
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 24 May 2021
Sec. Nuclear Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.671869
With the goal of using chiral interactions at various orders to explore the properties of the few-body nuclear systems, we write the recently developed local chiral interactions as spherical irreducible tensors and implement them in the hyperspherical harmonics expansion method. We devote particular attention to three-body forces at next-to-next-to leading order, which play an important role in reproducing experimental data. We check our implementation by benchmarking the ground-state properties of 3H, 3He, and 4He against the available Monte Carlo calculations. We then confirm their order-by-order truncation error estimates and further investigate uncertainties in the charge radii obtained by using the precise muonic atom data for single-nucleon radii. Having local chiral Hamiltonians at various orders implemented in our hyperspherical harmonics suites of codes opens up the possibility to test such interactions on other light-nuclei properties, such as electromagnetic reactions.
In 1935 the seminal idea of Yukawa [1] laid the foundation to the theory of the nuclear forces. His one-pion exchange term is nowadays known as an important contribution to the interaction among nuclei in the long-distance range and is implemented in many nuclear interaction models. In the mid 1990s the first high-precision nucleon-nucleon (NN) potentials able to reproduce at the same time the deuteron properties, the proton-proton, and the proton-neutron scattering data were released. Some notable examples of these interactions are the Argonne v18 (AV18) [2], the Nijmegen (Nijm93) [3], and the charge-dependent Bonn (CD-Bonn) [4]. The subsequent development of three-nucleon (3N) interactions, see for instance references [5, 6], improved the description of the A > 2 nuclear dynamics, initiating a successful theoretical campaign of nuclear structure and reaction predictions, see e.g., references [7–9] and references therein. Despite the great success of the phenomenological interactions, there are still open questions to address, including the difficulty of providing solid uncertainty quantifications in the modeling of the forces, the lack of connection between the NN and 3N interactions and the missing direct link to quantum chromodynamic (QCD), the fundamental theory of the strong force.
An important step forward to address these issues was made when the concept of effective field theory (EFT) was introduced and applied to low-energy QCD. As suggested by Weinberg [10–13], the low-energy nuclear dynamic can be described by a Lagrangian written in terms of pions and nucleons fields and consistent with all the commonly accepted symmetries of QCD, including the (explicitly and spontaneously broken) chiral symmetry which strongly constrains the pion dynamics. The proposed Lagrangian contains an infinite number of terms and a systematic expansion must be introduced to make the theory applicable. Following Weinberg's proposal, in the early 2000s, modern versions of chiral-inspired nuclear interactions were released by many groups—for a compilation of results, see for instance references [14–16] and references therein—each interaction being different by the truncation order of the chiral expansion, by the inclusion or exclusion of the Δ-isobar, by the fitting procedure or by the regularization scheme used. Given that these interactions are derived in field theories written in momentum space, they are highly non-local. One of the consequences is that they are difficult to implement in some of the few- and many-body techniques which are developed in coordinate-space representation.
In recent years a new chiral-inspired set of nuclear interactions at the next-to-next-to-leading order (N2LO) has become available [17–20]. These interactions have a series of interesting properties which make them a promising framework for future nuclear computations. These interactions are completely written in coordinate space and contain only one non-local operator. Furthermore, the NN and 3N terms are regularized consistently, namely the same regulator form and cut-off is used. Here, these interactions are written for the first time as a product of irreducible tensors under space rotations, a required step for the implementation into the hyperspherical harmonics formalism. Using the method of hyperspherical harmonics, we perform benchmark tests in light-nuclear systems, where we compare to available results from the Green's function Monte Carlo (GFMC) and the auxiliary field diffusion Monte Carlo (AFDMC) methods. We note that analogous benchmarks between the hyperspherical harmonic and quantum monte-carlo methods have been successfully performed in recent years for an alternative set of local-chiral interactions that explicitly includes the excitation of the Δ-resonance [21–23].
This paper is summarized as follows. In section 2, we briefly overview the formulation of the hyperspherical harmonics method in coordinate-space representation. In section 3, we present the maximally-local chiral interactions developed in reference [20] and rewrite the 3N force as a product of irreducible tensors under space rotations. In section 4, we show our benchmark results for 3H, 3He, and 4He and we discuss uncertainties. Finally, section 5 is reserved for the conclusive remarks and the overview of future prospects.
The hyperspherical harmonic method was firstly introduced in 1935 by Zernike and Brinkman [24], reintroduced later in the 60's by Delves [25], Simonov [26], Zickendraht [27], and Smith [28] and it is extensively applied nowadays to the study of few-body systems. For recent reviews with applications to nuclear physics we refer the reader to the following references [29, 30]. In this work, the hyperspherical harmonic functions are constructed to form irreducible representations of the SO(3) group of space rotations, the O(N) group of dynamical rotations in the space spanned by the N Jacobi vectors, and the SA permutation group of the A-particle system. The method is briefly reviewed in this section, the formalism introduced follows closely references [31, 32].
We consider a system of A identical nucleons, the Jacobi coordinates {ηi} are commonly introduced in order to separate the internal degrees of freedom from the center of mass. There are several ways to construct the set of N = A − 1 Jacobi coordinates out of the A coordinate vectors {ri} of the nucleons. One commonly used definition for the relative Jacobi vectors is
From a given choice of Jacobi coordinates, the hyperspherical coordinates {ρN, φ(N), Ω(N)} can be introduced. In this notation, ρN is the hyper-radius, Ω(N) ≡ {Ω1, ..., ΩN} where Ωj = (θj, ϕj) gathers the angular coordinates of the Jacobi vectors, and φ(N) ≡ {φ2, ..., φN} is a set of hyper-angles.
The hyper-radial coordinates ρ1, ..., ρN and the hyper-angular coordinates φ2, ..., φN are constructed recursively. The transformation law for the first two Jacobi coordinates is
Assuming that we already know the hyper-radial coordinates ρ1, ..., ρj − 1 and the hyper-angular coordinates φ2, ..., φj−1 the transformation law for ρj and φj reads in analogy to Equation (2) as
The internal kinetic energy operator for the A-body system is given by the 3N-dimensional Laplace operator Δ(N). In terms of the hyperspherical coordinates it is written as
where the hyper-radial part is
with ρ ≡ ρN. is the grand-angular momentum operator whose eigenfunctions are known as the hyperspherical harmonics.
Denoting as the angular momentum operator related to ηj, and and as the total orbital angular momentum operator and z-projection of the system identified by the first j Jacobi coordinates, it is possible to define the grand-angular momentum operator of the system recursively in terms of and as [33]
where .
The operators , , , and commute with each other. As a consequence, it is possible to label hyperspherical states using the set of 3N − 1 quantum numbers {K} ≡ {KN, ..., K2, LN, ..., L2, lN, ..., l1, MN}. The hyperspherical harmonics functions are the eigenfunctions of the grand-angular momentum operator with eigenvalues KN(KN + 3N − 2). The explicit expression for the resulting hyperspherical harmonics functions is given by [34]
where are the Clebsch-Gordan coefficients, Yljmj(Ωj) are the spherical harmonics associated with ηj, are Jacobi polynomials and
is a normalization constant with 2nj = Kj − Kj−1 − lj.
In our formulation of the hyperspherical harmonics method we construct hyper-angular functions that form irreducible tensors under the SO(3) group of spatial rotations, the O(N) group of kinematic rotations and the SA group of permutations of the A nucleons. These symmetry-adapted hyperspherical harmonics, , are uniquely identified by the set of quantum numbers [KN] ≡ {KN, LN, MN, λN, αNYA, βA}. For the current purposes, it is enough to specify that λN identifies the irreducible representation of O(N), YA is the Yamanouchi symbol which specifies the irreducible representations of the group-subgroup chain S1 ⊂ … ⊂ SA presented by the appropriate Young diagrams Γ1, …, ΓA, while αN and βA are additional quantum numbers needed to remove further degeneracies. The O(N) and SA symmetry-adapted hyperspherical harmonics are constructed recursively. Assuming that have been already constructed, the Nth Jacobi coordinate is then coupled to this system, so that a state with total angular momentum LN and grand-angular momentum KN is formed, let us call this state . Note that is a irreducible tensor under O(N − 1) and SA−1 but not under O(N) and SA. The states are obtained as linear combinations of the states , where the coefficients of the linear combinations are labeled as [(KN−1, LN−1, λN−1, αN−1; lN)KNLN|}KNLNλNαN], [(λN−1ΓNβN)λN|}λNΓAβA] and are known as hyperspherical orthogonal group parentage coefficients (HSOPCs) and orthogonal group coefficients of fractional parentage (OCFPs), respectively.
The full expression of the symmetry-adapted hyperspherical harmonics reads
Nucleons also possess spin and isospin degrees of freedom. Because the nuclear Hamiltonian is rotationally invariant, nuclear states have the total angular momentum J as good quantum number. Furthermore, isospin is an approximate symmetry for the nuclear interaction with the consequence that the total isospin T of a nuclear state is a conserved quantum number. For these reasons we couple the symmetry-adapted hyperspherical harmonics to the SA symmetry-adapted spin-isospin wavefunction χ of the A-nucleon system
Here , , ΛΓA,YN is a phase factor, and |ΓA| is the dimension of the irreducible representation ΓA.
Analogously to what has been done with the hyperspherical harmonics, the spin-isospin wavefunctions are constructed recursively. Assuming that the symmetry-adapted wavefunction χ[Sj−1] have been obtained, the construction of the χ[Sj] is done by first coupling χ[Sj−1] to the spin-isospin wavefunction of the jth nucleon, let us call this state χ[Sj−1], SjTj, and then taking linear combinations of χ[Sj−1], SjTj using the coefficients of fractional parentage labeled as . Namely the full expression for χ[Sj] reads
We are finally able to expand the nuclear wavefunction in terms of hyperspherical harmonics. In practice, the expansion is performed up to a maximal value of the grand-angular quantum number Kmax as
When we insert this wavefunction into the Schrödinger equation, an eigenvalues equation is obtained for the hyper-radial wavefunction , the eigenvalue equation is then solved by expanding the hyper-radial wavefunction in terms of an orthogonal set of functions. In this work the set is taken as the generalized Laguerre polynomials . Again, the model space is truncated to a given maximum number of Laguerre polynomials nmax
With the introduction of this further model space, the resulting eigenvalue equation is solved with direct diagonalization routines, or with the Lanczos method when the model space is too big for a direct diagonalization. In essence, the hyperspherical harmonics method is a powerful technique that allows for an exact solution of the Schrödinger equation for few-body systems. In the limit where nmax → ∞ and Kmax → ∞ the solution correspond to the exact solution to the Schrödinger equation. While we observe that good convergence can be reached with nmax ≤ 50, the convergence in terms of Kmax will be carefully investigated. The uncertainty coming from the truncation of the model space, in particular of Kmax, can be estimated by looking at the convergence pattern of the observables of interest, for instance the binding energy and the radius. As a consequence, the method is an excellent candidate for uncertainty quantifications in nuclear physics, with the possibility of performing tests over commonly accepted nuclear Hamiltonians or making precise predictions for few-nucleon systems. Because the formulation we present here is developed in coordinate space, the method benefits from having local forces, such as the AV18 potential. While one can formulate hyperspherical harmonics also in momentum space [35], the goal of this paper is to work in coordinate space and implement local-chiral interactions. To further improve the convergence with respect to the model space, we make use of the effective interaction hyperspherical harmonics (EIHH) method. The interested reader can find more details on this approach in reference [36], and also in the more recent review [37].
Nuclear physics is mainly formulated in the framework of non-relativistic quantum mechanics. The relevant degrees of freedom are represented by the nucleons, whose interactions are remnants of the color forces among the quarks. In this picture, the nucleus is a compound object of A non-relativistic nucleons and the dynamic of the system is specified by the nuclear Hamiltonian operator
where is the sum of the non-relativistic kinetic energy operators of the individual nucleons, is a sum of NN interactions, and Ŵ is a sum of 3N interactions. The dots stand for higher order forces not explicitly included in this work.
Our goal is to solve the Schödinger equation
and when working with antisymmetrized wavefunctions, the expectation values of the NN and 3N terms become
where only the first two (or three) particles are involved.1
In the modern theory of nuclear forces, interactions are derived from the chiral effective field theory (ChEFT). In this theory, proposed first by Weinberg [10–13], the chiral Lagrangian is constructed in terms of pion and nucleon fields and is consistent with the commonly accepted symmetries of QCD, including the explicitly and spontaneously broken chiral symmetry. This effective Lagrangian has infinitely many terms, therefore one needs to introduce an ordering scheme to render the theory predictive.
In ChEFT, the terms in the chiral Lagrangian are analyzed counting powers of a small external momentum over the large scale: , where Q stands for an external momentum or a pion mass and Λχ is the chiral symmetry breaking scale, whose value is approximately given by the mass of the ρ-meson Λχ ~ mρ = 770 MeV. Determining systematically the power of ν has become known as power counting. The lowest possible value of ν is conventionally referred to as the leading order (LO), the second lowest is the next-to-leading order (NLO), the third lowest is the next-to-next-to leading order (N2LO), and so on. While there are many proposed power counting schemes [38–43], in this work we adopt the Weinberg power counting, which makes use of naive dimensional analysis [11, 12].
Given that ChEFT is naturally formulated in momentum space, the derived nuclear interactions are strongly non-local, which is a disadvantage for methods that are formulated in coordinate space. However, it has been recently found that it is possible to construct maximally local chiral interactions by regularizing in coordinate space and exploiting Fierz ambiguities to remove non-localities in the short-distance interactions [17–20].
The local chiral NN forces are composed of contact (ct) terms and pion-exchange (π) terms so that the interaction between particle 1 and 2 can be written as
When working with totally anti-symmetric systems, it is possible to exploit Fierz ambiguities for removing the non-local operators contributing to the contact NN interactions. This means that the interactions can be chosen to have the following operator structure [17] at LO
where r12 is the relative distance between nucleon 1 and nucleon 2, σ1/2 are the vector-spin Pauli matrices operating in the space of the first/second nucleon2 and δ is the delta function.
At NLO, the following new terms enter
where τ1/2 are the vector-isospin Pauli matrices, Δ is the Laplace operator, L and S are the total orbital angular momentum and spin operator in the two-body system represented by the two interacting nucleons3, is the unit vector related to the relative distance r12, and the δ-function will have to be regularized. The {Ci} are a set of low energy constants (LECs). The term proportional to the LEC C5 is the only non-local operator appearing in this maximally local chiral interaction.
Following references [17, 44], all the pion-exchange interactions up to N2LO can be written in a complete local form as
where, S12 is the well-known tensor operator, defined as
The local functions VC(r12), WC(r12), VS(r12), WS(r12), VT(r12), and WT(r12) have dependencies on the axial-vector coupling constant of the nucleon gA, on the pion decay constant Fπ and on the pion mass mπ. These functions are evaluated at each order in ChEFT (LO, NLO, and N2LO) and details can be found in reference [44]. In reference [20] pion loops are regularized using the spectral-function regularization (SFR) with an ultraviolet cut-off GeV and we follow this prescription.
The local chiral NN interactions up to N2LO are already written or can be written with minimal modifications as irreducible tensors under space rotations. Thus, they can be easily implemented in the hyperspherical harmonics formalism in coordinate space. In fact, they have pretty much the same structure as the Argonne potential AV8' [45] with the only difference being that, compared to this interaction, there is no isospin-dependent spin-orbit operator. The same does not apply to 3N interactions.
Three-body interactions arise at NLO in Weinberg power counting. However, at this order their contribution is canceled out. The first non-zero contributions start at N2LO. The 3N force at this order is composed of a two-pion (2π) exchange, a one-pion (1π) exchange and a 3N contact (ct) interaction (see Figure 1). On the one hand, the 2π-term comes with the LECs c1, c3, and c4 that already appear at the subleading two-pion-exchange interaction at the NN level at the same chiral order which highlights the consistency of the NN and 3N interactions in ChEFT. On the other hand, the one-pion exchange and the 3N contact diagrams introduce two new LECs, cD and cE, which must be fitted on A ≥ 3 observables.
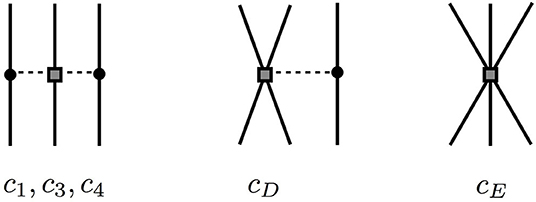
Figure 1. Feynman diagrams of the chiral 3N force at N2LO, from the left to the right: 2π-term, 1π-term, and ct-term.
With respect to reference [20], here the 3N interaction is written for a given triplet of nucleons, since at the end we use the fact that the wavefunction is anti-symmetric to compute the expectations values as in Equation (16). The 3N interaction reads
where the sum runs over the cyclic permutations of the particle triplet and the notation has the intention to highlight the symmetry of the interaction over the exchange of particles 2 and 3. Each term is denoted with a label that includes the associated LEC.
The 2π exchange terms are given by
where the coupling constants are and . The 2π-terms include the following functions
with analogous expressions for Y13 and U13. The operator χ12 (and analogously χ13) is defined as
with
In the last expression, r0 is the cut-off and following references [18–20] n is taken to be equal to 4.
For the 1π-interaction terms there are two options
with . While the difference between the two is due to regulator artifacts, in this work only the second choice is implemented, namely .
For the contact term there are different options on the operator structure, which come from different choices in the Fierz rearrangement. In this work only the following one is considered
with .
The value of all LECs entering the 3N forces at N2LO are shown in Table 1. In references [19, 20] cD and cE have been fitted in order to reproduce the 4He binding energy and the n-α P-wave phase shift.
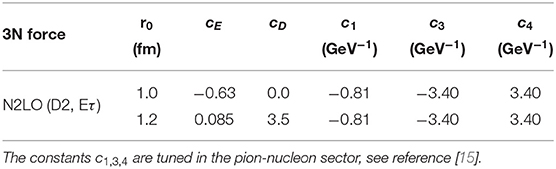
Table 1. Fit values for the couplings cD and cE for different choices of 3N cut-offs as reported in references [19, 20].
The above expressions for the 3N force are not written in terms of irreducible spherical tensors, so that they cannot be implemented directly into the hyperspherical formalism. In this section we address this point and write the interaction in terms of irreducible spherical tensors, both in coordinate-spin space and in isospin space.
For convenience, we denote the general spin space , and configuration space , irreducible tensor operators as
where i, j, k are generic particle indexes and is the rank 1 normalized spherical tensor associated to the relative distance between particle 1 and particle i. With the notation we intend the two rank-one coordinate space tensors coupled into a rank-λ tensor, and analogously for and in spin and isospin space, respectively. Furthermore, we define
where is the rank-1 normalized spherical tensor associated to the relative distance between particles i and j.
At this point, after rearranging the couplings with a few Racah algebra steps and by using the previously introduced notation, one can rewrite the 3N interactions of Equations (23), (27), (28) in terms of irreducible tensors in isospin space and in the coupled spin-configuration space.
The 2π-exchange term depending on c1 becomes
the 2π-exchange term that depends on c3 becomes
while the term that depends on c4 can be expressed as
To write the above expression in a compact form, we have introduced the following definitions
The 1π-exchange contribution takes the following form
while the contact term becomes
We have implemented these expressions in our hyperspherical harmonics codes. Since the interaction is now written in terms of irreducible tensors, the spin and isospin matrix elements can be computed analytically. For the calculation of the spatial matrix elements one can reduce the six-dimensional integration in the two Jacobi coordinates to a two-dimensional numerical quadrature, as explained in details in reference [46]. Below we present the benchmark results we obtained with these local-chiral forces on few-body systems, such as 3H, 3He, and 4He.
In this section we show the benchmark tests of the maximally-local-chiral interactions using the EIHH method. We compute ground-state energies and charge radii in three- and four-nucleon systems and compare to two Monte Carlo methods, namely the GFMC and AFDMC methods.
In the computations of nuclear charge radii, we use
where is the calculated point-proton radius, rp = 0.8751(61) fm [47] is the root-mean-square (rms) charge radius of the proton, fm2 [47] is the squared charge radius of the neutron, and Z is the number of protons in the nucleus. The last term is the Darwin-Foldy correction to the proton-charge radius [48] which depends on the proton mass mp. We neglect the spin-orbit relativistic contribution, since it is negligible in s-shell nuclei [49], as well as meson exchange currents.
Keeping in mind that the goal of this work is to benchmark our expressions for the 3N forces at N2LO by comparing to the Monte Carlo results, we have used the same numerical values for rp and rn as in reference [20], which follows the CODATA-2014 recommendations [47]. Hence, in a first stage we will not be using the more modern results for rp/n from references [50, 51].
A few words addressing the estimation of the numerical uncertainties are in line. As already said, the EIHH method allows for an exact solution of the Schrödinger equation, the computed wavefunction converges to the true eigenfunction of the Hamiltonian operator in the limit of infinite model space. The model space is mostly given by the maximal number, nmax, of Laguerre polynomials and the choice of the maximal value of the grand-angular momentum quantum number, Kmax, in the construction of the hyperspherical harmonics functions. It has been practically found that beyond a value nmax = 50, the expectation values are negligibly modified. The convergence in terms of Kmax is more delicate, so that in order to estimate the uncertainty coming from the truncation of the model space, we analyze the converging pattern at increasing values of Kmax.
To quantify our numerical uncertainty we proceed as follows: denoting with O(Kmax) the expectation value of an observable Ô computed by setting a given maximal value of the grand-angular momentum quantum number, Kmax, in the wavefunction, our uncertainty in this observable is estimated by
where δres is the residual uncertainty (not due to the Kmax behavior) obtained by varying: the number of radial grid points (from 70 to 90), the maximal values of the angular momentum in the construction of the two-body effective interaction (from 60 to 120) and the maximal number of three-body angular momentum (from 5/2 to 7/2) in the partial wave expansion of the 3N force.
First, we address and discuss the benchmark of the interactions at LO and NLO, so as to have a clean test on the NN interactions. Then we move to the N2LO, where the three-body forces are included.
We study the maximally-local chiral interactions for two different regulator cut-offs, indicated by r0, namely exploring the two possibilities of r0 = 1.0 fm and r0 = 1.2 fm. The latter gives rise to a softer interaction compared to the first one. For the benchmarks at LO and NLO, the 4He nucleus is used as a testing ground. We compute point-proton charge radii, , and ground-state energies, E0, for the two different cut-off choices at increasing values of the grand-angular momentum quantum number and compare to the GFMC calculations.
The final results are shown in Table 2, where the uncertainty is computed as explained above using Equation (38) with Kmax = 22. An extended table with all the various Kmax can be found in the Supplementary Material. We observe that as we enlarge the model space a nice converging pattern is obtained and our final EIHH results basically agree with the GFMC calculations when the uncertainties are taken into account. By looking at the converging pattern of the studied observables as the model space is increased (see Supplementary Material), we clearly observe that the interaction with r0 = 1.2 fm is much softer than the other, since the relative observables converge with a smaller model space. Finally, it is notable that, as shown in Table 2, the LO and NLO results do not reproduce the measured values, but the discrepancy decreases in going from LO to NLO.
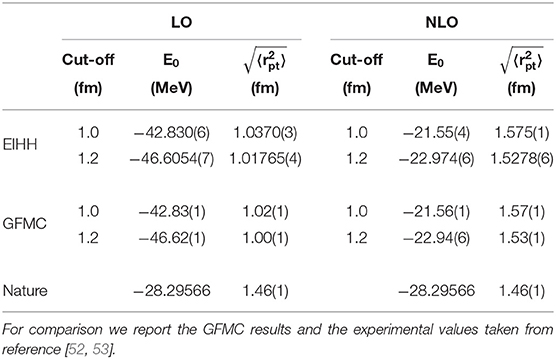
Table 2. Ground-state energies and point-proton radii for the 4He nuclear system at LO and NLO computed with the EIHH method.
We now turn to the benchmark at the next order. At N2LO we have the first appearance of 3N forces, so this will serve as a check of our irreducible tensor representation. The 3N interaction involves two new LECs, cD and cE, coming from the 1π-term and from the ct-term of the 3N forces, respectively, that cannot be fitted in the NN sector. In reference [19] these couplings have been fitted to reproduce the 4He binding energy and the n-α scattering P-wave phase shift, for which the values reported in Table 1 were obtained. We use the same values in this work, as our goal is to perform a benchmark. In particular, here we implement only the (D2, Eτ) 3N interactions, which we chose since the Eτ term has a more general isospin structure. Different choices of the 3N contact term have been shown to lead to different properties in neutron matter [18, 19].
As a testing ground for our N2LO Hamiltonian expressed in terms of spherical tensors outlined in the previous section, we study the three-body 3He and 3H and the four-body 4He nuclear systems. We compute ground-state energies, E0, and charge radii, , for the two different cut-off choices r0 = 1 and 1.2 fm and carefully study the convergence at increasing Kmax values. A complete table of our data is shown in the Supplementary Material. The Kmax convergence is also explicitly shown in a graphical manner in Figures 2–4, where a comparison to the GFMC method is made.
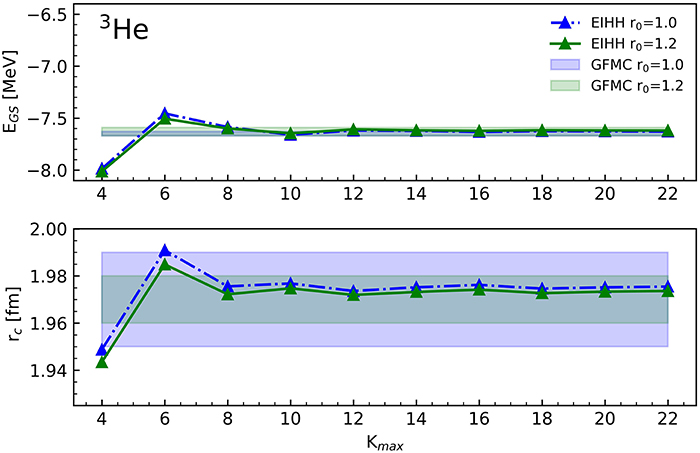
Figure 2. The ground-state energy and the charge radius of the nuclear 3He system as a function of the grand-angular momentum quantum number Kmax. The green and blue error-bands are the GFMC results with the relative statistical uncertainty.
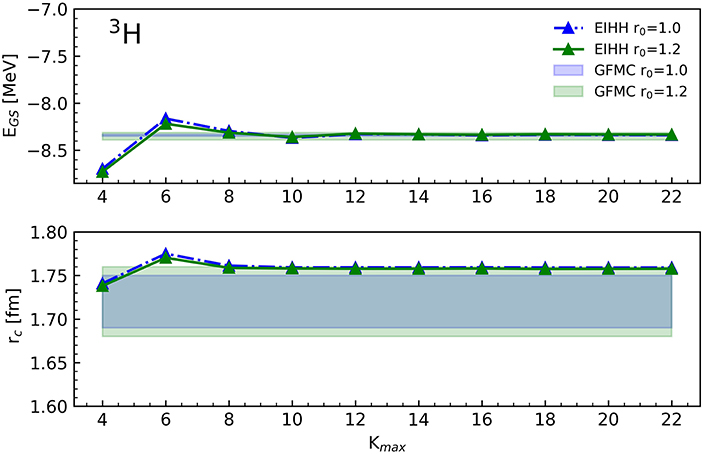
Figure 3. The ground-state energy and the charge radius of the nuclear 3H system as a function of the grand-angular momentum quantum number Kmax. The green and blue error-bands are the GFMC results with the relative statistical uncertainty.
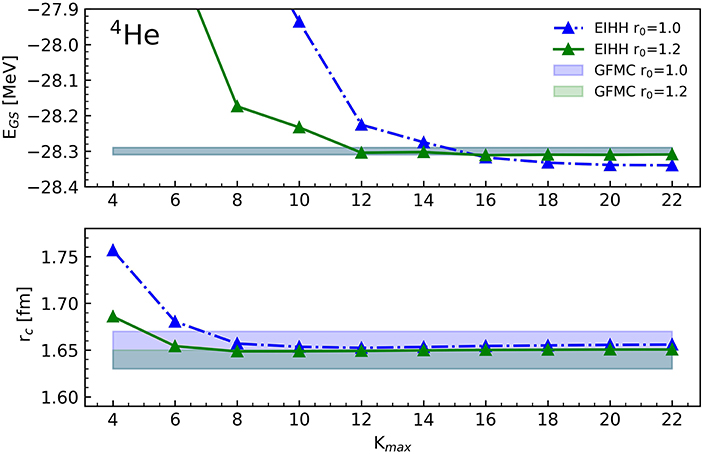
Figure 4. The ground state energy and the charge radius of the nuclear 4He system as a function of the grand-angular momentum quantum number Kmax. The green and blue error-bands are the GFMC results with the relative statistical uncertainty.
As it can be seen from Figures 2, 3, the EIHH method is in excellent agreement with the GFMC computations for the three-body nuclei, for both the ground-state energies and the charge radii. The typical non-monotonic convergence patter of the EIHH method is observed, and a very good convergence is reached already at Kmax = 12. This shows that these forces are softer than the AV18 potential, but harder than the low-k interactions [54].
For the 4He nucleus shown in Figure 4, we obtain a very nice agreement with the GFMC method for the cut-off value r0 = 1.2 fm, while for the cut-off r0 = 1.0 fm, we perfectly reproduce the charge radius, but we observe a small deviation for the ground-state energy with respect to the GFMC.
Our final EIHH results with uncertainties quantified as explained above using Equation (38) with Kmax = 22 are shown in Table 3 in comparison with the GFMC, AFDMC, and the experimental data. The theoretical computations agree with each other at a similar level as observed in other benchmarks [59]. In particular, for the cut-off r0 = 1.0 fm, which leads to a harder force, EIHH and GFMC are in agreement within error bars, while some discrepancy is seen with respect to the AFDMC results. Given that the latter method is known to be less accurate, we do not think that this difference is significant and we consider all these results to constitute a successful benchmark of our implementation of 3N forces.
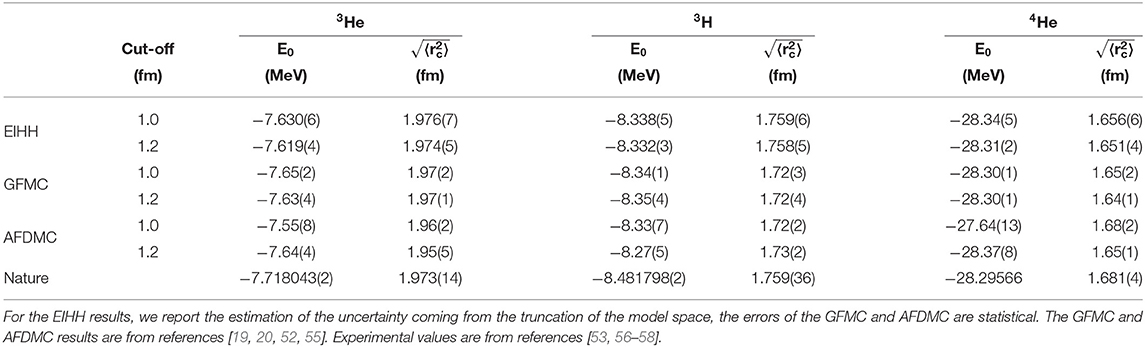
Table 3. Ground-state energies and charge radii for the nuclear 3He, 3H, and 4He systems at N2LO in the chiral expansion computed with the EIHH, GFMC, and AFDMC methods.
As can be seen in Table 3, at N2LO a much improved agreement with experiment is obtained. In fact, if one compares the experimental binding energies to the LO and NLO calculations in Table 2 one observes that these low orders overbind (LO) or underbind (NLO) the few-body nuclei, while at N2LO nice agreement is observed. This is expected for 4He, given that 3N forces are fit to reproduce the 4He binding energy, however a better agreement is also found for 3He and 3H due to the strong correlation between the three- and four-body binding energy. Interestingly, a nice converging pattern is also found for the nuclear charge radii.
From a careful look at Table 3, one can appreciate that our EIHH calculations are more precise than the GFMC and AFDMC results in the three-nucleon sector and that our numerical uncertainty is comparable to the experimental uncertainties for the radii. While this may be an advantage of our method, it is important to note that the error bars quoted in this table do not include the uncertainties coming from the ChEFT expansion, so they do not constitute the full uncertainty of the theory.
We conclude this section with a further investigation on the charge radii of light-nuclear systems. In reference [55] the proton-charge radius rp = 0.8751(61) fm and the neutron-charge radius fm2 recommended by CODATA-2014 were used in the evaluation of nuclear charge radii using Equation (37). Such single-nucleon data come from experiments that study the electron-nucleon system. Recently, these quantities were measured more precisely by investigating muonic atoms, and one could ask what is the effect of this increased precision in the nuclear charge radius when applying Equation (37). To address this point in Table 4 we compare our results for the charge radii of 3He, 3H, and 4He at N2LO using the CODATA-2014 single-nucleon input with the results obtained using the rms proton-charge radius coming from the muonic-hydrogen rp = 0.84087(39) [50] and the new value of the rms charge radius of the neutron fm2 [51]. We denote the first choice with e − rc and the second with μ − rc. The general effect of using this choice of the proton and neutron charge radii amounts to a systematic reduction of roughly 1% of the charge radii of these light nuclei. This has to be contrasted with the full uncertainty of the theory that includes not only the EIHH numerical error, but also considers the uncertainty coming from the order-by-order chiral expansion. The latter is estimated using the algorithm proposed first in reference [60] and is included in Table 4.
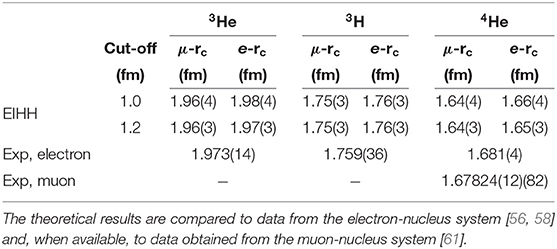
Table 4. Nuclear rms charge radii for 3He, 3H, and 4He systems at N2LO computed using either the single-nucleon CODATA-2014 values (columns e-rc) or the more precise muonic atoms data (columns μ-rc).
For a graphical representation of our findings, in Figure 5 we show the 4He nuclear charge radius at increasing chiral orders computed for different choices for the proton and neutron charge radii. We observe that the chiral order uncertainty is of the order of 2%, hence larger than the effect of the more precise single-nucleon input. Overall, we confirm the chiral order-by-order convergence patter, already discussed in references [19, 20], but there shown only for the binding energy and the point-proton radius, which does not include the single nucleon input.
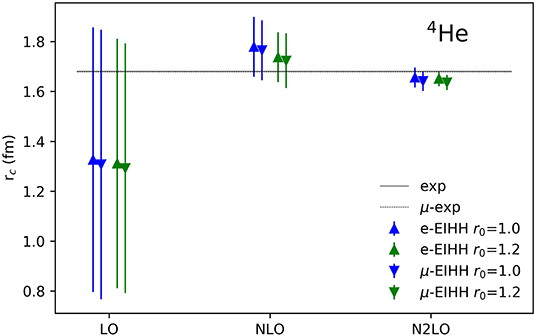
Figure 5. The 4He charge radius computed at increasing orders of the chiral expansion. The uncertainty bars include the numerical uncertainty of the EIHH method as well as the uncertainties coming from the truncation of the chiral expansion. The horizontal lines are the experimental values from electron scattering (solid line) [56] and from muonic atoms (dashed line) [61].
Interestingly, when comparing the 4He theoretical charge radius with the newest muonic atom measurement from reference [61], we see that the μ − rc results are still consistent with the experiment, leaving, however, space for meson exchange currents to help improve the theoretical precision, which is by far lower than the experimental one.
In this work, the maximally local chiral interactions are implemented for the first time in the hyperspherical harmonic formalism. The benchmark tests performed in light nuclei show general agreement between hyperspherical harmonic results and the previously available Monte Carlo calculations. As expected, at N2LO with the inclusion of the 3N forces the experimental results are much better reproduced with respect to the LO and NLO calculations. With this study we thus confirm the nice order-by-order convergence in the ground-state energies and in the radii that was already observed in the Monte Carlo studies.
While our numerical precision of the EIHH calculations lies in the sub-percent range, we find that the uncertainty due to the chiral order expansion is larger. In case of the charge radius, we observed that using the most updated values of the proton and nucleon radii instead of the CODATA-2014 values leads to a variation of 1%, which is smaller than the 2% uncertainty found in the chiral order-by-order truncation at N2LO. Addressing first the latter by going to N3LO should be the priority if the goal is to reduce theoretical uncertainties.
Having these new interactions implemented in our formalisms opens up the possibility of investigating other few-body observables in the future. Our most immediate goals include the investigation of muonic atoms [37], of the 4He monopole transition form factor [62], and the longitudinal response function [63] in order-by-order chiral expansions. We reserve these applications for future studies.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
NB derived the first expressions for the spherical tensors, which were then checked by SSL and SB. The two-body force was implemented by SB while SSL implemented the expressions of the 3N spherical tensors in the hyperspherical harmonics code and run the calculations, and results were discussed in the group at every step. All authors contributed in equal parts to this paper and contributed to the writing of the text.
This work was supported by the Deutsche Forschungsgemeinschaft (DFG) through the Collaborative Research Center [The Low-Energy Frontier of the Standard Model (SFB 1044)], and through the Cluster of Excellence Precision Physics, Fundamental Interactions, and Structure of Matter (PRISMA+ EXC 2118/1) funded by the DFG within the German Excellence Strategy (Project ID 39083149). Calculations were performed on the mogon2 cluster in Mainz.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
SSL and SB would like to acknowledge Joel Lynn, Ingo Tews, and Diego Lonardoni for useful discussions.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.671869/full#supplementary-material
1. ^This property will be used later when we will write explicitly the form of the nuclear forces between (among) two (three) particles.
2. ^Even though they are operators in spin space, we do not use the hat in our notation, as they are vectors, whose components are operators.
3. ^We drop the hat from vectors whose components are operators.
1. Yukawa H. On the interaction of elementary particles. I. Prog Theor Phys Suppl. (1955) 1:1–10. doi: 10.1143/PTPS.1.1
2. Wiringa RB, Stoks VGJ, Schiavilla R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys Rev C. (1995) 51:38–51. doi: 10.1103/PhysRevC.51.38
3. Stoks VGJ, Klomp RAM, Terheggen CPF, de Swart JJ. Construction of high-quality NN potential models. Phys Rev C. (1994) 49:2950–62. doi: 10.1103/PhysRevC.49.2950
4. Machleidt R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys Rev C. (2001) 63:024001. doi: 10.1103/PhysRevC.63.024001
5. Pudliner BS, Pandharipande VR, Carlson J, Wiringa RB. Quantum Monte Carlo Calculations of A ≤ 6 Nuclei. Phys Rev Lett. (1995) 74:4396–9. doi: 10.1103/PhysRevLett.74.4396
6. Pieper SC, Pandharipande VR, Wiringa RB, Carlson J. Realistic models of pion-exchange three-nucleon interactions. Phys Rev C. (2001) 64:014001. doi: 10.1103/PhysRevC.64.014001
7. Leidemann W, Orlandini G. Modern ab initio approaches and applications in few-nucleon physics with A ≥ 4. Prog Part Nucl Phys. (2013) 68:158–214. doi: 10.1016/j.ppnp.2012.09.001
8. Bacca S, Pastore S. Electromagnetic reactions on light nuclei. J Phys G Nucl Part Phys. (2014) 41:123002. doi: 10.1088/0954-3899/41/12/123002
9. Rocco N. Ab initio calculations of lepton-nucleus scattering. Front Phys. (2020) 8:116. doi: 10.3389/fphy.2020.00116
10. Weinberg S. Phenomenological Lagrangians. Physica. (1979) 96A:327–40. doi: 10.1016/0378-4371(79)90223-1
11. Weinberg S. Nuclear forces from chiral Lagrangians. Phys Lett B. (1990) 251:288–92. doi: 10.1016/0370-2693(90)90938-3
12. Weinberg S. Effective chiral Lagrangians for nucleon-pion interactions and nuclear forces. Nucl Phys B. (1991) 363:3–18. doi: 10.1016/0550-3213(91)90231-L
13. Weinberg S. Three-body interactions among nucleons and pions. Phys Lett B. (1992) 295:114–21. doi: 10.1016/0370-2693(92)90099-P
14. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773
15. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rep. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001
16. Epelbaum E, Krebs H, Reinert P. High-precision nuclear forces from chiral EFT: state-of-the-art, challenges, and outlook. Front Phys. (2020) 8:98. doi: 10.3389/fphy.2020.00098
17. Gezerlis A, Tews I, Epelbaum E, Freunek M, Gandolfi S, Hebeler K, et al. Local chiral effective field theory interactions and quantum Monte Carlo applications. Phys Rev C. (2014) 90:054323. doi: 10.1103/PhysRevC.90.054323
18. Tews I, Gandolfi S, Gezerlis A, Schwenk A. Quantum Monte Carlo calculations of neutron matter with chiral three-body forces. Phys Rev C. (2016) 93:024305. doi: 10.1103/PhysRevC.93.024305
19. Lynn J, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Chiral three-nucleon interactions in light nuclei, neutron-α scattering and neutron matter. Phys Rev Lett. (2016) 116:062501. doi: 10.1103/PhysRevLett.116.062501
20. Lynn J, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Quantum Monte Carlo calculations of light nuclei with local chiral two- and three-nucleon interactions and neutron matter. Phys Rev C. (2017) 96:054007. doi: 10.1103/PhysRevC.96.054007
21. Piarulli M, Girlanda L, Schiavilla R, Pérez RN, Amaro JE, Arriola ER. Minimally nonlocal nucleon-nucleon potentials with chiral two-pion exchange including Δ resonances. Phys Rev C. (2015) 91:024003. doi: 10.1103/PhysRevC.91.024003
22. Piarulli M, Girlanda L, Schiavilla R, Kievsky A, Lovato A, Marcucci LE, et al. Local chiral potentials with Δ-intermediate states and the structure of light nuclei. Phys Rev C. (2016) 94:054007. doi: 10.1103/PhysRevC.94.054007
23. Piarulli M, Baroni A, Girlanda L, Kievsky A, Lovato A, Lusk E, et al. Light-nuclei spectra from chiral dynamics. Phys Rev Lett. (2018) 120:052503. doi: 10.1103/PhysRevLett.120.052503
24. Zernike F, Brinkman HC. Hyperspharische Funktionen und die in sphärischen Bereichen orthogonalen Polynome. Proc K Ned Akad Wett. (1935) 38:161.
25. Delves LM. Tertiary and general-order collisions. Nucl Phys. (1959) 9:391–399. doi: 10.1016/0029-5582(58)90372-9
26. Simonov YA. The three-body problem. Complete system of angular functions. Sov J Nucl Phys. (1966) 3:461.
27. Zickendraht W. Construction of a complete orthogonal system for the quantum-mechanical three-body problem. Ann Phys. (1965) 35:18. doi: 10.1016/0003-4916(65)90067-9
28. Smith FT. Generalized angular momentum in many-body collisions. Phys Rev. (1960) 120:1058. doi: 10.1103/PhysRev.120.1058
29. Kievsky A, Rosati S, Viviani M, Marcucci LE, Girlanda L. A high-precision variational approach to three- and four-nucleon bound and zero-energy scattering states. J Phys G Nucl Part Phys. (2008) 35:063101. doi: 10.1088/0954-3899/35/6/063101
30. Marcucci LE, Dohet-Eraly J, Girlanda L, Gnech A, Kievsky A, Viviani M. The hyperspherical harmonics method: a tool for testing and improving nuclear interaction models. Front Phys. (2020) 8:69. doi: 10.3389/fphy.2020.00069
31. Barnea N. Exact Solution of the Schrödinger and Faddeev Equations for Few-Body Systems. Jerusalem: Hebrew University (1997).
32. Bacca S. Study of Electromagnetic Reactions on Light Nuclei With the Lorentz Integral Transform Method. Trento; Mainz: Universita' degli Studi di Trento; Johannes Gutenberg Universität Mainz (2005).
34. Fabre de la Ripelle M. The potential harmonic expansion method. Ann Phys. (1983) 147:281–320. doi: 10.1016/0003-4916(83)90212-9
35. Viviani M, Marcucci LE, Rosati S, Kievsky A, Girlanda L. Variational calculation on A = 3 and 4 nuclei with non-local potentials. Few Body Syst. (2006) 39:159–76. doi: 10.1007/s00601-006-0158-y
36. Barnea N, Leidemann W, Orlandini G. State dependent effective interaction for the hyperspherical formalism. Phys Rev C. (2000) 61:054001. doi: 10.1103/PhysRevC.61.054001
37. Ji C, Bacca S, Barnea N, Hernandez OJ, Nevo-Dinur N. Ab initio calculation of nuclear structure corrections in muonic atoms. J Phys G. (2018) 45:093002. doi: 10.1088/1361-6471/aad3eb
38. Kaplan DB, Savage MJ, Wise MB. A new expansion for nucleon-nucleon interactions. Phys Lett B. (1998) 424:390–6. doi: 10.1016/S0370-2693(98)00210-X
39. Kaplan DB, Savage MJ, Wise MB. Two-nucleon systems from effective field theory. Nucl Phys B. (1998) 534:329–55. doi: 10.1016/S0550-3213(98)00440-4
40. Nogga A, Timmermans RGE, Kolck U. Renormalization of one-pion exchange and power counting. Phys Rev C. (2005) 72:054006. doi: 10.1103/PhysRevC.72.054006
41. Pavón Valderrama M, Arriola ER. Renormalization of the NN interaction with a chiral two-pion-exchange potential: central phases and the deuteron. Phys Rev C. (2006) 74:054001. doi: 10.1103/PhysRevC.74.054001
42. Long B, Yang CJ. Renormalizing chiral nuclear forces: triplet channels. Phys Rev C. (2012) 85:034002. doi: 10.1103/PhysRevC.85.034002
43. van Kolck U. Few-nucleon forces from chiral Lagrangians. Phys Rev C. (1994) 49:2932–41. doi: 10.1103/PhysRevC.49.2932
44. Piarulli M, Tews I. Local nucleon-nucleon and three-nucleon interactions within chiral effective field theory, and neutron matter. Front Phys. (2020) 7:245. doi: 10.3389/fphy.2019.00245
45. Wiringa RB, Pieper SC. Evolution of nuclear spectra with nuclear forces. Phys Rev Lett. (2002) 89:182501. doi: 10.1103/PhysRevLett.89.182501
46. Barnea N, Efros VD, Leidemann W, Orlandini G. Incorporation of three-nucleon force in the effective interaction hyperspherical harmonics approach. Few Body Syst. (2004) 35:155–67. doi: 10.1007/s00601-004-0066-y
47. Mohr PJ, Newell DB, Taylor BN. CODATA recommended values of the fundamental physical constants: 2014. Rev Mod Phys. (2016) 88:035009. doi: 10.1103/RevModPhys.88.035009
48. Friar JL, Martorell J, Sprung DWL. Nuclear sizes and the isotope shift. Phys Rev A. (1997) 56:4579–86. doi: 10.1103/PhysRevA.56.4579
49. Ong A, Berengut JC, Flambaum VV. Effect of spin-orbit nuclear charge density corrections due to the anomalous magnetic moment on halonuclei. Phys Rev C. (2010) 82:014320. doi: 10.1103/PhysRevC.82.014320
50. Antognini A, Nez F, Schuhmann K, Amaro FD, Biraben F, Cardoso JMR, et al. Proton structure from the measurement of 2S-2P transition frequencies of muonic hydrogen. Science. (2013) 339:417–20. doi: 10.1126/science.1230016
51. Filin AA, Baru V, Epelbaum E, Krebs H, Möller D, Reinert P. Extraction of the neutron charge radius from a precision calculation of the deuteron structure radius. Phys Rev Lett. (2020) 124:082501. doi: 10.1103/PhysRevLett.124.082501
52. Lynn JE, Carlson J, Epelbaum E, Gandolfi S, Gezerlis A, Schwenk A. Quantum Monte Carlo calculations of light nuclei using chiral potentials. Phys Rev Lett. (2014) 113:192501. doi: 10.1103/PhysRevLett.113.192501
53. NuDat. Available online at: https://www.nndc.bnl.gov/nudat2 (accessed January 22, 2021).
54. Bacca S, Schwenk A, Hagen G, Papenbrock T. Helium halo nuclei from low-momentum interactions. Eur Phys J A. (2009) 42:553. doi: 10.1140/epja/i2009-10815-5
55. Lonardoni D, Gandolfi S, Lynn JE, Petrie C, Carlson J, Schmidt KE, et al. Auxiliary field diffusion Monte Carlo calculations of light and medium-mass nuclei with local chiral interactions. Phys Rev C. (2018) 97:044318. doi: 10.1103/PhysRevC.97.044318
56. Sick I. Zemach moments of 3He and 4He. Phys Rev C. (2014) 90:064002. doi: 10.1103/PhysRevC.90.064002
57. Purcell JE, Kelley JH, Kwan E, Sheu CG, Weller HR. Energy levels of light nuclei A=3. Nucl Phys A. (2010) 848:1–74. doi: 10.1016/j.nuclphysa.2010.08.012
58. Angeli I, Marinova KP. Table of experimental nuclear ground state charge radii: an update. Atomic Data Nucl Data Tables. (2013) 99:69–95. doi: 10.1016/j.adt.2011.12.006
59. Nevo Dinur N, Hernandez OJ, Bacca S, Barnea N, Ji C, Pastore S, et al. Zemach moments and radii of 2, 3H and 3, 4He. Phys Rev C. (2019) 99:034004. doi: 10.1103/PhysRevC.99.034004
60. Epelbaum E, Krebs H, Meißner UG. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J A. (2015) 51:53. doi: 10.1140/epja/i2015-15053-8
61. Krauth J, Schuhmann K, Ahmed MA, Amaro FD, Amaro P, Biraben F, et al. Measuring the α-particle charge radius with muonic helium-4 ions. Nature. (2022) 589:527–31. doi: 10.1038/s41586-021-03183-1
62. Bacca S, Barnea N, Leidemann W, Orlandini G. Isoscalar monopole resonance of the alpha particle: a prism to nuclear Hamiltonians. Phys Rev Lett. (2013) 110:042503. doi: 10.1103/PhysRevLett.110.042503
Keywords: nuclear interactions, hyperspherical harmonics, light nuclei, ab-initio theory, chiral effective field theory
Citation: Li Muli SS, Bacca S and Barnea N (2021) Implementation of Local Chiral Interactions in the Hyperspherical Harmonics Formalism. Front. Phys. 9:671869. doi: 10.3389/fphy.2021.671869
Received: 24 February 2021; Accepted: 06 April 2021;
Published: 24 May 2021.
Edited by:
Dean Lee, Michigan State University, United StatesReviewed by:
Alessandro Lovato, Argonne National Laboratory (DOE), United StatesCopyright © 2021 Li Muli, Bacca and Barnea. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Simone Salvatore Li Muli, c2lsaW11bGlAdW5pLW1haW56LmRl
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.