Numerical Simulation of Long-Wave Infrared Generation Using an External Cavity Diamond Raman Laser

Introduction

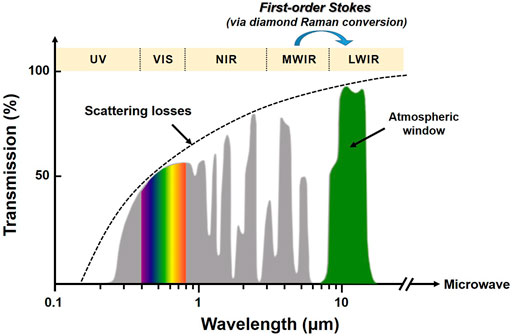
The long-wave infrared (LWIR) range (>8 μm) falls in the atmospheric window, where has lower atmospheric absorption and scattering loss compared with that of the near-infrared region, as shown in Figure 1. Hence, LWIR lasers are able to strongly penetrate fog and smoke. Therefore, these lasers have important applications in defense, laser remote sensing, and biochemical detection [1, 2]. Limitations on crystal growth (viz. limited size, limited transmission spectrum range, low damage threshold, or low gain coefficient, etc.) pose a limitation on the performance of the inversion lasers in the LWIR band. At present, the common approaches toward 10 μm band lasing include CO₂ laser, quantum cascade laser (QCL), free-electron laser, as well as frequency conversion via nonlinear optical techniques. Among these methods, the optical parametric oscillator (OPO) based on nonlinear frequency conversion is one of the most well-known techniques to realize all-solid-state LWIR lasing [3, 4]. However, it is very difficult to obtain high-power LWIR output by using OPO because of its large quantum defect and low optical conversion efficiency. Owing to the limited depth of quantum wells, the output power of QCLs in LWIR is usually less than hundreds of milliwatts, and it is difficult to achieve high peak power output [5]. The CO₂ laser is a mature method to generate tunable laser output in the range from 9.2 to 10.8 μm. However, continuous CO₂ gas injection is required for the operation of CO₂ lasers, and this results in large footprint and high operational cost. As a third-order nonlinear frequency conversion technology, stimulated Raman scattering (SRS) is automatic phase-matched and not affected by the “spatial hole burning” effect existing in traditional inversion lasers. Wideband laser output can be achieved by controlling the pump wavelength and cascade process in a Raman oscillator [6]. In addition, the “beam cleanup” effect makes SRS an effective technical method to obtain a high beam quality laser source [7–9].

FIGURE 1

FIGURE 1. Atmospheric windows (inset: LWIR laser generation via diamond Raman conversion).

Diamond is an excellent Raman crystal with an extremely high Raman gain coefficient, wide spectral transmission range (from 0.2 to >50 μm), large Raman frequency shift (1,332.3 cm⁻¹), and extremely high thermal conductivity (>2000 W m⁻¹ K⁻¹) [10–13]. The thermal conductivity of diamond is dozens or even hundreds of times that of common laser host materials (thermal conductivity of Y₃Al₅O₁₂ is 14 W m⁻¹ K⁻¹ and that of quartz fiber is 1.17 W m⁻¹ K⁻¹) and widely used mid-infrared OPO crystals (thermal conductivity of ZnGeP₂ is 35 W m⁻¹ K⁻¹ and that of KTiOAsO₄ is 2 W m⁻¹ K⁻¹). The near infrared 1.5 μm (eye-safe) [14] and mid-infrared 3–5 μm [15] band laser outputs have been achieved through diamond Raman conversion. Combined with the excellent photothermal properties of the diamond crystal and the many significant advantages of the SRS process, the diamond Raman laser (DRL) has become a potentially effective means to obtain LWIR lasing output. Utilizing the large Raman frequency shift of diamond and a 4.3 μm laser as the pump source, a 10 μm LWIR lasing output can be obtained through the first-order diamond Raman conversion, as shown in the inset of Figure 1.

In this paper, we propose a model of a first-order Raman laser with 10 μm output by utilizing diamond Raman conversion. Based on the steady-state model of the DRL, the relationships between the cavity parameters, crystal length, and output characteristics, such as the conversion rate are simulated and analyzed. The optimal pump waist size, output coupler transmission, and crystal length are determined. In addition, the intensity changes of pump and Stokes in the time domain during the Raman conversion are analyzed.

Numerical Simulation and Analysis

Model for Simulation

The experimental setup for the simulation analysis in this study is shown in Figure 2. Pump wavelength 4.3 μm (no challenge to realize in an OPO at present) was applied in the simulation for >10 μm Raman lasing. The long-band pumped far-infrared Raman laser has a larger intrinsic mode size under the condition of certain cavity parameters compared to the traditional short-band pumped Raman lasers; meanwhile, the Raman gain coefficient is inversely proportional to the wavelength [6]. Therefore, these increase the pump threshold of LWIR generation, the maximum pump power that the crystal can bear, and the maximum output power that can be obtained. The Raman oscillator adopts a near-concentric cavity structure. The curvature radius of the input and output couplers is 50 mm. The surface of the input coupler is antireflection-coated at the pump (4.3 μm) and high-reflection-coated at the Stokes (10 μm); the surface of the output coupler is high-reflection-coated at 4.3 μm. The total length of the cavity is 102 mm, and the corresponding intrinsic beam waist size is 251 μm (380 μm at the t-plane and 122 μm at the s-plane). As the refractive index of diamond is constant (n = 2.38) at wavelengths greater than 2 μm [11], a Brewster-cut (∼67.2°) single-crystal diamond is applied for the transmittance of both pump and Stokes beams, while avoiding the problems caused by crystal coating and film damage. The diamond is 5 mm in length and placed at the beam waist of the Stokes. To achieve better mode matching to improve the conversion efficiency, a focusing lens F3 with a focal length of 100 mm is used to focus the pump beam to the center of the diamond, and the corresponding pump waist size is 252 μm, as shown in the inset of Figure 2.

FIGURE 2

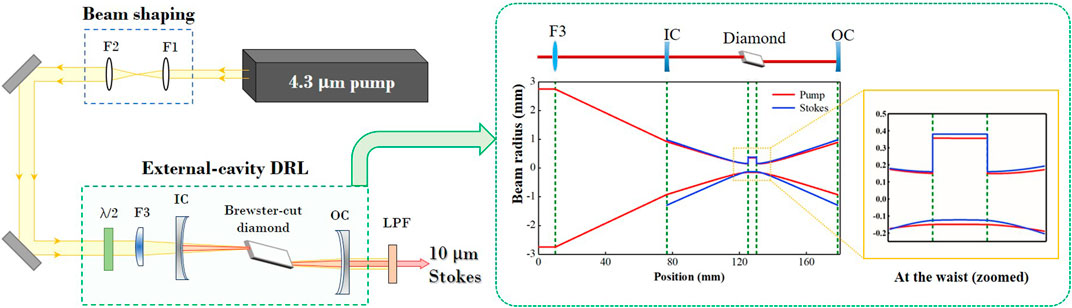
FIGURE 2. Schematic of 10 μm external-cavity DRL (inset: pump and intrinsic mode of diamond Raman resonator).

Simulation Analysis

For crystalline Raman gain materials, the time of Raman phase transition is usually in the order of picosecond. This means that the pump pulse duration in tens of nanoseconds is consistent with the steady-state operating conditions [16, 17]. However, affected by the build-up and amplification time of Stokes, usually the pulse duration of Stokes is often shorter than that of the pump until the pump pulse width is longer than hundreds of nanoseconds. Therefore, based on the resonator structure proposed above, we first used the steady-state model of an external cavity Raman laser to simulate and analyze the output characteristics (conversion efficiency, output power, etc.) under different resonators and pump parameters. Subsequently, time-domain characteristics of a short pulse pumped DRL is discussed to better understand the effect of oscillator parameters on the output pulse.

When the Raman laser operates in a steady-state, the following relationship is satisfied [18, 19].

${{\displaystyle P}}_p=\frac{T+2\alpha L}{\eta T}{{\displaystyle P}}_s{{\displaystyle \left[1-\exp \left(-\frac{2G}{T}{{\displaystyle P}}_s\right)\right]}}^{-1}(1)$

${{\displaystyle P}}_{res}={{\displaystyle P}}_p-\frac{\left(T+2\alpha L\right){{\displaystyle P}}_s}{\eta T}(2)$

where T is the output coupler transmittance, α (=0.03 cm⁻¹) and L (=5 mm) are the absorption coefficient and the length of the diamond crystal, respectively; η is the quantum defect in the Raman conversion process (η = λp/λs); G is the Raman power gain in the focused geometry; P_p, P_s and P_res are the powers of pump, Stokes, and the residual pump, respectively.

$G=\frac{{{\displaystyle g}}_s\arctan \left(\frac{L}{2}\sqrt{\frac{{{\displaystyle \left({{\displaystyle w}}_p/{{\displaystyle z}}_p\right)}}^2+{{\displaystyle \left({{\displaystyle w}}_s/{{\displaystyle z}}_s\right)}}^2}{{{\displaystyle w}}_p^2+{{\displaystyle w}}_s^2}}\right)}{\eta \frac{\pi }{4}\sqrt{{{\displaystyle \left({{\displaystyle w}}_p^2+{{\displaystyle w}}_s^2\right)}}^2\left[{{\displaystyle \left({{\displaystyle w}}_p/{{\displaystyle z}}_p\right)}}^2+{{\displaystyle \left({{\displaystyle w}}_s/{{\displaystyle z}}_s\right)}}^2\right]}}(3)$

${{\displaystyle z}}_{p,s}=\frac{\pi {{\displaystyle n}}_{p,s}{{\displaystyle w}}_{p,s}^2}{{{\displaystyle M}}_{p,s}^2{{\displaystyle \lambda }}_{p,s}}(4)$

where g_s is the Raman gain coefficient of the diamond crystal, n_p,s (n_p = n_s = 2.38), w_p,s (w_p = 252 μm and w_s = 251 μm) and $M_{p,s}^2$ ($M_p^2$ = 2 and $M_s^2$ = 1.1) are the indices of refraction, waist size and beam quality factors of the pump and Stokes, respectively. As the gain coefficient is inversely proportional to the wavelength, the gain coefficient is set to be 1 cm/GW in the simulation, based on the previous reports g_s = ∼10 cm/GW at 1 μm [6]. According to Eq. 2, when the pump power increases to infinity, the slope efficiency of Stokes light (σ) is equal to the maximum conversion efficiency of Raman generation, i.e.,

$\sigma =\frac{\eta T}{T+2\alpha L}(5)$

When Stokes output power approaches zero infinitely, the threshold P_thr of Raman generation is calculated by Eq. 1:

${{\displaystyle P}}_{thr}=\frac{\pi \left(T+2\alpha L\right)\sqrt{{{\displaystyle \left({{\displaystyle w}}_p^2+{{\displaystyle w}}_s^2\right)}}^2\left[{{\displaystyle \left({{\displaystyle w}}_p/{{\displaystyle z}}_p\right)}}^2+{{\displaystyle \left({{\displaystyle w}}_s/{{\displaystyle z}}_s\right)}}^2\right]}}{8{{\displaystyle g}}_s\arctan \left(\frac{L}{2}\sqrt{\frac{{{\displaystyle \left({{\displaystyle w}}_p/{{\displaystyle z}}_p\right)}}^2+{{\displaystyle \left({{\displaystyle w}}_s/{{\displaystyle z}}_s\right)}}^2}{{{\displaystyle w}}_p^2+{{\displaystyle w}}_s^2}}\right)}(6)$

According to Eqs. 5, 6, we can obtain the maximum conversion efficiency and Raman generation threshold at different output coupler transmittances. As shown in Figures 3A,B, the Raman generation threshold of DRL is much higher than that in the near-infrared band owing to its relatively low Raman gain and high absorption loss in the LWIR band [11]. The Raman generation threshold increases linearly with the output coupler transmittance. When the output coupler transmittance increases to about 60%, the maximum conversion efficiency can approach the quantum conversion limit (∼43%). Using Eqs. 1, 2, the output power and the residual pump curves when T = 0.5% are obtained for the double-pass pump mode. As shown in Figure 3C, when T = 0.5%, the corresponding Stokes generation threshold is 34.8 kW. When the pump power is greater than this value, owing to the consumption of Raman conversion, the residual pump power rapidly reduces, and the Stokes power generated increases accordingly.

FIGURE 3

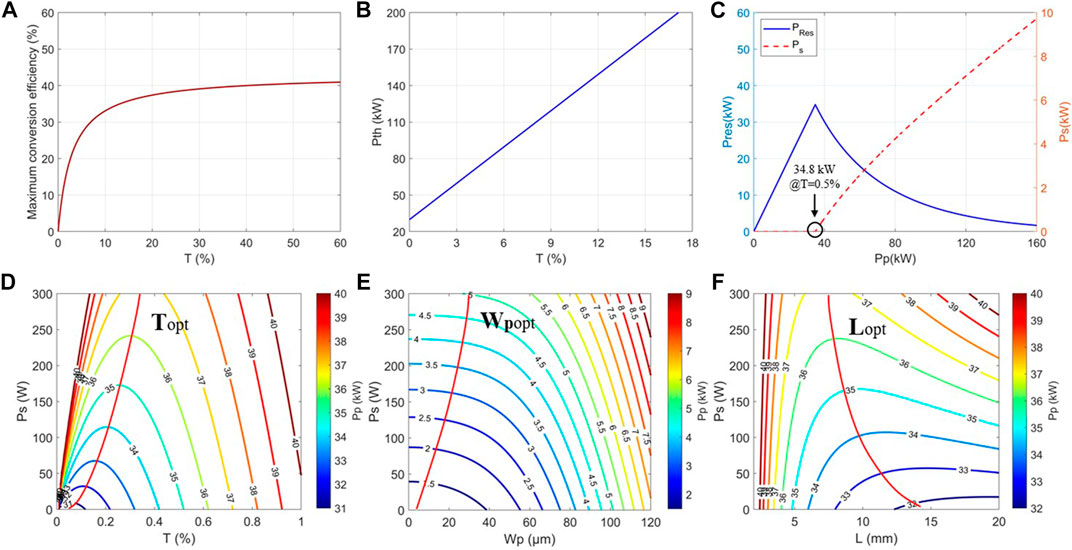
FIGURE 3. Numerical simulation results. (A) Maximum conversion efficiency, and (B) Raman generation threshold as a function of output coupler transmittance at Stokes; (C) output and residual pump curves at T = 0.5%. Stokes output power as a function of (D) output coupling transmittance, (E) pump waist radius, and (F) the crystal length, for different pump powers. The red line indicates optimal values of output coupler transmission, pump waist radius, and length of the crystal, respectively.

The output transmittance, pump waist size, and crystal length are three key factors that affect the output power of the DRL. Utilizing Eq. 1, we obtained the relationship between the output power of Stokes and the output transmittance, the size of the pump waist, and the crystal length under different pump powers, as shown in Figure 3. When the pump waist size and the crystal length are fixed, different pump powers correspond to different values of the optimal output transmittance. As shown in Figure 3D, the optimal output transmittance increases with the increase in pump power. The threshold of Stokes generation corresponds to a fixed pump power density, and the size of the pump focus is directly related to the power density. When the pump power is constant, the smaller the pump focus size (corresponding to the higher power density), and the easier it is to obtain Stokes output, as shown in Figure 3E. However, the pump spot size cannot be infinitely small, which is particularly difficult for LWIR lasers. Thus, there is an experimental optimum beam waist size that is small enough to get close to the maximum output power and yet not be experimentally problematic, for example, by shortening the length of the Raman oscillator combining with a shorter pump focus lens (F3, as illustrated in Figure 1). Even if the pump waist size is smaller than this value, the improvement of the output Stokes power is very limited. Meanwhile, the small size of the pump waist may increase the risk of diamond damage and aggravate the thermal effect. The crystal length is another key factor affecting the output power of the Raman laser, which affects the absorption loss of the crystal, as well as the interaction length of the pump and Stokes beams during the Raman conversion. As shown in Figure 3F, the Stokes power increases with the increase of diamond length in the initial stage, however, decreases when the diamond length increases continuously due to the relatively large absorption loss in the pump band. Therefore, it is critical to choose an optimal length of the crystal, especially for LWIR Raman lasing.

Theoretically, as the dephasing time of the vibrational excitation is of order of 10 ps for crystals [20], the Stokes pulse width is close to that of the pump when the overall gain of the oscillator is large enough for a crystalline Raman laser pumped by tens of nanoseconds pulse (or longer). However, restricted by Raman gain coefficient, crystal length, intracavity diffraction loss, as well as resonator structure, Stokes beam cannot oscillate and output in a very short time, which leads to an obvious pulse compression effect during Raman conversion [21, 22]. In view of this situation, we simply analyze the changes of pump and Stokes intensity in time domain in a Raman oscillator. It is assumed that the time-domain distribution of the pump pulse is Gaussian and only the first order Stokes generation is existed, as shown in Figure 4. At the beginning, the pump pulse remains in the input state before reaching the Raman threshold. When reaches the Stokes generation threshold, Stokes pulse is amplified rapidly with pump pulse depleted until the end of the pump cycle. It can be seen from the comparison of Figures 4A,B, when the overall gain of the Raman oscillator is small, a relatively long time is required to Stokes generation, showing low output power intensity and strong pulse width compression effect. By contrast, Stokes with high power intensity and negligible pulse compression effect is presented, while the gain is high. As gain coefficient in the specific operating wavelength and waist radii of the pump and Stokes beams, are the main parameters that the overall gain of a Raman oscillator depended on, it can be predicted that relatively strong pulse width compression will occur in a LWIR-DRL if the pump pulse width is in the order of nanoseconds. Therefore, compared with short pulse pumping (∼ns), increasing the pump pulse width in a certain range is an alternative way to improve the pump efficiency of LWIR-DRLs.

FIGURE 4

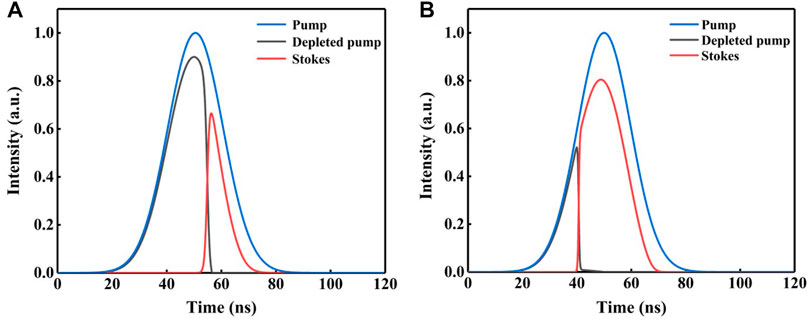
FIGURE 4. Tracings diagram of pump, depleted pump and Stokes with (A) small gain, and (B) large gain.

Conclusion and Outlook

In this paper, we proposed a new scheme to realize LWIR lasing output through diamond Raman conversion by utilizing the excellent photothermal properties of diamond crystals and the advantages of SRS. Based on the large Raman frequency shift of the diamond crystal, a 10 μm far-infrared laser was obtained by using a 4.3 μm laser as the pump source through the first-order Raman conversion. Using the diamond Raman steady-state model, we simulated the relationship between the output transmittance and the maximum conversion efficiency, Raman generation threshold, and residual pump power. The relationship between the relevant parameters (the size of the pump waist, output transmittance, and crystal length) and the output power was analyzed. And the pulse compression effect as the function of the oscillator gain in the process of Raman conversion is discussed. It can be predicted that when the diamond size is 1 × 1 × 1 cm³, the maximum Stokes peak power output close to 123 MW can be generated with the transmittance of 40%. However, since the steady-state Raman gain coefficient is inversely proportional to the linewidth [23, 24], considering the intrinsic gain linewidth of the diamond (∼40 GHz), it is necessary to control the linewidth of the mid-wave infrared (MWIR) pump beam in the experiment to ensure the Raman conversion efficiency.

The simulation results in this study provide important theoretical guidance and prediction for the subsequent development of LWIR lasers based on the DRL. In addition, due to the excellent thermophysical properties of diamond, stable LWIR Raman operation without heat accumulation can be realized when the pump pulse width is in the order of 100 microseconds, meanwhile, the repetition rate can be up to kHz-level [10, 25], even if its quantum defect is significantly higher than that of the short wave. As there is no spatial hole burning effect in the process of Raman conversion [26–29], the theoretical study also provides a preliminary reference for realizing the operation of narrow linewidth LWIR lasing. Besides, the excellent Brillouin characteristics of diamond also make it possible to realize low-noize LWIR Brillouin lasing and Brillouin frequency combs in the future [30, 31].

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

HC: Methodology, Formal analysis, Writing - original draft. ZB: Conceptualization, Writing - review and editing, Formal analysis, Supervision, Funding acquisition. CZ: Investigation, Writing - original draft. XY: Writing - review and editing, Formal analysis. JD: Writing - review and editing. YQ: Writing - review and editing. YW: Conceptualization, Supervision. ZL: Conceptualization, Supervision.

Funding

This work was supported by the National Natural Science Foundation of China (61905061 and 61927815), Key Laboratory of Functional Crystals and Laser Technology Foundation (FCLT202004), and Postgraduate Innovation Ability Training Program of Hebei Province (CXZZSS2021039).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Shaw LB, Cole B, Thielen PA, Sanghera JS, Aggarwal ID. Mid-Wave IR and Long-Wave IR Laser Potential of Rare-Earth Doped Chalcogenide Glass Fiber. IEEE J Quan Electron (2001) 37:1127–37. doi:10.1109/3.945317

CrossRef Full Text | Google Scholar

2. Miyamoto K, Ito H. Wavelength-agile Mid-infrared (5-10 μm) Generation Using a Galvano-Controlled KTiOPO_4 Optical Parametric Oscillator. Opt Lett (2007) 32:274–6. doi:10.1364/ol.32.000274

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Badikov VV, Laptev VB, Panyutin VL, Ryabov EA, Shevyrdyaeva GS. Study of Nonlinear-Optical Characteristics of AgGa1-xInxSe2crystals. Quan Electron (2005) 35(3):263–7. doi:10.1070/qe2005v035n03abeh002795

CrossRef Full Text | Google Scholar

4. Watson MA, O’Connor MV, Shepherd DP, Hanna DC. Synchronously Pumped CdSe Optical Parametric Oscillator in the 9-10 μm Region. Opt Lett (2003) 28(20):1957–9. doi:10.1364/ol.28.001957

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Razeghi M, Zhou W, Slivken S, Lu Q-Y, Wu D, McClintock R. Recent Progress of Quantum cascade Laser Research from 3 to 12 μm at the Center for Quantum Devices [Invited]. Appl Opt (2017) 56(31):H30–H44. doi:10.1364/ao.56.000h30

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Williams RJ, Kitzler O, Bai Z, Sarang S. High Power diamond Raman Lasers. IEEE J Selected Top Quan Electronics (2018) 24(5):1602214. doi:10.1109/jstqe.2018.2827658

CrossRef Full Text | Google Scholar

7. Murray JT, Austin WL, C. Powell R. Intracavity Raman Conversion and Raman Beam Cleanup. Opt Mater (1999) 11(4):353–71. doi:10.1016/s0925-3467(98)00033-0

CrossRef Full Text | Google Scholar

8. Bai Z, Williams RJ, Jasbeer H, Sarang S, Kitzler O, Mckay A, et al. Large Brightness Enhancement for Quasi-Continuous Beams by diamond Raman Laser Conversion. Opt Lett (2018) 43(3):563–6. doi:10.1364/ol.43.000563

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Bai Z, Williams RJ, Kitzler O, Sarang S, Spence DJ, Mildren RP. 302 W Quasi-Continuous Cascaded diamond Raman Laser at 15 Microns with Large Brightness Enhancement. Opt Express (2018) 26(16):19797–803. doi:10.1364/oe.26.019797

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Williams RJ, Kitzler O, Mckay A, Mildren RP. Investigating diamond Raman Lasers at the 100 W Level Using Quasi-Continuous-Wave Pumping. Opt Lett (2014) 39(14):4152–5. doi:10.1364/ol.39.004152

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Mildren RP. Intrinsic Optical Properties of Diamond. Optical Engineering of Diamond. New Jersey: John Wiley&Sons (2013) p. 1–34. doi:10.1002/9783527648603.ch1

CrossRef Full Text

12. Balmer RS, Brandon JR, Clewes SL, Dhillon HK, Dodson JM, Friel I, et al. Chemical Vapour Deposition Synthetic diamond: Materials, Technology and Applications. J Phys Condens Matter (2009) 21(36):364221. doi:10.1088/0953-8984/21/36/364221

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Friel I, Geoghegan SL, Twitchen DJ, Scarsbrook GA. Development of High Quality Single crystal diamond for Novel Laser Applications [C]. Proc SPIE (2010) 13:783819. doi:10.1117/12.864981

Google Scholar

14. Li Y, Bai Z, Chen H, Jin D, Yang X, Qi Y, et al. Eye-safe diamond Raman Laser. Results Phys (2020) 16:102853. doi:10.1016/j.rinp.2019.102853

CrossRef Full Text | Google Scholar

15. Sabella A, Piper JA, Mildren RP. Diamond Raman Laser with Continuously Tunable Output from 3.38 to 3.80 μm. Opt Lett (2014) 39(13):4037–40. doi:10.1364/ol.39.004037

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Piper JA, Pask HM. Crystalline Raman Lasers. IEEE J Select Top Quan Electron (2007) 13(3):692–704. doi:10.1109/jstqe.2007.897175

CrossRef Full Text | Google Scholar

17. Warrier AM, Lin J, Pask HM, Mildren RP, Coutts DW, Spence DJ. Highly Efficient Picosecond diamond Raman Laser at 1240 and 1485 nm. Opt Express (2014) 22(3):3325–33. doi:10.1364/oe.22.003325

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kitzler O, McKay A, Spence DJ, Mildren RP. Modelling and Optimization of Continuous-Wave External Cavity Raman Lasers. Opt Express (2015) 23:8590–602. doi:10.1364/oe.23.008590

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Boyd G, Johnston W, Kaminow I. Optimization of the Stimulated Raman Scattering Threshold. IEEE J Quan Electron (1969) 5(4):203–6. doi:10.1109/jqe.1969.1075751

CrossRef Full Text | Google Scholar

20. Pask HM. The Design and Operation of Solid-State Raman Lasers. Prog Quan Electronics (2003) 27(1):3–56. doi:10.1016/s0079-6727(02)00017-4

CrossRef Full Text | Google Scholar

21. Wang Y, Peng W, Yang X, Peng J. Efficient Operation Near the Quantum Limit in External Cavity diamond Raman Laser. Laser Phys (2020) 30(9):095002. doi:10.1088/1555-6611/ab9d76

CrossRef Full Text | Google Scholar

22. Ma S, Tu H, Lu D, Hu Z, Jiang N, Wang X, et al. Efficient Raman Red Laser with Second-Order Stokes Effect of diamond crystal. Opt Commun (2020) 22:126399. doi:10.1016/j.optcom.2020.126399

Google Scholar

23. Spence DJ. Spectral Effects of Stimulated Raman Scattering in Crystals. Prog Quan Electronics (2017) 51:1–45. doi:10.1016/j.pquantelec.2016.11.001

CrossRef Full Text | Google Scholar

24. Sheng Q, Lee A, Spence D, Pask H. Wavelength Tuning and Power Enhancement of an Intracavity Nd:GdVO₄-BaWO₄ Raman Laser Using an Etalon. Opt Express (2018) 26(24):32145–55. doi:10.1364/oe.26.032145

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Bai Z, Zhang Z, Wang K, Gao J, Zhang Z, Yang X, et al. Comprehensive thermal Analysis of diamond in a High-Power Raman Cavity Based on FVM-FEM Coupled Method. Nanomaterials (2021) 11(6):1572. doi:10.3390/nano11061572

CrossRef Full Text | Google Scholar

26. Lux O, Sarang S, Kitzler O, Spence DJ, Mildren RP. Intrinsically Stable High-Power Single Longitudinal Mode Laser Using Spatial Hole Burning Free Gain. Optica (2016) 3(8):876–81. doi:10.1364/optica.3.000876

CrossRef Full Text | Google Scholar

27. Sheng Q, Li R, Lee AJ, Spence DJ, Pask HM. A Single-Frequency Intracavity Raman Laser. Opt Express (2019) 27(6):8540–53. doi:10.1364/oe.27.008540

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yang X, Kitzler O, Spence DJ, Williams RJ, Bai Z, Sarang S, et al. Single-frequency 620 Nm diamond Laser at High Power, Stabilized via Harmonic Self-Suppression and Spatial-hole-burning-free Gain. Opt Lett (2019) 44(4):839–42. doi:10.1364/ol.44.000839

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Yang X, Kitzler O, Spence DJ, Bai Z, Feng Y, Mildren RP. Diamond Sodium Guide star Laser. Opt Lett (2020) 45(7):1898–901. doi:10.1364/ol.387879

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Bai Z, Robert JW, Ondrej K, Kitzler O. Diamond Brillouin Laser in the Visible. APL Photon (2020) 5(3):031301. doi:10.1063/1.5134907

CrossRef Full Text | Google Scholar

31. Williams RJ, Bai Z, Sarang S, Kitzler O, Spence DJ, Mildren RP. Diamond Brillouin Lasers. arXiv preprint arXiv:1807.00240 (2018).