Optical Parameters of Atomically Heterogeneous Systems Created by Plasma Based Low Energy Ion Beams: Wavelength Dependence and Effective Medium Model

The article presents the irradiation effects of low energy (∼0.5 keV) inert gaseous Argon ion beams on optical constants [real (n) and imaginary (k) parts of the refractive index], dielectric constants, skin depth, and optical conductivity of copper (Cu), silver (Ag), and aluminum (Al) metallic thin films (MTF). The optical constants of pristine MTF are obtained by employing the universal Kramers-Kronig (KK) technique. The reflectivity of pristine MTF measured using UV-VIS-NIR spectrophotometry is used as an input parameter in the KK technique to determine the optical constants as a function of energy [or wavelength (λ)] of incident light ranging between ∼1–4.96 eV (or 250–1,200 nm). For the irradiated MTF, the optical constants including the skin depth (δ = λ/2πk), optical conductivity (σ = nkc/λ), and dielectric constants (ϵ₁ = n² − k² and ϵ₂ = 2nk) with varying ion fluence have been investigated by implementing the Maxwell-Garnett (MG) approximation, used to determine the effective dielectric constants of a random mixture of two different mediums. Additionally, n and k obtained from MG approximation have been compared with those obtained using the pseudo- Brewster angle technique for four different laser wavelengths (405, 532, 632.8 and 670 nm) and are found to be in good agreement with each other. It is observed that the optical constants and optical conductivity of the MTF decrease with increase in ion beam fluence, while the skin depth increases. Besides the optical constants, the behavior of skin depth, dielectric constants, and optical conductivity of the irradiated MTF with varying fluence are discussed in this article.

1 Introduction

The field of employing low energy plasma ion beams for creating atomically heterogeneous systems in metals, dielectric and organic compounds for realizing their novel optical, electrical, and surface properties has initiated a growing interest in the research community [1–5]. During low energy ion beam bombardment, ions enter the subsurface layers (few tens of nm [2]) of the host and create an atomically heterogeneous system with heterogeneity at the atomic length scale, which modifies the optical, electrical and surface properties of the host [2, 4, 5]. It is known that the optical parameters such as the optical constants (n and k) provide critical information about the electronic structure, polarizability, refractive index, skin depth, optical conductivity, energy loss function, surface plasmon characteristics (propagation length, lifetime etc.) along with the interband and intraband transitions in the medium [6–15]. For example, frequency dependent dielectric constants describe lattice vibration, free carrier absorption, interband transitions, and chemical bonding excitations [16, 17]. The dielectric constants of metals such as silver, copper, and gold having one valence electron are related to the electronic intraband transitions within the conduction band in the lower energy range of the electromagnetic spectrum. Optical response of the material in this energy range is mainly governed by the free electron contribution and provides the critical information of scattering and mean free path of electrons. The interband transition from the d- bands (occupied) to the sp- bands (partially filled) are excited at higher energies, which is observed in the behaviour of dielectric constants [10]. The various optical properties such as transmission, reflection, absorption, and dispersion are fundamentally connected to the optical (or dielectric) constants of the material.

Owing to the importance of the subject, there have been different ways to determine the optical constants of pristine MTF such as: 1) measuring reflectivity or transmissivity and applying the KK technique [18–20], 2) inversion of Fresnel’s equation of reflectivity and transmissivity [21, 22], and 3) employing the KK technique to obtain n from the k values or vice-versa [23]. The optical constants of noble metals measured by Johnson and Christy (JC) are considered to be amongst the most reliable data [6]. S. Babar et al. have also obtained the dielectric constants by measuring the absorption experimentally (R = 1 - A) and applying KK reflectivity transformation [24] for the metals, which are in good agreement with JC and other researchers [7–9, 21, 24]. In this regard the works of Ordal et al. [25] and Palik [26] are also found to be quite useful. A. B. Kuzmenko has proposed a different approach to obtain the dielectric constants by parameterization of the imaginary part independently at each node of frequency and the real part calculated by employing the KK technique [27]. The KK technique has also been applied for layered media structure at oblique incident angle for the study of NaCl and BaF₂ [28]. The transmissivity instead of reflectivity has been employed as an input in the KK technique to obtain the optical constants of a thin absorbing film by Palmer et al. [19]. Therefore, the KK method has been established as an important technique widely employed to obtain the optical constants of metals, dielectrics, and semiconductors [18, 19, 29].

All the afore-mentioned methods have been successfully applied to describe mediums that are essentially homogeneous (pristine MTF). In order to deal with optical properties of mixed mediums, there are effective medium models that have been developed, such as the Maxwell-Garnett approximation, Bruggeman approximation and other effective medium approximations [30–33]. The MG and Bruggeman approximations have been employed in our previous study, and the outcome of the MG approximation was found to be more close to the results obtained from the experimental pseudo- Brewster angle technique for determining n and k for ion beam irradiated copper, silver, aluminum, and gold MTF [5]. Therefore, the MG approximation has been implemented in the present work to investigate the effective dielectric constants of ion beam irradiated MTF as a function of fluence and energy of incident light.

The present article reports the variation of optical parameters (optical constants, dielectric constants, skin depth, and optical conductivity) of Ag, Al, and Cu MTF upon irradiation of low energy ion beams with varying fluence ranging from (1.6–7.2) × 10¹⁵ cm⁻². The reflectivity of each MTF is measured experimentally by UV-VIS-NIR spectrophotometry in the wavelength range 250–1,200 nm [5] and thereafter, the KK reflectivity transformation is employed to obtain the phase information, and further to obtain the optical constants. To further corroborate the results, the pseudo- Brewster angle technique has also been employed to obtain the optical constants for both pristine and irradiated MTF, at four different wavelengths in the visible region (405, 532, 632.8 and 670 nm) produced by different laser sources that were available with us. It is observed that the values of both n and k obtained from MG approximation decrease with increase in fluence of Argon ions and are found to be in close agreement with the results obtained from the pseudo- Brewster angle technique. The decrease in k with ion fluence enhances the skin depth inside the atomically heterogeneous medium that results in increase in transmission as observed in our earlier experiment [5]. An increase in ion fluence results in increase of real part and decrease of imaginary part of dielectric constants, respectively as suggested by approximation methods [30–32]. The optical conductivity decreases with increase in ion beam fluence for all MTF. The principal motivation of the article is to demonstrate a way of controlling the optical parameters mentioned above, using low energy ion beams derived from plasmas, and present applicability of different techniques available to determine these optical constants for mixed media created by low energy ion beam irradiation of MTF. The vast applications of Ag and Al as reflector coatings and antennas of spacecrafts and satellites, respectively, make them a relevant subject for looking into their behavior. Hence Ag and Al, along with the widely available copper are chosen for investigation purposes [5]. Apart from the above mentioned applications, metallic thin films also have potential applications in solar cells [34, 35], and biosensors [36, 37].

This article is divided into the following sections. Section 2 presents the experimental setup and methodology. Section 3 is on the Kramers-Kronig analysis and the Maxwell-Garnett approximation method. Section 4 presents a discussion of results obtained from KK, pseudo- Brewster angle techniques and MG approximation. Finally, section 5 summarizes the results and concludes the paper.

2 Experimental Setup and Methodology

The complete experimental setup with its schematic and digital picture is shown in Figure 1. It consists of two main parts, i.e., the plasma production region and the ion extraction region. In the plasma production region, plasma is created using microwaves of 2.45 GHz using a generator (Richardson PM 740) of frequency 2.45 GHz. The water-cooled isolator (ISO), directional coupler (DC), and triple stub tuner (TST) helps to isolate the magnetron from reflected waves, measure the forwarded and reflected powers simultaneously, and match the source (magnetron) and load (plasma) impedance for maximum power transfer, respectively. All experiments are performed at a constant microwave power of 180 W and a pressure of ∼1 × 10⁻⁴ Torr. The plasma is produced by electron cyclotron resonance heating inside a magnetic multicusp (octupole) kept inside the vacuum chamber (VC), having a length of 50 cm and diameter of 20 cm. VC is evacuated to a base pressure of ∼1 × 10⁻⁶ Torr using a Turbo-molecular pump (TMP) (Varian 301 Navigator) backed by a rotary pump. The experiments are carried out at a working pressure of ∼1 × 10^–4 Torr. Argon is used as an experimental gas which is fed into VC through gas inlet (GI), and the gas flow is maintained by a mass flow controller (MFC, MKS 1179A). The second part, i.e., the ion extraction region, is used to extract the ions from the plasma region by applying a negative voltage (∼0.5 kV) at the collector. Another pumping set consisting of a TMP backed by a rotary pump is connected to the ion extraction region to maintain a good vacuum in the extraction region, so as to minimize the collisions of extracted ions with any neutral particles. Differential pumping is used in the two chambers by the help of turbo molecular and rotary pumps, and the pressure in the ion extraction region is kept one order lower than the plasma chamber (typically ∼10⁻⁵ Torr), such that no plasma forms in the ion extraction region. In the plasma chamber, the plasma is formed inside the multicusp which not only provides radial confinement, but axial confinement as well due to end-plugging of the multicusp, where the polarity of the magnets at both ends are reversed [38, 39]. The samples are mounted in the extraction chamber ∼8–10 mm away from the multicusp boundary. Ions from the plasma sheath edge reach the grounded plasma facing electrode (PLE) with Bohm velocity (∼4.8 × 10³ m/s) and energy eV_P, where V_P is the difference between the plasma potential (typically ∼40 V) and the ground potential (PLE). A plasma sheath of a few microns is formed near the plasma aperture at PLE. Thereafter, the ions from the sheath are extracted in the form of a beam by applying a negative voltage on the collector in the extraction region. Earlier work by A. Chowdhury et al. [40] has demonstrated that the current voltage characteristics of extracted ion beams exhibit the different behaviour of space charge limited region than the conventional Child- Langmuir’s law and the extracted voltage limited region shows the features similar to a vacuum diode. Various low energy ion beam sources have been developed, however most of them suffer from lack of control of ion beam energy [41]. In this regard, K. Takahashi et al. [42] has developed a dc discharge plasma source to obtain low energy ions (up to 100 eV) in a controlled manner.

FIGURE 1

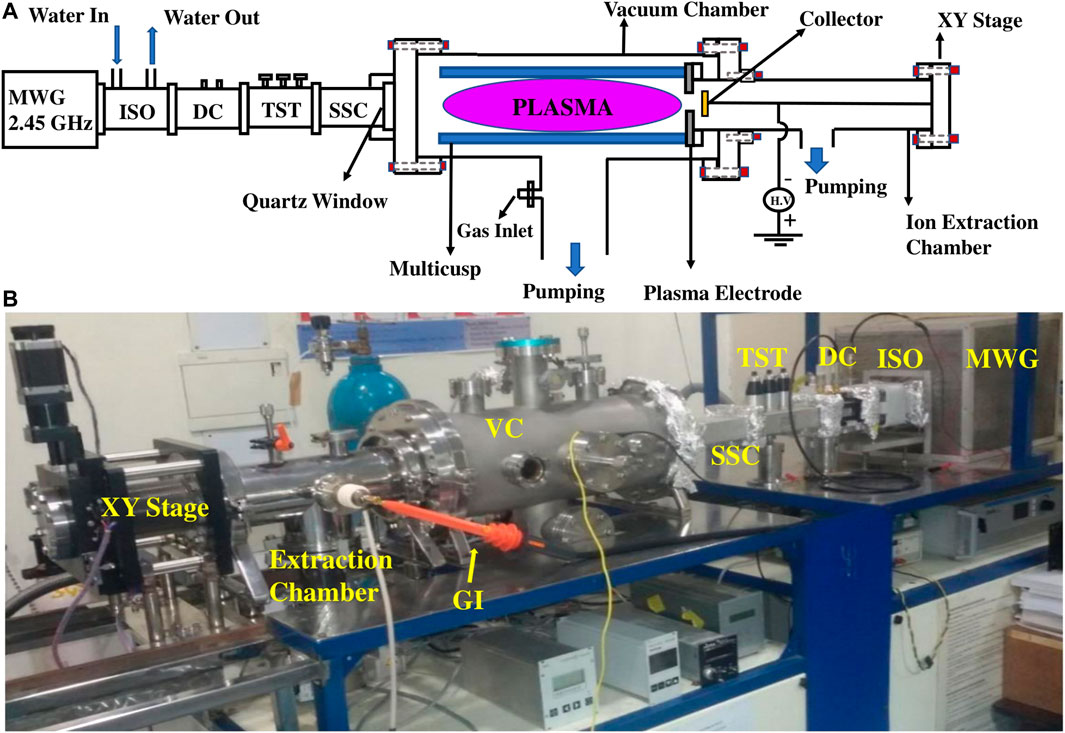
FIGURE 1. (A) Schematic diagram and (B) digital picture of experimental setup. MWG, microwave generator; ISO, isolator; DC, directional coupler; TST, triple stub tuner; SSC, straight section; GI, gas inlet; and VC, vacuum chamber.

The thermal evaporation technique is utilized to deposit various types of MTF such as Cu, Ag, and Al of thickness around 200 nm on a glass substrate. The glass substrates are ultrasonicated with acetone and isopropyl alcohol and rinsed with deionized water, before the deposition. In addition to the thickness monitor in the thermal evaporation system, a separate profilometer is used to confirm the thickness of the thin films used in the experiments. The thickness of the MTF used in the experiment is 205 ± 5 nm. The as-prepared samples are mounted on the collector plate in the ion extraction region and are bombarded with low energy (0.5 keV) Argon ions extracted from the plasma chamber. The voltage on the collector plate is also applied to the metallic film by connecting them electrically with a conducting silver paste. The extracted ions hit the sample at normal incidence. It has been reported that the actual ion penetration depth/range obtained from energy dispersive X-ray spectroscopy (EDAX) differs significantly from the SRIM/TRIM data. A. Chowdhury et al. [4] has reported that the range of 0.3 keV Ar ions inside the copper thin film (thickness ∼175 nm) is approximately ∼75 nm which is much higher than the SRIM data (∼2 nm). S. Chatterjee et al. [2] has also reported the penetration depth of 0.5 keV Ar ions inside the Au film, which is approximately ∼20 nm, and this also does not match with SRIM data (∼0.8 nm). The reason of the mismatch of SRIM/TRIM data could be due to the exclusion of many body interaction, inelastic collision, thermal diffusion of implanted ions due to heat generated at the time of irradiation, in the Monte Carlo simulation [4]. Thermal diffusion is considered to be the main cause of higher penetration depth as suggested in Ref. [4]. Hence, the penetration depth of 0.5 keV Ar ions inside the Al, Cu, and Ag is expected to be ∼50 nm or more, which is much higher than SRIM/TRIM data of 9, 12, and 20 Å for Cu, Ag, and Al respectively. The skin depth (min-max) of electromagnetic radiation (250–1,200 nm) for Al, Cu, and Ag lies ∼15–24, 22–36, and 34–132 nm, respectively. Hence, the radiation of wavelength 250–1,200 nm mostly sees the inhomogeneity up to its skin depth which is comparable to the penetration depth of the ions. The low energy (∼0.5 keV) Ar ions contribute to both target atom sputtering as well as electron emission from the target. It has been investigated that the secondary electron emission rate coefficient is quite less (less than 0.1 [43]) in case of ion bombardment compared to the electron bombardment. Because in case of ion bombardment, the low energy ions lose most of their energy in elastic collision with target nuclei (nuclear scattering). In case of electron bombardment, the rate coefficient of secondary electron emission for Ag, Al, and Cu for electron energy (∼0.5 keV) has been reported ∼1.4, 0.8, and 1.2, respectively by H. Burning et al. [44] while the Al rate coefficient 0.5 keV energy Ar ion bombardment is reported ∼0.07 by A. Marcak et al. [45]. Hence, the measured dose of Ar ions in our experiment would have maximum error of ∼7–10% and this error has already been reported and incorporated in flux measurement in our previous article [5]. In case of sputtering, it has been reported that the periodic patterns induced by sputtering on the substrate dominate for oblique angle incidence while normal incidence may be favourable for smoothening of sample due to atomic flux gradient parallel to the surface [46–48]. Sputtering leads to the formation of different type of periodic patterns such as: ripple like structures, nanostructures etc [49]. These periodic patterns change the optical properties of the material [50]. In our study, no pattern formation is found in the AFM images of silver MTF (data not presented here). Hence, sputtering only changes the surface roughness of the samples that in turn modifies the optical properties of the samples as mentioned in our earlier paper [5]. Sputtering by low energy ion beam bombardment has also been used to prepare the multi-layer metal thin films by K. Takahashi et al. [51]. The irradiation or treatment time decides the fluence of the ions. The fluence is varied between (1.6–7.2) × 10¹⁵ cm⁻². The details of ion beam flux variation with neutral gas pressure and microwave power along with the measurement technique may be found in [5]. A beam diameter of 2 cm is used to provide uniform irradiation of the samples of size ∼1.25 × 1.25 cm². The samples are always kept inside vacuum desiccator to prevent atmospheric contamination and oxidation. More details about the experimental setup and sample description may be found in [5].

The PerkinElmer Lambda 950 UV/VIS/NIR spectrophotometer has been employed to measure the reflectivity of each pristine MTF at 8° of normal incidence angle. The slit size of incoming incident light beam is 0.5 × 1 cm². The wavelength range of incident light coming from the spectrophotometer can be varied from 175 to 3,300 nm, having UV/VIS and NIR resolutions of (0.05–5.00) nm and (0.20–20.00) nm, respectively. The pseudo- Brewster angle technique has been employed to obtain the refractive index of each pristine as well as the irradiated MTF. In this technique, a laser light (unpolarized or semi polarized) of desired wavelength passes through the polarizer (linear sheet polarizer) and the transmitted light from the polarizer becomes polarized along the horizontal axis. Thereafter, the polarized light is made to fall on to the half wave plate (HWP) and the polarization axis of light shifts 45° to the initial after passing through the HWP, producing same horizontal (p- polarized) and vertical (s- polarized) components of light. The p- polarized component of light reaches to the detector (silicon photodiode) after getting reflected from the sample (mounted on an angular rotatory stage) and after passing through the analyzer (placed between detector and sample). More details on the measurement methods can be found in Ref. [5]. The detector and analyzer are mounted on the movable arm of spectrometer. The angle of incidence is varied by rotating the sample with the help of angular rotatory stage and the corresponding rotation is set by the movable arm of spectrometer to detect the p- polarized light. Hence, the reflectivity of p- polarized light is measured at various angles of incidence. The analyzer, polarizer, and HWP all have 1° of angular resolution. The reflectivity of p- polarized light attains its minimum value (R_PB) at the pseudo-Brewster angle (θ_B). The optical constants can be obtained using the following relations [5],

$n=\frac{1-R_{PB}}{1+R_{PB}}sec{\theta }_B,\text{\hspace{0.17em}and\hspace{0.17em}}k=\frac{2\sqrt{R_{PB}}}{1+R_{PB}}sec{\theta }_B.(1)$

3 Kramers-Kronig Technique and Maxwell-Garnett Approximation

The KK technique works on measuring the phase shift of the reflected light to the incident light. The phase information retrieved from the KK technique along with Fresnel’s equations provide the optical constants of the media. The equations of reflection coefficient for air (n₁ = 1) - metal (n₂ = n + ik) interface are given below [18].

$\tilde{r}(\omega )=\rho (\omega )\exp i\theta (\omega )=\frac{1-(n+ik)}{1+(n+ik)},(2)$

where ρ(ω) is the reflectivity modulus and θ(ω) is the phase difference between the incident and reflected light. Reflectivity is defined by the following relation:

$R=|\tilde{r}(\omega ){|}^2=\rho {(\omega )}^2\Rightarrow \rho (\omega )=\sqrt{R}.(3)$

We can obtain the following relation by taking natural logarithm of Equation 2 and using Equation 3,

$\ln r(\omega )=\ln \sqrt{R}+i\theta (\omega ).(4)$

The phase information θ(ω) can be obtained as follows by employing KK relations [18] for ln r(ω),

$\theta ({\omega }_0)=-\frac{2{\omega }_0}{\pi }{\int }_0^{\infty }\frac{\ln \sqrt{R}}{{\omega }^2-{\omega }_0^2}d\omega =\frac{1}{2\pi }{\int }_0^{\infty }\ln \left|\frac{\omega -{\omega }_0}{\omega +{\omega }_0}\right|\frac{d(\ln R(\omega ))}{d\omega }d\omega .(5)$

Equation 5 calculates the phase difference θ(ω₀) between incident and reflected beam for a particular frequency ω₀ using the log of reflectivity i.e.,   ln R. θ(ω) can be obtained by solving Equation 5 for various ω. The frequency limits of integral in the KK analysis vary from zero to infinity to obtain the actual phase information of reflected radiation. However, it is not feasible to measure the reflectivity experimentally in the infinite range. Hence, it is reported that the reflectivity has to be extrapolated to the extent possible to get the phase information more accurately from the KK technique [24, 52]. The first part of integrand in Equation 5 vanishes for both ω ≫ ω₀ or ω ≪ ω₀, while the second term vanishes for the range of ω where reflectivity remains almost constant. Thus, it is not needed to measure the reflectivity in infinite range to analyze any particular absorption band for ω₀. In the present investigation, the experimentally measured range of reflectivity from UV-VIS-NIR spectrophotometer is ∼1–4.96 eV (or 250–1,200 nm) in the interval of 2 nm for all the concerned MTF [5]. Reflectivity for Cu, Ag, and Al has been extrapolated up to 0.8 and 10 eV in the lower and higher energy range, respectively by using the previously measured reflectivity for copper [53], silver [53], and aluminum [52] in the literature.

The optical constants of the media can be readily obtained in terms of the reflectivity and phase angle by solving Equations 2, 3 as follows,

$n=\frac{1-R}{1+R+2\sqrt{R}\cos \theta },(6)$

$k=\frac{2\sqrt{R}\sin \theta }{1+R+2\sqrt{R}\cos \theta }.(7)$

Both n and k are functions of experimentally measured reflectivity R and numerically evaluated θ(ω) from Equation 5. The above Equations 6, 7 are derived for linear, isotropic and homogeneous medium [18] and this formulation is not valid for inhomogeneous medium. Hence, the KK analysis is employed only to the pristine (linear and homogeneous) metallic thin films to obtain the optical constants.

The above procedure of obtaining optical constants as a function of incident energy of light has been used for pristine MTF. Thereafter, the following MG approximation is employed to obtain the dielectric constants of each type of irradiated MTF using the pristine dielectric data obtained from the KK technique. The effect of ion beam irradiation on optical parameters of irradiated MTF can be understood using the concept of the effective dielectric constant of mixed media given by [5, 32],

${\widetilde{ϵ}}_{eff}^{MG}={\widetilde{ϵ}}_m+3f{\widetilde{ϵ}}_m\frac{({ϵ}_{Ar}-{\widetilde{ϵ}}_m)}{{ϵ}_{Ar}+2{\widetilde{ϵ}}_m-f({ϵ}_{Ar}-{\widetilde{ϵ}}_m)},(8)$

where, ${\widetilde{ϵ}}_{eff}^{MG}$ = complex effective dielectric constant of the mixed medium using MG approximation, ${\widetilde{ϵ}}_m$ = complex dielectric constant of the host (pristine) metallic medium, ϵ_Ar = dielectric constant of the inclusive Argon atoms, and f = nV fractional volume of Argon ions, n = number density of Argon ions, V = volume of each Argon ion. The effective complex refractive index of the atomically heterogeneous system can be calculated as follows

${\tilde{r}}_{eff}^{MG}=\sqrt{{\widetilde{ϵ}}_{eff}^{MG}}=n+ik,(9)$

where both ${\tilde{r}}_{eff}^{MG}$ and ${\widetilde{ϵ}}_{eff}^{MG}$ are complex.

4 Results and Discussion

4.1 Dielectric Constants

The dielectric constants for Al, Cu, and Ag MTF have been investigated and presented in Figure 2. Figures 2A–C describe the real part of dielectric constants for aluminum, copper, and silver, respectively, while the imaginary part is shown in Figures 2D–F. The Ar ions modify the polarizability of the medium by changing the response of the electric field. The effective dielectric constants of the heterogeneous medium in the approximation models (Maxwell-Garnett and Bruggeman approximation [30, 31]) is decided by the individual dielectric constant of the host medium and inclusion along with the fractional volume (f = nV, n: number density of Ar ions and V: volume of each Ar ion) of the inclusion. As the fluence of Ar ions increases, the fractional volume of Ar ions also increases, which increases the real part of the dielectric function and decreases both real and imaginary parts of the refractive index. The position of interband transitions can be figured out from the real as well as imaginary parts of the dielectric constants. The real part shows the peak, while imaginary part shows a dip in its profile wherever the interband transitions occur. The position of interband transition is observed in aluminum at ∼1.5 eV [54] and it can be seen for copper, and silver at ∼2.25 eV [55] and ∼3.8 eV [53], respectively. The real part of the dielectric constants of each MTF shows an increase with energy of the incident light and it also increases with increase in ion beam fluence as shown in Figures 2A–C. The increase in real part of the dielectric constants with increase in impurity concentration has also been reported earlier for different mixtures of mediums in theoretical models [56]. It is observed that the imaginary part decreases with increase in the fluence of ions for each MTF. However, the change in the imaginary part of the dielectric constants with fluence is very small for silver MTF, while for copper it is quite large as compared to silver. It can also be concluded from the results of dielectric constants that the position of interband transition does not shift with change in ion beam fluence.

FIGURE 2

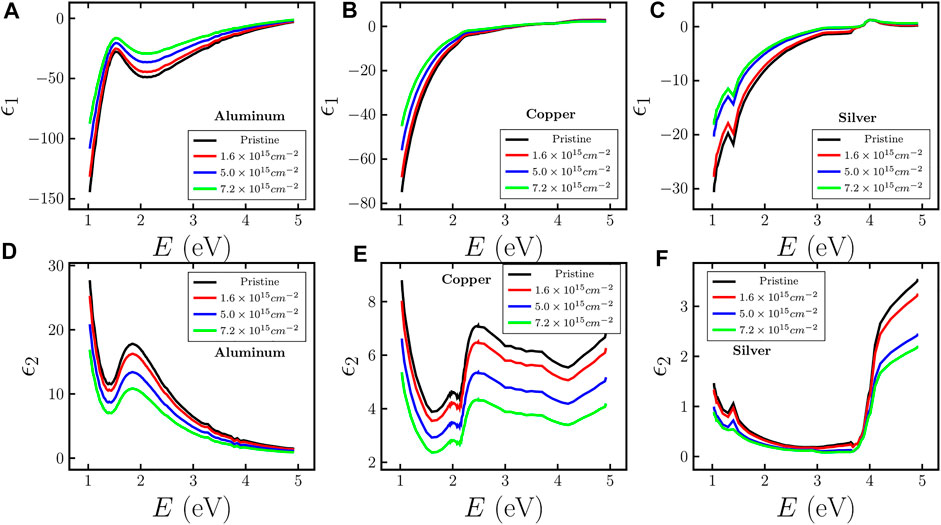
FIGURE 2. Variation of real and imaginary parts of dielectric constants for aluminum [(A,D)], copper [(B,E)], and silver [(C,F)], respectively, with energy of incident light as well as varying fluence of Argon ions. Black solid line represents the data obtained from KK technique and colored (red, blue, and green) solid lines represent the data obtained from MG approximation.

4.2 Optical Constants

Figure 3 shows the optical constants of pristine MTF (Ag, Cu, and Al) obtained from the KK technique and compared with standard data from JC [6] and Palik [26], and the results are found to be in good agreement. Figures 4A–C show the variation of the real part of the refractive index n of pristine and irradiated MTF with varying ion fluence and energy of incident light, while Figures 4D–F describe the variation of the imaginary part k. n of pristine aluminum shows a dip around ∼1.5 eV and a peak around ∼1.9 eV and it decreases with energy after 1.9 eV as shown in Figure 4A. The variation of n with ion beam fluence has also been shown in the same figure, and found that n decreases as the fluence increases without any change in the position of dip and peak. The energy corresponding to dip i.e., 1.5 eV matches with the position of interband transition in aluminum [54]. k also shows a dip corresponding to interband transition at 1.5 eV and it also decreases with fluence as shown in Figure 4D. In case of Cu (Figures 4B,E), n increases with energy and shows a sharp transition at around ∼2.25 eV, which is an interband transition [55] for pristine Cu MTF (see Figure 4B). It is noted that with increase in ion beam fluence both n and k are seen to decrease and the decrease in n is more significant in the higher energy side. Similarly, Figures 4C,F show the change in n and k of Ag with energy as well as fluence of ion beams. n of pristine MTF almost does not change with energy up to ∼3.8 eV and thereafter sharply increases. It can also be seen that there is no significant variation in n with ion fluence up to 3.8 eV. The sharp transition represents the interband transition for silver [53], while k for pristine as well as irradiated MTF decreases with energy and shows a dip at the position of interband transition. k also decreases with increase in ion fluence. In Figure 4F, behaviour of k changes near ∼3.8 eV (interband transition) for 5.0 × 10¹⁵ cm⁻² and 7.2 × 10¹⁵ cm⁻² fluence values. As fluence of Ar ions increase, more number of Ar ions accumulate within few nanometers depth of surface layers of Ag and it increases the density of Ar ions inside the silver surface layers and that in turn enhances the fractional volume. For the same value of fluence, the fractional volume will be higher for silver as compared to Al, because of lower penetration depth and in turn higher concentration of Ar ions. It can be seen from the Maxwell-Garnett approximation [31] that as the fractional volume increases the behaviour of effective dielectric constants (or refractive index) changes and it becomes highly non-linear from linear as fractional volume tends to unity.

FIGURE 3

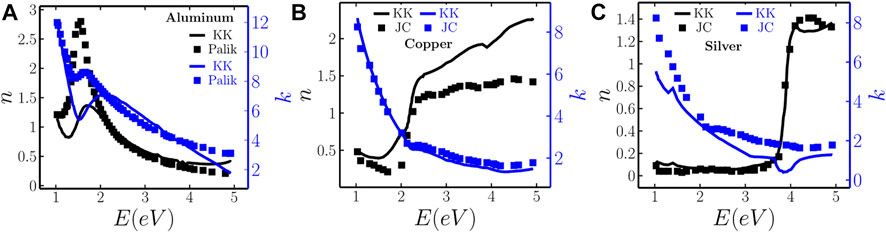
FIGURE 3. Comparison of optical constants of pristine (A) aluminum, (B) copper, and (C) silver MTF with results of Johnson and Christy (JC) [6], and Palik [26]. Black and blue solid lines represent the real and imaginary parts of the refractive index obtained from KK analysis and the respective solid squares represent the data of Palik for Al and JC for copper and silver.

FIGURE 4

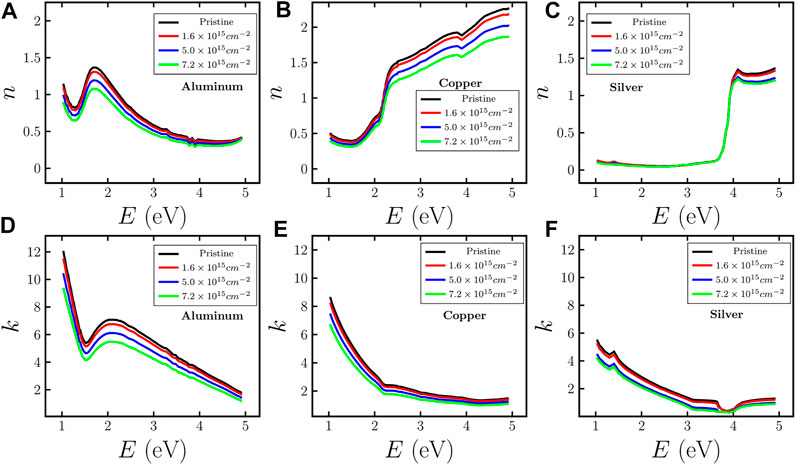
FIGURE 4. Variation of real and imaginary parts of the refractive index for aluminum [(A,D)], copper [(B,E)], and silver [(C,F)], respectively, with energy of incident light as well as varying fluence of Argon ions. Black solid line represents the data obtained from KK technique and colored (red, blue, and green) solid lines represent the data obtained from MG approximation.

In order to further verify the results obtained through the MG approximation, the optical constants of Ag, Al, and Cu have also been experimentally evaluated by employing the pseudo- Brewster angle technique at wavelengths of 405, 532, 632.8 and 670 nm. The data for 632.8 nm is taken from our earlier article [5]. The obtained results are presented in tabular form for copper (Table 1), aluminum (Table 2), and silver (Table 3). The optical constants of pristine as well as irradiated MTF, obtained from pseudo- Brewster angle technique and combined KK and MG approximation are found to be close to each other. It is found that the results obtained by employing combined KK and MG techniques are in reasonably good agreement with the results from the pseudo- Brewster angle technique. As discussed in paragraph below, the possible reason behind the small differences in experimental and earlier reported data (JC and Palik) of optical constants could be due to difference in surface morphology, film preparation technique, and deposition rate.

TABLE 1

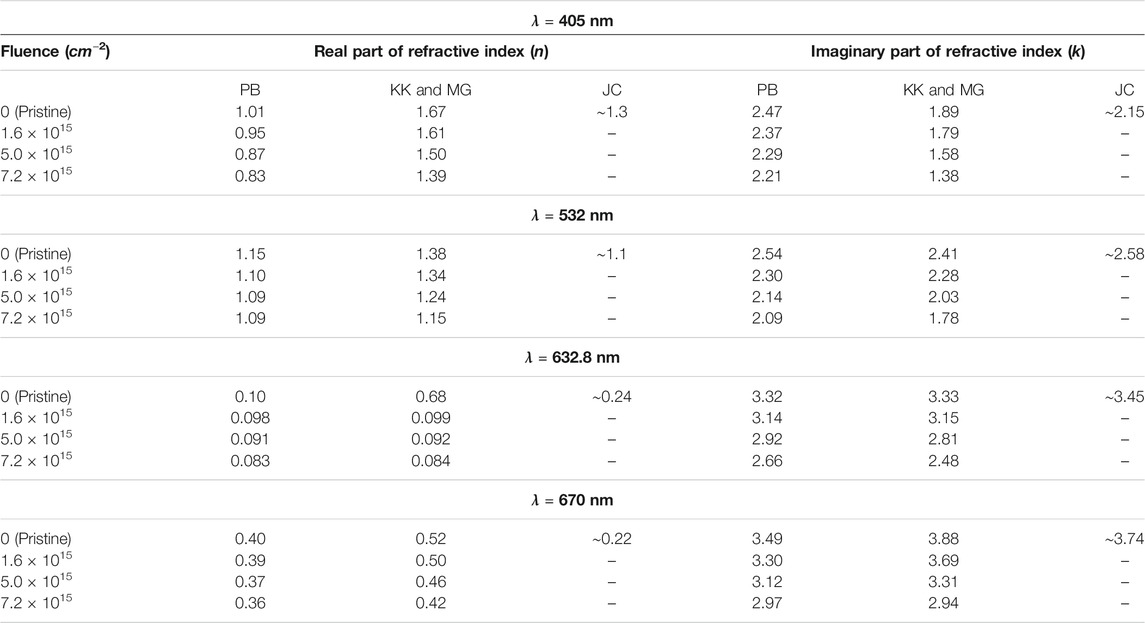
TABLE 1. Optical constants of copper MTF where PB: pseudo- Brewster angle technique, KK: Kramers-Kronig technique, MG: Maxwell-Garnett technique, JC: Johnson and Christy [6] data.

TABLE 2

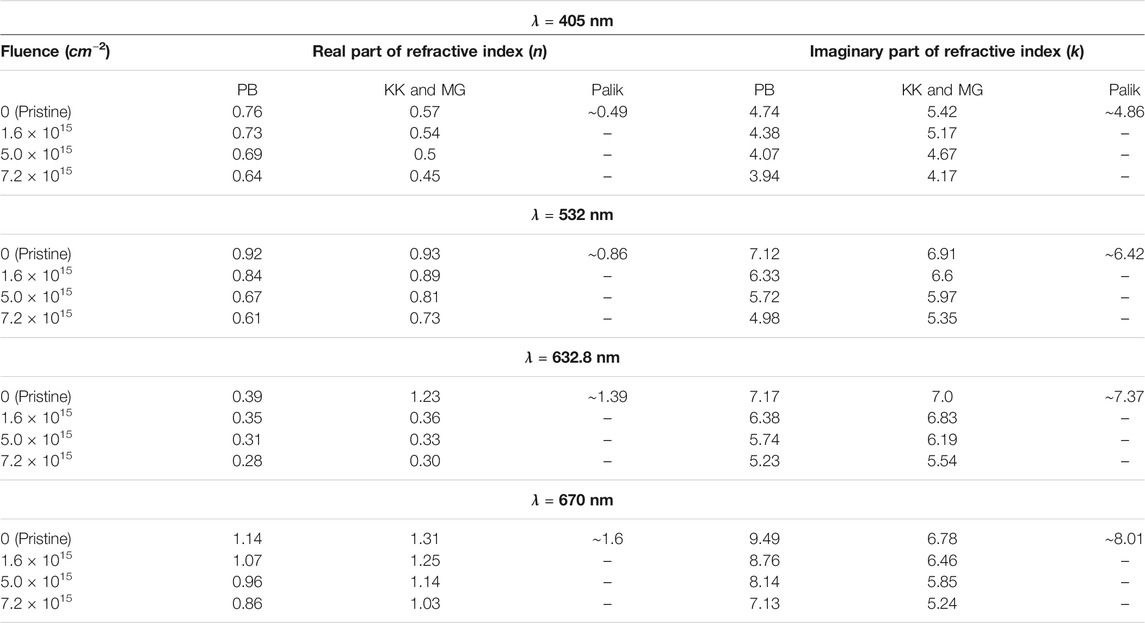
TABLE 2. Optical constants of aluminum MTF where PB: pseudo- Brewster angle technique, KK: Kramers-Kronig technique, MG: Maxwell-Garnett technique, Palik [26] data.

TABLE 3

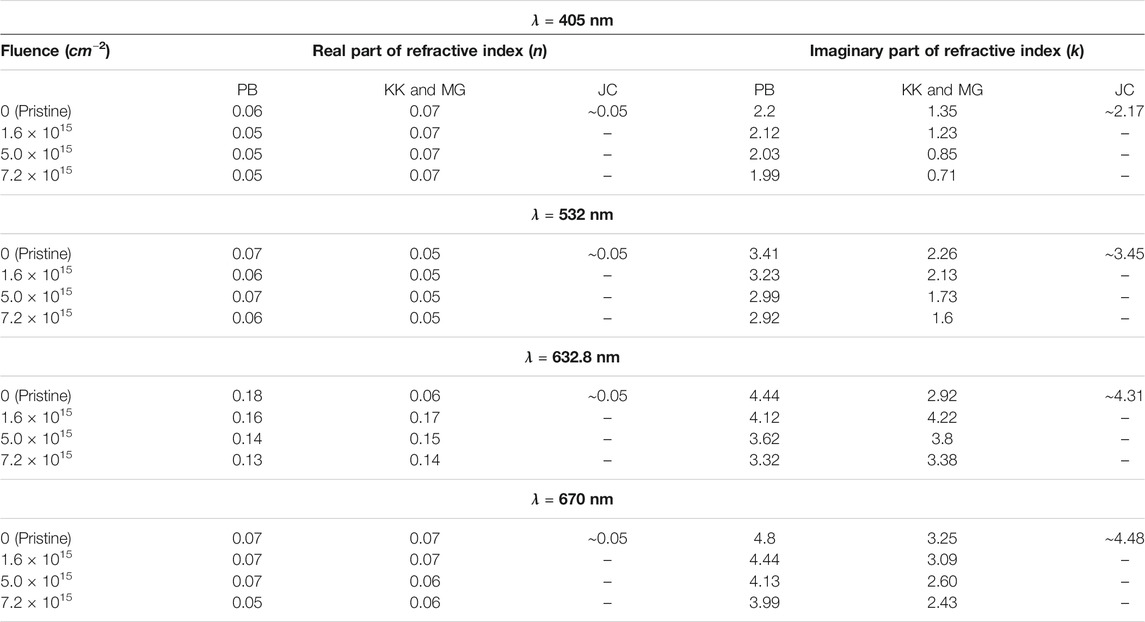
TABLE 3. Optical constants of silver MTF where PB: pseudo- Brewster angle technique, KK: Kramers-Kronig technique, MG: Maxwell-Garnett technique, JC: Johnson and Christy [6] data.

In Tables 1–3, the optical constants of metallic thin films are compared with the bulk optical data. However, thin film optical constants data deviates from the bulk because the continuous energy bands of the bulk materials are expected to be replaced by discrete energy levels along the direction of spatial confinement, leading to energy sub-band structure for thin films and discrete energy levels for nanoparticles [57]. Additionally, the optical constants of thin films also depend upon the measurement methods, deposition techniques (thermal evaporation technique, sputtering techniques etc.) used to prepare the thin films, and deposition rate during time of deposition because the electron density (or atomic density) in the metallic thin films vary depending upon the deposition technique [58]. The difference in optical constants obtained from various measurement methods has already been reported, and the imaginary part of dielectric constant is compared to JC and it is found that the difference between Babar et al. [24] and JC data is more than 2 in the energy range ∼1–1.5 eV, in case of copper and gold [24]. The reflectivity of metallic thin films differs slightly from the bulk reflectivity and this change reflects in the results of the optical constants obtained from KK analysis because the reflectivity has been used as input parameter in the KK analysis. Hence, there is a slight mismatch between the results of KK analysis and those obtained from Brewster- angle technique. The optical constants of each pristine MTF obtained from pseudo- Brewster angle technique are close to the JC data for Ag and Cu [6], and Palik for Al [26].

4.3 Skin Depth

Skin depth δ is the key parameter to determine how far an electromagnetic wave penetrates into the medium. While this information can easily be evaluated for pristine metallic samples, δ for atomically heterogeneous mediums is not known due to the lack of information of k. It is observed from the experimental results on optical constants that k decreases with ion fluence, which in turn increases δ. This increase in δ enhances the transmission probability of electromagnetic waves through the MTF, as observed in our previous work [5]. A sharp peak is observed in δ at the interband position in case of each MTF because of a sharp transition of the imaginary part of the refractive index. The variation of δ with energy of incoming light and fluence of low energy ion beams for each MTF (Al, Cu, and Ag) is shown in Figures 5A–C, respectively. It is observed that δ shows an increase with fluence of Argon ions. δ is found to be largest in silver and smallest for aluminum, which confirms the fact that silver has more transmissivity compared to aluminum as discussed in Ref. [5]. δ can provide important information regarding the selection of film thickness depending upon the desired application.

FIGURE 5

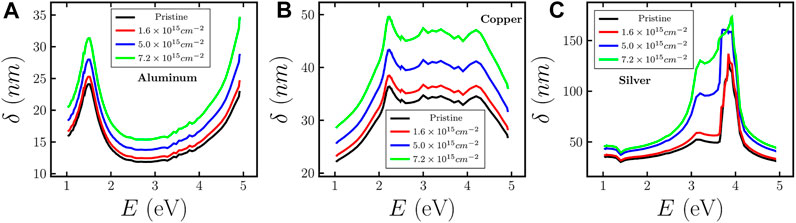
FIGURE 5. Variation of skin depth for (A) aluminum, (B) copper, and (C) silver, respectively, with energy of incident light as well as varying fluence of Argon ions.

4.4 Optical Conductivity

Optical conductivity σ of any metallic media can be calculated using optical constants (n and k) and wavelength (λ) of incident light. σ of aluminum, copper, and silver MTF are shown in Figures 6A–C, respectively. The σ of pristine aluminum shows a dip at the position of interband transition and increases thereafter up to ∼2 eV and then decreases almost linearly with the energy of incident light as shown in Figure 6A. The irradiation of low energy ion beams reduces aluminum’s optical conductivity. The position of the dip in σ does not shift with varying fluence of ion beams, while the σ of pristine copper (Figure 6B) shows an overall increment with the energy of incident light, which is unlike the behavior shown by aluminum. The sudden increase in σ is because of the interband transition around 2.25 eV. It is also noted that the position of interband transition remains unchanged after the irradiation. Finally, the pristine silver MTF does not show significant variation in σ up to 3.8 eV, and thereafter it shows a sudden enhancement in the value of σ (Figure 6C). The irradiation does not seem to have much effect on σ up to the critical energy value. The position of the dip in case of aluminum, critical energy values in case of copper and silver remains unchanged after irradiation by low energy ion beams.

FIGURE 6

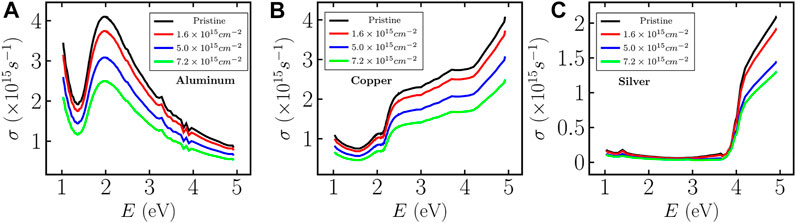
FIGURE 6. Variation of optical conductivity for (A) aluminum, (B) copper, and (C) silver, respectively, with energy of incident light as well as varying fluence of Argon ions.

5 Summary and Conclusion

The optical parameters such as refractive index, dielectric constants, skin depth, and optical conductivity of copper, silver, and aluminum MTF upon irradiation of low energy Argon ion beams have been examined over a wide range covering UV to NIR (250–1,200 nm) region of the electromagnetic spectrum. The universal KK technique and MG approximation have been employed to explore the aforementioned optical parameters of pristine as well as irradiated MTF for varying ion fluences. Additionally, the pseudo- Brewster angle technique has been employed to obtain the optical constants of pristine as well as irradiated MTF at four different wavelengths (405, 532, 632.8 and 670 nm), which further corroborates the results obtained using the MG approximation. It is observed from the obtained results that these optical parameters not only depends upon the material but also on the fluence of implanted impurities. The optical constants as well as the optical conductivity of each MTF decrease with increase in the ion fluence. Thus, low energy ion beams can provide a way of controlling the optical properties of the materials. The skin depth of electromagnetic radiation inside the materials has been found to increase with ion beam fluence, which clearly depicts the enhancement in the transmission of incoming radiation through the material. The real part of the dielectric constants increases, while the imaginary part decreases with increase in ion beam fluence. The irradiation technique presented here is found to the have the influence on various type of optical parameters. The present study may be helpful in selection of materials along with the desired fluence, for a wide variety of applications ranging from sensors, photonic devices and metallic thin film mirrors used for space applications.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

KPS and SB contributed to conception of the study and planning of the experiment. KPS performed the experiments and carried out the analysis of experimental data, which is guided by SB. KPS wrote the manuscript with valuable feedback at all stages from SB. Both the authors have made a substantial, direct and intellectual contribution to the work and contributed to manuscript revision, reading, and approved the submitted version.

Funding

This work was supported by Indian Space Research Organisation (ISRO) (STC/PHY/2019433) and partly from Department of Science and Technology (DST-SERB), Government of India under grant No. EMR/2016/006235. KPS gratefully acknowledges Council of Scientific and Industrial Research (CSIR), India for award of a Senior Research Fellowship under grant No. 09/092 (0954)/2016-EMR-I.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We gratefully acknowledge Prof. A. K. Jha (incharge Optics Laboratory), for providing equipment support from Optics Laboratory, IIT Kanpur to conduct some experiments. We also thank Prof. R. Vijaya, for providing Profilometer and UV-VIS-NIR spectrophotometer facilities for thickness and reflectivity measurements. KPS thanks Prof. M. K. Harbola and Prof. S. M. Tripathi for valuable suggestions, and to Sushanta Barman for helping in the Python programming to evaluate the optical constants using KK technique.

References

1. Jain IP, Agarwal G. Ion Beam Induced Surface and Interface Engineering. Surf Sci Rep (2011) 66:77–172. doi:10.1016/j.surfrep.2010.11.001

CrossRef Full Text | Google Scholar

2. Chatterjee S, Bhattacharjee S, Maurya SK, Srinivasan V, Khare K, Khandekar S. Surface Wettability of an Atomically Heterogeneous System and the Resulting Intermolecular Forces. Epl (2017) 118:68006. doi:10.1209/0295-5075/118/68006

CrossRef Full Text | Google Scholar

3. Chatterjee S, Pal Singh K, Bhattacharjee S. Wetting Hysteresis of Atomically Heterogeneous Systems Created by Low Energy Inert Gas Ion Irradiation on Metal Surfaces: Liquid Thin Film Coverage in the Receding Mode and Surface Interaction Energies. Appl Surf Sci (2019) 470:773–82. doi:10.1016/j.apsusc.2018.11.143

CrossRef Full Text | Google Scholar

4. Chowdhury A, Bhattacharjee S. Experimental Investigation of Change in Sheet Resistance and Debye Temperatures in Metallic Thin Films Due to Low-Energy Ion Beam Irradiation. J Phys D Appl Phys (2013) 46:435304. doi:10.1088/0022-3727/46/43/435304

CrossRef Full Text | Google Scholar

5. Pal Singh K, Majumdar J, Bhattacharjee S. Tuning Optical Properties of Atomically Heterogeneous Systems Created by Plasma-Based Low-Energy Ion Beams. Appl Opt (2020) 59:4507–16. doi:10.1364/AO.390751

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Johnson PB, Christy RW. Optical Constants of the noble Metals. Phys Rev B (1972) 6:4370–9. doi:10.1103/PhysRevB.6.4370

CrossRef Full Text | Google Scholar

7. Yang HU, D'Archangel J, Sundheimer ML, Tucker E, Boreman GD, Raschke MB. Optical Dielectric Function of Silver. Phys Rev B (2015) 91:235137. doi:10.1103/PhysRevB.91.235137

CrossRef Full Text | Google Scholar

8. Rioux D, Vallières S, Besner S, Muñoz P, Mazur E, Meunier M. An Analytic Model for the Dielectric Function of Au, Ag, and Their Alloys. Adv Opt Mater (2014) 2:176–82. doi:10.1002/adom.201300457

CrossRef Full Text | Google Scholar

9. Etchegoin PG, Le Ru EC, Meyer M. An Analytic Model for the Optical Properties of Gold. J Chem Phys (2006) 125:164705. doi:10.1063/1.2360270

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Olmon RL, Slovick B, Johnson TW, Shelton D, Oh S-H, Boreman GD, et al. Optical Dielectric Function of Gold. Phys Rev B (2012) 86:235147. doi:10.1103/physrevb.86.235147

CrossRef Full Text | Google Scholar

11. Barnes WL, Dereux A, Ebbesen TW. Surface Plasmon Subwavelength Optics. Nature (2003) 424:824–30. doi:10.1038/nature01937

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Homola J, Yee SS, Gauglitz G. Surface Plasmon Resonance Sensors: Review. Sensors Actuators B: Chem (1999) 54:3–15. doi:10.1016/S0925-4005(98)00321-9

CrossRef Full Text | Google Scholar

13. Zhang J, Zhang L, Xu W. Surface Plasmon Polaritons: Physics and Applications. J Phys D Appl Phys (2012) 45:113001. doi:10.1088/0022-3727/45/11/113001

CrossRef Full Text | Google Scholar

14. Degiron A, Ebbesen TW. The Role of Localized Surface Plasmon Modes in the Enhanced Transmission of Periodic Subwavelength Apertures. J Opt A: Pure Appl Opt (2005) 7:S90–S96. doi:10.1088/1464-4258/7/2/012

CrossRef Full Text | Google Scholar

15. Bekhti W, Ghamnia M. Optical Properties of SiO₂ Determined by Reflection Electron Energy Loss Spectroscopy. Catal Today (2004) 89:303–6. doi:10.1016/j.cattod.2003.12.005

CrossRef Full Text | Google Scholar

16. Martin Dressel GG. Electrodynamics of Solids: Optical Properties of Electrons in Matter. 1st ed. Cambridge University Press (2002).

17. Kuzmany H. Solid-State Spectroscopy: An Introduction. 2 edn. Springer-Verlag Berlin Heidelberg (2009).

18. Bazkir Ö. Determination of Optical Constants of Silicon Photodiode from Reflectivity Measurements at normal Incidence of Light. Opt Lasers Eng (2007) 45:245–8. doi:10.1016/j.optlaseng.2006.06.003

CrossRef Full Text | Google Scholar

19. Palmer KF, Williams MZ. Determination of the Optical Constants of a Thin Film from Transmittance Measurements of a Single Film Thickness. Appl Opt (1985) 24:1788–98. doi:10.1364/AO.24.001788

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Sharma P, Katyal SC. Determination of Optical Parameters of a-(As₂Se₃)₉₀Ge₁₀ thin Film. J Phys D Appl Phys (2007) 40:2115–20. doi:10.1088/0022-3727/40/7/038

CrossRef Full Text | Google Scholar

21. Denton RE, Campbell RD, Tomlin SG. The Determination of the Optical Constants of Thin Films from Measurements of Reflectance and Transmittance at normal Incidence. J Phys D: Appl Phys (1972) 5:852–63. doi:10.1088/0022-3727/5/4/329

CrossRef Full Text | Google Scholar

22. Kutavichus VP, Filippov VV, Huzouski VH. Determination of Optical Parameters and Thickness of Weakly Absorbing Thin Films from Reflectance and Transmittance Spectra. Appl Opt (2006) 45:4547–53. doi:10.1364/AO.45.004547

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Nitsche R, Fritz T. Determination of Model-free Kramers-Kronig Consistent Optical Constants of Thin Absorbing Films from Just One Spectral Measurement: Application to Organic Semiconductors. Phys Rev B (2004) 70:195432. doi:10.1103/physrevb.70.195432

CrossRef Full Text | Google Scholar

24. Babar S, Weaver JH. Optical Constants of Cu, Ag, and Au Revisited. Appl Opt (2015) 54:477–81. doi:10.1364/AO.54.000477

CrossRef Full Text | Google Scholar

25. Ordal MA, Bell RJ, Alexander RW, Long LL, Querry MR. Optical Properties of Fourteen Metals in the Infrared and Far Infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl Opt (1985) 24:4493–9. doi:10.1364/AO.24.004493

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Palik E. Handbook of Optical Constants of Solids. Academic Press (1998). p. 1–4.

27. Kuzmenko AB. Kramers-Kronig Constrained Variational Analysis of Optical Spectra. Rev Scientific Instr (2005) 76:083108. doi:10.1063/1.1979470

CrossRef Full Text | Google Scholar

28. Grosse P, Offermann V. Analysis of Reflectance Data Using the Kramers-Kronig Relations. Appl Phys A (1991) 52:138–44. doi:10.1007/BF00323731

CrossRef Full Text | Google Scholar

29. Yamamoto K, Masui A. Complex Refractive index Determination of Bulk Materials from Infrared Reflection Spectra. Appl Spectrosc (1995) 49:639–44. doi:10.1366/0003702953964048

CrossRef Full Text | Google Scholar

30. Niklasson GA, Granqvist CG, Hunderi O. Effective Medium Models for the Optical Properties of Inhomogeneous Materials. Appl Opt (1981) 20:26–30. doi:10.1364/AO.20.000026

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Sihvola A. Mixing Rules with Complex Dielectric Coefficients. Subsurface sensing Tech Appl (2000) 1:393–415. doi:10.1023/A:1026511515005

CrossRef Full Text | Google Scholar

32. Koledintseva MY, DuBroff RE, Schwartz RW. A Maxwell Garnett Model for Dielectric Mixtures Containing Conducting Particles at Optical Frequencies. Pier (2006) 63:223–42. doi:10.2528/PIER06052601

CrossRef Full Text | Google Scholar

33. Videen G, Chýlek P. Scattering by a Composite Sphere with an Absorbing Inclusion and Effective Medium Approximations. Opt Commun (1998) 158:1–6. doi:10.1016/S0030-4018(98)00557-4

CrossRef Full Text | Google Scholar

34. Antonaia A, Addonizio ML, Esposito S, Ferrara M, Castaldo A, Guglielmo A, et al. Adhesion and Structural Stability Enhancement for Ag Layers Deposited on Steel in Selective Solar Coatings Technology. Surf Coat Tech (2014) 255:96–101. doi:10.1016/j.surfcoat.2014.02.045

CrossRef Full Text | Google Scholar

35. Frey L, Parrein P, Virot L, Pellé C, Raby J. Thin Film Characterization for Modeling and Optimization of Silver-Dielectric Color Filters. Appl Opt (2014) 53:1663–73. doi:10.1364/AO.53.001663

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Ge J, Li Y, Wang J, Pu Y, Xue W, Liu X. Green Synthesis of Graphene Quantum Dots and Silver Nanoparticles Compounds with Excellent Surface Enhanced Raman Scattering Performance. J Alloys Comp (2016) 663:166–71. doi:10.1016/j.jallcom.2015.12.055

CrossRef Full Text | Google Scholar

37. Watanabe M, Kajikawa K. An Optical Fiber Biosensor Based on Anomalous Reflection of Gold. Sensors Actuators B: Chem (2003) 89:126–30. doi:10.1016/S0925-4005(02)00453-7

CrossRef Full Text | Google Scholar

38. Bhattacharjee S, Amemiya H. Production of Microwave Plasma in Narrow Cross Sectional Tubes: Effect of the Shape of Cross Section. Rev scientific Instr (1999) 70:3332–7. doi:10.1063/1.1149914

CrossRef Full Text | Google Scholar

39. Bhattacharjee S, Amemiya H. Microwave Plasma in a Multicusp Circular Waveguide with a Dimension below Cutoff. Jpn J Appl Phys (1998) 37:5742–5. doi:10.1143/jjap.37.5742

CrossRef Full Text | Google Scholar

40. Chowdhury A, Chatterjee S, Dutta A, Bhattacharjee S. Stopping Potential and Ion Beamlet Control for Micro-resistive Patterning through Sub-debye Length Plasma Apertures. AIP Adv (2014) 4:127127. doi:10.1063/1.4904371

CrossRef Full Text | Google Scholar

41. Al-Bayati A, Marton D, Todorov S, Boyd K, Rabalais J, Armour D, et al. Performance of Mass Analyzed, Low-Energy, Dual Ion Beam System for Materials Research. Rev scientific Instr (1994) 65:2680–92. doi:10.1063/1.1144670

CrossRef Full Text | Google Scholar

42. Takahashi K, Kaneko T, Hatakeyama R. Simultaneous Control of Ion Flow Energy and Electron Temperature in Magnetized Plasmas. Appl Phys Lett (2006) 88:111503. doi:10.1063/1.2181653

CrossRef Full Text | Google Scholar

43. Mattox DM. Handbook of Physical Vapor Deposition (PVD) Processing. Burlington, United States: William Andrew (2010).

44. Bruining H. Physics and Applications of Secondary Electron Emission: Pergamon Science Series: Electronics and Waves—A Series of Monographs. Elsevier (2016).

45. Marcak A, Corbella C, de los Arcos T, von Keudell A. Note: Ion-Induced Secondary Electron Emission from Oxidized Metal Surfaces Measured in a Particle Beam Reactor. Rev Scientific Instr (2015) 86:106102. doi:10.1063/1.4932309

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Bradley RM, Harper JME. Theory of Ripple Topography Induced by Ion Bombardment. J Vacuum Sci Tech A: Vacuum, Surf Films (1988) 6:2390–5. doi:10.1116/1.575561

CrossRef Full Text | Google Scholar

47. Kumar T, Kumar A, Agarwal DC, Lalla NP, Kanjilal D. Ion Beam-Generated Surface Ripples: New Insight in the Underlying Mechanism. Nanoscale Res Lett (2013) 8:1–5. doi:10.1186/1556-276X-8-336

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Bhowmik D, Mukherjee J. Study of Low Energy Ion Beam Induced Sputtering Parameters of Muscovite Mica [KAl2(Si3Al)O10(OH)2] Using Monte Carlo Simulation. Mater Today Proc (2021) doi:10.1016/j.matpr.2021.03.161

CrossRef Full Text | Google Scholar

49. Chiappe D, Toma A, de Mongeot FB. Transparent Plasmonic Nanowire Electrodes via Self-Organised Ion Beam Nanopatterning. small (2013) 9:913–9. doi:10.1002/smll.201201146

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Kumar M, Jangid T, Panchal V, Kumar P, Pathak A. Effect of Grazing Angle Cross-Ion Irradiation on Ag Thin Films. Nanoscale Res Lett (2016) 11:1–9. doi:10.1186/s11671-016-1665-5

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Takahashi K, Saito T, Ando A, Yabuta Y, Mizuguchi H, Yamamoto N, et al. Minimal Multi-Target Plasma Sputtering Tool. Vacuum (2020) 171:109000. doi:10.1016/j.vacuum.2019.109000

CrossRef Full Text | Google Scholar

52. Shiles E, Sasaki T, Inokuti M, Smith DY. Self-consistency and Sum-Rule Tests in the Kramers-Kronig Analysis of Optical Data: Applications to Aluminum. Phys Rev B (1980) 22:1612–28. doi:10.1103/PhysRevB.22.1612

CrossRef Full Text | Google Scholar

53. Ehrenreich H, Philipp HR. Optical Properties of Ag and Cu. Phys Rev (1962) 128:1622–9. doi:10.1103/PhysRev.128.1622

CrossRef Full Text | Google Scholar

54. Rakić AD. Algorithm for the Determination of Intrinsic Optical Constants of Metal Films: Application to Aluminum. Appl Opt (1995) 34:4755–67. doi:10.1364/AO.34.004755

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Segall B. Fermi Surface and Energy Bands of Copper. Phys Rev (1962) 125:109–22. doi:10.1103/PhysRev.125.109

CrossRef Full Text | Google Scholar

56. Aspnes DE, Kinsbron E, Bacon DD. Optical Properties of Au: Sample Effects. Phys Rev B (1980) 21:3290–9. doi:10.1103/PhysRevB.21.3290

CrossRef Full Text | Google Scholar

57. Mishra KC, Piquette A, Schmidt PC, Johnson KH. Electronic Structures and Optical Properties of Al, Cu, and Ag in Zero, Two, and Three Dimensional Structures. J Appl Phys (2017) 122:063104. doi:10.1063/1.4998164

CrossRef Full Text | Google Scholar

58. Axelevitch A, Gorenstein B, Golan G. Investigation of Optical Transmission in Thin Metal Films. Phys Proced (2012) 32:1–13. doi:10.1016/j.phpro.2012.03.510

CrossRef Full Text | Google Scholar