Classical Limit of Quantum Mechanics for Damped Driven Oscillatory Systems: Quantum–Classical Correspondence

The investigation of quantum–classical correspondence may lead to gaining a deeper understanding of the classical limit of quantum theory. I have developed a quantum formalism on the basis of a linear invariant theorem, which gives an exact quantum–classical correspondence for damped oscillatory systems perturbed by an arbitrary force. Within my formalism, the quantum trajectory and expectation values of quantum observables precisely coincide with their classical counterparts in the case where the global quantum constant $\hslash$ has been removed from their quantum results. In particular, I have illustrated the correspondence of the quantum energy with the classical one in detail.

1 Introduction

A fundamental issue in physics is to elucidate how classical mechanics (or Newtonian mechanics) emerges from a more general theory of physics, the so-called relativistic quantum mechanics. While the appearing of classical mechanics as a low velocity limit of relativistic mechanics is well known, the classical limit of quantum mechanics is a subtle problem yet. Planck’s $\hslash \to 0$ limit [1] and Bohr’s $n\to \infty$ limit [2] are the oldest proposals for the formulation of the classical limit of quantum theory. However, there has been controversy from the early epoch of quantum mechanics concerning this limit through different ideas and thoughts [3–9]. Accordingly, the mechanism on how to interlace the exact correspondence between the quantum and the classical theories has not yet been fully understood. Man’ko and Man’ko argued that the picture of extracting classical mechanics with the simple limitation $\hslash \to 0$ does not have universal applicability [4]. Some physicists believe that quantum mechanics is not concerned with a single particle problem but an ensemble of particles, and its $\hslash \to 0$ limit is not classical mechanics but classical statistical mechanics instead (see Ref. [5] and references therein). For more different opinions concerning the classical limit of quantum mechanics, refer in particular to Refs. [7, 8].

The purpose of this research is to establish a theoretical formalism concerning the classical limit of quantum mechanics for damped driven oscillatory systems, which reveals the quantum and classical correspondence, without any approximation or assumption except for the fundamental limitation $\hslash \to 0$. To deduce Newtonian mechanics from quantum one along this line, canonical quantum mechanics with fundamental Hamiltonian dynamics will be used. My theory is based on an invariant operator method [10–13] which is generally employed for mathematically treating quantum mechanical systems. This method enables us to derive exact quantum mechanical solutions for time-varying Hamiltonian systems. I will interpret and discuss the physical meanings of the consequences in order to derive insight into the correspondence principle.

2 Invariant-Based Dynamics and Quantum Solutions

To investigate quantum–classical correspondence, I consider a damped driven harmonic oscillator of mass m and frequency ${\omega }_0$, whose Hamiltonian is given by [13–16]

$\widehat{H}=e^{-\gamma t}\frac{{\widehat{p}}^2}{2m}+\frac{1}{2}{e}^{\gamma t}m\left[{\omega }_0^2{\widehat{q}}^2-2f\left(t\right)\widehat{q}\right],(1)$

where γ is a damping constant and $f\left(t\right)$ is a time-dependent driving force divided by m. From canonical Hamiltonian dynamics, one can confirm that this Hamiltonian gives an exact equation of motion for the damped driven harmonic oscillator. In the case of $f\left(t\right)=0$, this becomes the conventional Caldirola–Kanai (CK) Hamiltonian [17, 18] which has been widely used in a phenomenological approach for the dissipation of the damped harmonic oscillator.

If I denote the classical solution of the system in configuration space as $Q\left(t\right)$, it can be written in the form $Q\left(t\right)=Q_{\text{h}}\left(t\right)+Q_{\text{p}}\left(t\right)$ where $Q_{\text{h}}\left(t\right)$ is a homogeneous solution and $Q_{\text{p}}\left(t\right)$ a particular solution. From the basic algebra in classical dynamics, we have [19]

$Q_{\text{h}}\left(t\right)=Q_0{e}^{-\gamma t/2}\text{cos}\left(\omega t+\phi \right),(2)$

$Q_{\text{p}}\left(t\right)={\displaystyle {\int }_0^t\left[f\left(t\mathit{\prime }\right)/\omega \right]}{e}^{-\gamma \left(t-t\mathit{\prime }\right)/2}\text{sin}\left[\omega \left(t-t\mathit{\prime }\right)\right]dt\mathit{\prime },(3)$

where $Q_0$ is the amplitude of the mechanical oscillation at $t=0$, ω is a modified frequency which is $\omega ={\left({\omega }_0^2-{\gamma }^2/4\right)}^{1/2}$, and φ is an arbitrary phase. The canonical classical solution in the momentum space can also be represented in a similar form: $P\left(t\right)=P_{\text{h}}\left(t\right)+P_{\text{p}}\left(t\right)$, where $P_{\text{h}}\left(t\right)=m{\dot{Q}}_{\text{h}}\left(t\right)e^{\gamma t}$ and $P_{\text{p}}\left(t\right)=m{\dot{Q}}_{\text{p}}\left(t\right)e^{\gamma t}$.

In order to describe quantum solutions of the system, it is useful to introduce an invariant operator which is a powerful tool in elucidating mechanical properties of dynamical systems that are expressed by a time-dependent Hamiltonian like Eq. 1. A linear invariant operator of the system can be derived by means of the Liouville–von Neumann equation and it is given by (see Appendix A)

$\widehat{I}=c[e^{-\gamma t/2}{\widehat{p}}_{\text{p}}+m\left(\frac{\gamma }{2}-i\omega \right)e^{-\gamma t/2}{\widehat{q}}_{\text{p}}]e^{i\omega t},(4)$

where ${\widehat{p}}_{\text{p}}=\widehat{p}-P_{\text{p}}\left(t\right)$, ${\widehat{q}}_{\text{p}}=\widehat{q}-Q_{\text{p}}\left(t\right)$ and $c={\left(2\hslash m\omega \right)}^{-1/2}{e}^{i\chi }$ with a real constant phase χ. The eigenvalue equation of this operator can be expressed in the form

$\widehat{I}|\varphi \rangle =\lambda |\varphi \rangle ,(5)$

where λ is the eigenvalue and $|\varphi \rangle$ is the eigenstate. I have represented the formulae of λ and the eigenstate $\langle q|\varphi \rangle$ in the configuration space in Appendix A, including detailed derivation of them.

According to the Lewis–Riesenfeld theory [10, 20], the wave function that satisfies the Schrödinger equation is closely related to the eigenstate of the invariant operator. In fact, the wave function of the system in the coherent state is represented in terms of $\langle q|\varphi \rangle$ as [10]

$\langle q|\psi \rangle =\langle q|\varphi \rangle e^{i\theta \left(t\right)},(6)$

where $\theta \left(t\right)$ is a time-dependent phase. If we insert this equation together with Eq. 1 into the Schrödinger equation, we have $\theta \left(t\right)=-\omega t/2$. The wave function described here is necessary for investigating quantum–classical correspondence through the evolution of the system. It is notable that the probability density ${\left|\langle q|\psi \rangle \right|}^2$ is Gaussian and such a Gaussianity is maintained through the lapse of time as in the case of other Gaussian waves [21, 22] proposed in the literature. The fact that the wave function, Eq. 6, exactly satisfies the Schrödinger equation may guarantee the validity of the research unfolded in this work.

3 Correspondence Between Quantum and Classical Trajectories

Let us now see whether the expectation values of the position and the momentum operators under this formalism agree with the corresponding classical trajectories or not. Considering that the position operator is represented in terms of $\widehat{I}$ as (see Appendix A)

$\widehat{q}=i\sqrt{\hslash /\left(2m\omega e^{\gamma t}\right)}\left[\widehat{I}{e}^{-i\left(\omega t+\chi \right)}-{\widehat{I}}^{†}{e}^{i\left(\omega t+\chi \right)}\right]+Q_{\text{p}}\left(t\right),(7)$

and using Eq. 6, it can be easily verified that

$\langle \widehat{q}\rangle =Q\left(t\right),(8)$

where $\langle \cdot \rangle =\langle \psi |\cdot |\psi \rangle$. Hence, the quantum expectation value of the position operator is exactly the same as that of the classical trajectory $Q\left(t\right)$. In a similar way, the expectation value of the canonical momentum is also derived such that $\langle \widehat{p}\rangle =m\dot{Q}\left(t\right)e^{\gamma t}$. However, in general, the physical momentum in a damped system is not equivalent to the canonical one. Because the physical momentum operator is defined in the form ${\widehat{p}}_k=\widehat{p}{e}^{-\gamma t}$ [23] in the present case, its expectation value is given by

$\langle {\widehat{p}}_k\rangle =m\dot{Q}\left(t\right)\left(\equiv P_k\left(t\right)\right),(9)$

where $P_k\left(t\right)$ is the classical physical momentum. We thus confirm that the linear invariant operator theory admits quantum expectation values of $\widehat{q}$ and ${\widehat{p}}_k$ in a simple manner, of which results precisely coincide with the corresponding classical values. We can regard this outcome as an initial step for verifying that the invariant formalism of quantum mechanics reconciles with the principle of quantum and classical correspondence.

The above consequence, however, does not mean that the quantum particle (oscillator) follows the exact classical trajectory that is uniquely defined. Quantum mechanics is basically nonlocal and there are numerous possible paths allowed, within the width of a wave packet, for a quantum particle that has a definite initial condition. It is impossible to indicate exactly which path the quantum particle actually follows, but some paths may be more likely than others, especially those close to the classically predicted path. As a consequence of the Ehrenfest’s theorem [24], the trajectory of the quantum particle can be approximated to that of the classical one only when the width of the quantum wave packet is sufficiently narrow. Details of the Ehrenfest’s theorem for a particular case of the system where the oscillator is driven by a sinusoidal force are shown in Ref. [25].

4 Quantum Energy and Its Classical Limit

As pointed out by Hen and Kalev [9] and some other authors [26], obtaining a quantum–classical correspondence from a test performed at the level concerned expectation values is the key for achieving the genuine correspondence. Hence, it is necessary to compare the expectation values of quantum observables with their counterpart classical quantities. I will now analyze the expectation value of the quantum energy which is one of the most common observables in the system. Notice that quantum energy $E\left(t\right)$ for a nonconservative system is different from the expectation value of the Hamiltonian and the expression of the energy operator, in the present case, is [16, 27]

$\widehat{E}=e^{-2\gamma t}{\widehat{p}}^2/\left(2m\right)+\left(1/2\right)m{\omega }_0^2{\widehat{q}}^2.(10)$

After representing this operator in terms of $\widehat{I}$ and ${\widehat{I}}^{†}$, it is able to evaluate the expectation value of $\widehat{E}$ with the help of Eq. 6. Through this procedure, I finally have (see Appendix B)

$E\left(t\right)=\frac{1}{2}\hslash \text{Ω}+e^{-2\gamma t}\frac{P^2\left(t\right)}{2m}+\frac{1}{2}m{\omega }_0^2{Q}^2\left(t\right),(11)$

where $\text{Ω}=\left({\omega }_0^2/\omega \right)e^{-\gamma t}$. This is the main consequence of my present research. The first term that contains $\hslash$ is the zero-point energy that does not vanish even when the displacement of the oscillator is zero. Note that this term varies over time. Although $q^2$ ($p^2$) can be obtained by raising q (p) squared classically, the quantum expectation value $\langle {\widehat{q}}^2\rangle$ ($\langle {\widehat{p}}^2\rangle$) is different from ${\langle \widehat{q}\rangle }^2$ (${\langle \widehat{p}\rangle }^2$) because it involves a zero-point quantity. Such zero-point quantities also act as the origin of the zero-point quantum energy. When it comes to a measure of energy, great care must be taken in order to distinguish its classicality from the quantum nature. Fundamentally, the behavior of energy and its variance are directly related to the uncertainty principle [28, 29]. The (quantum) energy is, in general, not conserved over time in dissipative systems like this, while it is possible to predict its amount at any given instant in time.

For better understanding of the time behavior of Eq. 11, let us consider a specific system which is the cantilever in the tapping mode atomic force microscopy (TMAFM) [30]. This system is widely used as a dynamic imaging technique. For a mechanical description of TMAFM, see Appendix C. The time evolutions of quantum energy for TMAFM are illustrated in Figure 1 using Eq. 11 with comparison to its counterpart classical one. This figure exhibits complete consistency between the quantum energy (with $\hslash \to 0$) and the corresponding classical one. I have also applied the present theory to another system which is the familiar damped harmonic oscillator driven by a periodic sawtooth force (see Appendix D and Figure 2 for its mechanical description). Sawtooth forces or signals are typically observed from atomic force microscopy with biomolecules like proteins [31] and from a modulation of current density in a nuclear-fusion tokamak [32]. Figure 3 shows that the quantum description of this system using my theory also coincides with the classical one. We thus confirm that the formalism of quantum mechanics based on the linear invariant yields exact quantum–classical correspondence.

FIGURE 1

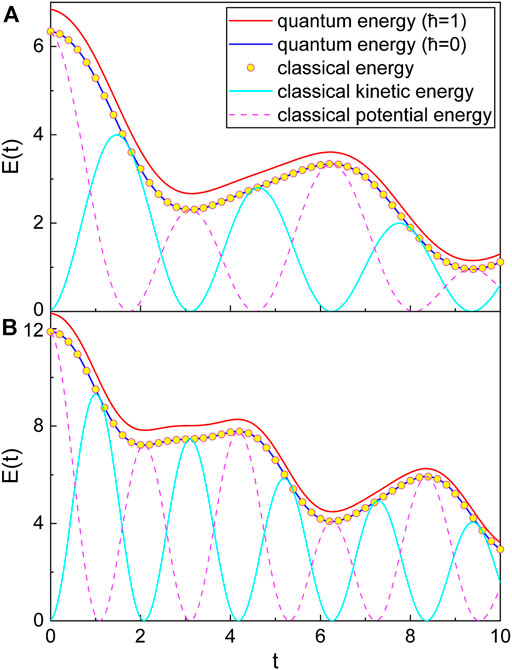
FIGURE 1. Exact quantum energy (red line), quantum energy with $\hslash \to 0$ (blue line), and classical mechanical energy (circle) of the oscillating cantilever in TMAFM as a function of t where $k=0.5$, $a_0=0.3$, $D_0=0.5$, $\hslash =1$, $m_{\text{eff}}=1$, $Q_0=3$, $\gamma =0.1$, $F_{\text{ext}}=0.3$, and $\phi =0$. The values of $\left({\omega }_0,{\omega }_{\text{d}}\right)$ are $\left(\mathrm{1,0.3}\right)$ for (A) and $\left(1.5,0.6\right)$ for (B). All values are taken to be dimensionless for convenience; this convention will also be used in subsequent figures.

FIGURE 2

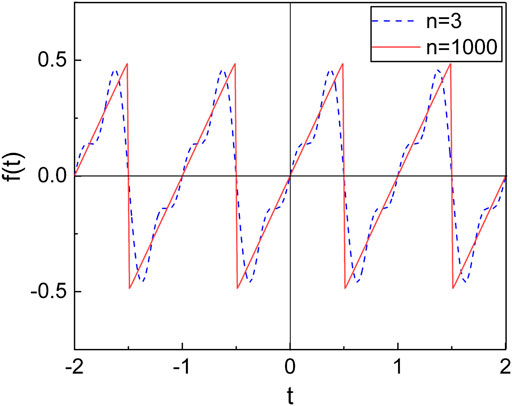
FIGURE 2. Sawtooth driving force $f\left(t\right)$ with $f_0=1$, $m=1$, and $\tau =1$, where the mathematical formula of $f\left(t\right)$ with a period τ is defined in Appendix D. n is the natural number (see Appendix D). I have considered n up to three for the blue dashed line and up to 1,000 for the red solid line. As n increases, the form of the obtained sawtooth driving force becomes more exact.

FIGURE 3

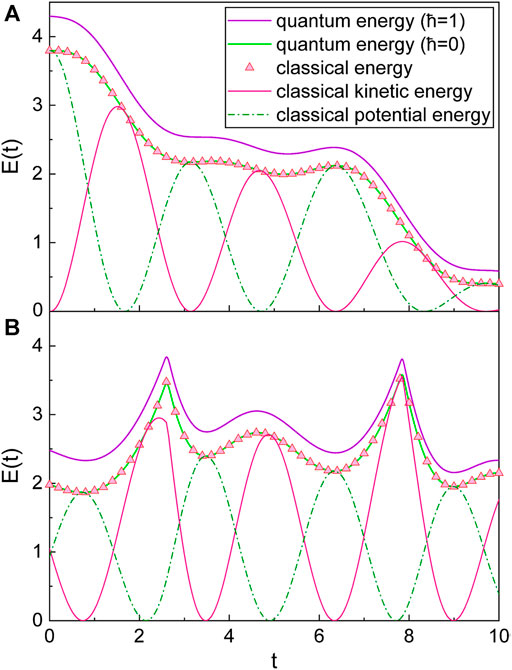
FIGURE 3. Exact quantum energy (violet line), quantum energy with $\hslash \to 0$ (green line), and classical mechanical energy (triangle) of the oscillator driven by the sawtooth force as a function of t where $m=1$, $\hslash =1$, $\gamma =0.1$, ${\omega }_0=1$, $\phi =0$, and $n=1000$. The values of $\left(Q_0,{\omega }_{\text{d}},f_0\right)$ are $\left(\mathrm{3,0.3},1\right)$ for (A) and $\left(\mathrm{1,1.2},2\right)$ for (B).

For further analysis, let us consider the case where the driving force disappears ($f\left(t\right)\to 0$). We can then confirm using Eq. 2 that Eq. 11 reduces to that of Ref. [33], which is of the form

$E\left(t\right)=\frac{1}{2}\hslash \text{Ω}+E_0{e}^{-\gamma t}\left(1+\frac{\gamma }{2{\omega }_0}\text{cos}\left[2\left(\omega t+\phi \right)-\delta \right]\right),(12)$

where $E_0=m{\omega }_0^2{Q}_0^2/2$ and $\delta ={\text{tan}}^{-1}\left(2\omega /\gamma \right)$. Except for the first term which is a purely quantum one, this is the well-known formula of the classical mechanical energy for the damped harmonic oscillator. Of course, for the high displacement limit $Q_0\gg \hslash /\left(m\omega \right)$, it is possible to neglect the quantum effect via the use of the assumption $\hslash \sim 0$ and, consequently, the quantum energy can be successfully approximated to the classical one. Though the quantum energy is considered now as a model example in order to explain the correspondence principle, one can easily check, using the formalism developed here, that the analytical expectation values of other observables are also in precise congruence with their classical counterparts under the limit $\hslash \to 0$. For other formulae of quantum energies and their interpretation for this reduced system ($f\left(t\right)\to 0$), which were derived using other methods such as the SU(1,1) Lie algebraic approach, refer to Ref. [34].

5 Uncertainty and The Correspondence Principle

An important feature of quantum mechanics, which distinguishes it from classical mechanics, is the appearance of a minimum uncertainty product between the arbitrary two noncommutative operators. One cannot simultaneously know the values of position and momentum with an arbitrary precision from a quantum measurement, while the classical theory of measurement has nothing to do with such a limitation.

The quantum variance of an observable $\widehat{\mathcal{O}}$ in the state $|\psi \rangle$ is given by $\text{Δ}\widehat{\mathcal{O}}={\left[\langle {\widehat{\mathcal{O}}}^2\rangle -{\langle \widehat{\mathcal{O}}\rangle }^2\right]}^{1/2}$. From this identity and the use of Eq. 6, the quantum uncertainty product for position and momentum of the system can be directly derived as

$\text{Δ}\widehat{q}\text{Δ}\widehat{p}=\hslash {\omega }_0/\left(2\omega \right).(13)$

Because this consequence is independent of the particular solutions, $Q_{\text{p}}\left(t\right)$ and $P_{\text{p}}\left(t\right)$, the driving force does not affect the uncertainty product. In other words, the uncertainty product of the system is the same as that of the undriven damped harmonic oscillator [12]. Due to the obvious inequality ${\omega }_0\ge \omega$, the uncertainty principle holds in this case. For the case $\gamma \to 0$, this uncertainty product reduces to $\hslash /2$ which is its minimal value allowed in quantum mechanics for the harmonic oscillator. On the other hand, for $\hslash \to 0$, this becomes zero, showing the classical prediction.

6 Other Formalisms and Approaches

There are several other quantum formalisms for describing the damped harmonic oscillator, such as the Lindblad dynamics [35–38], non-Hermitian Hamiltonian dynamics [39–41], and the Schwinger action method [15, 42]. Let’s look into the relatively well-known Lindblad dynamics here. Whereas my approach uses invariant operators $\widehat{I}$ and ${\widehat{I}}^{†}$ as basic tools for unfolding quantum theory, the approach based on the Lindblad theory uses an annihilation operator and its Hermitian adjoint operator (creation operator). The definition of the annihilation operator in that theory is given by $\widehat{a}=\sqrt{m\omega /\left(2\hslash \right)}\widehat{q}+i\widehat{\mathsf{p}}/\sqrt{2m\omega \hslash },$ where $\widehat{\mathsf{p}}$ is a momentum which is defined in terms of the notation in this work as (see Eq. 46 of Ref. [35])

$\widehat{\mathsf{p}}={\widehat{p}}_k+m\left(\gamma /2\right)\widehat{q}.(14)$

Although the momentum given above seems similar to the physical momentum, it is not exactly the same due to the presence of the additional second term.

In particular, Korsch evaluated the expectation value of ${\widehat{a}}^{†}\widehat{a}$ for the damped oscillator driven by a sinusoidal force of the form

$f\left(t\right)=f_{\text{d}}\text{cos}\left({\omega }_{\text{d}}t\right).(15)$

If we denote the expectation value of an observable $\widehat{\mathcal{O}}$ in the Lindblad theory as ${\langle \widehat{\mathcal{O}}\rangle }_{\text{L}}$, Korsch’s result for ${\widehat{a}}^{†}\widehat{a}$ with $\hslash =1$ and $m=1$ is given by (see Eq. 98 of Ref. [35])

${\langle {\widehat{a}}^{†}\widehat{a}\rangle }_{\text{L}}=\frac{1}{b\left(t\right)}-1+{\left|\alpha \left(t\right)\right|}^2,(16)$

where

$b\left(t\right)=\frac{\left(\mu -\nu \right)\left(1-u_0\right)e^{\gamma t}}{\mu u_0-\nu +\mu \left(1-u_0\right)e^{\gamma t}},(17)$

$\alpha \left(t\right)={\alpha }_0{e}^{-\left(i\omega +\gamma /2\right)t}-\frac{f_{\text{d}}}{2\sqrt{2\omega }}\left(\frac{e^{-\left(i\omega +\gamma /2\right)t}-e^{i{\omega }_{\text{d}}t}}{\omega +{\omega }_{\text{d}}-i\gamma /2}+\frac{e^{-\left(i\omega +\gamma /2\right)t}-e^{-i{\omega }_{\text{d}}t}}{\omega -{\omega }_{\text{d}}-i\gamma /2}\right),(18)$

while $\mu =\gamma \prime +\gamma /2$ and $\nu =\gamma \prime -\gamma /2$, $\gamma \prime$ is a diffusion constant [38], and $u_0$ is a constant chosen within the range $0<u_0<1$.

Let us now compare the present result with Korsch’s together with the classical one. The expectation value of ${\widehat{a}}^{†}\widehat{a}$ in my theory is given by

$\langle {\widehat{a}}^{†}\widehat{a}\rangle =\frac{m\omega }{2\hslash }\langle {\widehat{q}}^2\rangle +\frac{\langle {\widehat{\mathsf{p}}}^2\rangle }{2m\omega \hslash }-\frac{1}{2}{e}^{-\gamma t}.(19)$

The expectation values $\langle {\widehat{q}}^2\rangle$ and $\langle {\widehat{\mathsf{p}}}^2\rangle$ are provided in Appendix E. On the other hand, a classical counterpart of the expectation value of ${\widehat{a}}^{†}\widehat{a}$ can be defined as $A^{\text{*}}A$, where

$A=\sqrt{m\omega /\left(2\hslash \right)}Q\left(t\right)+i\mathsf{P}\left(t\right)/\sqrt{2m\omega \hslash },(20)$

with

$\mathsf{P}\left(t\right)=P_k\left(t\right)+\frac{m\gamma }{2}Q\left(t\right).(21)$

Figures 4, 5 are the comparison of the time behavior between $\langle {\widehat{a}}^{†}\widehat{a}\rangle$, ${\langle {\widehat{a}}^{†}\widehat{a}\rangle }_{\text{L}}$, and $A^{\text{*}}A$. The difference of Figure 5 compared with Figure 4 is the chosen amplitude ${\alpha }_0$, that is, ${\alpha }_0$ in Figure 5 is relatively smaller than that used in Figure 4. Although the result in this work agrees well with the Korsch’s one for the case of Figure 4, the two results in Figure 5 are somewhat different from each other. Especially, the discrepancy between them is very large for the case ${\omega }_{\text{d}}<{\omega }_0$ (see Figure 5B). By the way, my results in both Figures 4, 5 agree with the classical ones. From a lengthy calculation after substituting Equations E1 and E2 in Eq. 19, it can also be verified that $\langle {\widehat{a}}^{†}\widehat{a}\rangle$ is exactly the same as $A^{\text{*}}A$ analytically.

FIGURE 4

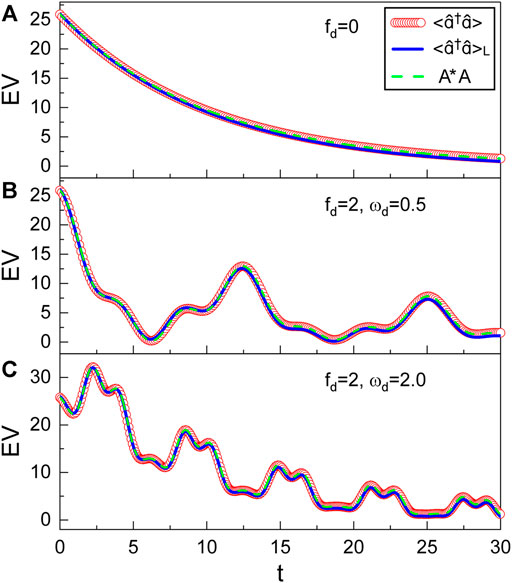
FIGURE 4. Time evolution of the expectation values (EV), $\langle {\widehat{a}}^{†}\widehat{a}\rangle$ (Eq. 19), ${\langle {\widehat{a}}^{†}\widehat{a}\rangle }_{\text{L}}$ (Eq. 16), and $A^{\text{*}}A$, for several different choices of the sinusoidal driving force characterized by $f_{\text{d}}$ and ${\omega }_{\text{d}}$. The chosen values of $f_{\text{d}}$ and ${\omega }_{\text{d}}$ are designated in each panel. I have used ${\alpha }_0=5$, $u_0=0.5$, ${\omega }_0=1$, $\gamma =0.1$, $\gamma \text{'}=0$, $m=1$, $\hslash =1$, $\chi =0$, and $\phi =0$. The value of $Q_0$ is 7.21 for A, 4.54 for B, and 7.85 for C.

FIGURE 5

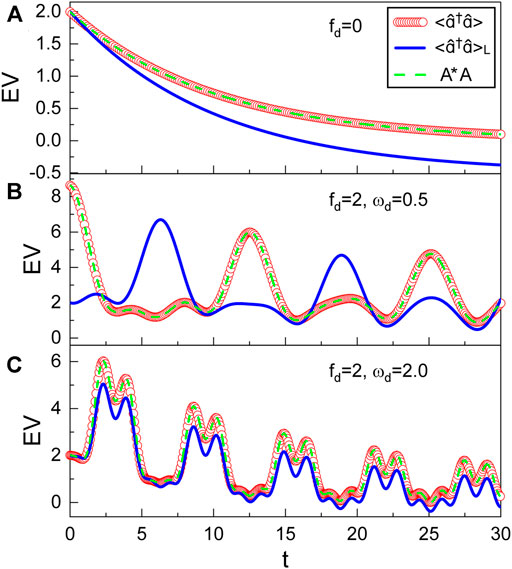
FIGURE 5. Time evolution of $\langle {\widehat{a}}^{†}\widehat{a}\rangle$, ${\langle {\widehat{a}}^{†}\widehat{a}\rangle }_{\text{L}}$, and $A^{\text{*}}A$ for the case where the amplitude is relatively small (${\alpha }_0=1$). The value of $Q_0$ is 2.00 for A, 1.50 for B, and 2.67 for C. Other unspecified values used here are the same as those of Figure 4.

There are lots of different approaches for the classical limit of quantum mechanics with their own viewpoints. The problem of quantum–classical transition has been extensively investigated for the quartic oscillator by Oliveira et al. [29, 43–45]. They argued that quantum–classical correspondence can be achieved via the convergence of three factors, which are large classical actions, the object-environment interaction, and experimentally induced limitations. It was reported by Zurek [46] that the quantum–classical limit is governed by decoherence that takes place through environmental perturbations. As a quantum chaotic system is decohered, it restores classical behavior as a consequence of the destruction of quantum superpositions. Wiebe and Ballentine [47] examined quantum–classical differences by computing the chaotic tumbling of the satellite Hyperion from both classical and quantum points of view regarding the hypothesis of Zurek.

7 Conclusion

Classical limit of quantum mechanics for a driven damped harmonic oscillator has been investigated based on the linear invariant operator. The full wave function of the system was represented in terms of the eigenstate of the linear invariant operator according to the Lewis–Riesenfeld theory [10]. The expectation values of observables, such as position, momentum, and quantum energy, have been derived by using the wave function, and I have compared them with their classical counterparts. From this, it was shown that $\hslash \to 0$ limit of quantum mechanics for the system coincides with the counterpart classical mechanics within my formulation. The quantum formalism adopted here may be extended to other systems beyond the harmonic oscillator, provided that a given system admits a linear invariant quantity as a tool for its analysis.

The recent trend [48, 49] of the reimplementation of classical mechanics in particle optics using quantum particles is a clear testimony of the close relationship between quantum and classical mechanics. Some essential knowledge of quantum information theory is developed on the basis of classical-like wave properties, while the quantum nature of a physical system is unquestionable especially when nonlocal entanglement is concerned [50]. It may be the very common opinion that every new physical theory should not only precisely describe facts that cannot be covered by existing theories but must also reproduce the predictions of classical mechanics in an appropriate classical limit.

Quantum systems exhibit various nonclassical properties such as entanglement, superposition, nonlocality, and negative Wigner distribution function. While such nonclassicalities are important in the next-generation quantum information science, the description of nonclassical properties is valid and reliable only when the underlying quantum formalism used in such descriptions is precise and complete. A formalism of quantum theory may be acceptable only when it gives classical results in the classical limit ($\hslash \to 0$ limit). This is the reason why a complete quantum formalism that obeys quantum–classical correspondence is important. Such a formalism may admit to explaining the various characteristics of dynamical systems in a reasonable and consistent way from every possible angle. The result for a correspondence principle that I have developed in this research beyond simple static systems may provide a deep insight into understanding how classical mechanics emerges from quantum mechanics through a limiting situation.

8 Methods

I considered a time-dependent Hamiltonian, which is composed of the basic CK Hamiltonian and an additional term associated with a time-varying driving force. This Hamiltonian corresponds to a damped driven harmonic oscillator.

The linear invariant operator of the system is constructed from the Liouville–von Neumann equation. The eigenvalue and the eigenstate of the linear invariant operator are derived by solving its eigenvalue equation through a fundamental mathematical procedure. If a system is described by a time-dependent Hamiltonian like the case given here, the eigenstate of the (linear) invariant operator is important because the full wave function of the system is expressed in terms of such an eigenstate [10]. More clearly speaking, the wave function in this case is represented by the eigenstate and a phase factor (see Eq. 6 in the text). Because we now know the formula of the eigenstate, the phase of the wave function can be easily evaluated by means of the Schrödinger equation. In this way, we can derive the full wave function eventually. This wave function is necessary in order to investigate the $\hslash \to 0$ limit of quantum mechanics.

The quantum expectation values of observables, such as position, momentum, and the energy operator, are derived using the wave function. By comparing such expectation values with their classical counterparts, the correspondence principle between quantum and classical mechanics is analyzed.

Data Availability Statement

The original contributions presented in the study are included in the article, and further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (No.: NRF-2021R1F1A1062849).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Planck M. Vorlesungen uber die Theorie der Wärmestralhung. 978-0270103878. New York: Dover Publications (1959).

2. Bohr N. The Theory of Spectra and Atomic Constitution. 978-1107669819. London: Cambridge University Press (1922).

3. Liboff RL. On the Potential x^2Nand the Correspondence Principle. Int J Theor Phys (1979) 18(3):185–91. doi:10.1007/BF00670395

CrossRef Full Text | Google Scholar

4. Man’ko OV, Man’ko VI. Classical Mechanics Is Not the Limit ℏ→0 of Quantum Mechanics. J Russ Laser Res (2004) 25(5):477–92. doi:10.1023/B:JORR.0000043735.34372.8f

CrossRef Full Text | Google Scholar

5. Huang XY. Correspondence between Quantum and Classical Descriptions for Free Particles. Phys Rev A (2008) 78(2):022109. doi:10.1103/PhysRevA.78.022109

CrossRef Full Text | Google Scholar

6. Kay KG. Hamiltonian Formulation of Quantum Mechanics with Semiclassical Implications. Phys Rev A (1990) 42(7):3718–25. doi:10.1103/PhysRevA.46.1213

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Klein U. What Is the ℏ → 0 Limit of Quantum Theory. Am J Phys (2012) 80(11):1009–16. doi:10.1119/1.4751274

CrossRef Full Text | Google Scholar

8. Oliveira AC. Classical Limit of Quantum Mechanics Induced by Continuous Measurements. Physica A (2014) 393:655–68. doi:10.1016/j.physa.2013.09.025

CrossRef Full Text | Google Scholar

9. Hen I, Kalev A. Classical States and Their Quantum Correspondence. arXiv:0701015v2 [quant-ph] (2007).

10. Lewis HR, Riesenfeld WB. An Exact Quantum Theory of the Time-dependent Harmonic Oscillator and of a Charged Particle in a Time-dependent Electromagnetic Field. J Math Phys (1969) 10(8):1458–73. doi:10.1063/1.1664991

CrossRef Full Text | Google Scholar

11. Abdalla MS, Choi JR. Propagator for the Time-dependent Charged Oscillator via Linear and Quadratic Invariants. Ann Phys (2007) 322(12):2795–810. doi:10.1016/j.aop.2007.01.006

CrossRef Full Text | Google Scholar

12. Choi JR, Zhang S. Quantum and Classical Correspondence of Damped-Amplified Oscillators. Phys Scr (2002) 66(5):337–41. doi:10.1238/Physica.Regular.066a00337

CrossRef Full Text | Google Scholar

13. Choi JR, Ju S. Properties of the Geometric Phase in Electromechanical Oscillations of Carbon-Nanotube-Based Nanowire Resonators. Nanoscale Res Lett (2019) 14:44. doi:10.1186/s11671-019-2855-8

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Yeon K-H, Kim S-S, Moon Y-M, Hong S-K, Um C-I, George TF. The Quantum under-, Critical- and Over-damped Driven Harmonic Oscillators. J Phys A: Math Gen (2001) 34(37):7719–32. doi:10.1088/0305-4470/34/37/321

CrossRef Full Text | Google Scholar

15. Urrutia LF, Hernandez E. Calculation of the Propagator for a Time-dependent Damped, Forced Harmonic Oscillator Using the Schwinger Action Principle. Int J Theor Phys (1984) 23(12):1105–27. doi:10.1007/BF02213423

CrossRef Full Text | Google Scholar

16. Um C-I, Yeon K-H, George TF. The Quantum Damped Harmonic Oscillator. Phys Rep (2002) 362(2-3):63–192. doi:10.1016/S0370-1573(01)00077-1

CrossRef Full Text | Google Scholar

17. Caldirola P. Porze Non Conservative Nella Meccanica Quantistica. Nuovo Cimento (1941) 18(9):393–400. doi:10.1007/BF02960144

CrossRef Full Text | Google Scholar

18. Kanai E. On the Quantization of Dissipative Systems. Prog Theor Phys (1948) 3(4):440–2. doi:10.1007/BF01313310

CrossRef Full Text | Google Scholar

19. Flores-Hidalgo G, Barone FA. The One Dimensional Damped Forced Harmonic Oscillator Revisited. Eur J Phys (2011) 32(2):377–9. doi:10.1088/0143-0807/32/2/010

CrossRef Full Text | Google Scholar

20. Choi JR, Nahm IH. SU(1,1) Lie Algebra Applied to the General Time-dependent Quadratic Hamiltonian System. Int J Theore Phys (2006) 46(1):1–15. doi:10.1007/s10773-006-9050-2

CrossRef Full Text | Google Scholar

21. Schumaker BL. Quantum Mechanical Pure States with Gaussian Wave Functions. Phys Rep (1986) 135(6):317–408. doi:10.1016/0370-1573(86)90179-1

CrossRef Full Text | Google Scholar

22. Marhic MF. Oscillating Hermite-Gaussian Wave Functions of the Harmonic Oscillator. Lett Nuovo Cim (1978) 22(9):376–8. doi:10.1007/BF02820587

CrossRef Full Text | Google Scholar

23. Greenberger DM. A Critique of the Major Approaches to Damping in Quantum Theory. J Math Phys (1979) 20(5):762–70. doi:10.1063/1.524148

CrossRef Full Text | Google Scholar

24. Ehrenfest P. Bemerkung über die angenäherte gültigkeit der klassischen mechanik innerhalb der quantenmechanik. Z Phys (1927) 45(7-8):455–7. doi:10.1007/BF01329203

CrossRef Full Text | Google Scholar

25. Medjber S, Bekkar H, Menouar S, Choi JR. Testing the Validity of the Ehrenfest Theorem beyond Simple Static Systems: Caldirola-Kanai Oscillator Driven by a Time-dependent Force. Chin Phys B (2016) 25(8), 080301. doi:10.1088/1674-1056/25/8/080301

CrossRef Full Text | Google Scholar

26. Bolivar AO. In: Quantum-Classical Correspondence: Dynamical Quantization and the Classical Limit. 978-3-662-09649-9. New York: Springer (2004).

27. Colegrave RK, Abdalla MS. A Canonical Description of the Fabry-Perot Cavity. Optica Acta (1981) 28(4):495–501. doi:10.1080/713820584

CrossRef Full Text | Google Scholar

28. Caves CM, Milburn GJ. Quantum-mechanical Model for Continuous Position Measurements. Phys Rev A (1987) 36(12):5543–55. doi:10.1103/PhysRevA.36.5543

CrossRef Full Text | Google Scholar

29. Oliveira AC, Oliveira ZT, Correia NS, Complementarity and Classical Limit of Quantum Mechanics: Energy Measurement Aspects. arXiv:1307.0528v1 [quant-ph] (2013).

Google Scholar

30. Legleiter J, Park M, Cusick B, Kowalewski T. Scanning Probe Acceleration Microscopy (SPAM) in Fluids: Mapping Mechanical Properties of Surfaces at the Nanoscale. PNAS (2006) 103(13):4813–8. doi:10.1073/pnas.0505628103

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Hornyak GL, Tibbals HF, Dutta J, Moore JJ. Introduction to Nanoscience & Nanotechnology 978-1420047790. Boca Raton: CRC Press (2009).

32. Soltwisch H. Measurement of Current-Density Changes during Sawtooth Activity in a Tokamak by Far-Infrared Polarimetry. Rev Sci Instrum (1988) 59(8):1599–604. doi:10.1063/1.1140159

CrossRef Full Text | Google Scholar

33. Choi JR. Interpreting Quantum States of Electromagnetic Field in Time-dependent Linear media. Phys Rev A (2010) 82(5):055803. doi:10.1103/PhysRevA.82.055803

CrossRef Full Text | Google Scholar

34. Choi JR. Analysis of Quantum Energy for Caldirola-Kanai Hamiltonian Systems in Coherent States. Results Phys (2013) 3(1):115–21. doi:10.1016/j.rinp.2013.06.003

CrossRef Full Text | Google Scholar

35. Korsch HJ. Lindblad Dynamics of the Damped and Forced Quantum Harmonic Oscillator. arXiv 1908.01187v2 [quant-ph] (2019).

36. Fujii K. Quantum Damped Harmonic Oscillator. In: P Bracken, editor. Advances in Quantum Mechanics. 978-953-51-1089-7. Rijeka: Intech (2013). p. 133–56.

Google Scholar

37. Isar A. Uncertainty, Entropy and Decoherence of the Damped Harmonic Oscillator in the Lindblad Theory of Open Quantum Systems. Fortschr Phys (1999) 47(7-8):855–79. doi:10.1002/(SICI)1521-3978(199909)47:7/8¡855::AID-PROP855¿3.0.CO;2-Z

CrossRef Full Text | Google Scholar

38. Piilo J, Maniscalco S. Driven Harmonic Oscillator as a Quantum Simulator for Open Systems. Phys Rev A (2006) 74(3):032303. doi:10.1103/PhysRevA.74.032303

CrossRef Full Text | Google Scholar

39. Graefe EM, Höning M, Korsch HJ. Classical Limit of Non-Hermitian Quantum Dynamics—A Generalized Canonical Structure. J Phys A: Math Theor (2010) 43(7):075306. doi:10.1088/1751-8113/43/7/075306

CrossRef Full Text | Google Scholar

40. Grimaldi A, Sergi A, Messina A. Evolution of a Non-Hermitian Quantum Single-Molecule Junction at Constant Temperature. Entropy (2021) 23(2):147. doi:10.3390/e23020147

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Nigam K, Banerjee K. Quantum Dynamics of Complex Hamiltonians. arXiv:1602.00157v2 [quant-ph] (2016).

42. Pepore S, Sukbot B. Schwinger Method for Dual Damped Oscillators. Chin J Phys (2015) 53(5):100002. doi:10.6122/CJP.20150803

CrossRef Full Text | Google Scholar

43. Oliveira AC, Nemes MC, Romero KMF. Quantum Time Scales and the Classical Limit: Analytic Results for Some Simple Systems. Phys Rev E (2003) 68(3):036214. doi:10.1103/PhysRevE.68.036214

CrossRef Full Text | Google Scholar

44. Oliveira AC, de Faria JGP, Nemes MC. Quantum-classical Transition of the Open Quartic Oscillator: The Role of the Environment. Phys Rev E (2006) 73(4):046207. doi:10.1103/PhysRevE.73.046207

CrossRef Full Text | Google Scholar

45. Oliveira AC, de Magalhães ARB, Faria JGP. Influence of Experimental Resolution on the Quantum-To-Classical Transition in the Quartic Oscillator. Physica A (2012) 391(21):5082–9. doi:10.1016/j.physa.2012.05.064

CrossRef Full Text | Google Scholar

46. Zurek WH. Decoherence, Chaos, Quantum-Classical Correspondence, and the Algorithmic Arrow of Time. Phys Scr (1998) 1998(T76):186–98. doi:10.1238/Physica.Topical.076a00186

CrossRef Full Text | Google Scholar

47. Wiebe N, Ballentine LE. Quantum Mechanics of Hyperion. Phys Rev A (2005) 72(2):022109. doi:10.1103/PhysRevA.72.022109

CrossRef Full Text | Google Scholar

48. Wang Y-M, Liang J-Q. Repulsive Bound-Atom Pairs in an Optical Lattice with Two-Body Interaction of Nearest Neighbors. Phys Rev A (2010) 81(4):045601. doi:10.1103/PhysRevA.81.045601

CrossRef Full Text | Google Scholar

49. Hawkes PW. Examples of Electrostatic Electron Optics: The Farrand and Elektros Microscopes and Electron Mirrors. Ultramicroscopy (2012) 119:9–17. doi:10.1016/j.ultramic.2011.11.009

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Goldin MA, Francisco D, Ledesma S. Classical Images as Quantum Entanglement: An Image Processing Analogy of the GHZ Experiment. Opt Commun (2011) 284(7):2089–93. doi:10.1016/j.optcom.2010.12.057

CrossRef Full Text | Google Scholar

51. Louisell WH. Quantum Statistical Properties of Radiation. 0-471-54785-9. New York: John Wiley & Sons (1973). p. 104–9.

52. Choi JR. Exact Solution of a Quantized LC Circuit Coupled to a Power Source. Phys Scr (2006) 73(6):587–95. doi:10.1088/0031-8949/73/6/010

CrossRef Full Text | Google Scholar

Appendix A: Linear Invariant Operator and its Eigenstate

From a straightforward evaluation of the Liouville-von Neumann equation,

$d\widehat{I}/dt=\partial \widehat{I}/\partial t+[\widehat{I},\widehat{H}]/\left(iħ\right)=0,(\mathrm{A1})$

using the Hamiltonian given in Eq. 1 in the text, we can easily derive the linear invariant operator $\widehat{I}$ that is given in Eq. 4 in the text (see Ref. 13). Notice that the Hermitian adjoint of this operator, ${\widehat{I}}^{†}$, is also an invariant operator. From a combined evaluation of the two equations for $\widehat{I}$ and ${\widehat{I}}^{†}$, it is possible to eliminate $\widehat{p}$ and, as a consequence, the expression for $\widehat{q}$ which appeared in Eq. 7 in the text can be obtained. From a similar method, we can also obtain the expression for $\widehat{p}$. By solving the eigenvalue equation of the invariant operator, Eq. 5, in the configuration space on the basis of the technique adopted in Ref. 20, we obtain the eigenvalue as

$\lambda =\beta e^{i\omega t},(\mathrm{A2})$

where $\beta =-i\sqrt{m\omega /\left(2ħ\right)}{Q}_0{e}^{-i\left(\omega t+\phi -\chi \right)}$, and the eigenstate of the form

$\langle q|\varphi \rangle =\sqrt{\frac{m\omega }{ħ\pi }}\text{exp}\left[e^{\gamma t/2}\frac{C_1{q}_{\text{p}}-C_2{q}_{\text{p}}^2}{ħ}+C_3\right],(\mathrm{A3})$

where $q_{\text{p}}=q-Q_{\text{p}}\left(t\right)$ and

$C_1=\sqrt{2ħm\omega }\beta ,(\mathrm{A4})$

$C_2=\frac{1}{2}m{e}^{\gamma t/2}\left(\omega +i\gamma /2\right),(\mathrm{A5})$

$C_3=\frac{i{P}_{\text{p}}\left(t\right)q}{ħ}+\frac{\gamma t}{4}-\frac{{\beta }^2}{2}-\frac{{\left|\beta \right|}^2}{2}.(\mathrm{A6})$

Appendix B: Expectation Value of the Energy Operator

I present how to evaluate the expectation value of the energy operator. From a minor evaluation with the energy operator using the expression of $\widehat{I}$ (and its Hermitian conjugate ${\widehat{I}}^{†}$), it is possible to represent the energy operator in terms of $\widehat{I}$ and ${\widehat{I}}^{†}$ such that

$\widehat{E}=\left[\frac{ħ}{4}\left(\frac{2{\omega }_0^2}{\omega }\left(2{\widehat{I}}^{†}\widehat{I}+1\right)-\epsilon {\widehat{I}}^2-{\epsilon }^{*}{\widehat{I}}^{†2}\right)+\sqrt{\frac{ħ}{2}}\left(\text{Θ}\widehat{I}+{\text{Θ}}^{\text{*}}{\widehat{I}}^{†}\right)\right]e^{-\gamma t}+E_{\text{p}},(\mathrm{B1})$

where $\epsilon =\gamma [\gamma /\left(2\omega \right)+i]e^{-2i\left(\omega t+\chi \right)}$ and

$\text{Θ}=\left[\sqrt{\frac{\omega }{m}}{e}^{-\gamma t/2}\eta P_{\text{p}}\left(t\right)+i{e}^{\gamma t/2}\sqrt{\frac{m}{\omega }}{\omega }_0^2{Q}_{\text{p}}\left(t\right)\right]e^{-i\left(\omega t+\chi \right)},(\mathrm{B2})$

$E_{\text{p}}=e^{-2\gamma t}\frac{P_{\text{p}}^2\left(t\right)}{2m}+\frac{1}{2}m{\omega }_0^2{Q}_{\text{p}}^2\left(t\right),(\mathrm{B3})$

with $\eta =1-i\gamma /\left(2\omega \right)$. Here, I have used the relation $\widehat{I}{\widehat{I}}^{†}={\widehat{I}}^{†}\widehat{I}+1$, i.e., all $\widehat{I}{\widehat{I}}^{†}$ are replaced by ${\widehat{I}}^{†}\widehat{I}+1$: this procedure of operator ordering is necessary when we manage a coherent state (see, for example, Ref. 51). Now by considering the fact that the eigenvalues of $\widehat{I}$ and ${\widehat{I}}^{†}$ are λ and ${\lambda }^{\text{*}}$ respectively, we can easily identify the expectation value of the energy operator, $\langle \psi \left|\widehat{E}\right|\psi \rangle$, which is given in Eq. 11 in the text. Notice that the $ħ$ must not be taken simplistically to zero at the initial stage of the evaluation under the pretext of obtaining the classical limit. We should keep it until we arrive at the final representation, Eq. 11.

Appendix C: Cantilever System

Description of the cantilever system appears in Ref. 30. If we denote the effective mass of the cantilever as $m_{\text{eff}}$, the force acted on the lever is represented in the form

$f\left(t\right)=\left[F_{\text{ext}}+k\left(D_0-a_0\text{sin}{\omega }_{\text{d}}t\right)\right]/m_{\text{eff}},(\mathrm{C1})$

where $F_{\text{ext}}$ is the tip-sample force, $k\left(=m_{\text{eff}}{\omega }_0^2\right)$ is the cantilever spring constant, $D_0$ is the resting position of the cantilever base, $a_0$ is the driving amplitude, and ${\omega }_{\text{d}}$ is the drive frequency [30].

Appendix D: Damped Harmonic Oscillator with a Sawtooth Force

I regard the damped harmonic oscillator to which applied an external sawtooth force with the period $\tau =2\pi /{\omega }_{\text{d}}$. The sawtooth force can be represented as $f\left(t\right)=f_{0}t/\left(m\tau \right)$ for a period $-\tau /2<t<\tau /2$ (see Figure 2), where $f_0$ is a constant that represents the strength of the force. In this case, $f\left(t\right)$ can be rewritten in terms of an infinite series such that [52]

$f\left(t\right)=\left[f_0/\left(\pi m\right)\right]{\displaystyle \sum }_{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{n}\text{sin}\left(n{\omega }_{\text{d}}t\right).(\mathrm{D1})$

Appendix E: Expectation Values of ${\widehat{\mathit{q}}}^2$ and ${\widehat{\mathrm{p}}}^2$

The expectation values of ${\widehat{q}}^2$ and ${\widehat{\mathsf{p}}}^2$ in the state $|\psi \rangle$, which are necessary in the development of a consequence in Section 6, are given by

$\langle {\widehat{q}}^2\rangle =-\hspace{0.17em}\frac{ħ}{2m\omega e^{\gamma t}}\left[{\lambda }^2{e}^{-2i\left(\omega t+\chi \right)}+{\lambda }^{\text{*}2}{e}^{2i\left(\omega t+\chi \right)}-2|\lambda {|}^2-1\right]+i{Q}_{\text{p}}\left(t\right)\sqrt{\frac{2ħ}{m\omega e^{\gamma t}}}[\lambda e^{-i\left(\omega t+\chi \right)}-{\lambda }^{\text{*}}{e}^{i\left(\omega t+\chi \right)}]+Q_{\text{p}}^2\left(t\right),(\mathrm{E1})$

$\langle {\widehat{\mathsf{p}}}^2\rangle =\frac{m\omega ħ}{2}{e}^{-\gamma t}[{\lambda }^2{e}^{-2i\left(\omega t+\chi \right)}+{\lambda }^{\text{*}2}{e}^{2i\left(\omega t+\chi \right)}+2|\lambda {|}^2+1]+G_{\text{p}}\left(t\right)\sqrt{2m\omega ħ}{e}^{-\gamma t/2}[\lambda e^{-i\left(\omega t+\chi \right)}+{\lambda }^{\text{*}}{e}^{i\left(\omega t+\chi \right)}]+G_{\text{p}}^2\left(t\right),(\mathrm{E2})$

where $G_{\text{p}}\left(t\right)=P_{\text{p}}\left(t\right)e^{-\gamma t}+\gamma m{Q}_{\text{p}}\left(t\right)/2$. The particular solutions that correspond to the driving force of Eq. 15 are given by

$Q_{\text{p}}\left(t\right)=\frac{f_{\text{d}}}{\sqrt{{\left({\omega }_0^2-{\omega }_{\text{d}}^2\right)}^2+{\gamma }^2{\omega }_{\text{d}}^2}}\text{cos}\left({\omega }_{\text{d}}t-{\delta }_{\text{d}}\right),(\mathrm{E3})$

$P_{\text{p}}\left(t\right)=-\frac{m{f}_{\text{d}}{\omega }_{\text{d}}}{\sqrt{{\left({\omega }_0^2-{\omega }_{\text{d}}^2\right)}^2+{\gamma }^2{\omega }_{\text{d}}^2}}\hspace{0.17em}{e}^{\gamma t}\text{sin}\left({\omega }_{\text{d}}t-{\delta }_{\text{d}}\right),(\mathrm{E4})$

where

${\delta }_{\text{d}}=\text{atan}\left({\omega }_0^2-{\omega }_{\text{d}}^2,\gamma {\omega }_{\text{d}}\right).(\mathrm{E5})$

Here, $\vartheta \equiv \text{atan}\left(x,y\right)$ is a two-argument inverse function of $\text{tan}\vartheta =y/x$. This function is defined in the range $0\le \vartheta <2\pi$.