Existing and Potential Applications of Elastography for Measuring the Viscoelasticity of Biological Tissues In Vivo

Mechanical tissue properties contribute to tissue shape change during development. Emerging evidence suggests that gradients of viscoelasticity correspond to cell movement and gene expression patterns. To accurately define mechanisms of morphogenesis, a combination of precise empirical measurements and theoretical approaches are required. Here, we review elastography as a method to characterize viscoelastic properties of tissue in vivo. We discuss its current clinical applications in mature tissues and its potential for characterizing embryonic tissues.

Introduction

Viscoelasticity, among other mechanical properties, is intrinsic to biological tissue. The term implies that tissue exhibits time-dependent responses to an applied force [1–3]. Characterization of the viscoelastic behavior of biological tissue has been performed in vitro [4, 5], ex vivo [6], and in vivo [7, 8] to gain insight into tissue stiffness and fluidity. In vivo assessment is preferable to determine tissue properties in their native environment, and elastography has the advantage of minimally disturbing that environment. In brief, elastography introduces a disturbance to displace specific regions within a tissue, which is subsequently imaged and analyzed to determine the local viscoelastic response.

It is worth noting that elastography was not originally developed for the purpose of measuring viscoelastic properties. As the name indicates, in its earlier development, only elasticity (in terms of Young’s modulus) was at the center of attention, lacking viscosity information (coefficient of viscosity) [9, 10]. However, as the properties of biological tissue were progressively understood, a variety of theoretical frameworks were developed and integrated with earlier elastography techniques. In recent years, although the name of elastography remains largely unchanged (some studies have adopted the term “viscoelastography” [11, 12]), it has become more common that quantitative values of various moduli, as we will discuss in detail in later sections, include information of material viscoelasticity.

In clinical settings, elastography techniques for measuring the viscoelastic properties of mature tissues have been well established in vivo to diagnose and distinguish among different pathologies [7, 13–16]. The motivation of shifting from measuring elasticity information to viscoelasticity information lies within the fact that as mature tissues exhibit varying degrees of viscoelastic behavior, the sufficiency and validity of solely relying on elasticity information have been questioned [17]. For instance, elastography-based studies on assessing hepatic tumor malignancy [15, 18], benign/normal breast tissues [19], and the efficacy of cornea disease treatment [20] have reported a more prominent effect by using viscosity as the differentiator rather than elasticity. Thus, assessing the viscoelastic behavior of mature tissues is necessary to provide more accurate in vivo measurements and characterization, subsequently improving tumor diagnostic accuracy.

In studies of embryonic tissues, it is increasingly understood how forces generated by cells can coordinate morphogenesis [21–23]. In response to forces, embryonic tissues, which are both liquid- and solid-like, exhibit viscoelastic behavior [3, 24]. Cells have receptors that can sense physical forces as well as chemical cues. For example, cadherin molecules have both mechanical and sensory properties which are applied for adhesion and signaling, respectively [24]. It is currently challenging to perform loss and gain of function experiments of mechanical cues to define their roles in vivo as one can with chemical cues. Although increasingly precise tools are being developed to characterize the mechanical and viscoelastic properties of embryonic tissues [25], data supporting their efficacy are currently sparse. Albeit less explicitly discussed, the motivation to study viscoelasticity in the context of developmental biology is twofold. At the single-cell level, various membrane-enclosed and membrane-less organelles exhibit viscoelastic behavior to different degrees. The latter can take on the form of liquid droplets that undergo controlled dissolution and condensation via phase separation [26, 27]. The occurrence of irreversible aggregation promotes further transition of some condensates from liquid-like to solid-like [28], underlying the pathologies in many neurodegenerative diseases [29]. Thus, probing viscoelasticity at the single-cell level would potentially facilitate our understanding of how changes in compartmental viscoelasticities correlate to the phase change in condensates and overall cell behavior. At the multicell level within an embryonic tissue, gradients of stiffness measured by the Young’s modulus were discovered as a cue that potentially guides cell migration by a process called durotaxis [30]. However, due to the omission of the viscous properties of ECM, durotaxis may need to be reexamined in the context of viscoelasticity to incorporate the potential role of viscosity in impeding the migratory speed. Viscoelasticity and Developmental Biology is dedicated to the in-depth discussion of existing and potential roles of viscoelasticity in the context of developmental biology.

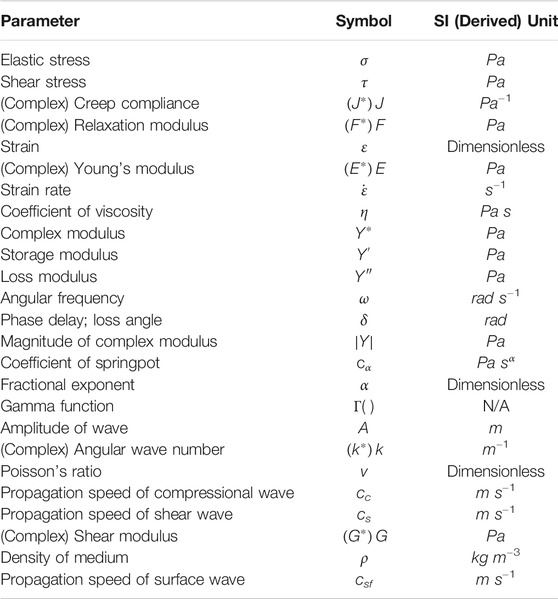
For the purpose of this review, the common assumption made in elastography techniques, that is, biological tissues are isotropic and homogenous, is also assumed. The definitions of elastic stress (σ), whether compressive or tensile, and shear stress (τ) are illustrated in Figures 1A,B, respectively. A glossary of the major parameters discussed throughout this review, in order of appearance, is given in Table 1. Here, the basics of rheological models and properties of waves necessary to understand elastography (Estimation of Material Moduli and Wave Properties and Parameters), as well as the classification of existing elastography techniques used to characterize material viscoelastic properties (Viscoelasticity Measurement with Elastography) have been discussed. The role of viscoelasticity in the context of developmental biology (Viscoelasticity and Developmental Biology), the clinical applications on mature tissues and potential extension to embryonic tissues (Current Applications of Elastography), and an outlook to future directions (Challenge and Outlook) have been outlined.

FIGURE 1

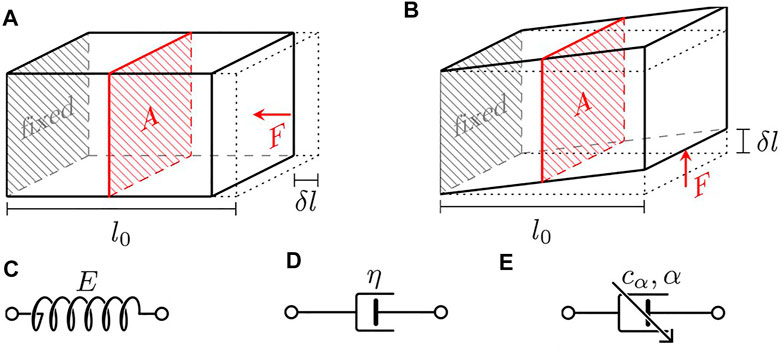
FIGURE 1. Illustration of the definition of stress and schematics of the basic rheological elements. (A) Normal stress, (B) shear stress, (C) Hookean spring, (D) Newtonian dashpot, and (E) fractional springpot.

TABLE 1

TABLE 1. Glossary of parameters.

Estimation of Material Moduli

The classical approach to estimating moduli that reflect the viscoelastic properties of a material is implemented by performing one of the following three canonical tests: creep, stress relaxation, and oscillatory loading. Once the data obtained from the tests, whether time-dependent or frequency-dependent, is fitted with the constitutive equation of a selected rheological model, the coefficient of each parameter within the model can be determined as an approximate representation of the viscoelastic properties of the material. Alternatively, if the constitutive equation is solved in the time domain, the Fourier transform can be taken to derive the solution in the frequency domain [31].

Classical Rheological Models

A common approach to the study of material viscoelasticity is to derive the expression of creep compliance, relaxation modulus, or their complex forms, from the constitutive equation of a linear theoretical framework. Depending on the properties of the material, differently structured rheological models can generate different levels of fit. Expressions of the creep compliance (J) and relaxation modulus (F) are commonly derived in the time domain via creep and stress relaxation tests. If their frequency-dependent complex forms, $\left(J^{\ast }\right)$ and $\left(F^{\ast }\right)$, need to be determined, oscillatory tests are conducted.

Elements of Rheological Models

Classical linear rheological models consist of various combinations of different numbers of Hookean springs, which model elastic behavior, and Newtonian dashpots, which model viscous behavior. Schematics of a Hookean spring and a Newtonian dashpot are shown in Figures 1C,D, respectively. Upon an applied elastic stress (σ), a Hookean spring exhibits linear elastic behavior and immediately produces an elastic strain (ε). The elasticity can be quantitatively represented by the Young’s modulus (E), which determines the stiffness of the material (with units of Pa), via Hooke’s law as follows:

$E=\frac{\sigma }{\epsilon }.(1)$

A Newtonian dashpot exhibits a viscous behavior that is proportional to the strain rate ($\dot{\epsilon }$), which represents the change in strain with respect to time. The viscous behavior is representative of the material fluidity and is expressed (with units of Pa s) via the coefficient of viscosity (η) as follows:

$\eta =\frac{\sigma }{\dot{\epsilon }}.(2)$

Common two-element rheological models include the Maxwell model and the Kelvin–Voigt model. The Maxwell model consists of a Hookean spring of Young’s modulus E in series with a Newtonian dashpot of coefficient of viscosity η. The Kelvin–Voigt model consists of a Hookean spring E and a Newtonian dashpot η in parallel. Models with three elements were also developed to more realistically characterize the creep-recovery and stress relaxation behavior of a viscoelastic material. These include notably the standard linear solid model, also known as the Zener model, which consists of two Hookean springs and one Newtonian dashpot arranged in one of the two equivalent configurations. The schematics of the above rheological models are illustrated in Figures 2A–C.

FIGURE 2

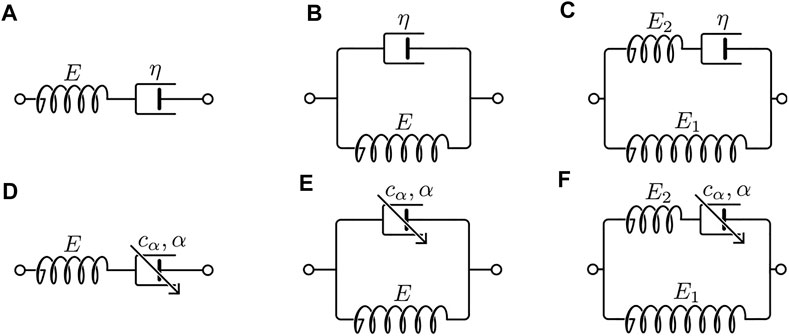
FIGURE 2. Schematics of the classical rheological models and their fractional analogs. (A) Maxwell, (B) Kelvin–Voigt, (C) Zener, (D) fractional Maxwell, (E) fractional Kelvin–Voigt, and (F) fractional Zener.

Creep and Stress Relaxation

There are two one-dimensional tests that utilize the application of a step input to examine material viscoelasticity, namely, creep and stress relaxation. The creep test assesses the time-dependent change in material strain, ε(t), upon the introduction of a step stress. A stress relaxation (or relaxation) response is the time-dependent change in material stress, σ(t), after a step strain is introduced. Data from the creep and relaxation tests are often acquired and analyzed in the time domain. For a linear viscoelastic material, the stress response to a step strain input of ε₀ is defined as follows:

$\sigma \left(t\right)=F\left(t\right){\epsilon }_0.(3)$

Here, F(t) is a monotonically decreasing function of time defined as the relaxation modulus. Similarly, if a step input of stress, σ₀, is introduced, the corresponding creep response is given as follows:

$\epsilon \left(t\right)=J\left(t\right){\sigma }_0.(4)$

Here, J(t) is a monotonically increasing function of time defined as the creep compliance. The mathematical representation of creep compliance and relaxation modulus of the three classical rheological models is summarized in Table 2.

TABLE 2

TABLE 2. Summary of equations of the classical rheological models.

Oscillatory Loading

In an oscillatory loading test, an oscillatory excitation, instead of a step input, is used to disturb the material. The material can be loaded in a time-varying manner such that the response can be examined over a range of frequencies. The complex modulus of the material, $Y^{\ast }$, can be determined using dynamic mechanical analysis (DMA) on the data collected with dynamic mechanical analyzers and rheometers [4, 32]. The complex modulus [33] consists of a real component, the storage modulus $Y^{\text{'}}$, which is the slope of the loading curve that characterizes the elastic behavior and measures the stored energy, and an imaginary component, the loss modulus $Y^{\text{'}\text{'}}$, which is the area bounded by the loading and unloading curves that characterizes the viscous behavior and measures the energy loss. The repetitive depiction of the stress–strain relationship allows for individual estimation of the frequency-dependent storage and loss moduli.

If an oscillatory strain input with an amplitude of ε₀ is applied to a linear material, following the Euler’s formula, its time-dependent form can be written as an exponential:

$\epsilon \left(t\right)={\epsilon }_0{e}^{i\omega t}.(5)$

The corresponding stress response will also be oscillatory with an amplitude of σ₀, but out of phase by δ with the strain input as follows:

$\sigma \left(t\right)={\sigma }_0{e}^{i(\omega t+\delta )}.(6)$

This phase delay, δ, is referred to as the loss angle of the material and reflects to what degree the material is viscoelastic. If the stress and strain curves are completely in phase, the loss angle is at its minimum value of 0 and the material is considered purely elastic. If, however, completely out of phase, the loss angle maximizes at π/2 and the material is purely viscous. The material is considered viscoelastic when the phase delay is away from the boundary limits.

The complex modulus, $Y^{\ast }$, is calculated from the ratio of oscillatory stress to strain, in a similar fashion as how the creep compliance and the relaxation modulus were defined. The storage and loss moduli are directly equated to the real and imaginary components of the ratio as follows:

$Y^{\ast }=\frac{\sigma \left(t\right)}{\epsilon \left(t\right)}=\frac{{\sigma }_0}{{\epsilon }_0}{e}^{i\delta }=\frac{{\sigma }_0}{{\epsilon }_0}\left(\cos \delta +i\sin \delta \right)=Y^{\prime }+i{Y}^{″}.(7)$

The tangent of the loss angle, tan δ, as well as the magnitude of the complex modulus, $\left|Y\right|$, are alternative ways to characterize the complex modulus as follows:

$\tan \delta =\frac{Y^{″}}{Y^{\prime }},(\mathrm{8a})$

$\left|Y\right|=\sqrt{{Y^{\prime }}^2+{Y^{″}}^2}.(\mathrm{8b})$

Similarly, if an oscillatory stress is applied such that σ(t) = σ₀e^iωt, the ratio of oscillatory strain to stress is defined as the complex compliance $J^{\ast }$ that is also composed of a real storage compliance ($J^{\mathit{\prime }}$) and an imaginary loss compliance $\left(J^{″}\right)$ [33]. The complex compliance is used less often due to the practical difficulty to apply and control an oscillatory stress in comparison to an oscillatory strain.

As the oscillatory loading test is often conducted in the frequency domain, the expression of the complex modulus is more often a function of frequency ($Y^{\ast }(\omega$)). Once fitted to a rheological model, the coefficients of each parameter within the model can be determined at a given frequency. The expressions of the complex moduli derived from the constitutive equations of classical rheological models are summarized in Table 2.

Limitation of Classical Rheological Models

Although classical rheological models serve as a foundational theoretical basis for the characterization of material viscoelastic behavior, they are limited by modeling accuracy. The creep and stress relaxation behaviors of the three classical rheological models are shown in Figures 3A–F. When an assumed Maxwell material is subjected to a step stress input of σ₀, the creep response follows a linear relationship as a function of time, which fails to realistically represent the “creeping” behavior as should be observed in a viscoelastic material (Figure 3A). The Kelvin–Voigt model, in comparison, can predict the creep response of a viscoelastic material more realistically as an assumed Kelvin–Voigt material creeps following an increasing exponential decay (Figure 3B). However, it is limited in the ability to model the relaxation response of a viscoelastic material since an impulse at t = 0 is only idealistic (Figure 3E). As models of more elements were developed, including the three-element Zener model and the more generalized Maxwell and Kelvin models, the modeling accuracy was consequently improved. However, as the constitutive equations of multielement models became more complex, the analysis of model parameters became more computationally expensive.

FIGURE 3

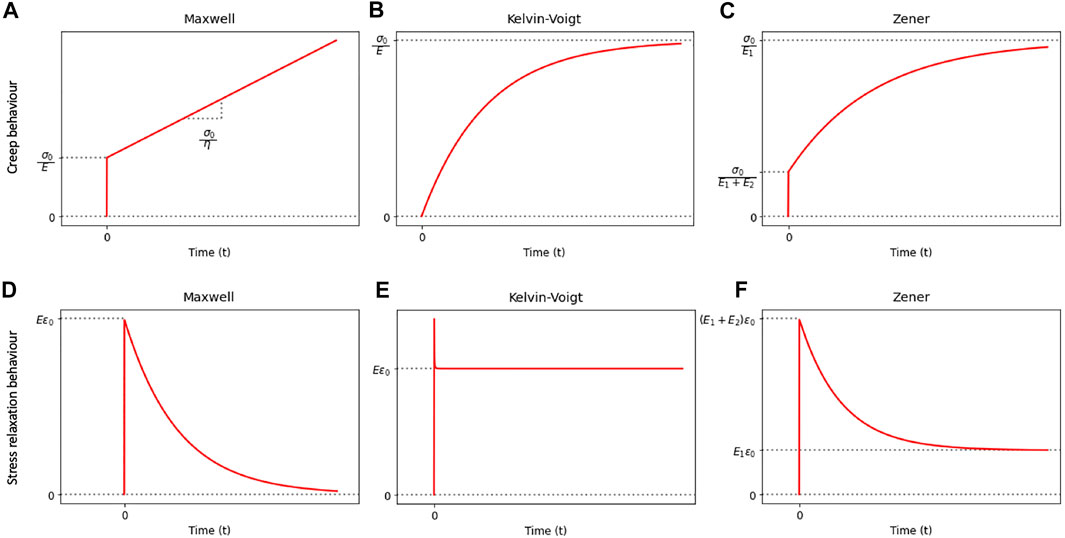
FIGURE 3. Illustration of the creep and stress relaxation behaviors of the classical rheological models.

In fact, studies using generalized models have revealed that the viscoelastic response of several biological tissues [34–37], such as the epithelial tissue, the kidney, and the liver, follows a distinctive power law behavior such that the stress–time, strain–time, and complex modulus–frequency relationships are approximately linear on a log–log scale [31, 38]. For the purpose of modeling the viscoelastic behavior of biological tissues in the common elastography frequency range of 40–1,000 Hz [31], studies have shown that the incorporation of fractional calculus into classical rheology bears modeling advantages [31, 38, 39].

Fractional Models

In fractional models, a fractional derivative element, the fractional springpot (Figure 1E), is introduced. The springpot is defined by its coefficient, c_α, similar to E for a Hookean spring and η for a Newtonian dashpot. The stress–strain relation as defined by a springpot [38] is given as follows:

$\sigma \left(t\right)=c_{\alpha }\frac{d^{\alpha }\epsilon \left(t\right)}{d{t}^{\alpha }}, \alpha \in \left[\mathrm{0,1}\right].(9)$

Conceptually, a springpot is a generalization of the classical viscoelastic components. At the two limiting conditions, one such that the fractional exponent α = 0, the springpot reduces to a Hookean spring and its coefficient c_α becomes E, whereas when α = 1, the springpot reduces to a Newtonian dashpot and its coefficient becomes η. Naturally, a springpot of varying α can exhaustively represent any intermediate viscoelastic behavior bounded by the limiting conditions.

The creep and relaxation behaviors as defined in Eqs 3, 4 can now be characterized by the fractional creep compliance and the relaxation modulus, respectively [38], as follows:

$J\left(t\right)=\frac{1}{c_{\alpha }\text{Γ}(1+\alpha )}{t}^{\alpha },(\mathrm{10a})$

$F\left(t\right)=\frac{c_{\alpha }}{\text{Γ}(1-\text{α})}{t}^{-\alpha }.(\mathrm{10b})$

The creep and relaxation behaviors of the springpot have been adapted to assess the viscoelastic response of a single cell alongside its subcompartments [40–42].

Under an oscillatory input, the complex modulus of a springpot, following the definition from Eq. 7, can be expressed as follows:

$Y^{\ast }=c_{\alpha }{\omega }^{\alpha }{e}^{i\delta }=c_{\alpha }{\omega }^{\alpha }(\cos \delta +i\sin \delta )=Y^{\prime }+i{Y}^{″}, \delta =\frac{\pi }{2}\alpha .(11)$

Fractional models can be constructed from the classical models by replacing the Newtonian dashpot(s) within the original models with springpot(s). Common fractional analogs of the classical models include the fractional Maxwell model, the fractional Kelvin–Voigt model, and the fractional Zener model. Schematics of the fractional analogs are shown in Figures 2D–F. Expressions [38, 43] of the moduli derived based on these fractional models are summarized in Table 3. The creep and relaxation behaviors exhibited by the fractional models with selective values of the fractional exponent are qualitatively illustrated in Figures 4A–F. When α=0, η, as shown in Figures 4A–F, is simply replaced by an E of a different value. Furthermore, a generalized fractional model can be constructed by replacing all model elements with springpots. For an elaborated list of fractional models, analytical expressions of moduli, and illustrative behaviors, please refer to reference [38].

TABLE 3

TABLE 3. Summary of equations of the fractional models.

FIGURE 4

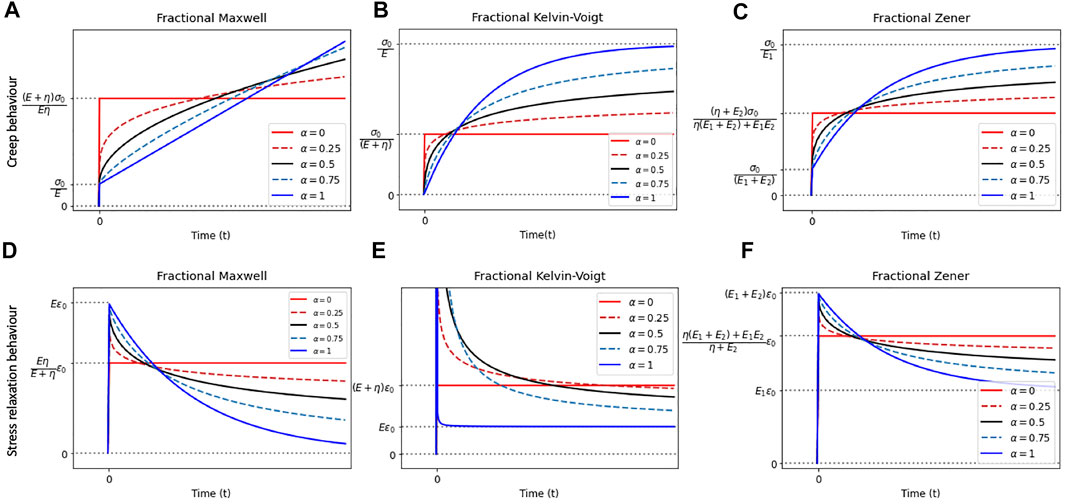
FIGURE 4. Illustration of the creep and stress relaxation behaviors of the fractional rheological models with selective values of α.

Wave Properties and Parameters

This section includes the relevant wave equations that are necessary in facilitating our understanding of how a sample medium can be excited by the propagating waves and how wave parameters can be derived and used to quantify viscoelasticity of the medium. In the context of wave-based elastography techniques, the assumption of one-dimensional, time-harmonic waves that propagate rightward along the +x direction in an unbounded biological medium is sufficient. We, first, restrict our discussion to pure elastic waves that propagate with no energy loss, before expanding to consider wave attenuation in a viscoelastic medium.

Wave Propagation in a Purely Elastic Medium

For a one-dimensional, time-harmonic wave that propagates rightward along the +x direction in an unbounded biological medium, several equations (Eqs 12)–b(16b) have been adapted from [31, 33, 44] to demonstrate the derivation of relevant wave parameters. The displacement of particles along x at time t can be defined as follows:

$u\left(x,t\right)=A{e}^{i(\omega t-kx)}.(12)$

Here, A is the wave amplitude, and k is the wave number which is given as follows:

$k=\frac{\omega }{c}.(13)$

In an elastic medium with known values of Poisson’s ratio (v) and the Young’s modulus (E), the propagation speed of compressional wave (c_c) is as follows:

$c_c=\sqrt{\frac{E(1-v)}{\rho (1+v)(1-2v)}}.(14)$

The propagation speed of shear wave (c_s) in an elastic medium is related to the shear modulus (G) of the medium, medium density (ρ), angular frequency (ω), phase delay (δ), and displacement between two points that the wave propagated through (Δx), which is given as follows:

$c_s=\frac{\omega \text{Δ}x}{\delta },(\mathrm{15a})$

$c_s=\sqrt{\frac{G}{\rho }}.(\mathrm{15b})$

The shear modulus (G) can be inferred from the angular frequency (ω) and wave number (k), or known values of Poisson’s ratio (v) and the Young’s modulus (E), which is given as follows:

$G=\rho c_s^2=\rho \frac{{\omega }^2}{k^2},(\mathrm{16a})$

$G=\frac{E}{2(1+v)}.(\mathrm{16b})$

Another important parameter is the propagation speed of surface acoustic waves (c_sf), which can be related to c_s if evaluated in an elastic medium [45, 46], and is given as follows:

$c_{sf}=c_s\frac{0.87+1.12v}{1+v}=\sqrt{\frac{G}{\rho }}\frac{0.87+1.12v}{1+v}=\sqrt{\frac{E}{2\rho (1+v)}}\frac{0.87+1.12v}{1+v}.(17)$

For nearly incompressible medium, the Poisson’s ratio is approximately 0.5, allowing Eqs 14, 16b, 17 to be further simplified.

Wave Propagation in a Viscoelastic Medium

When waves propagate in a viscoelastic medium, hysteresis occurs due to its viscous nature such that the waves attenuate as they propagate, dissipating energy [31, 47]. In comparison to a purely elastic medium, the stress–strain relationship of a viscoelastic medium is no longer linear. Instead of an instantaneous response to a step input, a complex response is characterized by the complex modulus $Y^{\ast }$, as mentioned in Estimation of Material Moduli. The storage modulus is determined by the restoration of energy due to the elastic property of the medium, while the loss modulus is related to its ability to dissipate energy [33]. The fraction of stored-to-dissipated energy determines whether the medium behaves more like a viscoelastic solid or viscoelastic liquid.

Depending on whether compressional (longitudinal) waves or shear (transverse) waves are propagated, the notation of the generalized complex modulus $Y^{\ast }$ takes on $E^{\ast }$ or $G^{\ast }$, respectively. The equations of the propagation speed of various wave types subsequently reflect the change in medium property. If shear wave propagation is used as an example, Eq. 15b becomes as follows:

$c_s=\sqrt{\frac{G^{\prime }+i{G}^{″}}{\rho }}.(18)$

The wave number also takes a complex form of $k^{\ast }$. Eq. 16a becomes as follows:

$G^{\prime }+i{G}^{″}=\rho \frac{{\omega }^2}{{(k^{\prime }+i{k}^{″})}^2}.(19)$

Equating the real and imaginary components of $G^{\ast }$, expressions of the storage and loss moduli can be individually obtained [47], which is given as follows:

$G^{\prime }=\rho {\omega }^2\frac{k^{\prime 2}-k^{″2}}{{(k^{\prime 2}+k^{″2})}^2},(\mathrm{20a})$

$G^{″}=-2\rho {\omega }^2\frac{k^{\prime }{k}^{″}}{{(k^{\prime 2}+k^{″2})}^2}.(\mathrm{20b})$

Equation 12 can be rewritten to reflect the added influence of attenuation as follows:

$u\left(x,t\right)=A{e}^{i(\omega t-(k^{\prime }+i{k}^{″})x)}=A{e}^{k^{″}x}{e}^{i(\omega t-k^{\prime }x)},(21)$

The real component of the complex wave number, $k^{\prime }$, remains in the same form as Eq. 13. Combining with Eq. 15a, $k^{\prime }$ can be related with the 1D gradient of the phase delay as follows:

$k^{\prime }=\frac{\omega }{c_s}=\frac{\delta }{\text{Δ}x}.(22)$

The term $e^{k^{″}x}$ describes an exponential decay along the +x direction, of which the attenuation coefficient $k^{″}$ has a leading term relating to the first power of frequency [31] as follows:

$k^{″}=-\left(\omega \sqrt{\frac{\rho }{\left|G\right|}}\right){\left(\frac{1}{2}(1-\frac{G^{\prime }}{\left|G\right|})\right)}^{\frac{1}{2}}.(23)$

For biological tissues that exhibit a power law viscoelastic behavior, the wave attenuation may also follow a power law behavior such that ω is replaced with ω^α. The significance and inclusion of these equations will become clear as we move into the details of how elastography techniques are built upon various actuation methods.

Viscoelasticity Measurement With Elastography

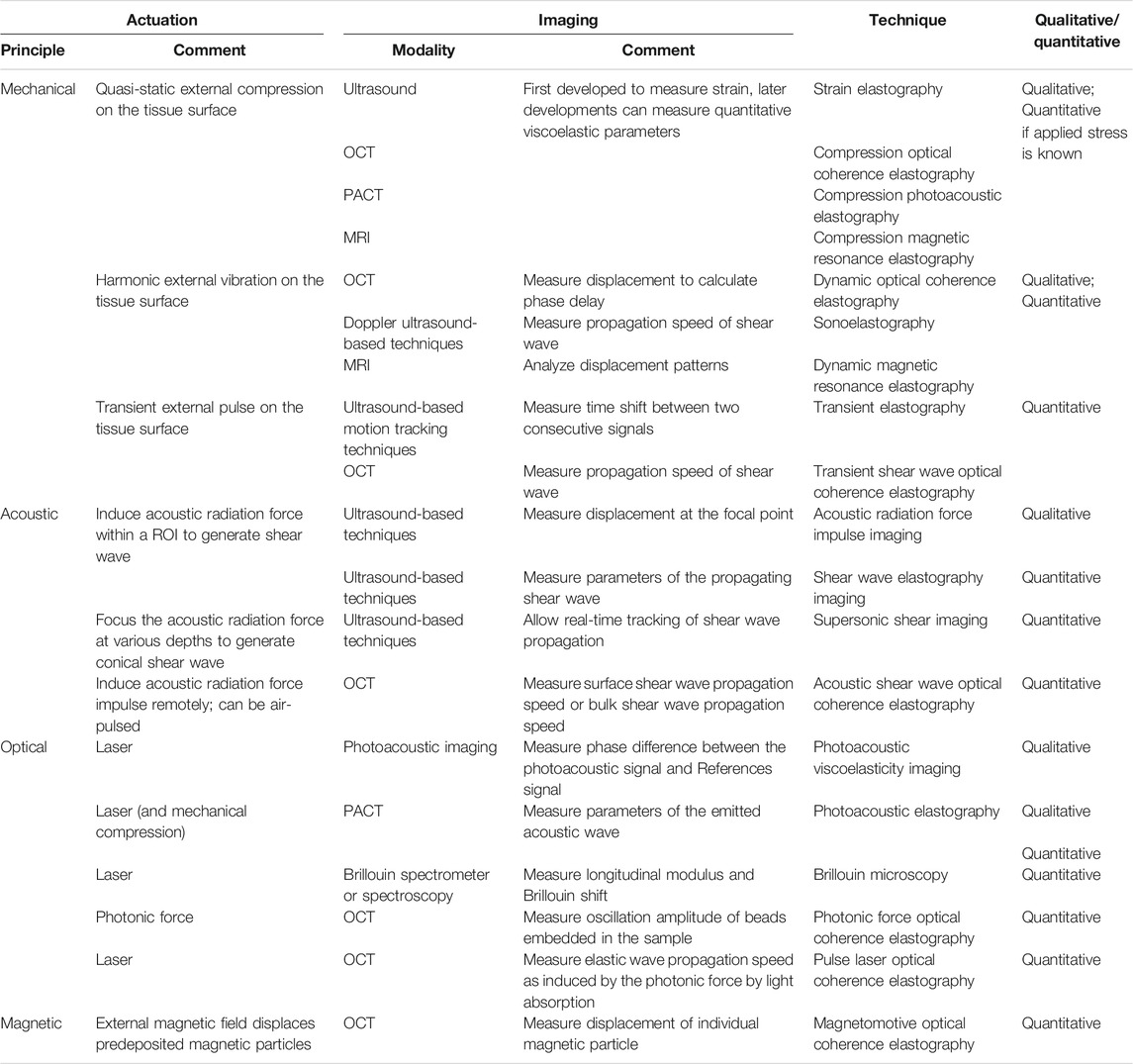
Palpation has long been a principal method to externally examine tissue stiffness. Although it is still commonly used as a preliminary assessment method to detect abnormal tissue, it is unable to provide quantifiable data. With an increasing interest in probing properties deeper within the tissue, the concept of elastography was brought to attention by Ophir et al. in 1991 [9]. Elastography techniques first require a method of actuation that introduces disturbance to the tissue, which is then assessed with an imaging tool, most commonly including ultrasound, magnetic resonance imaging (MRI), optical coherence tomography (OCT), alongside photoacoustic (PA) imaging, and Brillouin spectroscopy (BS). In combination with an actuation method, these form the measuring basis for the earliest ultrasound elastography (USE) [9], magnetic resonance elastography (MRE) [48], optical coherence elastography (OCE) [49], photoacoustic elastography (PAE) [50], and Brillouin Microscopy (BM) [51], respectively. Elastography techniques can often output quantitative values of the storage and loss moduli and/or parameters of a fitted rheological model. In this section, we provide a classification of the types of elastography that have been used on biological tissues and how viscoelasticity can be measured through each method of actuation.

The actuation methods are conceptually illustrated in Figure 5. Mechanical, acoustic, optical, and magnetic means of actuation have been principally developed. They could be quasi-static, transient, or oscillatory. Data gathered through elastography techniques based on oscillatory input are usually analyzed in the frequency domain, and the others in the time domain. In the case of optical actuation, the disturbance is caused by photon absorption or scattering within the tissue, whereas the other methods result in mechanical deformation. A summary of the elastography techniques discussed in this section is provided in Table 4.

FIGURE 5

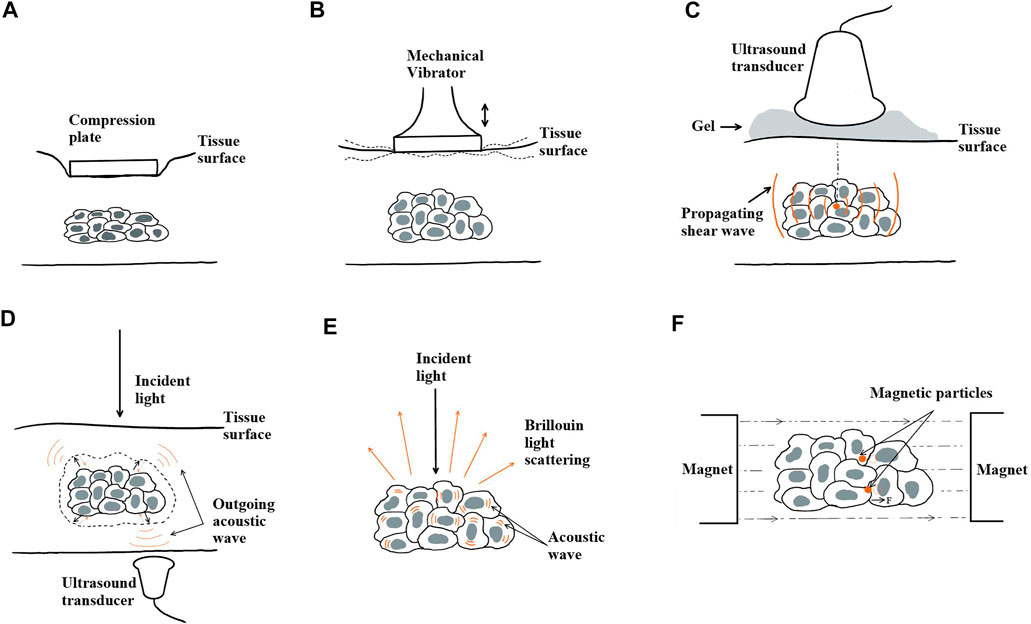
FIGURE 5. Actuation principles of elastography techniques. (A) Quasi-static mechanical actuation, (B) dynamic mechanical actuation, (C) acoustic actuation, (D) optical actuation with photoacoustic effect, (E) optical actuation with Brillouin light scattering, and (F) magnetic actuation.

TABLE 4

TABLE 4. Summary of elastography techniques.

Mechanical Actuation

The mechanical load can be quasi-static (Figure 5A) or dynamic (Figure 5B). Elastography was first developed on the basis of quasi-static mechanical actuation to assess only the elasticity of a sample [9]. In the experimental setup, a compression plate was placed onto the sample surface to alter the local strain within the sample. An ultrasonic transducer was used to send echo signals into the sample. By cross-correlating the pre- and post-compression curves of the echo amplitude, the time delay between two segments of A-lines was determined at the point where the maximum correlation value occurred. From a series of time delays estimated from the cross-correlation of multiple A-line pairs, the axial displacements, a strain profile ε(x), and a Young’s modulus profile E(x), if the applied compressional stress is known, as a function of depth (x) can be estimated. In combination with ultrasonic imaging, this technique is referred to as quasi-static elasticity imaging or strain elastography. Cross-correlation became a fundamental analytical method in strain elastography and was later used to evaluate the viscoelastic behavior of a sample. Once the data gathered through cross-correlation were fitted to a rheological model [52], the Young’s modulus and coefficient of viscosity of the model elements could then be calculated using the constitutive equation of the fitted model. The ease of implementation and cost efficiency in computation have allowed quasi-static compression to be combined with other imaging modalities besides ultrasound. For instance, OCT and MRI have been used in the development of compression OCE [53, 54] and compression MRE [55], respectively. Similarly, upon a quasi-static load or strain, a time-dependent creep or relaxation profile can be obtained via the corresponding imaging modality and used to derive the parameter coefficients once fitted to a rheological model.

Dynamic mechanical actuation requires the placement of a mechanical vibrator onto the sample surface (Figure 5B). The vibrator can produce transient impulses or oscillatory waves that propagate deeper into the sample along the +x direction. If the actuation is induced transiently, a single cycle of sinusoidal wave at low frequency (∼50 Hz) is typically applied to the sample surface, generating both compressional and shear waves that propagate spherically into the sample with distinguishable wave properties [56]. In particular, the propagation speed (c_s) and attenuation $\left(k^{\text{'}\text{'}}\right)$ of the shear wave as functions of depth (x) can be deduced if combined with an appropriate imaging modality of a frame rate in the kHz range [57]. Once fitted to a rheological model, the coefficients of model parameters can be determined [58–60]. Combined with ultrasound-based imaging techniques, this technique is referred to as compression transient elastography [56]. The earlier OCE was also coupled with a transient stepwise mechanical pulse [49].

Sonoelastography is an ultrasound-based elastography technique that applies continuous mechanical vibration to produce low amplitude (less than 0.1 mm) and low frequency (less than 1 kHz) harmonic shear waves [61–63]. Parameters from the vibration patterns at various input frequencies, including the propagation speed of shear wave (c_s) and phase delay (δ), are analyzed from the Doppler shift and fitted into a rheological model to obtain coefficients of viscoelasticity [64]. Using MRI, one of the first viscoelasticity studies was performed by Muthupillai et al. in 1995 in conjunction with dynamic mechanical actuation [48]. This combination was termed dynamic compression MRE, where harmonic mechanical waves of frequency on the lower spectrum (less than 1 kHz) were propagated to induce shear stress. The three-dimensional displacement fields, including u(x,t), and the phase delay extracted from MRI with harmonic motion-sensitizing gradient waveforms were then used to either reconstruct the viscoelastic parameters by inversion of the Helmholtz equation [7, 13], or directly calculate the frequency-dependent complex shear storage $G\text{'}(\omega$) and loss moduli $G\text{'}\text{'}\left(\omega \right)$ of the sample [13, 15]. In the latter case, a rheological model is needed to further determine the shear modulus and coefficient of viscosity of the model elements. Some OCE studies have also been coupled with dynamic compression, including a branch of shear wave OCE that is actuated by direct contact [65–68]. The complex wave number and shear wave speed can be extracted and used to derive the complex shear modulus. A rheological model is necessary if coefficients of viscoelasticity need to be quantified. Spectroscopic OCE (S-OCE) [69] is another representative of dynamic compression OCE. A frequency sweep (0–1,000 Hz) allows the frequency-dependent viscoelastic behavior of the sample to be examined within a range of frequencies. The raw OCT data often undergo several steps of processing to eventually arrive at relationships that can depict the complex viscoelastic response of the sample. A complex OCT signal is first obtained by sampling in the k-space and filtered to minimize phase noise, from which the phase difference, frequency-dependent complex displacement, modulus, and strain rate can be estimated [69, 70]. If the complex modulus is further fitted with a rheological model, individual coefficient of the components within the model can be determined.

Acoustic Actuation

Acoustic actuation relies on focused ultrasound beams produced by an ultrasound transducer to propagate acoustic waves within the tissue sample (Figure 5C). The displacement fields and properties of the propagating acoustic waves can be obtained through the coupled imaging tool to further characterize the viscoelastic behavior of the sample.

A technique referred to as acoustic radiation force impulse (ARFI) imaging developed by Nightingale et al. combined contactless transient acoustic actuation with ultrasound-based imaging [71, 72]. ARFI relies on focused ultrasound beams to deliver a high-intensity burst that generates acoustic radiation force, deforming the sample within a specific region of interest (ROI). The spatiotemporal relaxation behavior of the sample at the focal point is then recorded by the same transducer, and the resulting time-dependent tissue displacements are mapped. By fitting the relaxation behavior to a rheological model, the viscous and elastic parameters of the model may be determined [73].

Another type of acoustic actuation used is based on the properties of acoustic shear wave. A technique that utilizes oscillatory shear waves induced by and propagating in the orthogonal direction of the acoustic actuation is shear wave elasticity imaging (SWEI) [74]. SWEI offers a quantitative assessment of local material viscoelasticity in terms of shear storage modulus ($G^{\text{'}}$) and shear loss modulus ($G^{\text{'}\text{'}}$) derived from the propagation speed of shear wave (c_s) and phase delay (δ). The quantification of sample viscoelasticity is typically carried out by fitting to appropriate rheological models [75]; however, model-independent methods have also been developed [12, 76, 77]. To allow for an extended imaging region and an increased data acquisition speed (∼5,000 fps), supersonic shear imaging (SSI) [78] was developed with the added ability to focus the impulses at multiple focal depths such that conical shear waves can be generated [14, 79]. Another popular coupling modality is OCT, upon which surface acoustic wave OCE (SAW-OCE), acoustic radiation force OCE (ARF-OCE), and shear wave OCE (SW-OCE) have been developed. In SAW-OCE, the phase velocity of the propagating surface wave (c_sf) laterally across the surface of the sample and its dispersion curve can be determined from the phase delay via OCT. Values of the parameters can then be fitted into the Rayleigh wave dispersion equation [80] or a rheological model [81] to extract the viscoelastic parameters. A subset of SAW-OCE termed air-coupled OCE utilizes contactless air puffs to generate SAW, under the influence of which the sample’s time-dependent deformation can be mapped with OCT [45, 80, 82]. The slope and area bounded by the hysteresis curve can be calculated to derive the loss in energy that corresponds to the viscous behavior and storage modulus to the elastic behavior [82]. A rheological model can be used to derive numerical values of the Young’s modulus and coefficient of viscosity. In ARF-OCE, similar to ARFI, an ultrasound transducer is used to propagate pulsed ARF to remotely initiate local sample displacements [83]. The phase delay between adjacent A-lines can be obtained under OCT and used to estimate time-dependent axial displacements and strain. When model-dependent, further estimation of the parameter coefficients can be achieved. ARF-OCE can also be model-independent where the complex shear modulus can be estimated from a direct measurement of the propagation speed of surface wave [83]. Acoustically actuated SW-OCE can sometimes be induced by ARF [84], where the propagation speed of bulk shear waves is used to derive model parameters once fitted.

Optical Actuation

Optical actuation is enabled by the optical properties of biological tissues including absorption and scattering. For example, photoacoustic imaging (Figure 5D) was developed based on the photoacoustic effect by which a sample of biological tissue absorbs the energy from optical beams and releases it in the form of acoustic waves. A technique referred to as photoacoustic viscoelasticity (PAVE) imaging was developed by Gao et al., using intensity-modulated laser beams emitted toward the tissue sample [85]. Developed based on the photoacoustic effect as well, the tissue absorbs incoming light waves and undergoes thermal expansion. The viscoelastic nature of biological tissues introduces a phase delay (δ) in the detected photoacoustic signal, which relates to the viscosity–elasticity ratio (η/E) of the tissue and the modulation frequency (ω) [85], which is given as follows:

$\delta =\text{arctan} \left(\frac{\eta \omega }{E}\right),(24)$

thus providing a qualitative comparison between the viscous and elastic behavior of the tissue sample. Recent advances have demonstrated the feasibility of quantifying the Young’s modulus by establishing a photoacoustic shear wave model [86]. The viscosity parameter can be subsequently determined viaEq. 24.

Using a combination of optical beams, an external vibration source, and a measurement technique based on photoacoustic computed tomography (PACT), photoacoustic elastography (PAE) has emerged in recent years, attempting to measure strain concurrently with the functional parameters of a tissue sample [50, 87, 88]. A strain profile can be obtained from cross-correlating A-line pairs using photoacoustic imaging. If the stress applied by the external vibrator is known, a model can be fitted to quantify the elasticity of the sample. Although only quantitative values of the Young’s modulus have been demonstrated, an extension to viscosity may be achieved if the strain profile can be obtained as a function of time, in a way that is similar to how strain elastography can be used to quantify viscoelastic parameters.

Another optically actuated elastography technique, Brillouin microscopy, uses inelastic Brillouin light scattering as a contrast mechanism to measure properties of biological tissues (Figure 5E). The incident light interacts with the inherent acoustic phonons within the tissue sample. A frequency shift, referred to as the Brillouin shift, is then introduced to the outgoing light. This change in frequency can be directly related to the mechanical properties of the sample by calculating the complex longitudinal modulus containing a real and an imaginary part [51]. The real part yields a measurable frequency shift (v_B), which can be used to derive the longitudinal modulus of the tissue that characterizes its elastic properties [89], whereas the imaginary part is related to the spectral width (Г_B) that can be further used to determine the longitudinal coefficient of viscosity of the material [51, 90].

In combination with OCT, several optically actuated OCE techniques are worth mentioning, namely, photonic force OCE (PH-OCE) and pulse laser OCE. PH-OCE offers a contactless method that induces a harmonically modulated ultra–low radiation pressure force generated by a low-numerical aperture beam [91, 92]. The radiation pressure force subsequently causes sub-nanometer oscillations of predeposited microbeads in a sample. A linear model is used to decouple the mechanical and photothermal responses of the sample to the incoming radiation pressure such that the mechanical response can be isolated. The oscillation amplitude of a microbead can then be captured under OCT and estimated, as it is a function of the input radiation pressure force and radius of the microbead. The oscillation amplitude is also directly related to the complex shear modulus of the sample from which further extraction of viscoelastic parameters can be achieved depending on the choice of a suitable rheological model. In pulse laser OCE [93], wave generation is achieved by focusing pulsed laser irradiation toward the sample. By absorption of the light and localized thermal expansion within the sample, the irradiation is converted into compressional and shear waves that further propagate within the sample. The propagation of the laser-induced elastic waves can be profiled and the local time-dependent displacements can be mapped. A derivation of pulse laser OCE uses dye-loaded perfluorocarbon nanodroplets [94]. When excited by the laser pulse, the nanodroplets undergo rapid liquid–gas phase transition, inducing elastic waves.

Magnetic Actuation

Magnetic actuation introduces a disturbance to the sample using a magnetomotive force generated by an external magnetic field. First, magnetic nanoparticles (MNPs) are predeposited into the sample that is placed within the external magnetic field (Figure 5F). The magnitude and direction of the magnetomotive force can be controlled by adjusting gradients of the magnetic field. The viscoelastic behavior of the surrounding microenvironment of the MNPs in response to the disturbance can be inferred by analyzing the time-dependent displacement of the MNPs. One common imaging modality that magnetic actuation, whether static or dynamic, can be implemented with is OCT. Collectively, this technique is referred to as magnetomotive OCE (MM-OCE) [95–97]. MM-OCE allows for contactless manipulation, through which local MNP displacement in the sub-nanometer range can be detected. Static MM-OCE typically uses OCT to map the time-dependent phase variation in response to a step stress, from which the nanoscale time-dependent local displacements, amplitude with decay, and resonant frequency can be deduced. A rheological model can be fitted to determine the elastic modulus and coefficient of viscosity of the model parameters. Swept-frequency loading techniques have also been implemented in dynamic MM-OCE studies to determine the frequency-dependent viscoelastic behavior of the tissue [97].

Viscoelasticity and Developmental Biology

Physical forces, whether externally applied or internally generated, drive tissue shape changes during embryogenesis [24]. For instance, anisotropic tensional stress orients ectodermal remodeling in the early mouse limb bud [98], anteroposterior (AP) tensile force mediates Drosophila germ band extension [22, 99], contractile force of an actin cable initiates Drosophila dorsal closure [100], tensile convergence force drives Xenopus blastopore closure [23], and the formation of head fold in a chick embryo is driven by a mechanical force that is likely associated with neurulation [101].

Since embryonic tissues exhibit both solid- and liquid-like characteristics, they undergo viscoelastic changes under an applied force [3]. Substrates with various storage-to-loss moduli ratios can be artificially manufactured to mimic properties of the extracellular environment. It has been demonstrated that cells are sensitive to both elasticity and viscosity, resulting in morphological changes, proliferation, spreading, stiffening, softening, migration, and differentiation of cells [102–104]. Changes in the viscoelastic properties of extracellular matrix (ECM) have been shown to affect the functional and migratory behaviors of cells [105]. In an in vivo study of the Drosophila embryo during morphogenesis, myosin II pulses were used to assess how viscous dissipation in response to transient forces can stabilize local cell deformation [106]. Thus, to understand how physical forces regulate morphogenetic movements, characterization of the viscoelastic response within an embryo at both the cellular and tissue scales is necessary. In this section, emphasis is placed on the phase separation and transition of the intracellular membrane-less organelles, durotaxis and viscotaxis, respectively, along with the capability of existing techniques to examine viscoelastic properties at cellular and tissue scales.

Liquid–Liquid Phase Separation and Liquid–Solid Phase Transition

Intracellular mechanics have been shown to directly correlate with intracellular rheology and mechanotransduction [107]. Many intracellular compartments such as subcompartments within the nucleus, stress granules, germ cell granules, actin bodies, and other ribonucleoprotein (RNP) bodies are membrane-less and exhibit liquid-like behavior [108–110]. At the subcellular level, thermodynamic force drives intracellular compartmentalization toward a more energy-favorable state, sequestering molecules that assemble into phase-separated liquid droplets [26, 111]. The process by which condensates form is referred to as liquid–liquid phase separation (LLPS) [112]. During the dynamic dissolution and condensation of intracellular condensates, a cell will likely exhibit any combination of elastic and viscous behaviors as its properties reflect the collective properties of membrane-less and membrane-bound intracellular compartments. In vivo studies have suggested that some condensates, such as the fibrillarin (FIB1) protein, exhibit viscoelastic behavior [27, 108]. As many of the condensates reside within the nucleus and are constituted by RNP bodies [113], the assembly and disassembly of intracellular condensates will likely have an effect on the protein concentration [27, 108, 114] and subsequently the rate at which the condensates contribute to genetic activities that regulate the functional behavior of a cell [113]. For instance, it has been demonstrated in vitro that an increase in the concentration of the RNA LAF-1 within RNP bodies can decrease their viscosity [114]. However, there have been rather limited studies on the mechanical properties of intracellular condensates. Thus, a deeper look into the viscoelastic properties of intracellular and, especially, intranucleolar condensates will likely refine our understanding of the role viscoelasticity plays in nuclear and cellular activities.

During LLPS, liquid droplets can, often undesirably and irreversibly, undergo further liquid–solid phase transition (LSPT) during which compartments progress to a more viscoelastic or even solid-like state [26, 27, 112]. In studies of neurodegenerative diseases, LSPT has been proposed as an explanation for undesirable stiffening and inhibited molecular dynamics [26] due to protein aggregation. For example, LSPT involving a mutant FUS protein is believed to contribute to the progression of ALS [115]. Hence, a shift on the viscoelastic spectrum exhibited by a condensate that is normally fluid-like toward a more solid-like state can suggest a pathological tendency. The protein aggregation driven by LSPT is often irreversible, suggesting it is of value to investigate the exact phase boundary where liquid droplets become solid-like in vivo [116]. The long-term motivation is to detect the onset and monitor the progression of neurodegenerative diseases to assess the adequacy of medical intervention.

Durotaxis and Viscotaxis

Durotaxis was proposed in the early 2000s by Lo et al. as a mechanism by which cells migrate collectively toward greater substrate stiffness [117]. Despite the fact that biological tissues are intrinsically viscoelastic, pioneering in vitro studies in which stiffness gradients were artificially generated to mimic the ECM environment were often conducted on purely elastic substrates [118, 119]. Later studies identified stiffness gradients in vivo during embryogenesis, where the stiffness is commonly quantified using elastic (Young’s or shear) modulus. For example, the apparent elastic modulus of Xenopus cranial mesoderm was measured using atomic force microscopy (AFM), revealing that the collective migration of neural crest cells is triggered by mesodermal stiffening [120]. Also using AFM, it was shown that axonal growth, while not strictly durotaxis, is guided by a stiffness gradient in the brain of the Xenopus embryo [121]. Magnetic tweezers were used to uncover a mesodermal stiffness gradient along which cells migrate within the early mouse limb bud [122].

As the stiffness of ECM is sometimes attributed to the abundance of collagen [123], which can be realistically modeled as a viscoelastic material with quantifiable storage and loss moduli [124], cell-matrix interactions and resulting cell migration thus exhibit dynamic time-dependent mechanical responses [105]. Paths of migration and areas that cells migrate toward are likely of different viscosity in addition to higher elasticity, thereby impacting the timescale of the responses of migrating cells to stiffness gradients [125]. To elucidate the effect of ECM viscosity on cell movements, several in vitro studies have either isolated the effects of the viscosity of substrates or implemented tunable storage-to-loss moduli ratios of substrates. An increase in the substrate loss modulus can lead to viscous drag and cell-matrix energy dissipation that impedes the migratory speed of cells [104, 105, 126–130]. In a separate study using viscoelastic substrates, it was proposed that within a viscous environment, greater migratory speed corresponds to greater apparent modulus [131]. Therefore, the empirically measured Young’s moduli for characterizing local tissue stiffness may differ from the theoretical values in the absence of ECM viscosity considerations. A more recent study constructed a substrate with gradients of viscosity while keeping the elasticity constant, and demonstrated that human mesenchymal stem cells migrate along a viscosity gradient [132]. Viscosity-dependent cell migration has been given the name “viscotaxis” in some studies [132, 133].

To further test the validity of these in vitro observations and to more physiologically evaluate how mechanical cues correlate with cell migration patterns, we believe there is sufficient motivation to examine the role of viscoelasticity gradients in vivo. Results obtained from studies of stiffness, viscosity, and viscoelasticity gradients should be compared to more rigorously delineate the collective migratory behavior of cells in response to mechanical cues.

Existing Techniques for Measuring Embryonic Tissue Viscoelasticity

A handful of methods have been applied to measure the viscoelastic properties of embryonic tissues, including, predominantly, AFM (Figure 6A), magnetic tweezers using magnetic particles or ferrofluid droplets (Figure 6B), and micropipette aspiration (Figure 6C). AFM has been used to quantify the viscoelastic properties of embryonic tissues by indenting the tissue surface and analyzing the approach–retraction hysteresis using rheological models [134, 135]. For instance, AFM has been applied to quantify the elasticity and viscosity of the mouse mandibular arch in vivo [136]. Magnetic tweezers have been used to probe tissue viscoelastic behavior in the early mouse limb bud [122], mouse mandibular arch [137], and Drosophila embryo during cellularization [138]. Other magnetically actuated systems to measure viscoelasticity include ferrofluid oil droplets deployed in the zebrafish tailbud [139] and the Drosophila embryo [140, 141]. Confocal imaging has been combined with computer-aided cell tracking to calculate local tissue strain rate (a measurement of viscosity) during Drosophila germ band extension [22, 99]. Micropipette aspiration, which applies a known suction force to deform a region of interest, has been applied to determine the local viscoelastic response of a tissue or a single cell [142, 143]. For the purpose of measuring the viscoelastic properties of intracellular condensates, microrheology techniques have also been used to quantify the viscosity of the condensates through the Stokes–Einstein relation by assuming the condensates behave as equilibrium Newtonian liquids [112, 114]. For other intracellular structures such as the nuclear actin network, microrheology has also been used to probe the viscoelastic creep response [144]. Magnetic micron-size wires in combination with rotational magnetic spectroscopy have been adapted to measure the shear viscoelasticity of cytoplasm and to quantify the shear modulus and coefficient of viscosity [145]. At the single-cell level, a rheometer has been used in vitro to estimate the time-dependent power law creep function [40], relaxation behavior, and frequency-dependent complex modulus [146].

FIGURE 6

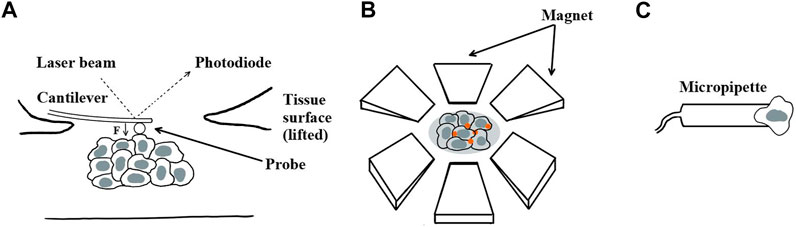
FIGURE 6. Existing techniques for measuring the viscoelasticity of embryonic tissues. (A) Atomic force microscopy, (B) magnetic tweezers, and (C) micropipette aspiration.

However, existing in vivo measurement techniques either require direct contact, are invasive, lack cellular spatial resolution, lack adequate throughput, or are unable to retrieve depth information. A limitation of AFM is that only two-dimensional surface measurements can be reliably taken. Deeper tissue assessment by AFM either requires dissection for exposure or model-based derivation [135, 136], both of which are suboptimal. Magnetic devices allow measurements within a bulk tissue sample but require the injection of magnetic particles or fluids by skilled individuals. Although the use of magnetic particles allows for the simultaneous assessment of multiple locations within a 3D sample, existing magnetic techniques lack broad spatial coverage within an embryo. To define mechanisms of cell migration in 3D, ECM properties and cellular behaviors need to be considered, and techniques that provide noninvasive, continuous, volumetric, and spatially resolved measurements without sacrificing acquisition speed would be ideal.

Current Applications of Elastography

Since quantitative measurements of viscoelasticity have been clinically realized in vivo on a variety of mature tissue types, we selectively list examples of in vivo clinical elastography applications. In comparison, the in vivo application of elastography on embryonic tissues is far less developed. Several examples of using elastography techniques on embryonic animal tissues in vivo are discussed. The challenge in advancing current techniques is discussed in Challenge and Outlook.

Adult Tissue

Transient elastography has been used in vivo for the detection and mapping of aggregated breast tumors within surrounding soft tissues [57], the assessment of stages of liver fibrosis [60], and the quantification of properties of blood clots [59]. Dynamic mechanical actuation has been adapted in compression MRE on assessing a variety of adult tissues such as liver fibrosis [15], breast lesions [7, 147], gray and white matter within the brain [13], and glioblastoma [148]. In the case of liver fibrosis, for instance, the purpose is usually to diagnose and classify stages of fibrosis. Among breast lesions, it is mainly for detecting and distinguishing between malignant and benign tumors. In glioblastoma, viscoelastic measurements are for the purpose of presurgical evaluation. More recently, dynamic compression MRE has been used to assess the differences of subcortical gray matter among adults in different age-groups [149].

SWEI-based elastography has been used to probe the viscoelastic properties of a healthy liver [150], a posttransplant liver [77], liver fibrosis [75], and normal breast tissue [151]. Sonoelastography has been used to assess the shear modulus and viscosity of healthy skeletal muscle [16]. During contraction, an increase in both shear modulus and viscosity has been observed in comparison to the relaxed state [16]. In vivo applications of supersonic shear imaging (SSI) include assessment of the complex shear modulus of breast lesions [79], measuring the viscoelastic and anisotropic properties of muscle tissue [14], and liver tissue [152].

OCE (compression, ARF based, and shear wave.) is extensively used to assess the viscoelastic properties of the human cornea in vivo as the superior submicron scale resolution of OCT can capture subtle changes in wave properties [153] and tissue properties, making it suitable for the detection of early-onset disease such as keratoconus [154]. In addition, in vivo dynamic OCE has been performed on human skin to assess its mechanical properties [155]. BM has, in recent years, been used in noncontact assessment of corneal biomechanics with and without keratoconus [156]. Although the current BM application focuses only on extracting the elastic information in terms of the longitudinal modulus, it is capable of decoupling the viscous component if needed [157].

Embryonic Tissue

Elastography has emerged to measure the viscoelastic properties of embryonic tissues. Most applications have been optically actuated due to the intricate nature of light’s ability to achieve subcellular spatial resolution. The attenuation of light in embryonic tissues is also less of a concern since the tissue can be considered as homogenous and isotropic, such that there is a minimal difference in the refractive indices of different parts of the embryo. Recent advances in OCE have acknowledged its potential for facilitating our understanding of the viscoelastic properties of embryonic tissues [53, 158, 159]. For instance, transient-compression OCE was used for the quantification of viscoelasticity of a living chicken embryo in vivo [160]. BM was used to quantify the longitudinal modulus and viscosity of spinal cord tissue [161], and ECM [162] in vivo in a zebrafish larva. For the purpose of examining the viscoelastic properties of intracellular condensates within a developing cell, a form of magnetic actuation has been used in combination with optical imaging [144].

Challenge and Outlook

Elastography techniques for assessing the viscoelasticity of mature tissues have been established, and future considerations may include tissue anisotropy and heterogeneity to improve measurement accuracy.

Substantial instrument development is still necessary to facilitate further application of the aforementioned elastography techniques to embryonic tissues in vivo. For elastography actuated by quasi-static compression, quantification of the elastic modulus cannot be achieved without known values of the applied stress. Moreover, coupling of the stress applied to the embryo surface requires additional attention and may vary case by case. USE- and MRE-based techniques, regardless of the coupled actuation method, have spatial resolutions of 100–200 μm at best, and therefore generally cannot achieve a spatiotemporal resolution sufficient for capturing the viscoelastic behavior of embryonic tissues [163–165]. Acoustically actuated elastography often requires additional time gain compensation as it suffers from the trade-off between spatial resolution, which increases with increasing frequency of the incoming wave, and attenuation of the wave intensity as the wave travels deeper into the tissue, which also increases with higher frequency. Actuating magnetically, as previously mentioned, requires the deposition of foreign particles into the tissue sample and can only provide measurements at a limited number of locations within a volume. Optical actuation methods are thermally induced. Overabsorption of light energy by the tissue may lead to phototoxicity and tissue damage. In addition, the advantageous cellular resolution offered by OCT is achieved at the sacrifice of depth penetration, although this may be insignificant as the depth of embryonic tissues may be up to several millimeters at most. A unified consideration, therefore, leaves the potential advancements of BS- and OCE-based elastography techniques in the spotlight.

However, there are some limitations. A pitfall of implementing BM on embryonic tissues is that a standardized systematic approach is not yet formulated. The biophysical basis on which the measurements and relationships were derived as well as the appropriateness of applying high frequencies (in GHz range) on biological tissues remain contentious [51, 166]. Furthermore, to be able to quantify the longitudinal modulus, known numerical values of the optical properties of the tissue, including the local refractive index and tissue density, are prerequisites [51]. The complex longitudinal modulus, a parameter also used to characterize viscoelastic behavior, differs from the complex modulus (Young’s or shear) used in existing elastography techniques. The lack of a universal correlation between complex moduli may require additional calibration.

A crucial issue hampering the assessment of mechanisms of morphogenesis is the lack of an appropriate approach for mapping viscoelastic properties in vivo. Despite current drawbacks, BM and OCE are among the few techniques that have the ability to generate 3D in vivo quantitative viscoelasticity data for an embryonic sample. BM can achieve submicron-scale spatial resolution [25, 167], which is sufficient for visualizing subcellular structures. A recent study used BM to reveal a liquid–solid phase transition in intracellular stress granules by measuring the elastic longitudinal modulus [168]. Although no direct measurement was made on the viscoelastic properties, it demonstrated the feasibility of probing intracellular compartments with BM. OCT enables rapid 3D imaging within seconds with millimeter-scale depth penetration [169], can achieve a spatial resolution of 1–10 μm [170, 171], and is able to resolve local displacements at the nanometer scale [172]. Therefore, it may be a fit for more embryonic animal models and possibly human embryos.

To advance the applicability of elastography techniques for assessing embryonic tissue properties, an ideal derivative of current methods would entail an actuation approach that is contactless, or at the minimum, easy to couple, noninvasive, and nondestructive. The technique should neither disturb the surrounding environment of the embryo nor interfere with its natural development. In addition, nontoxicity, which is a property that most optically actuated techniques lack, needs to be considered and carefully calibrated. The imaging method should provide adequate contrast, signal-to-noise ratio, data acquisition speed, and spatial resolution (submicron scale) to capture time-dependent movement of individual cells during a substantive developmental interval. During the next few years, we hope to witness the emergence of such elastography techniques and their applications to developmental biology.

Author Contributions

KZ drafted the manuscript. MZ, ET, SH, and YS edited the manuscript.

Funding

This work was supported by a project grant from the Canadian Institutes of Health Research (#168992).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Fung YC. Biomechanics: Mechanical Properties of Living Tissues. New York, NY: Springer-Verlag (1981).

2. Sasaki N. “Viscoelastic Properties of Biological Materials”, in Viscoelasticity – From Theory to Biological Applications. Editor J. de Vicente IntechOpen (2012).

CrossRef Full Text | Google Scholar

3. Forgacs G, Foty RA, Shafrir Y, Steinberg MS. Viscoelastic Properties of Living Embryonic Tissues: a Quantitative Study. Biophys J (1998) 74(5):2227–34. doi:10.1016/S0006-3495(98)77932-9

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kiss MZ, Varghese T, Hall TJ. Viscoelastic Characterization of In Vitro Canine Tissue. Phys Med Biol (2004) 49(18):4207–18. doi:10.1088/0031-9155/49/18/002

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Pan L, Zan L, Foster FS. Ultrasonic and Viscoelastic Properties of Skin Under Transverse Mechanical Stress In Vitro. Ultrasound Med Biol (1998) 24(7):995–1007. doi:10.1016/S0301-5629(98)00071-4

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Guertler CA, Okamoto RJ, Schmidt JL, Badachhape AA, Johnson CL, Bayly PV. Mechanical Properties of Porcine Brain Tissue In Vivo and Ex Vivo Estimated by MR Elastography. J Biomech (2018) 69:10–8. doi:10.1016/j.jbiomech.2018.01.016

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sinkus R, Tanter M, Xydeas T, Catheline S, Bercoff J, Fink M. Viscoelastic Shear Properties of In Vivo Breast Lesions Measured by MR Elastography. Magn Reson Imaging (2005) 23(2):159–65. doi:10.1016/j.mri.2004.11.060

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Nava A, Mazza E, Furrer M, Villiger P, Reinhart WH. In Vivo Mechanical Characterization of Human Liver. Med Image Anal (2008) 12(2):203–16. doi:10.1016/j.media.2007.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Ophir J, Céspedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: A Quantitative Method for Imaging the Elasticity of Biological Tissues. Ultrason Imaging (1991) 13(2):111–34. doi:10.1177/016173469101300201

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Sarvazyan AP, Skovoroda AR, Emelianov SY, Fowlkes JB, Pipe JG, Adler RS, et al. “Biophysical Bases of Elasticity Imaging,” in Acoustical Imaging. Editor J. P. Jones Boston, MA: Springer (1995), 223–40. doi:10.1007/978-1-4615-1943-0_23

CrossRef Full Text | Google Scholar

11. Pitre JJ, Koziol LB, Kruger GH, Vollmer A, Ophir J, Ammann J-J, et al. Design and Testing of a Single-Element Ultrasound Viscoelastography System for Point-of-Care Edema Quantification. Ultrasound Med Biol (2016) 42(9):2209–19. doi:10.1016/j.ultrasmedbio.2016.04.013

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Kazemirad S, Bernard S, Hybois S, Tang A, Cloutier G. Ultrasound Shear Wave Viscoelastography: Model-Independent Quantification of the Complex Shear Modulus. IEEE Trans Ultrason Ferroelectr Freq Control (2016) 63(9):1399–408. doi:10.1109/TUFFC.2016.2583785

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Green MA, Bilston LE, Sinkus R. In Vivo Brain Viscoelastic Properties Measured by Magnetic Resonance Elastography. NMR Biomed (2008) 21(7):755–64. doi:10.1002/nbm.1254

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Gennisson JL, Deffieux T, Macé E, Montaldo G, Fink M, Tanter M. Viscoelastic and Anisotropic Mechanical Properties of In Vivo Muscle Tissue Assessed by Supersonic Shear Imaging. Ultrasound Med Biol (2010) 36(5):789–801. doi:10.1016/j.ultrasmedbio.2010.02.013

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Garteiser P, Doblas S, Daire J-L, Wagner M, Leitao H, Vilgrain V, et al. MR Elastography of Liver Tumours: Value of Viscoelastic Properties for Tumour Characterisation. Eur Radiol (2012) 22:2169–77. doi:10.1007/s00330-012-2474-6

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Hoyt K, Kneezel T, Castaneda B, Parker KJ. Quantitative Sonoelastography for the In Vivo assessment of Skeletal Muscle Viscoelasticity. Phys Med Biol (2008) 53(15):4063–80. doi:10.1088/0031-9155/53/15/004

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Rus G, Faris IH, Torres J, Callejas A, Melchor J. Why are Viscosity and Nonlinearity Bound to Make an Impact in Clinical Elastographic Diagnosis? Sensors (2020) 20(8):2379. doi:10.3390/s20082379

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Doblas S, Garteiser P, Haddad N, Daire J, Wagner M, Leitão H, et al. Magnetic Resonance Elastography Measurements of Viscosity: A Novel Biomarker for Human Hepatic Tumor Malignancy?. Proc Int Soc Magn Reson Med ISMRM, Canada (2011) 19:389.

Google Scholar

19. Kumar V, Denis M, Gregory A, Bayat M, Mehrmohammadi M, Fazzio R, et al. Viscoelastic Parameters as Discriminators of Breast Masses: Initial Human Study Results. PLoS One (2018) 13(10):e0205717. doi:10.1371/journal.pone.0205717

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Han Z, Aglyamov SR, Li J, Singh M, Wang S, Vantipalli S, et al. Quantitative Assessment of Corneal Viscoelasticity Using Optical Coherence Elastography and a Modified Rayleigh-Lamb Equation. J Biomed Opt (2015) 20(2):020501. doi:10.1117/1.JBO.20.2.020501

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Krieg M, Arboleda-Estudillo Y, Puech P-H, Käfer J, Graner F, Müller DJ, et al. Tensile Forces Govern Germ-Layer Organization in Zebrafish. Nat Cell Biol (2008) 10:429–36. doi:10.1038/ncb1705

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Butler LC, Blanchard GB, Kabla AJ, Lawrence NJ, Welchman DP, Mahadevan L, et al. Cell Shape Changes Indicate a Role for Extrinsic Tensile Forces in Drosophila Germ-Band Extension. Nat Cell Biol (2009) 11:859–64. doi:10.1038/ncb1894

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Shook DR, Kasprowicz EM, Davidson LA, Keller R. Large, Long Range Tensile Forces Drive Convergence During Xenopus Blastopore Closure and Body axis Elongation. Elife (2018) 7:e26944. doi:10.7554/eLife.26944

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Keller R. Physical Biology Returns to Morphogenesis. Science (2012) 338(6014):201–3. doi:10.1126/science.1230718

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Sánchez-Iranzo H, Bevilacqua C, Diz-Muñoz A, Prevedel R. A 3D Brillouin Microscopy Dataset of the In-Vivo Zebrafish Eye. Data Brief (2020) 30:105427. doi:10.1016/j.dib.2020.105427

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Alberti S, Gladfelter A, Mittag T. Considerations and Challenges in Studying Liquid-Liquid Phase Separation and Biomolecular Condensates. Cell (2019) 176(3):419–34. doi:10.1016/j.cell.2018.12.035

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Weber SC. Sequence-Encoded Material Properties Dictate the Structure and Function of Nuclear Bodies. Curr Opin Cell Biol (2017) 46:62–71. doi:10.1016/j.ceb.2017.03.003

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Mongera A, Rowghanian P, Gustafson HJ, Shelton E, Kealhofer DA, Carn EK, et al. A Fluid-to-Solid Jamming Transition Underlies Vertebrate Body Axis Elongation. Nature (2018) 561:401–5. doi:10.1038/s41586-018-0479-2

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Patel A, Lee HO, Jawerth L, Maharana S, Jahnel M, Hein MY, et al. A Liquid-to-Solid Phase Transition of the ALS Protein FUS Accelerated by Disease Mutation. Cell (2015) 162(5):1066–77. doi:10.1016/j.cell.2015.07.047

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Sunyer R, Trepat X. Durotaxis. Curr Biol (2020) 30(9):R383–7. doi:10.1016/j.cub.2020.03.051

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Parker KJ, Szabo T, Holm S. Towards a Consensus on Rheological Models for Elastography in Soft Tissues. Phys Med Biol (2019) 64(21):215012. doi:10.1088/1361-6560/ab453d

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zhu Y, Zhang X, Zheng Y, Chen X, Shen Y, Lin H, et al. Quantitative Analysis of Liver Fibrosis in Rats with Shearwave Dispersion Ultrasound Vibrometry: Comparison with Dynamic Mechanical Analysis. Med Eng Phys (2014) 36(11):1401–7. doi:10.1016/j.medengphy.2014.04.002

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Bland DR. The Theory of Linear Viscoelasticity. Mineola, NY: Dover Publications (2016).

34. Sack I, Jöhrens K, Würfel J, Braun J. Structure-Sensitive Elastography: On the Viscoelastic Powerlaw Behavior of In Vivo Human Tissue in Health and Disease. Soft Matter (2013) 9(24):5672–80. doi:10.1039/C3SM50552A

CrossRef Full Text | Google Scholar

35. Khalilgharibi N, Fouchard J, Asadipour N, Barrientos R, Duda M, Bonfanti A, et al. Stress Relaxation in Epithelial Monolayers is Controlled by the Actomyosin Cortex. Nat Phys (2019) 15:839–47. doi:10.1038/s41567-019-0516-6

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Nicolle S, Vezin P, Palierne J-F. A Strain-Hardening Bi-Power Law for the Nonlinear Behaviour of Biological Soft Tissues. J Biomech (2010) 43(5):927–32. doi:10.1016/j.jbiomech.2009.11.002

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Fabry B, Maksym GN, Butler JP, Glogauer M, Navajas D, Fredberg JJ. Scaling the Microrheology of Living Cells. Phys Rev Lett (2001) 87:148102. doi:10.1103/PhysRevLett.87.148102

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Bonfanti A, Kaplan JL, Charras G, Kabla A. Fractional Viscoelastic Models for Power-Law Materials. Soft Matter (2020) 16(26):6002–20. doi:10.1039/d0sm00354a

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Taylor LS, Lerner AL, Rubens DJ, Parker KJ. “A Kelvin-Voight Fractional Derivative Model for Viscoelastic Characterization of Liver Tissue”, in Proceedings of the ASME 2002 International Mechanical Engineering Congress and Exposition. Advances in Bioengineering, November 17–22, 2002, New Orleans, LA, 447–8.

Google Scholar

40. Desprat N, Richert A, Simeon J, Asnacios A. Creep Function of a Single Living Cell. Biophys J (2005) 88(3):2224–33. doi:10.1529/biophysj.104.050278

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Zhou EH, Quek ST, Lim CT. Power-Law Rheology Analysis of Cells Undergoing Micropipette Aspiration. Biomech Model Mechanobiol (2010) 9:563–72. doi:10.1007/s10237-010-0197-7

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Pullarkat P, Fernandez P, Ott A. Rheological Properties of the Eukaryotic Cell Cytoskeleton. Phys Rep (2007) 449(1–3):29–53. doi:10.1016/j.physrep.2007.03.002

CrossRef Full Text | Google Scholar

43. Mainardi F, Spada G. Creep, Relaxation and Viscosity Properties for Basic Fractional Models in Rheology. Eur Phys J Spec Top (2011) 193(1):133–60. doi:10.1140/epjst/e2011-01387-1

CrossRef Full Text | Google Scholar

44. Truell R, Elbaum C, Chick BB. Ultrasonic Methods in Solid State Physics. Cambridge, MA: Academic Press (2013).

45. Wang S, Li J, Manapuram RK, Menodiado FM, Ingram DR, Twa MD, et al. Noncontact Measurement of Elasticity for the Detection of Soft-Tissue Tumors Using Phase-Sensitive Optical Coherence Tomography Combined with a Focused Air-Puff System. Opt Lett (2012) 37(24):5184–6. doi:10.1364/OL.37.005184

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Kirkpatrick SJ, Duncan DD, Fang L. Low-Frequency Surface Wave Propagation and the Viscoelastic Behavior of Porcine Skin. J Biomed Opt (2004) 9(6):1311. doi:10.1117/1.1803843

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Vappou J, Maleke C, Konofagou EE. Quantitative Viscoelastic Parameters Measured by Harmonic Motion Imaging. Phys Med Biol (2009) 54(11):3579–94. doi:10.1088/0031-9155/54/11/020

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Muthupillai R, Lomas D, Rossman P, Greenleaf J, Manduca A, Ehman R. Magnetic Resonance Elastography by Direct Visualization of Propagating Acoustic Strain Waves. Science (1995) 269(5232):1854–7. doi:10.1126/science.7569924

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Schmitt JM. OCT Elastography: Imaging Microscopic Deformation and Strain of Tissue. Opt Express (1998) 3(6):199–211. doi:10.1364/OE.3.000199

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Hai P, Yao J, Li G, Li C, Wang LV. Photoacoustic Elastography. Opt Lett (2016) 41(4):725–8. doi:10.1364/OL.41.000725

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Prevedel R, Diz-Muñoz A, Ruocco G, Antonacci G. Brillouin Microscopy: An Emerging Tool for Mechanobiology. Nat Methods (2019) 16:969–77. doi:10.1038/s41592-019-0543-3

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Sridhar M, Insana MF. Ultrasonic Measurements of Breast Viscoelasticity. Med Phys (2007) 34(12):4757–67. doi:10.1118/1.2805258

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Kennedy BF, Wijesinghe P, Sampson DD. The Emergence of Optical Elastography in Biomedicine. Nat Photon (2017) 11:215–21. doi:10.1038/nphoton.2017.6

CrossRef Full Text | Google Scholar

54. Wijesinghe P, Mclaughlin RA, Sampson DD, Kennedy BF. Parametric Imaging of Viscoelasticity Using Optical Coherence Elastography. Phys Med Biol (2015) 60(6):2293–307. doi:10.1088/0031-9155/60/6/2293

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Clarke EC, Cheng S, Green M, Sinkus R, Bilston LE. Using Static Preload with Magnetic Resonance Elastography to Estimate Large Strain Viscoelastic Properties of Bovine Liver. J Biomech (2011) 44(13):2461–5. doi:10.1016/j.jbiomech.2011.06.023

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Gennisson J-L, Deffieux T, Fink M, Tanter M. Ultrasound Elastography: Principles and Techniques. Diagn Interv Imaging (2013) 94(5):487–95. doi:10.1016/j.diii.2013.01.022

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Bercoff J, Chaffai S, Tanter M, Sandrin L, Catheline S, Fink M, et al. In Vivo Breast Tumor Detection Using Transient Elastography. Ultrasound Med Biol (2003) 29(10):1387–96. doi:10.1016/S0301-5629(03)00978-5

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Catheline S, Gennisson J-L, Delon G, Fink M, Sinkus R, Abouelkaram S, et al. Measurement of Viscoelastic Properties of Homogeneous Soft Solid Using Transient Elastography: An Inverse Problem Approach. J Acoust Soc Am (2004) 116(6):3734–41. doi:10.1121/1.1815075

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Gennisson J-L, Lerouge S, Cloutier G. Assessment by Transient Elastography of the Viscoelastic Properties of Blood During Clotting. Ultrasound Med Biol (2006) 32(10):1529–37. doi:10.1016/j.ultrasmedbio.2006.06.008

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Zhao J, Zhai F, Cheng J, He Q, Luo J, Yang X, et al. Evaluating the Significance of Viscoelasticity in Diagnosing Early-Stage Liver Fibrosis with Transient Elastography. PLoS One (2017) 12(1):e0170073. doi:10.1371/journal.pone.0170073

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Lerner RM, Parker KJ, Holen J, Gramiak R, Waag RC. Sono-Elasticity: Medical Elasticity Images Derived from Ultrasound Signals in Mechanically Vibrated Targets. Acoust Imaging (1988) 16:317–27. doi:10.1007/978-1-4613-0725-9_31

CrossRef Full Text | Google Scholar

62. Lerner RM, Huang SR, Parker KJ. “Sonoelasticity” Images Derived from Ultrasound Signals in Mechanically Vibrated Tissues. Ultrasound Med Biol (1990) 16(3):231–9. doi:10.1016/0301-5629(90)90002-t

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Taylor LS, Porter BC, Rubens DJ, Parker KJ. Three-Dimensional Sonoelastography: Principles and Practices. Phys Med Biol (2000) 45(6):1477–94. doi:10.1088/0031-9155/45/6/306

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Cortes DH, Suydam SM, Silbernagel KG, Buchanan TS, Elliott DM. Continuous Shear Wave Elastography: A New Method to Measure Viscoelastic Properties of Tendons In Vivo. Ultrasound Med Biol (2015) 41(6):1518–29. doi:10.1016/j.ultrasmedbio.2015.02.001

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Ramier A, Tavakol B, Yun SH. Measuring Mechanical Wave Speed, Dispersion, and Viscoelastic Modulus of the Cornea Using Optical Coherence Elastography. Opt Express (2019) 27(12):16635–49. doi:10.1364/OE.27.016635

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Nguyen TM, Song S, Arnal B, Wong EY, Huang Z, Wang RK, et al. Shear Wave Pulse Compression for Dynamic Elastography Using Phase-Sensitive Optical Coherence Tomography. J Biomed Opt (2014) 19(1):016013. doi:10.1117/1.JBO.19.1.016013

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Kearney SP, Khan A, Dai Z, Royston TJ. Dynamic Viscoelastic Models of Human Skin Using Optical Elastography. Phys Med Biol (2015) 60(17):6975–90. doi:10.1088/0031-9155/60/17/6975

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Jin Z, Zhou Y, Shen M, Wang Y, Lu F, Zhu D. Assessment of Corneal Viscoelasticity Using Elastic Wave Optical Coherence Elastography. J Biophotonics (2019) 13(1):e201960074. doi:10.1002/jbio.201960074

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Adie SG, Liang X, Kennedy BF, John R, Sampson DD, Boppart SA. Spectroscopic Optical Coherence Elastography. Opt Express (2010) 18(25):25519–34. doi:10.1364/OE.18.025519

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Liang X, Adie SG, John R, Boppart SA. Dynamic Spectral-Domain Optical Coherence Elastography for Tissue Characterization. Opt Express (2010) 18(13):14183. doi:10.1364/OE.18.014183

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Nightingale KR, Palmeri ML, Nightingale RW, Trahey GE. On the Feasibility of Remote Palpation Using Acoustic Radiation Force. J Acoust Soc Am (2001) 110(1):625–34. doi:10.1121/1.1378344

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Nightingale K, Soo MS, Nightingale R, Trahey G. Acoustic Radiation Force Impulse Imaging: In Vivo Demonstration of Clinical Feasibility. Ultrasound Med Biol (2002) 28(2):227–35. doi:10.1016/s0301-5629(01)00499-9

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Walker WF, Fernandez FJ, Negron LA. A Method of Imaging Viscoelastic Parameters with Acoustic Radiation Force. Phys Med Biol (2000) 45(6):1437–47. doi:10.1088/0031-9155/45/6/303

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Sarvazyan AP, Rudenko OV, Swanson SD, Fowlkes JB, Emelianov SY. Shear Wave Elasticity Imaging: a New Ultrasonic Technology of Medical Diagnostics. Ultrasound Med Biol (1998) 24(9):1419–35. doi:10.1016/S0301-5629(98)00110-0

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Chen S, Sanchez W, Callstrom MR, Gorman B, Lewis JT, Sanderson SO, et al. Assessment of Liver Viscoelasticity by Using Shear Waves Induced by Ultrasound Radiation Force. Radiology (2013) 266(3):964–70. doi:10.1148/radiol.12120837

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Amador C, Urban MW, Chen S, Greenleaf JF. Loss Tangent and Complex Modulus Estimated by Acoustic Radiation Force Creep and Shear Wave Dispersion. Phys Med Biol (2012) 57(5):1263–82. doi:10.1088/0031-9155/57/5/1263

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Nenadic IZ, Urban MW, Heng Zhao H, Sanchez W, Morgan PE, Greenleaf JF, et al. “Application of Attenuation Measuring Ultrasound Shearwave Elastography in 8 Post-Transplant Liver Patients”, in IEEE International Ultrasonics Symposium, Chicago, IL, September 3–4, 2014, 987–90. (2014). doi:10.1109/ULTSYM.2014.0242

CrossRef Full Text | Google Scholar

78. Bercoff J, Tanter M, Fink M. Supersonic Shear Imaging: A New Technique for Soft Tissue Elasticity Mapping. IEEE Trans Ultrason Ferroelect Freq Contr (2004) 51(4):396–409. doi:10.1109/TUFFC.2004.1295425

CrossRef Full Text | Google Scholar

79. Tanter M, Bercoff J, Athanasiou A, Deffieux T, Gennisson J-L, Montaldo G, et al. Quantitative Assessment of Breast Lesion Viscoelasticity: Initial Clinical Results Using Supersonic Shear Imaging. Ultrasound Med Biol (2008) 34(9):1373–86. doi:10.1016/j.ultrasmedbio.2008.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Han Z, Singh M, Aglyamov SR, Liu C-H, Nair A, Raghunathan R, et al. Quantifying Tissue Viscoelasticity Using Optical Coherence Elastography and the Rayleigh Wave Model. J Biomed Opt (2016) 21(9):090504. doi:10.1117/1.JBO.21.9.090504

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Zvietcovich F, Rolland JP, Parker KJ. An Approach to Viscoelastic Characterization of Dispersive Media by Inversion of a General Wave Propagation Model. J Innov Opt Health Sci (2017) 10(6):1742008. doi:10.1142/S1793545817420081

CrossRef Full Text | Google Scholar

82. Maczynska E, Karnowski K, Szulzycki K, Malinowska M, Dolezyczek H, Cichanski A, et al. Assessment of the Influence of Viscoelasticity of Cornea in Animal Ex Vivo Model Using Air-Puff Optical Coherence Tomography and Corneal Hysteresis. J Biophotonics (2018) 12(2):e201800154. doi:10.1002/jbio.201800154

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Leartprapun N, Iyer R, Adie SG. “Model-Independent Quantification of Soft Tissue Viscoelasticity with Dynamic Optical Coherence Elastography. Opt Coherence Tomogr Coherence Domain Opt Methods Biomed (2017) XXI:1005322. doi:10.1117/12.2251626

CrossRef Full Text | Google Scholar

84. Zhu J, Qi L, Miao Y, Ma T, Dai C, Qu Y, et al. 3D Mapping of Elastic Modulus Using Shear Wave Optical Micro-Elastography. Sci Rep (2016) 6(1):1–9. doi:10.1038/srep35499

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Gao G, Yang S, Xing D. Viscoelasticity Imaging of Biological Tissues with Phase-Resolved Photoacoustic Measurement. Opt Lett (2011) 36(17):3341–3. doi:10.1364/OL.36.003341

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Wang Q, Shi Y, Yang F, Yang S. Quantitative Photoacoustic Elasticity and Viscosity Imaging for Cirrhosis Detection. Appl Phys Lett (2018) 112:211902. doi:10.1063/1.5021675

CrossRef Full Text | Google Scholar

87. Wang LV, Hu S. Photoacoustic Tomography: In Vivo Imaging from Organelles to Organs. Science (2012) 335(6075):1458–62. doi:10.1126/science.1216210

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Singh MS, Thomas A. Photoacoustic Elastography Imaging: A Review. J Biomed Opt (2019) 24(4):040902. doi:10.1117/1.JBO.24.4.040902

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Elsayad K, Werner S, Gallemi M, Kong J, Sanchez Guajardo ER, Zhang L, et al. Mapping the Subcellular Mechanical Properties of Live Cells in Tissues with Fluorescence Emission-Brillouin Imaging. Sci Signal (2016) 9(435):rs5. doi:10.1126/scisignal.aaf6326

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Mattana S, Caponi S, Tamagnini F, Fioretto D, Palombo F. Viscoelasticity of Amyloid Plaques in Transgenic Mouse Brain Studied by Brillouin Microspectroscopy and Correlative Raman Analysis. J Innov Opt Health Sci (2017) 10(6):1742001. doi:10.1142/s1793545817420019

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Leartprapun N, Iyer RR, Untracht GR, Mulligan JA, Adie SG. Photonic Force Optical Coherence Elastography for Three-Dimensional Mechanical Microscopy. Nat Commun (2018) 9:2079. doi:10.1038/s41467-018-04357-8

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Leartprapun N, Lin Y, Adie SG. Microrheological Quantification of Viscoelastic Properties with Photonic Force Optical Coherence Elastography. Opt Express (2019) 27:22615. doi:10.1364/oe.27.022615

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Das S, Schill A, Liu C-H, Aglyamov S, Larin KV. Laser-Induced Elastic Wave Classification: Thermoelastic Versus Ablative Regimes for All-Optical Elastography Applications. J Biomed Opt (2020) 25:1–13. doi:10.1117/1.jbo.25.3.035004

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Liu CH, Nevozhay D, Sokolov KV, Larin KV. “Tissue Biomechanics with Nanobomb Optical Coherence Elastography”, in Biophotonics Congress: Biomed Optics Congress, Hollywood, FL, April 3–6, 2018 (2018).

CrossRef Full Text | Google Scholar

95. Huang PC, Iyer RR, Liu YZ, Boppart SA. Single-Shot Two-Dimensional Spectroscopic Magnetomotive Optical Coherence Elastography with Graphics Processing Unit Acceleration. Opt Lett (2020) 45(15):4124. doi:10.1364/OL.397900

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Crecea V, Oldenburg AL, Liang X, Ralston TS, Boppart SA. Magnetomotive Nanoparticle Transducers for Optical Rheology of Viscoelastic Materials. Opt Express (2009) 17(25):23114. doi:10.1364/OE.17.023114

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Oldenburg AL, Boppart SA. Resonant Acoustic Spectroscopy of Soft Tissues Using Embedded Magnetomotive Nanotransducers and Optical Coherence Tomography. Phys Med Biol (2010) 55(4):1189–201. doi:10.1088/0031-9155/55/4/019

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Lau K, Tao H, Liu H, Wen J, Sturgeon K, Sorfazlian N, et al. Anisotropic Stress Orients Remodelling of Mammalian Limb Bud Ectoderm. Nat Cell Biol (2015) 17:569–79. doi:10.1038/ncb3156

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Blanchard GB, Kabla AJ, Schultz NL, Butler LC, Sanson B, Gorfinkiel N, et al. Tissue Tectonics: Morphogenetic Strain Rates, Cell Shape Change and Intercalation. Nat Methods (2009) 6:458–64. doi:10.1038/nmeth.1327

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Solon J, Kaya-Çopur A, Colombelli J, Brunner D. Pulsed Forces Timed by a Ratchet-Like Mechanism Drive Directed Tissue Movement During Dorsal Closure. Cell (2009) 137(7):1331–42. doi:10.1016/j.cell.2009.03.050

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Varner VD, Voronov DA, Taber LA. Mechanics of Head Fold Formation: Investigating Tissue-Level Forces During Early Development. Development (2010) 137:3801–11. doi:10.1242/dev.054387

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Charrier EE, Pogoda K, Wells RG, Janmey PA. Control of Cell Morphology and Differentiation by Substrates with Independently Tunable Elasticity and Viscous Dissipation. Nat Commun (2018) 9:449. doi:10.1038/s41467-018-02906-9

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Barriga EH, Mayor R. Adjustable Viscoelasticity Allows for Efficient Collective Cell Migration. Semin Cell Dev Biol (2019) 93:55–68. doi:10.1016/j.semcdb.2018.05.027

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Cameron AR, Frith JE, Cooper-White JJ. The Influence of Substrate Creep on Mesenchymal Stem Cell Behaviour and Phenotype. Biomaterials (2011) 32:5979–93. doi:10.1016/j.biomaterials.2011.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Chaudhuri O, Cooper-White J, Janmey PA, Mooney DJ, Shenoy VB. Effects of Extracellular Matrix Viscoelasticity on Cellular Behaviour. Nature (2020) 584:535–46. doi:10.1038/s41586-020-2612-2

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Clément R, Dehapiot B, Collinet C, Lecuit T, Lenne P-F. Viscoelastic Dissipation Stabilizes Cell Shape Changes during Tissue Morphogenesis. Curr Biol (2017) 27(20):3132–42. doi:10.1016/j.cub.2017.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Mathieu S, Manneville J-B. Intracellular Mechanics: Connecting Rheology and Mechanotransduction. Curr Opin Cell Biol (2019) 56:34–44. doi:10.1016/j.ceb.2018.08.007

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Feric M, Vaidya N, Harmon TS, Mitrea DM, Zhu L, Richardson TM, et al. Coexisting Liquid Phases Underlie Nucleolar Subcompartments. Cell (2016) 165:1686–97. doi:10.1016/j.cell.2016.04.047

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Hyman AA, Weber CA, Jülicher F. Liquid-Liquid Phase Separation in Biology. Annu Rev Cell Dev Biol (2014) 30:39–58. doi:10.1146/annurev-cellbio-100913-013325

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Malinovska L, Kroschwald S, Alberti S. Protein Disorder, Prion Propensities, and Self-Organizing Macromolecular Collectives. Biochim Biophys Acta (2013) 1834(5):918–31. doi:10.1016/j.bbapap.2013.01.003

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Banani SF, Lee HO, Hyman AA, Rosen MK. Biomolecular Condensates: Organizers of Cellular Biochemistry. Nat Rev Mol Cell Biol (2017) 18:285–98. doi:10.1038/nrm.2017.7

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Brangwynne CP, Eckmann CR, Courson DS, Rybarska A, Hoege C, Gharakhani J, et al. Germline P Granules are Liquid Droplets that Localize by Controlled Dissolution/Condensation. Science (2009) 324(5935):1729–32. doi:10.1126/science.1172046

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Shin Y, Chang Y-C, Lee DSW, Berry J, Sanders DW, Ronceray P, et al. Liquid Nuclear Condensates Mechanically Sense and Restructure the Genome. Cell (2019) 176:1518. doi:10.1016/j.cell.2019.02.025

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Elbaum-Garfinkle S, Kim Y, Szczepaniak K, Chen CC, Eckmann CR, Myong S, et al. The Disordered P Granule Protein LAF-1 Drives Phase Separation into Droplets with Tunable Viscosity and Dynamics. Proc Natl Acad Sci USA (2015) 112(23):7189-94. doi:10.1073/pnas.1504822112

CrossRef Full Text | Google Scholar

115. Li YR, King OD, Shorter J, Gitler AD. Stress Granules as Crucibles of ALS Pathogenesis. J Cell Biol (2013) 201(3):361–72. doi:10.1083/jcb.201302044

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Loewe B, Chiang M, Marenduzzo D, Marchetti MC. Solid-Liquid Transition of Deformable and Overlapping Active Particles. Phys Rev Lett (2020) 125(3):038003. doi:10.1103/PhysRevLett.125.038003

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Lo CM, Wang HB, Dembo M, Wang Y. Cell Movement is Guided by the Rigidity of the Substrate. Biophys J (2000) 79(1):144–52. doi:10.1016/S0006-3495(00)76279-5

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Hartman CD, Isenberg BC, Chua SG, Wong JY. Vascular Smooth Muscle Cell Durotaxis Depends on Extracellular Matrix Composition. Proc Natl Acad Sci USA (2016) 113(40):11190–5. doi:10.1073/pnas.1611324113

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Sunyer R, Conte V, Escribano J, Elosegui-Artola A, Labernadie A, Valon L, et al. Collective Cell Durotaxis Emerges from Long-Range Intercellular Force Transmission. Science (2016) 353(6304):1157–61. doi:10.1126/science.aaf7119

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Barriga EH, Franze K, Charras G, Mayor R. Tissue Stiffening Coordinates Morphogenesis by Triggering Collective Cell Migration In Vivo. Nature (2018) 554:523–7. doi:10.1038/nature25742

PubMed Abstract | CrossRef Full Text | Google Scholar

121. Koser DE, Thompson AJ, Foster SK, Dwivedy A, Pillai EK, Sheridan GK, et al. Mechanosensing is Critical for Axon Growth in the Developing Brain. Nat Neurosci (2016) 19(12):1592–8. doi:10.1038/nn.4394

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Zhu M, Tao H, Samani M, Luo M, Wang X, Hopyan S, et al. Spatial Mapping of Tissue Properties In Vivo Reveals a 3D Stiffness Gradient in the Mouse Limb Bud. Proc Natl Acad Sci USA (2020). 117(9):4781–91. doi:10.1073/pnas.1912656117

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Clément B. “Extracellular Matrix Remodelling and Matrix Metalloproteinases in the Liver”, in Matrix Metalloproteinases in Tissue Remodelling and Inflammation. Editors V Lagente, and E. Boichot Birkhäuser Basel (2008). doi:10.1007/978-3-7643-8585-9_9

Google Scholar

124. Forgacs G, Newman SA, Hinner B, Maier CW, Sackmann E. Assembly of Collagen Matrices as a Phase Transition Revealed by Structural and Rheologic Studies. Biophysical J (2003) 84:1272–80. doi:10.1016/s0006-3495(03)74942-x

CrossRef Full Text | Google Scholar

125. Collinet C, Lecuit T. Programmed and Self-Organized Flow of Information during Morphogenesis. Nat Rev Mol Cell Biol (2021) 22:245–65. doi:10.1038/s41580-020-00318-6

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Cai D, Dai W, Prasad M, Luo J, Gov NS, Montell DJ. Modeling and Analysis of Collective Cell Migration in an In Vivo Three-dimensional Environment. Proc Natl Acad Sci USA (2016) 113(15):E2134–41. doi:10.1073/pnas.1522656113

CrossRef Full Text | Google Scholar

127. Müller C, Müller A, Pompe T. Dissipative Interactions in Cell-Matrix Adhesion. Soft Matter (2013) 9:6207. doi:10.1039/c3sm50803j

CrossRef Full Text | Google Scholar

128. Schultz KM, Kyburz KA, Anseth KS. Measuring Dynamic Cell-Material Interactions and Remodeling During 3D Human Mesenchymal Stem Cell Migration in Hydrogels. Proc Natl Acad Sci USA (2015) 112:E3757–E3764. doi:10.1073/pnas.1511304112

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Murrell M, Kamm R, Matsudaira P. Substrate Viscosity Enhances Correlation in Epithelial Sheet Movement. Biophys J (2011) 101:297–306. doi:10.1016/j.bpj.2011.05.048

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Charrier EE, Pogoda K, Li R, Wells RG, Janmey PA. Elasticity-Dependent Response of Malignant Cells to Viscous Dissipation. Biomech Model Mechanobiol (2020) 20:145–54. doi:10.1007/s10237-020-01374-9

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Martinez JS, Lehaf AM, Schlenoff JB, Keller TCS. Cell Durotaxis on Polyelectrolyte Multilayers with Photogenerated Gradients of Modulus. Biomacromolecules (2013) 14:1311–20. doi:10.1021/bm301863a

PubMed Abstract | CrossRef Full Text | Google Scholar

132. Shirke PU, Goswami H, Kumar V, Shah D, Das S, Bellare J, et al. “Viscotaxis”- Directed Migration of Mesenchymal Stem Cells in Response to Loss Modulus Gradient. bioRxiv (2020) 804492. doi:10.1101/804492

CrossRef Full Text | Google Scholar

133. Liebchen B, Monderkamp P, ten Hagen B, Löwen H. Viscotaxis : Microswimmer Navigation in Viscosity Gradients. Phys Rev Lett (2018) 120:120. doi:10.1103/physrevlett.120.208002

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Krieg M, Fläschner G, Alsteens D, Gaub BM, Roos WH, Wuite GJL, et al. Atomic Force Microscopy-Based Mechanobiology. Nat Rev Phys (2019) 1:41–57. doi:10.1038/s42254-018-0001-7

CrossRef Full Text | Google Scholar

135. Efremov YM, Wang W-H, Hardy SD, Geahlen RL, Raman A. Measuring Nanoscale Viscoelastic Parameters of Cells Directly from AFM Force-Displacement Curves. Sci Rep (2017) 7:1541. doi:10.1038/s41598-017-01784-3

PubMed Abstract | CrossRef Full Text | Google Scholar

136. Tao H, Zhu M, Lau K, Whitley OKW, Samani M, Xiao X, et al. Oscillatory Cortical Forces Promote Three Dimensional Cell Intercalations that Shape the Murine Mandibular Arch. Nat Commun (2019) 10:1703. doi:10.1038/s41467-019-09540-z

PubMed Abstract | CrossRef Full Text | Google Scholar

137. Zhu M, Zhang K, Tao H, Hopyan S, Sun Y. Magnetic Micromanipulation for In Vivo Measurement of Stiffness Heterogeneity and Anisotropy in the Mouse Mandibular Arch. Research (2020) 2020:7914074. doi:10.34133/2020/7914074

PubMed Abstract | CrossRef Full Text | Google Scholar

138. D'Angelo A, Dierkes K, Carolis C, Salbreux G, Solon J. In Vivo Force Application Reveals a Fast Tissue Softening and External Friction Increase during Early Embryogenesis. Curr Biol (2019) 29(9):1564–71. doi:10.1016/j.cub.2019.04.010

PubMed Abstract | CrossRef Full Text | Google Scholar

139. Serwane F, Mongera A, Rowghanian P, Kealhofer DA, Lucio AA, Hockenbery ZM, et al. In Vivo quantification of Spatially Varying Mechanical Properties in Developing Tissues. Nat Methods (2017) 14:181–6. doi:10.1038/nmeth.4101

PubMed Abstract | CrossRef Full Text | Google Scholar

140. He B, Doubrovinski K, Polyakov O, Wieschaus E. Apical Constriction Drives Tissue-Scale Hydrodynamic Flow to Mediate Cell Elongation. Nature (2014) 508(7496):392–6. doi:10.1038/nature13070

PubMed Abstract | CrossRef Full Text | Google Scholar

141. Doubrovinski K, Swan M, Polyakov O, Wieschaus EF. Measurement of Cortical Elasticity inDrosophila Melanogasterembryos Using Ferrofluids. Proc Natl Acad Sci USA (2017) 114(5):1051–6. doi:10.1073/pnas.1616659114

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Dassow MV, Strother JA, Davidson LA. Surprisingly Simple Mechanical Behavior of a Complex Embryonic Tissue. PLoS One (2010) 5:e15359. doi:10.1371/journal.pone.0015359

PubMed Abstract | CrossRef Full Text | Google Scholar

143. Guevorkian K, Gonzalez-Rodriguez D, Carlier C, Dufour S, Brochard-Wyart F. Mechanosensitive Shivering of Model Tissues Under Controlled Aspiration. Proc Natl Acad Sci (2011) 108:13387–92. doi:10.1073/pnas.1105741108

PubMed Abstract | CrossRef Full Text | Google Scholar

144. Feric M, Broedersz CP, Brangwynne CP. Soft Viscoelastic Properties of Nuclear Actin Age Oocytes Due to Gravitational Creep. Sci Rep (2015) 5:16607. doi:10.1038/srep16607

PubMed Abstract | CrossRef Full Text | Google Scholar

145. Berret J-F. Local Viscoelasticity of Living Cells Measured by Rotational Magnetic Spectroscopy. Nat Commun (2016) 7:10134. doi:10.1038/ncomms10134

PubMed Abstract | CrossRef Full Text | Google Scholar

146. Desprat N, Guiroy A, Asnacios A. Microplates-Based Rheometer for a Single Living Cell. Rev Scientific Instr (2006) 77(5):055111. doi:10.1063/1.2202921

CrossRef Full Text | Google Scholar

147. Sinkus R, Siegmann K, Xydeas T, Tanter M, Claussen C, Fink M. MR Elastography of Breast Lesions: Understanding the Solid/liquid Duality Can Improve the Specificity of Contrast-Enhanced MR Mammography. Magn Reson Med (2007) 58(6):1135–44. doi:10.1002/mrm.21404

PubMed Abstract | CrossRef Full Text | Google Scholar

148. Streitberger K-J, Reiss-Zimmermann M, Freimann FB, Bayerl S, Guo J, Arlt F, et al. High-Resolution Mechanical Imaging of Glioblastoma by Multifrequency Magnetic Resonance Elastography. PLoS One (2014) 9:e110588. doi:10.1371/journal.pone.0110588

PubMed Abstract | CrossRef Full Text | Google Scholar

149. Hiscox LV, Johnson CL, McGarry MDJ, Perrins M, Littlejohn A, van Beek EJR, et al. High-Resolution Magnetic Resonance Elastography Reveals Differences in Subcortical Gray Matter Viscoelasticity between Young and Healthy Older Adults. Neurobiol Aging (2018) 65:158–67. doi:10.1016/j.neurobiolaging.2018.01.010

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Amador Carrascal C, Chen S, Urban MW, Greenleaf JF. Acoustic Radiation Force-Induced Creep-Recovery (ARFICR): A Noninvasive Method to Characterize Tissue Viscoelasticity. IEEE Trans Ultrason Ferroelectr Freq Control (2018) 65:3–13. doi:10.1109/tuffc.2017.2768184

PubMed Abstract | CrossRef Full Text | Google Scholar

151. Rzymski P, Skórzewska A, Skibińska-Zielińska M, Opala T. Factors Influencing Breast Elasticity Measured by the Ultrasound Shear Wave Elastography - Preliminary Results. Arch Med Sci (2011) 7(1):127–33. doi:10.5114/aoms.2011.20617

PubMed Abstract | CrossRef Full Text | Google Scholar

152. Muller M, Gennisson J-L, Deffieux T, Tanter M, Fink M. Quantitative Viscoelasticity Mapping of Human Liver Using Supersonic Shear Imaging: Preliminary In Vivo Feasability Study. Ultrasound Med Biol (2009) 35(2):219–29. doi:10.1016/j.ultrasmedbio.2008.08.018

PubMed Abstract | CrossRef Full Text | Google Scholar

153. Lan G, Aglyamov SR, Larin KV, Twa MD. In Vivo Human Corneal Shear-Wave Optical Coherence Elastography. Optom Vis Sci (2021) 98(1):58–63. doi:10.1097/OPX.0000000000001633

PubMed Abstract | CrossRef Full Text | Google Scholar

154. Ramier A, Eltony AM, Chen Y, Clouser F, Birkenfeld JS, Watts A, et al. In Vivo Measurement of Shear Modulus of the Human Cornea Using Optical Coherence Elastography. Sci Rep (2020) 10:10. doi:10.1038/s41598-020-74383-4

PubMed Abstract | CrossRef Full Text | Google Scholar

155. Kennedy BF, Hillman TR, Mclaughlin RA, Quirk BC, Sampson DD. In Vivo Dynamic Optical Coherence Elastography Using a Ring Actuator. Opt Express (2009) 17(24):21762–72. doi:10.1364/OE.17.021762

PubMed Abstract | CrossRef Full Text | Google Scholar

156. Yun SH, Chernyak D. Brillouin Microscopy. Curr Opin Ophthalmol (2018) 29(4):299–305. doi:10.1097/ICU.0000000000000489

PubMed Abstract | CrossRef Full Text | Google Scholar

157. Bailey M, Alunni-Cardinali M, Correa N, Caponi S, Holsgrove T, Barr H, et al. Viscoelastic Properties of Biopolymer Hydrogels Determined by Brillouin Spectroscopy: A Probe of Tissue Micromechanics. Sci Adv (2020) 6:eabc1937. doi:10.1126/sciadv.abc1937

PubMed Abstract | CrossRef Full Text | Google Scholar

158. Wang S, Larin KV. Optical Coherence Elastography for Tissue Characterization: a Review. J Biophoton (2015) 8(4):279–302. doi:10.1002/jbio.201400108

PubMed Abstract | CrossRef Full Text | Google Scholar

159. Larin KV, Sampson DD. Optical Coherence Elastography - OCT at Work in Tissue Biomechanics [Invited]. Biomed Opt Express (2017) 8(2):1172–202. doi:10.1364/BOE.8.001172

PubMed Abstract | CrossRef Full Text | Google Scholar

160. Marrese M, Antonovaite N, Nelemans BKA, Smit TH, Iannuzzi D. Micro-Indentation and Optical Coherence Tomography for the Mechanical Characterization of Embryos: Experimental Setup and Measurements on Chicken Embryos. Acta Biomater (2019) 97:524–34. doi:10.1016/j.actbio.2019.07.056

PubMed Abstract | CrossRef Full Text | Google Scholar

161. Schlüßler R, Möllmert S, Abuhattum S, Cojoc G, Müller P, Kim K, et al. Mechanical Mapping of Spinal Cord Growth and Repair in Living Zebrafish Larvae by Brillouin Imaging. Biophys J (2018) 115(5):911–23. doi:10.1016/j.bpj.2018.07.027

PubMed Abstract | CrossRef Full Text | Google Scholar

162. Bevilacqua C, Sánchez-Iranzo H, Richter D, Diz-Muñoz A, Prevedel R. Imaging Mechanical Properties of Sub-Micron ECM in Live Zebrafish Using Brillouin Microscopy. Biomed Opt Express (2019) 10:1420. doi:10.1364/boe.10.001420

PubMed Abstract | CrossRef Full Text | Google Scholar

163. Qian X, Ma T, Yu M, Chen X, Shung KK, Zhou Q. Multi-Functional Ultrasonic Micro-Elastography Imaging System. Sci Rep (2017) 7:1230. doi:10.1038/s41598-017-01210-8

PubMed Abstract | CrossRef Full Text | Google Scholar

164. Braun J, Tzschätzsch H, Körting C, Ariza de Schellenberger A, Jenderka M, Drießle T, et al. A Compact 0.5 T MR Elastography Device and its Application for Studying Viscoelasticity Changes in Biological Tissues during Progressive Formalin Fixation. Magn Reson Med (2017) 79(1):470–8. doi:10.1002/mrm.26659

PubMed Abstract | CrossRef Full Text | Google Scholar

165. Bigot M, Chauveau F, Beuf O, Lambert SA. Magnetic Resonance Elastography of Rodent Brain. Front Neurol (2018) 9:1010. doi:10.3389/fneur.2018.01010

PubMed Abstract | CrossRef Full Text | Google Scholar

166. Wu P-J, Kabakova IV, Ruberti JW, Sherwood JM, Dunlop IE, Paterson C, et al. Water Content, Not Stiffness, Dominates Brillouin Spectroscopy Measurements in Hydrated Materials. Nat Methods (2018) 15:561–2. doi:10.1038/s41592-018-0076-1

PubMed Abstract | CrossRef Full Text | Google Scholar

167. Raghunathan R, Zhang J, Wu C, Rippy J, Singh M, Larin KV, et al. Evaluating Biomechanical Properties of Murine Embryos Using Brillouin Microscopy and Optical Coherence Tomography. J Biomed Opt (2017) 22(8):086013. doi:10.1117/1.JBO.22.8.086013

PubMed Abstract | CrossRef Full Text | Google Scholar

168. Antonacci G, Braakman S. Erratum: Corrigendum: Biomechanics of Subcellular Structures by Non-Invasive Brillouin Microscopy. Sci Rep (2017) 7:46789. doi:10.1038/srep46789

PubMed Abstract | CrossRef Full Text | Google Scholar

169. Kennedy BF, Kennedy KM, Sampson DD. A Review of Optical Coherence Elastography: Fundamentals, Techniques and Prospects. IEEE J Sel Top Quan Electron (2014) 20(2):272–88. doi:10.1109/JSTQE.2013.2291445

CrossRef Full Text | Google Scholar

170. Sun C, Standish B, Yang VXD. Optical Coherence Elastography: Current Status and Future Applications. J Biomed Opt (2011) 16(4):043001. doi:10.1117/1.3560294

PubMed Abstract | CrossRef Full Text | Google Scholar

171. Curatolo A, Villiger M, Lorenser D, Wijesinghe P, Fritz A, Kennedy BF, et al. Ultrahigh-Resolution Optical Coherence Elastography. Opt Lett (2016) 41(1):21–4. doi:10.1364/OL.41.000021

PubMed Abstract | CrossRef Full Text | Google Scholar

172. Wang RK, Kirkpatrick S, Hinds M. Phase-Sensitive Optical Coherence Elastography for Mapping Tissue Microstrains in Real Time. Appl Phys Lett (2007) 90(16):164105. doi:10.1063/1.2724920

CrossRef Full Text | Google Scholar

173. Mainardi F. On Some Properties of the Mittag-Leffler Function E_α (−t^α), Completely Monotone for t > 0 with 0 < α < 1. Discrete Continuous Dynamical Syst (2014) 19(7):2267–78. doi:10.3934/dcdsb.2014.19.2267

CrossRef Full Text | Google Scholar