- 1Max Planck Institute for Mathematics in the Sciences, Leipzig, Germany
- 2Department of Physics, Sharif University of Technology, Tehran, Iran
We consider a population of mobile agents able to make noisy observations of the environment and communicate their observation by production and comprehension of signals. Individuals try to align their movement direction with their neighbors. Besides, they try to collectively find and travel towards an environmental direction. We show that, when the fraction of informed individuals is small, by increasing the noise in communication, similarly to the Vicsek model, the model shows a discontinuous order-disorder transition with strong finite-size effects. In contrast, for a large fraction of informed individuals, it is possible to go from the ordered phase to the disordered phase without passing any phase transition. The ordered phase is composed of two phases separated by a discontinuous transition. Informed collective motion, in which the population collectively infers the correct environmental direction, occurs for a high fraction of informed individuals. When the fraction of informed individuals is low, the misinformed collective motion, where the population fails to find the environmental direction, becomes stable as well. Besides, we show that an amount of noise in the production of signals is more detrimental for the inference capability of the population and increases temporal fluctuations, the density fluctuations, and the probability of group fragmentation, compared to the same amount of noise in the comprehension.
1 Introduction
Many species, from bacteria [1–3] and cells [4, 5] to insects [6, 7], large animals [8–11] and humans [12] show collective motion, an intriguing phenomena in which individuals in a population move in ordered groups, presumably due to local interactions [13]. Such a collective motion is suggested to endow many advantages, such as avoiding predators [14], or enhancing the information acquisition capability of the population in noisy environments [15, 16]. Besides the biological examples, similar phenomena and similar challenges to address these phenomena can arise in the collective motion of artificial agents [17–20].
Although the collective motion has been subject to intense study [3, 13, 21–31], an important point not considered in the relevant literature, is that in many cases, the information individuals reach from others in the population is provided through communication by exchanging signals [5, 32–36]. Besides, in many cases, collectively moving populations try to find and travel to a preferred goal, such as a nutrient source or a migration root [8, 12, 16, 24]. They may do so, while only a fraction of individuals have information about the preferred root and try to lead the group [8, 12, 16, 24]. These considerations raise the important question that how collective motion in a population of individuals who exchange their social information by production and comprehension of signals is formed, and how the noise inherent in the communication system affects the collective information acquisition capability of the moving population?
To answer this question, we consider a population of mobile agents trying to collectively find and travel towards an environmental direction. Individuals communicate information about their movement by production and comprehension of signals. Individuals can be uninformed or informed. Uninformed individuals make decisions over their direction of motion based on the information they receive from their neighboring individuals. Informed individuals, on the other hand, can make noisy observations of an environmental direction and make decisions over their direction of motion by combining this information with the information they receive from the direction of motion of their neighboring individuals. We show that an ordered phase, where individuals move towards the same direction, emerges for a low level of noise in communication, and a disordered phase, where individuals travel to different directions, emerges for high levels of noise. The ordered phase is composed of two phases. Informed collective motion, in which the population collectively moves towards the environmental direction, emerges if the noise in communication is low enough and the fraction of informed individuals is high enough. As the fraction of informed individuals decreases (for small communication noise), the model shows a discontinuous phase transition to a misinformed collective motion phase in which the population moves collectively, but towards a direction other than the environmental direction. The fraction of informed individuals needed for the population for collectively travel to the environmental direction is larger for higher noise levels.
By increasing the noise in communication, for a low fraction of informed individuals, the model shows a discontinuous phase transition to the disordered phase in which individuals move towards random directions. As is the case in Vicsek-like models [21–23], the order-disorder transition suffers from strong finite-size effects that make its discontinuous nature apparent only in large system sizes. On the other hand, when the fraction of informed individuals is high, such that the system is well into the informed collective motion phase, by increasing the communication noise, contrary to the Viscek-like models, the population moves gradually from the ordered phase to the disordered phase without any phase transition. This shows how the amount of information about the environment contained in the population can change the nature of the order-disorder transition observed in Vicsek-like models.
Finally, we show an amount of noise in the production of signals is more detrimental for the collective information acquisition capability of the population compared to the same amount of noise in the comprehension of signals. This result is in keeping with a recently found comprehension-production asymmetry in a model of collective decision making, where individuals residing on a network try to form a consensus about an environment that can be found in a finite number of possible states [37]. While Ref. [42] provides theoretical evidence for a comprehension-production asymmetry in a case where a population of immobile individuals has access to a Potts variable as their belief variable, our finding here provides evidence for a similar asymmetry in the case of collective motion, where agents can move on space and need to make decisions over their direction of motion. Besides, we show that the production noise increases the density fluctuations and the probability of group fragmentation, and temporal fluctuations compared to comprehension noise. Thus, in this regard, by extending results found in Ref. [37], our findings suggest asymmetry between signal comprehension and production is a fundamental characteristic of biological communication systems.
2 The Model
A schematic representation of the model is provided in Figure 1. We consider a population of N mobile agents, moving with constant speed
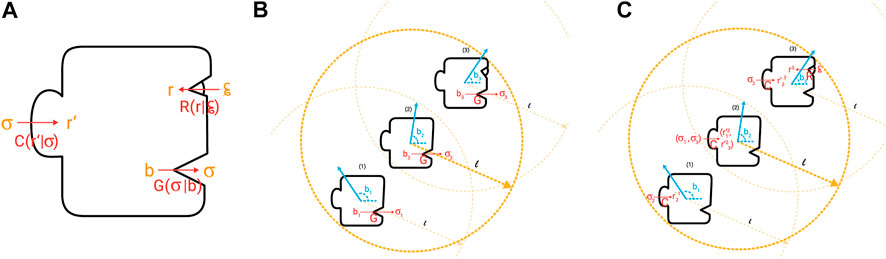
FIGURE 1. Schematic representation of the model. (A): Each agent is equipped with two information channels to communicate. Production channel
Observation. Personal information is acquired by noisy observation of the environmental direction. We assume observation is made through a noisy channel
Communication. Social information is acquired by production and comprehension of signals. To communicate its direction of motion b, each individual produces a signal σ, using its signal production channel
Signals are transmitted up to a distance l. That is all the individuals in a circle of radius l centered around the transmitter receive the signal. The receivers, comprehend a signal to refer to a direction of travel
Decision making. As a result of signals an individual receives, it reaches a set of representations
Here,
An uninformed individual, β, makes a decision about its direction of motion by simply averaging the social information it receives:
As in the Vicsek model [21], the dynamic is synchronous. At each time step, informed individuals make an observation using
In the following we use two variables to distinguish different phases of the system. The absolute value of the normalized average velocity of the population is defined as
3 Results
3.1 Collective Motion Phases
We begin by studying the behavior of the system as a function of the noise level and the fraction of informed individuals. To do this, in Figure 2A, we plot the absolute value of the normalized average velocity of the population in the case that an amount of noise η is in the comprehension and production is noiseless,
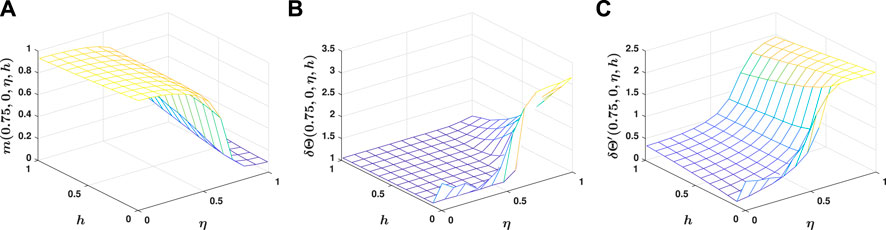
FIGURE 2. Different phases of the system. From (A) to (C), respectively,
Interestingly, the ordered phase is composed of two distinct phases. To see this, in Figure 2B, we plot the angular deviation of the average direction of motion from the environmental direction,
In 2 (c), we plot average angular deviation of the direction of motion of individuals from the environmental direction
3.2 Phase Transitions
The nature of the order-disorder transition in the Vicsek and related models has been the subject of intense research [13, 21–23]. It is well known that the order-disorder transition is discontinuous in many cases (depending on the parameter values and the way noise is implemented in the model) [13]. However, due to strong finite-size effects, the discontinuous nature of the transition shows up only in very large sizes [22]. Our model shows a similar phenomenology only for small h. However, the situation is different for large h. This can be seen in Figure 3A and Figure 3B for respectively, the production and comprehension noise, where the probability distribution of the order parameter for different noise levels and constant (large) h is plotted. Here, the distribution is derived from a single time series of the system of length
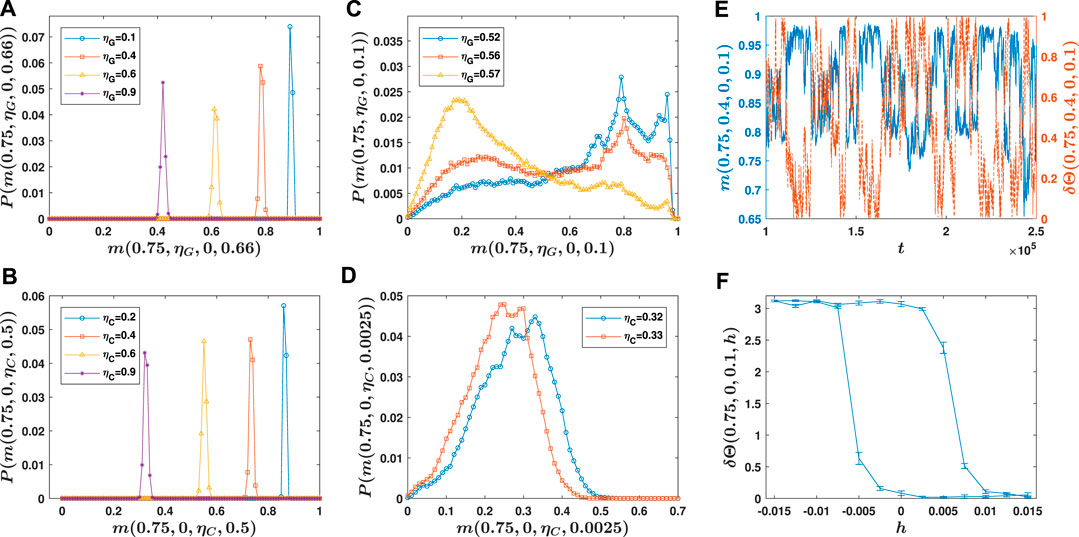
FIGURE 3. Phase transitions. (A) and (B): The probability distribution of the order parameter as a function of the order parameter for large fraction of informed individuals, h, is plotted. For large h, the order parameter decrease gradually as noise in communication increases, for both production (A) and comprehension (B) noise. Here
In Figure 3C and Figure 3D, by plotting the distribution of the order parameter for fixed h and different noise levels, we study the discontinuous nature of the order-disorder transition for small h. In Figure 3C the case of production noise is considered. Here,
Returning to Figure 3C, we see that for the case of production noise the distribution of the order parameter has two major peaks in the ordered phase. This happens only for small enough h, i.e., when the ordered phase is bistable, and the system can be found in both informed and misinformed collective motion phases. The two major peaks of m correspond to these two phases. This can be seen in Figure 3E, where m together with
For comprehension noise, m does not show a similar bi-modality that indicates intermittency between informed and misinformed collective motion. The reason is that, contrary to the production noise, with comprehension noise, the population rarely is decomposed into different dense groups with different directions of travel, and the strong fission-fusion dynamics observed for production noise is absent in the case of comprehension noise (see the Supplementary Video). We will shortly return to this difference between comprehension and production noise.
The bi-stability associated with a discontinuous transition results in hysteresis, which provides an alternative way to test the nature of the informed-misinformed phase transition [44]. This is shown in Figure 3F, where the hysteresis loop for the case of comprehension noise is shown. Production noise shows similar hysteresis effects. Here, we run a simulation beginning with
3.3 Noise in Signal Production Increases the Density Fluctuations, Temporal Fluctuations, and Degrades Collective Information Acquisition Capability
We have already seen that production noise increases the probability of group fragmentation and leads to a strong fission-fusion dynamic absent for the comprehension noise. This can be shown more quantitatively. For this purpose, we define the (relative) asymmetry in density fluctuations as
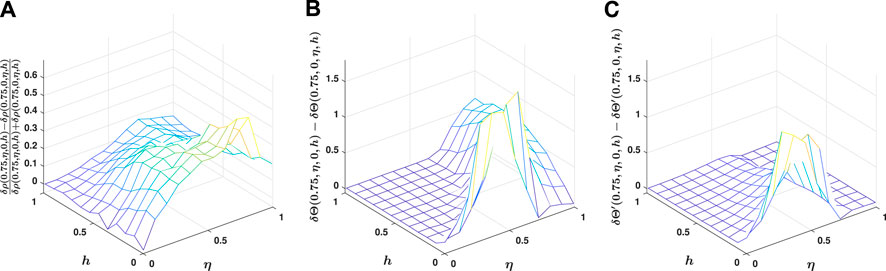
FIGURE 4. Asymmetry between signal comprehension and production. Asymmetry in density fluctuations
There is another asymmetry between the comprehension and production of signals. This asymmetry arises in the collective information acquisition capability of the population. To see this, we define the asymmetry in the inference capability of the population as the difference between the angular deviation of the average population direction from the environmental direction when an amount of noise is in signal production compared to the case when the noise is in signal comprehension,
As a second measure of asymmetry in the inference capability of the population, we consider the difference between the average deviation of the individuals’ direction of motion from the environmental direction, when an amount of noise is of production type compared to the case where the noise is of comprehension type
We note that the positivity of the measures of asymmetry in collective information acquisition results from two shifts in the phase transitions. First, production noise shifts the order-disorder transition to smaller noise levels. This shows production noise is more detrimental to the ordering of the population. Second, production noise shifts the monostable informed collective motion phase to larger values of h. This means with production noise, a larger fraction of informed individuals is necessary for the population to successfully infer the correct environmental direction. As shown in the Supplementary Material, both asymmetries in the density fluctuation and collective information acquisition are robust features of the model, valid for all the parameter values.
Finally, we note that noise in signal production also increases temporal fluctuations. To see this, in Figures 5A,B, we plot the normalized average velocity, m, and average angular deviation of the individuals from the environmental direction,
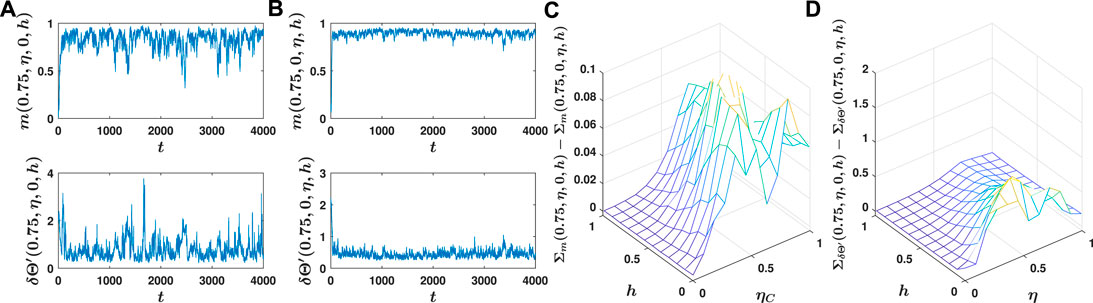
FIGURE 5. Production noise increases temporal fluctuations. (A) and (B): m(top) and
4 Discussion
We have introduced a model of collective movement in which individuals in a population try to collectively find and travel in a preferred direction. To do so, a fraction of individuals, informed individuals, can use private information provided by the noisy observation of the environment, and social information, provided by communication between individuals by exchanging signals. Others, uninformed individuals, can only use social information provided by communication. By analysis of the model, we showed that signal production noise not only decreases the inference capability of the population but also increases density fluctuations and the probability of group fragmentation. Besides, by identifying two different phases of collective motion (informed and misinformed) separated by a discontinuous transition, we have identified the mechanism by which a fraction of informed individuals able to only make noisy observations of the environment can lead the group. Finally, we have cast the much-studied order-disorder transition in Vicsek-like models into a broader context by showing that the nature of this transition depends on the amount of information about the environment available in the population, in other words, the fraction of informed individuals and the accuracy of their observation.
A similar comprehension-production asymmetry in the inference capability and similar phase transitions had been recently observed in a model of collective decision making in a population of immobile agents [37]. In this model, a population of agents who reside on a fixed communication network and live in an environment that can take one out of a finite number of possible states, try to collectively infer the environmental state [37, 45]. Similarly to the environmental state, in this model, individuals can take one out of a finite number of beliefs and are equipped with a production and a comprehension probability transition matrices to produce and comprehend a set of a finite number of signals. It is shown that such a model of collective decision making with signaling shows a similar comprehension-production asymmetry, according to which an amount of noise in signal production is more detrimental for the collective capability of the population to infer the environmental state, compared to the same amount of noise in signal production [37]. Our work here extends this study in different ways. In previous models of biological communication by production and comprehension of signals [37, 42, 45], or more generally, models of a proto-language [46–49], individuals try to communicate a finite number of states, which lack a distance measure. In other words, in that case, the state or belief variable is a categorical variable. In contrast, here, we have explored a case when individuals can form beliefs over a continuous space and produce and comprehend a continuous set of signals, which possesses a distance measure i.e., an ordinal variable. In this regard, in the limit of zero movement speed, our model reduces to a model of biological communication in a population of immobile agents, who can form beliefs and produce and comprehend signals over a continuous space of possible beliefs which possesses a distance measure. Second, by introducing movement into the model, we have been able to study collective movement in a communicating population. Our finding here shows that a similar asymmetry in the collective inference capability of biological populations is at work in this case as well. Furthermore, by showing that the production noise also increases temporal fluctuations, the density fluctuations, and the probability of group fragmentation, our analysis reveals new ways in which noise in signal production can be more detrimental than noise in the comprehension. This theoretical study thus strengthens the case for the existence of a comprehension production asymmetry and calls for empirical investigations to shed light on the question that whether such an asymmetry exists in biological populations.
Our study also provides insight on the question that how a fraction of informed individuals can lead the group on the move. Previous work has shown that enough fraction of informed individuals can indeed lead the collective movement of the group [24, 50]. Our study extends this line of research in two ways. First, our model introduces the more realistic possibility that informed individuals have only noisy and imperfect information of a preferred goal, such as a nutrient source. Second, our model studies how different types of noise in communication can affect the ability of the informed individuals to lead the group and the group’s ability to find the preferred direction of motion. In this regard, our finding reveals that depending on the fraction of informed individuals and noise in observation and communication, a collectively moving population can be found in different ordered or disordered phases, separated by phase transitions. Besides, our analysis reveals that the fraction of informed individuals needed to successfully lead the group increases by increasing noise in communication. This can be interpreted to result from the fact that a higher noise level in communication disrupts the flow of information in the population, and thus, a higher fraction of informed individuals and a higher information flow from the environment to the population through informed individuals is necessary for finding the environmental direction.
Finally, we note that the similarity between the phenomenology of the two apparently different systems, that is, the model of collective movement introduced here and the model of collective decision making mentioned before [37, 45, 49], can be understood by noting that movement decision involves choosing a direction between a continuous set of possible directions. This observation highlights the similarity of collective movement with collective decision making, which can provide insights into the physics of collective movements such as the nature of the phase transitions observed in such models or the mechanisms by which such populations can optimize their information acquisition capabilities [45], which can be subject to future researches.
5 Methods
5.1 The Simulations
All the simulations are started with a random distribution of positions and directions of motions. The parameter values used in the simulations differ for each figure and are given in the figure captions. To derive the hysteresis loop in Figure 3.f, we consider a population of size
5.2 Density Fluctuations
To calculate the density fluctuation, we first define the density field,
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
MS designed the research, SR contributed new reagents to the research, MS performed the research, MS wrote the paper. All the authors revised the manuscript.
Funding
MS acknowledges funding from Alexander von Humboldt Foundation in the framework of the Sofja Kovalevskaja Award endowed by the German Federal Ministry of Education and Research during part of this research.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are indebted to Yasser Roudi for many fruitful discussions and insightful ideas. MS was at Sharif University of Technology when this work started.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.668283/full#supplementary-material
References
1. Czirók A, Ben-Jacob E, Cohen I, Vicsek T. Formation of Complex Bacterial Colonies via Self-Generated Vortices. Phys Rev E (1996) 54(2):1791–801. doi:10.1103/physreve.54.1791
2. Sokolov A, Aranson IS, Kessler JO, Goldstein RE. Concentration Dependence of the Collective Dynamics of Swimming Bacteria. Phys Rev Lett (2007) 98(15):158102. doi:10.1103/physrevlett.98.158102
4. Szabo B, Szöllösi GJ, Selmeczi D, Vicsek TZs Jurányi. Phase Transition in the Collective Migration of Tissue Cells: experiment and Model. Phys Rev E (2006) 74(6):061908. doi:10.1103/physreve.74.061908
5. Friedl P, Gilmour D. Collective Cell Migration in Morphogenesis, Regeneration and Cancer. Nat Rev Mol Cel Biol (2009) 10(7):445–57. doi:10.1038/nrm2720
6. Buhl JDJTS, Couzin ID, Hale JJ, Despland E, Miller ER, Simpson SJ. From Disorder to Order in Marching Locusts. Science (2006) 312:5778–1406. doi:10.1126/science.1125142
7. Couzin ID, Franks NR. Self-organized Lane Formation and Optimized Traffic Flow in Army Ants. Proc R Soc Lond B (2003) 270:139–46. doi:10.1098/rspb.2002.2210
8. Ward AJW, Sumpter DJT, Couzin ID, Hart PJB, Krause J. Quorum decision-making Facilitates Information Transfer in Fish shoals. Proc Natl Acad Sci (2008) 105:6948–53. doi:10.1073/pnas.071034410519
9. Bajec IL, Heppner FH, Frank H. Organized Flight in Birds. Anim Behav (2009) 78(4):777–89. doi:10.1016/j.anbehav.2009.07.007
10. Fischhoff IR, Sundaresan SR, Cordingley J, Larkin HM, Sellier M-J, Rubenstein DI. Social Relationships and Reproductive State Influence Leadership Roles in Movements of plains Zebra, Equus Burchellii. Anim Behav (2007) 73(5):825–31. doi:10.1016/j.anbehav.2006.10.012
11. Sueur C, Petit O. Organization of Group Members at Departure Is Driven by Social Structure in Macaca. Int J Primatol (2008) 29(4):1085–98. doi:10.1007/s10764-008-9262-9
12. Faria JJ, Dyer JRG, Tosh CR, Krause. J. Leadership and Social Information Use in Human Crowds. Anim Behav (2010) 79(4):895–901. doi:10.1016/j.anbehav.2009.12.039
13. Vicsek T, Zafeiris A. Collective Motion. Phys Rep (2012) 517(3-4):71–140. doi:10.1016/j.physrep.2012.03.004
14. Ward AJW, Herbert-Read JE, Sumpter DJT, Krause J, Krause J. Fast and Accurate Decisions through Collective Vigilance in Fish shoals. Proc Natl Acad Sci (2011) 108(6):2312–5. doi:10.1073/pnas.1007102108
15. Grünbaum D. Schooling as a Strategy for Taxis in a Noisy Environment. Evol Ecol (1998) 12(5):503–22. doi:10.1023/a:1006574607845
16. Berdahl AM, Kao AB, Flack A, Peter AHWEAC, Couzin ID, Dell AI, et al. Collective Animal Navigation and Migratory Culture: from Theoretical Models to Empirical Evidence. Phil Trans R Soc B: Biol Sci (2018) 373:1746. doi:10.1098/rstb.2017.0009
17. Monaco JD, Hwang GM, Schultz KM, Zhang K, May. Cognitive Swarming: an Approach from the Theoretical Neuroscience of Hippocampal Function, In Micro-and Nanotechnology Sensors, Systems, and Applications XI. Vol. 10982. (Baltimore, MD, United States: International Society for Optics and Photonics (2019). p. 109822D.
18. Savkin AV. Coordinated Collective Motion of Groups of Autonomous Mobile Robots: Analysis of Vicsek′s Model. IEEE Trans Automat Contr (2004) 49(6):981–3. doi:10.1109/tac.2004.829621
19. Zhao H, Liu H, Leung Y-W, Chu X. Self-adaptive Collective Motion of Swarm Robots. IEEE Trans Automat Sci Eng (2018) 15(4):1533–45. doi:10.1109/tase.2018.2840828
20. Monaco JD, Hwang GM, Schultz KM, Zhang K. Cognitive Swarming in Complex Environments with Attractor Dynamics and Oscillatory Computing. Biol Cybern (2020) 114(2):269–84. doi:10.1007/s00422-020-00823-z
21. Vicsek T, Czirók A, Ben-Jacob E, Cohen I, Shochet O. Novel Type of Phase Transition in a System of Self-Driven Particles. Phys Rev Lett (1995) 75(6):1226–9. doi:10.1103/physrevlett.75.1226
22. Chaté H, Ginelli F, Grégoire G, Peruani F, Raynaud F. Modeling Collective Motion: Variations on the Vicsek Model. The Eur Phys J B (2008) 64(3-4):451–6. doi:10.1140/epjb/e2008-00275-9
23. Grégoire G, Chaté H. Onset of Collective and Cohesive Motion. Phys Rev Lett (2004) 92(2):025702. doi:10.1103/physrevlett.92.025702
24. Couzin ID, Krause J, Franks NR, Levin SA. Effective Leadership and Decision-Making in Animal Groups on the Move. Nature (2005) 433(7045):513–516. doi:10.1038/nature03236
25. Bricard A, Caussin J-B, Desreumaux N, Dauchot O, Bartolo D. Emergence of Macroscopic Directed Motion in Populations of Motile Colloids. Nature (2013) 503:7474. doi:10.1038/nature12673
26. Cucker F, Smale S. Emergent Behavior in Flocks. IEEE Trans Automat Contr (2007) 52(5):852–62. doi:10.1109/tac.2007.895842
27. Nagai KH, Sumino Y, Montagne R, Aranson IS, Chaté H. Collective Motion of Self-Propelled Particles with Memory. Phys Rev Lett (2015) 114(16):168001. doi:10.1103/physrevlett.114.168001
28. De Luca G, Mariani P, MacKenzie BR, Marsili M. Fishing Out Collective Memory of Migratory Schools. J R Soc Interf (2014) 11:20140043. doi:10.1098/rsif.2014.0043
30. Shaebani MR, Wysocki A, Winkler RG, Gompper G, Rieger H. Computational Models for Active Matter. Nat Rev Phys (2020) 2(4):181–99. doi:10.1038/s42254-020-0152-1
31. Bär M, Großmann R, Heidenreich S, Peruani F. Self-propelled Rods: Insights and Perspectives for Active Matter. Annu Rev Condens Matter Phys (2020) 11:441–66. doi:10.1146/annurev-conmatphys-031119-050611
32. McCann CP, Kriebel PW, Parent CA, Losert W. Cell Speed, Persistence and Information Transmission during Signal Relay and Collective Migration. J Cel Sci (2010) 123(10):1724–31. doi:10.1242/jcs.060137
33. Haas P, Gilmour D. Chemokine Signaling Mediates Self-Organizing Tissue Migration in the Zebrafish Lateral Line. Dev Cel (2006) 10:673–80. doi:10.1016/j.devcel.2006.02.0195
34. Rappel W-J. Cell-cell Communication during Collective Migration. Proc Natl Acad Sci USA (2016) 113(6):1471–3. doi:10.1073/pnas.1524893113
35. Leonhardt SD, Menzel F, Nehring V, Schmitt T. Ecology and Evolution of Communication in Social Insects. Cell (2016) 164:1277–87. doi:10.1016/j.cell.2016.01.035
36. Sumpter DJT. The Principles of Collective Animal Behaviour. Phil Trans R Soc B (2005) 361(1465):5–22. doi:10.1098/rstb.2005.1733
37. Salahshour M, Rouhani S, Roudi Y. Phase Transitions and Asymmetry between Signal Comprehension and Production in Biological Communication. Scientific Rep (2019) 9(no. 1):3428. doi:10.1038/s41598-019-40141-4
38.H Brumm, editor. Animal Communication and Noise, Vol. 2. Springer Science & Business Media (2013).
39. Schuster S, Zollinger SA, Lesku JA, Brumm H. On the Evolution of Noise-dependent Vocal Plasticity in Birds. Biol Lett (2012) 8(6):913–6. doi:10.1098/rsbl.2012.0676
40. Wiley RH. How Noise Determines the Evolution of Communication. Anim Behav (2017) 124:307–13. doi:10.1016/j.anbehav.2016.07.014
41. Hotchkin C, Parks S. The Lombard Effect and Other Noise-Induced Vocal Modifications: Insight from Mammalian Communication Systems. Biol Rev (2013) 88(4):809–24. doi:10.1111/brv.12026
42. Salahshour M, Rouhani S. Evolutionary Value of Collective Sensing (2018) (arXiv preprint arXiv:1802.03524.
44. Binder K. Theory of First-Order Phase Transitions. Rep Prog Phys (1987) 50:783–859. doi:10.1088/0034-4885/50/7/0017
45. Salahshour M. Phase Diagram and Optimal Information Use in a Collective Sensing System. Phys Rev Lett (2019) 123(6):068101. doi:10.1103/physrevlett.123.068101
46. Nowak MA, Krakauer DC. The Evolution of Language. Proc Natl Acad Sci (1999) 96(14):8028–33. doi:10.1073/pnas.96.14.8028
47. Nowak MA, Komarova NL. Towards an Evolutionary Theory of Language. Trends Cognitive Sciences (2001) 5(7):288–95. doi:10.1016/s1364-6613(00)01683-1
48. Ke J, Minett JW, Au C-P, Wang WS-Y. Self-organization and Selection in the Emergence of Vocabulary. Complexity (2002) 7(3):41–54. doi:10.1002/cplx.10030
49. Salahshour M. Coevolution of Cooperation and Language. Phys Rev E (2020) 102(4):042409. doi:10.1103/physreve.102.042409
Keywords: collective movement, collective information acquisition, flocking, communication, signaling, comprehension-production asymmetry
Citation: Salahshour M and Rouhani S (2021) Collective Movement and Collective Information Acquisition With Signaling. Front. Phys. 9:668283. doi: 10.3389/fphy.2021.668283
Received: 16 February 2021; Accepted: 17 May 2021;
Published: 02 June 2021.
Edited by:
Víctor M. Eguíluz, Institute of Interdisciplinary Physics and Complex Systems (IFISC), SpainReviewed by:
Gil Ariel, Bar-Ilan University, IsraelBikas K. Chakrabarti, Saha Institute of Nuclear Physics (SINP), India
Copyright © 2021 Salahshour and Rouhani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mohammad Salahshour, bW9oYW1tYWQuc2FsYWhzaG91ckBtaXMubXBnLmRl; Shahin Rouhani, c3JvdWhhbmlAc2hhcmlmLmly
 Mohammad Salahshour
Mohammad Salahshour Shahin Rouhani2*
Shahin Rouhani2*