Flipping Interferometric Module for Simultaneous Dual-Wavelength Unwrapping of Quantitative Phase Maps of Biological Cells

We present an imaging platform for stain-free quantitative imaging of biological cells using a simultaneous dual-wavelength holographic module. We use this module to experimentally solve the problem of 2π phase ambiguities that occurs in spatial locations where the optical thickness of the sample is larger than the wavelength. Thus, the process does not require using digital phase unwrapping that is computational heavy and impairs real-time processing. The proposed method is not limited to sequential acquisition of two quantitative phase maps in different times, but rather allows optical multiplexing of two off-axis holograms on the camera at once, enabling acquisition of fast dynamic processes. The module is simple and portable, making it attractive for clinical use. We demonstrate using the module for quantitative phase imaging of cancer and sperm cells.

Introduction

Digital holographic microscopy (DHM) can record the optical thickness profile of biological samples, such as cells in vitro. This profile, also referred to as the optical path delay (OPD) profile, is defined as the product of the sample thickness and its integral refractive-index (RI) profiles, allowing to visualize transparent or semitransparent samples in high and quantitative contrast, without using cell staining [1]. The OPD profile can be used to calculate the cell dry mass, which is an indicator for the physical density of the cell, as well as other quantitative parameters of biological relevance [2]. The OPD profile can be recorded in a single camera exposure using off-axis holography, where two beams interfere on the camera at a small off-axis angle, one beam interacts with the sample and the other beam is the reference beam that does not contain sample modulation. The resulting off-axis hologram is a cosine pattern, modulated by the off-axis angle plus the phase difference of the sample, and defined as follows:

$\begin{array}{ll}\Delta \phi \left(x,y\right)=\frac{2\pi }{\lambda }{H}_c\left({\overline{n}}_c-n_m\right)=\frac{2\pi }{\lambda }OPD\left(x,y\right),& (1)\end{array}$

where H_c is the sample thickness, ${\overline{n}}_c$ is the sample integral RI, n_m is the surrounding medium RI, and λ is the illumination wavelength. When creating this profile, 2π phase ambiguities occur in locations where the OPD is larger than the illumination wavelength.

Digital phase unwrapping algorithms can solve this problem [3]. However, they are computational heavy and cannot typically cope with samples which experience more than 2π jumps in neighboring locations. For this reason, two-wavelength phase unwrapping is used [4]. This technique acquires the OPD profile of the sample in two different wavelengths, and creates a new OPD profile at a larger synthetic wavelength, so that the sample is no longer optically thicker than the synthetic wavelength, and 2π phase ambiguities do not occur.

Two-wavelength phase unwrapping is pruned to coherence induced disturbances that may be caused by highly coherent laser light sources and the presence of scattering system components. Typically, this two-wavelength acquisition is done sequentially, in two exposures, which cannot be done for highly dynamic samples that might change between the exposures; Alternatively, if two cameras are used for parallel acquisition, image segmentation problems might occur. Simultaneous, single-camera two-wavelength holography can be used to solve this problem [5]. This can be done by multiplexing two off-axis holograms of the same sample imaged under different wavelengths on the same sensor, providing real-time holographic capabilities without 2π phase ambiguities. In this case, the camera records a multiplexed off-axis hologram composed of two 90°-rotated, or orthogonal, off-axis interference fringes [6–9]. These methods use separate reference beams, independent of the sample beam along most of the optical path, yielding increased temporal noise. Self-interference holography allows decreased temporal noise due to the nearly common-path geometry. A setup that uses a long-distance objective and two beam splitters positioned within the working distance was proposed for two-wavelength phase unwrapping [10]. Alternative approach is generating the reference beam externally, after the image plane of the optical system. Previously, we proposed an external, portable, and nearly common-path interferometric module, which is capable of forming a multiplexed off-axis hologram for two-wavelength phase unwrapping. It externally creates the reference beam using spatial filtering, as implemented by two lenses and a confocally positioned pinhole [11]. This setup requires meticulous pinhole alignment for implementing the spatial filtering, and it also suffers from loss of power in the reference arm, reducing the fringe visibility. To solve this issue, in [12], we proposed the flipping interferometry, which uses half of the optical beam as the reference beam for the other half of the beam; and thus, it does not require pinhole alignment. Since no pinhole is used, the system is not more sensitive to the sample meniscus than in regular holography with external reference beam, provided that half of the optical field of view used as the reference beam is empty and does not any contain a sample modulation such as additional meniscus. Flipping interferometry requires a high spatial coherence source, for obtaining interference in spite of the flipping operation. In addition, a high temporal coherence is preferred to obtain high modulation interference fringes on the entire sensor size. Inexpensive HeNe or many DPSS lasers have both high spatial coherence and temporal coherence and are suitable for flipping interferometry. This system is specifically suitable for acquiring biological cells during flow in a microfluidic channel, since the beam can be easily positioned on the border of the channel to meet the requirement for a half-empty optical beam. Still, in contrast to most shearing interferometers, the off-axis angle, determining the fringe spatial frequency, can be fully controlled, without the requirement for sample sparsity to avoid ghost image overlaps. In [13], we proposed flipping interferometry with doubled imaging area, an external portable module that combines simultaneous acquisition of two fields of view of the sample by spatial off-axis holographic multiplexing, without using a pinhole alignment. It projects two holographic fields of view on the camera at once, where each field of view is encoded into interference fringes of different orientation. Therefore, both fields of view can be reconstructed, while using the same number of camera pixels typically needed for acquiring a single field of view in off-axis holography. The flipping interferometry idea was adjusted for two-wavelength off-axis holographic multiplexing using an interferometric module that contains two lenses, two retro-reflectors, a mirror, and regular and polarizing beam splitters [14]. However, the use of polarizing elements makes the system unsuitable for imaging polarizing samples.

The current paper proposes a new alternative for a module that performs two-wavelength off-axis holographic multiplexing with flipping interferometry. The module uses no lenses and no polarizing elements, making it more portable and suitable even for imaging samples inducing polarization changes. We use this module for simultaneous two-wavelength phase unwrapping and demonstrate dynamic quantitative phase imaging of microbeads, sperm cells and cancer cells.

Materials and Methods

The F-2WL Setup

The proposed dual-wavelength flipping interferometry module (F-2WL) setup that allows simultaneous two-wavelength off-axis holography, and therefore two-wavelength phase unwrapping, is shown in Figure 1. It is an external interferometric module that is compact, nearly common path, and does not use any lenses or polarizer inside, hence easing its alignment. As in our previous flipping interferometry module that is used for field of view multiplexing [13], here too, the empty half of the optical spot illuminating the sample is used as the reference beam. It is optically flipped over the sample field of view to create an off-axis hologram of the sample on the monochromatic camera. However, in contrast to field of view multiplexing, here two orthogonal fringe patterns of the same sample field of view are acquired at once, each of which under a different wavelength illumination. As shown in Figure 1, the system is illuminated by two temporally coherent lasers 632.8 nm, helium-neon (HeNe) laser (Thorlabs) and 532 nm, diode-pump solid-state (DPSS) laser (Laserglow, Technologies), after being combined by a high-precision plate beam splitter (BSW10R). The sample is illuminated by a plane wave, thus no condenser lens is used. The inverted microscope includes a 1.35-NA microscope objective (UPlanSApo, 60×, oil-immersion, Olympus) and an achromatic lens tube lens (f = 200, 2” diameter). The F-2WL module is positioned after the tube lens, wherein the sample is imaged onto the camera. Alternatively, to make the module completely external, a 4f imaging system can be positioned at the exit if the microscope, where the module is located after the second lens, within is focal distance. Inside the module 50:50 beam splitter (BS013, Thorlabs) is used in order to split the beam to reference and sample arms. In the reference arm, one two-mirror retro-reflector is used to flip (mirror) both red and green beams. In the sample arm, a dichroic mirror (cut-off wavelength 567 nm, DMSP567R, Thorlabs) is placed, to split the red and green beams, so that each of them is reflected by a different mirror and is tilted in a different angle, so that each of them create, together with the reference arm from the retroreflector, an off-axis hologram on the CMOS monochrome camera (8 bit depth, 5.2 μm/pixel, DCC1545M, Thorlabs), so that the two off-axis holograms have orthogonal fringes patterns with respect to each other.

FIGURE 1

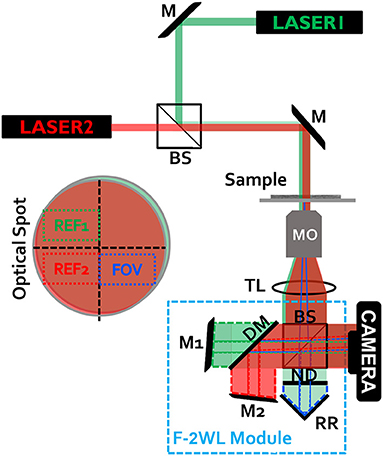
Figure 1. Experimental setup with the simultaneous flipping dual-wavelength interferometry (F-2WL) module, connected to an inverted microscope. M, mirror; BS, beam splitter; MO, microscope objective; TL, tube lens; RR, two-mirror retro-reflector; ND, neutral density filter; DM, dichroic mirror. The optical spot projected on the camera plane is shown on the left. The projected beams create two-wavelength multiplexed off-axis hologram on the camera. Ref₁, reference beam in the green channel; Ref₂, reference beam in the red channel; FOV, field of view containing the biological cells.

It is assumed that the beam spot projected onto the camera is at least as twice as large as the camera sensor, which is the typical case when using large-magnification objectives. The purpose of the ND filter in Figure 1 is to balance the intensity levels from each arm of the multiplexing interferometer, enhancing the final multiplexed hologram fringe visibility.

Phase Reconstruction Algorithm

The recorded multiplexed hologram is digitally Fourier transformed, and the resulting spatial spectrum is comprised of a DC term and two non-overlapping pairs of cross-correlation (CC) terms, each pair is from a different wavelength channel. Since the two interference fringe patterns recorded on the camera are orthogonal with respect to each other, the resulting CC terms are located on orthogonal axes in the spatial spectrum. In contrast to field-of-view multiplexing [13], no cross-terms occur between the wavelength channels, since the two different lasers do not create mutual interference resulted in unwanted terms between the useful CC terms.

Figure 2 demonstrates each of the interference channels (regular off-axis holograms) independently, green channel in Figure 2A and red channel in Figure 2B, indicating the active mirrors each time, as obtained on the monochromatic camera by blocking the other mirror. Figure 2C shows both wavelength channels together, creating the multiplexed off-axis hologram on the monochromatic camera.

FIGURE 2

Figure 2. Demonstration of the optical multiplexing operation, while imaging an empty field of view. (A) Off-axis hologram at λ₁, comprised of the green beams reflected from M₁ and RR. (B) Off-axis hologram at λ₂, comprised of red beams reflected from M₂ and RR. (C) The dual-wavelength multiplexed off-axis hologram, containing simultaneous orthogonal-fringe patterns. (D) The power spatial spectrum obtained by digital Fourier transforming of the multiplexed hologram. λ₁ and λ₂ are used to denote the selected CC terms of green and red channels, respectively, each of which containing the OPD profile of the sample at a different wavelength.

From the spatial spectrum, we crop one CC from each pairs of CCs, as marked in Figure 2D, and then inverse Fourier-transformed them, resulting in the complex wavefronts of the same sample, each acquired under a different illumination wavelength. To reduce stationary coherent noise and beam curvature, we can divide each of the cell sample wavefront by this sample-free background wavefront that does not contain any biological cell sample on the entire beam spot. For this stage, a multiplexed hologram without the sample present is recorded, containing the reference background profiles for both wavelength channels. This stage is not obligatory, but even if performed it does not disturb the recording of the dynamic process since it is done only once, before or after the recording of the dynamic process.

Since the phase arguments of the resulting complex wavefronts are periodically bounded to the range of 0 and 2π, phase ambiguities occur in places where the sample is optically thicker than the illumination wavelength. These ambiguities occur in different spatial locations in each wavelength channel. The setup is designed to resolve this issue by applying the synthetic phase unwrapping process that recovers the true phase values without ambiguities. Hence, it reduces the need for computationally heavy algorithms. The quantitative phase profile extracted from each digitally processed interference pattern is digitally refocused first by assessing the Tamura's coefficient for best refocusing criteria [15].

The two separate illumination wavelengths λ_i, where i = 1, 2, record 0 < φ_i (x,y,λ_i) < 2π, respectively for each wavelength. The synthetic OPD is obtained by simply subtracting the two wrapped phase maps, as follows:

$\begin{array}{ll}OP{D}_{12}\left(x,y\right)=\left[\frac{{\phi }_2\left(x,y,{\lambda }_2\right)-{\phi }_1\left(x,y,{\lambda }_1\right)}{2\pi }\right]\Lambda ,& (2)\end{array}$

where Λ = λ₁λ₂/|λ₁ − λ₂| is the synthetic (beat) wavelength, which, in our case, is equal to approximately 3.37 μm. This synthetic wavelength is larger than both individual wavelengths, and it is also larger than the maximal object optical thickness. Having an object that is optically thinner than the synthetic wavelength ensures no phase unwrapping. For thicker samples, larger synthetic wavelength can be reached by selecting closer illumination wavelengths. On the other hand, the technique is more pruned to noise as result of image subtraction in this case.

Human Colon Cancer Cell Line Preparation

HT-29 human colon cancer cell line was acquired from the ATCC. The growth medium used for these cells was Dulbecco's Modified Eagle's Medium (DMEM) (BI, SN. 01-55-1A) supplemented with 10% fetal bovine serum (FBS) [Biological industries (BI), SN. 04-007-1A], 4 mM L-Glutamin (BI, SN. 03-020-1B) and 1% antibiotics (BI, SN. 03-033-1B). The cell lines were incubated under standard cell culture conditions at 37°C and 5% CO₂ in a humidified incubator. For imaging, the cells were seeded on 24 × 60 mm #1 glass microscope cover-slip placed inside a Petri dish. After 48 h in growth medium, the cells reached about 20% confluence and washed with PBS, and then fixed by methanol for 1 min.

Sperm Cell Collection and Preparation

Upon obtaining the Tel Aviv University's IRB approval, we imaged human sperms. The collected raw semen samples were liquefied at room temperature for half an hour. Standard density gradient based-centrifugation for sperm enrichment was applied for separation of the cells before allowing it to liquefy again. Next, the spermatozoa were cleaned and isolated using the PureCeption Bi-layer kit (Origio, Målov, Denmark). Briefly, upper phases were removed to obtain the leftover pellet, which was resuspended in 5 mL modified human tubal fluid (HTF) medium (Irvine Scientific, CA, USA), and was centrifuged at 500 g for 5 min at 400 RCF in room temperature. Following this, micropipette collection of the sorted sperm cells is performed and the resulted sample is resuspended in 0.1 mL HTF. Ten milliliter of 3:1 methanol to acetic acid solution were then applied on the sample for 5 min. Then, the cells were centrifuged at 800 g for 5 min, the supernatant was discarded, and the pellet was resuspended in 0.2 mL of fixative solution. The sperm was imaged after being dried.

Results

Figures 3, 4 shows the wrapped quantitative OPD profiles of a 5 μm silica microbead in water and a cancer cell, respectively, as obtained while imaged under the green channel (Figures 3A, 4A), under the red channel (Figures 3B, 4B), and under two-wavelength phase unwrapping using the proposed F-2WL module (Figures 3C, 4C), each is obtained in a single camera exposure. Dynamic imaging of the microbead and the cancer cell are shown in Supplementary Videos 1, 2, respectively. Figure 3D shows a vertical cross-section through the center of the OPD profile. It demonstrates that after two-wavelength unwrapping, the final image is continuous and does not contain large jumps, as apparent in both cross-sections of the OPD profiles obtained under a single-wavelength illumination.

FIGURE 3

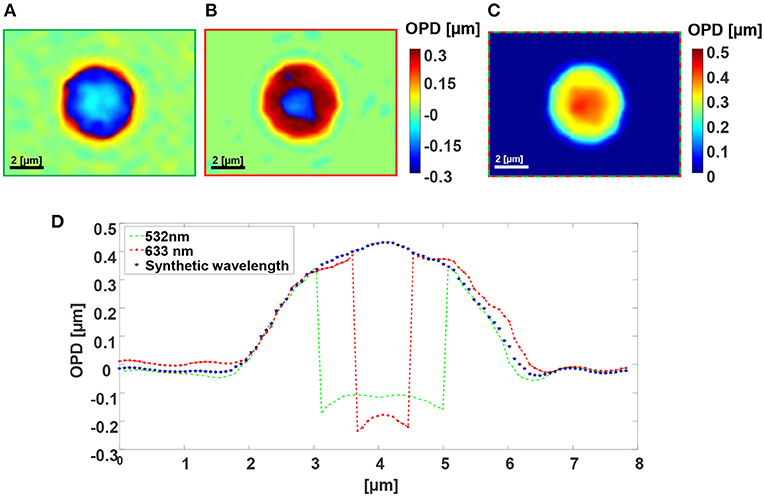
Figure 3. Dual-wavelength OPD reconstruction of a 5 μm silica microbead in water. (A) Wrapped OPD profile as obtained in the green channel. (B) Wrapped OPD profile as obtained in the red channel. (C) OPD profile obtained after using the proposed simultaneous F-2WL module. See dynamics in Supplementary Video 1. (D) Vertical cross-sections across the center of the cell in (A–C).

FIGURE 4

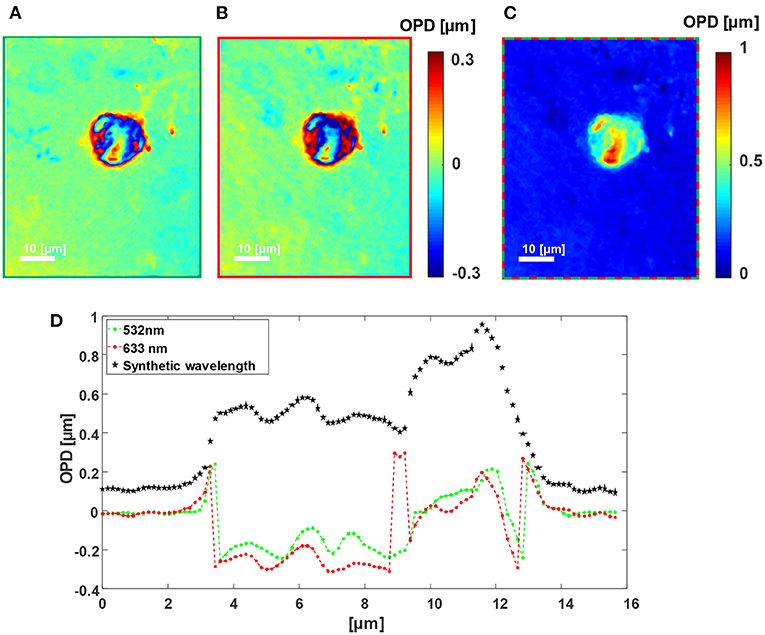
Figure 4. Dual-wavelength OPD reconstruction of a human cancer cell. (A) Wrapped OPD profile as obtained in the greed channel. (B) Wrapped OPD profile as obtained in the red channel. (C) OPD profile obtained after using the proposed simultaneous F-2WL module. See dynamics in Supplementary Video 2. (D) Vertical cross-sections across the center of the cell in (A–C).

Figure 5A shows the quantitative OPD profile of a human sperm cell as imaged under the green channel, and Figure 5B shows the same cell as imaged under the red channel, demonstrating that ambiguities occur in different locations. Figure 5C presents the quantitative OPD profile, as imaged by the simultaneous F-2WL module proposed here. Again, no phase ambiguities occur in the latter profile and still the acquisition is done in a single camera exposure. Supplementary Video 3 shows the cell, scanned while moving the sample stage, demonstrating the capability of the method for dynamic imaging.

FIGURE 5

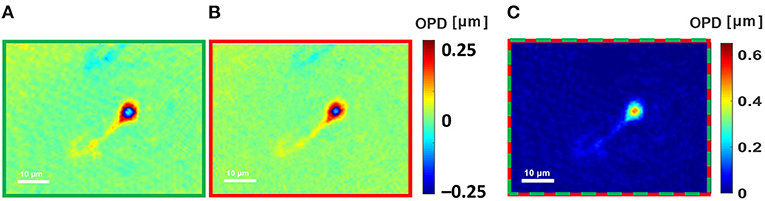
Figure 5. Dual-wavelength OPD reconstruction of a human sperm cell. (A) Wrapped OPD profile as obtained in the greed channel. (B) Wrapped OPD profile as obtained in the red channel. (C) OPD profile obtained after using the proposed simultaneous dual-wavelength module. See dynamics in Supplementary Video 3.

Conclusions

In summary, the F-2WL module is a flipping interferometer, allowing simultaneous acquisition of the complex wavefront of the sample under two different illumination wavelengths. This module is compact and contains only a few and simple components; hence it is accessible, affordable and can fit as a portable device at the output of a routine laboratory microscope, illuminated by two wavelengths of temporally coherent light sources. We used this module for two-wavelength phase unwrapping, using which thicker transparent objects can be acquired without using digital phase unwrapping algorithms that are computationally heavy. Since the module allows the acquisition of a multiplexed off-axis hologram containing the complex wavefronts in the two wavelength channels in a single camera exposure, it is highly suitable for imaging dynamic samples. The method assumes that the sample is empty in three-quarters of the optical field of view. In the fourth quarter, used as the sample beam, the sample can be dense. This is possible by controlling the seeding of the cells, by cleaning cells from the culture before imaging, or by using square chambers and locating the beam at one of the corners of the square. In addition to two-wavelength phase unwrapping, the proposed module can be used for simultaneous interferometric acquisition of two-wavelength channels for other applications, such as interferometric spectroscopy [16] and reduction of coherence-induced disturbances [17, 18]. We expect that in the future, this module will be used for quantitative phase imaging of highly dynamic samples, such as for flow cytometry, while enabling both faster acquisition and processing.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by Tel Aviv University's IRB. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

LK designed and built the setup, conducted experiments, designed and implemented the algorithms, processed the data, and wrote the paper. RG designed the algorithms and processed the data. IB prepared the biological samples for imaging. NS conceived the idea, designed the setup and algorithms, wrote the paper, and supervised the project. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by Tel Aviv University's Light-Matter Interactions Center.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.667023/full#supplementary-material

Supplementary Video 1. Dynamic OPD maps of a 5 μm silica microbead.

Supplementary Video 2. Dynamic OPD maps of a cancer cell.

Supplementary Video 3. Dynamic OPD maps of a sperm cell.

References

1. Shaked NT, Satterwhite LL, Wax A. Quantitative analysis of biological cells using digital holographic microscopy. In: Rosen J, editor. Holography, Research and Technologies. London: InTech (2011). p. 219–36.

Google Scholar

2. Girshovitz P, Shaked NT. Generalized cell morphological parameters based on interferometric phase microscopy and their application to cell life cycle characterization. Biomed Opt Express. (2012) 3:1757–73. doi: 10.1364/BOE.3.001757

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Ghihlia DC, Pritt MD. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software. Hoboken, NJ: Wiley (1998).

Google Scholar

4. Gass J, Dakoff A, Kim MK. Phase imaging without 2π ambiguity by multiwavelength digital holography. Opt Lett. (2003) 28:1141–3. doi: 10.1364/OL.28.001141

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Rinehart MT, Shaked NT, Jenness NJ, Clark RL, Wax A. Simultaneous two-wavelength transmission quantitative phase microscopy with a color camera. Opt Lett. (2010) 35:2612–4. doi: 10.1364/OL.35.002612

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kühn J, Colomb T, Montfort F, Charrière F, Emery Y, Cuche E, et al. Real-time dual-wavelength digital holographic microscopy with a single hologram acquisition. Opt Express. (2007) 15:7231–42. doi: 10.1364/OE.15.007231

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Khmaladze A, Kim M, Lo C-M. Phase imaging of cells by simultaneous dual-wavelength reflection digital holography. Opt Express. (2008) 16:10900–11. doi: 10.1364/OE.16.010900

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Shaked NT, Micó V, Trusiak M, Kus A, Mirsky SK. Off-axis digital holographic multiplexing for rapid wave front acquisition and processing. Adv Optics Photon. (2020) 12:556–611. doi: 10.1364/AOP.384612

CrossRef Full Text | Google Scholar

9. Abdelsalam DG, Kim D. Real-time dual-wavelength digital holographic microscopy based on polarizing separation. Opt Commun. (2012) 285:233–7. doi: 10.1016/j.optcom.2011.09.044

CrossRef Full Text | Google Scholar

10. Guo R, Wang F. Compact and stable real-time dual-wavelength digital holographic microscopy with a long-working distance objective. Opt Express. (2017) 25:24512–20. doi: 10.1364/OE.25.024512

CrossRef Full Text | Google Scholar

11. Turko NA, Shaked NT. Simultaneous two-wavelength phase unwrapping using an external module for multiplexing off-axis holography. Opt Lett. (2017) 42:73–6. doi: 10.1364/OL.42.000073

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Roitshtain D, Turko NA, Javidi B, Shaked NT. Flipping interferometry and its application for quantitative phase microscopy in a micro-channel. Opt Lett. (2016) 41:2354–7. doi: 10.1364/OL.41.002354

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Rotman-Nativ N, Turko NA, Shaked NT. Flipping interferometer with doubled imaging area. Opt Lett. (2018) 43:5543–6. doi: 10.1364/OL.43.005543

CrossRef Full Text | Google Scholar

14. Liu L, Shan M, Zhong Z, Liu B, Luan G, Diao M, et al. Simultaneous dual-wavelength off-axis flipping digital holography. Opt Lett. (2017) 42:4331–4. doi: 10.1364/OL.42.004331

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Tamamitsu M, Zhang Y, Wang H, Wu Y, Ozcan A. A robust holographic autofocusing criterion based on edge sparsity: comparison of Gini index and Tamura coefficient for holographic autofocusing based on the edge sparsity of the complex optical wavefront. Proc SPIE. (2018) IV:105030J. doi: 10.1117/12.2291179

CrossRef Full Text | Google Scholar

16. Turko NA, Shaked NT. Erythrocyte volumetric measurements in imaging flow cytometry using simultaneous three-wavelength digital holographic microscopy. Biomed Opt Express. (2020) 11:6649–58. doi: 10.1364/BOE.404368

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Kosmeier S, Langehanenberg P, von Bally G, Kemper B. Reduction of parasitic interferences in digital holographic microscopy by numerically decreased coherence length. Appl Phys B. (2012) 106:107–15. doi: 10.1007/s00340-011-4667-0

CrossRef Full Text | Google Scholar

18. Larivière-Loiselle C, Bélanger E, Marquet P. Polychromatic digital holographic microscopy: a quasicoherent-noise-free imaging technique to explore the connectivity of living neuronal networks. Neurophoton. (2020) 7:040501. doi: 10.1117/1.NPh.7.4.040501

PubMed Abstract | CrossRef Full Text | Google Scholar