Importance of Viscosity Contrast for the Motion of Erythrocytes in Microcapillaries

The dynamics and deformation of red blood cells (RBCs) in microcirculation affect the flow resistance and transport properties of whole blood. One of the key properties that can alter RBC dynamics in flow is the contrast λ (or ratio) of viscosities between RBC cytosol and blood plasma. Here, we study the dependence of RBC shape and dynamics on the viscosity contrast in tube flow, using mesoscopic hydrodynamics simulations. State diagrams of different RBC dynamical states, including tumbling cells, parachutes, and tank-treading slippers, are constructed for various viscosity contrasts and wide ranges of flow rates and tube diameters (or RBC confinements). Despite similarities in the classification of RBC behavior for different viscosity contrasts, there are notable differences in the corresponding state diagrams. In particular, the region of parachutes is significantly larger for λ = 1 in comparison to λ = 5. Furthermore, the viscosity contrast strongly affects the tumbling-to-slipper transition, thus modifying the regions of occurrence of these states as a function of flow rate and RBC confinement. Also, an increase in cytosol viscosity leads to a reduction in membrane tension induced by flow stresses. Physical mechanisms that determine these differences in RBC dynamical states as a function of λ are discussed.

1. Introduction

Microvascular blood flow is essential for the homeostasis of organism tissues, as it transports nutrients and waste products and mediates various physiological processes. This research field has received enormous attention directed at understanding complex microvascular transport and regulation [1–5]. Blood is a liquid tissue whose major cellular component is erythrocytes or red blood cells (RBCs) which constitute about 45% of blood volume. A healthy RBC has a biconcave shape with a diameter of 6–8 μm and thickness of 2 μm [6]. The RBC membrane consists of a lipid bilayer and spectrin network (cytoskeleton) attached to the inside of the bilayer [7]. These structures supply cell deformability and durability, as RBCs have to frequently pass capillaries with a diameter comparable to the RBC size. The ability of RBCs to deform is vital for microvascular perfusion, as an increased membrane rigidity is generally associated with pathological conditions [8, 9] such as sickle-cell anemia [10] and malaria [11, 12].

One of the important steps toward understanding microvascular blood flow is a detailed description of RBC behavior in microcapillaries. Early experiments [13–15] have shown that RBCs passing through small vessels either deform into cup-like parachute shapes at the vessel center or assume elongated slipper shapes at an off-center position. A number of more recent microfluidic experiments [16–20] have systematically studied and confirmed these observations and suggested a connection between RBC elasticity and its shape in flow. From the physics point of view, it is interesting to understand how such shapes develop and which cell and flow properties determine their stability. First simple axisymmetric models of RBCs flowing in microvessels [21] have demonstrated the ability of RBCs to attain parachute and bullet-like (in very narrow vessels) shapes due to the stresses exerted by fluid flow. Two dimensional (2D) simulations of fluid vesicles mimicking RBCs have shown that cell behavior in microcapillary flow is quite complex [22–27]. In addition to the parachute and slipper shapes, snaking dynamics (a periodic cell swinging around the tube center) at low flow rates and a region of co-existing parachutes and slippers at high flow rates were reported [24, 25]. These 2D simulations have also demonstrated that the transition between parachute and slipper shapes can be triggered by changes in flow rate or RBC membrane elasticity. This transition can be characterized by the distance between the cell's center-of-mass and the channel center, which has been shown to have a similar behavior as a pitchfork bifurcation [23]. Nevertheless, it is still not fully clear why the parachute-to-slipper transition takes place.

Three dimensional (3D) simulations of RBCs flowing in microchannels [28–34] have confirmed the existence of stable slippers in 3D. Despite some similarities between the results obtained from 2D and 3D simulations, RBC dynamics in microchannels is inherently three dimensional, so that the results from 2D simulations are at most qualitative. For instance, 3D simulations have shown the existence of a dynamic state of RBC tumbling at a radial position away from the tube center [29, 34]. In fact, the transition from tumbling to slipper state with increasing flow rate is reminiscent of the well-known tumbling-to-tank-treading transition of RBCs in simple shear flow [35–38]. Furthermore, recent experiments on RBCs in flow within square microchannels have found a tumbling trilobe state at large flow rates and low confinements [34]. Such trilobe dynamics has so far only been reproduced in simulations of RBCs in simple shear flow, and occurs at large shear rates and for large enough viscosity contrasts λ defined as the ratio between viscosities of RBC cytosol and suspending medium [39, 40], with λ ≳ 3.5.

Most of the current simulation studies assume for simplicity the viscosity contrast of unity, even though the average physiological value of λ is about five [41, 42]. The viscosity contrast is an important parameter that significantly affects RBC behavior in simple shear flow [39, 40, 43–45]. However, it remains unclear whether the viscosity contrast is equally important for RBC dynamics in microcapillary flow. Therefore, we focus on the effect of λ on RBC dynamical states in tube flow. Several state diagrams of RBC dynamics, including snaking, tumbling, tank-treading slipper, and parachute, are presented for different viscosity contrasts, tube diameters, and flow rates. Even though the dynamical states are similar for λ = 1 and λ = 5, there are differences in flow conditions at which they appear. In particular, the region of tumbling dynamics for λ = 5 expands toward larger flow rates in comparison to λ = 1, since an increased dissipation inside the cell suppresses membrane tank-treading in favor of tumbling motion. Furthermore, the region of parachute shapes is larger for λ = 1 than that for λ = 5. A larger viscosity inside the RBC also leads to a decrease in membrane tension for the same flow conditions. Physical mechanisms that determine these differences in dynamical state diagrams for various viscosity contrasts are discussed.

2. Models and Methods

2.1. Red Blood Cell Model

A RBC is modeled as a triangulated surface with N_v = 3, 000 vertices, N_e edges, and N_f triangular faces [28, 46–48]. The total potential energy of the system is given by

$\begin{array}{ll}V=V_{\text{in}-\text{plane}}+V_{\text{bend}}+V_{\text{area}}+V_{\text{vol}}.& (1)\end{array}$

The term V_in−plane represents an in-plane elastic energy as [47, 48]

$\begin{array}{ll}{V}_{\text{in}-\text{plane}}={\displaystyle \sum _{i=1}^{N_{\text{e}}}}\frac{k_{B}T{\ell }_{\text{m}}(3x_i^2-2x_i^3)}{4p(1-x_i)}+{\displaystyle \sum _{i=1}^{N_{\text{e}}}}\frac{k_{\text{p}}}{{\ell }_i},& (2)\end{array}$

where the first term is an attractive worm-like chain potential and the second term is a repulsive potential with a strength coefficient k_p. In the attractive potential, p is the persistence length, ℓ_i is the extension of edge i, ℓ_m is the maximum edge extension, and x_i = ℓ_i/ℓ_m.

The second term in Equation (1) corresponds to bending resistance of the membrane,

$\begin{array}{ll}{V}_{\text{bend}}={\displaystyle \sum _{i=1}^{N_{\text{e}}}}{\kappa }_{\text{b}}\left(1-cos({\theta }_i-{\theta }_0)\right),& (3)\end{array}$

where κ_b is the bending coefficient, θ is the angle between two neighboring faces, and θ₀ is the spontaneous angle. Equation (3) is a basic discretization of the Helfrich bending energy [49], which is acceptable for RBCs as their dynamics and deformation are primarily governed by shear-elastic properties. Other discretizations of the Helfrich energy are also available [50, 51].

The last two terms in Equations (1), V_area, and V_vol, represent surface area and volume constraints given by

$\begin{array}{l}{V}_{\text{area}}=\frac{k_{\text{a}}{(A-A_0)}^2}{2A_0}+{\displaystyle \sum _{i=1}^{N_{\text{f}}}}\frac{k_{\text{d}}{(A_i-A_i^0)}^2}{2A_i^0},\\ V_{\text{vol}}=\frac{k_{\text{v}}{(V-V_0)}^2}{2V_0},\hfill & (4)\end{array}$

where k_a, k_d, and k_v are local area, total surface area and volume constraint coefficients, respectively. $A_i^0$, A₀, and V₀ are local area of individual faces, total surface area and total volume of the RBC, respectively. Note that the membrane viscosity is omitted in the employed RBC model for simplicity.

2.2. Modeling Hydrodynamic Flow

Fluid flow is modeled by the smoothed dissipative particle dynamics (SDPD) method which is a Lagrangian discretization of the Navier-Stokes equations [52, 53]. The SDPD fluid consists of N fluid particles which interact through conservative (C), translational dissipative (D), rotational dissipative (R), and random forces (~). The forces between particles i and j are given by,

$\begin{array}{ll}{\text{F}}_{ij}^{\text{C}}=\left(\frac{p_i}{{\rho }_i^2}+\frac{p_j}{{\rho }_j^2}\right)F_{ij}{\text{r}}_{ij},& (5)\end{array}$

$\begin{array}{ll}{\text{F}}_{ij}^{\text{D}}=-{\gamma }_{ij}({\text{v}}_{ij}+({\text{v}}_{ij}·{\text{e}}_{ij}){\text{e}}_{ij}),& (6)\end{array}$

$\begin{array}{ll}{\text{F}}_{ij}^{\text{R}}=-{\gamma }_{ij}\frac{{\text{r}}_{ij}}{2}\times ({\omega }_i+{\omega }_j),& (7)\end{array}$

$\begin{array}{ll}{\tilde{\text{F}}}_{ij}={\sigma }_{ij}\left(d{\overline{{W}}}_{ij}^{\text{S}}+\frac{1}{3}tr\left[d{{W}}_{ij}\right]𝟙\right)·\frac{{\text{e}}_{ij}}{dt},& (8)\end{array}$

where r_i, v_i, and ω_i are the particle position, velocity, and angular velocity, and r_ij = r_i − r_j, v_ij = v_i − v_j, and e_ij = r_ij/|r_ij|. ${\rho }_i=\sum _{j\left[i\right]}{m}_j{W}_{ij}$ is the particle density, where the sum runs over the particle i and its neighbors within a smoothing length (or cutoff radius) h, m_i is the particle mass, and W_ij = W(r_ij) is the smoothing kernel represented by the Lucy function [54]

$\begin{array}{ll}W(r)=\frac{105}{16\pi h^3}\left(1+3\frac{r}{h}\right){\left(1-\frac{r}{h}\right)}^3.& (9)\end{array}$

The function F_ij is calculated from W_ij as ∇_iW_ij = −r_ijF_ij. The particle pressure p_i is defined as $p_i=p_0{({\rho }_i/{\rho }_0)}^{\alpha }-b$, where ρ₀ is the reference density and the parameters p₀, α, and b control fluid compressibility, and can be freely selected [55]. tr[d${W}$_ij] is the trace of matrix of independent Wiener increments d${W}$_ij and $d{\overline{{W}}}_{ij}^{\mathrm{\text{S}}}$ is the traceless symmetric part. The dissipative γ_ij = 20ηF_ij/(7ρ_iρ_j) and random σ_ij force coefficients are related as ${\sigma }_{ij}=2\sqrt{k_{\mathrm{\text{B}}}T{\gamma }_{ij}}$ where η is the dynamic viscosity, k_B is the Boltzmann constant, and T is temperature. dt is the time step.

The solvent inside the RBC (cytosol) is separated from outside fluid (plasma) by the membrane. The number density of fluid particles is set to n = 12 (per unit volume in model units) for both cytosol and plasma, providing a good resolution for fluid flow inside and outside the RBC. The reference density is set to ρ₀ = mn with m = 1. Solid walls are modeled by frozen SDPD particles. Fluid-membrane interactions have two contributions: (i) fluid particles bounce back from the membrane surface and (ii) the dissipative force coefficient between fluid particles and membrane vertices is set such that no-slip boundary conditions are attained. Note that the conservative force for fluid-membrane interactions is turned off. Fluid particles are also reflected back at the solid wall. In addition, an adaptive shear force is added to fluid particles near the wall to ensure no-slip boundary conditions [56].

2.3. Simulation Setup and Parameters

Poiseuille flow with a single RBC suspended in a viscous fluid inside a cylindrical tube of length L = 50 μm is simulated. The tube axis is aligned with the flow direction along the x axis. Diameter of the tube D = 2R determines RBC confinement as χ = D_r/D, where $D_r=\sqrt{A_0/\pi }$ is the effective RBC diameter. To generate flow, a force f is applied on every solvent particle, representing a pressure gradient ΔP/L = f · n with the pressure drop ΔP along the tube length.

In simulations, cell properties correspond to average characteristics of a healthy RBC with a membrane area $A_0=133\mu {\mathrm{\text{m}}}^2$, cell volume $V_0=93\mu {\mathrm{\text{m}}}^3$, shear modulus μ = 4.8 μN/m, and bending rigidity κ = 70 k_BT = 3 × 10⁻¹⁹ J [6, 57–59]. This leads to D_r = 6.5 μm (D_r = 6.5 in model units) and a RBC reduced volume of $V^{*}=6V_0/(\pi D_r^3)\approx 0.64$. Note that the stress-free shape of a RBC elastic network (Equation 2) is assumed to be an oblate spheroid with a reduced volume of 0.96. The biconcave shape of a RBC with V^* = 0.64 is obtained by deflating the stress-free spheroid with a reduced volume of 0.96. Furthermore, the energy unit k_BT is selected to be k_BT = 0.2 in simulations, corresponding to a physiological temperature of 37° C.

To characterize different flow conditions, several non-dimensional parameters are employed

  (i) Reynolds number $Re=\rho \overline{\stackrel{.}{\gamma }}{D}_r^2/\eta$ is the ratio of inertial and viscous forces, where ρ is the mass density, $\overline{\stackrel{.}{\gamma }}=\bar{v}/D=Dfn/(32\eta )$ is the average (or pseudo) shear rate, and η is the external fluid viscosity. In all simulations, Re ≤ 0.3.

 (ii) λ = η_i/η_o is the viscosity contrast between internal (cytosol) and external (plasma) fluids. The average value of λ under physiological conditions is λ = 5 [41, 42].

(iii) $\stackrel{.}{\gamma }*=\overline{\stackrel{.}{\gamma }}·\tau$ is the dimensionless shear rate that characterizes flow strength. τ is the RBC relaxation time given by τ = ηD_r/μ.

To keep Reynolds number low enough (i.e., Re ≤ 0.3), in most simulations $\stackrel{.}{\gamma }*$ is controlled by varying η instead of changing the flow rate for a fixed viscosity.

2.4. Dynamical Characteristics and Membrane Tension

To analyze dynamical properties of a flowing RBC, the gyration tensor

$\begin{array}{ll}{T}_{ij}=\frac{1}{N}{\displaystyle \sum _{n=1}^N}(r_{n,i}-r_{c,i})·(r_{n,j}-r_{c,j})& (10)\end{array}$

is employed, where i and j denote x, y, or z, r_n is the position of membrane vertex n, and r_c is the center of mass of the RBC. Then, the eigenvalues ξ_i of the gyration tensor T_ij characterize RBC deformation. The eigenvector that corresponds to the smallest eigenvalue is used to define the orientational axis of the cell. Orientation angle θ₁ of the RBC is defined as the angle between its orientational axis and the flow direction. The eigenvalues are also used to compute cell asphericity ${O}$, which characterizes its deviation from a spherical shape

$\begin{array}{ll}{O}=\left[{({\xi }_1-{\xi }_2)}^2+{({\xi }_2-{\xi }_3)}^2+{({\xi }_3-{\xi }_1)}^2\right]/\left(2R_g^4\right),& (11)\end{array}$

where $R_g^2={\xi }_1+{\xi }_2+{\xi }_3$.

To calculate local membrane tension G_i at vertex i, virial stress is used as

$\begin{array}{ll}{G}_i=-\frac{1}{2a_i}{\displaystyle \sum _{j(i)}}{\text{r}}_{\text{i},\text{j}}·{\text{F}}_{\text{i},\text{j}},& (12)\end{array}$

where a_i is the vertex area computed as one third of a sum of all face areas adjacent to vertex i, j(i) represents all neighboring vertices connected to i by an edge, and r_i,j and F_i,j are position and force vectors at the edge (i,j), respectively. Note that the in-plane elastic energy, bending potential, surface area, and volume constraints can contribute to the membrane tension. The kinetic energy contribution to tension is omitted, as it is very small under a significant membrane stretching in flow.

3. Results

In microcapillary flow, RBCs are known to exhibit different dynamical states, including snaking, tumbling, tank-treading, and parachute [15, 17, 20, 24, 25, 29, 34]. Snaking is characterized by a periodic swinging in RBC orientation around the tube axis [24, 25, 29]. Tumbling is an off-axis rigid-body-like rotation, similar to RBC tumbling in simple shear flow [37, 40, 60]. Tank-treading is represented by membrane rotation with a nearly fixed cell orientation, which also occurs in simple shear flow at low enough λ [37, 40, 61]. The tank-reading state of a RBC in microcapillary flow is also often referred to as slipper. Finally, parachute is a stable stomatocyte-like RBC deformation in the tube center. These dynamical states depend on RBC mechanical properties (e.g., shear modulus, bending rigidity, viscosity contrast), cell confinement, and the flow rate. Here, we primarily focus on how the viscosity contrast affects these dynamical states for a wide range of RBC confinements and flow rates.

3.1. Dynamic State Diagram

Figure 1 presents dynamic state diagram for the viscosity contrast λ = 5 and different χ and ${\stackrel{.}{\gamma }}^{*}$ values. The representative snapshots of tumbling, tank-treading, and parachute states are also displayed (see Supplementary Movies 1–3). The snaking state exhibits minimal deformation and appears at very low shear rates ${\stackrel{.}{\gamma }}^{*}\lesssim 0.01$ for all confinements χ. The tumbling state occurs for small confinements and moderate shear rates. As the shear rate increases, a tumbling RBC transits into a tank-treading state. The critical shear rate, at which the tumbling-to-tank-treading transition takes place, depends on χ and increases with increasing confinement. For large enough confinements and shear rates, the RBC adopts a parachute shape which exhibits least dynamics out of all observed states. Note that the classification of different states becomes difficult close to the transition boundaries, because the RBC may exhibit complex deformations. Therefore, these boundaries are approximate and intended to provide a visual guidance.

FIGURE 1

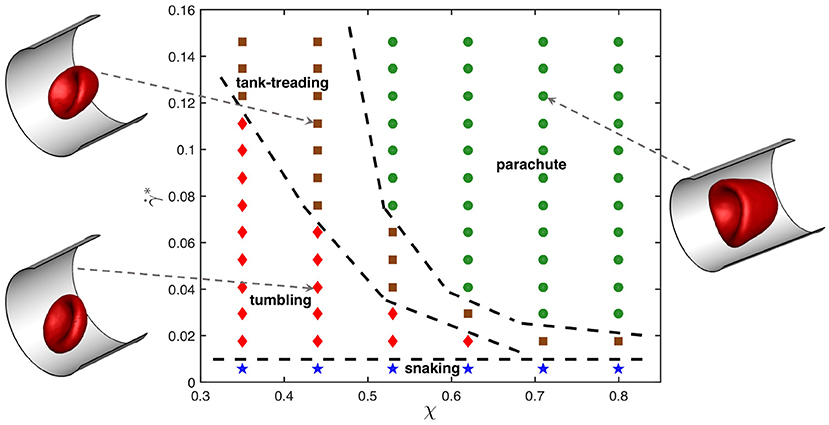
Figure 1. State diagram for λ = 5 showing different dynamical states of the RBC for various confinement ratios χ and non-dimensional shear rates ${\stackrel{.}{\gamma }}^{*}$. The states include snaking (blue stars), tumbling (red diamonds), tank-treading (brown squares), and parachute (green circles). Dashed lines separating regions with different states are drawn for visual guidance. Representative snapshots for tumbling, tank-treading, and parachute states are also displayed.

To understand the effect of viscosity contrast on dynamical states of the RBC in microcapillary flow, the state diagrams for λ = 1 and λ = 3 are shown for comparison in Figure 2. As the viscosity contrast is decreased from λ = 5 to λ = 1, the parachute region widens toward smaller confinement values. This is a surprising result considering the fact that an increase in viscosity contrast suppresses tank-treading in simple shear flow [39, 40], which will be discussed later. The tumbling-to-tank-treading transition shifts toward larger shear rates as the viscosity contrast is increased from λ = 1 to λ = 5. This result is consistent with our expectations that an increase in internal viscosity leads to increased fluid stresses inside the RBC, suppressing membrane tank-treading. A similar observation has also been made in the context of adhered malaria-infected RBCs (iRBCs) under flow, such that an increase in viscosity contrast suppresses iRBC crawling at the surface and results in iRBC flipping or its complete detachment [62]. Note that the snaking state remains nearly unchanged by the viscosity contrast.

FIGURE 2

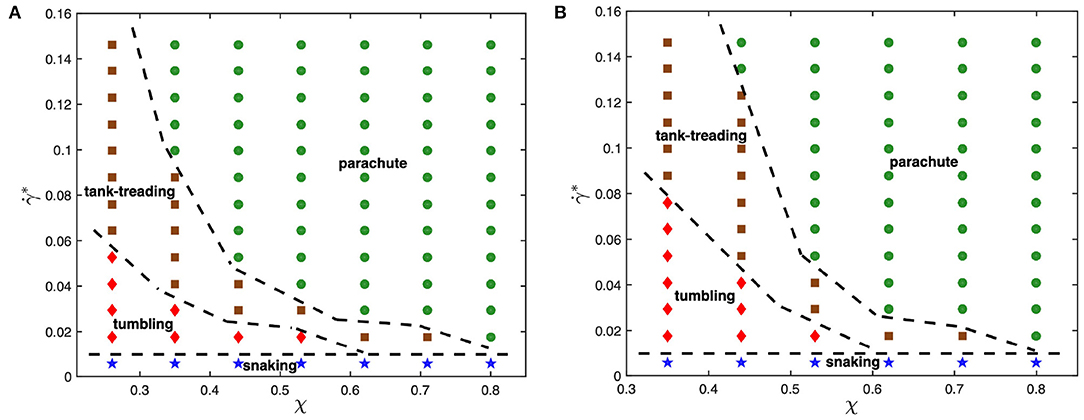
Figure 2. State diagrams for viscosity contrasts (A) λ = 1 and (B) λ = 3 with snaking (blue stars), tumbling (red diamonds), tank-treading (brown squares), and parachute (green circles) states. Dashed lines separating regions with different states are drawn for visual guidance.

3.2. Dynamical Characteristics

To examine differences in dynamical characteristics of RBCs with a change in viscosity contrast, multiple dynamical measures which uniquely characterize each state are computed. Figure 3 presents time evolution of the orientation angle θ₁ and asphericity ${O}$ for two different flow conditions (χ = 0.35 & $\stackrel{.}{\gamma }*=0.076$; χ = 0.44 & $\stackrel{.}{\gamma }*=0.1$) and viscosity contrasts λ = 1 and λ = 5. For the case with χ = 0.35 and $\stackrel{.}{\gamma }*=0.076$ in Figures 3A,B, the RBC tank-treads for λ = 1, whereas it tumbles for λ = 5. In an idealized tank-treading state with only membrane rotation and without cell deformation, both θ₁ and ${O}$ should remain constant. However, a moderate periodic deformation and oscillatory orientation swinging is observed in Figure 3A for λ = 1. For the tumbling state in Figure 3B with λ = 5, membrane deformation is significantly reduced, and the orientation angle spans a much wider range, indicating whole-cell flipping. For the case with χ = 0.44 and $\stackrel{.}{\gamma }*=0.1$ in Figures 3C,D, λ = 1 results in a parachute state with nearly constant θ₁ and ${O}$, while λ = 5 leads to a tank-treading state with variations in θ₁ and ${O}$ resembling those in Figure 3A. Interestingly, the frequency of the variations in θ₁ and ${O}$ for λ = 5 in Figure 3D is significantly smaller than that for λ = 1 in Figure 3A, even though the shear rate is larger for λ = 5. This means that an increased internal viscosity slows down membrane dynamics in microcapillary flow due to an increased dissipation, which is consistent with the results of a study on discocyte (fluid) vesicles for various viscosity contrasts and membrane viscosities [63].

FIGURE 3

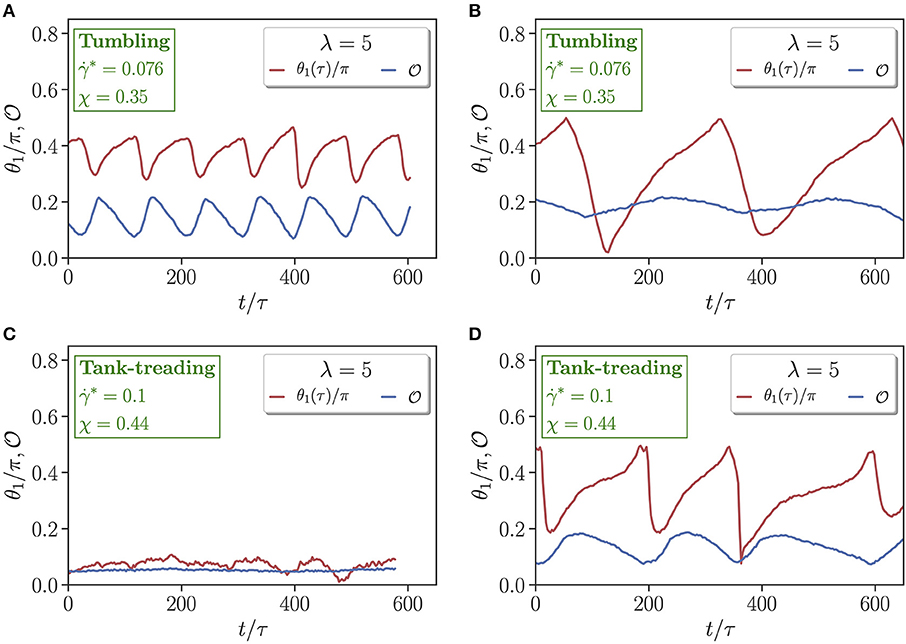
Figure 3. Comparison of time-dependent cell orientation θ₁ and asphericity ${O}$ for (A,C) λ = 1 and (B,D) λ = 5. Two flow conditions are selected, including (A,B) χ = 0.35 and ${\stackrel{.}{\gamma }}^{*}=0.076$, and (C,D) χ = 0.44 and ${\stackrel{.}{\gamma }}^{*}=0.1$. Both (A,D) represent tank-treading states, whereas (B) corresponds to a tumbling state and (C) to a parachute state.

Another difference in Figures 3A,D for the tank-treading state is that the amplitude of oscillations in cell orientation angle is larger for λ = 5 than for λ = 1. Note that, a RBC at large enough viscosity contrasts (λ ≳ 3.5) in an unbounded shear flow does not exhibit tank-treading, but shows a rotational dynamics [40]. In the microchannel, the tank-treading motion of a RBC for λ = 5 is facilitated by cell confinement [64]. Therefore, the aforementioned tendency of the RBC at λ = 5 for rotation likely results in the larger amplitude of oscillations in the orientation angle in comparison to that for λ = 1.

3.3. Membrane Tension

It is interesting to take a look at the effect of viscosity contrast on local membrane tension, as it might be important for the activation of mechano-sensitive channels within the membrane [65, 66]. Figure 4A shows the distribution of local tension G for a parachute shape normalized by the shear modulus μ. The local tension G is calculated using Equation (12), where all contributions from model potentials in Equation (1) are considered, even though the in-plane elastic-energy term supplies the maximum contribution to G. The concave part of the parachute shape has a significantly lower tension than the convex front of the RBC exposed to strong fluid stresses. The tension distribution for tumbling and tank-treading RBCs has a qualitatively similar trend, in which the frontal part of the cell has larger tension than the back portion. However, for tumbling and tank-treading states, local tension fluctuates in accord with the discussed RBC dynamics, while for the parachute state, temporal tension changes are generally small.

FIGURE 4

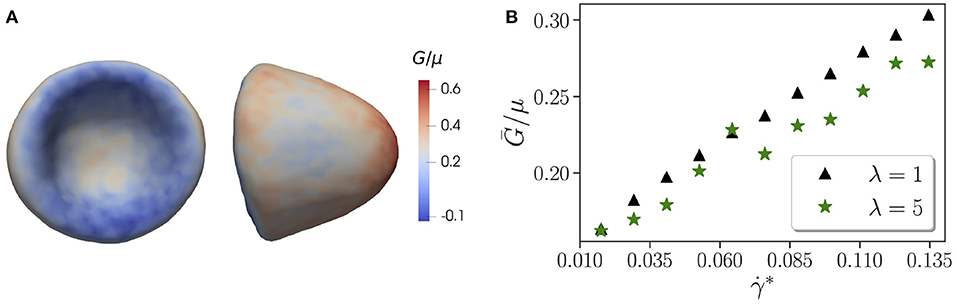
Figure 4. Membrane tension. (A) Side and front views of the parachute shape with a local tension G indicated by the color code and normalized by the shear modulus μ. Here, λ = 5, χ = 0.71, and $\stackrel{.}{\gamma }*=0.076$. (B) Average tension Ḡ/μ of the whole RBC as a function of non-dimensional shear rate $\stackrel{.}{\gamma }*$. Here, the confinement is fixed at χ = 0.53. The data are shown for two different viscosity contrasts λ = 1 and λ = 5. A jump in tension for λ = 5 at $\stackrel{.}{\gamma }*\simeq 0.065$ corresponds to the tank-treading-to-parachute transition.

Figure 4B presents tension Ḡ averaged over the RBC surface as a function of $\stackrel{.}{\gamma }*$ for two different viscosity contrasts λ = 1 and λ = 5. The average tension increases with the shear rate $\stackrel{.}{\gamma }*$ in an almost linear fashion for both viscosity contrasts. Interestingly, λ = 5 generally leads to a lower tension in comparison with λ = 1, which is consistent with a previous numerical investigation [67] showing that the maximum tension increases with the flow rate and decreases with increasing viscosity contrast. For λ = 5, there is a jump in tension at approximately $\stackrel{.}{\gamma }*\simeq 0.065$ that corresponds to the tank-treading-to-parachute transition as shown in Figure 1. Note that such jump is not present for λ = 1.

An average tension of about Ḡ = 10⁻⁶ N/m (or Ḡ/μ ≈ 0.2) is comparatively large. For example, in a recent study on sculpting of lipid vesicles by enclosed active particles [68], complex vesicle shapes have been observed for floppy vesicles with a tension of about 10⁻⁸ N/m, while a high membrane tension of about 10⁻⁵ N/m completely suppresses any vesicle shape changes. Apart from the average tension, it is also instructive to look at the maximum tension G_max = max{G_i} for different χ and $\stackrel{.}{\gamma }*$. As expected, G_max increases with increasing shear rate. For λ = 5, the maximum tension at χ = 0.62 is G_max/μ = 0.7 for $\stackrel{.}{\gamma }*=0.053$ and G_max/μ = 0.77 for $\stackrel{.}{\gamma }*=0.076$ (both are parachute states). For a given shear rate, an increase in confinement results in elevation of G_max, e.g., for $\stackrel{.}{\gamma }*=0.053$, G_max/μ = 0.64 for χ = 0.35 (tumbling state) and G_max/μ = 0.7 for χ = 0.62 (parachute state). These trends are similar for λ = 1. However, differences in G_max with respect to the viscosity contrast are rather small, indicating that external fluid stresses mainly govern the membrane tension. The magnitudes of maximal tension from our simulations are consistent with the values reported in [67].

4. Discussion and Conclusions

In our study, we have focused on the effect of viscosity contrast λ on RBC dynamic states in microcapillary flow. State diagrams with different dynamic states, such as snaking, tumbling, tank-treading, and parachute, have been constructed for several λ values and wide ranges of non-dimensional shear rates $\stackrel{.}{\gamma }*$ and confinements χ. Our central result is that there are significant changes in the state diagram when the viscosity contrast is decreased from λ = 5 to λ = 1. In particular, the region of stable parachutes becomes larger and expands toward lower confinements with decreasing λ. This result seems to be in contradiction to the fact that a large viscosity inside the RBC dampens membrane dynamics and hence, should suppress the dynamic tank-treading state [39, 40]. To verify the robustness of our simulation predictions, we have performed simulations with a consecutive change in the viscosity contrast for several conditions where parachutes are stable for λ = 1 and tank-treading is stable for λ = 5. Thus, after reaching a stable parachute state for λ = 1, the viscosity contrast is instantaneously switched to λ = 5, leading to the tank-treading state. Then, switching back to λ = 1 brings the initially tank-treading RBC to the parachute state. Furthermore, a larger parachute region for λ = 1 than that for λ = 5 has also been observed in 2D simulations of vesicles [24, 25].

To reconcile this seeming contradiction, physical mechanisms that govern the parachute-to-tank-treading transition in tube flow have to be uncovered. A study based on 2D simulations of vesicles in an unbounded parabolic flow [23] suggests that the parachute-to-slipper transition can be described well by a pitchfork bifurcation and that a slipper shape provides a higher flow efficiency for 2D RBC-like vesicles. In particular, there is a lag between the vesicle velocity and the imposed parabolic flow in the parachute state, which is proposed to trigger this instability. This lag increases as the parachute conforms less with the parabolic flow profile for decreasing flow rate or increasing bending rigidity of the vesicle. Unfortunately, this argument has not been connected in any way to the viscosity contrast or internal cell dissipation. From existing experimental and simulation studies [15, 17, 20, 24, 25, 29, 34], it is clear that the parachute state requires large enough flow rates, such that flow stresses in the tube center are sufficient to deform the RBC into a parachute shape. Therefore, only when a RBC conforms well enough to the flow profile, the parachute state is stable. Nevertheless, the change in the parachute-to-slipper transition for different λ cannot be attributed to differences in the parachute shape (or conformity with the flow), as we have not found substantial differences in parachute shapes for different viscosity contrasts. The insensitivity of the parachute shape to λ is likely due to the fact that a non-dynamic parachute state of the RBC depends primarily on its elastic properties, and is nearly independent of internal dissipation.

Our hypothesis is that membrane dynamics is also important for parachute stability at the tube center. As the parachute-to-tank-treading transition is approached, a perturbation (e.g., due to cell diffusion) in RBC position from the tube center leads to the asymmetry in fluid-flow stresses which pull the RBC away from the center and set the membrane into a tank-treading-like motion. A slight motion of the membrane in the parachute state is observed in our simulations, as the RBC is never perfectly symmetric and is often located slightly away from the tube center. For λ = 1, the membrane can rotate faster than in case of λ = 5, and therefore, the mismatch between local membrane motion and fluid flow is smaller, resulting in reduced local fluid stresses that pull the RBC away from the center. For λ = 5, the local fluid stresses on the RBC are larger due to slow membrane tank-treading, leading to the destabilization of parachute shape at larger confinements in comparison to λ = 1.

Another important difference in the state diagrams for λ = 1 and λ = 5 is that the tumbling-to-tank-treading transition occurs at larger shear rates for λ = 5 than for λ = 1. This can be explained by the fact that an increased dissipation inside the RBC for λ = 5 suppresses tank-treading motion and delays the transition in terms of $\stackrel{.}{\gamma }*$. In fact, in simple shear flow, the tank-treading state does not exist for λ = 5 [39, 40]. For microcapillary flow, RBC tank-treading becomes possible at λ = 5 due to the confinement which can trigger the tumbling-to-tank-treading transition even when cell dimensions are smaller than the distance between two walls [64]. For a large enough vessel diameter, it is plausible to expect that the tank-treading state should disappear for λ = 5, as local flow conditions should closely resemble simple shear flow at the scale of RBC size. For instance, recent microfluidic experiments in a square channel [34] have reported the existence of rotating trilobe shapes at low confinements and high flow rates, which are consistent with RBC shapes in simple shear flow at λ = 5 [39, 40].

Membrane tension must be directly related to mechano-transduction as the RBC membrane contains many mechano-sensitive channels [65, 66]. We have shown that an increase in the viscosity contrast lowers the membrane tension. A high viscosity of the cytosol provides a large dissipation, reducing membrane tension. Furthermore, the maximum tension increases with increasing shear rate $\stackrel{.}{\gamma }*$ and confinement χ. Several experimental studies show that flow stresses can change RBC biochemical properties. For instance, when RBCs pass through small constrictions, they release ATP which can participate in vasodilation signaling [69, 70]. Furthermore, a recent investigation [71] reports that when RBCs pass through small constrictions, the mechano-sensitive channels (e.g., Piezo1 and Gardos channels) that participate in RBC volume control become activated. The relevance of membrane tension has also been demonstrated for malaria disease, such that an increased RBC membrane tension in the Dantu blood group significantly reduces the invasion of RBCs by malaria parasites, which is a protective mechanism from malaria infection [72].

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

AD and JM performed simulations and analyzed the data. GG and DF designed the research. DF supervised the project. All authors discussed the results and wrote the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.666913/full#supplementary-material

References

1. Popel AS, Johnson PC. Microcirculation and hemorheology. Annu Rev Fluid Mech. (2005) 37:43–69. doi: 10.1146/annurev.fluid.37.042604.133933

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Lipowsky HH. Microvascular rheology and hemodynamics. Microcirculation. (2005) 12:5–15. doi: 10.1080/10739680590894966

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Pries AR, Secomb TW. Blood flow in microvascular networks. In: Tuma RF, Duran WN, Ley K, editors, Handbook of Physiology, The Cardiovascular System, Microcirculation. San Diego, CA: Academic Press (2008). p. 3–36.

Google Scholar

4. Secomb TW. Blood flow in the microcirculation. Annu Rev Fluid Mech. (2017) 49:443–61. doi: 10.1146/annurev-fluid-010816-060302

CrossRef Full Text | Google Scholar

5. Gompper G, Fedosov DA. Modeling microcirculatory blood flow: current state and future perspectives. WIREs Syst Biol Med. (2016) 8:157–68. doi: 10.1002/wsbm.1326

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Evans EA, Skalak R. Mechanics and Thermodynamics of Biomembranes. Boca Raton, FL: CRC Press, Inc. (1980).

Google Scholar

7. Discher DE, Mohandas N, Evans EA. Molecular maps of red cell deformation: hidden elasticity and in situ connectivity. Science. (1994) 266:1032–5. doi: 10.1126/science.7973655

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Diez-Silva M, Dao M, Han J, Lim CT, Suresh S. Shape and biomechanical characteristics of human red blood cells in health and disease. MRS Bull. (2010) 35:382–8. doi: 10.1557/mrs2010.571

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Tomaiuolo G. Biomechanical properties of red blood cells in health and disease towards microfluidics. Biomicrofluidics. (2014) 8:051501. doi: 10.1063/1.4895755

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Kaul DK, Fabry ME, Windisch P, Baez S, Nagel RL. Erythrocytes in sickle cell anemia are heterogeneous in their rheological and hemodynamic characteristics. J Clin Invest. (1983) 72:22–31.

PubMed Abstract | Google Scholar

11. Cranston HA, Boylan CW, Carroll GL, Sutera SP, Williamson JR, Gluzman IY, et al. Plasmodium falciparum maturation abolishes physiologic red cell deformability. Science. (1984) 223:400–3. doi: 10.1126/science.6362007

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Fedosov DA, Caswell B, Suresh S, Karniadakis GE. Quantifying the biophysical characteristics of Plasmodium-falciparum-parasitized red blood cells in microcirculation. Proc Natl Acad Sci USA. (2011) 108:35–9. doi: 10.1073/pnas.1009492108

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Skalak R, Branemark PI. Deformation of red blood cells in capillaries. Science. (1969) 164:717–9. doi: 10.1126/science.164.3880.717

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Gaehtgens P, Dührssen C, Albrecht KH. Motion, deformation, and interaction of blood cells and plasma during flow through narrow capillary tubes. Blood Cells. (1980) 6:799–812.

PubMed Abstract | Google Scholar

15. Bagge U, Branemark PI, Karlsson R, Skalak R. Three-dimensional observations of red blood cell deformation in capillaries. Blood Cells. (1980) 6:231–7.

PubMed Abstract | Google Scholar

16. Tomaiuolo G, Preziosi V, Simeone M, Guido S, Ciancia R, Martinelli V, et al. A methodology to study the deformability of red blood cells flowing in microcapillaries in vitro. Ann Ist Super Sanita. (2007) 43:186–92.

PubMed Abstract | Google Scholar

17. Tomaiuolo G, Simeone M, Martinelli V, Rotoli B, Guido S. Red blood cell deformation in microconfined flow. Soft Matter. (2009) 5:3736–40. doi: 10.1039/b904584h

CrossRef Full Text | Google Scholar

18. Guido S, Tomaiuolo G. Microconfined flow behavior of red blood cells in vitro. C R Phys. (2009) 10:751–63. doi: 10.1016/j.crhy.2009.10.002

CrossRef Full Text | Google Scholar

19. Abkarian M, Faivre M, Stone HA. High-speed microfluidic differential manometer for cellular-scale hydrodynamics. Proc Natl Acad Sci USA. (2006) 103:538–42. doi: 10.1073/pnas.0507171102

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Abkarian M, Faivre M, Horton R, Smistrup K, Best-Popescu CA, Stone HA. Cellular-scale hydrodynamics. Biomed Mater. (2008) 3:034011. doi: 10.1088/1748-6041/3/3/034011

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Secomb TW, Skalak R, Özkaya N, Gross JF. Flow of axisymmetric red blood cells in narrow capillaries. J Fluid Mech. (1986) 163:405–23. doi: 10.1017/S0022112086002355

CrossRef Full Text | Google Scholar

22. Secomb TW, Styp-Rekowska B, Pries AR. Two-dimensional simulation of red blood cell deformation and lateral migration in microvessels. Ann Biomed Eng. (2007) 35:755–65. doi: 10.1007/s10439-007-9275-0

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Kaoui B, Biros G, Misbah C. Why do red blood cells have asymmetric shapes even in a symmetric flow? Phys Rev Lett. (2009) 103:188101. doi: 10.1103/PhysRevLett.103.188101

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kaoui B, Tahiri N, Biben T, Ez-Zahraouy H, Benyoussef A, Biros G, et al. Complexity of vesicle microcirculation. Phys Rev E. (2011) 84:041906. doi: 10.1103/PhysRevE.84.041906

CrossRef Full Text | Google Scholar

25. Tahiri N, Biben T, Ez-Zahraouy H, Benyoussef A, Misbah C. On the problem of slipper shapes of red blood cells in the microvasculature. Microvasc Res. (2013) 85:40–5. doi: 10.1016/j.mvr.2012.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Aouane O, Thiébaud M, Benyoussef A, Wagner C, Misbah C. Vesicle dynamics in a confined Poiseuille flow: from steady state to chaos. Phys Rev E. (2014) 90:033011. doi: 10.1103/PhysRevE.90.033011

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lázaro GR, Hernández-Machado A, Pagonabarraga I. Rheology of red blood cells under flow in highly confined microchannels: I. Effect of elasticity. Soft Matter. (2014) 10:7195–206. doi: 10.1039/C4SM00894D

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Noguchi H, Gompper G. Shape transitions of fluid vesicles and red blood cells in capillary flows. Proc Natl Acad Sci USA. (2005) 102:14159–64. doi: 10.1073/pnas.0504243102

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Fedosov DA, Peltomäki M, Gompper G. Deformation and dynamics of red blood cells in flow through cylindrical microchannels. Soft Matter. (2014) 10:4258–67. doi: 10.1039/C4SM00248B

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Ye T, Phan-Thien N, Khoo BC, Lim CT. Dissipative particle dynamics simulations of deformation and aggregation of healthy and diseased red blood cells in a tube flow. Phys Fluids. (2014) 26:111902. doi: 10.1063/1.4900952

CrossRef Full Text | Google Scholar

31. Fedosov DA, Noguchi H, Gompper G. Multiscale modeling of blood flow: from single cells to blood rheology. Biomech Model Mechanobiol. (2014) 13:239–58. doi: 10.1007/s10237-013-0497-9

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Ye T, Shi H, Peng L, Li Y. Numerical studies of a red blood cell in rectangular microchannels. J Appl Phys. (2017) 122:084701. doi: 10.1063/1.5000357

CrossRef Full Text | Google Scholar

33. Guckenberger A, Kihm A, John T, Wagner C, Gekle S. Numerical-experimental observation of shape bistability of red blood cells flowing in a microchannel. Soft Matter. (2018) 14:2032–43. doi: 10.1039/C7SM02272G

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Reichel F, Mauer J, Nawaz AA, Gompper G, Guck J, Fedosov DA. High-throughput microfluidic characterization of erythrocyte shapes and mechanical variability. Biophys J. (2019) 117:14–24. doi: 10.1016/j.bpj.2019.05.022

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Fischer TM. Shape memory of human red blood cells. Biophys J. (2004) 86:3304–13. doi: 10.1016/S0006-3495(04)74378-7

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Skotheim JM, Secomb TW. Red blood cells and other nonspherical capsules in shear flow: oscillatory dynamics and the tank-treading-to-tumbling transition. Phys Rev Lett. (2007) 98:078301. doi: 10.1103/PhysRevLett.98.078301

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Abkarian M, Faivre M, Viallat A. Swinging of red blood cells under shear flow. Phys Rev Lett. (2007) 98:188302. doi: 10.1103/PhysRevLett.98.188302

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Dupire J, Socol M, Viallat A. Full dynamics of a red blood cell in shear flow. Proc Natl Acad Sci USA. (2012) 109:20808–13. doi: 10.1073/pnas.1210236109

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Lanotte L, Mauer J, Mendez S, Fedosov DA, Fromental JM, Claveria V, et al. Red cells' dynamic morphologies govern blood shear thinning under microcirculatory flow conditions. Proc Natl Acad Sci USA. (2016) 113:13289–94. doi: 10.1073/pnas.1608074113

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Mauer J, Mendez S, Lanotte L, Nicoud F, Abkarian M, Gompper G, et al. Flow-induced transitions of red blood cell shapes under shear. Phys Rev Lett. (2018) 121:118103. doi: 10.1103/PhysRevLett.121.118103

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Cokelet GR, Meiselman HJ. Rheological comparison of hemoglobin solutions and erythrocyte suspensions. Science. (1968) 162:275–77. doi: 10.1126/science.162.3850.275

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Wells R, Schmid-Schönbein H. Red cell deformation and fluidity of concentrated cell suspensions. J Appl Physiol. (1969) 27:213–7. doi: 10.1152/jappl.1969.27.2.213

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Yazdani AZK, Bagchi P. Phase diagram and breathing dynamics of a single red blood cell and a biconcave capsule in dilute shear flow. Phys Rev E. (2011) 84:026314. doi: 10.1103/PhysRevE.84.026314

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Sinha K, Graham MD. Dynamics of a single red blood cell in simple shear flow. Phys Rev E. (2015) 92:042710. doi: 10.1103/PhysRevE.92.042710

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Cordasco D, Yazdani A, Bagchi P. Comparison of erythrocyte dynamics in shear flow under different stress-free configurations. Phys Fluids. (2014) 26:041902. doi: 10.1063/1.4871300

CrossRef Full Text | Google Scholar

46. Gompper G, Kroll DM. Triangulated-surface models of fluctuating membranes. In: Nelson DR, Piran T, Weinberg S, editors. Statistical Mechanics of Membranes and Surfaces, 2nd Edn. Singapore: World Scientific (2004). p. 359–426.

Google Scholar

47. Fedosov DA, Caswell B, Karniadakis GE. A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys J. (2010) 98:2215–25. doi: 10.1016/j.bpj.2010.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Fedosov DA, Caswell B, Karniadakis GE. Systematic coarse-graining of spectrin-level red blood cell models. Comput Meth Appl Mech Eng. (2010) 199:1937–48. doi: 10.1016/j.cma.2010.02.001

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z Naturforschung C. (1973) 28:693–703. doi: 10.1515/znc-1973-11-1209

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Gompper G, Kroll DM. Random surface discretizations and the renormalization of the bending rigidity. J Phys I France. (1996) 6:1305–20. doi: 10.1051/jp1:1996246

CrossRef Full Text | Google Scholar

51. Guckenberger A, Gekle S. Theory and algorithms to compute Helfrich bending forces: a review. J Phys. (2017) 29:203001. doi: 10.1088/1361-648X/aa6313

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Español P, Revenga M. Smoothed dissipative particle dynamics. Phys Rev E. (2003) 67:026705. doi: 10.1103/PhysRevE.67.026705

CrossRef Full Text | Google Scholar

53. Müller K, Fedosov DA, Gompper G. Smoothed dissipative particle dynamics with angular momentum conservation. J Comp Phys. (2015) 281:301–15. doi: 10.1016/j.jcp.2014.10.017

CrossRef Full Text | Google Scholar

54. Lucy LB. A numerical approach to the testing the fission hypothesis. Astronom J. (1977) 82:1013–24. doi: 10.1086/112164

CrossRef Full Text | Google Scholar

55. Alizadehrad D, Fedosov DA. Static and dynamic properties of smoothed dissipative particle dynamics. J Comp Phys. (2018) 356:303–18. doi: 10.1016/j.jcp.2017.12.009

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Fedosov DA, Karniadakis GE. Triple-decker: interfacing atomistic-mesoscopic-continuum flow regimes. J Comp Phys. (2009) 228:1157–71. doi: 10.1016/j.jcp.2008.10.024

CrossRef Full Text | Google Scholar

57. Evans EA. Bending elastic modulus of red blood cell membrane derived from buckling instability in micropipet aspiration tests. Biophys J. (1983) 43:27–30. doi: 10.1016/S0006-3495(83)84319-7

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Dao M, Lim CT, Suresh S. Mechanics of the human red blood cell deformed by optical tweezers. J Mech Phys Solids. (2003) 51:2259–80. doi: 10.1016/j.jmps.2003.09.019

CrossRef Full Text | Google Scholar

59. Yoon YZ, Kotar J, Yoon G, Cicuta P. The nonlinear mechanical response of the red blood cell. Phys Biol. (2008) 5:036007. doi: 10.1088/1478-3975/5/3/036007

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Goldsmith HL, Marlow J. Flow behaviour of erythrocytes. I. Rotation and deformation in dilute suspensions. Proc R Soc Lond B. (1972) 182:351–84. doi: 10.1098/rspb.1972.0084

CrossRef Full Text | Google Scholar

61. Fischer TM, Stöhr-Liesen M, Schmid-Schönbein H. The red cell as a fluid droplet: tank tread-like motion of the human erythrocyte membrane in shear flow. Science. (1978) 202:894–6. doi: 10.1126/science.715448

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Dasanna AK, Fedosov DA, Gompper G, Schwarz US. State diagram for wall adhesion of red blood cells in shear flow: from crawling to flipping. Soft Matter. (2019) 15:5511–20. doi: 10.1039/C9SM00677J

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Noguchi H, Gompper G. Dynamics of fluid vesicles in shear flow: effect of the membrane viscosity and thermal fluctuations. Phys Rev E. (2005) 72:011901. doi: 10.1103/PhysRevE.72.011901

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Kaoui B, Krüger T, Harting J. How does confinement affect the dynamics of viscous vesicles and red blood cells? Soft Matter. (2012) 8:9246–52. doi: 10.1039/c2sm26289d

CrossRef Full Text | Google Scholar

65. Coste B, Mathur J, Schmidt M, Earley TJ, Ranade S, Petrus MJ, et al. Piezo1 and Piezo2 are essential components of distinct mechanically activated cation channels. Science. (2010) 330:55–60. doi: 10.1126/science.1193270

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Zarychanski R, Schulz VP, Houston BL, Maksimova Y, Houston DS, Smith B, et al. Mutations in the mechanotransduction protein PIEZO1 are associated with hereditary xerocytosis. Blood. (2012) 120:1908–15. doi: 10.1182/blood-2012-04-422253

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Omori T, Ishikawa T, Barthés-Biesel D, Salsac AV, Imai Y, Yamaguchi T. Tension of red blood cell membrane in simple shear flow. Phys Rev E. (2012) 86:056321. doi: 10.1103/PhysRevE.86.056321

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Vutukuri HR, Hoore M, Abaurrea-Velasco C, van Buren L, Dutto A, Auth T, et al. Active particles induce large shape deformations in giant lipid vesicles. Nature. (2020) 586:52–6. doi: 10.1038/s41586-020-2730-x

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Wan J, Ristenpart WD, Stone HA. Dynamics of shear-induced ATP release from red blood cells. Proc Natl Acad Sci USA. (2008) 105:16432–7. doi: 10.1073/pnas.0805779105

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Forsyth AM, Wan J, Owrutsky PD, Abkarian M, Stone HA. Multiscale approach to link red blood cell dynamics, shear viscosity, and ATP release. Proc Natl Acad Sci USA. (2011) 108:10986–91. doi: 10.1073/pnas.1101315108

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Danielczok JG, Terriac E, Hertz L, Petkova-Kirova P, Lautenschläger F, Laschke MW, et al. Red blood cell passage of small capillaries is associated with transient Ca²⁺-mediated adaptations. Front Physiol. (2017) 8:979.

PubMed Abstract | Google Scholar

72. Kariuki SN, Marin-Menendez A, Introini V, Ravenhill BJ, Lin YC, Macharia A, et al. Red blood cell tension protects against severe malaria in the Dantu blood group. Nature. (2020) 585:579–83. doi: 10.1038/s41586-020-2726-6

PubMed Abstract | CrossRef Full Text | Google Scholar