Using Monte Carlo to Simulate Complex Polymer Systems: Recent Progress and Outlook

Introduction

Metropolis Monte Carlo is a powerful simulation technique for equilibrating the dense phases of complex systems and predicting their key physicochemical properties because of the freedom it provides to sample new points in phase space thanks to the design of artificial (even fictitious) trial moves that can take the system completely away from its natural trajectory. It is particularly suited for simulating the bulk phases of chain-like (polymer or macromolecular) systems, because one can think of several such moves (both simple and complex) and combinations thereof that can design in order to generate trial states. Combined, in particular, with methods such as replica exchange, these moves can accelerate system equilibration by several orders of magnitude compared to dynamic methods such as Molecular Dynamics (MD). This is especially important at low temperatures or for systems characterized by highly dense structures, since dynamics becomes too slow to be followed reliably and ergodically by a detailed dynamic method.

In the last years, the method has expanded considerably through numerous applications in a variety of systems, often in the form of hybrid schemes with theoretic methods, thus providing invaluable insight into their thermodynamic, structural and conformational properties (and indirectly the dynamic ones). Our goal in this rather short report is to highlight important advances over the last 10 years or so, with some more emphasis on new applications to complex systems. We start by presenting the basic concepts underlying the method, then we review progress in the development of new Monte Carlo moves or interesting implementations of existing moves to new systems, then we discuss the development of new software for the more friendly execution of Monte Carlo simulations, and finally we discuss findings from several applications to polymer systems. These include the use of Monte Carlo in addressing polymer self-assembly, structure and conformation in polymer nanocomposites, polymers under flow, confined polymers, grafted polymers, polymer rings and knots, semiflexible polymers, polymer networks, polymer crystallization, and polymerization reactions. We discuss recent advances in all these areas and outline interesting future directions. Given the brief character of the review, we would like to deeply apologize in advance if we failed to include some significant contributions over the period (last decade or so) covered. For exactly the same reason, we have restricted our presentation to applications related with system equilibration and relaxation for soft materials made up of oligomers or polymers. Thus, extremely interesting extensions such as implementations to calculate rate constants or to track physicochemical processes in the form of kinetic Monte Carlo are not covered.

Basic Concepts

Let ρ^eq be the probability density in the equilibrium ensemble wherein the Monte Carlo simulation is carried out, and let us assume that in a given Monte Carlo step a move is attempted from an old state (o) to a new or trial state (n). Let us also denote by a(o → n) the corresponding stochastic matrix a of attempt probabilities, which is usually symmetric, i.e., it satisfies

$\begin{array}{ll}a(o\to n)=a(n\to o)& (1)\end{array}$

Then, in the Metropolis Monte Carlo method, the new state is accepted with probability [1]:

$\begin{array}{ll}{p}_{\text{acc}}(o\to n)=min\left[1,\frac{{\rho }^{\text{eq}}(n)}{{\rho }^{\text{eq}}(o)}\right]& (2)\end{array}$

with ρ^eq(o) and ρ^eq(n) denoting the probabilities of the system to be in state o or in state n, respectively. The corresponding Markov chain of states thus generated samples asymptotically the probability distribution ρ^eq. In the canonical (NVT) ensemble, Equation (2) reduces to [2–5]:

$\begin{array}{ll}{p}_{\text{acc}}(o\to n)=min\left(1,exp\left[-\frac{{\displaystyle U_{pot}^{(n)}}-U_{pot}^{(o)}}{k_{B}T}\right]\right)& (3)\end{array}$

where $U_{pot}^{(n)}-U_{pot}^{(o)}$ is the difference ΔU_pot in the potential energies between new and old states, k_B denotes the Boltzmann constant, and T is the absolute temperature.

The power of the Monte Carlo method in simulating complex physical systems lies in the fact that one has considerable freedom in choosing the matrix a as long as the requirement a(o → n) = a(n → o) is satisfied. For example, one can even think of applying totally unphysical moves for the system at hand, as far as the internal geometry and the molecular architecture of the constituent molecules are not destroyed. This can substantially speed up the rate with which the system moves through configuration space, which is particularly advantageous in the case of the dense phases of chain-like molecules (e.g., synthetic polymers and biopolymers) that are known to be characterized by a very broad distribution of relaxation times that renders their direct MD simulation a formidable task.

An interesting point in the Metropolis Monte Carlo scheme is that one can replace Equation (1) with the following more general condition:

$\begin{array}{ll}{\rho }^{\text{eq}}(o)a(o\to n)p_{\text{acc}}(o\to n)={\rho }^{\text{eq}}(n)a(n\to o)p_{\text{acc}}(n\to o)& (4)\end{array}$

also known as detailed balance or condition of microscopic reversibility [3–5]. Then, the Metropolis criterion, Equation (2), becomes

$\begin{array}{ll}{p}_{\text{acc}}(o\to n)=min\left(1,\frac{{\rho }^{\text{eq}}(n)a(n\to o)}{{\rho }^{\text{eq}}(o)a(o\to n)}\right)& (5)\end{array}$

If, in addition, the elementary move is designed in a set of coordinates that differs from the configuration-space coordinates wherein the equilibrium probability density ρ^eq was defined, then Equation (5) must be modified to account for the Jacobian of transformation J from one coordinate system to the other:

$\begin{array}{ll}{p}_{\text{acc}}(o\to n)=min\left(1,\frac{\rho (n)}{\rho (o)}\frac{J(n)}{J(o)}\frac{a(n\to o)}{a(o\to n)}\right)& (6)\end{array}$

From the elements of the underlying matrix a, the transition probability matrix π is defined next according to

$\begin{array}{l}{\pi }_{no}=\pi (o\to n)\\ =\{\begin{array}{l}a(o\to n),\text{ if }{\rho }^{\text{eq}}(n)\ge {\rho }^{\text{eq}}(o),n\ne o\\ a(o\to n)\frac{{\rho }^{\text{eq}}(n)}{{\rho }^{\text{eq}}(o)},\text{ if }{\rho }^{\text{eq}}(n)<{\rho }^{\text{eq}}(o),n\ne o\end{array}\\ {\pi }_{oo}=1-{\displaystyle \sum _{n\ne o}}{\pi }_{no}& (7)\end{array}$

and, by definition, is stochastic [2]. Then, as the Monte Carlo iterations progress, the row vector ρ_t = (ρ_t(1), ρ_t(2), …, ρ_t(o), …, ρ_t(n), …) containing the a priori probabilities of all states after step t of the simulation converges to the desired equilibrium distribution $\underset{t\to \infty }{\text{lim}}{\rho }_t={\rho }^{\text{eq}}$ satisfying [4, 5]:

$\begin{array}{ll}{\rho }^{\text{eq}}=\pi ·{\rho }^{\text{eq}}& (8)\end{array}$

Equation (8) implies that the equilibrium distribution ρ^eq is an eigenvector of the transition probability matrix π, with the corresponding eigenvalue equal to one [4, 5].

Monte Carlo Moves for Polymers

Due to difficulties associated with excluded volume interactions, chain connectivity, and conformational stiffness [6], early Monte Carlo simulations were performed on lattice models [7], but soon implementations in continuous space appeared. Today, we can categorize Monte Carlo moves developed for polymers roughly into three groups: simple, complex, and advanced.

Simple Monte Carlo Moves

Simple Monte Carlo moves include [4]: reptation [8], end-mer rotation [9], libration or flip [9], dimer flip [10, 11], configurational bias (CB) [12–15], extended configurational bias [16–22], concerted rotation (ConRot) [23], intra-chain and inter-chain concerted rotation [24, 25], generalized reptation [9, 26], parallel rotation [27], (g) pivot [28, 29], atom identity exchange [30], and volume fluctuation [9]. These moves apply only to a single polymer chain; moreover, reptation, configurational bias, end-mer rotation and generalized reptation apply only at chain ends. With these simple moves, only chains up to about 70 units long can be simulated. Special mention should be made of the reptation move (Figure 1), perhaps the very first Monte Carlo move devised for polymer chains; it is realized by cutting out a monomer from one end of the chain and appending it to the other end. Thus, the move simulates the diffusive (slithering-snake) motion of the chain. In the configurational bias move (Figure 2), on the other hand, one cuts out an entire segment composed of many monomers at one end of the chain and regrows it monomer by monomer in a biased way so as to avoid overlaps with the monomers on the same or nearby chains. The bias introduced in the construction of the new configuration is removed at the final stage of the move when the acceptance criterion is applied, by appropriately modifying it. As far as the local conformation at the interior of a chain is concerned, this is typically equilibrated with the help of the ConRot move, which involves the concerted rotation of an internal segment of the chain, of size equal to 5 monomers (Figure 3).

FIGURE 1

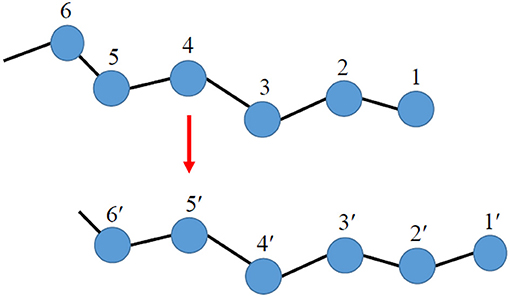
Figure 1. Schematic illustration of the reptation (slithering-snake) Monte Carlo move for polymer simulations in continuous space.

FIGURE 2

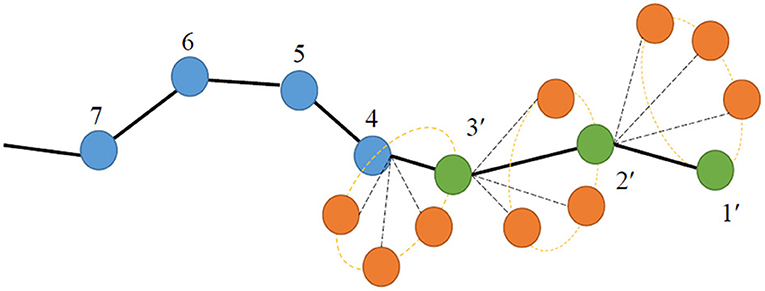
Figure 2. Schematic illustration of the configurational bias Monte Carlo move for polymer simulations in continuous space.

FIGURE 3

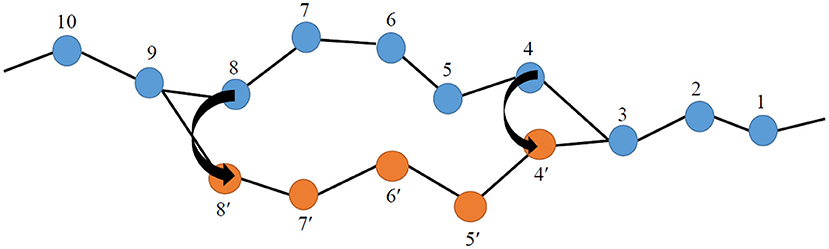
Figure 3. Schematic illustration of the ConRot Monte Carlo move for polymer simulations in continuous space.

Complex Monte Carlo Moves

Complex Monte Carlo moves induce drastic reconfigurations of large internal sections within one or two polymer chains simultaneously. Initially they appeared in the form of chain breaking moves [31] in Monte Carlo simulations of polymers on lattices; later they gave rise to the so-called family of chain-connectivity altering moves. Following some rigorous schemes, these moves effect large conformational changes at the level of the end-to-end distance of one or two chains at the same time, which can dramatically accelerate the rate with which the long-range conformational features of the polymer are sampled, often however at the expense of introducing polydispersity in the polymer. The family of complex Monte Carlo moves includes [9, 26, 32, 33]: end-bridging, directed internal bridging, directed end-bridging, self end-bridging, and fusion-scission [34]. Introduction of these moves almost revolutionized the field of the molecular simulation of polymers [4, 5]. Figure 4 presents a design of the end-bridging move.

FIGURE 4

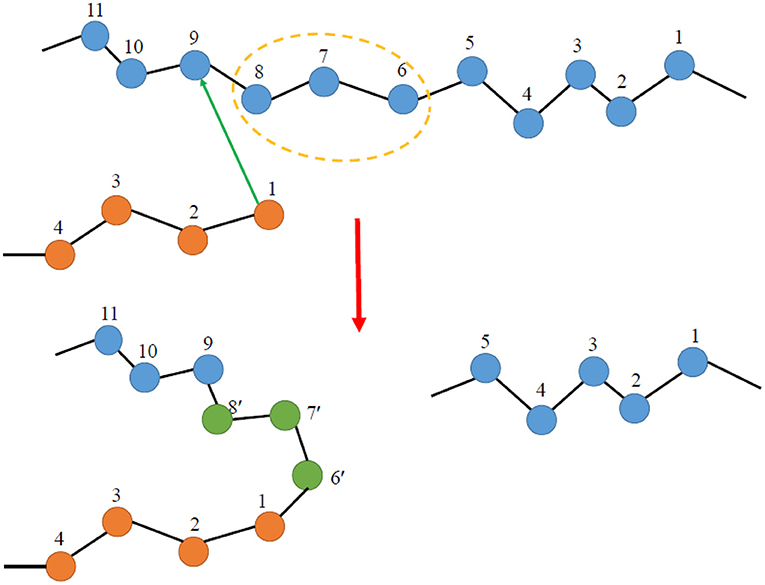
Figure 4. Schematic illustration of the end-bridging Monte Carlo move for polymer simulations in continuous space.

From a technical point of view, and in order not to violate the very important condition of microscopic reversibility, in a variable connectivity Monte Carlo move proper care should be taken to: (a) evaluate all possible geometric solutions to the underlying bridging problem, (b) incorporate appropriate Jacobians in the acceptance criterion (because the solution of the geometric problem is typically carried out in the space of generalized coordinates), and (c) address both the forward and the reverse problem pertinent to the move.

As already mentioned, chain connectivity altering algorithms typically induce polydispersity in the sample because the molecular lengths of the chains involved in these moves are altered. Because of this, the corresponding Monte Carlo simulations are carried out in a semigrand canonical ensemble, wherein the following quantities are kept constant: the total number of chains N_ch, the total number of mers n, the pressure P, the temperature T, and the spectrum of relative chemical potentials μ^* of all chain species within the system except two that are taken as reference species [26, 35]. Such an ensemble is typically denoted as [N_chnPTμ^*] and the average molecular length is estimated from the distribution of chain lengths eventually sampled, which in turn is dictated by the applied spectrum of relative chemical potentials μ^*.

Advanced Monte Carlo Moves: Simulation of Non-linear Chain Systems

Advanced Monte Carlo moves include Double Bridging (DB) and Intramolecular Double Rebridging (IDR) [36, 37]. These are generalizations of the end-bridging move in the sense that they involve the sequential or simultaneous construction of two trimer bridges (instead of one). The latter family of moves has found tremendous applications in simulations of polymers with a non-linear chain architecture such as long-chain branched, tri-arm star, and H-shaped polymers [10, 11, 37, 38]; they have helped to understand how chain dimensions and other important conformational quantities depend on the precise molecular architecture of the chains [39–41] (frequency and length of branches). A typical design of the double bridging move for linear polymers is shown in Figure 5.

FIGURE 5

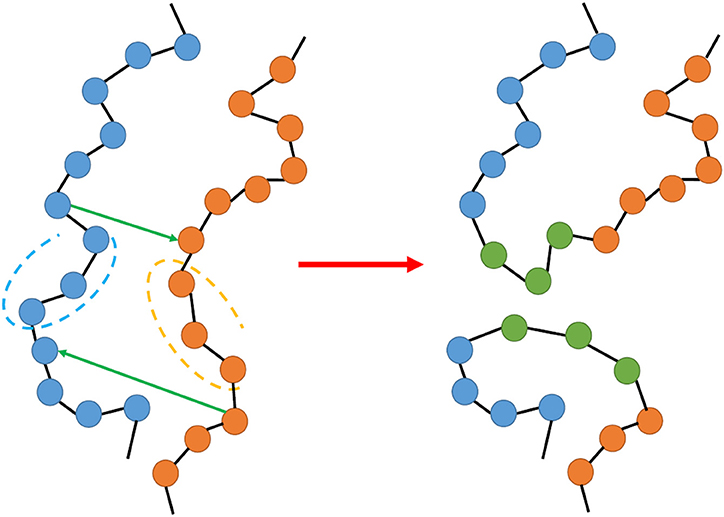
Figure 5. Schematic illustration of the double bridging Monte Carlo move for polymer simulations in continuous space. In general, given an internal atom in one chain and an internal atom in the other chain, there are four possible combinations with which this move can be realized (based on what pairs of trimers are chosen to be cut out), and in the Figure we have included only one of these combinations.

New Monte Carlo Software

In their majority, the Monte Carlo moves discussed in the preceding section have been implemented for specific polymer chemistries and architectures using home-made algorithms. However, there exist a few software packages offering these Monte Carlo moves for generic polymer structures. Available Monte Carlo software includes: (a) the Enhanced Monte Carlo code [42] which was used in simulations of semicrystalline polymers [43–46]; (b) Towhee [47]; (c) Cassandra [48]; and (d) RASPA [49].

Recently, Alexiadis et al. [50] presented Chameleon, a new simulation software in C++ wherein several chain connectivity altering Monte Carlo moves were implemented. The new software can handle several polymer structures such as polyethylene (PE), polystyrene (PS) and polyvinyl chloride (PVC), and many different polymer architectures (e.g., linear and branched), described either through an all-atom, a united-atom, or a coarse-grained model. Direct comparison of several structural and volumetric properties of the above systems obtained with Chameleon against available experimental data and previous computational works demonstrated excellent agreement.

For solute-solvent systems in liquid or gas phase, Cezar et al. [51] have introduced a new version of DICE (https://portal.if.usp.br/dice), a Monte Carlo algorithm for the molecular simulation of long flexible molecules, based on an improved implementation of the configurational bias move.

Monte Carlo Simulation of Self-Organized Polymer Phases

A family of polymer systems for which molecular modeling could provide significant insight is that of soft nanostructured materials (e.g., organic semiconducting polymers, polypeptides, polymerosomes, micellar surfactants and many others) because of the capabilities it offers to follow chain self-organization into a variety of structures and morphologies depending on operating (e.g., temperature) and physicochemical (e.g., concentration, type of solvent present, pH) conditions. Because self-organization can occur over long time scales, many of these systems cannot be simulated by a brute force application of the MD method. This explains why people resort to coarse-graining [52], an approach, however, that suffers from many drawbacks [53, 54]. In this case, atomistic Monte Carlo offers an excellent alternative, as one can still maintain the detailed molecular representation while overcoming the problem of long relaxation times through the application of the artificial moves presented in section Monte Carlo Moves for Polymers. Directly simulating ordered phases of polymers or oligomers with Monte Carlo is best exemplified by the work of Alexiadis et al. [30] for an alkanethiol self-assembled monolayer on Au. These authors proposed a Monte Carlo algorithm involving a mix of moves such as reptation, flip, concerted rotation, atom identity exchange, configurational bias, and intramolecular double rebridging which led to the formation of a self-assembled monolayer (SAM) on the gold substrate starting from a completely random configuration of a certain number of alkanethiols above the substrate. The conformational characteristics of the formed monolayer (especially the tilt angle) came out to be in very favorable agreement with measured data already known in the literature. This was an excellent demonstration of the limitless capabilities of Monte Carlo, as the formation of the corresponding monolayer is practically impossible to achieve with MD except if one starts from a pre-assembled structure very close to the final (equilibrium) one. In a later study, a similar Monte Carlo algorithm was developed for the bulk phase self-assembly of semi-fluorinated alkanes [55].

Recently, Tsourtou et al. [56, 57] redesigned several of the Monte Carlo moves discussed in section Monte Carlo Moves for Polymers for bulk models of oligo and polythiophenes by properly accounting for the regular presence of thiophene rings along their backbones. Monte Carlo moves implemented included bias reptation of an end thiophene ring, flip of an internal thiophene ring, rotation of an end thiophene ring, concerted rotation of three consecutive thiophene rings, rigid translation of an entire molecule, rotation of an entire molecule, and volume fluctuation. A schematic representation of the ring ConRot move is shown in Figure 6. According to this, the C-S-C trimer of a randomly selected thiophene ring (e.g., segment C12-S13-C14 in Figure 6) is re-positioned by having the two atoms C9 and C17 neighboring the trimer being displaced following small rotations of the rings on the left and right of the central ring around their respective bonds; this alters also the positions of atoms C6, C10, C16, and C20. At the end of a successful ring ConRot move, eleven inner atoms (C6, C9, C10, C11, C12, S13, C14, C15, C16, C17, and C20) have been displaced to new positions.

FIGURE 6

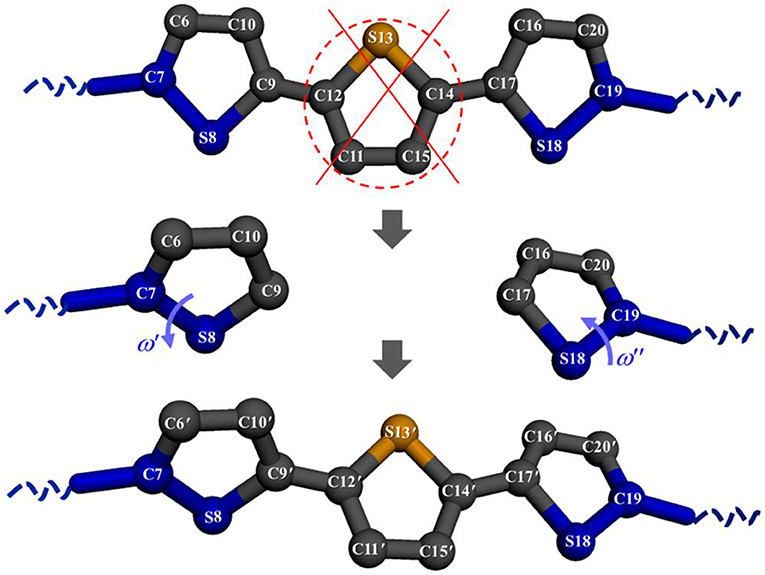
Figure 6. Schematic illustration of the ring ConRot move. Reprinted (adapted) with permission from Tsourtou et al. [56]. Copyright (2018) American Chemical Society.

In the work of Tsourtou et al. [56], thiophene ring atoms in all moves implemented were assumed to remain rigid and strictly coplanar while inter-ring torsion and bond bending angles were assumed to be fully flexible governed by suitable potential energy functions.

With the new algorithm, the authors studied (Figure 7) the different phases formed when α-sexithiophene (α-6T), an important thiophene oligomer, is cooled down to lower temperatures isobarically, starting from the isotropic (Iso) phase at a relatively high temperature (above 700 K). To avoid system size effects, a rather large simulation cell was used in the simulations. The Monte Carlo simulations were performed with a new united-atom model specifically developed for the purpose of the study. For comparison, the authors carried out similar MD simulations with a detailed, well-validated all-atom model, which showed four phase transitions: an isotropic-to-nematic (Iso-to-Nem) at 640 K, a nematic-to-smectic A (Nem-to-SmA) at 630 K, a smectic A-to-smectic C (SmA-to-SmC) at 620 K (demonstrating smectic polymorphism), and a SmC-to-crystal-like (SmC-to-Cry) at 600 K. Similar transitions were observed in the Monte Carlo simulations except that no Nem phase was seen, which was attributed to the stiffer nature of the corresponding forcefield. Indirectly, this provides evidence that predictions of morphology from coarse-grained models should not be fully trusted because of the highly approximate character of the effective potentials utilized in such models.

FIGURE 7

Figure 7. Characteristic atomistic snapshots from the Monte Carlo simulations of Tsourtou et al. [57] of a model system of α-unsubstituted sexithiophene (α-6T). (a) The isotropic (Iso) phase at T = 700 K, (b) the smectic-C (SmC) phase at T = 680 K with α-6T molecules self-organized into layered states, and (c) a zoom into the SmC phase showing the layer normal vector $\widehat{\text{l}}$ and the director $\widehat{\text{n}}$ of the phase. Sulfur, carbon, and end-carbon atoms of the outer rings are represented with yellow, white, and red color, respectively. Reproduced from Tsourtou et al. [57] by permission of The Royal Society of Chemistry.

Monte Carlo moves similar to those discussed above have been adapted [58–61] over the last years for simulations of jamming and crystallization of polymer molecules modeled as freely-jointed chains of tangent hard spheres of uniform size, both in the bulk and under confinement. Simulations carried out over a wide range of concentrations, from the very dilute up to the maximally random jammed state, addressed how factors like chain length, chain flexibility and volume fraction affect the structure and packing of polymer chains, with emphasis on phase transitions from disordered to more ordered structures. Recently, the work was extended to polymer chains interacting with the square well-potential [62]. The authors also tested highly confined systems of such chains by letting the inter-wall distance approach the size of the polymer bead [61]. Due to attraction, distinct morphologies were developed, spanning the entire spectrum of structures from purely amorphous to well-ordered ones depending on the specific values of the model parameters assigned [62].

For similar systems (dense hard sphere polymer melts), Kampmann et al. [63] proposed a Monte Carlo algorithm for their off-lattice simulation using both cluster and swap moves. The algorithm was validated by comparing against other Monte Carlo and MD simulations for the same system. At short time scales, the event chain Monte Carlo algorithm was shown to exhibit Rouse dynamics. At intermediate or long time scales, on the other hand, and in the absence of swap moves, it followed reptation dynamics.

Monte Carlo moves have also been implemented by Reith and Virnau [64] for single flexible globular homopolymer chains. For chains larger than a few hundreds of monomers, analysis of correlation times between unknotted globular states showed that bridging moves become more efficient than slithering-snake ones. However, the performance of the moves should depend on long-range correlations (which were not considered in the analysis) as well as on the specific molecular model considered. Also, if chain stiffness is included, efficiency is expected to drop.

Monte Carlo as a Tool for Understanding the Structure of Polymer Nanocomposites

Connectivity-altering Monte Carlo algorithms have been coupled with preferential sampling techniques by Pandey and Doxastakis [65] and Pandey et al. [66, 67], together with an extended reptate algorithm to facilitate polymer mass transfer from the nanoparticle surface to the bulk polymer, to explore structural and conformational features of polymers in a polymer nanocomposite melt containing highly curved nanoparticles. Using a rather detailed molecular model, the authors found that when the size of nanoparticle becomes comparable to the Kuhn segment length of the polymer, long train segments are disfavored.

Vogiatzis et al. [68] and Vogiatzis and Theodorou [69] combined Monte Carlo simulations with a field theoretic approach to address structural effects of long polymer chains next to nanoparticles. For example, the authors investigated the dependence of several physical properties (such as local polymer density around the nanoparticle, thickness of the depletion layer, bond orientation and scattering patterns) on chain length and grafting density. This was one of the very first times that a real experimental nanocomposite system was studied, since the coarse-grained nature of the model employed could address length scales comparable to those accessed by small angle neutron scattering experiments, thereby allowing for a direct comparison between simulation and experiments. For example, the scattering of the whole corona was analyzed (Figure 8). An important conclusion of the work was that the brush thickness increases with increasing molecular weight of the grafted chains, thus causing a shift of scattering peaks to lower q-values.

FIGURE 8

Figure 8. Monte Carlo predictions for the scattering curve $\frac{S_g(q)}{n_g(N_g+1)}$ (S_g(q) denotes the corona structure factor, n_g the number of grafted chains on the nanoparticle, and N_g the length of grafted chains in Kuhn segments) of a system consisting of an 8 nm-radius silica nanoparticle on the surface of which atactic polystyrene chains of molecular weight equal to 20 kg/mol have been grafted at surface density equal to 0.5 nm⁻². The grafted corona is inside a 100 kg/mol atactic polystyrene matrix. A piecewise cubic Hermite (PcH) spline interpolation scheme has been used. Results from two theoretical models [the form factor of a spherical shell of uniform density and thickness equal to the estimated brush thickness, and the model proposed by Pedersen and Gerstenberg [70] and Pedersen [71] for block copolymer micelles] are also included. Reprinted (adapted) with permission from Vogiatzis and Theodorou [69]. Copyright (2013) American Chemical Society.

Dodd and Jayaraman [72] employed Monte Carlo to study polydispersity effects in the structure of polymers grafted on spherical surfaces. They examined the conformation of grafted polymer chains, the thickness of the polymer layer formed, and the distribution of free-end monomers within the grafted layer. At brush-like grafting densities, with increasing polydispersity index, the scaling exponent describing the variation of the radius of gyration of the grafted chains with their molecular weight was observed to approach that of a single chain grafted on the same nanoparticle; this happens because polydispersity decongests the brush from monomer crowding. At high polydispersity indices, chains shorter than the number average chain length had more compressed conformations while chains longer than the number average chain length stretched less than in the monodisperse case. Monte Carlo simulations were also employed to obtain intramolecular structure factors needed in theoretical approaches to polymer nanocomposites through the self-consistent polymer reference interaction site model (PRISM) [73]. Such a combined approach allows mapping out equilibrium structure and phase behavior of polymer nanocomposites involving polymer-grafted nanoparticles in the matrix. Heterogeneous (e.g., copolymer-grafted nanoparticles) as well as polydisperse (e.g., bidisperse graft chain lengths) systems were studied [73].

At low enough temperatures, nanoparticles can act as effective heterogeneous nucleation sites, thus promoting polymer crystallization [74–76]. Here, Monte Carlo can provide information concerning the role of factors such as nanoparticle shape and size on polymer crystallization. According to the work of Gu et al. [74], one-dimensional nanoparticles are the most effective in inducing crystallization, leading to uniformly-oriented crystals. Additional Monte Carlo simulations by Nie et al. [75] addressed the competition for crystallization of mixed polymers grafted on a substrate. It was found that stereo-complex crystallites have higher thermal stability compared to homo-crystallites, which appears to be supported by experimental observations. Such simulations are of relevance (e.g.) in studies involving stereo-complex formation in poly(L-lactide)-poly(D-lactide) (PLLA/PDLA) blends. Ming et al. [76] used Monte Carlo simulations to study how polymer crystallization is affected by chain grafting onto the surface of the filler. It was found that the induction period for nucleation in a grafted system is shorter than in the system where chains are not grafted, but eventually the same degree of crystallinity is obtained. With increasing molecular weight, the induction period for nucleation decreases followed by an increase in the degree of crystallinity finally observed.

Monte Carlo Simulation of Polymers Under Flow

Metropolis Monte Carlo was originally designed to sample equilibrium states. However, as Kikuchi et al. [77] showed, the method can also be used as a numerical technique for solving the Fokker-Planck equation, thus providing information for the diffusive motion of a Brownian particle. Later, Sanz and Marenduzzo [78] presented a comparative study between Monte Carlo and Brownian Dynamics simulations for colloidal suspensions and reported that for the results from the two methods to be in agreement, the Monte Carlo time must be rescaled by the acceptance probability. A subsequent study [79] demonstrated that one can achieve quantitative agreement between Brownian Monte Carlo and Brownian Dynamics simulations also in the case of systems with orientational degrees of freedom.

From a strict statistical mechanics point of view, using Metropolis Monte Carlo to sample states in systems beyond equilibrium requires the introduction of expanded (generalized) ensembles wherein, in addition to the typical macroscopic variables routinely employed, a coarse-grained variable should be included accounting for the average polymer conformation that develops in response to the external field. For melts of unentangled polymer chains, a good such structural variable is the dimensionless conformation tensor $\tilde{\text{c}}$ [80, 81]. Then, guided from non-equilibrium thermodynamics [80–86], one can postulate the following expression for the internal energy function U of the polymer melt under the external field a:

$\begin{array}{ll}\text{d}U(S,V,N_{ch},\tilde{\text{c}})=T\text{d}S-P\text{d}V+\mu \text{d}{N}_{ch}+N_{ch}{k}_{B}T\text{a}:\text{d}\tilde{\text{c}}& (9)\end{array}$

In Equation (9), T is the absolute temperature, k_B the Boltzmann constant, S the entropy, P the pressure, V the volume, μ the chain chemical potential, N_ch the number of chains in the system, $\tilde{\text{c}}$ the dimensionless conformation tensor, and a a tensorial variable (the synthetic field) carrying information about the underlying (true) flow field that cannot be used directly in the Monte Carlo simulation. Equation (9) defines the so called $\left[N_{ch},V,U,\widetilde{\mathbf{\text{c}}}\right]$ ensemble, an expanded [N, V, E] ensemble accounting for the overall conformation of polymer chains in response to the field a.

From Equation (9), all other thermodynamic functions can be derived through appropriate Legendre transforms [82–84]. From a statistical mechanics point of view, it is more suitable to work with the [N_ch, P, T, a] ensemble, for which a Legendre transform with respect to variables S, V, and $\widetilde{\mathbf{\text{c}}}$ leads to

$\begin{array}{ll}\text{d}G(T,P,N_{ch},\text{a})=-S\text{d}T+V\text{d}P+\mu \text{d}{N}_{ch}-N_{ch}{k}_{B}T\tilde{\text{c}}:\text{d}\text{a}& (10)\end{array}$

Equation (10) allows one to carry out simulations in the generalized [N_ch, P, T, a] ensemble involving (in addition to the typical variables N_ch, T, and P) the synthetic field a. If we further allow for changes in the connectivity of chains implying a polydisperse system (this is important in cases where drastic Monte Carlo moves are incorporated in the algorithm such as the generalized reptation and the end-bridging ones), the simulation must be carried out in the expanded semi-grand canonical ensemble $\left[N_{ch},n,P,T,{\mu }^{*},\mathbf{\text{a}}\right]$ where the spectrum of chemical potentials μ^* also appears controlling the chain length distribution together with the total number of atomistic segments (or monomers) n which remains constant in the course of the simulation. The corresponding probability density function is [82]:

$\begin{array}{l}\text{}\text{}\text{}\text{}\text{}{\rho }^{N_{ch}nPT{\mu }^{*}\text{a}}\left(r_1,r_2,\dots ,r_n,V\right)\\ ~\exp [-\beta (U_{pot}\left(r_1,r_2,\dots ,r_n,V\right)+PV\\ -{\displaystyle \sum _{k=1}^{N_{ch}}{\mu }_k^{*}{N}_k}-k_{B}Ta:{\displaystyle \sum _{k=1}^{N_{ch}}{\tilde{c}}_k})]& (11)\end{array}$

implying that system configurations are sampled according to the following generalized Metropolis criterion:

$\begin{array}{l}{p}_{\text{acc}}^{N_{ch}nPT{\mu }^{*}\text{a}}\\ ~exp\left[-\beta \left(\Delta U_{pot}+P\Delta V-{\displaystyle \sum _{k=1}^{N_{ch}}}{\mu }_k^{*}\Delta N_k-k_{B}T\text{a}:{\displaystyle \sum _{k=1}^{N_{ch}}}\Delta {\tilde{\text{c}}}_k\right)\right]& (12)\end{array}$

or, for the case of a system simulated under conditions of constant volume V (i.e., constant density ρ) according to:

$\begin{array}{l}{p}_{\text{acc}}^{N_{ch}nVT{\mu }^{*}\text{a}}\\ ~exp\left[-\beta \left(\Delta U_{pot}-{\displaystyle \sum _{k=1}^{N_{ch}}}{\mu }_k^{*}\Delta N_k-k_{B}T\text{a}:{\displaystyle \sum _{k=1}^{N_{ch}}}\Delta {\tilde{\text{c}}}_k\right)\right]& (13)\end{array}$

where $\beta \equiv \frac{1}{k_{B}T}$. In the above equations, {r} = {r₁, r₂, …, r_n} denotes the space of atomic position vectors, U_pot is the potential energy of the system, ${\left\{{\mu }_k^{*}\right\}}_{k=1}^{N_{ch}}$ the set of chain relative chemical potentials, and ${\left\{{\widetilde{\mathbf{\text{c}}}}_k\right\}}_{k=1}^{N_{ch}}$ the set of chain conformation tensors.

For the method to be applied, one needs to provide input data for the tensor a. Defining, however, a for a given flow field is not an easy task. Here, we can get help by looking at the corresponding evolution equation for the variable $\widetilde{\mathbf{\text{c}}}$ as derived from the generalized bracket [80] and GENERIC [81] formalisms of non-equilibrium thermodynamics. Through this, we find that a conveys information related to the underlying dissipative or relaxation matrix of the viscoelastic model describing the polymeric fluid under study. Any proposition, therefore, for a from theory would be model-dependent, and thus also approximate. For example, in the case of steady shear flow described by the following velocity gradient tensor

$\begin{array}{ll}\nabla \text{u}=\left(\begin{array}{ccc}0& 0& 0\\ \stackrel{.}{\gamma }& 0& 0\\ 0& 0& 0\end{array}\right)& (14)\end{array}$

and for the simple upper-convected Maxwell model, we find that

$\begin{array}{ll}\text{a}=\left[\begin{array}{c}\frac{1}{2}\frac{{({\lambda }_0\stackrel{.}{\gamma })}^2}{1+{({\lambda }_0\stackrel{.}{\gamma })}^2}\frac{1}{2}\frac{{\lambda }_0\stackrel{.}{\gamma }}{1+{({\lambda }_0\stackrel{.}{\gamma })}^2}0\\ \frac{1}{2}\frac{{\lambda }_0\stackrel{.}{\gamma }}{1+{({\lambda }_0\stackrel{.}{\gamma })}^2}-\frac{1}{2}\frac{{({\lambda }_0\stackrel{.}{\gamma })}^2}{1+{({\lambda }_0\stackrel{.}{\gamma })}^2}0\\ 000\end{array}\right]& (15)\end{array}$

where λ₀ denotes the longest relaxation time of the polymer.

To compute model-independent values of a one should run GENERIC Monte Carlo simulations in parallel with direct non-equilibrium molecular dynamics (NEMD) simulations for the specified value of shear rate $\stackrel{.}{\gamma }$ using (e.g.) the following more general form of a

$\begin{array}{ll}\text{a}=\left[\begin{array}{ccc}{a}_{xx}& a_{xy}& 0\\ a_{xy}& a_{yy}& 0\\ 0& 0& 0\end{array}\right]& (16)\end{array}$

and then match the resulting chain conformation tensors from the two methods [84]. An interesting feature of such an approach is that by comparing the values of a computed from the GENERIC Monte Carlo simulations with those suggested by the macroscopic model, one can validate the model or deduce information how to modify it so that model predictions and simulation data for the same flow superimpose. It suggests therefore a solid framework for improving available macroscopic models for the viscoelasticity of polymer melts [84, 85]. It can also be used to test fundamental thermodynamic equations far away from equilibrium. For example, the form of a provided by Equation (16) for a_yy = 0 implies the following generalized Maxwell relation [86]:

$\begin{array}{ll}{\left(\frac{\partial c_{xx}}{\partial {\alpha }_{xy}}\right)}_{T,V,N_{ch},{\alpha }_{xx}}=2{\left(\frac{\partial c_{xy}}{\partial {\alpha }_{xx}}\right)}_{T,V,N_{ch},{\alpha }_{xy}}& (17)\end{array}$

Test GENERIC Monte Carlo simulations provide direct evidence for the validity of this equation over a wide range of field strengths (Figure 9).

FIGURE 9

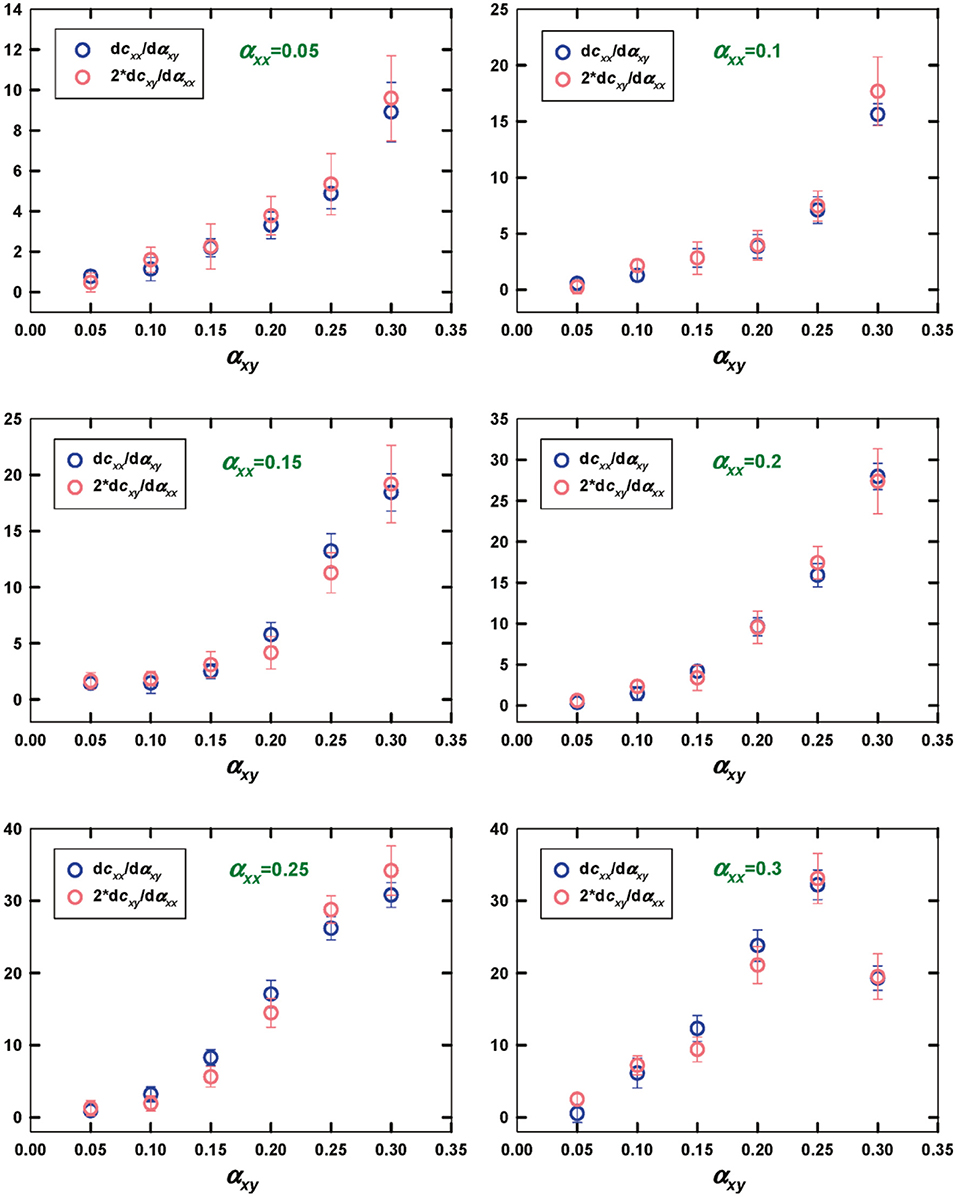
Figure 9. Validity of the generalized Maxwell equation, Equation (17), from GENERIC Monte Carlo simulations with an unentangled C₇₈ PE melt at 450 K over a wide range of fields a. Reprinted (adapted) with permission from Baig et al. [86]. Copyright (2011) American Chemical Society.

The methodology was implemented initially for unentangled polymer melts although recently Roh and Baig [87] proposed a simple extension to an entangled polyethylene melt by treating each chain as a sequence of entanglement segments (each one consisting of approximately 68 carbon atoms), with the synthetic field a coupled simultaneously and independently with the conformation tensors of all these entanglement segments. Although all components of the tensor a had to be recomputed (compared to those estimated for an unentangled PE melt at the same temperature and flow conditions) in order for the GENERIC Monte Carlo predictions to match the direct NEMD ones for the overall conformational properties of the polymer (Figure 10), gratifying agreement was observed between the two methodologies in the regime of weak flows, but some systematic deviations were noted in the regime of weak-to-strong flows. These deviations were attributed to the fact that the synthetic field a was coupled independently to all entanglement strands along a chain, which fails to account for the inter-dependence of deformation between entanglement strands either intra-molecularly or inter-molecularly.

FIGURE 10

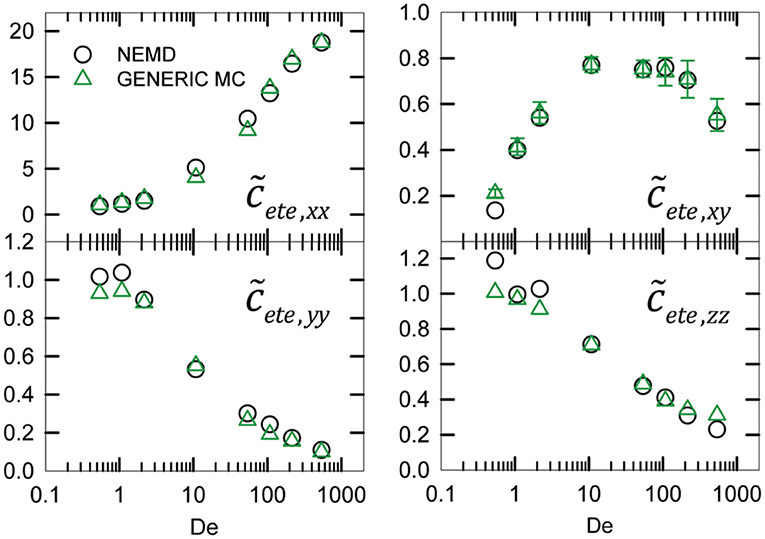
Figure 10. Direct comparison between GENERIC Monte Carlo calculations and NEMD simulations for the four (xx, xy, yy, and zz) components of the dimensionless conformation tensor based on the chain end-to-end unit vector, $\widetilde{\mathbf{\text{c}}}$_ete, as a function of applied Deborah number (the dimensionless shear rate) De. Results shown are for a C₄₀₀ PE melt at T = 450 K. Reproduced with permission from Roh and Baig [87].

Other Applications

In addition to addressing soft nanostructured materials, polymer nanocomposites, and steady-state polymer flows, Metropolis Monte Carlo has been used in the past few years to provide a wealth of information for other polymer systems and/or properties. We briefly review many of them in the next paragraphs.

Polymer Chain Stiffness

On the basis of single chain Metropolis Monte Carlo simulations, Tzounis et al. [88] proposed a methodology for computing the unperturbed chain dimensions of any polymer chain, irrespective of its chemical or architectural complexity. The authors tested many Monte Carlo moves and the most efficient ones in terms of their capability to relax both linear and branched polymer chains were found to be the rotate strand (pivot) and rotate branch ones, as they could induce drastic changes to the conformation of long strands and branches along the polymer chain. In addition, an iterative scheme was proposed to define local interactions. The method was used to predict the characteristic ratio of a series of polymers (Figure 11) and satisfactory agreement with experimental data was obtained.

FIGURE 11

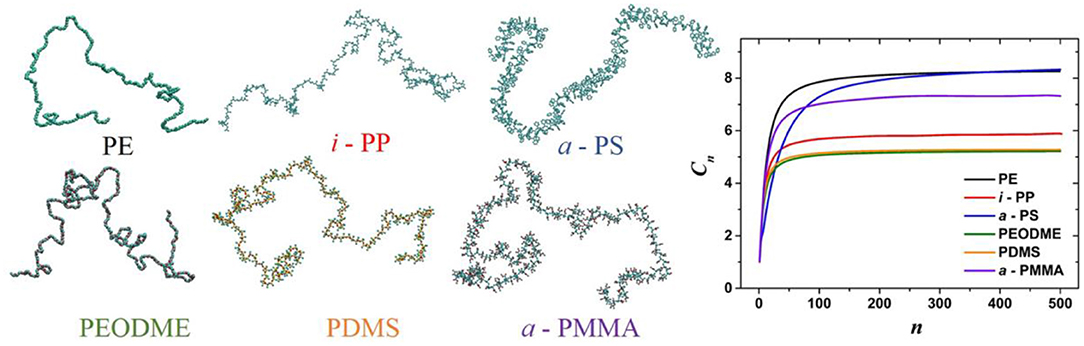
Figure 11. Characteristic snapshots from the single chain Monte Carlo simulations of Tzounis et al. [88] for six different polymers [polyethylene (PE), isotactic polypropylene (i-PP), atactic polystyrene (a-PS), poly(ethylene oxide) dimethyl ether (PEODME), poly(dimethylsiloxane) (PDMS), and atactic poly(methyl methacrylate) (a-PMMA)], and the simulation predictions for the dependence of chain characteristic ratio C_n on the number of backbone bonds n at 450 K. Reprinted (adapted) with permission from Tzounis et al. [88]. Copyright (2017) American Chemical Society.

Confined Polymers

Lattice Monte Carlo simulations have been combined with lattice self-consistent field (SCF) theory [89] to study athermal homopolymer solutions confined between parallel, non-absorbing surfaces at equilibrium with a bulk solution. Calculations of the effective interaction between the two surfaces provided support for a fluctuation-induced repulsion between the confining surfaces at intermediate separation as had been suggested by Obukhov and Semenov [90] and Semenov and Obukhov [91].

Despite being inherently a non-dynamic method, Monte Carlo has been exploited to capture also the main features of polymer dynamics. It has been used [92] to simulate polymer diffusion in narrow periodic channels with alternating attractive and repulsive parts, and to study [93] the dynamics of a semiflexible polymer chain in the presence of an array of periodically distributed nanoparticles. In the former work, the diffusion coefficient was found to change periodically with the polymer length. In the latter work, the authors investigated polymer dynamics for repulsive, weak attractive, and strong attractive nanoparticles. An interesting finding in the case of strongly attractive nanoparticles was that a stiff polymer may move faster than a flexible one, since chain stiffness effectively weakens nanoparticle attraction. Monte Carlo has also been employed [94] to study the rupture of ultra-thin polymer film melts under strong confinement.

Grafted Polymers

The Monte Carlo moves described in section Monte Carlo Moves for Polymers were extended quite early by Daoulas et al. [95] to address melts of polymer chains grafted by one of their ends onto a solid substrate. The simulations were used to test theoretical scaling laws for the conformation and orientational order of grafted chains as a function of chain length and grafting density [96]. To account for the effect of grafting on the polydispersity of the melt (as induced by the chain connectivity moves included in the Monte Carlo algorithm), an iterative scheme was presented [35] capable of controlling the spectrum of chain relative chemical potentials discussed in section Complex Monte Carlo Moves so that the chain length distribution sampled in the course of the simulation is the desired one. This was achieved by accounting explicitly for interatomic interactions and is very important in reproducing and maintaining in the course of the simulation the desired polydispersity in applications of the method to inhomogeneous or anisotropic polymers.

Mendonça et al. [97] developed a configurational bias Monte Carlo method, as an alternative to dissipative particle dynamics (DPD) method, to study friction between grafted polymers in good solvent. The friction was examined as a function of intramolecular flexibility (controlled through the bond-stretching and bond-angle bending potentials imposed in the simulation) based on predictions for the tangential component of the pressure induced by imposing a certain degree of mismatch in the registry of the two grafting surfaces. The main conclusion was that, the more flexible the polymer layer, the much lower the value of the shear force at which slip occurs.

Monte Carlo simulations with a single-site bond fluctuation model have also been used [98] to study protein adsorption on end-grafted polymers and investigate the role of polymer hydrophilicity and grafting density on the conformation and height of the brush.

We also mention the Monte Carlo method introduced by Pakula [99] and Polanowski and Pakula [100] based on the dynamic lattice liquid model which was employed by Polanowski et al. [101] to simulate the growth of polymer brushes by the grafting-from method using atom transfer radical polymerization (ATRP). It allowed the authors to study the influence of the overall polymerization rate and the relationship between monomer attachment probability and activation/deactivation probabilities on polymer dispersity, polymer concentration profile and distribution of active chain ends in space. The work was extended to include also the dynamics of such realistic, polydisperse brushes starting from the “as obtained” (and usually non-equilibrium) state. This allowed investigating chain relaxation independently of chain growth, which in real ATRP synthesis is a much slower process, and results for various grafting densities and polymerization rates were presented.

Polymer Rings and Knots

Polymer rings is an intriguing class of polymers whose properties cannot be described by the reptation theory due to lack of chain ends. They have been the subject of intense research work in the past few years, especially after the pioneering work of Kapnistos et al. [102] was published according to which contamination by linear chains even at very small levels can dramatically affect the stress relaxation properties. Given the capabilities offered by simulations to precisely control sample composition, molecular simulation techniques such as Molecular Dynamics and Monte Carlo have emerged as excellent tools for studying the conformational and dynamic properties of polymer rings and ring-linear blends including their dependence on the relative concentration of the two species (ring and linear).

Lee and Jung [103] used lattice Monte Carlo simulations to study the connection between slow diffusional processes in melts of polymer rings and topological constraints associated with threading events between different ring molecules. Monte Carlo simulations on a face-centered-cubic lattice were employed by Suzuki and collaborators in a series of papers [104–108] to study: (a) the size and conformation of non-concatenated polymer rings in the melt state [104], (b) molecular conformations of trivial, 3₁-knot, and 5₁-knot ring polymers at their theta points [105, 106], (c) the temperature dependence of the second virial coefficient of ring polymers [107], and (d) the size and conformation of catenated ring polymers in dilute solution, over a wide range of chain lengths [108].

Lattice Monte Carlo simulations have been used by Reigh and Yoon [109] to study concentration effects on the conformation of ring polymers. Shanbhag [110] and Henke and Shanbhag [111] have made use of Monte Carlo simulations with the bond fluctuation model to study dynamics (chain center-of-mass diffusion) and conformational properties (radius–of-gyration and end-to-end distance) in symmetric and asymmetric ring-linear polymer blends.

In a very recent study, Monte Carlo simulations based on the reptation (slithering-snake) and flip (crankshaft) moves were employed to sample configurational space and thus parameterize a generic soft repulsive potential of a mesoscopic, worm-like chain model for polymer knots (i.e., closed loops typically categorized according to the minimum number of crossings in a projection onto a plane) [112]. A similar method had been followed in the past to determine knotting probabilities and typical sizes of knots in double-stranded DNA containing up to half a million base pairs [113].

Semiflexible Polymers

Monte Carlo simulations of self-avoiding walks on a simple cubic lattice have been employed to study semiflexible polymers (chains with variable flexibility) and test the applicability of the Kratky-Porod model [114] and the structure of bottle-brush polymers [115], as well as to get information for the force-vs.-extension behavior of flexible chains and semiflexible bottle-brush polymers adsorbed from a good solvent on a planar substrate using the bond fluctuation model [116, 117]. The same bond fluctuation model was used to study transitions associated with orientational ordering in thin films [118] or near walls [119], at nematic ordering. For example, Monte Carlo simulations have confirmed [120] surface-induced nematic ordering in semi-dilute solutions of chains with a moderate stiffness in films that are thick enough for their central region to exhibit bulk behavior.

Greco et al. [121] used coarse-grained Monte Carlo simulations to study conjugated polymers forming nematic mesophases. In the method, polymer chains were described in the context of the discrete worm-like chain model subject to a soft non-bonded potential containing an isotropic repulsive and an anisotropic attractive term (of the type of Maier-Saupe) capable of inducing nematic order.

Manca et al. [122] used Monte Carlo to study how flexible and semiflexible single polymer chains anchored by one of their ends stretch due to an applied external field, and the results were used to validate a statistico-mechanical analytical model on the basis of the freely-jointed and worm-like chain models.

In the past, Monte Carlo simulations of long, single linear polymer chains subjected to uniform stretching by Pierleoni et al. [123] provided confirmation of the tensile blob concept introduced earlier by Pincus [124] and de Gennes [125]. In a later study, Titantah et al. [126] used Monte Carlo to study the thermo-elastic properties of individual polyethylene chains at theta and good solvent conditions by employing a realistic model for polyethylene, in two different ensembles (fixed-external stretching force on chain and fixed relative extension of chain).

Physical Gels, Hydrogels, and Networks

Monte Carlo simulations with the bond fluctuation model have been employed [127–129] for star-polymer networks. Lange et al. [128] reported Monte Carlo simulations of the network structure of a tetra-PEG hydrogel (formed by an A-B reaction of two symmetric four-arm polymers), which was experimentally characterized using proton multiple-quantum NMR measurements at low field. Different connectivity modes (regular single links and double links) between the macromonomers were suggested for individual stars, together with some other network structures characterized by lower order parameters. In this case, the simulations confirmed the concentration-dependence of the network structure and the fraction of double links probed experimentally. Monte Carlo simulations with the bond-fluctuation model were also performed by Lang et al. [129] to test the predictions of a rate theory for the formation of short cyclic structures in networks formed by the homo- and co-polymerization of f-functional molecules.

Bergsma et al. [130] combined Monte Carlo with the Scheutjens-Fleer self-consistent field theory to address gels of ABA triblock copolymers as a function of polymer volume fraction. Associative A blocks were confined to small volumes called nodes, the number of polymers per node being a parameter. B blocks, on the other hand, were allowed to move freely as long as they were connected to A blocks. With Monte Carlo, the authors could sample node configurations on a lattice (Figure 12) while with the Scheutjens-Fleer theory they could determine changes in free energy. The proposed method (a hybrid Monte Carlo—SCF scheme) has the advantage that the interaction potential between nodes needs not to have been defined in advance.

FIGURE 12

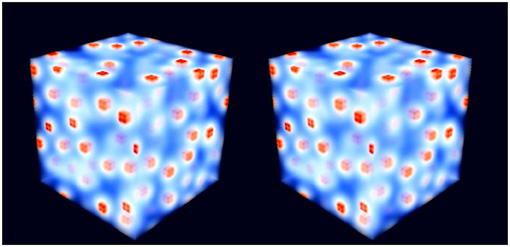
Figure 12. An example of the system simulated by Bergsma et al. [130]. Dark red cubes indicate nodes (whose cores are shown with a slightly lighter red color). Due to steric repulsion, polymer molecules push each other away from the node, this drags anchoring groups outside the core, and therefore the density within the core decreases. Figure reprinted with permission from Bergsma et al. [130]. Notice to readers: further permissions related to the material excerpted should be directed to the ACS.

Polymer Crystallization

Monte Carlo has also been used to study the kinetics and morphology of polymers undergoing crystallization under an applied 3-d flow [131], or strain-enhanced stereo-complex polymer crystallization [132]. In another study [133], the method was extended to binary blends of symmetric crystallizable polymers in which the authors enhanced (separately) the driving forces leading to polymer-uniform and polymer-staggered crystals. Under parallel enhancements, polymer-uniform crystals were observed to exhibit faster nucleation and growth, more chain folds and less lamellar thickening than polymer-staggered ones. Tahara et al. [134] used Monte Carlo to simulate 2-d small-angle X-ray scattering (SAXS) patterns exhibited by oriented crystalline polymer samples, and thus indirectly deduce information concerning the structure of lamellar aggregates (Figure 13). The 2-d model corresponded to the projection of the 3-d lamellar structure or to the averaged structure viewed along the direction of the beam.

FIGURE 13

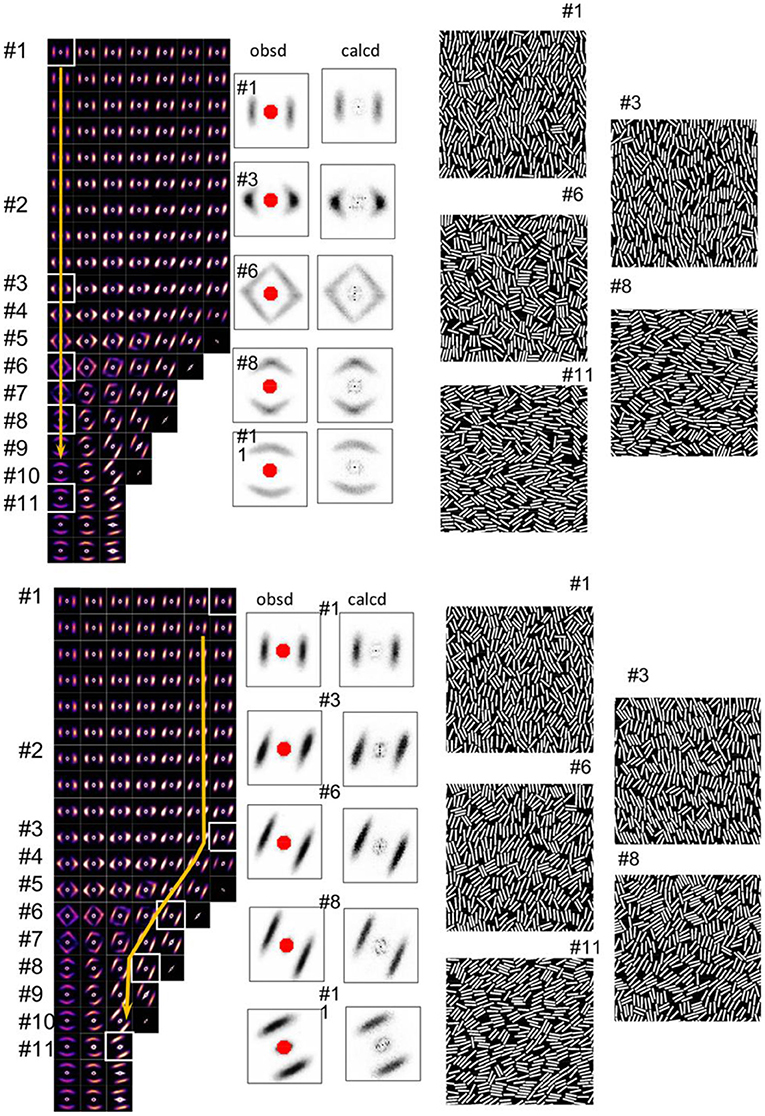
Figure 13. Stacked lamellar models proposed [134] on the basis of information extracted from the Monte Carlo simulations of observed SAXS patterns of a biaxially oriented LLDPE (linear low density polyethylene) sample. Different sets of data are shown corresponding to SAXS patterns measured at different positions in the sample. Also shown is the comparison between experimentally observed and Monte Carlo simulated SAXS patterns. Reprinted (adapted) with permission from Tahara et al. [134]. Copyright (2020) American Chemical Society.

Polymer Reaction Engineering

The Monte Carlo method has also been very popular in polymer reaction engineering because of its capability to describe polymerization reactions. This is an interesting subject by itself and we refer readers to the detailed review by Brandão et al. [135].

Summary and Outlook

Out of our short review we hope it has been shown that, thanks to the development and efficient implementation of advanced moves that can induce large conformational changes in the interior of a polymer chain and, consequently, considerably accelerate the rate with which configurational space is sampled, Metropolis Monte Carlo has advanced today to a powerful computational tool that can be used to address several physico-chemical properties of real polymers (structural, conformational, thermodynamic, and morphological) with remarkable accuracy. We should emphasize, in particular, the capability to treat polymer molecular organization and morphology at several scales. Direct observation of self-organization starting from a purely random configuration of an ensemble of polymer chains with the detailed Molecular Dynamics method is often impossible for polymers with high molecular weight due to the long time scales involved in the course of the phase transition, despite that molecular organization in condensed phases is determined predominantly by short-range repulsive or attractive forces between polymer atoms or groups of atoms. Resorting to a non-dynamic method such as atomistic Monte Carlo in which the path followed in going from the original completely disordered state to the final self-organized one departs considerably from the natural trajectory seems to be much more promising.

The benefits of using a non-dynamic method to simulate ordered phases without making big compromises in the degree of atomistic detail accounted for are far more reaching and important than what has been discussed here, since tiny details in the chemical structure (e.g., exact length of a side alkyl group, or exact degree of flexibility of the main chain) can dramatically affect the phase behavior of the system. For example, it can influence the precise morphological structure or even the number of intermediate ordered phases predicted as the value of a physical parameter (e.g., temperature, concentration or volume fraction) is varied. Failure to take proper account of the full complexity of interactions may lead to erroneous predictions concerning the full spectrum of morphologies manifested by the system under study. This renders atomistic Monte Carlo a much more reliable and attractive method to employ than techniques based on structural coarse-graining and the use of effective potentials that offer only an approximate treatment of the problem, the possible dependence of the parameters of the effective potentials on the conditions of the simulation (e.g., temperature and pressure or density) notwithstanding.

Despite its unlimited potential (the method is only limited by our imagination to devise new moves), there is still many issues and problems to be addressed for the method to reach the level of maturity of Molecular Dynamics. First of all, most Monte Carlo simulation algorithms today are highly system-specific, in the sense that the corresponding Monte Carlo moves are tailored for a particular polymer chemistry (e.g., polyethylene or polypropylene or polybutadiene) and/or molecular architecture (e.g., linear polymer, branched polymer, cyclic polymer). This strongly prohibits code transferability from the original polymer system for which the moves were developed to another. We are clearly in the need of further algorithmic developments before Monte Carlo can be regarded as a friendly, ready-to-use simulation tool for different polymers. The problem becomes more acute considering the great complexity of certain polymers such as the simultaneous presence on the same chain of side groups, branches, rings, functional groups etc., or the emphasis today on multicomponent systems (e.g., polymer nanocomposites, polymer mixtures, block copolymers, etc.). Even if the corresponding moves are rigorously adapted for a new polymer ensuring an ergodic simulation, it is not at all clear that their acceptance rates will be sufficient to ensure complete relaxation at all length scales. This is often the case when the polymer contains relatively long side groups or stiff units or when specific structural features exclude the implementation of some key Monte Carlo moves like ConRot or end-bridging.

The obstacles discussed in the previous paragraph doubtless pose significant limitations to the applicability of Metropolis Monte Carlo to polymer systems of considerable industrial and technological interest presently. At the same time, however, they call for important developments in the next years along several directions. One such direction would be to develop new moves for the more efficient treatment of polymer segments around branch points or junctions; the latter would be of relevance to polymer networks. Although procedures for treating such points have already appeared, devising moves to further enhance equilibration around branch points or junctions would be an important step forward, since these points constitute the Achilles heel of the majority of Monte Carlo algorithms presently available. Even under the hypothesis that no new moves are introduced, significant progress could be made by extending existing ones (in particular, the most advanced chain-connectivity altering moves) to systems that depart structurally from the original polymer system for which the moves were developed (e.g., linear or branched polyethylene, or polybutadiene) but whose complexity remains simple enough to offer a relatively straightforward implementation. This is the case of block copolymers. To the best of our knowledge, casting Monte Carlo moves already developed for specific pairs of homopolymers (e.g., polystyrene and polyisoprene or polybutadiene) to their copolymers with the object of exploring their rich phase diagram has not been undertaken thus far. A direct treatment of the full phase diagram of block copolymers with Monte Carlo would not be prohibitively difficult and would constitute a significant step forward in the field indeed.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. J Chem Phys. (1953) 21:1087–92. doi: 10.1063/1.1699114

CrossRef Full Text | Google Scholar

2. Allen MP, Tildesley DJ. Computer Simulation of Liquids. Clarendon, TX: Oxford (1987).

Google Scholar

3. Sadus RJ. Molecular Simulation of Fluids: Theory, Algorithms and Object-Orientation. Elsevier (1999).

Google Scholar

4. Theodorou DN. Variable-connectivity Monte Carlo algorithms for the atomistic simulation of long-chain polymer systems. In: Nielaba P, Mareschal M, Ciccotti G, editors. Bridging Time Scales: Molecular Simulations for the Next Decade. Springer Verlag) (2002). p. 64–127.

Google Scholar

5. Theodorou DN. Progress and outlook in Monte Carlo simulations. Ind Eng Chem Res. (2010) 49:3047–58. doi: 10.1021/ie9019006

CrossRef Full Text | Google Scholar

6. Mavrantzas VG. Monte Carlo simulation of chain molecules. In: Yip S, editor. The Encyclopedia of Modeling for Advanced Materials. New York, NY: Marcel Dekker (2004).

Google Scholar

7. Alexandrowicz Z, Accad Y. Monte Carlo of chains with excluded volume: distribution of intersegmental distances. J Chem Phys. (1971) 54:5338–45. doi: 10.1063/1.1674833

CrossRef Full Text | Google Scholar

8. Vacatello M, Avitabile G, Corradini P, Tuzi A. A computer model of molecular arrangement in a n-paraffinic liquid. J Chem Phys. (1980) 73:548–52. doi: 10.1063/1.439853

CrossRef Full Text | Google Scholar

9. Mavrantzas VG, Boone TD, Zervopoulou E, Theodorou DN. End-Bridging Monte Carlo: a fast algorithm for atomistic simulation of condensed phases of long polymer chains. Macromolecules. (1999) 32:5072–96. doi: 10.1021/ma981745g

CrossRef Full Text | Google Scholar

10. Peristeras LD, Economou IG, Theodorou DN. Structure and volumetric properties of linear and triarm star polyethylenes from atomistic Monte Carlo simulation using new internal rearrangement moves. Macromolecules. (2005) 38:386–97. doi: 10.1021/ma048364p

CrossRef Full Text | Google Scholar

11. Ramos J, Peristeras LD, Theodorou DN. Monte Carlo simulation of short chain branched polyolefins in the molten state. Macromolecules. (2007) 40:9640. doi: 10.1021/ma071615k

CrossRef Full Text | Google Scholar

12. Rosenbluth MN, Rosenbluth AW. Monte Carlo calculation of the average extension of molecular chains. J Chem Phys. (1955) 23:356–9. doi: 10.1063/1.1741967

CrossRef Full Text | Google Scholar

13. de Pablo JJ, Laso M, Suter UW. Simulation of phase equilibria for chain molecules. J Chem Phys. (1992) 97:2817–9. doi: 10.1063/1.463022

CrossRef Full Text | Google Scholar

14. Siepmann JI, Frenkel D. Configurational bias Monte Carlo: a new sampling scheme for flexible chains. Mol Phys. (1992) 75:59–70. doi: 10.1080/00268979200100061

CrossRef Full Text | Google Scholar

15. Panagiotopoulos AZ. Direct determination of fluid phase equilibria by simulation in the Gibbs ensemble: a review. Mol Phys. (1992) 9:1–23. doi: 10.1080/08927029208048258

CrossRef Full Text | Google Scholar

16. Escobedo FA, de Pablo JJ. Extended continuum configurational bias Monte Carlo methods for simulation of flexible molecules. J Chem Phys. (1995) 102:2636–52. doi: 10.1063/1.468695

CrossRef Full Text | Google Scholar

17. Uhlherr A. Monte Carlo conformational sampling of the internal degrees of freedom of chain molecules. Macromolecules. (2000) 33:1351–60. doi: 10.1021/ma9908595

CrossRef Full Text | Google Scholar

18. Wick CD, Siepmann JI. Self-adapting fixed end-point configurational-bias Monte Carlo method for the regrowth of interior segments of chain molecules with strong intramolecular interactions. Macromolecules. (2000) 33:7207–18. doi: 10.1021/ma000172g

CrossRef Full Text | Google Scholar

19. Lyubartsev AP, Martsinovskii AA, Shavkunov SV, Vorontsov-Velyaminov PN. New approach to Monte Carlo calculation of the free energy: method of expanded ensembles. J Chem Phys. (1992) 96:1776–83. doi: 10.1063/1.462133

CrossRef Full Text | Google Scholar

20. Wang F, Landau DP. Efficient, multiple-range random walk algorithm to calculate the density of states. Phys Rev Lett. (2001) 86:2050–3. doi: 10.1103/PhysRevLett.86.2050

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Jain TS, de Pablo JJ. A biased Monte Carlo technique for calculation of density of states of polymer films. J Chem Phys. (2002) 116:7238–43. doi: 10.1063/1.1463422

CrossRef Full Text | Google Scholar

22. Shell MS, Debenedetti PG, Panagiotopoulos AZ. An improved Monte Carlo method for direct calculation of the density of states. J Chem Phys. (2003) 119:9406–11. doi: 10.1063/1.1615966

CrossRef Full Text | Google Scholar

23. Dodd LR, Boone TD, Theodorou DN. A concerted rotation algorithm for atomistic Monte Carlo simulation of polymer melts and glasses. Mol Phys. (1993) 78:961–96. doi: 10.1080/00268979300100641

CrossRef Full Text | Google Scholar

24. Balijepalli S, Rutledge GC. Simulation study of semi-crystalline polymer interphases. Macromol Symp. (1998) 133:71–99. doi: 10.1002/masy.19981330108

CrossRef Full Text | Google Scholar

25. Veld PJ, Rutledge GC. Temperature-dependent elasticity of a semicrystalline interphase composed of freely rotating chains. Macromolecules. (2003) 36:7358–65. doi: 10.1021/ma0346658

CrossRef Full Text | Google Scholar

26. Pant PVK, Theodorou DN. Variable connectivity method for the atomistic Monte Carlo simulation of polydisperse polymer melts. Macromolecules. (1995) 28:7224–34. doi: 10.1021/ma00125a027

CrossRef Full Text | Google Scholar

27. Santos S, Suter UW, Müller M, Nievergelt J. A novel parallel-rotation algorithm for atomistic Monte Carlo simulation of dense polymer systems. J Chem Phys. (2001) 114:9772–9. doi: 10.1063/1.1371496

CrossRef Full Text | Google Scholar

28. Lal M. ‘Monte Carlo’ computer simulation of chain molecules. I. Mol Phys. (1969) 17:57–64. doi: 10.1080/00268976900100781

CrossRef Full Text | Google Scholar

29. Madras N, Sokal AD. The pivot algorithm: a highly efficient Monte Carlo method for the self-avoiding walk. J Stat Phys. (1988) 50:109–86. doi: 10.1007/BF01022990

CrossRef Full Text | Google Scholar

30. Alexiadis O, Daoulas KCh, Mavrantzas VG. An efficient Monte Carlo algorithm for the fast equilibration and atomistic simulation of alkanethiol self-assembled monolayers on a Au(111) substrate. J Phys Chem B. (2008) 112:1198–211. doi: 10.1021/jp076417+

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Olaj OF, Lantschbauer W. Simulation of chain arrangement in bulk polymer, 1. Chain dimensions and distribution of the end-to-end distance. Makromol Chem Rapid Commun. (1982) 3:847–58. doi: 10.1002/marc.1982.030031202

CrossRef Full Text | Google Scholar

32. Wu MG, Deem MW. Efficient Monte Carlo for cyclic peptides. Mol Phys. (1999) 97:559–80. doi: 10.1080/00268979909482855

CrossRef Full Text | Google Scholar

33. Uhlherr A, Leak SJ, Adam NE, Nyberg PE, Doxastakis M, Mavrantzas VG, et al. Large scale atomistic polymer simulations using Monte Carlo methods for parallel vector processors. Comp Phys Comm. (2002) 144:1–22. doi: 10.1016/S0010-4655(01)00464-7

CrossRef Full Text | Google Scholar

34. Zervopoulou E, Mavrantzas VG, Theodorou DN. A new Monte Carlo simulation approach for the prediction of sorption equilibria of oligomers in polymer melts: solubility of long alkanes in linear polyethylene. J Chem Phys. (2001) 115:2860–75. doi: 10.1063/1.1383050

CrossRef Full Text | Google Scholar

35. Daoulas KCh, Terzis AF, Mavrantzas VG. Variable connectivity methods for the atomistic Monte Carlo simulation of inhomogeneous and/or anisotropic polymer systems of precisely defined chain length distribution: tuning the spectrum of chain relative chemical potentials. Macromolecules. (2003) 36:6674–82. doi: 10.1021/ma021570h

CrossRef Full Text | Google Scholar

36. Karayiannis NCh, Mavrantzas VG, Theodorou DN. A novel Monte Carlo scheme for the rapid equilibration of atomistic model polymer systems of precisely defined molecular architecture. Phys Rev Lett. (2002) 88:105503. doi: 10.1103/PhysRevLett.88.105503

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Karayiannis NCh, Giannousaki AE, Mavrantzas VG. An advanced Monte Carlo method for the equilibration of model long-chain branched polymers with a well-defined molecular architecture: detailed atomistic simulation of an H-shaped polyethylene melt. J Chem Phys. (2003) 118:2451–4. doi: 10.1063/1.1543580

CrossRef Full Text | Google Scholar

38. Baig C, Alexiadis O, Mavrantzas VG. Advanced Monte Carlo algorithm for the atomistic simulation of short- and long-chain branched polymers: implementation for model H-shaped, A₃AA₃ multiarm (pom-pom) and short-chain branched polyethylene melts. Macromolecules. (2010) 43:986–1002. doi: 10.1021/ma902199g

CrossRef Full Text | Google Scholar

39. Moorthi K, Kamio K, Ramos J, Theodorou DN. Monte Carlo simulation of short chain branched polyolefins: structure and properties. Macromolecules. (2012) 45:8453–66. doi: 10.1021/ma301322v

CrossRef Full Text | Google Scholar

40. Moorthi K, Kamio K, Ramos J, Theodorou DN. Monte Carlo simulations of structure and entanglements in polymer melts. Mol Simulat. (2015) 41:993–5. doi: 10.1080/08927022.2014.931583

CrossRef Full Text | Google Scholar

41. Jeong SH, Kim JM, Yoon J, Tzoumanekas C, Kröger M, Baig C. Influence of molecular architecture on the entanglement network: topological analysis of linear, long- and short-chain branched polyethylene melts via Monte Carlo simulations. Soft Matter. (2016) 12:3770–86. doi: 10.1039/C5SM03016A

PubMed Abstract | CrossRef Full Text | Google Scholar

42. A Multi-Purpose Modular and Easily Extendable Solution to Molecular and Mesoscale Simulations. Available online at: montecarlo.sourceforge.net (accessed March 28, 2021).

43. Lee S, Rutledge GC. Plastic deformation of semicrystalline polyethylene by molecular simulation. Macromolecules. (2011) 44:3096–108. doi: 10.1021/ma1026115

CrossRef Full Text | Google Scholar

44. Kim JM, Locker R, Rutledge GC. Plastic deformation of semicrystalline polyethylene under extension, compression, and shear using molecular dynamics simulation. Macromolecules. (2014) 47:2515–28. doi: 10.1021/ma402297a

CrossRef Full Text | Google Scholar

45. Yeh I-C, Andzelm JW, Rutledge GC. Mechanical and structural characterization of semicrystalline polyethylene under tensile deformation by molecular dynamics simulations. Macromolecules. (2015) 48:4228–39. doi: 10.1021/acs.macromol.5b00697

CrossRef Full Text | Google Scholar

46. Kumar V, Locker CR, in t' Veld PJ, Rutledge GC. Effect of short chain branching on the interlamellar structure of semicrystalline polyethylene. Macromolecules. (2017) 50:1206–14. doi: 10.1021/acs.macromol.6b02458

CrossRef Full Text | Google Scholar

47. Martin MG. MCCCS towhee: a tool for Monte Carlo molecular simulation. Mol Simul. (2013) 39:1212–22. doi: 10.1080/08927022.2013.828208

CrossRef Full Text | Google Scholar

48. Shah JK, Marin-Rimoldi E, Mullen RG, et al. Cassandra: an open source Monte Carlo package for molecular simulation. J Comput Chem. (2017) 38:1727–39. doi: 10.1002/jcc.24807

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Dubbeldam D, Calero S, Ellis DE, Snurr RQ. RASPA: molecular simulation software for adsorption and diffusion in flexible nanoporous materials. Mol Simul. (2016) 42:81–101. doi: 10.1080/08927022.2015.1010082

CrossRef Full Text | Google Scholar

50. Alexiadis O, Cheimarios N, Peristeras LD, Bick A, Mavrantzas VG, Theodorou DN, et al. Chameleon: a generalized, connectivity altering software for tackling properties of realistic polymer systems. WIREs Comput Mol Sci. (2019) 9:e1414. doi: 10.1002/wcms.1414

CrossRef Full Text | Google Scholar

51. Cezar HM, Canuto S, Coutinho K. DICE: a Monte Carlo code for molecular simulation including the configurational bias Monte Carlo method. J Chem Inf Model. (2020) 60:3472–3488. doi: 10.1021/acs.jcim.0c00077

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Müller-Plathe F. Coarse-graining in polymer simulation: from the atomistic to the mesoscopic scale and back. ChemPhysChem. (2002) 3:754–69. doi: 10.1002/1439-7641(20020916)3:9<754::AID-CPHC754>3.0.CO;2-U

PubMed Abstract | CrossRef Full Text | Google Scholar

53. de Pablo JJ, Curtin WA. Multiscale modeling in advanced materials research: challenges, novel methods, and emerging applications. MRS Bull. (2007) 32:905–11. doi: 10.1557/mrs2007.187

CrossRef Full Text | Google Scholar

54. Öttinger HC. Systematic coarse graining: “four lessons and a caveat” from nonequilibrium statistical mechanics. MRS Bull. (2007) 32:936–40. doi: 10.1557/mrs2007.191

CrossRef Full Text | Google Scholar

55. Tsourtou FD, Alexiadis O, Mavrantzas VG, Kolonias V, Housos E. Atomistic Monte Carlo and molecular dynamics simulation of the bulk phase self-assembly of semifluorinated alkanes. Chem Eng Sci. (2015) 121:32–50. doi: 10.1016/j.ces.2014.09.009

CrossRef Full Text | Google Scholar

56. Tsourtou FD, Peroukidis SD, Peristeras LD, Mavrantzas VG. Monte Carlo algorithm based on internal bridging moves for the atomistic simulation of thiophene oligomers and polymers. Macromolecules. (2018) 51:8406–23. doi: 10.1021/acs.macromol.8b01344

CrossRef Full Text | Google Scholar

57. Tsourtou FD, Skountzos EN, Peroukidis SD, Mavrantzas VG. Molecular simulation of the high temperature phase behaviour of α-unsubstituted sexithiophene. Soft Matter. (2018) 14:8253–66. doi: 10.1039/C8SM01492B

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Karayiannis NCh, Foteinopoulou K, Laso M. Jamming and crystallization in athermal polymer packings. Philos Mag. (2013) 93:4108–31. doi: 10.1080/14786435.2013.815377

CrossRef Full Text | Google Scholar

59. Karayiannis NCh, Foteinopoulou K, Laso M. Spontaneous crystallization in athermal polymer packings. Int J Mol Sci. (2013) 14:332–58. doi: 10.3390/ijms14010332

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Foteinopoulou K, Karayiannis NCh, Laso M. Monte Carlo simulations of densely-packed athermal polymers in the bulk and under confinement. Chem Eng Sci. (2015) 121:118–32. doi: 10.1016/j.ces.2014.08.021

CrossRef Full Text | Google Scholar

61. Ramos PM, Karayiannis NCh, Laso M. Off-lattice simulation algorithms for athermal chain molecules under extreme confinement. J Comput. Phys. (2018) 375:918–34. doi: 10.1016/j.jcp.2018.08.052

CrossRef Full Text | Google Scholar

62. Herranz M, Santiago M, Foteinopoulou K, Karayiannis NCh, Laso M. Crystal, fivefold and glass formation in clusters of polymers interacting with the square well potential. Polymers. (2020) 12:1111. doi: 10.3390/polym12051111

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Kampmann TA, Boltz HH, Kierfeld J. Monte Carlo simulation of dense polymer melts using event chain algorithms. J Chem Phys. (2015) 143:044105. doi: 10.1063/1.4927084

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Reith D, Virnau P. Implementation and performance analysis of bridging Monte Carlo moves for off-lattice single chain polymers in globular states. Comput Phys Commun. (2010) 181:800–5. doi: 10.1016/j.cpc.2009.12.012

CrossRef Full Text | Google Scholar

65. Pandey YN, Doxastakis M. Detailed atomistic Monte Carlo simulations of a polymer melt on a solid surface and around a nanoparticle. J Chem Phys. (2012) 136:094901. doi: 10.1063/1.3689316

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Pandey YN, Brayton A, Burkhart C, Papakonstantopoulos GJ, Doxastakis M. Multiscale modeling of polyisoprene on graphite. J Chem Phys. (2014) 140:054908. doi: 10.1063/1.4863918

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Pandey YN, Papakonstantopoulos GJ, Doxastakis M. Polymer/nanoparticle interactions: Bridging the gap. Macromolecules. (2013) 46:5097–106. doi: 10.1021/ma400444w

CrossRef Full Text | Google Scholar

68. Vogiatzis GG, Voyiatzis E, Theodorou DN. Monte Carlo simulations of a coarse grained model for an athermal all-polystyrene nanocomposite system. Euro Polym J. (2011) 47:699712. doi: 10.1016/j.eurpolymj.2010.09.017

CrossRef Full Text | Google Scholar

69. Vogiatzis GG, Theodorou DN. Structure of polymer layers grafted to nanoparticles in silica-polystyrene nanocomposites. Macromolecules. (2013) 46:4670–83. doi: 10.1021/ma400107q

CrossRef Full Text | Google Scholar

70. Pedersen JS, Gerstenberg MC. Scattering form factor of block copolymer micelles. Macromolecules. (1996) 29:1363–5. doi: 10.1021/ma9512115

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Pedersen, JS. Structure factors effects in small-angle scattering from block copolymer micelles and star polymers. J Chem Phys. (2001) 114:2839–46. doi: 10.1063/1.1339221

CrossRef Full Text | Google Scholar

72. Dodd PM, Jayaraman A. Monte Carlo simulations of polydisperse polymers grafted on spherical surfaces. J Polym Sci Part B Polym Phys. (2012) 50:694–705. doi: 10.1002/polb.23057

CrossRef Full Text | Google Scholar

73. Jayaraman A, Nair N. Integrating PRISM theory and Monte Carlo simulation to study polymer-functionalised particles and polymer nanocomposites. Mol Simulat. (2012) 38:751–61. doi: 10.1080/08927022.2012.683528

CrossRef Full Text | Google Scholar

74. Gu Z, Yang R, Yang J, Qiu X, Liu R, Liu Y, et al. Dynamic Monte Carlo simulations of effects of nanoparticle on polymer crystallization in polymer solutions. Comput Mat Sci. (2018) 147:217–26. doi: 10.1016/j.commatsci.2018.02.009

CrossRef Full Text | Google Scholar

75. Nie Y, Liu Y, Liu R, Zhou Z, Hao T. Dynamic Monte Carlo simulations of competition in crystallization of mixed polymers grafted on a substrate. J Polym Sci Part B Polym Phys. (2019) 57:89–97. doi: 10.1002/polb.24757

CrossRef Full Text | Google Scholar

76. Ming Y, Zhou Z, Xu D, Liu R, Nie Y, Hao T. The effect of molecular weight of polymers grafted in two-dimensional filler on crystallization behaviors studied by dynamic Monte Carlo simulations. Comput Mater Sci. (2018) 155:144–50. doi: 10.1016/j.commatsci.2018.08.046

CrossRef Full Text | Google Scholar

77. Kikuchi K, Yoshida M, Maekawa T, Watanabe H. Metropolis Monte Carlo method as a numerical technique to solve the Fokker-Planck equation. Chem Phys Lett. (1991) 185:335–8. doi: 10.1016/S0009-2614(91)85070-D

CrossRef Full Text | Google Scholar

78. Sanz E, Marenduzzo, D. Dynamic Monte Carlo versus Brownian dynamics: a comparison for self-diffusion and crystallization in colloidal fluids. J Chem Phys. (2010) 132:194102. doi: 10.1063/1.3414827

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Romano F, De Michele C, Marenduzzo D, Sanz E. Monte Carlo and event-driven dynamics of Brownian particles with orientational degrees of freedom. J Chem Phys. (2011) 135:124106. doi: 10.1063/1.3629452

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Beris AN, Edwards BJ. Thermodynamics of Flowing Systems: With Internal Microstructure. New York, NY: Oxford University Press (1994). doi: 10.1093/oso/9780195076943.001.0001

CrossRef Full Text | Google Scholar

81. Öttinger HC. Beyond Equilibrium Thermodynamics. New York, NY: Wiley-Interscience (2004).

Google Scholar

82. Mavrantzas VG, Theodorou DN. Atomistic simulation of polymer melt elasticity: calculation of the free energy of an oriented polymer melt. Macromolecules. (1998) 31:6310–32. doi: 10.1021/ma9714878

CrossRef Full Text | Google Scholar

83. Mavrantzas VG, Öttinger HC. Atomistic Monte Carlo simulations of polymer melt elasticity: their nonequilibrium thermodynamics GENERIC formulation in a generalized canonical ensemble. Macromolecules. (2002) 35:960–75. doi: 10.1021/ma010688f

CrossRef Full Text | Google Scholar

84. Baig C, Mavrantzas VG. Thermodynamically guided nonequilibrium Monte Carlo method for generating realistic shear flows in polymeric systems. Phys Rev Lett. (2007) 99:257801. doi: 10.1103/PhysRevLett.99.257801

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Baig C, Mavrantzas VG. Multiscale simulation of polymer melt viscoelasticity: expanded-ensemble Monte Carlo coupled with atomistic nonequilibrium molecular dynamics. Phys Rev B. (2009) 79:144302. doi: 10.1103/PhysRevB.79.144302

CrossRef Full Text | Google Scholar

86. Baig C, Mavrantzas VG, Öttinger HC. On Maxwell's relations of thermodynamics for polymeric liquids away from equilibrium. Macromolecules. (2011) 44:640–6. doi: 10.1021/ma101813q

CrossRef Full Text | Google Scholar

87. Roh EJ, Baig C. Nonequilibrium Monte Carlo simulations of entangled polymer melts under steady shear flow. Soft Matter. (2019) 15:5271–81. doi: 10.1039/C9SM00556K

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Tzounis PN, Anogiannakis SD, Theodorou DN. General methodology for estimating the stiffness of polymer chains from their chemical constitution: a single unperturbed chain Monte Carlo algorithm. Macromolecules. (2017) 50:4575–87. doi: 10.1021/acs.macromol.7b00645

CrossRef Full Text | Google Scholar

89. Zhang P, Wang Q. Repulsion between colloidal particles mediated by nonadsorbing polymers: lattice Monte Carlo simulations and the corresponding self-consistent field calculations. Macromolecules. (2019) 52:5777–90. doi: 10.1021/acs.macromol.9b00545

CrossRef Full Text | Google Scholar

90. Obukhov SP, Semenov, AN. Long-range interactions in polymer melts: the anti-Casimir effect. Phys Rev Lett. (2005) 95:038305. doi: 10.1103/PhysRevLett.95.038305

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Semenov AN, Obukhov SP. Fluctuation-induced long-range interactions in polymer systems. J Phys Condens Matter. (2005) 17:S1747. doi: 10.1088/0953-8984/17/20/007

CrossRef Full Text | Google Scholar

92. Chen YC, Zhou YL, Wang C. Monte Carlo simulation on the diffusion of polymer in narrow periodical channels. Int J Modern Phys B. (2017) 31:1750144. doi: 10.1142/S0217979217501442

CrossRef Full Text | Google Scholar

93. Peng Y, Zhang H, Huang XW, Huang JH, Luo MB. Monte Carlo simulation on the dynamics of a semi-flexible polymer in the presence of nanoparticles. Phys Chem Chem Phys. (2018) 20:26333. doi: 10.1039/C8CP05136D

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Singh SP. A molecular scale perspective: Monte Carlo simulation for rupturing of ultra thin polymer film melts. Phys Lett A. (2017) 381:1321–7. doi: 10.1016/j.physleta.2017.02.011

CrossRef Full Text | Google Scholar

95. Daoulas KCh, Terzis AF, Mavrantzas VG. Detailed atomistic Monte Carlo simulation of grafted polymer melts. I. Thermodynamic and conformational properties. J Chem Phys. (2002) 116:11028. doi: 10.1063/1.1478055

CrossRef Full Text | Google Scholar

96. Daoulas KCh, Mavrantzas VG, Photinos DJ. Detailed atomistic Monte Carlo simulation of grafted polymer melts: II. Orientational order and nuclear magnetic resonance spectra. J Chem Phys. (2003) 118:1521. doi: 10.1063/1.1526466

CrossRef Full Text | Google Scholar

97. Mendonça ACF, Goujon F, Malfreyt P, Tildesley DJ. Monte Carlo simulations of the static friction between two grafted polymer brushes. Phys Chem Chem Phys. (2016) 18:6164. doi: 10.1039/C5CP07374J

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Han Y, Jin J, Cui J, Jiang W. Effect of hydrophilicity of end-grafted polymers on protein adsorption behavior: a Monte Carlo study. Colloids Surf B Biointerfaces. (2016) 142:38–45. doi: 10.1016/j.colsurfb.2016.01.064

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Pakula T. Collective dynamics in simple supercooled and polymer liquids. J Mol Liq. (2000) 86:109–21. doi: 10.1016/S0167-7322(99)00132-4

CrossRef Full Text | Google Scholar

100. Polanowski P, Pakula T. Studies of polymer conformation and dynamics in two dimensions using simulations based on the dynamic lattice liquid (DLL) model. J Chem Phys. (2002) 117:4022–9. doi: 10.1063/1.1495836

CrossRef Full Text | Google Scholar

101. Polanowski P, Jeszka JK, Matyjaszewski K. Polymer brush relaxation during and after polymerization—Monte Carlo simulation study. Polymer. (2019) 173:190–6. doi: 10.1016/j.polymer.2019.04.023

CrossRef Full Text | Google Scholar

102. Kapnistos M, Lang M, Vlassopoulos D, Pyckhout-Hintzen W, Richter D, Cho D, et al. Unexpected power-law stress relaxation of entangled ring polymers. Nat Mater. (2008) 7:997–1002. doi: 10.1038/nmat2292

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Lee E, Jung YJ. Slow dynamics of ring polymer melts by asymmetric interaction of threading configuration: Monte Carlo study of a dynamically constrained lattice model. Polymers. (2019) 11:516. doi: 10.3390/polym11030516

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Suzuki J, Takano A, Deguchi T, Matsushita Y. Dimension of ring polymers in bulk studied by Monte-Carlo simulation and self-consistent theory. J Chem Phys. (2009) 131:144902. doi: 10.1063/1.3247190

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Suzuki J, Takano A, Matsushita Y. Topological constraint in ring polymers under theta conditions studied by Monte Carlo simulation. J Chem Phys. (2013) 138:024902. doi: 10.1063/1.4773822

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Suzuki J, Takano A, Matsushita Y. Chain conformations of ring polymers under theta conditions studied by Monte Carlo simulation. J Chem Phys. (2013) 139:184904. doi: 10.1063/1.4829046

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Suzuki J, Takano A, Matsushita Y. Interactions between ring polymers in dilute solution studied by Monte Carlo simulation. J. Chem. Phys. (2015) 142:044904. doi: 10.1063/1.4906556

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Suzuki J, Takano A, Matsushita Y. Dimensions of catenated ring polymers in dilute solution studied by Monte-Carlo simulation. J Chem Phys. (2018) 149:204901. doi: 10.1063/1.5050840

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Reigh SY, Yoon DY. Concentration dependence of ring polymer conformations from Monte Carlo simulations. ACS Macro Lett. (2013) 2:296–300. doi: 10.1021/mz300587v

CrossRef Full Text | Google Scholar

110. Shanbhag S. Unusual dynamics of ring probes in linear matrices. J Polym Sci Part B Polym Phys. (2017) 55:169–77. doi: 10.1002/polb.24252

CrossRef Full Text | Google Scholar

111. Henke SF, Shanbhag S. Self-diffusion in asymmetric ring-linear blends. React Funct Polym. (2014) 80:57–60. doi: 10.1016/j.reactfunctpolym.2013.11.005

CrossRef Full Text | Google Scholar

112. Zhang J, Meyer H, Virnau P, Daoulas KCh. Can soft models describe polymer knots? Macromolecules. (2020) 53:10475–86. doi: 10.1021/acs.macromol.0c02079

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Rieger FC, Virnau P. A Monte Carlo study of knots in long double-stranded DNA chains. PLoS Comput Biol. (2016) 12:e1005029. doi: 10.1371/journal.pcbi.1005029

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Hsu HP, Paul W, Binder K. Polymer chain stiffness vs. excluded volume: a Monte Carlo study of the crossover towards the worm-like chain model. EPL. (2010) 92:28003. doi: 10.1209/0295-5075/92/28003

CrossRef Full Text | Google Scholar

115. Hsu HP, Paul W, Binder K. Understanding the multiple length scales describing the structure of bottle-brush polymers by Monte Carlo simulation methods. Macromol Theor Simulat. (2011) 20:510–25. doi: 10.1002/mats.201000092

CrossRef Full Text | Google Scholar

116. Hsu H-P, Paul W, Binder K. Pulling single adsorbed bottle-brush polymers off a flat surface: A Monte Carlo simulation. Macromolecules. (2014) 47:427–437. doi: 10.1021/ma401996n

CrossRef Full Text | Google Scholar

117. Hsu H-P, Binder K. Stretching semiflexible polymer chains: evidence for the importance of excluded volume effects from Monte Carlo simulation. J Chem Phys. (2012) 136:024901. doi: 10.1063/1.3674303

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Ivanov VA, Rodionova AS, An EA, Martemyanova JA, Stukan MR, Müller M, et al. Orientational ordering transitions of semiflexible polymers in thin films: A Monte Carlo simulation. Phys Rev E. (2011) 84:041810. doi: 10.1103/PhysRevE.84.041810

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Ivanov VA, Rodionova AS, Martemyanova JA, Stukan MR, Müller M, Paul W, et al. Wall-induced orientational order in athermal semidilute solutions of semiflexible polymers: Monte Carlo simulations of a lattice model. J Chem Phys. (2013) 138:234903. doi: 10.1063/1.4810745

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Ivanov VA, Rodionova AS, Martemyanova JA, Stukan MR, Müller M, Paul W, et al. Conformational properties of semiflexible chains at nematic ordering transitions in thin films: a Monte Carlo simulation. Macromolecules. (2014) 47:1206–20. doi: 10.1021/ma402138c

CrossRef Full Text | Google Scholar

121. Greco C, Jiang Y, Chen JZY, Kremer K, Daoulas KCh. Maier-Saupe model of polymer nematics: comparing free energies calculated with self consistent field theory Monte Carlo simulations. J Chem Phys. (2016) 145:184901. doi: 10.1063/1.4966919

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Manca F, Giordano S, Palla PL, Cleri F, Colombo L. Theory and Monte Carlo simulations for the stretching of flexible and semiflexible single polymer chains under external fields. J Chem Phys. (2012) 137:244907. doi: 10.1063/1.4772656

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Pierleoni C, Arialdi G, Ryckaert JP. On the signature of tensile blobs in the scattering function of a stretched polymer. Phys Rev Lett. (1997) 79:2990–3. doi: 10.1103/PhysRevLett.79.2990

CrossRef Full Text | Google Scholar

124. Pincus P. Excluded volume effects and stretched polymer chains. Macromolecules. (1976) 9:386–8. doi: 10.1021/ma60051a002

CrossRef Full Text | Google Scholar

125. de Gennes PG. Scaling Concepts in Polymer Physics. Ithaca, NY: Cornell University Press (1979).

Google Scholar

126. Titantah JT, Pierleoni C, Ryckaert, JP. Single chain elasticity and thermoelasticity of polyethylene. J Chem Phys. (2002) 117:9028. doi: 10.1063/1.1514974

CrossRef Full Text | Google Scholar

127. Schwenke K, Lang M, Sommer JU. On the structure of star-polymer networks. Macromolecules. (2011) 44:9464–72. doi: 10.1021/ma202022q

CrossRef Full Text | Google Scholar

128. Lange F, Schwenke K, Kurakazu M, Akagi Y, Chung Y, Lang M, et al. Connectivity and structural defects in model hydrogels: a combined proton NMR and Monte Carlo simulation study. Macromolecules. (2011) 44:9666–74. doi: 10.1021/ma201847v

CrossRef Full Text | Google Scholar

129. Lang M, Schwenke K, Sommer J-U. Short cyclic structures in polymer model networks: a test of mean field approximation by Monte Carlo simulations. Macromolecules. (2012) 45:4886–95. doi: 10.1021/ma300317z

CrossRef Full Text | Google Scholar

130. Bergsma J, Leermakers FAM, Kleijn JM, van der Gucht J. A hybrid Monte Carlo self-consistent field model of physical gels of telechelic polymers. J. Chem. Theory Comput. (2018) 14:6532–6543. doi: 10.1021/acs.jctc.7b01264

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Ruan C. Kinetics and morphology of flow induced polymer crystallization in 3D shear flow investigated by Monte Carlo simulation. Crystals. (2017) 7:51. doi: 10.3390/cryst7020051

CrossRef Full Text | Google Scholar

132. Guan X, Wang J, Hu W. Monte Carlo simulation of strain-enhanced stereocomplex polymer crystallization. J Phys Chem B. (2018) 122:10928–10933. doi: 10.1021/acs.jpcb.8b07499

PubMed Abstract | CrossRef Full Text | Google Scholar

133. Zhang R, Zha L, Hu W. Intramolecular crystal nucleation favored by polymer crystallization: Monte Carlo simulation evidence. J Phys Chem B. (2016) 120:6754–60. doi: 10.1021/acs.jpcb.6b01757

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Tahara D, Ninh TH, Yamamoto H, Tashiro K. Metropolis Monte Carlo simulation of two-dimensional small-angle X-ray scattering patterns of oriented polymer materials. Macromolecules. (2020) 53:276–87. doi: 10.1021/acs.macromol.9b01522

CrossRef Full Text | Google Scholar

135. Brandão ALT, Soares JBP, Pinto JC, Alberton AL. When polymer reaction engineers play dice: applications of Monte Carlo models in PRE. Macromol React Eng. (2015) 9:141–185. doi: 10.1002/mren.201500020

CrossRef Full Text | Google Scholar