Co-evolutionary Game Dynamics of Competitive Cognitions and Public Opinion Environment

Liu, Haoyan; Wang, Xin; Liu, Longzhao; Li, Zhoujun

doi:10.3389/fphy.2021.658130

ORIGINAL RESEARCH article

Front. Phys., 11 May 2021

Sec. Social Physics

Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.658130

Co-evolutionary Game Dynamics of Competitive Cognitions and Public Opinion Environment

$\nHaoyan Liu$ Haoyan Liu¹

Xin Wang^1,2,3

Longzhao Liu^1,2,3,4

Zhoujun Li^1,5^*

¹State Key Lab of Software Development Environment, Beihang University, Beijing, China
²Key Laboratory of Mathematics, Informatics and Behavioral Semantics (LMIB), Advanced Innovation Center of Big Data and Brain Computing (BDBC), School of Mathematical Sciences, Beihang University, Beijing, China
³PengCheng Laboratory, Shenzhen, China
⁴ShenYuan Honor School, Beihang University, Beijing, China
⁵College of Computer Science and Software Engineering, Shenzhen University, Shenzhen, China

Competitive cognition dynamics are widespread in modern society, especially with the rise of information-technology ecosystem. While previous works mainly focus on internal interactions among individuals, the impacts of the external public opinion environment remain unknown. Here, we propose a heuristic model based on co-evolutionary game theory to study the feedback-evolving dynamics of competitive cognitions and the environment. First, we show co-evolutionary trajectories of strategy-environment system under all possible circumstances. Of particular interest, we unveil the detailed dynamical patterns under the existence of an interior saddle point. In this situation, two stable states coexist in the system and both cognitions have a chance to win. We highlight the emergence of bifurcation phenomena, indicating that the final evolutionary outcome is sensitive to initial conditions. Further, the attraction basins of two stable states are not only influenced by the position of the interior saddle point but also affected by the relative speed of environmental feedbacks.

1. Introduction

Individual cognitive process and public cognition evolution have aroused great concern and have been widely studied in recent years due to the rapid development of information-technology ecosystem consisting of news medias, blogs, large-scale social networks, etc. [1–6]. Throughout this paper, “cognition” is a psychological representation that can be any piece of “knowledge” an individual holds, including information, attitude, beliefs, and behaviors, in accordance with Festinger's definition [7, 8]. In modern society, online social networks reshape the way of public discourse and cognition consumption patterns, amplify sociocognitive biases, which further influences the evolution of public opinions or collective behaviors [9–13]. A recent work reveals that the combination of external political campaigns (or mass medias) and online social influence processes could give rise to partisan echo chambers [14]. Complicating matters further, the complex interplay between different social networks could also affect cognition diffusion [15, 16], leading to the emergence of rich and important physical phenomena such as non-monotonic promotion [17], phase transition [18], and bistability [19], which has been demonstrated by numerous studies using multiplex networks [20–23].

Of particular interest, an important line of research focuses on competitive cognition dynamics, which mimic the ubiquitous scenarios where individuals are confronted with multiple and mutually exclusive cognitions [24–26]. Understanding the spreading processes as well as predicting the evolutionary outcomes of competitive cognitions is of fundamental significance for overcoming a series of real-world challenges, ranging from public health problems, social polarization to economic development [27–29]. For instance, pro-vaccination vs. anti-vaccination beliefs, adopting social distancing behaviors during COVID-19 pandemic or not, Biden vs. Trump, supporting the use of new technologies or not, truths vs. rumors, etc. [30–32]. Originally, the competing dynamics were considered in the field of infectious disease, where the classic susceptible-infected-susceptible (SIS) model and susceptible-infected-recovered (SIR) model are extended to study the co-contagion process of two competitive diseases [33–35]. These epidemic-like models were subsequently extended to describe the competitive information diffusion [36, 37]. Further, the complex contagion models that incorporate the complicated behavioral patterns were also developed, along with the emerging empirical studies exploring dynamical characteristics via real data [38–40].

While previous models interpret the evolution of competitive cognitions mainly as a result of internal interactions among individuals, either described by the effects of social influence or by the spreading dynamics such as contact-based transmission, the impact of external public opinion environment, especially the media atmosphere of supporting a certain cognition, is ignored [14]. For example, when exposed to a new cognition, the increasing number of adopters or supporters may attract the attention of medias and promotes the supportive level of public opinion environment. In turn, an ascending public opinion environment could encourage more people to adopt or support a new cognition, providing positive evidence for the supporters in public discourse. Therefore, the evolutionary outcome of the competitive cognitions is actually determined by both the benefit from the new cognition and the feedback from public opinion environment, especially in the era of social medias. However, it remains largely unknown how the public opinion environment influences the evolutionary dynamics of competitive cognitions.

To advance this important issue, in this paper, we propose a theoretical framework to describe the co-evolution of competitive cognitions and public opinion environment using co-evolutionary game theory, which has been developed recently to study the feedback loops between environment and strategies that are widely observed in biological and ecological systems [41–46]. The “cooperators” are defined as individuals who support the new cognition while the “defectors” are those who support the old cognition. Hence, the evolution of competitive cognitions can be characterized by the replicator dynamics in evolutionary game theory. The core idea of our model is to incorporate the impact of environmental feedback into cognition dynamics through an additional payoff from public discourse. Conversely, the external public opinion environment is a function of the current proportions of cooperators and defectors. First, we conduct theoretical analysis for the stability of all fixed points and present co-evolutionary dynamics of cooperation and environment under different situations. We find that cooperation or defection can be the sole dominant strategy among population, i.e., one of the cognitions always wins the competition, but only if the benefit or the loss from adopting the new cognition exceeds a threshold related to the influence of public discourse. In other cases, the system has a saddle point and the two cognitions both have a chance to survive, depending on the initial conditions. We further explore the dynamical properties under the existence of an interior saddle point and find the emergence of bifurcation phenomena. In other words, the evolutionary directions of the co-evolution system can be changed through a tiny disturbance, which indicates the existence of “randomness” or “luckiness” in real-world cognition competitions, making it difficult to steer the evolution to a desired direction [46, 47]. Furthermore, we show how the parameters in our model affect the position of the interior saddle point and that the relative feedback speed of public opinion not only influences the convergence speed but also changes the attraction basin of the two stable states. Finally, we incorporate systematic stochasticity into our deterministic model and reveal the detailed impact of stochastic environmental fluctuations.

2. Model

In this section, we introduce a modeling framework of two-strategy co-evolutionary game in a well-mixed population to characterize the competition of two cognitions under the influence of modern information-technology ecosystem. When exposed to two cognitions, an individual can choose either to support the new cognition (be a cooperator) or support the old cognition (be a defector). The cooperator receives a fixed payoff P_c from the new cognition and takes the risk of “innovation” c, while the defector receives P_d for adopting the old cognition. Meanwhile, the player receives an extra payoff or loss during public discourse, the value of which is decided by the supportive level for the two cognitions from external environment, i.e., public opinion environment n, n ∈ [0, 1]. The schematic of our model is illustrated in Figure 1. The payoff matrix of this game can be written as

\begin{array}{l} A = [\begin{matrix} P_{c} - c + n k_{1} & P_{c} - c - k_{2} ((1 - n) - n) \\ P_{d} - k_{2} (n - (1 - n)) & P_{d} + (1 - n) k_{1} \end{matrix}] & (1) \end{array}

where n and 1 − n denote the environments for supporting the new cognition and the old cognition, and k₁, k₂ > 0 are the rates of receiving payoffs/losses from homogeneous interactions and heterogeneous conflicts during public discourse, respectively. For example, if a cooperator plays with a cooperator, they talk to each other and both satisfy with the discussion, receiving nk₁ from the interaction in addition to P_c − c from the new cognition itself. If a cooperator plays with a defector, however, they debate each other and the virtual conflict makes the cooperator loses k₂((1 − n) − n). Note that here ((1 − n) − n) indicates the current environmental advantage of defectors over cooperators. If ((1 − n) − n) < 0, the cooperator actually wins the argument and receives a positive benefit. Thus, the fitnesses of cooperators and defectors, f_c and f_d, are

\begin{array}{l} {\begin{cases} f_{c} = (P_{c} - c + n k_{1}) x + (P_{c} - c - k_{2} (1 - 2 n)) (1 - x) \\ f_{d} = (P_{d} - k_{2} (2 n - 1)) x + (P_{d} + (1 - n) k_{1}) (1 - x) \end{cases} & (2) \end{array}

The standard replicator dynamics for the fraction of cooperators x is

\begin{array}{l} \dot{x} = x (f_{c} - \bar{f}) \\ = x (1 - x) (f_{c} - f_{d}) \\ = x (1 - x) (k_{1} x + (k_{1} + 2 k_{2}) n + P_{1} - k_{1} - k_{2}) & (3) \end{array}

where $\bar{f} = x f_{c} + (1 - x) f_{d}$ represents the average fitness of the population, P₁ = P_c − c − P_d indicates the inherent fixed payoff of cooperation (adopting the new cognition) vs. defection (adopting the old cognition). Meanwhile, the public opinion environment is modified by the population states, and the environmental evolution is given by

\begin{array}{l} \dot{n} = ϵ n (1 - n) (θ x - (1 - x)) & (4) \end{array}

where ϵ denotes the relative feedback speed of the environment compared to cognition dynamics. The logistic term n(1 − n) ensures n ∈ [0, 1]. And θ > 0 is the relative strength of enhancing the environment by cooperators vs. decreasing the environment by defectors.

FIGURE 1

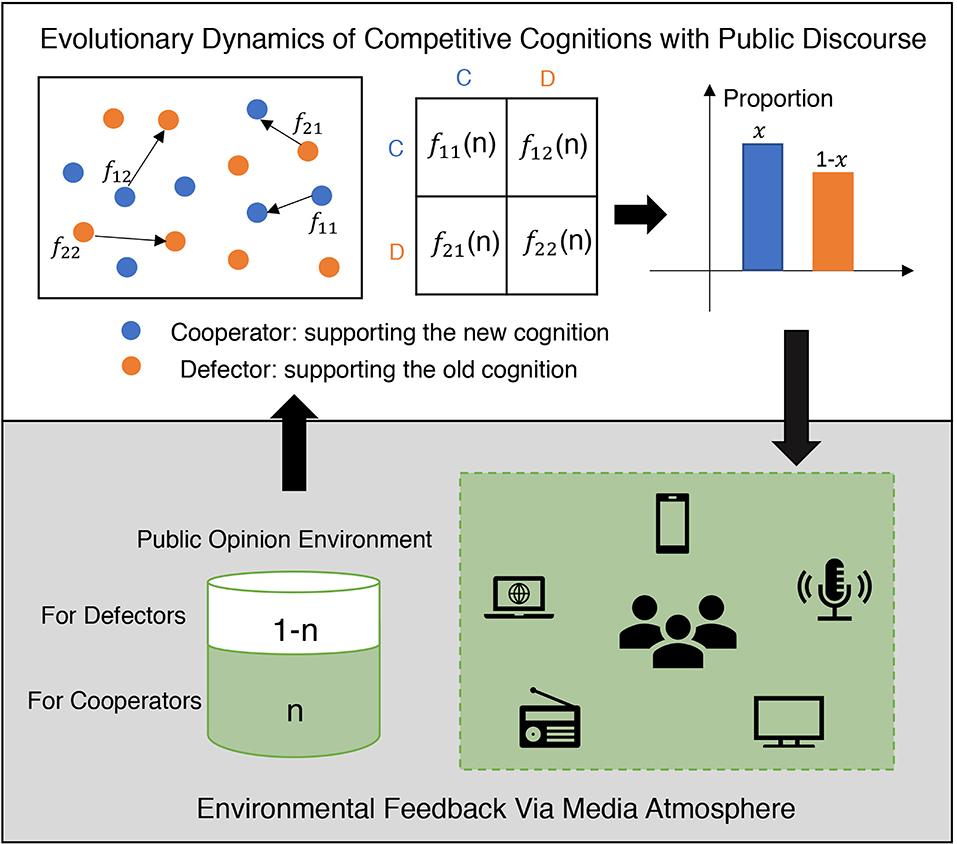
Figure 1. Schematic of our co-evolutionary modeling framework. (Top) The evolution of competitive cognitions, described by the fraction of cooperators who support the new cognition, is determined by a payoff matrix. (Top, Bottom) The fraction of cooperators x modifies the public opinion environment n, which in turn influences the payoffs f_ij.

Therefore, the co-evolutionary game dynamics of competitive cognitions and public opinion environment can be written as follows:

\begin{array}{l} {\begin{cases} \dot{x} = x (1 - x) (k_{1} x + (k_{1} + 2 k_{2}) n + P_{1} - k_{1} - k_{2}) \\ \dot{n} = ϵ n (1 - n) (θ x - (1 - x)) \end{cases} & (5) \end{array}

3. Results

3.1. Co-evolution of Cooperation and Environment Under Different Circumstances

First, we provide trajectory diagrams of x − n system to illustrate co-evolutions of cooperation and environment in the well-mixed population under all possible circumstances in Figure 2. Since the environment n is confined in [0, 1], all parameters should naturally be in the same order of magnitude. In order to provide a typical case close to reality, we assume the rate of receiving payoffs from homogeneous interactions (k₁) is larger than that from heterogeneous conflicts during public discourse (k₂). And cooperators have advantages over defectors in terms of enhancing the environment (i.e., θ ≥ 1), which means the new cognition or social innovation is favored by the media atmosphere. In addition, we assume the environment evolves faster than cognition dynamics (ϵ ≥ 1). For simplicity and without loss of generality, we set k₁ = 2, k₂ = 1, θ = 2, ϵ = 2 and change P₁ = −4, −2, −1.3, 0.5, 1.4, 2.4, 4, respectively. There are seven possible fixed points in the system: four locate in the corners, two on the boundary and the remaining one is an interior fixed point. The detailed theoretical analysis for the existence conditions and the stability of these fixed points are provided in Supplementary Materials.

FIGURE 2

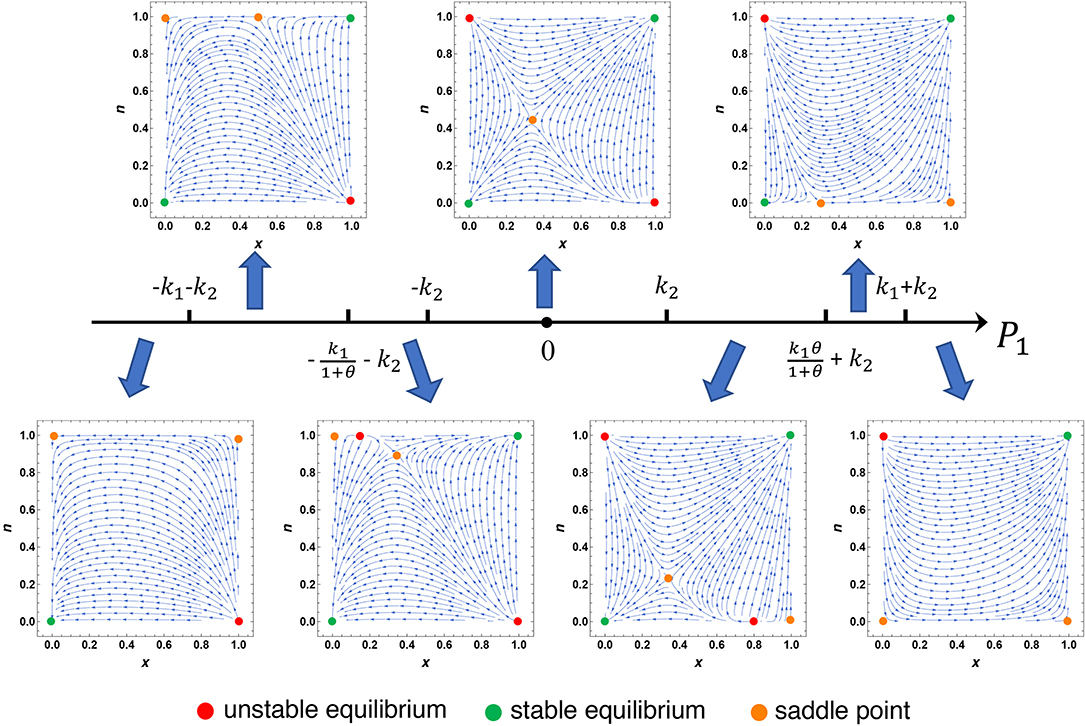
Figure 2. Trajectory diagrams of x − n system in the well-mixed population under all possible situations. The red dots represent unstable equilibriums, the green dots represent stable equilibriums while the orange dots represent saddle points. Parameters: k₁ = 2, k₂ = 1, θ = 2, ϵ = 2. From left to right, P₁ = −4, −2, −1.3, 0.5, 1.4, 2.4, 4, respectively.

When P₁ > k₁ + k₂, the system has four corner fixed points, within which (1, 1) is the only stable equilibrium, corresponding to the state where the population is dominated by cooperators and the external environment fully supports the new cognition. Similarly, when P₁ < −k₁−k₂, (0, 0) is the only stable equilibrium and the old cognition will win the competition with the environment reaches its minimum value.

When −k₁ − k₂ < P₁ < k₁ + k₂, however, (0, 0) and (1, 1) are both stable equilibriums and the final state of the system depends on initial conditions. More specifically, when $- k_{1} - k_{2} < P_{1} < - \frac{k_{1}}{1 + θ} - k_{2}$ or $\frac{θ k_{1}}{1 + θ} + k_{2} < P_{1} < k_{1} + k_{2}$ , there exists a boundary saddle point $(\frac{- k_{2} - P_{1}}{k_{1}}, 1)$ or $(\frac{k_{1} + k_{2} - P_{1}}{k_{1}}, 0)$ in addition to four corner fixed points, respectively. And the phase plane is divided into two regions: one evolves to (0, 0) and one evolves to (1, 1).

In particular, when $- \frac{k_{1}}{1 + θ} - k_{2} < P_{1} < \frac{θ k_{1}}{1 + θ} + k_{2}$ , we find the emergence of an interior saddle point:

\begin{array}{l} {\begin{cases} x^{*} = \frac{1}{1 + θ} \\ n^{*} = \frac{k_{2} + \frac{θ k_{1}}{1 + θ} - P_{1}}{k_{1} + 2 k_{2}} \end{cases} & (6) \end{array}

Within this interval, the boundary fixed point becomes an unstable equilibrium when $- \frac{k_{1}}{1 + θ} - k_{2} < P_{1} < - k_{2}$ and $k_{2} < P_{1} < \frac{θ k_{1}}{1 + θ} + k_{2}$ , and vanishes when −k₂ < P₁ < k₂.

To summarize, we show that when the inherent payoff of adopting a certain cognition is large enough to ignore the environmental influence through public discourse, that cognition will eventually dominant the population with a fully supportive environment. Nevertheless, if the impact of public opinion environment is comparable to the inherent benefit from the competitive cognitions, there are opportunities for both cognitions to win, depending on initial conditions and model parameters.

3.2. Evolutionary Dynamics With Interior Saddle Points

We are particularly interested in exploring dynamical patterns under the existence of interior saddle points. In Figure 3, we show the phase plane dynamics of a typical case where the cooperation and the environment co-evolve toward either (1, 1) or (0, 0). Here, k₁ = 2, k₂ = 1, θ = 1, ϵ = 1, P₁ = −0.5 and the interior fixed point is $(\frac{1}{2}, \frac{5}{8})$ according to equation 6. Four typical trajectories are highlighted in Figure 3A and the corresponding variations of strategies as well as the public opinion environment over time are provided in Figures 3B,C. We find that all trajectories experience two stages of dynamics. During the first stage, the cooperation and the environment evolve to opposite directions: either the supporters of new cognition increase while the external environment becomes worse (pink and red trajectories), or the public opinion environment gets better while the supporters of new cognition become fewer (orange and green trajectories). During the second stage, on the other hand, the cooperation and the environment benefit from the mutual positive feedbacks and co-evolve toward the same direction: the population adopts the new cognition with a fully supportive environment (pink and orange trajectories) or adopts the old cognition with a fully unsupportive environment (red and green trajectories).

FIGURE 3

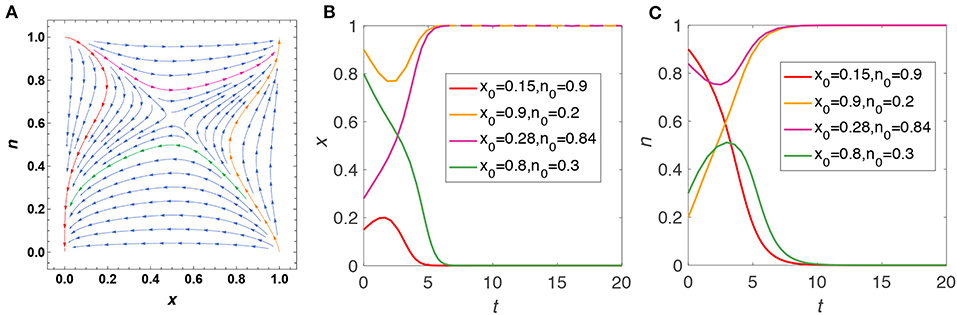
Figure 3. A typical case in which the cooperation and the environment co-evolve toward either (1, 1) or (0, 0), indicating that the social innovation of new cognition succeeds or fails, respectively. We provide phase plane dynamics in (A) and highlight four typical trajectories in different colors. The detailed time evolutions of strategies and the environment for each trajectory are presented in (B,C), correspondingly. Parameters: k₁ = 2, k₂ = 1, θ = 1, ϵ = 1, P₁ = −0.5.

To conclude, the intuitive understanding of this dynamical character can be explained as follows. The eventual evolutionary direction of this system actually depends on the results of two types of “competition” at initial stage: (i) whether the increasing public opinion environment could save the loss of new cognition adopters (orange trajectory succeeds while green trajectory fails), and (ii) whether the increasing new cognition supporters would arouse enough external supports from media environment (pink trajectory succeeds while red trajectory fails).

Unfortunately, the existence of interior saddle point in co-evolution system leads to the emergence of bifurcation phenomena, as shown in Figure 4, which indicates that it is difficult to steer the social evolution to a desired direction. The parameters are k₁ = 2, k₂ = 1, θ = 2, ϵ = 2, P₁ = 0.5, and the x − n phase diagram can be found in Figure 1. The final evolutionary direction, to some extent, can be significantly affected by “randomness” or “luckiness” in real-world practice: both a tiny disturbance in public opinion environment given a certain fraction of cooperators (Figure 4A) and a tiny disturbance in the fraction of cooperators given a certain level of environment (Figure 4B) could change the evolutionary directions of the dynamical system.

FIGURE 4

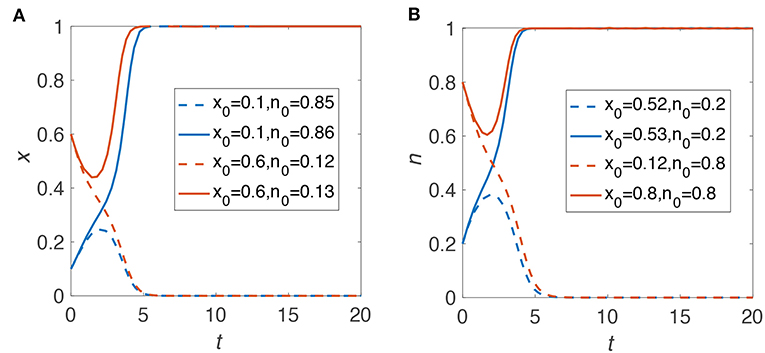
Figure 4. Emergence of bifurcation phenomena: sensitivity to initial conditions. The existence of interior saddle points in x − n system can lead to “randomness” in real-world practice: either (A) a small disturbance in initial public opinion environment given a certain level of initial cooperation, or (B) a small disturbance in initial fraction of cooperators given a certain initial environment could change the evolutionary directions of the dynamical system. Parameters: k₁ = 2, k₂ = 1, θ = 2, ϵ = 2, P₁ = 0.5.

These dynamical properties just highlight the importance of the interior saddle point. We further analyze how our model parameters affect the position of the interior saddle point (x^*, n^*), which determines the attraction basin of the two stable equilibriums [(0, 0) and (1, 1)]. Generally, a larger x^* or n^* indicates that more initial cooperators or a more supportive initial environment is needed for successfully promoting the new cognition. According to equation 6, x^* is only influenced by θ, the relative strength of enhancing the environment by cooperators vs. decreasing the environment by defectors. Obviously, x^* increases as θ decreases, calling for more cooperators participating the social innovation if each of them has less impact. On the other hand, n^* is influenced by four parameters: θ, P₁, k₁ and k₂. It is easy to see that n^* increases as θ increases or P₁ decreases, whereas k₁ and k₂ have more complicated influence. The formula of n^* can be rewritten as

\begin{array}{l} n^{*} = \frac{θ}{1 + θ} + \frac{\frac{1 - θ}{1 + θ} k_{2} - P_{1}}{k_{1} + 2 k_{2}} & (7) \end{array}

Therefore, (i) when $P_{1} < \frac{1 - θ}{1 + θ} k_{2}$ , n^* increases as k₁ decreases; (ii) when $P_{1} = \frac{1 - θ}{1 + θ} k_{2}$ , $n^{*} = \frac{θ}{1 + θ}$ ; (iii) when $P_{1} > \frac{1 - θ}{1 + θ} k_{2}$ , n^* increases as k₁ increases. Similarly, we have

\begin{array}{l} n^{*} = \frac{1}{2} + \frac{\frac{θ - 1}{2 (1 + θ)} k_{1} - P_{1}}{k_{1} + 2 k_{2}} & (8) \end{array}

Hence, (i) when $P_{1} < \frac{θ - 1}{2 (1 + θ)} k_{1}$ , n^* increases as k₂ decreases; (ii) when $P_{1} = \frac{θ - 1}{2 (1 + θ)} k_{1}$ , $n^{*} = \frac{1}{2}$ ; (iii) when $P_{1} > \frac{θ - 1}{2 (1 + θ)} k_{1}$ , n^* increases as k₂ increases.

Furthermore, we show the impact of the relative feedback speed in Figure 5. We fix k₁ = 2, k₂ = 1, θ = 2, P₁ = 0.5, and change ϵ = 0.1, 3, 20 from Figures 5A–C. Aside from changing the convergence speed of the dynamical system, we find the relative feedback speed can also influence the attraction basin of the two stable states, though not affecting the position of interior saddle point. A larger ϵ gives advantage to the environmental feedback compared to the strategy dynamics, resulting in the occurrence of more steep trajectories.

FIGURE 5

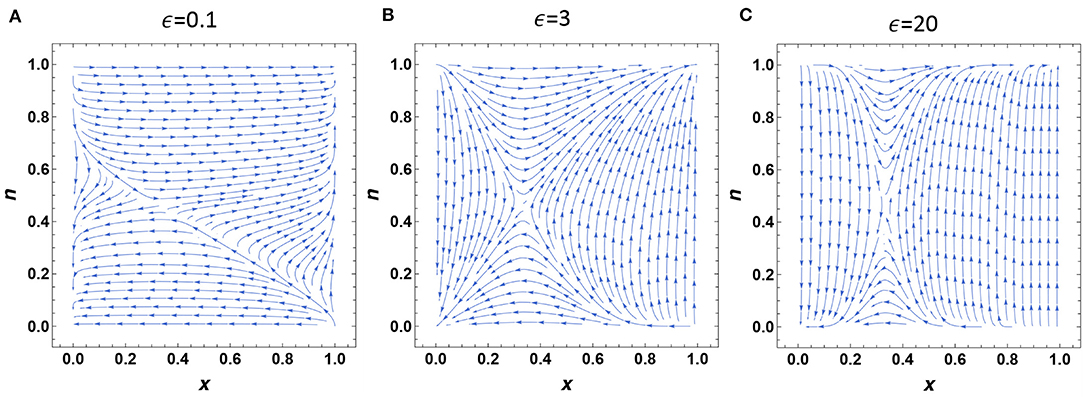
Figure 5. Effects of the relative feedback speed. We fix k₁ = 2, k₂ = 1, θ = 2, P₁ = 0.5, and change ϵ = 0.1, 3, 20 in (A–C), respectively.

3.3. Impact of Stochastic Environmental Fluctuations

While the power of external stochasticity (via direct disturbance on either strategy or environment) has been stressed in Figure 4, it is meaningful to further explore the influence of systematic stochasticity on our deterministic model. Here, we consider a simple stochastic fluctuation embedded in environmental evolution, which is given by

\begin{array}{l} \dot{n} = ϵ n (1 - n) ((θ x - (1 - x)) + ϕ_{T} (δ)) & (9) \end{array}

where ϕ_T(δ) = δ or −δ with the same probability 0.5 at each time interval [T, T + 1), T ∈ {0, 1, 2, ...}, and δ > 0 describes the relative fluctuation speed of the environment.

In Figure 6, we study the impact of stochastic environmental fluctuations in two scenarios: (i) the initial state (x₀, n₀) = (0.1, 0.84) is close to the boundary of the two attraction basins (Figures 6A–C), or (ii) the initial state (x₀, n₀) = (0.1, 0.7) locates inside the attraction basin of (0, 0) and is relatively far away from the boundary (Figures 6D–F). Note that the actual changing speed of the environment caused by the systematic stochasticity at time t can be calculated by ϵn_t(1 − n_t)ϕ_t(δ), which is small under all our parameters. In scenario (i), we find that even a tiny stochastic fluctuation is capable of changing the co-evolutionary direction, i.e., driving the x − n system toward (1, 1) instead of (0, 0). In addition, a larger δ significantly promotes such changes, bring about more (1, 1) states when system becomes stable. In scenario (ii), however, the final evolutionary results can be changed only when δ is large enough.

FIGURE 6

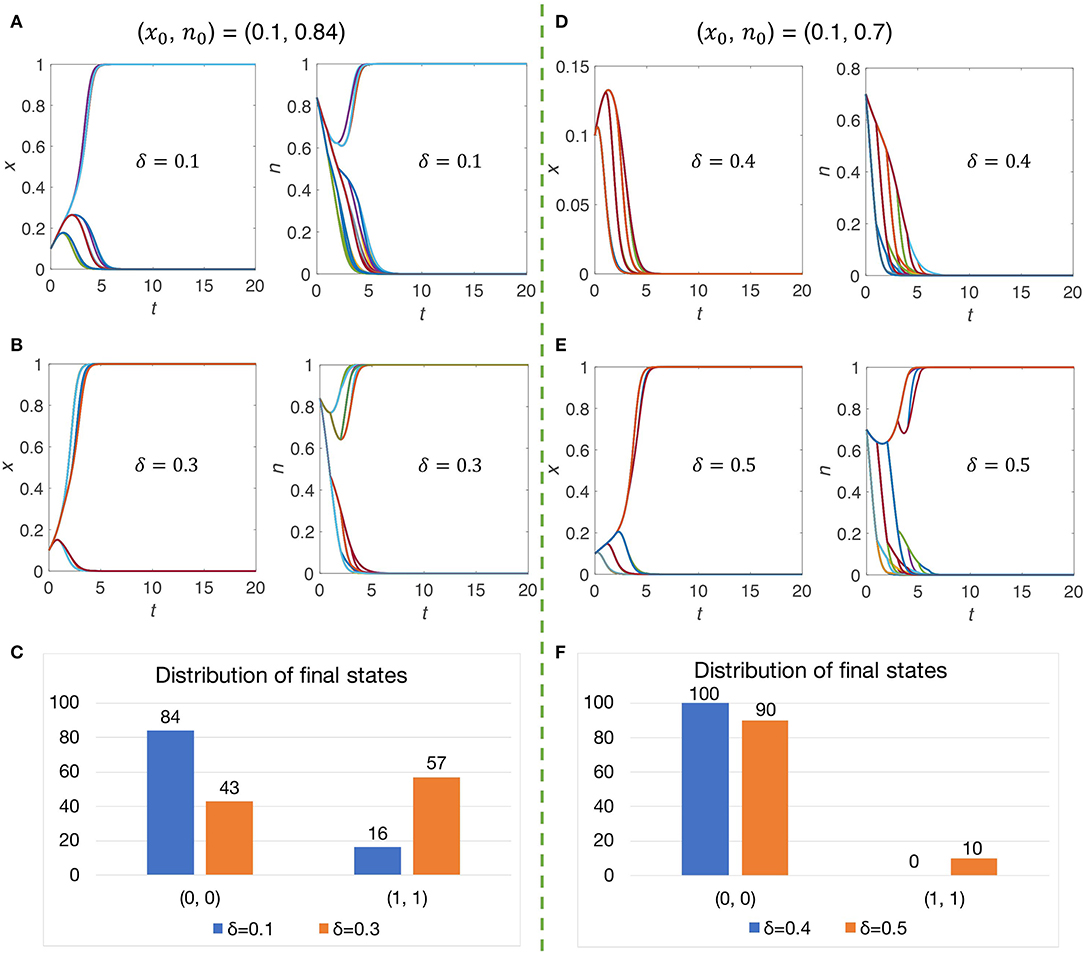
Figure 6. Evolutionary dynamics under the influence of stochastic environmental fluctuations. (A,B) and (D,E) show time evolutions of strategies and the environment under different fluctuation speeds [δ = 0.1, 0.3 for (A,B) and δ = 0.4, 0.5 for (D,E)] and different initial conditions [(x₀, n₀) = (0.1, 0.84) for (A,B) and (x₀, n₀) = (0.1, 0.7) for (D,E)]. Each subfigure presents result of 100 independent runs. Panels (C,F) provide distributions of the final states corresponding to (A,B) and (D,E), respectively. Other parameters for all subfigures: k₁ = 2, k₂ = 1, θ = 2, ϵ = 2, P₁ = 0.5.

4. Conclusions and Discussions

Evolutionary game theory is an effective approach to study the incentive-driven dynamical evolutions, where different strategies “compete” for a higher payoff in order to survive in the natural systems [48, 49]. In particular, recent advance highlights the importance of coupled interactions between strategies and external environment [50]. The strategy-dependent environmental feedbacks give rise to the oscillating dynamics of both cooperation and environment states, which provides profound insights toward many important issues, such as overexploitation problem [51], social distancing behavior during COVID-19 pandemic [31], vaccine refusal [52–54], etc. Further studies show that such co-evolution could lead to the emergence of persistent cooperation if the relative feedback speed exceeds a threshold, breaking the tragedy of the commons in traditional public goods game [55]. Despite the progress, few works have extended this powerful theoretical framework to the field of cognition (information, beliefs, ideas, behaviors, etc.) evolution. Specifically, it remains largely unknown how public opinion environment influences the competition of two opposite cognitions, which is ubiquitous and is of vital importance in a polarizing society [56].

In this paper, we introduce this co-evolutionary game theory into our new model to study the dynamics of feedback loops between competitive cognitions and public opinion environment. We find that when the inherent payoff or loss from the new cognition exceeds a critical value with regard to the environmental impact, individuals will neglect the feedbacks from public opinion and the population will be dominated by one cognition regardless of initial conditions. Otherwise, a saddle point occurs in the system and both cooperation (the new cognition) domination with a fully supportive environment and defection (the old cognition) domination with a fully unsupportive environment are stable states. Under this circumstance, the final result of the competition depends on the parameters and initial conditions. A further exploration on dynamical patterns under the existence of interior saddle point is also performed. Results unveil the sensitivity of the system to tiny disturbance in some areas, indicating that the eventual evolutionary direction of the competitive cognition sometimes might be determined by “randomness” or “luckiness” in real world. Similar phenomena are also observed when a simple systematic stochastic fluctuation is considered in the environmental evolution. Finally, we show that the relative feedback speed not only influences the convergence speed, but also changes the attraction basin of the two stable states.

A noteworthy limitation of our work is that our model cannot reproduce the possible stable state where the two cognitions both survive. Previous works have revealed many mechanisms that contribute to the coexistence in competitive dynamics or the emergence of persistent cooperation, such as the existence of inactive individuals [57], the network structures [58–62], the homogeneous trends [26], etc. [63–68]. Further studies may consider the incorporation of these influential factors based on our heuristic modeling framework.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

HL conceived the project. XW conceived the model. HL, XW, and LL performed the analysis and wrote the paper. ZL provided funding and supervised the research. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the National Natural Science Foundation of China (Grant Nos. U1636211, 61672081, 61370126), and the Fund of the State Key Laboratory of Software Development Environment (Grant No. SKLSDE-2019ZX-17).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.658130/full#supplementary-material

References

1. Vespignani A. Modelling dynamical processes in complex socio-technical systems. Nat Phys. (2012) 8:32–9. doi: 10.1038/nphys2160