Predicting Motion Patterns Using Optimal Paths

The ability to navigate safely and efficiently through a given landscape is relevant for any intelligent moving object. Examples range from robotic science and traffic analysis, to the behavior within an ecosystem. Many objects tend to move in patterns depending on their nature. By establishing models of patterns of motion one may estimate the future motion within an area. We propose here a method for detecting regular patterns of motion by modeling the environment as an energy landscape, and locating optimal paths through it. As an example, we use maritime position Automatic Identification System (AIS) data as input to work out optimal routes between different start and end points when these are not located along the standard shipping lanes. These initial tests show that the method has potential for analyzing and determining regular patterns of motion.

1 Introduction

Imagine a large town square. The square has fixed structures such as fountains etc. that block direct pathways across it. It is a busy place where many pass across it in all directions. Cameras have been set up that record the motion of people across the town square. The question we will address in this paper is the following: Based on the recordings, is it possible to predict the motion of a single person from some start point A to some end point B across the town square, even when the points A and B are not located along the typical paths that people use across the square. This question has since long been posed in different contexts [1]. Examples range from the behavior of ecosystems to robotic navigation and traffic systems. A predator needs to account for the future motion of its prey in order to catch it, just as a ship needs to consider the future positions of other ships to avoid collisions [2].

Moving objects are influenced by both the landscape in which they move, as well as other objects, moving or not, within the same area [3–5]. There are several different ways to approach motion prediction. The most straight forward approach is to predict the motion of each object in a system individually, by assigning to each object a position as a function of time [6]. However, for large systems, this method would produce a large number of coupled equations. Hence, this approach would be unproductive in this case. A better approach is to exploit the fact that objects tend to move in patterns [3, 7]. Depending on their nature and surroundings, moving objects tend to move in regular patterns. By establishing a model of these motion-patterns in a given area, one may use the pattern itself when predicting future motion. This is the core idea of our approach.

When applying methods of pattern recognition to motion prediction, the process typically operates in two stages. The first stage is the actual pattern recognizing, which learns the regular patterns of motion using a set of training data. The next stage applies the learned pattern to predict the future motion. Further, this two-stage process may be grouped into two main groups of techniques; Grid-based techniques and cluster-based techniques [3].

The grid-based techniques are derived from the occupancy grid concept [8]. That is, the landscape is modeled as a grid and transition probabilities between the cells are calculated from the training data. The grid is then used directly for motion prediction. Grid-based techniques are frequently used in robot navigation systems [9–11].

Cluster-based techniques on the other hand, apply statistical decision tools in order to group similar trajectories into representative clusters. Several different clustering techniques exists, the Expectation-Maximization approach [12] is considered to be the state of the art [3]. Future motion of a moving object is then estimated as the representative cluster which the given route is most likely to belong to.

In this paper, we propose a dynamic grid-based technique for learning motion patterns by mapping it onto the optimal paths in a disordered landscape problem [13, 14]. We describe this problem as follows. Imagine a plane and that $\overrightarrow{x}$ is a point on this plane. There is a stochastic field $e\left(\overrightarrow{x}\right)$ associated with the plane. We choose a path $\mathcal{P}$ through the plane starting at point ${\overrightarrow{x}}_A$ and ending at point ${\overrightarrow{x}}_B$. We integrate the field $e\left(\overrightarrow{x}\right)$ along the path $\mathcal{P}$,

$E_{\mathcal{P}}={\displaystyle {\int }_{\overrightarrow{x}\in \mathcal{P}}e\left(\overrightarrow{x}\right)}\text{d}\overrightarrow{x}\text{.}(1)$

The optimal path is found by the minimization

$E_{\mathcal{O}}=\underset{\mathcal{P}}{\text{min}}{E}_{\mathcal{P}}=\underset{\mathcal{P}}{\text{min}}{\displaystyle {\int }_{\overrightarrow{x}\in \mathcal{P}}e\left(\overrightarrow{x}\right)\text{d}\overrightarrow{x}}\text{.}(2)$

This problem has produced a large body of work within the statistical physics community. It is also closely related to the optimal path problem which is central in a large number of applications and fields [15–18].

The central idea we present in this paper is to relate the function $e\left(\overrightarrow{x}\right)$ to the inverse of the density earlier paths raised to some power. We then identify the optimal path from ${\overrightarrow{x}}_A$ to ${\overrightarrow{x}}_B$ through this landscape.

We apply this idea to vessel traffic, using marine automatic identification system coordinates. We transform the coordinates to a dimensionless area and introduce a grid over the area. We associate each grid point with the local density of AIS coordinates. We implement the optimal paths through the area using the iterative algorithm of Hansen and Kertész [19, 21], but any other algorithms may be used, e.g., the Bellman-Ford or the Dijkstra algorithms [22–24].

We emphasize that we are not attempting here to present a fully implementable algorithm ready to be used on ships. Rather, this is a feasibility study testing whether the central ideas may work.

We note that optimal paths have been used earlier in connection with marine motion prediction [20]. However, the paths in this case are optimized with respect to length. This is a very different concept than what we present here.

We organize this paper as follows. Section 2 describes the method we propose. In Section 3, we implement the method for marine AIS data. We end by a brief summary and discussion.

2 Algorithm

We now describe how we transform the AIS coordinates, given in terms of continuous longitude and latitude, into grid points. We then go on to describe the concept of optimal paths in this context and the algorithm used to extract it. Lastly, we describe how we turn this into path prediction.

2.1 From Automatic Identification System Coordinates to Grid

The automatic tracking system AIS uses tranceivers to allow ships to view surrounding marine traffic and to be seen themselves. It provides, among other services, a record of the position as a function of time for the equipped vessels passing through the area. This includes most large vessels.

We define our area of interest as the rectangle defined by the corners given by the longitudinal and latitudinal coordinates ${\text{long}}_{\min }$, ${\text{long}}_{\text{max}}$, ${\text{lae}}_{\text{min}}$ and ${\text{lae}}_{\text{max}}$. A given ship at a given time is at position $\left({\text{long}}_k,{\text{lae}}_k\right)$ where the subscript refers to the position record (i.e., which ship and at what time). We introduce dimensionless Cartesian coordinates to describe its position, $x_k\in \left\{0,N-1\right\}$ and $y_k\in \left\{0,N-1\right\}$, where N is an integer, given by

$x_k=\frac{{\text{long}}_k-{\text{long}}_{\text{min}}}{{\text{long}}_{\text{max}}-{\text{long}}_{\text{min}}}\left(N-1\right)\text{,}(3)$

and

$y_k=\frac{{\text{lae}}_k-{\text{lae}}_{\text{min}}}{{\text{lae}}_{\text{max}}-{\text{lae}}_{\text{min}}}\left(N-1\right)\text{.}(4)$

The position of a given ship at a given time k at $\left(x_k,y_k\right)$ is then located within grid cell defined by the corner nodes $i_k^1\text{mod}\left(x_k\right)$, $i_k^2\text{mod}\left(x_k\right)+1$, $j_k^1\text{mod}\left(y_k\right)$ and $j_k^2\text{mod}\left(y_k\right)+1$. In order to construct a path density defined at the nodes $\left(i,j\right)$, ${\rho }_{i,j}$, we assign a weight to the position of ship position and time k, $\left(x_k,y_k\right)$ distributed among the four corned nodes $\left(i_k^1,j_k^1\right)$, $\left(i_k^2,j_k^1\right)$, $\left(i_k^2,j_k^2\right)$ and $\left(i_k^1,j_k^2\right)$. If $r_{i_k^1,j_k^1}$ is the distance between $\left(x_k,y_k\right)$ and $\left(i_k^1,j_k^1\right)$, and likewise for $r_{i_k^2,j_k^1}$, $r_{i_k^2,j_k^2}$ and $r_{i_k^1,j_k^2}$, we define

$R_{x_k,y_k}=r_{i_k^1,j_k^1}+r_{i_k^2,j_k^1}+r_{i_k^2,j_k^2}+r_{i_k^1,j_k^2}\text{.}(5)$

We define the weights

$\begin{array}{l}{W}_{i_k^1,j_k^1}=\frac{1}{3R_{x_k,y_k}}\left(R_{x_k,y_k}-r_{i_k^1,j_k^1}\right)\text{,}\\ W_{i_k^2,j_k^1}=\frac{1}{3R_{x_k,y_k}}\left(R_{x_k,y_k}-r_{i_k^2,j_k^1}\right)\text{,}\\ W_{i_k^2,j_k^2}=\frac{1}{3R_{x_k,y_k}}\left(R_{x_k,y_k}-r_{i_k^2,j_k^2}\right)\text{,}\\ W_{i_k^1,j_k^2}=\frac{1}{3R_{x_k,y_k}}\left(R_{x_k,y_k}-r_{i_k^1,j_k^2}\right)\text{.}\end{array}(6)$

The path density may then be defined as

${\rho }_{i,j}={\displaystyle \sum _{k=1}^K{W}_{i_k,j_k}}\text{,}(7)$

when K is the number of position recordings within the grid cell.

We now associate a weight with node $\left(i,j\right)$,

$e_{i,j}=\{\begin{array}{cc}{\rho }_{i,j}^{-\alpha },& \text{if}{\rho }_{i,j}>0\text{,}\\ m,& \text{if}{\rho }_{i,j}=0\text{,}\\ M,& \text{if}\left(i,j\right)\text{is}\text{on}\text{land,}\end{array}(8)$

where α is an adjustable parameter controlling the magnitude of the fluctuations of $e_{i,j}$: if $\alpha \to 0$ the fluctuations are smoothened out and disappear when $\alpha =0$ as all nodes then are assigned the same weight. The parameter m is chosen so that there is a balance between the tendency for a path to follow the normal shipping lanes (where ${\rho }_{i,j}$ is large) and a path being as short as possible. The other value $M\gg m$ ensures that no paths crosses land.

The last step in setting up the system is to assign weights to the links between neighboring nodes. Let the node $\left(i_{nn},j_{nn}\right)$ be one of the four nearest neighbors of node $\left(i,j\right)$. Then, the link between them is given the weight

$e_{i,j;i_{nn},j_{nn}}=\frac{1}{2}\left(e_{i,j}+e_{i_{nn},j_{nn}}\right)\text{.}(9)$

We also allow for diagonal paths. The link between node $\left(i,j\right)$ and its diagonal neighbors $\left(i_{nn},j_{nn}\right)$ as

$e_{i,j;i_{nn},j_{nn}}=\frac{\sqrt{2}}{2}\left(e_{i,j}+e_{i_{nn},j_{nn}}\right),(10)$

where the factor $\sqrt{2}$ is introduced to take into account the additional length of the diagonal edges.

2.2 Optimal Path Construction

We define a path $\mathcal{P}$ between two nodes A at $\left(i_A,j_A\right)$ and B at $\left(i_B,j_B\right)$ as a continuous chain of neighboring links linking the two nodes. We associate a weight of the path in the same way as in Eq. 1,

$E_{\mathcal{P}}={\displaystyle \sum _{\left(i,j\right)\in \mathcal{P}}{e}_{i,j;i_{nn},j_{nn}}}\text{.}(11)$

The optimal path is then

$E_{\mathcal{O}}=\underset{\mathcal{P}}{\text{min}}{E}_{\mathcal{P}}=\underset{\mathcal{P}}{\text{min}}{\displaystyle \sum _{\left(i,j\right)\in \mathcal{P}}{e}_{i,j;i_{nn},j_{nn}}}\text{.}(12)$

We will in the following assume that both nodes A and B lie on the edges of the grid. In order to identify the optimal path, we use the algorithm of Hansen and Kertész [19]. It consists of two main steps; first an initialization and then an updating process. A variable $e_{i,j}$ is assigned to each node. For the nodes on the edges of the grid, the values $e_{i,j}$ stay fixed, while it is updated for the internal nodes iteratively. The iteration algorithm for the internal nodes is

$e_{i,j}\to e_{i,j}=\underset{i_{nn},j_{nn}}{\text{min}}\left(e_{i,j;i_{nn},j_{nn}}+e_{i_{nn},j_{nn}}\right)\text{.}(13)$

After M iterations, the variable $e_{i,j}$ will contain the sum of the weights along the optimal path starting at node $\left(i,j\right)$ of length M. The end point of the optimal path is not specified. Furthermore, the optimal path may curl up on itself, creating a tadpole configuration.

Consider now a node $\left(i_A,j_A\right)$ on the boundary of the grid. In order to find the optimal path from an internal node $\left(i,j\right)$ to $\left(i_A,j_A\right)$, we set the value $e_{i_A,j_A}$ to zero, while for the remaining boundary nodes the value $e_{i_c,j_c}$ is set to a very large positive value. The updating process for the internal nodes is carried out according to Eq. 13, until all values $e_{i,j}$ no longer change. At this point, the value of $e_{i,j}$ contains the value of $E_{\mathcal{O}}=E_{i,j;i_A,j_A}$ along the optimal path between nodes $\left(i,j\right)$ and $\left(i_A,j_A\right)$.

We now choose another boundary node $\left(i_B,j_B\right)$ as end point for the optimal paths. Hence, we fix $e_{i_B,j_B}=0$ and fix all the other boundary nodes to a large positive value, including boundary node $\left(i_A,j_A\right)$. The internal node values are initially set to zero, $e_{i,j}=0$. We then iterate according to Eq. 13. When numbers no longer change, $e_{i,j}$ will contain $E_{i,j;i_B,j_B}=E_{\mathcal{O}}$ for the optimal path between nodes $\left(i,j\right)$ and $\left(i_B,j_B\right)$.

We may now combine the optimal paths starting at boundary node $\left(i_A,j_A\right)$ and ending at internal node $\left(i,j\right)$ with the optimal path starting at internal node $\left(i,j\right)$ and ending at boundary node $\left(i_B,j_B\right)$. The optimal weight $E_{\mathcal{O}}$ for this combined path is then given by,

$E_{i_A,j_A;i,j;i_B,j_B}=\underset{i_{nn},j_{nn}}{\text{min}}\left(E_{i_A,j_A;i,j}+e_{i,j;i_{nn},j_{nn}}+E_{i_{nn},j_{nn};i_B,j_B},E_{i_A,j_A;i_{nn},j_{nn}}+e_{i_{nn},j_{nn};i,j}+E_{i,j;i_B,j_B}\right).(14)$

Associating each internal node $\left(i,j\right)$ with the value $e_{i,j}=E_{i_A,j_A;i,j;i_B,j_B}$ leads to the construction of a pathscape [21]. The optimal path between edge nodes $\left(i_A,j_A\right)$ and $\left(i_B,j_B\right)$ is the sequence of nodes associated with the smallest $e_{i,j}$ values. There will then be a sequence of nodes having the second smallest values $e_{i,j}$. This sequence will branch out from the globally optimal path as some node, to rejoin it at a different node along the path. Then there will be sequence with the third smallest values $e_{i,j}$ branching off and rejoining nodes belonging to the two paths containing the two smaller $e_{i,j}$—and so on. Each internal node will belong to some path in this hierarchy.

2.3 Predicting Paths

We now focus our attention on pathscapes where boundary nodes $\left(i_A,j_A\right)$ and $\left(i_B,j_B\right)$ are placed along different edges. There are $6N^2$ possible combinations. It may be convenient to coarse grain the end points of the optimal paths. Hence, we divide each edge into intervals of length $L_I$. This means that we set the weight of all the edge nodes nodes $\left({i^{\prime }}_A,{j^{\prime }}_A\right)$ belonging to the interval, $e_{i_{A\text{'}},j_{A\text{'}}}=0$. The pathscape will then consist of all optimal paths starting somewhere in the first interval, $\left({i^{\prime }}_A,{j^{\prime }}_A\right)$, passing through internal node $\left(i,j\right)$ and then ending at a node $\left(i_{B\text{'}},j_{B\text{'}}\right)$ somewhere in the end interval. Hence, the number of pathscapes is then reduced from $6N^2$ to $6n^2$, where $n=N/L_I$.

Suppose the optimal path $\left(i_{A\text{'}},j_{A\text{'}};i,j;i_{B\text{'}},j_{B\text{'}}\right)$ has a length $L_{i_{A\text{'}},j_{A\text{'}};i,j;i_{B\text{'}},j_{B\text{'}}}$ and a weight $E_{i_{A\text{'}},j_{A\text{'}};i,j;i_{B\text{'}},j_{B\text{'}}}$. Using the weight alone in predicting paths does not function well since a short path through a high-weight region may be as optimal as a longer path through a low-weight region. We therefore renormalize the weights, $E_{i_{A\text{'}},j_{A\text{'}};i,j;i_{B\text{'}},j_{B\text{'}}}\to E{\text{'}}_{i_{A\text{'}},j_{A\text{'}};i,j;i_{B\text{'}},j_{B\text{'}}}$ by setting

$E{\text{′}}_{i_{A^{\prime }},j_{A^{\prime }};i,j;i_{B\text{'}},j_{B^{\prime }}}=C_p\frac{E_{i_{A^{\prime }},j_{A^{\prime }};i,j;i_{B^{\prime }},j_{B^{\prime }}}}{{\left(L_{i_{A^{\prime }},j_{A^{\prime }};i,j;i_{B^{\prime }},j_{B^{\prime }}}\right)}^{\beta }}\text{,}(15)$

where β is an adjustable parameter. The constant $C_p$ is introduced to further separate between different optimal paths. We note that higher β makes longer paths more favorable.

3 Analysis of Two Automatic Identification System Patterns

We denote the two AIS sets we consider in the following A and B. Figures 1, 2 show the two areas and the subsets that we use in our analysis. Both subsets, shown in Figures 1B, 2B, have size 100 × 100 and where each grid block has size 100 × 100 m² (area A) and 1000 × 1000 m² (area B). We see that A has a simpler structure than B, consisting of two vertical clusters, while B includes multiple clusters with different orientation. By “cluster” we mean an area with high density of position recordings.

FIGURE 1

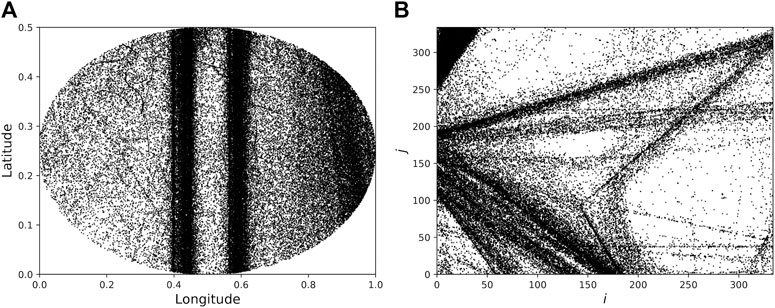
FIGURE 1. (A) Data set A showing AIS position recordings with positions in degrees relative to the origin. (B) A selected subset of area A spanning ${0.3}^{\circ }$ in both the longitudinal and latitudinal directions, transformed into a grid of dimensions 334 × 334 with grid size 100 × 100 m².

FIGURE 2

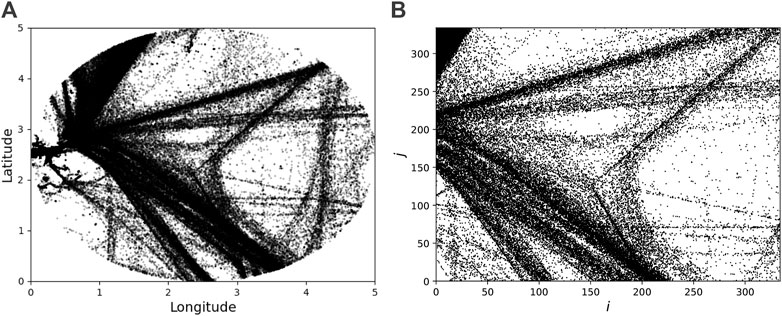
FIGURE 2. (A) Data set B showing AIS position recordings with positions in degrees relative to the origin. (B) A selected subset of area B spanning $3^{\circ }$ in both the longitudinal and latitudinal directions, transformed into a grid of dimensions 334 × 334 with cell size 1000 × 1000 m².

We now consider area A. Setting parameter $\beta =0$ in Eq. 15, we show in Figure 3 the optimal path between the lower left and upper right corners of the grid 1b for different values of α.

FIGURE 3

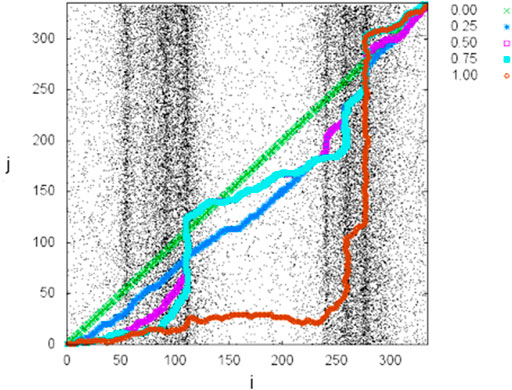
FIGURE 3. Optimal paths between the lower left and upper right corner of the grid in Figure 1B for $\alpha =0$, 0.25, 0.50, 0.75 and 1. The parameter β, defined in Eq. 15 was set to zero.

We show in Figure 4 the length of the optimal path between the lower left and upper right corner in Figure 3 for different values of α and with $\beta =0$, $L_{\mathcal{O}}$. We note that $L_{\mathcal{O}}$ is approximately linear in α for $\alpha <0.75$, at which there is a jump.

FIGURE 4

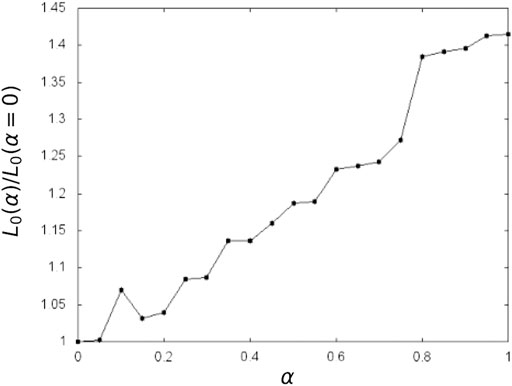
FIGURE 4. The length of the optimal paths, $L_{\mathcal{O}}$ between the lower left and upper right corner of III as a function of α, while keeping $\beta =0$.

Turning to area B, we show in Figure 5 the optimal paths starting from the lower left corner and ending at the upper right corner of the grid shown in Figure 2B as a fuction of α while keeping $\beta =0$.

FIGURE 5

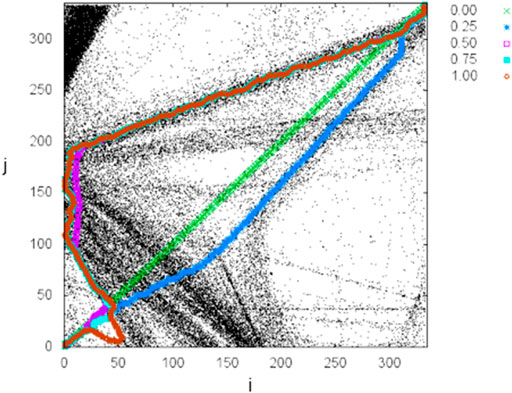
FIGURE 5. Optimal paths between the lower left and upper right corner of the grid in Figure 2B for $\alpha =0$, 0.25, 0.50, 0.75 and 1. The parameter β, defined in Eq. 15 was set to zero.

We show in Figure 6 the length of the optimal path between the lower left and upper right corner in Figure 5 for different values of α and $\beta =0$. As in Figure 4 for area A, we find a jump in the length of the optimal paths for a given value of α, here $\alpha \approx 0.4$. However, there are clearly defined plateaus in the optimal path length, e.g., for $0.05<\alpha <0.4$.

FIGURE 6

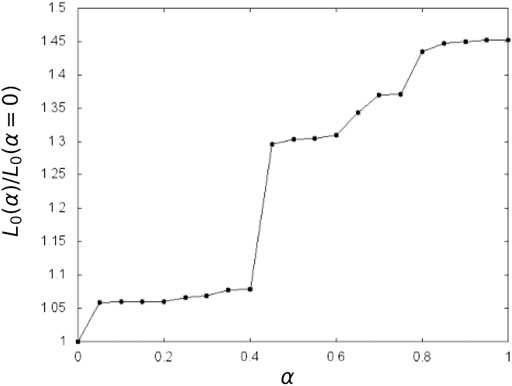
FIGURE 6. The length of the optimal paths, $L_{\mathcal{O}}$ between the lower left and upper right corner of V as a function of α, while keeping $\beta =0$.

We now introduce intervals $L_I$ as described in Section C. We consider first a more coarse grained section of area A, covered by a grid of size 148 × 148 with grid size 100 × 100 m². We divide each edge into two sections. Figure 7A shows the two most optimal paths in this system. In Figure 7B, we show the five most optimal paths. We see in Figure 7B that several of the five optimal paths overlap considerably, creating an impression that there are fewer paths in the figure than there is in reality.

FIGURE 7

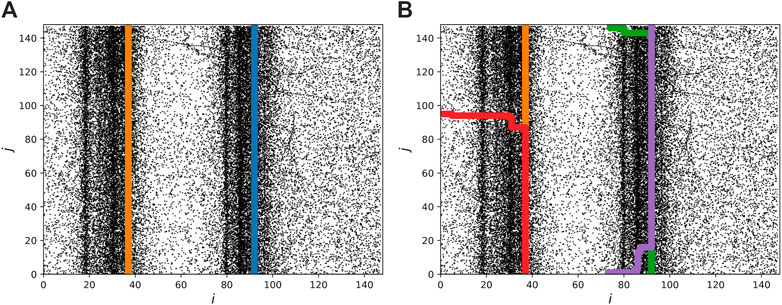
FIGURE 7. Area A: (A) The two most optimal paths between the intervals along different edges. (B) The five most optimal paths between different edges. Each edge has been divided into two intervals, and fixing $\alpha =0.8$, and $\beta =0.8$.

Figure 8 shows the ordered sequence of weights $E{\text{'}}_{\mathcal{O}}$ for the optimal paths in Figure 7. We see that the weights of the first five paths is quite similar, whereas from the sixth and onwards, it is significantly higher. Generating this flat region is accomplished by adjusting β and it signifies that these optimal paths are equally good.

FIGURE 8

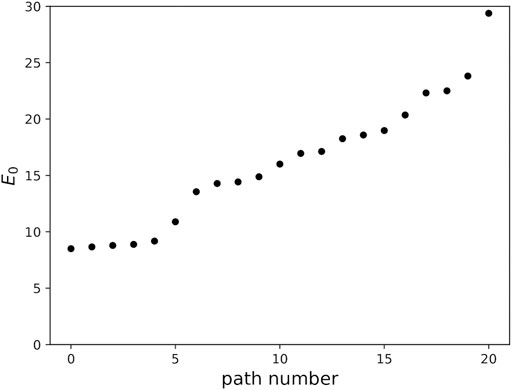
FIGURE 8. The weight $E_{\mathcal{O}}$ ranging from the most optimal (No. 0) to the least optimal (No. 20) for paths between intervals on different edges as shown in Figure 7.

We do the same construction as in Figure 7 for area B in Figure 9. We divide the edges into three intervals and choose the values $\alpha =0.08$ and $\beta =0.8$ for the two adjustable parameters.

FIGURE 9

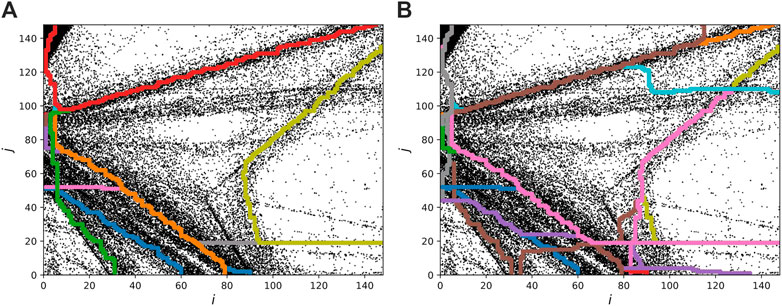
FIGURE 9. Area B: Here the grid has been divided into three segments along each edge. In (A) we show the 24 most optimal paths and in (B) we show the 48 most optimal paths. We fixed the parameter values to $\alpha =0.08$ and $\beta =0.8$.

Figure 10 shows the ascending sequence of renormalized weights $E{\text{'}}_{\mathcal{O}}$ for the two cases shown in Figures 9A,B. We find 48 optimal paths with slowly increasing weights before it jumps to a much higher value.

FIGURE 10

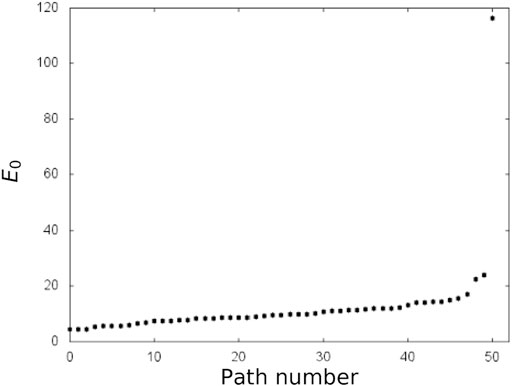
FIGURE 10. The weight $E_{\mathcal{O}}$ ranging from the most optimal (No. 0) to the least optimal (No. 50) for paths between intervals on different edges as shown in Figure 9.

Figure 9 shows the same area as in Figure 5. We have here divided the edges into three intervals. The weight of the 50 most optimal paths is shown if Figure 10. As in the much simpler pucture in Figure 7, there is also in this case considerable overlap between the optimal paths.

4 Discussion and Conclusion

We have in this paper introduced a method to predict motion in an area based on earlier motion in the same region. That is, given the history of traffic in the area, what would be the most likely path a new traveler would take between positions A and B, even if these positions are outside the usual routes of travel in the area. The method is based on the concept of optimal paths through a landscape formed by the paths taken earlier. It is a dynamic method as each new trajectory taken in the area is added to the history.

We have tested the method on marine Automatic Identification System (AIS) data. From a visual point of view, the method locates the motion patterns efficiently in both the simple case we studied (A) and in the more complex traffic picture (B). However, a proper performance test has not been performed. Further, the results showed that sectioning the edges into only a few intervals, were enough to generate a good estimate of the pattern. As all the grid nodes along the edges, may be represented by only a few intervals, with a short running time of the algorithm. The grid dimension and size of the cells does not seem to influence the results that are found.

This work shows that the method we propose manages to identify sensible paths that optimize between path length and frequency of use—two seemingly very different quantities. In order to turn this into a practical method, much more work is needed, e.g. with respect to the cluster identification, grid construction, type of vessel (if it is to be implemented as a marine tool).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

MF did the numerical work based on an idea by AH. MF write the first draft of the manuscript. AH wrote the second version.

Funding

This work was partly supported by the Research Council of Norway through its Centers of Excellence funding scheme, project number 262644.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Hirakawa T, Yamashita T, Tamaki T, Fujiyoshi H, Umezu Y, Takeuchi I, et al. Can AI Predict Animal Movements? Filling Gaps in Animal Trajectories Using Inverse Reinforcement Learning. Ecosphere (2018) 9:e02447. doi:10.1002/ecs2.2447

CrossRef Full Text | Google Scholar

2. Pallotta G, Vespe M, Bryan K. Vessel Pattern Knowledge Discovery from AIS Data: A Framework for Anomaly Detection and Route Prediction. Entropy (2013) 15:2218–45. doi:10.3390/e15062218

CrossRef Full Text | Google Scholar

3. Vasquez D, Fraichard T. Motion Prediction for Moving Objects: A Statistical Approach. Proc ICRA’04, IEEE (2004) 4:3931–6. doi:10.1109/ROBOT.2004.1308883

CrossRef Full Text | Google Scholar

4. Martinez J, Black MJ, Romero J. On Human Motion Prediction Using Recurrent Neural Networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2017). p. 2891–900.

Google Scholar

5. González D, Pérez J, Milanés V, Nashashibi F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE Trans Intell Transport Syst (2016) 17:1135–45. doi:10.1109/TITS.2015.2498841

CrossRef Full Text | Google Scholar

6. Zhu Q. A Stochastic Algorithm for Obstacle Motion Prediction in Visual Guidance of Robot Motion. In: IEEE International Conference on Systems EngineeringIEEE (1990). doi:10.1109/ICSYSE.1990.203136

CrossRef Full Text | Google Scholar

7. Weiming Hu W, Xuejuan Xiao X, Zhouyu Fu Z, Xie D, Tieniu Tan T, Maybank S. A System for Learning Statistical Motion Patterns. IEEE Trans Pattern Anal Mach Intell (2006) 28:1450–64. doi:10.1109/TPAMI.2006.176

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Elfes A. Using Occupancy Grids for mobile Robot Perception and Navigation. Computer (1989) 22:46–57. doi:10.1109/2.30720

CrossRef Full Text | Google Scholar

9. Tadokoro S, Hayashi M, Manabe Y, Nakami Y, Takamori T. Motion Planner of mobile Robots Which Avoid Moving Human Obstacles on the Basis of Stochastic Prediction. Intell Syst 21st Century (1995) 4:3286–91. doi:10.1109/ICSMC.1995.538292

CrossRef Full Text | Google Scholar

10. Kruse E, Gutsche R, Wahl FM. Estimation of Collision Probabilities in Dynamic Environments for Path Planning with Minimum Collision Probability. In: Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. IROS’96, 3 (1996). p. 1288–95. doi:10.1109/IROS.1996.568983

CrossRef Full Text | Google Scholar

11. Tanaka K. Detecting Collision-free Paths by Observing Walking People. In: IEEE/RSJ International Conference on Intelligent Robots and Systems, 1 (2002). p. 55–60. doi:10.1109/IRDS.2002.1041362

CrossRef Full Text | Google Scholar

12. Bennewitz M, Burgard W, Thrun S. Learning Motion Patterns of Persons for mobile Service Robots. In: Proceedings 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), 4 (2002). p. 3601–6. doi:10.1109/ROBOT.2002.1014268

CrossRef Full Text | Google Scholar

13. Halpin-Healy T, Zhang Y-C. Kinetic Roughening Phenomena, Stochastic Growth, Directed Polymers and All that. Aspects of Multidisciplinary Statistical Mechanics. Phys Rep (1995) 254:215–414. doi:10.1016/0370-1573(94)00087-J

CrossRef Full Text | Google Scholar

14. Alava M, Duxbury P, Moukarzel C, Rieger H. Combinatorial Optimization and Disordered Systems. In: C Domb, and JL Lebowitz, editors. Phase Transitions and Critical Phenomena, Vol. 18. Amsterdam: Elsevier (2000).

Google Scholar

15. Alur R, La Torre S, Pappas GJ. Optimal Paths in Weighted Timed Automata. In: International Workshop on Hybrid Systems: Computation and Control, 49–62. Berlin: Springer (2001). p. 49–62. doi:10.1007/3-540-45351-2_8

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Xia Q. Optimal Paths Related to Transport Problems. Commun Contemp Math (2003) 05:251–79. doi:10.1142/S021919970300094X

CrossRef Full Text | Google Scholar

17. Gendreau M, Ghiani G, Guerriero E. Time-dependent Routing Problems: A Review. Comput Operations Res (2015) 64:189–97. doi:10.1016/j.cor.2015.06.001

CrossRef Full Text | Google Scholar

18. Yu J, LaValle SM. Planning Optimal Paths for Multiple Robots on Graphs. In: IEEE International Conference on Robotics and Automation (2013). p. 3612–7. doi:10.1109/ICRA.2013.6631084

CrossRef Full Text | Google Scholar

19. Hansen A, Kertész J. Phase Diagram of Optimal Paths. Phys Rev Lett (2004) 93:040601. doi:10.1103/PhysRevLett.93.040601

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Soleimani BH, De Souza EN, Hilliard C, Matwin S. Anomaly Detection in Maritime Data Based on Geometrical Analysis of Trajectories. In: 18th International Conference on Information Fusion (Fusion) (2015). p. 1100–5.

Google Scholar

21. Talon L, Auradou H, Pessel M, Hansen A. Geometry of Optimal Path Hierarchies. EPL (2013) 103:30003. doi:10.1209/0295-5075/103/30003

CrossRef Full Text | Google Scholar

22. Ford LR. Network Flow Theory, No. P–923. Rand Corp Santa Monica Ca (1956).

23. Bellman R. On a Routing Problem. Quart Appl Math (1958) 16:87–90. doi:10.1090/qam/102435

CrossRef Full Text | Google Scholar

24. Dijkstra EW. A Note on Two Problems in Connexion with Graphs. Numer Math (1959) 1:269–71. doi:10.1007/bf01386390

CrossRef Full Text | Google Scholar