Superconductivity in Cubic A15-type V–Nb–Mo–Ir–Pt High-Entropy Alloys

We report the crystal structure and superconducting properties of new V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ high-entropy alloys (HEAs) for x in the range of 0 $\le$x$\le$ 10. These HEAs are found to crystallize in a cubic A15-type structure and have a weakly coupled, fully gapped superconducting state. A maximum T_c of 5.18 K and zero-temperature upper critical field $B_{\text{c}2}$(0) of 6.4 T are observed at x = 0, and both quantities decrease monotonically with the increase of V content x. In addition, T_c shows an increase with increasing valence electron concentration from 6.4 to 6.5, which is compared with other A15-type HEA and binary superconductors.

1 Introduction

High-entropy alloys (HEAs) consisting of five or more constituent elements have received a lot of attention as an emerging class of multicomponent alloys [1–5]. These alloys are stabilized by the high mixing entropy rather than the formation enthalpy, and often refereed to as metallic glasses on ordered lattices. Despite the presence of strong chemical disorder, some HEAs exhibit collective quantum phenomena such as superconductivity [6, 7]. So far, a number of HEA superconductors have been discovered and their crystal structures can be categorized into body-centered cubic (bcc)-type [8–11], a-Mn-type [12, 13], CsCl-type [14], hcp-type [15–17], A15-type [18], and s-type [19]. In particular, the A15-type $V_{1.4}$${\text{Nb}}_{1.4}$${\text{Mo}}_{0.2}$${\text{Al}}_{0.5}$${\text{Ga}}_{0.5}$ HEA has a T_c of 10.2 K and a disorder-enhanced upper critical field of 20.1 T [18], both of which are the highest among HEA superconductors. It is worthy noting that, for binary A15-type superconductors, the T_c values exhibit two maxima at valence electron concentrations (VECs) of 4.7 and 6.5, respectively [20]. Since the VEC of the V–Nb–Mo–Al–Ga HEAs is limited below around 5, it is desirable to search for other A15-type HEA superconductors with VEC close to 6.5.

Motivated by this, we replace Al and Ga in the V–Nb–Mo–Al–Ga HEAs with Ir and Pt to form new V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs. A nearly single A15 phase is found for 0 $\le$x$\le$ 10, which corresponds to a VEC range of 6.4–6.5. Physical property measurements indicate that these A15-type HEAs are weakly coupled, fully gapped superconductors with T_c and $B_{\text{c}2}$ (0) up to 5.18 K and 6.4 T, respectively. In addition, their T_c increases with increasing VEC, in contrast to the V–Nb–Mo–Al–Ga HEAs. A comparison of the T_c vs. VEC plots is made between the A15-type HEA and binary superconductors, and its implication is discussed.

2 Materials and Methods

The V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs were prepared by the arc melting method. Stoichiometric amounts of high purity V (99.99%), Nb (99.999%), Mo (99.995%), Ir (99.99%), Pt (99.99%) elements were mixed thoroughly and pressed into pellets in an argon-filled glove box. The pellets were then melted in an arc furnace under high-purity argon atmosphere. To ensure homogeneity, the melts were flipped several times, followed by rapid cooling on a water-chilled copper plate. The phase purity of as-cast HEAs was checked by powder x-ray diffraction (XRD) at room temperature using a Bruker D8 Advance x-ray diffractometer with Cu-Kα radiation. The structural refinements were performed using the JANA2006 program [21]. The morphology and elemental composition were examined by a Zeiss field emission scanning electron microscope (SEM) equipped with an energy dispersive x-ray (EDX) spectrometer. The four-probe resistivity and specific heat were measured in a Quantum Design Physical Property Measurement System (PPMS-9 Dynacool). The dc magnetization measurements were carried out in a commercial SQUID magnetometer (MPMS3).

3 Results and Discussion

3.1 X-Ray Diffraction and Chemical Composition

The XRD patterns for the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs are displayed in Figure 1A. For all x values, the major diffraction peaks can be well indexed on a cubic lattice with the $Pm\overline{3}$n space group, indicative of a dominant A15 phase. With increasing x, the (004) peak shifts toward higher 2θ values. This points to a decrease of the a-axis with the increase of V content, in consistent with its smaller atomic radius compared with those of Nb and Mo [22]. In addition to the A15 phase, small impurity peaks are observed in the vicinity of main (102) diffraction and probably comes from the NbAl₂-type sigma phase [18]. In the A15 structure, there are two crystallographic sites (0, 0, 0) and (0.25, 0, 0.5). Following Reference [18], all the five constituent elements are assumed to be distributed randomly on these sites for the structural refinement (see the inset of Figure 1A), and their occupancies are fixed by the stoichiometry. This assumption is based on the previous studies of binary A15 compounds, which show that the antisite disorder is the most common point defects [23]. In Nb₃Sn, it has been argued that the Nb and Sn atoms occupy randomly the two sites after a certain period of mechanical milling [24]. The refinement profiles are shown in Figures 1B–D and the statistics are listed in Table 1. Both the difference plot and $R_{\text{wp}}$ ($R_{\text{p}}$) factor indicate a reasonably good agreement between the observed and calculated XRD patterns, which supports the validity of the employed structural model. Note that a more definitive conclusion requires atomic-level spectroscopies in future. The refined lattice parameter a = 5.0324, 5.0130, and 4.9848 Å for x = 0, 5 and 10, respectively, close to those of the A15-type V-Nb-Mo-Al-Ga HEAs. Figures 2A–C show the typical SEM images for the HEAs, all of which appear to be dense and homogeneous. Indeed, EDX elemental mapping reveals the uniform distribution of V, Nb, Mo, Ir, and Pt, and, as an example, the results for x = 0 are shown in Figures 2D–H. Furthermore, the EDX measurements allow us to determine the chemical compositions to be V_7.1Nb_33.8Mo_37.1Ir_10.7Pt_11.3, V_17.0Nb_28.9Mo_29.2Ir_11.2Pt_13.7 and V_26.3Nb_25.4Mo_26.0Ir_10.5Pt_11.8 for the HEAs with x = 0, 5, and 10, respectively. These agree well with the nominal compositions within the experimental error of ±2.5 at%.

FIGURE 1

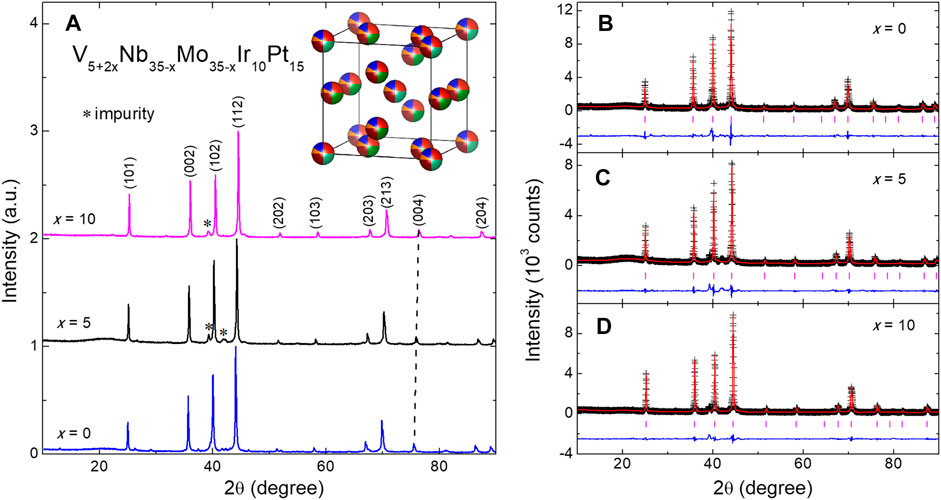
FIGURE 1. (A) X-ray diffraction patterns for the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs. The major peaks are indexed on a cubic unit-cell with the Pm$\overline{3}$n space group and the small impurity peaks are marked by the asterisks (B–D) Structural refinement profiles for the HEAs with x = 0, 5 and 10, respectively.

TABLE 1

TABLE 1. Structural and physical parameters of the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs.

FIGURE 2

FIGURE 2. (A–C) Typical SEM images for the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs with x = 0, 5 and 10, respectively. (D–H) Elemental mapping of V, Nb, Mo, Ir, and Pt, respectively, for the HEA with x = 0.

3.2 Resistivity and Magnetic Susceptibility

Figures 3A,B show the temperature dependencies of resistivity (ρ) and magnetic susceptibility (χ) for the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs, respectively. For each x value, a sharp drop in ρ and strong diamagnetic χ are observed, signifying a superconducting transition. As indicated by the vertical dashed line, the midpoint of ρ drop coincides well with the onset of diamagnetic transition. By this criterion, T_c is determined to be 5.18, 4.49, and 3.61 K for the HEAs with x = 0, 5, and 10, respectively. Below T_c, there is a clear bifurcation between the zero-field cooling (ZFC) and field cooling (FC) χ data measured under an applied field of 1 mT, which is characteristic of a type-II superconductor. At 1.8 K, the ${\chi }_{\text{ZFC}}$ data correspond to superconducting shielding fractions ranging from 101 to 174%. Although the demagnetization effect is difficult to correct due to irregular sample shapes, these large values suggest bulk superconductivity in these HEAs.

FIGURE 3

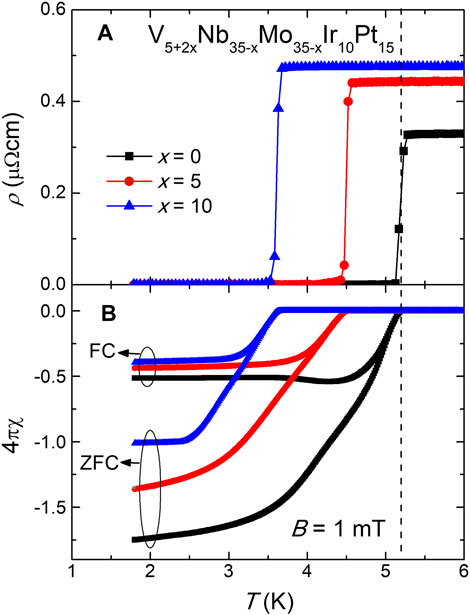
FIGURE 3. (A) Temperature dependence of resistivity for the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs below 6 K. (B) Temperature dependence of magnetic susceptibility measured under 1 mT for these HEAs in the same temperature range. The ZFC as well as FC curves are labeled, and the vertical dashed line is a guide to the eyes.

3.3 Specific Heat

To confirm the bulk nature of superconductivity, the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs were further characterized by specific heat ($C_{\text{p}}$) measurements, whose results are shown in Figure 4. As can be seen in Figures 4A, a C_p jump is indeed detected around T_c for these HEAs. Above T_c, the data are analyzed by the Debye model

$C_p/T=\gamma +\beta T^2+\delta T^4,(1)$

where γ and β(δ) are the Sommerfeld and phonon specific heat coefficients, respectively. With β, the Debye temperature ${\Theta }_D$ is calculated as

${\Theta }_D={\left(12{\pi }^{4}R/5\beta \right)}^{1/3},(2)$

where R is the molar gas constant 8.314 J/molK². This gives γ = 4.59, 4.94, and 5.03 mJ/molatomK², and ${\text{Θ}}_{\text{D}}$ = 419, 440, and 393 K for x = 0, 5, and 10, respectively. Figure 4B shows the normalized electronic specific heat C_el/γT after subtraction of the phonon contribution. For all HEAs, the ΔC_el/γT are significantly smaller than the BCS value of 1.43 [25]. Nevertheless, the C_el/γT data can still be fitted by a modified BCS model or the α-model [26] with α = 1.39, 1.41 and 1.56 for x = 0, 5 and 10, respectively, where α = Δ₀/T_c and Δ₀ is the gap size at 0 K. These results suggest that the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs are BCS-like superconductors in the weak coupling regime. This is corroborated by their electron-phonon coupling constants ${\lambda }_{\text{ep}}$ in the range of 0.55–0.59, as calculated using the inverted McMillan formula [27],

${\lambda }_{ep}=\frac{1.04+{\mu }^{\ast }\ln \left({\Theta }_D/1.45T_c\right)}{\left(1-0.62{\mu }^{\ast }\right)\ln \left({\Theta }_D/1.45T_c\right)-1.04},(3)$

with ${\mu }^{\text{*}}$ = 0.13 being the Coulomb repulsion pseudopotential. In passing, it is pointed out that the decrease in T_c with increasing x is accompanied by the decrease in ${\lambda }_{\text{ep}}$ but the increase in γ. Hence the T_c in the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs is mainly governed by the electron-phonon coupling strength rather than the density of states at the Fermi level. In passing, it is worth noting that the T_c, γ and ${\lambda }_{\text{ep}}$ values of the V–Nb–Mo–Pt–Ir HEAs are very similar to those of the ($V_{0.5}$${\text{Nb}}_{0.5}$)_3−x Mo_x${\text{Al}}_{0.5}$${\text{Ga}}_{0.5}$ HEAs for x$\ge$ 1.2 [18], pointing to a common phonon-mediated pairing mechanism.

FIGURE 4

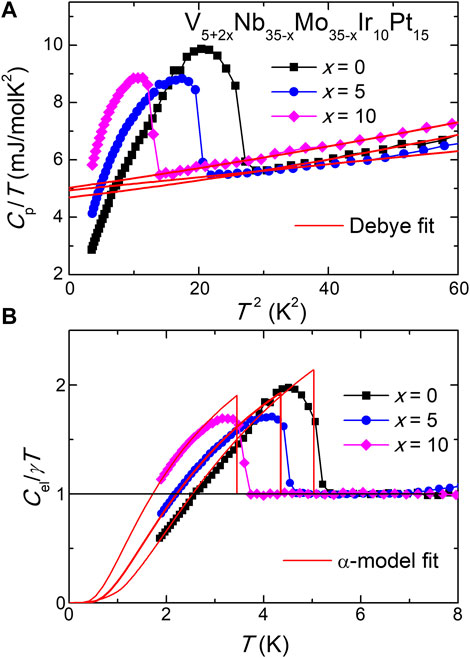
FIGURE 4. (A) Low-temperature specific heat for the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs plotted as $C_{\text{p}}$/T vs. $T^2$. The solid lines are results of Debye fits to the data. (B) Normalized electronic specific heat for these HEAs. The solid lines are fits to the data by the a-model.

3.4 Upper Critical Field

The upper critical fields $B_{\text{c}2}$ of these HEAs were investigated by resistivity measurements under magnetic fields. As an example, the result for the HEA with x = 0 is shown in Figure 5A. The resistive transition is gradually suppressed to low temperatures as the field increases. For each field, the T_c is determined using the same criterion as above, and the obtained $B_{\text{c}2}$ vs. T phase diagrams are displayed in Figure 5B. Extrapolating the $B_{\text{c}2}$(T) data to 0 K using the Wathamer-Helfand-Hohenberg model [28] yields $B_{\text{c}2}$(0) = 6.4, 5.7 and 4.4 T for the HEAs with x = 0, 5, and 10, respectively. These values are well below the corresponding Pauli limiting fields [29] of ∼9.6, ∼8.4, and ∼6.7 T, suggesting that $B_{\text{c}2}$ in these HEAs is orbitally limited. In addition, the Ginzburg–Landau coherence lengths ${\xi }_{\text{GL}}$ can be calculated using the equation

${\xi }_{\text{GL}}\left(0\right)=\sqrt{{\text{Φ}}_0/2\pi B_{c2}\left(0\right)},(4)$

where ${\text{Φ}}_0$ = 2.07 $\times$${10}^{-15}$ Wb is the flux quantum. This yields ${\xi }_{\text{GL}}$ = 7.2, 7.6 and 8.7 nm for the HEAs with x = 0, 5, and 10, respectively. The above results are summarized in Table 1.

FIGURE 5

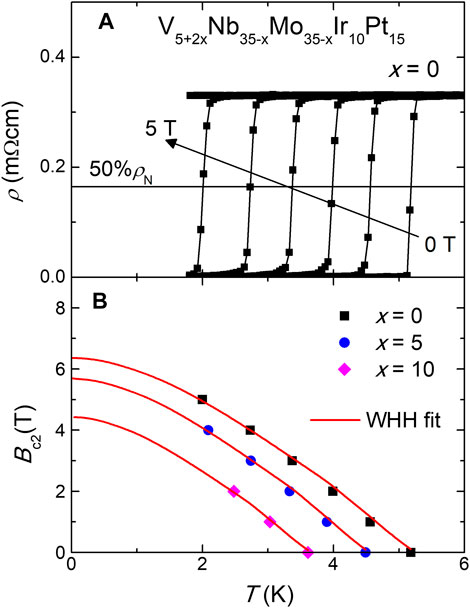
FIGURE 5. (A) Temperature dependence of resistivity for the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEA with x = 0 under various field up to 6 T with an field increment of 1 T. The horizontal line and the arrow mark the level corresponding to half of the resistivity drop and the increasing field direction, respectively. (B) Temperature dependence of the upper critical fields for these HEAs. The solid lines are WHH fits to the data.

3.5 VEC Dependence of T_c

Figure 6 shows the VEC dependence of T_c for the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs, together with the data for A15-type V-Nb-Mo-Al-Ga HEA [18] and binary [20] superconductors for comparison. One can see that superconductivity in all these materials occurs near the VEC values of 4.7 and 6.5, consistent with the expectation from the Matthias rule [30]. Compared with the V–Nb–Mo–Al–Ga HEAs, the V–Nb–Mo–Ir–Pt HEAs have higher VEC values in the range of 6.4–6.5 and their VEC dependence of T_c is in the opposite trend, increasing monotonically with the increase of VEC. Nevertheless, the maximum T_c is considerably lower for the V–Nb–Mo–Ir–Pt HEAs than for the V-Nb-Mo-Al-Ga ones. This indicates that optimal VEC for T_c in A15-type HEA superconductors is around 4.7, which is reminiscent of the case in binary A15 compounds [20]. Moreover, for similar VEC values, the T_c values for V–Nb–Mo–Al–Ga and V–Nb–Mo–Ir–Pt HEAs are always no more than half those of the binary compounds. It is thus reasonable to speculate that the upper limit of T_c for A15-type HEA superconductors is about one-half the highest T_c in binary A15 superconductors.

FIGURE 6

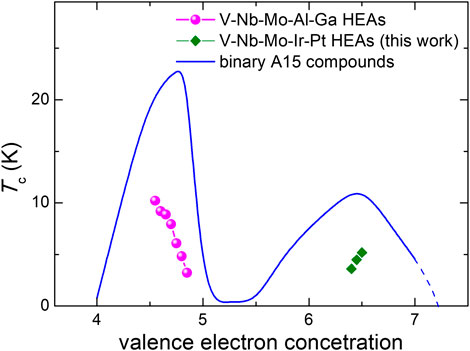
FIGURE 6. VEC dependence of T_c for the A15-type HEA superconductors. The solid line denotes the T_c behavior of binary A15 superconductors.

4 Conclusion

In summary, we have studied the structure, electronic, magnetic and thermodynamic properties of the V_5+2xNb_35−xMo_35−xIr₁₀Pt₁₅ HEAs with 0 $\le$x$\le$ 10. In this x range, the HEAs adopt a cubic A15-type structure and exhibit bulk superconductivity. The analysis of their specific-heat jumps points to a weakly coupled, fully gapped superconducting state. The T_c and $B_{\text{c}2}$(0) reach 5.18 K and 6.4 T, respectively, at x = 0, and decrease monotonically with the increase of V content x. In addition, T_c increases with increasing VEC from 6.4 to 6.5 and its comparison with isostructural HEA and binary superconductors suggests that the upper limit of T_c for A15-type HEA superconductors is about half that for binary compounds. Our study helps to better understand the effect of chemical disorder in A15-type superconductors.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, upon reasonable request.

Author Contributions

LB synthesized the samples and did the physical property measurements with the assistance from WJF, CYW, ZQQ, XGR. WSQ and CGH contributed in the magnetic measurements. RZ supervised the project and wrote the paper.

Funding

The authors thank the foundation of Westlake University and the National Key Research Development Program of China (No. 2017YFA0303002) for financial support.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Yeh JW, Chen SK, Lin SJ, Gan JY, Chin ST, Shun TT, et al. Nanostructured high-entropy alloys with multiple principal elements: novel alloy Design concepts and outcomes. Adv Eng Mater (2004) 6:299. doi:10.1002/adem.200300567

CrossRef Full Text | Google Scholar

2. Ye YF, Wang Q, Lu J, Liu CT, Yang Y High-entropy alloy: challenges and prospects. Mater Today (2016) 19:349. doi:10.1016/j.mattod.2015.11.026

CrossRef Full Text | Google Scholar

3. Miracle DB, Senkov ON A critical review of high entropy alloys and related concepts. Acta Mater (2017) 122:448. doi:10.1016/j.actamat.2016.08.081

CrossRef Full Text | Google Scholar

4. Zhang WR, Liaw PK, Zhang Y Science and technology in high-entropy alloys. Sci China Mater (2018) 61:2. doi:10.1007/s40843-017-9195-8

CrossRef Full Text | Google Scholar

5. George EP, Rabbe D, Ritchie RO High-entropy alloys. Nat Rev Mater (2019) 4:515. doi:10.1038/s41578-019-0121-4

CrossRef Full Text | Google Scholar

6. Sun LL, Cava RJ High entropy alloy superconductors -status, opportunities and challenges. Phys Rev Mater (2019) 3:090301. 10.1016/j.mattod.2015.11.026

CrossRef Full Text | Google Scholar

7. Kitagawa J, Hamamoto S, Ishizu N Cutting edge of high-entropy alloy superconductors from the perspective of materials research. Metals (2020) 10:1078. doi:10.3390/met10081078

CrossRef Full Text | Google Scholar

8. Kozelj K, Vrtnik S, Jelen A, Jazbec S, Jaglicic Z, Maiti S, et al. Discovery of a superconducting high-entropy alloy. Phys Rev Lett (2014) 113:107001. doi:10.1103/PhysRevLett.113.107001

PubMed AbstractGoogle Scholar

9. vonn Rohr F, Winiarski MJ, Tao J, Klimczuk T, Cava RJ The effect of electron count and chemical complexity on the superconductivity of the Ta-Nb-Hf-Zr-Ti high-entropy alloy. Proc Nat Acad Sci USA (2016) 113:E7144. doi:10.1073/pnas.1615926113

PubMed AbstractGoogle Scholar

10. Yuan Y, Wu Y, Luo HQ, Wang ZS, Liang X, Yang Z, et al. Superconducting Ti₁₅Zr₁₅Nb₃₅Ta₃₅ high-entropy alloy with intermediate electron-phonon coupling. Front Mater (2018) 5:72. doi:10.3389/fmats.2018.00072

CrossRef Full Text | Google Scholar

11. Nelson WL, Chemey AT, Hertz M, Choi E, Graf DE, Latturner S, et al. Superconductivity in a uranium containing high entropy alloy. Sci Rep (2020) 10:4717. doi:10.1038/s41598-020-61666-z

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Stolze K, Cevallos FA, Kong T, Cava RJ High-entropy alloy superconductors on an α-Mn lattice. J Mater Chem C (2018) 6:10441. doi:10.1039/C8TC03337D

CrossRef Full Text | Google Scholar

13. Liu B, Wu JF, Cui YW, Zhu QQ, Xiao GR, Wang HD, et al. Structural evolution and superconductivity tuned by valence electron concentration in the Nb–Mo–Re–Ru–Rh high-entropy alloys. J Mater Sci Technol (2021) 85:11. doi:10.1016/j.jmst.2021.02.002

CrossRef Full Text | Google Scholar

14. Stolze K, Tao J, von Rohr FO, Kong T, Cava RJ Sc–Zr–Nb–Rh–Pd and Sc–Zr–Nb–Ta–Rh–Pd high-entropy alloy superconductors on a CsCl-type lattice. Chem Mater (2018) 20:906. doi:10.1021/acs.chemmater.7b04578

CrossRef Full Text | Google Scholar

15. Marik S, Molta K, Varghese M, Sajilesh KP, Singh D, Breard Y, et al. Superconductivity in a new hexagonal high-entropy alloy. Phys Rev Mater (2019) 3:060602. doi:10.1103/PhysRevMaterials.3.060602

CrossRef Full Text | Google Scholar

16. Lee YS, Cava RJ Superconductivity in high and medium entropy alloys based on MoReRu. Physica C. (2019) 566:1353520. doi:10.1016/j.physc.2019.1353520

CrossRef Full Text | Google Scholar

17. Liu B, Wu JF, Cui YW, Zhu QQ, Xiao GR, Wu SQ, et al. Superconductivity in hexagonal Nb–Mo–Ru–Rh–Pd high-entropy alloys. Scripta Mater (2020) 182:109. doi:10.1016/j.scriptamat.2020.03.004

CrossRef Full Text | Google Scholar

18. Wu JF, Liu B, Cui YW, Zhu QQ, Xiao GR, Wang HD, et al. Polymorphism and superconductivity in the V–Nb–Mo–Al–Ga high-entropy alloys. Sci China Mater (2020) 63:823. doi:10.1007/s40843-019-1237-5

CrossRef Full Text | Google Scholar

19. Liu B, Wu JF, Cui YW, Zhu QQ, Xiao GR, Wang HD, et al. Formation and superconductivity of single-phase high-entropy alloys with a tetragonal structure. ACS Appl Electron Mater (2020) 2:1130. doi:10.1021/acsaelm.0c00108

CrossRef Full Text | Google Scholar

20. Dew-Hughes D Superconducting A-15 compounds: a review. Cryogenics (1975) 15:435. doi:10.1016/0011-2275(75)90019-3

CrossRef Full Text | Google Scholar

21. Petricek V, Dusek M, Palatinus L Crystallographic computing system JANA2006: general features. Z Kristallogr (2014) 229:345. doi:10.1515/zkri-2014-1737

Google Scholar

22. Tarutani Y, Kudo M Atomic radii and lattice parameters of the A15 crystal structure. J Less Common Met (1977) 55:221. doi:10.1016/0022-5088(77)90196-5

CrossRef Full Text | Google Scholar

23. Besson R, Guyot S, Legris A Atomic-scale study of diffusion in A15 Nb3Sn. Phys Rev B (2007) 75:054105. doi:10.1103/PhysRevB.75.054105

CrossRef Full Text | Google Scholar

24. Takano H, Sugiue T, Amakai Y, Momono N, Murayama S Site random supercoductivity of A15 compound Nb3Sn induced by mechanical milling. J Phys Conf Ser (2010) 200:032073. doi:10.1088/1742-6596/200/3/032073

CrossRef Full Text | Google Scholar

25. Bardeen J, Cooper LN, Schreiffer JR Theory of superconductivity. Phys Rev (1957) 108:1175. doi:10.1201/9780429495700

CrossRef Full Text | Google Scholar

26. Johnston DC Elaboration of the $\alpha$-model derived from the BCS theory of superconductivity. Supercond Sci Technol (2013) 26:115011. doi:10.1088/0953-2048/26/11/115011

CrossRef Full Text | Google Scholar

27. McMillan WL Transition temperature of strong-coupled superconductors. Phys Rev (1968) 167:331.

CrossRef Full Text | Google Scholar

28. Werthamer NR, Helfand E, Hohenberg PC Temperature and Purity Dependence of the Superconducting Critical Field, $H_{\rm c2}$. III. Electron Spin and Spin-Orbit Effects. Phys Rev (1966) 147:295. doi:10.1103/PhysRev.147.295

CrossRef Full Text | Google Scholar

29. Clogston AM Upper Limit for the Critical Field in Hard Superconductors. Phys Rev Lett (1962) 9:266. doi:10.1103/PhysRevLett.9.266

CrossRef Full Text | Google Scholar

30. Matthias BT Empirical Relation between Superconductivity and the Number of Valence Electrons per Atom. Phys Rev (1955) 97:74. doi:10.1103/PhysRev.97.74

CrossRef Full Text | Google Scholar