Average Intensity and Beam Quality of Hermite-Gaussian Correlated Schell-Model Beams Propagating in Turbulent Biological Tissue

The propagation characteristics of a Hermite-Gaussian correlated Schell-model (HGCSM) beam in the turbulence of biological tissue are analyzed. The average intensity, spectral degree of coherence, and the dependence of the propagation factors on the beam orders, transverse coherence width, fractal dimension, characteristic length of heterogeneity, and small length-scale factor are numerically investigated. It is shown that the HGCSM beam does not exhibit self-splitting properties on propagation in tissues due to the strong turbulence in the refractive index of biological tissue. The larger the beam orders, the fractal dimension, and the small length-scale factor are, or the smaller the transverse coherence width and the characteristic length of heterogeneity are, the smaller the normalized propagation factor is, and the better the beam quality of HGCSM beams in turbulence of biological tissue is. Moreover, under the same condition, the HGCSM beam is less affected by turbulence than of Gaussian Schell-model (GSM) beam. It is expected that the results obtained in this paper may be useful for the application of partially coherent beams in tissue imaging and biomedical diagnosis.

Introduction

In recent years, the propagation of laser beams in biological tissues has been a hot topic of tissue optics research, which plays an important role in medical diagnosis and treatment [1–8]. The structures that comprise biological tissues span several orders of magnitude in size and are composed of a wide range of materials. However, there are differences in the refractive indices of the components in living tissues, and the non-uniformity of the materials leads to a complex spatial distribution of refractive indices over a range. Such heterogeneity gives rise to turbulence and optical turbidity. So far, several power spectral models of the refractive index of animal tissues have been reported, which can be used to quantitative study light propagation and scattering in the tissues [9–13]. For example, Gao et al. investigated the degree of polarization and coherence of a random electromagnetic beam on propagation in tissue by using the power spectrum of tissue turbulence that fits the classical Kolmogorov model, and found that the refractive index fluctuations of biological tissues are much larger than those of the atmosphere, the degree of polarization changes greatly although the propagation distance is very short [14, 15]. Based on a fractal continuous power spectrum model of tissue refractive-index variation, Wu et al. found that the GSM beam is less affected by turbulence than the Laguerre-Gaussian Schell-model (LGSM) beam and Bessel-Gaussian Schell-model (BGSM) beam beams [16]. Yu and Zhang investigated the beam spreading and wander of a partially coherent Lommel-Gaussian beam propagation in turbulent tissue using a power spectrum model of the tissue considering the structural length-scale and fractal dimension, and the results reveal that laser beam with low-order vortex suffers less turbulence interference [17]. Shi et al. experimentally investigated light transmission in mouse brain tissues, and found that the transmittance of Gaussian and Laguerre-Gaussian (LG) beams is not significantly different, while the transmittance of circularly polarized LG beams increases significantly and is affected by the topological charge [18, 19]. Duan et al. analyzed the influences of the spatial correlation length on the relative spectral shift of GSM vortex beam propagation in turbulent tissue, and discovered that the spatial coherence of beams can accelerate spectral changes and slow down spectral jumps [20]. In addition, the propagation characteristics of anomalous hollow vortex beam [21], quasi-diffraction-free beam [22], partially coherent circular flattened Gaussian vortex beam [23], and other laser beams [24, 25] in biological tissue have been studied. From the above theoretical and experimental studies, it can be found that due to the strong fluctuation of tissue refractive index, the laser beams can only transport a very short distance within the tissue, and the properties of the optical field change rapidly. Partially coherent beams and vector beams may be effective means to resist the destructive effect of tissue turbulence and to improve the information and energy transfer of the laser within the tissue.

Based on the sufficient condition for devising genuine correlation functions of partially coherent beams proposed by Gori et al. [26, 27], Chen et al. introduced a class of partially coherent beam with a special spatially correlation function named Hermite-Gaussian correlated Schell-model (HGCSM) beam in 2015 [28]. The propagation properties of the HGCSM beam in free space, focusing optical system, Kolmogorov and non-Kolmogorov turbulent atmosphere have been investigated in detail [28–31]. It was found that the HGCSM beam exhibits many extraordinary properties, such as self-splitting on propagation in free space, splitting and combining in focusing optical system, and turbulent atmosphere, and self-healing properties when a portion of the spot is obscured. With these properties, such beams may overcome refractive index turbulence to some extent, as well as transmit deeper. However, as far as we know, the statistical properties of a HGCSM beam propagating in biological tissue have not been given. The aim of this paper is to investigate the intensity evolution and beam quality of the HGCSM beam in turbulent tissue.

The paper is organized as follows. In section The Theories of a HGCSM Beam Propagating in a Turbulent Biological Tissue, the analytical expression for the cross-spectral density function of the HGCSM beam propagating through turbulent biological tissue is derived. The average intensity, the spectral degree of coherence, and the dependence of propagation factors on the parameters of the beam and of the turbulent tissue are analyzed and illustrated by numerical examples in section Numerical Simulations and Analysis. Finally, section Conclusion provides the concluding remarks.

The Theories of a HGCSM BEAM Propagating in a Turbulent Biological Tissue

In the space-frequency domain, the cross-spectral density function of a HGCSM beam at the source plane z = 0 is expressed as [28].

$\begin{array}{ll}{W}_0\left({\text{r}}_1,{\text{r}}_2,0\right)=G_{0}exp\left(-\frac{{\text{r}}_1^2+{\text{r}}_2^2}{4{\sigma }_0^2}\right){\mu }_0({\text{r}}_2-{\text{r}}_1)& (1)\end{array}$

where r₁ = (r_1x, r_1y) and r₂ = (r_2x, r_2y) are two-dimensional position vectors of points in the source plane, G₀ is a constant, σ₀ denotes the transverse beam width of the Gaussian part, and μ₀(r₂−r₁) is the spectral degree of coherence of the HGCSM beam at the z = 0 plane and takes the following form

$\begin{array}{l}{\mu }_0(r_2-r_1)=\frac{H_{2m}[(r_{2x}-r_{1x})/\sqrt{2}{\delta }_{0x}]}{H_{2m}\left(0\right)}\frac{H_{2n}[(r_{2y}-r_{1y})/\sqrt{2}{\delta }_{0y}]}{H_{2n}\left(0\right)}\\ \exp \left[-\frac{{(r_{2x}-r_{1x})}^2}{2{\delta }_{0x}^2}-\frac{{(r_{2y}-r_{1y})}^2}{2{\delta }_{0y}^2}\right]& (2)\end{array}$

in which δ_0x and δ_0y denote the transverse coherence widths along x and y directions, respectively, H_m(·) represents the mth-order Hermite polynomial. For m = n = 0 and δ_0x = δ_0y, the HGCSM beam is reduces the GSM beam. When m = n = 0 and δ_0x≠δ_0y, the HGCSM beam reduces to the elliptical GSM beam. We now proceed to consider the propagation of a HGCSM beam in a turbulent biological tissue, as illustrated in Figure 1, where the left plot is the intensity distribution of the beam at the input plane, and the varying colors in the graph on the right indicate the non-uniformity of the refractive index.

FIGURE 1

Figure 1. Illustration of the propagation of a HGCSM beam in a turbulence tissue.

Based on the extended Huygens-Fresnel principle [32], and within the validity of the paraxial approximation, the cross-spectral density function of the HGCSM beam propagating through turbulent biological tissue can be expressed as

$\begin{array}{l}W({\rho }_1,{\rho }_2,z)={\left(\frac{k}{2z\pi }\right)}^2{\displaystyle \int {\displaystyle \int {\displaystyle \int {\displaystyle \int W_0}}}}(r_1,r_2,0)\exp \{-\frac{ik}{2z}[{\left(r_1-{\rho }_1\right)}^2\\ -{\left(r_2-{\rho }_2\right)}^2]\}\\ \times \langle \exp [\psi (r_1,{\rho }_1)+{\psi }^{*}(r_2,{\rho }_2)]\rangle d^2{r}_1{d}^2{r}_2,& (3)\end{array}$

where z is the propagation distance, ρ₁ = (ρ_1x, ρ_1y) and ρ₂ = (ρ_2x, ρ_2y) denote the position vectors of points in the z plane, k = 2πn₀/λ is the wavenumber with λ being the wavelength of source and n₀ being the refractive index of propagating medium. 〈·〉 denotes ensemble average, superscript “^*” stands for the complex conjugate, and ψ(r, ρ) is the solution to the Rytov method that represents the random part of the complex phase of a spherical wave propagating in turbulence. The ensemble average term in Equation (3) can be given by [33].

$\begin{array}{l}\langle \exp [\psi (r_1,{\rho }_1)+{\psi }^{*}(r_2,{\rho }_2)]\rangle \\ \cong \exp -\{\frac{{\pi }^2{k}^{2}z}{3}\left[{(r_1-r_2)}^2+(\rho 1-{\rho }_2)2+(r_1-r_2)({\rho }_1-{\rho }_2)\right]& (4)\\ {\displaystyle {\int }_0^{\infty }{\kappa }^3\Phi (\kappa )d\kappa }\}\\ =\exp \left\{-\frac{1}{{\rho }_0^2}\left[{(r_1-r_2)}^2+{({\rho }_1-{\rho }_2)}^2+(r_1-r_2)({\rho }_1-{\rho }_2)\right]\right\},\end{array}$

where κ is the spatial frequency, Φ(κ) is the power spectrum of the refractive-index fluctuations of the biological tissue, and ρ₀ is the spherical-wave lateral coherence radius due to the turbulence. Considering the fractional dimension and structural length-scale of the biological tissue, Φ(κ) is expressed as [12, 17].

$\begin{array}{ll}\Phi (\kappa )=\frac{S{l}_c^3\Gamma (D_f/2)}{{\pi }^{3/2}{2}^{(5-D_f)/2}{(1+{\kappa }^2{l}_c^2)}^{D_f/2}}\exp \left(-\frac{{\kappa }^2{l}_0^2}{8In2}\right),& (5)\end{array}$

where S is strength coefficient of fluctuations, D_f is the fractal dimension, Γ(·) is the gamma function, l_c is the characteristic length of heterogeneity, l₀ is the small length-scale filter. On substituting Equation (5) into Equation (4), we obtain the spatial coherence radius of a laser beam propagating in turbulent biological tissue

$\begin{array}{l}{\rho }_0^{-2}=\frac{{\pi }^2{k}^{2}z}{3}{\displaystyle {\int }_0^{\infty }{\kappa }^3\Phi (\kappa )d\kappa }\\ =\frac{{\pi }^{1/2}{k}^{2}z}{6}\frac{S{l}_c^3\Gamma (D_f/2)}{2^{(5-D_f)/2}}\frac{b^{-2-d}[-a^2{b}^d+a^{d}b\exp (a/b)(a+b(d-1))\Gamma (2-d,a/b)]}{a^2(d-1)},& (6)\end{array}$

where $a=l_0^2/(8In2)$, $b=l_c^2$, and d = D_f/2. Then, substituting Equations (1) and (4) into Equation (3) and using the following formulation [34].

$\begin{array}{ll}{H}_n(x+y)=2^{-n/2}{\displaystyle \sum _{c=0}^n\left(\begin{array}{c}n\\ c\end{array}\right)}{H}_{n-c}\left(\sqrt{2}x\right)H_c\left(\sqrt{2}y\right),& (7)\end{array}$

$\begin{array}{l}{\displaystyle {\int }_{-\infty }^{\infty }\exp \left[-{(x-y)}^2\right]H_n\left(\alpha x\right)dx=\sqrt{\pi }{\left(1-{\alpha }^2\right)}^{n/2}{H}_n}\\ \left[\frac{\alpha y}{{\left(1-{\alpha }^2\right)}^{1/2}}\right],& (8)\end{array}$

$\begin{array}{ll}{H}_n(x)={\displaystyle \sum _{c=0}^{\left[n/2\right]}}\frac{{(-1)}^{c}n!}{c!(n-2c)!}{(2x)}^{n-2c},& (9)\end{array}$

$\begin{array}{ll}{\displaystyle {\int }_{-\infty }^{\infty }}{x}^{n}exp\left[-{(x-b)}^2\right]dx=\sqrt{\pi }{(2i)}^{-n}{H}_n(ib),& (10)\end{array}$

one can obtain the resulting expression of the cross-spectral density function of the HGCSM beam in the output plane

$\begin{array}{ll}W({\rho }_1,{\rho }_2,z)=G_0{\left(\frac{k}{2z\pi }\right)}^2\exp \left[-\frac{ik}{2z}({\rho }_1^2-{\rho }_2^2)\right]G_x{G}_y,& (11)\end{array}$

in which

$\begin{array}{l}{G}_x=\frac{1}{H_{2m}(0)}{\displaystyle \sum _{c_1=0}^{2m}{\displaystyle \sum _{e_1=0}^{c_1}{\displaystyle \sum _{e_2=0}^{[e_1/2]}{\displaystyle \sum _{d_1=0}^{[(2m-c_1)/2]}\left(\begin{array}{c}2m\\ c_1\end{array}\right)}}}}\left(\begin{array}{c}{c}_1\\ e_1\end{array}\right)2^{-m-c_1/2}\frac{\pi }{\sqrt{M_{1x}}\sqrt{M_{2x}}}{\left(\frac{1}{2i\sqrt{M_{2x}}}\right)}^{{}^{2m-c_1-2d_1+e_1-2e_2}}\\ \times {\left(1-F_{3x}^2\right)}^{c_1/2}\frac{{(-1)}^{e_2+d_1}{e}_1!}{e_2!(e_1-2e_2)!}\frac{(2m-c_1)!}{d_1!(2m-c_1-2d_1)!}{\left(\frac{\sqrt{2}{F}_{3x}{F}_{2x}}{{(1-F_{3x}^2)}^{1/2}\sqrt{M_{1x}}}\right)}^{e_1-2e_2}{\left(\frac{2}{{\delta }_{0x}}\right)}^{2m-c_1-2d_1}& (\mathrm{12a})\\ \times \exp \left(\frac{F_{1x}^2}{4M_{1x}}\right)\exp \left(\frac{F_{4x}^2}{4M_{2x}}\right)H_{c_1-e_1}\left(\frac{\sqrt{2}{F}_{3x}{F}_{1x}}{2{\left(1-F_{3x}^2\right)}^{1/2}\sqrt{M_{1x}}}\right)H_{2m-c_1-2d_1+e_1-2e_2}\left(\frac{i{F}_{4x}}{2\sqrt{M_{2x}}}\right),\end{array}$

$\begin{array}{l}{G}_y=\frac{1}{H_{2n}(0)}{\displaystyle \sum _{c_2=0}^{2n}{\displaystyle \sum _{e_3=0}^{c_2}{\displaystyle \sum _{e_4=0}^{[e_3/2]}{\displaystyle \sum _{d_2=0}^{[(2n-c_2)/2]}\left(\begin{array}{c}2n\\ c_2\end{array}\right)}}}}\left(\begin{array}{c}{c}_2\\ e_3\end{array}\right)2^{-n-c_2/2}\frac{\pi }{\sqrt{M_{1y}}\sqrt{M_{2y}}}{\left(\frac{1}{2i\sqrt{M_{2y}}}\right)}^{2n-c_2-2d_2+e_3-2e_4}\\ \times {\left(1-F_{3y}^2\right)}^{c_2/2}\frac{{(-1)}^{e_4+d_2}{e}_1!}{e_4!(e_3-2e_4)!}\frac{(2n-c_2)!}{d_2!(2n-c_2-2d_2)!}{\left(\frac{\sqrt{2}{F}_{3y}{F}_{2y}}{{(1-F_{3x}^2)}^{1/2}\sqrt{M_{1x}}}\right)}^{e_3-2e_4}{\left(\frac{2}{{\delta }_{0y}}\right)}^{2n-c_2-2d_2}\\ \times \exp \left(\frac{F_{1y}^2}{4M_{1y}}\right)\exp \left(\frac{F_{4y}^2}{4M_{2y}}\right)H_{c_2-e_3}\left(\frac{\sqrt{2}{F}_{3y}{F}_{1y}}{2{(1-F_{3y}^2)}^{1/2}\sqrt{M_{1y}}}\right)H_{2n-c_2-2d_2+e_3-2e_4}\left(\frac{i{F}_{4y}}{2\sqrt{M_{2y}}}\right),& (\mathrm{12b})\end{array}$

$\begin{array}{ll}{M}_{1x}=\frac{1}{4{\sigma }_0^2}+\frac{1}{2{\delta }_{0x}^2}+\frac{ikA}{2z}+\frac{1}{{\rho }_0^2},& (\mathrm{12c})\end{array}$

$\begin{array}{ll}{M}_{2x}=\frac{1}{4{\sigma }_0^2}+\frac{1}{2{\delta }_{0x}^2}-\frac{ikA}{2z}+\frac{1}{{\rho }_0^2}-\frac{F_{2x}^2}{4M_{1x}},& (\mathrm{12d})\end{array}$

$\begin{array}{ll}{F}_{1x}=\frac{ik{\rho }_{1x}}{z}+\frac{{\rho }_{2x}-{\rho }_{1x}}{{\rho }_0^2},& (12e)\end{array}$

$\begin{array}{ll}{F}_{2x}=\frac{1}{{\delta }_{0x}^2}+\frac{2}{{\rho }_0^2},& (\mathrm{12f})\end{array}$

$\begin{array}{ll}{F}_{3x}=-\frac{1}{{\delta }_{0x}\sqrt{M_{1x}}},& (\mathrm{12g})\end{array}$

$\begin{array}{ll}{F}_{4x}=-\frac{ik{\rho }_{2x}}{z}+\frac{{\rho }_{1x}-{\rho }_{2x}}{{\rho }_0^2}+\frac{F_{1x}{F}_{2x}}{2M_{1x}}.& (\mathrm{12h})\end{array}$

Duo to the symmetry, M_1y, M_2y, F_1y, F_2y, F_3y, and F_4y can be obtained by replacement of δ_0x, ρ_1x, and ρ_2x in M_1x, M_2x, F_1x, F_2x, F_3x, and F_4x with δ_0y, ρ_1y and ρ_2y.

After obtaining the cross-spectral density function, we now consider the average intensity and spectral degree of coherence of HGCSM beams. The average intensity of the HGCSM beam propagating through turbulent biological tissue in the output plane is obtained as

$\begin{array}{ll}I(\rho ,z)=W(\rho ,\rho ,z),& (13)\end{array}$

and the spectral degree of coherence is defined as

$\begin{array}{ll}\mu ({\rho }_1,{\rho }_2,z)=\frac{W({\rho }_1,{\rho }_2,z)}{\sqrt{I({\rho }_1,z)I({\rho }_2,z)}}.& (14)\end{array}$

In addition, the propagation factor (also named M² factor) is the ratio of the actual space-beam width product of laser beam to the ideal conditions, which takes into account both the beam width and the far-field divergence angle variation on the beam quality. Using the Wigner distribution function, we can obtain the propagation factor of a beam. The propagation factors of HGCSM beam propagating in turbulence are given by [30].

$\begin{array}{l}{M}_x^2(z)=2\{\left[\frac{z^2}{{\delta }_{0x}^2{k}^2}(2m+1)+\frac{z^2}{4k^2{\sigma }_0^2}+{\sigma }_0^2+\frac{2{\pi }^2{z}^{3}T}{3}\right]\\ \left[\frac{1}{{\delta }_{0x}^2}(2m+1)+\frac{1}{4{\sigma }_0^2}+2{\pi }^2{k}^{2}zT\right]& (15)\\ -{{\left[\frac{z}{k{\delta }_{0x}^2}(2m+1)+\frac{z}{4k{\sigma }_0^2}+{\pi }^2{z}^{2}kT\right]}^2\}}^{1/2},\end{array}$

$\begin{array}{l}{M}_y^2(z)=2\{\left[\frac{z^2}{{\delta }_{0y}^2{k}^2}(2n+1)+\frac{z^2}{4k^2{\sigma }_0^2}+{\sigma }_0^2+\frac{2{\pi }^{2}zT}{3}\right]\\ \left[\frac{1}{{\delta }_{0y}^2}(2n+1)+\frac{1}{4{\sigma }_0^2}+2{\pi }^2{k}^{2}zT\right]& (16)\\ -{{\left[\frac{z}{k{\delta }_{0y}^2}(2n+1)+\frac{z}{4k{\sigma }_0^2}+{\pi }^2{z}^{2}kT\right]}^2\}}^{1/2},\end{array}$

where T is turbulence intensity, which can be expressed as

$\begin{array}{ll}T={\displaystyle {\int }_0^{\infty }{\kappa }^3\Phi (\kappa )}d\kappa =\frac{3}{{\pi }^2{k}^{2}z{\rho }_0^2}.& (17)\end{array}$

With the above formulas, one can explore the evolution properties of HGCSM beams in the turbulent biological tissue.

Numerical Simulations and Analysis

In this section, we analyze the average intensity, the spectral degree of coherence, and the propagation factor of HGCSM beams propagating in the turbulent biological tissue based on the analytical formulas derived in the previous section.

To start, we consider the propagation of HGCSM beams in free space under the condition of Φ(κ) = 0. The average intensity distributions of a HGCSM beam propagating in free space are displayed in Figure 2. The calculation parameters of the beam are chosen as G₀ = 1, λ = 0.83 μm, σ₀ = 10 μm, δ_0x = δ_0y = 2λ, m = 5, and n = 0. From Figure 2, it is found that as the propagation distance increases, the HGCSM beam gradually splits into two spots along the x direction, and the distance between these two spots gradually increases. This phenomenon shows the self-splitting property of the HGCSM beam. When the beam orders m and n are both non-zero (m and n are non-negative integers), the HGCSM beam splits into four spots. In addition, the peak value of intensity gradually decreases with the increase of the propagation distance. This is due to the fact that the divergence of the beam.

FIGURE 2

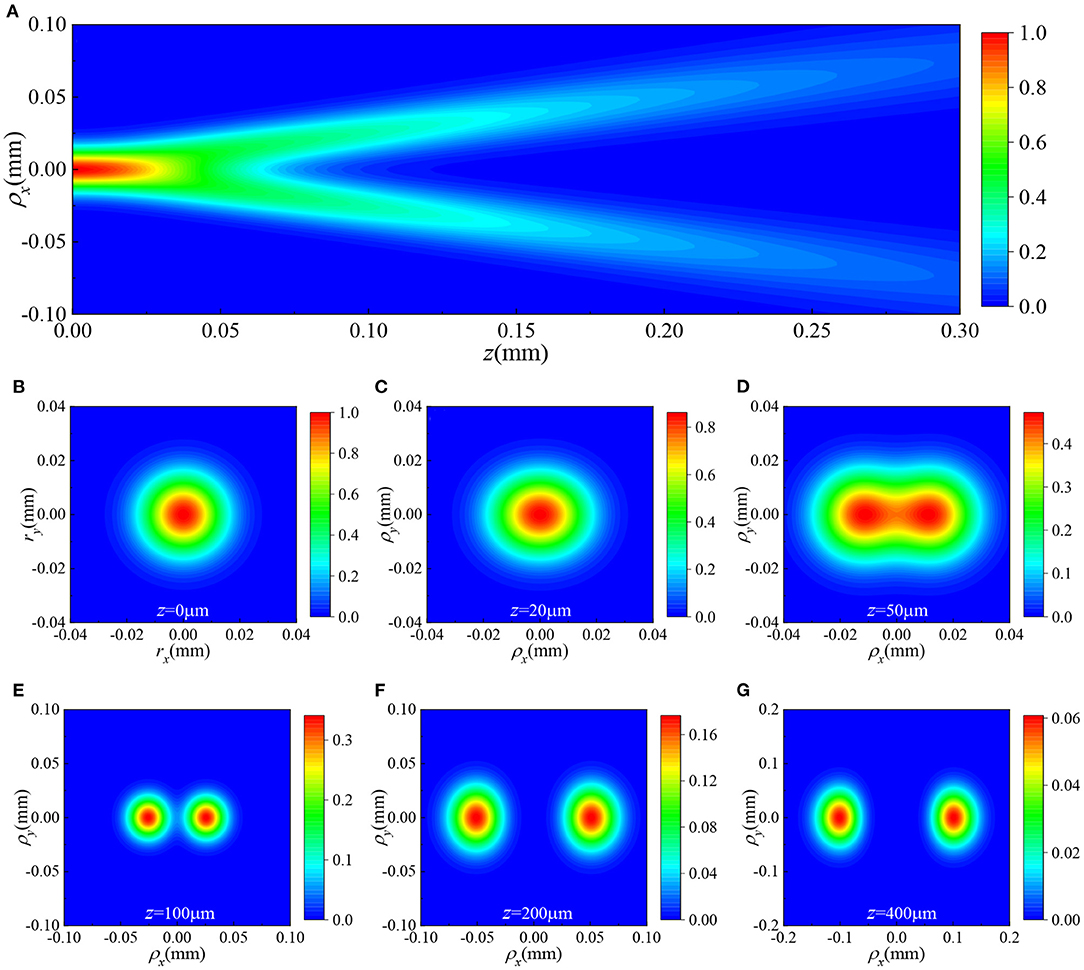
Figure 2. The average intensity distributions of a HGCSM beam with m = 5 and n = 0 propagating in free space (A) in the ρ_x−z plane with, ρ_y = 0, and (B–G) in the ρ_x−ρ_y plane at different propagation distances.

We now turn to investigate the propagation of HGCSM beams in biological tissues. Figure 3 gives the average intensity distributions of a HGCSM beam propagating in turbulent biological tissue. The parameters of tissues are n₀ = 1.53, l_c = 2 μm, l₀ = 1 μm, S = 2 × 10⁻⁴, D_f = 3, and the beam parameters are the same as Figure 2. Comparing Figure 3 with Figure 2, it is obvious that unlike the HGCSM beam in free space, the HGCSM beam does not split into two spots when transmitted in biological tissues. It is due to the influence of turbulence, and the beam eventually evolved into an elliptical intensity distribution. Furthermore, in general, the attenuation of the average intensity in the turbulent tissue is larger than in free space when the absorption of the tissue is not taken into account. In other words, the fluctuation of tissue refractive index affects the attenuation of light intensity.

FIGURE 3

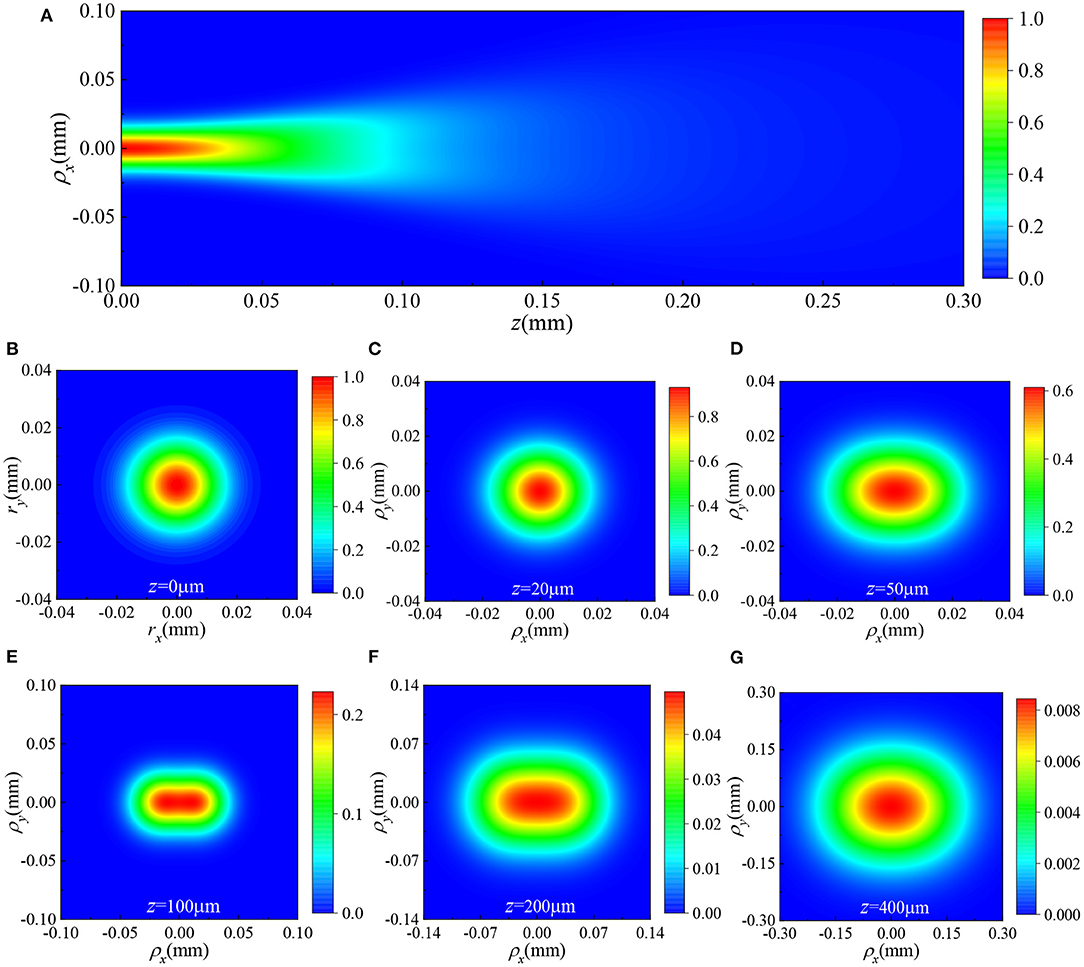
Figure 3. The spectral intensity distributions of a HGCSM beam with m = 5 and n = 0 propagating in turbulent biological tissue (A) in the ρ_x−z plane with, ρ_y = 0, and (B–G) in the ρ_x−ρ_y plane at different propagation distances.

Figure 4 depicts the density plot of the spectral degree of coherence of a HGCSM beam at different propagation distances in the biological tissue with m = n = 5. Other parameters used in the simulation are the same as Figure 3. It is seen that the spectral degree of coherence of the HGCSM beam exhibits array distribution, and the number of arrays is highest in the plane and decreases as the propagation distance increases. Finally, the array distribution evolves into Gaussian distribution.

FIGURE 4

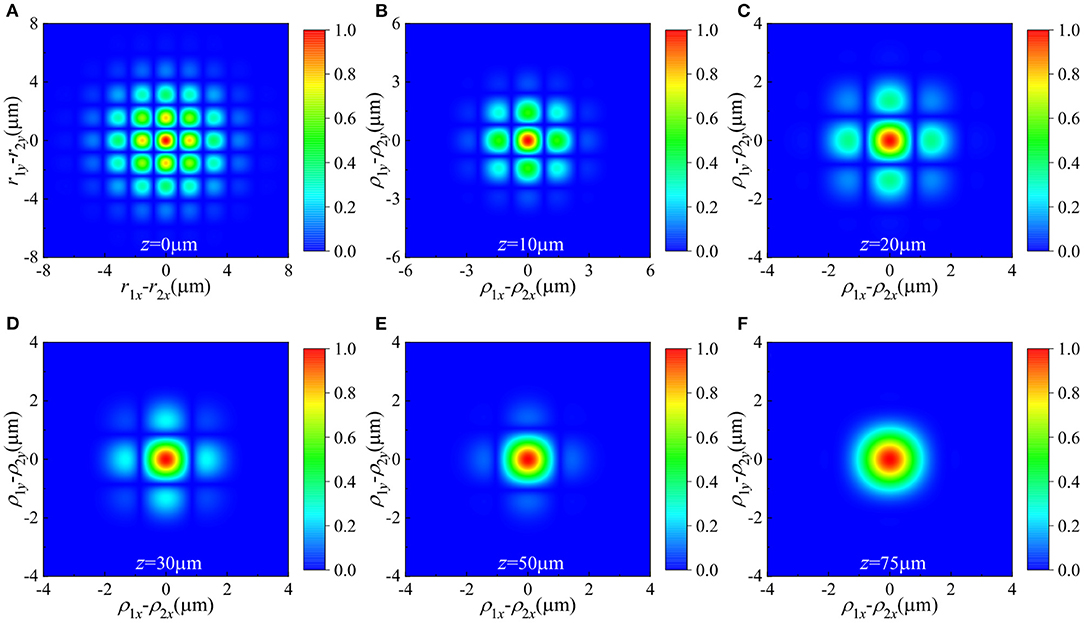
Figure 4. Density plot of the spectral degree of coherence of a HGCSM beam with m = n = 0 propagating through a turbulent biological tissue at different propagation planes. (A) z = 0μm, (B) z = 10μm, (C) z = 20μm, (D) z = 30μm, (E) z = 50μm, and (F) z = 75 μm.

To investigate the influence of beam parameters on the beam quality of HGCSM beams in biological tissues, Figure 5 shows the normalized propagation factors of HGCSM beams vs. propagation distance in turbulent biological tissue for different values of the beam orders m, n, and the transverse coherence width. The calculation parameters are m = n = 0, 1, 3, 5 in Figures 5A,B, δ_0x or δ_0y = 1λ, 2λ, 3λ, 5λ in Figures 5C,D, and other parameters used in the simulation are the same as Figure 3. Note that the propagation factor remains constant when the laser is propagating in free space. From Figure 5, one can find that normalized propagation factor increases with increasing the propagation distance z. That is, the longer the propagation distance z is, the poorer the beam quality. The normalized propagation factors of the HGCSM beam with large beam orders or small transverse coherence width increase slower than the HGCSM beam with small beam orders or large transverse coherence width on propagation. In other words, the larger the beam order or the smaller the transverse coherence width, the smaller the influence of refractive-index fluctuations of the biological tissue on the HGCSM beams. In addition, it can also be seen from Figures 5A,B that the HGCSM beam is less affected by turbulence than of the GSM beam (m=n=0) under the same condition. The normalized propagation factor in the direction is equal to the normalized propagation factor in the direction when the corresponding beam parameters are the same.

FIGURE 5

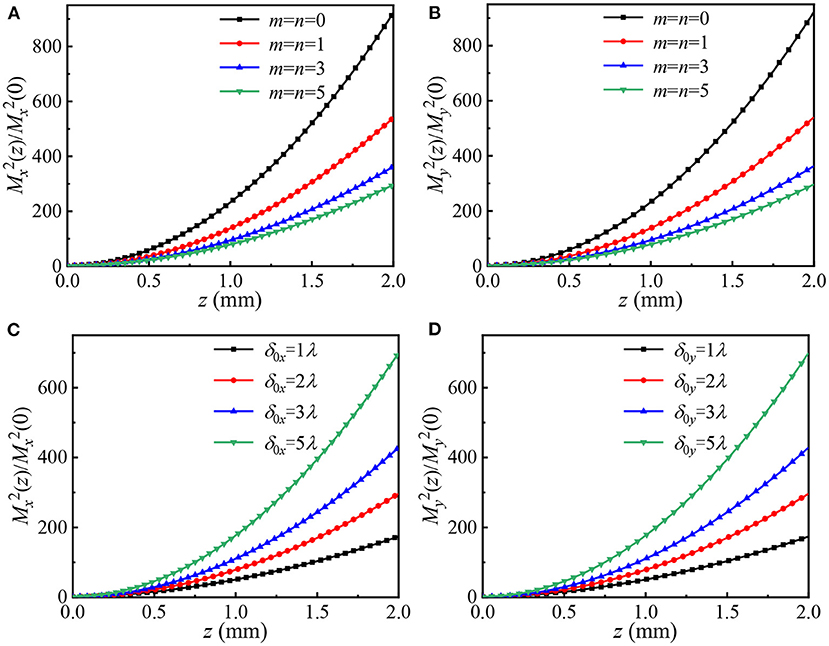
Figure 5. Normalized propagation factors of HGCSM beams vs. propagation distance in turbulent biological tissue for different values of the mode orders m, n, and the transverse coherence width. (A,C) along x direction, (B,D) along y direction.

Figures 6A–C, respectively, display the normalized propagation factors of HGCSM beams propagation through turbulent biological tissue vs. propagation distance for different fractal dimension D_f, characteristic length of heterogeneity l_c, and small length-scale factor l₀. The calculation parameters are D_f=3, 3.3, 3.67, 4 in Figure 6A, l_c=0.6, 0.8, 1.0, 1.2μ m in Figure 6B, l₀=0.6, 0.8, 1.0, 1.2μ m in Figure 6C, and other calculation parameters are the same as in Figure 4. From Figures 6A–C, one sees that the normalized propagation factor decreases with increasing the fractal dimension, and the small length-scale factor, as well as, decreasing the characteristic length of heterogeneity. This analysis suggests that the larger the fractal dimension and the small length-scale factor are, or the smaller the characteristic length of heterogeneity is, the weaker tissue turbulence is, the smaller the normalized propagation factor is, and the better the beam quality of HGCSM beams propagating in turbulent biological tissue is.

FIGURE 6

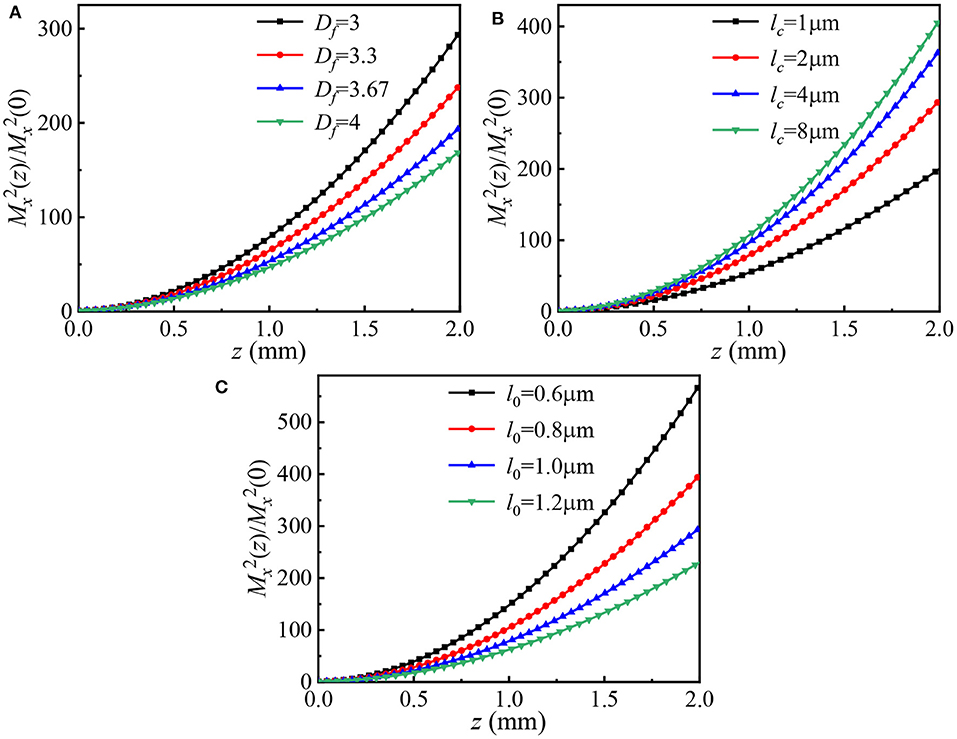
Figure 6. Normalized propagation factors of HGCSM beams vs. propagation distance in turbulent biological tissue for different values of (A) the fractal dimension, (B) the characteristic length of heterogeneity, and (C) the small length-scale factor.

Conclusion

In this paper, based on the extended Huygens-Fresnel principle, the expressions for the average intensity and the spectral degree of coherence of HGCSM beams propagation in turbulence of biological tissue are derived. The average intensity, the spectral degree of coherence, and the dependence of the propagation factors on the beam orders, the transverse coherence width, the fractal dimension D_f, the characteristic length of heterogeneity l_c, and the small length-scale factor are numerically investigated. The results show that the HGCSM beam does not exhibit self-splitting characteristics on propagation in tissues due to the strong turbulence in refractive index of biological tissue. The spectral degree of coherence evolves from an array to a Gaussian distribution over a short propagation distance. The larger the beam orders, the fractal dimension and the small length-scale factor are, or the smaller the transverse coherence width and the characteristic length of heterogeneity are, the smaller the normalized propagation factor is, and the better the beam quality of HGCSM beams in turbulence of biological tissue is. In addition, the HGCSM beam is less affected by turbulence than of GSM beam under the same condition. The results presented in this paper may be helpful to improving the propagation quality of structured beams in tissue optics field.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

YH and HZ proposed the project. HZ and JG conducted the equation derivation, simulation, and image processing. HZ, ZC, and CC wrote the manuscript. All authors reviewed the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No.61675159), and the Natural Science Foundation of Shaanxi Province (Grant No. 2020JM-210).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Horstmeyer R, Ruan H, Yang C. Guidestar-assisted wavefront-shaping methods for focusing light into biological tissue. Nat Photonics. (2015) 9:563–71. doi: 10.1038/nphoton.2015.140

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Yu H, Park J, Lee K, Yoon J, Kim K, Lee S, et al. Recent advances in wavefront shaping techniques for biomedical applications. Curr Appl Phys. (2015) 15:632–41. doi: 10.1016/j.cap.2015.02.015

CrossRef Full Text | Google Scholar

3. Blackberrie E, Lediju BMA. Design of a multifiber light delivery system for photoacoustic-guided surgery. J Biomed Opt. (2017) 22:041011. doi: 10.1117/1.JBO.22.4.041011

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Lu G, Fei B. Medical hyperspectral imaging: a review. J Biomed Opt. (2014) 19:10901. doi: 10.1117/1.JBO.19.1.010901

CrossRef Full Text | Google Scholar

5. Puxiang L, Lidai W, Wei TJ, Wang LV. Photoacoustically guided wavefront shaping for enhanced optical focusing in scattering media. Nat Photonics. (2015) 9:126–132. doi: 10.1038/nphoton.2014.322

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Jacques SL. Optical properties of biological tissues: a review. Phys Med Biol. (2013) 58:R37–R61. doi: 10.1088/0031-9155/58/11/R37

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Aymar G, Becker T, Boogert S, Borghesi M, Xiao R. LhARA: the laser-hybrid accelerator for radiobiological applications. Front Phys-Lausanne. (2020) 8:567738. doi: 10.3389/fphy.2020.567738

CrossRef Full Text | Google Scholar

8. Goto A, Otomo K, Nemoto T. Real-time polarization-resolved imaging of living tissues based on two-photon excitation spinning-disk confocal microscopy. Front Phys-Lausanne. (2019) 7:56. doi: 10.3389/fphy.2019.00056

CrossRef Full Text | Google Scholar

9. Schmitt JM, Kumar G. Turbulent nature of refractive-index variations in biological tissue. Opt Lett. (1996) 21:1310–2. doi: 10.1364/OL.21.001310

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Xu M, Alfano RR. Fractal mechanisms of light scattering in biological tissue and cells. Opt Lett. (2005) 30:3051–3. doi: 10.1364/OL.30.003051

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Sheppard CJ. Fractal model of light scattering in biological tissue and cells. Opt Lett. (2007) 32:142–4. doi: 10.1364/OL.32.000142

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Radosevich AJ, Yi J, Rogers JD, Backman V. Structural length-scale sensitivities of reflectance measurements in continuous random media under the Born approximation. Opt Lett. (2012) 37:5220–2. doi: 10.1364/OL.37.005220

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ye L, Yixin Z, Yun Z, Lin Y. Modified biological spectrum and SNR of Laguerre-Gaussian pulsed beams with orbital angular momentum in turbulent tissue. Opt Express. (2019) 27:9749–62. doi: 10.1364/OE.27.009749

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Gao W. Changes of polarization of light beams on propagation through tissue. Opt Commun. (2006) 260:749–54. doi: 10.1016/j.optcom.2005.10.064

CrossRef Full Text | Google Scholar

15. Gao W, Korotkova O. Changes in the state of polarization of a random electromagnetic beam propagating through tissue. Opt Commun. (2007) 270:474–8. doi: 10.1016/j.optcom.2006.09.061

CrossRef Full Text | Google Scholar

16. Wu Y, Zhang Y, Wang Q, Hu Z. Average intensity and spreading of partially coherent model beams propagating in a turbulent biological tissue. J Quant Spectrosc Radiat Transf. (2016) 184:308–15. doi: 10.1016/j.jqsrt.2016.08.001

CrossRef Full Text | Google Scholar

17. Lin Y, Yixin Z. Beam spreading and wander of partially coherent Lommel-Gaussian beam in turbulent biological tissue. J Quant Spectrosc Radiat Transf. (2018) 217:315–20. doi: 10.1016/j.jqsrt.2018.05.036

CrossRef Full Text | Google Scholar

18. Lingyan S, Lukas L, Wubao W, Robert A, Adrián R-C. Propagation of Gaussian and Laguerre-Gaussian vortex beams through mouse brain tissue. J Biophotonics. (2017) 10:1756–60. doi: 10.1002/jbio.201700022

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Mamani S, Shi L, Ahmed T, Karnik R, Rodríguez-Contreras A, Nolan D, et al. Transmission of classically entangled beams through mouse brain tissue. J Biophotonics. (2018) 11:e201800096. doi: 10.1002/jbio.201800096

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Duan M, Tian Y, Zhang Y, Li J. Influence of biological tissue and spatial correlation on spectral changes of Gaussian-Schell model vortex beam. Opt Lasers Eng. (2020) 134:106224. doi: 10.1016/j.optlaseng.2020.106224

CrossRef Full Text | Google Scholar

21. Liu D, Zhong H, Wang Y. Intensity properties of anomalous hollow vortex beam propagating in biological tissues. Optik. (2018) 170:61–9. doi: 10.1016/j.ijleo.2018.05.098

CrossRef Full Text | Google Scholar

22. Katsev IL, Prikhach AS, Kazak NS, Kroening M. Peculiarities of propagation of quasi-diffraction-free light beams in strongly scattering absorbing media. Quantum Electron. (2006) 36:357–62. doi: 10.1070/QE2006v036n04ABEH013151

CrossRef Full Text | Google Scholar

23. Ni Y, Zhou Y, Zhou G, Chen R. Characteristics of partially coherent circular flattened gaussian vortex beams in turbulent biological tissues. Appl Sci. (2019) 9:969. doi: 10.3390/app9050969

CrossRef Full Text | Google Scholar

24. Gke MC, Baykal Y, Ata Y. Laser array beam propagation through liver tissue. J Vis. (2020) 23:331–8. doi: 10.1007/s12650-020-00630-5

CrossRef Full Text | Google Scholar

25. Saad F, Belafhal A. A theoretical investigation on the propagation properties of Hollow Gaussian beams passing through turbulent biological tissues. Optik. (2017) 141:72–82. doi: 10.1016/j.ijleo.2017.05.054

CrossRef Full Text | Google Scholar

26. Gori F, Santarsiero M. Devising genuine spatial correlation functions. Opt Lett. (2008) 32:3531–3. doi: 10.1364/OL.32.003531

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Gori F, Ramírez-Sánchez V, Santarsiero M, Shirai T. On genuine cross-spectral density matrices. J Opt A. (2009) 11:85706–7. doi: 10.1088/1464-4258/11/8/085706

CrossRef Full Text | Google Scholar

28. Chen Y, Gu J, Wang F, Cai Y. Self-splitting properties of a Hermite-Gaussian correlated Schell-model beam. Phys Rev A. (2015) 91:013823. doi: 10.1103/PhysRevA.91.013823

CrossRef Full Text | Google Scholar

29. Chen Y, Wang F, Yu J, Liu L, Cai Y. Vector Hermite-Gaussian correlated schell-model beam. Opt Express. (2016) 24:15232–15250. doi: 10.1364/OE.24.015232

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Jiayi Y, Yahong C, Lin L, Xianlong L, Yangjian C. Splitting and combining properties of an elegant Hermite-Gaussian correlated Schell-model beam in Kolmogorov and non-Kolmogorov turbulence. Opt Express. (2015) 23:13467–81. doi: 10.1364/OE.23.013467

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Liang C, Xu Z, Liu X, Chen Y, Cai Y. Self-healing properties of Hermite-Gaussian correlated Schell-Model beams. Opt Express. (2020) 28:2828–37. doi: 10.1364/OE.383805

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Andrews LC, Phillips RL. Laser Beam Propagation Through Random Media. Bellingham, WA: SPIE Press (2005) doi: 10.1117/3.626196

CrossRef Full Text | Google Scholar

33. Wang SCH, Plonus MA. Optical beam propagation of a partially coherent source in the turbulent atmosphere. J Opt Soc Am. (1979) 69:1297–304. doi: 10.1364/JOSA.69.001297

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Gradshteyn IS, Ryzhik IM. Table of Integrals, Series and Products. New York, NY: Academic Press (2007).

PubMed Abstract | Google Scholar