Experimental Approaches to Neutrino Nuclear Responses for ββ Decays and Astro-Neutrinos

1 Neutrinoless ββ‐Decays and Astro-Neutrino Nuclear Interactions

Fundamental properties of neutrinos such as the Majorana nature and the neutrino masses, which are beyond the standard electro-weak model, are well investigated by studying neutrinoless double beta decays ($\beta \beta$-decays) in nuclei. Inverse beta decays (inverse β-decays) induced by neutrino nuclear interactions are used to study astro-neutrino nucleo-syntheses and astro-neutrino productions [1–3].

The $\beta \beta$ rate $T^{0\nu }$ for the light Majorana-neutrino mass mode is expressed as [4–6].

$T^{0\nu }=g_A^4{G}^{0\nu }|M^{0\nu }{m}^{eff}{|}^2,B^{0\nu }=|M^{0\nu }{|}^2,(1)$

where $G^{0\nu }$ is the phase space, $B^{0\nu }$ is the nuclear response and $m^{eff}$ is the effective neutrino mass. $M^{0\nu }$ is the nuclear matrix element (NME). The axial vector weak coupling is $g_A=1.27$ in units of the vector coupling for a free nucleon. The $\beta \beta$ nuclei to be considered are even-even nuclei.

Astro-neutrino (supernova- and solar-neutrinos) nuclear interaction rate $T^{\nu }\left(i\right)$, i.e., the inverse β-decay rate, for the ith nuclear state is given as [1, 2].

$T^{\nu }\left(i\right)={\displaystyle \int g_A^2{G}^{\nu }\left(i,E_{\nu }\right)B_i^{\nu }{f}_{\nu }\left(E_{\nu }\right)d{E}_{\nu },B_i^{\nu }=|M_i^{\nu }{|}^2{\left(2J+1\right)}^{-1},}(2)$

where $G^{\nu }\left(i,E_{\nu }\right)$ is the phase space volume, $B_i^{\nu }$ is the nuclear response, and $f_{\nu }\left(E_{\nu }\right)$ is the neutrino flux. $B_i^{\nu }$ is expressed in terms of the NME $M_i^{\nu }$ and the initial state spin J.

The $\beta \beta$ NME $M^{0\nu }$ and the inverse β-decay NME $M_i^{\nu }$ are crucial for extracting the effective neutrino-mass of the particle physic interest and the neutrino flux of the astro-physics interest from the experimental $\beta \beta$ rate and the inverse β-decay rate, respectively. They are important to design the $\beta \beta$ and astro-neutrino detectors since the nuclear isotopes used in $\beta \beta$ and astro-neutrino detectors depend on their NMEs [2, 3]. Accurate theoretical calculations for the $\beta \beta$ and inverse β-decay NMEs, however, are very hard since they depend much on models and parameters used for the calculations [1, 2, 7–9].

Recently, nuclear and muon (lepton) charge-exchange reactions (CERs) have been shown to be used to provide experimentally single-${\beta }^{\pm }$ NMEs associated with the $\beta \beta$ and astro-neutrino NMEs [1–3, 6]. The present report aims at critical reviews on perspectives of experimental approaches to the $\beta \beta$ and astro-neutrino nuclear responses by means of the nuclear and leptonic (muon) CERs and others.

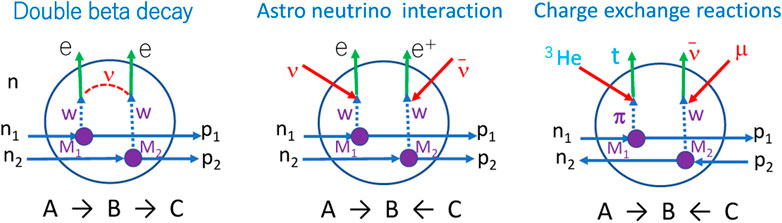
We consider mainly the ground-state to ground-state $\left(0^{+}\to 0^{+}\right)$$\beta \beta$ decay of ${}_Z{}^A\mathrm{X}\leftrightarrow {}_{Z+2}{}^A\mathrm{X}$, the ground-state to the ith state astro-neutrino transition of ${}_Z{}^A\mathrm{X}{\to }_{Z+1}^A{\mathrm{X}}_i$ and the ground-state to the ith state astro-antineutrino transition of ${}_{Z+1}{}^A\mathrm{X}\leftarrow {}_{Z+2}{}^A\mathrm{X}$. The $\beta \beta$ decay and astro-neutrino transition schemes are illustrated in Figure 1. Hereafter $\beta \beta$ and astro-neutrino stand for, respectively, neutrinoless $\beta \beta$ and astro-neutrino and astro-antineutrino unless specified. The $\beta \beta$ NME is expressed as [1, 2, 6].

$M^{0\nu }={\displaystyle \sum }_{\alpha }{g}_{\alpha }^2{M}^{0\nu }\left(\alpha \right),M^{0\nu }\left(\alpha \right)={\displaystyle \sum }_i{M}_i^{0\nu }\left(\alpha \right),(3)$

where α = GT, T, F stand for the Gamow-Teller, tensor and Fermi transitions and $g_{\alpha }$ is the weak coupling in units of $g_A$ and $M_i^{0\nu }\left(\alpha \right)$ is the α mode $\beta \beta$ NME via the ith state in the intermediate nucleus of ${}_{Z+1}{}^A\mathrm{X}$. The $\beta \beta$ NME $M_i^{0\nu }\left(\alpha \right)$ associated with the ν-exchange between two neutrons is expressed as $M_i^{0\nu }\left(\alpha \right)=<T_{\alpha }{h}_i\left(\alpha \right){>}_i$ with $T_{\alpha }$ and $h_i\left(\alpha \right)$ being the α mode transition operator and the neutrino potential for the $\beta \beta$ decay via the ith intermediate state [2, 4, 6, 7]. $T_{\alpha }$ operators for α = GT. F and T are given, respectively, by $\tau \tau \sigma \sigma ,\tau \tau ,\mathrm{and}\tau \tau \left(\sigma r\sigma r-\sigma \sigma /3\right)$ where $\tau ,\sigma$ are the isospin and spin operators and r is the distance between the two neutrons. Among GT, F, and T NMEs, the GT and F NMEs are dominant. Experimental measurements of the $\beta \beta$ NMEs are not possible unless the $\beta \beta$ rates and the neutrino-masses are measured, while two-neutrino $\beta \beta$$\left(2\nu \beta \beta \right)$ NMEs have been derived from the measured rates.

FIGURE 1

FIGURE 1. Decay and interaction schemes. (A): Double beta decay. (B): Astro-neutrino and astro-antineutrino interactions. (C): Nuclear (³He) and leptonic (muon) charge-exchange reactions (CERs). W and π are weak boson and pion involved in the weak and nuclear CERs, respectively.

The astro-neutrino NME for the ith state is expressed as [1, 2].

$M_i^{\nu }={\displaystyle \sum }_{\alpha \prime }{M}_i^{\pm }\left({\alpha }^{\prime }\right),(4)$

where $M_i^{\pm }\left({\alpha }^{\prime }\right)$ is the ${\alpha }^{\prime }$-mode single-${\beta }^{\pm }$ NME for the ith state. Here ${\beta }^{+}$ and ${\beta }^{-}$ refer to the anti-neutrino ${\tau }^{+}$ transition of ${}_{Z+1}{}^A\mathrm{X}\leftarrow {}_{Z+2}{}^A\mathrm{X}$ and the neutrino ${\tau }^{-}$ transition of ${}_Z{}^A\mathrm{X}{\to }_{Z+1}^A$ respectively, as shown in Figure 1. The transition modes include the allowed F transition, the allowed GT transition, the first-forbidden unique transition, the first forbidden non-unique transition, and so on.

2 Neutrino Nuclear Responses for ββ‐Decays and Astro-Neutrinos

So far, neutrino nuclear responses and their NMEs have been measured mainly by ${\beta }^{\pm }$ and electron capture, and thus they are limited mostly to ground-state and low-momentum GT (1⁺) transitions. There are several specific features of $\beta \beta$ and astro-neutrino nuclear responses (NMEs) to be considered [1, 2].

1. $\beta \beta$ and astro-neutrino NMEs involve wide ranges of momentum, spin and excitation energy [2, 6, 7]. In case of the light neutrino-mass mode $\beta \beta$, the Majorana neutrino is exchanged between two nucleons with distance r in the nucleus. Then the linear and angular momenta and the excitation energy involved in $\beta \beta$ are around 1/r = 30–120 MeV/c, $l\hslash \approx 0\text{–}5\hslash$ and E_i = 0–30 MeV. Supernova neutrinos are in the wide energy range of 10–50 MeV, depending on the temperature. Then the energetic neutrinos may excite final states up to around 40 MeV with spin transfers of $\text{Δ}{J}^{\pi }=0^{\pm },1^{\pm },2^{\pm }$ and so on.

2. $\beta \beta$ and astro-neutrino interactions are expressed in terms of the isospin (τ) and spin (σ) operators. Thus the NMEs are necessarily very sensitive to nucleonic and non-nucleonic τ and $\tau \sigma$ interactions and correlations. Nuclear τ and $\tau \sigma$ interactions are repulsive in nature, and thus most τ and $\tau \sigma$ strengths are pushed up to the τ and $\tau \sigma$-type giant resonances in the high excitation region, leaving little strengths in the low-lying quasi-particle states involved in the DBDs and astro-neutrinos [1–3].

3. The τ and $\tau \sigma$ interactions and correlations are associated with both the nucleons (protons and neutrons) and non-nucleonic hadrons (mesons, $\text{Δ}$-baryons). The $\beta \beta$ and astro-neutrino NMEs are sensitive to nuclear medium changes from the initial to final states, resulting in the reduction of the NMEs.

4. Axial-vector NMEs for nuclear $\beta \gamma$ transitions are quenched with respect to the NMEs calculated by the proton-neutron quasi-particle random-phase approximation, which includes nucleonic $\tau \sigma$ interactions and correlations but not explicitly the non-nucleonic correlations and nuclear medium effects [1, 2, 10, 11]. Such quenching effect is incorporated by using the effective axial-vector coupling $g_A^{eff}=k{g}_A$, where $g_A=1.27$ is the coupling for a free nucleon and k is the quenching coefficient [1–3].

5. Accurate theoretical calculations for the $\beta \beta$ and astro-neutrino NMEs are very hard since the medium heavy nuclei involved in the NMEs are very complex many-body strongly interacting hadron (nucleon, meson, $\text{Δ}$-baryon, and others) systems [2, 7, 8]. Then the NMEs are very sensitive to all kinds of nucleonic, non-nucleonic and nuclear medium effects. Furthermore, the NMEs themselves are only a very tiny (10⁻²–10⁻³) fraction of the total strength. Actually, theoretical $\beta \beta$ NMEs scatter over an order of magnitude depending on the models and the parameters such as $g_A^{eff}$ and nuclear interactions [2, 6].

3 Experimental Approaches to $\beta \beta$ and Astro-Neutrino Responses

The $\beta \beta$ and astro-neutrino NMEs have recently been studied by using nuclear and muon CERs as given in the reviews and references there in [1, 2]. Here we discuss mainly the single ${\beta }^{-}$ NME $M_i^{-}\left({\alpha }^{\prime }\right)$ for ${}_Z{}^A\mathrm{X}\to {}_{Z+1}{}^A\mathrm{X}$ and single ${\beta }^{+}$NME $M_i^{+}\left(\alpha \prime \right)$ for ${}_{Z+1}{}^A\mathrm{X}\leftarrow {}_{Z+2}{}^A\mathrm{X}$ (see Figure 1). They are the ${\tau }^{-}$ and ${\tau }^{+}$-side NMEs, which the $\beta \beta$ NME for the ith intermediate state is associated with through the neutrino potential, and are the NMEs relevant to the astro-neutrino and astro-antineutrino reactions for the ith state in ${}_{Z+1}{}^A\mathrm{X}$, respectively. The $M_i^{-}\left(\text{GT}\right)$ and $M_i^{+}\left(\text{GT}\right)$ for low-lying quasi-particle states have been used to evaluate the $2\nu \beta \beta$ NMEs, and the evaluated NMEs agree with the NMEs derived from the observed $2\nu \beta \beta$ rates [12].

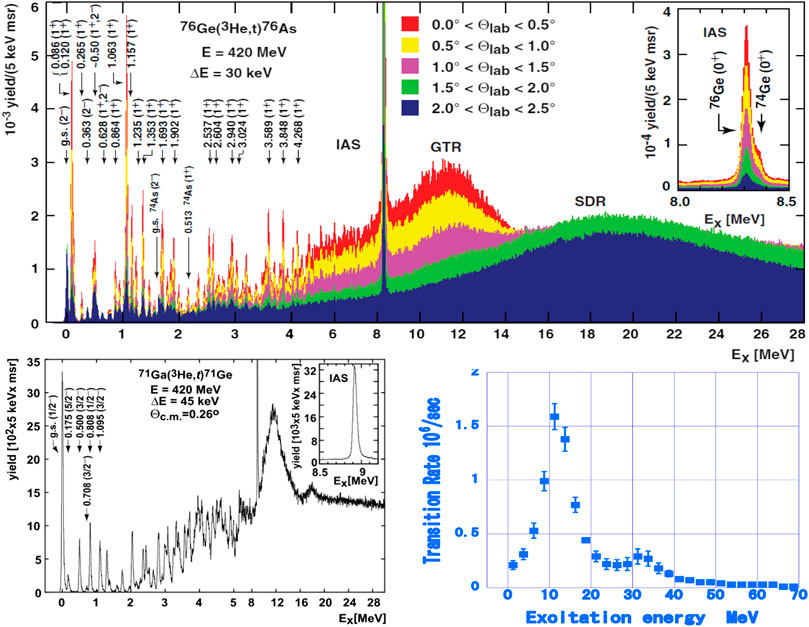
Medium energy (³He,t) reactions with E(³He) = 0.42 GeV at Research Center for Nuclear Physics (RCNP) are shown to be powerful for studying ${\tau }^{-}$-side $\tau \sigma$ responses in the wide momentum (0–120 MeV/c) and excitation energy (0–30 MeV) regions [1, 2]. The axial-vector ${\alpha }^{\prime }=\mathrm{GT}\left({\mathrm{1}}^{\mathrm{+}}\right)$ and ${\alpha }^{\prime }=\mathrm{SD}$ (spin dipole 2⁻) NMEs in nuclei of $\beta \beta$ and astro-neutrino interests are measured [1, 2, 13–17]. The measured spectrum for ⁷⁶Ge [13] is shown in Figure 2. GT NMEs are the NMEs involved mainly in the $2\nu \beta \beta$ decays and the low-energy astro-neutrinos, while SD NMEs are major components associated with the neutrinoless DBDs and medium energy astro-neutrinos [2].

FIGURE 2

FIGURE 2. CER strengths as a function of the excitation energy. Top: The ⁷⁶Ge(³He,t)⁷⁶As reaction for $\beta \beta$ responses, where the GT s-wave strengths (red lines) are preferentially excited at the forward angles, while SD p-wave strengths (blue lines) at larger angles [13]. Bottom left-panel: The ⁷¹Ga(³He,t) ⁷¹Ge reaction for solar neutrino responses [14]. Bottom right-panel: The ${}^{100}\mathrm{M}\mathrm{o}\left(\mu ,{\nu }_{\mu }\right)$ Nb reactions [20]. The strong GT and SD giant resonances, GTR and SDR, at around 12 and 20 MeV are seen in the spectrum of ⁷⁶Ge(³He,t)⁷⁶ As.

The measured GT and SD NMEs are quenched by the coefficient $k=g_A^{eff}/g_A\approx 0.4\text{–}0.6$ with respect to the NMEs by the quasi-particle random-phase approximation [1, 2, 11]. The measured GT and SD responses (square of NME) for low excitation region are only a few % of the total strength and most of them are located at the highly excited giant resonances, as shown in Figure 2. The giant resonances are coherent $\tau \sigma$ excitations with the large NMEs. They mix in the low-lying GT and SD states with the negative (out-phase) mixing coefficient via the repulsive interaction. Thus the GT and SD NMEs for the low-lying states are quenched by the mixing effect of the high-lying GT and SD giant resonances, respectively.

Ordinary muon capture (OMC) [18] is a muon charge-exchange reaction (μ-CER). It is used for studying the $M_i^{+}\left({\alpha }^{\prime }\right)$ NMEs [2]. A negative muon trapped in an inner atomic orbit is captured into the nucleus. The process is a lepton CER of $\mathrm{\mu }{\mathrm{+}}_{Z+2}^A\mathrm{X}\to {\nu }_{\mu }{+}_{Z+1}^A{\mathrm{X}}_{\mathit{i}}$. The momentum and energy transferred to the nucleus are around 95–50 MeV/c and 5–50 MeV, which are the regions of DBDs and astro-neutrinos.

μ-CERs on Mo isotpes [19] and $\beta \beta$ nuclei have been studied by using low-momentum muons from the MuSIC beam line at RCNP [2, 20]. The ith excited state of ${}_{Z+1}{}^A{{\displaystyle \mathrm{X}}}_{\mathit{i}}$ produced by the μ-CER on ${}_{Z+2}{}^A\mathrm{X}$ decays by emitting a number (x) of neutrons and gamma rays to the ground state of ${}_{Z+1}{}^{A-x}\mathrm{X}$. The number x depends on the excitation energy $E_i$. The residual nuclei are identified by measuring γ rays characteristic of them. Then the μ-CER strength distribution in ${}_{Z+1}{}^A\mathrm{X}$ as a function of the excitation energy $E_i$ is obtained from the measured mass-number ($A-x$) distribution by using the neutron cascade-emission model [20]. The μ-CER strength distribution for ¹⁰⁰Mo [20] show a strong μ-giant resonance around $E_i\approx 12\mathrm{MeV}$, as shown in Figure 2. Since μ-CER excites mainly states with $J^{\pi }=0^{\pm },1^{\pm },2^{\pm },\mathrm{and}{3}^{\pm }$, the giant resonance is a composite of the resonances with these spins. The observed strength distribution agrees with the calculation using the quasi-particle random-phase approximation [21]. The muon-capture rate is smaller by a factor around 5 with respect to the calculated rate, suggesting the quenching coefficient of $g_A^{eff}/g_A\approx 0.5$ [21].

4 Perspectives and Remarks on Neutrino Nuclear Responses

The high energy-resolution (³He,t) CERs at RCNP are well used for studying the ${\tau }^{-}$-side $M_i^{-}\left({\alpha }^{\prime }\right)$ NMEs with ${\alpha }^{\prime }=\mathrm{GT}\left({\mathrm{1}}^{\mathrm{+}}\right)$ and SD (2⁻) in the wide momentum and energy regions involved in $\beta \beta$-decays and astro-neutrinos. They are extended to higher-multipole NMEs $M_i^{-}\left({\alpha }^{\prime }\right)$ with ${\alpha }^{\prime }=\mathrm{SQ}$ (spin quadra-pole 3⁺) and SO (spin octa-pole 4⁻). The ${\tau }^{+}$-side NMEs of $M_i^{+}\left({\alpha }^{\prime }\right)$ are studied by using (d,²He) [22] and (t,³He) CERs [1]. Higher energy-resolution studies of unbound ²He from the (d,²He) CER is interesting to study the ${\tau }^{+}$-side NMEs for individual states.

The axial-vextor (GT, SD, and higher multi-pole) strength distributions in the wide excitation region are interesting to see how the axial vector NMEs at the low lying quasi-particle states are quenched due to the destructive interference with the high-lying giant resonances, and how the summed strengths over the giant resonances are somewhat reduced by the possible effects of the $\text{Δ}$ baryons [2, 11].

Double charge-exchange reactions explore double τ and $\tau \sigma$ responses for $\beta \beta$ responses [2, 3, 23]. The RCNP (¹¹B, ¹¹Li) data indicate a large strength at the high excitation region and little one at the low-lying states. Extensive studies of double charge-exchange reactions are under progress at INFN-LNS [23].

μ-CERs are used to study the NME $M_i^{+}\left({\alpha }^{\prime }\right)$ in wide momentum and energy regions relevant to $\beta \beta$-decays and astro-neutrinos. The observed μ giant resonance around $E_i\approx 12\mathrm{MeV}$ suggests concentration of the ${\tau }^{+}$-strengths at the highly excited giant resonance, resulting in the quenching of the NMEs at low-lying states, as in case of the ${\tau }^{-}$-side responses. In fact, the absolute μ-CER strength is much smaller than the calculated one [21, 24], suggesting the severe quenching as in case of ${\tau }^{-}$ responses. The recent calculations, however, reproduce the observed rates with the bare $g_A$ [25]. The two calculations are based on the quasi-particle random-phase approximation, but use different nuclear parameters. Thus the calculated strength distributions and the calculated multipole components are different between the two calculations. So the origins of the differences are open questions. Actually, the μ-CER rate is a product of the phase space factor and the neutrino nuclear response (square of the NME). It is important to compare the experimental μ-CER NME with the theoretical NME to see if one needs a quenched $g_A^{eff}$ as in case of the NMEs studied in single ${\beta }^{\pm }$. Further experimental and theoretical studies of the μ-CERs for nuclei of $\beta \beta$ and astro-neutrino interests are interesting to investigate the NMEs $M_i^{+}\left({\alpha }^{\prime }\right)$ up to around 50 MeV.

Medium-energy neutrinos are of potential interest for direct measurements of neutrino nuclear responses [26]. High-intensity medium-energy (1–3 GeV) proton accelerators at SNS ORNL and MLF KEK and others are used to produce intense pions, and neutrinos of the order of 10¹⁵/sec are obtained from the $\pi -\mu$ decays. Neutrino and anti-neutrino CERs of $\nu \left(\overline{\nu }\right)\to {\mathrm{e}}^{-}\left({\mathrm{e}}^{+}\right)$ are used to study $\left(M_i^{+}\left({\alpha }^{\prime }\right)\right)$ NMEs. Neutrino nuclear cross-sections are of the order of 10⁻⁴⁰ cm². Then one may use multi-ton scale isotopes as used for $\beta \beta$ experiments to study neutrino nuclear responses.

Electro-magnetic interaction includes isovector and isoscalar components. They are analogous to the charged and neutral current responses of the neutrino (weak) interaction, respectively. Thus one gets information of the neutrino NME by studying the isovector component of the EM transition [2, 9]. The special case is the photo-nuclear excitation of the isobaric analogue state of T${}^{-}|\text{i}>$ with ${\mathrm{T}}^{-}$ being the isosin lowering operator [1, 2, 27]. The NME for the weak transition of $|\text{i}>\to |\text{f}>$ is obtained from the analogous EM NME for the γ transition from the isobaric analogue state to $|\text{f}>$ [2].

Nucleon transfer reactions are used to measure single quasi-particle occupation probabilities. The summed probability is quenched by 0.5–0.6 with respect to the nucleon-based model value [28]. This suggests some non-nucleonic and nuclear medium effects as in the neutrino responses [2].

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Ejiri H. Nuclear spin isospin responses for low-energy neutrinos. Phys Rep (2000) 338:265. doi:10.1016/s0370-1573(00)00044-2

CrossRef Full Text | Google Scholar

2. Ejiri H, Suhonen J, Zuber K. Neutrino-nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys Rep (2019) 797:1. doi:10.1016/j.physrep.2018.12.001

CrossRef Full Text | Google Scholar

3. Ejiri H. Neutrino-mass sensitivity and nuclear matrix element for neutrinoless double beta decay. Universe (2020) 6:225. doi:10.3390/universe6120225

CrossRef Full Text | Google Scholar

4. Doi M, Kotani T, Takasugi E. Double beta decay and majorana neutrino. Prog Theor Phys Suppl (1985) 83:1–175. doi:10.1143/ptps.83.1

CrossRef Full Text | Google Scholar

5. Avignone FT, Elliott SR, Engel J. Double beta decay, majorana neutrinos, and neutrino mass. Rev Mod Phys (2008) 80:481. doi:10.1103/revmodphys.80.481

CrossRef Full Text | Google Scholar

6. Vergados JD, Ejiri H, Šimkovic F. Theory of neutrinoless double-beta decay. Rep Prog Phys (2012) 75:106301. doi:10.1088/0034-4885/75/10/106301

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Suhonen J, Civitarese O. Double-beta decay nuclear matrix elements in the QRPA framework. J Phys G Nucl Part Phys (2012) 39:035105. doi:10.1088/0954-3899/39/8/085105

CrossRef Full Text | Google Scholar

8. Engel J, Menéndez J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: a review. Rep Prog Phys (2017) 80:046301. doi:10.1088/1361-6633/aa5bc5

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Jokiniemi L, Ejiri H, Frekers D, Suhonen J. Neutrinoless nuclear matrix elements using isovector spin-dipole data. Phys Rev C (2018) 98:024608. doi:10.1103/physrevc.98.024608

CrossRef Full Text | Google Scholar

10. Suhonen J. Impact of the quenching of the on the sensitivities of 0 experiments. Phys Rev C (2017) 96:05501. doi:10.1103/physrevc.96.055501

CrossRef Full Text | Google Scholar

11. Ejiri H. Nuclear matrix elements for β and decays and quenching of the weak coupling in QRPA. Front Phys (2019).2165:020007.doi:10.1063/1.5130968

CrossRef Full Text | Google Scholar

12. Ejiri H. Fermi surface quasi particle model nuclear matrix elements for two neutrino double beta decays. J Phys Nucl Part Phys (2017) 44:15201. doi:10.1088/1361-6471/aa8a1f

CrossRef Full Text | Google Scholar

13. Thies JH, Frekers D, Adachi T, Dozono M, Ejiri H, Fujita H, et al. The (³He,t) reaction on ⁷⁶Ge, and double-β decay matrix element. Phys Rev C (2012) 86:014304. doi:10.1103/physrevc.86.014304

CrossRef Full Text | Google Scholar

14. Frekers D, Ejiri H, Akimune H, Adachi T, Bilgier B, Brown BA, et al. The ⁷¹Ga(³He,t) reaction and the low-lying neutrino response. Phys Lett B (2011) 706:134–8. doi:10.1016/j.physletb.2011.10.061

CrossRef Full Text | Google Scholar

15. Ejiri H, Frekers D. Spin dipole nuclear matrix elements for double beta decay nuclei by charge-exchange reactions. J Phys G: Nucl Part Phys (2016) 43:11LT01. doi:10.1088/0954-3899/43/11/11lt01

CrossRef Full Text | Google Scholar

16. Akimune H, Ejiri H, Hattori F, Agodi C, Alanssari M, Cappuzzello F, et al. Spin-dipole nuclear matrix element for double beta decay of ⁷⁶Ge by the (³He,t) charge-exchange reaction. J Phys G Nucl Part Phys (2020) 47:05LT01. doi:10.1088/1361-6471/ab7a87

CrossRef Full Text | Google Scholar

17. Ejiri H. Axial-vector weak coupling at medium momentum for astro neutrinos and double beta decays. J Phys G: Nucl Part Phys (2019) 46:125202. doi:10.1088/1361-6471/ab4dcb

CrossRef Full Text | Google Scholar

18. Measday DF. The nuclear physics of muon capture. Phys Rep (2001) 354:243–409. doi:10.1016/s0370-1573(01)00012-6

CrossRef Full Text | Google Scholar

19. Ejiri H, Engel J, Hazama R, Krastev P, Kudomi N, Robertson RGH. Spectroscopy of double-beta and inverse-beta decays from ¹⁰⁰Mo for neutrinos. Phys Rev Lett (2000) 85:2917. doi:10.1103/physrevlett.85.2917

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hashim I, Ejiri H, Shima T, Takahisa K, Sato A, Kuno Y, et al. Muon capture reaction on Mo to study neutrino nuclear responses for double-β decays and neutrinos of astro-physics origins. Phys Rev C (2018) 97:014617. doi:10.1103/physrevc.97.014617

CrossRef Full Text | Google Scholar

21. Jokiniemi L, Suhonen J, Ejiri H, Hashim IH. Pinning down the strength function for ordinary muon capture on ¹⁰⁰Mo. Phys Lett B (2019) 794:143–7. doi:10.1016/j.physletb.2019.05.037

CrossRef Full Text | Google Scholar

22. Dohmann H, Ba̋mer C, Frekers D, Grewe E -W, Harakeh MN, Hollstein S, et al. The (d,²He) reaction on Mo and the double-β decay matrix elements for Zr. Phys Rev C (2008) 78:041602. doi:10.1103/physrevc.78.041602

CrossRef Full Text | Google Scholar

23. Cappuzzello F, Cavallaro M, Agodi C, Bondì M, Carbone D, Cunsolo A, et al. Heavy ion double charge exchange reactions: a tool toward 0 nuclear matrix elements. Eur Phys J (2015) 51:145. doi:10.1140/epja/i2015-15145-5

CrossRef Full Text | Google Scholar

24. Jokiniemi L, Suhonen J. Muon-capture strength functions in intermediate nuclei of 0 decays. Phys Rev C (2019) 100:014619. doi:10.1103/physrevc.100.014619

CrossRef Full Text | Google Scholar

25. Simkovic F, Dvornieky R, Vogel P. Muon capture rates: evaluation within the quasiparticle random phase approximation. Phys Rev C (2020) 102:034301. doi:10.1103/PhysRevC.102.034301

CrossRef Full Text | Google Scholar

26. Ejiri H. Neutrino studies in nuclei and intense neutrino sources. Nucl Instr Methods Phys Res Sec. A (2003) 503:276–8. doi:10.1016/s0168-9002(03)00695-8

CrossRef Full Text | Google Scholar

27. Ejiri H, Titov A, Bosewell M, Yang A. Neutrino nuclear response and photonuclear reactions. Phys Rev C (2013) 88:054610. doi:10.1103/physrevc.88.054610

CrossRef Full Text | Google Scholar

28. Kay BP, Schiffer JP, Freeman SJ. Quenching of cross sections in nuclear transfer reactions. Phys Rev Lett (2013) 111:042502. doi:10.1103/physrevlett.111.042502

PubMed Abstract | CrossRef Full Text | Google Scholar