Activity-Induced Fluidization and Arrested Coalescence in Fusion of Cellular Aggregates

At long time scales, tissue spheroids may flow or appear solid depending on their capacity to reorganize their internal structure. Understanding the relationship between intrinsic mechanical properties at the single cell level, and the tissue spheroids dynamics at the long-time scale is key for artificial tissue constructs, which are assembled from multiple tissue spheroids that over time fuse to form coherent structures. The dynamics of this fusion process are frequently analyzed in the framework of liquid theory, wherein the time scale of coalescence of two droplets is governed by its radius, viscosity and surface tension. In this work, we extend this framework to glassy or jammed cell behavior which can be observed in spheroid fusion. Using simulations of an individual-cell based model, we demonstrate how the spheroid fusion process can be steered from liquid to arrested by varying active cell motility and repulsive energy as established by cortical tension. The divergence of visco-elastic relaxation times indicates glassy relaxation near the transition toward arrested coalescence. Finally, we investigate the role of cell growth in spheroid fusion dynamics. We show that the presence of cell division introduces plasticity in the material and thereby increases coalescence during fusion.

1 Introduction

A general understanding of the rheological properties of multicellular tissues is important to gain insight into the physics of morphogenetic processes during development. Furthermore, robust models of these materials allow for the design and characterization of generic unit operations, such as aggregation, dispersion, and fusion, which are used for the production of artificial tissues. Given its analogy to the merging of two liquid droplets, the fusion of tissue spheroids has received considerable interest as a model for soft tissue rheology. An analytical expression of the onset of coalescence of two equal viscous droplets under influence of their surface tension was first derived by Frenkel [1] and was improved and extended upon so that the dynamics of complete coalescence could be accurately modeled [2, 3]. Furthermore, various extensions to this framework have been proposed to take into account specific properties of multicellular materials, for example differences in spheroid size [4], and the presence of biological processes such as proliferation, differentiation and apoptosis, which may conflict with the assumption of conservation of mass [4, 5].

However, the liquid model cannot consistently reproduce in vitro tissue behavior. For instance, Kosheleva et al. showed that fusion dynamics did not correspond to liquid model predictions based on nano-indentation surface tension measurements [6]. Furthermore, arrested fusion has been observed between spheroids treated with Rho-kinase inhibitor affecting acto-myosin contractility [7, 8]. Arrested fusion was shown to be controlled by cancer cell activity in tumors [9]. To explain these observations, Oriola et al. recently proposed to model spheroids during fusion as visco-elastic materials instead of simple liquid droplets [10]. Such an approach has already been applied to parallel plate compression [11], micro-pipette aspiration [12], and tissue-detachment/fracture assays [13]. In general, a tissue may behave like an elastic solid at short time scales and like a liquid at longer time scales [14]. However, they can also appear solid-like at long time scales. This may occur when tissues change from a fluid-like to a solid-like state by undergoing a jamming transition [15]. In the jammed state, individual cells are caged by their neighbors preventing the cells from rearranging, resulting in glassy rheology, whereas in the unjammed state cells are able to move freely, resembling a fluid-like state.

Multiple computational approaches such as phase field models [16], Monte Carlo based models [17–19], and individual cell-based models [4, 10, 18–22], allow for the characterization of tissue-scale rheological behavior as a function of cell-scale mechanical properties or to simulate fusion of spheroids in more complex geometries. Schötz et al. calibrated an individual cell-based model to better describe the random motion of cells in tissues close to a glass transition. Nevertheless, when investigating fusion with that model, it could still be described by a liquid model. On the other hand, simulations that resulted in a solidification during spheroid fusion have already been mentioned by Kosztin et al. [20]. This observation was attributed to high levels of cell adhesion, but was not further analyzed. Recently, using individual cell-based computational models, it was demonstrated that a divergence of the visco-elastic relaxation time can be observed within a transition region of arrested fusion, indicative of a jammed system [10]. The existence of arrested fusion could thus be traced back to the build up of elastic energy during fusion.

In this work, we derive a simplified analytical expression for the coalescence of visco-elastic tissue spheroids on the basis of elasticity caused by internal structure of the droplet [23, 24]. Doings so we obtain similar results to [10]. We demonstrate the applicability of this expression by using an individual-cell based model approach to simulate the fusion process and, using this expression, we are able to compare the relaxation dynamics of fusion to the characteristic timescales involved in the preceding aggregation (or compaction) process in which the individual tissue spheroids have been formed. Finally, we extend this simulation framework to include a morphological model of the cell cycle. In analogy to active motility, cell division and growth may introduce excitation that may induce fluidization, as was observed in other systems [25–28]. Here, we investigate whether, in spheroid fusion, there is an additional active contribution of cell division beyond a mere correction for the increase in volume, and assess to what extent this contribution may unjam the cellular material [4, 5] and recover tissue coalescence.

2 Materials and Methods

2.1 Individual Cell-Based Model

We follow an individual cell-based model approach as described in detail in Smeets et al. [29, 30]. This model has already been used to study cell aggregation and compaction dynamics. In this paper we extend the model by taking into account cell proliferation. All details of the individual cell based model can be found in Supplementary Section S1. In brief, the model is based on a simulation framework introduced by Delile et al. [31], in which cells are simulated as self-propelled particles. Conservative active forces are exchanged between neighboring cells, similar to [10]. The connectivity network is based on a Delaunay triangulation of the cell center coordinates. For the edges of this network, a symmetric central potential is calculated, which is parameterized by adhesion $w_a$ and cortical tension $w_{\text{r}}$. Protrusive active forces are responsible for active migration with velocity $v_t$. These forces are calculated in the direction of the cell’s polarization which is randomly diffusing with rotational diffusivity $D_r$. Hence, activity from cell motility may be parameterized as $D_{\text{eff}}:=v_t^2/\left(2D_r\right)$. Overdamped equations of motion are integrated to evolve the system over time. Finally, cells are able to grow and multiply based on a cell cycle model, which is explained in Supplementary Section S1.2. The model parameters are listed in tables in Supplementary Tables S1, S2.

2.2 Simulation Setup

The simulation pipeline is shown in Figure 1 and follows a sequence of generic unit operations to form a small tissue via fusion. In the first step we simulate the seeding and spontaneous aggregation of two aggregates for 24 h, each in their own micro-well, similar to [30]. This guarantees that the shape of each spheroid is consistent with respect to its underlying mechanical properties. It should be noted that, depending on the mechanical properties that govern the aggregation process, this relaxed configuration may have a highly irregular shape. Any (few) remaining cells that did not get incorporated in the main aggregates, are removed from the simulation in analogy to a real fusion experiment. In the second step, the two aggregates are transferred to a larger micro-well and are brought into contact with each other, simulating another 50 h during which the fusion process naturally progresses. In the final step, we extract the spheroid contours and fit two circles to compute the contact angle θ for each simulation, as explained in (Supplementary Section S2). Each realization of a simulated fused spheroid is initialized independently. To calculate the average fusion dynamics, i.e., the average of $\text{sin}{\left[\theta \left(t\right)\right]}^2$ across all repeats, we take into account that not all spheroids start fusing at the same time, because the initial contact between the spheroids can be weak. To account for this, we define the time at which fusion starts as the last time at which we observe two distinct objects in the extracted contours. For further analysis, the extracted shape measures are shifted in time using this offset.

FIGURE 1

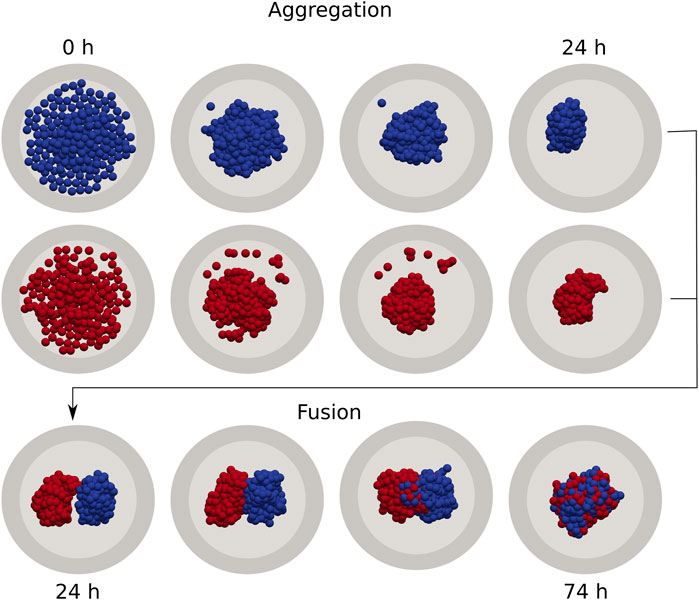
FIGURE 1. Individual cell-based model of cell aggregation and spheroid fusion. First, gravitationally deposited cells aggregate in independent cylindrical wells for 24 h (top). Next, two aggregates are extracted and combined in a single fusion simulation, which continues for a further 50 h (bottom).

2.3 Visco-Elastic Approximation of the Fusion Process

The fusion dynamics of two equal visco-elastic spheres can be approximated by the differential equation

$\dot{\theta }=\frac{\text{Γ}}{2a_0\eta }\text{cot}\left(\theta \right)-\frac{G\prime }{8\eta }\text{sin}\left(\theta \right)=\frac{\text{cot}\left(\theta \right)}{2{\tau }_{\text{Γ}}}-\frac{\text{sin}\left(\theta \right)}{2{\tau }_{\epsilon }}(1)$

as derived in (Supplementary Section S3). Here, θ is the angle as shown in Figure 2, and is influenced by the surface tension $\text{Γ}$, the radius of the spheroid before fusion $a_0$, the apparent viscosity of the tissue η and the shear modulus of the tissue $G\prime$. We combine these parameters into two characteristic time constants; ${\tau }_{\text{Γ}}:=a_0\eta /\text{Γ}$ is the visco-capillary time, and ${\tau }_{\epsilon }:=4\eta /G\prime$ is the visco-elastic time. The analytical solution of Eq. 1 is

$\text{cos}\left(\theta \right)=-\frac{{\tau }_{\epsilon }}{2{\tau }_{\text{Γ}}}+\sqrt{\frac{{\tau }_{\epsilon }^2}{4{\tau }_{\text{Γ}}^2}+1}\times \text{tanh}\left(\frac{\sqrt{4{\tau }_{\text{Γ}}^2+{\tau }_{\epsilon }^2}}{4{\tau }_{\text{Γ}}{\tau }_{\epsilon }}\left(t+C\right)\right)(2)$

in which the complex number C (Supplementary Section S3) can be obtained from the initial conditions $\theta \left(t=0\right)={\theta }_0$

$C=\frac{4{\tau }_{\text{Γ}}{\tau }_{\epsilon }}{\sqrt{4{\tau }_{\text{Γ}}^2+{\tau }_{\epsilon }^2}}\text{arctanh}\left(\frac{2{\tau }_{\text{Γ}}\text{cos}\left({\theta }_0\right)+{\tau }_{\epsilon }}{\sqrt{4{\tau }_{\text{Γ}}^2+{\tau }_{\epsilon }^2}}\right)(3)$

FIGURE 2

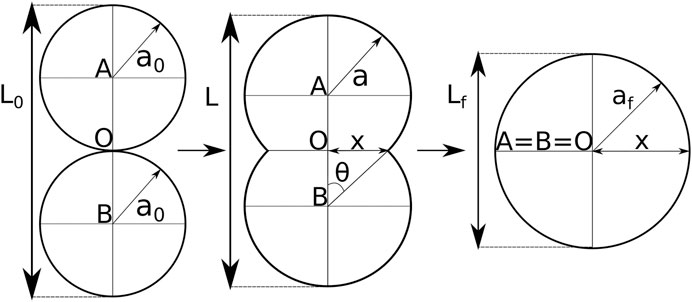
FIGURE 2. Shape evolution during spheroid fusion adapted from [3]. The shape is described by two intersecting circles with equal radius a, and center A and B. O marks the center of the axis system, and depicts the initial contact point. Based on the intersections one defines the neck radius x and the angle θ. During fusion the centers A and B gradually move toward point O, the radius a increases and the doublet length L decreases. $a_0$ and $a_f$ is the radius of the spheroids before, and after complete fusion, respectively. $L_0$ and $L_f$ is the length of the spheroid doublet before, and after complete fusion, respectively.

In analogy to previous studies on spheroid fusion, the fusion dynamics are reported as ${\text{sin}}^2\left(\theta \right)={\left(x/a\right)}^2$ with a the radius of the spheroid and x the contact radius which both vary in time [4, 10, 18, 20, 21]. Other studies perform the analysis based on ${\left(x/a_0\right)}^2$ [5, 6, 17, 19], but this is less consistent with the underlying theory (see Supplementary Section S4). Eq. 2 is used to calculate ${\text{sin}}^2\left(\theta \right)$. When fitting, we use this equation with free variables: ${\tau }_{\text{Γ}}$, ${\tau }_{\epsilon }$ and ${\theta }_0$. In order to compare simulated fusion experiments, ${\theta }_0$ is retained as a free variable since the discrete initial adhesion between the first contacting cell pair will permit a rapid relaxation toward a non-zero initial angle, ${\theta }_0$. Based on the fitted values, the predicted equilibrium angle ${\theta }_{eq}$ can be obtained as

$\text{cos}\left({\theta }_{eq}\right)=-\frac{{\tau }_{\epsilon }}{{2\tau }_{\text{Γ}}}+\sqrt{\frac{{\tau }_{\epsilon }^2}{4{\tau }_{\text{Γ}}^2}+1}=-\frac{2\text{Γ}}{G{a}_0}+\sqrt{\frac{4{\text{Γ}}^2}{G^2{a}_0^2}+1}(4)$

3 Results

3.1 Arrested Coalescence Dynamics

The average dynamics of simulated tissue spheroid fusion are consistent with the derived visco-elastic material model, expressed in the time evolution of contact angle θ, Eq. 1, as shown in Figure 3B where we varied the cell activity $D_{\text{eff}}$. At sufficiently low $D_{\text{eff}}$, coalescence appears arrested and complete fusion is not attained. Given the correspondence to the visco-elastic model, the parameters ${\tau }_{\text{Γ}}$ and ${\tau }_{\epsilon }$ can be interpreted as characteristic timescales of the multi-cellular visco-elastic material. From the fit of ${\tau }_{\text{Γ}}$, ${\tau }_{\epsilon }$ and the instantaneous initial angle ${\theta }_0$, we are able to calculate the equilibrium fusion angle, ${\theta }_{eq}$, using Eq. 4. When varying the cell activity $D_{\text{eff}}$ and the repulsive energy $w_{\text{r}}$, two distinct regions can be recognized based on ${\theta }_{eq}$, Figure 3F. For low activity $\left(D_{\text{eff}}\right)$ fusion is arrested, while at higher activities fusion is complete. Higher levels of repulsion $w_{\text{r}}$ require more cell activity to fluidize the material and hence to attain complete fusion. Similarly, the characteristic visco-capillary time ${\tau }_{\text{Γ}}$ increases when cell activity decreases and when cell repulsion increases, Figure 3E. When reducing cell activity within the fluidized region, the visco-elastic time ${\tau }_{\epsilon }$ gradually increases and displays a divergence near the transition line toward arrested coalescence. This divergence of elastic relaxation time is indicative of an underlying glass transition, as was already pointed out in [10], although based on somewhat different analytical and computational models. The transition from arrested to complete fusion as characterized by ${\theta }_{eq}$, coincides with the glass transition as characterized by the divergence of ${\tau }_{\epsilon }$, as shown in Figure 3D. Since this computational model is based on the same individual cell-based framework that was used to simulate the aggregate formation process, we are able to make a direct comparison between dynamics of aggregation and dynamics of tissue spheroid fusion. At sufficient cell activity, the aggregation process is consistent with the dewetting of a liquid film from a surface, as was demonstrated in [30]. Upon decrease in activity, this correspondence is lost. Instead, the aggregate density ${\rho }_a$ follows the dynamics of granular compaction, characterized by stretched exponential relaxation (KWW law):

${\rho }_a\left(t\right)={\rho }_f-\left({\rho }_f-{\rho }_0\right)\text{exp}\left[-{\left(t/{\tau }_{\text{agg}}\right)}^{\beta }\right](5)$

with initial density ${\rho }_0$, final density ${\rho }_f$, exponent β and characteristic timescale ${\tau }_{\text{agg}}$, see Figure 3A. In this equation the apparent packing density is expressed by ${\rho }_a=3V_a/\left(4\pi R_a^3\right)$ Here, $V_a$ is the apparent volume of the spheroid approximated as the sum of cell volumes using an average cell radius. $R_a$ is the radius of the spheroid, which is obtained based on the projected area on the bottom of the micro-well, assuming a circular geometry. During compaction, a similar glass transition as observed during the fusion process can be recognized from the divergence of ${\tau }_{\text{agg}}$ [30]. For the same underlying cell properties $D_{\text{eff}}$ and $w_{\text{r}}$, these two transitions closely align, as demonstrated in Figure 3B, although the transition in the fusion process consistently occurs at higher values of cell activity. We hypothesize that this discrepancy is due to the additional constraints in cell movement imposed by the geometry of the spheroid during the fusion process, compared to the loose network connectivity that characterizes the aggregation phase. Due to the sequential simulation of aggregation and fusion, which mimics the experimental procedure, additional compaction may occur during fusion, particularly at low activity when compaction proceeds slowly. We verified that the effect of this additional compaction on the predicted equilibrium angle ${\theta }_{eq}$ is minor, as shown in Supplementary Figure S7, where we compare fusion of self-assembled aggregates to artificially compacted spheroid structures.

FIGURE 3

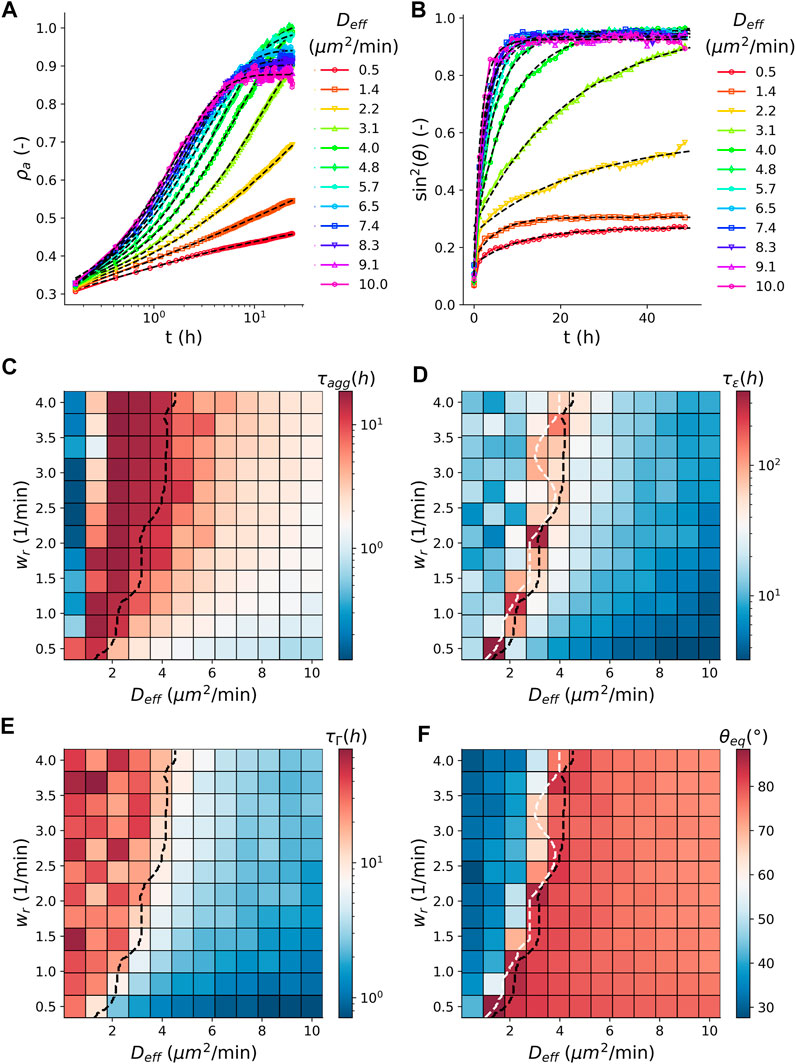
FIGURE 3. Comparison between aggregation and fusion. (A) Time evolution of the average (N = 100) apparent density ${\rho }_a$ for varying activity $D_{\text{eff}}$ at constant level of cell repulsion $w_{\mathrm{r}}=2.09{\min }^{-1}$. The fits of the KWW law Eq. 5, are shown as black dashed lines. (B) Average (N = 50) fusion dynamics, represented as ${\text{sin}}^2\left(\theta \right)$, for varying cell activity $D_{\text{eff}}$ at constant level of cell repulsion $w_{\text{r}}=2.09{\min }^{-1}$. Based on the fusion dynamics equation Eqs. 2, 3, the simulated data is fitted in the form ${\text{sin}}^2\left(\theta \right)$. These fits are shown as black dashed lines. (C) Estimated values of ${\tau }_{agg}$ based on KWW law Eq. 5 during aggregation for varying cell repulsion $w_{\text{r}}$ and cell activity $D_{\text{eff}}$. The black dashed line shows the separation of arrested versus complete fusion based on ${\theta }_{eq}$. A similar trend between this black dashed line and the divergence in ${\tau }_{\text{agg}}$ can be observed. (D–F) Estimated values of the visco-elastic time constant ${\tau }_{\epsilon }$, the visco-capillary time constant ${\tau }_{\text{Γ}}$ based on fitting fusion dynamics in ${\text{sin}}^2\left(\theta \right)$ using Eqs. 2, 3, and the equilibrium angle ${\theta }_{\text{eq}}$ calculated using Eq. 4. The black dashed line shows the separation of arrested versus complete fusion based on ${\theta }_{\text{eq}}$. The white dashed line represents the separation between two regions of low ${\tau }_{\epsilon }$. Both lines are obtained by performing a watershed segmentation on the images of ${\theta }_{\text{eq}}$ and $\text{log}\left({\theta }_{\epsilon }\right)$, respectively, and show a similar trend.

3.2 Increase of Coalescence Due to Cell Division

Next, we turn to the role of cell division in the arrest of coalescence. For this, we simulated the fusion dynamics in the presence of cell proliferation, see (Supplementary Section S1.2) Although cell proliferation is not explicitly accounted for in the derivation of our analytical model, Eq. 1 still fits the fusion dynamics of our simulated spheroid fusion in the presence of cell division well, Figure 4A. Figures 4B,C compares the characteristic visco-elastic time constant ${\tau }_{\epsilon }$ and the predicted equilibrium angle ${\theta }_{eq}$ without $\left(k_{\text{div}}=2\times {10}^{-8}{\text{h}}^{-1}\right)$ and with $\left(k_{\text{div}}=0.06{\text{h}}^{-1}\right)$ cell division, when varying cell motility $D_{\text{eff}}$ at repulsive energy $w_{\text{r}}=2.09{\min }^{-1}$. This enables us to evaluate the effect of cell growth/division as an additional source of biological excitation compared to active cell motility. The simulated cell division rate corresponds to a cell cycle period of approximately 16.7 h, which is lower than many commonly used cell lines which are used for spheroid fusion. Yet, even at this relatively high division rate, we do not see a strong shift in critical activity beyond which the material appears fluid-like, as indicated by the coincidence of the peak in ${\tau }_{\epsilon }$ for varying $D_{\text{eff}}$ with and without cell division (Figure 4B). However, we do observe that the presence of cell division greatly increases the overall visco-elastic relaxation time, indicating a decrease in the apparent elasticity of the multi-cellular material. Furthermore, cell division markedly increases the equilibrium angle ${\theta }_{eq}$ in the arrested fusion region. Hence, in the simulated configuration, cell division appears to recover coalescence by increasing the plasticity of the tissue. However, it has no strong influence on the location of the fluidization transition.

FIGURE 4

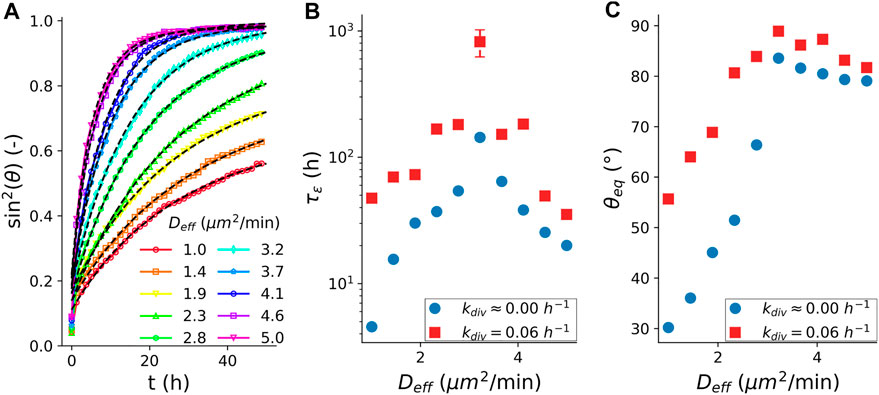
FIGURE 4. Fusion characteristics in the presence of cell division. (A) Average (N = 100) fusion dynamics with simulated cell cycle, quantified as ${\text{sin}}^2\left(\theta \right)$, during 50 h for varying cell activity $D_{\text{eff}}$ at constant $w_{\mathrm{r}}=2.09{\min }^{-1}$ and $k_{\text{div}}=0.06{\text{h}}^{-1}$. The simulated data is fitted by calculating ${\text{sin}}^2\left(\theta \right)$ based on the solution for θEqs. 2, 3. Although cell division is not taken into account in the fusion dynamics model, it still fits the data well. Fitting results of have to be interpret as effective parameters. (B–C) Comparison of fusion dynamics characteristics in presence and in absence of cell division, as a function of cell activity $D_{\text{eff}}$ at a constant $w_{\text{r}}=2.09{\min }^{-1}$. The estimated values for the visco-elastic time constant ${\tau }_{\epsilon }$ are based on fitting the average fusion dynamics in ${\text{sin}}^2\left(\theta \right)$ using Eqs. 2, 3, the predicted equilibrium angle ${\theta }_{\text{eq}}$ calculated by Eq. 4. The error bars for ${\tau }_{\epsilon }$ correspond to two times the standard error obtained from the fits. In these graphs, the error bars are only one time larger than the marker. These graphs show that cell division promotes spheroid fusion, although the system remains arrested at low levels of cell activity.

4 Discussion

In this work, we derived an expression for the arrested coalescence of tissue spheroid fusion, based on visco-elastic material properties. Simulations of a minimal individual cell-based model of the fusion process showed that this expression is able to describe the transition of liquid-like to arrested coalescence dynamics. Furthermore, a divergence in the visco-elastic relaxation time indicates the presence of jammed or glassy relaxation behavior near the transition toward arrested coalescence. These findings are highly similar to recent work from Oriola et al. [10], hence a brief comparison between these contemporary results is appropriate. First, the analytical expressions for the dynamics of θ (Eq. 1 in [10], compared to Eq. 1) are based on somewhat different assumptions. Our model is an extension of the model of Pokluda [3] by adding an elastic energy term in the equation which was suggested by [23, 24]. This has the advantage that in the absence of elasticity, the model of Pokluda is retrieved. The downside of our approach is that this leads to an inconsistency in the strain and strain rate for viscous energy dissipation rate and the elastic energy rate (we note this difference as ε and ε). For the viscous dissipation term, we have, according to Pokluda [3] $\dot{\mathit{ϵ}}=\left(1/a\right)\left(\text{d}/\text{d}t\right)\left[a\left(\theta \right)\text{cos}\left(\theta \right)\right]$. On the other hand, the strain in arrested coalescence is suggested to be $\epsilon =1-a\left(\theta \right)\left(1+\text{cos}\left(\theta \right)/\left(2a_0\right)\right)$ [23, 24]. Therefore the strain rate is $\dot{\epsilon }=-\left(1/2a_0\right)\left(\text{d}/\text{d}t\right)\left[a\left(\theta \right)\left(1+\text{cos}\left(\theta \right)\right)\right]$. These expressions are equivalent in magnitude only for the onset of fusion i.e. $\theta \approx 0$ and $a\left(\theta \right)=a_0$. In contrast to our hybrid model, Oriola et al. [10] consistently use the strain rate as suggested for arrested coalescence [23, 24]. Furthermore, they introduce elasticity by considering the spheroid as an incompressible Kelvin-Voigt material, instead of adding a separate elastic energy term, hence obtaining a critical value for the Young’s modulus for which fusion is inhibited. Moreover, whereas they include a “pre-strain” to account for the initial fusion onset, we allow for an instantaneous initial angle ${\theta }_0$. Still, both models are parameterized by two essential characteristic timescales: the visco-capillary timescale ${\tau }_{\text{Γ}}$ and the visco-elastic timescale ${\tau }_{\epsilon }$. Secondly, one key difference between the individual cell-based model in this work and the one in [10] is the implementation of the active cell motility. Their model is based on “protrusions” defined on the level of cell-cell bonds, and effectuates persistence by means of a protrusion lifetime per bond. Our model is based on a polarization direction defined for each cell which diffuses over time. Nonetheless, the similarity of the main results underpins that the transition of liquid-like to arrested coalescence is a generic phenomenon that is not dependent on the precise assumptions of the visco-elastic description, nor on the implementation details of the individual cell-based model. Additionally, because arrested fusion is the main discrepancy for fusion of the jammed tissue, the simulation of shötz et al. [22] of cells close to the jamming transition can still adequately be described by a liquid model.

The glassy relaxation dynamics during fusion mirror the dynamics of the aggregation process during which the initial tissue spheroids are formed. A direct comparison between these two unit processes shows that there is a clear correspondence between, on the one hand, the transition from granular compaction to liquid dewetting during the aggregation phase, and on the other hand, the transition from arrested coalescence to liquid behavior during the fusion phase. However, this transition occurs for slightly smaller values of cell activity in the case of aggregate formation. Experimental confirmation of this correspondence can be found in studies involving Rho kinase inhibitor, which has been observed to cause arrested dynamics during aggregate formation of human periosteum-derived cells [30], as well as inhibit fusion of spheroids from human mesenchymal stem cells [8] and of embryonal chicken organoids [7]. The role of cell activity in fluidization has been experimentally shown [9]. They related cell activity as obtained from cell tracking to the outcome of fusion. The fusion of low cell activity tumor spheroids appears like a jammed tissue and results in arrested coalescence, while in high cell activity tumor spheroids, fusion is completed. They also noted that the dynamics of this arrested fusion process could not be captured with the classical model. The equation, as derived in this paper will therefore contribute to a better understanding of spheroid fusion in general.

In addition, we considered the effect of cell division on the dynamics of the fusion process. In the framework of arrested coalescence, we showed that the presence of cell division may recover coalescence of fusion. Other studies on the role of cell growth in biological active matter systems, for example in simulations of two-dimensional epithelial tissues [27], or in growing 3D cell aggregates [25], observed an increase of fluidization induced by cell division. More generally, an overview of the role of cell division in tissue rheology and mechanics is provided in [32]. However, in our simulations, the effect of cell division on the location of the fluidization transition was limited, at least for realistic cell division rates compared to the timescale of fusion. Instead, cell division appeared to increase plasticity of the glassy material and thereby improves coalescence in the arrested phase. However, it should be noted that the absence of fluidization as a result of cell division in simulations could be partly due to the minimal representation of cell shape, which introduces artificial energy barriers and thereby overly penalizes neighbor exchanges. This shortcoming could be addressed in more detailed tissue models, such as vertex models [33] or deformable cell models [34, 35]. On the other hand, our representation of the cell cycle was limited to cell growth and cell division, while fluidization is often investigated in the presence of apoptosis when the number of cells is stationary or at a homeostatic pressure [28]. We expect that including apoptosis will further fluidize the tissue as this creates random vacancies around caged cells, offering a low energy route for local relaxation. Additional complexities on fusion dynamics could arise as cells enter a pressure-dependent dormant state, increasing tissue heterogeneity. For example, the increased pressure in the core of tumor spheroids results in a jammed stage with dormant cells, while cells at the periphery grow and motility is super-diffusive [36].

In practice, technologies that involve the production of artificial tissues frequently incorporate subsequent steps of micro-aggregation and tissue assembly, where the latter often relies on the (partial) fusion of spheroids to create larger tissue constructs [37]. To complicate matters, all these steps are typically accompanied by biological processes such as cell division, production of extracellular matrix, cell differentiation or apoptosis. However, since the physical description of the underlying aggregation and fusion dynamics is highly generic, each of these steps may be parameterized in terms of its characteristic material properties, allowing for the comparison within and between different culture conditions and production formats. As such, continued efforts toward the characterization of structure, rheology and mechanics of these artificial tissues will become indispensable.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the Zenodo repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author Contributions

BS and HR conceived the project, SO and BS designed and conducted the simulations, SO performed the mathematical analysis, SO performed data analysis. SO, MC, JV, and BS wrote the manuscript. All authors commented on the manuscript.

Funding

This work is part of Prometheus, the KU Leuven R&D Division for Skeletal Tissue Engineering. SO acknowledges support from KU Leuven internal funding C14/18/055. MC acknowledges support form the Research Foundation Flanders (FWO), grant 1S46817N. BS acknowledges support from the Research Foundation Flanders (FWO) grant 12Z6118N.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Jiří Pešek for proofreading the derivations.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.649821/full#supplementary-material

References

1. Frenkel JJ. Viscous Flow of Crystalline Bodies under the Action of Surface Tension. J Phys (1945) 9:385. doi:10.1007/BF03398399

Google Scholar

2. Eshelby J. Discussion,’ in a.J. Shuler, ‘seminar on the Kinetics of Sintering’. Met Trans (1949) 185:806.

Google Scholar

3. Pokluda O, Bellehumeur CT, Vlachopoulos J. Modification of Frenkel's Model for Sintering. Aiche J (1997) 43:3253–6. doi:10.1002/aic.690431213

CrossRef Full Text | Google Scholar

4. McCune M, Shafiee A, Forgacs G, Kosztin I. Predictive Modeling of post Bioprinting Structure Formation. Soft matter (2014) 10:1790–800. doi:10.1039/c3sm52806e

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dechristé G, Fehrenbach J, Griseti E, Lobjois V, Poignard C. Viscoelastic Modeling of the Fusion of Multicellular Tumor Spheroids in Growth Phase. J Theor Biol 454 (2018) 102 – 9. doi:10.1016/j.jtbi.2018.05.005

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kosheleva NV, Efremov YM, Shavkuta BS, Zurina IM, Zhang D, Zhang Y, et al. Cell Spheroid Fusion: beyond Liquid Drops Model. Sci Rep (2020) 10:12614. doi:10.1038/s41598-020-69540-8

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Pierzchalska M, Panek M, Grabacka M. The Migration and Fusion Events Related to Rock Activity Strongly Influence the Morphology of Chicken Embryo Intestinal Organoids. Protoplasma (2019) 256:575–81. doi:10.1007/s00709-018-1312-3

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Tsai A-C, Liu Y, Yuan X, Ma T. Compaction, Fusion, and Functional Activation of Three-Dimensional Human Mesenchymal Stem Cell Aggregate. Tissue Eng Part APart A (2015) 21:1705–19. doi:10.1089/ten.TEA.2014.0314

CrossRef Full Text | Google Scholar

9. Grosser S, Lippoldt J, Oswald L, Merkel M, Sussman DM, Renner F, et al. Cell and Nucleus Shape as an Indicator of Tissue Fluidity in Carcinoma. Phys Rev X (2021) 11:011033. doi:10.1103/physrevx.11.011033

CrossRef Full Text | Google Scholar

10. Oriola D, Marin-Riera M, Aalderink G, Anlas K, Gritti N, Sharpe J, et al. Arrested Coalescence of Multicellular Aggregates (2020) arXiv:2012.01455.

11. Yu M, Mahtabfar A, Beelen P, Demiryurek Y, Shreiber DI, Zahn JD, et al. Coherent Timescales and Mechanical Structure of Multicellular Aggregates. Biophysical J 114 (2018) 2703 – 16. doi:10.1016/j.bpj.2018.04.025

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Guevorkian K, Colbert M-J, Durth M, Dufour S, Brochard-Wyart F, Aspiration of Biological Viscoelastic Drops. Phys Rev Lett (2010) 104:218101. doi:10.1103/PhysRevLett.104.218101

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Gonzalez-Rodriguez D, Bonnemay L, Elgeti J, Dufour S, Cuvelier D, Brochard-Wyart F. Detachment and Fracture of Cellular Aggregates. Soft Matter (2013) 9:2282–90. doi:10.1039/C2SM26648B

CrossRef Full Text | Google Scholar

14. Forgacs G, Foty RA, Shafrir Y, Steinberg MS. Viscoelastic Properties of Living Embryonic Tissues: a Quantitative Study. Biophysical J 74 (1998) 2227–34. doi:10.1016/S0006-3495(98)77932-9

CrossRef Full Text | Google Scholar

15. Mongera A, Rowghanian P, Gustafson HJ, Shelton E, Kealhofer DA, Carn EK, et al. A Fluid-To-Solid Jamming Transition Underlies Vertebrate Body axis Elongation. Nature (2018) 561:401–5. doi:10.1038/s41586-018-0479-2

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Yang X, Mironov V, Wang Q. Modeling Fusion of Cellular Aggregates in Biofabrication Using Phase Field Theories. J Theor Biol 303 (2012) 110–8. doi:10.1016/j.jtbi.2012.03.003

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Fleming PA, Argraves WS, Gentile C, Neagu A, Forgacs G, Drake CJ. Fusion of Uniluminal Vascular Spheroids: A Model for Assembly of Blood Vessels. Dev Dyn (2010) 239:398–406. doi:10.1002/dvdy.22161

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Flenner E, Janosi L, Barz B, Neagu A, Forgacs G, Kosztin I. Kinetic Monte Carlo and Cellular Particle Dynamics Simulations of Multicellular Systems. Phys Rev E (2012) 85:031907. doi:10.1103/PhysRevE.85.031907

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Flenner E, Marga F, Neagu A, Kosztin I, Forgacs G. Relating Biophysical Properties across Scales. Schnell S, Maini PK, Newman SA, and Newman TJ, editors. Relating Biophysical Properties across Scales. Multiscale Modeling of Developmental SystemsCurrent Topics in Developmental Biology, 81. Academic Press (2008). p. 461–83. doi:10.1016/S0070-2153(07)81016-7

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kosztin I, Vunjak-Novakovic G, Forgacs G. Colloquium: Modeling the Dynamics of Multicellular Systems: Application to Tissue Engineering. Rev Mod Phys (2012) 84:1791–805. doi:10.1103/RevModPhys.84.1791

CrossRef Full Text | Google Scholar

21. Shafiee A, McCune M, Forgacs G, Kosztin I. Post-deposition Bioink Self-Assembly: a Quantitative Study. Biofabrication (2015) 7:045005. doi:10.1088/1758-5090/7/4/045005

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Schötz E-M, Lanio M, Talbot JA, Manning ML. Glassy Dynamics in Three-Dimensional Embryonic Tissues. J R Soc Interf (2013) 10:20130726. doi:10.1098/rsif.2013.0726

CrossRef Full Text | Google Scholar

23. Pawar AB, Caggioni M, Hartel RW, Spicer PT. Arrested Coalescence of Viscoelastic Droplets with Internal Microstructure. Faraday Discuss (2012) 158:341–35. doi:10.1039/c2fd20029e

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Dahiya P, Caggioni M, Spicer PT. Arrested Coalescence of Viscoelastic Droplets: Polydisperse Doublets. Phil Trans R Soc A (2016) 374:20150132. doi:10.1098/rsta.2015.0132

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Ranft J, Basan M, Elgeti J, Joanny J-F, Prost J, Jülicher F. Fluidization of Tissues by Cell Division and Apoptosis. Proc Natl Acad Sci (2010) 107:20863–8. doi:10.1073/pnas.1011086107

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Malmi-Kakkada AN, Li X, Samanta HS, Sinha S, Thirumalai D. Cell Growth Rate Dictates the Onset of Glass to Fluidlike Transition and Long Time Superdiffusion in an Evolving Cell colony. Phys Rev X (2018) 8:021025. doi:10.1103/PhysRevX.8.021025

CrossRef Full Text | Google Scholar

27. Matoz-Fernandez DA, Martens K, Sknepnek R, Barrat JL, Henkes S. Cell Division and Death Inhibit Glassy Behaviour of Confluent Tissues. Soft Matter (2017) 13:3205–12. doi:10.1039/C6SM02580C

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Basan M, Prost J, Joanny J-F, Elgeti J. Dissipative Particle Dynamics Simulations for Biological Tissues: Rheology and Competition. Phys Biol (2011) 8:026014. doi:10.1088/1478-3975/8/2/026014

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Smeets B, Pešek J, Deckers T, Hall GN, Cuvelier M, Ongenae S, et al. Compaction Dynamics during Progenitor Cell Self-Assembly Reveal Granular Mechanics. Matter 2 (2020) 1283 – 95. doi:10.1016/j.matt.2020.02.016

CrossRef Full Text | Google Scholar

30. Smeets B, Pešek J, Deckers T, Hall GN, Cuvelier M, Ongenae S, et al. Compaction Dynamics during Progenitor Cell Self-Assembly Reveal Granular Mechanics. Matter 2 (2020) 1283 – 95. doi:10.1016/j.matt.2020.02.016

CrossRef Full Text | Google Scholar

31. Delile J, Herrmann M, Peyriéras N, Doursat R. A Cell-Based Computational Model of Early Embryogenesis Coupling Mechanical Behaviour and Gene Regulation. Nat Commun (2017) 8:13929. doi:10.1038/ncomms13929

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Godard BG, Heisenberg C-P. Cell Division and Tissue Mechanics. Curr Opin Cel Biol 60 (2019) 114 – 20. doi:10.1016/j.ceb.2019.05.007

CrossRef Full Text | Google Scholar

33. Krajnc M, Dasgupta S, Ziherl P, Prost J. Fluidization of Epithelial Sheets by Active Cell Rearrangements. Phys Rev E (2018) 98:022409. doi:10.1103/PhysRevE.98.022409

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Van Liedekerke P, Neitsch J, Johann T, Alessandri K, Nassoy P, Drasdo D. Quantitative Cell-Based Model Predicts Mechanical Stress Response of Growing Tumor Spheroids over Various Growth Conditions and Cell Lines. Plos Comput Biol (2019) 15:e1006273. doi:10.1371/journal.pcbi.1006273

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Smeets B, Cuvelier M, Pešek J, Ramon H. The Effect of Cortical Elasticity and Active Tension on Cell Adhesion Mechanics. Biophysical J (2019) 116:930–7. doi:10.1016/j.bpj.2019.01.015

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Sinha S, Malmi-Kakkada AN, Li X, Samanta HS, Thirumalai D. Spatially Heterogeneous Dynamics of Cells in a Growing Tumor Spheroid: Comparison between Theory and Experiments. Soft Matter (2020) 16:5294–304. doi:10.1039/C9SM02277E

PubMed Abstract | CrossRef Full Text | Google Scholar

37. De Moor L, Fernandez S, Vercruysse C, Tytgat L, Asadian M, De Geyter N, et al. Hybrid Bioprinting of Chondrogenically Induced Human Mesenchymal Stem Cell Spheroids. Front Bioeng Biotechnol (2020) 8:484. doi:10.3389/fbioe.2020.00484

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Ongenae S, Cuvelier M, Vangheel J, Ramon H, Smeets B. mpacts_arrested_coalescence-master (2021) doi:10.5281/zenodo.4745560

CrossRef Full Text