Social Simulation of Intergroup Conflicts Using a New Model of Opinion Dynamics

The social identity theory proposed by Tajfel et al. provides insight into how group membership and self-categorization cause intergroup prejudice and discrimination, finally leading to social conflicts. However, unanswered questions remain: under what conditions can an “in-group” and an “out-group” transform conflictual intergroup behavior into a more harmonious relationship and avoid social conflict? Opinion dynamics theory and social simulation are appropriate methods to answer this question. In this study, a new model of opinion dynamics proposed by Ishii is adopted, and we conduct simulations of intergroup conflicts. The new model, along with social simulations, presents how an in-group and an out-group can develop social harmony and avoid social conflict. According to our simulations, when the two groups trust their members 100%, the opinion inside an in-group converges. However, intragroup opinion diverges as trust within the group gets lower. On the other hand, intergroup opinion converges when the intergroup trust is higher than 50%. If intergroup trust is higher than 80%, then the intergroup opinions of the two perfectly overlap. Furthermore, if intragroup trust is 70% and intergroup trust is as low as 50%, the two groups' opinions completely polarize. We also calculated additional cases where intragroup trust was fixed at 70%, but for one-third of an in-group member trust an out-group with various values. Finally, a method to avoid further social crises can be obtained by examining real-world cases of partisan conflicts in recent America.

1. Introduction

Throughout world history, too many cases of social conflict have been observed. By examining cases of social conflicts, we can develop a method to avoid further social crises. Therefore, we conducted a simulation of conflict between the two groups in this study.

Prejudice and discrimination are the causes of social conflicts. According to social identity theory, intrapersonal or interpersonal psychological processes are not a cause of prejudice and discrimination. If anything, prejudice and discrimination derive from intergroup antagonism [1, 2]. People decide which social group to belong to for a sense of pride, involvement, stability, and meaning [3–5]. In deciding which group to support, they identify the social group they belong to as their “in-group” and distinguish other groups as “out-groups,” often in harmful or discriminative ways [6]. They strengthen a sense of unity with the party members of the in-group and start to support its issues. This self-categorization and group membership work as a social-cognitive schema (norms, values, and beliefs) for their group-related behavior. The perception of belonging to the in-group is sufficient to cause intergroup prejudice, ethnocentrism, stereotypes, and discrimination, even in the absence of material conflict or previous group hostility [2, 3].

Social identity theory is critical because it offers a foundation for understanding how group membership and self-categorization cause intergroup prejudice and discrimination, and they finally lead to social conflicts [2]. Thousands of empirical studies have been conducted by scholars of social science, and most of these empirical studies adopt experimental methods [1, 7, 8]. However, there remain unanswered questions. Under what conditions can an in-group and an out-group transform conflictual intergroup behavior into a more harmonious relationship and avoid social conflict? From prior empirical studies, achieving or sustaining a harmonious relationship is assumed to be nearly impossible for an in-group and an out-group [1]. Here, opinion dynamics theory and social simulation are appropriate methods to answer the question. Based on the bounded confidence model [9–11], opinion dynamics can present how an in-group and an out-group can develop social harmony and avoid social conflict.

Grounded upon opinion dynamics theory, several models have been developed to explain social conflicts [12–16]. In particular, Javarone established a variation of the classical voter model to study the best strategies to gain a popular consensus with two competitors [16–18]. Our model is distinct in two aspects. First, we use the theory originating from Ishii [19, 20], a straightforward extension of the bounded confidence model to the theory of opinion dynamics that sets trust and distrust for intergroup dimension and intragroup dimension. According to Ishii's theory, D_ij, which appeared in Hegselmann-Krause's opinion dynamics theory before, is considered a coefficient of trust, and if it posits a negative value, that means a relationship is distrustful. Second, we refer to the social identity theory initially proposed by Tajfel as a key [6]. With the opinion dynamics model and social simulations, the social identity theory helps understand how consensus within social groups is formed, and intergroup conflicts arise or mitigate.

In this study, we simulate intergroup and intragroup opinion dynamics using Ishii's model. In previous works, based on the foundational model developed by Ishii and Kawahata [19, 20], we incorporated trust and distrust into the model. It was also established that consensus-building aspects depend on the ratio between trust and distrust coefficients [21, 22]. Thus, it is recognized that the model can be applied to illustrate real-world examples of social conflicts [22]. Therefore, in this study, we adopt a model to examine real-world examples of social conflicts. We assume that a society consists of two groups, and the severity of the conflict between the two is related to the intragroup and intergroup relatability.

2. Theory of Opinion Dynamics

Opinion dynamics is a discipline that follows the process of consensus building within societies. The theory of opinion dynamics can be divided into a theory that treats people's opinions in society as binary values and a theory that treats the opinions of people in society as continuous values. Theories that treat binary opinions include the voter model [23] and theories that apply magnetism theory in solid-state physics [24].

The theory that expresses people's opinions in society as continuous values is called the bounded confidence model. In the bounded confidence model, if person i's opinion is expressed as I_i(t), it is considered to be influenced by the opinions of others I_j(t) by the following formula:

$\begin{array}{ll}{I}_i(t+\Delta t)=I_i(t)+\lambda (I_j(t)-I_i(t)).& (1)\end{array}$

where λ is a convergence factor, and the time required for consensus building differs depending on the value of λ. The above equation is the fundamental equation of the bounded confidence model by Deffuant et. al. [9, 10]. On the other hand, the fundamental equation of the Hegselmann-Krause model [11] is the following equation,

$\begin{array}{ll}{I}_i(t+\Delta t)=I_i(t)+{\lambda }_{ij}(I_j(t)-I_i(t)).& (2)\end{array}$

where λ_ij is a convergence factor, and the time required for consensus building differs depending on the value of λ_ij. The above two models, the Deffuant model and the Hegselmann-Krause model, are almost equivalent. The time convergent factor λ_ij is a positive number so that society's opinions form a consensus. The difference in the initial settings of the bounded confidence model calculation is related to how many opinions the society agrees.

In contrast to the bounded confidence model shown above, Ishii et al. modified the meaning of time convergence coefficient λ_ij to D_ij as the coefficient of trust. Here, Ishii assumes that D_ij > 0 for a trust relationship between two people, and D_ij < 0 for a distrust relationship between two people [19, 20]. According to the extension, the value of opinion I_i(t) could be either positive or negative. In Ishii's opinion dynamics theory, opinions within the society are assumed to be on a one-dimensional axis. Thus, the negative opinion merely indicates an opinion opposite to the positive opinion. For example, if the positive opinion is a liberal one, the negative opinion would be conservative. If the positive opinion is conservative, the negative opinion would be liberal.

Following the grounding theory [20], we assume that people disregard an opinion far from their opinion. An opinion that is close to themselves' will not be affected. Thus, we use the following function instead of D_ijI_j(t) to include the two effects:

$\begin{array}{ll}{D}_{ij}\Phi (I_i,I_j)(I_j(t)-I_i(t))& (3)\end{array}$

where

$\begin{array}{ll}\Phi (I_i,I_j)=\frac{1}{1+exp(\beta (|I_i-I_j|-b))}& (4)\end{array}$

This function is called the Sigmoid function, and it works as a smooth cutoff function at |I_i−I_j| = b. Using the Sigmoid function, we assume that if the opinions of the two are far apart, one's opinion will not be influenced by the opinion of the other. The factor I_j(t) − I_i(t) means that agent i is not affected by agent j. As a result, an opinion that is close to the subject or an opinion that is far away from the subject will not be affected. In the theory of Hegselmann-Krause [7], they only use the step function instead of the Sigmoid function. The Sigmoid function should be used here because the function makes the cutoff smooth; however, there is no significant difference from the step function in the actual opinion dynamics calculation.

The influence of the mass media can be added to the following mathematical model [25, 26]: In the actual calculation, the effect A(t) of the mass media is, for example, the number of seconds spent in reporting or advertising on a relevant item [25]. A(t) denotes the pressure from mass media at a time t. The coefficient c_i shows how much impact media gives to each agent. The coefficient c_i can have different values for each person, and it can be either positive or negative. If the coefficient c_i is positive, person i moves their opinion toward the mass media. On the contrary, if the coefficient c_i is negative, a person's opinion changes against the mass media [27, 28].

Therefore, including mass media effects, the change of opinion of an agent can be expressed as follows:

$\begin{array}{ll}\Delta I_i(t)=c_{i}A(t)\Delta t+{\displaystyle \sum _{j=1}^N}{D}_{ij}\Phi (I_i(t),I_j(t))(I_j(t)-I_i(t))\Delta t,& (5)\end{array}$

where ΔI_i(t) = I_i(t + Δt) − I_i(t). According to the Ishii's opinion dynamics theory [20], D_ij is an asymmetric matrix. D_ij and D_ji, D_ij ≠ D_ji, and D_ij and D_ji can have different signs. Here, D_ij > 0 corresponds to the trust relationship between the two people, and D_ij < 0 corresponds to the distrust relationship between the two.

Long-term behavior requires attenuation; that is, topics will be forgotten over time. Hence, we introduced exponential attenuation to the model as follows:

$\begin{array}{ll}\Delta I_i(t)=-\alpha I_i(t)\Delta t+c_{i}A(t)\Delta t+{\displaystyle \sum _{j=1}^N}{D}_{ij}\Phi (I_i(t),I_j(t))(I_j(t)-I_i(t))\Delta t.& (6)\end{array}$

In previous studies [25, 26], the mass media effect was defined as the amount of time for a television advertisement. The definition worked without any issues. We obtained a suggestion from those studies, and here we define the mass media effect of the model as c_iA(t). In the actual simulation shown below, we assume that c_i = 1, for simplicity.

$\begin{array}{ll}\Delta I_i(t)=c_{i}A(t)\Delta t+{\displaystyle \sum _{j=1}^N}{D}_{ij}\Phi (I_i(t),I_j(t))(I_j(t)-I_i(t))\Delta t& (7)\end{array}$

In the calculation below, we set A(t) as 0.00, and c_i is set as unity. Throughout this article, A(t) is set to be zero for simplicity to concentrate on the effect of D_ij.

We assumed a case of two people, N = 2. Based on the model [20], the equations for the two-people model are

$\begin{array}{ll}\Delta I_A(t)=c_{A}A(t)\Delta t+D_{AB}\Phi (I_A(t),I_B(t))(I_B(t)-I_A(t))\Delta t& (8)\end{array}$

$\begin{array}{ll}\Delta I_B(t)=c_{B}A(t)\Delta t+D_{BA}\Phi (I_B(t),I_A(t))(I_A(t)-I_B(t))\Delta t& (9)\end{array}$

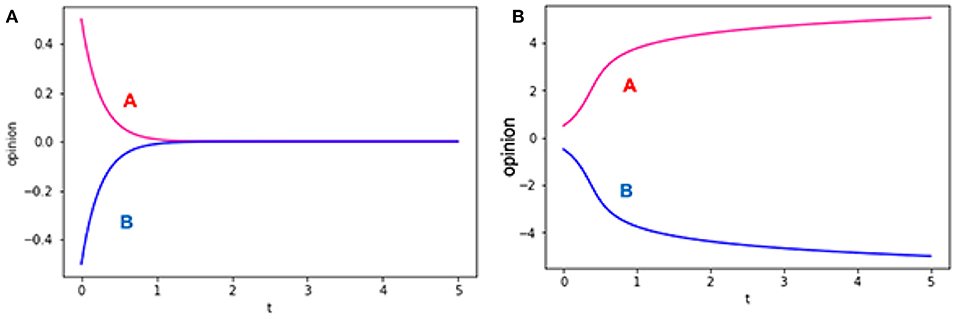
Let us suppose two-people cases: In the first case, the two trust each other, and the two distrust each other in the second case. The former case is shown in Figure 1A, and the latter case is shown in Figure 1B. If the two trust each other, their opinions converge: they form a consensus. However, if the two distrust each other, their opinions diverge: they never reach an agreement

FIGURE 1

Figure 1. Calculation result for N = 2. (A) D_AB > 0 and D_BA > 0. (B) D_AB < 0 and D_BA < 0.

In the bounded confidence model, the multi-polarization of social opinions is brought about by ignoring distant opinions (shown in Equation 4) or by the step function. However, in Ishii's opinion dynamics theory, it is assumed that the multi-polarization of social opinions is brought about by repulsion of opinions or distrust. According to Ishii's theory, the repulsion of opinions could occur even among people whose opinions are relatively close. Ishii's theory is more realistic in setting than the ordinally bounded confidence model.

The theory of opinion dynamics shown in this section can be applied to studies on real-world social conflicts using social simulations. With this opinion dynamics theory, calculating the convergence of opinions is enabled. In the same manner, calculating the divergence of opinions is enabled. The calculation with social simulation performed for the cases with 300 people is shown in the following sections. In the calculations, a connection of the people was simulated by a random network model. Here, 30% of the people are assumed to be connected. Figure 2 shows an example of a consensus building, where the coefficient D represents trust between people. The coefficient D posited a positive value by a random number from 0 to 1. In Figure 3, coefficient D presents trust among people. The coefficient D posited a random number in the range of −1 to 1, and the ratio of the positive and negative values was set to be equal. In this case, people's opinions were diffused and never reached a consensus.

FIGURE 2

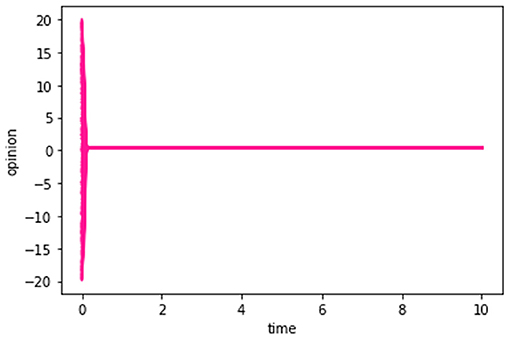
Figure 2. Calculation result for N = 300. D_ij for every person is set to be a positive random number between 0 and +1.

FIGURE 3

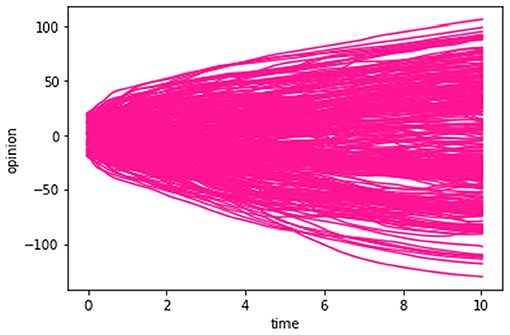
Figure 3. Calculation result for N = 300. D_ij for every persons are set to be random numbers between −1 to +1.

3. Setting of Social Simulation Calculation

In this section, we explain how to check the division of society using a social simulation. Owing to the capacity of our computer, the number of people used in the simulations had to be limited to 300. We confirmed that our calculations with 300 people presented the same results with 500 or even 1,000 people. However, we limited the number of people to 300 because calculations with 1,000 people took a long time. Additionally, if we set more than 1,000 people, it is reasonable to assume that the way people connect in the real world should be scale-free [29]. In implementing calculations with the scale-free network, it is essential to set a person as a “hub.” In a given scale-free network, a “hub” person maintains strong influence within a network, that is, each scale-free network is determined by the hub's opinion and hence unique: it is difficult to identify the general characteristics of the scale-free network from its uniqueness. Let us inform Ishii's opinion dynamics model calculations with a scale-free network have already been done elsewhere [21, 30]. Hence, calculations using the scale-free network are technically feasible for us; however, because of the aforementioned reason, a scale-free network is not adopted in this study.

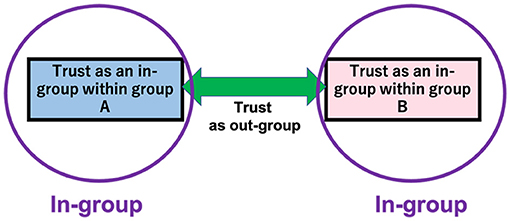
We evenly divide the 300 population society: we create two groups with 150 members within a society. Let us name the two groups as group A (an “in-group”) and group B (an “in-group”). As it is supposed in the social identity theory [1–3, 6], group A is an “out-group” if seen from group B and vice versa. In this study, we assume that the members of a group sometimes trust and sometimes distrust members of the other group. Figure 4 shows a schematic illustration of our model in the calculation.

FIGURE 4

Figure 4. Model of social division in the calculation.

We set the initial opinion value for the 300 population society to be randomly assigned between −20 and +20. We randomly set the coefficient of trust (D_ij). For cases of positive value, D_ij posits between 0 and +1 as a random number. For the cases of negative value, D_ij is between −1 and 0 as a random number.

As shown in Figure 3, opinions converge within an in-group, and a consensus is formed when a degree of trust among the people who belong to the in-group posits a positive value. Our calculation shows that when coefficient D is higher than 55%, an in-group forms a consensus [21, 30]. Since this result can be applied to any of the two coexisting in-groups, we can assume consensus will be built when the degree of trust among members of an in-group is higher than 55%. However, how intergroup trust against an out-group from an in-group matters is still unknown. Therefore, we calculate that in the next section of this article.

We performed the following two calculations in the following section. In the first calculation (Figure 5), intergroup trust was set to zero, and intragroup trust was set to varying degrees. Then, we changed intragroup trust to 55% (Figure 6) and changed intergroup trusts to varying degrees.

FIGURE 5

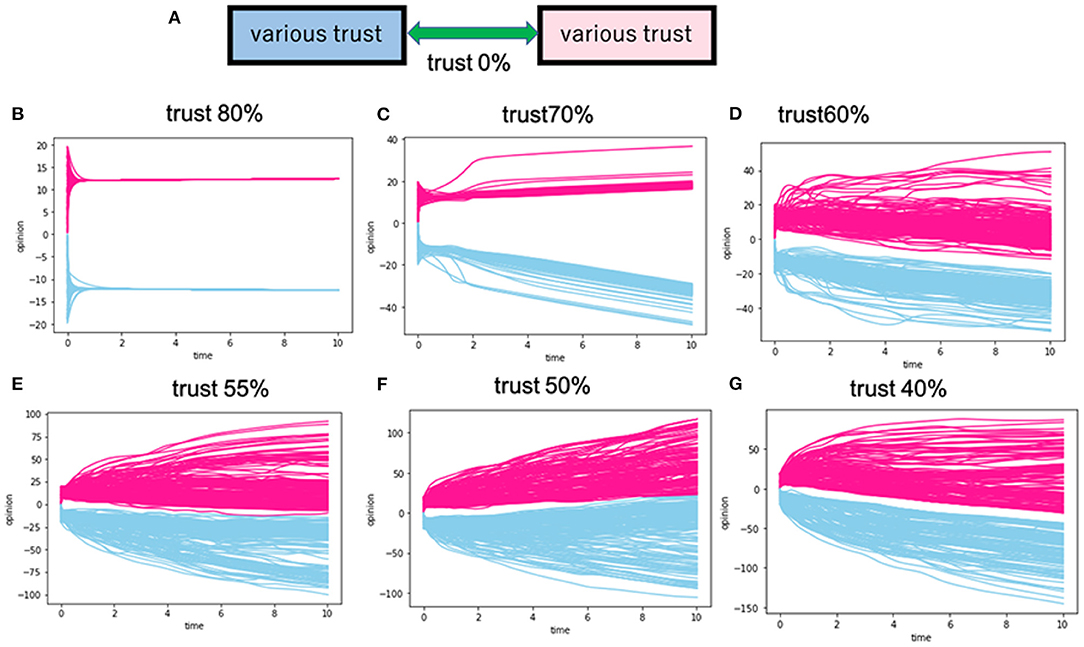
Figure 5. Calculation for the cases of no intergroup trusts between group A and group B. (A) Is the schematic view of this model. (B–G) Correspond to the various intragroup trusts. The red lines in the figures indicate the opinion trajectories of group A, and the blue lines are those of group B. For instance, the trust of 80% in (B) means that 80% of the intragroup trusts (D_ij) for A and B are positive values.

FIGURE 6

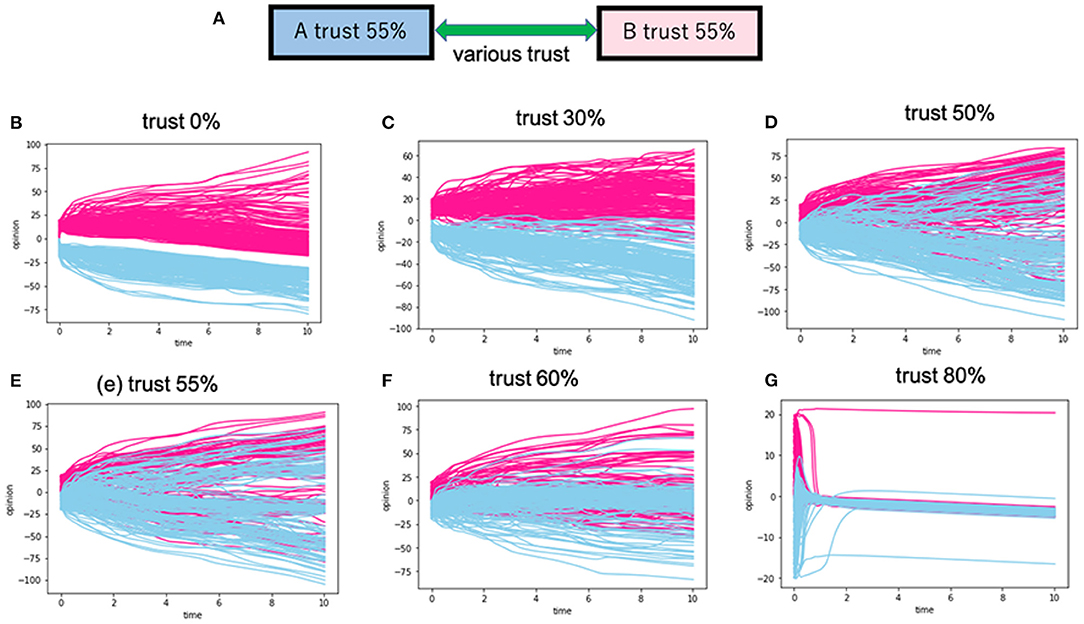
Figure 6. Various calculations for the intergroup trusts between group A and group B. (A) Is the model's schematic view. (B–G) Correspond to the various intergroup trusts (Dij) between group A and the group B. For example, the trust of 30% in (C) means that the intergroup trust (D_ij) between group A and group B posits a positive value of 30%. The red lines correspond to the opinion trajectories for group A, and the blue lines correspond to those of group B.

In the second calculation, we examined cases with members of Group B. In those cases, group B's 50 members (B-1) embrace intergroup trust toward group A (Figure 7). Members of group B maintained intragroup trust at 70% (Figure 7), and members of group B maintained intragroup trust at 50% (Figure 8). We calculated with varying values of intergroup trust from B-1 toward group A. It is assumed that group A trusts B-1 with the same degree as B-1 trusts group A.

FIGURE 7

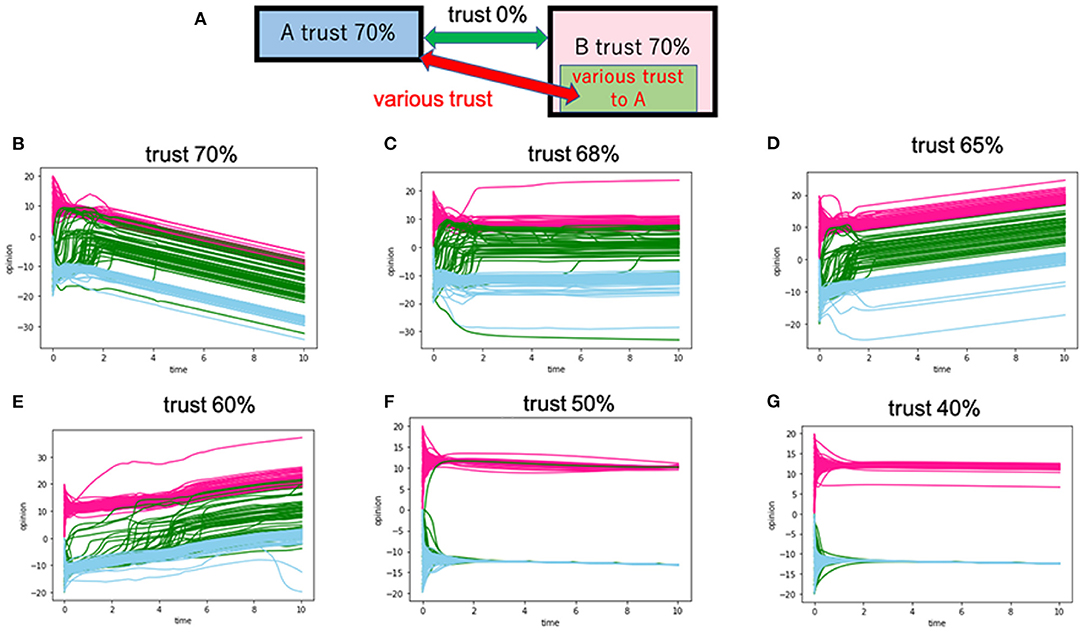
Figure 7. Cases in which no intergroup trust exists between group A and group B. The intragroup trusts for group A and group B are fixed to 70%. Furthermore, 50 people in group B (B-1) have intergroup trust toward group A. (A) Presents this model's schematic view. (B–G) Correspond to the various intergroup trusts between B-1 and group A. For example, the trust of 70% means that the intergroup trust (D_ij) between B-1 and group A posits a positive value of 70%. The red lines represent the opinion trajectories of group A. The blue lines show those of group B except for the B-1 subgroup. The green lines are the opinion trajectories of B-1.

FIGURE 8

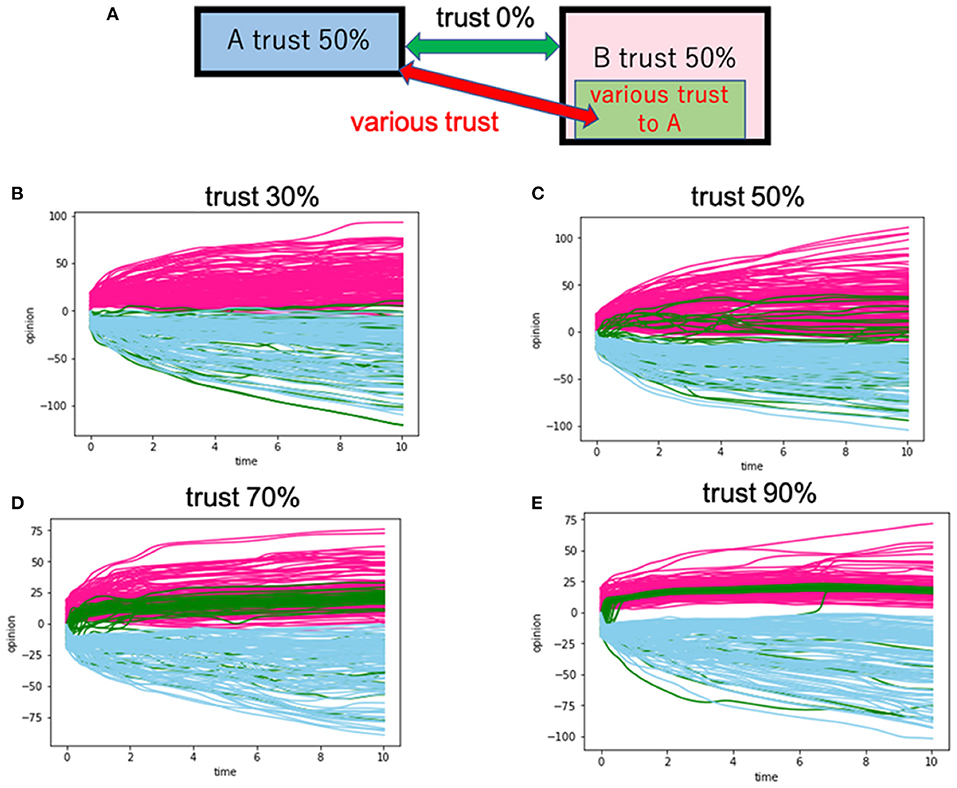
Figure 8. Cases in which no intergroup trust exists between group A and group B. The intragroup trusts for group A and group B are fixed at 50%. However, 50 people in group B (B-1) have intergroup trust toward group A. (A) Is the model's schematic view. In (B–E), there are various intergroup trusts between the B-1 and group A. For instance, the trust 70% means that 70% of the trust (D_ij) exists between the B-1 and group A. The red lines correspond to the opinion trajectories of group A. The blue lines are those of group B except for the B-1 subgroup. The green lines are the opinion trajectories of B-1.

4. Results

In Figure 5, we set the intergroup trusts against out-groups as 0%, and we changed the intragroup trust to varying degrees. Our prior studies show that two groups can reach an intragroup consensus, as shown in Figures 5B,C [17, 18]. In the cases shown in Figures 5D–G, we cannot even confirm intragroup consensus formation. Since the intergroup trusts are set to zero, intragroup opinions diverge. Furthermore, in those cases, the two groups never reached an intergroup consensus.

In Figure 6, we set the intragroup trust as 55%. Then, we changed the intergroup trust to varying degrees. The results are shown in Figure 6. In Figure 6B, there is no intergroup consensus, as shown in Figure 5. However, in Figures 6C–F, the intergroup opinions between groups A and B overlapped because of the high intergroup trust. This result shows that there were no serious conflicts between the two groups. A complete consensus building occurs when intergroup trusts are as high as 80% (Figure 6G).

We then assumed that the members of group B are not united. In our assumption, 50 out of the 150 members of group B (we call this subgroup B-1) maintain intergroup trust toward group A and vice versa. However, there is no trust between group A and the rest of the group B members. The members of groups A and B, including members of B-1, have an intragroup trust of 70% (Figure 7). In Figure 8, the members of group A and group B, including the members of B-1, have an intragroup trust of 50%. In Figure 8, we changed the value of intergroup trust for B-1. Whereas, the members of B-1 have intergroup trust toward group A and vice versa, there is no trust between group A and the rest of group B members.

The green line in Figure 7 represents B-1. When the intergroup trust of B-1 toward group A is lower than 50%, both group A and group B form intragroup consensuses (see Figures 7F,G). In Figure 7F, we can see that few people from B-1 reached a consensus with Group A. Here, very few members from B-1 function as “out-group” inside of group B. However, in Figures 7B,C, a large number of B-1 members reach consensus with group A. In those cases, intragroup consensus-buildings within group B (depicted in the blue line) are hindered as B-1 leans toward group A.

Figure 8 shows a case where the intragroup trusts of the two groups are 50%. In this case, they can form no consensus. When the intergroup trust of B-1 exceeds 50%, group B-1 starts to overlap with group A. In Figure 8E, the B-1 members form a consensus with group A (the opinion distribution for this case is shown in Figure 9). Members of B-1 (depicted in the green line) and group A members work together to form a consensus. This consensus building is due to the high intergroup trust between group A and group B-1.

FIGURE 9

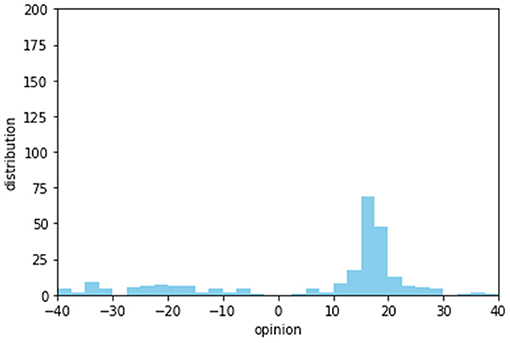
Figure 9. Opinion distribution for the case shown in Figure 8E at time = 10.

5. Discussion and Conclusion

In this study, we evaluated the conflict between two groups by applying opinion dynamics with simulations. We simulated the society, which was divided into two groups. Social division becomes decisive when an in-group embraces strong distrust against an out-group. If both an in-group and an out-group present a mixture of trust and distrust, the division is not decisive.

According to our simulation shown in Figure 5, when the two groups trust their members 100%, the opinion inside an in-group converges. However, intragroup opinion diverges as trust within the group gets lower, as shown in Figure 5. In Figure 6, intragroup trust is fixed at 55%. Here, intergroup opinion converges when the intergroup trust is higher than 50%. If intergroup trust is higher than 80%, then the intergroup opinions of the two perfectly overlap.

Furthermore, in Figure 7, the intragroup trusts of the two groups are fixed at 70%. Intergroup opinions do not overlap, even when intergroup trust is 70%. If intragroup trust is 70% and intergroup trust is as low as 50%, the two groups' opinions completely polarize.

We also calculated additional cases where intragroup trust was fixed at 70%, but for one-third of an in-group member (B-1), trust an out-group (group A) with various values (Figure 7). For example, when one-third of the in-group members, i.e., B-1, trust an out-group with 60% of trust or higher, group B's opinion diverges and comes closer to the opinion of A (Figures 7B–E). In contrast, when B-1 trusts its out-group with a trust of 50% or lower, group B's opinion converges and will not get closer to A's opinion (Figures 7F,G). In Figure 8, the intragroup trusts of the two groups are fixed at 50%. The opinion of group B starts to diverge as the intergroup trust from B-1 to A grows large.

The most important limitation lies in that there is much randomness in the model. As the authors tested only a single realization of the model in this article, it is still unclear how representative the results in this article are. Those uncertainties of the estimates are going to be studied as the next step of the research project. Hence, in subsequent studies, we will run several model realizations to check the robustness of trust threshold estimates. Please see forthcoming papers by Okano and Ishii [31, 32] and other related articles [21, 30].

Finally, after intergroup conflict studies using opinion dynamics theory with simulations, how can we explain examples of the real world? Recently in the United States, conflicts have arisen between the two political groups, that is, Republicans and Democrats. From a social identity perspective, partisanship functions in similar ways to other forms of group membership. American voters think of themselves as partisans, either the Republicans or Democrats, by calling to mind a mental image of the sort of people they associate with each party and then assessing the coherence of this image with their self-image [2]. The two parties have been severely divided, and each party has become more cohesive than ever in the last two decades. To say nothing about political ideology, Republicans and Democrats nowadays differ in lifestyles [33, 34]. They do not marry each other. The cars they ride, the food they eat, and the TV programs they prefer are all different. In other words, in-party members trust those who belong to the same party in all respects. However, they do not even try to nurture trust between an out-party. Under these circumstances, the two parties' intragroup trusts are supposed to be very high, as shown in Figure 5B: Republicans and Democrats become more cohesive and antagonistic toward its out-group.

Nowadays, Republicans and Democrats struggle over many issues. There are many conflicts of controversial issues within the society of the United States. For example, gun control, gay marriage, abortion, immigration, racial equality, health insurance, legalization of marijuana, and belief in conspiracy theory are such cases. In the United States, these fierce conflicts have arisen between Republicans and Democrats [35]. On a feeling thermometer, a scale ranging from cold (0) to neutral (50) to warm (100), affinity among co-partisans has consistently hovered within the 70–75 range. By contrast, affinity between opposing partisans has plummeted from 48 in the 1970s to 20 today [36]. Correspondingly, Republicans and Democrats will not agree on the issues because of their hate for an out-party. This situation is similar to our simulations shown in Figures 5B,C.

How can the United States survive this interparty hostility and avoid falling into a social crisis? As we see in Figure 5, if intraparty trusts go down to 55%, the two parties will not reach a consensus because interparty trust is 0%. However, interparty consensus will be achieved when intraparty trusts are lower than 55%, and interparty trusts are higher than 50% (Figure 6). To fix interparty antagonism and reach an agreement, both parties have to endeavor to create divergence of opinions within the party and find ways to enhance interparty trust.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

NO did almost calculation and modeling of the calculation. AI and MN supervised her as graduate student. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by JSPS KAKENHI (Grant Number JP19K04881).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Hogg M. Social identity theory. In: Mckeown S, Haji R, Ferguson N, editors. Understanding Peace and Conflict Through Social Identity Theory: Contemporary Global Perspectives. Cham, CH: Springer (2016). p. 3–17. doi: 10.1007/978-3-319-29869-6_1

CrossRef Full Text | Google Scholar

2. Kalin M, Sambanis N. How to think about identity theory. Annu Rev Polit Sci. (2018) 21:239–57. doi: 10.1146/annurev-polisci-042016-024408

CrossRef Full Text

3. Korte RF. A review of social identity theory with implications for training and development. J Eur Ind Train. (2007) 31:166–80. doi: 10.1108/03090590710739250

CrossRef Full Text | Google Scholar

4. Berelson B, Lazarsfeld P, McPhee W. Voting: A Study of Opinion Formation in a Presidential Campaign. Chicago, IL: The University of Chicago Press (1954).

Google Scholar

5. Achen C, Bartels L. Democracy for Realists: Why Elections Do Not Produce Responsive Government. Princeton, NJ: Princeton University Press (2016).

Google Scholar

6. Tajfel H, Turner J. An integrative theory of inter-group conflict. In: Austin W, Worchel S, editors. The Social Psychology of Inter-Group Relations. Monterey, CA: Brooks/Cole (1979). p. 33–47.

7. Jetten J, McAuliffe BJ, Hornsey MJ, Hogg MA. Differentiation between and within groups: the influence of individualist and collectivist group norms. Eur J Soc Psychol. (2006) 36:825–43. doi: 10.1002/ejsp.322

CrossRef Full Text | Google Scholar

8. Abrams D, Hogg M. Social identity and self-categorization. In: Dovidio J, Hewstone M, Glick P, Esses V, editors. The SAGE Handbook of Prejudice, Stereotyping and Discrimination. London: Sage (2010). p. 179–93. doi: 10.4135/9781446200919.n11

CrossRef Full Text | Google Scholar

9. Deffuant G, Neau D, Amblard F, Weisbuch G. Mixing beliefs among interacting agents. Adv Complex Syst. (2000) 3:87–98. doi: 10.1142/S0219525900000078

CrossRef Full Text | Google Scholar

10. Weisbuch G, Deffuant G, Amblard F, Nadal J. Meet, discuss and segregate! Complexity. (2002) 7:55–63. doi: 10.1002/cplx.10031

CrossRef Full Text | Google Scholar

11. Hegselmann R, Krause U. Opinion dynamics and bounded confidence models, analysis, and simulation. J Artif Soc Soc Simul. (2002) 5:1–33.

Google Scholar

12. Douven I. Simulating peer disagreements. Stud Hist Philos Sci A. (2010) 41:148–57. doi: 10.1016/j.shpsa.2010.03.010

CrossRef Full Text | Google Scholar

13. Sîrbu A, Loreto V, Servedio VDP, Tria F. Opinion dynamics with disagreement and modulated information. J Stat Phys. (2013) 151:218–37. doi: 10.1007/s10955-013-0724-x

CrossRef Full Text | Google Scholar

14. Jarman M, Nowak A, Borkowski W, Serfass D, Wong A, Vallacher R. The critical few: anticonformists at the chrossroads of minority opinion survival and collapse. J Artif Sci Soc Simul. (2015) 18:6. doi: 10.18564/jasss.2663

CrossRef Full Text | Google Scholar

15. Galam S, Javarone MA. Modeling radicalization phenomena in heterogeneous populations. PLoS ONE. (2016) 11:e0155407. doi: 10.1371/journal.pone.0155407

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Javarone MA. Network strategies in election campaigns. J Stat Mech Theory Exp. (2014) 2014:08013. doi: 10.1088/1742-5468/2014/8/P08013

CrossRef Full Text | Google Scholar

17. Javarone MA. Social influences in opinion dynamics: the role of conformity. Phys A Stat Mech Appl. (2014) 414:19–30. doi: 10.1016/j.physa.2014.07.018

CrossRef Full Text | Google Scholar

18. Javarone M, Squartini T. Conformism-driven phases of opinion formation on heterogeneous networks: the q-voter model case. J Stat Mech Theory Exp. (2015) 2015:10002. doi: 10.1088/1742-5468/2015/10/P10002

CrossRef Full Text | Google Scholar

19. Ishii A, Kawahata Y. Opinion dynamics theory for analysis of consensus formation and division of opinion on the internet. arXiv. (2018).

Google Scholar

20. Ishii A. opinion dynamics theory considering trust and suspicion in human relations. In: Morais D, Carreras A, de Almeida A, Vetschera R, editors. Group Decision and Negotiation: Behavior, Models, and Support. 19th International Conference, GDN 2019, Proceedings. Loughborough, UK: Springer (2019). doi: 10.1007/978-3-030-21711-2_15

CrossRef Full Text | Google Scholar

21. Ishii A, Yomura I, Okano N. Opinion dynamics including both trust and distrust in human relation for various network structure. In: The Proceeding of TAAI2020. Taipei (2021).

Google Scholar

22. Ishii A, Okano N. Social simulation of a divided society using opinion dynamics. In: Proceedings of the 2020 IEEE/WIC/ACM International Joint Conference on Web Intelligence and Intelligent Agent Technology. Melbourne, VIC (2021).

23. Holley RA, Liggett TM. Ergodic theorems for weakly interacting infinite systems and the voter model. Ann Probab. (1975) 3:643–63. doi: 10.1214/aop/1176996306

CrossRef Full Text | Google Scholar

24. Galam S. Sociophysics: A Physicist's Modeling of Psycho-Political Phenomena. New York, NY: Springer (2012).

Google Scholar

25. Ishii A, Arakaki H, Matsuda N, Umemura S, Urushidani T, Yamagata N, et al. The “Hit” phenomenon: a mathematical model of human dynamics interactions as s stochastic process. New J Phys. (2012) 14:063018. doi: 10.1088/1367-2630/14/6/063018

CrossRef Full Text | Google Scholar

26. Ishii A, Kawahata Y. Sociophysics analysis of the dynamics of peoples' interests in society. Front Phys. (2018) 6:89. doi: 10.3389/fphy.2018.00089

CrossRef Full Text | Google Scholar

27. Ishii A, Okano N. Sociophysics approach of simulation of mass media effects in society using new opinion. In: Arai K, Kapoor S, Bhatia R, editors. Advances in Intelligent Systems and Computing as the Proceedings of the 2020 Intelligent Systems Conference (IntelliSys). AISC; Amsterdam: Springer Nature (2020). p. 13–28. doi: 10.1007/978-3-030-55190-2_2

CrossRef Full Text | Google Scholar

28. Fujii M, Ishii A. The simulation of diffusion of innovations using new opinion dynamics. In: The Proceedings of 2020 IEEE/WIC/ACM International Joint Conference on Web Intelligence and Intelligent Agent Technology. Melbourne, VIC (2021).

29. Barabashi A. Network Science. Cambridge: Cambridge University Press (2016).

Google Scholar

30. Ishii A, Kawahata Y. Theory of opinion distribution in human relations where trust and distrust mixed. In: Czarnowski I, Howlett R, Jain L, editors. Intelligent Decision Technologies. Smart Innovation, Systems and Technologies. IDT 2020, Vol. 193. Singapore: Springer (2020). p. 471–8. doi: 10.1007/978-981-15-5925-9_40

CrossRef Full Text | Google Scholar

31. Okano N, Ishii A. Simulation by opinion dynamics of the movement of opinions of people in society who are not influenced by the mass media. In: The Proceedings of the Annual Meeting of Computational Social Science Japan. Sendai.

32. Okano N, Ishii A. Simulation by Opinion Dynamics of the Movement of Opinions of People in Society Who Are Not Influenced by the Mass Media. Working Paper.

33. Frank T. What's the Matter With Kansas? How Conservatives Won the Heart of America. New York, NY: Metropolitan Books (2007).

Google Scholar

34. Hetherington M, Weiler J. Prius or Pickup? How the Answers to Four Simple Questions Explain America's Great Divide. New York, NY: Houghton Mifflin (2018).

Google Scholar

35. Pew Research Center. Political Polarization in the American Public: How Increasing Ideological Uniformity and Partisan Antipathy Affect Politics, Compromise and Everyday Life. (2014). Available online at: https://www.pewresearch.org/politics/2014/06/12/political-polarization-in-the-american-public/

36. Finkel EJ, Bail CA, Cikara M, Ditto PH, Iyengar S, Klar S, et al. Political sectarianism in America. Science. (2020) 370:533–6. doi: 10.1126/science.abe1715

CrossRef Full Text | Google Scholar