Conditional Neutral Reward Promotes Cooperation in the Spatial Prisoner’s Dilemma Game

Reward is an effective mechanism that promotes cooperation. However, an individual usually reward her opponents in certain cases. Inspired by this, a conditional neutral reward mechanism has been introduced. In detail, an individual will reward his or her neighbors with the same strategy when the payoff of the focal one is higher than that of his or her neighbors. And simulations are conducted to investigate the impact of our mechanism on the evolution of cooperation. Interestingly, cooperation can survive and dominate the system. Nominal antisocial reward that defectors reward each other is rarely because of the greed of defectors. By contrast, cooperators inside the cooperative clusters share the payoff with cooperators on the boundary so that the latter can form shields to protect cooperators.

Introduction

How cooperation among selfish individuals can emerge and maintain of has been an attractive question in biology, sociology, and many different fields [1–5]. For example, worker ants give up their reproductive capacity to build nests and collect food. And human beings play different roles in social division of labor. In order to explain the widespread phenomenon of cooperation, evolutionary game theory has been proposed and provides a powerful mathematical framework [6–11]. In many game models, PDG (prisoner's dilemma game) is regarded as a paradigm due to capturing the essence of cooperation. In the PDG, two players choose cooperation (C) or defection (D) at the same time without being known by the opponent. If they both choose cooperation or defection, they will both receive the reward (R) or get the punishment (P). However, if one chooses cooperation but the other chooses cooperation, the defector will get the temptation (T) while the cooperator will get the sucker’s payoff (S). For PDG, the ranking rules are T > R > P > S and 2R > T + S. Obviously, the better choice is always defection no matter which strategy the other chooses. But if two individuals both defects, they will receive the less payoff than both cooperating. This is the dilemma.

In the landmark work of Nowak, the mechanism of spatial topology, widely known as spatial reciprocity, has proved to be an effective mechanism to promote cooperative coevolution [12–38]. Inspired by this, many kinds of spatial topologies are applicated to study the cooperative dynamics in evolution, such as square lattice network, ER random network, small-world network, BA scale-free network and so on [39–47]. Besides, to explain cooperation on the spatial topologies, different mechanisms have been proposed, such as reputation, asymmetric interaction, different update rule, co-evolution of dynamical rules, reward or punishment and so on [48–53].

Recent research has shown that rewarding is an effective way to promote cooperation. Various rewards are often given to those who perform well, which is very common in the real society. In this paper, we consider a reward mechanism that the individual could pay a cost to reward the neighbors who has the same strategy. Meanwhile, he could be rewarded by his neighbors. We find that rewards have a positive effect on the maintenance of cooperation, which is manifested in the fact that the weakened cooperators are supported against the invasion of defectors by the population of their kinds, in the form of rewards, while it is opposite for defectors. This creates a unique boundary structure. The reminder of this paper is organized as follows. First, we describe our model detailly. Then, we show the simulation results with figures and try to give an explanation. Finally, we summarize and give the discussion about the conclusions.

Methods

We introduce social reward in the PDG (prisoner’s dilemma game) on L*L square lattices, where each player occupies one and is surrounded by four neighbors. Each player will be initialized as either C (cooperator) or D (defector) with the same possibility. We use the standard PDG by setting T = b (1 < b < 2), R = 1, P = 0, and S = 0. The value of b specifies the strength of the dilemma [54–56]. Hence, the payoff matrix of PDG is described as follows:

$\begin{array}{c} \begin{array}{cc}& \begin{array}{cc}C& D\end{array}\\ \begin{array}{c}C\\ D\end{array}& \left(\begin{array}{cc}1& 0\\ b& 0\end{array}\right)\end{array}.\end{array}(1)$

A player x is chosen randomly at the beginning of each time step, whose payoff $p_x$ can be calculated:

$p_x={\displaystyle \sum _{y=1}^4{p}_{xy}},(2)$

where $p_{xy}$ is the payoff of player x obtained from neighbor y, and it is defined by the payoff matrix. Four neighbors of player x get their payoffs in the same way. Thus, the average payoff of player x’s neighbors $p_{avN}$ is calculated as follows:

$p_{avN}=\frac{{\displaystyle {\sum }_{y=1}^4{p}_y}}{4}.(3)$

If payoff of player x is higher than his neighbors’ or equal, he will pay a cost to reward each his neighbors who have the same strategy. Otherwise, his payoff remains the same. Meanwhile, his four neighbors follow the same procedure. The accumulated payoff of player x at current time step is:

$p_x=\{\begin{array}{cc}{p}_x+N_r\times r-N_c\times c,& p_x\ge p_{avN},\\ p_x,& p_x<p_{avN},\end{array}(4)$

where $N_r$ ($0\le N_r\le 4$) is the number of neighbors rewarding player x, $N_c$ ($0\le N_c\le 4$) is the number of neighbors whom player x rewards, and $r$ and $c$ is the value of rewards and cost.

Finally, player x updates his strategy. A neighbor y is chosen and player x learns the strategy of y randomly with the probability as following:

$P_{x\leftarrow y}=\frac{1}{1+\exp \left((p_x+p_y)/K\right)},(5)$

where K indicates the amplitude of noise that also called intensity of selection [57–62]. Without loss of generality, we set K = 0.1.

The Monte Carlo simulation is carried out with setting L = 200, and the number of all step is set to $5\times {10}^4$. We choose the data of last $5\times {10}^3$ steps to calculate the ultimate average fraction of cooperation. To eliminate the random errors, the final results is the average value of 10 independent repeated experiments for each value of parameters.

Results

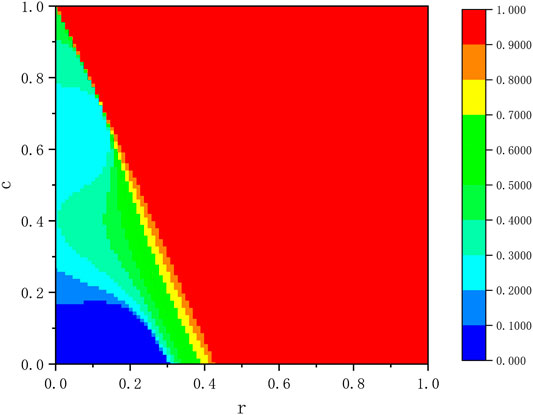
In order to verify the impact of our reward mechanism on cooperation, we give a contour plot as Figure 1, where the simulation result of fraction of cooperation ${\rho }_c$ with a fixed parameter cost $c$ (0.01) and two changing parameters reward $r$ and temptation of defect $b$ is shown. From the figure we can see that first, it is obviously that when the $b$ is relatively large, due to the introduction of reward mechanism ($r>0$), the fraction of cooperation ${\rho }_c$ is still at a high level. In sharp contrast, in the traditional case, when b > 1.04, the cooperation disappears. Second, the contour plot has an obvious dividing line. The area at the upper left of this line, which represents smaller b and larger r, is the area where the cooperation survives. In other words, when the reward mechanism is introduced, for the same b, a higher level of reward $r$ leads to a higher fraction of cooperation ${\rho }_c$. All in all, our reward mechanism strongly promotes cooperation.

FIGURE 1

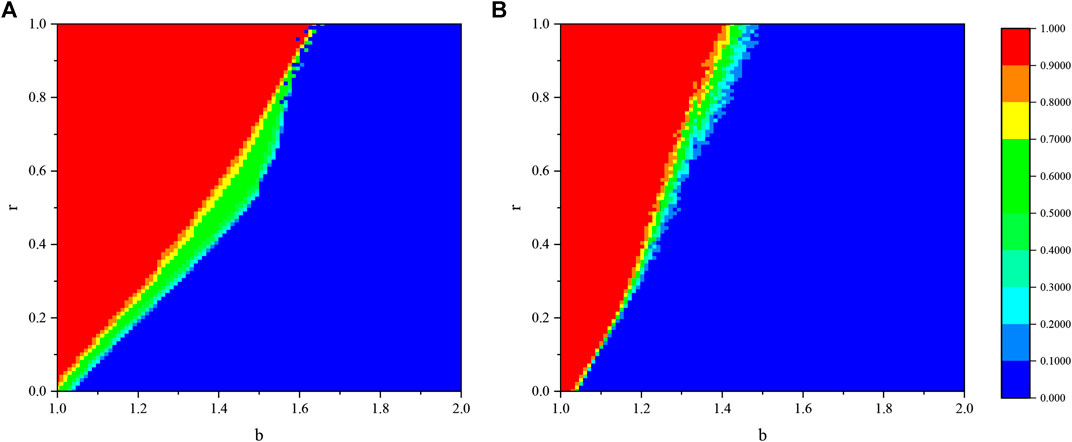
FIGURE 1. Fraction of cooperation on the b-r parameter space when c = 0.01. (A) and (B) give the results simulated on square lattice and WS small world network.

Figure 2 shows the impact of both cost $c$ and reward $r$ on the evolution of cooperation. Interestingly, in Figure 2 we can see that the both increasements of $c$ and $r$ lead to more appropriate condition for survival of cooperation. What’s more, the boundaries among cooperation phase, mixed phase and defection phase are close to straight lines. The phenomenon can be described as under what conditions complete cooperation be formed, which is explained as follows. The key point lies in whether the cooperator can resist the invasion of the defector on the boundary between the cooperator cluster and the defector cluster, which depends on the payoffs of the two type players. Let’s consider a common situation on the boundary, as shown in Figure 3.

FIGURE 2

FIGURE 2. Fraction of cooperation on the r-c parameter space when b = 1.3.

FIGURE 3

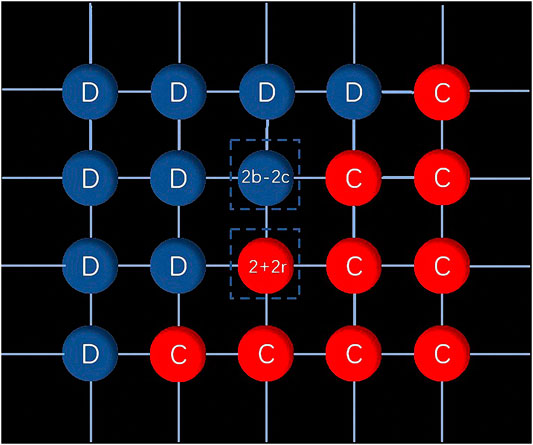
FIGURE 3. Schematic of the boundary structure. Cooperator (defectors) are presented in red (blue). We show the payoffs of the nodes in the dotted boxes.

In Figure 3, we show the payoffs of a cooperator and a defector on the boundary, which are marked with dotted boxes. For the defector, first, he gets payoff $2b$ from his two cooperative neighbors and 0 from his two defective neighbors. It is obviously that his payoff ($2b$) is higher than the average payoff of his four neighbors (1) because of the interaction with cooperators on the boundary. According to the reward mechanism we introduced, he must pay costs of $2c$ to reward his two defective neighbors, but he doesn’t get any reward from his neighbor with the same strategy due to their low payoff. Therefore, his updated payoff is $2b-2c$. However, it is different for the cooperator, who gets $2$ from his two neighbors with cooperation strategy firstly. Interacting with defectors makes his payoff (2) lower than the average payoff of his four neighbors ($2+b$). Thus, he is from paying the cost, but gets the rewards from his neighbors, which increases his payoff to $2+2r$. Obviously, the critical condition is $2+2r=2b-2c$, or $r+c=b-1$. For this situation, if $r+c<b-1$, the cooperator will be at a disadvantage in the game, and vice versa. In this way, we can give the reason why the both increasements of c and r lead to more appropriate condition for survival of cooperation. What’s more, the critical condition is also a linear function, which explains that boundaries among different phases are close to straight lines as shown in Figure 2.

As mentioned before, the supports of cooperation clusters to cooperators on the boundaries, and on the contrary for defectors on the boundaries of defection clusters, may be the potential reasons for promoting cooperation. To confirm that, we show the characteristic snapshots in Figure 4, where different types of nodes called cooperator (C), cooperative rewarder (CR), defector (D) and defective rewarder (DR), are marked in four different colors. Here we fixed cost = 0.1 and from top to bottom, the reward is set as 0.1, 0.3, 0.6 respectively. Obviously, the evolution of game is very different under different values of reward when the value of cost is fixed. It is worth mentioning that distributions CR-C-DR-D as shown in Figure 3 indeed appear on the boundaries among cluster of cooperators and cluster of defectors at any value of reward. However, different $r$ led to different evolution Tendency, which further led to different results. When $r$ is relatively small (0.1), cooperation clusters cannot provide adequate support to cooperators on the boundaries. Hence the cooperators can’t resist the invasion of the defectors. As $r$ increases, cooperators begin to take advantage on the boundaries. When $r=0.5$, it can be observed that while the cooperation cluster invaded the defection cluster, it is also invaded by the defectors. For this phenomenon, our explanation is that when the cluster expands, its boundary structure changes. In particular, the expansion of clusters will produce ragged boundaries, which weakens the role of the cluster to the boundary player. When $r=1$, cooperation has an absolute advantage over defection, so it has expanded rapidly and soon occupied the entire region.

FIGURE 4

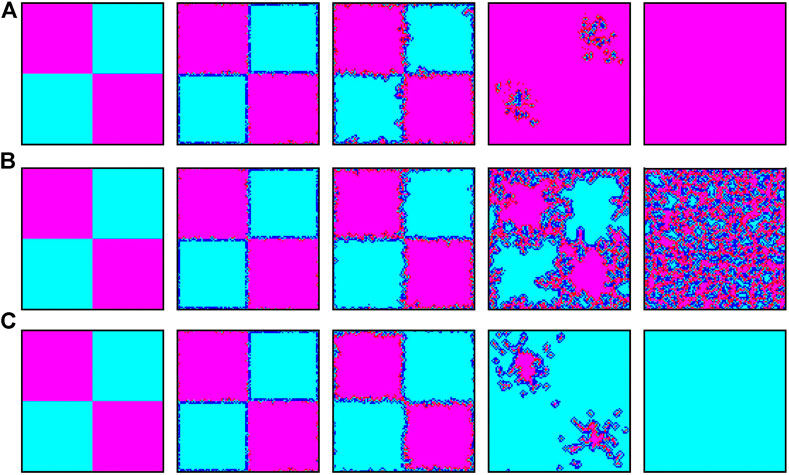
FIGURE 4. Initial evolution of the prepared scenario. The top, medium and bottom correspond to r values of 0.1, 0.3, 0.6 respectively. From left to right, the snapshots correspond to MCS = 0, 1, 10, 100, and 50,000. Cooperator (C), cooperative rewarder (CR), defector (D) and defective rewarder (DR) are shown in color cyan, blue, magenta, and red respectively.

Figure 5 shows how the size of the largest cluster of all kinds of cooperators (including cooperators and cooperative rewarders) $S_{cr}$ and the cooperators who isn’t a rewarder $S_c$ at the last MC step evolves respectively when cost = 0.1 and reward = 0.3. When $b\le 1.1$, there is only one cluster of cooperators and its size is equal to the scale of the network, due to the fact that cooperation dominates the system. Now there is no rewarder in populations of cooperators. As $b$ increases, the clusters of cooperators are invaded, and its size decreases. It should be noted that $S_c$ is smaller $S_{cr}$, which suggests that cooperative clusters are surrounded by cooperative rewarders to free from invasion. When $b$ further increases, the huge cooperation cluster disintegrates rapidly and decomposes into many small cooperation clusters until it disappears completely.

FIGURE 5

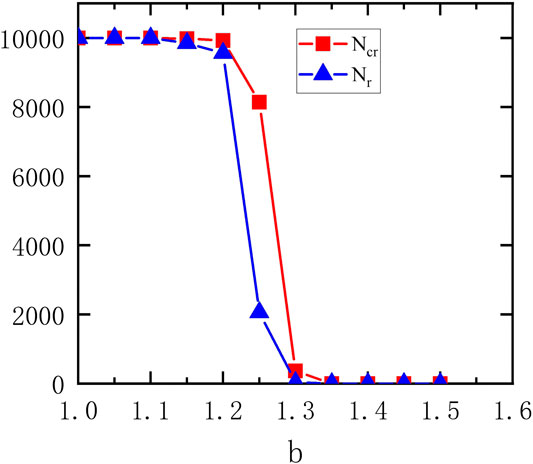
FIGURE 5. The size of the largest cluster of all kinds of cooperators (including cooperators and cooperative rewarders) $S_{cr}$ and the cooperators who isn’t a rewarder $S_c$ at the last MC step evolves respectively when cost = 0.1 and reward = 0.3.

Conclusion

In the real world, individuals are more willing to reward other participants according to certain conditions rather than directly reward them. Hence, we explore the effects of neutral and conditional rewards in structural groups. By numerical simulation, we find that cooperation can be greatly promoted, while conditional antisocial reward does not prevent the evolution of cooperation. From the micro perspective, we provide some evidence to prove that our mechanism enhances the spatial reciprocity and is conducive to the formation of cooperation clusters. In our model, the individuals in the cooperative cluster reward the same kind of individuals on the boundary, so that the latter can form a shield to protect the former. On the contrary, defectors on the border will gradually reduce themselves after rewarding similar individuals inside. By and large, Social reward rather than antisocial reward shapes the direction of collective behavior when an individual rewards others under the condition that her payoff is higher. We hope our work is helpful to resolve the social dilemmas in real society.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

YT designed the research, YT and YY performed the research, MJ and YY analyzed the results, YT and MJ wrote the manuscript. All authors reviewed and approved the manuscript.

Funding

This work was supported by the Science Foundation of Yunnan Province under Grant No. 202001BB050063 and the Open Foundation of Key Laboratory in Software Engineering of Yunnan Province under Grant No. 2020SE315.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Axelrod R, Hamilton WD. The evolution of cooperation. Science (1981) 211(80):1390–6. doi:10.1126/science.7466396

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Wingreen NS, Levin SA. Cooperation among microorganisms. Plos Biol (2006) 4:e299–1488. doi:10.1371/journal.pbio.0040299

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Morgenstern O, von Neumann J. Theory of games and economic behavior. commemorative edition. Princeton, NJ: Princeton University Press (2007).

4. Nowak MA, Sasaki A, Taylor C, Fudenberg D. Emergence of cooperation and evolutionary stability in finite populations. Nature (2004) 428:646–50. doi:10.1038/nature02414

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev Mod Phys (2009) 81:591–646. doi:10.1103/RevModPhys.81.591

CrossRef Full Text | Google Scholar

6. Jm S. Evolution and the theory of games. Cambridge, United Kingdom: Cambridge university press (1982) doi:10.1017/CBO9780511806292

CrossRef Full Text

7. Ritzberger K, Weibull JW. Evolutionary selection in normal-form games. Econometrica (1995) 63:1371. doi:10.2307/2171774

CrossRef Full Text | Google Scholar

8. Hofbauer J, Sigmund K. Evolutionary games and population dynamics. Cambridge, United Kingdom: Cambridge University Press (1998). doi:10.1017/cbo9781139173179

CrossRef Full Text

9. Szabó G, Tőke C. Evolutionary prisoner’s dilemma game on a square lattice. Phys Rev E - Stat Physics, Plasmas Fluids Relat Interdiscip Top (1998) 58:69–73. doi:10.1103/PhysRevE.58.69

CrossRef Full Text | Google Scholar

10. Hill K. Altruistic cooperation during foraging by the Ache, and the evolved human predisposition to cooperate. Hum Nat (2002) 13:105–28. doi:10.1007/s12110-002-1016-3

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hammond RA, Axelrod R. Evolution of contingent altruism when cooperation is expensive. Theor Popul Biol (2006) 69:333–8. doi:10.1016/j.tpb.2005.12.002

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Hardin G. The tragedy of the commons. Science (1968) 162(80):1243–8. doi:10.1126/science.162.3859.1243

CrossRef Full Text | Google Scholar

13. Nowak MA, Sigmund K. Evolution of indirect reciprocity by image scoring. Nature (1998) 393:573–7. doi:10.1038/31225

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Perc M, Szolnoki A. Social diversity and promotion of cooperation in the spatial prisoner’s dilemma game. Phys Rev E Stat Nonlin Soft Matter Phys (2008) 77:011904. doi:10.1103/PhysRevE.77.011904

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Szolnoki A, Perc M. Emergence of multilevel selection in the prisoner’s dilemma game on coevolving random networks. New J Phys (2009) 11:93033. doi:10.1088/1367-2630/11/9/093033

CrossRef Full Text | Google Scholar

16. Zhang H, Small M, Yang H, Wang B. Adjusting learning motivation to promote cooperation. Phys A Stat Mech Its Appl (2010) 389:4734–9. doi:10.1016/j.physa.2010.06.023

CrossRef Full Text | Google Scholar

17. Wang Z, Wang Z, Zhu X, Arenzon JJ. Cooperation and age structure in spatial games. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85:011149. doi:10.1103/PhysRevE.85.011149

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Shen C, Chu C, Shi L, Perc M, Wang Z. Aspiration-based coevolution of link weight promotes cooperation in the spatial prisoner's dilemma game. R Soc Open Sci (2018) 5:180199. doi:10.1098/rsos.180199

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Wang Z, Szolnoki A, Perc M. Evolution of public cooperation on interdependent networks: the impact of biased utility functions. Epl (2012) 97:48001. doi:10.1209/0295-5075/97/48001

CrossRef Full Text | Google Scholar

20. Liu C, Shi J, Li T, Liu J. Aspiration driven coevolution resolves social dilemmas in networks. Appl Math Comput (2019) 342:247–54. doi:10.1016/j.amc.2018.09.034

CrossRef Full Text | Google Scholar

21. Shen C, Chu C, Guo H, Shi L, Duan J. Coevolution of vertex weights resolves social dilemma in spatial networks. Sci Rep (2017) 7:15213. doi:10.1038/s41598-017-15603-2

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Shen C, Chu C, Geng Y, Jin J, Chen F, Shi L. Cooperation enhanced by the coevolution of teaching activity in evolutionary prisoner’s dilemma games with voluntary participation. PLoS One (2018) 13:e0193151. doi:10.1371/journal.pone.0193151

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Perc M, Wang Z. Heterogeneous aspirations promote cooperation in the prisoner’s dilemma game. PLoS One (2010) 5:e15117. doi:10.1371/journal.pone.0015117

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Wang Z, Perc M. Aspiring to the fittest and promotion of cooperation in the prisoner’s dilemma game. Phys Rev E Stat Nonlin Soft Matter Phys (2010) 82:021115. doi:10.1103/PhysRevE.82.021115

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Barabási AL, Albert R. Emergence of scaling in random networks. Science (1999) 80-286:509–12. doi:10.1126/science.286.5439.509

CrossRef Full Text | Google Scholar

26. Chu C, Mu C, Liu J, Liu C, Boccaletti S, Shi L, et al. Aspiration-based coevolution of node weights promotes cooperation in the spatial prisoner’s dilemma game. New J Phys (2019) 21:63024. doi:10.1088/1367-2630/ab0999

CrossRef Full Text | Google Scholar

27. Watts DJ, Strogatz SH. Collective dynamics of “small-world” networks. Nature (1998) 393:440–2. doi:10.1038/30918

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Wang Z, Wang L, Szolnoki A, Perc M. Evolutionary games on multilayer networks: a colloquium. Eur Phys J B (2015) 88:124. doi:10.1140/epjb/e2015-60270-7

CrossRef Full Text | Google Scholar

29. Nowak MA. Five rules for the evolution of cooperation. Science (2006) 314(80):1560–3. doi:10.1126/science.1133755

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Shi J, Hu D, Tao R, Peng Y, Li Y, Liu J. Interaction between populations promotes cooperation in voluntary prisoner’s dilemma. Appl Math Comput (2021) 392:125728. doi:10.1016/j.amc.2020.125728

CrossRef Full Text | Google Scholar

31. Liu J, Meng H, Wang W, Li T, Yu Y. Synergy punishment promotes cooperation in spatial public good game. Chaos, Solitons & Fractals (2018) 109:214–8. doi:10.1016/j.chaos.2018.01.019

CrossRef Full Text | Google Scholar

32. Wang Z, Wang L, Perc M. Degree mixing in multilayer networks impedes the evolution of cooperation. Phys Rev E Stat Nonlin Soft Matter Phys (2014) 89:052813. doi:10.1103/physreve.89.052813

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Wang Z, Wang L, Yin ZY, Xia CY. Inferring reputation promotes the evolution of cooperation in spatial social dilemma games. PLoS One (2012) 7:e40218. doi:10.1371/journal.pone.0040218

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Jin Q, Wang L, Xia CY, Wang Z. Spontaneous symmetry breaking in interdependent networked game. Sci Rep (2014) 4:4095. doi:10.1038/srep04095

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wang Z, Andrews MA, Wu ZX, Wang L, Bauch CT. Coupled disease-behavior dynamics on complex networks: a review. Phys Life Rev (2015) 15:1–29. doi:10.1016/j.plrev.2015.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Li X, Sun S, Xia C. Reputation-based adaptive adjustment of link weight among individuals promotes the cooperation in spatial social dilemmas. Appl Math Comput (2019) 361:810–20. doi:10.1016/j.amc.2019.06.038

CrossRef Full Text | Google Scholar

37. Zhang Y, Wang J, Ding C, Xia C. Impact of individual difference and investment heterogeneity on the collective cooperation in the spatial public goods game. Knowl-based Syst (2017) 136:150–8. doi:10.1016/j.knosys.2017.09.011

CrossRef Full Text | Google Scholar

38. Wang J, Lu W, Liu L, Li L, Xia C. Utility evaluation based on one-to-N mapping in the prisoner's dilemma game for interdependent networks. PLoS One (2016) 11:e0167083. doi:10.1371/journal.pone.0167083

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Huang K, Chen X, Yu Z, Yang C, Gui W. Heterogeneous cooperative belief for social dilemma in multi-agent system. Appl Math Comput (2018) 320:572–9. doi:10.1016/j.amc.2017.10.018

CrossRef Full Text | Google Scholar

40. Szolnoki A, Perc M. Promoting cooperation in social dilemmas via simple coevolutionary rules. Eur Phys J B (2009) 67:337–44. doi:10.1140/epjb/e2008-00470-8

CrossRef Full Text | Google Scholar

41. Droz M, Szwabiński J, Szabó G. Motion of influential players can support cooperation in prisoner’s dilemma. Eur Phys J B (2009) 71:579–85. doi:10.1140/epjb/e2009-00160-1

CrossRef Full Text | Google Scholar

42. Perc M, Szolnoki A, Szabó G. Restricted connections among distinguished players support cooperation. Phys Rev E Stat Nonlin Soft Matter Phys (2008) 78:066101. doi:10.1103/PhysRevE.78.066101

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Raihani NJ, Bshary R. The evolution of punishment in n-player public goods games: a volunteer's dilemma. Evolution (2011) 65:2725–8. doi:10.1111/j.1558-5646.2011.01383.x

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Chu C, Liu J, Shen C, Jin J, Tang Y, Shi L. Coevolution of game strategy and link weight promotes cooperation in structured population. Chaos, Solitons and Fractals (2017) 104:28–32. doi:10.1016/j.chaos.2017.07.023

CrossRef Full Text | Google Scholar

45. Chu C, Hu X, Shen C, Li T, Boccaletti S, Shi L, et al. Self-organized interdependence among populations promotes cooperation by means of coevolution. Chaos (2019) 29:13139. doi:10.1063/1.5059360

CrossRef Full Text | Google Scholar

46. Dai X, Zhu P, Guo Y, Wang Z. Coevolution of vaccination opinions and awareness affecting the spread of epidemics. IEEE Access (2019) 7:61558–69. doi:10.1109/ACCESS.2019.2902856

CrossRef Full Text | Google Scholar

47. Huang K, Wang Z, Jusup M. Incorporating latent constraints to enhance inference of network structure. IEEE Trans Netw Sci Eng (2020) 7:466–75. doi:10.1109/TNSE.2018.2870687

CrossRef Full Text | Google Scholar

48. Huang K, Liu Y, Zhang Y, Yang C, Wang Z. Understanding cooperative behavior of agents with heterogeneous perceptions in dynamic networks. Phys A Stat Mech Its Appl (2018) 509:234–40. doi:10.1016/j.physa.2018.06.043

CrossRef Full Text | Google Scholar

49. Wang Z, Jusup M, Shi L, Lee JH, Iwasa Y, Boccaletti S. Exploiting a cognitive bias promotes cooperation in social dilemma experiments. Nat Commun (2018) 9:2954. doi:10.1038/s41467-018-05259-5

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Wang Z, Jusup M, Wang RW, Shi L, Iwasa Y, Moreno Y, et al. Onymity promotes cooperation in social dilemma experiments. Sci Adv (2017) 3:e1601444. doi:10.1126/sciadv.1601444

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Chu C, Liu J, Shen C, Jin J, Shi L. Win-stay-lose-learn promotes cooperation in the prisoner's dilemma game with voluntary participation. PLoS One (2017) 12:e0171680. doi:10.1371/journal.pone.0171680

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Liu J, Meng H, Wang W, Xie Z, Yu Q. Evolution of cooperation on independent networks: the influence of asymmetric information sharing updating mechanism. Appl Math Comput (2019) 340:234–41. doi:10.1016/j.amc.2018.07.004

CrossRef Full Text | Google Scholar

53. Shen C, Lu J, Shi L. Does coevolution setup promote cooperation in spatial prisoner’s dilemma game?. Appl Math Comput (2016) 290:201–7. doi:10.1016/j.amc.2016.05.044

CrossRef Full Text | Google Scholar

54. Tanimoto J, Sagara H. Relationship between dilemma occurrence and the existence of a weakly dominant strategy in a two-player symmetric game. BioSystems (2007) 90:105–14. doi:10.1016/j.biosystems.2006.07.005

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Wang Z, Kokubo S, Jusup M, Tanimoto J. Dilemma strength as a framework for advancing evolutionary game theory: reply to comments on “Universal scaling for the dilemma strength in evolutionary games”. Phys Life Rev (2015) 14:56–8. doi:10.1016/j.plrev.2015.07.012

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Ito H, Tanimot J. Scaling the phase-planes of social dilemma strengths shows game-class changes in the five rules governing the evolution of cooperation. R Soc Open Sci (2018) 5:181085. doi:10.1098/rsos.181085

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Tanimoto J. Evolutionary games with sociophysics. Singapore: Springer (2018).

CrossRef Full Text

58. Tanimoto J. Fundamentals of evolutionary game theory and its applications. Singapore: Springer (2015) Available from: http://link.springer.com/10.1007/978-4-431-54962-8 (Accessed October 7, 2020).

CrossRef Full Text

59. Alam M, Nagashima K, Tanimoto J. Various error settings bring different noise-driven effects on network reciprocity in spatial prisoner’s dilemma. Chaos, Solitons and Fractals (2018) 114:338–46. doi:10.1016/j.chaos.2018.07.014

CrossRef Full Text | Google Scholar

60. Alam M, Kuga K, Tanimoto J. Three-strategy and four-strategy model of vaccination game introducing an intermediate protecting measure. Appl Math Comput (2019) 346:408–22. doi:10.1016/j.amc.2018.10.015

CrossRef Full Text | Google Scholar

61. Alam M, Tanaka M, Tanimoto J. A game theoretic approach to discuss the positive secondary effect of vaccination scheme in an infinite and well-mixed population. Chaos, Solitons and Fractals (2019) 125:201–13. doi:10.1016/j.chaos.2019.05.031

CrossRef Full Text | Google Scholar

62. Zhu P, Wang X, Jia D, Guo Y, Li S, Chu C. Investigating the co-evolution of node reputation and edge-strategy in prisoner’s dilemma game. Appl Math Comput (2020) 386:125474. doi:10.1016/j.amc.2020.125474

CrossRef Full Text | Google Scholar