1 Introduction
In one of his foundational studies, Stokes established the existence of traveling nonlinear periodic wave trains in deep water [1]. The stability of these waves was resolved when Benjamin and Feir proved that in sufficiently deep water the Stokes wave is modulationally unstable. Small perturbations of Stokes waves were found to lead to exponential growth of the side bands [2, 3]. More recently, modulational instability (MI) of the background state is considered to play a prominent role in the development of rogue waves in oceanic sea states, nonlinear optics, and plasmas [4–9].
The nonlinear Schrödinger (NLS) equation (when in Eq. 1) is one of the simplest models for studying phenomena related to MI; as such, special solutions of the NLS equation are regarded as prototypes of rogue waves. Among the more tractable “rogue wave” solutions of the NLS equation are the rational solutions (with the Peregrine breather being the lowest order) and the spatially periodic breathers (SPBs) which are constructed as heteroclinic orbits of modulationally unstable Stokes waves [10–12]. In the case of the Stokes waves with N unstable modes (UMs), the associated SPBs can be of dimension and are referred to as M-mode SPBs; the single mode SPB is the Akhmediev breather [13]. For more realistic sea states with non-uniform backgrounds, heteroclinic orbits of unstable N-phase solutions have been used to describe rogue waves [14–16].
For theoretical and practical purposes it is important to understand the stability of the SPBs with respect to small variations in initial data and small perturbations of the NLS equation. Using the squared eigenfunction connection between the Floquet spectrum of the NLS equation and the linear stability problem, the SPBs were shown to be typically unstable [17]. The effects of damping on deep water wave dynamics, even when weak, can be significant and in many instances must be included in models to enable accurate predictions of laboratory and field data [18–22].
In a recent study the authors examined the stabilization of symmetric SPBs using the linear damped NLS equation (a near-integrable system that preserves even symmetry of solutions) [23]. The route to stability for these damped SPBs was determined by appealing to the Floquet spectral theory of the NLS equation. Degenerate complex elements of the periodic spectrum (referred to as complex double points) are associated with instabilities of the solution and may split under perturbation to the system. In the restricted subspace of even solutions complex double points can reform as time evolves. The damped solutions were found to be unstable as long as complex double points were present in the spectral decomposition of the data (either by persisting or reforming). A key issue in analyzing the route to stability is determining which complex double points in the spectrum of the SPB are split by damping. For an initial SPB with a given mode structure, perturbation analysis showed that only the complex double points associated with resonant modes split under damping while those associated with nonresonant modes remained closed [23].
The evolution of deep water waves is described only to leading order by the NLS equation. A more accurate description of the wave dynamics is provided by the Dysthe equation, obtained by extending the asymptotic analysis used to derived the NLS equation to fourth order. The Dysthe equation has been shown to accurately predict laboratory data for a wider range of wave parameters than the NLS equation [24, 25, 26]. Gramstad and Trulsen brought the Dysthe equation into Hamiltonian form obtaining a new higher order NLS (HONLS) equation (Eq. 1 with ) [27]. Damped versions of the HONLS equation have successfully described ocean swell and frequency downshift of wave trains on deep water [28, 29].
In this paper we examine the competing effects of dissipation and higher order nonlinearities on the routes to stability of the N-mode SPBs in the framework of the linear damped HONLS equation over a spatially periodic domain:
where is the complex envelope of the wave train, is the Hilbert transform of f, and . The initial data used in the numerical experiments is generated using exact SPB solutions of the integrable NLS equation. The SPBs are over Stokes waves with N unstable modes (referred to as the N-UM regime) for . We interpret the damped HONLS (near-integrable) dynamics by appealing to the NLS Floquet spectral theory.
The higher order nonlinearities in Eq. 1 break the even symmetry of both the initial data and the equation. This raises several interesting questions regarding the damped HONLS equation. Which integrable instabilities are excited by the damped HONLS flow and which elements of the Floquet spectrum are associated with these instabilities? What are the routes to stability under damping; i.e., what remnants of integrable NLS structures are detected in the damped HONLS evolution?
In the present study we observe the onset of novel instabilities as a result of symmetry breaking and the development of critical states in the damped HONLS flow which were nonexistent in the previously examined damped NLS system with even symmetry. Significantly, we determine these instabilities are associated with degenerate complex elements of both the periodic and continuous spectrum, i.e., with both complex “double points” and complex “critical points”, respectively. This association was not previously recognized. With regard to teminology, although double points are among the critical points of , in this paper we exclusively call degenerate complex periodic spectrum where “double points” and reserve the term “critical points” for degenerate complex spectrum where .
The paper is organized as follows. In Section 2 we present elements of the NLS Floquet spectral theory which we use to distinguish instabilities in the numerical experiments. Whether higher phase solutions, such as the even 3-phase solution given in Eq. 8, are unstable with respect to general noneven perturbations and what the Floquet “signature” is of the possible instabilities, has been an open question. The closest stability results we are aware of are for the elliptic solutions of the focusing NLS equation [30]. We numerically show an even 3-phase solution of the NLS equation is unstable with respect to generic perturbations of initial data and find the relevant element of the Floquet spectrum associated with the instability in order to develop a broadened Floquet characterization of instabilities of the NLS equation.
A brief overview of the SPB solutions of the NLS is provided at the end of Section 2 before numerically examining their stabilization under the damped HONLS flow in Section 3. The Floquet decompositions of the numerical solutions are computed for . Complex double points are initially present in the spectrum. If one of the complex double points present initially splits due to the damped HONLS perturbation, the subsequent evolution involves repeated formation and splitting of complex critical points (not double points) which we correlate with the observed instabilities. The Floquet spectral analysis is complemented by an examination of the growth of small perturbations in the SPB initial data under the damped HONLS flow. We determine that the instabilities saturate and the solutions stabilize once all complex double points and complex critical points vanish in the spectral decomposition of the perturbed flow. Variations in the spectrum under the HONLS flow are correlated with deformations of certain NLS solutions to determine the routes to stability for the damped HONLS SPBs.
In Section 4, via perturbation analysis, we examine splitting of the complex double points, present in the SPB initial data, under the damped HONLS flow. We find that for short time, the complex double points associated with modes that resonate with the SPB structure split producing disjoint asymmetric bands, while the complex double points associated with nonresonant modes remain closed, substantiating the initial spectral evolutions observed in the numerical experiments. The nonresonant double points are observed to remain closed for the duration of the experiments, beyond the time-frame of the short time analysis, even though the solution evolves as a damped asymmetric multi-phase state. In this study resonances have a stabilizing effect; the instabilities of nonresonant modes persist on a longer time scale than the instabilities associated with resonant modes.
2 Analytical Framework
The nonlinear Schrödinger equation (when in Eq. 1) arises as the solvability condition of the Zakharov-Shabat (Z-S) pair of linear systems [31]:
where λ is the spectral parameter, ϕ is a complex vector valued eigenfunction, and is a solution of the NLS equation itself. Associated with an periodic NLS solution is it’s Floquet spectrum
Given a fundamental matrix solution of the Z-S system, , one defines the Floquet discriminant as the trace of the transfer matrix across one period L, . The Floquet spectrum has an explicit representation in terms of the discriminant:
The Floquet discriminant is analytic and is a conserved functional of the NLS equation. As such, the spectrum of an NLS solution is invariant under the time evolution.
The spectrum consists of the entire real axis and curves or “bands of spectrum” in the complex λ plane ( is not self-adjoint). The periodic/antiperiodic points (abbreviated here as periodic points) of the Floquet spectrum are those at which . The endpoints of the bands of spectrum are given by the simple points of the periodic spectrum . Located within the bands of spectrum are two important spectral elements:
1. Critical points of spectrum, , determined by the condition .
2. Double points of periodic spectrum .
Double points are among the critical points of . However, in this paper, we exclusively call the degenerate periodic spectrum where “double points” and reserve the term “critical points” for degenerate elements of the spectrum where .
The Floquet spectrum can be used to represent a solution in terms of a set of nonlinear modes where the structure and stability of the modes are determined by the band-gap structure of the spectrum. Simple periodic points are associated with stable active modes. The location of the double points is particularly important. Real double points correspond to zero amplitude inactive nonlinear modes. On the other hand, complex double points are associated with degenerate, potentially unstable, nonlinear modes with either positive or zero growth rate. When restricted to the subpace of even solutions, exponential instabilities of a solution are associated with complex double points in the spectrum [32].
A concrete example illustrating the correspondence between complex double points in the spectrum and linear instabilities is the Stokes wave solution . For small perturbations of the form , , one finds ϵ satisfies the linearized NLS equation
Representing ϵ as a Fourier series with modes , , gives . As a result, the jth mode is unstable if . The number of UMs is the largest integer M such that .
The Floquet discriminant for the Stokes wave is . The Floquet spectrum consists of continuous bands and a discrete part containing and the infinte number of double points
as shown in Figure 1. Note that the condition for to be complex is precisely the condition for the jth Fourier mode to be unstable. The remaining for are real double points.
As the NLS spectrum is symmetric under complex conjugation, we subsequently only display the spectrum in the upper half λ-plane.
2.1 A Broadened Floquet Spectral Characterization of Instabilities
Earlier work on perturbations of the NLS equation dealt primarily with solutions with even symmetry whose instabilities were identified solely via complex double points [33, 34]. In general, imposing symmetry on a solution restricts it’s dynamical behavior and may suppress instabilities. In the current damped HONLS experiments we find instabilities arise due to the asymmetry of the system that are not captured by complex double points. Although complex double points, if present in the damped HONLS flow, still identify instabilities, we need to develop a broader Floquet spectral characterization of instabilities to capture the instabilities of generic solutions.
A clue as to which new spectral elements are associated with instabilities in the full solution space of the NLS equation is provided by considering generic perturbations of initial data for even solutions of the NLS equation. One of the simplest solutions to examine is the following even 3-phase solution of the NLS equation [13],
With respect to t the solution has a double frequency; a frequency determined by the exponential function and a modulation frequency determined by the elliptic functions. Equation 8 describes an even standing wave, periodic in space and time, arising as the degeneration of a 3-phase solution due to symmetry in it’s spectrum. The spatial period L and temporal period T are functions of and , respectively, where is the complete elliptic integral of the first kind. As in Eq. 8, and , the SPB given in Eq. 10 associated with one complex double point.
The surface and Floquet spectrum for are shown in Figures 2A,B. The spectrum forms an even “cross” state with two bands of spectrum in the upper half plane with endpoints given by the simple periodic spectrum and . These two bands intersect transversally at on the imaginary axis. Since at transverse intersections of bands of continuous spectrum, is a critical point. There are no complex double points in .
To numerically address the stability of the cross state Eq. 8 with respect to initial data we consider small perturbations (both symmetric and asymmetric) of the following form:
where , , and . We examine 1) the Floquet spectrum of as compared with and 2) the growth of the perturbations as δ is varied. We consider a solution of the NLS equation to be stable if for every there exists a such that if , then , for all t. Therefore, to determine whether u and stay close as time evolves, we monitor the evolution of the difference
where .
Symmetric Perturbations of Initial Data
As ϕ and δ are varied, the surface and spectrum for for perturbation are qualitatively the same as in Figures 2A,B. The endpoints of the band of spectrum, , are slightly shifted maintaining even symmetry. Due to analyticity of , does not split under even perturbations and the spectrum is not topologically different. Figure 2C shows the evolution of for even perturbations . The small osciallations in , typical in Hamiltonian systems, do not grow. The Floquet spectrum and the evolution of show that when restricted to the subspace of even solutions, is stable.
Asymmetric Perturbations of Initial Data
The surface and spectrum of for are shown in Figures 3A,B. A topologically different spectral configuration is obtained and the waveform is a modulated right traveling wave. The critical point has split into and the two disjoint bands of spectrum form a “right” state: the upper band with endpoints and in the right quadrant and the lower band with endpoint extending to the real axis in the left quadrant. On the other hand, if e.g., , the waveform is a modulated left traveling wave. In this case the orientation of the bands of spectrum is reversed, forming a “left” state with the upper band in the left quadrant and the lower band in the right quadrant. As the parameters in are varied these are the two possible noneven spectral configurations for . The perturbation analysis in Section 4 is related and shows noneven perturbations of the SPB split complex double points into left and right states.
Figure 3C shows grows to for asymmetric perturbations . Clearly does not remain close to for these perturbations. We associate the transverse complex critical points with instabilities arising from symmetry breaking which are not excited when evenness is imposed. The exact nature of the instability associated with complex critical points is under investigation. The current damped HONLS experiments in Section 3 corroborate the significance of transverse critical points in identifying instabilities in the unrestricted solution space.
2.2 Spatially Periodic Breather Solutions of the NLS Equation
A variety of dressing methods can be used to derive new nontrivial solutions to integrable equations [see [35] for applications of the Darboux transformation to generate solutions of generalized NLS models]. Here we use the Bäcklund-gauge transformation (BT) for the NLS equation [36] to generate the heteroclinic orbits of a spatially periodic unstable NLS potential with complex double points, , in its Floquet spectrum. Given a Stokes wave with N complex double points, a single BT of at yields the one mode SPB, , associated with the jth UM, . Introducing , , , and one obtains [13, 33]:
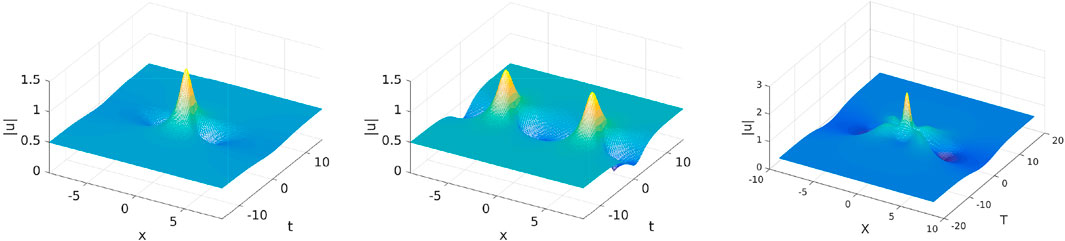
exponentially approaches a phase shift of the Stokes wave, , at a rate depending on . Figures 4A,B show the amplitudes of two distinct single mode SPBs, and over a Stokes waves with UMs. and are both unstable as the BT based at saturates the instability of the jth UM while the other instabilities of the background persist.
When the Stokes wave posesses two or more UMs, the BT can be iterated to obtain multi mode SPBs. For example, the two-mode SPB with wavenumbers and , obtained by applying the BT successively at complex and , is of the following form:
The exact formula is provided in [11]. The parameters ρ and τ determine the time at which the first and second modes become excited, respectively. Figure 4C shows the amplitude of the “coalesced” two mode SPB (, ) over a Stokes waves with UMs where the two modes are excited simultaneously.
An important property of the Bäcklund transformation: The BT is isospectral, i.e., . For example, the Stokes wave with UMs (given in Figure 1) and each of the SPBs shown in Figure 4A–C share the same Floquet spectrum.
3 Numerical Investigation of Routes to Stability OF SPBS IN the Damped Higher Order NLS Equation
In our examination of the even 3-phase solution in Section 2 we found that when evenness is relaxed novel instabilities arise which are associated with complex critical points. Armed with this result, in this section we return to the questions posed at the outset of our study: 1) Which integrable instabilities are excited by the damped HONLS flow and what is the Floquet criteria for their saturation? 2) What remnants of integrable NLS structures are detected in the damped HONLS evolution?
The notation used in this section is as follows: 1) The “N UM regime” refers to the range of parameters a and L for which the underlying Stokes wave initially has N unstable modes. 2) The initial data used in the numerical experiments is generated using exact SPB solutions of the integrable NLS equation. The perturbed SPBs are indicated with subscripts: refers to the solution of the damped HONLS Eq. 1 for one-mode SPB initial data . Likewise is the solution to Eq. 1 for iterated SPB initial data.
The damped HONLS equation is solved numerically using a high-order spectral method due to Trefethen [37]. The integrator uses a Fourier-mode decomposition in space with a fourth-order Runge-Kutta discretization in time. The number of Fourier modes and the time step used depends on the complexity of the solution. For example, for initial data in the three UM regime, Fourier modes are used with time step . As a benchmark the first three global invariants of the HONLS equation, the energy , momentum , and Hamiltonian
are preserved with an accuracy of for . The invariant for the damped HONLS system, the spectral center , is preserved with an accuracy of at least in the experiments.
Nonlinear mode decomposition of the damped HONLS flow: At each time t we compute the spectral decomposition of the damped HONLS data using the numerical procedure developed by Overman et. al. [34]. After solving system Eq. (2), the discriminant is constructed. The zeros of are determined using a root solver based on Müller’s method and then the curves of spectrum filled in. The spectrum is calculated with an accuracy of which is sufficient given the perturbation parameters ϵ and γ used in the numerical experiments are .
Notation used in the spectral plots: The periodic spectrum is indicated with a large when and a large box when . The continuous spectrum is indicated with small when the is negative and a small box when is positive.
Interpreting the damped HONLS flow via the NLS spectral theory: A tractable example which illustrates the use of the Floquet spectrum to interpret near integrable dynamics is the spatially uniform solution (there is no depenence on ϵ) of the damped HONLS Eq. 1,
At a given time the nonlinear spectral decomposition of Eq. 12 can be explicitly determined by substituting into . We find the periodic Floquet spectrum consists of and infinitely many double points
where is complex if . Under the damped HONLS evolution the endpoint of the band of spectrum and the complex double points move down the imaginary axis and then onto the real axis. Similarly, at , a linearized stability analysis about shows the growth rate of the jth mode . Thus the number of complex double points and the number of unstable modes diminishes in time due to damping. As a result, stabilizes when the growth rate , i.e., when , giving .
Saturation time of the instabilities: Since the association of complex critical points with instabilities is a new result, we supplement the spectral analysis with an examination of the saturation time of the instabilities for the damped SPBs and as follows: we examine the growth of small asymmetric perturbations in the initial data of the following form,
and
where.
i., , ,
ii., is random noise.
To determine the closeness of and as time evolves we monitor the evolution of , as given by Eq. 9. We consider the solution to have stabilized under the damped HONLS flow once saturates.
In the damped HONLS numerical experiments we obtain a new criteria for the saturation of instabilities: saturates and the SPB stabilizes once damping eliminates all complex double points and complex critical points in the spectrum.
3.1 Damped HONLS SPB in the One Unstable Mode Regime
in the one UM regime
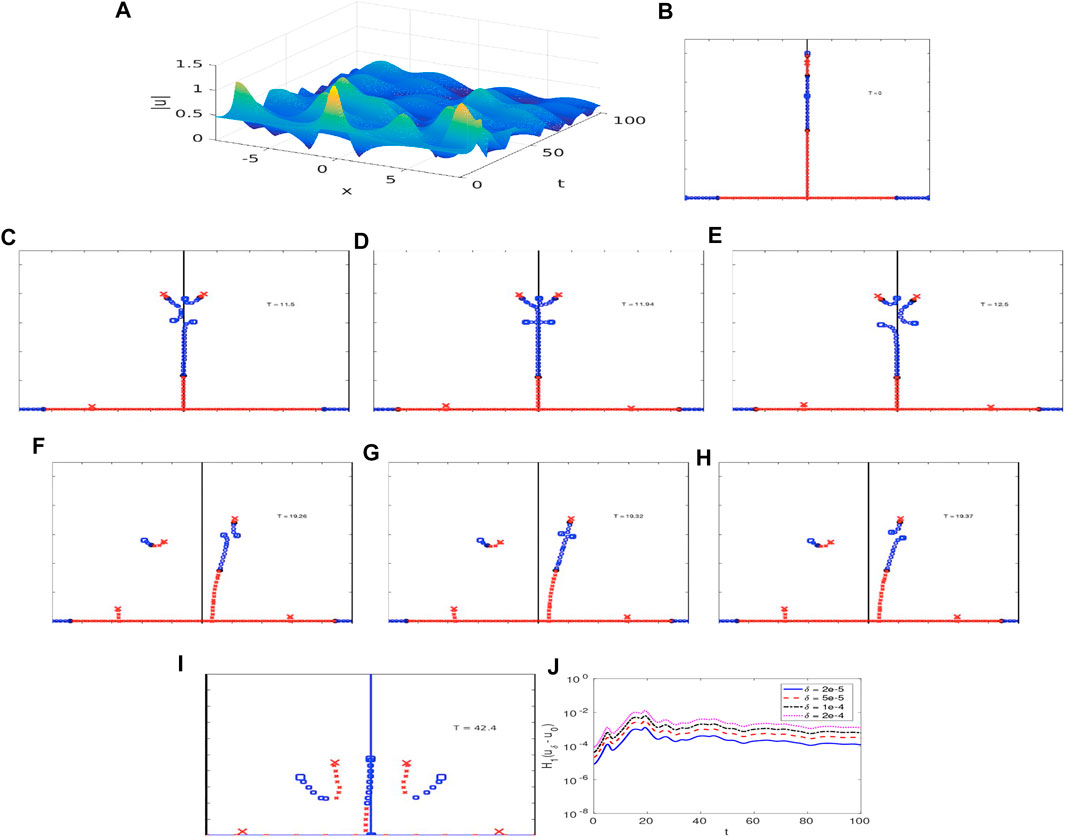
We begin by considering for and in the one UM regime with initial data generated using Eq. 10 with , and . Figure 5A shows the surface for .
The evolution of the Floquet spectrum for is as follows: At , the spectrum in the upper half plane consists of a single band of spectrum with end point at , indicated by a large “box”, and one imaginary double point at , indicated by a large “” (Figure 5B). Under the damped HONLS splits asymmetrically forming a right state, with the upper band of spectrum in the right quadrant and the lower band in the left quadrant, consistent with the short time perturbation analysis in Section 4. The right state is clearly visible at in Figure 5C with the waveform characterized by a single damped modulated mode traveling to the right. The spectrum persists in a right state with the separation distance between the two bands varying until , Figure 5D, when a cross state forms with an embedded critical point indicating an instability. Subsequently the critical point splits into a right state. As damping continues the band in the right quadrant widens, Figure 5E, and the vertex of the loop eventually touches the origin at The spectrum then has three bands emanating off the real axis, with endpoints which, as damping continues, diminish in amplitude and move away from the imaginary axis, Figure 5F.
Figure 5G shows the evolution of for using and The saturation of at is consistent with the Floquet criteria that the solution stabilizes after complex double points and complex critical points are eliminated in the damped HONLS flow.
From the spectral analysis of in the one UM regime, we find it may be characterized as a continuous deformation of a noneven generalization of the 3-phase solution, the right state, given by Eq. 8. The amplitude of the oscillations of decreases and the frequency increases until small fast oscillations about the damped Stokes wave, visible in Figure 5A, are obtained.
An alternate approach to studying the effect of small damping (or gain) on the one mode SPB is to consider the evolution of asymmetric initial data in the neighborhood of the SPB under the linearly damped NLS equation. Using the finite gap method of the periodic NLS equation [38], the solution is analytically approximated to leading order with a sum of SPBs shifted in space and time. The quantitative agreement between the leading order analytical formula and the corresponding numerical experiments was found to be good [21]. It is interesting to note that, although we use exact SPB initial data under the linearly damped HONLS equation, with different damping values, the asymmetric evolution of the Floquet spectral data is qualitatively consistent with the numerical experiments described in [21].
3.2 Damped HONLS SPBs in the Two Unstable Mode Regime
For the two UM regime we let , and consider the two distinct perturbed single mode SPBs and and the perturbed iterated SPB . The damped HONLS perturbation parameters are and .
in the two UM regime
Figure 6A shows the surface for for initial data given by Eq. 10 with . The Floquet spectrum at is given in Figure 6B. The end point of the band of spectrum at is indicated by a “box”. There are two complex double points at and , indicated by a “” and “box”, respectively. For both double points split asymmetrically: , the complex double point at which is constructed, splits at leading order into such that a right state forms with the first mode traveling to the right. The second double point splits at higher order into such that a left state forms with the second mode traveling to the left. These disjoint asymmetric bands of spectrum are consistent with the short time perturbation analysis in Section 4 for damped HONLS data of the form Eq. 18.
This spectral configuration is representative of the spectrum during the initial stage of it’s evolution and is still observable in Figure 6C at . A sequence of bifurcations occur at , Figure 6D, when two complex critical points emerge in rapid succession in the spectrum, indicating instabilities associated with both nonlinear modes. Subsequently both complex critical points split, Figure 6E, with the upper band in the left quadrant and the second band in the right quadrant corresponding to a damped waveform with the first mode traveling to the left and the second mode traveling to the right.
The bifurcation at corresponds to transitioning through the remnant of an unstable 5-phase solution (with two instabilities) of the NLS equation. The bands eventually become completely detached from the imaginary axis and a second complex critical point forms at . The bifurcation sequence is shown in Figure 6F–H. The main band emanating from the real axis then reestablishes itself close to the imaginary axis, Figure 6I, and the spectrum settles into a configuration corresponding to a stable 5 phase solution. The bands move apart and downwards and hit the real axis with no further development of complex critical points. From the Floquet spectral perspective, once damping eliminates complex critical points in the spectrum at approximately , stabilizes.
Figure 6J shows the evolution of for with for The perturbation is chosen in the direction of the unstable mode associated with . stops growing by , confirming the instabilities associated with the complex critical ponts and time of stabilization obtained from the nonlinear spectral analysis.
For in the 2-UM regime, both and resonate with the perturbation. The route to stability is characterized by the appearance of the double cross state of the NLS and the proximity to this state is significant in organazing the damped HONLS dynamics. Once stabilized, may be characterized as a continuous deformation of a stable 5-phase solution.
in the two UM regime
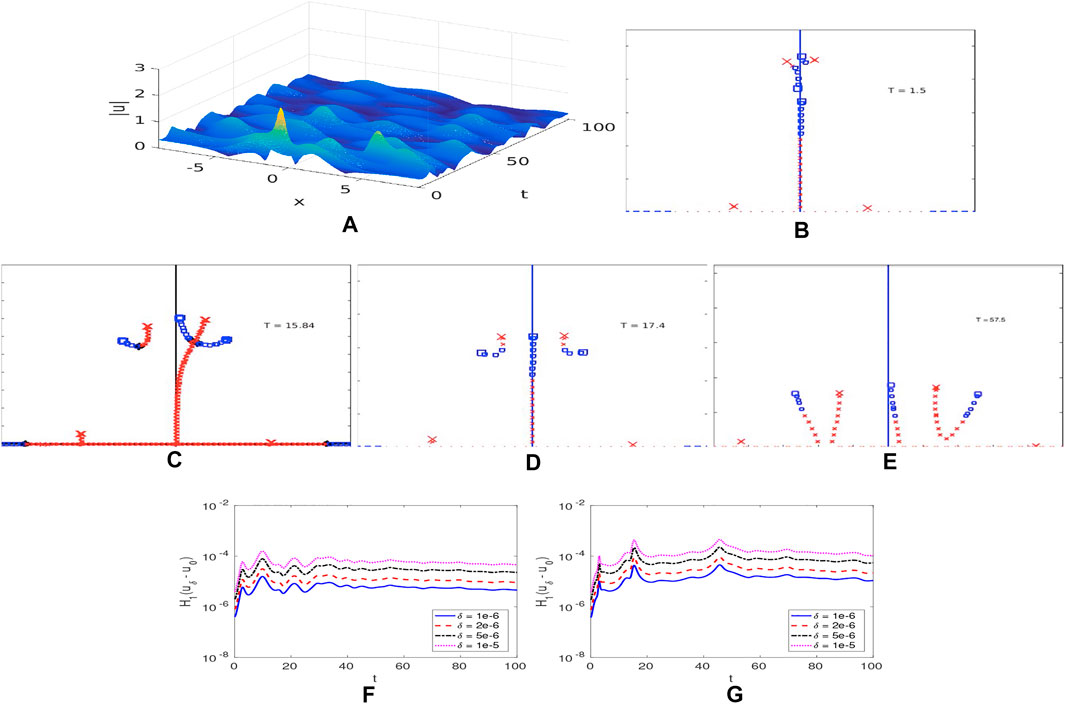
We now consider whose initial data is given by Eq. 10 with . Although and are both single mode SPBs over the same Stokes wave, their respective routes to stability under damping are quite different. Notice in Figure 7A the surface of for is a damped modulated traveling state, exhibiting regular behavior, in contrast to the irregular behavior of in the two UM regime.
The spectrum of at is the same as in Figure 6B. Under perturbation immediately splits asymmetrically into with the upper band in the right quadrant and the lower band in the left quadrant, while the first double point (indicated by the large “”) does not split. Figure 7B clearly shows that at damping has only split , i.e., the double point at which the SPB is constructed. In fact does not split for the duration of the damped HONLS evolution, . In Figure 7C, by , the two bands have aligned forming a cross state with a complex critical point at the transverse intersection of the bands while is still intact and has simply translated down the imaginary axis.
The complex critical point subsequently splits with the upper band of spectrum again in the right quadrant, Figure 7D. Complex critical points do not reappear in the spectrum. At the vertex of the upper band of spectrum touches the real axis Figure 7E. As damping continues moves down the imaginary axis and the two bands move away from the imaginary axis with diminishing amplitude. In Figure 7F the complex double point has moved almost all the way down the imaginary axis. At , and complex double points do not arise in the subsequent spectral evolution.
We find grows until , Figure 7G, consistent with the expectation that will stabilize once all complex critical points and complex double points vanish in the spectrum. Until moves onto the real axis, perturbations to the initial data can excite the first mode associated with causing and to grow apart.
Why doesn’t the HONLS perturbation split when given initial data? In Section 4, for short time, a suitable linearization of the damped HONLS SPB data is found to be given by Eq. 19 for , respectively where . The perturbation analysis shows that at leading order damping asymmetrically splits only the double point associated with . The endpoint of spectrum, , decreases in amplitude and the rest of the double points simply move along curves of continuous spectrum without splitting. The resonant modes which correspond to split asymmetrically at higher order . The splitting of , , is zero and is termed “closed”.
The spectral evolution for in the 2 UM regime is reminiscent of the spectral evolution of in the one UM regime. There is an important difference though: The nearby cross state that appears in the spectral decomposition of has two different types of instabilites: the instability associated with the complex critical point (potentially a phase instability) and the exponential instability associated with the (nonresonant) complex double point . The numerical results suggest that when nonresonant modes are present in the damped HONLS, their instabilities persist and organize the dynamics on a longer time scale. As remains closed for , can be characterized as a continuous deformation of a noneven generalization of the degenerate 3 phase solution given by Eq. 8 (the parameter values change due to doubling the period L; i,e., a th mode excitation with period L becomes a th mode excitation with period 2L.)
in the two UM regime
Figure 8A shows the surface for for initial data obtained from Eq. 11 by setting and , . The spectrum of at is given by Figure 6B. As we’ve seen in the previous examples, once complex double points split they do not reform in the perturbed system; if they are present in the spectral decomposition of the damped HONLS, it is because the modes corresponding to didn’t resonate under perturbation. Here both double points and split at leading order under the damped HONLS perturbation. Figure 8B shows for short time () the spectrum has a band gap structure indicating the first mode travels to the right and the second travels to the left. As time evolves the bands shift and align and Figure 8C shows at two bands in the right quadrant intersect with an embedded complex critical point. The critical point splits with one band moving back toward the imaginary axis. There are now two bands detached from the primary band and evolving towards the real axis, Figures 8D,E. Complex critical points do not appear for .
Figure 8F shows for the example under consideration () when ,. We find saturates at indicating has stabilized. For is characterized as a continuous deformation of a stable NLS five-phase solution. The numerically observed initial splitting of complex double points and is consistent with the perturbation analysis of damped HONLS SPB data (19).
Among the two mode SPBs in the 2 UM regime, the one of highest amplitude due to coalescence of the modes appeared to be more robust [17]. An interesting observation is obtained if we examine the evolution of spectrum and of using the initial data for the special coalesced two mode SPB, generated from Eq. 11 by setting , , and . For the coalesced case, complex critical points form 4 times for in the damped HONLS system. Figure 8G shows saturates for . A comparison with the results of the non-coalesced two mode SPB given above indicate that remnants of the coalesced and it’s instabilities influence the damped HONLS dynamics over a longer time period, suggesting enhanced robustness with respect to perturbations of the NLS equation.
3.3 Damped SPBs in the Three Unstable Mode Regime
The parameters used for the three UM regime are and . The damped HONLS perturbation parameters are and . We present the results of two damped HONLS SPBs, and , which exhibit an interesting or new feature. The evolutions of the other damped HONLS SPBs in the three UM regime in the three UM regime are discussed in relation to these cases.
in the three UM regime
The surface for initial data given by Eq. 10 with is shown in Figure 9A for . Notice in the 3 UM regime exhibits regular behavior and is a damped modulated right traveling wave as was in the 2 UM regime. The spectrum at is given in Figure 9B. The end point of the band of spectrum, is indicated by a “box”. There are three complex double points at , , and indicated by an “”, “box” and “”, respectively. Under the damped HONLS perturbation the complex double point at which is constructed, , splits into a right state as shown in Figure 9C. The complex double points and remain closed; lies on the upper band in the right quadrant and lies on the lower band. Transverse cross states with embedded complex critical points form frequently in the spectrum until , e.g., a cross state is shown at in Figure 9D. Figures 9E,F show the complex double points persist on the bands of spectrum until damping sufficiently diminishes the amplitude of the background and the complex double points reach the real axis at . In Figure 9G saturates at . Due to the presence of the complex double points for , can be viewed as a continuous deformation of an unstable 3 phase solution (with two instabilities). As discussed previously, the instabilities associated with the nonresonant modes persist longer than for the resonant modes.
In the 3 UM regime the behavior of the SPB is similar to . In this case initially splits asymmetrically into the right state (which we’ve now seen frequently in the initial damped HONLS system when only one mode is activated). The double points and do not split, they move along the band of spectrum created by and . As a result stabilizes only when and become real, at . As in the previous cases, it is striking that the prediction from a short time perturbation analysis that certain double points remain closed, holds for the duration of the experiments (even while the solution evolves as a perturbed degenerate 3-phase state (with two instabilities). In contrast, for the higher order nonlinearities and damping excite all the modes. The solution is characterized by the formation of complex critical points and irregular behavior before stabilizing at .
in the three UM regime
Figure 10A shows the surface for for initial data given by Eq. 11 with .
The spectrum at is as in Figure 9B. The perturbation initially splits the double points and into and that correspond to a left and right modulated traveling modes, respectively. The new feature here is that the first complex double point, , splits at higher order into (see the analysis in Section 4 showing that a multi-mode perturbation in a higher UM regime introduces new resonances not seen with single mode perturbations). The higher order splitting is visible in Figure 10B at .
Complex double points are not observed in the spectral evolution for .The formation of complex critical points in the spectrum occurs frequently as shown, for example, in Figure 10C and Figure 10D. Since the amplitude of the background state at is initially very close to the 4 UM regime, in this example we observe that nearby real double points are noticeably split by the perturbation. Figure 10E shows the spectrum at when the last complex critical point forms. This is reflected in Figure 10G which shows saturates at . Each of the bursts of growth in can be correlated with a complex critical point crossing. As time evolves disspiation diminshes the strength of the instability captured by the complex critical points or complex double points. exhibits quite rich and compex dynamics before damping saturates the instabilities and it’s behavior is not easy to characterize as when dealing with the perturbed SPBs in the UM regimes. For the evolution of may be characterized as a continuous deformation of a stable 7-phase solution (Figure 10F).
As a comparison, and exhibit shorter term irregular behavior with all the dominant modes excited and they stabilize at . respectively. was observed to take longer to stabilize due to the higher order splitting in .
The exact nature of the instability associated with complex critical points in under investigation. They may be weaker than the exponential instabilities associated with complex double points but the evolution of illustrates their cumulative impact can be significant.
4 Perturbation Analysis
While examining the route to stability of the SPBs under the damped HONLS several novel results arose. One feature was that the instabilities of nonresonant modes persist longer than the instabilities of the resonant modes. We are interested in the fate of complex double points under noneven perturbations induced by HONLS as they characterize the SPB. Following the perturbation analysis in [39] used to determine the splitting of double points for single mode perturbations, we carry the analysis to higher order for noneven multi mode perturbations of the SPBs. We find 1) additional modes resonate with the perturbation and 2) complex double points associated with nonresonant modes remain closed.
To obtain linearized initial conditions for the one and two mode SPBs we use the Hirota formulation of the SPBs [40]. For example for the one mode SPB one obtains,
where , , , , and γ is an arbitrary phase.
The appropriate linearized initial conditions for the one and two mode SPBs, and respectively, are obtained by choosing t and γ such that , , are small. After neglecting second-order terms we obtain:
The damped HONLS yields the following noneven first order approximation for small time,
where and are functions of h and the damped HONLS parameters ϵ and γ, for . For simplicity we set and suppress their explicit dependence on :
where and Q can be 0 or 1, depending on whether a one or two mode SPB is under consideration.
Since and the eigenfunctions are analytic functions of their arguments, at the double points we assume the following expansions:
Substituting these expansions into Eq. 25 we obtain the following:
where
The leading order Eq. 22 provides the spectrum for the Stokes wave. At the double points the two dimensional eigenspace is spanned by the eigenfunctions
where , and the general solution is given by
4.1 First Order Results
For periodic v, the solvability condition for the system is given by the orthogonality condition
for all w in the nullspace of the Hermitian operator
At the double points the nullspace of is spanned by the eigenfunctions and the orthogonality condition becomes
Applying this orthogonality condition to Eq. 23 yields the system of equations
where
Non trivial solutions are obtained only at the complex double points , at which the SPB was constructed providing the first order correction
where and for . As a result where and the double point splits asymmetrically in any direction. Examining in a neighborhood of we find that when resonates with a particular mode, the band of continuous spectrum along the imaginary axis splits asymmetrically into two disjoint bands in the upper half plane. The other double points do not experience an correction.
The spectral configuration is determind by the location of . determines the speed and direction of the associated phase. For example, in the one complex double point regime there are only two spectral configurations associated with noneven perturbation: 1) For , Re and the upper band of spctrum lies in the first quadrant. The wave form is characterized by a single modulated mode traveling to the right. 2) For , Re , the upper band of spectrum is in the second quadrant, and the wave form is characterized by a single modulated mode traveling to the left.
As observed in the damped HONLS numerical experiments, the spectrum evolves between two distinct configurations when the continuous spectrum develops a complex critical point (not double point) due to the formation of transverse bands which then splits.
4.2 Second Order Results
Determining the corrections to the double points for , requires determining the eigenfunctions at . When the right hand side of Eq. 23 simplifies to
where is given by Eq. 26. We assume where
Substituting into Eq. 23 we find the coefficient vectors to be (with , )
With in hand, applying the orthogonality condition to Eq. 24 yields the system
giving an correction of the form
Consequently only the double points with , or experience an splitting. All other double points experience an translation. This calculation can be carried to higher order . In the simpler case of a damped single mode SPB, , only corresponding to the resonant mode will split at order whereas the splitting is zero for , [41].
For the two mode damped SPB in the 3 UM regime we find and will split at . The mode associated with resonates also with at . All 3 complex double points split, in contrast with the one mode where and do not split.
5 Conclusions
In this paper we investigated the route to stability for even N-mode SPB solutions of the NLS equation in the framework of a damped HONLS equation using the Floquet spectral theory of the NLS equation. We found novel instabilities emerging in the symmetry broken solution space of the damped HONLS which are not captured by complex double points in the Floquet spectrum. We developed a broadened Floquet characterization of instabilities by examining the stability of an even 3-phase solution of the NLS equation with respect to noneven perturbations. We found the transverse complex critical point in its spectrum is associated with an instability which is not excited when evenness is imposed.
The association of instabilities excited by symmetry breaking with complex critical points of the Floquet spectrum was corroborated by the numerical experiments. If one of the complex double points present at splits in the damped HONLS system, the subsequent spectral evolution involves repeated formation and splitting of complex critical points (not double points) which we correlated with the observed instabilities.
In the numerical study we presented experiments using fixed values of the perturbation parameters ϵ and γ. As these parameters are varied fewer or more critical points may form and the time the damped HONLS solution stabilizes may vary but the following interesting results are independent of their specific value: 2) Instabilities excited by symmetry breaking are associated with complex critical points. 2) Solutions stabilize once damping eliminates all the complex critical points and complex double points in the spectral deomposition of the damped HONLS data. 3) Only certain modes resonate with the damped HONLS perturbation. Resonant modes aid in stabilizing the solution. If nonresonant modes are present, their instabilities persist and appear to organize the dynamics on a longer timescale.
Each burst of growth in can be correlated with the emergence of a complex critical point. The numerics suggest the instabilities associated with complex critical points may be weaker than those associated with complex double points. Even so the exact nature of the instability warrants further investigation. As demonstrated by the evolution of their cumulative impact can be significant.
Via a short time perturbation analysis we find that resonant complex double points split producing disjoint asymmetric bands, while the nonresonant complex double points remain closed as they move along the bands of spectrum, corroborating the initial spectral evolutions observed in the numerical experiments. Further, the nonresonant double points remain closed for the duration of the experiments, beyond the time-frame of the short time analysis, even though the solution evolves as a damped asymmetric multi-phase state.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
CS was responsible for the theoretical framework, calculations, and the writing of the manuscript. CS and AI performed the numerical simulations. Both authors approve the manuscript.
Funding
This work was partially supported by Simons Foundation, Grant No. #527565.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Stokes GG. On the theory of oscillatory waves. Trans Cambridge Philos Soc (1847) 8:441–73.
Google Scholar
2. Benjamin TB, Feir JE. The disintegration of wave trains in deep water. J Fl Mech (1967) 27:417–30. doi:10.1017/s002211206700045x
CrossRef Full Text | Google Scholar
3. Zakharov VE. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J Appl Mech Tech Phys (1968) 9:190–4. doi:10.1007/BF00913182
CrossRef Full Text | Google Scholar
4. Peregrine D. Water waves, nonlinear Schrödinger equations and their solutions. J Austral Math Soc Ser B (1983) 25:16–43. doi:10.1017/s0334270000003891
CrossRef Full Text | Google Scholar
5. Dysthe KB, Trulsen K. Note on breather type solutions of the NLS as models for freak-waves. Physica Scripta (1999) T82:48–52. doi:10.1238/physica.topical.082a00048
CrossRef Full Text | Google Scholar
6. Kibbler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The Peregrine soliton in nonlinear fibre optics. Nat Phys (2010) 6:790–5. doi:10.1038/nphys1740
CrossRef Full Text | Google Scholar
7. Kharif C, Pelinovsky E, Slunyaev A. Rogue waves in the ocean. Berlin Heidelberg: Springer-Verlag (2009).
8. Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi FT. Rogue waves and their generating mechanisms in different physical contexts. Phys Rep (2013) 528:47–89. doi:10.1016/j.physrep.2013.03.001
CrossRef Full Text | Google Scholar
10. Osborne A, Onorato M, Serio M. The nonlinear dynamics of rogue waves and holes in deep-water gravity wave train. Phys Lett A (2000) 275:386–93. doi:10.1016/s0375-9601(00)00575-2
CrossRef Full Text | Google Scholar
11. Calini A, Schober CM. Homoclinic chaos increases the likelihood of rogue wave formation. Phys Lett A (2002) 298:335–49. doi:10.1016/s0375-9601(02)00576-5
CrossRef Full Text | Google Scholar
12. Akhmediev N, Soto-Crespo JM, Ankiewicz A. Extreme waves that appear from nowhere: on the nature of rogue waves. Phys Lett A (2009) 373:2137–45. doi:10.1016/j.physleta.2009.04.023
CrossRef Full Text | Google Scholar
13. Akhmediev NN, Eleonskii VM, Kulagin NE. Exact first-order solutions of the nonlinear Schrödinger equation. Theor Math Phys (Ussr) (1987) 72:809–18. doi:10.1007/bf01017105
CrossRef Full Text | Google Scholar
14. Calini A, Schober CM. Characterizing JONSWAP rogue waves and their statistics via inverse spectral data. Wave Motion (2017) 71:5–17. doi:10.1016/j.wavemoti.2016.06.007
CrossRef Full Text | Google Scholar
15. Chen J, Pelinovsky D. Rogue periodic waves of the focusing nonlinear Schrödinger equation. Proc Math Phy Eng Sci (2018) 474:20170814. doi:10.1098/rspa.2017.0814
CrossRef Full Text | Google Scholar
16. Chen J, Pelinovsky DE, White RE. Rogue waves on the double-periodic background in the focusing nonlinear Schrödinger equation. Phys Rev E (2019) 100:052219. doi:10.1103/physreve.100.052219 |
PubMed Abstract | CrossRef Full Text | Google Scholar
17. Calini A, Schober CM. Numerical investigation of stability of breather-type solutions of the nonlinear Schrödinger equation. Nat Hazards Earth Syst Sci (2014) 14:1431–40. doi:10.5194/nhess-14-1431-2014
CrossRef Full Text | Google Scholar
18. Segur H, Henderson D, Carter J, Hammack J, Li C, Pheiff D, et al. Stabilizing the benjamin-feir instability. J Fluid Mech (2005) 539:229–71. doi:10.1017/s002211200500563x
CrossRef Full Text | Google Scholar
19. Chabchoub A, Hoffmann NP, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett (2011) 106:1–4. doi:10.1103/physrevlett.106.204502
CrossRef Full Text | Google Scholar
20. Fotopoulos G, Frantzeskakis DJ, Karachalios NI, Kevrekidis PG, Koukouloyannis V, Vetas K. Extreme wave events for a nonlinear Schrödinger equation with linear damping and Gaussian driving. Commun Nonlinear Sci Numer Simul (2019) 82:105058. doi:10.1016/j.cnsns.2019.105058
CrossRef Full Text | Google Scholar
21. Coppini F, Grinevich PG, Santini PM. Effect of a small loss or gain in the periodic nonlinear Schrödinger anomalous wave dynamics. Phys Rev E (2020) 101:032204. doi:10.1103/physreve.101.032204 |
PubMed Abstract | CrossRef Full Text | Google Scholar
22. Kimmoun O, Hsu HC, Branger H, Li MS, Chen YY, Kharif C, et al. Modulation instability and phase-shifted Fermi-Pasta-Ulam recurrence. Sci Rep (2016) 6:28516. doi:10.1038/srep28516 |
PubMed Abstract | CrossRef Full Text | Google Scholar
23. Schober CM, Islas AL. The routes to stability of spatially periodic solutions of the linearly damped NLS equation. The Eur Phys J Plus (2020) 135:1–20. doi:10.1140/epjp/s13360-020-00660-w
CrossRef Full Text | Google Scholar
24. Dysthe K. Note on a modification to the nonlinear Schrödinger equation for deep water. Proc R Soc London Ser A Math Phys Sci (1979) 369:105–14. doi:10.1098/rspa.1979.0154
CrossRef Full Text | Google Scholar
25. Lo E, Mei CC. A numerical study of water wave modulation based on a higher-order nonlinear Schrödinger equation. J Fluid Mech (2020) 150:395–416. doi:10.1017/s0022112085000180
CrossRef Full Text | Google Scholar
26. Ablowitz MJ, Herbst B, Schober CM. Long-time dynamics of the modulational instability of deep water waves. Physica D (2001) 152-153:416–33. doi:10.1016/s0167-2789(01)00183-x
CrossRef Full Text | Google Scholar
27. Gramstad O, Trulsen K. Hamiltonian form of the modified nonlinear Schrödinger equation for gravity waves on arbitrary depth. J Fluid Mech (2011) 670:404–26. doi:10.1017/s0022112010005355
CrossRef Full Text | Google Scholar
29. Carter JD, Henderson D, Butterfield I. A comparison of frequency downshift models of wave trains on deep water. Phys Fluids (2019) 31:013103. doi:10.1063/1.5063016
CrossRef Full Text | Google Scholar
30. Deconinck B, Segal BL. The stability spectrum for elliptic solutions to the focusing NLS equation. Physica D (2017) 346:1–19. doi:10.1016/j.physd.2017.01.004
CrossRef Full Text | Google Scholar
31. Zakharov VE, Shabat AB. Exact theory of two-dimensional self-focusing and onedimensional self-modulation of waves in nonlinear media. Soviet Phys JETP (1972) 34:62–9.
Google Scholar
32. Ercolani N, Forest MG, McLaughlin DW. Geometry of the modulational instability. iii. homoclinic orbits for the periodic Sine-Gordon equation. Physica D (1990) 43:349–84. doi:10.1016/0167-2789(90)90142-c
CrossRef Full Text | Google Scholar
33. McLaughlin DW, Overman EA. Whiskered tori for integrable pdes and chaotic behavior in near integrable pdes. Surv Appl Math (1995) 1:83–203. doi:10.1007/978-1-4899-0436-2_2
CrossRef Full Text | Google Scholar
34. Overman EA, II, McLaughlin DW, Bishop AR. Coherence and chaos in the driven damped Sine-Gordon equation: measurement of the soliton spectrum. Physica D (1986) 19:1–14. doi:10.1016/0167-2789(86)90052-7
CrossRef Full Text | Google Scholar
35. Lu X, Ma WX, Yu J, Khalique CM. Solitary waves with the Madelung fluid description: a generalized derivative nonlinear Schrödinger equation. Commun Nonlinear Sci Numer Simul (2016) 31:40–6. doi:10.1016/j.cnsns.2015.07.007
CrossRef Full Text | Google Scholar
36. Sattinger DH, Zurkowski VD. Gauge theory of BÃcklund transformations. ii. Physica D Nonlinear Phenom (1987) 26:225–50. doi:10.1016/0167-2789(87)90227-2
CrossRef Full Text | Google Scholar
37. Trefethen LN. Spectral methods. Philadelphia: SIAM (2000).
38. Grinevich PG, Santini PM. The finite gap method and the analytic description of the exact rogue wave recurrence in the periodic NLS Cauchy problem. Nonlinearity (2018) 31:5258–308. doi:10.1088/1361-6544/aaddcf
CrossRef Full Text | Google Scholar
39. Ablowitz MJ, Herbst BM, Schober CM. Computational chaos in the nonlinear Schrödinger equation without homoclinic crossings. Physica A (1996) 228:212–35. doi:10.1016/0378-4371(95)00434-3
CrossRef Full Text | Google Scholar
40. Hirota R. Lecture notes in mathematics. New York, NY: Springer-Verlag (1976), 515.
41. Ablowitz MJ, Schober CM. Effective chaos in the nonlinear Schrödinger equation. Contemp Math (1994) 172:253. doi:10.1090/conm/172/01808
CrossRef Full Text | Google Scholar

 C. M. Schober*
C. M. Schober* A. L. Islas
A. L. Islas