Monte Carlo and Kinetic Monte Carlo Models for Deposition Processes: A Review of Recent Works

Monte Carlo (MC) and kinetic Monte Carlo (kMC) models are widely used for studying the physicochemical surface phenomena encountered in most deposition processes. This spans from physical and chemical vapor deposition to atomic layer and electrochemical deposition. MC and kMC, in comparison to popular molecular methods, such as Molecular Mechanics/Dynamics, have the ability to address much larger time and spatial scales. They also offer a far more detailed approach of the surface processes than continuum-type models, such as the reaction-diffusion models. This work presents a review of the modern applications of MC/kMC models employed in deposition processes.

Introduction

Monte Carlo (MC) and kinetic Monte Carlo (kMC) are widely used methods in many fields of science and engineering: From materials science and polymers properties [1], astrophysics and black holes mergers [2] to computational geometry and volume approximation [3]. Their popularity in materials science stems from their inherit ability to simulate the molecular level of materials seamlessly. In MC/kMC, the particles (molecules, atoms, beads) move stochastically according to specific rules (events/processes), transferring the system randomly over the phase-space and approximating the mean values of various properties. In contrast to other molecular methods such as molecular dynamics (MD), the system in MC cannot easily be trapped in local energy minima and even if it is trapped, it can be “kicked out” to other states by incorporating sophisticated events. Furthermore, kMC filters out vibrational movements, allowing it to run over much larger spatial and time scales than MD. Especially in film growth, snapshots of MC/kMC simulation can be directly related and compared to scanning tunneling microscopy images.

MC/kMC have notable applications in the study of film deposition processes—probably the most important in the fabrication of semiconductor devices. Because of their importance, deposition processes have extensively studied via MC/kMC models either standalone or combined with other models in the context of multiscale modeling [4]. Nevertheless, there is no current review of the works that use MC or kMC concerning film deposition. This work is a critical review of the works on deposition processes utilizing MC/kMC models published within the last 5 years. Following the introduction, the deposition processes are shortly presented and the works that use MC/kMC models are reviewed. The paper ends with summary and outlook.

The MC and kMC Methods for Deposition Processes

In MC and kMC algorithms, sequential events are performed stochastically. MC solves the steady state Master Equation (ME) and kMC the transient one. The transient ME reads,

$\begin{array}{ll}\frac{\partial p_j(t)}{\partial t}={{\displaystyle \sum }}_{i\ne j}{p}_i(t)T_{ij}-{{\displaystyle \sum }}_{i\ne j}{p}_j(t)T_{ji}& (1)\end{array}$

where p_j(i) is the probability of the system to be found in state j(i) at time t. T_ij and T_ji denote the transition rate or transition probability from state i to j and vice versa.

Each event occurs at a certain probability/rate to form a Markov chain [5]. To generate the Markov chain the desired probability distribution p_i(j) must obey the detailed balanced condition,

$\begin{array}{ll}{p}_i{T}_{ij}=p_j{T}_{ji}& (2)\end{array}$

p_i(j) are Boltzmann distributions,

$\begin{array}{ll}{p}_{i(j)}=exp\left(-\frac{E_{i(j)}}{k_{b}T}\right)& (3)\end{array}$

where E_i(j)is the energy of the system in state i(j). Metropolis et al. [6] proposed that,

$\begin{array}{ll}{T}_{ij}=\{\begin{array}{c}1,if\Delta E\le 0\hfill \\ exp\left(-\frac{\Delta E}{k_{b}T}\right),if\Delta E>0\hfill \end{array}\hfill & (4)\end{array}$

so that the system will unconditionally move from state i to j if ΔE < 0 and with a probability $exp\left(-\frac{\Delta E}{k_{b}T}\right)$ if ΔE > 0, where ΔE = E_j−E_i. Practically, a random number ξ is chosen between (0, 1] and if $\xi <exp\left(-\frac{\Delta E}{k_{b}T}\right)$, the system moves to the state j, otherwise the move is rejected. In this way, different states of the system are generated and the thermodynamic average of a quantity q_ireads

$\begin{array}{ll}\langle q\rangle =\frac{{\displaystyle {{\displaystyle \sum }}_i}{q}_i{p}_i}{{\displaystyle {{\displaystyle \sum }}_i}{p}_i}& (5)\end{array}$

kMC method solves Equation (1). The most popular algorithm proposed by Bortz et al. [7] is termed as the N-fold method. In the N-fold method random transitions from i to j are performed unconditionally based on the transition rates, so that more likely transitions are selected more often. Every transition event i is assigned a rate which reads,

$\begin{array}{ll}{r}_i=v_{i}exp\left(-\frac{E_i}{k_{b}T}\right)& (6)\end{array}$

where ν_i is a frequency prefactor, E_i is the energy barrier and T is the temperature. Practically, the simulation starts by defining all rates (rate catalog) r_i of all possible processes that describe the physical problem. The total rate, $R={\sum }_i{r}_i$, is first computed and then a process n is randomly chosen according to,

$\begin{array}{ll}{\displaystyle {\displaystyle \sum }_{i=1}^n}\frac{r_i}{R}<{\xi }_1<{\displaystyle {\displaystyle \sum }_{i=1}^{n+1}}\frac{r_i}{R}& (7)\end{array}$

where ξ₁ is randomly chosen in (0, 1) and a single event is performed. The time advances as t = t + Δt with Δt being,

$\begin{array}{ll}\Delta t=-\frac{ln{\xi }_2}{R}& (8)\end{array}$

where ξ₂ is an additional random number chosen in (0, 1). R is recalculated based on the new system state. The algorithm stops when the desired time interval is reached.

kMC rates must obey also the detailed balance condition (Equation 2), even if the system is not in equilibrium, to ensure the dynamic evolution will correspond to a physical system [8]. kMC rates depend on both the particle and the lattice type that participate in the process and can be calculated via Transition State and Harmonic Transition State Theories (TST – HTST) [8], Density Functional Theory (DFT) and ab initio methods (e.g., [9–12]).

Focusing on the deposition processes, the notion of lattice is of great importance. The lattice represents the deposition surface and is composed of sites upon which all events occur, simplifying the construction of the rate catalog. Depending on how the lattice is represented, the atomistic information can either be presented in full detail (e.g., [13]) or in a coarse-grained way where microscopic neighboring sites are coalesced into coarse cells (e.g., [14, 15]). Off-lattice kMC [16] methods have also been proposed in atomistic representation where the rate catalog is computed “on the fly” in every step.

In MC/kMC the number and types of processes that occur upon a lattice site differ depending on the physical/chemical phenomena of interest. For deposition processes, adsorption, desorption, surface diffusion, and surface reaction events are used. This set of events is customized to capture the physical and chemical mechanisms unique to each deposition process (Figure 1). The ultimate goal of an MC/kMC model is to describe the interactions of particles with the surface, define the growth rate and predict the profile of the growing film on the surface.

FIGURE 1

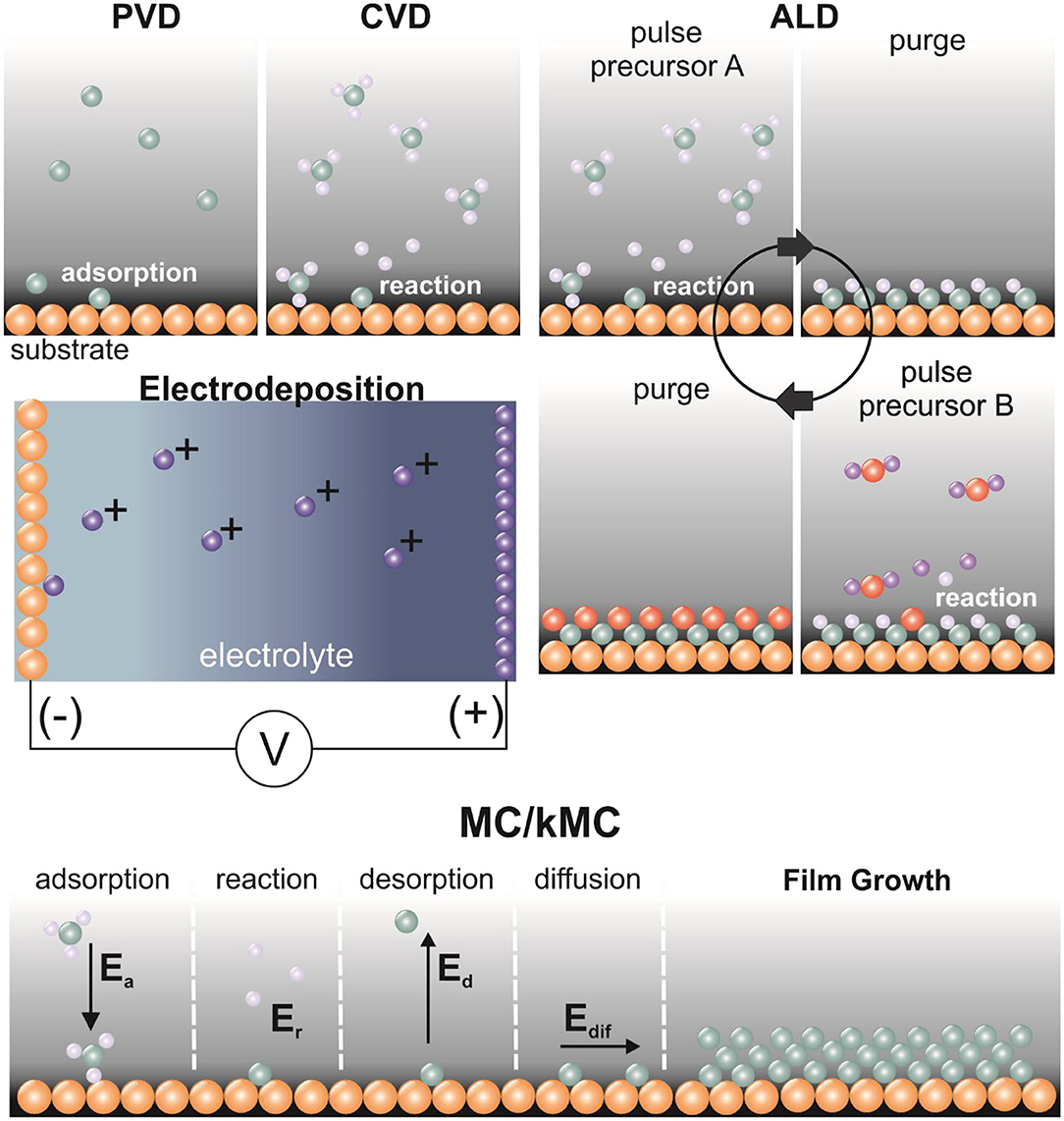
Figure 1. Schematic representation at the molecular level of the basic principles in deposition processes. In PVD, particles are adsorbed in the substrate. In CVD, particles (here an arbitrary molecule is shown) react on the substrate surface to grow the film. In ALD, multiple precursors (here A and B) are injected into the reactor though pulses in a cyclic way of pulses-purges and grow the film through self-limiting surface reactions. In electrodeposition, the voltage (V) is applied causing the particles from the cathode to move to the anode through an electrolyte where the film is grown through adsorption or surface reactions. In MC/kMC methods, an activation energy is assigned to each event. In MC, if the event leads the system to a smaller energy, it is accepted unconditionally. If not, it is selected with a probability according to Equation (2). In kMC, an event is selected from a predefined rate catalog containing all possible rates and performed unconditionally. Then the system evolves in time according to Equation (4). The four basic events - adsorption, reaction, desorption and diffusion- whose combination can describe a deposition process, with their activation energies, E_a, E_r, E_d, and E_dif are shown.

Deposition Processes

During any deposition process the material is deposited upon a surface either by physical or chemical processes. In physical processes, the material is injected as a gas and sticks on the deposition surface with a probability (or rate). Physical Vapor Deposition (PVD), which encompasses sputtering and evaporation, belongs to this category of deposition processes. In chemical processes, the material is grown on the deposition surface through surface reactions. Examples of chemical deposition processes are Chemical Vapor Deposition (CVD), Atomic Layer Deposition (ALD) and electrochemical deposition.

Physical Vapor Deposition

PVD is performed in vacuum chambers where the coating material is evaporated—via a method such as electron or laser beam, arc discharge or sputtering—and is guided to the substrate. Upon hitting the substrate, the vapor condenses to form a film. It is used extensively for the production of metallic nanorods. The applications of the nanorods, e.g., integrated circuit, metallic glue, lithium-ion batteries and fuel cells to name a few, demand conformal shell layer with minimized defects. Compared to CVD and ALD, which offer highly conformal and uniform films on nanostructures, PVD entails a lower cost, higher availability of materials, greater growth rates, and no need for high substrate temperatures. PVD is thus the preferred method for large-scale fabrication. During PVD, the basic growth mechanisms are adsorption and surface diffusion, making MC/kMC models very popular to study the formation of nanorods.

In a series of works, Cansizoglu et al. [17, 18] and later Yurukcu et al. [19], studied the growth of nanorods via MC. They applied their MC model in PVD of Ag on In₂S₃ nanorods and were able to assess the favorable conditions that lead to a conformal shell coating (Figure 2A). They concluded that a wider angular distribution of incident atomic flux can provide conformal coatings around nanowires. Wang et al. [20] coupled Computational Fluid Dynamics (CFD) simulations with an MC model to predict the columnar growth of Cu nanorods for different operating pressures of a plasma reactor. Du and Huang [21, 22] used kMC to verify their theory for the transition from thin film to nanorod Cu growth. They found a critical coverage condition at which multiple-layer surface growth form for the onset of nanorod growth. Yang et al. [23] created a kMC model for metallic nanorods growth considering 3D Ehrlich–Schwoebel (ES) diffusion effects. They concluded that larger 3D ES barrier leads to multiple steps formation and eventually nanorods formation.

FIGURE 2

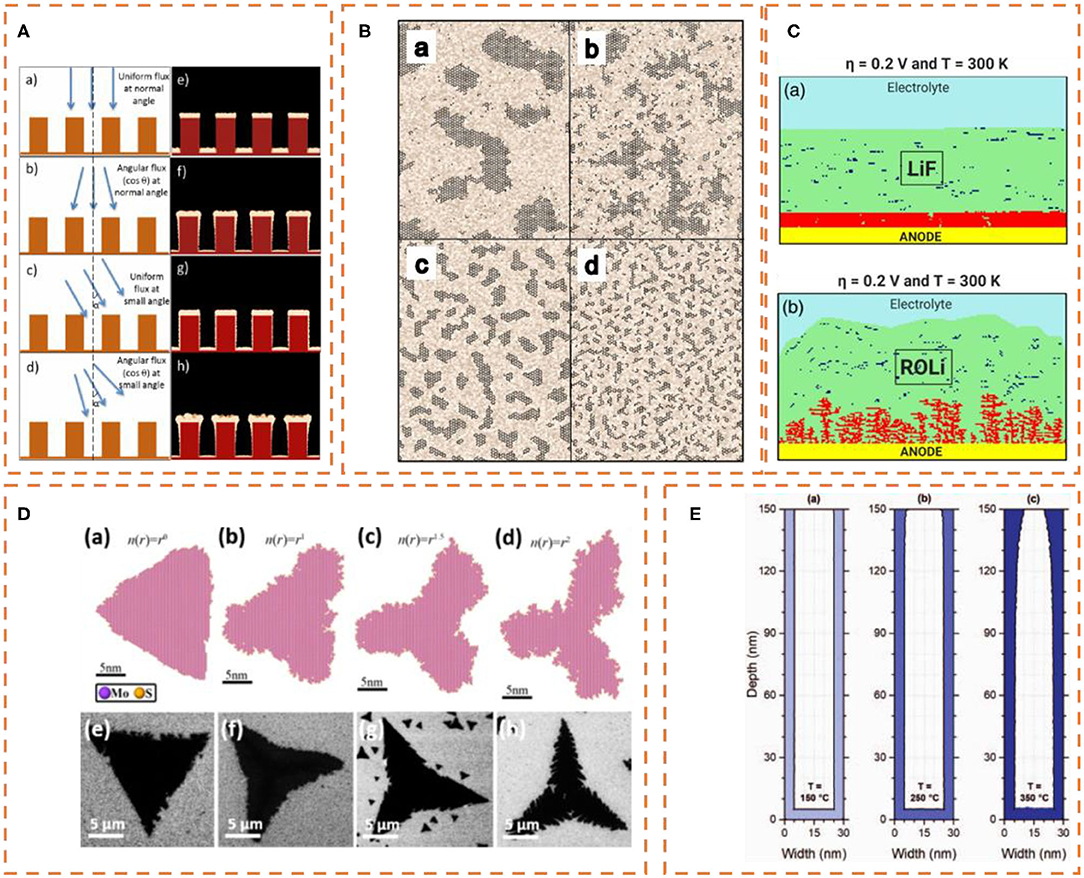
Figure 2. (A) PVD of Ag core/shell on In₂S₃ nanorods: MC results for four different conditions: (a,e) Uniform incident flux, α = 0° (α is the angle between the incoming flux and the surface normal to the substrate), (b,f) angular flux ~cos(θ) with α = 0°, (c,g) uniform flux with α = 30° and (d,h) angular flux ~ cos(θ) with α = 30°. Reprinted with permission from Metropolis et al. [6] - Published by the IEEE. (B) Graphene CVD: MC results for varying strength of surface roughness parameter ξ and mobility parameter T_s for (a) ξ = 1.2, T_s = ∞ (b) ξ = 1.5, T_s = ∞ (c), ξ = 1.5, T_s = 0 and (d) ξ = 1.2, T_s =0. The color represents roughness. Reprinted with permission from Yang et al. [23] - Published by the PCCP Owner Societies. (C) Electrodeposition in Li metal anode: kMC results for (a) uniform Li deposition in LiF electrolyte, (b) dendrite growth in ROLi electrolyte. The red particles represent the Li metal which is being deposited, and the dark-blue particles represent the Li+ ions which are diffusing. The process conditions (η - activation overpotential and T – temperature) are also shown. Reprinted with permission from Ding et al. [67] - Published by the AIChe. (D) MoS₂ CVD: kMC results for the morphology of MoS₂ as a function of the Mo density gradient, n(r) – r distance from Mo source (a) no Mo density gradient, n(r) = r⁰ (b–d) n(r) = r¹, n(r) = r^1.5, and n(r) = r² (e–h) corresponding SEM images. Reprinted with permission from Jiang and Hou [35] - Published by the ACS. (E) SiN_x ALD: Thickness profile in a micro-structure with aspect ratio equal to 5 for parasitic CVD (no-ALD) reactions at different substrate temperatures (a) 150°C, (b) 250°C and (c) 350°C, determined by kMC computations. Reprinted with permissions from Poodt et al. [56] - Published by the IEEE.

Alongside nanorods works, Pflug et al. [24] studied the growth of ZnO:Al during reactive sputtering by expanding direct simulation MC to include surface reactions. Chernogor et al. [25, 26] performed MC computations to study the properties of TiCrN-Mo₂ N-Ni films during arc discharge PVD. Chen et al. [27] proposed a kMC model for predicting the grain boundary during MoS₂ growth. Finally, Evrard et al. [28] proposed a multiscale framework based on an MC model to predict film's thickness as a function of the mass flux reaching the deposition surface during magnetron sputtering.

Chemical Vapor Deposition

CVD is the most widely used deposition process in industry. Applications range from coatings and integrated circuits to powders and nanomaterials. During CVD, a compound (precursor) containing the material to be deposited, is transferred to the substrate for deposition where the film is grown via surface reactions. The deposition of two-dimensional (2D) materials is one of the main applications of CVD in the literature of the past 5 years. 2D materials, such as graphene and transition metal dichalcogenides (TMDs e.g., MoS₂, WSe₂, WS₂), have attracted considerable interest due to their potential in the semiconductor industry, particularly applied to electronic and spintronic devices. Such devices demand high quality orientationally-ordered films with low nucleation density and low number of defects, properties supported by CVD.

Most published works focus on graphene growth. During CVD, graphene can grow in different shapes, such as hexagons, multiple-lobed islands, snowflake-like structures or hexagons with dendritic edges. The shape and size of these graphene domains are affected by many process and physical parameters such as deposition flux, temperature and state/orientation of the substrate. To predict the growth shape, new diffusion processes, whose activation energies are calculated via DFT, are designed. Gaillard et al. [9] showed that zigzag edges of graphene flakes arise from low fluxes and higher deposition rates and lower temperature conditions produce less compact islands formations. Their predicted shapes are in qualitative agreement with experimental reports for hexagons, multiple-lobed and snowflakes with fractal shapes. Additives, such as N₂, does not affect the shape of graphene flakes [29]. By introducing etching process on their rate catalog, Chen et al. [30, 31] predicted dodecagon with a hexagonal hole, double hexagonal rings, honeycomb-like networks and nanoribbons. In a recent work [32], they studied graphene growth on Cu (1 1 1) as a function of deposition flux and temperature. They concluded that at high temperatures, an increase in the deposition flux leads to graphene transforming from a circular shape to an intermediate compact hexagonal shape, before finally transitioning to a fractal with six-fold symmetry. Göltl et al. [33] by combining experiments and kMC computations proposed a qualitative description for the growth of high aspect ratios nanoribbons on a Ge (0 0 1).

Because of the 2D nature of graphene, most works only consider the early stages (monolayer) of growth. The mechanism of graphene growth depends on the specific substrate. Graphene growth on transition metals such as Ni, Co, and Fe, is a precipitate of carbon atoms dissolved in the substrate, making carbon solubility a key indicator for the growth rate. Graphene growth on a Cu substrate is due to the diffusion of carbon atoms on the Cu surface with the latter having low solubility and catalyst activity. Enstone et al. [34] proposed an MC model for graphene growth on a Cu substrate to study the effects of the substrate's roughness on graphene nucleation. They showed that the key factors which determine the island size and formation are roughness amplitude and mobility parameters (Figure 2B). Conversely, on active catalytic surfaces, such as Ir, Rh, and Ru, the interaction of carbon-substrate atoms is strong. Since the graphene and substrate lattices are of differing structures, the graphene spreads like a carpet, forming moiré patterns of super unit cells of hundreds of atoms. Jiang and Hou [35], used a multiscale “standing-on-the-front” (SOF) kMC [36] approach for graphene growth on an Ir surface. In SOF-kMC the growth kinetics are determined by the attachment and detachment of different carbon clusters at a growth front. Their computations showed that the rate-dominating event for concave growth-front segments is carbon monomer attachment—and five-atom carbon clusters attachment for other segments—leading to time-resolved growth behavior that was consistent with scanning tunneling microscopy experiments.

TMDs, such as MoS₂, WSe₂, and WS₂, have gain the attention of the semiconductor industry due to their relatively inert surfaces and thickness-dependent electrical and optical properties [37]. The factors that control the size and shape of the evolving monolayer during CVD of TMDs is still an open issue. The first works [10, 38] attempted to connect the reactor operating conditions to the geometric characteristics of TMDs. Both works applied kMC models that take into account the explicit formation of chemical bonds. Govind Rajan et al. [38] developed a kMC model based on the terrace-ledge-kink formalism. They were able to accurately predict the geometric shape, size, and aspect ratio of triangular and hexagonal MoS₂ and WS₂ structures and link them to the CVD reactor operating conditions. Nie et al. [10] performed kMC coupled with DFT computations to study the deposition of a WSe₂ monolayer on graphene. They constructed a phase diagram of regions of triangular compact, fractal and dendritic structures of WSe₂ based on various operating conditions. Yue et al. [37] detailed the growth of WSe₂ grains and Wu et al. [39] included growth anisotropy during the growth of WS₂ on quartz by incorporating local substrate effects in their kMC model. Chen et al. [11] developed a combined DFT–kMC model to elucidate the mechanism for ultrafast growth of regular triangular WSe₂ monolayer with compact edges on Au (111). They concluded that this ultrafast growth was due to fast kink nucleation and ultrafast kink propagation along the edge. Li et al. [12] studied MoS₂ growth and concluded that Mo concentration gradient is the key factor for the morphological evolution of MoS₂ from dendritic shape to compact triangular geometry (Figure 2D).

Besides 2D materials, in the context of nanoparticle and nanorod growth, MC simulations [12, 40], multiscale modeling [41, 42] and enhanced multiscale modeling with Artificial Neural Network (ANN) [43–46] have been performed. “Classical” kMC models have also used for the deposition of diamond [47], AlN [48] and GaAs [49] film, plasma enhanced a-Si:H CVD [50], hybrid MD/kMC [51] and for growth in extereme pressure conditions [52].

Atomic Layer Deposition

ALD is a subset of CVD that is based on sequential and self-limiting surface reactions. In contrast to CVD, multiple precursors are cyclically pulsed and purged to grow the desired material. ALD offers exceptional conformality on high aspect ratio micro-structures, high thickness and film composition control [53] which makes it prevalent in modern complementary metal–oxide–semiconductor (CMOS) and dynamic random-access memory (DRAM) fabrication processes. Concerning deposition inside micro-structures, MC/kMC methods have been used for over three decades in the context of CVD [4]. Nevertheless, CVD could not provide good step coverage in high aspect ratio structures, for which ALD came as a solution.

Schwille et al. [54, 55] proposed a new MC method to study the deposition inside micro-structures. Their direct simulation MC-derived method models only the walls of the geometrical structure, rather than partitioning the entire domain into grid cells. This assumes that deposited particles can only collide with the molecules of the carrier gas and can only interact with the walls of the structure [55]. The simplification drastically decreased the computational demands. Poodt et al. [56] proposed an MC model to study the step coverage inside pores by considering reactor pressure effects through a gas-phase collision model whose frequency is determined by the mean free path of the precursor molecules. They concluded that ALD is in the diffusion-limited regime for various experimental conditions, even when low reactor pressures are used. Cremers et al. [57] used a 3D MC model to compare step coverage in arrays of holes and pillars and concluded that the latter are suitable for fabrication processes where large surface areas are desired, such as in sensors, solar cells, fuel cells, and batteries. Muneshwar et al. [58] used a scalable kMC model to study the effects of parasitic reactions (no-ALD) in the step coverage inside high aspect ratio features (Figure 2E). They concluded that it is essential that parasitic side surface reactions must be restricted, either by operating a lower temperatures or adjusting dosages.

Furthermore, a series of MC/kMC studies regarding ALD of 2D materials [59, 60] for conductive bridge random access memory cells, quantum dots [61] and nanoparticle reactivity [62] were also published. In a series of works, Christofides et al. [63–68] conducted multiscale simulations of plasma assisted ALD processes, combining CFD and kMC models to characterize and control the process. Taken a step further, they enhanced their computations with an ANN to characterize the microscopic domain film growth dynamics.

Electrochemical Deposition (Electrodeposition)

During electrodeposition, a thin layer of one metal is coated on top of a different metal. An electrical current within a conductive substrate reduces the cations within an electrolyte, growing them as a thin film. Electrodeposition has become an increasingly popular method of fabrication for the next generation of batteries. Conventional Li-ion batteries are reaching their theoretical energy density limits, pushing researchers to investigate alternative materials. Li metal anodes are conventionally used because of their high energy density. However, Li metals show irregular deposition patterns such as dendrite formations. The irregularities result in poor cycling efficiency, capacity fade, and can cause batteries to short-circuit [69], disqualifying its commercial viability. Sitapure et al. [69] studied the multiscale formation of dendritic structures during Li metal anode electrodeposition, using MD computations for the heterogeneous solid-electrolyte interphase (SEI) and kMC for the growth of the dendrites. This formulation considered the effects of the mechanical properties of the heterogeneous SEI in dendritic formation (Figure 2C). Vishnugopi et al. [70] constructed a kMC model based on self-diffusion processes without accounting for the existence of SEI. Rather, they considered three types of self-diffusion: terrace diffusion, diffusion away from a step and interlayer diffusion. Their computations showed that, neglecting interlayer diffusion, the growth mode of metal undergoes two transitions as the deposition rate increases. The transitions are from film-type to mossy and from mossy to dendritic. When included in the model, interlayer diffusion favors the deposition of smooth films, even at high deposition rates.

Besides Li anodes metal studies, Carim et al. [1, 71] used an MC model along with experiments of photoelectrochemical growth to study the spontaneous growth of highly ordered, nanoscale lamellar morphologies of Se-Te films. In a series of works, Li et al. [72–74] applied a 3D kMC model to study the electrodeposition of Cu₂ZnSnS₄ for photovoltaic applications. Zargarnezhad and Dolati [75] combined experiments and kMC computations for the electrodeposition of Ni. Crevillén-García et al. [76] proposed a kMC model based on Gaussian process (GP) emulation to predict the final shape of the film. The authors concluded that the use of GP greatly accelerates the kMC computations without substantial precision loss.

Summary and Outlook

MC and kMC models that have been used during the last 5 years to study the physicochemical phenomena of deposition processes were discussed. The various categories of deposition processes (PVD, CVD, ALD and electrodeposition) were introduced and selected applications were highlighted. This work maintains a broad perspective of process types and applications, and contributes to recent reviews regarding the computational approaches for the theoretical investigation of graphene growth [77, 78], multiscale modeling in CVD [4] and the implementation of surface reactions in kMC [79].

Though old in conception, MC/kMC methods continue to provide a deep insight of the physical/chemical mechanisms during deposition of novel high-end materials by introducing simple, yet effective, customized processes. MC/kMC are expected to play an important role on the study of Xenes materials [80] which—in contrast to the other 2D materials—can be produced with deposition processes alone. Algorithmically, emergent deep learning techniques provide promising methods to produce detailed and realistic rate catalogs with minimum input from the user. This, combined with parallel processing techniques, is expected to increase the robustness and applicability of kMC methods.

Author Contributions

NC and GK had the initial idea for this review. NC and DT wrote the initial version of the manuscript. NC, DT, and GM reviewed the MC/kMC methods. AB contributed in shaping up the general framework of the review in the context of deposition processes. All authors contributed in the literature review and in the final version of the manuscript.

Funding

This research was co-financed by Greece and the European Union (European Social Fund- ESF) through the Operational Program Human Resources Development, Education and Lifelong Learning in the context of the project Reinforcement of Postdoctoral Researchers - 2nd Cycle (MIS-5033021), implemented by the State Scholarships Foundation (IKY).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Carim AI, Batara NA, Premkumar A, Atwater HA, Lewis NS. Self-optimizing photoelectrochemical growth of nanopatterned Se-Te films in response to the spectral distribution of incident illumination. Nano Lett. (2015) 15:7071–6. doi: 10.1021/acs.nanolett.5b03137

PubMed Abstract | CrossRef Full Text | Google Scholar

2. McKernan B, Ford KES, O'Shaugnessy R, Wysocki D. Monte Carlo simulations of black hole mergers in AGN discs: low χeff mergers and predictions for LIGO. Mon Not R Astron Soc. (2020) 494:1203–16. doi: 10.1093/mnras/staa740

CrossRef Full Text | Google Scholar

3. Emiris IZ, Fisikopoulos V. Practical polytope volume approximation. ACM Trans Math Softw. (2018) 44:38. doi: 10.1145/3194656

CrossRef Full Text | Google Scholar

4. Cheimarios N, Kokkoris G, Boudouvis AG. Multiscale modeling in chemical vapor deposition processes: models and methodologies. Arch Comput Methods Eng. (2020) 28:637–72. doi: 10.1007/s11831-019-09398-w

CrossRef Full Text | Google Scholar

5. Spade DA. Chapter 1 - Markov chain Monte Carlo methods: theory practice. In: Srinivasa ASR, Rao CRB, Rao S, editors. Principles Methods for Data Science. Elsevier. p. 1–66.

Google Scholar

6. Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. J Chem Phys. (1953) 21:1087–92. doi: 10.1063/1.1699114

CrossRef Full Text | Google Scholar

7. Bortz AB, Kalos MH, Lebowitz JL. A new algorithm for Monte Carlo simulation of Ising spin systems. J Comput Phys. (1975) 17:10–8. doi: 10.1016/0021-9991(75)90060-1

CrossRef Full Text | Google Scholar

8. Voter AF. Introduction to the kinetic Monte Carlo method - radiation effects in solids. In: Sickafus KE, Kotomin EA, Uberuaga BP, editors. Radiation Effects in Solids. Dordrecht: Springer Netherlands. p. 1–23.

Google Scholar

9. Gaillard P, Chanier T, Henrard L, Moskovkin P, Lucas S. Multiscale simulations of the early stages of the growth of graphene on copper. Surf Sci. (2015) 637–638:11–8. doi: 10.1016/j.susc.2015.02.014

CrossRef Full Text | Google Scholar

10. Nie Y, Liang C, Zhang K, Zhao R, Eichfeld SM, Cha P-R, et al. First principles kinetic Monte Carlo study on the growth patterns of WSe 2 monolayer. 2D Mater. (2016) 3:025029. doi: 10.1088/2053-1583/3/2/025029

CrossRef Full Text | Google Scholar

11. Chen S, Gao J, Srinivasan BM, Zhang G, Sorkin V, Hariharaputran R, et al. Origin of ultrafast growth of monolayer WSe2 via chemical vapor deposition. npj Comput Mater. (2019) 5:28. doi: 10.1038/s41524-019-0167-2

CrossRef Full Text | Google Scholar

12. Li X, Zhang S, Chen S, Zhang X, Gao J, Zhang Y-W, et al. Mo concentration controls the morphological transitions from dendritic to semicompact, and to compact growth of monolayer crystalline MoS2 on various substrates. ACS Appl Mater Interfaces. (2019) 11:42751–9. doi: 10.1021/acsami.9b14577

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Balbuena JP, Martin-Bragado I. Lattice kinetic Monte Carlo simulation of epitaxial growth of silicon thin films in H2/SiH4 chemical vapor deposition systems. Thin Solid Films. (2017) 634:121–33. doi: 10.1016/j.tsf.2017.05.013

CrossRef Full Text | Google Scholar

14. Collins SD, Chatterjee A, Vlachos DG. Coarse-grained kinetic Monte Carlo models: Complex lattices, multicomponent systems, and homogenization at the stochastic level. J Chem Phys. (2008) 129:184101. doi: 10.1063/1.3005225

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zheng Z, Stephens RM, Braatz RD, Alkire RC, Petzold LR. A hybrid multiscale kinetic Monte Carlo method for simulation of copper electrodeposition. J Comput Phys. (2008) 227:5184–99. doi: 10.1016/j.jcp.2008.01.056

CrossRef Full Text | Google Scholar

16. Trochet M, Mousseau N, Béland LK, Henkelman G. Off-lattice kinetic monte carlo methods BT - handbook of materials modeling: methods: theory modeling. In: Andreoni W, Yip S. Cham: Springer International Publishing. p. 715–43.

Google Scholar

17. Cansizoglu H, Cansizoglu MF, Karabacak T. Effect of Shell Coating Technique on Carrier Collection Properties of Core/Shell Nanostructures. Department of Physics and Astronomy, University of Arkansas at Little Rock, Little Rock, AR 72204, United States: Institute of Electrical and Electronics Engineers Inc.

Google Scholar

18. Cansizoglu H, Yurukcu M, Cansizoglu MF, Karabacak T. Investigation of physical vapor deposition techniques of conformal shell coating for core/shell structures by Monte Carlo simulations. Thin Solid Films. (2015) 583:122–8. doi: 10.1016/j.tsf.2015.03.071

CrossRef Full Text | Google Scholar

19. Yurukcu M, Cansizoglu H, Cansizoglu MF, Karabacak T. Conformality of PVD shell layers on vertical arrays of rods with different aspect ratios investigated by Monte Carlo simulations. In: MRS Advances. Department of Physics and Astronomy, University of Arkansas at Little Rock, Little Rock, AR 72211, United States: Materials Research Society. p. 465–470.

Google Scholar

20. Wang P, Mücke R, He W, Mauer G, Vaßen R. Fluid Dynamics and Modelling of Plasma Jet in PS-PVD Process and Monte Carlo Simulations of PS-PVD Columns. Jülich, Germany: ASM International. p. 190–195. Available online at: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85034778196&partnerID=40&md5=589d6065645191d773bab5455a87e615 (accessed April 1, 2021).

Google Scholar

21. Du F, Huang H. A theory of growing crystalline nanorods – mode I. Surf Sci. (2018) 674:18–24. doi: 10.1016/j.susc.2018.03.016

CrossRef Full Text | Google Scholar

22. Du F, Huang H. A generalized theory of thin film growth. Surf Sci. (2018) 669:154–9. doi: 10.1016/j.susc.2017.12.002

CrossRef Full Text | Google Scholar

23. Yang J, Zhou Y, Pu B. Three-dimensional ES barrier promotes the steps formation. (2018) 783:115–9. doi: 10.4028/www.scientific.net/KEM.783.115

CrossRef Full Text | Google Scholar

24. Pflug A, Siemers M, Melzig T, Sittinger V, Schäfer L. Heuristic modeling of the doping efficiency in sputtered TCO layers. Surf Coatings Technol. (2015) 267:81–9. doi: 10.1016/j.surfcoat.2014.11.046

CrossRef Full Text | Google Scholar

25. Chernogor AV, Blinkov IV, Belov DS, Sergevnin VS, Volkhonskii AO. Analysis of the structure of multilayer nanocrystalline coatings based on plasma mass transfer parameters calculated by the Monte Carlo method. Tech Phys Lett. (2019) 45:75–8. doi: 10.1134/S1063785019020056

CrossRef Full Text | Google Scholar

26. Chernogor AV, Blinkov IV, Belov DS, Volkhonskiy AO, Sergevnin VS. Influence of Bias Voltage on Structure and Mechanical Properties of TiCrN-Mo2N-Ni Coatings. National University of Science and Technology MISiS, Moscow, Russian Federation: Institute of Physics Publishing.

PubMed Abstract | Google Scholar

27. Chen S, Gao J, Srinivasan BM, Zhang G, Yang M, Chai J, et al. Revealing the Grain Boundary Formation Mechanism and Kinetics during Polycrystalline MoS2 Growth. ACS Appl Mater Interfaces. (2019) 11:46090–100. doi: 10.1021/acsami.9b15654

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Evrard M, Besnard A, Lucas S. Study of the influence of the pressure and rotational motion of 3D substrates processed by magnetron sputtering: a comparative study between Monte Carlo modelling and experiments. Surf Coatings Technol. (2019) 378:125070. doi: 10.1016/j.surfcoat.2019.125070

CrossRef Full Text | Google Scholar

29. Gaillard P, Schoenhalz AL, Moskovkin P, Lucas S, Henrard L. Growth of nitrogen-doped graphene on copper: multiscale simulations. Surf Sci. (2016) 644:102–8. doi: 10.1016/j.susc.2015.08.038

CrossRef Full Text | Google Scholar

30. Chen S, Gao J, Srinivasan BM, Zhang G, Sorkin V, Hariharaputran R, et al. A kinetic Monte Carlo model for the growth and etching of graphene during chemical vapor deposition. Carbon N Y. (2019) 146:399–405. doi: 10.1016/j.carbon.2019.02.016

CrossRef Full Text | Google Scholar

31. Chen S, Gao J, Srinivasan BM, Zhang G, Sorkin V, Hariharaputran R, et al. Unveiling the competitive role of etching in graphene growth during chemical vapor deposition. 2D Mater. (2019) 6:015031. doi: 10.1088/2053-1583/aaf59c

CrossRef Full Text | Google Scholar

32. Chen S, Gao J, Srinivasan BM, Zhang G, Sorkin V, Hariharaputran R, et al. An all-atom kinetic Monte Carlo model for chemical vapor deposition growth of graphene on Cu(1 1 1) substrate. J Phys Condens Matter. (2020) 32:155401. doi: 10.1088/1361-648X/ab62bf

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Göltl F, Murray EA, Chen BWJ, Jacobberger RM, Arnold MS, Mavrikakis M. Exploring driving forces for length growth in graphene nanoribbons during chemical vapor deposition of hydrocarbons on Ge(0 0 1) via kinetic Monte Carlo simulations. Appl Surf Sci. (2020) 527:146784. doi: 10.1016/j.apsusc.2020.146784

CrossRef Full Text | Google Scholar

34. Enstone G, Brommer P, Quigley D, Bell GR. Enhancement of island size by dynamic substrate disorder in simulations of graphene growth. Phys Chem Chem Phys. (2016) 18:15102–9. doi: 10.1039/C6CP00788K

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Jiang H, Hou Z. Large-scale epitaxial growth kinetics of graphene: a kinetic Monte Carlo study. J Chem Phys. (2015) 143:084109. doi: 10.1063/1.4929471

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wu P, Jiang H, Zhang W, Li Z, Hou Z, Yang J. Lattice mismatch induced nonlinear growth of graphene. J Am Chem Soc. (2012) 134:6045–51. doi: 10.1021/ja301791x

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Yue R, Nie Y, Walsh LA, Addou R, Liang C, Lu N, et al. Nucleation and growth of WSe2: enabling large grain transition metal dichalcogenides. 2D Mater. (2017) 4:045019. doi: 10.1088/2053-1583/aa8ab5

CrossRef Full Text | Google Scholar

38. Govind Rajan A, Warner JH, Blankschtein D, Strano MS. Generalized mechanistic model for the chemical vapor deposition of 2D transition metal dichalcogenide monolayers. ACS Nano. (2016) 10:4330–44. doi: 10.1021/acsnano.5b07916

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Wu L, Yang W, Wang G. Mechanism of substrate-induced anisotropic growth of monolayer WS2 by kinetic Monte Carlo simulations. npj 2D Mater Appl. (2019) 3:6. doi: 10.1038/s41699-019-0088-4

CrossRef Full Text | Google Scholar

40. Liu Q, Zhang Y, Shen H, Zhao Z, Li H. Fractal characteristics and quantitative descriptions of messily grown nanowire morphologies. Mater Des. (2018) 153:287–97. doi: 10.1016/j.matdes.2018.05.003

CrossRef Full Text | Google Scholar

41. Aviziotis IG, Cheimarios N, Duguet T, Vahlas C, Boudouvis AG. Multiscale modeling and experimental analysis of chemical vapor deposited aluminum films: linking reactor operating conditions with roughness evolution. Chem Eng Sci. (2016) 155:449–58. doi: 10.1016/j.ces.2016.08.039

CrossRef Full Text | Google Scholar

42. Aviziotis IG, Duguet T, Vahlas C, Boudouvis AG. Combined macro/nanoscale investigation of the chemical vapor deposition of Fe from Fe(CO)5. Adv Mater Interfaces. (2017) 4:1601185. doi: 10.1002/admi.201601185

CrossRef Full Text | Google Scholar

43. Kimaev G, Chaffart D, Ricardez-Sandoval LA. Multilevel Monte Carlo applied for uncertainty quantification in stochastic multiscale systems. AIChE J. (2020) 66:1–6. doi: 10.1002/aic.16262

CrossRef Full Text | Google Scholar

44. Kimaev G, Ricardez-Sandoval LA. Artificial neural networks for dynamic optimization of stochastic multiscale systems subject to uncertainty. Chem Eng Res Des. (2020) 161:11–25. doi: 10.1016/j.cherd.2020.06.017

CrossRef Full Text | Google Scholar

45. Kimaev G, Ricardez-Sandoval LA. Artificial Neural Network Discrimination for Parameter Estimation and Optimal Product Design of Thin Films Manufactured by Chemical Vapor Deposition. J Phys Chem C. (2020) 124:18615–627. doi: 10.1021/acs.jpcc.0c05250

CrossRef Full Text | Google Scholar

46. Kimaev G, Ricardez-Sandoval LA. Nonlinear model predictive control of a multiscale thin film deposition process using artificial neural networks. Chem Eng Sci. (2019) 207:1230–45. doi: 10.1016/j.ces.2019.07.044

CrossRef Full Text | Google Scholar

47. Reshi BA, Kartha MJ, Misra A, Varma R. Investigation of diamond deposition on the diamond, silicon and quartz substrates by microwave plasma chemical vapor deposition and Monte Carlo simulations. Mater Res Express. (2019) 6:096420. doi: 10.1088/2053-1591/ab2e8e

CrossRef Full Text | Google Scholar

48. An J, Dai X, Wu W, Guo R, Feng L. Kinetic Monte Carlo simulation of the growth of AlN films by metal organic chemical vapor deposition. Phys Status Solidi Basic Res. (2019) 256:1900114-1–8. doi: 10.1002/pssb.201900114

CrossRef Full Text | Google Scholar

49. Saxena PK, Srivastava P, Trigunayat R. An innovative approach for controlled epitaxial growth of GaAs in real MOCVD reactor environment. J Alloys Compd. (2019) 809:151752. doi: 10.1016/j.jallcom.2019.151752

CrossRef Full Text | Google Scholar

50. Babahani O, Hadjadj S, Khelfaoui F, Kebaili HO, Lemkeddem S. Monte Carlo simulation of chemical reactions in plasma enhanced chemical vapor deposition: from microscopic view to macroscopic results. Silicon. (2019) 11:1267–74. doi: 10.1007/s12633-018-9916-y

CrossRef Full Text | Google Scholar

51. Zhang Y, Wang H, Gou Y, Jiang S. Evolution of medium-range order and surface compositions by mechanism-driven model with realistic network. Appl Surf Sci. (2019) 464:321–7. doi: 10.1016/j.apsusc.2018.09.090

CrossRef Full Text | Google Scholar

52. Pittman N, Lu T-M. Growth front smoothing effects in extremely high pressure vapor deposition. Sci Rep. (2020) 10:12355. doi: 10.1038/s41598-020-69269-4

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Johnson RW, Hultqvist A, Bent SF. A brief review of atomic layer deposition: from fundamentals to applications. Mater Today. (2014) 17:236–46. doi: 10.1016/j.mattod.2014.04.026

CrossRef Full Text | Google Scholar

54. Schwille MC, Schössler T, Barth J, Knaut M, Schön F, Höchst A, et al. Experimental and simulation approach for process optimization of atomic layer deposited thin films in high aspect ratio 3D structures. J Vac Sci Technol A Vacuum Surfaces Film. (2017) 35:01B118-1–10. doi: 10.1116/1.4971196

CrossRef Full Text | Google Scholar

55. Schwille MC, Barth J, Schössler T, Schön F, Bartha JW, Oettel M. Simulation approach of atomic layer deposition in large 3D structures. Model Simul Mater Sci Eng. (2017) 25:035008-1–18. doi: 10.1088/1361-651X/aa5f9d

CrossRef Full Text | Google Scholar

56. Poodt P, Mameli A, Schulpen J, Kessels WMM, Roozeboom F. Effect of reactor pressure on the conformal coating inside porous substrates by atomic layer deposition. J Vac Sci Technol A Vacuum Surfaces Film. (2017) 35:021502-1–9. doi: 10.1116/1.4973350

CrossRef Full Text | Google Scholar

57. Cremers V, Geenen F, Detavernier C, Dendooven J. Monte Carlo simulations of atomic layer deposition on 3D large surface area structures: required precursor exposure for pillar- versus hole-type structures. J Vac Sci Technol A Vacuum Surfaces Film. (2017) 35:01B115. doi: 10.1116/1.4968201

CrossRef Full Text | Google Scholar

58. Muneshwar T, Shoute G, Barlage D, Cadien K. Parasitic surface reactions in high-aspect ratio via filling using ALD: a stochastic kinetic model. In: Technical Digest - International Electron Devices Meeting, IEDM. Institute of Electrical and Electronics Engineers Inc. p. 40.2.1–40.2.4.

Google Scholar

59. Letourneau S, Young MJ, Bedford NM, Ren Y, Yanguas-Gil A, Mane AU, et al. Structural evolution of molybdenum disulfide prepared by atomic layer deposition for realization of large scale films in microelectronic applications. ACS Appl Nano Mater. (2018) 1:4028–37. doi: 10.1021/acsanm.8b00798

CrossRef Full Text | Google Scholar

60. Dong Z, Zhao H, DIMarzio D, Han M-G, Zhang L, Tice J, et al. Atomically thin CBRAM enabled by 2-D materials: scaling behaviors and performance limits. IEEE Trans Electron Dev. (2018) 65:4160–6. doi: 10.1109/TED.2018.2830328

CrossRef Full Text | Google Scholar

61. Surrente A, Carron R, Gallo P, Rudra A, Dwir B, Kapon E. Self-formation of hexagonal nanotemplates for growth of pyramidal quantum dots by metalorganic vapor phase epitaxy on patterned substrates. Nano Res. (2016) 9:3279–90. doi: 10.1007/s12274-016-1206-7

CrossRef Full Text | Google Scholar

62. Soethoudt J, Grillo F, Marques EA, van Ommen JR, Tomczak Y, Nyns L, et al. Diffusion-Mediated growth and size-dependent nanoparticle reactivity during ruthenium atomic layer deposition on dielectric substrates. Adv Mater Interfaces. (2018) 5:1800870-1–11. doi: 10.1002/admi.201800870

CrossRef Full Text | Google Scholar

63. Zhang Y, Ding Y, Christofides PD. Integrating feedback control and run-to-run control in multi-wafer thermal atomic layer deposition of thin films. Processes. (2020) 8:18. doi: 10.3390/pr8010018

CrossRef Full Text | Google Scholar

64. Ding Y, Zhang Y, Orkoulas G, Christofides PD. Microscopic modeling and optimal operation of plasma enhanced atomic layer deposition. Chem Eng Res Des. (2020) 159:439–54. doi: 10.1016/j.cherd.2020.05.014

CrossRef Full Text | Google Scholar

65. Zhang Y, Ding Y, Christofides PD. Multiscale computational fluid dynamics modeling and reactor design of plasma-enhanced atomic layer deposition. Comput Chem Eng. (2020) 142:107066. doi: 10.1016/j.compchemeng.2020.107066

CrossRef Full Text | Google Scholar

66. Zhang Y, Ding Y, Wu Z, Christofides PD. Run-to-run control of thermal atomic layer deposition. In: 2020 28th Mediterranean Conference on Control and Automation, MED 2020. Institute of Electrical and Electronics Engineers Inc. p. 1080–6.

Google Scholar

67. Ding Y, Zhang Y, Ren YM, Orkoulas G, Christofides PD. Machine learning-based modeling and operation for ALD of SiO2 thin-films using data from a multiscale CFD simulation. Chem Eng Res Des. (2019) 151:131–45. doi: 10.1016/j.cherd.2019.09.005

CrossRef Full Text | Google Scholar

68. Ding Y, Zhang Y, Kim K, Tran A, Wu Z, Christofides PD. Microscopic modeling and optimal operation of thermal atomic layer deposition. Chem Eng Res Des. (2019) 145:159–72. doi: 10.1016/j.cherd.2019.03.004

CrossRef Full Text | Google Scholar

69. Sitapure N, Lee H, Ospina-Acevedo F, Balbuena PB, Hwang S, Kwon JS-I. A computational approach to characterize formation of a passivation layer in lithium metal anodes. AIChE J. (2020) 67:1–11. doi: 10.1002/aic.17073

CrossRef Full Text | Google Scholar

70. Vishnugopi BS, Hao F, Verma A, Mukherjee PP. Surface diffusion manifestation in electrodeposition of metal anodes. Phys Chem Chem Phys. (2020) 22:11286–95. doi: 10.1039/D0CP01352H

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Carim AI, Batara NA, Premkumar A, Atwater HA, Lewis NS. Polarization control of morphological pattern orientation during light-mediated synthesis of nanostructured se-Te films. ACS Nano. (2016) 10:102–11. doi: 10.1021/acsnano.5b05119

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Tan K, Lin P, Tan J, Wu L, Wang G, Jin S, et al. The film morphology evolution and growth simulation of Cu2ZnSnS4 (CZTS) solar cells during electrodeposition. In: 2015 IEEE 42nd Photovoltaic Specialist Conference, PVSC 2015. Institute of Electrical and Electronics Engineers Inc.

Google Scholar

73. Tan K, Wang G, Liu Y, Xu Z, Jin S, Wei Q, et al. Film morphology and growth evolution of copper electrodeposition in stacking Cu2ZnSnS4 (CZTS) precursor: a kinetic Monte Carlo-embedded atom method simulation. J Electrochem Soc. (2016) 163:D608–14. doi: 10.1149/2.0801610jes

CrossRef Full Text | Google Scholar

74. Wu Z, Tan K, Zhang R, Wei Q, Lin Y. Atomistic kinetic Monte Carlo - embedded atom method simulation on growth and morphology of Cu-Zn-Sn precursor of Cu2ZnSnS4 solar cells. J Mater Res. (2020) 35:252–62. doi: 10.1557/jmr.2019.413

CrossRef Full Text | Google Scholar

75. Zargarnezhad H, Dolati A. A 3D continuum-kinetic monte carlo simulation study of early stages of nucleation and growth in Ni electrodeposition. Electrochim Acta. (2017) 236:1–9. doi: 10.1016/j.electacta.2017.02.103

CrossRef Full Text | Google Scholar

76. Crevillén-García D, Leung P, Shah AA. An emulator for kinetic Monte Carlo simulations of kinetically controlled metal electrodeposition. J Phys Conf Ser. 1053:012081. doi: 10.1088/1742-6596/1053/1/012081

CrossRef Full Text | Google Scholar

77. Habib MR, Liang T, Yu X, Pi X, Liu Y, Xu M. A review of theoretical study of graphene chemical vapor deposition synthesis on metals: nucleation, growth, and the role of hydrogen and oxygen. Reports Prog Phys. (2018) 81:036501. doi: 10.1088/1361-6633/aa9bbf

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Li P, Li Z. Multiscale theoretical studies of graphene growth on copper surfaces. Kexue Tongbao Chin Sci Bull. (2018) 63:3419–26. doi: 10.1360/N972018-00905

CrossRef Full Text | Google Scholar

79. Andersen M, Panosetti C, Reuter K. A practical guide to surface kinetic monte carlo simulations. Front Chem. (2019) 7:202. doi: 10.3389/fchem.2019.00202

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Wang T, Wang H, Kou Z, Liang W, Luo X, Verpoort F, et al. Xenes as an emerging 2D monoelemental family: fundamental electrochemistry and energy applications. Adv Funct Mater. (2020) 30:2002885. doi: 10.1002/adfm.202002885

CrossRef Full Text | Google Scholar