- School of Basic Sciences, Indian Institute of Technology Bhubaneswar, Odisha, India
In this paper, we study the effect of dark energy on the extended thermodynamic structure and interacting microstructures of black holes in AdS, through an analysis of thermodynamic geometry. Considering various limiting cases of the novel equation of state obtained in charged rotating black holes with quintessence, and taking enthalpy H as the key potential in the extended phase space, we scrutinize the behavior of the Ruppeiner curvature scalar R in the entropy-pressure
1 Introduction
Cosmological data points toward an accelerated expansion of our Universe due to the presence of a large negative pressure leading to the conjectured existence of an anti-gravitational force, namely dark energy [1–3]. Despite the prevalence of several theoretical models in efforts to explain astronomical observations, the key traits of dark energy such as its source and nature still remain mysterious. Some of the models for dark energy employ a cosmological constant
An interesting aspect of black hole thermodynamics ensues while generalizing the notion of ADM mass from asymptotically flat to (A) dS spacetimes, namely the requirement of a dynamical cosmological constant. A variable
where
The fact that a black hole horizon can be assigned the notion of a temperature indicates toward a microscopic description of black holes where microstructures share the degrees of freedom of the Bekenstein-Hawking entropy [38–42]. These microscopic structures have associated with them, thermal degrees of freedom and respect equipartition theorems (see for example [43]). With this picture in mind, it is useful to think of the microstructures of the black hole in parallel with the molecules that constitute a fluid system in standard thermodynamics and the study of thermodynamic geometry proves to be of outmost importance in its usefulness in probing the nature of interactions between the microstructures [44–73]. To the best of our knowledge, Ruppeiner geometry for black holes was first used in [44], to gain a statistical understanding of the underlying degrees of freedom, with extensions to Reissner-Nordström, Kerr and Reissner-Nordström-AdS black holes with internal energy and electric potential (or angular velocity for Kerr black hole case) as the fluctuation variables [47]. For example, based on empirical analysis, it is now known that charged AdS black holes are associated with both attraction and repulsion dominated regions as shown in remarkable works [62, 63]. Extending to theories with higher derivative terms, including those with a Gauss-Bonnet term in the action, the attraction-repulsion dominated regions are determined by their electric charge (and Gauss-Bonnet coupling,
where
where
Motivation and plan: In this work, thermodynamic geometry is pursued in extended thermodynamics where enthalpy in Eq. 1 is identified as the correct thermodynamic potential [17] for the proper identification of microstructure interactions with quintessence, keeping the vdW analogy in mind. Using enthalpy as the key potential, the effect of dark energy on microstructures using thermodynamic geometry is appropriately studied in
1.1 Thermodynamics of AdS Kerr-Newman Black Holes Surrounded by Dark Energy
Making use of Newman-Penrose formalism [83], the solution for a Kerr-Newman-AdS black hole generalizing the Kiselev’s model metric with quintessence, was obtained by Xu and Wang [36], with the line-element in Boyer-Lindquist coordinates given as,
Here,
where a is the rotation parameter and
Quintessence has been introduced as an alternative to the cosmological constant scenario to account for the current acceleration of the Universe. This new dark energy component allows values of the equation of state parameter
Useful expressions for mass, entropy and temperature are given respectively as,
In extended black hole thermodynamics, the cosmological constant is identified with pressure as,
with its thermodynamic conjugate volume obtained as,
Here mass M, angular momentum J and charge Q, are related to parameters m, a and q as follows,
The physical parameters M, J and Q now satisfy the Smarr-Gibbs-Duhem relation [37],
where the electric potential
Let us note that when
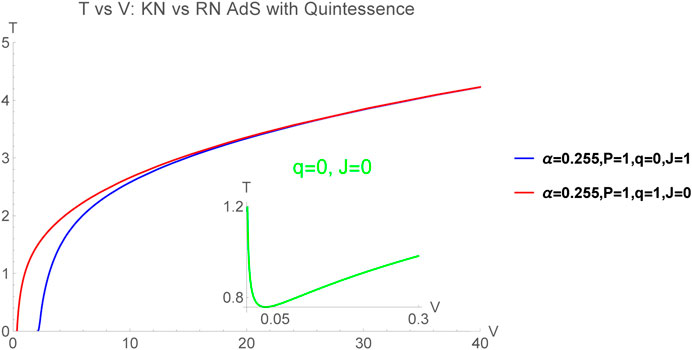
The plot of temperature vs volume is shown in Figure 1.
The above equation needs to be inverted to obtain the equation of state of the general Kerr-Newman AdS black holes. However, as noted in [30], it is in general not possible to obtain an exact expression and hence one resorts to the slowly rotating charged black hole case, where the equation of state is [37],
which is an expansion in powers of J and terms of order
2 Ruppeiner Geometry and Microscopic Interactions
To begin with, consider a thermodynamic system with some n independent thermodynamic variables which can fluctuate about their mean values. A prototypical example with
where
where we have used Eq. 18 and have written,
Clearly, Eq. 20 defines a length element on the space of independent thermodynamic variables describing the system. However, such a length has great physical meaning. Indeed, from Eq. 19 it is clear that for any two points on the space of independent thermodynamic variables, the probability of them being related by a fluctuation more, the closer they are! The reader is referred to [79–81] for a much more detailed account on the role of the Ruppeiner metric in thermodynamic fluctuation theory. Note that taking any arbitrary thermodynamic potential,
This would still in some sense define a length between different thermodynamic equilibrium states. However, in general it may not have a good connection with thermodynamic fluctuation theory and may not result in curvature scalar with nice interpretation (like the one provided by Ruppeiner scalar R) as the measure of interactions of the system. The metric in Eq. 21 may be meaningful if it is obtained from Eq. 20 by an appropriate coordinate transformation. More details are given in the Supplementary Appendix.
2.1 Line Element and Ruppeiner Curvature
To proceed with the study of thermodynamic geometry of the black holes in AdS with quintessence background, we note that even though the Ruppeiner metric [Eq. 2] is initially defined as the Hessian of the entropy, one can calculate equivalent forms of the metric using other potentials such as the enthalpy,
where
where
Now that it is understood that the Ruppeiner metric defines a physically meaningful distance on the spaces of thermodynamic equilibrium states, let us go further and analyze the meaning of the corresponding Ricci scalar. For a two dimensional metric, i.e., with two fluctuation coordinates as we shall be using in this work, the components of the metric can be written down as a
where
3 Effect of Dark Energy on Thermodynamic Geometry
From the form of the equation of state given in Eq. 17, it is helpful to first discuss the thermodynamic geometry of cases
3.1 Schwarzschild and Reissner-Nordström Black Holes in AdS
Setting the rotation parameter in Eq. 4 to zero, we get a Reissner-Nordström-AdS (RN-AdS) black hole surrounded by quintessence, whose lapse function
Making the usual identification that the ADM mass of the black hole and expressing it as function of entropy and pressure, one gets enthalpy to be,
Note that in this non-rotating case, one has
and is found to be same as geometric volume [33]. With all definitions of fundamental thermodynamic variables available, the first law of black holes in the extended thermodynamic phase space can be written to be,
where
Further, setting
which corresponds to that of a non-ideal fluid, i.e., one with non-trivial interactions between molecules. Each of the last three terms in Eq. 31 signify interactions between the microstructures. The limit
where
and
It should be noted that both
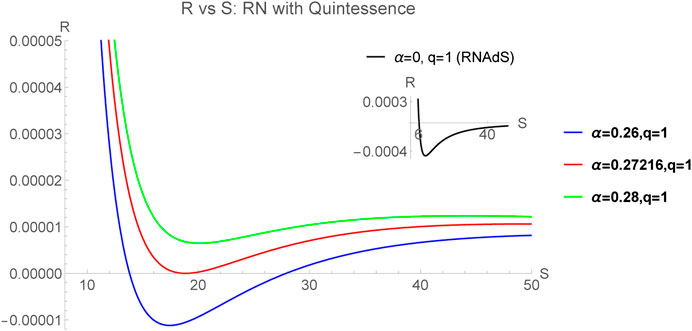
On either of the thermodynamic planes, it is found that the Ruppeiner curvature admits zero crossings indicating existence of points where the dominant kind of interactions can switch from attractive to repulsive and vice versa, since the sign of the Ruppeiner curvature indicates the nature of microscopic interactions. Let us first note that for
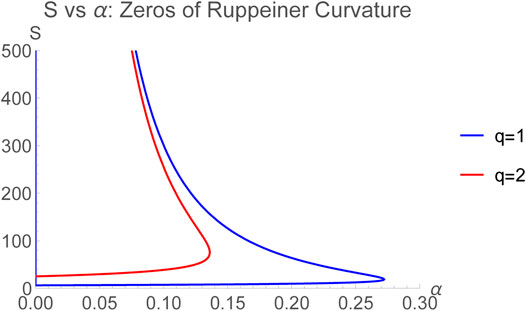
The crossing points therefore depend on the parameters α and q of the black hole. A plot of S vs α shown in Figure 4 gives interesting insights.
As seen from Figure 4 the number of zero crossing points are either zero, one or two depending for a particular case on how many real solutions Eq. 35 admits based on the values of α and q. As mentioned above, the existence of one zero of the Ruppeiner curvature at small value of S6 at which the attractive and repulsive interactions balance each other is well known for the RN-AdS system [68]. The cases where there’s a second zero (see Figure 2) at a higher entropy (or equivalently horizon size), are new and of particular interest here, because they are associated with the presence of quintessence in the background. In fact, there are two further remarkable results. First is the existence of a point on the S-axis (the red curve in Figure 2) corresponding to a threshold value of
The existence of such an
We now consider the
or equivalently
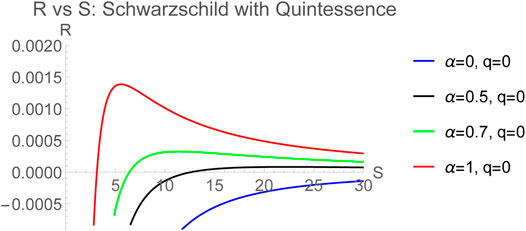
FIGURE 5. Ruppeiner curvature for Schwarzschild-AdS black hole surrounded by quintessence on the
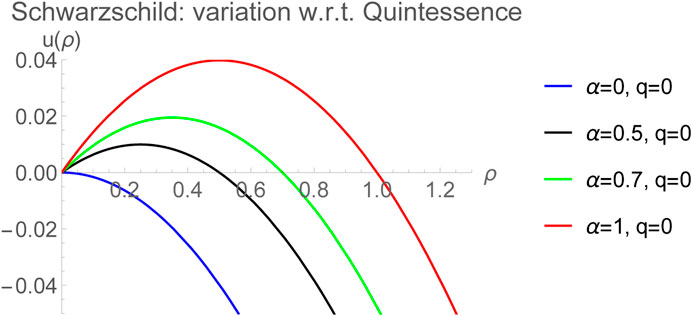
There is another important novel consequence of the quintessence parameter α on the thermodynamic volume of Schwarzschild AdS black hole. In general in fluids, such as the vdW fluid, there is a minimum volume dictated by the fact that temperature does not become negative. This can be obtained from the equation of state evaluated at
It is clear that there is no minimum volume when
3.2 Slowly Rotating Black Holes in AdS
The general expression for Ruppeiner curvature can be obtained analytically in the case
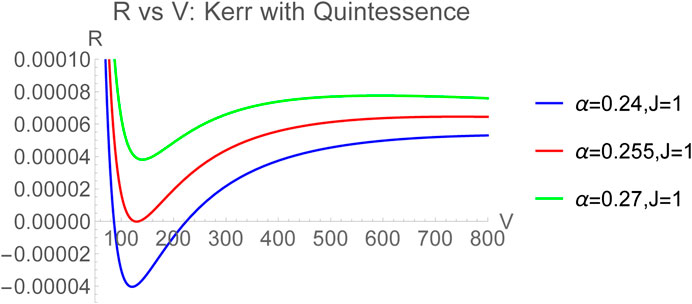
FIGURE 6. Ruppeiner curvature for Kerr-AdS black hole surrounded by quintessence on the
Furthermore, there is a minimum volume dictated by the equation of state given in Eq. 17 so that the temperature is not negative, which cannot be obtained analytically, but one can obtain its values numerically. For instance, considering the case
4 Microstructures of Black Holes and a Mean Field Description
Analysis of Ruppeiner curvature of AdS black holes in last section, shows a subtle interplay between the attraction and repulsion dominated regimes, which heuristically suggests the presence of both attractive and repulsive interactions in the system, akin to the behavior of microstructures in a vdW fluid [62, 63]. Despite long standing efforts, the true nature of microscopic degrees of freedom of black holes are not known yet. Following Boltzmann’s lines, “if you can heat it, it has microstructure,” current studies have tried to obtain whatever valuable information from connection between thermodynamic and gravitation properties of black holes. The black hole chemistry paradigm [27, 28] has shown that charged black holes in AdS have a rich phase structure similar to vdW systems, suggesting a possible molecular kind of microstructure emerging from the degrees of freedom for black holes as well. However, the analysis of thermodynamic curvature shows that the behavior of microstructures of the two systems is not the same, with the case of black holes being more subtle [62, 63, 65, 68]. There are also proposals that a general interacting system can probably also be modeled as a binary mixture [65, 68] of both attractive and repulsive microstructures which share the degrees of freedom of the total entropy. Here, we take these issues forward and show that within a mean field approximation, the interactions can be described by an effective mean field interaction potential whose extremum points correspond to points where the Ruppeiner metric is flat. However, we particularly emphasize on the fact that any analysis in this spirit is phenomenological and is possible due to the resemblance of the thermodynamic structure of AdS black holes with that of hydrostatic systems such as the vdW fluid. Therefore, we shall be exploring a fluid-like description of black hole microstructures which may be thought of as being analogous to the molecules present in a fluid. Since
The first term, which depends on the temperature is clearly the kinetic energy density7 whereas the remaining terms signify non-trivial microscopic interactions. In fact, one can think of the remaining terms to correspond to a mean field potential energy density containing coarse grained information of the interactions and is given by,
where
In the following subsection, we demonstrate the utility of the mean field interaction potential approach, by considering the special case
4.1 RN-AdS Black Holes
For the case of RN-AdS black holes without quintessence in the background, the mean field interaction potential is given as,
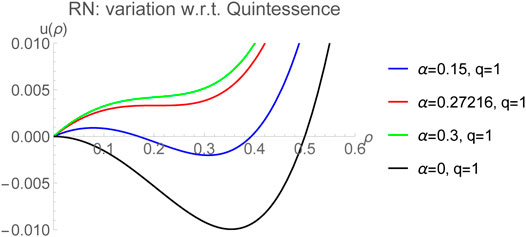
and is plotted as a function of ρ for various values of the electric charge q in Figure 7.
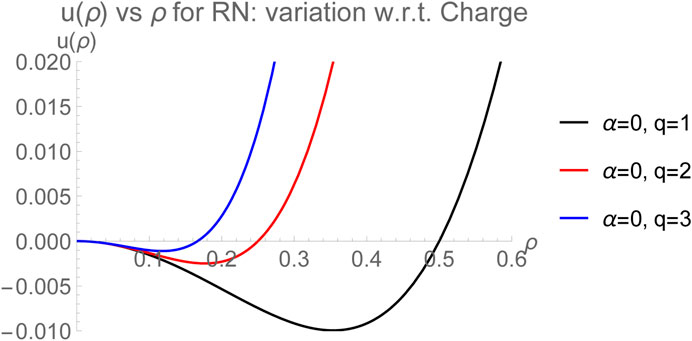
FIGURE 7. Mean field interaction potential
In all the cases, there exists a minimum8 of the potential where the attractive and repulsive interactions balance out. This point corresponds to
where c and d are appropriate positive constants. The mean field approach is therefore consistent with the previously known results for RN-AdS black holes and provides a satisfactory picture of interactions among microstructures.
4.2 Effect of Dark Energy on the Mean Field Interaction Potential
We shall now consider the effect of quintessence on the microstructures of AdS black holes. The mean field interaction potential in this case takes the form,
Interestingly, the crossing point of the Ruppeiner curvature corresponds to a maximum, i.e., an unstable equilibrium of the mean field interaction potential,
A plot of the mean field interaction potential is shown in Figure 8. This means that with
where b and c are both positive constants. The first and second terms respectively correspond to the repulsive and attractive parts of the intermolecular interaction. Naively, such an observation looks bizarre, but can be explained from the fact that quintessence, which corresponds to a negative pressure responsible for the expansion of the Universe is essentially a long ranged repulsive interaction with a range that is naturally longer than the range of attractive interactions between microstructures of the Schwarzschild-AdS black hole. Microstructures associated with quintessence are therefore not just repulsive, but have long ranged interactions, which typically go as an inverse cube of the distance.
The presence of a non-trivial electric charge makes the behaviour of the mean field interaction potential all the more interesting and is shown in Figure 9.
Note that the black curve corresponds to the RN-AdS case without quintessence, i.e.,
In this paper, we restricted to the special case where the quintessence equation of state parameter took the value
5 Remarks
In this work, we have focused on probing the nature of interactions among the microstructures for asymptotically AdS black holes surrounded by quintessence using methods of thermodynamic geometry. From the empirical behavior of thermodynamic scalar R, charged black holes in
It would be interesting to see the effects of quintessence on the microstructures for black holes in higher derivative theories such as Gauss-Bonnet-AdS black holes or even the more general Lovelock-AdS and pure Lovelock-AdS black holes, leading to a complete classification of attraction and repulsion dominated regions for wide variety of black holes. Another important avenue for future work is to include thermal fluctuations, as it is known that fluctuations give additional contributions and modify the points where the Ruppeiner scalar R goes to zero. The effect of statistical fluctuations on thermodynamics and phase transitions is well studied and is known to change the definitions of entropy and free energy, with particularly novel consequences for large black holes [37, 89–94]. Thus, it should be intriguing to consider additional effects due to thermal fluctuations on the thermodynamic geometry of black holes with quintessence studied in this work.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
A.S. wishes to thank the Council of Scientific and Industrial Research (CSIR), Government of India, for financial support. A.G. would like to acknowledge the financial support received from IIT Bhubaneswar in the form of an institute research fellowship. The authors are grateful to the anonymous referees for a careful reading of the manuscript and their useful comments which have led to an improvement of the article. C.B. would like to thank the Science and Engineering Research Board (SERB), Government of India, for financial support through the Mathematical Research Impact Centric Support (MATRICS) grant number MTR/2020/000135.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.631471/full#supplementary-material.
Footnotes
1For a rotating black hole one can write the first law as:
2The Weinhold metric is originally defined in the energy representation [82], taking U as the key potential. In standard black hole thermodynamics U is identified with mass M of the black hole to evaluate the metric on the space of thermodynamic equilibrium states. However, in extended thermodynamics M is identified with enthalpy H and hence it is appropriate to call it an enthalpy representation.
3Typically, temperature is conjugate to the entropy as is clear from the first law,
4As also pointed out in [66], an internal energy representation, i.e., the
5See for example the recent work [63] where the Ruppeiner curvature of the vdW fluid in the novel
6Indicating that the smaller black holes are dominated by repulsive interactions among microstructures [62,63]
7Indeed from the equipartition theorem,
8Since
9The fluid in our discussions always assumes three spatial dimensions, irrespective of the number of spacetime dimensions in which the black hole (whose thermodynamics gets mapped into that of the fluid) resides in.
10With the assumption that the fluid density is spatially uniform, without any loss of generality one can consider some arbitrarily small length scale r of the order of the mean free path of the molecules such that in a volume
11See [85] for a deeper connection between zero crossings of Ruppeiner curvature and intermolecular interactions involving Lennard-Jones type potentials in a different context.
12The presence of electric charge would of course shift the position of this maximum but does not change the qualitative behavior of
References
1. Riess AG, Filippenko AV, Challis P, Clocchiatti A, Diercks A, Garnavich PM, et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron J (1998) 116:1009. doi:10.1086/300499
2. Perlmutter S, Aldering G, Goldhaber G, Knop RA, Nugent P, Castro PG, et al. Measurements of omega and lambda from 42 high redshift supernovae. Astrophys J (1999) 517:565. doi:10.1086/307221
3. Sahni V, Starobinsky AA. The case for a positive cosmological Λ-term. Int J Mod Phys D (2000) 9:373–444. doi:10.1142/s0218271800000542
4. Caldwell RR, Dave R, Steinhardt PJ. Cosmological imprint of an energy component with general equation of state. Phys Rev Lett (1998) 80:1582. doi:10.1103/physrevlett.80.1582
5. Chen S, Wang B, Su R. Hawking radiation in a $d$-dimensional static spherically-symmetric black Hole surrounded by quintessence. Phys Rev D (2008) 77:124011. doi:10.1103/physrevd.77.124011
6. Azreg-Aïnou M. Charged de Sitter-like black holes: quintessence-dependent enthalpy and new extreme solutions. Eur Phys J C (2015) 75(1):34. doi:10.1140/epjc/s10052-015-3258-3
7. Kiselev VV. Quintessence and black holes. Class Quan Grav (2003) 20:1187. doi:10.1088/0264-9381/20/6/310
8. Thomas BB, Saleh M, Kofane TC. Thermodynamics and phase transition of the Reissner-Nordström black hole surrounded by quintessence. Gen Relativ Gravit (2012) 44:2181–9. doi:10.1007/s10714-012-1382-z
9. Ghosh SG, Maharaj SD, Baboolal D, Lee T. Lovelock black holes surrounded by quintessence. Eur Phys J C (2018) 78(2):90. doi:10.1140/epjc/s10052-018-5570-1
10. Ghosh SG, Amir M, Maharaj SD. Quintessence background for 5D Einstein–Gauss–Bonnet black holes. Eur Phys J C (2017) 77(8):530. doi:10.1140/epjc/s10052-017-5099-8
11. Ghaderi K, Malakolkalami B. Effects of quintessence on thermodynamics of the black holes. Astrophys Space Sci (2016) 361(5):161. doi:10.1007/s10509-016-2744-x
12. Ghaderi K, Malakolkalami B. Thermodynamics of the Schwarzschild and the Reissner-Nordström black holes with quintessence. Nucl Phys B (2016) 903:10–8. doi:10.1016/j.nuclphysb.2015.11.019
13. Toledo JM, Bezerra VB. The Reissner–Nordström black hole surrounded by quintessence and a cloud of strings: thermodynamics and quasinormal modes. Int J Mod Phys D (2018) 28(1):1950023.
14. Chabab M, Iraoui S. Thermodynamic criticality of d-dimensional charged AdS black holes surrounded by quintessence with a cloud of strings background. Gen Relat Gravit (2020) 52:75. doi:10.1007/s10714-020-02729-4
15. Visser M. The Kiselev black hole is neither perfect fluid, nor is it quintessence. Class. Quant Grav (2020) 37:4. doi:10.1088/1361-6382/ab60b8
16. Cvetic M, Gibbons GW, Pope CN. Photon spheres and sonic horizons in black holes from supergravity and other theories. Phys Rev D (2016) 94:106005. doi:10.1103/PhysRevD.94.106005
17. Kastor D, Ray S, Traschen J. Enthalpy and the mechanics of AdS black holes. Class Quan Grav (2009) 26:195011. doi:10.1088/0264-9381/26/19/195011
18. Cvetic M, Gibbons G, Kubiznak D, Pope C. Black hole enthalpy and an entropy inequality for the thermodynamic volume. Phys Rev D (2011) 84:024037. doi:10.1103/PhysRevD.84.024037
19. Hawking SW, Page DN. Thermodynamics of black holes in anti-de sitter space. Commun Math Phys (1983) 87:577. doi:10.1007/bf01208266
20. Dolan BP. The cosmological constant and black-hole thermodynamic potentials. Class Quan Grav (2011) 28:125020. doi:10.1088/0264-9381/28/12/125020
21. Dolan BP. Pressure and volume in the first law of black hole thermodynamics. Class Quan Grav (2011) 28:235017. doi:10.1088/0264-9381/28/23/235017
22. Chamblin A, Emparan R, Johnson CV, Myers RC. Charged AdS black holes and catastrophic holography. Phys Rev D (1999) 60:064018. doi:10.1103/physrevd.60.064018
23. Chamblin A, Emparan R, Johnson CV, Myers RC. Holography, thermodynamics and fluctuations of charged AdS black holes. Phys Rev D Bf (1999) 60:104026. doi:10.1103/physrevd.60.104026
24. Kubiznak D, Mann RB. P-V criticality of charged AdS black holes. J High Energ Phys (2012) 07:033. doi:10.1007/JHEP07(2012)033
25. Cai RG, Cao LM, Li L, Yang RQ. P-V criticality in the extended phase space of Gauss-Bonnet black holes in AdS space. J High Energ Phys (2013) 09:005. doi:10.1007/JHEP09(2013)005
26. Caceres E, Nguyen PH, Pedraza JF. Holographic entanglement entropy and the extended phase structure of STU black holes. JHEP (2015) 09:184. doi:10.1007/JHEP09(2015)184
27. Karch A, Robinson B. Holographic black hole chemistry. JHEP (2015) 12:073. doi:10.1007/JHEP12(2015)073
28. Kubiznak D, Mann RB, Teo M. Black hole chemistry: thermodynamics with Lambda. Class Quant Grav (2017) 34(6):063001. doi:10.1088/1361-6382/aa5c69
29. Majhi BR, Samanta S. P-V criticality of AdS black holes in a general framework. Phys Lett B (2017) 773:203–7. doi:10.1016/j.physletb.2017.08.038
30. Gunasekaran S, Kubiznak D, Mann RB. Extended phase space thermodynamics for charged and rotating black holes and Born-Infeld vacuum polarization. JHEP (2012) 11:110. doi:10.1007/JHEP11(2012)110
31. Wei SW, Liu YX. Critical phenomena and thermodynamic geometry of charged Gauss-Bonnet AdS black holes. Phys Rev D (2013) 87:044014. doi:10.1103/physrevd.87.044014
32. Li GQ. Effects of dark energy on P-V criticality of charged AdS black holes. Phys Lett B (2014) 735:256–60. doi:10.1016/j.physletb.2014.06.047
33. Liu H, Meng X. Effects of dark energy on the efficiency of charged AdS black holes as heat engines. Eur Phys J C (2017) 77(8):556. doi:10.1140/epjc/s10052-017-5134-9
34. Guo XY, Li HF, Zhang LC, Zhao RContinuous Phase Transition and Microstructure of Charged AdS Black Hole with Quintessence. Eur Phys J C (2020) 80:168. doi:10.1140/epjc/s10052-019-7601-y
35. Wu Y, Xu W. Effect of dark energy on Hawking–page transition. Phys Dark Univ (2020) 27:100470. doi:10.1016/j.dark.2020.100470
36. Xu Z, Wang J. Kerr-Newman-AdS black hole in quintessential dark energy. Phys Rev D (2017) 95:064015. doi:10.1103/physrevd.95.064015
37. Sharif M, Ama-Tul-Mughani Q. Phase transition and thermal fluctuations of quintessential Kerr-Newman-AdS black hole. Phys Dark Universe (2020) 30:100723. doi:10.1016/j.dark.2020.100723
38. Bekenstein JD. Black holes and entropy. Phys Rev D (1973) 7:2333–46. doi:10.1103/physrevd.7.2333
39. Bekenstein JD. Generalized second law of thermodynamics in black-hole physics. Phys Rev D (1974) 9:3292–300. doi:10.1103/physrevd.9.3292
40. Hawking SW. Particle creation by black holes. Commun.Math Phys.Commun Math Phys (1975) 43:199–206. doi:10.1007/bf02345020
41. Hawking SW. Black holes and thermodynamics. Phys Rev D (1976) 13:191. doi:10.1103/physrevd.13.191
42. Bardeen JM, Carter B, Hawking SW. The Four laws of black hole mechanics. Commun Math Phys (1973) 31:161. doi:10.1007/bf01645742
43. Padmanabhan T. Equipartition of energy in the horizon degrees of freedom and the emergence of gravity. Mod Phys Lett A (2010) 25:1129. doi:10.1142/s021773231003313x
44. Cai RG, Cho JH. Thermodynamic curvature of the BTZ black hole. Phys Rev D (1999) 60:067502. doi:10.1103/physrevd.60.067502
45. Mirza B, Zamaninasab M. Ruppeiner geometry of RN black holes: flat or curved? J High Energ Phys (2007) 6:059. doi:10.1088/1126-6708/2007/06/059
46. Aman J, Bengtsson I, Pidokrajt N. Geometry of black hole thermodynamics. Gen Relativity Gravitation (2003) 35:1733. doi:10.1023/a:1026058111582
47. Shen JY, Cai RG, Wang B, Su RK. Thermodynamic geometry and critical behavior of black holes. Int J Mod Phys A (2007) 22:11. doi:10.1142/s0217751x07034064
48. Quevedo H, Sanchez A. Geometric description of BTZ black holes thermodynamics. Phys Rev D (2009) 79:024012. doi:10.1103/physrevd.79.024012
49. Sahay A, Sarkar T, Sengupta G. Thermodynamic geometry and phase transitions in Kerr-Newman-AdS black holes. JHEP (2010) 04:118. doi:10.1007/JHEP04(2010)118
50. Sahay A, Sarkar T, Sengupta G. On the thermodynamic geometry and critical phenomena of AdS black holes. J High Energ Phys (2010) 07:82. doi:10.1007/JHEP07(2010)082
51. Banerjee R, Ghosh S, Roychowdhury D. New type of phase transition in Reissner Nordström-AdS black hole and its thermodynamic geometry. Phys Lett B (2011) 696:156. doi:10.1016/j.physletb.2010.12.010
52. Niu C, Tian Y, Wu XN. Critical phenomena and thermodynamic geometry of Reissner-Nordström-anti-de Sitter black holes. Phys Rev D (2012) 85:024017. doi:10.1103/physrevd.85.024017
53. Mansoori SAH, Mirza B. Correspondence of phase transition points and singularities of thermodynamic geometry of black holes. Eur Phys J C (2014) 74:2681. doi:10.1140/epjc/s10052-013-2681-6
54. Quevedo H. Geometrothermodynamics of black holes. Gen Relativ Gravit (2008) 40:971. doi:10.1007/s10714-007-0586-0
55. Hendi SH, Panahiyan S, Eslam Panah B, Momennia M. A new approach toward geometrical concept of black hole thermodynamics. Eur Phys J C (2015) 75(10):507. doi:10.1140/epjc/s10052-015-3701-5
56. Dehyadegari A, Sheykhi A, Montakhab A. Critical behavior and microscopic structure of charged AdS black holes via an alternative phase space. Phys Lett B (2017) 768:235. doi:10.1016/j.physletb.2017.02.064
57. Bhattacharya K, Majhi BR. Thermogeometric description of the van der Waals like phase transition in AdS black holes. Phys Rev D (2017) 95(10):104024. doi:10.1103/PhysRevD.95.104024
58. Chabab M, Moumni HE, Iraoui S, Masmar K, Zhizeh S. More insight into microscopic properties of RN-AdS black hole surrounded by quintessence via an alternative extended phase space. Int J Geom Methods Mod Phys (2018) 15:1850171. doi:10.1142/s0219887818501712
59. Kumara AN, Rizwan CA, Vaid D, Ajith K. Critical behaviour and microscopic structure of charged AdS black hole with a global monopole in extended and alternate phase spaces. Gen. Relat. Quant. Cosmol. (1906) 1906:11550, 1906. arXiv:1906.11550 [gr-qc].
60. Kumara AN, Rizwan CL, Hegde K, Ajith KM, Ali MS. Microstructure and continuous phase transition of a regular Hayward black hole in anti-de Sitter spacetime. Gen Relat Quant Cosmol (2003) 2003:0889. arXiv:2003.00889 [gr-qc].
61. Kumara AN, Rizwan CLA, Hegde K, Ajith KM. Repulsive interactions in the microstructure of regular Hayward black hole in anti-de Sitter spacetime. Phys Lett B (2020) 807:135556. doi:10.1016/j.physletb.2020.135556
62. Wei SW, Liu YX, Mann RB. Repulsive interactions and universal properties of charged Antiâde Sitter black hole microstructures. Phys Rev Lett (2019) 123(7). doi:10.1103/physrevlett.123.071103
63. Wei SW, Liu YX, Mann RB. Ruppeiner geometry, phase transitions, and the microstructure of charged AdS black holes. Phys Rev D (2019) 100:124033. doi:10.1103/physrevd.100.124033
64. Zangeneh MK, Dehyadegari A, Sheykhi A. Insight into the microscopic structure of an AdS black hole from a thermodynamical phase transition. Phys Rev Lett (2015) 115:111302. doi:10.1103/PhysRevLett.115.111302
65. Guo XY, Li HF, Zhang LC, Zhao R. Microstructure and continuous phase transition of a Reissner-Nordström-AdS black hole. Phys Rev D (2019) 100:064036. doi:10.1103/physrevd.100.064036
66. Xu ZM, Wu B, Yang WL. Ruppeiner thermodynamic geometry for the Schwarzschild-AdS black hole. Phys Rev D (2020) 101:024018. doi:10.1103/physrevd.101.024018
67. Wei SW, Liu YX. Intriguing microstructures of five-dimensional neutral Gauss-Bonnet AdS black hole. Phys Lett B (2020) 803:135287. doi:10.1016/j.physletb.2020.135287
68. Ghosh A, Bhamidipati C. Thermodynamic geometry for charged Gauss-Bonnet black holes in AdS spacetimes. Phys Rev D (2020) 101:046005. doi:10.1103/physrevd.101.046005
69. Zhou R, Liu YX, Wei SW. Phase transition and microstructures of five-dimensional charged Gauss-Bonnet-AdS black holes in the grand canonical ensemble. Phys Rev D (2008) 102:124015. doi:10.1103/PhysRevD.102.124015
70. Wei SW, Liu YX, Mann RB. Novel dual relation and constant in Hawking-Page phase transition. Phys Rev D (2020) 102:104011. doi:10.1103/PhysRevD.102.104011
71. Dehyadegari A, Sheykhi A, Wei SW. Microstructure of charged AdS black hole via P−V criticality. Phys Rev D (2020) 102(10):104013. doi:10.1103/PhysRevD.102.104013
72. Yerra PK, Bhamidipati C. Constancy of Ruppeiner curvature along a renormalization group flow (2007). arXiv:2007.11515 [hep-th].
73. Ghosh A, Bhamidipati C. Thermodynamic geometry and interacting microstructures of BTZ black holes. Phys Rev D (2020) 101:106007. doi:10.1103/physrevd.101.106007
74. Ruppeiner G. Thermodynamics: a Riemannian geometric model. Phys Rev A (1979) 20:1608. doi:10.1103/physreva.20.1608
75. Ruppeiner G. Application of Riemannian geometry to the thermodynamics of a simple fluctuating magnetic system. Phys Rev A (1981) 24:488. doi:10.1103/physreva.24.488
76. Janyszek H, Mrugala R. Riemannian geometry and the thermodynamics of model magnetic systems. Phys Rev A Gen Phys (1989) 39:6515. doi:10.1103/physreva.39.6515
77. Janyszek H. Riemannian geometry and stability of thermodynamical equilibrium systems. J Phys A Math Gen (1990) 23:477. doi:10.1088/0305-4470/23/4/017
78. Janyszek H, Mrugaa R. Riemannian geometry and stability of ideal quantum gases. J Phys A: Math Gen (1990) 23:467. doi:10.1088/0305-4470/23/4/016
79. Ruppeiner G. Riemannian geometry in thermodynamic fluctuation theory. Rev Mod Phys Rev Mod Phys (1996) 6768:605313. doi:10.1103/RevModPhys.67.605
80. Ruppeiner G. Thermodynamic curvature measures interactions. Am J Phys (2010) 78:1170. doi:10.1119/1.3459936
81. Ruppeiner G. Thermodynamic curvature from the critical point to the triple point. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 86:021130. doi:10.1103/PhysRevE.86.021130
82. Weinhold F. Metric geometry of equilibrium thermodynamics. The J Chem Physics J Chem Phys (1975) 63:2479. doi:10.1063/1.431689
83. Newman E, Penrose R. An approach to gravitational radiation by a method of spin coefficients. J Math Phys (1962) 3(3):566–78. doi:10.1063/1.1724257
84. Hawking SW. The conservation of matter in general relativity. Commun Math Phys (1970) 18:301. doi:10.1007/bf01649448
85. May HO, Mausbach P, Ruppeiner G. Thermodynamic curvature for attractive and repulsive intermolecular forces. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 88:032123. doi:10.1103/PhysRevE.88.032123
86. Wei SW, Liu YX. Insight into the microscopic structure of an AdS black hole from a thermodynamical phase transition. Phys Rev Lett Phys Rev Lett (2015) 115(16):111302. doi:10.1103/PhysRevLett.115.111302
87. Das Bairagya J, Pal K, Pal K, Sarkar T. The geometry of RN-AdS fluids. Phys Lett B (2020) 805:135416. doi:10.1016/j.physletb.2020.135416
88. Miao YG, Xu ZM. On thermal molecular potential among micromolecules in charged AdS black holes. Phys Rev D (2018) 98:044001. doi:10.1103/physrevd.98.044001
89. Pourhassan B, Faizal M, Debnath U. Effects of thermal fluctuations on the thermodynamics of modified Hayward black hole. Eur Phys J C (2016) 76:145. doi:10.1140/epjc/s10052-016-3998-8
90. Pourhassan B, Kokabi K, Rangyan S. Thermodynamics of higher dimensional black holes with higher order thermal fluctuations. Gen Relativ Gravit (2017) 49:144. doi:10.1007/s10714-017-2315-7
91. Sinha AK. Thermal fluctuations of stable quantum ADS Kerr-Newman black hole. Gen Relat Quant Cosmol (2016) 1608:08359, 2016. arXiv:1608.08359 [gr-qc].
92. Upadhyay S, Hendi SH, Panahiyan S, Panah BE. Thermal fluctuations of charged black holes in gravity’s rainbow. Prog Theor Exp Phys (2018) 1809:093E01, 2018. [arXiv:1809.01078 [gr-qc]].
93. Zhang M. Corrected thermodynamics and geometrothermodynamics for anti-de Sitter black hole. Nucl Phys B (2018) 935:170. doi:10.1016/j.nuclphysb.2018.08.010
Keywords: black holes, thermodynamic geometry, anti de Sitter space, thermodynamics, quantum gravity
Citation: Singh A, Ghosh A and Bhamidipati C (2021) Thermodynamic Curvature of AdS Black Holes with Dark Energy. Front. Phys. 9:631471. doi: 10.3389/fphy.2021.631471
Received: 20 November 2020; Accepted: 25 January 2021;
Published: 23 March 2021.
Edited by:
Oscar Dias, University of Southampton, United KingdomReviewed by:
George Ruppeiner, New College of Florida, United StatesJennie Traschen, University of Massachusetts Amherst, United States
Copyright © 2021 Singh, Ghosh and Bhamidipati. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chandrasekhar Bhamidipati, Y2hhbmRyYXNla2hhckBpaXRiYnMuYWMuaW4=
 Aditya Singh
Aditya Singh Aritra Ghosh
Aritra Ghosh Chandrasekhar Bhamidipati
Chandrasekhar Bhamidipati