Deformation Parameters and Collective Temperature Changes in Photofission Mass Yields of Actinides Within the Systematic Statistical Scission Point Model

The photofission fragment mass yields of actinides are evaluated using a systematic statistical scission point model. In this model, all energies at the scission point are presented as a linear function of the mass numbers of fission fragments. The mass yields are calculated with a new approximated relative probability for each complementary fragment. The agreement with the experimental data is quite good, especially with a collective temperature T_col of 2 MeV at intermediate excitation energy and T_col = 1 MeV for spontaneous fission. This indicates that the collective temperature is greater than the value obtained by the initial excitation energy. The generalized superfluid model is applied for calculating the fragment temperature. The deformation parameters of fission fragments have been obtained by fitting the calculated results with the experimental values. This indicates that the deformation parameters decrease with increasing excitation energy. Also, these parameters decrease for fissioning systems with odd mass numbers.

1 Introduction

Since the fission discovery, the experimental and theoretical fission mass yields have been continuously developed. The most widely used theoretical model to study mass yields is the statistical model which was founded by Fong and Wilkins [1, 2]. This model has been developed in many branches, such as the Gaussian model [3, 4] and modified scission point models [6–13]. The time-dependent model has been significantly developed by Randrup [14–16] and others [17–22] to predict the shape of mass yields (symmetric or asymmetric modes). Because all of them have sophisticated computations, a systematic method is needed to evaluate the mass distribution of fission fragments in an easy way.

Although the statistical model can predict transitions between symmetric and asymmetric modes in the region of heavy actinides, the calculated results are inaccurate compared to the experimental data. This problem is found where the calculated results were smeared (refined) by the Gaussian model with the width 1.5 amu to obtain a smoother curve [8].

On the other hand, some researchers [6–9] added some terms to neutron kinetic energy or gamma endpoint energy, E (as the initial excitation energy), to obtain the excitation energy of the fissioning nucleus, E^*, for example, Pasca [7, 9] added the Q-factor and the difference between the potential energy of the fissioning nucleus and the potential energy of one of the fragments at the scission point to the initial excitation energy to obtain excitation energy (i.e., E^* = Q+E+U_cn−U_i). Some others [10, 11] took available energy as the difference between the potential energy of the fissioning system at the scission point and the energy of the excited compound nucleus, which is the sum of Q-factor and initial excitation energy (E^* = Q+E). This addition of energies to the initial excitation energy is more pronounced in time-dependent models [14] when nuclear excitation energy measured relative to potential energy (E^* = E-U). Also, fragment temperature, instead of collective temperature, has been used to calculate the mass yield of ²³⁸U in my previous work [13]. Also, collective temperature is usually calculated by the excitation energy of fissioning systems. Here, the role of collective temperature is examined by selecting two values (1 and 2 MeV) independently.

In the next section, a systematic method is presented to calculate mass yields for actinides; the fewer parameters and refinements are included in this framework. For this reason, all energies at the scission point are formulated as a function of the mass number of fission fragments. Then, all mass yields for photofission of actinides are calculated and compared with the experimental data (Section 3).

2 Theoretical Framework

The relative yield is usually calculated as the ratio between the probabilities of a given fragmentation and the sum of probabilities of all possible fragmentations as follows:

$Y\left(A_i,Z_i\right)=\frac{P\left(A_i,Z_i\right)}{{\displaystyle \sum P\left(A_i,Z_i\right)}}(1)$

where $P\left(A_i,Z_i\right)$ is the relative probability of formation of any fission fragment. In the statistical method, the relative probability of any fission fragment pair is given by Ref. 2.

$P={\displaystyle {\int }_0^{{\beta }_{\max }}{\displaystyle {\int }_0^{{\beta }_{\max }}{e}^{V\frac{\left(N,Z,s,{\beta }_1,{\beta }_2\right)}{T_{coll}}}d{\beta }_1}d{\beta }_2}(2)$

where $V\left(N,Z,s,{\beta }_1,{\beta }_2\right)$ is the total potential energy of the fissioning system at the scission point; T_coll is the collective temperature of the fissioning system; s is the spherical coaxial distance; and β_is (i = L, H) are the deformation parameters for the light and heavy fragments.

The total potential energies at the scission point are defined as follows:

$V\left(N,Z,s,{\beta }_1,{\beta }_2\right)=V_{\text{Interac}}+{\displaystyle \sum _{A_L,A_H}{V}_{\text{indiv},i}}(3)$

The first term is the interaction energy between complementary fragments, $V_{Interac}=V_{Coul}+V_{prox}$. The individual energy includes the macroscopic energy ($V_{Mac}$), shell correction energy, and pairing energy as microscopic energies ($V_{Mic}$), that is, $V_{indiv}=V_{Mac,i}+E_{shell,i}+E_{pair,i}$. In the following sections, these energies are presented.

2.1 Interaction Energy

The nuclear proximity potential ($V_{prox}$) is presented [23, 24] by the following equation:

$V_{prox}\left(s\right)=4\pi \gamma b\left[\frac{C_1{C}_2}{C_1+C_2}\right]\text{Φ}\left(\frac{s}{b}\right),(4)$

where the width (diffuseness) of the nuclear surface is b$\approx$0.88. C₁ and C₂ are the Süsmann central radii of fragments that is related to the sharp radius R_i as follows:

$C_i=R_{0,i}-\left[\frac{b^2}{R_{0,i}}\right],(5)$

$R_{0,i}$ is the net radius of each fission fragment obtained through a semi-empirical equation that is a function of the mass number of fission fragments [24] as follows:

$R_{0,i}\left(fm\right)=1.28A_i^{1/3}-0.76+0.8A_i^{-1/3}(6)$

In Eq. 4, γ is the surface tension coefficient of the nucleus and obtained from the Lysekil mass formula (Ref. 25) by

$\gamma =0.9517\sqrt{\left(1-2.61I_1^2\right)\left(1-2.61I_2^2\right)}MeV/f{m}^2;I_i=\frac{{\left(N_i-Z_i\right)}^2}{A_i^2},(7)$

where $N_i$, $Z_i$, and $A_i$ are neutron, atomic, and mass numbers of any fission fragments, respectively. In Eq. 4, $\text{Φ}$ is the universal proximity relation which is a function of distance between two interaction fragments and is defined [23] as follows:

$\text{Φ}\left(\frac{s}{b}\right)=\{\begin{array}{l}-1.7817+0.9270+0.0169{\left(\frac{s}{b}\right)}^2-0.0514{\left(\frac{s}{b}\right)}^3\hfill \\ for0\le \frac{s}{b}\le 1.9475\hfill \\ -4.41\text{exp}\left(-\frac{s}{0.7176b}\right)\hfill \\ for\frac{s}{b}\ge 1.9475\hfill \end{array}(8)$

Coulomb energy is written as [4, 12] follows:

$E_{Coul}=\frac{Z_1{Z}_2{e}^2}{r}\left(\begin{array}{c}\left(1+n_1\left(R_{\mathrm{0,1}}^2{\beta }_1+R_{\mathrm{0,2}}^2{\beta }_2\right)\right)+n_2\left(R_{\mathrm{0,1}}^2{\beta }_1^2+R_{\mathrm{0,2}}^2{\beta }_2^2\right)\\ +n_3\left(R_{\mathrm{0,1}}^4{\beta }_1^2+R_{\mathrm{0,2}}^4{\beta }_2^2\right)+n_4{\beta }_1{\beta }_2\end{array}\right),(9)$

where $r=s+R_1+R_2$, $n_1=\frac{3}{2\sqrt{5\pi }{r}^2}$, $n_2=\frac{3}{7\pi r^2}$, $n_3=\frac{9}{14\pi r^4}$, and $n_4=\frac{27R_1^2{R}_2^2}{10\pi r^4}$. R_i is the radii of deformed nuclei that can be evaluated using the deformation-dependent expansion of nuclear radii as follows:

$R_i\left(\theta \right)=R_{0,i}\left(1+{\beta }_i{Y}_{20}\left(\theta \right)\right),(10)$

where θ is the angle made by the axis of symmetry with fission axis, β_i is the quadrupole deformation parameter of fragments, and Y₂₀ is the spherical harmonic functions.

2.2 Individual Energies

The individual energies include the macroscopic energy, shell correction energy, and pairing energy. The macroscopic energy is calculated in the framework of the FRLDM model from Ref. 26, and the spheroidally deformed is applied as [27].

$V_{surf,i}=21.18466\text{B}1\left(1-2.345\frac{{\left(N_i-Z_i\right)}^2}{A_i^2}\right)\sqrt[3]{A_i^2}\left(1-0.009266T_i^2\right),(11)$

$V_{coul,i}=\left(0.7448\frac{\text{B}3{\text{Z}}_i^2}{\sqrt[3]{A_i}}-0.5689\frac{Z_i^{4/3}}{\sqrt[3]{A_i}}+\frac{f{Z}_i^2}{A_i}\right)\left(1-\frac{0.0032}{3}{T}_i^2\right),(12)$

where the quantity B1 is the relation generalized surface or nuclear energy in a model that accounts for the effect of infinite range of nuclear force. The quantity f is the proton form factor correction to Coulomb energy. Relative Coulomb energy B3 is used in the first approximate. All parameters are chosen from Ref. 26.

The pairing correction energy (E_pair in MeV) is calculated by a simple relation as follows:

$E_{pair}=\{\begin{array}{l}0\text{for}{Z}_{i}and{N}_i\text{even}\hfill \\ 12/\sqrt{Z_i}\text{for}{Z}_i\text{even}\text{and}{N}_i\text{odd}\hfill \\ 12/\sqrt{N_i}\text{for}{N}_i\text{even}\text{and}{Z}_i\text{odd}\hfill \\ 24/\sqrt{A_i}\text{for}{Z}_i\text{and}{N}_i\text{odd}.\hfill \end{array}(13)$

The shell correction energy is calculated according to Ref. 13. The systematic formalism of this method is used to calculate the shell correction energy of fragments. Also, the results of this method agree with the results of the Strutinsky model [28].

2.3 Temperature

The temperature-dependent relation for pairing energy is given by Ref. 29.

$E_{pair}\left(T\right)=\frac{E_{pair}\left(0\right)}{1+e^{\left(\frac{T}{0.03}-\frac{7.37}{0.03\sqrt{A}}\right)}}.(14)$

Temperature dependence of shell energy is applied as [29] follows:

$E_{shell}\left(T\right)=E_{shell}\left(0\right)\left(\frac{\left(e^{-E_1{E}_0}-1\right)}{\left(e^{\left(E^{\text{*}}-E_1\right)E_0}-1\right)}+\frac{{\text{TS}}_0\left(\tau \text{cosh}\left(\tau \right)-1\right)}{\text{sinh}\left(\tau \right)}\right),(15)$

where $E_{shell}\left(T\right)$ is the shell correction energy for each excitation energy and $E_{shell}\left(0\right)$ is the zero excitation energy. Also, S₀ = 2.5 MeV⁻¹, $\tau =2{\pi }^2{A}^{1/3}T/41$, E₁ = −18.54 MeV, and E₀ = 42.28 MeV, and E is energy corresponding to temperature.

Temperature (T) usually calculate with Fermi gas relation, but we used the generalized superfluid model as follows:

$T=\sqrt{\left(E^{\text{*}}+E_{pair}-E_{con}\right)/a},(16)$

where E is the excitation energy and E_con is the condensation energy for the even–even nucleus. We have

$E_{con}=\frac{3a}{2{\pi }^2}{E}_{pair,0^2}^2,(17)$

where $E_{pair,0}=12/\sqrt{A}$ and the level density parameters are given by

$a=\tilde{a}\left(1+E_{shell}\left(1-{\text{e}}^{-0.05E^{\text{*}}}\right)/E^{\text{*}}\right),(18)$

where

$\tilde{a}=0.0984A-0.253A^{2/3}+2.07\sqrt[3]{A}-\mathrm{4.04.}(19)$

3 Results and Discussion

Similar to Refs. 30 and 31, the atomic number of fission fragments are obtained with the unchanged charge density distribution as [32] follows:

$Z_{UCD}=\frac{Z_{\text{cn}}\left(A_i+\nu \right)}{A_{\text{cn}}},(20)$

where Z_cn is the atomic number of compound nucleus, A_cn is the mass number of compound nucleus, and ν is post-scission neutrons and is defined by Refs. 33 and 34.

Pasca [9] added the height of the fission barrier to the potential energy at the scission point to calculate the collective temperature. In this study, the height of the fission barrier is chosen as the excitation energy for spontaneous fission. Thus, for photofission, the height of the fission barrier is added to the initial excitation energy (the bremsstrahlung endpoint energy) (i.e., 6+E MeV for ²³⁸U). Thus, E^* in Eqs 15, 16 is the height of the fission barrier of the target nucleus plus the initial excitation energies.

On the other hand, the collective temperature is not dependent on the excitation energy in this study such as Ref. 2. Therefore, here, the excitation energy only affects the total potential energy of the fissioning system. These calculations indicate that the excitation energy has little change in the values of fission fragment mass distributions. For example, by increasing the excitation energy by 20 MeV, the mass distribution changes by less than 1 percent. Therefore, this small effect indicates that the major effect of the excitation energy in mass yield values is due to the change in collective temperature. Of course, the excitation energies are divided between the fragments proportional to their masses.

Equation 2 is an exponential function that is strongly upward-sloping, and the collective temperature is usually taken to be constant in Refs. 2 and 7 (the change in collective temperature is discussed later). Therefore, the values of deformation parameters provide the minimal value of the total potential energy. On the other hand, the minimal values of the total potential energy of the fissioning system at the scission point correspond to the minimal values of the deformation parameters. Therefore, only the maximum values of deformation parameters could be considered in Eq. 2 as follows:

$P_i\approx e^{-\frac{V_{Interac}\left(N_i,Z_i,s,{\beta }_{m,1},{\beta }_{m,2}\right)+V_{Mac}\left(N_i,Z_i,T,{\beta }_{m,1},{\beta }_{m,2}\right)+V_{Mic}\left(N_i,Z_i,T,{\beta }_{m,1},{\beta }_{m,2}\right)}{T_{coll}}}(21)$

Here, ${\beta }_{m,i}$ are the values of the deformation parameter of each fragment associated with the minimum total energy at the scission point. Also, according to Ref. 2, the distance of two fragments, s, is 1.44 fm. The pairing correction energy is not included in the calculations.

3.1 Investigation on Fission of ²³⁸U

The mass yield for spontaneous fission of ²³⁸U is presented in Figure 1. In the left side of Figure 1, the results of systematic calculation are presented for T_coll = 1 MeV, and the results of systematic calculation are presented for T_coll = 2 MeV in the right side of this figure. The deformation parameters have been changed to fit the calculated results and the experimental values, so when T_coll = 1 MeV, we have ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.4\hfill & \text{for }{A}_L<91\hfill \\ 0.42\hfill & \text{for }91\le A_L\le 96\hfill \\ 0.47\hfill & \text{for }96\le A_L\le 98\hfill \\ 0.53\hfill & \text{for }{A}_L>98\hfill \end{array}.(22)$

It can be seen that ${\beta }_{m,L}$ values increase with increasing mass numbers of fission fragments. This indicates that the probability of the formation of symmetric fragments is reduced, which shows the dominance of the asymmetric fission mode. When T_coll = 2 MeV, the deformation parameters are obtained as ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.4\hfill & \text{for }{A}_L<91\hfill \\ 0.38\hfill & \text{for }91\le A_L\le 97\hfill \\ 0.55\hfill & \text{for }96\le A_L\le 102\hfill \\ 0.43\hfill & \text{for }{A}_L>102\hfill \end{array},(23)$

also, for $A_L=96$, ${\beta }_{m,L}$ equals to 0.43. However, ${\beta }_{m,L}$ values increase significantly for mass numbers between 102 and 96. This increase could be due to the magic neutron number (N_L = 50) of fission fragments with the mass number $A_L=96$. Figure 1 shows that the calculated results for mass yield are in good agreement with the experimental data for two collective temperatures. But, as the collective temperature increases, the order of ${\beta }_{m,L}$ values is disturbed for spontaneous fission of ²³⁸U. This indicates that $T_{coll}=1$ is better for spontaneous fission of ²³⁸U.

FIGURE 1

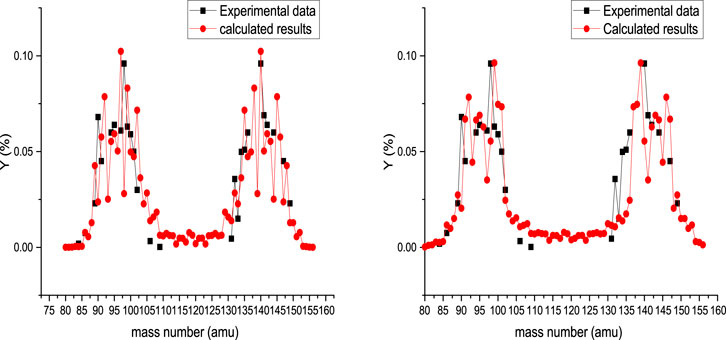
FIGURE 1. Calculated mass yield for spontaneous fission of ²³⁸U accompanied by experimental data [35]. In the left and right sides are presented the calculated results obtained for T_coll = 1 MeV and T_coll = 2 MeV, respectively.

Also, the obtained ${\beta }_{m,L}$ values, especially for fragments with a mass number around 98, are close to the results of Ref. 13, which used Eq. 2 and close to the results of Ref. 38 obtained from the study of the total kinetic energy. However, in the recent reference, the values of deformation parameters are the same for the two complementary fission fragments, which caused differences in the β values for some fragments.

The photofission mass yield of ²³⁸U is presented in Figure 2 at 8 MeV bremsstrahlung endpoint energy. In the left side of Figure 2, the results of systematic calculation are presented for T_coll = 1 MeV, and the results of systematic calculation are presented for T_coll = 2 MeV in the right side of this figure. The changing of deformation parameters are the same as the deformation parameters for spontaneous fission of ²³⁸U for T_coll = 1 MeV. This shows that with increasing excitation energy up to 8 MeV, the behavior of photofission and spontaneous fission is the same. But for T_coll = 2 MeV, the deformation parameters are obtained as ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.4\hfill & \text{for }{A}_L<91\hfill \\ 0.41\hfill & \text{for }91\le A_L\le 95\hfill \\ 0.50\hfill & \text{for }98\le A_L\le 102\hfill \\ 0.58\hfill & \text{for }{A}_L>102\hfill \end{array},(24)$

also, when $A_L=96$ and 97, ${\beta }_{m,L}$ equals to 0.44. It can be seen that ${\beta }_{m,L}$ values increase with increasing mass number of fission fragments. Also, the light fission fragments around mass number 96 are zirconium, which has the semi-magic number in the proton number (Z_L = 40). Figure 2 shows that the mass yield has a good agreement to the experimental data for T_coll = 2 MeV.

FIGURE 2

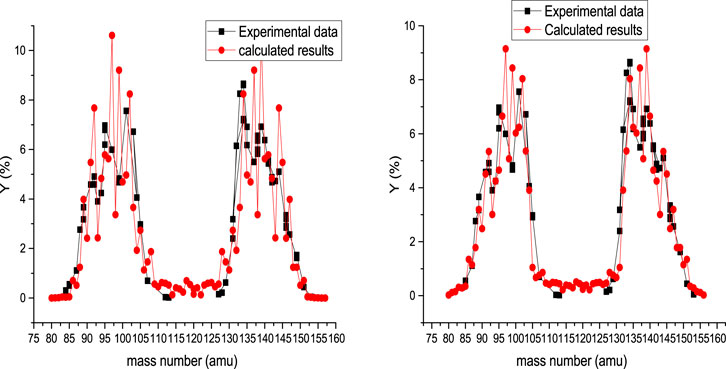
FIGURE 2. Calculated mass yield for photofission of ²³⁸U at 8 MeV bremsstrahlung endpoint energy, accompanied by experimental data [36]. In the left and right sides are presented the calculated results obtained for T_coll = 1 MeV and T_coll = 2 MeV, respectively.

In Figure 3, the photofission mass yield of ²³⁸U is presented at 67.8 MeV bremsstrahlung endpoint energy. In the left and right sides of this figure, the calculated results, along with the experimental data, are presented for T_coll = 1 MeV and T_coll = 2 MeV, respectively. When the deformation parameters are obtained by fitting the calculated results to the experimental values for T_coll = 1 MeV, we have ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.33\hfill & \text{for }{A}_L<90\hfill \\ 0.37\hfill & \text{for }90\le A_L\le 98\hfill \\ 0.5\hfill & \text{for }{A}_L>98\hfill \end{array}.(25)$

Also, for $A_L=95$, ${\beta }_{m,L}$ equals to 0.4; for $A_L=96$ and 97, ${\beta }_{m,L}$ equals to 0.45; for $A_L=99$, ${\beta }_{m,L}$ equals to 0.53; and for $A_L=102$, ${\beta }_{m,L}$ equals to 0.52. It can be seen again that ${\beta }_{m,L}$ values increase with increasing mass number of fission fragments. But the increase in ${\beta }_{m,L}$ values is significant only for fragments with a mass number greater than 98. For T_coll = 2 MeV, the deformation parameters are obtained as ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.33\hfill & \text{for }{A}_L<90\hfill \\ 0.35\hfill & \text{for }90\le A_L\le 98\hfill \\ 0.48\hfill & \text{for }98\le A_L\le 102\hfill \\ 0.5\hfill & \text{for }{A}_L>102\hfill \end{array}.(26)$

Also, for $A_L=95$, ${\beta }_{m,L}$ equals to 0.39; for $A_L=96$ and $A_L=97$, ${\beta }_{m,L}$ equals to 0.41 and 0.45; for $A_L=99$, ${\beta }_{m,L}$ equals to 0.50, and for $A_L=102$, ${\beta }_{m,L}$ equals to 0.52. ${\beta }_{m,L}$ values increase with increasing mass number of fission fragments similar other cases. Also, For this excitation energy, the fission fragments with mass numbers between A_L = 96 and 102 have the semi-magic number protons or magic number neutrons (Z_L = 50 and N_H = 82), which make the large ${\beta }_{m,L}$ values in this region.

FIGURE 3

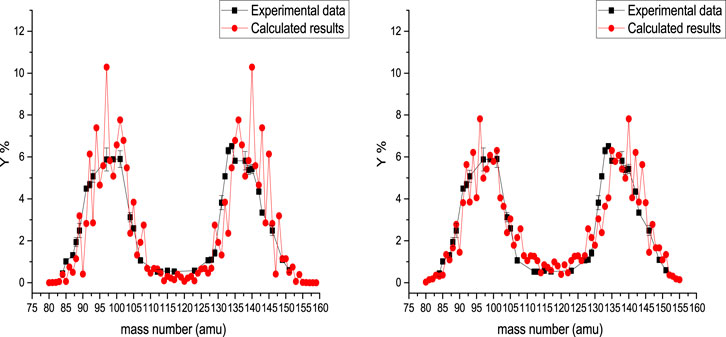
FIGURE 3. Calculated mass yield for photofission of ²³⁸U at 67.8 MeV bremsstrahlung endpoint energy, accompanied by experimental data [37]. In the left and right sides are presented the calculated results obtained for T_coll = 1 MeV and T_coll = 2 MeV, respectively.

As the excitation energy increases from 8 to 68 MeV, ${\beta }_{m,L}$ decrease and the number of cases where the value of the deformation parameter is expressed separately increases (special in Eqs 24 and 26). This indicates the increase in excitation energy causes a chaos. On the other hand, ${\beta }_{m,L}$ values decrease with increasing excitation energy. This indicates that there is no need to deform the fragments much for fission with increasing excitation energy.

But why does the fission fragment with the mass number A_L = 102, corresponding to the heavy fission fragment ${135}_{53}I$ with the magic number 82, have a large ${\beta }_{m,L}$ value at 68 MeV excitation energy but this fragment does not have this large value at 8 MeV excitation energy? This may be because the magic fragment with mass number A_H = 132 is much heavier than the magic fragment with the mass number A_L = 96, so stimulating a heavier nucleus needs more excitation energy.

3.2 Investigation on the Plutonium Isotopes

The photofission mass yield of ²⁴⁰Pu is presented in Figure 4 at 10 MeV bremsstrahlung endpoint energy. In the left side of Figure 4, the results of systematic calculation are presented for T_coll = 1 MeV, and the results of systematic calculation are presented for T_coll = 2 MeV in the right side of this figure. The deformation parameters of fission fragments are obtained by fitting the calculated results with the experimental values for T_coll = 1 MeV, so we have ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.37\hfill & \text{for }{A}_L<88\hfill \\ 0.41\hfill & \text{for }88\le A_L\le 97\hfill \\ 0.45\hfill & \text{for }97\le A_L\le 101\hfill \\ 0.5\hfill & \text{for }{A}_L>101\hfill \end{array}.(27)$

Also, for $A_L=99$, ${\beta }_{m,L}$ equals to 0.5; for $A_L=101$, ${\beta }_{m,L}$ equals to 0.55; for $A_L=102$ and 104, ${\beta }_{m,L}$ equals to 0.53; and for $A_L=107$, ${\beta }_{m,L}$ equals to 0.52. These ${\beta }_{m,L}$ values, especially for fragments with a mass number greater than 101, are similar to results of Ref. 38 in which the total kinetic energy of actinide were studied within statistical scission point model.

FIGURE 4

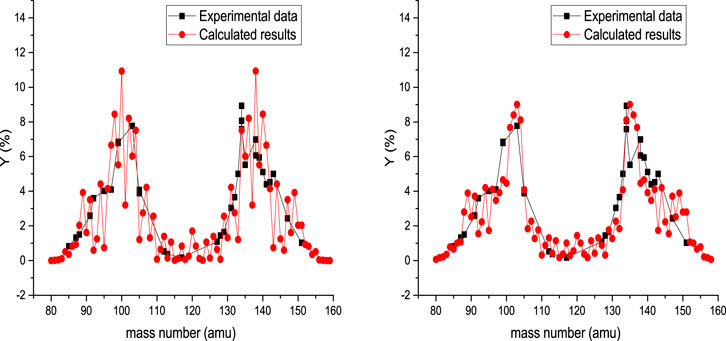
FIGURE 4. Calculated mass yield for photofission of ²⁴⁰Pu at 10 MeV bremsstrahlung endpoint energy, accompanied by experimental data [39]. In the left and right sides are presented the calculated results obtained for T_coll = 1 MeV and T_coll = 2 MeV, respectively.

For T_coll = 2 MeV, the deformation parameters are obtained as ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.37\hfill & \text{for }{A}_L<88\hfill \\ 0.38\hfill & \text{for }88\le A_L\le 97\hfill \\ 0.44\hfill & \text{for }97\le A_L\le 101\hfill \\ 0.5\hfill & \text{for }{A}_L>101\hfill \end{array}.(28)$

Also, for $A_L=99$, ${\beta }_{m,L}$ equals to 0.47; for $A_L=101$, ${\beta }_{m,L}$ equals to 0.48; for $A_L=102$ and $A_L=104$, ${\beta }_{m,L}$ equals to 0.48; and for $A_L=107$, ${\beta }_{m,L}$ equals to 0.52. It is seen that the heavy fission fragments with mass numbers around 102 have a magic neutron number (N_H = 82), which makes large changes in ${\beta }_{m,L}$ values. Also, the heavy fission fragments with mass numbers around 106 have a magic neutron number (${134}_{52}Te$), which make the large change in ${\beta }_{m,L}$ values.

The photofission mass yield of ²³⁹Pu is presented in Figure 5 at 28 MeV bremsstrahlung endpoint energy. In the left side of Figure 5, the results of systematic calculation are presented for T_coll = 1 MeV, and the results of systematic calculation are presented for T_coll = 2 MeV in the right side of this figure. The deformation parameters of fission fragments are obtained by fitting the calculated results with the experimental values for T_coll = 1 MeV, so we have ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.25\hfill & \text{for }{A}_L<86\hfill \\ 0.32\hfill & \text{for }86\le A_L\le 98\hfill \\ 0.42\hfill & \text{for }98\le A_L\le 110\hfill \\ 0.4\hfill & \text{for }{A}_L>110\hfill \end{array}.(29)$

Also, for $A_L=94$, $A_L=96$, and $A_L=97$, ${\beta }_{m,L}$ equals to 0.36; for $A_L=99$, ${\beta }_{m,L}$ equals to 0.47; for $A_L=101$, ${\beta }_{m,L}$ equals to 0.45; for $A_L=103$, ${\beta }_{m,L}$ equals to 0.43; and for $A_L=104$, ${\beta }_{m,L}$ equals to 0.46. ${\beta }_{m,L}$ values do not increase with increasing mass numbers of fission fragments, so T_coll = 1 MeV may not be suitable for this excitation energy.

FIGURE 5

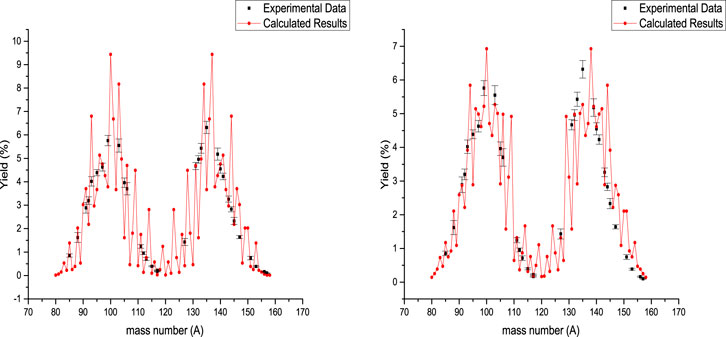
FIGURE 5. Calculated mass yield for photofission of ²³⁹Pu at 28 MeV bremsstrahlung endpoint energy, accompanied by experimental data [40]. In the left and right sides are presented the calculated results obtained for T_coll = 1 MeV and T_coll = 2 MeV, respectively.

For T_coll = 2 MeV, the deformation parameters are obtained as ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.25\hfill & \text{for }{A}_L<86\hfill \\ 0.30\hfill & \text{for }86\le A_L\le 98\hfill \\ 0.38\hfill & \text{for }98\le A_L\le 110\hfill \\ 0.4\hfill & \text{for }{A}_L>110\hfill \end{array}.(30)$

Also, for $A_L=94$, ${\beta }_{m,L}$ equals to 0.36; for $A_L=96$ and $A_L=97$, ${\beta }_{m,L}$ equals to 0.32; for $A_L=99$, $A_L=101$, and $A_L=103$, ${\beta }_{m,L}$ equal to 0.42; and for $A_L=104$, ${\beta }_{m,L}$ equals to 0.40.

Also, the ${\beta }_{m,L}$ values in plutonium-239 fission are lower than the ${\beta }_{m,L}$ values in plutonium-240 fission. This decrease can be due to both an increase in excitation energy and the odd effect of the plutonium-239 nucleus. Of course, since the compound nucleus does not absorb neutrons in the photofission process, the number of neutrons remains odd; it shows that the fission of nucleus with the odd number of neutrons can be easier than the fission of an even nucleus. To examine the odd–even effect, we investigate the neptunium nucleus in the next section.

3.3 Investigation on Neptunium Isotopes

The photofission mass yield of ²³⁷Np is presented in Figure 6 at 28 MeV bremsstrahlung endpoint energy. In the left side of Figure 6, the results of systematic calculation are presented for T_coll = 1 MeV, and the results of systematic calculation are presented for T_coll = 2 MeV in the right side of this figure. The deformation parameters of fission fragments are obtained by fitting the calculated results with the experimental values for T_coll = 1 MeV, so we have ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.3\hfill & \text{for }{A}_L<88\hfill \\ 0.39\hfill & \text{for }88\le A_L\le 96\hfill \\ 0.45\hfill & \text{for }96\le A_L\le 101\hfill \\ 0.45\hfill & \text{for }{A}_L>101\hfill \end{array}.(31)$

It can be seen that ${\beta }_{m,L}$ values increase with increasing mass numbers of fission fragments like in other studies [42]. As can be seen, the ${\beta }_{m,L}$ values for photofission of ²³⁷Np are higher than the ${\beta }_{m,L}$ values for photofission of ²³⁹Pu, while the excitation energy of both is equal. This indicates that the odd neutron number can play a major role in reducing the ${\beta }_{m,L}$ values. Also, the odd mass number reduces the deformation parameters.

FIGURE 6

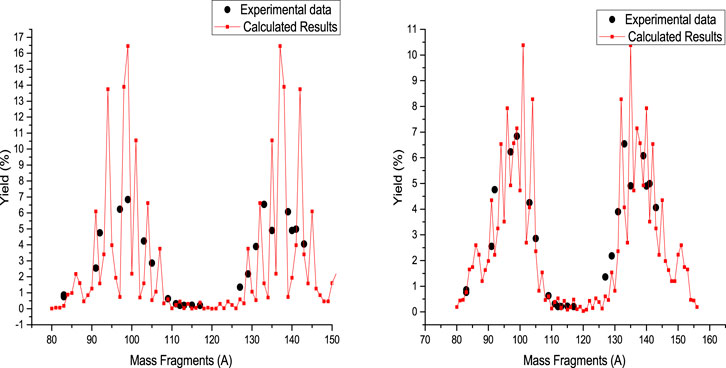
FIGURE 6. Calculated mass yield for photofission of ²³⁷Np at 25 MeV bremsstrahlung endpoint energy, accompanied by experimental data [41]. In the left and right sides are presented the calculated results obtained for T_coll = 1 MeV and T_coll = 2 MeV, respectively.

For T_coll = 2 MeV, the deformation parameters are obtained as ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.3\hfill & \text{for }{A}_L<88\hfill \\ 0.39\hfill & \text{for }88\le A_L\le 96\hfill \\ 0.42\hfill & \text{for }96\le A_L\le 101\hfill \\ 0.49\hfill & \text{for }{A}_L>101\hfill \end{array},(32)$

and for $A_L=98$ and $A_L=99$, ${\beta }_{m,L}$ equals to 0.45. ${\beta }_{m,L}$ values for symmetric fragments are higher than those values for the previous case, and these values are slightly lower for fragments with mass numbers between 96 and 101. These changes and the closeness of the calculated results to the experimental results indicate that the choice of collective temperature as T_coll = 2 MeV is more appropriate than T_coll = 2 MeV.

The photofission mass yield of ²³⁷Np is presented in Figure 7 at 9.5 MeV bremsstrahlung endpoint energy. In the left side of Figure 7, the results of systematic calculation are presented for T_coll = 1 MeV, and the results of systematic calculation are presented for T_coll = 2 MeV in the right side of this figure. The deformation parameters of fission fragments are obtained by fitting the calculated results with the experimental values for T_coll = 1 MeV, so we have ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.3\hfill & \text{for }{A}_L<88\hfill \\ 0.39\hfill & \text{for }88\le A_L\le 96\hfill \\ 0.45\hfill & \text{for }{A}_L>96\hfill \end{array}.(33)$

Unlike plutonium fission, ${\beta }_{m,L}$ values do not change much with decreasing excitation energy. This confirms that the ${\beta }_{m,L}$ values decrease in plutonium-239 fission is related to the odd neutron number. For T_coll = 2 MeV, the deformation parameter is chosen as ${\beta }_{m,H}=0.5$ and

${\beta }_{m,L}=\{\begin{array}{ll}0.38\hfill & \text{for }{A}_L<88\hfill \\ 0.39\hfill & \text{for }88\le A_L\le 98\hfill \\ 0.45\hfill & \text{for }{A}_L>98\hfill \end{array}.(34)$

The calculated results for the neptunium even–odd nucleus are in good agreement with the experimental values, and the deformation parameters have the least variations. Also, the deformation parameters reduce oscillations when T_coll = 2 MeV. These conditions are true for all actinides, so it is best to use T_coll = 2 MeV for intermediate energy of photofission.

FIGURE 7

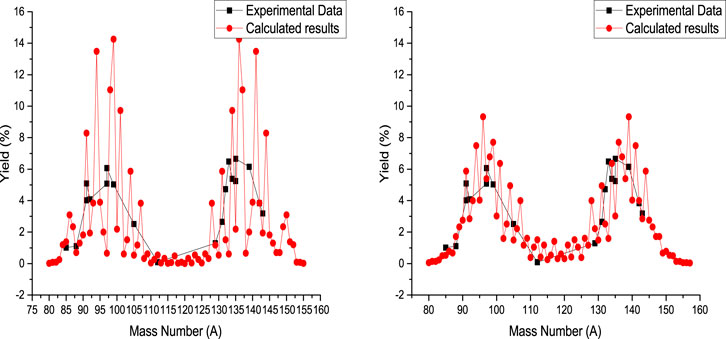
FIGURE 7. Calculated mass yield for photofission of ²³⁷Np at 9.5 MeV bremsstrahlung endpoint energy, accompanied by experimental data [43]. In the left and right sides are presented the calculated results obtained for T_coll = 1 MeV and T_coll = 2 MeV, respectively.

Therefore, by using the fragment temperature, instead of collective temperature in Eq. 2, the values of mass distribution are better obtained like in Ref. 13. Unlike the Gaussian models to calculate mass yields [5], where the excitation energy (bremsstrahlung endpoint energy) is used to evaluate mass distribution, in the statistical scission point model, the Q-factor energy and the height of the fission barrier are better added to the initial excitation energy.

Naik and Pomme [39, 44, 45] showed that the fission fragment mass yields around mass numbers 94–95, 99–100, and 104–105 are higher than other fission fragment mass yields for photofission of ²³⁸U and ²⁴⁰Pu in the low-energy region. Therefore, our calculated results confirm the changes in the mass yields of experimental data in some fragments. But these changes are seen for all nuclei studied in this systematic study.

4 Summary

The mass yield for spontaneous fission and photofission of actinides are calculated within a systematic scission point model. The calculated results are compared with the available experimental data. There is good agreement with the experimental data, especially for a collective temperature of 2 MeV.

For intermediate excitation energy, the calculated results with T_coll = 2 MeV have better agreement with the experimental data, so it is better to add initial excitation energy (E) with the height of the fission barrier (and other energies such as Q-factor) to evaluate the mass yields. But for spontaneous fission, it is better not to change the excitation energy because the calculated results with T_coll = 1 are in good agreement with the experimental data. Therefore, by using the fragment temperature, instead of collective temperature and adding other energies to initial excitation energy, the values of mass yield are closer to the experimental data.

In this study, the collective temperature is constant and also the change in mass distribution values was small with the change in excitation energy; therefore, the major effect of excitation energy (in other studies) is due to change in collective temperature.

The deformation parameters of fission fragments are presented by fitting the calculated results to the experimental data. There are close to the values in other studies obtained by the total kinetic energy and the integral form. The deformation values increase with increasing mass numbers of fission fragments (symmetric fragments) for all fissioning systems, which is due to the dominance of the asymmetric fission mode for photofission of actinides. On the other hand, the deformation parameter values decrease with increasing excitation energy. This increase in excitation energy also causes the deformation parameter changes to be irregular. Also, these parameters decrease for odd mass number fissioning systems. Also, the fissioning systems with odd neutron numbers have less deformation parameter values than the fissioning systems with even neutron numbers. The mass yield values for photofission of other actinides can be predicted by this method.

It is seen that the higher values in mass numbers of fission fragments around 104–105 and 99–100 in experimental data for photofission are related to the potential energy of the fissioning system at the scission point, and it can be seen for all photofission of nuclei actinide. But for some nuclei, these peaks are so small that they are not seen in the measurements.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Fong P. Statistical theory of nuclear fission: asymmetric fission. Phys. Rev (1956) 102:434. doi:10.1103/physrev.102.434

CrossRef Full Text | Google Scholar

2. Wilkins BD, Steinberg EP, Chasman RR. Scission-point model of nuclear fission based on deformed-shell effects. Phys Rev C (1976) 14:1832. doi:10.1103/physrevc.14.1832

CrossRef Full Text | Google Scholar

3. Brosa U, Grossmann S, Müller A. Nuclear scission. Phys Rep (1990) 197(4):167–262. doi:10.1016/0370-1573(90)90114-h

CrossRef Full Text | Google Scholar

4. Denisov VY, Margitych TO, Sedykh IY. Mass yields and kinetic energy of fragments from fission of highly-excited nuclei with A ≲ 220. Nucl Phys (2017) 958:101–128. doi:10.1016/j.nuclphysa.2016.11.007

CrossRef Full Text | Google Scholar

5. Mehdipour Kaldiani P. The perusal of photofission fragments mass yields for actinide isotopes by systematics neutron models. Phys Atom Nucl (2019) 82(5):450–461. doi:10.1134/s1063778819050089

CrossRef Full Text | Google Scholar

6. Andreev AV, Adamian GG, Antonenko NV. Mass distributions for induced fission of different Hg isotopes. Phys Rev C (2012) 86:044315. doi:10.1103/physrevc.86.044315

CrossRef Full Text | Google Scholar

7. Pasca H, Andreev AV, Adamian GG, Antonenko NV. Extraction of potential energy in charge asymmetry coordinate from experimental fission data. Eur Phys J A (2016) 52:369. doi:10.1140/epja/i2016-16369-5

CrossRef Full Text | Google Scholar

8. Pasca H, Andreev AV, Adamian GG, Antonenko NV. Physical origin of the transition from symmetric to asymmetric fission fragment charge distribution. Acta Phys Pol Ser B (2017) 48(3):431. doi:10.5506/aphyspolb.48.431

CrossRef Full Text | Google Scholar

9. Pasca H, Andreev AV, Adamian GG, Antonenko NV. Transitions between symmetric and asymmetric modes in the region of heavy actinides. Nucl Phys (2018) 969:226–236. doi:10.1016/j.nuclphysa.2017.10.001

CrossRef Full Text | Google Scholar

10. Lemaître J-F, Dubray N, Hilaire S, Panebianco S, Sida J-L. SPY: a new scission point model based on microscopic ingredients to predict fission fragments properties. EPJ Web Conf (2013) 62:04002. doi:10.1051/epjconf/20136204002

CrossRef Full Text | Google Scholar

11. Lemaître JF, Goriely S, Hilaire S, Sida J-L. Fully microscopic scission-point model to predict fission fragment observables. Phys Rev C (2019) 99:034612. doi:10.1103/physrevc.99.034612

CrossRef Full Text | Google Scholar

12. Karthika C, Balasubramaniam M. Scission point model for the mass distribution of ternary fission. Eur Phys J A (2019) 55:59. doi:10.1140/epja/i2019-12729-y

CrossRef Full Text | Google Scholar

13. Mehdipour Kaldiani P. Mass yield of spontaneous fission of 238 U within the systematic statistical scission-point model. Phys Scripta (2020) 95(7):075306. doi:10.1088/1402-4896/ab93a9

CrossRef Full Text | Google Scholar

14. Randrup J, Möller P. Brownian shape motion on five-dimensional potential-energy surfaces: nuclear fission-fragment mass distributions. Phys Rev Lett (2011) 106:132503. doi:10.1103/physrevlett.106.132503

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Randrup J, Möller P. Energy dependence of fission-fragment mass distributions from strongly damped shape evolution. Phys Rev Lett (2013) 88:064606. doi:10.1103/physrevc.88.064606

CrossRef Full Text | Google Scholar

16. Möller P, Randrup J. Calculated fission-fragment yield systematics in the region 74 ≤ Z ≤94 and 90 ≤ N ≤ 150. Phys Rev C (2015) 91:044316. doi:10.1103/physrevc.91.044316

CrossRef Full Text | Google Scholar

17. Nadtochy PN, Karpov AV, Vanin DV, Adeev GD. Mass-energy distribution of fragments from the fission of excited nuclei within three-dimensional Langevin dynamics. Phys Atom Nucl (2001) 64(5):861–869. doi:10.1134/1.1378876

CrossRef Full Text | Google Scholar

18. Ivanyuk F, Chiba S, Aritomo Y. Scission-point configuration within the two-center shell model shape parameterization. Phys Rev C (2014) 90(5). doi:10.1103/physrevc.90.054607

CrossRef Full Text | Google Scholar

19. Ivanyuk F, Kawano T, Chiba S, Paris MW, Talou P. The scission point configuration of fissioning nuclei. EPJ Web Conf (2016) 122:01002. doi:10.1051/epjconf/201612201002

CrossRef Full Text | Google Scholar

20. Mirea M, Delion DS, Sandulescu A. Microscopic cold fission yields ofCf252. Phys Rev C (2010) 81:044317. doi:10.1103/physrevc.81.044317

CrossRef Full Text | Google Scholar

21. Pomorski K, Nerlo-Pomorska B, Bartel J, Schmitt C. Fission fragment mass and total kinetic energy distributions of spontaneously fissioning plutonium isotopes. EPJ Web Conf (2018) 169:00016. doi:10.1051/epjconf/201816900016

CrossRef Full Text | Google Scholar

22. Goutte H, Casoli P, Berger J-F. Mass and kinetic energy distributions of fission fragments using the time dependent generator coordinate method. Nucl Phys (2004) 734:217. doi:10.1016/j.nuclphysa.2004.01.038

CrossRef Full Text | Google Scholar

23. Blocki J, Świątecki WJ. A generalization of the proximity force theorem. Ann Phys (1981) 132:53–65. doi:10.1016/0003-4916(81)90268-2

CrossRef Full Text | Google Scholar

24. Blocki J, Randrup J, Swiatecki WJ, Tsang CF. Proximity forces. Anna Phys NY (1977) 105:427–462. doi:10.1016/0003-4916(77)90249-4

CrossRef Full Text | Google Scholar

25. Bao X, Zhang H, Royer G, Li J. Spontaneous fission half-lives of heavy and superheavy nuclei within a generalized liquid drop model. Nucl Phys A (2013) 906:1–13. doi:10.1016/j.nuclphysa.2013.03.002

CrossRef Full Text | Google Scholar

26. Moller P, Nix JR, Myers WD, Swiatecki WJ. Nuclear ground-state masses and deformations. At Data Nucl Data Tables (1995) 59:185–381. doi:10.1006/adnd.1995.1002

CrossRef Full Text | Google Scholar

27. Duijvestijn MC, Koning AJ, Hambsch F-J. Mass distributions in nucleon-induced fission at intermediate energies. Phys Rev C (2001) 64:014607. doi:10.1103/physrevc.64.014607

CrossRef Full Text | Google Scholar

28. Strutinsky VM. Shell effects in nuclear masses and deformation energies. Nucl Phys (1967) 95:420. doi:10.1016/0375-9474(67)90510-6

CrossRef Full Text | Google Scholar

29. Ivanyuk FA, Ishizuka C, Usang MD, Chiba S. Temperature dependence of shell corrections. Phys Rev C (2018) 97:054331. doi:10.1103/physrevc.97.054331

CrossRef Full Text | Google Scholar

30. Manailescu C, Tudora A, Hambsch F-J, Morariu C, Oberstedt S. Possible reference method of total excitation energy partition between complementary fission fragments. Nucl Phys (2011) 867(1):12–40. doi:10.1016/j.nuclphysa.2011.08.001

CrossRef Full Text | Google Scholar

31. Morariu C, Tudora A, Hambsch F-J, Oberstedt S, Manailescu C. Modelling of the total excitation energy partition including fragment deformation and excitation energies at scission. J Phys G Nucl Part Phys (2012) 39:055103. doi:10.1088/0954-3899/39/5/055103

CrossRef Full Text | Google Scholar

32. Sugarman N, Turkevich A. Radiochemical studies: the fission product In: CD Coryell, and N Sugarman, editors , Vol. 3. New York: McGraw-Hill (1951). p 1396.

Google Scholar

33. Pahlavani MR, Mehdipour P. Product yields for the photofission of 232Th, 234,238U, 237Np, and 239,240,242Pu actinides at various incident photon energies. Nucl Sci Tech (2018) 29:146. doi:10.1007/s41365-018-0482-1

CrossRef Full Text | Google Scholar

34. Umezawa H, Baba S, Baba H. Systematic behaviour of the most probable charge in the medium-energy fission. Nucl Phys (1971) 160:65. doi:10.1016/0375-9474(70)90174-0

CrossRef Full Text | Google Scholar

35. Swindle DL, Wright RJ, Kuroda PK. Yields of ruthenium isotopes from the spontaneous fission of 238U. J Inorg Nucl Chem (1971) 33:876–879. doi:10.1016/0022-1902(71)80491-8

CrossRef Full Text | Google Scholar

36. Naik H, Shivashankar BS, Raj Prakash HG, Raj D, Sanjeev G, Karunakara N, et al. Measurements of fission yield in 8 MeV bremsstrahlung induced fission of 232Th and 238U. J Radioanal Nucl Chem (2014) 299:127. doi:10.1007/s10967-013-2719-0

CrossRef Full Text | Google Scholar

37. Belyshev SS, Ishkhanov BS, Kuznetsov AA, Stopani KA. Mass yield distributions and fission modes in photofission ofU238below 20 MeV. Phys Rev (2015) 91:034603. doi:10.1103/physrevc.91.034603

CrossRef Full Text | Google Scholar

38. Mehdipour Kaldiani P. Kinetic energy distribution for photofission of light actinides. Phys Rev C (2020) 102:044612. doi:10.1103/physrevc.102.044612

CrossRef Full Text | Google Scholar

39. Naik H, Nimje VT, Raj D, Suryanarayana SV, Goswami A, Singh S, et al. Mass distribution in the bremsstrahlung-induced fission of 232Th, 238U and 240Pu. Nucl Phys (2011) 853:1–25. doi:10.1016/j.nuclphysa.2011.01.009

CrossRef Full Text | Google Scholar

40. Kondratko MY, Mosesov AV, Petrzhak KA. Yields of products of the photofission of239Pu. Sov Atom Energy (1981) 50:41–43. doi:10.1007/BF01141251

CrossRef Full Text | Google Scholar

41. Kondratko MY, Korinets VN, Petrzhak KA, Teodorovich OA. At Energ (1973) 35:211.

Google Scholar

42. Zhao YL, Nishinaka I, Nagame Y, Tanikawa M, Tsukada K, Ichikawa S, et al. Symmetric and asymmetric scission properties: identical shape elongations of fissioning nuclei. Phys Rev Lett (1999) 82:3408–3411. doi:10.1103/physrevlett.82.3408

CrossRef Full Text | Google Scholar

43. Parlag OO. EXFOR experimental nuclear reaction data base; targets: Np-237. In: International conference current problems in nuclear physics atomic energy, Kyiv (2006), p 369, Reactions: (g,f), quantity: FY.

Google Scholar

44. Naik H, Carrel F, Kim GN, Laine F, Sari A, Normand S, et al. Mass yield distributions of fission products from photo-fission of 238U induced by 11.5–17.3 MeV bremsstrahlung. Eur Phys J A (2013) 49:94. doi:10.1140/epja/i2013-13094-7

CrossRef Full Text | Google Scholar

45. Pommé S, Jacobs E, Piessens M, De Frenne D, Persyn K, Govaert K, et al. Fragment characteristics for the photofission of 238U with 6.1-13.1 MeV bremsstrahhmg. Nucl Phys (1994) 572:237. doi:10.1016/0375-9474(94)90174-0

CrossRef Full Text | Google Scholar