3D Human Pose Estimation Based on a Fully Connected Neural Network With Adversarial Learning Prior Knowledge

3D human pose estimation is more and more widely used in the real world, such as sports guidance, limb rehabilitation training, augmented reality, and intelligent security. Most existing human pose estimation methods are designed based on an RGB image obtained by one optical sensor, such as a digital camera. There is some prior knowledge, such as bone proportion and angle limitation of joint hinge motion. However, the existing methods do not consider the correlation between different joints from multi-view images, and most of them adopt fixed spatial prior constraints, resulting in poor generalizations. Therefore, it is essential to build a multi-view image acquisition system using optical sensors and customized algorithms for a 3D reconstruction of the human pose in the image. Inspired by generative adversarial networks (GAN), we used a data-driven method to learn the implicit spatial prior information and classified joints according to the natural connection characteristics. To accelerate the proposed method, we proposed a fully connected network with skip connections and used the SMPL model to make the 3D human body reconstruction. Experimental results showed that compared with other state-of-the-art methods, the joints’ average error of the proposed method was the smallest, which indicated the best performance. Moreover, the running time of the proposed method was 1.3 seconds per frame, which may not meet real-time requirements, but is still much faster than most existing methods.

Introduction

Human pose estimation (HPE) refers to the detection and positioning of the joint points of the people from the given optical sensor (cameras) input via algorithms. Estimating human pose is the key to analyzing human behavior. HPE is the basic research in computer vision, which can be applied to many applications, such as Human-computer interaction, human action recognition [1–4], intelligent security, motion capture, and action detection [5].

3D human pose estimation methods were roughly categorized into two types: 1) predicting the 3D human pose from the RGB image in an end-to-end manner; 2) two-stage methods, in which the 2D human pose was estimated from the RGB image firstly, and then the 3D human pose was predicted based on the results of the 2D human pose.

Rogez et al. [6] presented an end-to-end architecture, named LCR-Net. The network included positioning, classification, and regression. First, the candidate human body regions were obtained by the candidate pose region generator, and the potential poses were located in the candidate regions. Scores of pose proposals were counted by the classifier. Finally, the 3D human poses were obtained by regression. Pavlakos et al. [7] directly regressed the 2D heatmap to 3D space and optimize the network from coarse to fine to obtain a more accurate 3D human pose. Pavlakos et al. [8] used a weaker supervision signal provided by the ordinal depths of human joints. This method could evaluate the image in the wild quantitatively.

Through the depth learning network model, the end-to-end mapping from the RGB images to the 3D joint coordinates was directly established. Although rich information can be obtained from the images, there was no intermediate supervision process, and the model was vulnerable to the background of the images, the lighting, the human dress, and other factors. More and more researchers preferred to use deep neural networks to learn the mapping relationship from 2D joint points to 3D joint points. In the first stage, the positions of 2D human joint points were obtained by 2D human pose detectors [9–11], and then the mapping relationship between 2D and 3D human poses was estimated by regression [12, 13] or model matching. Zhou et al. [14] presented a two-stage cascaded unified deep neural network that predicted 3D pose from the 2D heatmap. They augmented a state-of-the-art 2D pose estimation structure to obtain a 2D heatmap. Tekin et al. [15] proposed novel two-branch architecture with a trainable fusion scheme to fuse the 2D heatmaps information optimally. There was an inverse for the human posture projected from a 2D feature map to 3D. To resolve this problem, Li and Lee et al. [16] proposed a new method to generate multiple feasible hypotheses of 3D posture from 2D input that can choose the best solution from 2D reprojections. Qammaz and Argyros [17] presented MocapNET which offered a conquer-and-divide strategy to get 3D Bio Vision Hierarchical (BVH) [18] format. To tackle 3D human pose estimation, Wang et al. [19] proposed a depth ranking method (DRPose3D) that contains rich 3D information. They estimated 3D pose from 2D joint locations and depth rankings.

In the above algorithms, researchers only focused on the 3D coordinates of joints, which were composed of dots and lines, and showed no details about the human body shape and appearance. Therefore, some researchers proposed a method to predict the 3D human model from 2D images. Sigal et al. [20] predicted the 3D human model by the outline shape of the body in the image and adopted a shape completion and animation of people [21] (SCAPE) to match the outline of the human body in the image. Federica et al. [22] estimated a full 3D mesh model from a single image, called SMPLify. They estimated the 2D body joint locations through the 2D joint point detector Deepcut [23] and then fitted the skinned multi-person linear (SMPL) model [24] to the joint data. Lassner et al. [25] made further improvement on SMPLify and used the random forest method to estimate the 3D pose. Riza et al. [26] created a dense mapping between an image and a surface-based model of the human, called DensePose. They, respectively, designed a fully convolution dense pose regression network and region-based dense pose regression network, and the experimental comparison found that the latter performed better. Yao et al. [27] proposed an end-to-end learning convolutional neural network for directly regressing a 3D human mesh model from an image. Muhammed et al. [28] proposed a novel recurrent neural network with a self-attention mechanism for estimating human posture and shape from the video.

Although the above methods can obtain the 3D human mesh model, none of them can meet the real-time requirements in practical application, the correlation of different joints was not considered, and most of them adopted fixed spatial prior constraints, resulting in a relatively poor generalization of the model.

In the presented method, we used multiple optical sensors to build an image capture system in a fixed scene and used efficient algorithms for 3D human reconstruction, which can be used as the basis for the analysis of the character's movements and the limb rehabilitation training. Inspired by generative adversarial networks, we adopted a data-driven method to learn the implicit prior information of the spatial structure and classify joints according to the natural connection of the human body. The outputs of our model included not only the 3D mesh model of the human but also the 3D coordinates of the joints. Therefore, under the premise of ensuring the accuracy of 3D human body estimation, real-time performance was also a factor that needed to be considered. We specifically designed a fully connected neural network with skip connections to estimate the parameters of the SMPL model. The parameters of proposed network model were much less than other state-of-the-art algorithms.

Methods

Multi-View Image Capture System

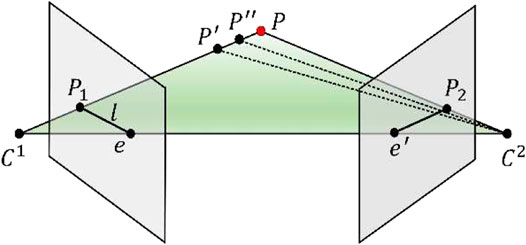
Compared with the 2D plane, the dimension of spatial depth increases in the 3D space. Inspired by epipolar geometry, we note that images from multiple perspectives have some corresponding relations, which can reduce the ambiguity of projection. As shown in Figure 1, $C^1$ and $C^2$ are the centers of the two cameras, $e$ and $e^{\text{'}}$ are the epipoles, and the green plane area represents the epipolar plane. The point $P_{1 }$ means the joint in the image plane (gray box), which is projected into 3D space. The point P exists on a straight line but the specific position is uncertain. The corresponding joint is a point $P_2$ in another view, and the intersection point of two projection lines can determine the position of the point P in the 3D space. Epipolar constraint is a significant property that can be written as

${\mathit{P}}_2^{\mathit{T}}\mathit{E}{\mathit{P}}_1=0,(1)$

where E represents the essential matrix.

FIGURE 1

FIGURE 1. Epipolar geometry.

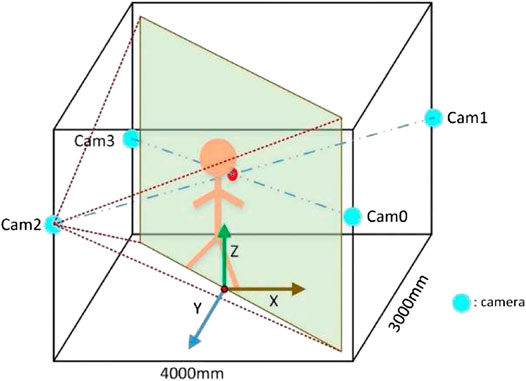
Our method performs information fusion on images collected by four cameras at different positions in a certain activity space, and the implicit camera parameter relationship is learned through a multilayer fully connected neural network. Therefore, our image acquisition system needs four optical sensors to acquire images of the experimenter in this certain activity space. The overall structure of the system is shown in Figure 2. Four optical sensors are used for image acquisition. The computer analyzes the image data through the algorithm we proposed to estimate the 3D human model and the position of 3D joint points.

FIGURE 2

FIGURE 2. Multi-view acquisition system architecture.

The image acquisition instrument selects the industrial vision inspection camera named Basler piA1000. This model of camera uses KAI-1020 CCD photosensitive chip, and the resolution is 1,000 × 1,000, which meets the requirements of experimental data acquisition. The KAI-1020 CCD image sensor is a megapixel interline transfer CCD with an integrated clock driver and associated on-chip double sampling, and the size of the photosensitive chip is 7.4 mm × 7.4 mm. The data transmission uses the GigE interface, and the data is transmitted to the computer directly without a frame grabber. The camera has provided a set of basic preprocessing functions, such as debayering, anti-false color, sharpening enhancement, and denoising. Besides, the preprocessing function can greatly improve the brightness, detail, and sharpness of the image, while reducing noise.

To reduce the ambiguity in predicting the 3D posture of the human from the 2D image, and to be able to effectively take a photo of the whole body of the experimenter, the four cameras are placed on the same level and the same plane. The experimental system has an active area of 4000 mm × 3000 mm, as shown in Figure 3. The plane center of the active area is the origin of the three-dimensional world coordinate system. In this coordinate system, the spatial positions (mm) of cameras were camera 0 (2,000, 1,500, 1,550), camera 1 (2,000, −1,500, 1,550), camera 2 (−2,000, 1,500, 1,550), and camera 3 (−2,000, −1,500, 1,550). In the process of horizontal arrangement and vertical placement, a certain direction allows error ±100 mm and ±50 mm, respectively.

FIGURE 3

FIGURE 3. Position distribution of four cameras.

For the multi-view acquisition system, it is crucial to acquire images synchronously. We set the time and date for multiple cameras using the Precision Time Protocol (PTP). According to time, the image is added timestamp. The operation instructions are sent to multiple cameras to allow each camera to accurately capture images at a predefined time point. Camera calibration is also an essential step in image acquisition using multi-view cameras. The geometric model is established through camera calibration, which is the object mapped from the 3D world to the imaging plane of the camera. In the process of camera calibration, we used the Zhang–Calibration method. Through the chessboard calibration board composed of black and white squares at intervals and Pylon development software, we obtained the relevant parameters.

3D Human Pose Estimation Algorithm

Our goal is to estimate the 3D human pose from the RGB images, where the 3D human pose includes the 3D joint point coordinates and the 3D human mesh model. Our method combines the simplest fully connected neural network with the SMPL model to obtain the 3D human posture, as shown in Figure 4, which consists of three stages:

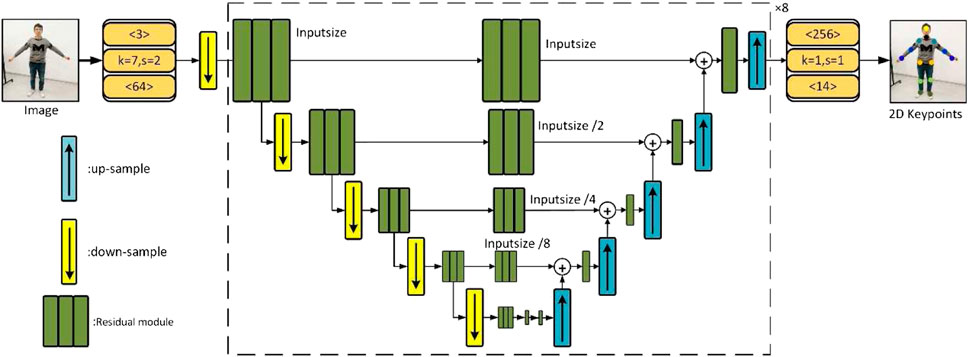
1 The first stage is to estimate the 2D joint coordinates of the human through the convolutional neural network. The images of four cameras with different angles are taken as inputs, and the Hourglass Network proposed by Newell et al. [9] is used to estimate the multi-view 2D pose.

2 In the second stage, we design a multi-layer cascaded fully connected neural network whose input is multi-view 2D joint coordinates and outputs are SMPL model pose and shape parameters. We classify joints according to the natural connection characteristics and design discriminators to learn the implicit spatial prior information.

3 In the third stage, the 3D human mesh model and human posture are calculated by the SMPL model parameters. The 3D human mesh model more specifically and vividly shows the 3D human body.

FIGURE 4

FIGURE 4. 3D human pose estimation structure.

2D Human Pose Detector

At present, most convolutional neural networks adopt deeper layers, such as VGG-16 [29], Resnet-50, or Resnet-101 [30]. The network of different depths can extract different levels of features. The shallow network extracts local features, such as human head feature information or shoulder texture contours, which belong to low-level feature information. The features extracted by the deep network are global features, which are more comprehensive and abstract, such as the relative position relationship between different parts of the human body. It is necessary to fuse the shallow features with deep features at the same time.

The input image size is 256 × 256 × 3. In the convolution operation block (orange box), the number above represents the number of input channels, the number below represents the number of output channels, k denotes the size of the convolution kernel, and s represents the step value. All downsampled blocks in the network use the maximum pooling operation, and upsampling blocks use the nearest neighbor operation. The dotted line part in Figure 5 is the hourglass basic model that can be expanded into cascades of multiple modules. The output of the network is the 2D joint coordinates. Each green rectangle represents the residual module in Figure 5. The residual connection is used to fuse the extracted shallow features with the following deep features of the same size, and more robust joint positions are obtained by using the information of spatial position distribution between joints.

FIGURE 5

FIGURE 5. Overall structure of the 2D stacked hourglass network.

The network module structure is symmetrical and similar to the shape of an hourglass, so it is called the stacked hourglass network. The input images from the four angles of view are used to extract the joint point features through the stacked hourglass network, and the joint point coordinates of the human body are calculated. The above is the main content of the first stage of the algorithm model in this paper. According to the analysis of the Numbers of Hourglass Network Modules section, the number of hourglass basic modules in this paper is finally set to 8.

Fully Connected 3D Parameters Regression Network

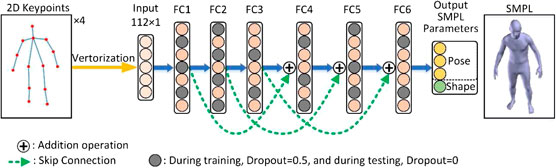
At this stage, our goal is to learn the mapping relationship between the 2D joint coordinates and the pose and shape parameters of the SMPL model. To learn this mapping relationship, this paper specially designs a multi-level fully connected neural network. The input data is the 2D joint coordinates $\text{X}\in {\mathrm{ℝ}}^{4\times 2\times N}$ from the four cameras (in this paper, 14 joint points are taken, so N = 14). The output of the network is the shape and pose parameters of the SMPL mesh model (where shape parameters are $\text{β}\in {\mathrm{ℝ}}^{10},$ and pose parameters are $\text{θ}\in {\mathrm{ℝ}}^{72}).$

We use the SMPL model, introduced by Loper et al. [24], due to their low-dimensional parameter space, compared to voxelized or point cloud representations, which is very suitable for direct network prediction. We describe the SMPL body model and provide the essential notation here. For more details, you can read this paper [24]. The SMPL model is a parametric human body mode, so the parameters of the human are divided into pose parameters $\theta \in {\mathrm{ℝ}}^{72}$ and shape parameters $\beta \in {\mathrm{ℝ}}^{10}.$ The shape parameters are the linear coefficients of a 10-dimension shape space, which reduce to low-dimensional by principal component analysis (PCA). The different shape parameters show the height, weight, body proportion, and body shape of people with various body types. The pose parameters $\theta$ denote the axis-angle representation $({\theta }_i\in {\mathrm{ℝ}}^3)$ of the relative rotation between parts in the 3D space. The pose parameters $(\theta \in {\mathrm{ℝ}}^{23\times 3+3},$ 3 for each of the 23 joints, plus 3 for the global rotation) consist of the root orientation and 23 joints which are defined by a skeleton rig.

The essence is to find a functional mapping relationship $(F:{\mathrm{ℝ}}^{4\times 2\times 14}\mapsto {\mathrm{ℝ}}^{72+20}).$ In this regression calculation, we adopt a simple and efficient fully connected neural network, thus greatly reducing the operation time while ensuring certain joint accuracy. Based on the above considerations, this paper designs a 3D human pose estimation neural network as shown in Figure 6, specifically as shown in Algorithm 1.

FIGURE 6

FIGURE 6. Fully connected 3D parameters regression network.

Algorithm 1 Fully connected neural network regressing SMPL parameters.The fully connected neural network we designed has six layers, including an input layer, four intermediate layers, and an output layer. The selection of the number of layers is explained in detail in the Number of Fully Connected Layers section. According to the characteristics of the fully connected network, the input data needs to be converted into a vector before being sent to the 3D human posture regression network, so the input data is 112 dimensions. The output layer reduces to 82-dimensional SMPL model parameters. The hidden layers (FC2, FC3, FC4, and FC5) use the same number of neurons. The network uses 2,048 neurons for network learning. The selection of this parameter is analyzed in the The Number of Neurons section.At the same time, to achieve the fusion of feature information between different layers, every two layers use skip connection. Skip connection is to merge the input information of the front layer with the output information of the back layer network and send it to the next fully connected layer, as shown in Figure 6. The skip connection is denoted as

$\mathit{H}\left(\mathit{x}\right)=\mathit{F}\left(\mathit{x}\right)+\mathit{x}.(2)$

Even if skip connections are added to the neural network, the efficiency is not affected, because it is very easy to learn the identity function for a fully connected network. The addition of skip connections not only improves the performance of the network but also reduces the possibility of gradient disappearance during training. In our method, because the number of neurons in each hidden layer is the same, direct skip connections can be used, and there is no need to change the dimension of the feature information. The whole network completes the regression from 2D joint to 3D human parameters, and the network is simpler and lighter. Compared with the convolutional neural network, the fully connected neural network can integrate the local features of the previous layer to obtain the global features and obtain more abstract features.

Learnable Adversarial Prior

The human joints have high flexibility, and various actions and postures are produced in 3D space, which brings great challenges to the prediction of the spatial position of joints. However, the skeletal structure of the human has strict symmetry and a certain limited position of the relative hinge motion between the human joints. Therefore, there are some prior constraints between the joints, such as the bone ratio and the limit of the rotation angle between the joint points.

Inspired by the idea of generating adversarial networks (GAN) [31], we adopt a data-driven approach to learn the implicit prior information of the spatial structure of human joint points. Unlike directly providing the model with fixed joint point prior constraints [32–35], our method continues to learnable and flexible, which improves the generalization ability of the model. Besides, we also group the joints of the human according to the correlation between the joints of the human body. For a group of joints with a strong correlation, the same simple discriminant neural network is used.

Due to the relative hinge movement of human joints, it is natural for us to think that the position information of some joints provides important reference information and geometric constraints for the positioning of other joints, such as between the knee and the ankle. However, due to the high flexibility of the human body, not all joints are very close, such as the wrist and ankle. Based on the natural connection between human structures and the correlation between joints [36, 37], we classify the joint points of the human body. The joint points related to this paper are divided into six classes: 1) head and neck; 2) left wrist, left elbow, and left shoulder; 3) right wrist, right elbow, and right shoulder; 4) left knee and left ankle; 5) right knee and right ankle; 6) left hip and right hip.

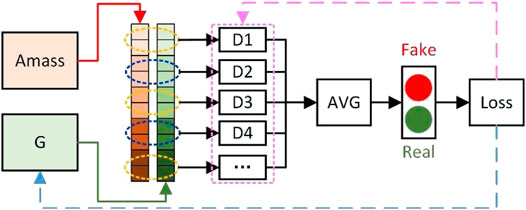
We design a set of human 3D pose discriminators (D1, D2, etc.) to distinguish the pose and shape parameters of the human body predicted by the previously fully connected neural network and determine whether it is a real human body. A learnable discriminator is designed for each group of joints to learn the distribution of normal human joint position data, thus reducing the generation of exaggerated data. To reduce the possibility of abnormal body shape (such as abnormal thick or abnormal small joints), we designed a shape discriminator. At the same time, to learn the joint prior knowledge of all parameters, we also designed a discriminator for all parameters of the human body parameterized by SMPL. Therefore, we design eight discriminators in this article. Finally, the average value of the discriminators is calculated as the final discrimination result.

As shown in Figure 7, the fully connected neural network serves as a generator (G) to generate the pose and shape parameters of the 3D human $G(\theta ,\beta )\in {\mathrm{ℝ}}^{82}.$ Amass is a large-scale human 3D motion dataset. We select the corresponding parameters in the Amass dataset [38] as the real data $R(\theta ,\beta )\in {\mathrm{ℝ}}^{82}.$ These two sets of data are fed into discriminators (D1, D2, etc.) to judge whether the SMPL parameters generated by the fully connected neural network conform to the real human body parameter data distribution. Through adversarial training, we learn the implicit prior knowledge of the spatial structure of key human nodes, so that the results generated by the fully connected network are more in line with the shape of the real human body.

FIGURE 7

FIGURE 7. Prior knowledge network for adversarial learning in groups.

Considering that the task of the discriminator is a simple binary classification, our discriminators (D) also adopt a simple fully connected neural network. Since the number of joints in each group is different, the dimensions of the input layer of each discriminator are different, and the output layer is the result of judging whether the input parameters conform to the distribution of real human body data. The middle two hidden layers of the network use 1,024 neurons for training to learn the real distribution of joint rotation vectors in the same group.

Experiments

Experimental Equipment

The training and testing of the experimental model in this article are completed on the NVIDIA GeForce RTX 2070, with the operating system of Linux and the CPU model of Intel Core i5-7500 CPU @3.40 GHz.

Implementation Details

In the stacked hourglass network for detecting the 2D joint coordinates, the number of hourglass modules was 8, the learning rate was set to 1 × 10⁻⁴, and the batch-size was set to 16, and the network had undergone 50,000 iterative training processes. The regressed network learned the mapping relationship between the 2D joint coordinates and the parameters of the SMPL model. The Adam optimizer was used, the learning rate was set to 0.001, the exponential decay optimization method was used, and the batch size was set to 64, with 250 epochs.

Experiment on 3D Pose of Human3.6M

To compare with other state-of-the-art human pose estimation methods, we conduct experimental evaluations of the proposed method on the public 3D human pose estimation dataset Human 3.6M [39], which consists of 3.6 million images and collects 15 daily activities performed by 11 experimenters under four camera views. To facilitate the evaluation and recording of the experimental results, each action in the dataset was marked with abbreviations, for example, Directions as Direc, Discussion as Disc, Eating as Eat, Greeting as Greet, and so on.

We follow the standard protocols to evaluate our approach. Images of subjects S1, S5, S6, and S7 are used for model training, and S9 and S11 are used for testing. Protocol #1 is the Mean Per Joint Position Error (MPJPE, millimeter) between the ground-truth and the prediction. In some works, the predicted 3D pose is firstly aligned with a rigid transformation using Procrustes Analysis [40] and then compute the Mean Per Joint Position Error (PA-MPJPE), which is called Protocol #2. The MPJPE is denoted as

$MPJPE=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{H}_{pre}\left(i\right)-H_{gt}\left(i\right),(3)$

where N represents the number of joints of the human, $H_{pre}\left(i\right)$ represents the predicted position at the ith joint point, and similarly $H_{gt}\left(i\right)$ represents the ground-truth of the ith joint point.

We compared the results with those achieved in the past three years and conducted quantitative comparisons of the two standard protocols in Tables 1 and 2, respectively. The best score is marked in bold. We performed three sets of tests on the number of different cameras. V1, V2, and V4 represent images from 1, 2, and 4 viewing angles, respectively. The results showed that our method outperforms other methods in all evaluation protocols.

TABLE 1

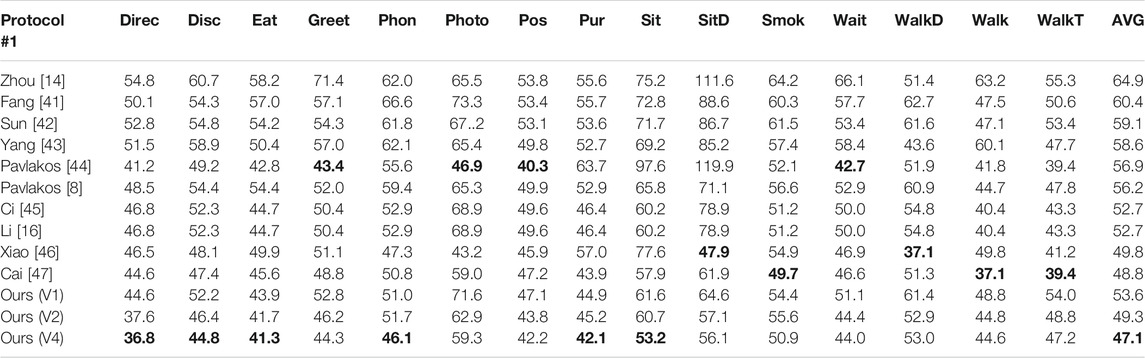
TABLE 1. Comparative results of MPJPE for predicting 3D joints under Protocol #1. The best score is marked in bold.

TABLE 2

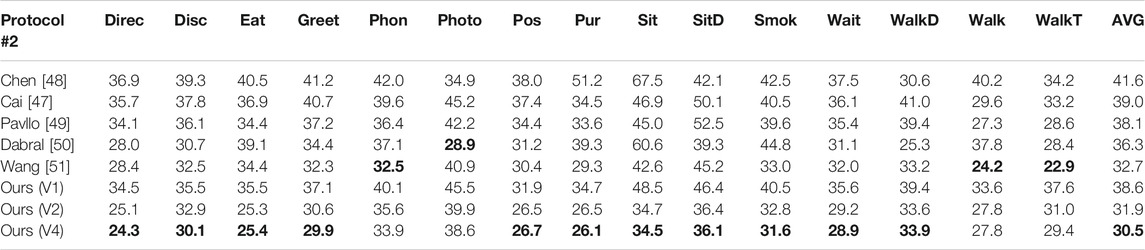
TABLE 2. Results showing the PA-MPJPE on Human3.6M under Protocol #2. The best score is marked in bold.

From the experimental results in Tables 1 and 2, it can be seen that the overall ranking of this method was the first, and all the sub-items were in the top three, and the overall error calculated by the model was small. The method proposed by Cai et al. [47] used the spatial-temporal information to obtain the spatial prior knowledge between joints, and the effect was superior to other algorithms. The method we proposed was to group the joints with strong correlation, and the designed antagonistic prior knowledge module was used for each group of joints to learn the spatial prior knowledge between joint points, thus reducing the generation of exaggerated data. The effect was better, MPJPE was reduced from 48.8 to 47.1 mm, and PA-MPJPE was reduced by 8.5 mm.

For the problem of depth ambiguity, Li et al. [16] introduced the mixture density model into 3D human pose estimation to solve the problem of projecting multiple feasible solutions. We used images from multiple perspectives as input to solve the multi-solution problem and reduce the ambiguity of projection from 2D to 3D. The experimental analysis was performed with images from 1, 2, and 4 viewing angles as input (V1, V2, and V4). In Tables 1 and 2, MPJPE and PA-MPJPE were reduced from 53.6 to 47.1 mm and from 38.6 to 30.5 mm, respectively.

Figure 8 showed the changing process of MPJPE in our training process by using images with different visual angles as input. The horizontal axis represented the number of training epochs, and the vertical axis represented MPJPE. We discovered that, with the increase in the number of input views, our method worked better. This was because the image information from multiple views can well solve the depth blur problem and made up for the inaccurate detection of the 2D joint detector.

FIGURE 8

FIGURE 8. MPJPE curve under different number of perspectives in the training.

Compared with other methods, we not only calculated the 3D space position of the human body joint points but also estimated the 3D mesh model of the human body. Our representation method was more vivid and lifelike than the representation of the line between the joint points, so the method in this paper was better than other algorithms in the overall prediction effect.

Running Time

To test the running time of the proposed algorithm in the 3D human pose estimation, it was compared with Simplify and HMR under the same experimental conditions (see the Experimental Equipment section). Table 3 summarizes the results from the different algorithms. The average time per frame of Simplify [22] algorithm was 199.2 s. The reason was that the model was based on the parameter optimization method to match the SMPL model with 2D joint points, and the optimization process took a lot of time. HMR [52] algorithm needed 7.8 s per frame, and the model obtains the parameters of the 3D human model from the images by iterative regression, which improved the operational efficiency to a certain extent. The proposed algorithm is 1.3 s per frame, where the average cost was 75 ms for the 2D human pose estimation and 1.225 s for the 3D SMPL model parameter estimation and 3D human mesh model rendering, which took a large part of the time. Therefore, the fully connected network structure proposed in this paper saved a large amount of model calculation time, improved the accuracy, and maintained high efficiency.

TABLE 3

TABLE 3. Running time comparison of 3D human mesh model estimation algorithm.

Ablation Experiment

Considering that there are a large number of parameters that can be optimized in the network structure designed in this paper, the use of different parameter settings will have different effects on the accuracy and operation efficiency of the model, so we analyze the ablation experiments with different parameter configurations.

Numbers of Hourglass Network Modules

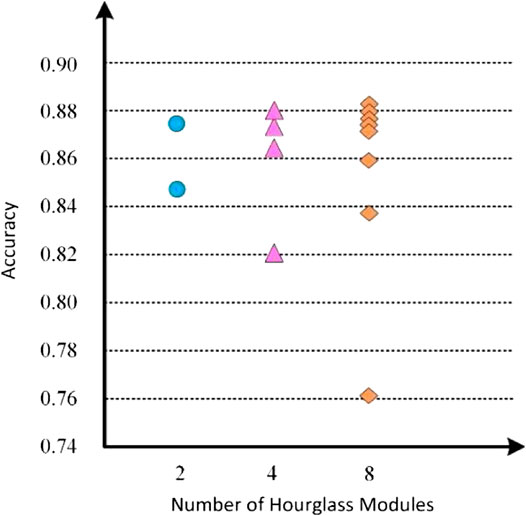
The model estimation effect was different for different numbers of hourglass modules. To determine the effect of the number of hourglass modules on model accuracy, we compared the performance of the 2D human pose estimation model on the test set, when different numbers of modules are used, and showed the changing process of the model estimation effected by calculating the accuracy of each hourglass module in Figure 9.

FIGURE 9

FIGURE 9. Accuracy of different numbers of hourglass network modules on evaluation.

The abscissa represented the number of hourglass modules, and the ordinate represented the accuracy of the corresponding different numbers of hourglass modules on the verification set. Each column icon in the figure corresponded to a situation. For example, the horizontal axis 2 indicated that the number of hourglass modules was 2, and there were two icons in the column, which, respectively, indicated the estimation accuracy of the first and second hourglass modules in the model from bottom to top, and so on.

Through comparison, it was found that, with the increase in the number of hourglass modules, the accuracy rate was gradually improved. The highest accuracy of hourglass module numbers 2, 4, and 8 is 0.875, 0.880, and 0.884, respectively. It can be seen that the larger the number of hourglass modules, the better the model estimation effect. However, with the deepening of the network layer, the number of model parameters increases, and the gradient easily disappears. Moreover, the variation amplitude of the accuracy of model estimation decreased and tended to a stable state. Therefore, the algorithm in this paper set the number of hourglass modules to 8.

Number of Fully Connected Layers

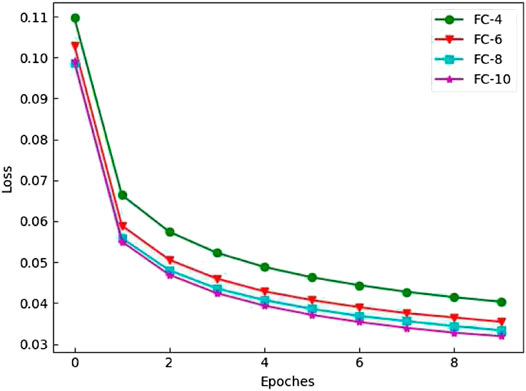
We analyzed the effect of choosing a different number of fully connected layers on the algorithm in the training process through experiments. In the experiment, we set the training process as 10 epochs in total, and the number of fully connected layers was set to 4 (FC-4), 6 (FC-6), 8 (FC-8), and 10 (FC-10). It can be seen that as the number of fully connected layers increases, the loss value of the model decreases gradually and tended to convergence from Figure 10. When the number of fully connected layers was larger, the model converged faster. It can be seen from the curve that the convergence speed of the model had little difference when the number of fully connected layers was 6, 8, and 10, and the number of parameters of the model was relatively less when the number of fully connected layers was 6.

FIGURE 10

FIGURE 10. Training loss curve of 3D pose regression network.

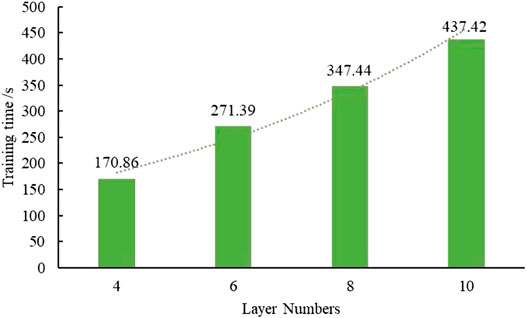
For further illustration of the training process’s efficiency, we conducted a statistical analysis of the training time of different numbers of fully connected layer models, as shown in Figure 11. As the number of fully connected layers increased, the time consumed by the model also increased. Comprehensive analysis of the results, We considered that the number of fully connected layers was set to 6.

FIGURE 11

FIGURE 11. Model training time comparison.

The Number of Neurons

In this paper, the 3D pose estimation was implemented using a fully connected network, and the number of neurons in the fully connected layer had a certain impact on the number of model parameters and the prediction effect. Therefore, a comparative analysis is performed on networks with different numbers of neurons (Linear_size, which represents the number of neurons in the fully connected layer).

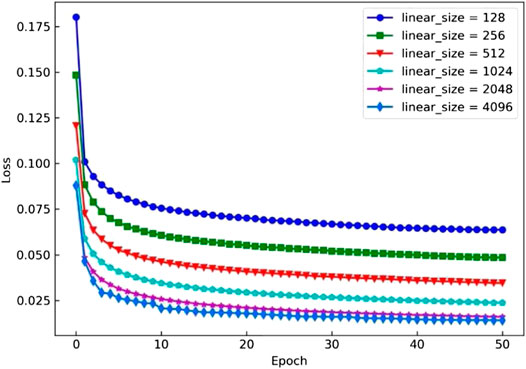
To compare the effect of different neuron numbers on the model performance, we selected several classic parameter values 128, 256, 512, 1,024, 2,048, 4,096 for experiments. As shown in Figure 12, The horizontal axis represented the number of epochs of model training (we selected the first 50 epochs for analysis), and the vertical axis represented the loss function value of the training process. We can observe that when the number of neurons increases from 128 to 4,096, the loss value gradually declines. It indicated that the accuracy of model training was approximately positively correlated with the number of neurons; that is, the higher the number of neurons is, the higher the accuracy of model estimation will be.

FIGURE 12

FIGURE 12. Loss curves of different numbers of neurons.

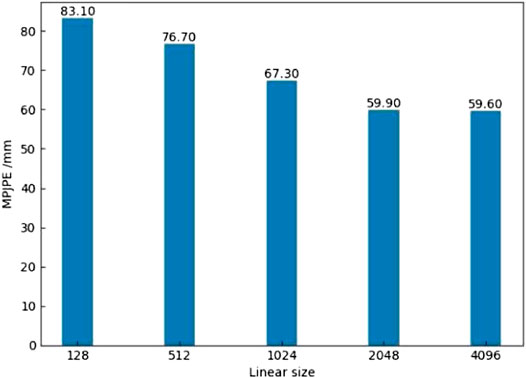
To determine the effect of the number of neurons on the model performance better, we further conducted comparative experiments on the network prediction effects with different numbers of neurons. The 50 batches of test images were randomly selected to verify the model prediction effect. The number of images in each batch was 64, and 3,200 images were used for this experiment. The abscissa represented the number of neurons in each layer, the parameters were set to 128, 512, 1,024, 2,048, and 4,096, and the ordinate represented the MPJPE (mm) of the joint errors in Figure 13. By comparing the prediction results of different numbers of neurons, it was found that the error value of 4,096 neurons was only 0.3 mm lower than the error value of 2,048 neurons. This indicated that the prediction effects of the two models were not much different. Compared with the model with 4,096 neurons, the model with 2,048 neurons had fewer parameters. Considering comprehensively, this article set the number of neurons in the fully connected layer to 2,048.

FIGURE 13

FIGURE 13. Average joint error of different neuron numbers (mm).

Optimization Method

To make the fully connected network better learn the mapping relationship between 2D joint points and 3D model parameters, we added optimization methods such as batch normalization, dropout, and skip connection between layers. For whether these optimization methods had a positive impact on the model, and how to choose the best combination plan, we further conducted experiments and analysis.

The abscissa represented the number of epochs of model training, and the ordinate indicated the value of the loss function during the training process, shown in Figure 14. The purple-red curve at the top indicated that no optimization measures were added to the network. It can be seen that the loss function (Loss) value of model training was the highest. When only Dropout and Residual were added to the network, the green curve which was in the second place in the corresponding figure shows a significant reduction in the loss value compared with the case without optimization. When only Batch Normalization (BN) layer and Dropout operations were added to the network, corresponding to the light blue curve in the third place in the figure, it can be seen that the loss had dropped more significantly, which showed that the batch normalization affects the loss value. The effect was remarkable. The curves in the fourth and fifth places corresponded to the cases where the BN, Dropout, and Residual optimization methods are added at the same time, and the BN and Residual optimization methods were added only. Through comparison, it was found that the red curve had the lowest value. The network model without Dropout will have higher prediction results for the batch of training data, but the prediction effect of the model on the new test data is often unsatisfactory. Because Dropout operations were used to solve the over-fitting problem of the model, the parameters of model training will be biased toward overfitting, so the loss value will be relatively low. This is disadvantageous for our model.

FIGURE 14

FIGURE 14. Comparison of loss curves by using different methods.

Based on the above curve analysis, BN improved the prediction effect of the network, and the extracted feature information was fused by the skip connection method. Compared with the model without the Dropout method, the smallest loss was obtained. But considering the generalization ability of the model, it was necessary to finally choose to add the Dropout layer.

Experiment of Multi-View Capturing Images

The capturing system was used for image acquisition. The experimental subjects moved in the active area and did some actions in daily life, to ensure that the experimental subjects were located in the perspective of the camera as far as possible. The stacked hourglass convolutional network was used as the 2D detector to detect the 2D joint point of the image under four perspectives $(\text{X},\text{ Y}\in {\mathrm{ℝ}}^{4\times 14\times 2}).$ The 2D coordinates were input into the fully connected neural network designed in this paper, and the parameters of the SMPL model were obtained by regression calculation $(\text{θ},\text{β}\in {\mathrm{ℝ}}^{82}).$ The 3D human mesh model was obtained through the SMPL model, and the 3D joint point coordinates of the human body were further calculated. Using this experimental system, experimenter 1 and experimenter 2 were tested with 5,000 images, and the test results were quantitatively analyzed by quantitative index MPJPE. The analysis results were shown in Table 4.

TABLE 4

TABLE 4. MPJPE index experimental results for each joint of two experimenters (1, 2).

The joints such as the right ankle, left ankle, right hand, and left wrist had higher error values than other joint points. The reason was that these joint points of the human body were flexible, and the ankle joints were easy to be occluded compared with other joints, so the error of the model in estimating the position of these joint points was larger. To improve the accuracy of model prediction, the next step is to focus on improving the prediction accuracy of these easily occluded joints and joints with greater flexibility, which should be constrained by the symmetry of the human structure and the proportion of the joints, thus reducing the error in the estimation of joint point coordinates.

Conclusion

We proposed a multi-layer fully connected neural network with skip connections to learn the mapping relationship between the 2D joint coordinates and the parameters of the SMPL model. we classified joints according to the natural connection characteristics and used a data-driven method to learn the implicit spatial prior information. Besides, we constructed a multi-view image acquisition system. The experimenter performs some daily behavioral activities in a certain activity space. We used four optical sensors to collect images of the experimenter, and the computer analyzed the image via the algorithm we proposed to estimate the 3D human mesh model and the 3D joint locations. The experimental results showed that the MPJPE of the 3D human pose estimated by the algorithm in this paper was the smallest, and it ranked first among all the algorithms participating in the comparison. The future work is to analyze multi-frame video sequences and restore the distortion of postures by studying the continuity information of postures.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Ethics Statement

Written informed consent was obtained from the individuals for the publication of any potentially identifiable images or data included in this article.

Author Contributions

LM is the main contributor of this work, and Hengshang Gao focused on the experimental design and debug.

Funding

This research was funded by National Key Research and Development Project (2018YFB2003203), National Natural Science Foundation of China (62073061), and Fundamental Research Funds for the Central Universities (N2004020).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Yang F, Sakti S, Wu Y, Nakamura S. Make skeleton-based action recognition model smaller, faster and better. In: Proceedings of the ACM multimedia asia (2019). p. 1–6. doi:10.1145/3338533.3366569

CrossRef Full Text | Google Scholar

2. Liu J, Wang G, Duan LY, Abdiyeva K, Kot AC. Skeleton-based human action recognition with global context-aware attention LSTM networks. IEEE Trans Image Process (2018) 27(4):1586–99. doi:10.1109/TIP.2017.2785279

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Shi L, Zhang Y, Cheng J, Lu H. Skeleton-based action recognition with multi-stream adaptive graph convolutional networks. IEEE Trans Image Process (2020) 29:9532–45. doi:10.1109/TIP.2020.3028207

CrossRef Full Text | Google Scholar

4. Li M, Chen S, Chen X, Zhang Y, Wang Y, Tian Q. Actional-structural graph convolutional networks for skeleton-based action recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2019). p. 3590–8. doi:10.1109/CVPR.2019.00371

CrossRef Full Text | Google Scholar

5. Su K, Liu X, Shlizerman E. Predict & cluster: unsupervised skeleton based action recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2020). p. 13–9. doi:10.1109/CVPR42600.2020.00965

CrossRef Full Text | Google Scholar

6. Rogez G, Weinzaepfel P, Schmid C. LCR-net: localization-classification-regression for human pose. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2017). p. 21–6. doi:10.1109/CVPR.2017.134

CrossRef Full Text | Google Scholar

7. Pavlakos G, Zhou X, Derpanis KG, Daniilidis K. Coarse-to-Fine volumetric prediction for single-image 3D human pose. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2017). p. 21–6. doi:10.1109/CVPR.2017.139

CrossRef Full Text | Google Scholar

8. Pavlakos G, Zhou X, Daniilidis K. Ordinal depth supervision for 3D human pose estimation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2018). p. 7307–16. doi:10.1109/CVPR.2018.00763

CrossRef Full Text | Google Scholar

9. Newell A, Yang K, Deng J. Stacked hourglass networks for human pose estimation. In: Proceedings of the European conference on computer vision (2016). p. 483–99. doi:10.1007/978-3-319-46484-8_29

CrossRef Full Text | Google Scholar

10. Wei S, Ramakrishna V, Kanade T, Sheikh Y. Convolutional pose machine. In: IEEE conference on computer vision and pattern recognition (2016). p. 4724–32. doi:10.1109/CVPR.2016.511

CrossRef Full Text | Google Scholar

11. Zhou X, Zhu M, Leonardos S, Derpanis KG, Daniilidis K. Sparseness meets deepness: 3D human pose estimation from monocular video. In: IEEE conference on computer vision and pattern recognition (2016). p. 4966–75. doi:10.1109/CVPR.2016.537

CrossRef Full Text | Google Scholar

12. Martinez J, Hossain R, Romero J, Little JJ. A simple yet effective baseline for 3d human pose estimation. In: IEEE international conference on computer vision (2017). p. 2640–9. doi:10.1109/ICCV.2017.288

CrossRef Full Text | Google Scholar

13. Ramakrishna V, Kanade T, Sheikh Y. Reconstructing 3D human pose from 2D image landmarks. In: European conference on computer vision (2012). p. 573–86. doi:10.1007/978-3-642-33765-9_41

CrossRef Full Text | Google Scholar

14. Zhou X, Huang Q, Sun X, Xue X, Wei Y. Towards 3D human pose estimation in the wild: a weakly-supervised approach. In: IEEE international conference on computer vision (2017). p. 398–407. doi:10.1109/ICCV.2017.51

CrossRef Full Text | Google Scholar

15. Tekin B, Márquez-Neila P, Salzmann M, Fua P. Learning to fuse 2D and 3D image cues for monocular body pose estimation. In: IEEE international conference on computer vision (2017). p. 3941–50. doi:10.1109/ICCV.2017.42

CrossRef Full Text | Google Scholar

16. Li C, Lee GH. Generating multiple hypotheses for 3D human pose estimation with mixture density network. In: IEEE conference on computer vision and pattern recognition (2019). p. 9887–95. doi:10.1109/CVPR.2019.01012

CrossRef Full Text | Google Scholar

17. Qammaz A, Argyros A. MocapNET: ensemble of SNN encoders for 3D human pose estimation in RGB images. In: British machine vision conference (2019). p. 46–63.

Google Scholar

18. Meredith M, Maddock SC. Motion capture file formats explained. Dep Comput Sci (2001) 211:241–4.

Google Scholar

19. Wang M, Chen X, Liu W, Qian C, Lin L, Ma L. DRPose3D: depth ranking in 3D human pose estimation. In: Twenty-Seventh international joint conference on artificial intelligence (2018). p. 1805. doi:10.24963/ijcai.2018/136

CrossRef Full Text | Google Scholar

20. Sigal L, Balan A, Black MJ. Combined discriminative and generative articulated pose and non-rigid shape estimation. Adv Neural Inf Process Syst (2007) 25:1337–44.

Google Scholar

21. Anguelov D, Srinivasan P, Koller D, Thrun S, Rodgers J, Davis J. Scape. ACM Trans Graph (2005) 24(3):408–16. doi:10.1145/1073204.1073207

CrossRef Full Text | Google Scholar

22. Bogo F, Kanazawa A, Lassner C, Gehler P, Romero J, Black MJ. Keep it SMPL: automatic estimation of 3D human pose and shape from a single image. In: European conference on computer vision (2016). p. 561–78. doi:10.1007/978-3-319-46454-1_34

CrossRef Full Text | Google Scholar

23. Pishchulin L, Insafutdinov E, Tang S, Andres B, Andriluka M, Gehler P, et al. DeepCut: joint subset partition and labeling for multi person pose estimation. In: IEEE conference on computer vision and pattern recognition (2016). p. 4929–37. doi:10.1109/CVPR.2016.533

CrossRef Full Text | Google Scholar

24. Loper M, Mahmood N, Romero J, Pons-Moll G, Black MJ. SMPL. ACM Trans Graph (2015) 34(6):1–16. doi:10.1145/2816795.2818013

CrossRef Full Text | Google Scholar

25. Lassner C, Romero J, Kiefel M, Bogo F, Black MJ, Gehler PV. Unite the people: closing the loop between 3D and 2D human representations. In: IEEE conference on computer vision and pattern recognition (2017). p. 6050–9. doi:10.1109/CVPR.2017.500

CrossRef Full Text | Google Scholar

26. Güler RA, Neverova N, Kokkinos I. DensePose: dense human pose estimation in the wild. In: IEEE conference on computer vision and pattern recognition (2018). p. 7297–306. doi:10.1109/CVPR.2018.00762

CrossRef Full Text | Google Scholar

27. Yao P, Fang Z, Wu F, Feng Y, Li J. DenseBody: directly regressing dense 3D human pose and shape from a single color image. arXiv [Preprint] (2019). Available from: arXiv:1903.10153

Google Scholar

28. Kocabas M, Athanasiou N, Black MJ. VIBE: video inference for human body pose and shape estimation. In: IEEE conference on computer vision and pattern recognition (2020). p. 5253–63. doi:10.1109/CVPR42600.2020.00530

CrossRef Full Text | Google Scholar

29. Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv [Preprint] (2014). Available from: arXiv:1409.1556.

Google Scholar

30. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2016). p. 770–8. doi:10.1109/CVPR.2016.90

CrossRef Full Text | Google Scholar

31. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial nets. Adv Neural Inf Process Syst (2014) 90:2672–80.

Google Scholar

32. Akhter I, Black MJ. Pose-conditioned joint angle limits for 3D human pose reconstruction. In: IEEE conference on computer vision and pattern recognition (2015). p. 1446–55. doi:10.1109/CVPR.2015.7298751

CrossRef Full Text | Google Scholar

33. Zell P, Wandt B, Rosenhahn B. Joint 3D human motion capture and physical analysis from monocular videos. In: IEEE conference on computer vision and pattern recognition workshops (2017). p. 17–26. doi:10.1109/CVPRW.2017.9

CrossRef Full Text | Google Scholar

34. Wang C, Wang Y, Lin Z, Yuille AL, Gao W. Robust estimation of 3D human poses from a single image. In: IEEE conference on computer vision and pattern recognition (2014). p. 2361–8. doi:10.1109/CVPR.2014.303

CrossRef Full Text | Google Scholar

35. Marcard T, Henschel R, Black M, Rosenhahn B, Pons-Moll G. Recovering accurate 3D human pose in the wild using IMUs and a moving camera. In: Proceedings of the European conference on computer vision (2018). p. 601–17. doi:10.1007/978-3-030-01249-6_37

CrossRef Full Text | Google Scholar

36. Tang W, Yu P, Wu Y. Deeply learned compositional models for human pose estimation. In: European conference on computer vision (2018). p. 197–214. doi:10.1007/978-3-030-01219-9_12

CrossRef Full Text | Google Scholar

37. Tian Y, Zitnick CL, Narasimhan SG. Exploring the spatial hierarchy of mixture models for human pose estimation. In: European conference on computer vision (2012). p. 256–69. doi:10.1007/978-3-642-33715-4_19

CrossRef Full Text | Google Scholar

38.1 Mahmood N, Ghorbani N, Troje NF, Pons-Moll G, Black M. AMASS: archive of motion capture as surface shapes. In: Proceedings of the IEEE international conference on computer vision (2019). p. 5442–51. doi:10.1109/ICCV.2019.00554

CrossRef Full Text | Google Scholar

39. Ionescu C, Papava D, Olaru V, Sminchisescu C. Human3.6M: large scale datasets and predictive methods for 3D human sensing in natural environments. IEEE Trans Pattern Anal Mach Intell (2014) 36(7):1325–39. doi:10.1109/TPAMI.2013.248

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Gower JC Generalized procrustes analysis. Psychometrika (1975) 40(1):33–51. doi:10.1007/BF02291478

CrossRef Full Text | Google Scholar

41. Fang H, Xu Y, Wang W, Liu X, Zhu S. Learning pose grammar to encode human body configuration for 3D pose estimation. In: Proceedings of the AAAI (2018).

Google Scholar

42. Sun X, Shang J, Liang S, Wei Y. Compositional human pose regression. In: IEEE international conference on computer vision (2017). p. 2602–11. doi:10.1109/ICCV.2017.284

CrossRef Full Text | Google Scholar

43. Yang W, Ouyang W, Wang X, Ren J, Li H, Wang X. 3D human pose estimation in the wild by adversarial learning. In: IEEE conference on computer vision and pattern recognition (2018). p. 5255–64. doi:10.1109/CVPR.2018.00551

CrossRef Full Text | Google Scholar

44. Pavlakos G, Zhou X, Derpanis K, Daniilidis K. Harvesting multiple views for marker-less 3D human pose annotations. In: IEEE conference on computer vision and pattern recognition (2017). p. 6988–97. doi:10.1109/CVPR.2017.138

CrossRef Full Text | Google Scholar

45. Ci H, Wang C, Ma X, Wang Y. Optimizing network structure for 3D human pose estimation. In: IEEE international conference on computer vision (2019). p. 2262–71. doi:10.1109/ICCV.2019.00235

CrossRef Full Text | Google Scholar

46. Sun X, Xiao B, Wei F, Liang S, Wei Y. Integral human pose regression. In: Proceedings of the European conference on computer vision (2018). p. 536–53. doi:10.1007/978-3-030-01231-1_33

CrossRef Full Text | Google Scholar

47. Cai Y, Ge L, Liu J, Cai J, Cham T-J, Yuan J, et al. Exploiting spatial-temporal relationships for 3D pose estimation via graph convolutional networks. In: International conference on computer vision (2019). p. 227–2281. doi:10.1109/ICCV.2019.00236

CrossRef Full Text | Google Scholar

48. Chen X, Lin K, Liu W, Qian C, Lin L. Weakly-supervised discovery of geometry-aware representation for 3D human pose estimation. In: Conference on computer vision and pattern recognition (2019). p. 10895–904. doi:10.1109/CVPR.2019.01115

CrossRef Full Text | Google Scholar

49. Pavllo D, Feichtenhofer C, Grangier D, Auli M. 3D human pose estimation in video with temporal convolutions and semi-supervised training. In: Conference on computer vision and pattern recognition (2019). p. 7753–62. doi:10.1109/CVPR.2019.00794

CrossRef Full Text | Google Scholar

50. Dabral R, Mundhada A, Kusupati U, Afaque S, Sharma A, Jain A. Learning 3D human pose from structure and motion. In: Proceedings of the European conference on computer vision (2018). p. 679–96. doi:10.1007/978-3-030-01240-3_41

CrossRef Full Text | Google Scholar

51. Wang J, Yan S, Xiong Y, Lin D. Motion guided 3D pose estimation from videos. arXiv [Preprint] (2020). Available from: arXiv:2004.1398.

Google Scholar

52. Kanazawa A, Black MJ, Jacobs DW, Malik J End-to-End recovery of human shape and pose. In: Conference on computer vision and pattern recognition (2018). p. 7122–31. doi:10.1109/CVPR.2018

CrossRef Full Text | Google Scholar