Joule-Thomson Expansion of the Quasitopological Black Holes

In this paper, we investigate the thermal stability and Joule-Thomson expansion of some new quasitopological black hole solutions. We first study the higher-dimensional static quasitopological black hole solutions in the presence of Born-Infeld, exponential, and logarithmic nonlinear electrodynamics. The stable regions of these solutions are independent of the types of the nonlinear electrodynamics. The solutions with horizons relating to the positive constant curvature, $k=+1$, have a larger region in thermal stability, if we choose positive quasitopological coefficients, ${\mu }_i>0$. We also review the power Maxwell quasitopological black hole. We then obtain the five-dimensional Yang-Mills quasitopological black hole solution and compare it with the quasitopological Maxwell solution. For large values of the electric charge, q, and the Yang-Mills charge, e, we showed that the stable range of the Maxwell quasitopological black hole is larger than the Yang-Mills one. This is while thermal stability for small charges has the same behavior for these black holes. Thereafter, we obtain the thermodynamic quantities for these solutions and then study the Joule-Thomson expansion. We consider the temperature changes in an isenthalpic process during this expansion. The obtained results show that the inversion curves can divide the isenthalpic ones into two parts in the inversion pressure, $P_i$. For $P<P_i$, a cooling phenomenon with positive slope happens in $T-P$ diagram, while there is a heating process with a negative slope for $P>P_i$. As the values of the nonlinear parameter, β, the electric and Yang-Mills charges decrease, the temperature goes to zero with a small slope and so the heating phenomena happens slowly.

1 Introduction

Black holes as thermodynamic systems have been one of the most interesting subjects in theoretical physics for several decades. The main motivation for studying thermodynamics of AdS black holes originates from the AdS/CFT correspondence. In this correspondence, the dynamics of the quantum field theory in $\left(d-1\right)$-dimensions are related to the dynamics of an AdS black hole in d-dimensions [1]. The first-order phase transition of the AdS Schwarzschild black holes was studied by Hawking and Page [2] and prompted many physicists to study the phase structure of black holes. For example, the thermodynamic phase structures of the charged AdS black holes have been studied in Refs. [3, 4]. In this paper, the cosmological constant has been considered as the dynamical pressure, while its conjugate is the thermodynamic volume of the black hole. P-V diagram of charged AdS black holes is similar to the van der Waals liquid-gas phase transition.

Joule-Thomson expansion is another thermodynamic issue which has attracted many people. For the van der Waals gases, the Joule-Thomson expansion is an isenthalpic process in which we can probe the temperature changes as the gas expands from the high pressure to the low one, through porous plugs. In fact, the Joule-Thomson expansion is a tool used to know whether a cooling or heating process is happening for a gas. The zero value of the Joule-Thomson coefficient is called the inversion point in which the two cooling to heating processes intersect. Considering the mass of a black hole as an enthalpy [5], the Joule-Thomson expansion of charged AdS black holes was studied for the first time in Ref. [6]. The Joule-Thomson expansion was studied in many papers [7–14]. Joule-Thomson expansion of the higher dimensional charged AdS and Gauss-Bonnet AdS black holes have been broadly probed in Refs. [7, 8]. Joule-Thomson expansion of charged AdS black holes in rainbow gravity has also been studied in Ref. [15]. In Refs. [16, 17], the Joule-Thomson expansion of the usual and regular (Bardeen)-AdS black holes have been investigated. Joule-Thomson expansion of Born-Infeld AdS black holes has been investigated in Ref. [18]. Born-Infeld nonlinear electrodynamics was introduced by Born and Infeld with the main aim to remove the divergence of the electric field [19]. Other types of the nonlinear electrodynamics such as logarithmic nonlinear (LN) and exponential nonlinear (EN) were introduced in Refs. [20, 21]. The main purpose of this paper is to obtain the Joule-Thomson expansion for the nonlinear quasitopological black holes.

Quasitopological gravity is a higher curvature modified theory in d dimensions. This gravity has some advantages which has attracted us to investigating it further. Based on the AdS/CFT correspondence, this gravity can provide a one-to-one duality between .the central charges of the conformal field theory and the parameters in the gravitational side [22–24]. Also, Einstein’s gravity is a low energy limit of the string theory which predicts higher dimensions. As the terms of the quasitopological gravity are not true topological invariants, so they can generate nontrivial gravitational terms in lower dimensions. This is the benefit of this gravity to the other modified gravities such as Lovelock. This gravity can also provide a dual CFT which respects the causality [25]. Quasitopological black holes and $P-V$ criticality behavior have been studied in Refs. [26, 27]. Thermodynamics of the AdS black hole and holography in generalized quasi-topological gravity was investigated in Refs. [28, 29].

We also obtained the five-dimensional Yang-Mills (YM) quasitopological black hole solutions and compared them with the ones in quasitopological Maxwell theory. The YM theory is one of the attractive non-abelian gauge theories that comes from the low energy limit of the string theory model’s spectrum. Non-abelian gauge fields beside the gravitational ones can be an effective subject in the physical phenomena of the results of superstring models. The analytic black hole solution of the Einstein-YM (EYM) was first developed by Yasskin in Ref. [30]. Black hole solutions in the presence of nonabelian Yang-Miils theory have been obtained in Refs. [31–34]. Black holes in a non-abelian Born-Infeld theory and supersymmetric EYM theories were studied in [35, 36], respectively. Using the Wu-Yang ansatz [37], black hole solutions of the various gravities coupled to the YM field have been explored in Refs. [38–44]. It is interesting to look at the Joule-Thomson expansion of the Yang-Mills quasitopological solutions.

This paper is arranged as follows: We start with the quasitopological gravity and the nonlinear electrodynamic theory in Sec. 2 and find the related static solutions. We then obtain the thermodynamic quantities and study the thermal stability of the related solutions in the sections III and IV, respectively. We also probe the Joule-Thomson expansion of the Power Maxwell quasitopological black hole in Sec.VI. In Sec. VII, we obtain the solution of the Yang-Mills black hole in the presence of the quasitopological gravity and then probe the thermal stability and Joule-Thomson expansion for this black hole. Lastly, we provide a conclusion of the paper in Sec. 8.

2 The Static Solutions of the $\left(n+1\right)$-Dimensional Nonlinear Quasitopological Gravity

The main structure of the $\left(n+1\right)$-dimensional quasitopological gravity starts from the action [45–47]

$I_{\mathrm{bulk}}=\frac{1}{16\pi }{\displaystyle \int d^{n+1}x\sqrt{-g}\left\{-2\Lambda +R+{\widehat{\mu }}_2{\mathrm{ℒ}}_2+{\widehat{\mu }}_3{\mathrm{ℒ}}_3+{\widehat{\mu }}_4{\mathrm{ℒ}}_4+\mathrm{ℒ}\left(F\right)\right\}},(1)$

where $\mathrm{ℒ}\left(F\right)$ is the matter source that for the nonlinear electrodynamics is considered as follows:

$\mathrm{ℒ}\left(F\right)=\{\begin{array}{l}4{\beta }^2\left[1-\sqrt{1+\frac{F^2}{2{\beta }^2}}\right],BI\\ 4{\beta }^2\left[\exp \left(-\frac{F^2}{4{\beta }^2}\right)-1\right],EN\\ -8{\beta }^2\ln \left[1+\frac{F^2}{8{\beta }^2}\right],LN\end{array}(2)$

where $BI$, $EN$, and $LN$ are the abbreviations of the Born-Infeld, exponential, and logarithmic forms, respectively [19–21].

We define $F^2=F_{\mu \nu }{F}^{\mu \nu }$, where the electromagnetic field tensor is described as $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$ with $A_{\mu }$ as the vector potential. The Lagrangians ${\mathrm{ℒ}}_2$, ${\mathrm{ℒ}}_3$ and ${\mathrm{ℒ}}_4$ are respectively referred to as the second-order Lovelock (Gauss-Bonnet), cubic and quartic quasitopological gravity with the constant coefficients ${\widehat{\mu }}_2$, ${\widehat{\mu }}_3$ and ${\widehat{\mu }}_4$. It should be noted that a hat (ˆ) is not the sign of an operator. ${\mathrm{ℒ}}_2$, ${\mathrm{ℒ}}_3$ and ${\mathrm{ℒ}}_4$ are defined as [45]

${\mathrm{ℒ}}_2=R_{abcd}{R}^{abcd}-4R_{ab}{R}^{ab}+R^2,(3)$

${\mathrm{ℒ}}_3={{\displaystyle R_a^c}}_b^d{{\displaystyle R_c^e}}_d^f{{\displaystyle R_e^a}}_f^b+\frac{1}{\left(2n-1\right)\left(n-3\right)}\left[\begin{array}{c}\frac{3\left(3n-5\right)}{8}{R}_{abcd}{R}^{abcd}R-3\left(n-1\right)R_{abcd}{R}^{abc}{{\displaystyle {}_{e}R}}^{de}\\ +3\left(n+1\right)R_{abcd}{R}^{ac}{R}^{bd}+6\left(n-1\right)R_a^b{R}_b^c{R}_c^a-\frac{3\left(3n-1\right)}{2}{R}_a^b{R}_b^{a}R+\frac{3\left(n+1\right)}{8}{R}^3\end{array}\right](4)$

$\begin{array}{c}{\mathrm{ℒ}}_4=c_1{R}_{abcd}{R}^{cdef}{R}^{hg}{{\displaystyle {}_{ef}R}}_{hg}^{ab}+c_2{R}_{abcd}{R}^{abcd}{R}_{ef}^{ef}+c_{3}R{R}_{ab}{R}^{ac}{R}_c^b+c_4{\left(R_{abcd}{R}^{abcd}\right)}^2\\ +c_5{R}_{ab}{R}^{ac}{R}_{cd}{R}^{db}+c_{6}R{R}_{abcd}{R}^{ac}{R}^{db}+c_7{R}_{abcd}{R}^{ac}{R}^{be}{R}_e^d+c_8{R}_{abcd}{R}^{acef}{R}^b{{\displaystyle {}_{e}R}}_f^d\\ +c_9{R}_{abcd}{R}^{ac}{R}_{ef}{R}^{bedf}+c_{10}{R}^4+c_{11}{R}^2{R}_{abcd}{R}^{abcd}+c_{12}{R}^2{R}_{ab}{R}^{ab}\\ +c_{13}{R}_{abcd}{R}^{abef}{R}_{ef}^c{{\displaystyle {}_{g}R}}^{dg}+c_{14}{R}_{abcd}{R}^{aecf}{R}_{gehf}{R}^{gbhd},\end{array}(5)$

where the coefficients $c_i$’s are written in the Supplementary Appendix A. To find a handle of the static topological solutions, we use the metric.

$d{s}^2=-f\left(r\right)d{t}^2+\frac{d{r}^2}{f\left(r\right)}+r^{2}d{\Omega }_{k,n-1}^2,(6)$

where $d{\Omega }_{k,n-1}^2$ represents the line element of a $\left(n-1\right)$-dimensional hypersurface $\Sigma$ with the constant curvature $k=\mathrm{1,0},-1$ as the spherical, flat, and hyperbolic geometries, respectively. By varying the action (1) with respect to $A_{\mu }$ and solving the related equation, the electromagnetic field tensor is obtained as

$F_{tr}=\{\begin{array}{l}\frac{q}{r^{n-1}}{\left(\sqrt{1+\eta }\right)}^{-1},BI\\ \beta \sqrt{L_W\left(\eta \right)},EN\\ \frac{2q}{r^{n-1}}{\left(1+\sqrt{1+\eta }\right)}^{-1},LN\end{array}(7)$

where $\eta =\frac{q^2}{{\beta }^2{r}^{2n-2}}$ and q is an integration constant. If we vary the action (1) with respect to $g_{\mu \nu }$ and redefine the quasitopological gravity coefficients as

${\mu }_2=\left(n-2\right)\left(n-3\right){\widehat{\mu }}_2,(8)$

${\mu }_3=\frac{\left(n-2\right)\left(n-5\right)\left(3n^2-9n+4\right)}{8\left(2n-1\right)}{\widehat{\mu }}_3,(9)$

${\mu }_4=n\left(n-1\right)\left(n-3\right)\left(n-7\right){\left(n-2\right)}^2\left(n^5-15n^4+72n^3-156n^2+150n-42\right){\widehat{\mu }}_4,(10)$

so the gravitational field equation is gained as

${\mu }_4{\Psi }^4+{\mu }_3{\Psi }^3+{\mu }_2{\Psi }^2+\Psi +\xi =0,(11)$

where we have the definitions $\Psi \left(r\right)=\left[k-f\left(r\right)\right]/r^2$ and

$\begin{array}{l}\xi =-\frac{2\Lambda }{n\left(n-1\right)}-\frac{m}{r^n}+\\ \{\begin{array}{l}\frac{4{\beta }^2}{n\left(n-1\right)}\left\{1-{{\displaystyle {}_{2}F}}_1\left\{\left[-\frac{1}{2},-\frac{n}{2\left(n-1\right)}\right],\left[\frac{n-2}{2\left(n-1\right)}\right],-\eta \right\}\right\},BI\\ -\frac{4{\beta }^2}{n\left(n-1\right)}+\frac{4\left(n-1\right)\beta q}{n\left(n-2\right)r^n}{\left(\frac{q}{\beta }\right)}^{\frac{1}{n-1}}{\left[L_W\left(\eta \right)\right]}^{\frac{n-2}{2\left(n-1\right)}}\times {{\displaystyle {}_{2}F}}_1\left\{\left[\frac{n-2}{2\left(n-1\right)}\right],\left[\frac{3n-4}{2\left(n-1\right)}\right],-\frac{1}{2\left(n-1\right)}{L}_W\left(\eta \right)\right\}\\ -\frac{4\beta q}{\left(n-1\right)r^{n-1}}{\left[L_W\left(\eta \right)\right]}^{\frac{1}{2}}\times \left\{1-\frac{1}{n}{\left[L_W\left(\eta \right)\right]}^{-1}\right\},EN\\ \frac{8\left(2n-1\right)}{n^2\left(n-1\right)}{\beta }^2\left[1-\sqrt{1+\eta }\right]+\frac{8\left(n-1\right)q^2}{n^2\left(n-2\right)r^{2n-2}}{{\displaystyle {}_{2}F}}_1\left\{\left[\frac{n-2}{2\left(n-1\right)},\frac{1}{2}\right],\left[\frac{3n-4}{2\left(n-1\right)}\right],-\eta \right\}\\ -\frac{8}{n\left(n-1\right)}{\beta }^2\ln \left[\frac{2\sqrt{1+\eta }-2}{\eta }\right],LN\end{array}\end{array}(12)$

where m is an integration constant relating to the mass of the black hole. In the above relation, $L_W\left(x\right)$ and ${}_2{{\displaystyle F}}_1\left[\left(a,b\right),\left(c\right),z\right]$ are, respectively, the Lambert and hypergeometric functions. We get to the solution for Eq. 11

$f\left(r\right)=k-r^2\times \{\begin{array}{l}-\frac{{\mu }_3}{4{\mu }_4}+\frac{-W+\sqrt{-\left(3A+2y-\frac{2B}{W}\right)}}{2},{\mu }_4>0,\\ -\frac{{\mu }_3}{4{\mu }_4}+\frac{W-\sqrt{-\left(3A+2y+\frac{2B}{W}\right)}}{2},{\mu }_4<0,\end{array}(13)$

where for brevity reasons, we have described W, A, y, and B in the Supplementary Appendix B.

3 Thermodynamic Behavior of the $\left(n+1\right)$-Dimensional Static Nonlinear Quasitopological Black Hole

Via the AdS/CFT correspondence, the thermodynamic behaviors of an AdS black hole can provide a set of knowledge for a certain dual conformal field theory (CFT). So, in this section, we are eager to obtain the thermodynamic quantities of the static nonlinear quasitopological black hole. Using the subtraction method [48], the mass of this black hole is gained as

$M=\frac{\left(n-1\right)}{16\pi }m,(14)$

where m can be obtained from Eq. 11 by the fact that $f\left(r_{+}\right)=0$. The electric charge of the black hole can be determined from the Gauss law

$Q=\frac{1}{4\pi }{\displaystyle \int F_{tr}{r}^{n-1}d{\Omega }_k}=\frac{q}{4\pi },(15)$

and the electric potential U is defined by the formula $U={A_{\nu }{\chi }^{\nu }|}_{\infty }-{A_{\nu }{\chi }^{\nu }|}_{r=r_{+}}$, where ${\chi }^{\nu }$ is the killing vector. So, we can obtain the electric potential as follows

$U=\{\begin{array}{l}\frac{q}{\left(n-2\right)r_{+}^{n-2}}{{\displaystyle {}_{2}F}}_1\left\{\left[\frac{1}{2},\frac{n-2}{2\left(n-1\right)}\right],\left[\frac{3n-4}{2\left(n-1\right)}\right],-{\eta }_{+}\right\},BI\\ \frac{n-1}{n-2}\beta {\left(\frac{q}{\beta }\right)}^{\frac{1}{n-1}}{\left[L_W\left({\eta }_{+}\right)\right]}^{\frac{n-2}{2\left(n-1\right)}}{{\displaystyle {}_{2}F}}_1\left\{\left[\frac{n-2}{2\left(n-1\right)}\right],\left[\frac{3n-4}{2\left(n-1\right)}\right],-\frac{1}{2\left(n-1\right)}{L}_W\left({\eta }_{+}\right)\right\}-\beta r_{+}\sqrt{L_W\left({\eta }_{+}\right)},EN\\ \frac{q}{\left(n-2\right)r_{+}^{n-2}}{{\displaystyle {}_{3}F}}_2\left\{\left[\frac{n-2}{2\left(n-1\right)},\frac{1}{2},1\right],\left[\frac{3n-4}{2\left(n-1\right)},2\right],-{\eta }_{+}\right\},LN\end{array}(16)$

where ${\eta }_{+}\equiv \eta \left(r=r_{+}\right)$. The entropy [49] and the Hawking temperature of the static nonlinear quasitopological black hole can be obtained by

$S=\frac{n-1}{4}{r}_{+}^{n-1}\left[\frac{1}{n-1}+\frac{2k{\mu }_2}{\left(n-3\right)r_{+}^2}+\frac{3k^2{\mu }_3}{\left(n-5\right)r_{+}^4}+\frac{4k^3{\mu }_4}{\left(n-7\right)r_{+}^6}\right],(17)$

$T=\frac{f^{\text{'}}\left(r_{+}\right)}{4\pi }=\frac{1}{4\pi r_{+}\left(4{\mu }_4{k}^3+3{\mu }_3{k}^2{r}_{+}^2+2{\mu }_{2}k{r}_{+}^4+r_{+}^6\right)}\times \left[{\mu }_4{k}^4\left(n-8\right)+{\mu }_3{k}^3\left(n-6\right)r_{+}^2+{\mu }_2{k}^2\left(n-4\right)r_{+}^4+k\left(n-2\right)r_{+}^6-\frac{2\Lambda }{n-1}{r}_{+}^8+\{\begin{array}{l}\frac{4{\beta }^2}{n-1}{r}_{+}^8\left(1-\sqrt{1+{\eta }_{+}}\right),BI\\ -\frac{4{\beta }^2}{n-1}{r}_{+}^8\left\{1-\left[1-L_W\left({\eta }_{+}\right)\right]\exp \left[\frac{L_W\left({\eta }_{+}\right)}{2}\right]\right\},EN\\ \frac{8{\beta }^2}{n-1}{r}_{+}^8\left\{1-\sqrt{1+{\eta }_{+}}-\ln \left[\frac{2\left(\sqrt{1+{\eta }_{+}}-1\right)}{{\eta }_{+}}\right]\right\}.LN\end{array}\right](18)$

If we consider the thermodynamic volume and pressure as below [50]

$\begin{array}{l}V=\frac{r_{+}^n}{n},\\ P=-\frac{\Lambda }{8\pi },\end{array}(19)$

therefore, the first law of the thermodynamics in the extended phase space follows from the formula

$dM=TdS+UdQ+VdP+Bd\beta +{\Psi }_{2}d{\mu }_2+{\Psi }_{3}d{\mu }_3+{\Psi }_{4}d{\mu }_4,(20)$

where B and ${\Psi }_i$’s, $\left(i=\mathrm{1,2,3}\right)$ are denoted, respectively, as the potentials conjugate to the nonlinear parameter β and couplings ${\mu }_i$’s, respectively. They are defined as follows

$\begin{array}{l}B=\frac{\partial M}{\partial \beta },\\ {\Psi }_2=\frac{\partial M}{\partial {\mu }_2}=\frac{\left(n-1\right)k^2{r}_{+}^{n-4}}{16\pi }-\frac{\left(n-1\right)k{r}_{+}^{n-3}}{2\left(n-3\right)}T,\\ {\Psi }_3=\frac{\partial M}{\partial {\mu }_3}=\frac{\left(n-1\right)k^3{r}_{+}^{n-6}}{16\pi }-\frac{3\left(n-1\right)k^2{r}_{+}^{n-5}}{4\left(n-5\right)}T,\\ {\Psi }_4=\frac{\partial M}{\partial {\mu }_4}=\frac{\left(n-1\right)k^4{r}_{+}^{n-8}}{16\pi }-\frac{\left(n-1\right)k^3{r}_{+}^{n-7}}{\left(n-7\right)}T,\end{array}(21)$

that the relations $T=\frac{\partial M}{\partial S},U=\frac{\partial M}{\partial Q},V=\frac{\partial M}{\partial P}$ are established. In the extended phase space, we can write the Smarr-type formula of this black hole as

$M=\frac{1}{n-2}\left[\left(n-1\right)TS-2PV+\left(n-2\right)UQ-\beta B+2{\mu }_2{\Psi }_2+4{\mu }_3{\Psi }_3+6{\mu }_4{\Psi }_4\right].(22)$

If we determine the specific volume $v=\frac{4r_{+}}{n-1}$ and use the pressure (III) in Eq. (III), we can specify the equation of state for the static nonlinear quasitopological black hole as $P\left(v,T\right)$. The critical points of the static nonlinear quasitopological black hole can be derived from the following conditions

$\frac{\partial P}{\partial v}{|}_{v_C}=0,\frac{{\partial }^{2}P}{\partial v^2}{|}_{v_C}=0.(23)$

Critical behavior of the cubic quasitopological black hole has been investigated in Ref. [27]. As the critical behavior of the quartic quasitopological black hole is similar to the cubic one, we refrain from repeating them here.

4 Thermal Stability of the $\left(n+1\right)$-Dimensional Static Nonlinear Quasitopological Black Hole

In order to know where a black hole may exist physically or not, we should discuss its thermal stability. To study the thermal stability of the static nonlinear quasitopological black hole, we define the heat capacity $C_P$ at the constant pressure as follows

$C_P=T{\left(\frac{\partial S}{\partial T}\right)}_P=T\frac{{\left(\frac{\partial S}{\partial r_{+}}\right)}_P}{{\left(\frac{\partial T}{\partial r_{+}}\right)}_P}.(24)$

The positive value of $C_P$ may lead to the thermal stability of the mentioned black hole, while the negative value shows the instability. We should note that the positive value of the temperature is a requirement to having physical solutions. To show the stability of the static nonlinear quasitopological black hole, we have plotted $C_P$ and T for the BI black hole in Figures 1, 2 with $k=1$ and ${\widehat{\mu }}_2>0$ and ${\widehat{\mu }}_3>0$. The obtained results show that the type of the nonlinear electrodynamics has a trivial effect on the thermal stability. Therefore, we have refrained from probing all of them and just included the stability of the BI theory. In Figure 1 with ${\widehat{\mu }}_4>0$, we can see a $r_{+\min }$ for each $n=4$ and 6 dimensions, that $C_P$ and T are both positive for $r_{+}>r_{+\min }$. For ${\widehat{\mu }}_4<0$ in Figure 2B, there are two $r_{+\min }$ and $r_{+\max }$ which $C_P$ is positive for both regions $r_{+}<r_{+\min }$ and $r_{+}>r_{+\max }$. According the temperature diagram in Figure 2A, a unit positive region for both $C_P$ and T can be gained for just $r_{+}>r_{+\max }$. Comparing Figures 1, 2 shows that for the same parameters, a black hole with ${\widehat{\mu }}_4>0$ may have a larger region in thermal stability than the one with ${\widehat{\mu }}_4<0$. We can also understand this result from Eqs. 3, 17, 24. The nonlinear quasitopological black holes with $k=1$ and positive ${\widehat{\mu }}_2$ and ${\widehat{\mu }}_3$ can have larger positive regions for $\partial S/\partial r_{+}$, T and $C_P$, if we choose ${\widehat{\mu }}_4>0$.

FIGURE 1

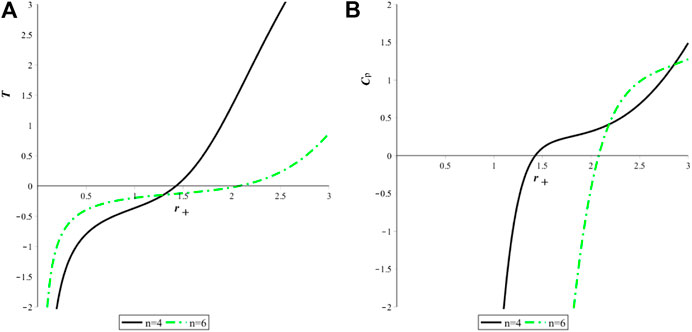
FIGURE 1. Thermal stability of the BI quasitopological black hole with respect to $r_{+}$ for different values of dimension n with ${\widehat{\mu }}_2=0.2$, ${\widehat{\mu }}_3=0.1$, ${\widehat{\mu }}_4=0.001$$k=1$, $q=1$ and $\beta =6$(A) Temperature T, (B) Heat capacity C_P.

FIGURE 2

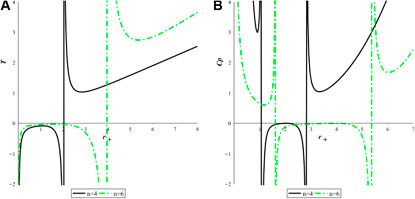
FIGURE 2. Thermal stability of the BI quasitopological black hole with respect to $r_{+}$ for different values of dimension n with ${\widehat{\mu }}_2=0.2$, ${\widehat{\mu }}_3=0.1$, ${\widehat{\mu }}_4=-0.001$$k=1$, $q=1$ and $\beta =6$(A) Temperature T, (B) Heat capacity C_P.

5 Joule-Thomson Expansion of the $\left(n+1\right)$-Dimensional Static Nonlinear Quasitopological Black Hole

In this section, we intend to study the Joule-Thomson expansion of the obtained quasitopological black hole coupled to the nonlinear electrodynamics. In the classical thermodynamics, the Joule-Thomson expansion is an isenthalpic process in which we can probe the temperature changes as the gas expands from the high pressure to the low one through porous plugs. The Joule-Thomson coefficient is obtained by the Eq. 6

$\mu ={\left(\frac{\partial T}{\partial P}\right)}_H=\frac{1}{C_P}\left[T{\left(\frac{\partial V}{\partial T}\right)}_P-V\right],(25)$

where the enthalpy of the system, H, is fixed. In the gas expansion, the pressure always decreases. So, when the value of the coefficient µ is positive during the expansion, it means that the temperature decreases and therefore it is called a cooling phenomenon. However, when µ is negative, the temperature increases, and this is called a heating process. For $\mu =0$, we can obtain the inversion temperature in which the process of the temperature changes vice versa. It can be obtained by the formula

$T_i=V{\left(\frac{\partial T}{\partial V}\right)}_P.(26)$

Because a black hole behaves like a thermodynamic system, we can consider the mass of a black hole as the enthalpy and probe the Joule-Thomson expansion for it.

Now, we would like to investigate the Joule-Thomson expansion of the higher-dimensional nonlinear quasitopological black hole and identify the region in which cooling, or heating occurs. Therefore in Figure 3, we have plotted the Joule-Thomson coefficient µ versus $r_{+}$ for different values of β and compared it with the temperature of the black hole. In Figure 3A, there is a $r_{+\mathrm{ext}}$ for each value of β in which the coefficient µ diverges. This point is in accordance with $T=0$ in Figure 3B where there is an extreme black hole. So, we can get some knowledge about the external black hole by recognizing the infinite points of µ. This figure also shows that by increasing the nonlinear parameter β, the value of $r_{+\mathrm{ext}}$ increases. For $r_{+}>r_{+\mathrm{ext}}$ in Figure 3A, there is also an inversion phenomenon in $r_{+\mathrm{inv}}$ in which the black hole goes from a heating process to a cooling one. For small β, inversion happens in a smaller $r_{+}$.

FIGURE 3

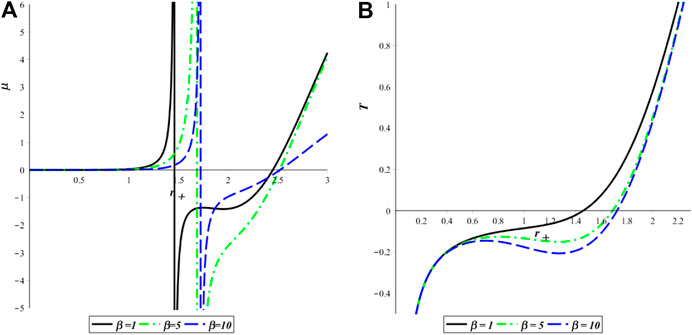
FIGURE 3. The Joule-Thomson coefficient µ and temperature T of the BI quasitopological black hole with respect to $r_{+}$ for different values of the nonlinear parameter β with ${\widehat{\mu }}_2=0.1$, ${\widehat{\mu }}_3=0.1$, ${\widehat{\mu }}_4=0.002$, $k=1$, $Q=2$ and $n=4$(A) Joule-Thomson coefficient µ, (B) Temperature T.

We have also plotted the isenthalpic curves and the inversion curve of the nonlinear quasitopological black hole for different values of Q and β in Figure 4. In each subfigure, we can see three isenthalpic curves with constant M and the related inversion curve happening at the maximum value of the isenthalpic curves. We define the inversion temperature and pressure of each isenthalpic as $T_i$ and $P_i$. The inversion curve divides the isenthalpic curves in to two parts where for $P<P_i$, the slope of the isenthalpic curve is positive and so cooling happens in the expansion. But, for $P>P_i$, the slope of the isenthalpic curve is negative, so there is heating for the black hole. For small values of parameter β in Figures 4B,C, the same behaviors are repeated, but for $P>P_i$, the temperature decreases to zero with a steeper slope. So, the heating process happens slowly. This is unlike the Einstein-Born-Infeld black hole for which the slope of the curve in the range $P>P_i$ is unchanged as β increases [18]. By decreasing the parameter β in Figure 4B with respect to the one in Figure 4A, the extreme black hole will happen in a larger pressure. In Figure 4C with a small electric charge, the heating happens very slowly and so the temperature gets to zero for a higher-pressure value than the Figure 4B with a larger charge. We have also checked the Joule-Thomson expansion of the obtained black hole for ${\widehat{\mu }}_4<0$ in Figure 5. The result shows that we can face isenthalpic curves with ${\widehat{\mu }}_4<0$ just for the hyperbolic geometry, $k=-1$.

FIGURE 4

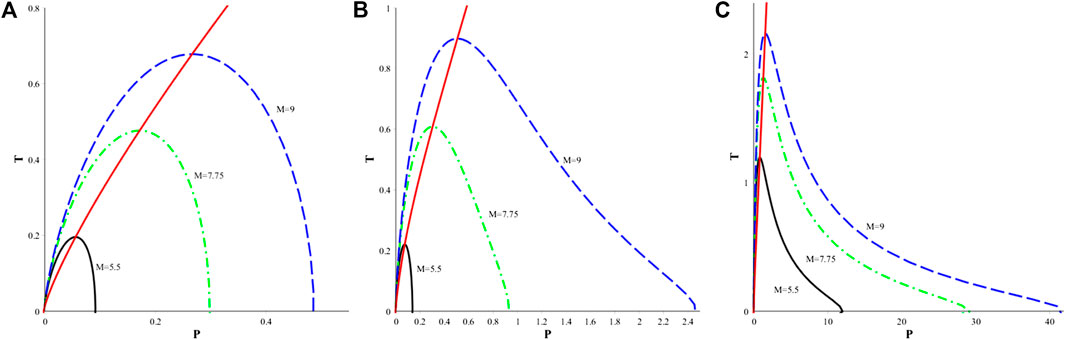
FIGURE 4. Isenthalpic curves and inversion curve of the BI quasitopological black hole with ${\widehat{\mu }}_2=0.1$, ${\widehat{\mu }}_3=0.1$, ${\widehat{\mu }}_4=0.001$, $k=1$ and $n=4$(A)Q = 3, β = 10; (B)Q = 3, β = 1; (C)Q = 1, β = 1.

FIGURE 5

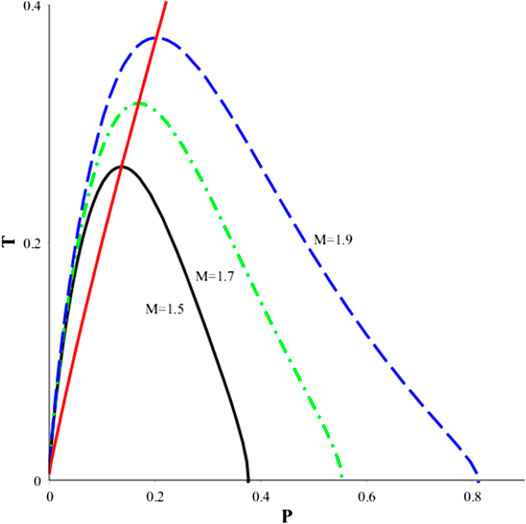
FIGURE 5. Isenthalpic curves and inversion curve of the BI quasitopological black hole with ${\widehat{\mu }}_2=0.1$, ${\widehat{\mu }}_3=0.1$, ${\widehat{\mu }}_4=-0.001$, $k=-1$, $Q=1$, $n=4$ and $\beta =20$.

6 Joule-Thomson Expansion of the Power Maxwell Quasitopological Black Hole

Power Maxwell is another nonlinear electrodynamics which can preserve the conformal invariance of the theory in higher dimensions. It has the form

$\mathrm{ℒ}\left(F\right)={\left(-F_{\mu \nu }{F}^{\mu \nu }\right)}^s,(27)$

where for the nonlinear parameter $s=1$, it is reduced to the linear Maxwell theory. In order to have an $\left(n+1\right)$-dimensional conformal invariant action, the energy-momentum tensor should be traceless which leads to the value, $s=\left(n+1\right)/4$. For a general study, we consider an arbitrary value for the parameter s. Quasitopological black hole solutions in the presence of the power Maxwell matter field have been obtained in Refs. [51, 52]. In this section, we aim to investigate the Joule-Thomson expansion of these solutions. The temperature of this black hole follows from [51, 52]

$T=\frac{1}{4\pi r_{+}\left(4{\mu }_4{k}^3+3{\mu }_3{k}^2{r}_{+}^2+2{\mu }_{2}k{r}_{+}^4+r_{+}^6\right)}\times \left[\begin{array}{c}{\mu }_4{k}^4\left(n-8\right)+{\mu }_3{k}^3\left(n-6\right)r_{+}^2+{\mu }_2{k}^2\left(n-4\right)r_{+}^4\\ +k\left(n-2\right)r_{+}^6-\frac{2\Lambda }{n-1}{r}_{+}^8\end{array}\right]-\frac{q^{2s}{2}^s{\left(n-2s\right)}^{2s}{r}_{+}^{2s\left(1-n\right)/\left(2s-1\right)}}{4\pi \left(4{\mu }_4{k}^3{r}_{+}^{-6}+3{\mu }_3{k}^2{r}_{+}^{-4}+2{\mu }_{2}k{r}_{+}^{-2}+1\right)\left(n-1\right){\left(2s-1\right)}^{2s-1}}{r}_{+},(28)$

where $r_{+}$ has a range between $r_0\le r_{+}<\infty$ that $r_0\ne 0$. Using Eq. 26, we plot the isenthalpic and inversion curves of the power Maxwell quasitopological solutions in Figure 6. It is clear that for a general parameter s, the inversion curve has divided the isenthalpic curves into two cooling and heating parts. In the cooling/heating process, the temperature decreases/increases as the pressure decreases in the isenthalpic process. If we compare our results with the Joule-Thomson expansion of the power Maxwell black holes in Einstein gravity [53], they show that the quasitopological gravity cannot make an enhancement for the isenthalpic curves. It is also clear from Figure 6 that by increasing the parameter value, s, an extreme black hole happens at lower pressure. This is unlike the Einstein-power-Maxwell black hole, in which the extreme black hole with larger s has a larger pressure.

FIGURE 6

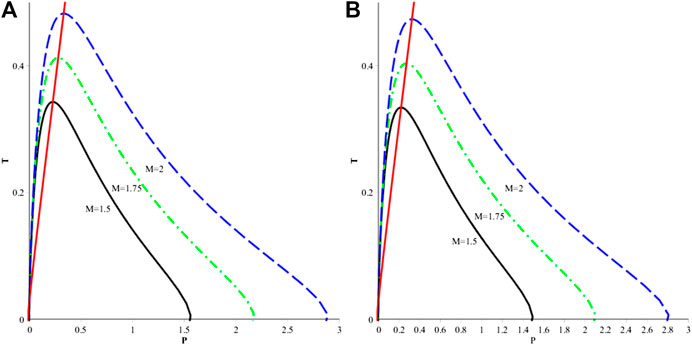
FIGURE 6. Isenthalpic curves and inversion curve of the PM quasitopological black hole with ${\widehat{\mu }}_2=0.1$, ${\widehat{\mu }}_3=0.1$, ${\widehat{\mu }}_4=0.001$, $k=1$, $n=4$ and $q=1$(A)S = 0.7, (B)S = 1.4.

7 Joule-Thomson Expansion of the Five-Dimensional Yang-Mills Quasitopological Black Hole

In this section, we consider the non-abelian Yang-Mills theory with the quasitopological gravity and obtain the related five-dimensional solutions. We also obtain the thermodynamic quantities of this black hole and then probe the Joule-Thomson expansion for it. In five dimensions, we can just consider the six-parameters gauge groups, $SO\left(4\right)$ and $SO\left(\mathrm{3,1}\right)$, where the action is defined by the relation (1) with the matter source

$\mathrm{ℒ}\left(F\right)=-{\gamma }_{ab}{F}_{\mu \nu }^{\left(a\right)}{F}^{\left(b\right)\mu \nu }.(29)$

The gauge field tensor $F_{\mu \nu }$ is described as follows

$F_{\mu \nu }^{\left(a\right)}={\partial }_{\mu }{A}_{\nu }^{\left(a\right)}-{\partial }_{\nu }{A}_{\mu }^{\left(a\right)}+\frac{1}{e}{C}_{bc}^a{A}_{\mu }^{\left(b\right)}{A}_{\nu }^{\left(c\right)},(30)$

where e is a coupling constant and $C_{bc}^a$’s are the structure constants of the gauge groups that $a,b$ go from 1 to 6. In order to have analytical solutions, we use the Wu-Yang ansatz [37] and obtain the gauge potentials of the gauge groups. Using the appropriate coordinates, we have written the gauge potentials and the structure constants of the groups $SO\left(4\right)$ and $SO\left(\mathrm{3,1}\right)$ in the Supplementary Appendix C. If we vary the Yang-Mills quasitopological action with respect to $g_{\mu \nu }$, we get to Eq. 11, where ξ obeys from

$\xi =-\frac{\Lambda }{6}+\frac{m}{r^4}-\frac{2e^2}{r^4}\ln \left(\frac{r}{r_0}\right),(31)$

and $r_0$ is a constant that for simplicity, we chose, $r_0=1$. In order to have the static Yang-Mills quasitopological solutions, we use the metric (6) with $k=-1,+1$ that leads to the solutions (13) with the ξ defined in Eq. 31. The mass and entropy of the five-dimensional Yang-Mills quasitopological black hole can be gained as Eqs. 14Eqs. 17 where m is obtained as below

$m={\mu }_4\frac{k^4}{r_{+}^4}+{\mu }_3\frac{k^3}{r_{+}^2}+{\mu }_2{k}^2+k{r}_{+}^2-\frac{\Lambda }{6}{r}_{+}^4-2e^2\ln \left(r_{+}\right).(32)$

We can also determine the temperature and the Yang-Mills charge of this black hole as

$T=-\frac{6{\mu }_4{k}^4+3{\mu }_3{k}^3{r}_{+}^2-3k{r}_{+}^6+\Lambda r_{+}^8+3e^2{r}_{+}^4}{6\pi r_{+}\left(4{\mu }_4{k}^3+3{\mu }_3{k}^2{r}_{+}^2+2{\mu }_{2}k{r}_{+}^4+r_{+}^6\right)},(33)$

$Q=\frac{1}{4\pi \sqrt{6}}{\displaystyle \int d{\Omega }_3\sqrt{Tr\left[F_{\mu \nu }^{\left(a\right)}{F}_{\mu \nu }^{\left(a\right)}\right]}}=\frac{e}{4\pi }.(34)$

This black hole obeys the first law of thermodynamics

$dM=TdS+UdQ,(35)$

where $T={\left(\frac{\partial M}{\partial S}\right)}_Q$ is equal to the temperature (33) and the Yang-Mills potential U can be obtained by

$U={\left(\frac{\partial M}{\partial Q}\right)}_S=-12\pi Q\ln \left(r_{+}\right).(36)$

This relation restricts the range of the horizon value $r_{+}$ to $1\le r_{+}<\infty$. To study the thermal stability of the Yang-Mills quasitopological black hole, we obtain the heat capacity from Eq. 24 and plot it in Figure 7A. We also compare the stability of this black hole with the Maxwell quasitopological black hole in Figure 7B. These figures show that for each value of e and q, there is a $r_{+\min }$(the condition $r_{+\min }>1$ is established for the Yang-Mills theory) that both $C_P$ and T are positive for $r_{+}>r_{+\min }$. For small charges e and q, $r_{+\min }$ has a same value in both Yang-Mills and Maxwell quasitopological theories, while for large charges, $r_{+\min }$ has a larger value in the Yang-Mills quasitopological gravity. Therefore, for large q, the Maxwell quasitopological black holes have a larger region in thermal stability than the Yang-Mills quasitopological black holes. We are also eager to investigate the Joule-Thomson expansion of the five-dimensional Yang-Mills quasitopological black hole in Figure 8A and to then compare it with the Maxwell quasitopological one in Figure 8B. In both Figures 8A,B, we can see a cooling/heating process for different mass values with a positive/negative slope in the isenthalpic curves. In fact, as the pressure decreases during this expansion, according to Eq. 25, a decrease/increase of the temperature is related to the positive/negative slope in the $T-P$ diagram. For each isenthalpic curve, there is an inversion temperature and pressure, $T_i$ and $P_i$, which there is a cooling and heating process for $P<P_i$ and $P>P_i$, respectively. The heating process for the Yang-Mills quasitopological black hole in Figure 8A happens with a slower slope than the one in Maxwell quasitopological theory. So, the extreme Yang-Mills quasitopological black holes are described with larger pressures than the extreme Maxwell quasitopological black holes.

FIGURE 7

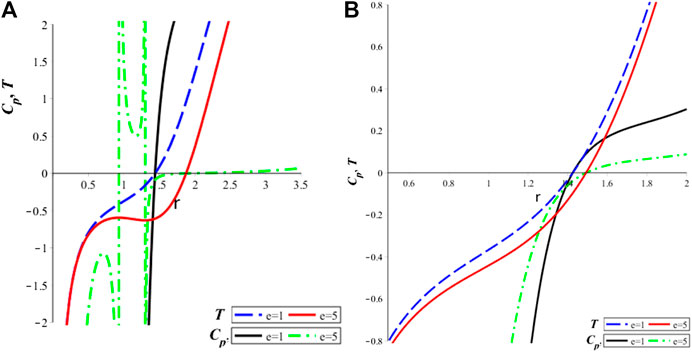
FIGURE 7. Thermal stability with respect to $r_{+}$ for different values e and q with ${\widehat{\mu }}_2=0.1$, ${\widehat{\mu }}_3=0.2$, ${\widehat{\mu }}_4=0.001$, $k=1$ and $n=4$(A) Yang-Mills quasitopological, (B) Maxwell quasitopological.

FIGURE 8

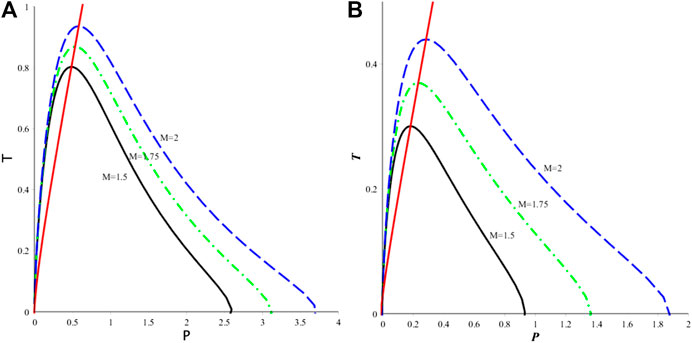
FIGURE 8. Isenthalpic curves and inversion curve with ${\widehat{\mu }}_2=0.1$, ${\widehat{\mu }}_3=0.2$, ${\widehat{\mu }}_4=0.001$, $k=1$, $e=q=5$ and $n=4$(A) Yang-Mills quasitopological, (B) Maxwell quasitopological.

8 Concluding Remarks

In this paper, we reviewed some quasitopological black hole solutions and obtained their thermodynamic properties such as their thermal stability and Joule-Thomson expansion. At first, we achieved the $\left(n+1\right)$-dimensional static quasitopological black hole solutions in the presence of three BI, EN, and LN forms of nonlinear electrodynamics. The obtained solutions are divided into two parts, for ${\mu }_4>0$ and ${\mu }_4<0$. We also obtained the thermodynamic quantities of this black hole and wrote the first law of thermodynamics in the extended phase space. Then, we looked for the physical existence of the black hole by studying the thermal stability. The stable region of this black hole is independent of the types of the nonlinear electrodynamics. Also, for $k=1$, the solutions with ${\widehat{\mu }}_i>0$ may lead to a larger stable region than the one with negative ${\widehat{\mu }}_i$. Joule-Thomson expansion was the other goal we paid attention to for this black hole. So, we probed the temperature changes of this black hole in an isenthalpic process during the expansion in which the pressure decreases. For the nonlinear quasitopological black hole with ${\widehat{\mu }}_4>0$ and $k=1$, we obtained an inversion curve which can divide the isenthalpic curves in to two parts. The part with the positive slope in the isenthalpic curve leads to a cooling process, while for the negative slope, heating may happen. For the black hole with a small charge q and nonlinear parameter β, the temperature reduces to zero with a very slow slope. It is possible to have an isenthalpic curve for ${\widehat{\mu }}_4<0$ just for $k=-1$.

We also studied the Joule-Thomson expansion of the power Maxwell quasitopological black holes. The results showed that for the large nonlinear parameter, s, the extreme black hole has a smaller pressure. This is while for the Einstein-power-Maxwell black hole, an extreme black hole with a small parameter s happens in low pressure. At the end, we looked at the Yang-Mills theory and gained the five-dimensional Yang-Mills solutions in the quasitopological gravity. We also carefully examined the thermodynamic quantities such as thermal stability and Joule-Thomson for this black hole and compared the results with the five-dimensional Maxwell quasitopological black hole. They show that there is a $r_{+\min }$, which the Yang-Mills quasitopological black hole is thermally stable for $r_{+}>r_{+\min }$. For small values of the charges e and q, the value of $r_{+\min }$ is independent of the Yang-Mills or Maxwell theories, while, for large charges, $r_{+\min }$ has a larger value in Yang-Mills theory. Also, the heating process for the Yang-Mills quasitopological black hole happens more slowly than the one in the Maxwell black hole.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is supported by Iranian National Science Foundation (INSF).

Acknowledgments

FN would like to thank physics department of Isfahan University of Technology for warm hospitality.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.628727/full#supplementary-material.

References

1. Aharony O, Gubser SS, Maldacena J, Ooguri H, Oz Y. Large N field theories, string theory and gravity. Phys Rep (2000) 323:183. arXiv:hep-th/9905111. doi:10.1016/s0370-1573(99)00083-6

CrossRef Full Text | Google Scholar

2. Hawking SW, Page DN. Thermodynamics of black holes in anti-de Sitter space. Commun Math Phys (1983) 87:577. doi:10.1007/bf01208266

CrossRef Full Text | Google Scholar

3. Chamblin A, Emparan R, Johnson CV, Myers RC. Charged AdS black holes and catastrophic holography. Phys Rev D (1999) 60:064018. arXiv:hep-th/9902170. doi:10.1103/physrevd.60.064018

CrossRef Full Text | Google Scholar

4. Chamblin A, Emparan R, Johnson CV, Myers RC. Holography, thermodynamics, and fluctuations of charged AdS black holes. Phys Rev D (1999) 60:104026. arXiv:hep-th/9904197. doi:10.1103/physrevd.60.104026

CrossRef Full Text | Google Scholar

5. Kastor D, Ray S, Traschen J. Enthalpy and the mechanics of AdS black holes. Classical Quantum Gravity (2009) 26:195011. arXiv:0904.2765 [hep-th]. doi:10.1088/0264-9381/26/19/195011

CrossRef Full Text | Google Scholar

6. Ökcü Ö, Aydiner E. Joule-Thomson expansion of charged AdS black holes. Eur Phys J C (2017) 77:24. arXiv:1611.06327 [gr-qc]. doi:10.1140/epjc/s10052-017-4598-y

CrossRef Full Text | Google Scholar

7. Mo JX, Li GQ, Lan SQ, Xu XB. Joule-Thomson expansion of d-dimensional charged AdS black holes. Phys Rev D (2018) 98:124032, 2018. arXiv:1804.02650 [gr-qc]. doi:10.1103/physrevd.98.124032

CrossRef Full Text | Google Scholar

8. Lan SQ. Joule-Thomson expansion of charged Gauss-Bonnet black holes in AdS space. Phys Rev D (2018) 98:084014. arXiv:1805.05817 [gr-qc]. doi:10.1103/physrevd.98.084014

CrossRef Full Text | Google Scholar

9. Ghaffarnejad H, Yaraie E, Farsam M. Quintessence Reissner Nordström anti de Sitter black holes and Joule Thomson effect. Int J Theor Phys (2018) 57:1671. arXiv:1802.08749 [gr-qc]. doi:10.1007/s10773-018-3693-7

CrossRef Full Text | Google Scholar

10. Almeida RD, Yogendran KP. Thermodynamic properties of holographic superfluids. (2018). arXiv:1802.05116.

Google Scholar

11. Ahmed Rizwan CL, Naveena Kumara A, Deepak V, Ajith KM. Joule-Thomson expansion in AdS black hole with a global monopole. Int J Mod Phys A (2018) 33(35):1850210. doi:10.1142/S0217751X1850210XarXiv:1805.11053

CrossRef Full Text | Google Scholar

12. Chabab M, El Moumni H, Iraoui S, Masmar K, Zhizeh S. Joule-Thomson expansion of RN-AdS black holes in f(R) gravity. Lett High Energy Phys (2018) 02(05):5. doi:10.2018/LHEP000001 arXiv:1804.10042 [gr-qc].

CrossRef Full Text | Google Scholar

13. Rostami M, Sadeghi J, Miraboutalebi S, Masoudi AA, Pourhassan B. Charged accelerating AdS black hole of f(R) gravity and the Joule-Thomson expansion. Int J Geom Methods Mod Phys (2019) 17(09):2050136. doi:10.1142/S0219887820501364 arXiv:1908.08410.

CrossRef Full Text | Google Scholar

14. Mo JX, Li GQ. Effects of lovelock gravity on the Joule-Thomson expansion. Classical Quantum Gravity (2020) 37(4):045009. doi:10.1088/1361-6382/ab60b9 arXiv:1805.04327.

CrossRef Full Text | Google Scholar

15. Yekta DM, Hadikhani A, Ökcü Ö. Joule-Thomson expansion of charged AdS black holes in rainbow gravity. Phys Lett B (2019) 795:521. doi:10.1016/j.physletb.2019.06.049

CrossRef Full Text | Google Scholar

16. Pu J, Guo S, Jiang QQ, Zu XT. Joule-Thomson expansion of the regular (Bardeen)-AdS black hole. Chin Phys C (2020) 44:035102. doi:10.1088/1674-1137/44/3/035102 arXiv:1905.02318 [gr-qc].

CrossRef Full Text | Google Scholar

17. Li C, He P, Li P, Deng JB. Joule-Thomson expansion of the Bardeen-AdS black holes. Gen Relativ Gravitation (2020) 52:50. arXiv:1904.09548 [gr-qc] doi:10.1007/s10714-020-02704-z

CrossRef Full Text | Google Scholar

18. Bi S, Du M, Tao J, Yao F. Joule-Thomson expansion of Born-Infeld AdS black holes. Chin Phys C (2020) 45(2):025109. doi:10.1088/1674-1137/abcf23 arXiv:2006.08920 [gr-qc].

CrossRef Full Text | Google Scholar

19. Born M, Infeld L. Foundations of the new field theory. Proc R Soc A (1934) 144:425. doi:10.1098/rspa.1934.0059

CrossRef Full Text | Google Scholar

20. Soleng HH. Charged black points in general relativity coupled to the logarithmic U(1) gauge theory. Phys Rev D (1995) 52:6178. doi:10.1103/physrevd.52.6178

CrossRef Full Text | Google Scholar

21. Hendi SH. Asymptotic charged BTZ black hole solutions. J High Energy Phys (2012) 03:065. doi:10.1007/JHEP03(2012)065 arXiv:1405.4941 [hep-th].

CrossRef Full Text | Google Scholar

22. Lemos JP. Cylindrical black hole in general relativity. Phys Lett B (1995) 353:46–51. arXiv:gr-qc/9404041. doi:10.1016/0370-2693(95)00533-q

CrossRef Full Text | Google Scholar

23. Cai R-G, Zhang Y-Z. Black plane solutions in four-dimensional spacetimes. Phys Rev D (1996) 54:4891. doi:10.1103/physrevd.54.4891

CrossRef Full Text | Google Scholar

24. Mann RB. Pair production of topological anti-de Sitter black holes. Classical Quantum Gravity (1997) 14:L109. doi:10.1088/0264-9381/14/5/007

CrossRef Full Text | Google Scholar

25. Myers RC, Paulos MF, Sinha A. Holographic studies of quasi-topological gravity. J High Energy Phys (2010) 08:035. doi:10.1007/JHEP08(2010)035 arXiv:1004.2055 [hep-th].

CrossRef Full Text | Google Scholar

26. Dehghani MH, Bazrafshan A, Mann RB, Mehdizadeh MR, Ghanaatian M, Vahidinia MH. Black holes in (quartic) quasitopological gravity. Phys Rev D (2012) 85(10):104009, 2012. arXiv:1109.4708 [hep-th] doi:10.1103/physrevd.85.104009

CrossRef Full Text | Google Scholar

27. Hennigar RA, Brenna WG, Mann RB. P-v criticality in quasitopological gravity. J High Energy Phys (2015) 07:77. doi:10.1007/JHEP07(2015)077 arXiv:1505.05517 [hep-th].

CrossRef Full Text | Google Scholar

28. Mir M, Hennigar RA, Ahmed J, Mann RB. Black hole chemistry and holography in generalized quasi-topological gravity. J High Energy Phys (2019) 2019(8):68, 2019. arXiv:1902.02005 [hep-th]. doi:10.1007/jhep08(2019)068

CrossRef Full Text | Google Scholar

29. Mir M, Mann RB. On generalized quasi-topological cubic-quartic gravity: thermodynamics and holography. J High Energy Phys (2019) 2019(7):1–58. doi:10.1007/JHEP07(2019)012 arXiv:1902.10906 [hep-th].

CrossRef Full Text | Google Scholar

30. Yasskin PB. Solutions for gravity coupled to massless gauge fields. Phys Rev D (1975) 12:2212. doi:10.1103/physrevd.12.2212

CrossRef Full Text | Google Scholar

31. Lavrelashvili G, Maison D. Regular and black hole solutions of Einstein-Yang-Mills Dilaton theory. Nucl Phys B (1993) 410:407. doi:10.1016/0550-3213(93)90441-q

CrossRef Full Text | Google Scholar

32. Donets EE, Gal'tsov DV. Stringy sphalerons and non-abelian black holes. Phys Lett B (1993) 302:411, 1993. arXiv:hep-th/9212153. doi:10.1016/0370-2693(93)90418-h

CrossRef Full Text | Google Scholar

33. Torii T, Maeda KI. Black holes with non-Abelian hair and their thermodynamical properties. Phys Rev D (1993) 48:1643. doi:10.1103/physrevd.48.1643

CrossRef Full Text | Google Scholar

34. Brihaye Y, Radu E. Euclidean solutions in Einstein-Yang-Mills-Dilaton theory. Phys Lett B (2006) 636:212. arXiv:gr-qc/0602069. doi:10.1016/j.physletb.2006.04.001

CrossRef Full Text | Google Scholar

35. Wirschins M, Sood A, Kunz J. Non-Abelian Einstein-Born-Infeld black holes. Phys Rev D (2001) 63:084002. arXiv:hep-th/0004130. doi:10.1103/physrevd.63.084002

CrossRef Full Text | Google Scholar

36. Huebscher M, Meessen P, Ortin T, Vaula S. N=2 Einstein-Yang-Mills’s BPS solutions. J High Energy Phys (2008) 09:099. doi:10.1088/1126-6708/2008/09/099 arXiv:0806.1477 [gr-qc].

CrossRef Full Text | Google Scholar

37. Wu TT, Yang CN, Mark H. Properties of Matter Under Unusual Conditions. New York, London: Interscience (1969). 349 p.

38. Mazharimousavi SH, Halilsoy M. 5D black hole solution in Einstein-Yang-Mills-Gauss-Bonnet theory. Phys Rev D (2007) 76:087501. arXiv:0801.1562 [gr-qc]. doi:10.1103/physrevd.76.087501

CrossRef Full Text | Google Scholar

39. Mazharimousavi SH, Halilsoy M. Black hole solutions in Einstein-Maxwell-Yang-Mills-Gauss-Bonnet theory. J Cosmol Astropart Phys (2008) 2008:005. arXiv:0801.2110 [gr-qc]. doi:10.1088/1475-7516/2008/12/005

CrossRef Full Text | Google Scholar

40. Mazharimousavi SH, Halilsoy M. Higher dimensional Yang Mills black holes in third order lovelock gravity. Phys Lett B (2008) 665:125–130. 10.1016/j.physletb.2008.06.007 arXiv:0801.1726 [gr-qc].

CrossRef Full Text | Google Scholar

41. Mazharimousavi SH, Halilsoy M. Lovelock black holes with a power-Yang-Mills source. Phys Lett B (2009) 681:190. 2009. arXiv:0908.0308 [gr-qc]. doi:10.1016/j.physletb.2009.10.006

CrossRef Full Text | Google Scholar

42. Bostani N, Dehghani MH. Topological black holes of (N+1)-dimensional Einstein-Yang-Mills gravity. Mod Phys Lett A (2010) 25:1507. arXiv:0908.0661 [gr-qc]. doi:10.1142/s0217732310032809

CrossRef Full Text | Google Scholar

43. Dehghani MH, Bostani N, Pourhasan R. Topological black holes of Gauss-Bonnet-Yang-Mills gravity. Int J Mod Phys D (2010) 19:1107, 2010. arXiv:0908.0663 [gr-qc]. doi:10.1142/s0218271810017196

CrossRef Full Text | Google Scholar

44. Dehghani MH, Bazrafshan A. Topological black holes of Einstein-Yang-Mills Dilaton gravity. Int J Mod Phys D (2010) 19:293. arXiv:1005.2387 [gr-qc]. doi:10.1142/s0218271810016403

CrossRef Full Text | Google Scholar

45. Bazrafshan A, Naeimipour F, Ghanaatian M, Khajeh A. Physical and thermodynamic properties of quartic quasitopological black holes and rotating black branes with a nonlinear source. Phys Rev D (2019) 100:064062. arXiv:1905.12428 [gr-qc]. doi:10.1103/physrevd.100.064062

CrossRef Full Text | Google Scholar

46. Ghanaatian M. Quartic quasi-topological-BornInfeld gravity. Gen Relativ Gravitation (2015) 47:105. doi:10.1007/s10714-015-1951-z

CrossRef Full Text | Google Scholar

47. Ghanaatian M, Naeimipour F, Bazrafshan A, Abkar M. Charged black holes in quartic quasi-topological gravity. Phys Rev D (2018) 97:104054. arXiv:1801.05692 [gr-qc]. doi:10.1103/physrevd.97.104054

CrossRef Full Text | Google Scholar

48. Brown JD, York JW. Quasilocal energy and conserved charges derived from the gravitational action. Phys Rev D (1993) 47:1407. doi:10.1103/physrevd.47.1407

CrossRef Full Text | Google Scholar

49. Wald RM. Black hole entropy is the Noether charge. Phys Rev D (1993) 48:3427. arXiv:gr-qc/9307038. doi:10.1103/physrevd.48.r3427

CrossRef Full Text | Google Scholar

50. Dolan BP. Pressure and volume in the first law of black hole thermodynamics. Classical Quantum Gravity (2011) 28:235017. arXiv:1106.6260 [gr-qc] doi:10.1088/0264-9381/28/23/235017

CrossRef Full Text | Google Scholar

51. Ghanaatian M, Naeimipour F, Bazrafshan A, Eftekharian M, Ahmadi A. Third order quasitopological black hole with a power-law Maxwell nonlinear source. Phys Rev D (2019) 99:024006, 2019. arXiv:1809.05198 [gr-qc]. doi:10.1103/physrevd.99.024006

CrossRef Full Text | Google Scholar

52. Ghanaatian M, Bazrafshan A. Nonlinear charged black holes in AdS quasi-topological gravity. Int J Mod Phys D (2013) 22:1350076. arXiv:1304.2311 [gr-qc]. doi:10.1142/s0218271813500764

CrossRef Full Text | Google Scholar

53. Feng ZW, Zhou X, Zhou SQ. Joule-Thomson expansion of higher dimensional nonlinearly charged AdS black hole in Einstein-PMI gravity. Commun Theor Phys (2020). doi:10.1088/1572-9494/abecd9 arXiv:2009.02172 [gr-qc].

CrossRef Full Text | Google Scholar