On the Origin of High–Frequency Magnetic Fluctuations in the Interplanetary Medium: A Brownian–like Approach

Low–frequency fluctuations in the interplanetary medium have been extensively investigated and described in the framework of turbulence, and the observed universal scaling behavior represents a clear signature of the underlying energy cascade. On the contrary, the interpretation of observations of plasma fluctuations at high frequencies, where wave–wave coupling, collisionless dissipation, and anomalous plasma heating play a key role, still represents a challenge for theoretical modeling. In this paper the high frequency fluctuations occurring in the interplanetary space are described through a Brownian–like approach, where the plasma dynamics at small scales is described through a stochastic process. It is shown that a simple model based on this framework is able to successfully reproduce the main features of the spectrum of the observed magnetic fluctuations. Moreover, the Fluctuation-Dissipation Relation, derived by our model, leads to a power law between dissipation rate and temperature, which is compatible with the occurrence of Landau damping, interpreted thus as the main mechanism of dissipation in the solar wind plasma.

1 Introduction

Since the first measurements of magnetic fluctuations in the interplanetary space [1], showing that the spectral magnetic energy density decays with the frequency ω as $E\left(\omega \right)\sim {\omega }^{-5/3}$, it has been argued that they can be described in the framework of turbulence [2]. This approach has been also successfully applied to interpret anomalous scalings due to intermittency of fluctuations [3–6] through multifractal models [7–11], and the nonlinear energy cascade, described by a Yaglom relation for the mixed third–order moment of fluctuations [12–15]. The scale–free behavior breaks down at a frequency $f_i$, usually found in the range between 0.1 and 1 Hz [16, 17], beyond which fluid or Magnetohydrodynamic (MHD) regimes are not valid anymore. Beyond this scale, a steeper power spectrum is observed $E\left(\omega \right)\sim {\omega }^{-\alpha }$ [17–19], the slope being strongly dependent on the analyzed sample. A statistical analysis of spectral slopes shows that α covers the range $\sim$[2, 3], with a peak at about $\alpha \simeq 2.8$ [19]. The presence of fluctuations at high frequencies has been attributed to dispersive phenomena generated by velocity–space effects and electron dynamics [20, 21, 22], and interpreted in terms of a further turbulent energy cascade driven by wave–wave coupling, as for example a quasi two–dimensional cascade of Kinetic Alfvén Waves (KAWs) [17] for which $E\left(\omega \right)\sim {\omega }^{-7/3}$. However, a clear detection of single wave modes in the frequency-wavenumber diagram is difficult due to the presence of large scattering, sideband modes, sporadic wave–trains as envelope solitons, and zero–frequency modes [23, 24]. Moreover, the situation is complicated by the failure of the Taylor hypothesis, implying that measurements in the time domain cannot be simply translated into the wave-vector domain [25]. Statistical analyses of many intervals of magnetic field data from Cluster spacecraft (see e.g., [17, 18]) indicate the presence of another breakpoint $f_e$ in the magnetic energy power spectrum at higher frequencies, of the order of few tens of Hz, associated with electron scales.

Contrary to the low frequency spectrum ($\omega <{\omega }_i$, where ${\omega }_i=2\pi f_i$), succesfully described in the nonlinear energy cascade turbulence framework, the interpretation of the spectrum at high frequencies ($\omega >{\omega }_i$) is less clear. Indeed, several models, which differs in their physical assumptions, have been developed to reproduce the observed spectra. The power spectrum for $\omega >{\omega }_i$ has been fitted either through a function made by a combination of ${\omega }^{-8/3}$ decay and an exponential decay, compatible with the proton Landau damping of magnetic fluctuations [18], or by a combinantion of two power laws [17, 19]. In the latter case, the statistical distributions of the two slopes, as obtained by the analysis of a large number of CLUSTER spectra, are narrow and centered around $\alpha \simeq 2.8$ (for ${\omega }_i\mathrm{\lesssim }\omega \mathrm{\lesssim }{\omega }_e$, where ${\omega }_e=2\pi f_e$) and $\alpha \simeq 4$ (for $\omega \mathrm{\gtrsim }{\omega }_e$), respectively. In this paper we deal with the problem of the origin of high frequency magnetic fluctuations in the interplanetary medium through a novel approach, to investigate whether the whole spectrum for $\omega >{\omega }_i$ can be described by means of a single physical model.

2 Model and Results

At small scales (high frequencies), smaller than the ion gyro–radius or inertial length, the plasma dynamics in the interplanetary space is extremely complex. More specifically, the linear mode waves become kinetic, exhibiting simultaneously a dispersive and dissipative character due to wave–particle interactions such as coherent scattering processes or incoherent processes (like pitch angle scattering). The collissionless damping mechanisms include cyclotron damping [26], Landau damping [27], energization of particles at current sheets, that can be spontaneously generated by an intermittent turbulent cascade [28–33], and stochastic heating [34–38].

It is generally agreed that the nonlinear energy cascade, which is surely active at the largest scales, transfers energy beyond the ion–cyclotron frequency (see e.g., [2] and Refs. therein), mainly exciting electric fluctuations [39], while the energy content in the magnetic fluctuations is lower (see e.g., [40]. At the same time, fluctuations are damped by plasma kinetic effects, thus providing a mechanism for heating in the collisionless plasma. The wave–particle mechanism involved in the dissipation acts as a feedback for fluctuations, as it generates particle beams which, in turn, are able to excite further fluctuations. The complex plasma dynamics at small scales, well documented in literature, involves a medium where random fluctuations and dissipation compete in generating magnetic fluctuations. In a range of scales where collisionless dissipation and plasma heating could take place and the presence of a lot of characteristic frequencies and lengths (e.g., cyclotron frequencies and inertial lenghts) breaks the scale–free behavior, the role of dispersion and dissipation is still poorly understood, and the origin of fluctuations is far from being clearly established. This framework is rather diffrent, even if compatible, from the “classical” turbulent dynamics where the nonlinear cascade operates within a scale–free range which is well separated from the smallest scales where dissipation occurs.

In order to provide a description of the high-frequency dynamics of magnetic fuctuations, a novel scenario, based on a stochastic Brownian approach, is introduced in the present work. This approach allows an interpretation of the observed high frequency magnetic spectra with no assumptions about dispersion relations from plasma turbulence theory. Based on the above considerations, we consider a simple framework where magnetic fuctuations $b\left(t\right)$ at small scales can be roughly described by a Itô stochastic differential equation

$db\left(t\right)=\Gamma \left[b\left(t\right),t\right]dt+\Psi \left[b\left(t\right),t\right]dW\left(t\right)(1)$

Here, without loss of generality, we consider only the time evolution of a single component of the fluctuations, but the model can be easily generalized to three-dimensional fluctuations or specific wavenumbers. In the simplest case, we assume that the dynamics of the fluctuations is due to two different contributions. The first contribution (first term in the right hand side) is due to the collisionless dissipative processes, which we parametrize with a linear damping term $\Gamma \left[b\left(t\right),t\right]\simeq -\gamma b\left(t\right)$, proportional to a constant damping rate γ. The second contribution, which mimics all the complex plasma wave dynamics, is described through the stochastic process $dW\left(t\right)$. For the sake of simplicity, $\Psi \left[b\left(t\right),t\right]$ is assumed to be constant, equal to the r.m.s of the fluctuations $\Psi \left[b\left(t\right),t\right]=F_0={<b^2>}^{1/2}$. The random forcing is expressed as $dW\left(t\right)=\xi \left(t\right)dt$, which is the natural physically acceptable choice for an interpretation which assumes $\xi \left(t\right)$ as a real noise, possibly different from a white noise, with finite correlation times [41]. Moreover, we assume that $\xi \left(t\right)$ is uncorrelated with the initial values of magnetic fluctuations $b\left(0\right)$, say $<\xi \left(t\right)b\left(0\right)>=0$. With these assumptions, Eq. (1) takes the following form:

$db\left(t\right)=-\gamma b\left(t\right)dt+F_0\xi \left(t\right)dt$

Under the hypotheses described above, the Itô equation can be solved by Fourier transforms. This gives an obvious relation between the correlations of the Fourier modes of the forcing ${\xi }_{\omega }$ and the power spectrum of magnetic energy modes $b_{\omega }$

$\langle b_{\omega }{b}_{\omega }^{\mathrm{\star }}\rangle =\frac{F_0^2\langle {\xi }_{\omega }{\xi }_{\omega }^{\mathrm{\star }}\rangle }{\left(\gamma -i\omega \right)\left(\gamma +i\omega \right)}(2)$

where brackets denote time averaging and $\mathrm{\star }$ stands for complex conjugate. Using homogeneity, we can write the spectral correlations of the forcing term as

$\langle {\xi }_{\omega }{\xi }_{\omega ’}\rangle =2\pi G\left(\omega \right)\delta \left(\omega +\omega ’\right)$

so that we can immediately write again Eq. (2) in terms of the power spectrum $E\left(\omega \right)$ which can be compared to observations in the solar wind plasmas

$E\left(\omega \right)=F_0^2\left[\frac{G\left(\omega \right)}{{\omega }^2+{\gamma }^2}\right](3)$

The spectral energy is, therefore, related to the spectral shape $G\left(\omega \right)$ of the external forcing. As a simple example, let us suppose that magnetic fluctuations are generated by completely uncorrelated stochastic wave trains, so that $\langle {\xi }_{\omega }{\xi }_{\omega ’}\rangle =2\pi \delta \left(\omega +\omega ’\right)$. In this case the magnetic energy spectrum is given by a Lorentzian function $E\left(\omega \right)\simeq F_0^2/\left({\omega }^2+{\gamma }^2\right)$ which, of course, does not describe the magnetic energy density spectrum as observed in the high–frequency solar wind plasma (see e.g., [17]).

As a further example, let us consider the case in which, close to the ion breakpoint, a variety of waves takes part in the process through wave–wave couplings, wave–particles interactions and dispersive effects. In this situation we can expect that the two–point correlations of the stochastic forcing term decay exponentially in time

$\langle \xi \left(t’\right)\xi \left(t\right)\rangle \sim \exp \left[-{\lambda }_0\left(t’-t\right)\right](4)$

where ${\lambda }_0^{-1}$ represents the correlation time. This means that $\xi \left(t\right)$ can be considered, in a rough approximation, as a Brownian noise. The magnetic energy power spectrum $E\left(\omega \right)$ can be easily calculated from Eq. (3) by using the inverse Fourier transform to deduce $G\left(\omega \right)$ from Eq. (4), obtaining the following functional shape

$E\left(\omega \right)\simeq \frac{{\lambda }_0{F}_0^2}{\left({\omega }^2+{\lambda }_0^2\right)\left({\omega }^2+{\gamma }^2\right)}(5)$

In our framework, the values of the correlation time ${\lambda }_0^{-1}$ and of the dissipation rate γ correspond to the low–frequency and high–frequency breakpoints, respectively, that is ${\lambda }_0\approx {\omega }_i$ and $\gamma \approx {\omega }_e$. In particular, it is reasonable to assume, for the solar wind plasma, that the typical correlation time is represented by the proton gyration period and corresponds, thus, to the first breakpoint in our model. In the same way, the association between the second breakpoint and the dissipation rate is well-founded since the high frequency breakpoint, roughly corresponding to the electron gyro frequency, has been attributed to wave-particle interaction processes leading to the dissipation of KAWs. The main properties of the spectra observed in the interplanetary space at high frequencies ($\omega >{\omega }_i$) are reproduced by Eq. (5). The power spectrum $E\left(\omega \right)$, as a function of $\omega /{\lambda }_0$, is shown in Figure 1, where $\gamma /{\lambda }_0=100$ was chosen, as this represents a typical value of the ratio ${\omega }_e/{\omega }_i$ found in the interplanetary space (see e.g., [17]).

FIGURE 1

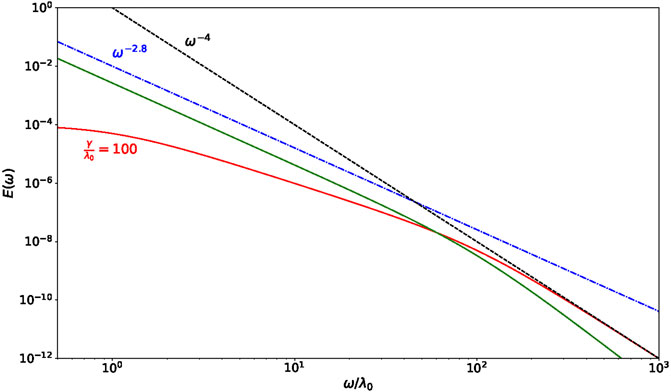
FIGURE 1. $E\left(\omega \right)$ vs. $\omega /{\lambda }_0$ as obtained from Eq. (5) for $\gamma /{\lambda }_0=100$ (red solid line) and from Eq. (7) for $\mu =1.8$ and $\gamma =100$ (green solid line). $E\left(\omega \right)\sim {\omega }^{-2.8}$ (blue dash-dotted line) and $E\left(\omega \right)\sim {\omega }^{-4}$ (black dashed line) are shown as reference.

Equation (5) is compatible with the presence of two power law ranges, similarly to what is reported for observations in some previous works [17, 19]: the first one, between the two breakpoints, with a spectral slope $\alpha \simeq 2$, and the second one, beyond the second breakpoint, with a slope $\alpha \simeq 4$. The separation between the spectral breakpoints is fixed by the ratio $\gamma /{\lambda }_0$ but the slopes of the two power law ranges are independent of the parameters of the model.

Since the power law index reported in observations for the range of scales between the ion and electron breaks varies in the interval $\alpha \in \left[2;3\right]$, we can consider a more realistic case in which a continuous distribution of relaxation rates λ exists. In this case, the power spectrum of the external forcing is calculated from the superposition of all λ′s. If we assume, for instance, a distribution with a probability of occurrence $dP\left(\lambda \right)\sim {\lambda }^{-\mu }d\lambda$ (where μ is a free parameter) in order to take into account phenomena with different correlation ranges, we obtain

$G\left(\omega \right)={\displaystyle {\int }_{{\lambda }_0}^{\gamma }\frac{{\lambda }^{-\mu }d\lambda }{{\omega }^2+{\lambda }^2}}\simeq A\left(\mu \right){\omega }^{-\left(1+\mu \right)}(6)$

where $A\left(\mu \right)={\displaystyle {\int }_{\Delta /\gamma }^{\infty }{x}^{-\mu }{\left(1+x^2\right)}^{-1}dx}$ is a smooth function of µ, and $\Delta$ is a typical scale of the exponential decay rate of stochastic two-points correlations. Assuming $\Delta \sim \gamma$, a simple direct numerical estimate gives $A\left(\mu \right)\simeq \left(0.5-0.13\mu \right)$. The magnetic energy spectrum then becomes

$E\left(\omega \right)\simeq A\left(\mu \right)F_0^2{\omega }^{-\left(1+\mu \right)}{\left({\omega }^2+{\gamma }^2\right)}^{-1}(7)$

The spectum $E\left(\omega \right)$ given by Eq. (7) is shown in Figure 1 for $\mu =1.8$ (green solid line). The same shape $E\left(\omega \right)$ was already used by [19] to fit solar wind magnetic energy spectra measured by Cluster, well reproducing the overall shape of the spectra. Also Eq. (7) is compatible with a double power law, with a slope $\alpha \simeq 1+\mu$ for the first range. Our approach provides a physical interpretation of Eq. (7) as the result of a whole class of colored noises $\xi \left(t\right)$, compatible with the excitation of sporadic wave trains.

When comparing the power spectra obtained from solar wind observations to those given by theoretical models, it is necessary, in general, to take into account the possible failure of the Taylor hypothesis. Measurements are obtained in the spacecraft reference frame, which is in relative motion with respect to the plasma frame of the solar wind. According to the Doppler shift formula, the measured frequency ${\omega }_{sc}$ (in the spacecraft frame), of a Fourier mode of wavevector $k$ and frequency ω, is given by ${\omega }_{sc}=\omega +\mathit{k}\cdot {\mathit{v}}_{\mathit{S}\mathit{W}}$, where $v_{SW}$ is the solar wind velocity. In the high frequency range, which represents the focus of the present work, two relevant situations can occur [42], depending on the ratio between the two terms at the right hand side. When the solar wind speed is slow enough, $\left|\omega \right|\mathrm{\gtrsim }\left|\mathit{k}\cdot {\mathit{v}}_{\mathit{S}\mathit{W}}\right|$ and this leads to a constant shift of the frequency spectrum to higher frequency, in the spacecraft-frame, without changes in the scaling of the spectrum [42]. Therefore, the scaling predictions of our model are still valid in this situation and the only change would be a shift of both low and high frequency breakpoints by a constant value ${\Omega }_0$, namely ${\omega }_i\approx {\lambda }_0+{\Omega }_0$ and ${\omega }_e\approx \gamma +{\Omega }_0$. The other significant case is the dispersive regime, when the plasma-frame frequency increases more rapidly than linearly and ${\omega }_{sc}$ is eventually dominated by the plasma-frequency term $\left({\omega }_{sc}\approx \omega \right)$. Also in this case, since ${\omega }_{sc}\approx \omega$, the spectra of our model can be directly compared to those measured by spacecraft. Problems would arise only if we wanted to map frequency spectra to wavenumber spectra, but this is not a aim of our work, as the nature of the model proposed here is such that high frequency magnetic fluctuations are described in the time/frequency domains and the spectra given by the model are frequency spectra. In other words, in our Brownian framework observations are not interpreted in terms of turbulence and no assumptions about dispersion relations, from plasma turbulence theory, are needed.

2.1 Statistical Properties

The statistical properties of the fluctuations can be related to the properties of the macroscopic dissipation through the Sinai-Ruelle-Bowen (SRB) measure [43]. To this purpose, Eq. (1) can be reformulated as

$\frac{d{b}_j}{dt}=-\alpha \left(b_j,{\xi }_j\right)b_j+F_0{\xi }_j(8)$

where $b_j$ denote the components of the magnetic field fluctuatons and the dissipation parameter is replaced by some unknown stochastic quantity. With a suitable choice of $\alpha \left(b_j,{\xi }_j\right)$, which we define as

$\alpha \left(b_j,{\xi }_j\right)=F_0\frac{{{\displaystyle \sum }}_j{b}_j{\xi }_j}{{{\displaystyle \sum }}_j{b}_j^2/2{\mu }_0}(9)$

(${\mu }_0$ being the vacuum permittivity) Eq. (8) conserves the energy

$\sigma \left(t\right)={\displaystyle \sum }_j\frac{b_j^2}{2{\mu }_0}$

According to the chaotic hypothesis [44, 45], in this case it can be shown [43] that there exists a SRB measure $\Omega \left(d{b}_j\right)$ such that the statistical properties of Eqs. (1) and (8) are the same, in the sense that for a smooth function $F\left(b_j\right)$ we have

$\underset{M\to \infty }{\lim }\frac{1}{M}{\displaystyle \sum }_{k=0}^{M-1}F\left(S^k{b}_j\right)={\displaystyle \underset{A}{\int }\Omega \left(d{b}_j’\right)F\left(b_j’\right)}(10)$

where A is the contracting phase space and $S^k$ represents the time evolution operator, that is, the r.h.s of Eq. (1) with $t=t_k$. The SRB measure is proportional to

$\Omega \left(d{b}_j\right)\sim \delta \left[b_j^2-\sigma \left(t\right)\right]d{b}_j$

and, as expected, the average of α defines the phase-space contraction rate and is proportional to the damping rate $\langle \alpha \rangle \simeq \gamma$.

For systems with reversible dynamics, as those described by Eq. (8), the chaotic hypothesis and the SRB measure generally imply the Onsager reciprocity and the fluctuation-dissipation relation [46]. We consider, from the Itô equation, an equation for the average energy of magnetic fluctuations $\epsilon \left(t\right)=\langle b_j^2/2{\mu }_0\rangle$ in the form

$\frac{d\epsilon }{dt}+\gamma \epsilon =F_0\langle b\left(t\right)\xi \left(t\right)\rangle (11)$

The relation between the magnetic fluctuations and the random forcing term can be formally obtained, from the Itô equation, in the following way

$b\left(t\right)=F_0{\displaystyle {\int }_0^{t}dt\text{'}\xi \left(t\text{'}\right)\exp \left[\gamma \left(t\text{'}-t\right)\right]}$

where we set $b\left(0\right)=0$ for simplicity. By using this result in Eq. (11), we obtain

$\frac{d\epsilon }{dt}=-2\gamma \epsilon +2F_0^{2}G\left(t\right)(12)$

where

$G\left(t\right)={\displaystyle {\int }_0^t\langle \xi \left(s\right)\xi \left(t\right)\rangle e^{\gamma \left(s-t\right)}ds}(13)$

A nearly–stationary solution $E_{stat}$ for the magnetic energy exists and is finite if $G\left(t\to \infty \right)\to G_0$ constant. In this case $E_{stat}\simeq \langle \sigma \rangle$ according to the chaotic hypothesis, so that we obtain the relation

$E_{stat}\simeq F_0^{2}g\left(\gamma ,\lambda ,\mu \right)(14)$

where the unknown function $g\left(\gamma ,\lambda ,\mu \right)$ involves the dissipation rate γ, the correlation rates λ and the scaling exponent μ.

On the other hand, from the definition of the magnetic energy power spectrum and using Eq. (3), we obtain

$\langle b_{\omega }{b}_{\omega }^{\mathrm{\star }}\rangle =\frac{F_0^{2}G\left(\omega \right)}{{\omega }^2+{\gamma }^2}={\displaystyle {\int }_0^{\infty }dt\langle b\left(t\right)b\left(0\right)\rangle \cos \omega t}(15)$

At equilibrium $\omega \simeq 0$ and $G\left(\omega \right)\simeq 1$, so that by eliminating $F_0$ from Eqs. (15) and (14), we obtain

$\left(\frac{B_0^2}{2{\mu }_0}\right){\gamma }^{2}g\left(\gamma ,\lambda ,\mu \right)\simeq E_{stat}(16)$

where $B_0^2$ is the square modulus of the total magnetic field. This last equation represents a kind of Fluctuation–Dissipation Relation (FDR) [41, 47]. The use of the FDR for the description of plasma fluctuations is known since a long time (see e.g., [48]). In the context of space magnetized plasmas the FDR approach has been utilized to study electromagnetic fluctuations associated to different wave modes in various configurations (see e.g., [49–52]). In the framework of the model proposed in this work, the FDR can be used to investigate the collisionless dissipation mechanism at work in the solar wind. To this aim, the function $g\left(\gamma ,\lambda ,\mu \right)$ can be calculated from Eq. (11), which can be formally integrated, thus obtaining, after some algebra,

$\epsilon \left(t\right)=\left(F_0^2/{\mu }_0\right)e^{-2\gamma t}{\displaystyle {\int }_0^{t}ds{e}^{2\gamma s}}{\displaystyle {\int }_0^{s}dt\text{'}{e}^{\gamma \left(t\text{'}-s\right)}\langle \xi \left(t\text{'}\right)\cdot \xi \left(s\right)\rangle }$

The last equation depends on the time correlations of the forcing. For example, by using Eq. (4), we obtain $g\left(\gamma ,\lambda ,\mu \right)=1/2\gamma \left(\gamma -{\lambda }_0\right)$, and hence

$\left(\frac{\gamma }{{\lambda }_0}\right)\simeq \frac{2\beta }{\beta -1}(17)$

where we defined $\beta ={\left(B_0^2/2{\mu }_0\right)}^{-1}{E}_{stat}$ proportional to $E_{stat}$. By using the more refined hypothesis involving a distribution of decorrelation times, we obtain the relation

$\begin{array}{c}\left(\frac{\gamma }{{\lambda }_0}\right)\simeq h\left(\mu \right){\left(\frac{B_0^2}{2{\mu }_0}\right)}^{1/\left(\mu -1\right)}{E}_{stat}^{-1/\left(\mu -1\right)}\\ \simeq h\left(\mu \right){\beta }^{-1/\left(\mu -1\right)}\end{array}(18)$

where $h\left(\mu \right)={\left[{\displaystyle {\int }_{\Delta /\gamma }^{\infty }{x}^{-\mu }{\left(x-1\right)}^{-1}dx}\right]}^{1/\left(\mu -1\right)}$ and assuming as before $\Delta \sim \gamma$, a simple direct numerical estimate gives $h\left(\mu \right)\simeq {\left(6-\mu /3\right)}^{1/\left(\mu -1\right)}$.

The FDR relation Eq. (18) is very interesting because it allows us to obtain information about the physical mechanism responsible for the dissipative term. If we conjecture that energy equipartition is present, as in standard statistical mechanics, we can interpret $E_{stat}$ as due to a statistical equilibrium at some temperature$k_{B}T$ corresponding to the second moment of the velocity distribution function measured by a spacecraft. Therefore, by using the value $1+\mu =8/3$, which roughly represents the center of the peak of the observed distribution of slopes in the ionic scale range, $E_{stat}^{-1/\left(\mu -1\right)}={\left(k_{B}T\right)}^{-3/2}$ and Eq. (18) gives

$\left(\frac{\gamma }{{\lambda }_0}\right)\sim {\left(k_{B}T\right)}^{-3/2}(19)$

which corresponds to the classical scaling for the electron Landau damping. Therefore, according to our model the observed spectral properties of magnetic fluctuations at ionic scales are compatible with the occurrence of electron Landau damping. It is worthwhile to remark that according to our approach, the spectral properties of magnetic fluctuations are not necessarily the result of a turbulent cascade process. Rather the spectrum is a direct consequence of the FDR, which governs at the same time both fluctuations and dissipation, which represent the two ingredients of the same physical process. Of course, in a classical turbulent environment [2] the fluctuations generated by the cascade process are not subject to dissipation, which starts beyond the Kolmogorov microscale breakpoint. Our approach can be linked to kinetic turbulent cascades by using nonequilibrium ensembles in turbulence models [53, 54].

Note that assuming that the β parameter in Eq. (18) is the usual plasma-β parameter, the FDR (Eq. 18) suggests that the high-frequency spectral breakpoint shifts toward higher frequencies as the solar wind plasma-β decreases, in agreement with observations. The electron break can be hardly or no observable in the data because it can be located out of the instrumental range or hidden by the high-frequency instrumental noise (see e.g., [55]). Our approach enables, at least, to obtain an estimate of the break position even when it is out of the observable instrumental range. This is because the FDR has a predictive meaning, as the spectral properties of magnetic fluctuations depend on the parameter used to describe the dissipation, so that by measuring the parameter µ, through the magnetic power spectra at ionic scales, and the plasma-β parameter, we are able to investigate the frequency location of the electron break, even when it can not be observed.

3 Discussion

In this paper we introduce a framework to describe the high–frequency dynamics of magnetic fluctuations in the interplanetary space. Our description is rather different from the nonlinear energy cascade framework, successfully used to describe low–frequency fluctuations. By using a Brownian–like approach, we are able to describe the main properties of the magnetic energy spectra observed at high frequencies in the solar wind. We remark that the same kind of phenomenology was used by [56] to describe the susceptibility of fluctuations under the action of random forcing, within the Direct Interaction Approximation of the complex nonlinear mode couplings generated by the fluid turbulent cascade. Of course, our approach does not rule out the importance of all the complex dynamics coming from plasma physics. Kinetic plasma physics describes, indeed, all the microscopic features involved in the dynamics of fluctuations, namely the birth of the many modes involved, their nonlinear coupling, their dispersive properties, and the collissionless dissipative processes which lead to anomalous plasma–heating.

Using our approach, we describe, at the same time, both fluctuations and dissipation in the high-frequency range of solar wind plasmas, where high-frequency microphysical plasma effects are modelled as a stochastic source, whose details, in this framework, are unessential. Through the FDR, we evidence the relationship between fluctuations and dissipation in a way that, independently of the specific microphysical plasma dynamics, we can account for the main features of the spectral properties of high-frequency fluctuations in the interplanetary space. In fact, as usual in a Brownian-like approach [41], the FDR has a predictive meaning for some microphysical quantities. In our case, Eq. (18) opens a window on the high-frequency fluctuations, allowing us to estimate the position of the electron break as a function of fully measurable quantities in the solar wind, similarly to the Einstein’s approach to Brownian motion. Moreover, the scaling of the damping rate results compatible with the presence of electron Landau damping, which therefore can be identified as the main dissipation mechanism in the collisionless solar wind plasma.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

VC conceived the study and the model. VC and FL prepared the article draft. All the authors contributed to scientific discussions, model refinement and writing of the article.

Funding

VC, FL, and FC were supported by Italian MIUR-PRIN Grant No. 2017APKP7T on Circumterrestrial Environment: Impact of Sun-Earth Interaction.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Coleman PJ. Jr. Turbulence, viscosity, and dissipation in the solar-wind plasma. Astrophys J (1968) 153:371. doi:10.1086/149674

CrossRef Full Text | Google Scholar

2. Bruno R, Carbone V. Turbulence in the solar wind. Berlin, Germany: Springer (2016). doi:10.1007/978-3-319-43440-7

CrossRef Full Text

3. Burlaga LF. Intermittent turbulence in the solar wind. J Geophys Res (1991) 96:5847–51. doi:10.1029/91JA00087

CrossRef Full Text | Google Scholar

4. Carbone V, Bruno R, Sorriso-Valvo L, Lepreti F. Intermittency of magnetic turbulence in slow solar wind. Planet Space Sci (2004) 52:953–6. doi:10.1016/j.pss.2004.02.005

CrossRef Full Text | Google Scholar

5. Marsch E, Liu S. Structure functions and intermittency of velocity fluctuations in the inner solar wind. Ann Geophysicae (1993) 11:227–38.

Google Scholar

6. Sorriso-Valvo L, Carbone V, Veltri P, Consolini G, Bruno R. Intermittency in the solar wind turbulence through probability distribution functions of fluctuations. Geophys Res Lett (1999) 26:1801–4. doi:10.1029/1999GL900270

CrossRef Full Text | Google Scholar

7. Burlaga LF. Multifractal structure of the interplanetary magnetic field: voyager 2 observations near 25 AU, 1987-1988. Geophys Res Lett (1991) 18:69–72. doi:10.1029/90GL02596

CrossRef Full Text | Google Scholar

8. Carbone V, Lepreti F, Sorriso-Valvo L, Veltri P, Antoni V, Bruno R. Scaling laws in plasma turbulence. Nuovo Cimento Rivista Serie (2004) 27:1–108. doi:10.1393/ncr/i2005-10003-1

CrossRef Full Text | Google Scholar

9. Carbone V. Cascade model for intermittency in fully developed magnetohydrodynamic turbulence. Phys Rev Lett (1993) 71:1546–8. doi:10.1103/PhysRevLett.71.1546

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Carbone V. Scaling exponents of the velocity structure functions in the interplanetary medium. Ann Geophys (1994) 12:585–90. doi:10.1007/s00585-994-0585-3

CrossRef Full Text | Google Scholar

11. Marsch E, Tu C-Y, Rosenbauer H. Multifractal scaling of the kinetic energy flux in solar wind turbulence. Ann Geophys (1996) 14:259–69. doi:10.1007/s00585-996-0259-4

CrossRef Full Text | Google Scholar

12. Banerjee S, Hadid LZ, Sahraoui F, Galtier S. Scaling of compressible magnetohydrodynamic turbulence in the fast solar wind. Astrophys J (2016) 829:L27. doi:10.3847/2041-8205/829/2/l27

CrossRef Full Text | Google Scholar

13. Carbone V, Marino R, Sorriso-Valvo L, Noullez A, Bruno R. Scaling laws of turbulence and heating of fast solar wind: the role of density fluctuations. Phys Rev Lett (2009) 103:061102. doi:10.1103/PhysRevLett.103.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

14. MacBride BT, Smith CW, Forman MA. The turbulent cascade at 1 AU: energy transfer and the third‐order scaling for MHD. Astrophys J (2008) 679:1644–60. doi:10.1086/529575

CrossRef Full Text | Google Scholar

15. Sorriso-Valvo L, Marino R, Carbone V, Noullez A, Lepreti F, Veltri P, et al. Observation of inertial energy cascade in interplanetary space plasma. Phys Rev Lett (2007) 99:115001. doi:10.1103/PhysRevLett.99.115001

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Leamon RJ, Smith CW, Ness NF, Matthaeus WH, Wong HK. Observational constraints on the dynamics of the interplanetary magnetic field dissipation range. J Geophys Res (1998) 103:4775–87. doi:10.1029/97JA03394

CrossRef Full Text | Google Scholar

17. Sahraoui F, Goldstein ML, Robert P, Khotyaintsev YV. Evidence of a cascade and dissipation of solar-wind turbulence at the electron gyroscale. Phys Rev Lett (2009) 102:231102. doi:10.1103/PhysRevLett.102.231102

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Alexandrova O, Lacombe C, Mangeney A, Grappin R, Maksimovic M. Solar wind turbulent spectrum at plasma kinetic scales. Astrophys J (2012) 760:121. doi:10.1088/0004-637x/760/2/121

CrossRef Full Text | Google Scholar

19. Sahraoui F, Huang SY, Belmont G, Goldstein ML, Rétino A, Robert P, et al. Scaling of the electron dissipation range of solar wind turbulence. Astrophys J (2013) 777:15. doi:10.1088/0004-637X/777/1/15

CrossRef Full Text | Google Scholar

20. Bruno R, Carbone V. The solar wind as a turbulence laboratory. Living Rev Solar Phys (2013) 10:2. doi:10.12942/lrsp-2013-2

CrossRef Full Text | Google Scholar

21. Marsch E. Kinetic physics of the solar corona and solar wind. Living Rev Solar Phys (2006) 3:1. doi:10.12942/lrsp-2006-1

CrossRef Full Text | Google Scholar

22. Parashar TN, Salem C, Wicks RT, Karimabadi H, Gary SP, Matthaeus WH. Turbulent dissipation challenge: a community-driven effort. J Plasma Phys (2015) 81:905810513. doi:10.1017/S0022377815000860

CrossRef Full Text | Google Scholar

23. Narita Y, Gary SP, Saito S, Glassmeier K-H, Motschmann U. Dispersion relation analysis of solar wind turbulence. Geophys Res Lett (2011) 38:L05101. doi:10.1029/2010GL046588

CrossRef Full Text | Google Scholar

24. Perschke C, Narita Y, Motschmann U, Glassmeier KH. Observational test for a random sweeping model in solar wind turbulence. Phys Rev Lett (2016) 116:125101. doi:10.1103/PhysRevLett.116.125101

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Narita Y. Space-time structure and wavevector anisotropy in space plasma turbulence. Living Rev Sol Phys (2018) 15:2. doi:10.1007/s41116-017-0010-0

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Hollweg JV, Isenberg PA. Generation of the fast solar wind: a review with emphasis on the resonant cyclotron interaction. J Geophys Res (2002) 107:1147. doi:10.1029/2001JA000270

CrossRef Full Text | Google Scholar

27. Schekochihin AA, Cowley SC, Dorland W, Hammett GW, Howes GG, Quataert E, et al. Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys J Suppl Ser (2009) 182:310–77. doi:10.1088/0067-0049/182/1/310

CrossRef Full Text | Google Scholar

28. Dmitruk P, Matthaeus WH, Seenu N. Test particle energization by current sheets and nonuniform fields in magnetohydrodynamic turbulence. Astrophys J (2004) 617:667–79. doi:10.1086/425301

CrossRef Full Text | Google Scholar

29. Karimabadi H, Roytershteyn V, Wan M, Matthaeus WH, Daughton W, Wu P, et al. Coherent structures, intermittent turbulence, and dissipation in high-temperature plasmas. Phys Plasmas (2013) 20:012303. doi:10.1063/1.4773205

CrossRef Full Text | Google Scholar

30. Parashar TN, Servidio S, Shay MA, Breech B, Matthaeus WH. Effect of driving frequency on excitation of turbulence in a kinetic plasma. Phys Plasmas (2011) 18:092302. doi:10.1063/1.3630926

CrossRef Full Text | Google Scholar

31. Parashar TN, Shay MA, Cassak PA, Matthaeus WH. Kinetic dissipation and anisotropic heating in a turbulent collisionless plasma. Phys Plasmas (2009) 16:032310. doi:10.1063/1.3094062

CrossRef Full Text | Google Scholar

32. Sundkvist D, Retinò A, Vaivads A, Bale SD. Dissipation in turbulent plasma due to reconnection in thin current sheets. Phys Rev Lett (2007) 99:025004. doi:10.1103/PhysRevLett.99.025004

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Wan M, Matthaeus WH, Karimabadi H, Roytershteyn V, Shay M, Wu P, et al. Intermittent dissipation at kinetic scales in collisionless plasma turbulence. Phys Rev Lett (2012) 109:195001. doi:10.1103/PhysRevLett.109.195001

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Chandran BDG, Verscharen D, Quataert E, Kasper JC, Isenberg PA, Bourouaine S. Stochastic heating, differential flow, and the alpha-to-proton temperature ratio in the solar wind. Astrophys J (2013) 776:45. doi:10.1088/0004-637X/776/1/45

CrossRef Full Text | Google Scholar

35. Chandran BDG. Alfvén-wave turbulence and perpendicular ion temperatures in coronal holes. Astrophys J (2010) 720:548–54. doi:10.1088/0004-637X/720/1/548

CrossRef Full Text | Google Scholar

36. Chaston CC, Bonnell JW, Carlson CW, McFadden JP, Ergun RE, Strangeway RJ, et al. Auroral ion acceleration in dispersive Alfvén waves. J Geophys Res (2004) 109:A04205. doi:10.1029/2003JA010053

CrossRef Full Text | Google Scholar

37. McChesney JM, Stern RA, Bellan PM. Observation of fast stochastic ion heating by drift waves. Phys Rev Lett (1987) 59:1436–9. doi:10.1103/PhysRevLett.59.1436

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Xia Q, Perez JC, Chandran BDG, Quataert E. Perpendicular ion heating by reduced magnetohydrodynamic turbulence. Astrophys J (2013) 776:90. doi:10.1088/0004-637X/776/2/90

CrossRef Full Text | Google Scholar

39. Bale SD, Kellogg PJ, Mozer FS, Horbury TS, Reme H. Measurement of the electric fluctuation spectrum of magnetohydrodynamic turbulence. Phys Rev Lett (2005) 94:215002. doi:10.1103/PhysRevLett.94.215002

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Cerri SS, Califano F. Reconnection and small-scale fields in 2d-3v hybrid-kinetic driven turbulence simulations. New J Phys (2017) 19:025007. doi:10.1088/1367-2630/aa5c4a

CrossRef Full Text | Google Scholar

41. Gardiner C. Stochastic methods. Berlin Heidelberg: Springer-Verlag (2009).

42. Klein KG, Howes GG, TenBarge JM. The violation of the taylor hypothesis in measurements of solar wind turbulence. Astrophys J (2014) 790, L20. doi:10.1088/2041-8205/790/2/L20

CrossRef Full Text | Google Scholar

43. Gallavotti G, Cohen EGD. Dynamical ensembles in nonequilibrium statistical mechanics. Phys Rev Lett (1995) 74:2694–7. doi:10.1103/PhysRevLett.74.2694

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Ruelle D. A review of linear response theory for general differentiable dynamical systems. Nonlinearity (2009) 22:855–70. doi:10.1088/0951-7715/22/4/009

CrossRef Full Text | Google Scholar

45. Ruelle D. General linear response formula in statistical mechanics, and the fluctuation-dissipation theorem far from equilibrium. Phys Lett A (1998) 245:220–4. doi:10.1016/S0375-9601(98)00419-8

CrossRef Full Text | Google Scholar

46. Gallavotti G. Chaotic hypothesis: Onsager reciprocity and fluctuation-dissipation theorem. J Stat Phys (1996) 84:899–925. doi:10.1007/BF02174123

CrossRef Full Text | Google Scholar

47. Callen HB, Welton TA. Irreversibility and generalized noise. Phys Rev (1951) 83:34–40. doi:10.1103/PhysRev.83.34

CrossRef Full Text | Google Scholar

48. Sitenko A. Electromagnetic fluctuations in plasmas. New York, NY: Academic Press (1967).

49. Araneda JA, Astudillo H, Marsch E. Interactions of alfvén-cyclotron waves with ions in the solar wind. Space Sci Rev (2012) 172:361–72. doi:10.1007/s11214-011-9773-0

CrossRef Full Text | Google Scholar

50. Navarro R, Moya P, Muñoz V, Araneda J, Valdivia J, et al. Solar wind thermally induced magnetic fluctuations. Phys Rev Lett (2014) 112:245001. doi:10.1103/physrevlett.112.245001

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Navarro RE, Araneda J, Muñoz V, Moya PS, F.-Viñas A, Valdivia JA. Theory of electromagnetic fluctuations for magnetized multi-species plasmas. Phys Plasmas (2014) 21:092902. doi:10.1063/1.4894700

CrossRef Full Text | Google Scholar

52. Viñas AF, Moya PS, Navarro R, Araneda JA. The role of higher-order modes on the electromagnetic whistler-cyclotron wave fluctuations of thermal and non-thermal plasmas. Phys Plasmas (2014) 21:012902. doi:10.1063/1.4861865

CrossRef Full Text | Google Scholar

53. Biferale L, Cencini M, De Pietro M, Gallavotti G, Lucarini V. Equivalence of nonequilibrium ensembles in turbulence models. Phys Rev E (2018) 98:012202. doi:10.1103/PhysRevE.98.012202

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Gallavotti G. Chaotic principle: some applications to developed turbulence. J Stat Phys (1997) 86:907–34. doi:10.1007/BF02183608

CrossRef Full Text | Google Scholar

55. Goldstein ML, Wicks RT, Perri S, Sahraoui F. Kinetic scale turbulence and dissipation in the solar wind: key observational results and future outlook. Phil Trans R Soc A (2015) 373:20140147. doi:10.1098/rsta.2014.0147

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Kraichnan RH. The structure of isotropic turbulence at very high Reynolds numbers. J Fluid Mech (1959) 5:497–543. doi:10.1017/S0022112059000362

CrossRef Full Text | Google Scholar