- 1P.P. Shirshov Institute of Oceanology of RAS, Moscow, Russia
- 2Skolkovo Institute of Science and Technology, Moscow, Russia
- 3Institute of Automation and Electrometry of SB RAS, Novosibirsk, Russia
In this brief report we study numerically the spontaneous emergence of rogue waves in 1) modulationally unstable plane wave at its long-time statistically stationary state and 2) bound-state multi-soliton solutions representing the solitonic model of this state. Focusing our analysis on the cohort of the largest rogue waves, we find their practically identical dynamical and statistical properties for both systems, that strongly suggests that the main mechanism of rogue wave formation for the modulational instability case is multi-soliton interaction. Additionally, we demonstrate that most of the largest rogue waves are very well approximated–simultaneously in space and in time–by the amplitude-scaled rational breather solution of the second order.
1 Introduction
The phenomenon of rogue waves (RWs)—unusually large waves that appear suddenly from moderate wave background–was intensively studied in the recent years. A number of mechanisms were suggested to explain their emergence, see e.g., the reviews [1–3]; with the most general idea stating that RWs could be related to breather-type solutions of the underlying nonlinear evolution equations [4–6]. Currently, ones of the most popular models for RWs are the Peregrine rational breather [7] and the higher-order rational breather [8] solutions of the one-dimensional nonlinear Schrödinger equation (1D-NLSE) of the focusing type,
These solutions belong to a family of localized in space and time algebraic breathers, which evolve on a finite background and lead to three-fold, five-fold, seven-fold, and so on, increase in amplitude at the time of their maximum elevation. Taking specific and carefully designed initial conditions, they were reproduced in well-controlled experiments performed in different physical systems [9–13].
The 1D-NLSE is integrable in terms of the inverse scattering transform (IST), as it allows transformation to the so-called scattering data, which is in one-to-one correspondence with the wavefield and, similarly to the Fourier harmonics in the linear wave theory, changes trivially during the motion. Thanks to its properties, the scattering data can be used to characterize the wavefield. For spatially localized case, the scattering data consists of the discrete (solitons) and the continuous (nonlinear dispersive waves) parts of eigenvalue spectrum, calculated for specific auxiliary linear system. For strongly nonlinear wavefields, such as the ones where emergence of rational breathers can be expected, the solitons provide the main contribution to the energy [14] and should therefore play the dominant role in the dynamics. In particular, as has been recently demonstrated in [15]; the modulationally unstable plane wave (the condensate) at its long-time statistically stationary state can be accurately modeled (in the statistical sense) with a certain soliton gas, designed to follow the solitonic structure of the condensate. The latter naturally raises a question of whether there is a difference between the RWs emerging in the two systems. Indeed, in a soliton gas all RWs are multi-soliton interactions by construction. Hence, if there is no significant difference, then we can draw a hypothesis that for the asymptotic stationary state of the MI (and, possibly, for other strongly nonlinear wavefields) the main mechanism of RW formation is interaction of solitons.
With the present paper, we contribute to the answer on this question by summarizing our observations of RWs for both systems. Specifically, we compute time evolution for 1,000 random realizations of the noise-induced MI of the condensate and also for 1,000 random realizations of 128-soliton solutions modeling the asymptotic state of the MI. For each realization, we analyze one largest RW emerging in the course of the evolution, thus focusing our analysis on the largest RWs. For both systems, we observe practically identical dynamical and statistical properties of the collected RWs. In particular, most of the RWs turn out to be very well approximated–simultaneously in space and in time–by the amplitude-scaled rational breather solution (RBS) of the second order. By measuring deviation between RWs and their fits with RBS as an integral of the difference in the
Note that in the present paper we consider solutions of the 1D-NLSE for three different types of boundary conditions: the MI of the condensate for which we use the periodic boundary, the multi-soliton solutions with vanishing border conditions and the RBS having constant border conditions at infinity. Globally, these solutions are fundamentally different, and the different border conditions require application of separate IST techniques, see e.g., [5, 14, 16, 17]. For instance, formally our MI case corresponds to finite-band scattering data. However, the characteristic widths of the structures (RWs, solitons, RBS) are small compared to the sizes of the studied wavefields, so that the eigenvalue bands are very narrow and we neglect their difference from solitons. The similar idea was suggested in [18]; where, vice versa, the soliton gas was considered as a limit of finite-band solutions. Effectively, we assume that formation of a RW, as a local phenomenon, represents a similar process for all three cases of border conditions. As we demonstrate in the paper, this assumption is supported by the presented results, that raises an important problem that we leave for future studies–explanation of how the three models may exhibit locally similar nonlinear patterns.
2 Numerical Methods
For both the MI of the condensate and the soliton gas initial conditions, we solve Eq. 1 numerically in a large box
Without loss of generality, the initial conditions for the noise-induced MI of the condensate can be written as
where
where
To generate soliton gas, modeling the asymptotic stationary state of the noise-induced MI, we use exact 128-soliton solutions of the 1D-NLSE. More precisely, we compute the corresponding wavefields using numerical implementation of the 1D-NLSE integration technique–the so-called dressing method [20]—with 100-digits precision arithmetics, as described in [21]. Each soliton has four parameters: amplitude
Following [15]; we distribute soliton amplitudes according to the Bohr-Sommerfeld quantization rule,
and set soliton velocities to zero,
For the soliton gas, we gather the RWs by simulating time evolution of the 128-soliton solutions in the interval
For the MI of the condensate, we collect the RWs similarly, but in the time interval
The rational breather solution of the first order (RBS1)—the Peregrine breather [7]—reads as
The RBS of the second order (RBS2)
Note that, in general, RBS may have nonzero velocity
Also note that in addition to the RBS1 and the RBS2, we have examined approximation with the RBS of the 3rd order [8]; as well. However, we have found that it works worse than either the RBS1, or the RBS2 for all 2000 examined RWs, and thereby excluded it from the analysis.
3 Rogue Waves With Rational Profiles
We start this Section with description of one RW event for the soliton gas case, and then continue with examination of RW properties for both systems–the noise-induced MI close to its asymptotic stationary state and the soliton gas representing the solitonic model of this state.
An example of one of the 10 largest RWs collected for the soliton gas case is shown in Figure 1. The space profile
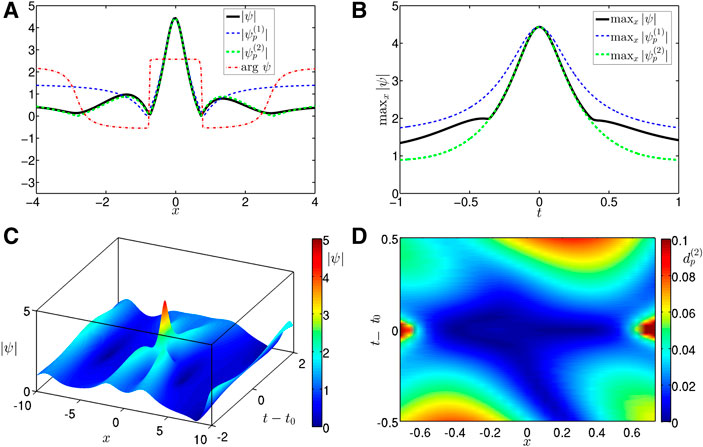
FIGURE 1. (Color on-line) One of the 10 largest RWs (the coordinate of maximum amplitude is shifted to zero for better visualization) for the soliton gas case with time of occurrence
The deviation between a RW and its approximation with a RBS can be measured locally as
Figure 1D shows this deviation
As an integral measure reflecting the deviation between a RW and a RBS, one can consider a quantity
Here we choose the region of integration over time
The quantity Eq. 7 can be used to assess how well a RW can be approximated by a RBS. Figure 2A shows the minimum deviation
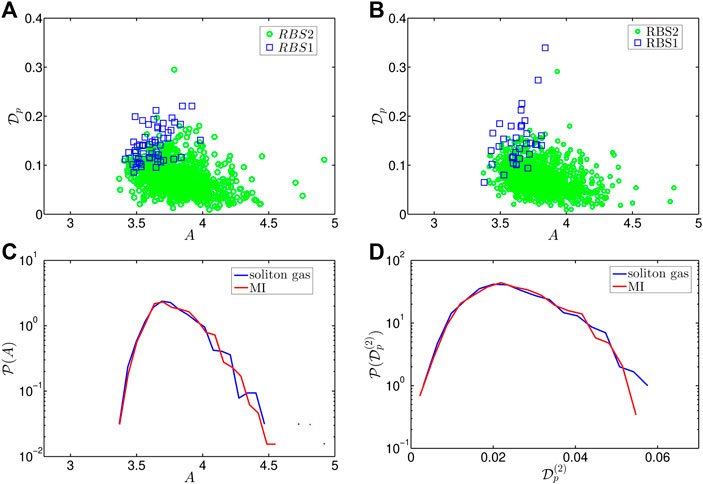
FIGURE 2. (Color on-line) (A,B) Deviation
RWs collected close to the statistically stationary state of the noise-induced MI show the same general properties as those for the soliton gas case. Figure 2B demonstrates very similar “clouds” of RWs approximated with either the RBS1, or the RBS2 on the diagram representing the minimum deviation
The RWs for the two types of initial conditions turn out to be practically identically distributed by their maximum amplitude, as demonstrated in Figure 2C with the corresponding probability density functions (PDFs). The PDFs of the deviation
4 Discussion and Future Directions
As we have mentioned in [21]; some two- and three-soliton collisions at the time of their maximum elevation have space profiles remarkably similar to those of the RBS1 and the RBS2. Moreover, we have presented an example of a phase-synchronized three-soliton collision, for which both the space profile and the temporal evolution of the maximum amplitude are very well approximated by the RBS2. The solitons in [21] had nonzero velocities; here we modify the two- and three-soliton examples for the case of zero velocities and also examine the local deviations
Figure 3 shows an example of three-soliton interaction with solitons having amplitudes
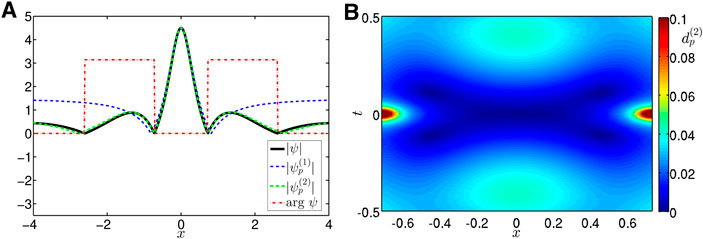
FIGURE 3. (Color on-line) Synchronized three-soliton interaction of solitons having amplitudes
To analyze how often phase-synchronized interactions of two and three solitons of various amplitudes may lead to such quasi-rational profiles, we have created 20 two-soliton and 20 three-soliton interactions with solitons of random amplitudes, zero velocities
We think that the presented elementary three-soliton model might provide an explanation of RW formation inside multi-soliton solutions. The most direct way for future studies might be a demonstration of a RW for synchronized many-soliton solution. Here, however, we face a new question, that is, whether formation of a RW is a collective phenomenon that requires synchronization of all the solitons, or a “local” event that can be achieved by synchronizing of a few with arbitrary parameters of the others. Note that even the latter case represents a challenging problem. Indeed, the few solitons that generate a RW acquire space and phase shifts due to the presence of the remaining solitons, that should influence their optimal synchronization condition. For remote solitons, the shifts can be computed analytically using the well-known asymptotic formulas, see e.g., [14]; which however do not work for our case of a dense soliton gas where all solitons effectively interact with each other. This leaves us two options: 1) a local numerical synchronization of a small group with “trial and error” method and 2) calculation of generalized space-phase shifts for closely located solitons. Both ways seem challenging at the moment.
Also note that our study is limited with respect to statistical analysis of RWs, as we have focused on the largest RWs, while the “common” RWs may have different dynamical and statistical properties. Nevertheless, we believe that, since the largest RWs for the two systems show identical properties, the “common” RWs have identical properties too. Identification of all the RWs according to the standard criterion
5 Conclusion
In this brief report we have presented our observations of RWs within the 1D-NLSE model for 1) the modulationally unstable plane wave at its long-time statistically stationary state and 2) the bound-state multi-soliton solutions representing the solitonic model of this state. Focusing our analysis on the largest RWs, we have found their practically identical dynamical and statistical properties for both systems. In particular, most of the RWs turn out to be very well approximated–simultaneously in space and in time–by the amplitude-scaled rational breather solution of the second order (RBS2), see Figures 1, 2 and the two sets of the collected RWs are identically distributed by their maximum amplitude and deviation from the RBS2, see Figures 2C,D. Additionally, we have demonstrated the appearance of quasi-rational profiles very similar to that of the RBS2 already for synchronized three-soliton interactions, see e.g., Figure 3.
The main messages of the present paper can be summarized as follows. First, a quasi-rational profile very similar to a RBS does not necessarily mean emergence of the corresponding rational breather, as it can be a manifestation of a multi-soliton interaction. Second, the identical dynamical and statistical properties of RWs collected for the two examined systems strongly suggest that the main mechanism of RW formation should be the same, i.e., that RWs emerging in the asymptotic stationary state of the MI (and, possibly, in other strongly nonlinear wavefields) are formed as interaction of solitons. However, more study is necessary to clarify exactly how interaction of solitons within a large wavefield may lead to formation of a RW, and we plan to continue this research in the future.
As future directions of our studies, we consider two problems. The first is about examination of whether formation of a RW in a soliton gas is a collective phenomenon that requires synchronization of all the solitons, or a “local” event that can be achieved by synchronizing of a few. The second problem relates to statistical analysis of all the RWs according to the standard criterion
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors contributed significantly to this work.
Funding
The work of DA on simulations and data analysis was supported by the state assignment of IO RAS, Grant No. 0128-2021-0003. The work of AG on generation of multi-soliton solutions and two- and three-soliton models was supported by RFBR Grant No. 19-31-60028.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Simulations were performed at the Novosibirsk Supercomputer Center (NSU).
References
1. Kharif C, Pelinovsky E. Physical mechanisms of the rogue wave phenomenon. Eur J Mech—B/Fluids (2003) 22:603–34. doi:10.1016/j.euromechflu.2003.09.002
2. Dysthe K, Krogstad HE, Müller P. Oceanic rogue waves. Annu Rev Fluid Mech (2008) 40:287–310. doi:10.1146/annurev.fluid.40.111406.102203
3. Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi FT. Rogue waves and their generating mechanisms in different physical contexts. Phys Rep (2013) 528:47–89. doi:10.1016/j.physrep.2013.03.001
4. Dysthe KB, Trulsen K. Note on breather type solutions of the NLS as models for freak-waves. Physica Scripta, T82 (1999) 48. doi:10.1238/physica.topical.082a00048
5. Osborne A. Nonlinear ocean waves and the inverse scattering transform. Cambridge, MA: Academic Press (2010).
6. Shrira VI, Geogjaev VV. What makes the peregrine soliton so special as a prototype of freak waves?. J Eng Math (2010) 67:11–22. doi:10.1007/s10665-009-9347-2
7. Peregrine DH. Water waves, nonlinear Schrödinger equations and their solutions. J Aust Math Soc Ser B, Appl. Math (1983) 25:16–43. doi:10.1017/s0334270000003891
8. Akhmediev N, Ankiewicz A, Soto-Crespo JM. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys Rev E (2009) 80:026601. doi:10.1103/physreve.80.026601
9. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The Peregrine soliton in nonlinear fibre optics. Nat Phys (2010) 6:790. doi:10.1038/nphys1740
10. Chabchoub A, Hoffmann NP, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett (2011) 106:204502. doi:10.1103/physrevlett.106.204502
11. Bailung H, Sharma SK, Nakamura Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011) 107:255005. doi:10.1103/physrevlett.107.255005
12. Chabchoub A, Hoffmann N, Onorato M, Akhmediev N. Super rogue waves: observation of a higher-order breather in water waves. Phys Rev X (2012) 2:011015. doi:10.1103/physrevx.2.011015
13. Chabchoub A, Hoffmann N, Onorato M, Slunyaev A, Sergeeva A, Pelinovsky E, et al. Observation of a hierarchy of up to fifth-order rogue waves in a water tank. Phys Rev E (2012) 86:056601. doi:10.1103/physreve.86.056601
14. Novikov S, Manakov SV, Pitaevskii LP, Zakharov VE. Theory of solitons: the inverse scattering method. Berlin, Germany: Springer Science and Business Media (1984).
15. Gelash A, Agafontsev D, Zakharov V, El G, Randoux S, Suret P. Bound state soliton gas dynamics underlying the noise-induced modulational instability. Phys Rev Lett (2019) 123:234102. doi:10.1103/physrevlett.123.234102
16. Belokolos ED, Bobenko AI, Enol’skii VZ, Its AR, Matveev VB. Algebro-geometric approach to nonlinear integrable equations. Berlin, Germany: Springer-Verlag (1994).
17. Bobenko AI, Klein C. Computational approach to Riemann surfaces. Berlin, Germany: Springer Science and Business Media (2011).
18. El GA, Krylov AL, Molchanov SA, Venakides S. Soliton turbulence as a thermodynamic limit of stochastic soliton lattices. Physica D: Nonlinear Phenomena (2001) 152-153:653–64. doi:10.1016/s0167-2789(01)00198-1
19. Agafontsev DS, Zakharov VE. Integrable turbulence and formation of rogue waves. Nonlinearity (2015) 28:2791. doi:10.1088/0951-7715/28/8/2791
20. Zakharov VE, Mikhailov AV. Relativistically invariant two-dimensional models of field theory which are integrable by means of the inverse scattering problem method. Soviet Phys JETP (1978) 47:1017–1027.
21. Gelash AA, Agafontsev DS. Strongly interacting soliton gas and formation of rogue waves. Phys Rev E (2018) 98:042210. doi:10.1103/physreve.98.042210
22. Zakharov VE, Shabat AB. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Soviet Phys JETP (1972) 34:62.
23. Lewis ZV. Semiclassical solutions of the Zaharov-Shabat scattering problem for phase modulated potentials. Phys Lett A (1985) 112:99–103. doi:10.1016/0375-9601(85)90665-6
24. Kedziora DJ, Ankiewicz A, Akhmediev N. The phase patterns of higher-order rogue waves. J Opt (2013) 15:064011. doi:10.1088/2040-8978/15/6/064011
Keywords: solitons, breathers, rogue waves, integrable systems, modulational instability
Citation: Agafontsev DS and Gelash AA (2021) Rogue Waves With Rational Profiles in Unstable Condensate and Its Solitonic Model. Front. Phys. 9:610896. doi: 10.3389/fphy.2021.610896
Received: 27 September 2020; Accepted: 20 January 2021;
Published: 09 April 2021.
Edited by:
Heremba Bailung, Ministry of Science and Technology, IndiaReviewed by:
Haci Mehmet Baskonus, Harran University, TurkeyMatteo Conforti, UMR8523 Physique des lasers, atomes et molécules (PhLAM), France
Copyright © 2021 Agafontsev and Gelash. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: D. S. Agafontsev, ZG1pdHJpakBpdHAuYWMucnU=
 D. S. Agafontsev
D. S. Agafontsev A. A. Gelash
A. A. Gelash