Peregrine Soliton as a Limiting Behavior of the Kuznetsov-Ma and Akhmediev Breathers

This article discusses a limiting behavior of breather solutions of the focusing nonlinear Schrödinger equation. These breathers belong to the family of solitons on a non-vanishing and constant background, where the continuous-wave envelope serves as a pedestal. The rational Peregrine soliton acts as a limiting behavior of the other two breather solitons, i.e., the Kuznetsov-Ma breather and Akhmediev soliton. Albeit with a phase shift, the latter becomes a nonlinear extension of the homoclinic orbit waveform corresponding to an unstable mode in the modulational instability phenomenon. All breathers are prototypes for rogue waves in nonlinear and dispersive media. We present a rigorous proof using the ϵ-δ argument and show the corresponding visualization for this limiting behavior.

1 Introduction

Although the study of wave phenomena traces its history back to the time of Pythagoras, research on nonlinear and rogue waves has attracted great scientific interest recently, both theoretically and experimentally. In particular, the focusing nonlinear Schrödinger (NLS) equation and its exact analytical solutions that belong to the family of soliton on constant background have been adopted as models and prototypes for rogue wave phenomena. The purpose of this article is to provide an overview of the relationship between these soliton solutions in this context. It also fills the gap in the details of limiting behavior. While the connection is well-known, the rigorous proof seems to be absent, and the visualizations found in the literature are incomplete. We will present this connection of the limiting behavior both analytically and visually. This introduction section covers a brief history of the NLS equation, exact solutions of the NLS equation, and a literature review on rogue waves.

1.1 A Brief Historical Background of the Nonlinear Schrödinger Equation

The NLS equation is a nonlinear evolution equation that models slowly varying envelope dynamics of a weakly nonlinear quasi-monochromatic wave packet in dispersive media. The model has an infinite set of conservation laws and belongs to a completely integrable system of nonlinear partial differential equations. It has a wide range of applications in various physical settings, such as surface water waves, nonlinear optics, plasma physics, superconductivity, and Bose-Einstein condensates (BEC) [1–8].

Among early derivations of the NLS equation were found in nonlinear optics [9, 10], plasma physics [11–15], and hydrodynamics [16–18]. In BEC, the NLS equation with the non-zero potential term is known as the Gross-Pitaevskii equation [19, 20]. In superconductivity, the time-independent NLS equation resembles some similarities with a simplified $\left(1+1\right)$-D form of the Ginzburg-Landau equation [21]. A further overview and extensive discussion of the NLS equation can be found in [7, 22–26].

1.2 Exact Solutions of the Nonlinear Schrödinger Equation

There are various techniques to derive analytical solutions of the NLS equation, among others, are the phase-amplitude algebraic ansatz [27–30], the Hirota method [31–34], nonlinear Fourier transform of inverse scattering transform (IST) [6, 35–40], symmetry reduction methods [41], variational formulation and displaced phase-amplitude equations [42–44]. Another derivation using IST with asymmetric boundary conditions is given in [45].

Throughout this article, we adopt the following $\left(1+1\right)$D, focusing-type of the NLS equation in a standard form:

$i{q}_t+q_{xx}+2{\left|q\right|}^{2}q=0,q\left(x,t\right)\in C.(1)$

Usually, the variables x and t denote the space and time variables, respectively. The simplest-solution is called the “plane-wave” or “continuous-wave” solution: $q\left(x,t\right)=q_0\left(t\right)=e^{2it}$. Another simple solution with a vanishing background is known as the “bright soliton” or “one-soliton solution”, given as follows:

$q\left(x,t\right)=q_S\left(x,t\right)=a\text{sech}\left(ax-2abt+{\theta }_0\right)e^{i\left(bx+\left(a^2-b^2\right)t+{\varphi }_0\right)},a,b,{\theta }_0,{\varphi }_0\in ℝ.(2)$

We focus our discussion on the family of exact solutions with constant and non-vanishing background, also called “breather soliton solutions” [46]. There are three types of breather, and all of them are considered as weakly nonlinear prototypes for freak waves. Other solutions of the NLS equation include cnoidal wave envelopes that can be expressed in terms of the Jacobi elliptic functions and can be derived using the Hirota bilinear transformation, theta functions, or with some clever algebraic ansatz [30, 47].

In this subsection, the coverage follows the historical order of the time when the breathers were found. Furthermore, the term “breather” and “soliton” can be used interchangeably in this article, and they can also appear as a single term “breather soliton”. All of them refer to the same object, i.e., the exact analytical solutions of the NLS equation with a non-vanishing, constant pedestal, or background of continuous-wave solution.

1.2.1 The Kuznetsov-Ma Breather

The first found solution is called the “Kuznetsov-Ma breather”, where Kuznetsov derived it for the first time in the 1970s [48]. The original Russian version of his paper was published as a preprint in 1976 by the Institute of Automation and Electrometry of the Siberian Branch of the USSR (now Russian) Academy of Sciences in Novosibirsk. This preprint was then reproduced in English and appeared in the Proceedings of the 13th International Conference on Phenomena in ionized Gases and Plasma, held in East Berlin, German Democratic Republic, on 12–17 September 1977 [49].

Although some authors stated that Kawata and Inoue, as well as Ma, also derived this solution independently, understanding the history behind its development might change our perspective [50, 51]. Between 1976 and 1977, Evgenii A. Kuznetsov met Tutomu Kawata (also spelled Tsutomu, 川田 勉) many times because the latter was a postdoctoral researcher in the Landau Institute for Theoretical Physics in Chernogolovka, near Moscow, under the mentorship of Professor Vladimir E. Zakharov. Kuznetsov personally gave Kawata his preprint on the soliton solution of the NLS equation. Furthermore, although Yan-Chow Ma has never really met with Kuznetsov, Ma was surely aware of Kuznetsov’s paper. In his work [51], Ma has cited another Kuznetsov’s paper that was written together with Alexander V. Mikhailov on the stability of stationary waves using the Korteweg-de Vries (KdV) equation [49, 52].

Although the term “Kuznetsov-Ma soliton” has been introduced earlier [53], we will adopt and use the terminology “Kuznetsov-Ma breather” throughout this article. When the breather dynamics were observed experimentally for the first time in optical fibers by Kibler and collaborators, this term is getting popular since then [54]. We denote it as $q_{\text{M}}$, and it is explicitly given by

$q\left(x,t\right)=q_{\text{M}}\left(x,t\right)=e^{2it}\left(\frac{{\mu }^3\cos \left(\rho t\right)+i\mu \rho \sin \left(\rho t\right)}{2\mu \cos \left(\rho t\right)-\rho \cosh \left(\mu x\right)}+1\right),(3)$

where $\rho =\mu \sqrt{4+{\mu }^2}$. The Kuznetsov-Ma breather does not represent a traveling wave. It is localized in the spatial variable x and periodic in the temporal variable t, and hence some authors also called it as the “temporal periodic breather” [55].

A minor typographical error found in Kawata and Inoue’s paper [50] has been corrected by Gagnon [56]. Kawata and Inoue [50], as well as Ma [51], derived the Kuznetsov-Ma breather solution using the IST for finite boundary conditions at $x\to \pm \infty$. The derivation using a direct method of Bäcklund transformation can be found in [57, 58], where the former analyzed solitary waves in the context of an optical bistable ring cavity.

Defining the amplitude amplification factor (AF) as the quotient of the maximum breather amplitude and the value of its background [43], we obtain that the amplitude amplification for the Kuznetsov-Ma breather is always larger than the factor of three, and it is explicitly given by

${\text{AF}}_{\text{M}}\left(\mu \right)=1+\sqrt{4+{\mu }^2},\mu >0.(4)$

The function is bounded below and is increasing as the parameter μ also increases. The plot of this AF can be found in [43, 44], and different expressions of the AF for this breather also appear in [59–62].

The Kuznetsov-Ma breather finds applications as a rogue wave prototype in nonlinear optics [30, 54, 63] and deep-water gravity waves [38, 39, 61, 64]. A numerical comparison of the Kuznetsov-Ma breather indicated that a qualitative agreement was reached in the central part of the corresponding wave packet and on the real face of the modulation [59]. The stability analysis of the Kuznetsov-Ma breather using a perturbation theory based on the IST verified that although the soliton is rather robust with respect to dispersive perturbations, damping terms strongly influence its dynamics [65].

The dynamics of the Kuznetsov-Ma breather in a microfabricated optomechanical array showed an excellent agreement between theory and numerical calculations [66]. The spectral stability analysis of this breather has been considered using the Floquet theory [67]. The mechanism of the Kuznetsov-Ma breather has been discussed and two distinctive mechanisms are paramount: modulational instability and the interference effects between the continuous-wave background and bright soliton [68]. New scenarios of rogue wave formation for artificially prepared initial conditions using the Kuznetsov-Ma and superregular breathers in small localized condensate perturbations are demonstrated numerically by solving the Zakharov-Shabat eigenvalue problem [69].

A higher-order Kuznetsov-Ma breather can be derived using the Hirota method and utilized in studying soliton propagation with an influence of small plane-wave background [70, 71]; or using the bilinear method [72].

1.2.2 The Akhmediev Soliton

The second one is called the Akhmediev-Eleonskiĭ-Kulagin breather and was found in the 1980s [27–29]. In short, we simply call it the “Akhmediev soliton” and denote it as $q_{\text{A}}$. This breather is localized in the temporal variable t and is periodic in the spatial variable x, and it can be written explicitly as follows:

$q\left(x,t\right)=q_{\text{A}}\left(x,t\right)=e^{2it}\left(\frac{{\nu }^3\cosh \left(\sigma t\right)+i\nu \sigma \sinh \left(\sigma t\right)}{2\nu \cosh \left(\sigma t\right)-\sigma \cos \left(\nu x\right)}-1\right).(5)$

Here, the parameter ν, $0\le \nu <2$ denotes a modulation frequency (or wavenumber) and $\sigma \left(\nu \right)=\nu \sqrt{4-{\nu }^2}$ is the modulation growth rate. The colleagues from nonlinear optics prefer calling this soliton “instanton” [73, 74] instead of “breather” since it breathes only once [75]. Other names for this solution include “modulational instability” [30], “homoclinic orbit” [34, 76], “spatial periodic breather” [55], and “rogue wave solution” [39].

The amplitude amplification for the Akhmediev soliton is at most of the factor of three, and it is explicitly given by

${\text{AF}}_{\text{A}}\left(\nu \right)=1+\sqrt{4-{\nu }^2},0<\nu <2.(6)$

This function is bounded above and below, $1<{\text{AF}}_{\text{A}}<3$, and is decreasing for an increasing value of the modulation parameter ν. Although the maximum growth rate occurs for $\nu =\sqrt{2}$, the maximum AF occurs when $\nu \to 0$, when the Akhmediev breather becomes the Peregrine soliton. To the best of our knowledge, this expression was introduced by Onorato et al. in their study on freak wave generation in random ocean waves where this AF depends on the wave steepness and number of waves under the envelope [77]. The plot for this AF can be found in [43, 78, 79]. Some variations in the AF expression for this soliton also appear in [59–62, 80, 81].

The Akhmediev soliton is rather well-known due to its characteristics being a nonlinear extension of linear modulational instability. This instability is also known as sideband (or Bespalov-Talanov) instability in nonlinear optics [82–84], or Benjamin-Feir instability in water waves [17, 85]. Some authors studied the modulational instability in plasma physics [11, 86–88] and in BEC [89–94]. Modulational instability is defined as the temporal growth of the continuous-wave NLS solution due to a small, side-band modulation, in a monochromatic wave train. A geometric condition for wave instability in deep water waves is given in [95] and for a historical review of modulational instability, see [96].

It has been shown numerically and experimentally that the modulated unstable wave trains grow to a maximum limit and then subside. In the spectral domain, the wave energy is transferred from the central frequency to its sidebands during the wave propagation for a certain period, and then it is recollected back to the primary frequency mode [97–101]. It turns out that the long-time evolution of these unstable wave trains leads to a sequence of modulation and demodulation cycles, known as the Fermi-Pasta-Ulam-Tsingou (FPUT) recurrence phenomenon [102, 103]. Although the FPUT recurrence using the NLS model has been observed experimentally in surface gravity waves in the late 1970s [98], it took more than 2 decades for the phenomenon to be successfully recovered in nonlinear optics [104].

Since the modulational instability extends nonlinearly to the Akhmediev soliton, it is no surprise that the former is considered as a possible mechanism for the generation of rogue waves while the latter acts as one prototype [105–107]. For wave trains with amplitude and phase modulation, there is a competition between the nonlinearity and dispersive factors. After the modulational instability occurs, the growth predicted by linear theory is exponential, and the nonlinear effect in the form of the Akhmediev soliton takes over before the wave trains return to the stage similar to the initial profiles with a phase-shift difference [64, 108]. On the other hand, Biondini and Fagerstrom argued that the major cause of modulational instability in the NLS equation is not the breather soliton solutions per se, but the existence of perturbations where discrete spectra are absence [109].

Experimental attempts on deterministic rogue wave generation using the Akhmediev solitons suggested that the symmetric structure is not preserved and the wave spectrum experiences frequency downshift even though wavefront dislocation and phase singularity are visible [43, 110–114]. A numerical calculation of rogue wave composition can be described in the form of the collision of Akhmediev breathers [115]. Another comparison of the Akhmediev breathers with the North Sea Draupner New Year and the Sea of Japan Yura wave signals also show some qualitative agreement [116]. The characteristics of the Akhmediev solitons have also been observed experimentally in nonlinear optics [117].

A theoretical, numerical, and experimental report of higher-order modulational instability indicates that a relatively low-frequency modulation on a plane-wave induces pulse splitting at different phases of evolution [118]. Second-order breathers composed of nonlinear combinations of the Kuznetsov-Ma breather and Akhmediev soliton reveal the dependence of the wave envelope on the degenerate eigenvalues and differential shifts [119]. Similar higher-order Akhmediev solitons visualized in [118, 119] have been featured earlier in [43, 120] and similar illustrations can also be found in [60, 121–127].

1.2.3 The Peregrine Soliton

The third one is called the “Peregrine soliton”, also known as the “rational solution” [128]. This soliton is localized in both spatial and temporal variables $\left(x,t\right)$ and is written as follows (denoted as $q_{\text{P}}$):

$q\left(x,t\right)=q_{\text{P}}\left(x,t\right)=e^{2it}\left(\frac{4\left(1+4it\right)}{1+16t^2+4x^2}-1\right).(7)$

This solution is neither a traveling wave nor contains free parameters. Johnson called it a “rational-cum-oscillatory solution” [129]. Others referred to it as the “isolated Ma soliton” [130], an “explode-decay solitary wave” [131], the “rational growing-and-decaying mode” [71], the “algebraic breather” [132], or the “fundamental rogue wave solution” [124].

The amplitude amplification for the Peregrine soliton is exactly of factor three, and this can be obtained by taking the limit of the parameters toward zero in the previous two breathers:

${\text{AF}}_{\text{P}}=\underset{\mu \to 0}{\lim }{\text{AF}}_{\text{M}}\left(\mu \right)=3=\underset{\nu \to 0}{\lim }{\text{AF}}_{\text{A}}\left(\nu \right).(8)$

Although the other two breather solitons are also proposed as rogue wave prototypes, some authors argued that the Peregrine soliton is the most likely freak wave event due to its appearance from nowhere and disappearance without a trace [79] as well as its closeness to all initial supercritical humps of small uniform envelope amplitude [133]. Some numerical and experimental studies may support this reasoning.

Henderson et al. studied numerically unsteady surface gravity wave modulations by comparing the fully nonlinear and NLS equations [130]. For steep-waves, their computations produced striking similarities with the Peregrine soliton. On the other hand, Voronovich et al. confirmed numerically that the bottom friction effect, even when it is small in comparison to the nonlinear term, could hamper the formation of a breather freak wave at the nonlinear stage of instability [134]. Investigations on linear stability demonstrated that the Peregrine soliton is unstable against all standard perturbations, where the analytical study is supported by numerical evidence [135–138].

An important breakthrough in the study of rogue waves is the observation of the Peregrine soliton in nonlinear media. In nonlinear optics, the existence of strongly localized temporal and spatial peaks on a non-vanishing background, which indicates near-ideal Peregrine soliton characteristics, was successfully implemented for the first time in optical fiber generating femtosecond pulses in 2010 [139]. Not long after that, the Peregrine soliton was also observed experimentally for the first time in a water wave tank [140]. A comparison between the predictions from the theoretical model and the measurement results exhibits an excellent qualitative agreement in terms of wave signal pattern, its amplification factor, and its symmetric structure. Another successful experimental observation of the Peregrine solitons is reported in ion-acoustic waves of a multicomponent plasma with negative ions when the density of negative ions is equal to the critical value [141].

A sequence of related experimental studies using the Peregrine soliton demonstrated reasonably good qualitative agreement with the theoretical prediction. Some discrepancies occur in the modulational gradients, spatiotemporal symmetries, and for larger steepness values [142], as well as the frequency downshift [143]. Interestingly, Chabchoub et al. shown further experimentally that the dynamics of the Peregrine soliton and its spectrum characteristics persist even in the presence of wind forcing with high velocity [144]. By selecting a target location and determining an initial steepness, an experiment using the Peregrine soliton of wave interaction with floating bodies during extreme ocean condition has also been successfully implemented [145].

The Peregrine soliton also finds applications in the evolution of the intrathermocline eddies, also known as the oceanic lenses [146]. It appeared as a special case of stationary limit in the solutions of the spinor BEC model [147], and it was observed experimentally emerging from the stochastic background in deep-water surface gravity waves [148].

Nonlinear spectral analysis using the finite gap theory showed that the spectral portraits of the Peregrine soliton represent a degenerate genus two of the NLS equation solution [149]. Higher-order Peregrine solitons in terms of quasi-rational functions are derived in [150]. Higher-order Peregrine solitons up to the fourth-order using a modified Darboux transformation has been presented with applications in rogue waves in the deep ocean and high-intensity rogue light wave pulses in optical fibers [151]. Super rogue waves modeled with higher-order Peregrine soliton with an amplitude amplification factor of five times the background value are observed experimentally in a water-wave tank [122].

1.3 A Literature Review on Rogue Waves

There are various excellent reviews on rogue wave phenomena based on the NLS equation as a mathematical model and its corresponding breather solitons. Onorato et al. covered rogue waves in several physical contexts including surface gravity waves, photonic crystal fibers, laser fiber systems, and 2D spatiotemporal systems [60]. Dudley et al. reviewed breathers and rogue waves in optical fiber systems with an emphasis on the underlying physical processes that drive the appearance of extreme optical structures [125]. They reasoned that the mechanisms driving rogue wave behavior depend very much on the system. Residori et al. presented physical concepts and mathematical tools for rogue wave description [62]. They highlighted the most common features of the phenomenon include large deviations of wave amplitude from the Gaussian statistics and large-scale symmetry breaking. Chen et al. discussed rogue waves in scalar, vector, and multidimensional systems [152] while Malomed and Mihalache surveyed some theoretical and experimental studies on nonlinear waves in optical and matter-wave media [153].

Rogue waves come from and are closely related to modulational instability with resonance perturbation on continuous background [154]. A comparison of breather solutions of the NLS equation with emergent peaks in noise-seeded modulational instability indicated that the latter clustered closely around the analytical predictions [155]. “Superregular breathers” is the term coined indicating creation and annihilation dynamics of modulational instability, and the evidence of the broadest group of these superregular breathers in hydrodynamics and optics has been reported [156]. An interaction between breather and higher-order rogue waves in a nonlinear optical fiber is characterized by a trajectory of localized troughs and crests [157].

Breather soliton solutions find several applications, among others in beam-plasma interactions [158], in the transmission line analog of nonlinear left-handed metamaterials [159], in a nonlinear model describing an electron moving along the axis of deformable helical molecules [160], and in the mechanisms underlying the formation and real-time prediction of extreme events [161]. Additionally, optical rogue waves also successfully simulated in the presence of nonlinear self-image phenomenon in the near-field diffraction of plane waves from lightwave grating, known as the Talbot effect [162].

Since the definitions of “rogue waves” and “extreme events” are varied, a roadmap for unifying different perspectives could stimulate further discussion [163]. Theoretical, numerical, and experimental evidence of the dissipation effect on phase-shifted FPUT dynamics in a super wave tank, which is related to modulational instability, can be described by the breather solutions of the NLS equation [164]. Since the behavior of a large class of perturbations characterized by a continuous spectrum is described by the identical asymptotic state, it turns out that the asymptotic stage of modulational instability is universal [165]. Surprisingly, the long-time asymptotic behavior of modulationally unstable media is composed of an ensemble of classical soliton solutions of the NLS equation instead of the breather-type solutions [166].

General N-solitonic solutions of the NLS equation in the presence of a condensate derived using the dressing method describe the nonlinear stage of the modulational instability of the condensate [167]. Rogue waves on a periodic background in the form of cnoidal functions that exhibit modulational instability not only generalize the Peregrine’s soliton but also potentially stimulate further discussion [168]. Recently, both theoretical description and experimental observation of the nonlinear mutual interactions between a pair of copropagative breathers are presented and it is observed that the bound state of breathers exhibits a behavior similar to a molecule with quasiperiodic oscillatory dynamics [169].

The paper will be presented as follows. After this introduction, Section 2 discusses rigorous proof for the limiting behavior of the breather wave solutions using the ϵ-δ argument. The limiting behavior will continue in Section 3, where we cover it from the visual viewpoint. We present the corresponding contour plots for various values of parameters and the parameterization sketches of the non-rapid oscillating complex-valued breather amplitudes. Finally, Section 4 concludes our discussion and provide remarks for potential future research.

2 Limiting Behavior

This section provides rigorous proof of the limiting behavior of breather wave solutions using the ϵ-δ argument. We have the following theorem:

Theorem 1. The Peregrine soliton is a limiting case for both the Kuznetsov-Ma breather and Akhmediev soliton:

$\underset{\mu \to 0}{\lim }{q}_{\text{M}}\left(x,t\right)=q_{\text{P}}\left(x,t\right)=\underset{\nu \to 0}{\lim }{q}_{\text{A}}\left(x,t\right).(9)$

We split the proof into four parts, and each limit consists of two parts corresponding to the real and imaginary parts of the solitons.

Proof. The following shows that the limit for the real parts of the Kuznetsov-Ma breather and Peregrine soliton is correct, i.e.,

$\underset{\nu \to 0}{\lim }\mathrm{Re}\left\{q_{\text{M}}\left(x,t\right)\right\}=\mathrm{Re}\left\{q_{\text{P}}\left(x,t\right)\right\}.$

For each $\epsilon >0$, there exists $\delta =\sqrt{{\left(\epsilon +2\right)}^2-4}>0$ such that if $0<\mu <\delta$, then $|\mathrm{Re}\left\{q_{\text{M}}\right\}-\mathrm{Re}\left\{q_{\text{P}}\right\}|<\epsilon$. We know that since

$\frac{\cosh \mu \left(x-x_0\right)}{\cos \rho \left(t-t_0\right)}\ge 1\text{for}\text{all}\left(x,t\right)\in {ℝ}^2,$

it then implies

$\rho \frac{\cosh \mu \left(x-x_0\right)}{\cos \rho \left(t-t_0\right)}-2\mu \ge \rho -2\mu ,$

It follows that

$\begin{array}{l}\left|\mathrm{Re}\left\{q_{\mathrm{M}}\right\}-\mathrm{Re}\left\{q_{\mathrm{P}}\right\}\right|=\left|\frac{{\mu }^3}{\rho \frac{\cosh \nu \left(x-x_0\right)}{\cos \rho \left(t-t_0\right)}-2\mu }-\frac{4}{1+16{\left(t-t_0\right)}^2+4{\left(x-x_0\right)}^2}\right|\\ \le \left|\frac{{\mu }^3}{\rho -2\mu }-4\right|=\left|\sqrt{{\mu }^2+4}-2\right|\\ \le \sqrt{{\delta }^2+4}-2=\sqrt{{\left(\sqrt{{\left(\epsilon +2\right)}^2-4}\right)}^2+4}-2=\epsilon .\end{array}$

The following verifies that the limit for the imaginary parts of the Kuznetsov-Ma breather and Peregrine soliton is accurate, i.e.,

$\underset{\nu \to 0}{\lim }\mathrm{Im}\left\{q_{\text{M}}\left(x,t\right)\right\}=\mathrm{Im}\left\{q_{\text{P}}\left(x,t\right)\right\}.$

For each $\epsilon >0$, there exists $\delta =\sqrt{-10+2\sqrt{25+4\epsilon /|t-t_0|}}>0$ such that if $0<\mu <\delta$, then $\left|\mathrm{Im}\left\{q_{\text{M}}\right\}-\mathrm{Im}\left\{q_{\text{P}}\right\}\right|<\epsilon$. We can write the imaginary parts of $q_{\text{M}}$ and $q_{\text{P}}$ as follows

$\begin{array}{l}\mathrm{Im}\left\{q_{\text{M}}\right\}=\frac{\mu \rho }{\rho \frac{\cosh \mu \left(x-x_0\right)}{\sin \rho \left(t-t_0\right)}-2\mu \cot \rho \left(t-t_0\right)}\le \frac{\mu {\rho }^2\left|t-t_0\right|}{\rho -2\mu },\\ \text{Im}\left\{q_{\text{P}}\right\}=\frac{16\left(t-t_0\right)}{1+16{\left(t-t_0\right)}^2+4{\left(x-x_0\right)}^2}\le 16\left|t-t_0\right|,\end{array}$

It follows that

$\begin{array}{l}\left|\mathrm{Im}\left\{q_{\mathrm{M}}\right\}-\mathrm{Im}\left\{q_{\mathrm{P}}\right\}\right|=\left|\frac{\mu \rho }{\rho \frac{\cosh \mu \left(x-x_0\right)}{\sin \rho \left(t-t_0\right)}-2\mu \cot \rho \left(t-t_0\right)}-\frac{16\left(t-t_0\right)}{1+16{\left(t-t_0\right)}^2+4{\left(x-x_0\right)}^2}\right|\\ \le \left|\frac{\mu {\rho }^2}{\rho -2\mu }-16\left|\right|t-t_0\right|=|\left({\mu }^2+4\right)\left(\sqrt{{\mu }^2+4}+2\right)-16\left|\right|t-t_0|\\ <|\left({\delta }^2+4\right)\left(\frac{{\delta }^2}{4}+4\right)-16\left|\right|t-t_0|=|\frac{{\delta }^4}{4}+5{\delta }^2\left|\right|t-t_0|=\epsilon .\end{array}$

In what follows, we present the limit of the real part of the Akhmediev soliton as $\nu \to 0$ is indeed the real part of the Peregrine soliton, i.e.,

$\underset{\nu \to 0}{\lim }\mathrm{Re}\left\{q_{\text{A}}\left(x,t\right)\right\}=\mathrm{Re}\left\{q_{\text{P}}\left(x,t\right)\right\}.$

For each $\epsilon >0$, there exists $\delta =\sqrt{\epsilon /3}>0$ such that if $0<\nu <\delta <2$, then $\left|\mathrm{Re}\left\{q_{\text{A}}\right\}-\mathrm{Re}\left\{q_{\text{P}}\right\}\right|<\epsilon$. We know that since

$-1\le \frac{\cos \nu \left(x-x_0\right)}{\cosh \sigma \left(t-t_0\right)}\le 1\text{for all}\left(x,t\right)\in {ℝ}^2,$

it then implies

$2\nu -\sigma \le 2\nu -\sigma \frac{\text{cos}\nu \left(x-x_0\right)}{\text{cosh}\sigma \left(t-t_0\right)}.$

We also have $1+16{\left(t-t_0\right)}^2+4{\left(x-x_0\right)}^2\ge 1$ for all $\left(x,t\right)\in {\mathrm{ℝ}}^2$. Furthermore, since $0\le \sqrt{4-{\nu }^2}\le 2$, $0\le 2-\sqrt{4-{\nu }^2}\le 2$,

$\begin{array}{l}\frac{1}{4}\le \frac{2-\sqrt{4-{\nu }^2}}{{\nu }^2}\le \frac{1}{2},\\ \frac{1}{2}\le \frac{1}{4}+\frac{2-\sqrt{4-{\nu }^2}}{{\nu }^2}\le \frac{3}{4},\\ \mathrm{and}\frac{2-\sqrt{4-{\nu }^2}}{4{\nu }^2}\ge \frac{1}{4{\delta }^2},\end{array}$

it follows that

$\begin{array}{l}\left|\mathrm{Re}\left\{q_{\mathrm{A}}\right\}-\mathrm{Re}\left\{q_{\mathrm{P}}\right\}\right|=\left|\frac{{\nu }^3}{2\nu -\sigma \frac{\cos \nu \left(x-x_0\right)}{\cosh \sigma \left(t-t_0\right)}}-\frac{4}{1+16{\left(t-t_0\right)}^2+4{\left(x-x_0\right)}^2}\right|\\ \le \left|\frac{{\nu }^3}{2\nu -\sigma }+4\right|=\left|\frac{1}{\frac{\left(2-\sqrt{4-{\nu }^2}\right)}{{\nu }^2}}+\frac{1}{\frac{1}{4}}\right|=\frac{\left|\frac{1}{4}+\frac{\left(2-\sqrt{4-{\nu }^2}\right)}{{\nu }^2}\right|}{\left|\frac{\left(2-\sqrt{4-{\nu }^2}\right)}{4{\nu }^2}\right|}\\ \le \frac{3}{4}\left(4{\delta }^2\right)=3{\left(\sqrt{\frac{\epsilon }{3}}\right)}^2=\epsilon .\end{array}$

In what follows, we demonstrate that the limit of the imaginary part of the Akhmediev soliton becomes the imaginary part of the Peregrine soliton, i.e.,

$\underset{\nu \to 0}{\lim }\mathrm{Im}\left\{q_{\text{A}}\left(x,t\right)\right\}=\mathrm{Im}\left\{q_{\text{P}}\left(x,t\right)\right\}.$

For each $\epsilon >0$, there exists $\delta =\sqrt{\epsilon /4}>0$ such that if $0<\nu <\delta <2$, then $\left|\mathrm{Im}\left\{q_{\text{A}}\right\}-\mathrm{Im}\left\{q_{\text{P}}\right\}\right|<\epsilon$. We can write the imaginary parts of $q_{\text{A}}$ and $q_{\text{P}}$ as follows

$\begin{array}{l}\mathrm{Im}\left\{q_{\text{A}}\right\}=\frac{\nu \sigma \tanh \sigma \left(t-t_0\right)}{2\nu -\sigma \frac{\cos \nu \left(x-x_0\right)}{\cosh \sigma \left(t-t_0\right)}}\le \frac{\nu {\sigma }^2\left|t-t_0\right|}{2\nu -\sigma },\\ \mathrm{Im}\left\{q_{\text{P}}\right\}=\frac{16\left(t-t_0\right)}{1+16{\left(t-t_0\right)}^2+4{\left(x-x_0\right)}^2}\le 16\left|t-t_0\right|.\end{array}$

Since $2+\sqrt{4-{\nu }^2}\le 4$ and $\left(4-{\nu }^2\right)\le 4+{\delta }^2/\left|t-t_0\right|$, it follows that

$\begin{array}{l}\left|\mathrm{Im}\left\{q_{\text{A}}\right\}-\mathrm{Im}\left\{q_{\text{P}}\right\}\right|=\left|\frac{\nu \sigma \tanh \sigma \left(t-t_0\right)}{2\nu -\sigma \frac{\cos \nu \left(x-x_0\right)}{\cosh \sigma \left(t-t_0\right)}}-\frac{16\left(t-t_0\right)}{1+16{\left(t-t_0\right)}^2+4{\left(x-x_0\right)}^2}\right|\\ \le \left|\frac{\nu {\sigma }^2}{2\nu -\sigma }-16\left|\right|t-t_0\right|=\left|\left(4-{\nu }^2\right)\left(2+\sqrt{4-{\nu }^2}\right)-16\left|\right|t-t_0\right|\\ <\left|4\left(4+\frac{{\delta }^2}{|t-t_0|}\right)-16\left|\right|t-t_0\right|=4{\delta }^2=4{\left(\sqrt{\frac{\epsilon }{4}}\right)}^2=\epsilon .\end{array}$

We have completed the proof.

In the following section, we will visualize the limiting behavior of the breather solutions as they approach toward the Peregrine soliton.

3 Limiting Behavior Visualized

In this section, we will visually confirm the limiting behavior of the Kuznetsov-Ma and Akhmediev breathers toward the Peregrine soliton as both parameter values approach zero. Subsection 3.1 presents the contour plots of the amplitude modulus, and Subsection 3.2 discusses the spatial and temporal parameterizations of the breathers. We select several parameter values in sketching the plots. Figure 1 displays the chosen parametric values for both breather solutions, where they can be visualized in the complex-plane for the parameter pair $\left(\mu ,\nu \right)$.

FIGURE 1

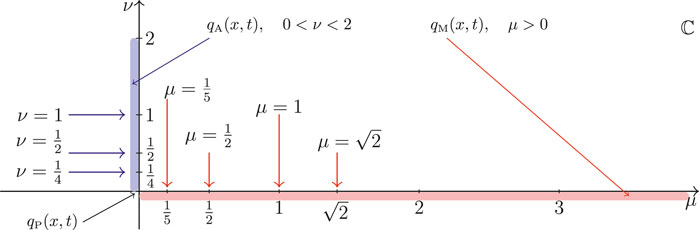
FIGURE 1. Selected parametric values ν and $\mu =i\nu$ displayed in the complex plane for the Kuznetsov-Ma breather and Akhmediev soliton visualized in this section.

3.1 Contour Plot

In this subsection, we observe the contour plots of the amplitude modulus of the breather and how the changes in the parameter values affect the envelope’s period and wavelength. Similar contour plots have been presented in the context of electronegative plasmas with Maxwellian negative ions [170]. In particular, the contour plot of the Peregrine soliton is also displayed in [142].

Figures 2A-E display the contour plots of the Kuznetsov-Ma breather for several values of parameters μ: $\sqrt{2},1,1/2$, and $1/5$. Figure 2E is a zoom-in version of the same contour plot given in Figure 2D. Figure 2F is the final stop when we let the parameter $\mu \to 0$, for which the Kuznetsov-Ma breather turns into the Peregrine soliton. It is interesting to note that for $\mu =1/5$, the contour plot is nearly identical to the one from the Peregrine soliton, as we can observe by qualitatively comparing panels (E) and (F) of Figure 2.

FIGURE 2

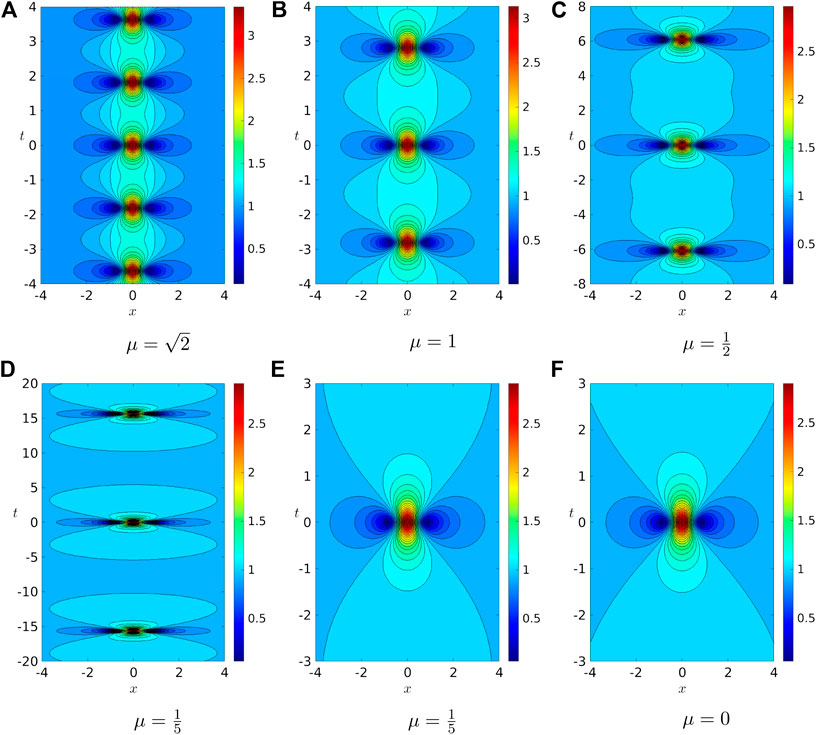
FIGURE 2. Contour plots for the moduli of the Kuznetsov-Ma breather for (A)$\mu =\sqrt{2}$, (B)$\mu =1$, (C)$\mu =0.5$, (D)$\mu =0.2$, (E) also $\mu =0.2$ but a zoom-in version, and (F)$\mu =0$, which gives the Peregrine soliton. Notice that the contour plots (e) and (f) are qualitatively nearly identical.

Let $T_{\text{M}}$ denote the temporal envelope period for the Kuznetsov-Ma breather, then we know that in general, $T_{\text{M}}=2\pi /\rho$. For $\mu \to \infty$, $T_{\text{M}}\to 0$ and vice versa, for $\mu \to 0$, $T_{\text{M}}\to \infty$. For any given value of $\mu >0$, $T_{\text{M}}$ can be easily calculated. Here are some examples. For $\mu =\sqrt{2}$, $T_{\text{M}}=\pi /\sqrt{3}\approx 1.814$ and we display five periods in Figure 2A along the temporal axis t. For $\mu =1$, $T_{\text{M}}=2\pi /\sqrt{5}\approx 2.81$ and for the same time interval as in panel (A), we can only capture three periods along the temporal axis t, as shown in Figure 2B. Furthermore, for $\mu =1/2$, $T_{\text{M}}=8\pi /\sqrt{17}\approx 6.1$ and we need to extend almost twice the length in the time interval in order to capture at least three periods. Figure 2C shows this contour plot. Finally, for $\mu =1/5$, $T_{\text{M}}=50\pi /\sqrt{101}\approx 15.63$. As we can observe in Figure 2D, extending the length of time interval to around 40 units is sufficient to capture at least three periods, albeit the detail around maximum and minimum is hardly visible. Table 1 displays selected parameter values of the Kuznetsov-Ma breather and their corresponding temporal envelope periods $T_{\text{M}}$.

TABLE 1

TABLE 1. Exact values of the temporal envelope period $T_{\text{M}}$ and their approximate values for selected parameter values μ corresponding to the Kuznetsov-Ma breather.

Figures 3A–C display the contour plot of the Akhmediev soliton for selected values of its parameters ν: 1, $1/2$, and $1/4$. Figure 3D shows the contour plot of the Peregrine soliton, which occurs as the final destination when letting the parameter $\nu \to 0$. Figure 3D is identical to Figure 2F, the only difference lies in the length-scale of both horizontal and vertical axes. Similar to the previous case, zooming-in the contour plot for $\nu =1/4$ in Figure 3C will yield a qualitatively nearly identical contour plot with the Peregrine soliton shown in the panel (D). (It is not shown in the figure.)

FIGURE 3

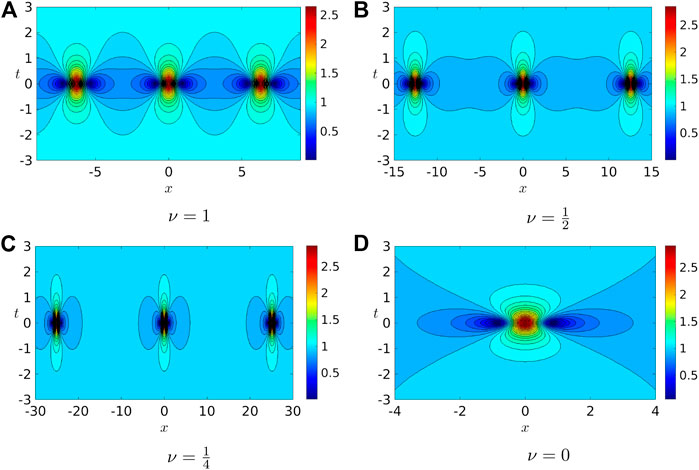
FIGURE 3. Contour plots for the moduli of the Akhmediev breather for (A)$\nu =1$, (B)$\nu =0.5$, and (C)$\nu =0.25$, as well as (D) the Peregrine soliton.

Let $L_{\text{A}}$ denote the spatial envelope wavelength for the Akhmediev soliton, then for $0<\nu <2$, $L_{\text{A}}=2\pi /\nu$, which gives $L_{\text{A}}>\pi$. For $\nu \to 2$, $L_{\text{A}}\to \pi$, and as $\nu \to 0$, $L_{\text{A}}\to \infty$. Table 2 displays selected values of the parameter ν and their corresponding spatial envelope wavelength $L_{\text{A}}$ for the Akhmediev soliton. For $\nu =1$, $L_{\text{A}}=2\pi$ and the spatial length of 20 units in Figure 3A is sufficient to capture three envelope wavelength. For $\nu =1/2$, $L_{\text{A}}=4\pi$ and the spatial length of 40 units in Figure 3B is required to capture at least three envelope wavelength. For $\nu =1/4$, $L_{\text{A}}=8\pi$ and the spatial length of 60 units in Figure 3C is needed to capture at least three envelope wavelength. The details around maxima and minima are hardly visible for the latter.

TABLE 2

TABLE 2. Exact values of the spatial envelope wavelength $L_{\text{A}}$ and their approximate values for selected parameter values ν corresponding to the Akhmediev soliton.

3.2 Parameterization in Spatial and Temporal Variables

In this subsection, we write the breather solutions as $q_{\text{X}}\left(x,t\right)=q_0\left(t\right){\tilde{q}}_{\text{X}}\left(x,t\right)$, where $q_0\left(t\right)$ is the plane-wave solution and $\text{X}=\left\{\text{M,A,P}\right\}$. Since the plane-wave solution gives a fast-oscillating effect, we only consider the non-rapid oscillating part of the breathers ${\tilde{q}}_{\text{X}}$ for the parameterization visualization. In the subsequent figures, we present both spatial and temporal parameterizations of the Kuznetsov-Ma breather, Akhmediev, and Peregrine solitons. A similar description has been briefly covered and discussed in [30, 61, 63, 164]. This article does not only complements and supplements but also provides detailed explanations to those references. Additionally, note that the unit circle centered at the origin appeared in each panel of Figures 4–7 (dotted black circle) corresponds to the phase of the continuous-wave pedestal, i.e., the manifold of the breathers for $x\to \pm \infty$ or $t\to \pm \infty$ [30].

FIGURE 4

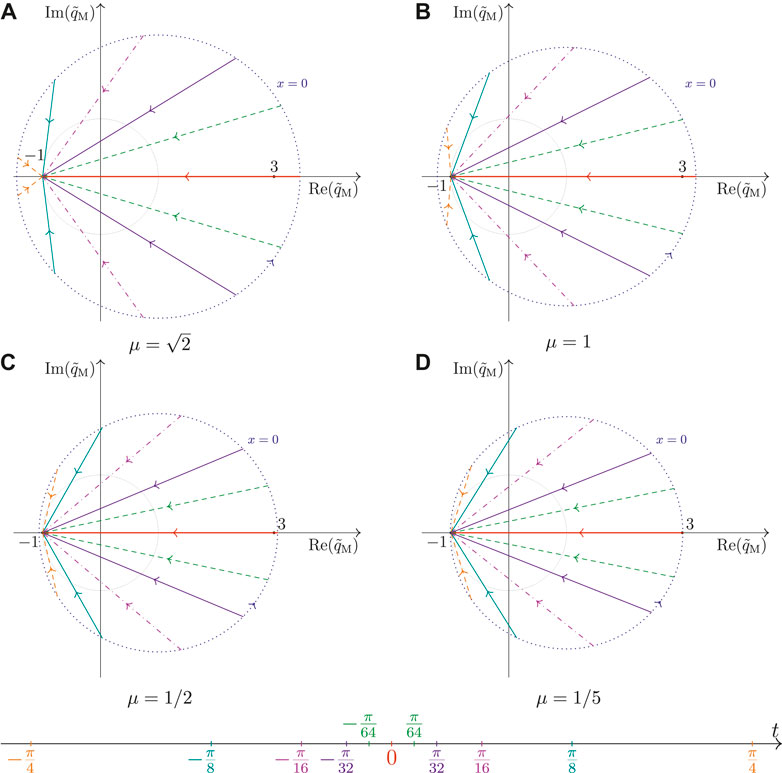
FIGURE 4. Parameterization of the non-rapid-oscillating complex-valued amplitude of the Kuznetsov-Ma breather ${\tilde{q}}_{\text{M}}$ in the spatial variable x, $x\ge 0$, for different values of temporal variable t and different values of the parameter μ: (A)$\mu =\sqrt{2}$, (B)$\mu =1$, (C)$\mu =1/2$, and (D)$\mu =1/5$. The selected values of t are $t=0$ (solid red), $t=\pm \pi /64$ (dashed green), $t=\pm \pi /32$ (solid purple), $t=\pm \pi /16$ (dash-dotted magenta), $t=\pm \pi /8$ (solid cyan), and $t=\pm \pi /4$ (dashed orange).

Figure 4 displays the parameterization of the non-rapid oscillating Kuznetsov-Ma breather ${\tilde{q}}_{\text{M}}$ in the spatial variable x for different values of the temporal variable t and parameter μ. Different panels indicate different parameter values μ and for each panel, different curves, for which in this particular case, they are merely straight lines, indicate different time t. For all cases, we consider $x\ge 0$ due to the symmetry nature of the breathers. The straight-line trajectories move inwardly focused from the dotted blue circle at $x=0$ toward $\left(-\mathrm{1,0}\right)$ as $x\to \infty$. The situation is simply reversed for $x<0$: the path of trajectories move outwardly defocused as x progresses from $\left(-\mathrm{1,0}\right)$ at $x\to -\infty$ toward the dotted blue circle at $x=0$. At the bottom of these four panels, we also present the t-axis and corresponding values of the selected values of t for $-T_{\text{M}}/2<-\pi /4\le t\le \pi /4<T_{\text{M}}/2$. The trajectories in the upper-part and lower-part of the complex-plane correspond to the positive and negative values of t, respectively. We observe that the trajectories shift faster in space around $t=0$ than around $t=\pm T_{\text{M}}/2=\pm \pi /\rho$.

In particular, for $t=n\pi /\rho$, $n\in \mathbb{Z}$, ${\tilde{q}}_{\text{M}}$ reduces to a real-valued function, i.e., Im$\left({\tilde{q}}_{\text{M}}\right)=0$ for all $\mu >0$. Hence, the parameterized curve is a straight line at the real-axis. For $t=2n\pi /\rho$, $n\in \mathbb{Z}$, this is shown by the horizontal solid red line lying on the real axis moving from a point larger than Re$\left({\tilde{q}}_{\text{M}}\right)=3$ to $\text{Re}\left({\tilde{q}}_{\text{M}}\right)=-1$ for $x>0$. The represented case $t=0$ is displayed in Figure 4 while the case $t=\pi /\rho$ is not shown in the figure. Indeed, from (3), we obtain the following limiting values for $n\in \mathbb{Z}$:

$\begin{array}{l}\underset{x\to 0}{\lim }{q}_{\mathrm{M}}\left(x,2n\pi /\rho \right)=1+\sqrt{{\mu }^2+4},\\ \mathrm{and}\underset{x\to 0}{\lim }{q}_{\mathrm{M}}\left(x,\left(2n+1\right)\pi /\rho \right)=1-\sqrt{{\mu }^2+4}.\end{array}(10)$

Additionally, $\underset{x\to \mathrm{\pm }\infty }{\lim }{q}_M\left(x,n\pi /\rho \right)=-1$. Using a similar analysis, vertical straight lines at $\mathrm{Re}\left({\tilde{q}}_{\text{M}}\right)=-1$ can be obtained by taking the values of $t=\left(n+1/2\right)\pi /\rho$, for $n\in \mathbb{Z}$. The line direction from the positive and negative regions of Im$\left({\tilde{q}}_{\text{M}}\right)$ is downward and upward toward $\left(-\mathrm{1,0}\right)$ for even and odd values of $n\in \mathbb{Z}$, respectively.

Figure 5 displays the sketch of the non-rapid-oscillating Kuznetsov-Ma breather ${\tilde{q}}_{\text{M}}$ in the complex-plane parameterized in the temporal variable t for different values of the spatial variable x and parameter μ. For each case, t is taken for one temporal envelope period, i.e., $-T_{\text{M}}/2=-\pi /\rho <t<\pi /\rho =T_{\text{M}}/2$. Instead of a set of straight lines, the trajectories form the shape of elliptical curves. For each $x=x_0\in ℝ$, the ellipse is centered at $\left(c\left(x_0\right),0\right)$ with semi-minor axis $a\left(x_0\right)$ and semi-major axis $b\left(x_0\right)$, where

$a\left(x_0\right)=\frac{\mu \rho \cosh \left(\mu x_0\right)}{d\left(x_0\right)}(11)$

$b\left(x_0\right)=\frac{\rho \cosh \left(\mu x_0\right)}{\sqrt{d\left(x_0\right)}}(12)$

$c\left(x_0\right)=\frac{2{\mu }^2}{d\left(x_0\right)}-1(13)$

$d\left(x_0\right)=2\cosh \left(2\mu x_0\right)+{\mu }^2-2.(14)$

FIGURE 5

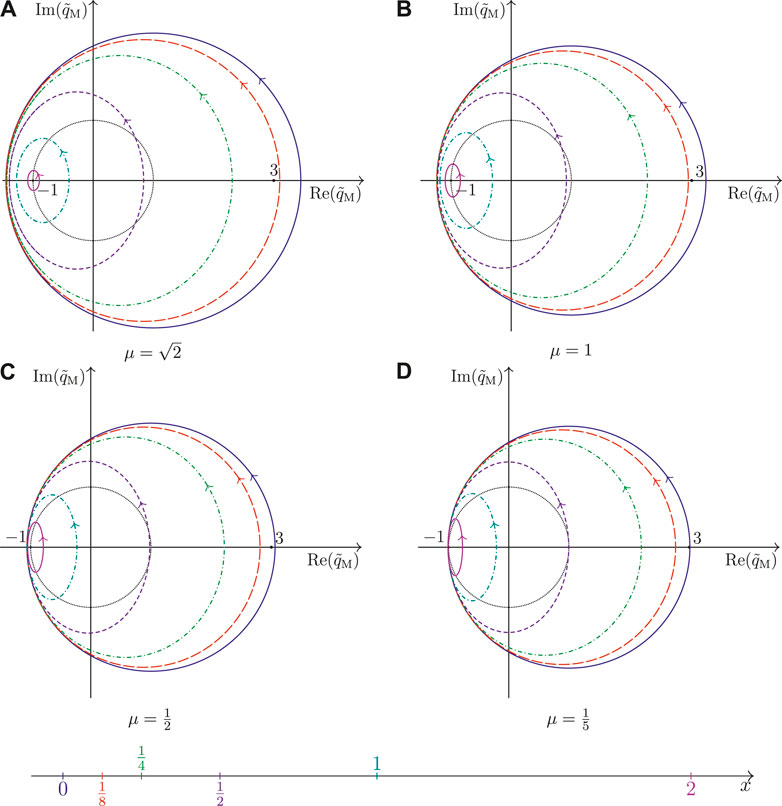
FIGURE 5. Parameterization of the non-rapid oscillating complex-valued amplitude of the Kuznetsov-Ma breather ${\tilde{q}}_{\text{M}}$ in the temporal variable t ($-\pi /\rho <t<\pi /\rho$) for different values of spatial variable x: $x=0$ (solid blue), $x=1/8$ (long-dashed red), $x=1/4$ (dash-dotted green), $x=1/2$ (dashed purple), $x=1$ (dash-dotted cyan), and $x=2$ (solid magenta) and different values of the parameter μ: (A)$\mu =\sqrt{2}$, (B)$\mu =1$, (C)$\mu =1/2$, and (D)$\mu =1/5$.

The special case of a circle is obtained for $x_0=0$ with the radius $r=\sqrt{{\mu }^2+4}$ centered at $\left(\mathrm{1,0}\right)$. All curves move in the counterclockwise direction for increasing t. For $x>0$, the larger the values of x, the smaller the ellipses become. The situation is the opposite for $x<0$: smaller values of x (but largely negatives in its absolute value sense) correspond to smaller ellipses in the complex plane. Due to its spatial symmetry, only the plots for positive values of x are displayed. The axis below the figure panels shows the selected x values for a better overview of the variable scaling: $x=0$, $1/8$, $1/4$, $1/2$, 1, and $x=2$.

In Figure 4, the starting points of the trajectories for $x=0$ are shrinking as μ decreases, as indicated by the dotted blue exterior circles. For the same interval of time t, these initial points also tend to be absorbed toward the right-hand side of the exterior circles while they focus toward $\left(-\mathrm{1,0}\right)$. As we can observe in panels (A) and (B), the trajectories at $t=\pm \pi /4$ originate from the left-hand side of the exterior circles for $\mu \ge 1$. A similar pattern was no longer observed as the values of μ get smaller, as we can see in panels (C) and (D). Meanwhile, the circles and ellipses are getting smaller in Figure 5 for decreasing values of μ. Except for the circles that are always centered at $\left(\mathrm{1,0}\right)$, the centers of the ellipses shift toward the left-hand side of the blue exterior circle near $\left(-\mathrm{1,0}\right)$ as μ decreases.

Figure 6 displays the sketch in the complex-plane of the non-rapid-oscillating Akhmediev soliton ${\tilde{q}}_{\text{A}}$ [panels (A)‐(C)] and Peregrine soliton ${\tilde{q}}_{\text{P}}$ [panel (D)] parameterized in the spatial variable x for different values of the temporal variable t and parameter ν. We only display the trajectories corresponding to the positive values of t, the trajectories for the negative values of t are simply the reflection over the horizontal axis $\mathrm{Re}\left({\tilde{q}}_{\text{P}}\right)=0$. The t-axis below the panels indicate the chosen values of t displayed in the figure. Similar to the trajectories for the Kuznetsov-Ma breather when they are parameterized in the spatial variable x, the trajectories for the Akhmediev soliton parameterized in x are also collections of straight lines shifting in the counterclockwise direction for increasing values of t. Different from the previous case, these straight lines are periodic in x. The experimental results of deterministic freak wave generation using the spatial NLS equation showed that instead of straight lines, we obtained non-degenerate Wessel curves, suggesting that the periodic lines might be perturbed during the downstream evolution [43, 113].

FIGURE 6

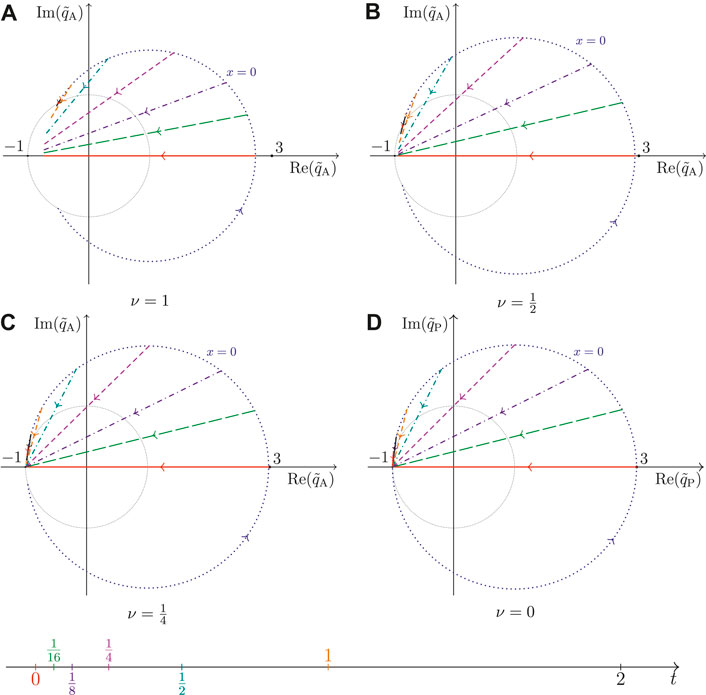
FIGURE 6. Parameterization of the non-rapid oscillating complex-valued amplitude $\tilde{q}$ in the spatial variable x for different values of temporal variable t: $t=0$ (solid red), $t=1/16$ (long-dashed green), $t=1/8$ (dash-dotted purple), $t=1/4$ (dash magenta), $t=1/2$ (dash-dotted cyan), $t=1$ (dashed orange), $t=2$ (solid black), and $t=4$ (solid red), and modulation frequencies of the Akhmediev solitons (A)$\nu =1$$\left(0\le x\le \pi \right)$, (B)$\nu =1/2$$\left(0\le x\le 2\pi \right)$, (C)$\nu =1/4$$\left(0\le x\le 4\pi \right)$, and (D)$\nu =0$, $x\ge 0$ (Peregrine soliton).

For each panel, we only sketch the trajectories for an interval of half the spatial envelope wavelength, i.e., $0\le x\le L_{\text{A}}/2=\pi /\nu$. For this limited space interval, the direction of the lines is moving inwardly focused, from the dotted-blue exterior circle for $x=0$ to some values in the left-part of the complex-plane near $\mathrm{Re}\left({\tilde{q}}_{\text{A}}\right)=-1$. As the value of x progresses, $L_{\text{A}}/2=\pi /\nu \le x\le L_{\text{A}}=2\pi /\nu$, the trajectories bounce back toward the initial points by following the identical paths. They then travel in the same manner periodically as $x\to \pm \infty$. For a decreasing value of the parameter ν, the endpoint of these lines tends to focus around the region near $\left(-\mathrm{1,0}\right)$, as we can observe in Figures 6A–C. For the Peregrine soliton, the trajectories are not periodic as $L_{\text{A}}\to \infty$, and they tend to $\left(-\mathrm{1,0}\right)$ for $x\to \pm \infty$, as can be seen in Figure 6D.

In Figure 6, a prominent difference in the trajectories for different values of the parameter ν is its lengths. The length of the trajectories is increasing for decreasing values of ν. While the starting points for the Kuznetsov-Ma breathers are shrinking, for this family of Akhmediev solitons, they are expanding as $\nu \to 0$ until the dotted blue exterior circle reaches a radius of 2 unit length. Moreover, the endpoints for larger values of ν stop at some points where their real values become negative but still larger than $-1$. These endpoints eventually approach $\left(-\mathrm{1,0}\right)$ as $\nu \to 0$.

Figure 7 displays the sketch of the non-rapid-oscillating part of the Akhmediev soliton ${\tilde{q}}_{\text{A}}$ [panels (A)‐(C)] and Peregrine soliton ${\tilde{q}}_{\text{P}}$ [panel (D)] in the complex-plane parameterized in the temporal variable t for different values of the spatial variable x and parameter ν. The values of t run from $t\to -\infty$ to $t\to +\infty$, and we only sketch the positive values of x. The plots for the negative values of x are identical and are not shown due to the symmetry property of the soliton. The x-axis below the panels shows the selected values of x ranging from $x=0$ to $x=\text{π}$. For ${\tilde{q}}_{\text{A}}$, the trajectories are composed of circular sectors, elliptical sectors, and straight lines instead of closed curves like circles or ellipses. Since this soliton is a nonlinear extension of the modulational instability, the trajectories for each value of the parameter ν, $0<\nu <2$, are the corresponding homoclinic orbit for an unstable mode, and the presence of a phase shift prevents closed-path trajectories [30, 34, 76, 164].

FIGURE 7

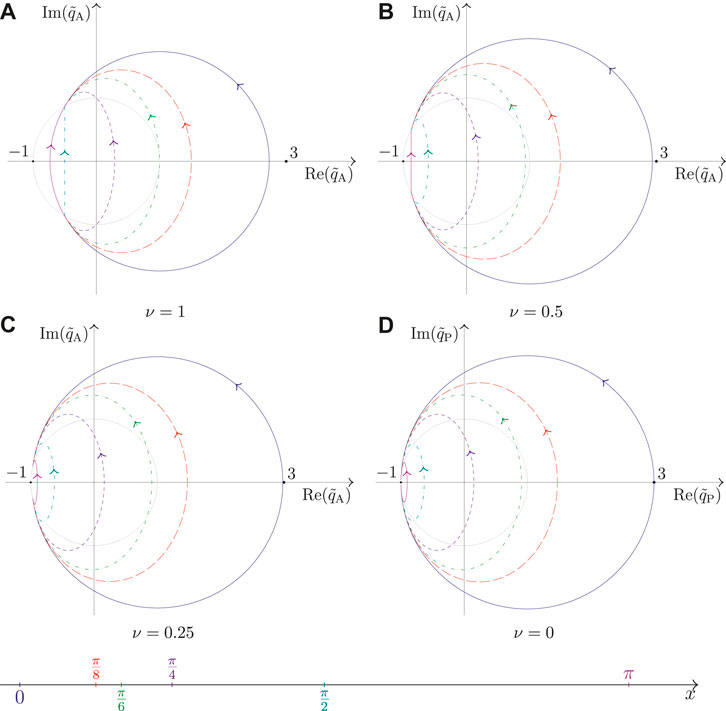
FIGURE 7. Parameterization of the non-rapid oscillating complex-valued amplitude $\tilde{q}$ in the temporal variable t$\left(-\infty <t<\infty \right)$ for different values of spatial variable x: $x=0$ (solid blue), $x=\pi /8$ (long-dashed red), $x=\pi /6$ (dash-dotted green), $x=\pi /4$ (dashed purple), $x=\pi /2$ (dash-dotted cyan), and $x=\pi$ (solid magenta), and modulation frequencies of the Akhmediev solitons (A)$\nu =1$, (B)$\nu =0.5$, (C)$\nu =0.25$, and (D)$\nu \to 0$ (the Peregrine soliton).

The circular sectors are attained for $x=0$ and the straight lines occur at $x=\left(n+1/2\right)\pi /\nu ,n\in \mathbb{Z}$, $n\in \mathbb{Z}$. Trajectories at other locations yield the elliptical sectors. The initial and final points are not identical, and this indicates a phase shift in the soliton. Let ${\varphi }_{+\infty }$ and ${\varphi }_{-\infty }$ be the phases for $x\to \pm \infty$, respectively. Let also $\Delta \varphi ={\varphi }_{+\infty }-{\varphi }_{-\infty }$ be the difference between the phases at $x=+\infty$ and $x=-\infty$, then we have the following phase relationships:

$\begin{array}{l}\tan {\varphi }_{\pm \infty }=\pm \frac{\sigma }{{\nu }^2-1},\end{array}(15)$

$\begin{array}{l}\mathrm{and}\Delta \varphi =2\arctan \left(\frac{\sigma }{{\nu }^2-1}\right).\end{array}(16)$

For the Peregrine soliton, the trajectories of time parameterization in the complex-plane are either a circle (for $x=0$) or ellipses (for other values of $x\ne 0$). The circle is centered at $\left(\mathrm{1,0}\right)$ with radius $r=2$. Let $x=x_0\in ℝ$ be the position for the Peregrine soliton, then the ellipse has the length of semi-minor axis $a\left(x_0\right)$, the length of semi-major axis $b\left(x_0\right)$, and is centered at $\left(c\left(x_0\right),0\right)$, where

$\begin{array}{l}a\left(x_0\right)=\frac{2}{1+4x_0^2},\end{array}(17)$

$\begin{array}{l}b\left(x_0\right)=\frac{2}{\sqrt{1+4x_0^2}},\end{array}(18)$

$\begin{array}{l}\mathrm{and}c\left(x_0\right)=a\left(x_0\right)-1.\end{array}(19)$

Nearly all trajectories in Figure 7 follow the right-hand side paths instead of the left-hand side. For decreasing values of ν, the trajectories are generally expanding in size, except for the curve at $x=\pi$ that becomes a straight line when the parameter value changes from $\nu =1$ to $\nu =1/2$. When the values of ν is further decreased, the trajectories at $x=\pi$ become an elliptical sector and an ellipse for $\nu =1/4$ and $\nu =0$, respectively.

Figure 8 should be viewed in connection to Figures 6D, 7D. It displays the plots of the real and imaginary parts of the non-rapid-oscillating complex-valued amplitude for the Peregrine soliton ${\tilde{q}}_{\text{P}}$ with respect to x and t, which are presented in the upper and lower panels, respectively. For the former, different curves correspond to selected values of time $t\in \left\{0,1/16,1/8,1/4,1/2,\mathrm{1,2}\right\}$. For the latter, different curves correspond to selected values of position $x\in \left\{0,\pi /8,\pi /6,\pi /4,\pi /2,\pi \right\}$. The phase difference in the time parameterization of ${\tilde{q}}_{\text{P}}$ is discernible from the behavior of Im$\left({\tilde{q}}_{\text{P}}\right)$ as $t\to \pm \infty$. While $\underset{x\to \pm \infty }{\lim }\mathrm{Re}\left({\tilde{q}}_P\right)=-1$, the quantity for $\underset{x\to \pm \infty }{\lim }\mathrm{Im}\left({\tilde{q}}_P\right)$ takes positive and negative values, respectively.

FIGURE 8

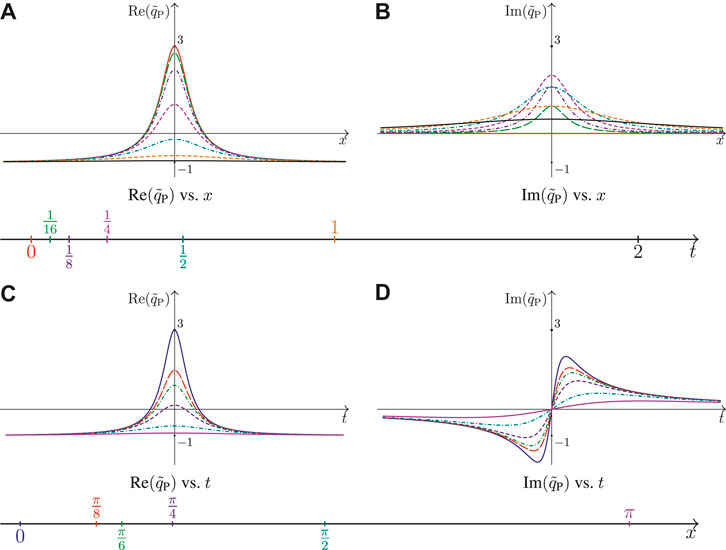
FIGURE 8. Plots of the real and imaginary parts of the non-rapid oscillating complex-valued amplitude for the Peregrine soliton with respect to the spatial and temporal variables, x (upper panels) and t (lower panels), respectively. For upper panels (A) and (B), various curves indicates different time: $t=0$ (solid red), $t=1/16$ (long-dashed green), $t=1/8$ (dash-dotted purple), $t=1/4$ (dash magenta), $t=1/2$ (dash-dotted cyan), $t=1$ (dashed orange), and $t=2$ (solid black). For lower panels (C) and (D), different curves indicates different positions: $x=0$ (solid blue), $x=\pi /8$ (long-dashed red), $x=\pi /6$ (dash-dotted green), $x=\pi /4$ (dashed purple), $x=\pi /2$ (dash-dotted cyan), and $x=\pi$ (solid magenta).

4 Conclusion

We have considered the exact analytical breather solutions of the focusing NLS equation, where the wave envelopes at infinity have a nonzero but constant background. These solutions have been adopted as weakly nonlinear prototypes for freak waves in dispersive media due to their fine agreement with various experimental results. We have provided not only a brief historical review of the breathers but also covered some recent progress in the field of rogue wave modeling in the context of the NLS equation.

In particular, we have discussed the Peregrine soliton as a limiting case of the Kuznetsov-Ma breather and Akhmediev soliton. We have verified rigorously using the ε-δ argument that as each of the parameter values from these two breathers is approaching zero, they reduce to the Peregrine soliton. We have also presented this limiting behavior visually by depicting the contour plots of the breather amplitude modulus for selected parameter values. We displayed the parameterization plots of the non-rapid-oscillating complex-valued breather amplitudes both spatially and temporally.

The trajectories for the spatial parameterization in the complex-plane exhibit a set of straight lines for all the breathers. From $x\to -\infty$ to $x\to +\infty$, the paths are passed twice for the Kuznetsov-Ma breather and are elapsed many times infinitely for the Akhmediev soliton due to its spatial periodic characteristics. The trajectories in the complex plane for the parameterization in the temporal variable of the Kuznetsov-Ma breather and Peregrine soliton feature a periodic circle and a set of periodic ellipses due to its temporal symmetry. For the Akhmediev soliton, on the other hand, the path does not only turn into circle and ellipse sectors but also becomes straight lines as it travels from $t\to -\infty$ to $t\to +\infty$, featuring homoclinic orbits with a phase shift.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Dedication

The author would like to dedicate this article to his late father Zakaria Karjanto (Khouw Kim Soey, 許金瑞) who not only taught him the alphabet, numbers, and the calendar in his early childhood but also cultivated the value of hard work, diligence, discipline, perseverance, persistence, and grit. Karjanto Senior was born in Tasikmalaya, West Java, Japanese-occupied Dutch East Indies on 1 January 1944 (Saturday Pahing) and died in Bandung, West Java, Indonesia on 18 April 2021 (Sunday Wage).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The author wishes to thank Bertrand Kibler, Amin Chabchoub, and Heremba Bailung for the invitation to contribute to the article collection “Peregrine Soliton and Breathers in Wave Physics: Achievements and Perspectives” and Marlena Radomska from the Production Team of Frontiers in Physics for her excellent and outstanding administrative assistance. The author also acknowledges E. (Brenny) van Groesen, Mark Ablowitz, Constance Schober, Frederic Dias, Roger Grimshaw, Panayotis Kevrekidis, Boris Malomed, Evgenii Kuznetsov, Nail Akhmediev, Alfred Osborne, Miguel Onorato, Gert Klopman, René Huijsmans, Andonowati, Stephan van Gils, Guido Schneider, Anthony Roberts, Shanti Toenger, Omar Kirikchi, Ardhasena Sopaheluwakan, Hadi Susanto, Alexander Iskandar, Agung Trisetyarso, Ade Irma Suriajaya, and Defrianto Pratama for fruitful discussion.

References

1. Osborne AR. Nonlinear Ocean Wave and the Inverse Scattering Transform. Cambridge, MA: Academic Press (2010).

2. Debnath L. Nonlinear Partial Differential Equations for Scientists and Engineers. Berlin, Germany: Springer Science + Business Media (2012).

CrossRef Full Text

3. Agrawal GP. Nonlinear Fiber Optics. 5th ed. Cambridge, MA: Academic Press (2012).

4. Kivshar YS, Agrawal GP. Optical Solitons: From Fibers to Photonic Crystals. Cambridge, MA: Academic Press (2003).

5. Infeld E, Rowlands G. Nonlinear Waves, Solitons and Chaos. 2nd ed. Cambridge, United Kingdom: Cambridge University Press (2000).

6. Newell AC. Solitons in Mathematics and Physics. Philadelphia, PA: SIAM (1985).

CrossRef Full Text

7. Sulem C, Sulem PL. The Nonlinear Schrödinger Equation: Self-Focusing and Wave Collapse. Berlin, Germany: Springer-Verlag (1999).

8. Kevrekidis PG, Frantzeskakis DJ, Carretero-González R. Emergent Nonlinear Phenomena in Bose-Einstein Condensates: Theory and Experiment. Berlin, Germany: Springer Science + Business Media (2007).

9. Chiao RY, Garmire E, Townes CH. Self-trapping of Optical Beams. Phys Rev Lett (1964) 13:479–82. doi:10.1103/physrevlett.13.479

CrossRef Full Text | Google Scholar

10. Kelley PL. Self-focusing of Optical Beams. Phys Rev Lett (1965) 15:1005–1008. doi:10.1103/physrevlett.15.1005

CrossRef Full Text | Google Scholar

11. Taniuti T, Washimi H. Self-trapping and Instability of Hydromagnetic Waves along the Magnetic Field in a Cold Plasma. Phys Rev Lett (1968) 21:209–212. doi:10.1103/physrevlett.21.209

CrossRef Full Text | Google Scholar

12. Karpman VI, Krushkal EM Modulated Waves in Nonlinear Dispersive Media. Soviet Phys JETP (1969) 28:277. doi:10.1007/3-540-46629-0_2

CrossRef Full Text | Google Scholar

13. Taniuti T, Yajima N. Perturbation Method for a Nonlinear Wave Modulation. I. J Math Phys (1969) 10:1369–1372. doi:10.1063/1.1664975

CrossRef Full Text | Google Scholar

14. Asano N, Taniuti T, Yajima N. Perturbation Method for a Nonlinear Wave Modulation. II. J Math Phys (1969) 10:2020–2024. doi:10.1063/1.1664797

CrossRef Full Text | Google Scholar

15. Tappert FD, Varma CM. Asymptotic Theory of Self-Trapping of Heat Pulses in Solids. Phys Rev Lett (1970) 25:1108–1111. doi:10.1103/physrevlett.25.1108

CrossRef Full Text | Google Scholar

16. Benney DJ, Newell AC The Propagation of Nonlinear Wave Envelopes. J Math Phys (1967) 46:133–139. doi:10.1002/sapm1967461133

CrossRef Full Text | Google Scholar

17. Zakharov VE. Stability of Periodic Waves of Finite Amplitude on the Surface of a Deep Fluid. J Appl Mech Tech Phys (1968) 9:190–194. doi:10.1007/BF00913182

CrossRef Full Text | Google Scholar

18. Hasimoto H, Ono H. Nonlinear Modulation of Gravity Waves. J Phys Soc Jpn (1972) 33:805–811. doi:10.1143/jpsj.33.805

CrossRef Full Text | Google Scholar

19. Gross EP. Structure of a Quantized Vortex in Boson Systems. Il Nuovo Cimento (1955–1965) 20:454–477. doi:10.1007/BF02731494

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Pitaevskii LP. Vortex Lines in an Imperfect Bose Gas. Soviet Phys JETP (1961) 13:451–454.

Google Scholar

21. Ginzburg VL, Landau LD. On the Theory of Superconductivity. On Superconductivity and Superfluidity. Berlin Heilderberg, Germany: Springer (2009). 113–137.

22. Malomed BA. Nonlinear Schrödinger Equation. In: A Scott, editor. Encyclopedia of Nonlinear Science. New York, NY: Routledge (2005). 639–643.

Google Scholar

23. Ablowitz M, Prinari B. Nonlinear Schrodinger Systems: Continuous and Discrete. Scholarpedia (2008) 3:5561. doi:10.4249/scholarpedia.5561

CrossRef Full Text | Google Scholar

24. Huang J. Nonlinear Schrödinger Equation. In: B Lembrikov, editor. Nonlinear Optics: Novel Results in Theory and Applications. London, UK and Rijeka, Croatia: IntechOpen (2018). 11–29.

Google Scholar

25. Karjanto N. The Nonlinear Schrödinger Equation: A Mathematical Model with its Wide Range of Applications. In: V Simpao, and H Little, editors. Understanding the Schrödinger Equation: Some (Non)Linear Perspectives. Hauppauge, New York: Nova Science Publishers (2020). 135–179. Accessible online at arXiv, preprint arXiv:1912.10683.

Google Scholar

26. Fibich G. The Nonlinear Schrödinger Equation: Singular Solutions and Optical Collapse. Cham, Switzerland: Springer (2015).

27. Akhmediev NN, Eleonskiĭ VM, Kulagin NE. Generation of Periodic Trains of Picosecond Pulses in an Optical Fiber: Exact Solutions. Soviet Phys JETP (1985) 62:894–899.

Google Scholar

28. Akhmediev NN, Korneev VI. Modulation Instability and Periodic Solutions of the Nonlinear Schrödinger Equation. Theor Math Phys (1986) 69:1089–1093. doi:10.1007/bf01037866

CrossRef Full Text | Google Scholar

29. Akhmediev NN, Eleonskii VM, Kulagin NE. Exact First-Order Solutions of the Nonlinear Schrödinger Equation. Theor Math Phys (1987) 72:809–818. doi:10.1007/bf01017105

CrossRef Full Text | Google Scholar

30. Akhmediev NN, Ankiewicz A. Solitons: Nonlinear Pulses and Beams. London, United Kingdom: Chapman & Hall (1997).

31. Hirota R. A New Form of Backlund Transformations and its Relation to the Inverse Scattering Problem. Prog Theor Phys (1974) 52:1498–1512. doi:10.1143/ptp.52.1498

CrossRef Full Text | Google Scholar

32. Hirota R. Direct Method of Finding Exact Solutions of Nonlinear Evolution Equations. In: Bäcklund Transformations, the Inverse Scattering Method, Solitons, and Their Applications. Lecture Notes in Mathematics, 515. Berlin, Germany: Springer (1976). 40–68. doi:10.1007/bfb0081162

CrossRef Full Text | Google Scholar

33. Hirota R, Satsuma J. A Variety of Nonlinear Network Equations Generated from the Bäcklund Transformation for the Toda Lattice. Prog Theor Phys Suppl (1976) 59:64–100. doi:10.1143/ptps.59.64

CrossRef Full Text | Google Scholar

34. Ablowitz MJ, Herbst BM. On Homoclinic Structure and Numerically Induced Chaos for the Nonlinear Schrödinger Equation. SIAM J Appl Math (1990) 50:339–351. doi:10.1137/0150021

CrossRef Full Text | Google Scholar

35. Zakharov VE, Shabat AB. Exact Theory of Two-Dimensional Self-Focusing and One-Dimensional Self-Modulation of Waves in Nonlinear Media. Soviet Phys JETP (1972) 34:62.

Google Scholar

36. Zakharov VE, Shabat AB. Interaction between Solitons in a Stable Medium. Soviet Phys JETP (1973) 37:823–828.

Google Scholar

37. Ablowitz MJ, Segur H. Solitons and the Inverse Scattering Transform. Philadelphia, PA: SIAM (1981).

38. Osborne AR, Onorato M, Serio M. The Nonlinear Dynamics of Rogue Waves and Holes in Deep-Water Gravity Wave Trains. Phys Lett A (2000) 275:386–393. doi:10.1016/s0375-9601(00)00575-2

CrossRef Full Text | Google Scholar

39. Osborne AR. The Random and Deterministic Dynamics of ‘Rogue Waves' in Unidirectional, Deep-Water Wave Trains. Mar Structures (2001) 14:275–293. doi:10.1016/s0951-8339(00)00064-2

CrossRef Full Text | Google Scholar

40. Biondini G, Kovačič G. Inverse Scattering Transform for the Focusing Nonlinear Schrödinger Equation with Nonzero Boundary Conditions. J Math Phys (2014) 55:031506. doi:10.1063/1.4868483

CrossRef Full Text | Google Scholar

41. Olver PJ. Applications of Lie Groups to Differential Equations. 2nd ed. Berlin, Germany: Springer Science + Business Media (1993).

CrossRef Full Text

42. van Groesen E, A ndonowati, Karjanto N. Displaced Phase-Amplitude Variables for Waves on Finite Background. Phys Lett A (2006) 354:312–319. doi:10.1016/j.physleta.2006.02.037

CrossRef Full Text | Google Scholar

43. Karjanto N. Mathematical Aspects of Extreme Water Waves (Enschede and Zutphen, the Netherlands: The University of Twente and Wöhrmann Print Service). [PhD thesis] (2006). Accessible online at arXiv, preprint arXiv:2006.00766.

44. Karjanto N, van Groesen E. Derivation of the NLS Breather Solutions Using Displaced Phase-Amplitude Variables. In: S Wahyuni, IE Wijayanti, and D Rosadi, editors. Proceedings of SEAMS-GMU Conference 2007. Indonesia: Applied Mathematics (Department of Mathematics, Gadjah Mada University (2007). 357–368. Accessible online at arXiv, preprint arXiv:1110.4704.

Google Scholar

45. Demontis F, Prinari B, Van Der Mee C, Vitale F. The Inverse Scattering Transform for the Focusing Nonlinear Schrödinger Equation with Asymmetric Boundary Conditions. J Math Phys (2014) 55:101505. doi:10.1063/1.4898768

CrossRef Full Text | Google Scholar

46. Dysthe KB, Trulsen K. Note on Breather Type Solutions of the NLS as Models for Freak-Waves. Physica Scripta (1999) T82:48. doi:10.1238/physica.topical.082a00048

CrossRef Full Text | Google Scholar

47. Chow KW. A Class of Exact, Periodic Solutions of Nonlinear Envelope Equations. J Math Phys (1995a) 36:4125–4137. doi:10.1063/1.530951

CrossRef Full Text | Google Scholar

48. Kuznetsov EA. Solitons in a Parametrically Unstable Plasma. Akademiia Nauk SSSR Doklady (1977) 236:575–577. English translation: Soviet Physics Doklady22 (1977) 507–508.

Google Scholar

49. Kuznetsov EA. Personal Communication (2020).

50. Kawata T, Inoue H, Adachihara H, McLaughlin DW, Moloney JV, Newell AC. Solitary Waves as Fixed Points of Infinite‐dimensional Maps for an Optical Bistable Ring Cavity: Analysis. J Math Phys (1988) 29:63–85. doi:10.1063/1.528136

CrossRef Full Text

51. Ma Y-C. The Perturbed Plane-Wave Solutions of the Cubic Schrödinger Equation. Stud Appl Math (1979) 60:43–58. doi:10.1002/sapm197960143

CrossRef Full Text | Google Scholar

52. Kuznetsov EA, Mikhailov AV. Stability of Stationary Waves in Nonlinear Weakly Dispersive Media. Zhurnal Eksperimentalnoi I Teoreticheskoi Fiziki 67 (1974). p. 1717–1727. English translation: Soviet Physics JETP40(2)1975855859.

Google Scholar

53. Slunyaev A. Nonlinear Analysis and Simulations of Measured Freak Wave Time Series. Eur J Mech - B/Fluids (2006) 25:621–635. doi:10.1016/j.euromechflu.2006.03.005

CrossRef Full Text | Google Scholar

54. Kibler B, Fatome J, Finot C, Millot G, Genty G, Wetzel B, et al. Observation of Kuznetsov-Ma Soliton Dynamics in Optical Fibre. Scientific Rep (2012) 2:463. doi:10.1038/srep00463

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Grimshaw R, Pelinovsky D, Pelinovsky E, Talipova T. Wave Group Dynamics in Weakly Nonlinear Long-Wave Models. Physica D: Nonlinear Phenomena (2001) 159:35–57. doi:10.1016/s0167-2789(01)00333-5

CrossRef Full Text | Google Scholar

56. Gagnon L. Solitons on a Continuous-Wave Background and Collision between Two Dark Pulses: Some Analytical Results. J Opt Soc Am B (1993) 10:469–74. doi:10.1364/josab.10.000469

CrossRef Full Text | Google Scholar

57. Adachihara H, McLaughlin DW, Moloney JV, Newell AC. Solitary Waves as Fixed Points of Infinite‐dimensional Maps for an Optical Bistable Ring Cavity: Analysis. J Math Phys (1988) 29:63–85. doi:10.1063/1.528136

CrossRef Full Text | Google Scholar

58. Mihalache D, Lederer F, Baboiu D-M. Two-parameter Family of Exact Solutions of the Nonlinear Schrödinger Equation Describing Optical-Soliton Propagation. Phys Rev A (1993) 47:3285–3290. doi:10.1103/physreva.47.3285

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Clamond D, Francius M, Grue J, Kharif C. Long Time Interaction of Envelope Solitons and Freak Wave Formations. Eur J Mech - B/Fluids (2006) 25:536–553. doi:10.1016/j.euromechflu.2006.02.007

CrossRef Full Text | Google Scholar

60. Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi FT. Rogue Waves and Their Generating Mechanisms in Different Physical Contexts. Phys Rep (2013) 528:47–89. doi:10.1016/j.physrep.2013.03.001

CrossRef Full Text | Google Scholar

61. Chabchoub A, Kibler B, Dudley JM, Akhmediev N. Hydrodynamics of Periodic Breathers. Phil Trans R Soc A (2014) 372:20140005. doi:10.1098/rsta.2014.0005

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Residori S, Onorato M, Bortolozzo U, Arecchi FT. Rogue Waves: a Unique Approach to Multidisciplinary Physics. Contemp Phys (2017) 58:53–69. doi:10.1080/00107514.2016.1243351

CrossRef Full Text | Google Scholar

63. Akhmediev NN, Wabnitz S. Phase Detecting of Solitons by Mixing with a Continuous-Wave Background in an Optical Fiber. J Opt Soc Am B (1992) 9:236–242. doi:10.1364/josab.9.000236

CrossRef Full Text | Google Scholar

64. Kharif C, Pelinovsky E, Talipova T, Slunyaev A. Focusing of Nonlinear Wave Groups in Deep Water. JETP Lett (2001) 73:170–175. doi:10.1134/1.1368708

CrossRef Full Text | Google Scholar

65. Garnier J, Kalimeris K. Inverse Scattering Perturbation Theory for the Nonlinear Schrödinger Equation with Non-vanishing Background. J Phys A: Math Theor (2011) 45:035202. doi:10.1088/1751-8113/45/3/035202

CrossRef Full Text | Google Scholar

66. Xiong H, Gan J, Wu Y. Kuznetsov-Ma Soliton Dynamics Based on the Mechanical Effect of Light. Phys Rev Lett (2017) 119:153901. doi:10.1103/physrevlett.119.153901

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Cuevas-Maraver J, Kevrekidis PG, Frantzeskakis DJ, Karachalios NI, Haragus M, James G. Floquet Analysis of Kuznetsov-Ma Breathers: A Path towards Spectral Stability of Rogue Waves. Phys Rev E (2017) 96:012202. doi:10.1103/physreve.96.012202

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Zhao LC, Ling L, Yang ZY. Mechanism of Kuznetsov-Ma Breathers. Phys Rev E (2018) 97:022218. doi:10.1103/physreve.97.022218

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Gelash A. Formation of Rogue Waves from a Locally Perturbed Condensate. Phys Rev E (2018) 97:022208. doi:10.1103/physreve.97.022208

CrossRef Full Text | Google Scholar

70. Bélanger N, Bélanger P-A. Bright Solitons on a CW Background. Opt Commun (1996) 124:301–308. doi:10.1016/0030-4018(95)00659-1

CrossRef Full Text | Google Scholar

71. Tajiri M, Watanabe Y. Breather Solutions to the Focusing Nonlinear Schrödinger Equation. Phys Rev E (1998) 57:3510–3519. doi:10.1103/physreve.57.3510

CrossRef Full Text | Google Scholar

72. Chow KW. Solitary Waves on a Continuous Wave Background. J Phys Soc Jpn (1995) 64:1524–1528. doi:10.1143/jpsj.64.1524

CrossRef Full Text | Google Scholar

73. Rajaraman R. Solitons and Instantons: An Introduction to Solitons and Instantons in Quantum Field Theory. Amsterdam, Netherlands: Elsevier/North Holland (1982).

74. Falkovich G, Kolokolov I, Lebedev V, Migdal A. Instantons and Intermittency. Phys Rev E (1996) 54:4896–907. doi:10.1103/physreve.54.4896

CrossRef Full Text | Google Scholar

75. Turitsyn SK, Bale BG, Fedoruk MP. Dispersion-managed Solitons in Fibre Systems and Lasers. Phys Rep (2012) 521:135–203. doi:10.1016/j.physrep.2012.09.004

CrossRef Full Text | Google Scholar

76. Calini A, Schober CM. Homoclinic Chaos Increases the Likelihood of Rogue Wave Formation. Phys Lett A (2002) 298:335–349. doi:10.1016/s0375-9601(02)00576-5

CrossRef Full Text | Google Scholar

77. Onorato M, Osborne AR, Serio M, Damiani T. Occurrence of Freak Waves from Envelope Equations in Random Ocean Wave Simulations. In: Rogue Waves 2000. editors M Olagnon, and M Prevosto, (Brest, France: IFREMER, French Research Institute for Exploitation of the Sea). (2001). 11.

Google Scholar

78. Karjanto N, van Groesen E, Peterson P. Investigation of the Maximum Amplitude Increase from the Benjamin-Feir Instability. J Indonesian Math Soc (2002) 8:39.

Google Scholar

79. Akhmediev N, Ankiewicz A, Taki M. Waves that Appear from Nowhere and Disappear without a Trace. Phys Lett A (2009) 373:675–678. doi:10.1016/j.physleta.2008.12.036

CrossRef Full Text | Google Scholar

80. Onorato M, Proment D, Toffoli A. Triggering Rogue Waves in Opposing Currents. Phys Rev Lett (2011) 107:184502. doi:10.1103/physrevlett.107.184502

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Slunyaev AV, Shrira VI. On the Highest Non-breaking Wave in a Group: Fully Nonlinear Water Wave Breathers versus Weakly Nonlinear Theory. J Fluid Mech (2013) 735:203–248. doi:10.1017/jfm.2013.498

CrossRef Full Text | Google Scholar

82. Bespalov VI, Talanov VI. Filamentary Structure of Light Beams in Nonlinear Liquids. Soviet Phys JETP Lett (1966) 3:307–312.

Google Scholar

83. Ostrovskii L. Propagation of Wave Packets and Space-Time Self-Focusing in a Nonlinear Medium. Soviet Phys JETP (1967) 24:797–800.

Google Scholar

84. Karpman VI. Self-modulation of Nonlinear Plane Waves in Dispersive Media. JETP Lett (1967) 6:277.

Google Scholar

85. Benjamin TB, Feir JE. The Disintegration of Wave Trains on Deep Water Part 1. Theory. J Fluid Mech (1967) 27:417–30. doi:10.1017/s002211206700045x

CrossRef Full Text | Google Scholar

86. Tam CKW. Amplitude Dispersion and Nonlinear Instability of Whistlers. Phys Fluids (1969) 12:1028–1035. doi:10.1063/1.2163663

CrossRef Full Text | Google Scholar

87. Hasegawa A. Observation of Self-Trapping Instability of a Plasma Cyclotron Wave in a Computer Experiment. Phys Rev Lett (1970) 24:1165–1168. doi:10.1103/physrevlett.24.1165

CrossRef Full Text | Google Scholar

88. Hasegawa A. Theory and Computer Experiment on Self-Trapping Instability of Plasma Cyclotron Waves. Phys Fluids (1972) 15:870–881. doi:10.1063/1.1693996

CrossRef Full Text | Google Scholar

89. Robins NP, Zhang W, Ostrovskaya EA, Kivshar YS. Modulational Instability of Spinor Condensates. Phys Rev A (2001) 64:021601. doi:10.1103/physreva.64.021601

CrossRef Full Text | Google Scholar

90. Konotop V, Salerno M. Modulational Instability in Bose-Einstein Condensates in Optical Lattices. Phys Rev A (2002) 65:021602. doi:10.1103/physreva.65.021602

CrossRef Full Text | Google Scholar

91. Smerzi A, Trombettoni A, Kevrekidis P, Bishop A. Dynamical Superfluid-Insulator Transition in a Chain of Weakly Coupled Bose-Einstein Condensates. Phys Rev Lett (2002) 89:170402. doi:10.1103/physrevlett.89.170402

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Baizakov BB, Konotop VV, Salerno M. Regular Spatial Structures in Arrays of Bose Einstein Condensates Induced by Modulational Instability. J Phys B: Mol Opt Phys (2002) 35:5105–5119. doi:10.1088/0953-4075/35/24/312

CrossRef Full Text | Google Scholar

93. Salasnich L, Parola A, Reatto L Modulational Instability and Complex Dynamics of Confined Matter-Wave Solitons. Phys Rev Lett (2003) 91:080405. doi:10.1103/physrevlett.91.080405

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Theocharis G, Rapti Z, Kevrekidis P, Frantzeskakis D, Konotop V. Modulational Instability of Gross-Pitaevskii-type Equations in 1 + 1 Dimensions. Phys Rev A (2003) 67:063610. doi:10.1103/physreva.67.063610

CrossRef Full Text | Google Scholar

95. Lighthill MJ. Contributions to the Theory of Waves in Non-linear Dispersive Systems. IMA J Appl Math (1965) 1:269–306. doi:10.1093/imamat/1.3.269

CrossRef Full Text | Google Scholar

96. Zakharov VE, Ostrovsky LA. Modulation Instability: The Beginning. Physica D: Nonlinear Phenomena (2009) 238:540–548. doi:10.1016/j.physd.2008.12.002

CrossRef Full Text | Google Scholar

97. Yuen HC, Lake BM. Nonlinear Deep Water Waves: Theory and Experiment. Phys Fluids (1975) 18:956–960. doi:10.1063/1.861268

CrossRef Full Text | Google Scholar

98. Lake BM, Yuen HC, Rungaldier H, Ferguson WE. Nonlinear Deep-Water Waves: Theory and Experiment. Part 2. Evolution of a Continuous Wave Train. J Fluid Mech (1977) 83:49–74. doi:10.1017/s0022112077001037

CrossRef Full Text | Google Scholar

99. Yuen HC, Ferguson WE Relationship between Benjamin-Feir Instability and Recurrence in the Nonlinear Schrödinger Equation. Phys Fluids (1978a) 21:1275–1278. doi:10.1063/1.862394

CrossRef Full Text | Google Scholar

100. Yuen HC, Ferguson WE Fermi-Pasta-Ulam Recurrence in the Two-Space Dimensional Nonlinear Schrödinger Equation. Phys Fluids (1978b) 21:2116–2118. doi:10.1063/1.862122

CrossRef Full Text | Google Scholar

101. Yuen HC, Lake BM. Instabilities of Waves on Deep Water. Annu Rev Fluid Mech (1980) 12:303–334. doi:10.1146/annurev.fl.12.010180.001511

CrossRef Full Text | Google Scholar

102. Fermi E, Pasta P, Ulam S, Tsingou M. Studies of the Nonlinear Problems. Technical Report No. LA-1940. New Mexico: Los Alamos Scientific Laboratory (1955). doi:10.2172/4376203

CrossRef Full Text

103. Janssen PAEM. Modulational Instability and the Fermi-Pasta-Ulam Recurrence. Phys Fluids (1981) 24:23–26. doi:10.1063/1.863242

CrossRef Full Text | Google Scholar

104. Van Simaeys G, Emplit P, Haelterman M. Experimental Demonstration of the Fermi-Pasta-Ulam Recurrence in a Modulationally Unstable Optical Wave. Phys Rev Lett (2001) 87:033902. doi:10.1103/physrevlett.87.033902

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Janssen PAEM. Nonlinear Four-Wave Interactions and Freak Waves. J Phys Oceanogr (2003) 33:863–884. doi:10.1175/1520-0485(2003)33863

CrossRef Full Text | Google Scholar

106. Dysthe K, Krogstad HE, Müller P. Oceanic Rogue Waves. Annu Rev Fluid Mech (2008) 40:287–310. doi:10.1146/annurev.fluid.40.111406.102203

CrossRef Full Text | Google Scholar

107. Kharif C, Pelinovsky E, Slunyaev A. Rogue Waves in the Ocean. Berlin, Germany: Springer Science + Business Media (2009).

108. Slunyaev A, Kharif C, Pelinovsky E, Talipova T. Nonlinear Wave Focusing on Water of Finite Depth. Physica D: Nonlinear Phenomena (2002) 173:77–96. doi:10.1016/s0167-2789(02)00662-0

CrossRef Full Text | Google Scholar

109. Biondini G, Fagerstrom E. The Integrable Nature of Modulational Instability. SIAM J Appl Math (2015) 75:136–163. doi:10.1137/140965089

CrossRef Full Text | Google Scholar

110. Huijsmans RH, Klopman G, Karjanto N, Andonowati. Experiments on Extreme Wave Generation Using the Soliton on Finite Background. in Rogue Waves 2004 (Brest, France: IFREMER, French Research Institute for Exploitation of the Sea) editors M. Olagnon, and M. Prevosto. (2005). 10. Accessible online at arXiv, preprint arXiv:1110.5119

Google Scholar

111. van Groesen E, Andonowati , Karjanto N. Deterministic Aspects of Nonlinear Modulation Instability. in Rogue Waves 2004 (Brest, France: IFREMER, French Research Institute for Exploitation of the Sea) editors. M Olagnon, and M Prevosto. (2005). 12. Accessible online at arXiv, preprint arXiv:1110.5120

Google Scholar

112. Andonowati, , Karjanto N, van Groesen E. Extreme Wave Phenomena in Down-Stream Running Modulated Waves. Appl Math Model (2007) 31:1425–1443. doi:10.1016/j.apm.2006.04.015

CrossRef Full Text | Google Scholar

113. Karjanto N, van Groesen E. Qualitative Comparisons of Experimental Results on Deterministic Freak Wave Generation Based on Modulational Instability. J Hydro-environment Res (2010) 3:186–192. doi:10.1016/j.jher.2009.10.008

CrossRef Full Text | Google Scholar

114. Karjanto N, van Groesen E. Note on Wavefront Dislocation in Surface Water Waves. Phys Lett A (2007b) 371:173–179. doi:10.1016/j.physleta.2007.06.064

CrossRef Full Text | Google Scholar

115. Akhmediev N, Soto-Crespo JM, Ankiewicz A. Extreme Waves that Appear from Nowhere: on the Nature of Rogue Waves. Phys Lett A (2009) 373:2137–2145. doi:10.1016/j.physleta.2009.04.023

CrossRef Full Text | Google Scholar

116. Chabchoub A, Vitanov N, Hoffmann N. Experimental Evidence for Breather Type Dynamics in Freak Waves. Proc Appl Math Mech (2010) 10:495–496. doi:10.1002/pamm.201010240

CrossRef Full Text | Google Scholar

117. Dudley JM, Genty G, Dias F, Kibler B, Akhmediev N. Modulation Instability, Akhmediev Breathers and Continuous Wave Supercontinuum Generation. Opt Express (2009) 17:21497–21508. doi:10.1364/oe.17.021497

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Erkintalo M, Hammani K, Kibler B, Finot C, Akhmediev N, Dudley JM, et al. Higher-order Modulation Instability in Nonlinear Fiber Optics. Phys Rev Lett (2011) 107:253901. doi:10.1103/physrevlett.107.253901

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Kedziora DJ, Ankiewicz A, Akhmediev N. Second-order Nonlinear Schrödinger Equation Breather Solutions in the Degenerate and Rogue Wave Limits. Phys Rev E (2012) 85:066601. doi:10.1103/physreve.85.066601

CrossRef Full Text | Google Scholar

120. Karjanto N, van Groesen E. Mathematical Physics Properties of Waves on Finite Background. In: SP Lang, and SH Bedore, editors. Handbook of Solitons: Research, Technology and Applications. Hauppauge, NY: Nova Science Publishers) (2009). 501–539.

Google Scholar

121. Branger H, Chabchoub A, Hoffmann N, Kimmoun O, Kharif C, Akhmediev N. Evolution of a Peregrine Breather: Analytical and Experimental Studies. In: Presented in the 13th Hydrodynamics Days (Saint-Venant Hydrodynamic Laboratory, Île des Impressionnistes, Chatou, Seine River. France): Yvelines department, Île-de-France region (2012). 12. The typographical error contained in the English version of the title has been corrected in this reference.

Google Scholar

122. Chabchoub A, Hoffmann N, Onorato M, Akhmediev N. Super Rogue Waves: Observation of a Higher-Order Breather in Water Waves. Phys Rev X (2012) 2:011015. doi:10.1103/physrevx.2.011015

CrossRef Full Text | Google Scholar

123. Calini A, Schober CM. Observable and Reproducible Rogue Waves. J Opt (2013) 15:105201. doi:10.1088/2040-8978/15/10/105201

CrossRef Full Text | Google Scholar

124. Ling L, Zhao LC. Simple Determinant Representation for Rogue Waves of the Nonlinear Schrödinger Equation. Phys Rev E (2013) 88:043201. doi:10.1103/physreve.88.043201

CrossRef Full Text | Google Scholar

125. Dudley JM, Dias F, Erkintalo M, Genty G. Instabilities, Breathers and Rogue Waves in Optics. Nat Photon (2014) 8:755–764. doi:10.1038/nphoton.2014.220

CrossRef Full Text | Google Scholar

126. Chabchoub A, Fink M. Time-reversal Generation of Rogue Waves. Phys Rev Lett (2014) 112:124101. doi:10.1103/physrevlett.112.124101

PubMed Abstract | CrossRef Full Text | Google Scholar

127. Bilman D, Miller PD. A Robust Inverse Scattering Transform for the Focusing Nonlinear Schrödinger Equation. Comm Pure Appl Math (2019) 72:1722–1805. doi:10.1002/cpa.21819

CrossRef Full Text | Google Scholar

128. Peregrine DH. Water Waves, Nonlinear Schrödinger Equations and Their Solutions. J Aust Math Soc Ser B, Appl. Math (1983) 25:16–43. doi:10.1017/s0334270000003891

CrossRef Full Text | Google Scholar

129. Johnson RS.  A Modern Introduction to the Mathematical Theory of Water Waves. Cambridge, United Kingdom: Cambridge University Press (1997).

130. Henderson KL, Peregrine DH, Dold JW. Unsteady Water Wave Modulations: Fully Nonlinear Solutions and Comparison with the Nonlinear Schrödinger Equation. Wave Motion (1999) 29:341–361. doi:10.1016/s0165-2125(98)00045-6

CrossRef Full Text | Google Scholar

131. Nakamura A, Hirota R A. New Example of Explode-Decay Solitary Waves in One-Dimension. J Phys Soc Jpn (1985) 54:491–499. doi:10.1143/jpsj.54.491

CrossRef Full Text | Google Scholar

132. Yan Z. Nonautonomous “rogons” in the Inhomogeneous Nonlinear Schrödinger Equation with Variable Coefficients. Phys Lett A (2010) 374:672–679. doi:10.1016/j.physleta.2009.11.030

CrossRef Full Text | Google Scholar

133. Shrira VI, Geogjaev VV. What Makes the Peregrine Soliton So Special as a Prototype of Freak Waves? J Eng Math (2010) 67:11–22. doi:10.1007/s10665-009-9347-2

CrossRef Full Text | Google Scholar

134. Voronovich VV, Shrira VI, Thomas G. Can Bottom Friction Suppress “Freak Wave” Formation? J Fluid Mech (2008) 604:263–296. doi:10.1017/s0022112008001171

CrossRef Full Text | Google Scholar

135. Klein C, Haragus M. Numerical Study of the Stability of the Peregrine Solution. Ann Math Sci Appl (2017) 2:217–239. doi:10.4310/amsa.2017.v2.n2.a1

CrossRef Full Text | Google Scholar

136. Muñoz C Instability in Nonlinear Schrödinger Breathers. Proyecciones (2017) 36:653–683. doi:10.4067/s0716-09172017000400653

CrossRef Full Text | Google Scholar

137. Calini A, Schober CM, Strawn M. Linear Instability of the Peregrine Breather: Numerical and Analytical Investigations. Appl Numer Math (2019) 141:36–43. doi:10.1016/j.apnum.2018.11.005

CrossRef Full Text | Google Scholar

138. Klein C, Stoilov N. Numerical Study of the Transverse Stability of the Peregrine Solution. Stud Appl Math (2020) 145:36–51. doi:10.1111/sapm.12306

CrossRef Full Text | Google Scholar

139. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The Peregrine Soliton in Nonlinear Fibre Optics. Nat Phys (2010) 6:790–795. doi:10.1038/nphys1740

CrossRef Full Text | Google Scholar

140. Chabchoub A, Hoffmann NP, Akhmediev N. Rogue Wave Observation in a Water Wave Tank. Phys Rev Lett (2011) 106:204502. doi:10.1103/physrevlett.106.204502

PubMed Abstract | CrossRef Full Text | Google Scholar

141. Bailung H, Sharma SK, Nakamura Y. Observation of Peregrine Solitons in a Multicomponent Plasma with Negative Ions. Phys Rev Lett (2011) 107:255005. doi:10.1103/physrevlett.107.255005

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Chabchoub A, Akhmediev N, Hoffmann N. Experimental Study of Spatiotemporally Localized Surface Gravity Water Waves. Phys Rev E (2012) 86:016311. doi:10.1103/physreve.86.016311

CrossRef Full Text | Google Scholar

143. Shemer L, Alperovich L. Peregrine Breather Revisited. Phys Fluids (2013) 25:051701. doi:10.1063/1.4807055

CrossRef Full Text | Google Scholar

144. Chabchoub A, Hoffmann N, Branger H, Kharif C, Akhmediev N. Experiments on Wind-Perturbed Rogue Wave Hydrodynamics Using the Peregrine Breather Model. Phys Fluids (2013) 25:101704. doi:10.1063/1.4824706

CrossRef Full Text | Google Scholar

145. Onorato M, Proment D, Clauss G, Klein M. Rogue Waves: From Nonlinear Schrödinger Breather Solutions to Sea-Keeping Test. PLOS One (2013) 8:e54629. doi:10.1371/journal.pone.0054629

PubMed Abstract | CrossRef Full Text | Google Scholar

146. Yurova A. A Hidden Life of Peregrine's Soliton: Rouge Waves in the Oceanic Depths. Int J Geom Methods Mod Phys (2014) 11:1450057. doi:10.1142/s0219887814500571

CrossRef Full Text | Google Scholar

147. Li S, Prinari B, Biondini G. Solitons and Rogue Waves in Spinor Bose-Einstein Condensates. Phys Rev E (2018) 97:022221. doi:10.1103/physreve.97.022221

PubMed Abstract | CrossRef Full Text | Google Scholar

148. Cazaubiel A, Michel G, Lepot S, Semin B, Aumaître S, Berhanu M, et al. Coexistence of Solitons and Extreme Events in Deep Water Surface Waves. Phys Rev Fluids (2018) 3:114802. doi:10.1103/physrevfluids.3.114802

CrossRef Full Text | Google Scholar

149. Randoux S, Suret P, Chabchoub A, Kibler B, El G. Nonlinear Spectral Analysis of Peregrine Solitons Observed in Optics and in Hydrodynamic Experiments. Phys Rev E (2018) 98:022219. doi:10.1103/physreve.98.022219

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Gaillard P. Multi-parametric Deformations of Peregrine Breathers Solutions to the NLS Equation. Adv Res (2015) 4:346–364. doi:10.9734/air/2015/16827

CrossRef Full Text | Google Scholar

151. Akhmediev N, Ankiewicz A, Soto-Crespo JM. Rogue Waves and Rational Solutions of the Nonlinear Schrödinger Equation. Phys Rev E (2009c) 80:026601. doi:10.1103/physreve.80.026601

CrossRef Full Text | Google Scholar

152. Chen S, Baronio F, Soto-Crespo JM, Grelu P, Mihalache D. Versatile Rogue Waves in Scalar, Vector, and Multidimensional Nonlinear Systems. J Phys A: Math Theor (2017) 50:463001. doi:10.1088/1751-8121/aa8f00

CrossRef Full Text | Google Scholar

153. Malomed BA, Mihalache D. Nonlinear Waves in Optical and Matter-Wave Media: A Topical Survey of Recent Theoretical and Experimental Results. Rom J Phys (2019) 64:106.

Google Scholar

154. Zhao L-C, Ling L. Quantitative Relations between Modulational Instability and Several Well-Known Nonlinear Excitations. J Opt Soc Am B (2016) 33:850–856. doi:10.1364/josab.33.000850

CrossRef Full Text | Google Scholar

155. Toenger S, Godin T, Billet C, Dias F, Erkintalo M, Genty G, et al. Emergent Rogue Wave Structures and Statistics in Spontaneous Modulation Instability. Scientific Rep (2015) 5:10380. doi:10.1038/srep10380

CrossRef Full Text | Google Scholar

156. Kibler B, Chabchoub A, Gelash A, Akhmediev N, Zakharov VE. Superregular Breathers in Optics and Hydrodynamics: Omnipresent Modulation Instability beyond Simple Periodicity. Phys Rev X (2015) 5:041026. doi:10.1103/physrevx.5.041026

CrossRef Full Text | Google Scholar

157. Liu XS, Zhao LC, Duan L, Gao P, Yang ZY, Yang WL. Interaction between Breathers and Rogue Waves in a Nonlinear Optical Fiber. Chin Phys Lett (2018) 35:020501. doi:10.1088/0256-307x/35/2/020501

CrossRef Full Text | Google Scholar

158. Veldes G, Borhanian J, McKerr M, Saxena V, Frantzeskakis D, Kourakis I. Electromagnetic Rogue Waves in Beam-Plasma Interactions. J Opt (2013) 15:064003. doi:10.1088/2040-8978/15/6/064003

CrossRef Full Text | Google Scholar

159. Shen Y, Kevrekidis P, Veldes G, Frantzeskakis D, DiMarzio D, Lan X, et al. From Solitons to Rogue Waves in Nonlinear Left-Handed Metamaterials. Phys Rev E (2017) 95:032223. doi:10.1103/physreve.95.032223

PubMed Abstract | CrossRef Full Text | Google Scholar

160. Albares P, Díaz E, Cerveró JM, Domínguez-Adame F, Diez E, Estévez P. Solitons in a Nonlinear Model of Spin Transport in Helical Molecules. Phys Rev E (2018) 97:022210. doi:10.1103/physreve.97.022210

PubMed Abstract | CrossRef Full Text | Google Scholar

161. Farazmand M, Sapsis TP. Extreme Events: Mechanisms and Prediction. Appl Mech Rev (2019) 71. doi:10.1115/1.4042065

CrossRef Full Text | Google Scholar

162. Zhang Y, Belić MR, Zheng H, Chen H, Li C, Song J, et al. Nonlinear Talbot Effect of Rogue Waves. Phys Rev E (2014) 89:032902. doi:10.1103/physreve.89.032902

CrossRef Full Text | Google Scholar

163. Akhmediev N, Kibler B, Baronio F, Belić M, Zhong WP, Zhang Y, et al. Roadmap on Optical Rogue Waves and Extreme Events. J Opt (2016) 18:063001. doi:10.1088/2040-8978/18/6/063001

CrossRef Full Text | Google Scholar

164. Kimmoun O, Hsu H, Branger H, Li M, Chen YY, Kharif C, et al. Modulation Instability and Phase-Shifted Fermi-Pasta-Ulam Recurrence. Scientific Rep (2016) 6:28516. doi:10.1038/srep28516

PubMed Abstract | CrossRef Full Text | Google Scholar

165. Biondini G, Mantzavinos D. Universal Nature of the Nonlinear Stage of Modulational Instability. Phys Rev Lett (2016) 116:043902. doi:10.1103/physrevlett.116.043902

PubMed Abstract | CrossRef Full Text | Google Scholar

166. Biondini G, Li S, Mantzavinos D Oscillation Structure of Localized Perturbations in Modulationally Unstable Media. Phys Rev E (2016) 94:060201. doi:10.1103/physreve.94.060201

PubMed Abstract | CrossRef Full Text | Google Scholar

167. Gelash AA, Zakharov VE. Superregular Solitonic Solutions: a Novel Scenario for the Nonlinear Stage of Modulation Instability. Nonlinearity (2014) 27:R1–38. doi:10.1088/0951-7715/27/4/r1

CrossRef Full Text | Google Scholar

168. Chen J, Pelinovsky DE. Rogue Periodic Waves of the Focusing Nonlinear Schrödinger Equation. Proc R Soc A (2018) 474:20170814. doi:10.1098/rspa.2017.0814

PubMed Abstract | CrossRef Full Text | Google Scholar

169. Xu G, Gelash A, Chabchoub A, Zakharov V, Kibler B. Breather Wave Molecules. Phys Rev Lett (2019) 122:084101. doi:10.1103/physrevlett.122.084101

PubMed Abstract | CrossRef Full Text | Google Scholar

170. El-Tantawy S, Wazwaz A, Ali Shan S. On the Nonlinear Dynamics of Breathers Waves in Electronegative Plasmas with Maxwellian Negative Ions. Phys Plasmas (2017) 24:022105. doi:10.1063/1.4975090

CrossRef Full Text | Google Scholar