Storage, Splitting, and Routing of Optical Peregrine Solitons in a Coherent Atomic System

We propose a scheme to realize the storage and retrieval of optical Peregrine solitons in a coherent atomic gas via electromagnetically induced transparency (EIT). We show that optical Peregrine solitons with very small propagation loss, ultraslow motional velocity, and extremely low generation power can be created in the system via EIT. We also show that such solitons can be stored, retrieved, split, and routed with high efficiency and fidelity through the manipulation of control laser fields. The results reported here are useful for the active control of optical Peregrine solitons and promising for applications in optical information processing and transmission.

1 Introduction

Rogue waves, first observed in ocean surfaces, are highly isolated spatial-temporal wave packets with very large amplitudes when some special conditions are attained [1]. Such waves are ubiquitous in nature and quite intriguing, since they “appear from nowhere and disappear without a trace” and have extremely destructive power [2]. Except for ocean waves, the study on rogue waves has been extended to many other different physical contexts, including atmosphere [3], superfluid helium [4], capillary waves [5], water waves [6], photorefractive ferroelectrics [7], plasmas [8], ferromagnetic materials [9], and so on [10, 11].

Peregrine soliton, firstly suggested by D. H. Peregrine in the early 1980s for nonlinear dynamics of deep waters [12], is commonly taken as a prototype of rogue waves [13, 14]. Such soliton, i.e., localized rational solution of nonlinear Schrödinger equation, can be taken as a limiting case of the one-parameter family of Kuznetsov–Ma breathers [15] or Akhmediev breathers [16]. There have been considerable interests on Peregrine solitons occurring in a variety of physical systems [17–39]. Many efforts have also been devoted to the new understanding of Peregrine solitons through the analysis of other types of nonlinear partial differential equations [40–51].

Among various rogue waves, optical rogue waves have received much attention due to their interesting properties and promising applications [10, 11, 25–39, 52–54]. However, the creation of the optical rogue waves is not an easy task in conventional optical media (such as optical fibers and waveguides). The reason is that the nonlinear optical effect in such media is very weak, and hence a large input optical power is needed to obtain a significant optical nonlinearity required for the formation of rogue waves. Although some resonance mechanisms may be exploited to enhance nonlinear effects, near resonances significant optical absorptions occur, which result in serious attenuation and distortion of optical pulses during propagation.

In recent years, many efforts have been focused on the investigation of electromagnetically induced transparency (EIT), a typical quantum interference effect occurring in three-level atomic systems, by which the light absorption due to resonance may be largely suppressed and giant Kerr nonlinearity may be obtained simultaneously [55]. By means of EIT, it has been shown that weak-light solitons and their storage and retrieval can be realized [56–58]. Recent works [59, 60] have demonstrated that it is possible to generate optical Peregrine solitons with low generation power in EIT-base atomic systems.

In this work, we suggest a scheme to realize the memory of optical Peregrine solitons in a $\text{Λ}$-shaped three-level atomic gas via EIT. We show that such solitons may have very small propagation loss, ultraslow motional velocity, and extremely low generation power; they can be stored, retrieved, split, and routed with high efficiency and fidelity through the manipulation of control laser fields. The results reported here are helpful for the active control of optical Peregrine solitons and promising for practical applications in optical information processing and transmission.

The article is arranged as follows. In Section 2, the physical model and ultraslow weak-light Peregrine solitons and their propagation are described. In Section 3, the storage, retrieval, splitting, and routing of such solitons are presented. Finally, Section 4 gives a summary of the main results obtained in this work.

2 Model and Ultraslow Weak-Light Peregrine Solitons

2.1 Model

We start to consider a cold three-state atomic gas with $\text{Λ}$-shaped level configuration, interacting with a weak, pulsed probe laser field (center wavenumber ${\mathbf{k}}_p$ and center angular frequency ${\omega }_p$) and a strong, continuous-wave (CW) control laser field (wavenumber ${\mathbf{k}}_c$ and angular frequency ${\omega }_c$). The probe (control) field drives the transition $|1\rangle \leftrightarrow |3\rangle$ ($|2\rangle \leftrightarrow |3\rangle$); see Figure 1A.

FIGURE 1

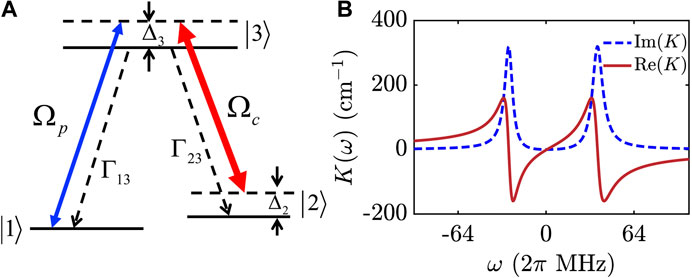
FIGURE 1. (A) Energy-level diagram and excitation scheme of the $\text{Λ}$-shaped three-level atomic system for realizing EIT. The probe field (with center angular frequency ${\omega }_p$ and half Rabi frequency ${\text{Ω}}_p$) couples the atomic levels $|1\rangle$ and $|3\rangle$; the CW control field (with angular frequency ${\omega }_c$ and half Rabi frequency ${\text{Ω}}_c$) couples the atomic levels $|2\rangle$ and $|3\rangle$; ${\text{Γ}}_{13}$ (${\text{Γ}}_{23}$) is the decay rate from $|3\rangle$ to $|1\rangle$ ($|3\rangle$ to $|2\rangle$); ${\text{Δ}}_3$ (${\text{Δ}}_2$) is one-photon (two-photon) detuning. (B) The imaginary part $\text{Im}\left(K\right)$ and real part $\text{Re}\left(K\right)$ of the linear dispersion relation K as a function of ω ($\omega =0$ corresponds to the central frequency of the probe pulse).

The total electric field in the system reads $\mathbf{E}={\mathbf{E}}_p+{\mathbf{E}}_c={\displaystyle \sum }_{l=p,c}{\mathbf{e}}_l{\mathrm{ℰ}}_l\text{exp}\left[i\left(k_{l}z-{\omega }_{l}t\right)\right]+\text{c}.\text{c}.$, where ${\mathbf{e}}_l$ (${\mathrm{ℰ}}_l$) is the unit polarization vector (envelope) of the electric field ${\mathbf{E}}_l$. To suppress Doppler effect, both the probe and control fields are assumed to propagate along z direction.

The Hamiltonian of the system in the interaction picture reads ${\widehat{H}}_{\text{int}}=-\hslash \left({{{\displaystyle \sum }}^{\text{}}}_{j=2}^3{\text{Δ}}_j|j\rangle \langle j|+{\text{Ω}}_p|3\rangle \langle 1|+{\text{Ω}}_c|3\rangle \langle 2|+\text{H}.\text{c}.\right)$, where ${\text{Δ}}_3={\omega }_p-\left(E_3-E_1\right)/\hslash$ (${\text{Δ}}_2={\omega }_p-{\omega }_c-\left(E_2-E_1\right)/\hslash$) is one-(two-) photon detuning; $E_j$ is the eigenvalue of the atomic state $|j\rangle$; ${\text{Ω}}_p=\left({\mathbf{e}}_p\cdot {\mathbf{p}}_{13}\right){\mathrm{ℰ}}_p/\hslash$ (${\text{Ω}}_c=\left({\mathbf{e}}_c\cdot {\mathbf{p}}_{23}\right){\mathrm{ℰ}}_{c1}/\hslash$) is the half Rabi frequency of the probe (control) field; ${\mathbf{p}}_{ij}$ is the electric-dipole matrix element associated with levels $|i\rangle$ and $|j\rangle$. The atomic dynamics is described by a $3\times 3$ density matrix σ, obeying the optical Bloch equation

$\frac{\partial \sigma }{\partial t}=-\frac{i}{\hslash }\left[{\widehat{H}}_{\text{int}},\sigma \right]-\text{Γ}\left[\sigma \right],(1)$

where $\text{Γ}$ is a relaxation matrix characterizing the spontaneous emission and dephasing [61]. The explicit form of Eq. 1 is presented in Section 1 of the Supplementary Material.

The evolution of the probe field ${\mathbf{E}}_p$ is governed by the Maxwell equation ${\nabla }^2{\mathbf{E}}_p-\left(1/c^2\right){\partial }^2{\mathbf{E}}_p/\partial t^2=\left(1/{\epsilon }_0{c}^2\right){\partial }^2{\mathbf{P}}_p/\partial t^2$, where ${\mathbf{P}}_p={\mathrm{N}}_a\left\{{\mathbf{p}}_{13}{\sigma }_{31}\text{exp}\left[i\left(k_{p}z-{\omega }_{p}t\right)\right]+\text{c}.\text{c}.\right\}$ is the electric polarization intensity, with ${\mathrm{N}}_a$ the atomic density. Under slowly varying envelope and paraxial approximations, the Maxwell equation is reduced into the form

$i\left(\frac{\partial }{\partial z}+\frac{1}{c}\frac{\partial }{\partial t}\right){\text{Ω}}_p+{\kappa }_{13}{\sigma }_{31}=0,(2)$

with ${\kappa }_{13}={\mathrm{N}}_a{\omega }_p{\left|{\mathbf{p}}_{13}\right|}^2/\left(2{\epsilon }_{0}c\hslash \right)$. Note that we have assumed that the probe field has a large transverse size so that its diffraction effect is negligible. The model described here may be realized, e.g., by a cold ⁸⁷Rb atomic gas [62], with the levels selected by $|1\rangle =|5^2{S}_{1/2},F=1,m_F=0\rangle$, $|2\rangle =|5^2{S}_{1/2},F=2,m_F=0\rangle$, and $|3\rangle =|5^2{P}_{1/2},F=1,m_F=0\rangle$. Thus we have ${\omega }_p=2.37\times {10}^{15}\text{ Hz}$, $\left|{\mathbf{p}}_{13}\right|=2.54\times {10}^{-27}\text{C}\text{cm}$. If the atomic density ${\mathrm{N}}_a=8.8\times {10}^{11}{\text{cm}}^{-3}$, ${\kappa }_{13}$ takes the value of $2.4\times {10}^{10}{\text{cm}}^{-1}{\text{s}}^{-1}$. This set of parameters will be used in the following analysis and calculation.

2.2 Ultraslow Weak-Light Peregrine Solitons and Their Propagation

We first investigate the linear propagation of the probe field. When a very weak probe pulse is applied, the system undergoes a linear evolution. In this case, the Maxwell–Bloch (MB) (Eqs. 1 and 2) admit the solution ${\text{Ω}}_p=F\text{exp}\left[i\left(Kz-\omega t\right)\right]$, where F is a constant,

$K\left(\omega \right)=\frac{\omega }{c}-{\kappa }_{13}\frac{\omega +d_{21}}{\left(\omega +d_{21}\right)\left(\omega +d_{31}\right)-{\left|{\text{Ω}}_c\right|}^2}(3)$

is linear dispersion relation, and $d_{\alpha \beta }={\text{Δ}}_{\alpha }-{\text{Δ}}_{\beta }+i{\gamma }_{\alpha \beta }$ (with ${\gamma }_{\alpha \beta }\equiv \left({\text{Γ}}_{\alpha }+{\text{Γ}}_{\beta }\right)/2+{\gamma }_{\alpha \beta }^{\text{dep}}$, ${\text{Γ}}_{\beta }\equiv {\displaystyle \sum }_{{\omega }_{\alpha }<{\omega }_{\beta }}{\text{Γ}}_{\alpha \beta }$, and ${\gamma }_{\alpha \beta }^{\text{dep}}$is the dephasing rate associated with the states $|\alpha \rangle$ and $|\beta \rangle$).

Shown in Figure 1B is the imaginary part $\text{Im}\left(K\right)$ and the real part $\text{Re}\left(K\right)$ of K as functions of ω. Due to the quantum interference effect induced by the control field, an EIT transparency window is opened in $\text{Im}\left(K\right)$ (dashed line), which implies that the probe field can propagate in this resonant atomic gas with a very small absorption. Parameters used for plotting the figure are ${\text{Δ}}_2=-2\pi \times 0.64\text{ MHz}$, ${\text{Δ}}_3=-2\pi \times 9.6\text{ MHz}$, ${\gamma }_{21}=2\pi \times 1.09\text{ kHz}$, ${\gamma }_{31}=2\pi \times 2.5\text{ MHz}$, and ${\text{Ω}}_c=2\pi \times 31.8\text{ MHz}$.

From the MB Eqs. 1 and 2 and using the method of multiple-scales [63], we can derive the controlling equation governing the nonlinear evolution of the probe-field envelope F (see Section 2 of the Supplementary Material), which reads

$i\frac{\partial }{\partial z}F-\frac{1}{2}{K}_2\frac{{\partial }^2}{\partial {\tau }^2}F+W{\left|F\right|}^{2}F=0,(4)$

where $\tau =t-z/{\tilde{V}}_g$ [${\tilde{V}}_g\equiv {\left(\partial \tilde{K}/\partial \omega \right)}^{-1}$ is the group velocity of the envelope; here and in the following, the quantity with a tilde represents the corresponding real part]; $K_2={\partial }^{2}K/\partial {\omega }^2$ is the coefficient describing group-velocity dispersion; W is the coefficient (describing self-phase modulation) proportional to Kerr nonlinearity. The explicit expression of W is given in Section 2 of the Supplementary Material.

If the imaginary parts of K and W are much smaller than their corresponding real parts, Eq. 4 admits the Peregrine soliton solution, which can be expressed by the half Rabi frequency

${\text{Ω}}_p\left(z,t\right)=U_0\left[1-4\frac{1+2iz/L_{\text{Non}}}{1+4z^2/L_{\text{Non}}^2+4{\left(t-z/{\tilde{V}}_g\right)}^2/{\tau }_0^2}\right]e^{i{K}_{0}z+iz/L_{\text{Non}}},(5)$

where $K_0\equiv K{|}_{\omega =0}$, $U_0$ and ${\tau }_0$ are respectively the characteristic half Rabi frequency and time duration of the probe field, and $L_{\text{Non}}\equiv 1/\left(U_0^2\left|\tilde{W}\right|\right)$ is the characteristic nonlinearity length (which has been assumed to equal the dispersion length defined by $L_{\text{Dis}}\equiv {\tau }_0^2/\left|{\tilde{K}}_2\right|$ for simplicity). One sees that the Peregrine soliton consists of a CW background and a bump in its envelope that first grows and then decay rapidly on the background. The physical reason for the formation of such optical Peregrine soliton can be understood as follows. When a plane-wave probe field with a finite amplitude is applied to and propagates in the atomic gas, the Kerr nonlinearity brings a modulational instability and a phase modulation to the probe field; due to the role played by the group-velocity dispersion, the phase modulation is converted into amplitude modulation and peak amplification. Because of the joint phase and amplitude modulations, the probe field reorganizes its spatial distribution and hence the Peregrine soliton is generated in the system.

As an example, we take ${\tau }_0=2.36\times {10}^{-7}\text{s}$, $U_0=2\pi \times 8.0\text{ MHz}$, and other system parameters which are the same as those used in Figure 1B. Then we obtain $K_0=-1.70+i0.02{\text{ cm}}^{-1}$, $K_1=\partial K/\partial \omega \approx \left(4.5-i0.05\right)\times {10}^{-7}{\text{ cm}}^{-1}\text{ s}$, $K_2\approx \left(-1.5-i0.1\right)\times {10}^{-14}{\text{ cm}}^{-1}{\text{ s}}^2$, and $W\approx \left(1.05-0.004\right)\times {10}^{-16}{\text{ cm}}^{-1}{\text{ s}}^2$ (estimated at $\omega =0$). We see that the imaginary parts of $K_j$ ($j=\mathrm{0,1,2}$) and W are much smaller than their corresponding real parts, which is due to the EIT effect that results in the suppression of the optical absorption in the system. Based on these results, we obtain $L_{\text{Non}}\simeq L_{\text{Dis}}\simeq 3.8\text{ cm}$ and

${\tilde{V}}_g\simeq 7.34\times {10}^{-5}c.(6)$

Thus, the propagation velocity of the optical Peregrine soliton is much slower than the light speed c in vacuum. If the transverse cross-section area of the probe pulse takes the value $S=8.0\times {10}^{-3}{\text{ cm}}^2$, the generation power of the soliton (which can be estimated by using the Poynting vector [56]) reads

$P_{\text{max}}\simeq 1.8\mathrm{\mu }\text{W},(7)$

i.e., very small power needed for creating such soliton. Consequently, the Peregrine solitons given here are different from those obtained in conventional optical systems [25, 27, 28, 31].

We now investigate the propagation of the ultraslow Peregrine soliton by exploiting Runge–Kutta method based on solving the MB Eqs. 1 and 2 numerically. Since solution (5) has an infinite energy due to the existence of the CW background, it cannot be generated in a real experiment. To avoid this, we assume the probe field at $z=0$ has the form

${\text{Ω}}_p\left(0,t\right)={\text{Ω}}_{p0}\left(t\right)\left[\frac{1}{2}\text{tanh}\left(\frac{t-T_{\text{on}}^p}{T_s^p}\right)-\frac{1}{2}\text{tanh}\left(\frac{t-T_{\text{off}}^p}{T_s^p}\right)\right].(8)$

Here ${\text{Ω}}_{p0}\left(t\right)=6.67\left[1-3.2/\left(1+4t^2/{\tau }_0^2\right)\right]$ is chosen to match the analytical solution (5); the hyperbolic tangent function is used to impose temporal boundaries on both sides of CW background (far from the pump part), which can make the soliton have finite energy and also have a clear illustration on its waveshape (similar to the case for generating dark solitons [64, 65]); $T_s^p=3.0{\tau }_0$ is the switching time when switching on and off the probe field; $T_{\text{on}}^p=-80{\tau }_0$ and $T_{\text{off}}^p=4{\tau }_0$ are parameters characterizing the two temporal boundaries, respectively. The waveshape of the input probe field at $z=0$ is shown by a solid blue line in the upper part of Figure 2A, where the dashed vertical lines represent temporal boundaries.

FIGURE 2

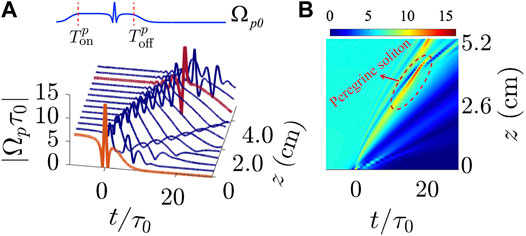
FIGURE 2. Propagation of ultraslow weak-light Peregrine solitons. (A)$\left|{\text{Ω}}_p{\tau }_0\right|$ as a function of $t/{\tau }_0$ and z. The solid blue line in the upper part is the input temporal shape of the probe field with the dashed vertical lines representing the temporal boundaries. The orange line in the lower part is the input Peregrine soliton at $z=0$. The red line represents the Peregrine soliton propagating to $z=4.3\text{ cm}$ with the maximum intensity $|{\text{Ω}}_p{\tau }_0{|}_{\text{max}}\simeq 15.2$ at $t=16.9{\tau }_0$(B) The contour map for the propagation of the Peregrine soliton (the red dashed circle) on the t-z plane. The upper color bar shows the intensity of the probe field.

The lower part of Figure 2A illustrates the result of a numerical simulation on the propagation of the Peregrine soliton (with ${\text{Δ}}_3=-2\pi \times 95.5\text{ MHz}$, ${\tau }_0=1.5\times {10}^{-7}\text{s}$, and other parameters the same as those used in Figure 1B), by taking $\left|{\text{Ω}}_p{\tau }_0\right|$ as a function of $t/{\tau }_0$ and z. The orange line is the input Peregrine soliton at $z=0$; the red line denotes the Peregrine soliton propagating to $z=4.3\text{ cm}$; the maximum value ($|{\text{Ω}}_p{\tau }_0{|}_{\text{max}}\simeq 15.2$) of the soliton along the trajectory appears sharply around $z=4.3\text{ cm}$ at $t=16.9{\tau }_0$. Figure 2B shows the contour map for the propagation of the Peregrine soliton, which can be taken as a projection of Figure 2A onto the t-z plane. One sees that the Peregrine soliton (indicated by the red dashed circle in Figure 2B) appears sharply and disappears suddenly; a secondary peak (soliton) emerges at longer distance, as a result of phase modulation when the first soliton is excited.

3 Storage, Retrieval, Splitting, and Routing of the Optical Peregrine Solitons

We now turn to consider the memory of the optical Peregrine solitons and related applications in optical splitting and routing through the manipulation of the control fields.

3.1 Storage and Retrieval of the Optical Peregrine Solitons

We first consider the storage and retrieval of optical Peregrine solitons obtained above, which can be implemented by switching off and on the control field described by the following switching function:

${\text{Ω}}_c={\text{Ω}}_{c0}\left[1-\frac{1}{2}\text{tanh}\left(\frac{t-T_{\text{off}}^c}{T_s^c}\right)+\frac{1}{2}\text{tanh}\left(\frac{t-T_{\text{on}}^c}{T_s^c}\right)\right],(9)$

where ${\text{Ω}}_{c0}$ is a constant, $T_s^c$ is the time interval for switching off and switching on the control field (switching time), and $T_{\text{off}}^c$ ($T_{\text{on}}^c$) is the time when the control field is switched off (on).

As an example, we take ${\text{Ω}}_{c0}=2\pi \times 31.8\text{MHz}$, $T_{\text{off}}^c=10.0{\tau }_0$, $T_{\text{on}}^c=20.0{\tau }_0$, $T_s^c=3.0{\tau }_0$ (${\tau }_0=1.5\times {10}^{-7}\text{s}$), and other system parameters are the same as those used in Figure 2. The upper part of Figure 3A shows the time sequences of the control field (black line) and the probe field (blue line); the red dashed vertical line (black dashed vertical line) represents the time $T_{\text{off}}^p$ ($T_{\text{off}}^c$). Symbols I, II, and III denote the CW background, the Peregrine soliton, and the low-intensity component of the probe field, respectively. The lower part of the figure shows the result of a numerical simulation on the storage and retrieval of the Peregrine soliton by taking $\left|{\text{Ω}}_p{\tau }_0\right|$ as a function of $t/{\tau }_0$ and z. Here the orange line is the input Peregrine soliton at $z=0$; the purple line represents the Peregrine soliton at the storage period; the red line represents the retrieved Peregrine soliton propagating to $z=4.1\text{ cm}$ with the maximum intensity $|{\text{Ω}}_p{\tau }_0{|}_{\text{max}}\simeq 15.4$ at $t=30.3{\tau }_0$. Shown in Figure 3B is the contour map of the storage and retrieval of the Peregrine soliton in the t-z plane with $T_{\text{off}}^p<T_{\text{off}}^c$. The retrieved Peregrine soliton is indicated by the red dashed circle (i.e., “Retrieved PS”). From the figure we see that the Peregrine soliton can be stored and retrieved some time later in the medium.

FIGURE 3

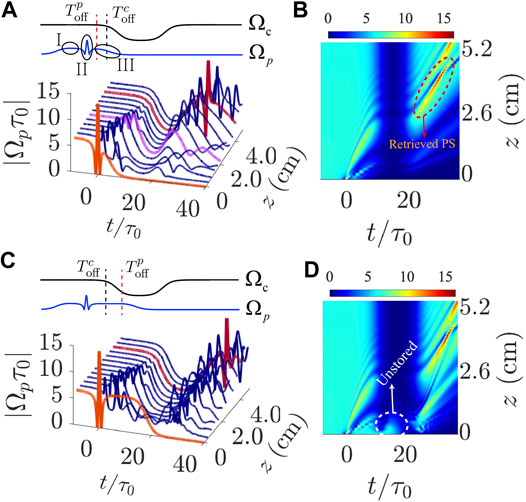
FIGURE 3. Storage and retrieval of optical Peregrine solitons. (A) Upper part: the black line (blue line) is the time sequence of the control (probe) field, the red dashed vertical line is $T_{\text{off}}^p$, and the black dashed vertical line is $T_{\text{off}}^c$. Symbols I, II, and III denote the CW background, the Peregrine soliton, and the low-intensity component of the probe field, respectively. Lower part: $\left|{\text{Ω}}_p{\tau }_0\right|$ vs. $t/{\tau }_0$ and z with $T_{\text{off}}^p<T_{\text{off}}^c$; i.e., the switching-off time of the input probe field is before the time when the control field is switched off. The orange line represents the input Peregrine soliton at $z=0$; the purple line represents the probe field at the storage period; the red line represents the retrieved Peregrine soliton propagating to $z=4.1\text{ cm}$ with the maximum intensity ${\left|{\text{Ω}}_p{\tau }_0\right|}_{\text{max}}\simeq 15.4$ at $t\simeq 30.3{\tau }_0$. (B) The contour map of the storage and retrieval of the Peregrine soliton in the t-z plane with $T_{\text{off}}^p<T_{\text{off}}^c$. The red dashed circle denotes the retrieved Peregrine soliton (i.e., “Retrieved PS”). The upper color bar shows the intensity of the probe field. (C) The same as panel (A) but with $T_{\text{off}}^p>T_{\text{off}}^c$. (D) The contour map of the Peregrine soliton in the t-z plane with $T_{\text{off}}^p>T_{\text{off}}^c$. The unstored component of the probe field is marked by the white circle.

The steps of the storage and retrieval of the Peregrine soliton can be described as follows:

• Firstly, the control field ${\text{Ω}}_c$ is switched on (to establish EIT) and the probe field (Peregrine soliton) of the form ${\text{Ω}}_{p0}{\tau }_0=6.67\left[1-3.2/\left(1+4t^2/{\tau }_0^2\right)\right]\left\{0.5\left[\left(t/{\tau }_0+80\right)/3.0\right]-0.5\text{tanh}\left[\left(t/{\tau }_0-4\right)/3.0\right]\right\}$ is incident into the system (i.e., the orange line in the lower part of Figure 3A).

• Then, the control field is switched off at time $t=T_{\text{off}}^c=10.0{\tau }_0$, with the switching time of the control and probe fields setting to be $T_s^c=T_s^p=3.0{\tau }_0$. The probe field (the Peregrine soliton) is thus stored in the system (i.e., it is converted into the atomic coherence ${\sigma }_{21}$ [66, 67]).

• Lastly, the control field is switched on again at $t=T_{\text{on}}^c=20.0{\tau }_0$. The atomic coherence ${\sigma }_{21}$ is converted back to the probe field, and hence the probe pulse is retrieved. Particularly, at time $t\simeq 30.3{\tau }_0$, the retrieved probe field manifests as a Peregrine soliton with the maximum intensity ${\left|{\text{Ω}}_p{\tau }_0\right|}_{\text{max}}\simeq 15.4$ at the position $z\simeq 4.1\text{ cm}$.

The efficiency of the Peregrine soliton memory can be characterized by the parameter $\eta ={{{\displaystyle \int }}^{\text{}}}_{-\infty }^{+\infty }{\left|E_p^{\text{Pere}}\left(t\right)\right|}^2\text{d}t/{{{\displaystyle \int }}^{\text{}}}_{-\infty }^{+\infty }{\left|E_p^{\text{in}}\left(t\right)\right|}^2\text{d}t$ [57, 67], where $E_p^{\text{in}}\left(t\right)=E_p^{\text{in}}\left(0,t\right)$ (i.e., the input Peregrine soliton) and $E_p^{\text{Pere}}\left(t\right)=E_p^{\text{Pere}}\left(L_{\text{Pere}},t\right)$ (i.e., the retrieved Peregrine soliton), with $L_{\text{Pere}}$ ($\simeq 4.1\text{cm}$) as the position where the Peregrine soliton is retrieved. Based on the result of Figure 3A, we obtain $\eta =85.9\text{\%}$.

The fidelity of the Peregrine soliton memory can be described by the parameter $\eta J^2$, where $J^2$ describes the degree of coincidence of the wave shapes for the input and retrieved solitons, defined by the overlap integral $J^2={{{\displaystyle \int }}^{\text{}}}_{-T_1}^{T_1}{\left|E_p^{\text{in}}\left(t\right)E_p^{\text{Pere}}\left(t-\text{Δ}T\right)\right|}^2\text{d}t/\left[{{{\displaystyle \int }}^{\text{}}}_{-T_1}^{T_1}{\left|E_p^{\text{in}}\left(t\right)\right|}^2\text{d}t{{{\displaystyle \int }}^{\text{}}}_{-T_1}^{T_1}{\left|E_p^{\text{Pere}}\left(t-\text{Δ}T\right)\right|}^2\text{d}t\right]$ [57, 67], where $T_1$ is a coefficient related to the temporal width of the Peregrine soliton (i.e., corresponding to symbol II in Figure 2A), and $\text{Δ}T$ is the time interval between the peak of the input soliton pulse $E_p^{\text{in}}$ and the peak of the retrieved soliton pulse $E_p^{\text{Pere}}$. Here we take $\text{Δ}T=30.3{\tau }_0$ and $T_1=10{\tau }_0$. We obtain $\eta J^2=84.3\text{\%}$. We see that the efficiency and fidelity of the storage and retrieval of the Peregrine soliton are quite high.

The numerical result shown in Figure 3C is similar to that of Figure 3A but for $T_{\text{off}}^p>T_{\text{off}}^c$. In this case, the storage and retrieval of the Peregrine soliton can also be implemented; however, compared with Figure 3A (which is for $T_{\text{off}}^p<T_{\text{off}}^c$), the retrieved waveshape is little more distorted. Figure 3D illustrates the contour map of the Peregrine soliton in the t-z plane with $T_{\text{off}}^p>T_{\text{off}}^c$. One sees that the probe field has a nonzero value in the region indicated by the dashed white circle, which means that some parts of the probe field are not stored when the control field is switched off. We obtain the efficiency and fidelity of the Peregrine soliton memory for $T_{\text{off}}^p>T_{\text{off}}^c$ are $\eta =77\text{\%}$ and $\eta J^2=65\text{\%}$, respectively. Based on these results, we conclude that in order to get a high memory quality, the choice of $T_{\text{off}}^p<T_{\text{off}}^c$ is better than that of $T_{\text{off}}^p>T_{\text{off}}^c$.

3.2 Splitting of the Optical Peregrine Solitons

To realize an optical splitting [67] of the Peregrine soliton, we generalize the system into a four-level one with a tripod-type level configuration. Here a probe field ${\text{Ω}}_p$ drives the transition $|1\rangle \leftrightarrow |3\rangle$; two CW control fields ${\text{Ω}}_{c1}$ and ${\text{Ω}}_{c2}$ drive respectively the transitions $|2\rangle \leftrightarrow |3\rangle$ and $|4\rangle \leftrightarrow |3\rangle$; ${\text{Γ}}_{j3}$ is the decay rate from $|3\rangle$ to $|j\rangle$ ($j=\mathrm{1,2,4}$), ${\text{Δ}}_3$ and ${\text{Δ}}_l$ ($l=\mathrm{2,4}$) are respectively one-photon and two-photon detunings (see Figure 4A). The Hamiltonian of the system and the optical Bloch equations controlling the dynamics of the atoms have been presented in Section 5 of the Supplementary Material.

FIGURE 4

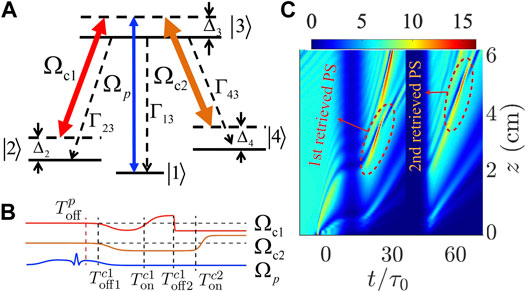
FIGURE 4. Splitting of optical Peregrine solitons. (A) Energy-level diagram and excitation scheme of the tripod-type four-level atomic system. Here, a probe laser field ${\text{Ω}}_p$ drives the transition $|1\rangle \leftrightarrow |3\rangle$; the two CW control fields ${\text{Ω}}_{c1}$ and ${\text{Ω}}_{c2}$ drive the transitions $|2\rangle \leftrightarrow |3\rangle$ and $|4\rangle \leftrightarrow |3\rangle$, respectively; ${\text{Γ}}_{j3}$ is the decay rate from $|3\rangle$ to $|j\rangle$ ($j=\mathrm{1,2,4}$); ${\text{Δ}}_3$ and ${\text{Δ}}_l$ ($l=\mathrm{2,4}$) are respectively one-photon and two-photon detunings. (B) Time sequences of the control and the probe fields for realizing the optical splitting. The vertical red dashed line is for $t=T_{\text{off}}^p$; the vertical black dashed lines represent the times when switching off and on the two control fields. For detailed meanings of the symbols $T_{\text{off}1}^{c1}$, etc., see text. (C) The contour map of the splitting process of the Peregrine soliton in the t-z plane. The intensities of two split Peregrine solitons are ${\left|{\text{Ω}}_p{\tau }_0\right|}_{\text{max}}=15.4$ when $t=23.0{\tau }_0$ at the position $z=3.7\text{ cm}$ (first retrieved Peregrine soliton, i.e., “1st retrieved PS” indicated in the figure) and ${\left|{\text{Ω}}_p{\tau }_0\right|}_{\text{max}}=14.0$ when $t=61.5{\tau }_0$ at the position $z=5.5\text{ cm}$ (second retrieved Peregrine soliton, i.e., “2nd retrieved PS” indicated in the figure), respectively.

The timing sequences of the switching-off and -on of ${\text{Ω}}_{cj}\left(t\right)$ for obtaining a Peregrine soliton splitter are shown in Figure 4B, with $T_{\text{off}}^p<T_{\text{off}1}^{c1}=T_{\text{off}1}^{c2}<T_{\text{on}}^{c1}<T_{\text{off}2}^{c1}<T_{\text{on}}^{c2}$. For jth control field ${\text{Ω}}_{cj}$ ($j=\mathrm{1,2}$), $T_s^{cj}$ ($T_{\text{on}}^{cj}$) is its switching-off (switching-on) time. The corresponding switching functions have been given in Section 5 of the Supplementary Material. When plotting the figure, we have set ${\text{Ω}}_{c1}\left(0\right)={\text{Ω}}_{c2}\left(0\right)=2\pi \times 31.8\text{ MHz}$, $T_{\text{off}1}^{c1}=T_{\text{off}1}^{c2}=6.0{\tau }_0$, $T_{\text{on}}^{c1}=15.0{\tau }_0$, $T_{\text{off}2}^{c1}=35.0{\tau }_0$, $T_{\text{on}}^{c2}=45.0{\tau }_0$, and $T_s^{c1}=T_s^{c2}=3.0{\tau }_0$.

Shown in Figure 4C is the numerical result on the simulation for obtaining the Peregrine soliton splitter by taking ${\text{Ω}}_p{\tau }_0$ as a function of $t/{\tau }_0$ and z (with ${\tau }_0=1.5\times {10}^{-7}\text{s}$). The operation steps can be described as follows: 1) Firstly, the two control fields ${\text{Ω}}_{c1}$ and ${\text{Ω}}_{c2}$ are applied and a probe field with the waveform ${\text{Ω}}_{p0}\left(0,t\right)=6.67\left[1-3.2/\left(1+4{\left(t+5\right)}^2/{\tau }_0^2\right)\right]\left\{0.5\text{tanh}\left[\left(t/{\tau }_0+80\right)/3.0\right]-0.5\text{tanh}\left[\left(t/{\tau }_0-4\right)/3.0\right]\right\}$ is incident to the system. 2) Then, both control fields are simultaneously switched off at time $t=T_{\text{off}1}^{c1}=T_{\text{off}1}^{c2}=6.0{\tau }_0$. Thus the probe field is stored in the two atomic coherences ${\sigma }_{21}$ and ${\sigma }_{41}$ simultaneously 67. 3) Later on, switching on ${\text{Ω}}_{c1}$ at $t=T_{\text{on}}^{c1}=15.0{\tau }_0$ (but ${\text{Ω}}_{c2}$ is remained to be switched off), the atomic coherence ${\sigma }_{21}$ is converted back into the probe field, and hence a new probe pulse is retrieved. At time $t\simeq 23.0{\tau }_0$, this retrieved probe pulse turns into a Peregrine soliton (i.e., “1st retrieved PS”, indicated by a red circle in Figure 4B) with the maximum intensity ${\left|{\text{Ω}}_p{\tau }_0\right|}_{\text{max}}\simeq 15.4$ at the position $z=3.7\text{ cm}$. 4) By switching off ${\text{Ω}}_{c1}$ at $t=T_{\text{off}2}^{c1}=35.0{\tau }_0$ and switching on ${\text{Ω}}_{c2}$ at $t=T_{\text{on}}^{c2}=45.0{\tau }_0$, the atomic coherence ${\sigma }_{41}$ converts back into the probe field; this retrieved probe field turns into another Peregrine soliton (i.e., “2nd retrieved PS”, indicated by another red circle in Figure 4B) with the maximum intensity ${\left|{\text{Ω}}_p{\tau }_0\right|}_{\text{max}}\simeq 14.0$ at the position $z=5.5\text{ cm}$ at $t\simeq 61.5{\tau }_0$.

In the simulation, we have taken ${\text{Δ}}_2={\text{Δ}}_4=-2\pi \times 0.64\text{MHz}$, ${\gamma }_{21}={\gamma }_{41}=2\pi \times 1.09\text{kHz}$, with the other parameters the same as those used in Figure 3A. The reason for taking ${\text{Δ}}_2={\text{Δ}}_4$ and ${\gamma }_{21}={\gamma }_{41}$ is to keep the symmetry of the tripod level configuration, which gives two nearly degenerated EITs in the system; for details, see [67]. The splitting efficiency and fidelity of the first (second) Peregrine soliton are ${\eta }_1=89.8\text{\%}$ and ${\eta }_1{J}_1^2=85.4\text{\%}$ (${\eta }_2=89.3\text{\%},{\eta }_2{J}_2^2=84.9\text{\%}$), respectively.

3.3 Routing of the Optical Peregrine Solitons

To realize all-optical routing [67, 68] of optical Peregrine solitons, we consider a four-level atomic system with a double-$\text{Λ}$-type level configuration. Here, two probe laser fields ${\text{Ω}}_{p1}$ and ${\text{Ω}}_{p2}$ drive the transitions $|1\rangle \leftrightarrow |3\rangle$ and $|1\rangle \leftrightarrow |4\rangle$, respectively; two CW control laser fields ${\text{Ω}}_{c1}$ and ${\text{Ω}}_{c2}$ drive the transitions $|2\rangle \leftrightarrow |3\rangle$ and $|2\rangle \leftrightarrow |4\rangle$, respectively; ${\text{Δ}}_3$ and ${\text{Δ}}_4$ are one-photon detunings, and ${\text{Δ}}_2$ is two-photon detuning (see Figure 5A).

FIGURE 5

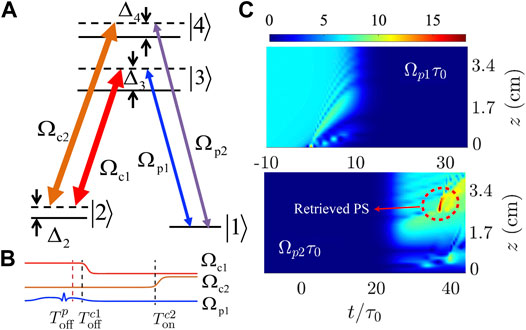
FIGURE 5. Routing of optical Peregrine solitons. (A) The energy-level diagram and excitation scheme of the double-$\text{Λ}$-type four-level atomic system. In this configuration, two probe laser fields ${\text{Ω}}_{p1}$ and ${\text{Ω}}_{p2}$ drive the transitions $|1\rangle \leftrightarrow |3\rangle$ and $|1\rangle \leftrightarrow |4\rangle$, respectively; two CW control laser fields ${\text{Ω}}_{c1}$ and ${\text{Ω}}_{c2}$ drive the transitions $|2\rangle \leftrightarrow |3\rangle$ and $|2\rangle \leftrightarrow |4\rangle$, respectively; ${\text{Δ}}_3$ and ${\text{Δ}}_4$ are one-photon detunings, and ${\text{Δ}}_2$ is two-photon detuning. (B) Time sequences of the two control fields ${\text{Ω}}_{c1}$, ${\text{Ω}}_{c2}$ and the probe field ${\text{Ω}}_{p1}$ for realizing the soliton routing. The vertical red dashed line denotes the time $t=T_{\text{off}}^p$; the vertical black dashed lines denote the times when switching off and on the control fields. (C) Contour maps for the routing process of the Peregrine soliton, where the upper panel is for ${\text{Ω}}_{p1}$ and the lower panel is for ${\text{Ω}}_{p2}$. The Peregrine soliton is input as the probe field ${\text{Ω}}_{p1}$, but it is retrieved as the probe field ${\text{Ω}}_{p2}$ (i.e., “retrieved PS” indicated by the red dashed circle in the lower panel of the figure).

The Hamiltonian of the system and the MB equations governing the dynamics of the atoms and light fields have been given in Section 6 of the Supplementary Material.

For simplicity, here we consider a frequency routing process, i.e., the probe field ${\text{Ω}}_{p1}$ is converted into the ${\text{Ω}}_{p2}$ (which has different frequency from ${\text{Ω}}_{p1}$). The time sequence of the switching off and on of ${\text{Ω}}_{cj}$ for obtaining routing of Peregrine soliton is shown in Figure 5B, with $T_{\text{off}}^p<T_{\text{off}}^{c1}<T_{\text{on}}^{c2}$, where $T_{\text{off}}^{c1}$ is the switching-off time of ${\text{Ω}}_{c1}$ and $T_{\text{on}}^{c2}$ is the switching-on time of ${\text{Ω}}_{c2}$. The corresponding switching functions have been given in Section 5 of the Supplementary Material. Without loss of generality, the system parameters are set to be ${\text{Ω}}_{c1}={\text{Ω}}_{c2}=2\pi \times 31.8\text{ MHz}$, $T_{\text{off}}^{c1}=10.0{\tau }_0$, $T_{\text{on}}^{c2}=25.0{\tau }_0$, and $T_s^{c1}=T_s^{c2}=3.0{\tau }_0$ (switching time).

The implementing procedure of the Peregrine soliton routing is as follows. First, by switching on the control field ${\text{Ω}}_{c1}$, the input probe field ${\text{Ω}}_{p1}$ with the initial condition ${\text{Ω}}_{p0}\left(t/{\tau }_0\right)=6.67\left[1-3.2/\left(1+4t^2/{\tau }_0^2\right)\right]\left\{0.5\text{tanh}\left[\left(t/{\tau }_0+80\right)/3.0\right]-0.5\text{tanh}\left[\left(t/{\tau }_0-4\right)/3.0\right]\right\}$ propagates in the system, as shown in the upper panel of Figure 5C as a function of propagation distance $t/{\tau }_0$ and z. One sees that a trajectory of the soliton shows up before its storage. Second, by switching off ${\text{Ω}}_{c1}$ at time $t=10{\tau }_0$, the probe field ${\text{Ω}}_{p1}$ is stored in the atomic coherence ${\sigma }_{21}$. Third, by switching on the control field ${\text{Ω}}_{c2}$ at $t=25{\tau }_0$, another probe pulse ${\text{Ω}}_{p2}$ appears from the atomic coherence ${\sigma }_{21}$, i.e., “retrieved PS” in the lower panel of Figure 5C. We stress that during this routing process, the Peregrine soliton in the probe field ${\text{Ω}}_{p1}$ is annihilated and a new Peregrine soliton in the probe field ${\text{Ω}}_{p2}$ (which has no input) is created. Since the frequency of ${\text{Ω}}_{p2}$ is different from that of ${\text{Ω}}_{p1}$, the system performs as a frequency router of the Peregrine soliton.

4 Conclusion

We have proposed a scheme for realizing the storage and retrieval of optical Peregrine solitons in a coherent atomic gas via EIT. We have shown that the optical Peregrine solitons with very small propagation loss, ultraslow motional velocity, and extremely low generation power can be generated in the system via EIT. We have demonstrated that such solitons can be stored, retrieved, split, and routed with high efficiency and fidelity through the manipulation of control laser fields.

The scheme can also be generalized to cases with more optical output channels through the use of more control fields, and hence the two-channel splitting and routing processes can be generalized to multiple channel ones. Furthermore, the storage and retrieval of the optical Peregrine solitons can be extended to solid materials, like on-chip optical resonator systems [69]. The research results reported here may be useful for the active control of optical Peregrine solitons and promising for potential applications in optical information processing and transmission.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

GH proposed the idea and supervised the whole work. CS carried out the analytical and numerical calculation. Both authors contributed to the writing of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China under grant no. 11975098.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.594680/full#supplementary-material.

References

1. Pelinovsky E, Kharif C. Extreme ocean waves. Berlin: Springer (2008).

2. Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Phys Lett A (2009a) 373:675–8. doi:10.1016/j.physleta.2008.12.036

CrossRef Full Text | Google Scholar

3. Stenflo L, Marklund M. Rogue waves in the atmosphere. J Plasma Phys (2010) 76:293–5. doi:10.1017/S0022377809990481

CrossRef Full Text | Google Scholar

4. Efimov V, Ganshin A, Kolmakov G, McClintock P, Mezhov-Deglin L. Rogue waves in superfluid helium. Eur Phys J Spec Top (2010) 185:181–93. doi:10.1140/epjst/e2010-01248-5

CrossRef Full Text | Google Scholar

5. Shats M, Punzmann H, Xia H. Capillary rogue waves. Phys Rev Lett (2010) 104:104503. doi:10.1103/PhysRevLett.104.104503

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Chabchoub A, Hoffmann NP, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett (2011) 106:204502. doi:10.1103/PhysRevLett.106.204502

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Pierangeli D, Di Mei F, Conti C, Agranat AJ, DelRe E. Spatial rogue waves in photorefractive ferroelectrics. Phys Rev Lett (2015) 115:093901. doi:10.1103/PhysRevLett.115.093901

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Moslem WM, Sabry R, El-Labany SK, Shukla PK. Dust-acoustic rogue waves in a nonextensive plasma. Phys Rev E (2011) 84:066402. doi:10.1103/PhysRevE.84.066402

CrossRef Full Text | Google Scholar

9. Li BQ, Ma YL. Characteristics of rogue waves for a (2+1)-dimensional heisenberg ferromagnetic spin chain system. J Magn Magn Mater (2019) 474:537–43. doi:10.1016/j.jmmm.2018.10.133

CrossRef Full Text | Google Scholar

10. Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi F. Rogue waves and their generating mechanisms in different physical contexts. Phys Rep (2013) 528:47–89. doi:10.1016/j.physrep.2013.03.001

CrossRef Full Text | Google Scholar

11. Dudley JM, Dias F, Erkintalo M, Genty G. Instabilities, breathers and rogue waves in optics. Nat Photon (2014) 8:755–64. doi:10.1038/nphoton.2014.220

CrossRef Full Text | Google Scholar

12. Peregrine DH. Water waves, nonlinear schrödinger equations and their solutions. J Aust Math Soc Ser B (1983) 25:16–43. doi:10.1017/S0334270000003891

CrossRef Full Text | Google Scholar

13. Akhmediev N, Soto-Crespo J, Ankiewicz A. Extreme waves that appear from nowhere: on the nature of rogue waves. Phys Lett A (2009b) 373:2137–45. doi:10.1016/j.physleta.2009.04.023

CrossRef Full Text | Google Scholar

14. Shrira VI, Geogjaev VV. What makes the peregrine soliton so special as a prototype of freak waves? J Eng Math (2010) 67:11–22. doi:10.1007/s10665-009-9347-2

CrossRef Full Text | Google Scholar

15. Ma YC. The perturbed plane-wave solutions of the cubic schrödinger equation. Stud Appl Math (1979) 60:43–58. doi:10.1002/sapm197960143

CrossRef Full Text | Google Scholar

16. Akhmediev NN, Eleonskii VM, Kulagin NE. Exact first-order solutions of the nonlinear schrödinger equation. Theor Math Phys (1987) 72:809–18. doi:10.1007/BF01017105

CrossRef Full Text | Google Scholar

17. Bailung H, Sharma SK, Nakamura Y. Observation of peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011) 107:255005. doi:10.1103/PhysRevLett.107.255005

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Chabchoub A, Neumann S, Hoffmann NP, Akhmediev N. Spectral properties of the eregrine soliton observed in a water wave tank. J Geophys Res (2012) 117:C00J03. doi:10.1029/2011JC007671

CrossRef Full Text | Google Scholar

19. Shemer L, Alperovich L. Peregrine breather revisited. Phys Fluids (2013) 25:051701. doi:10.1063/1.4807055

CrossRef Full Text | Google Scholar

20. Sharma SK, Bailung H. Observation of hole peregrine soliton in a multicomponent plasma with critical density of negative ions. J Geophys Res Space Phys (2013) 118:919–24. doi:10.1002/jgra.50111

CrossRef Full Text | Google Scholar

21. Al Khawaja U, Bahlouli H, Asad-uz-zaman M, Al-Marzoug S. Modulational instability analysis of the peregrine soliton. Commun Nonlinear Sci Numer Simulat (2014) 19:2706–14. doi:10.1016/j.cnsns.2014.01.002

CrossRef Full Text | Google Scholar

22. Chen S, Song LY. Peregrine solitons and algebraic soliton pairs in Kerr media considering space-time correction. Phys Lett A (2014) 378:1228–32. doi:10.1016/j.physleta.2014.02.042

CrossRef Full Text | Google Scholar

23. Dai CQ, Wang YY. Controllable combined peregrine soliton and Kuznetsov-Ma soliton in -symmetric nonlinear couplers with gain and loss. Nonlinear Dyn (2015) 91:715–21. doi:10.1007/s11071-015-1900-0

CrossRef Full Text | Google Scholar

24. Gupta SK, Sarma AK. Peregrine rogue wave dynamics in the continuous nonlinear schrödinger system with parity-time symmetric Kerr nonlinearity. Commun. Nonlinear Sci Numer Simulat (2016) 36:141–7. doi:10.1016/j.cnsns.2015.11.017

CrossRef Full Text | Google Scholar

25. Solli DR, Ropers C, Koonath P, Jalali B. Optical rogue waves. Nature (2007) 450:1054–7. doi:10.1038/nature06402

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Solli DR, Ropers C, Jalali B. Active control of rogue waves for stimulated supercontinuum generation. Phys Rev Lett (2008) 101:233902. doi:10.1103/PhysRevLett.101.233902

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Montina A, Bortolozzo U, Residori S, Arecchi FT. Non-Gaussian statistics and extreme waves in a nonlinear optical cavity. Phys Rev Lett (2009) 103:173901. doi:10.1103/PhysRevLett.103.173901

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The Peregrine soliton in nonlinear fibre optics. Nat Phys (2010) 6:790–5. doi:10.1038/NPHYS1740

CrossRef Full Text | Google Scholar

29. Bonatto C, Feyereisen M, Barland S, Giudici M, Masoller C, Leite JRR, et al. Deterministic optical rogue waves. Phys Rev Lett (2011) 107:053901. doi:10.1103/PhysRevLett.107.053901

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Hammani K, Kibler B, Finot C, Morin P, Fatome J, Dudley JM, et al. Peregrine soliton generation and breakup in standard telecommunications fiber. Opt Lett (2011) 36:112–4. doi:10.1364/OL.36.000112

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Zaviyalov A, Egorov O, Iliew R, Lederer F. Rogue waves in mode-locked fiber lasers. Phys Rev A (2012) 85:013828. doi:10.1103/PhysRevA.85.013828

CrossRef Full Text | Google Scholar

32. Akhmediev N, Dudley JM, Solli DR, Turitsyn SK. Recent progress in investigating optical rogue waves. J Opt (2013) 15:060201. doi:10.1088/2040-8978/15/6/060201

CrossRef Full Text | Google Scholar

33. Bludov YV, Driben R, Konotop VV, Malomed BA. Instabilities, solitons and rogue waves in -coupled nonlinear waveguides. J Opt (2013) 15:064010. doi:10.1088/2040-8978/15/6/064010

CrossRef Full Text | Google Scholar

34. Zhang Y, Belić MR, Zheng H, Chen H, Li C, Song J, et al. Nonlinear talbot effect of rogue waves. Phys Rev E (2014) 89:032902. doi:10.1103/PhysRevE.89.032902

CrossRef Full Text | Google Scholar

35. Yang G, Wang Y, Qin Z, Malomed BA, Mihalache D, Li L. Breatherlike solitons extracted from the peregrine rogue wave. Phys Rev E (2014) 90:062909. doi:10.1103/PhysRevE.90.062909

CrossRef Full Text | Google Scholar

36. Suret P, Koussaifi RE, Tikan A, Evain C, Randoux S, Szwaj C, et al. Single-shot observation of optical rogue waves in integrable turbulence using time microscopy. Nat Commun (2016) 7:13136. doi:10.1038/ncomms13136

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Tikan A, Billet C, El G, Tovbis A, Bertola M, Sylvestre T, et al. Universality of the peregrine soliton in the focusing dynamics of the cubic nonlinear schrödinger equation. Phys Rev Lett (2017) 119:033901. doi:10.1103/PhysRevLett.119.033901

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Randoux S, Suret P, Chabchoub A, Kibler B, El G. Nonlinear spectral analysis of peregrine solitons observed in optics and in hydrodynamic experiments. Phys Rev E (2018) 98:022219. doi:10.1103/PhysRevE.98.022219

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Xu G, Hammani K, Chabchoub A, Dudley JM, Kibler B, Finot C. Phase evolution of peregrine-like breathers in optics and hydrodynamics. Phys Rev E (2019a) 99:012207. doi:10.1103/PhysRevE.99.012207

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Yang G, Li L, Jia S. Peregrine rogue waves induced by the interaction between a continuous wave and a soliton. Phys Rev E. (2012) 85:046608. doi:10.1103/PhysRevE.85.046608

CrossRef Full Text | Google Scholar

41. Tiofack CGL, Coulibaly S, Taki M, De Bièvre S, Dujardin G. Comb generation using multiple compression points of Peregrine rogue waves in periodically modulated nonlinear Schrödinger equations. Phys Rev A (2015) 92:043837. doi:10.1103/PhysRevA.92.043837

CrossRef Full Text | Google Scholar

42. Li J, Han J, Du Y, Dai C. Controllable behaviors of Peregrine soliton with two peaks in a birefringent fiber with higher-order effects. Nonlinear Dyn (2015) 82:1393–8. doi:10.1007/s11071-015-2246-3

CrossRef Full Text | Google Scholar

43. Chowdury A, Kedziora DJ, Ankiewicz A, Akhmediev N. Breather-to-soliton conversions described by the quintic equation of the nonlinear Schrödinger hierarchy. Phys Rev E (2015) 91:032928. doi:10.1103/PhysRevE.91.032928

CrossRef Full Text | Google Scholar

44. Chen S, Baronio F, Soto-Crespo JM, Liu Y, Grelu P. Chirped Peregrine solitons in a class of cubic-quintic nonlinear Schrödinger equations. Phys Rev E (2016) 93:062202. doi:10.1103/PhysRevE.93.062202

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Wang L, Zhang JH, Liu C, Li M, Qi FH. Breather transition dynamics, peregrine combs and walls, and modulation instability in a variable-coefficient nonlinear Schrödinger equation with higher-order effects. Phys Rev E (2016) 93:062217. doi:10.1103/PhysRevE.93.062217

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Dai CQ, Liu J, Fan Y, Yu DG. Two-dimensional localized Peregrine solution and breather excited in a variable-coefficient nonlinear Schrödinger equation with partial nonlocality. Nonlinear Dyn (2017) 88:1373–83. doi:10.1007/s11071-016-3316-x

CrossRef Full Text | Google Scholar

47. Özkan YS, Yaşar E, Seadawy AR. On the multi-waves, interaction and Peregrine-like rational solutions of perturbed Radhakrishnan–Kundu–Lakshmanan equation. Phys Scr (2020) 95:085205. doi:10.1088/1402-4896/ab9af4

CrossRef Full Text | Google Scholar

48. Chen S. Twisted rogue-wave pairs in the Sasa-Satsuma equation. Phys Rev E (2013) 88:023202. doi:10.1103/PhysRevE.88.023202

CrossRef Full Text | Google Scholar

49. Chen S, Grelu P, Soto-Crespo JM. Dark- and bright-rogue-wave solutions for media with long-wave–short-wave resonance. Phys Rev E (2014a) 89:011201. doi:10.1103/PhysRevE.89.011201

CrossRef Full Text | Google Scholar

50. Chen S, Ye Y, Soto-Crespo JM, Grelu P, Baronio F. Peregrine solitons beyond the threefold limit and their two-soliton interactions. Phys Rev Lett (2018) 121:104101. doi:10.1103/PhysRevLett.121.104101

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Chen S, Pan C, Grelu P, Baronio F, Akhmediev N. Fundamental peregrine solitons of ultrastrong amplitude enhancement through self-steepening in vector nonlinear systems. Phys Rev Lett (2020) 124:113901. doi:10.1103/PhysRevLett.124.113901

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Xu G, Gelash A, Chabchoub A, Zakharov V, Kibler B. Breather wave molecules. Phys Rev Lett (2019b) 122:084101. doi:10.1103/PhysRevLett.122.084101

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Asgarnezhad-Zorgabad S, Berini P, Sanders BC. Polaritonic frequency-comb generation and breather propagation in a negative-index metamaterial with a cold four-level atomic medium. Phys Rev A (2019) 99:051802. doi:10.1103/PhysRevA.99.051802

CrossRef Full Text | Google Scholar

54. Asgarnezhad-Zorgabad S, Sadighi-Bonabi R, Kibler B, Özdemir ŞK, Sanders BC. Surface-polaritonic phase singularities and multimode polaritonic frequency combs via dark rogue-wave excitation in hybrid plasmonic waveguide. New J Phys (2020) 22:033008. doi:10.1088/1367-2630/ab7259

CrossRef Full Text | Google Scholar

55. Fleischhauer M, Imamoglu A, Marangos JP. Electromagnetically induced transparency: optics in coherent media. Rev Mod Phys (2005) 77:633–73. doi:10.1103/RevModPhys.77.633

CrossRef Full Text | Google Scholar

56. Huang G, Deng L, Payne MG. Dynamics of ultraslow optical solitons in a cold three-state atomic system. Phys Rev E (2005) 72:016617. doi:10.1103/PhysRevE.72.016617

CrossRef Full Text | Google Scholar

57. Chen Y, Bai Z, Huang G. Ultraslow optical solitons and their storage and retrieval in an ultracold ladder-type atomic system. Phys Rev A (2014b) 89:023835. doi:10.1103/PhysRevA.89.023835

CrossRef Full Text | Google Scholar

58. Xu D, Chen Z, Huang G. Ultraslow weak-light solitons and their storage and retrieval in a kagome-structured hollow-core photonic crystal fiber. Opt Express (2017) 25:19094–111. doi:10.1364/OE.25.019094

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Liu J, Hang C, Huang G. Weak-light rogue waves, breathers, and their active control in a cold atomic gas via electromagnetically induced transparency. Phys Rev A (2016) 93:063836. doi:10.1103/PhysRevA.93.063836

CrossRef Full Text | Google Scholar

60. Liu J, Hang C, Huang G. Weak-light vector rogue waves, breathers, and their Stern-Gerlach deflection via electromagnetically induced transparency. Opt Express (2017) 25:23408–23. doi:10.1364/OE.25.023408

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Boyd RW. Nonlinear Optics New York: Elsevier (2008).

62. Steck DA. Rubidium 87 D line data (2019) https://steck.us/alkalidata/ (Accessed August 3, 2020).

CrossRef Full Text

63. Newell AC, Moloney JC. Nonlinear Optics (California. Addison-Wesley Publishing Company (1991).

64. Kivshar YS, Luther-Davies B. Dark optical solitons: physics and applications. Phys Rep (1998) 298:81–197. doi:10.1016/S0370-1573(97)00073-2

CrossRef Full Text | Google Scholar

65. Shou C, Huang G. Storage and retrieval of slow-light dark solitons. Opt Lett (2020) 45:6787–90. doi:10.1364/OL.412247

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Mazets IE. Adiabatic pulse propagation in coherent atomic media with the tripod level configuration. Phys Rev A (2005) 71:023806. doi:10.1103/PhysRevA.71.023806

CrossRef Full Text | Google Scholar

67. Shou C, Huang G. Slow-light soliton beam splitters. Phys Rev A (2019) 99:043821. doi:10.1103/PhysRevA.99.043821

CrossRef Full Text | Google Scholar

68. Lemr K, Bartkiewicz K, Černoch A, Soubusta J. Resource-efficient linear-optical quantum router. Phys Rev A (2013) 87:062333. doi:10.1103/PhysRevA.87.062333

CrossRef Full Text | Google Scholar

69. Xu Q, Sandhu S, Povinelli ML, Shakya J, Fan S, Lipson M. Experimental realization of an on-chip all-optical analogue to electromagnetically induced transparency. Phys Rev Lett (2006) 96:123901. doi:10.1103/PhysRevLett.96.123901

PubMed Abstract | CrossRef Full Text | Google Scholar