Orbital Selectivity in Electron Correlations and Superconducting Pairing of Iron-Based Superconductors

Electron correlations play a central role in iron-based superconductors. In these systems, multiple Fe $3d$-orbitals are active in the low-energy physics, and they are not all degenerate. For these reasons, the role of orbital-selective correlations has been an active topic in the study of the iron-based systems. In this article, we survey the recent developments on the subject. For the normal state, we emphasize the orbital-selective Mott physics that has been extensively studied, especially in the iron chalcogenides, in the case of electron filling $n\sim 6$. In addition, the interplay between orbital selectivity and electronic nematicity is addressed. For the superconducting state, we summarize the initial ideas for orbital-selective pairing and discuss the recent explosive activities along this direction. We close with some perspectives on several emerging topics. These include the evolution of the orbital-selective correlations, magnetic and nematic orders, and superconductivity as the electron filling factor is reduced from 6 to 5, as well as the interplay between electron correlations and topological band structure in iron-based superconductors.

1 Introduction

Since the discovery of superconductivity in F-doped LaFeAsO [1], the study of iron-based superconductors (FeSCs) has been one of the most active fields in condensed matter physics. The FeSCs feature a large family of materials, which are divided into two major classes, the iron pnictides and iron chalcogenides. The highest superconducting transition temperature ($T_c$) is at 56 K for the iron pnictides [2, 3] and 65 K or even higher in the single-layer iron chalcogenide [4–8]. It is believed that the high-temperature superconductivity in the FeSCs originates from electron-electron interactions [9–14]. This motivates the consideration of similarities and differences between the FeSCs and other correlated superconductors, especially the cuprates [15]. Similar to the cuprates, most parent compounds of FeSCs have an antiferromagnetically (AFM) ordered ground state [12, 16], and the superconductivity emerges within a certain range of chemical doping. In contrast with the cuprates, most, though not all, parent iron pnictides and iron chalcogenides are metals [9–14], typically exhibiting electron and hole Fermi pockets as revealed by angle resolved photoemission spectroscopy (ARPES) measurements [17].

These properties raise important questions about the role of electron correlations in the FeSCs and how the correlations interplay with the superconductivity in these materials. In this review, we survey recent developments on the orbital-selective electron correlations in the FeSCs.

1.1 Electron Correlations in the FeSCs

We start by outlining the two important issues regarding the electron correlations of the FeSCs. The first issue concerns the overall strength of the electron correlations. The parent FeSCs are bad metals [18, 19], with the room-temperature electrical resistivities reaching the Mott-Ioffe-Regel limit and corresponding to the product of Fermi wave vector and mean-free path being of order unity. The Mott-Ioffe-Regel criterion [20] signifies a system with a metallic ground state and with strong electron correlations. Further evidence for the bad metal behavior comes from the optical conductivity measurement, which showed that the Drude weight is considerably reduced by the electron correlations [21–25]. In relation to this, the effective mass of the single-electron excitations is much enhanced from their non-interacting counterpart, with the enhancement factor ranging from 3 to 20 across the FeSC families [17, 26–30]. These bad-metal characteristics, together with the existence of a large spin spectral weight observed by neutron scattering experiments (already for the parent iron pnictides [31, 32]) and a number of other characteristics from measurements such as the X-ray emission [33] and Raman scattering [34] spectroscopies, imply that the parent FeSCs possess a considerable degree of electron correlations. Indeed, the integrated spin spectral weight measured from the dynamical spin susceptibility is at the order of 3 ${\mu }_B^2$ per Fe in the parent iron pnictides, which is too large to be generated by particle-hole excitations in the Fermi-surface nesting picture but is consistent with the spin degrees of freedom being dominated by the contributions from the incoherent electronic excitations [32]. The total spin spectral weight is even larger in the iron chalcogenides [11–13].

All of these experimental results suggest that the parent FeSCs are in the bad metal regime which is close to a metal-to-Mott-insulator transition (MIT). This regime can be described by a w-expansion around the MIT within the incipient Mott picture [18, 35, 36], where w is the overall fraction of the electron spectral weight that occupies the coherent itinerant part. To the zeroth order in w, the spin degrees of freedom appear in the form of quasilocalized magnetic moments with frustrated exchange interactions; this picture anchors the description of the AFM order and the associated magnetic fluctuations. The importance of such incoherent electronic excitations to the low-energy physics of the FeSCs has also been emphasized from related considerations [37–48, 50–56].

1.2 Orbital-Selective Correlations and Orbital-Selective Superconducting Pairing

The other, related, issue is the multiorbital nature of the low-energy electronic structure of FeSCs. As illustrated in Figures 1A,B, the Fermi surface of the parent FeSCs consists of several pockets, and each pocket contains contributions from multiple Fe $3d$ orbitals. The Fe ion has a valence of $+2$, corresponding to $n=6$ electrons occupying its five 3d orbitals. These orbitals are not all degenerate, and there are an even number of electrons per Fe site. Thus, the MIT in such systems, if it does take place, is expected to be quite distinct. The common tetragonal structure of FeSCs only preserves the degeneracy between the $d_{xz}$ and $d_{yz}$ orbitals. The partially lifted orbital degeneracy may cause the effects of the electron correlations to be orbital dependent. As a simple example, consider a system with two nondegenerate orbitals. The bandwidths or the electron fillings in these two orbitals are generically different. Thus, even for the same Coulomb repulsion, the degree of electron correlations is expected to be different, and this difference is denoted as orbital selectivity. The case of extreme distinction corresponds to an orbital-selective Mott phase (OSMP): as sketched in Figure 1C, orbital 2 becomes a MI where the electrons are fully localized, while orbital 1 remains metallic. The notion that some orbitals can be driven through a delocalization-localization transition while the others remain delocalized can be traced back to the physics of Kondo destruction in f-electron physics [57–59]. For d-electron systems, the OSMP was first considered for ${\text{Ca}}_{2-x}$ Sr_xRuO₄ [60] within a multiorbital model whose kinetic part is diagonal in the orbital basis, for which the orbital and band bases are the same.

FIGURE 1

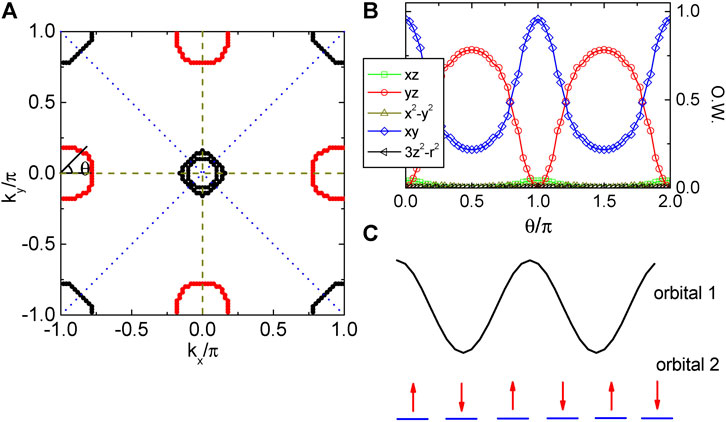
FIGURE 1. (A): Fermi surface of a five-orbital multiorbital Hubbard model for the iron pnictides, consisting of both hole (black symbols) and electron (red symbols) pockets. The 1-Fe Brillouin zone (BZ) is used hereafter. (B) Orbital weights (O.W.) along the electron pocket centered at $\left(\pi ,0\right)$. θ is defined in panel (A), adapted from [72]. (C) Sketch of the orbital-selective Mott phase in a two-orbital model. Orbital 1 is metallic, with its renormalized bandwidth being nonzero, and orbital 2 is a Mott insulator where the active degree of freedom is a magnetic moment localized at each site. Note that interorbital coupling is in general nonzero in the kinetic part of the Hamiltonian. The OSMP can develop only when the corresponding interorbital coupling is renormalized to zero.

An important characteristic of the FeSCs is that different orbitals are coupled to each other, as dictated by the crystalline symmetry, and this makes the consideration of the OSMP especially nontrivial. Here, the treatment of the orbital-selective correlation effect in multiorbital models with such interorbital coupling was introduced in [61]. The analysis of [61] sets the stage for realizing

(1) An OSMP in the multiorbital Hubbard models for the iron chalcogenides [62]. Here, the $d_{xy}$ states are localized while the other $3d$ states are delocalized with nonzero coherent spectral weight. This is so in spite of the fact that the bare Hamiltonian contains a kinetic coupling between the $d_{xy}$ and other $3d$ orbitals of Fe;

(2) A distinct crossover [dashed line, Figure 2A], with the increasing strength of the interactions, from the regime of a weakly correlated metal into an OSMP-proximate regime [62–64]. In this regime, dubbing a “strongly correlated metal” (SCM), all the orbitals remain itinerant but some of the orbitals have substantially reduced and orbitally differentiated quasiparticle weights.

FIGURE 2

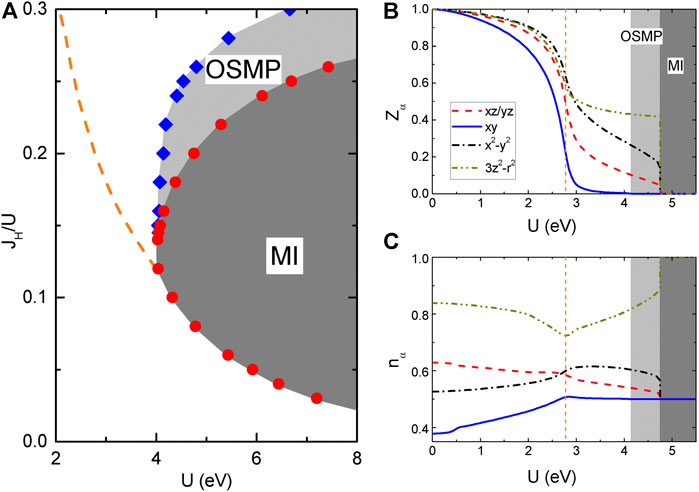
FIGURE 2. (A) Ground-state phase diagram of the five-orbital multiorbital model for alkaline iron selenides at commensurate filling $n=6$. The dark and light gray regions correspond to the MI and OSMP, respectively. The orange dashed line refers to a crossover between the weakly correlated metal (WCM) and bad metal (strongly correlated metal, SCM). (B) and (C) The evolution of the orbital resolved quasiparticle spectral weights [in (B)] and electron filling factor per spin [in (C)] with U in the five-orbital model at $J_H/U=0.2$, adapted from [62].

The theoretical work went together with the experimental observation of an OSMP in several iron chalcogenides [29, 30, 65]. The mechanism for the suppression of interorbital coupling by the correlation effects, which allows for the OSMP, is further clarified in terms of a Landau free-energy functional in [66]. (Related microscopic studies have been carried out in [67].) In all these analyses, the interplay between the Hund’s coupling ($J_{\text{H}}$) and Hubbard interaction (U) plays a crucial role (see the discussions below and in Figures 2, 3). A complementary approach to the correlation effects describes the localization-delocalization phenomena in the form of orbitally differentiated coherence-incoherence crossover, referred to as Hund’s metal [39, 68, 69]; this approach leads to results that share considerable commonality to those arising from the orbital-selective Mott physics. Very recently, the low-temperature emergence of the OSMP has been identified in ${\text{FeTe}}_{1-x}$ Se_x near the FeTe end ($x\to 0$) [70]. In addition, the orbital-selective Mott correlations have been advanced as the mechanism for the striking renormalization to the Fermi surface and low-energy electronic dispersion of LiFeAs [71].

FIGURE 3

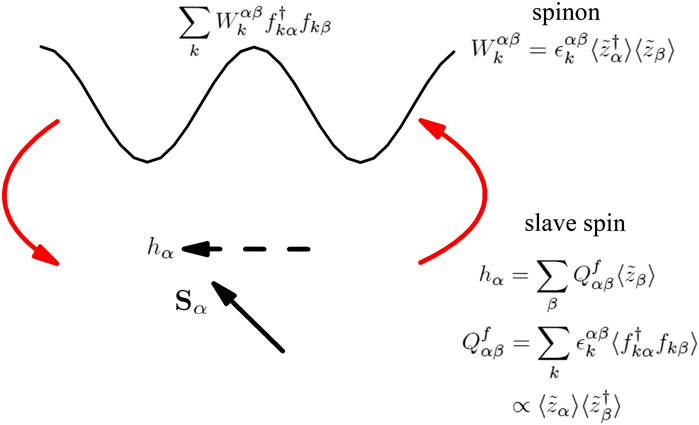
FIGURE 3. Illustrating the effect of the interorbital kinetic hybridization in the $U\left(1\right)$ slave-spin theory. The black curve shows the effective spinon dispersion, which is described by $W_k^{\alpha \beta }{f}_{\mathrm{k\alpha }\sigma }^{†}{f}_{\mathrm{k\beta }\sigma }$. (The physical spin index σ is suppressed in the figure legends.) Meanwhile, the slave-spin ${\mathbf{S}}_{\alpha }$ experiences a local field, $h_{\alpha }={\displaystyle {\sum }_{\beta }{Q}_{\alpha \beta }^f\langle {\tilde{z}}_{\beta }\rangle }$, where $Q_{\alpha \beta }^f\propto \langle {\tilde{z}}_{\alpha }\rangle \langle {\tilde{z}}_{\beta }^{†}\rangle$. The red arrows indicate the self-consistency between $W_k^{\alpha \beta }$ and $h_{\alpha }$, which results in a biquadratic interorbital coupling as shown in Eqs. 12,13, adapted from [66].

The recognition of the orbital-selective correlations has led to the initial work on the orbital-selective pairing [72]. This notion was motivated by—and applied to the analysis of—the properties of the superconducting state in the under-electron-doped NaFeAs [73]. In other theoretical approaches, various forms of orbital-selective pairing were considered in the contexts of the FeSCs [74, 75].

1.3 Perspective and Objective

Because most of the parent compounds are not Mott insulators (MIs), assessing the strength of electron correlations has been an important topic since the beginning of the FeSC field. In principle, the AFM ground state and the superconducting state nearby may originate from the Fermi surface nesting mechanism of a weak-coupling theory [76–80].

As outlined above, the correlation strength of the FeSCs is intermediate: here, the Coulomb repulsion and the bandwidth are similar in magnitude, and the competition between the electrons’ itineracy and localization is the most fierce. Spectroscopy measurements have provided ample evidence that, for the parent compounds of the FeSCs, the incoherent part of the electron spectral weight $\left(1-w\right)$ is larger than the coherent counterpart w, which provides a microscopic definition of a bad metal. The full force of the electron correlations in the FeSCs has now become quite apparent [13, 81–98]. In leading toward this understanding, the orbital-selective aspects of the correlations and pairing have played an important role.

Recognizing that the study of the orbital-selective correlations and pairing has had explosive developments in recent years, here we survey the recent theoretical progress on the orbital selectivity for both the normal and superconducting states in multiorbital models for FeSCs. We focus on the MIT at $n=6$ and show how the Hund’s coupling stabilizes a bad metal phase with a large orbital selectivity. Especially for the iron chalcogenides, an OSMP—with the $d_{xy}$ orbital being Mott localized and the other $3d$ orbitals remaining itinerant—appears in the phase diagram. We further discuss the experimental evidences for the orbital selectivity as well as the implications of the orbital-selective correlations for the magnetism, electronic nematicity, and superconductivity of FeSCs. For the superconducting state, we summarize how the orbital-selective superconducting pairing not only accounts for the strikingly large superconducting gap anisotropy, but also gives rise to novel pairing states. The latter clarifies a number of puzzles in alkaline iron selenides. We note that the orbital-selective correlations correspond to a very broad and active subject. Thus, instead of aiming to be comprehensive, here we review the conceptual and model studies of the orbital-selective Mott physics in the normal state and, relatedly, of the orbital-selective pairing in the superconducting state.

We also note that standard weak-coupling approaches (see, e.g., [99]) do not capture the orbital-selective Mott regime. However, the orbital-selective correlation effects, with some orbitals having substantially reduced and orbitally differentiated quasiparticle weights similar to what we summarize here, have more recently been incorporated in a phenomenological way [100, 101] into the weak-coupling approaches. Some of the limitations of the weak-coupling analyses have been suggested [100, 101] to be remedied by this phenomenological approach, but other issues inherent to the weak-coupling treatments—such as the under-accounting of the spin spectral-weight—remain [31] within the phenomenological approach.

The rest of the manuscript is organized as follows: in Section 2 we first briefly introduce the multiorbital Hubbard model for FeSCs and outline the $U\left(1\right)$ slave-spin theory [63, 66] used for studying the MIT in this model. This approach accounts for the proper symmetry of the involved phases. We also consider a Landau free-energy functional that demonstrates how an OSMP can be robust in spite of a nonzero bare interorbital kinetic hybridization. We proceed to address the bad metal behavior and the OSMP that is identified in the phase diagram of this model and discuss the implication for the nematic phase of iron selenide. In Section 3 we set up the multiorbital t-J model for studying the superconductivity of FeSCs and discuss the main results of the orbital-selective superconducting pairing and its implications. In Section 4 we present a brief summary and an outlook for several emerging directions.

2 Orbital-Selective Correlations in the Normal State of Iron-Based Superconductors

To study the effects of orbital-selective correlation, we consider a multiorbital Hubbard model for the FeSCs. The Hamiltonian reads

$H=H_{TB}+H_{\mathrm{int}}.(1)$

Here $H_{TB}$ is a tight-binding model that contains multiple Fe $3d$ orbitals and preserves the tetragonal lattice symmetry of the FeSCs in the normal state. The tight-binding parameters are obtained by fitting to the DFT band structure of specific compounds. A number of tight-binding models, ranging from two to five orbital models, have been proposed for FeSCs [77, 78, 102–106]. In principle, any of these models can be used to illustrate the correlation effects. In practice, we adopt the more realistic five-orbital models, which capture the salient features of the electronic structure and Fermi surface and facilitate a direct comparison to the experimental results. As already stressed, the tetragonal symmetry dictates that interorbital hopping amplitudes are allowed and the fitted tight-binding parameters do show that such hopping amplitudes are nonzero. Specifically, the noninteracting part of the Hamiltonian is written as

$H_{TB}=\frac{1}{2}{\displaystyle \sum _{ij\alpha \beta \sigma }{t}_{ij}^{\alpha \beta }{d}_{i\alpha \sigma }^{†}{d}_{j\beta \sigma }}+{\displaystyle \sum _{i\alpha \sigma }\left({\Lambda }_{\alpha }-\mu \right)d_{i\alpha \sigma }^{†}{d}_{i\alpha \sigma }}.(2)$

Here, $d_{i\alpha \sigma }^{†}$ creates an electron in orbital ($=1,\dots ,5$) with spin σ at site i; $t_{ij}^{\alpha \beta }$, with $i\ne j$, are the tight-binding parameters, with those for $\alpha \ne \beta$ describing the interorbital couplings; and ${\text{Λ}}_{\alpha }$ refers to the orbital-dependent energy levels, associated with the crystal field splittings, and is diagonal in the orbital basis. In particular, the C₄ symmetry dictates that $d_{xz}$ and $d_{yz}$ are degenerate, but no symmetry enforces any degeneracy between the $d_{xy}$ orbital and the other orbitals. Indeed, for any orbital $\beta \ne xy$, ${\text{Λ}}_{xy,\beta }\equiv {\text{Λ}}_{xy}-{\text{Λ}}_{\beta }\ne 0$. The chemical potential μ controls the total electron number n that occupies the $3d$ orbitals of each Fe site. In the model, $n=6$ for the parent (undoped) compound.

The onsite interaction $H_{\mathrm{int}}$ takes the following form:

$H_{\text{int}}=\frac{U}{2}{\displaystyle \sum _{i,\alpha ,\sigma }{n}_{i\alpha \sigma }{n}_{i\alpha \overline{\sigma }}}+{\displaystyle \sum _{i,\alpha <\beta ,\sigma }\left\{U^{\text{′}}{n}_{i\alpha \sigma }{n}_{i\beta \overline{\sigma }}+\left(U^{\prime }-J_{\text{H}}\right)n_{i\alpha \sigma }{n}_{i\beta \sigma }\right\}}-J_{\text{H}}{\displaystyle \sum }_{i,\alpha <\beta ,\sigma }\left(d_{i\alpha \sigma }^{†}{d}_{i\alpha \overline{\sigma }}{d}_{i\beta \overline{\sigma }}^{†}{d}_{i\beta \sigma }+d_{i\alpha \sigma }^{†}{d}_{i\alpha \overline{\sigma }}^{†}{d}_{i\beta \sigma }{d}_{i\beta \overline{\sigma }}\right),(3)$

where $n_{i\alpha \sigma }=d_{i\alpha \sigma }^{†}{d}_{i\alpha \sigma }$. Here, U and $U^{\prime }$ denote the intraorbital and interorbital repulsion, respectively, and $J_H$ is the Hund’s rule exchange coupling. These coupling parameters satisfy $U^{\prime }=U-2J_H$ [107].

2.1 The $U\left(1\right)$ Slave Spin Theory

The multiorbital system described by the model in Eq. 1 undergoes a MIT driven by the electron correlations at any commensurate electron filling. This transition can be studied by using a $U\left(1\right)$ slave-spin theory [63, 66]. In this subsection we summarize the theoretical approach for the MIT and show that, besides the conventional metallic and Mott insulating phases, there is also an OSMP as the ground state of the system.

Slave-particle (or parton) construction has a long history in the study of correlated systems [108–111]. For the single orbital Hubbard model, the slave boson method of [111] has been successfully applied. But the construction of this theory for an M-orbital Hubbard model would require $4^M$ slave bosons, which is not feasible for the case of FeSCs where $M=5$. More recent variations include slave rotor [112] and $Z_2$ slave-spin [113] formulations. For the purpose of describing the MIT, the $Z_2$ gauge structure [113–115] is problematic given that the MIT concerns the (de)localization of a $U\left(1\right)$-symmetric charge degrees of freedom [116]. The $U\left(1\right)$ slave-spin formulation is more suitable, given that it captures the symmetry of the pertinent phases.

In the $U\left(1\right)$ slave-spin formulation [63, 66], the electron creation operator is represented as

$d_{i\alpha \sigma }^{†}=S_{i\alpha \sigma }^{+}{f}_{i\alpha \sigma }^{†}.(4)$

Here the XY component of a quantum $S=1/2$ spin operator ($S_{i\alpha \sigma }^{+}$) is used to represent the charge degree of freedom of the electron at each site i, for each orbital α and each spin flavor σ. Correspondingly, the fermionic “spinon” operator, $f_{i\alpha \sigma }^{†}$, is used to carry the spin degree of freedom. To restrict the Hilbert space to the physical one, a local constraint

$S_{i\alpha \sigma }^z=f_{i\alpha \sigma }^{†}{f}_{i\alpha \sigma }-\frac{1}{2},(5)$

is implemented. This representation contains a $U\left(1\right)$ gauge redundancy corresponding to $f_{i\alpha \sigma }^{†}\to f_{i\alpha \sigma }^{†}{e}^{-i{\theta }_{i\alpha \sigma }}$ and $S_{i\alpha \sigma }^{+}\to S_{i\alpha \sigma }^{+}{e}^{i{\theta }_{i\alpha \sigma }}$. In parallel to the slave-rotor approach [112], in this representation, the slave spins carry the $U\left(1\right)$ charge. Correspondingly, the $U\left(1\right)$ slave-spin theory can naturally describe the MIT, including in multiorbital settings.

To construct a saddle-point theory, one has to work within the Schwinger boson representation of the slave spins. A detailed derivation of the saddle-point equations can be found in [63, 66]. Here, for conciseness, we will mostly stay in the slave-spin representation and simply describe the main results. To ensure that the quasiparticle spectral weight in the noninteracting limit is normalized to 1 at the saddle point level, and in analogy to the standard treatment in the slave-boson theory [111], we define a dressed operator:

${\widehat{z}}_{i\alpha \sigma }^{†}=P_{i\alpha \sigma }^{+}{S}_{i\alpha \sigma }^{+}{P}_{i\alpha \sigma }^{-},(6)$

where the projectors $P_{i\alpha \sigma }^{\pm }=1/\sqrt{1/2+\delta \pm S_{i\alpha \sigma }^z}$ and δ is an infinitesimal positive number to regulate $P_{i\alpha \sigma }^{\pm }$. Next we rewrite Eq. 4 with the dressed operator to $d_{i\alpha \sigma }^{†}={\widehat{z}}_{i\alpha \sigma }^{†}{f}_{i\alpha \sigma }^{†}$. The Hamiltonian, Eq. 1, is then effectively rewritten as

$H=\frac{1}{2}{\displaystyle \sum _{ij\alpha \beta \sigma }{t}_{ij}^{\alpha \beta }{\widehat{z}}_{i\alpha \sigma }^{†}{\widehat{z}}_{j\beta \sigma }{f}_{i\alpha \sigma }^{†}{f}_{j\beta \sigma }}+{\displaystyle \sum }_{i\alpha \sigma }\left({\text{Λ}}_{\alpha }-\mu \right)f_{i\alpha \sigma }^{†}{f}_{i\alpha \sigma }-{\lambda }_{i\alpha \sigma }\left[f_{i\alpha \sigma }^{†}{f}_{i\alpha \sigma }-S_{i\alpha \sigma }^z\right]+H_{\text{int}}^S.(7)$

Here, we have introduced the Lagrange multiplier ${\lambda }_{i\alpha \sigma }$ to enforce the constraint in Eq. 5. In addition, $H_{\text{int}}^S$ is the interaction Hamiltonian, Eq. 3, rewritten in terms of the slave-spin operators [61] as follows:

$H_{\mathrm{int}}^S={\displaystyle \sum _i\left\{\frac{U^{\prime }}{2}{\left({\displaystyle \sum _{\alpha \sigma }{S}_{i\alpha \sigma }^z}\right)}^2+\frac{U-U^{\prime }}{2}{\displaystyle \sum _{\alpha }{\left({\displaystyle \sum _{\sigma }{S}_{i\alpha \sigma }^z}\right)}^2}-\frac{J_H}{2}{\displaystyle \sum _{\sigma }{\left({\displaystyle \sum _{\alpha }{S}_{i\alpha \sigma }^z}\right)}^2}-J_H{\displaystyle \sum _{\alpha <\beta }\left[S_{i\alpha \uparrow }^{+}{S}_{i\alpha \downarrow }^{-}{S}_{i\beta \downarrow }^{+}{S}_{i\beta \uparrow }^{-}-S_{i\alpha \uparrow }^{+}{S}_{i\alpha \downarrow }^{+}{S}_{i\beta \downarrow }^{-}{S}_{i\beta \uparrow }^{-}+H.c.\right]}\right\}.}(8)$

One practical way is to neglect the spin flip terms in Eq. 8 without affecting the qualitative results [63]. The quasiparticle spectral weight is defined as

$Z_{i\alpha \sigma }={\left|z_{i\alpha \sigma }\right|}^2\equiv {\left|\langle {\widehat{z}}_{i\alpha \sigma }\rangle \right|}^2.(9)$

A metallic phase corresponds to $Z_{i\alpha \sigma }>0$ for all orbitals, and a Mott insulator corresponds to $Z_{i\alpha \sigma }=0$ in all orbitals with a gapless spinon spectrum.

At the saddle-point level, the slave-spin and spinon operators are decomposed and the constraint is treated on average. We obtain two effective Hamiltonians for the spinons and the slave spins, respectively:

$H_f^{\text{eff}}={\displaystyle \sum _{k\alpha \beta }\left[{\mathit{ϵ}}_k^{\alpha \beta }\langle {\tilde{z}}_{\alpha }^{†}\rangle \langle {\tilde{z}}_{\beta }\rangle +{\delta }_{\alpha \beta }\left({\text{Λ}}_{\alpha }-{\lambda }_{\alpha }+{\tilde{\mu }}_{\alpha }-\mu \right)\right]}{f}_{k\alpha }^{†}{f}_{k\beta },(10)$

$H_S^{\text{eff}}={\displaystyle \sum }_{\alpha \beta }\left[Q_{\alpha \beta }^f\left(\langle {\tilde{z}}_{\alpha }^{†}\rangle {\tilde{z}}_{\beta }+\langle {\tilde{z}}_{\beta }\rangle {\tilde{z}}_{\alpha }^{†}\right)+{\delta }_{\alpha \beta }{\lambda }_{\alpha }{S}_{\alpha }^z\right]+H_{\mathrm{int}}^S,(11)$

where ${\delta }_{\alpha \beta }$ is Kronecker delta function, ${\mathit{ϵ}}_k^{\alpha \beta }=1/N{\displaystyle {\sum }_{ij\sigma }{t}_{ij}^{\alpha \beta }{e}^{ik\left(r_i-r_j\right)}}$, $Q_{\alpha \beta }^f={\displaystyle {\sum }_{k\sigma }{\mathit{ϵ}}_k^{\alpha \beta }\langle f_{k\alpha \sigma }^{†}{f}_{k\beta \sigma }\rangle }/2$, and ${\tilde{z}}_{\alpha }^{†}=\langle P_{\alpha }^{+}\rangle S_{\alpha }^{+}\langle P_{\alpha }^{-}\rangle$. Finally, ${\tilde{\mu }}_{\alpha }$ is an effective onsite potential defined as ${\tilde{\mu }}_{\alpha }=2{\overline{\mathit{ϵ}}}_{\alpha }{\eta }_{\alpha }$, where ${\overline{\mathit{ϵ}}}_{\alpha }={\displaystyle {\sum }_{\beta }\left(Q_{\alpha \beta }^f\langle {\tilde{z}}_{\alpha }^{†}\rangle \langle {\tilde{z}}_{\beta }\rangle +\text{c}.\text{c}.\right)}$ and ${\eta }_{\alpha }=\left(2n_{\alpha }^f-1\right)/\left[4n_{\alpha }^f\left(1-n_{\alpha }^f\right)\right]$, with $n_{\alpha }^f=1/N{\displaystyle {\sum }_k\langle f_{k\alpha }^{†}{f}_{k\alpha }\rangle }$.

We study the MIT in the paramagnetic phase preserving the translational symmetry and can hence drop the spin and/or site indices of the slave spins and the Lagrange multiplier in the saddle-point equations, (10)(11). The parameters $z_{\alpha }$ and ${\lambda }_{\alpha }$ are then solved self-consistently.

2.2 Landau Free-Energy Functional for Orbital-Selective Mott Physics

As described earlier and illustrated in Figure 1C, the OSMP can develop only when (at least) one of the orbitals becomes localized, while the others remain delocalized. How can this be possible in a multiorbital model with nonzero bare interorbital coupling between orbitals? While the $U\left(1\right)$ slave-spin approach found an affirmative answer, it is important to ask whether the result of this microscopic approach is robust. To do so, we construct a Landau theory based on the slave-spin formulation [66]. We start from the saddle-point Hamiltonians Eq. 10. Consider first Eq. 10, where the kinetic hybridization between two different orbitals $\alpha \ne \beta$ is $W_k^{\alpha \beta }{f}_{k\alpha }^{†}{f}_{k\beta }$, with $W_k^{\alpha \beta }={\mathit{ϵ}}_k^{\alpha \beta }\langle {\tilde{z}}_{\alpha }^{†}\rangle \langle {\tilde{z}}_{\beta }\rangle \propto \langle {\tilde{z}}_{\alpha }^{†}\rangle \langle {\tilde{z}}_{\beta }\rangle$. Because $f_{k\alpha }^{†}{f}_{k\beta }$ is conjugate to $W_k^{\alpha \beta }$, from the linear response theory, it is easy to show that $\langle f_{k\alpha }^{†}{f}_{k\beta }\rangle \propto W_k^{\alpha \beta }\propto \langle {\tilde{z}}_{\alpha }\rangle \langle {\tilde{z}}_{\beta }^{†}\rangle$. As a result, the kinetic hybridization of the spinons is

${\langle H_f^{eff}\rangle }_{\alpha \beta }={\displaystyle \sum _k{\epsilon }_k^{\alpha \beta }\langle {\tilde{z}}_{\alpha }^{†}\rangle \langle {\tilde{z}}_{\beta }\rangle \langle f_{k\alpha }^{†}{f}_{k\beta }\rangle \propto {\left|\langle {\tilde{z}}_{\alpha }\rangle \right|}^2{\left|\langle {\tilde{z}}_{\beta }\rangle \right|}^2}.(12)$

Next for Eq. 11, we can define an effective field of $h_{\alpha }={\displaystyle {\sum }_{\beta }{Q}_{\alpha \beta }^f\langle {\tilde{z}}_{\beta }\rangle }$. For similar reasoning as mentioned above, we obtain $Q_{\alpha \beta }^f\propto \langle {\tilde{z}}_{\alpha }\rangle \langle {\tilde{z}}_{\beta }^{†}\rangle$, which leads to

${\langle H_S^{\text{eff}}\rangle }_{\alpha \beta }\to {\left|\langle {\tilde{z}}_{\alpha }\rangle \right|}^2{\left|\langle {\tilde{z}}_{\beta }\rangle \right|}^2.(13)$

Note that Eq. 13 are natural consequence of Eq. 11, and this self-consistent procedure of the saddle-point theory is illustrated in Figure 3. Based on Eq 12 we can construct a Landau free-energy functional in terms of the quasiparticle weights, $z_{\alpha }$. For simplicity of notation, we consider a two-orbital model, but our analysis straightforwardly generalizes to the case of more than two orbitals. The free-energy density reads

$f={\displaystyle \sum _{\alpha =\mathrm{1,2}}\left(r_{\alpha }{\left|z_{\alpha }\right|}^2+u_{\alpha }{\left|z_{\alpha }\right|}^4\right)+v{\left|z_1\right|}^2{\left|z_2\right|}^2},(14)$

in which the quadratic terms $r_{\alpha }{\left|z_{\alpha }\right|}^2$ arise from the kinetic energy of the saddle-point Hamiltonian in Eq. 11 [as well as in Eq. 10]. The biquadratic coupling v term comes from the kinetic hybridization in Eq 13. The biquadratic nature of this intraorbital coupling—as opposed to the bilinear form—is crucial to the stabilization of an OSMP. This can be seen by taking the derivatives of Eq. 14 with respect to $\left|z_{\alpha }\right|$. Besides the conventional metallic phase with $\left|z_1\right|\ne 0$, $\left|z_2\right|\ne 0$ and the MI with $\left|z_1\right|=\left|z_2\right|=0$, Eq. 14 supports a third solution with $\left|z_1\right|=0$, $\left|z_2\right|=\sqrt{-\left(r_2/2u_2\right)}$ (or $\left|z_2\right|=0$, $\left|z_1\right|=\sqrt{-\left(r_1/2u_1\right)}$), which corresponds to an OSMP.

2.3 Orbital-Selective Mott Physics in FeSCs

We now turn to microscopic studies of the MIT. A realistic microscopic model for FeSCs is described in Eq. 1. Owing to its multiorbital nature, the MIT in this model shows unique features. First, the parent compound corresponds to $n=6$, containing an even number of electrons per Fe ion. Since Mott transition is more readily defined in systems with an odd number of electrons per unit cell, this makes it a nontrivial question whether the model generally supports a MI in the strong correlation limit. Second, besides the Coulomb repulsion U, the Hund’s rule coupling $J_{\text{H}}$ also plays a very important role in settling the ground states of the model and, as we will see, plays an important role in realizing an OSMP.

The MIT in the multiorbital model for FeSCs at $n=6$ has been studied by using the slave-spin methods introduced in Section 2.1. In the following, we present the resulting phase diagram for alkaline iron selenides. As shown in Figures 2A, a MI is generally stabilized in the phase diagram when the Coulomb repulsion U is sufficiently strong. The critical value $U_c$ for the Mott transition displays a nonmonotonic dependence on the Hund’ coupling $J_H$. This is a general feature of the MIT of the multiorbital Hubbard model away from half-filling and can be understood as follows [63]: naively the MIT takes place when the Mott gap at the atomic limit $G_A$ approaches the bare bandwidth of the tight-binding model D. In the weak $J_H$ limit, the MI is dominated by the low-spin $S=1$ configuration and correspondingly $G_A\sim U+J_H$. This leads to $U_c\sim D/\left(1+J_{\text{H}}/U\right)$; namely, $U_c$ decreases with $J_{\text{H}}/U$. On the other hand, for large $J_{\text{H}}/U$, the high-spin $S=2$ configuration dominates in the MI state and $G_A\sim U-3J_H$. Consequently, $U_c\sim D/\left(1-3J_{\text{H}}/U\right)$ increases with $J_{\text{H}}/U$.

Importantly, the Hund’s coupling already strongly affects the properties of the metallic state. For $J_{\text{H}}/U\mathrm{\gtrsim }0.1$, the system undergoes a crossover from a weakly correlated metal (WCM) to a bad metal with increasing U [shown as the dashed line in Figure 2A]. As illustrated in Figure 2B, the orbital resolved quasiparticle spectral weight $Z_{\alpha }$ in each orbital α rapidly drops across this crossover. Inside the bad metal phase, $Z_{\alpha }$ becomes strongly orbital dependent. This large orbital-selective correlation is rather surprising given that the strength of the onsite interaction is identical for each orbital. To understand the strong orbital selectivity, note that the Hund’s coupling suppresses interorbital correlations. For large Hund’s coupling, this causes an effective orbital decoupling between any two nondegenerate orbitals and hence promotes the $S=2$ high-spin configuration in the bad metal regime. As a result of the orbital decoupling, the correlation effect in each nondegenerate orbital depends on its filling factor $n_{\alpha }$. This is clearly seen in Figures 2B,C: the $d_{xy}$ orbital experiences the strongest correlation effect and $n_{xy}$ is the closest to $1/2$; while the least correlated $3z^2-r^2$ orbital has the largest filling away from $1/2$.

Further increasing U in the bad metal phase, the system undergoes a transition to the OSMP. In this phase the $d_{xy}$ orbital is fully Mott localized ($Z_{xy}=0$) whereas the electrons in other Fe $3d$ orbitals are still itinerant ($Z_{\alpha }>0$). Besides the aforementioned orbital decoupling effect, several other factors are also important for stabilizing the OSMP. First, the bare bandwidth projected to the $d_{xy}$ orbital is smaller than that of the other orbitals. Second, the orbital fluctuations in the degenerate $d_{xz}$ and $d_{yz}$ orbitals make the threshold interaction needed for their Mott localization larger than that for the nondegenerate $d_{xy}$ orbital, although the filling factors of these three orbitals are all close to $1/2$. Taking into account all these factors, the $d_{xy}$ orbital has the lowest interaction threshold for the Mott transition, at which the OSMP takes place. Because only the $d_{xy}$ orbital is Mott localized, the OSMP survives nonzero doping, while the MI can only be stabilized as a ground state at commensurate fillings. It is worth noting that, for a particular system, whether an OSMP is stabilized depends on the competition of the above factors. For example, the OSMP is stabilized in the model for K_xFe_2−ySe₂ but not that for LaOFeAs [62, 63]. (However, the OSMP-proximate SCM regime, which displays strong orbital selectivity in the quasiparticle weight, does exist in the model for LaOFeAs [63].) This is mainly because the bare bandwidth of the $d_{xy}$ orbital is sufficiently smaller than that of the other orbitals in K_xFe_2−ySe₂, but the difference in the bare bandwidths is less pronounced in the case of LaOFeAs. Even though an OSMP is not stabilized as the true ground state for this iron pnictide, it is energetically competitive [63]. As such, the OSMP can be viewed as the anchoring point for the strong orbital-selective correlation effects and the associated bad metal behavior both in the case of the iron selenides and iron pnictides.

The OSMP is supported by additional theoretical studies. Orbital differentiation in K_xFe_2−ySe₂ has also been analyzed in DFT + DMFT calculations [117]. Besides the case of the multiorbital models for K_xFe_2−ySe₂ and related iron chalcogenides and LiFeAs, strong orbital-selective correlations and OSMP have been evidenced in several other multiorbital models for FeSCs [40, 118, 119]. Additionally, the conclusions of the U (1) slave-spin analysis, regarding both the rapid crossover into the OSMP-proximate SCM regime and the development of the OSMP phase, are confirmed by studies of the multiorbital Hubbard models for the FeSCs based on a Gutzwiller approximation [120]. Note that there has also been theoretical efforts to feed the results of the mechanistic studies on the orbital-selective correlations into the weak-coupling approaches, by incorporating the orbital selectivity in the weak-coupling calculations via phenomenological parameters [100, 101]. Experimentally, ARPES measurements provide clear evidence [29, 30] for OSMP in iron chalcogenides. As temperature goes above about 100 K, the spectral weight for the $d_{xy}$ orbital vanishes, while that for the $d_{xz/yz}$ orbitals does not change much [30]. The behavior is similar for all the iron chalcogenides studied as well as for the alkaline iron pnictide [121], which suggests a universal crossover to the OSMP in FeSCs [30]. Additional evidence for the OSMP has come from THz spectroscopy [122], Hall measurements [123], pump-probe spectroscopy [124], and high-pressure transport measurements [125]. Moreover, a variety of other Fe-based systems have been studied for the orbital-selective Mott behavior [82–87, 98]. We note in passing that related orbital-selective correlation effects have recently been discussed in the multiorbital $5f$-based actinide systems [126, 127].

2.4 Orbital Selectivity in the Nematic Phase of FeSe

In most iron pnictides, lowering the temperature in the parent compounds gives rise to a tetragonal-to-orthorhombic structural transition at $T_s$. Right at or slightly below $T_s$, the system exhibits a transition to a collinear $\left(\pi ,0\right)$ AFM state [12]. The origin of the nematicity below $T_s$ has been widely discussed [18, 36, 47–49], and a likely explanation is an Ising-nematic transition of quasilocalized magnetic moments, described by an effective $J_1-J_2$-like model [18, 36, 47, 48].

Experiments in bulk FeSe do not seem to fit into this framework. Under ambient pressure, a nematic phase without an AFM long-range order is stabilized in the bulk FeSe below the structural transition at $T_s\approx 90$ K. This suggests an unusual type of magnetism in the ground state [128, 129]. The nematic order parameter linearly couples to the splitting between the $d_{xz}$ and $d_{yz}$ orbitals, which can be experimentally detected. In the nematic phase of FeSe, ARPES measurements find this splitting to be momentum dependent, and the splittings at both the $\text{Γ}$ and M points of the Brillouin zone (BZ) [130–137], $\text{Δ}{E}_{\text{Γ}}$ and $\text{Δ}{E}_{\text{M}}$, respectively, are relatively small (less than 50 meV). Meanwhile, recent scanning tunneling microscopy (STM) experiments have revealed a strong orbital selectivity [138, 139]. Especially, the estimated ratio of the quasiparticle spectral weights between the $yz$ and $xz$ orbitals is very large: $Z_{yz}/Z_{xz}\sim 4$. Given the small splitting between these two orbitals [131, 136], such a strong orbital selectivity is surprising [140].

To resolve this puzzle, we examine the electron correlation effects in a multiorbital Hubbard model for the nematic phase of FeSe using the $U\left(1\right)$ slave-spin theory. To generate a momentum-dependent orbital splitting, besides the momentum-independent ferro-orbital order (${\delta }_f$), we have also taken into account a d- and an s-wave bond nematic order (${\delta }_d$ and ${\delta }_s$), which corresponds to the nearest-neighboring hopping anisotropy [141]. We add the Hamiltonian $H_{\text{nem}}$ that describes the effects of these nematic orders in the $d_{xz}$ and $d_{yz}$ orbital subspace ($\alpha =\mathrm{1,2}$) into Eq. 1. In the momentum space

$H_{\text{nem}}={\displaystyle {\sum }_k\left[-2{\delta }_d\left(\cos k_x-\cos k_y\right)\left(n_{k1}+n_{k2}\right)-2{\delta }_s\left(\cos k_x+\cos k_y\right)\left(n_{k1}-n_{k2}\right)+{\delta }_f\left(n_{k1}-n_{k2}\right)\right]}.(15)$

By solving the saddle-point equations, we show that the OSMP is promoted by any of these nematic orders, as illustrated in Figure 4A. This effect is delicate, because we also find that the full Mott localization of the system depends on the type and strength of the nematic order [142]. Remarkably, we find that, by taking a proper combination of the three types of nematic order, the system can exhibit a strong orbital selectivity with $Z_{yz}/Z_{xz}\sim 4$ while, at the same time, shows a small band splittings at the $\text{Γ}$ and M points of the BZ (with $\text{Δ}{E}_{\text{Γ}}$, $\Delta E_M\mathrm{\lesssim }50$ meV) as a result of a cancellation effect (see Figures 4B,C) [142]. These results reconcile the seemingly contradictory ARPES and STM results. The explanation of the unusually large orbital selectivity in the nematic phase of FeSe [138, 139] further shed light to the understanding of the superconductivity in this compound, which we will discuss in Section 3.3.

FIGURE 4

FIGURE 4. (A) Ground-state phase diagram of the five-orbital Hubbard model for FeSe with a ferro-orbital order ${\delta }_f$ at $J_H/U=0.25$. (B) The orbital-selective quasiparticle spectral weights in the nematic phase with a combined nematic order ${\delta }_f/4={\delta }_d={\delta }_s=0.2$ eV and with $J_{\text{H}}/U=0.25$. (C) Band splittings at $\text{Γ}$ ($\text{Δ}{E}_{\text{Γ}}$) and M ($\text{Δ}{E}_{\text{M}}$) points of the 2-Fe BZ in the nematic phase with the same set of parameters as in (B), adapted from [142].

3 Orbital-Selective Superconducting Pairing

In Section 2 we have discussed the orbital-selective electron correlations in the normal state of FeSCs. It is natural to ask whether the strong orbital selectivity can affect the pairing symmetry and amplitudes in the superconducting states. The effects of orbital selectivity on superconductivity are two-fold. The orbital selectivity modifies the band structure from its noninteracting counterpart. This has been verified by ARPES measurements [30, 65, 121]. In addition, the orbital selectivity influences the effective interactions projected to the pairing channel. In the following, we study these effects in a frustrated multiorbital t-J model. We show that any interorbital pairing has a negligible amplitude; the structure of the pairing state is then reflected in the pairing amplitude being orbital dependent, which is denoted as orbital-selective pairing. In FeSCs, this may give rise to superconducting gaps with unexpectedly strong anisotropy as well as new type of pairing states that has no single-orbital counterpart; we will discuss how both types of effects play an important role in several iron pnictide and iron chalcogenide compounds [72, 143, 144].

3.1 Superconducting Pairing in the Multiorbital t-J Model

The bad metal behavior in the normal state implies strong electron correlations in FeSCs. In strongly correlated systems, the effective superconducting pairing has to avoid the penalty from the Coulomb repulsion. Even though the parent compound is not a MI, the superconducting phase in most cases is in proximity to an AFM phase. This suggests that the AFM exchange interaction plays a very important role for superconductivity. It has been shown theoretically that the AFM exchange interaction is enhanced in the bad metal ($0<Z\ll 1$) regimes near the Mott transition [145]. In a multiorbital correlated system, similar enhancement is anticipated when the system is close to an OSMP. We therefore proceed to study the superconducting pairing within the framework of a multiorbital t-J model, such that the orbital selectivity in the normal state is taken into account.

The effective Hamiltonian of the model has the following form [144].

$H_{\text{eff}}={\displaystyle \sum _{ij,\alpha \beta \sigma }\left(\sqrt{Z_{\alpha }{Z}_{\beta }}{t}_{ij}^{\alpha \beta }-{\tilde{\lambda }}_{\alpha }{\delta }_{\alpha \beta }\right)f_{i,\alpha ,\sigma }^{†}{f}_{j,\beta ,\sigma }-{\displaystyle \sum _{ij,\alpha \beta }{J}_{ij}^{\alpha \beta }{f}_{j,\beta ,\downarrow }^{†}{f}_{i,\alpha ,\uparrow }^{†}{f}_{i,\alpha ,\downarrow }{f}_{j,\beta ,\uparrow }}}.(16)$

Here, the bands are renormalized by the quasiparticle spectral weights $Z_{\alpha }$’s; as we described in the previous section, the orbital (α) dependence of this weight reflects the orbital selectivity in the normal state. In addition, ${\tilde{\lambda }}_{\alpha }$ is the effective energy level that takes into account the correlation effect (see Eq. 10); $J_{ij}^{\alpha \beta }$ refers to the orbital-dependent AFM exchange couplings, which can be obtained by integrating out the incoherent single-electron excitations via either the slave-rotor [145] or slave-spin [146] approach. It is generically a matrix in the orbital space. However, the interorbital interactions have been found to generate negligible interorbital pairing [143]. Thus, the most important terms to the pairing are the diagonal interactions in the $t_{2g}$ ($d_{xz},d_{yz},d_{xy}$) orbital subspace. We focus on these spin-exchange interactions between the nearest ($J_1^{\alpha }$) and next-nearest neighboring ($J_2^{\alpha }$) sites, where the index α enumerates the $d_{xz},d_{yz},d_{xy}$ orbitals. We further introduce two ratios to quantify the effects of magnetic frustration and orbital differentiation, respectively, $A_L=J_1/J_2$ and $A_O=J^{xy}/J^{xz/yz}$. In principle $A_L$ and $A_O$ can be determined from the procedure of integrating out high-energy incoherent states [145]. In practice we take them as model parameters, so that a comprehensive understanding on the pairing states can be gained.

To study the superconducting pairing, we decompose the interaction term in Eq. 16 in the pairing channel by introducing the pairing fields in the real space: ${\Delta }_e^{\alpha }=1/\mathcal{N}{\displaystyle {\sum }_i{f}_{i,\alpha ,\uparrow }{f}_{i+e,\alpha ,\downarrow }}$, where $\mathbf{e}\in \left\{e_x,e_y,e_{x+y},e_{x-y}\right\}$ refers to a unit vector connecting the nearest and next nearest neighboring sites. Transforming to the momentum space we obtain different pairing channels, each of which corresponds to linear combinations of several pairing fields in the real space. In general, the pairing function ${\text{Δ}}_{g,\alpha ,\mathbf{k}}={\Delta }_{g,\alpha \left({\tau }_i\right)}g\left(\mathbf{k}\right){\left({\tau }_i\right)}_{\alpha }$, where ${\text{Δ}}_{g,\alpha \left({\tau }_i\right)}$ is the pairing strength of a particular pairing channel. For the nondegenerate $d_{xy}$ orbital, the symmetry of the pairing state is fully determined by the form factor $g\left(\mathbf{k}\right)$, and the four channels are usually denoted as $s_{x^2+y^2}=\text{cos}{k}_x+\text{cos}{k}_y$, $d_{x^2-y^2}=\text{cos}{k}_x-\text{cos}{k}_y$, $s_{x^2{y}^2}=\text{cos}{k}_x\text{cos}{k}_y$, and $d_{xy}=\text{sin}{k}_x\text{sin}{k}_y$, respectively. In the tetragonal phase, the degeneracy of $d_{xz}$ and $d_{yz}$ orbitals introduces additional pairing channels, and it is necessary to use the $2\times 2$ Pauli matrices ${\tau }_i$ in the orbital isospin space to construct the various possibilities. The pairing channels can be classified according to the one-dimensional irreducible representations of the tetragonal $D_{4h}$ point group to be $A_{1g}$, $B_{1g}$, $A_{2g}$, and $B_{2g}$. Note that different channels may exhibit the same symmetry, by combining the structure in both the form factor and the orbital structure. For example, both the $d_{x^2-y^2}$ wave channel in the $d_{xy}$ orbital and the $s_{x^2{y}^2}{\tau }_3$ channel in the $d_{xz/yz}$ orbitals have the $B_{1g}$ symmetry.

3.2 Orbital-Selective Pairing in FeSCs

Since the discovery of FeSCs, the pairing symmetry of the superconducting state has been one of the most important questions. The s-wave $A_{1g}$ channel has played a particularly important role. In addition, various subleading—in some cases, nearly-degenerate—pairing channels with compatible symmetry can coexist.

The notion of orbital-selective pairing was introduced [72] in the multiorbital t-J model for electron-doped NaFeAs. With the intraorbital pairing amplitudes being dominant, this leads to a multigap structure, with different pairing components coming from different orbitals. Because the orbital composition varies along each pocket as shown in Figure 1B, this orbital-selective pairing can give rise to an anisotropic superconducting gap.

For simplicity, the exchange couplings have been assumed to be orbital independent in the calculation, and the pairing state has an $A_{1g}$ symmetry with a full gap along the Fermi surfaces. The different bandwidths and electron fillings of the $d_{xy}$ and $d_{xz/yz}$ orbitals still make the pairing to be orbital selective. As shown in Figure 5A, the pairing amplitude of the leading channel, the $s_{x^2{y}^2}$ channel in the $d_{xy}$ orbital, is much larger than those of the subleading channels in the $d_{xz/yz}$ orbitals. This orbital-selective pairing is reflected in an anisotropy of the superconducting gap along the electron pocket, as shown in Figure 5B. It turns out that the superconducting gap strongly depends on the magnetic frustration. For $J_1/J_2=0.8$ as illustrated in Figure 5C, the gap becomes almost isotropic. Here, several competing channels become active, which makes the overall contributions to the gap from the $d_{xz/yz}$ and $d_{xy}$ orbitals comparable. In experiments, an almost isotropic superconducting gap has been reported for the optimally electron doped NaFeAs, but the gap becomes strongly anisotropic along the electron pocket in the underdoped compound [147]. This behavior is understood by the strong orbital-selective pairing [72], which also splits into two the neutron resonance peak as a function of energy in the superconducting state [73, 148]. The orbital-selective pairing is also being explored in other FeSCs [149].

FIGURE 5

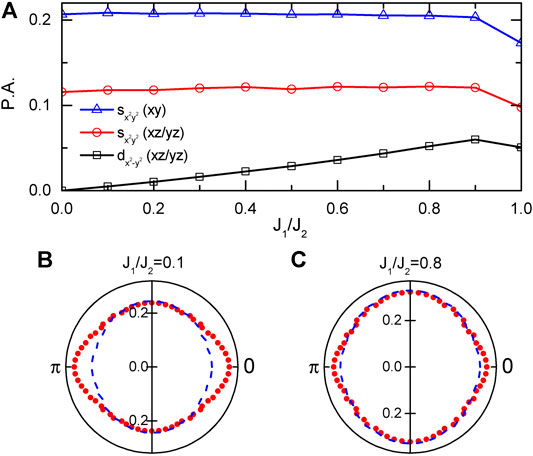
FIGURE 5. (A) Evolution of the leading pairing channels with $J_1/J_2$ in the multiorbital t-J model for electron doped NaFeAs. All the channels have the $A_{1g}$ symmetry. P.A. denotes pairing amplitude. (B), (C) Angular dependence of the superconducting gaps (red circles) along the electron pocket centered at $\left(\pi ,0\right)$ in the same model at $J_1/J_2=0.1$ [in (B)] and $J_1/J_2=0.8$ [in (C)], respectively. The blue dashed line is a fit to the single parameter gap function ${\text{Δ}}_0\text{cos}{k}_x\text{cos}{k}_y$. The deviation from this fit implies a multigap structure arising from the orbital-selective pairing, adapted from [72].

Besides the gap anisotropy, strong orbital selectivity may give rise to novel pairing states. In a multiorbital t-J model for the electron-doped alkaline iron chalcogenide compounds with only electron Fermi pockets, with orbital independent exchange couplings, the dominant pairing symmetry has been found to be either an s-wave $A_{1g}$ channel when $J_2$ is dominant or a d-wave $B_{1g}$ channel for dominant $J_1$ coupling [150, 151]. In the regime where the two types of pairing states are quasidegenerate, a novel orbital-selective pairing state, $s{\tau }_3$ pairing, with s-wave form factor but $B_{1g}$ symmetry in the $d_{xz/yz}$ orbital subspace can be stabilized as the leading pairing channel [143] (see Figure 6A). However, its nontrivial orbital structure makes it distinct from the other two pairing channels, and this successfully explains the unconventional superconductivity in alkaline iron chalcogenides [143]. It produces a full gap but the pairing function has a sign change between the two electron pockets, which causes a spin resonance around the wave vector $\left(\pi ,\pi /2\right)$, as shown in Figures 6B,C. These features are compatible with both the ARPES and neutron scattering measurements [152–156].

FIGURE 6

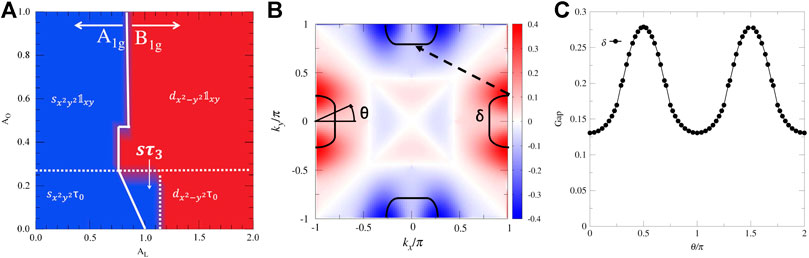
FIGURE 6. (A) Pairing phase diagram of the multiorbital t-J model for alkaline iron selenides. The blue shaded area corresponds to dominant pairing channels with an $s_{x^2{y}^2}$ form factor while the red shading covers those with a $d_{x^2-y^2}$ form factor. The continuous line separates regions where the pairing belongs to the $A_{1g}$ and the $B_{1g}$ representations, respectively. The orbital-selective $s{\tau }_3$ pairing occurs for $A_O<1$, $A_L$ near 1. (B) The Fermi surface (solid line) and the sign-change intraband pairing function of the corresponding band for the alkaline iron selenides. The dashed arrow indicates the $\mathbf{q}=\left(\pi ,\pi /2\right)$ wave-vector associated with the spin resonance found in experiment. (C) Superconducting gap along the electron pocket. In (B) and (C) the dominant $s{\tau }_3$ pairing state is stabilized with parameters $J_2=1.5$, $A_O=0.3$, and $A_L=0.9$, adapted from [143].

Importantly, the $s{\tau }_3$ pairing corresponds to an irreducible representation of the crystalline point group. Nonetheless, in the band basis, this multiorbital superconducting state has the form of a multiband $d+d$ pairing. The latter allows the state to contrast with the more familiar $d+id$ pairing in a way that the ³He-B superfluid state contrasts with ³He-A state [157]. This understanding elevates the $d+d$ pairing to the status of a natural multiorbital pairing state. We note in passing that an analogous $s{\tau }_3$ pairing has been constructed for the first unconventional superconductor CeCu₂ Si₂ [157], which provides a natural understanding of the recently discovered low-temperature behavior in this heavy fermion compound [158].

3.3 Orbital-Selective Pairing in the Nematic Phase of Iron Selenide

As we discussed in Section 2.4, recent STM measurements in the nematic phase of FeSe have uncovered not only a surprisingly large difference between the quasiparticle weights of the $d_{xz}$ and $d_{yz}$ orbitals, but also an unusually strong anisotropy of the superconducting gap [138, 139]. These experimental findings provide evidence for a strongly orbital-selective superconducting state.

Theoretically, the pairing structure in the nematic phase of FeSe has been investigated within the framework of the multiorbital t-J model in Eq. 16. The slave-spin calculation [142] produces $Z_{xz}:Z_{yz}:Z_{xy}=1:4:0.5$; an orbital-selective pairing was shown, with the leading pairing channel in the $d_{yz}$ orbital. Taking into account the mixed orbital character of both hole and electron pockets, such an orbital-selective pairing naturally leads to a large gap anisotropy as shown in Figure 7. This orbital-selective pairing not only provides the understanding of the experimental observations [133–135, 138], but also sheds new light on the interplay among the pairing state, Mott physics, and the nematic order, all of which appear to be important ingredients for the unconventional superconductivity in FeSCs. Experimentally, other signatures of orbital-selective superconductivity in nematic FeSC are also being explored [159].

FIGURE 7

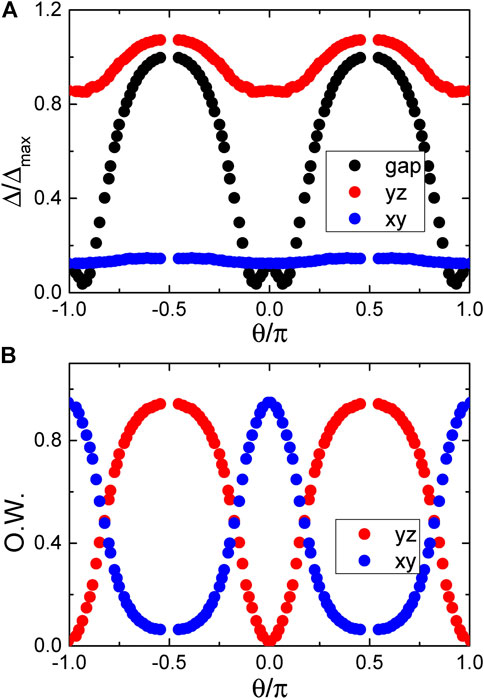
FIGURE 7. (A) Overall (blue symbols) and orbital resolved superconducting gaps along the M_x electron pocket. (B) Weight distributions of the $d_{xy}$ and $d_{yz}$ orbitals along the M_x electron pocket, adapted from [144].

4 Summary and Outlook

Since the discovery of superconductivity in FeSCs, clarifying the underlying microscopic physics of these materials has been the goal of extensive research, and considerable progress has been achieved. By now it has become abundantly clear that electron correlations play a key role. This includes both the Hubbard and Hund’s couplings, which combine to cause the normal state of the FeSCs to be a bad metal in proximity to a Mott transition. Theoretical studies on the pertinent microscopic models for the FeSCs not only confirm the existence of the bad metal in the phase diagram, but also reveal a strong orbital selectivity in this phase, which is anchored by an orbital-selective Mott phase. In this manuscript we have reviewed recent theoretical progress on the orbital selectivity. It has been found that the orbital selectivity not only is a universal property of the normal state of FeSCs, but also shows intriguing interplay with the nematicity. Equally important, it can strongly affect the superconducting states of the system.

It is worth reiterating that the FeSCs consist of a large family of materials, and superconductivity has been found over a broad range of tuning parameters, such as pressure and electron filling. For example, many electron-doped iron chalcogenides have a simpler Fermi surface, with only electron pockets, and the electron filling is $n\sim 6.1-6.2$. Even so, superconductivity is also discovered and, indeed, it is in this category of materials that the highest-$T_c$ FeSC belongs. Here, the strong orbital selectivity is shown to be universal in these systems and has been extensively studied.

Also of note is the case of extremely hole-doped iron pnictides, which likewise displays superconductivity. A prototype class of materials in this category is AFe₂As₂ (A = K, Rb, Cs), which contains hole pockets only, and the electron filling is at $n=5.5$. As illustrated in Figure 8, they are far from both the $n=6$ and $n=5$ MIs. Although the superconducting $T_c$ observed in these systems is much lower than that of the other iron-based systems, a number of recent experiments prompt the consideration of a completely different type of antiferromagnetism and nematicity [161–167], which are possibly associated with the Mott physics in the $n=5$ limit. In particular, the $d_{xy}$ orbital is shown to be closer to the Mott localization with reducing the total electron filling. Therefore, a systematic study on the evolution of orbital-selective correlations with doping from $n=6$ to $n=5$ would be important in clarifying the underlying physics and the connection to superconductivity in these heavily hole-doped materials.

FIGURE 8

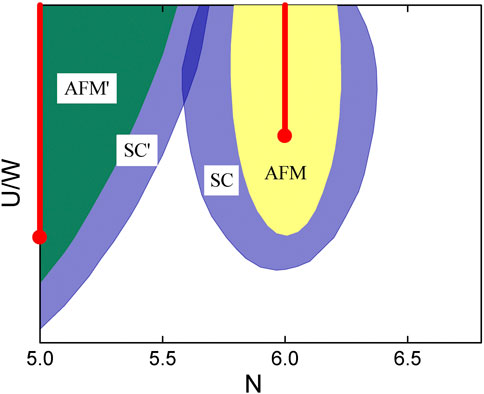
FIGURE 8. Schematic phase diagram as a function of $U/W$ (the ratio of the Coulomb interaction to bandwidth) and the electron filling $n$. Here the red lines denote the MIs at electron filling $n=6$ and $n=5$, respectively. AFM marks the $\left(\pi ,0\right)$ AFM order near the $n=6$ MI, while AFM′ represents the AFM order near the $n\to 5$ limit [64]. SC and SC′ denote two superconducting states near the two AFM phases, adapted from [160].

A topic of considerable recent interest in the area of FeSCs is the indication for a topologically nontrivial band structure and the possible Majorana zero mode in the superconducting iron chalcogenides [168]. This highlights the important role of spin-orbit coupling in these systems. Given the compelling evidence for the strongly orbital-selective correlations we have discussed here, it would be highly desirable to clarify how the interplay between the correlation effects and the spin-orbit coupling affects the topological properties of the electronic band structure. Such efforts promise to elucidate the extent to which the topological band structure develops in the various families of FeSCs.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

Work at Renmin University has been supported by the National Science Foundation of China, Grant number 11674392; the Ministry of Science and Technology of China, National Program on Key Research Project, Grant no. 2016YFA0300504; and the Fundamental Research Funds for the Central Universities and the Research Funds of Renmin University of China, Grant no. 18XNLG24. Work at Rice has been supported by the DOE BES Award, #DE-SC0018197, and the Robert A. Welch Foundation, Grant no. C-1411. Work at Los Alamos was carried out under the auspices of the U.S. Department of Energy (DOE) National Nuclear Security Administration under Contract no. 89233218CNA000001 and was supported by the LANL LDRD Program. Q.S. acknowledges the support of NSF Grant no. PHY-1607611 at the Aspen Center for Physics.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the late E. Abrahams, R. J. Birgeneau, P. C. Dai, W. Ding, P. Goswami, K. Jin, C. L. Liu, D. H. Lu, X. Y. Lu, P. Nikolic, Z.-X. Shen, Y. Song, M. Yi, and W. Yu for useful discussions. R.Y. acknowledges the hospitality of the T.D. Lee Institute.

References

1. Kamihara Y, Watanabe T, Hirano M, Hosono H. Iron-based layered superconductor La[OF_x]FeAs (x = 0.05−0.12) with = 26 K. J Am Chem Soc (2008) 130:3296. doi:10.1021/ja800073m

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Ren ZA, Wei L, Jie Y, Wei Y, Xiao-Li S, Zheng-Cai L, et al. Superconductivity at 55K in iron-based F-doped layered quaternary compound Sm[OF_x]FeAs. Chin Phys Lett (2008) 25:2215. doi:10.1088/0256-307X/25/6/080

Google Scholar

3. Wang C, Li L, Chi S, Zhu Z, Ren Z, Li Y, et al. Thorium-doping-induced superconductivity up to 56 K in GdTh_xFeAsO. EPL (2008) 83:67006. doi:10.1209/0295-5075/83/67006

CrossRef Full Text | Google Scholar

4. Wang Q-Y, Zhi L, Wen-Hao Z, Zuo-Cheng Z, Jin-Song Z, Wei L, et al. Interface-Induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO. Chin Phys Lett (2012) 29:037402. doi:10.1088/0256-307x/29/3/037402

CrossRef Full Text | Google Scholar

5. He S, He J, Zhang W, Zhao L, Liu D, Liu X, et al. Phase diagram and electronic indication of high-temperature superconductivity at 65 K in single-layer FeSe films. Nat Mater (2013) 12:605. doi:10.1038/nmat3648

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Lee JJ, Schmitt FT, Moore RG, Johnston S, Cui Y-T, Li W, et al. Interfacial mode coupling as the origin of the enhancement of T_c in FeSe films on SrTiO. Nature (2014) 515:245–8. doi:10.1038/nature13894

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zhang Z, Wang Y-H, Song Q, Liu C, Peng R, Moler KA, et al. Onset of the Meissner effect at 65 K in FeSe thin film grown on Nb-doped SrTiO₃ substrate. Sci Bull (2015) 60:1301–4. doi:10.1007/s11434-015-0842-8

CrossRef Full Text | Google Scholar

8. Ge J-F, Liu Z-L, Liu C, Gao C-L, Qian D, Xue Q-K, et al. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO. Nat Mater (2015) 14:285. doi:10.1038/nmat4153

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Johnston DC. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv Phys (2010) 59:803–1061. doi:10.1080/00018732.2010.513480

CrossRef Full Text | Google Scholar

10. Wang F, Lee D-H. The electron-pairing mechanism of iron-based superconductors. Science (2011) 332:200–4. doi:10.1126/science.1200182

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Dagotto E. Colloquium: the unexpected properties of alkali metal iron selenide superconductors. Rev Mod Phys (2013) 85:849. doi:10.1103/revmodphys.85.849

CrossRef Full Text | Google Scholar

12. Dai P. Antiferromagnetic order and spin dynamics in iron-based Superconductors. Rev Mod Phys (2015) 87:855–96. doi:10.1103/revmodphys.87.855

CrossRef Full Text | Google Scholar

13. Si Q, Yu R, Abrahams E High temperature superconductivity in iron pnictides and chalcogenides. Nat Rev Mater (2016) 1:16017. doi:10.1038/natrevmats.2016.17

CrossRef Full Text | Google Scholar

14. Hirschfeld PJ. Using gap symmetry and structure to reveal the pairing mechanism in Fe-based superconductors. Comptes Rendus Physique (2016) 17:197. doi:10.1016/j.crhy.2015.10.002

CrossRef Full Text | Google Scholar

15. Bednorz JG, Müller KA. Possible high superconductivity in the Ba-La-Cu-O system. Z Phys B- Condensed Matter (1986) 64:189. doi:10.1007/bf01303701

CrossRef Full Text | Google Scholar

16. de la Cruz C, Huang Q, Lynn JW, Li J, Ii WR, Zarestky JL, et al. Magnetic order close to superconductivity in the iron-based layered Lao1-xF x FeAs systems. Nature (2008) 453:899. doi:10.1038/nature07057

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Yi M., et al. Electronic structure of the BaFeAs family of iron pnictides. Phys Rev B (2009) 80:024515. doi:10.1103/PhysRevB.80.024515

Google Scholar

18. Si Q, Abrahams E. Strong correlations and magnetic frustration in the high iron pnictides. Phys Rev Lett (2008) 101:076401. doi:10.1103/physrevlett.101.076401

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Abrahams E, Si Q. Quantum criticality in the iron pnictides and chalcogenides. J Phys Condens Matter (2011) 23:223201. doi:10.1088/0953-8984/23/22/223201

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hussey NE, Takenaka K, Takagi H. Universality of the Mott-Ioffe-Regel limit in metals. Philoso Mag (2004) 84:2847. doi:10.1080/14786430410001716944

CrossRef Full Text | Google Scholar

21. Qazilbash MM, Hamlin JJ, Baumbach RE, Zhang L, Singh DJ, Maple MB, et al. Electronic correlations in the iron pnictides. Nat Phys (2009) 5:647. doi:10.1038/nphys1343

CrossRef Full Text | Google Scholar

22. Hu W Z, Dong Q, Li G, Li Z, Zheng P, Chen G F, Luo J L, Wang N L. Origin of the Spin Density Wave Instability in AFe₂As₂ (A=Ba,Sr) as Revealed by Optical Spectroscopy. Phys Rev Lett (2008) 101:257005. doi:10.1103/PhysRevLett.101.257005

PubMed Abstract

23. Yang J, Hüvonen D, Nagel U, Room T, Ni N, Canfield P C, Bud′ko P C, Carbotte J P, Timusk T, et al. Optical Spectroscopy of Superconducting Ba_0.55 K_0.45 Fe₂ As₂: Evidence for Strong Coupling to Low-Energy Bosons. Phys Rev Letters (2009) 102:187003. doi:10.1103/PhysRevLett.102.187003

PubMed Abstract

24. Boris AV, Kovaleva N N, Seo S S A, Kim J S, Popovich P, Matiks Y, Kremer R K, Keimer B. Signatures of Electronic Correlations in Optical Properties of LaFeAsO_1‐x F_x. Phy Rev Lett (2009) 102:027001. doi:10.1103/PhysRevLett.102.027001

PubMed Abstract

25. Degiorgi L. Measurement of Coherent Polarons in the Strongly Coupled Antiferromagnetically Ordered Iron-Chalcogenide Fe_1.02Te using Angle-Resolved Photoemission Spectroscopy. New J Phys (2011) 13:023011. doi:10.1088/1367-2630/13/2/023011

CrossRef Full Text | Google Scholar

26. Tamai A, Ganin AY, Emil Jerzy R, Bacsa J, Worawat M, Marco C, et al. Strong electron correlations in the normal state of the iron-based FeSeTe superconductor observed by angle-resolved photoemission spectroscopy. Phys Rev Lett (2010) 104:097002. doi:10.1103/physrevlett.104.097002

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Yi M, Lu DH, Morre RG, Kihou K, Lee CH, Lyo A, et al. Electronic reconstruction through the structural and magnetic transitions in detwinned NaFeAs. New J Phys (2012) 14:073019. doi:10.1088/1367-2630/14/7/073019

CrossRef Full Text | Google Scholar

28. Liu ZK., et al. Measurement of coherent polarons in the strongly coupled antiferromagnetically ordered iron-chalcogenide Fe_1.02Te using angle-resolved photoemission spectroscopy. Phys Rev Lett (2013) 110:037003. doi:10.1103/PhysRevLett.110.037003

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Yi M, Donghui L, Rong Y, Scott R, Jiun-Haw C, Bing L, et al. Observation of temperature-induced crossover to an orbital-selective Mott phase in A_xFe_2‐ySe₂ (A=K, Rb) superconductors. Phys Rev Lett (2013) 110:067003. doi:10.1103/physrevlett.110.067003

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yi M, Liu Z-K, Zhang Y, Yu R, Zhu J-X, Lee JJ, et al. Observation of universal strong orbital-dependent correlation effects in iron chalcogenides. Nat Commun (2015) 6:7777. doi:10.1038/ncomms8777

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Liu C, Lu X, Dai P, Yu R, Si Q. Anisotropic magnetic excitations of a frustrated bilinear-biquadratic spin model – implications for spin waves of detwinned iron pnictides. Phys Rev B (2020) 101:024510. doi:10.1103/physrevb.101.024510

CrossRef Full Text | Google Scholar

32. Liu M, Harriger LW, Luo H, Wang M, Ewings RA, Guidi T, et al. Nature of magnetic excitations in superconducting BaFe1.9Ni0.1As2. Nat Phys (2012) 8:376–81. doi:10.1038/nphys2268

CrossRef Full Text | Google Scholar

33. Gretarsson H, Lupascu A, Jungho K, Casa D, Gog T, Wu W, et al. Revealing the dual nature of magnetism in iron pnictides and iron chalcogenides using x-ray emission spectroscopy. Phys Rev B (2011) 84(R):100509. doi:10.1103/physrevb.84.100509

CrossRef Full Text | Google Scholar

34. Baum A, Ruiz HN, Lazarević N, Yao W, Böhm T, Hosseinian Ahangharnejhad R, et al. Frustrated spin order and stripe fluctuations in FeSe. Commun Phys (2019) 2:14. doi:10.1038/s42005-019-0107-y

CrossRef Full Text | Google Scholar

35. Si Q, Abrahams E, Dai J, Zhu J-X Correlation effects in the iron pnictides. New J Phys (2009) 11:045001. doi:10.1088/1367-2630/11/4/045001

CrossRef Full Text | Google Scholar

36. Dai J, Si Q, Zhu J-X, Abrahams E Iron pnictides as a new setting for quantum criticality. Proc Natl Acad Sci (2009) 106:4118–21. doi:10.1073/pnas.0900886106

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Laad MS, Craco L, Leoni&Rosner SH. Electrodynamic response of incoherent metals: normal phase of iron pnictides. Phys Rev B (2009) 79:024515. doi:10.1103/physrevb.79.024515

CrossRef Full Text | Google Scholar

38. Ishida H, Liebsch A. Fermi-liquid, non-Fermi-liquid, and Mott phases in iron pnictides and cuprates. Phys Rev B (2010) 81:054513. doi:10.1103/physrevb.81.054513

CrossRef Full Text | Google Scholar

39. Yin ZP, Haule K, Kotliar G. Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides. Nat Mater (2011) 10:932. doi:10.1038/nmat3120

PubMed Abstract | CrossRef Full Text | Google Scholar

40. de’Medici L, Giovannetti G, Capone M. Selective Mottness as a key to iron superconductors. Phys Rev Lett (2014) 112:177001.

PubMed AbstractGoogle Scholar

41. Seo K, Bernevig BA, Hu J. Pairing symmetry in a two-orbital exchange coupling model of oxypnictides. Phys Rev Lett (2008) 101:206404. doi:10.1103/physrevlett.101.206404

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Chen W-Q, Yang K-Y, Zhou Y, Zhang F-C. Strong coupling theory for superconducting iron pnictides. Phys Rev Lett (2009) 102:047006. doi:10.1103/physrevlett.102.047006

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Moreo A, Daghofer M, Riera JA, Dagotto E. Properties of a two-orbital model for oxypnictide superconductors: magnetic order, spin-singlet pairing channel, and its nodal structure. Phys Rev B (2009) 79:134502. doi:10.1103/physrevb.79.134502

CrossRef Full Text | Google Scholar

44. Bascones E, Valenzuela B, Calderón MJ. Orbital differentiation and the role of orbital ordering in the magnetic state of Fe superconductors. Phys Rev B (2012) 86:174508. doi:10.1103/physrevb.86.174508

CrossRef Full Text | Google Scholar

45. Berg E, Kivelson SA, Scalapino DJ. A twisted ladder: relating the Fe superconductors to the high- cuprates. New J Phys (2009) 11:085007. doi:10.1088/1367-2630/11/8/085007

CrossRef Full Text | Google Scholar

46. Lv W, Krüger F, Phillips P. Orbital ordering and unfrustrated (π,0) magnetism from degenerate double exchange in the iron pnictides. Phys Rev B (2010) 82:045125. doi:10.1103/physrevb.82.045125

CrossRef Full Text | Google Scholar

47. Fang C, Yao H, Tsai W-F, Hu JP, Kivelson SA. Theory of electron nematic order in LaFeAsO. Phys Rev B (2008) 77:224509. doi:10.1103/physrevb.77.224509

CrossRef Full Text | Google Scholar

48. Xu C, Müller M, Sachdev S. Ising and spin orders in the iron-based superconductors. Phys Rev B (2008) 78:(R):020501. doi:10.1103/physrevb.78.020501

CrossRef Full Text | Google Scholar

49. Fernandes RM, Chubukov AV, Schmalian J. What drives nematic order in iron-based superconductors? Nat Phys (2014) 10:97. doi:10.1038/nphys2877

CrossRef Full Text | Google Scholar

50. Ma F, Lu Z-Y, Xiang T. Antiferromagnetic superexchange interactions in LaOFeAs. Phys Rev B (2008) 78:224517. doi:10.1103/physrevb.78.224517

CrossRef Full Text | Google Scholar

51. Wysocki AL, Belashchenko KD, Antropov VP Consistent model of magnetism in ferropnictides. Nat Phys (2011) 7:485. doi:10.1038/nphys1933

CrossRef Full Text | Google Scholar

52. Uhrig GS, Holt M, Oitmaa J, Sushkov OP, Singh RRP. Pnictides as frustrated quantum antiferromagnets close to a quantum phase transition. Phys Rev B (2009) 79:092416. doi:10.1103/physrevb.79.092416

CrossRef Full Text | Google Scholar

53. Rodriguez JP, Rezayi EH. Low ordered magnetic moment by off-diagonal frustration in undoped parent compounds to iron-based high- superconductors. Phys Rev Lett (2009) 103:097204. doi:10.1103/physrevlett.103.097204

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Giavannetti G, Ortix C, Marsman M, Capone M, van den Brink J, Lorenzana J. Proximity of iron pnictide superconductors to a quantum tricritical point. Nat Commun (2011) 2:398. doi:10.1038/ncomms1407

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Arakawa N, Ogata M. Orbital-selective superconductivity and the effect of lattice distortion in iron-based superconductors. J Phys Soc Jpn (2011) 80:074704. doi:10.1143/jpsj.80.074704

CrossRef Full Text | Google Scholar

56. Liebsch A, Ishida H. Self-consistent determination of the interaction strength: Application to the iron arsenide superconductors. Phys Rev B (2010) 82:155106. doi:10.1103/physrevb.82.155106

CrossRef Full Text | Google Scholar

57. Si Q, Rabello S, Ingersent K, Smith JL. Locally critical quantum phase transitions in strongly correlated metals. Nature (2001) 413:804. doi:10.1038/35101507

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Coleman P, Pépin C, Si Q, Ramazashvili R. How do Fermi liquids get heavy and die? J Phys Condens Matter (2001) 13:R723. doi:10.1088/0953-8984/13/35/202

CrossRef Full Text | Google Scholar

59. Pépin C. Selective Mott transition and heavy fermions. Phys Rev B (2008) 77:245129. doi:10.1103/physrevb.77.245129

CrossRef Full Text | Google Scholar

60. Anisimov VI, Nekrasov IA, Kondakov DE, Rice TM, Sigrist M. Orbital-selective Mott-insulator transition in Ca Ca_2-xSr_xRuO₄. Eur Phys J B (2002) 25:191. doi:10.1140/epjb/e20020021

CrossRef Full Text | Google Scholar

61. Yu R, Si Q. Mott transition in multi-orbital models for iron pnictides’. Phys Rev B (2011) 84:235115. doi:10.1103/physrevb.84.235115

CrossRef Full Text | Google Scholar

62. Yu R, Si Q. Orbital-selective Mott phase in multiorbital models for alkaline iron selenides KFeSe. Phys Rev Lett (2013) 110:146402. doi:10.1103/physrevlett.110.146402

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Yu R, Si Q. Slave-spin theory and its application to Mott transition in a multiorbital model for iron pnictides. Phys Rev B (2012) 86:085104. doi:10.1103/physrevb.86.085104

CrossRef Full Text | Google Scholar

64. Yu R, Zhu J-X, Si Q. Orbital-dependent effects of electron correlations in microscopic models for iron-based superconductors. Curr Opin Solid State Mater Sci (2013) 17:65. doi:10.1016/j.cossms.2013.05.003

CrossRef Full Text | Google Scholar

65. Liu ZK, Ming Yi, Yan Z, Jin H, Rong Y, Jianxin Z, et al. Experimental observation of incoherent-coherent crossover and orbital-dependent band renormalization in iron chalcogenide superconductors. Phys Rev B (2015) 92:235138. doi:10.1103/physrevb.92.235138

CrossRef Full Text | Google Scholar

66. Yu R, Si Q. Orbital-selective Mott phase in multiorbital models for iron pnictides and chalcogenides. Phy Rev B (2017) 96:125110. doi:10.1103/physrevb.96.125110

CrossRef Full Text | Google Scholar

67. Komijani Y, Kotliar G. Analytical slave-spin mean-field approach to orbital selective Mott insulators. Phys Rev B (2017) 96:125111. doi:10.1103/physrevb.96.125111

CrossRef Full Text | Google Scholar

68. Aron C, Kotliar G. Analytic theory of Hund’s metals: a renormalization group perspective. Phys Rev B (2015) 91:041110. doi:10.1103/physrevb.91.041110

CrossRef Full Text | Google Scholar

69. Bascones E, Valenzuela B, Calderón MJ. Magnetic interactions in iron superconductors: a review. Comp Rend Phys (2017) 17:36. doi:10.1016/j.crhy.2015.05.004

CrossRef Full Text | Google Scholar

70. Huang J, Rong Y, Zhijun X, Jian-Xin Z, Qianni J, Meng W, et al. Low temperature emergence of an orbital-selective Mott phase in FeTe_1-xSe_x. arXiv:2010.13913.

Google Scholar

71. Lin H, Yu R, Zhu J-X, Si Q. Orbital-selective correlations and renormalized electronic structure in LiFeAs. arXiv:2101.05598.

Google Scholar

72. Yu R, Zhu J-X, Si Q. Orbital-selective superconductivity, gap anisotropy, and spin resonance excitations in a multiorbi--tal t model for iron pnictides. Phys Rev B (2014) 89:024509. doi:10.1103/physrevb.89.024509

CrossRef Full Text | Google Scholar

73. Zhang C, Rong Y, Yixi S, Yu S, Miaoyin W, Guotai T, et al. Double spin resonances and gap anisotropy in superconducting underdoped NaFeCoAs. Phys Rev Lett (2013) 111:207002. doi:10.1103/physrevlett.111.207002

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Yin ZP, Haule K, Kotliar G. Spin dynamics and orbital-antiphase pairing symmetry in iron-based superconductors. Nat Phys (2014) 10:845. doi:10.1038/nphys3116

CrossRef Full Text | Google Scholar

75. Ong T, Coleman P, Schmalian J. Concealed d-wave pairs in the s± condensate of iron-based superconductors. Proc Natl Acad Sci U.S.A. (2016) 113:5486. doi:10.1073/pnas.1523064113

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Dong J, Zhang HJ, Xu G, Li Z, Li G, Hu WZ, et al. Competing orders and spin-density-wave instability in La(O_1-xF_x)FeAs. Europhys Lett (2008) 83:27006. doi:10.1209/0295-5075/83/27006

CrossRef Full Text | Google Scholar

77. Kuroki K, Seiichiro O, Ryotaro A, Hidetomo U, Yukio T, Hiroshi K, et al. Unconventional pairing originating from the disconnected Fermi surfaces of superconducting LaFeAsOF_x. Phys Rev Lett (2008) 101:087004. doi:10.1103/physrevlett.101.087004

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Graser S, Maier TA, Hirschfeld PJ, Scalapino DJ. Near-degeneracy of several pairing channels in multiorbital models for the Fe pnictides. New J Phys (2009) 11:025016. doi:10.1088/1367-2630/11/2/025016

CrossRef Full Text | Google Scholar

79. Wang F, Zhai H, Ran Y, Vishwanath A, Lee D-H. Functional renormalization-group study of the pairing symmetry and pairing mechanism of the FeAs-based high-temperature superconductor. Phys Rev Lett (2009) 102:047005. doi:10.1103/physrevlett.102.047005

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Knolle J, Eremin I, Moessner R. Multiorbital spin susceptibility in a magnetically ordered state: orbital versus excitonic spin density wave scenario. Phys Rev B (2011) 83:224503. doi:10.1103/physrevb.83.224503

CrossRef Full Text | Google Scholar

81. Yi M, Zhang Y, Shen Z-X, Lu D Role of the orbital degree of freedom in iron-based superconductors. npj Quan Mater (2017) 2:57. doi:10.1038/s41535-017-0059-y

CrossRef Full Text | Google Scholar

82. Wang M, Ming Y, Huibo C, de la Cruz C, Mo SK, Huang QZ, et al. Mott localization in a pure stripe antiferromagnet. Phys Rev (2015) B92:121101. doi:10.1103/PhysRevB.92.121101

CrossRef Full Text | Google Scholar

83. Wang Q, Ming Y, Huibo C, de la Cruz C, Mo SK, Huang QZ, et al. Transition from sign-reversed to sign-preserved cooper-pairing symmetry in sulfur-doped iron selenide superconductors. Phys Rev Lett (2016) 116:197004. doi:10.1103/physrevlett.116.197004

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Yi M, Meng W, Kemper AF, Mo S-K, Hussain Z, Bourret-Courchesne E, et al. Bandwidth and electron correlation-tuned superconductivity in RbFe(SeS_z). Phys Rev Lett (2015) 115:256403. doi:10.1103/physrevlett.115.256403

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Niu XH, Chen S, Juan J, Ye Z, Yu T, Xu DF, et al. A unifying phase diagram with correlation-driven superconductor-to-insulator transition for the 122 series of iron chalcogenides. Phys Rev B (2016) 93:054516. doi:10.1103/physrevb.93.054516

CrossRef Full Text | Google Scholar

86. Song Y, Zahra Y, Chongde C, Yu L, Chenglin Z, Justin SC, et al. A Mott insulator continuously connected to iron pnictide superconductors. Nat Commun (2016) 7:13879. doi:10.1038/ncomms13879

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Iimura S, Matsuishi S, Hosono H. Heavy electron doping induced antiferromagnetic phase as the parent for the iron oxypnictide superconductor LaFeAsOH_x. Phys Rev B (2016) 94:024512. doi:10.1103/physrevb.94.024512

CrossRef Full Text | Google Scholar

88. Watson MD, Steffen B, Amir AH, Moritz H, Timur KK, Amalia IC, Roser V, et al. Formation of Hubbard-like bands as a fingerprint of strong electron-electron interactions in FeSe. Phys Rev B (2017) 95:081106. doi:10.1103/physrevb.95.081106

CrossRef Full Text | Google Scholar

89. Evtushinsky DV, Aichhorn M, Sassa Y, Liu Z-H, Maletz J, Wolf T, Yaresko AN, et al. Direct observation of dispersive lower Hubbard band in iron-based superconductor FeSe. arXiv preprint arXiv:1612.02313 (2016).

Google Scholar

90. Gerber S, Yang S-L, Zhu D, Soifer H, Sobota JA, Rebec S, et al. Femtosecond electron-phonon lock-in by photoemission and x-ray free-electron laser. Science (2017) 357:71. doi:10.1126/science.aak9946

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Lafuerza S, Gretarsson H, Hardy F, Wolf T, Meingast C, Giovannetti G, et al. Evidence of Mott physics in iron pnictides from x-ray spectroscopy. Phys Rev B (2017) 96:045133. doi:10.1103/physrevb.96.045133

CrossRef Full Text | Google Scholar

92. Miao H, Brito WH, Yin ZP, Zhong RD, Gu GD, Johnson PD, et al. Universal 2Δ_max/k_BT_c scaling decoupled from the electronic coherence in iron-based superconductors. Phys Rev B (2018) 98:020502. doi:10.1103/physrevb.98.020502

CrossRef Full Text | Google Scholar

93. Song Y, Cao H, Chakoumakos BC, Zhao Y, Wang A, Lei H, et al. Intertwined magnetic and nematic orders in semiconducting KFe_0.8Ag_1.2Te₂. Phys Rev Lett (2019) 122:087201. doi:10.1103/physrevlett.122.087201

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Song Y, Yuan D, Lu X, Xu Z, Bourret-Courchesne E, Birgeneau RJ, et al. Strain-Induced spin-nematic state and nematic susceptibility arising from Fe clusters in KFe_0.8Ag_1.2Te₂. Phys Rev Lett (2019) 123:247205. doi:10.1103/physrevlett.123.247205

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Hu Y, Yu X, Yi-Min Z, Qing-Yan W, Shao-Long H, De-Fa L, et al. Insulating parent phase and distinct doping evolution to superconductivity in single-layer FeSe/SrTiO₃ films. arXiv preprint arXiv:1904.04662 (2019).

Google Scholar

96. Patel N, Nocera A, Alvarez G, Moreo A, Johnston S, Dagotto E. Fingerprints of an orbital-selective Mott phase in the block magnetic state of BaFe Se ladders. Commun Phys (2019) 2:1. doi:10.1038/s42005-019-0155-3

CrossRef Full Text | Google Scholar

97. Ruiz H, Wang Y, Moritz B, Baum A, Hackl R, Devereaux TP. Frustrated magnetism from local moments in FeSe. Phys Rev B (2019) 99:125130. doi:10.1103/physrevb.99.125130

CrossRef Full Text | Google Scholar

98. Hiraishi M, Kojima KM, Okabe H, Takeshita S, Koda A, Kadono R, et al. Magnetism driven by strong electronic correlation in the heavily carrier-doped iron oxypnictide LaFeAsOH (2004):11547. arXiv:2004.11547.

Google Scholar

99. Ikeda H, Arita R, Kuneš J. Phase diagram and gap anisotropy in iron-pnictide superconductors. Phys Rev B (2010) 81:054502. doi:10.1103/physrevb.81.054502

CrossRef Full Text | Google Scholar

100. Kreisel A, Andersen BM, Sprau PO, Kostin A, Davis JCS, Hirschfeld PJ. Orbital selective pairing and gap structures of iron-based superconductors. Phys Rev B (2017) 95:174504. doi:10.1103/physrevb.95.174504

CrossRef Full Text | Google Scholar

101. Benfatto L, Valenzuela B, Fanfarillo L. Nematic pairing from orbital-selective spin fluctuations in FeSe. npj Quan Mater (2018) 3:56. doi:10.1038/s41535-018-0129-9

CrossRef Full Text | Google Scholar

102. Raghu S, Qi X-L, Liu C-X, Scalapino DJ, Zhang S-C. Minimal two-band model of the superconducting iron oxypnictides. Phys Rev B (2008) 77(R):220503. doi:10.1103/physrevb.77.220503

CrossRef Full Text | Google Scholar

103. Lee P-A, Wen X-G. Spin-triplet p-wave pairing in a three-orbital model for iron pnictide superconductors. Phys Rev B (2008) 78:144517. doi:10.1103/physrevb.78.144517

CrossRef Full Text | Google Scholar

104. Yu R, Trinh KT, Moreo A, Daghofer M, Riera JA, Haas S, et al. Magnetic and metallic state at intermediate Hubbard U coupling in multiorbital models for undoped iron pnictides. Phys Rev B (2009) 79:104510. doi:10.1103/physrevb.79.104510

CrossRef Full Text | Google Scholar

105. Daghofer M, Nicholson A, Moreo A, Dagotto E. Three orbital model for the iron-based superconductors. Phys Rev B (2010) 81:014511. doi:10.1103/physrevb.81.014511

CrossRef Full Text | Google Scholar

106. Graser S, Kemper AF, Maier TA, Cheng H-P, Hirschfeld PJ, Scalapino DJ. Spin fluctuations and superconductivity in a three-dimensional tight-binding model for BaFe₂As₂. Phys Rev B (2010) 81:214503. doi:10.1103/physrevb.81.214503

CrossRef Full Text | Google Scholar

107. Castellani C, Natoli CR, Ranninger J. Magnetic structure of V₂O₃ in the insulating phase. Phys Rev B (1978) 18:4945. doi:10.1103/physrevb.18.4945

CrossRef Full Text | Google Scholar

108. Barnes SE New method for the Anderson model. J Phys F: Met Phys (1976) 6:1375. doi:10.1088/0305-4608/6/7/018

CrossRef Full Text | Google Scholar

109. Coleman P. New approach to the mixed-valence problem. Phys Rev B (1984) 29:3035. doi:10.1103/physrevb.29.3035

CrossRef Full Text | Google Scholar

110. Read N, Newns DM. On the solution of the Coqblin-Schreiffer Hamiltonian by the large-N expansion technique. J Phys C: Solid State Phys (1983) 16:3273. doi:10.1088/0022-3719/16/17/014

CrossRef Full Text | Google Scholar

111. Kotliar G, Ruckenstein AE. New functional integral approach to strongly correlated Fermi systems: the gutzwiller approximation as a saddle point. Phys Rev Lett (1986) 57:1362. doi:10.1103/physrevlett.57.1362

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Florens S, Georges A. Slave-rotor mean-field theories of strongly correlated systems and the Mott transition in finite dimensions. Phys Rev B (2004) 70:035114. doi:10.1103/physrevb.70.035114

CrossRef Full Text | Google Scholar

113. de’Medici L, Georges A, Biermann S. Orbital-selective Mott transition in multiband systems: slave-spin representation and dynamical mean-field theory. Phys Rev B (2005) 72:205124.

Google Scholar

114. Hassan SR, de’Medici L. Slave spin cluster mean field theory away from half-filling: application to the Hubbard and the extended Hubbard Model. Phys Rev B (2010) 81:035106. doi:10.1103/physrevb.81.035106

CrossRef Full Text | Google Scholar

115. Rüegg A, Huber SD, Sigrist M. -slave-spin theory for strongly correlated fermions. Phys Rev B (2010) 81:155118. doi:10.1103/physrevb.81.155118

CrossRef Full Text | Google Scholar

116. Nandkishore R, Metlitski MA, Senthil T Orthogonal metals: the simplest non-Fermi liquids. Phys Rev B (2012) 86:045128. doi:10.1103/physrevb.86.045128

CrossRef Full Text | Google Scholar

117. Yin Z, Haule K, Kotliar G. Fractional power-law behavior and its origin in iron-chalcogenide and ruthenatesuperconductors: insights from first-principles calculations. Phys Rev B (2012) 86:195141. doi:10.1103/physrevb.86.195141

CrossRef Full Text | Google Scholar

118. Rincon J, Moreo A, Alvarez G, Dagotto E. Exotic magnetic order in the orbital-selective Mott regime of multiorbital systems. Phys Rev Lett (2014) 112:106405. doi:10.1103/physrevlett.112.106405

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Backes S, Jeschke HO, Valenti R. Microscopic nature of correlations in multiorbital AFe₂As₂ (A = K, Rb, Cs): Hund’s coupling. Phys Rev B (2015) 92:195128. doi:10.1103/physrevb.92.195128

CrossRef Full Text | Google Scholar

120. Lanatà N, Strand HUR, Giovannetti G, Hellsing B, de’ Medici L, Capone M Orbital Selectivity in Hund’s metals: The Iron Chalcogenides. Phys Rev B (2013) 87:045122. doi:10.1103/physrevb.87.045122

CrossRef Full Text | Google Scholar

121. Miao H, Yin ZP, Wu SF, Li JM, Ma J, Lv B-Q, et al. Orbital-differentiated coherence-incoherence crossover identified by photoemission spectroscopy in LiFeAs. Phys Rev B (2016) 94:201109. doi:10.1103/physrevb.94.201109

CrossRef Full Text | Google Scholar

122. Wang Z, Schmidt M, Fischer J, Tsurkan V, Greger M, Vollhardt D, et al. Orbital-selective metal-insulator transition and gap formation above in superconducting Rb(1-x)Fe(2-y)Se. Nat Commun (2014) 5:3202. doi:10.1038/ncomms4202

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Ding X, Pan Y, Yang H, Wen H-H. Strong and nonmonotonic temperature dependence of Hall coefficient in superconducting K_xFeSe single crystals. Phys Rev B (2014) 89:224515. doi:10.1103/physrevb.89.224515

CrossRef Full Text | Google Scholar

124. Li W, Chun-Feng Z, Sheng-hua L, Ding X, Xuewei W, Xiaoyong W, et al. Mott behaviour in K_xFeSe superconductors studied by pump-probe spectroscopy. Phys Rev B (2014) 89:134515. doi:10.1103/physrevb.89.134515

CrossRef Full Text | Google Scholar

125. Gao P, Rong Y, Liling S, Hangdong W, Zhen W, Qi W, et al. Role of the 245 phase in alkaline iron selenide superconductors revealed by high-pressure studies. Phys Rev B (2014) 89:094514. doi:10.1103/physrevb.89.094514

CrossRef Full Text | Google Scholar

126. Chen QY, Luo XB, Xie DH, Li ML, Ji XY, Zhou R, et al. Orbital-selective Kondo entanglement and antiferromagnetic order in USb. Phys Rev Lett (2019) 123:106402. doi:10.1103/physrevlett.123.106402

PubMed Abstract | CrossRef Full Text | Google Scholar

127. Giannakis I, Justin L, Mariam K, Sheng R, Chang-Jong K, Shanta RS, et al. Orbital-selective Kondo lattice and enigmatic f-electrons emerging from inside the antiferromagnetic phase of a heavy fermion. Sci Adv (2019) 5:eaaw9061. doi:10.1126/sciadv.aaw9061

PubMed Abstract | CrossRef Full Text | Google Scholar

128. Yu R, Si Q. Antiferroquadrupolar and Ising-nematic orders of a frustrated bilinear-biquadratic Heisenberg model and implications for the magnetism of FeSe. Phys Rev Lett (2015) 115:116401. doi:10.1103/physrevlett.115.116401

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Wang F, Kivelson SA, Lee D-H. Nematicity and quantum paramagnetism in FeSe. Nat Phys (2015) 11:959. doi:10.1038/nphys3456

CrossRef Full Text | Google Scholar

130. Watson MD, Yi M, Liu ZK, Li W, Lee JJ, Moore RG, et al. Emergence of the nematic electronic state in FeSe. Phys Rev B (2015) 91:155106. doi:10.1103/physrevb.91.199905

CrossRef Full Text | Google Scholar

131. Watson MD, Kim TK, Rhodes LC, Eschrig M, Hoesch M, Haghighirad AA, et al. Evidence for unidirectional nematic bond ordering in FeSe. Phys Rev B (2016) 94:201107. doi:10.1103/physrevb.94.201107

CrossRef Full Text | Google Scholar

132. Zhang Y, Yi M, Liu ZK, Li W, Lee JJ, Moore RG, et al. Distinctive orbital anisotropy observed in the nematic state of a FeSe thin film. Phys Rev B (2016) 94:115153. doi:10.1103/physrevb.94.115153

CrossRef Full Text | Google Scholar

133. Liu D, Cong L, Jianwei H, Bin L, Le W, Xianxin W, et al. Orbital origin of extremely anisotropic superconducting gap in nematic phase of FeSe superconductor. Phys Rev X (2018) 8:031033. doi:10.1103/physrevx.8.031033

CrossRef Full Text | Google Scholar

134. Rhodes LC, Watson MD, Haghighirad AA, Evtushinsky DV, Eschrig M, Kim TK Scaling of the superconducting gap with orbital character in FeSe. Phys Rev B (2018) 98:180503. doi:10.1103/physrevb.98.180503

CrossRef Full Text | Google Scholar

135. Kushnirenko YS, Fedorov AV, Haubold E, Thirupathaiah S, Wolf T, Aswartham S, et al. Three-dimensional superconducting gap in FeSe from angle-resolved photoemission spectroscopy. Phys Rev B (2018) 97:180501. doi:10.1103/physrevb.97.180501

CrossRef Full Text | Google Scholar

136. Yi M, Heike P, Yan Z, Yu H, Han W, Tong C, Zirong Y, et al. Nematic energy scale and the missing electron pocket in FeSe. Phys Rev X (2019) 9:041049. doi:10.1103/physrevx.9.041049

CrossRef Full Text | Google Scholar

137. Huh S, Jeongjin S, Beomseo K, Soohyun C, Jongkeun J, Sunghun K, et al. Lifted electron pocket and reversed orbital occupancy imbalance in FeSe. Commun Phys (2020) 3:52. doi:10.1038/s42005-020-0319-1

CrossRef Full Text | Google Scholar

138. Sprau PO, Kostin A, Kreisel A, Böhmer AE, Taufour V, Canfield PC, et al. Discovery of orbital-selective Cooper pairing in FeSe. Science (2017) 357:75. doi:10.1126/science.aal1575

PubMed Abstract | CrossRef Full Text | Google Scholar

139. Kostin A, Sprau PO, Kreisel A, Chong YX, Böhmer AE, Canfield PC, et al. Imaging orbital-selective quasiparticles in the Hund's metal state of FeSe. Nat Mater (2018) 17:869. doi:10.1038/s41563-018-0151-0

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Fanfarillo L, Giovannetti G, Capone M, Bascones E. Nematicity at the Hund’s metal crossover in iron superconductors. Phys Rev B (2017) 95:144511. doi:10.1103/physrevb.95.144511

CrossRef Full Text | Google Scholar

141. Su Y, Liao H, Li T. The form and origin of orbital ordering in the electronic nematic phase of iron-based superconductors. J Phys Condens Matter (2015) 27:105702. doi:10.1088/0953-8984/27/10/105702

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Yu R, Zhu J-X, Si Q. Orbital selectivity enhanced by nematic order in FeSe. Phys Rev Lett (2018) 121:227003. doi:10.1103/physrevlett.121.227003

PubMed Abstract | CrossRef Full Text | Google Scholar

143. Nica EM, Yu R, Si Q. Orbital selective pairing and superconductivity in iron selenides. Npj Quant Mater (2017) 2:24. doi:10.1038/s41535-017-0027-6

CrossRef Full Text | Google Scholar

144. Hu H, Yu R, Nica EM, Zhu J-X, Si Q. Orbital-selective superconductivity in the nematic phase of FeSe. Phys Rev B (2018) 98(R):220503. doi:10.1103/physrevb.98.220503

CrossRef Full Text | Google Scholar

145. Ding W, Yu R, Si Q, Abrahams E. Effective exchange interactions for bad metals and implications for iron-based superconductors. Phys Rev B (2019) 100:235113. doi:10.1103/physrevb.100.235113

CrossRef Full Text | Google Scholar

146. Ding W, Yu R Dynamical expansion of the doped hubbard model. arXiv:1906.12071.

Google Scholar

147. Ge Q, Ye ZR, Xu M, Zhang Y, Jiang J, Xie BP, et al. Anisotropic but nodeless superconducting gap in the presence of spin-density wave in iron-pnictide superconductor NaFeCo_xAs. Phys Rev X (2013) 3:011020. doi:10.1103/physrevx.3.011020

CrossRef Full Text | Google Scholar

148. Zhang C, Park JT, Xingye L, Rong Y, Yu L, Wenliang Z, et al. Neutron spin resonance as a probe of superconducting gap anisotropy in partially detwinned electron underdoped NaFeCoAs. Phys Rev B (2015) 91:104520. doi:10.1103/physrevb.91.104520

CrossRef Full Text | Google Scholar

149. Tian L, Liu P, Xu Z, Li Y, Lu Z, Walker HC, et al. Spin fluctuation anisotropy as a probe of orbital-selective hole-electron quasiparticle excitations in detwinned Ba(FeCo_x)As. Phys Rev B (2019) 100:134509. doi:10.1103/physrevb.100.134509

CrossRef Full Text | Google Scholar

150. Goswami P, Nikolic P, Si Q. Superconductivity in multi-orbital t-J 1 -J 2 model and its implications for iron pnictides. Epl (2010) 91:37006. doi:10.1209/0295-5075/91/37006

CrossRef Full Text | Google Scholar

151. Yu R, Goswami P, SiNikolic QP, Zhu J-X. Superconductivity at the border of electron localization and itinerancy. Nat Commun (2013) 4:2783. doi:10.1038/ncomms3783

PubMed Abstract | CrossRef Full Text | Google Scholar

152. Mou D, Shanyu L, Xiaowen J, Junfeng H, Yingying P, Lin Z, et al. Distinct Fermi surface topology and nodeless superconducting gap in a (TlRb)FeSe superconductor. Phys Rev Lett (2011) 106:107001. doi:10.1103/physrevlett.106.107001

PubMed Abstract | CrossRef Full Text | Google Scholar

153. Wang X-P, Qian T, Richard P, Zhang P, Dong J, Wang H-D, et al. Strong nodeless pairing on separate electron Fermi surface sheets in (Tl, K)Fe 1.78 Se 2 probed by ARPES. Epl (2011) 93:57001. doi:10.1209/0295-5075/93/57001

CrossRef Full Text | Google Scholar

154. Wang X-P, Richard P, Shi X, Roekeghem A, Huang Y-B, Razzoli E, et al. Observation of an isotropic superconducting gap at the Brillouin zone centre of Tl 0.63 K 0.37 Fe 1.78 Se 2. Epl (2012) 99:67001. doi:10.1209/0295-5075/99/67001

CrossRef Full Text | Google Scholar

155. Park JT, Friemel G, Yuan L, Kim J-H, Tsurkan V, Deisenhofe J, et al. Magnetic resonant mode in the low-energy spin-excitation spectrum of superconducting RbFeSe single crystals. Phys Rev Lett (2011) 107:177005. doi:10.1103/physrevlett.107.177005

PubMed Abstract | CrossRef Full Text | Google Scholar

156. Friemel G, Park JT, Maier TA, Tsurkan V, Yuan L, Deisenhofer J, et al. Reciprocal-space structure and dispersion of the magnetic resonant mode in the superconducting phase of Rb_xFeSe single crystals. Phys Rev B (2012) 85(R):140511. doi:10.1103/physrevb.85.140511

CrossRef Full Text | Google Scholar

157. Nica EM, Si Q. Multiorbital singlet pairing and d+d superconductivity. Npj Quant Mater (2021) 6:3. doi:10.1038/s41535-020-00304-3

Google Scholar

158. Pang G, Smidman M, Zhang J, Jiao L, Weng Z, Nica EM, et al. Fully gapped d-wave superconductivity in CeCu2Si2. Proc Natl Acad Sci USA (2018) 115:5343–7. doi:10.1073/pnas.1720291115

PubMed Abstract | CrossRef Full Text | Google Scholar

159. Chen T, Chen Y, Kreisel A, Lu X, Schneidewind A, Qiu Y, et al. Anisotropic spin fluctuations in detwinned FeSe. Nat Mater (2019) 18:709. doi:10.1038/s41563-019-0369-5

PubMed Abstract | CrossRef Full Text | Google Scholar

160. Wang Y, Hu W, Yu R, Si Q. Broken mirror symmetry, incommensurate spin correlations, and nematic order in iron pnictides. Phys Rev B (2019) 100(R):100502. doi:10.1103/physrevb.100.100502

CrossRef Full Text | Google Scholar

161. Liu X, Tao R, Ren M, Chen W, Yao Q, Wolf T, et al. Evidence of nematic order and nodal superconducting gap along [110] direction in RbFeAs. Nat Commun (2019) 10:1039. doi:10.1038/s41467-019-08962-z

PubMed Abstract | CrossRef Full Text | Google Scholar

162. Ishida K, Tsujii M, Hosoi S, Mizukami Y, Ishida S, Iyo A, et al. Novel electronic nematicity in heavily hole-doped iron pnictide superconductors. Proc Natl Acad Sci USA (2020) 117:6424. doi:10.1073/pnas.1909172117

PubMed Abstract | CrossRef Full Text | Google Scholar

163. Wang PS, Zhou P, Dai J, Zhang J, Ding XX, Lin H, et al. Nearly critical spin and charge fluctuations in KFeAs observed by high-pressure NMR. Phys Rev (2016) B93:085129. doi:10.1103/PhysRevB.93.085129

CrossRef Full Text | Google Scholar

164. Li J, Zhao D, Wu YP, Li SJ, Song DW, Zheng LX, Wang NZ, et al. Reemergeing electronic nematicity in heavily hole-doped Fe-based superconductors (2016). arXiv:1611.04694.

Google Scholar

165. Horigane K, Kihou K, Fujita K, Kajimoto R, Ikeuchi K, Ji S, et al. Spin excitations in hole-overdoped iron-based superconductors. Sci Rep (2016) 6:33303. doi:10.1038/srep33303

PubMed Abstract | CrossRef Full Text | Google Scholar

166. Eilers F, Grube K, Zocco DA, Wolf T, Merz M, Schweiss P, et al. Strain-driven approach to quantum criticality in A FeAs with A=K, Rb, and Cs. Phys Rev Lett (2016) 116:237003. doi:10.1103/physrevlett.116.237003

PubMed Abstract | CrossRef Full Text | Google Scholar

167. Wiecki P, Haghighirad A-A, Weber F, Merz M, Heid R, Böhmer AE, et al. Dominant in-plane symmetric elastoresistance in CsFe₂As₂. Phys Rev Lett (2020) 125:187001. doi:10.1103/physrevlett.125.187001

PubMed Abstract | CrossRef Full Text | Google Scholar

168. Zhang P, Yaji K, Hashimoto T, Ota Y, Kondo T, Okazaki K, et al. Observation of topological superconductivity on the surface of an iron-based superconductor. Science (2018) 360:182. doi:10.1126/science.aan4596

PubMed Abstract | CrossRef Full Text | Google Scholar