Quantum Interference Effects in Quantum Dot Molecular With Majorana Bound States

Non-invasive detection of the Majorana bound state (MBSs), a kind of quasiparticle without charge and mass, is one of the core issues in current condensed matter physics. Here we study in theory the quantum interference effect in parallel-coupled double quantum dots which are connected either by Majorana bound states (MBSs) or regular fermions. We find that the zero-energy conductance develops a sharp peak when the dots are connected by the MBSs, whereas that in the case of the dots are coupled via regular fermions shows a valley. By varying the coupling strength between the dots and the electron reservoirs, the conductance in the two structures changes in different ways. By comparing the properties of the linear conductance in the two systems, the information of the MBSs formed at the two ends of a topological superconductor nanowire then can be inferred. We also find that the MBSs in the present structure also induces the Fano effect, and is favorable in quantum information processing.

Introduction

In recent years, the preparation and detection of the exotic self-conjugate Majorana fermions have been extensively studied both experimentally and theoretically [1–3]. In solid platforms, they are realized in the form of zero-energy Majorana bound states (MBSs), and are promising in fault-tolerant quantum computing over the last two decades because of their non-Abelian statistics and robustness against decoherence [4, 5]. Up to now, MBSs have been prepared in various setups, in which the simplest and the most frequently studied one is perhaps the topological superconducting nanowires (TSNW). It involves the use of a nanowire having strong spin-orbit interactions under a uniform magnetic field in the proximity of an s-wave superconductor [5–7]. The magnetic field breaks the time-reversal symmetry in the TSNW and produces spinless electrons with p-wave superconducting pairing [5–7]. With the rapid developments of the nano-fabrications, the MBSs have also be successfully prepared in semiconducting nanowires [8, 9], magnetic atom chains [10], and planar Josephson junctions [11, 12].

The detection of the MBSs is quite challenging due to its charge neutrality and massless nature. One of the current strong evidence of the existence of MBSs is the zero-bias anomaly of the conductance peak in tunnel-spectroscopy experiments [7, 11], which means that under the condition zero bias, the conductance develops a peak other than the usual zero value. The zero-bias anomaly of the conductance arises from the hybridization between the quantum dot and the Majorana bound state, and then can be used for deducing the existence of the latter. However, such a phenomenon can also arise from some other mechanisms, such as the Kondo effect [13–15]. The Josephson effect has also been extensively investigated due to its phase-sensitive nature as the MBSs in a Josephson junction enable a nontrivial Josephson current having 4π periodicity in the Josephson phase [1, 11, 12]. This is quite different from the Josephson current with 2π periodicity in the usual junctions. Meanwhile, there were also some proposes of hybridizing a quantum dot (QD) to one end of a TSNW [16–20] in that the information of the MBSs will “leak” into the QD and then can be detected by spectroscopy transport measurements in a non-invasive way [21, 22]. Some other proposals such as the thermoelectric effect [23] and optical schemes [24, 25] based on QDs were also put forward. For example in Ref. 24, they argued that the MBSs will absorb and emit photons leading photon-assisted side band peaks. Such processes result in non-zero MBSs mode and then indicate a novel detection scheme for MBSs. The height of the photon-induced side band peaks is proportional to the magnitude of the photon field, and the time-dependent conductance is negative for a certain period of time in the presence of the MBSs [24].

Electronic transport through QD structures has been an active research subject during the past several decades [26, 27]. Due to the confinement of electrons in both the three directions, QD is characterized by the quantized energy levels, and is usually called ‘‘artificial atoms’’ [26]. Coherence of electrons tunneling through QD is greatly preserved, which has been demonstrated in phenomena such as the Aharonov-Bohm oscillations in closed ring-shape geometries [28], the subtle Kondo effect in QD connected to leads [13, 14, 29], and Fano resonances in systems with multiple channels [26–29]. In fact, two or more QDs coupled to each other will form an ‘‘artificial molecule’’ and result in the formation of bonding and antibonding states that are interesting in potential applications in quantum computing devices [26–29]. A lot of research works then have been carried out on the quantum interference effects in diverse parallel and T-shaped setups. In the systems of hybridized QD-TSNW, there is usually more than one electron transport channels and the quantum interference effect is an efficient mean to detect the existence of the MBSs formed at the ends of the TSNW [30–35]. For example, it was shown that when the MBSs is coupled to the QD in multiple channel systems, antiresonance in the conductance emerges and its location depends on the direct hybridization between the MBSs [32, 33]. If the coupling strengths between the QD and the two modes of the MBSs are the same, the Fano effect is induced as the Fano lineshape in the conductance or spectrum function [35]. Such interesting results may provide new information for the detection of the MBSs or find practical applications in design of high-efficiency quantum devices.

In the present paper, we study Fano effect in parallel double QDs in the presence of MBSs. We consider the cases of the two dots are simultaneously coupled to the left and right leads with different strengths, and to each other by the TNSW hosting MBSs (QD-MBSs). Our numerical results show that the zero-energy conductance is sensitive to the dot-lead coupling. We also compare the results in our QD-MBSs structure with those in the QDs connected to each other by the usual tunnel junction or regular fermions (another QD), and show that the central (zero-energy) peak in the two cases undergoes a peak to valley evolution, which can be used for detecting the MBSs.

Model and Methods

The schematic plot of the present structure is shown in Figure 1, in which two QDs are simultaneously coupled to the left and right leads with different coupling strengths, and connected to each other by a TNSW with MBSs. The Hamiltonian can be written as the following form Refs. 36–40,

$H={\displaystyle \sum _{k\alpha }{\epsilon }_{k\alpha }{\epsilon }_{k\alpha }^{†}{\epsilon }_{k\alpha }}+{\displaystyle \sum _{i=\mathrm{1,2}}{\epsilon }_i{d}_i^{†}{d}_i}+t_c\left(d_1^{†}{d}_2+h.c\right)+{\displaystyle \sum _{k\alpha i}\left(V_{k\alpha i}{d}_i^{†}{c}_{k\alpha }+h.c.\right)}+H_{MBSs},(1)$

where the creation (annihilation) operator $c_{k\alpha }^{†}\left(c_{k\alpha }\right)$ is for electrons having wave vector k, energy ${\epsilon }_{k\alpha }$ in the αth $\left(\alpha =L/R\right)$ normal metal lead. The second term in the right side of Eq. 1 is for electrons on the two QDs with energy level ε_iwith creation (annihilation) operator $d_i^{†}\left(d_i\right)$. The third term in the right side of Eq. 1 stands for possible hopping between the two QDs through a tunnel barrier with strength t_c. The forth term in the right side of Eq. 1corresponds to tunneling between the QDs and the leads with amplitude V_kαi. The last term in right side of Eq. 1 denotes the MBSs formed at opposite ends of the TSNW and their couplings to the QDs [35–37].

$H_{MBSs}=\frac{{\lambda }_1}{\sqrt{2}}\left(d_1-d_1^{†}\right){\gamma }_1+i\frac{{\lambda }_2}{\sqrt{2}}\left(d_2+d_2^{†}\right){\gamma }_2+i{\delta }_M{\gamma }_1{\gamma }_2,(2)$

in which λ_i is the hybridization amplitude between the QD-i and the mode-i of the MBSs, and the self-conjugate nature of the MBSs requires ${\gamma }_{1\left(2\right)}={\gamma }_{1\left(2\right)}^{†}$ and $\left\{{\gamma }_i,{\gamma }_j\right\}=2{\delta }_{ij}$. Following previous work [17], we transform the Majorana fermion operators γ₁₍₂₎into the regular fermion operators f and f^†by defining ${\gamma }_1=\frac{1}{\sqrt{2}}\left(f^{+}+f\right),{\gamma }_2=\frac{i}{\sqrt{2}}\left(f^{+}-f\right)$, and then Eq. 2 becomes into the following form,

$H_{MBSs}={\delta }_M\left(f^{†}f-\frac{1}{2}\right)+\frac{{\lambda }_1}{\sqrt{2}}\left(d_1-d_1^{†}\right)\left(f+f^{†}\right)+\frac{{\lambda }_2}{\sqrt{2}}\left(d_2+d_2^{†}\right)(f-f^{†}).(3)$

FIGURE 1

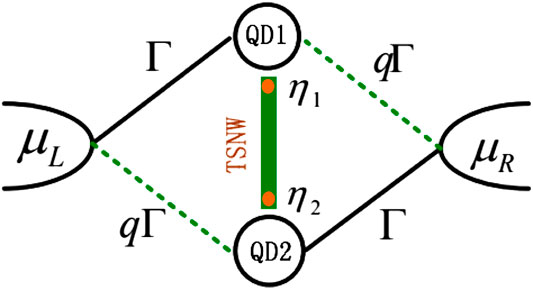
FIGURE 1. Schematic plot of the parallel double QDs coupled to the left and right leads with coupling strength ${\Gamma }_{ij}^{L/R}$, and to each other by a TSNW hosting MBSs. Dot 1(2) couples to the mode η₁₍₂₎ of the MBηSs with hybridization strength λ₁₍₂₎. The chemical potentials of the leads are μ_L and μ_R, which are set to be μ_L = μ_R = 0 in the linear response regime.

At ultra-low temperature favorable for the preparation of the MBSs, the linear conductance G is obtained with the help of the transmission T(ε) of an electron by the Landauer formula G = (2e²/h)T(ε). The transmission coefficient is calculated in terms of the Green’s functions as $T\left(\epsilon \right)=Tr\left\{{\widehat{G}}^a\left(\epsilon \right){\widehat{\Gamma }}^R{\widehat{G}}^r\left(\epsilon \right){\widehat{\Gamma }}^L\right\}$, in which ${\widehat{G}}^{r\left(a\right)}\left(\epsilon \right)$ is the retarded (advanced) Green’s function and ${\widehat{\Gamma }}^{L\left(R\right)}$ the line-width function denoting coupling between the dots and the leads. For the present structure, they are all 6×6matrixes. We calculate the retarded Green’s function ${\widehat{G}}^r\left(\epsilon \right)={\left[{\widehat{G}}^a\left(\epsilon \right)\right]}^{†}$ by using the Dyson’s equation method combined with the equation of motion technique. After some straightforward calculations, the Green’s function is given by Ref. 14${\widehat{G}}^r={\left({\widehat{g}}^{r-1}-{\widehat{T}}_c-\widehat{K}-i\left({\widehat{\Gamma }}^L+{\widehat{\Gamma }}^R\right)/2\right)}^{-1}$, in which ${\widehat{g}}^r$ is the retarded Green’s function of the central region free from couplings whose diagonal elements are $g_{11\left(22\right)}^r\left(\epsilon \right)=1/\left(\epsilon \mp {\epsilon }_1\right)$, $g_{33\left(44\right)}^r\left(\epsilon \right)=1/\left(\epsilon \mp {\epsilon }_2\right)$, and $g_{55\left(66\right)}^r\left(\epsilon \right)=1/\left(\epsilon \mp {\delta }_M\right)$. Matrix ${\widehat{T}}_c$ denotes the tunnel-coupling between the dots whose elements are ${\widehat{T}}_{c,13}={\widehat{T}}_{c,31}=-{\widehat{T}}_{c,24}=-{\widehat{T}}_{c,42}=t_c$. The matrix elements of are ${\widehat{K}}_{15\left(6\right)}={\widehat{K}}_{5\left(6\right)1}=-{\widehat{K}}_{25\left(6\right)}=-{\widehat{K}}_{5\left(6\right)}={\xi }_1$ and ${\widehat{K}}_{3\left(4\right)5}={\widehat{K}}_{53\left(4\right)}=-{\widehat{K}}_{3\left(4\right)6}=-{\widehat{K}}_{63\left(4\right)}={\xi }_2$, where ${\xi }_{1\left(2\right)}=\pi {\rho }_i{\lambda }_{1\left(2\right)}^2/2$ being the dot-MBSs coupling strength and ρ_i the density of the states in QDs i. In the present paper, we assume that the MBSs are coupled to the two QDs with equal strength, and fix ${\xi }_1={\xi }_2=\lambda$. The line-width function is given by

${\widehat{\Gamma }}^{L/R}=\left(\begin{array}{cccccc}{\Gamma }_{11}^{L/R}& 0& \sqrt{{\Gamma }_{11}^{L/R}{\Gamma }_{22}^{L/R}}& 0& 0& 0\\ 0& {\Gamma }_{11}^{L/R}& 0& \sqrt{{\Gamma }_{11}^{L/R}{\Gamma }_{22}^{L/R}}& 0& 0\\ \sqrt{{\Gamma }_{11}^{L/R}{\Gamma }_{22}^{L/R}}& 0& {\Gamma }_{22}^{L/R}& 0& 0& 0\\ 0& \sqrt{{\Gamma }_{11}^{L/R}{\Gamma }_{22}^{L/R}}& 0& {\Gamma }_{22}^{L/R}& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right),(4)$

in which the ${\Gamma }_{ij}^{\alpha }=2\pi V_{k\alpha i}{V}_{k\alpha j}^{\ast }{\rho }_{\alpha }$ with ρ_α being the local density of states in lead α.

Results and Discussion

In the following numerical calculations, we fix the line-width function ${\Gamma }_{11}^L={\Gamma }_{22}^R=\Gamma \equiv 1$ as the energy unit, and assume ${\Gamma }_{22}^L={\Gamma }_{11}^R=q\Gamma$ with q a dimensionless parameter throughout the paper. We also fix the dots’ levels at ${\epsilon }_1={\epsilon }_2=0$ in that the MBSs exert significant impacts on electronic transport around zero energy. For 0 < q ≤ 1, the two dots are parallel-coupled to the two leads, and q = 0 corresponds to the case of the serially coupled configuration. Figure 2 presents the results of linear conductance through the double QDs for different values of q. For q = 0 and t_c = 0, the system is an open circuit and the conductance is zero $\left(G=0\right)$ as indicated by the solid black line in Figure 2A. For 0 < q < 1, the two dots are connected in parallel configuration with asymmetrical left-right couplings, and the analytical expression of the linear conductance is Refs. 28 and 31

$G=\frac{2e^2}{h}\frac{4q{\epsilon }^2{\Gamma }^2}{{\left[{\epsilon }^2-{\left(\frac{1-q}{2}\Gamma \right)}^2\right]}^2+{\left[\epsilon \Gamma \left(1+q\right)\right]}^2}.(5)$

FIGURE 2

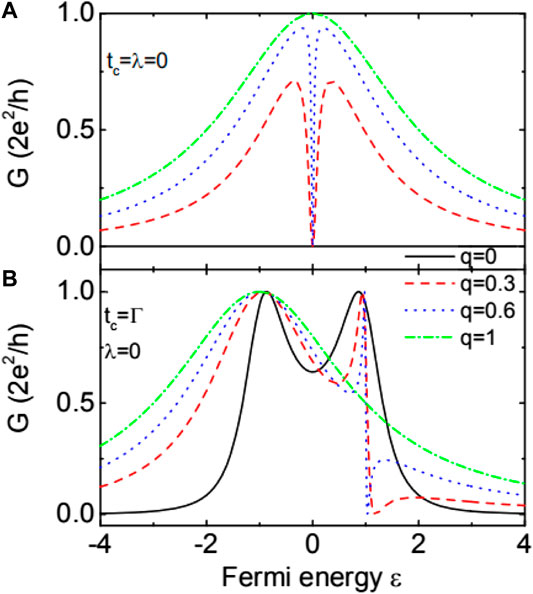
FIGURE 2. Linear conductance varying as a function of the Fermi energy in the absence of QD-MBSs coupling $\left(\lambda =0\right)$ for t_c = 0 in (A), and $t_c=\Gamma$ in (B). The configuration of the structure is varied by the value of q.

From above equation, one can see that G develops a dip at ε = 0, and has two resonances located at $\epsilon =\pm \left(1-q\right)\Gamma /2$ as shown by the red dashed and blue dotted lines in Figure 2A. For the two dots are coupled to the dots symmetrically q = 1, the conductance exhibits a single wide peak centered at as indicated by the green dash-dotted line, which can also be seen from Eq. 5. Under the condition of $t_c\ne 0$, the conductance is composed by one Breit-Wigner resonance at ε = t_c and a Fano one at ε = t_c, which respectively correspond to the bonding and antibonding states in this QDs molecular [28, 31]. The conductance now is given by

$G=\frac{2e^2}{h}\frac{4{\Gamma }^2{\left(\frac{1+q}{2}{t}_c-\sqrt{q}\epsilon \right)}^2}{{\left[{\epsilon }^2-t_c^2+{\left(\frac{1-q}{2}\Gamma \right)}^2\right]}^2+4{\Gamma }^2{\left[\frac{1+q}{2}\epsilon +\sqrt{q}{t}_c\right]}^2}.(6)$

For q = 0 (serially connected double QDs), the conductance shows two Lorentz peaks at the bonding and antibonding states, respectively. Whereas for 0 < q < 1, the resonance at the antibonding state ε = t_c shows the typical asymmetrical Fano line-shape, which has been systematically investigated in Refs. 28 and 31 and we do not discuss them in more detail.

We now study the case of the two QDs are connected by the MBSs (DQD-MBSs configuration) in Figure 3A, and also shows the results when the two dots are connected by regular fermions (TQD configuration). For q = 0, the conductance remains at zero in that the electrons can not transport through the TSNW for $t_c={\delta }_M=0$ as shown by the black solid line in Figure 3A. The conductance develops triple peaks for nonzero $q\ne 0$ which locate about at ε = 0 and $\epsilon =\pm \left(\lambda +\Gamma /2\right)$, respectively. Meanwhile, there are two antiresonances $\left(G=0\right)$ at ε = ±λ. With increasing q, the height of the three peaks increases with unchanged configuration, and reaches its quantum value $2e^2/h$ for q = 1. In structure of single QD hybridized with the MBSs, the zero energy conductance is half of its quantum value $G\left(\epsilon =0\right)\equiv e^2/h$, which is believed to be the evidence of the MBSs [19]. In the present DQD-MBSs systems, however, this criterion will not hold true, and the existence of the MBSs can only be deduced from the properties of the resonances and antiresonances in the conductance. For this reason, we show the results when the MBSs connecting the two QDs is replaced by another QD (dot-3) serving as a pair of regular fermions. For the convenience of comparison, we use similar symbols of the MBSs to denote dot-3, and then Hamiltonian in Eq. 1 is changed into

$H={\displaystyle \sum _{k\alpha }{\epsilon }_{k\alpha }{\epsilon }_{k\alpha }^{†}{\epsilon }_{k\alpha }}+{\displaystyle \sum _{i=\mathrm{1,2}}{\epsilon }_i{d}_i^{†}{d}_i}+t_c\left(d_1^{†}{d}_2+h.c\right)+{\delta }_M{d}_3^{†}{d}_3+\left(\lambda d_1^{†}{d}_3+\lambda d_3^{†}{d}_1+h.c\right)+{\displaystyle \sum _{k\alpha i}\left(V_{k\alpha i}{d}_i^{†}{c}_{k\alpha }+h.c.\right)},(7)$

from which the retarded Green’s function and the conductance can be easily obtained by the equation of motion method in the absence of Coulomb interaction between the electrons [41].

FIGURE 3

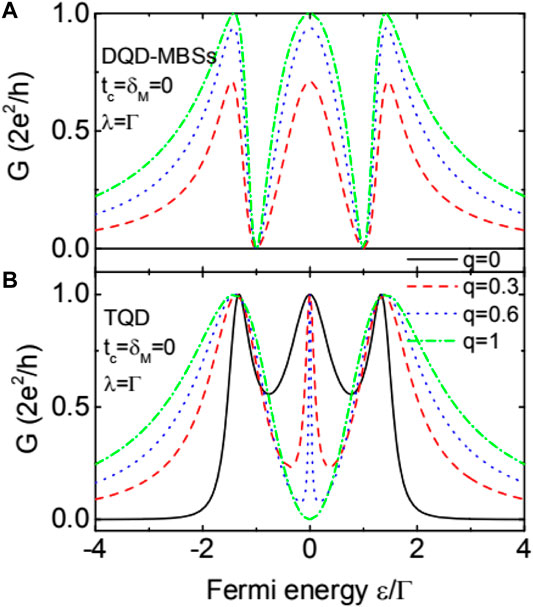
FIGURE 3. Dependence of the linear conductance on the Fermi energy for the case of the double QDs are coupled to each other by the MBSs (DQD-MBSs) in (A) and the case of the two QDs connected by regular fermions, i.e., another QD in (B). The latter corresponds to the triple-QD (TQD) configuration.

As shown in Figure 3B, the conductance develops triple peaks for 0 ≤ q < 1 with unchanged peaks’ value $2e^2/h$. With increasing q, the two dips move toward ε = 0 with the narrowing of the central peak. For, the central peak involves into an antiresonance $G\left(\epsilon =0\right)\equiv 0$ and the conductance reduces to a double-peak configuration. By comparing Figures 3A,B, one can find that the properties of the conductance in DQD-MBSs are quite different from those in TQD, and then the information of the MBSs can be then inferred. For example, the zero-energy conductance develops a peak when the two dots are symmetrically coupled to the leads $\left(q=1\right)$ in the DQD-MBSs, whereas it becomes to be zero when the two dots are connected by another QD (TQD). In fact, this is one of the interesting effects induced by the interaction between the MBSs and the electrons on the QDs that the behaviors of the conductance near the zero-energy point are mainly influenced. The reason is that the MBSs are zero energy like the electron-hole pair, and then induces a peak at zero Fermi energy, or a peak in the differential conductance when the bias voltage is zero (zero bias anomaly in the conductance found in Ref. 13). In higher energy regime, the impacts of the MBSs then are weak and the transport processes are dominated by the electrons from different channels. For this reason, the typical asymmetrical Fano line-shape in the conductance in higher energy regimes emerges, but vanishes around the zero-energy.

Figure 4 presents the calculation results in structures of DQD-MBSs (black solid line) and TQD (red dashed line) with varied inter-MBSs coupling strength δ_M (or energy level of dot-3). For small value ${\delta }_M=0.1\Gamma$ as shown in Figure 4A, the conductance’s configuration in both of the two structures remains almost unchanged, which is also quite different from the result in single dot coupled to MBSs [19], in which the value of the zero-energy conductance recovers $2e^2/h$ as long as ${\delta }_M\ne 0$. With increasing δ_M as shown in Figure 4B, the conductance peak in negative (positive) energy regimes moves toward (away from) the zero-energy state of ε = 0 for the case of DQD-MBSs (the solid black line). The conductance in the TQD, however, both the positions of the peaks and the dip move to higher energy level, as indicated by the red dashed line. When the hybridization between the MBSs is ${\delta }_M>\Gamma$, the conductance in high energy regime exhibits typical Fano line-shape, which holds true in both the DQD-MBSs and TQD configurations. Around the zero-energy state, however, the conductance in DQD-MBSs remains the double-peak configuration with an antiresonance. The conductance in TQD around ε = 0 shows the single wide peak configuration, which is completely different from that in DQD-MBSs.

FIGURE 4

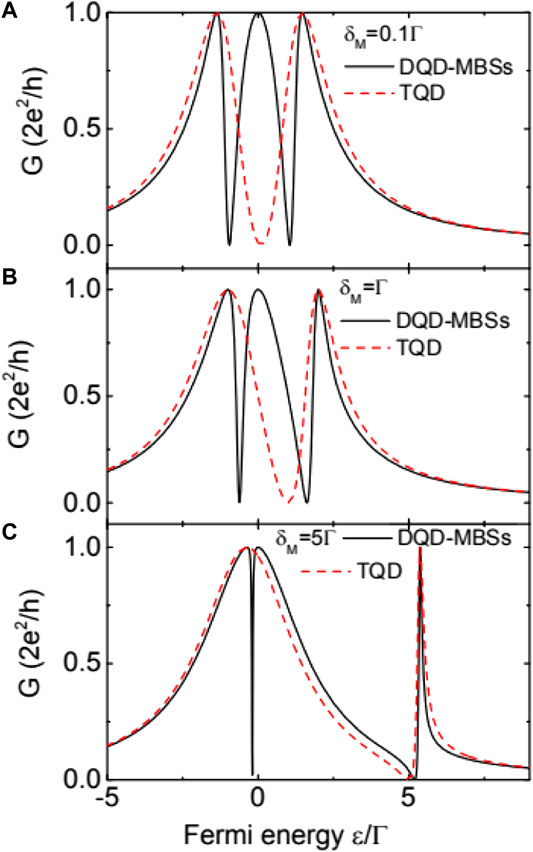
FIGURE 4. Linear conductance as a function of the Fermi energy for DQD-MBSs and TQD configurations and different values of direct overlap amplitude δ_M and fixed λ = 1 and q = 1. In (A) we set ${\delta }_M=0.1\Gamma$, and ${\delta }_M=\Gamma$ in (B), ${\delta }_M=5\Gamma$ in (C). The conductance in (C) displays typical asymmetric Fano line-shape in higher energy regimes.

Finally, we study the conductance in Figure 5 for different values of q and fixed ${\delta }_M=5\Gamma$. For nonzero δ_M, the conductance in serially coupled double QDs has three peaks individually abut at ε = 0 and $\epsilon =\pm \sqrt{{\lambda }^2+{\delta }_M^2}$ in DQD-MBSs, as shown by the solid black line in Figure 5A. The peaks are also equal in height but the width of the central peak is much wider than that of the other two. With increasing q as indicated by the sold lines in Figures 5B, C, the peak in the negative energy regime is destroyed with the splitting of the central one, exhibiting the Fano line-shape. The peak in higher energy regime becomes higher and then also displays the asymmetric Fano line-shape which is similar to the case in Figure 4. The conductance in TQD has only two peaks for q = 0, and then changes in similar way as that of DQD-MBSs. Interestingly, in the case of q = 1, we find in Figure 5A that the zero-energy conductance of DQD-MBSs develops a peak whereas that of TQD is a dip with the value of G = 0. Such an evolution from peak to valley is a good evidence of the MBSs. This difference between the two cases can be attributed to the fact that there is a resonant state at zero-energy induced by the MBSs.

FIGURE 5

FIGURE 5. Linear conductance as a function of the Fermi energy for DQD-MBSs and TQD configurations for q = 0 in (A), q = 0.3 in (B), q = 0.6 in (C). Except the parameters given in the figure, others are as in Figure 4.

Summary

In summary, we have studied the properties of the conductance in double QDs coupled to the left and right leads in parallel configuration within the framework of the Green’s function method. We find that when the two dots are connected by a TSNW with MBSs at its two ends, the conductance develops three peaks, whose height is enhanced with increasing left-right symmetry. Between the peaks, there are two dips with zero conductance. If the dots are connected by regular fermions, however, the dips is nonzero, and the central peaks will evolve into a dip if the system is totally symmetric in left-right coupling strength. Such a peak to valley change of the conductance provides a non-invasive detection of the MBSs. When the MBSs formed at the ends of the TSNW is overlapped, the resonances at zero and positive energy regimes will display the typical Fano line-shape, which is useful in quantum information processing or design of novel quantum devices.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

FC and Z-GF contributed the ideas equally and derived the formulae. JW and T-YH performed the numerical calculations. FC, Z-GF, and PZ wrote the original manuscript. X-WZ, LW, and ZL helped to discussed the results and polished the manuscript.

Funding

This research was supported by the NSFC (Grant No. 62075035), the Initial Project of UEST of China, Zhongshan Institute (415YKQ02), Project for Innovation Team of Guangdong University (No. 2018KCXTD033), Science and Technology Bureau of Zhongshan (Grant No. 2017B1116, 180809162197886), and the Research Funds for Beijing Universities (NO.KM201910009002). X-W Zhang acknowledges support from Key Research and Development Program of Guangxi (GuiKeAB19110032).

Conflict of Interest

Authors LW and ZL are employed by China Monferrous Metal (Guilin) Geology and Mining Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Kitaev AY Unpaired majorana fermions in quantum wires. Phys Usp (2001) 44(10):131–6. doi:10.1070/1063-7869/44/10S/S29

CrossRef Full Text | Google Scholar

2. Nayak C, Simon SH, Stern A, Freedman M, Das Sarma S Non-Abelian anyons and topological quantum computation. Rev Mod Phys (2008) 80(3):1083–1159. doi:10.1103/revmodphys.80.1083

CrossRef Full Text | Google Scholar

3. Alicea J New directions in the pursuit of Majorana fermions in solid state systems. Rep Prog Phys (2012) 75(7):076501. doi:10.1088/0034-4885/75/7/076501

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Sau JD, Lutchyn RM, Tewari S, Das Sarma S Generic new platform for topological quantum computation using semiconductor heterostructures. Phys Rev Lett (2010) 104(4):040502. doi:10.1103/PhysRevLett.104.040502

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Karzig T, Knapp C, Lutchyn RM, Bonderson P, Hastings MB, Nayak C, et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys Rev B (2017) 95(23):235305. doi:10.1103/physrevb.95.235305

CrossRef Full Text | Google Scholar

6. Oreg Y, Refael G, von Oppen F Helical liquids and Majorana bound states in quantum wires. Phys Rev Lett (2010) 105(17):177002. doi:10.1103/PhysRevLett.105.177002

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Mourik V, Zuo K, Frolov SM, Plissard SR, Bakkers EP, Kouwenhoven LP Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science (2012) 336(6084):1003–7. doi:10.1126/science.1222360

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Deng MT, Vaitiekėnas S, Hansen EB, Danon J, Leijnse M, Flensberg K, et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science (2016) 354(6319):1557–62. doi:10.1126/science.aaf3961

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhang H, Liu CX, Gazibegovic S, Xu D, Logan JA, Wang G, et al. Quantized Majorana conductance. Nature (2018) 556(7699):74–9. doi:10.1038/nature26142

PubMed Abstract | CrossRef Full Text | Google Scholar

10. KouwenhovenXu S, Xie Y, Li J, Wang Z, Bernevig BA, Yazdani A Distinguishing a Majorana zero mode using spin-resolved measurements. Science (2017) 358(6364):772–6. doi:10.1126/science.aan3670

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Fornieri A, Whiticar AM, Setiawan F, Portolés E, Drachmann ACC, Keselman A, et al. Evidence of topological superconductivity in planar Josephson junctions. Nature (2019) 569(7754):89–92. doi:10.1038/s41586-019-1068-8

PubMed Abstract | CrossRef Full Text | Google Scholar

12. NichelePortolés H, Pientka F, Hart S, Pierce A, Kosowsky M, Lunczerau L, et al. Topological superconductivity in a phase-controlled Josephson junction. Nature (2019) 569(7754):93–8. doi:10.1038/s41586-019-1148-9

PubMed Abstract | CrossRef Full Text | Google Scholar

13. YacobyPierce A, Das A, Ronen Y, Most Y, Oreg Y, Heiblum M, et al. Zero-bias peaks and splitting in an Al-InAs nanowire topological superconductor as a signature of Majorana fermions. Nat Phys (2012) 8(12):887–95. doi:10.1038/NPHYS2479

CrossRef Full Text | Google Scholar

14. Górski G, Kucab K The spin-dependent coupling in the hybrid quantum dot–Majorana wire system. Phys Status Solidi B-Basic Solid State Phys (2019) 256(3):1800492. doi:10.1002/pssb.201800492

CrossRef Full Text | Google Scholar

15. Weymann I, Wojcik KP, Majek P Majorana-Kondo interplay in T-shaped double quantum dots. Phys Rev B (2020) 101(23):235404. doi:10.1103/PhysRevB.101.235404

CrossRef Full Text | Google Scholar

16. Yi GY, Jiang C, Zhang LL, Zhong SR, Chu H, Gong WJ, et al. Manipulability of the Kondo effect in a T-shaped triple-quantum-dot structure. Phys Rev B (2020) 102(8):085418. doi:10.1103/PhysRevB.102.085418

CrossRef Full Text | Google Scholar

17. Feng JJ, Huang Z, Wang Z, Niu Q Josephson radiation from nonlinear dynamics of Majorana zero modes. Phys Rev B (2020) 101(18):180504. doi:10.1103/PhysRevB.101.180504

CrossRef Full Text | Google Scholar

18. Liu DE, Cheng M, Lutchyn RM Probing Majorana physics in quantum-dot shot-noise experiments. Phys Rev B (2015) 91(8):081405. doi:10.1103/PhysRevB.91.081405

CrossRef Full Text | Google Scholar

19. Liu DE, Baranger HU Detecting a Majorana-fermion zero mode using a quantum dot. Phys Rev B (2011) 84(20):201308. doi:10.1103/PhysRevB.84.201308

CrossRef Full Text | Google Scholar

20. Sherman D, Yodh JS, Albrecht SM, Nygård J, Krogstrup P, Marcus CM Normal, superconducting and topological regimes of hybrid double quantum dots. Nat Nanotechnol (2016) 12(3):212–7. doi:10.1038/nnano.2016.227

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ricco LS, Campo VL, Shelykh IA, Seridonio AC Majorana oscillations modulated by Fano interference and degree of nonlocality in a topological superconducting-nanowire–quantum-dot system. Phys Rev B (2018) 98(7):075142. doi:10.1103/PhysRevB.98.075142

CrossRef Full Text | Google Scholar

22. Ricco LS, de Souza M, Figueira MS, Shelykh IA, Seridonio AC Spin-dependent zero-bias peak in a hybrid nanowire-quantum dot system: distinguishing isolated Majorana fermions from Andreev bound states. Phys Rev B (2019) 99(15):155159. doi:10.1103/PhysRevB.99.155159

CrossRef Full Text | Google Scholar

23. López R, Lee M, Serra L, Lim JS Thermoelectrical detection of Majorana states. Phys Rev B (2014) 89(20):205418. doi:10.1103/PhysRevB.89.205418

CrossRef Full Text | Google Scholar

24. Tang HZ, Zhang YT, Liu JJ Photon-assisted tunneling through a topological superconductor with Majorana bound states. AIP Adv (2015) 5(12):127129. doi:10.1063/1.4939096

CrossRef Full Text | Google Scholar

25. Chi F, He TY, Wang J, Fu ZG, Liu LM, Liu P, et al. Photon-assisted transport through a quantum dot side-coupled to Majorana bound states. Front Phys (2020) 8:254. doi:10.3389/fphy.2020.00254

CrossRef Full Text | Google Scholar

26. Van der Wiel WG, De Franceschi S, Elzerman JM, Fujisawa T, Tarucha S, Kouwenhoven LP Electron transport through double quantum dots. Rev Mod Phys (2002) 75(1):1–22. doi:10.1103/RevModPhys.75.1

CrossRef Full Text | Google Scholar

27. Hanson R, Kouwenhoven LP, Petta JR, Tarucha S, Vandersypen LMK Spins in few-electron quantum dots. Rev Mod Phys (2007) 79(4):1217–65. doi:10.1103/RevModPhys.79.1217

CrossRef Full Text | Google Scholar

28. Chi F, Liu JL, Sun LL Fano-Rashba effect in a double quantum dot Aharonov-Bohm interferometer. J Appl Phys (2007) 101(9):093704. doi:10.1063/1.2720097

CrossRef Full Text | Google Scholar

29. Hofstetter W, König J, Schoeller H Kondo correlations and the Fano effect in closed Aharonov-Bohm interferometers. Phys Rev Lett (2001) 87(15):156803. doi:10.1103/PhysRevLett.87.156803

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Miroshnichenko AE, Flach S, Kivshar YS Fano resonances in nanoscale structures. Rev Mod Phys (2010) 82(3):2257–98. doi:10.1103/RevModPhys.82.2257

CrossRef Full Text | Google Scholar

31. de Guevara MLL, Claro F, Orellana PA Ghost Fano resonance in a double quantum dot molecule attached to leads. Phys Rev B (2003) 67(19):195335. doi:10.1103/PhysRevB.67.195335

CrossRef Full Text | Google Scholar

32. Li YX, Bai ZM Tunneling transport through multi-quantum-dot with Majorana bound states. J Appl Phys (2013) 114(3):033703. doi:10.1063/1.4813229

CrossRef Full Text | Google Scholar

33. Wang N, Lv SH, Li YX Quantum transport through the system of parallel quantum dots with Majorana bound states. J Appl Phys (2014) 115(8):083706. doi:10.1063/1.4867040

CrossRef Full Text | Google Scholar

34. Xia JJ, Duan SQ, Zhang W Detection of Majorana fermions by Fano resonance in hybrid nanostructures. Nanoscale Res Lett (2015) 10:223. doi:10.1186/s11671-015-0914-3

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Jiang C, Zheng YS Fano effect in the Andreev reflection of the Aharonov-Bohm-Fano ring with Majorana bound states. Solid State Commun (2015) 212:14–18. doi:10.1016/j.ssc.2015.04.001

CrossRef Full Text | Google Scholar

36. Ueda A, Yokoyama T Anomalous interference in Aharonov-Bohm rings with two Majorana bound states. Phys Rev B (2014) 90(8):081405. doi:10.1103/PhysRevB.90.081405

CrossRef Full Text | Google Scholar

37. Zeng QB, Chen S, Rong L Fano effect in an AB interferometer with a quantum dot side-coupled to a single Majorana bound state. Phys Lett (2016) 380:951–7. doi:10.1016/j.physleta.2015.12.026

CrossRef Full Text | Google Scholar

38. Ivanov TI Coherent tunneling through a double quantum dot coupled to Majorana bound states. Phys Rev B (2017) 96(3):035417. doi:10.1103/PhysRevB.96.035417

CrossRef Full Text | Google Scholar

39. Cifuentes JD, Dias da Silva LGGV Manipulating Majorana zero modes in double quantum dots. Phys Rev B (2019) 100(8):085429. doi:10.1103/PhysRevB.100.085429

CrossRef Full Text | Google Scholar

40. Tang LW, Mao WG Detection of Majorana bound states by sign change of the tunnel magnetoresistance in a quantum dot coupled to ferromagnetic electrodes. Front Phys (2020) 8(5):147. doi:10.3389/fphy.2020.00147

CrossRef Full Text | Google Scholar

41. Liu LM, Chi F, Fu ZG, Yu SC, Chen HW Spin-polarized transport and spin Seebeck effect in triple quantum dots with spin-dependent interdot couplings. Nanoscale Res Lett (2018) 13(1):358. doi:10.1186/s11671-018-2773-1

PubMed Abstract | CrossRef Full Text | Google Scholar