- High Energy and Astrophysics Laboratory, Physics Department, FSSM, Cadi Ayyad University, Marrakech, Morocco
In this paper, we have extended and deepened the study on fractional order phase transition (FPT) of a charged AdS black hole. We have carried out a detailed analysis of FPT for several AdS black hole prototypes: black hole surrounded by quintessence background, 5D Gauss-Bonnet, D dimensional RN-AdS BH, and lastly Kerr black holes. We have shown that the 4/3 order FPT at critical points holds for the first three black holes systems, while for Kerr black holes, the fractional order is rather 1/3. These results suggest two remarkable features: Firstly 4/3 order phase transition can be assumed for asymptotically AdS black holes spherical solutions; secondly the fractional order is not universal and can be affected by the geometric symmetry.
1 Introduction
Thermodynamic properties and particularly phase transitions of black holes in asymptotically Anti de-Sitter spacetime have been investigated extensively. This growing interest in phase transitions originates from their relation to holographic superconductivity in the context of the AdS/CFT correspondence [2]. Recently, many studies of black holes criticality have identified the cosmological constant with thermodynamic pressure and its conjugate quantity with thermodynamic volume [3–6]. Furthermore the inclusion of the
Originally outlined by Ehrenfest who used the discontinuities in derivatives of the free energy to probe and classify thermodynamic phase transitions, Ehrenfest’s classification scheme is based on the experimental observation of the density contrast between coexisting phases and latent heat during a phase transition. When a system undergoes a phase transition at a critical temperature, Ehrenfest defines its order of phase transition as the smallest integer
where
Hawking-Page phase transition is an example of first-order transition. The critical point is commonly presented as a witness of second-order phase transition in the sense of Ehrenfest. A much more general classification scheme based on fractional derivatives, viz. a derivative with noninteger order, along arbitrary curves in the thermodynamic state space, has been revealed [15–17]. Fractional phase transitions (FPT) go back to the work of Nagle on dipalmitoyl lecithin (DPL) system [18], where it has been observed that the order
The generalized Ehrenfest classification holds for all thermodynamic systems having phase structures, including AdS black holes with analogous behavior to Van der Waals gases. Indeed, a first study recently performed by Ma [1] showed that RN-AdS black holes can undergo 4/3 order FPT. In this paper, we aim to explore further this issue and see whether this fractional order holds for any AdS black hole solution, as in VdW systems. To this end, we consider four prototypes: First the charged AdS black hole surrounded by quintessence field to show the effect of an external source. Second, we use a D dimensional RN-AdS and five-dimensional Gauss-Bonnet-AdS black hole to probe whether higher spacetime dimensions,
This paper is organized as follows. In the next section, first we present the following AdS black hole solutions: Kiselev, D dimensional RN-AdS, and 5D Gauss-Bonnet solution, and their corresponding thermodynamic quantities. Then, we study their fractional phase transitions at critical points via the Caputo derivative of Gibbs free energy. Section 3 is devoted to the analysis of Kerr-AdS black hole and derivation of its FPT order. Our conclusion is drawn in the last section.
2 Thermodynamic Criticality and Fractional Order Phase Transitions of AdS Black Holes With Spherical Symmetry
In this section, we consider three spherical symmetric solutions of static asymptotically AdS black holes, namely: a charged AdS BH surrounded by quintessence, D dimensional RN-AdS BH, and a 5D Gauss-Bonnet AdS black holes. We first calculate their thermodynamic quantities and then describe the behaviors of corresponding Gibbs free energy and their fractional derivatives nearby the critical points. Our objective is to probe whether the extra factors, as quintessence parameter, higher dimensions, and/or higher derivatives in Gauss-Bonnet term parameters, could affect the FPT order.
2.1 Charged AdS Black Hole Surrounded by Quintessence
From high precision astronomical observations, it has been shown that the Universe is currently undergoing a phase of accelerated expansion [20, 21], which might be due to dark energy acting as a repulsive gravity. A possible origin of this phenomenon could come from the so-called quintessence field, which obeys an equation of state formulated through the relation between negative pressure and energy density as
We consider the Kiselev solution of four-dimensional charged AdS black holes surrounded by quintessence,
where a represents a positive normalization parameter, while M and Q are the mass and electric charge of the black hole, respectively. As usual, we treat the cosmological constant as a dynamical pressure of the black hole [7],
The Hawking temperature related to the surface gravity via the formula
where the horizon
where the specific volume v associated with the fluid volume is related to the horizon radius since
where the conjugate quantities of the parameters P, Q, and a read, respectively, as
while the Smarr relation is formulated by
Thereafter, without loss of generality, we will set
For subsequent analysis, it is more appropriate to introduce the following variables:
Thus with the new set of variables
Besides, the rescaled Gibbs free energy now takes the form
Next we probe the behavior of Gibbs free energy
The above equation can well be expressed in the Taylor series of t and written in a simple form as
Several definitions of fractional derivatives exist in literature [23]. Here we rely on Caputo definition which enables easy use of conventional boundaries and initial conditions [24]:
where ß is the order of derivative and n an integer. As a result of calculation we get
According to Refs. 11 and 13, the equation of state near the critical point (
where the slope k is given by
Therefore, we can calculate the values of
Obviously, for
When
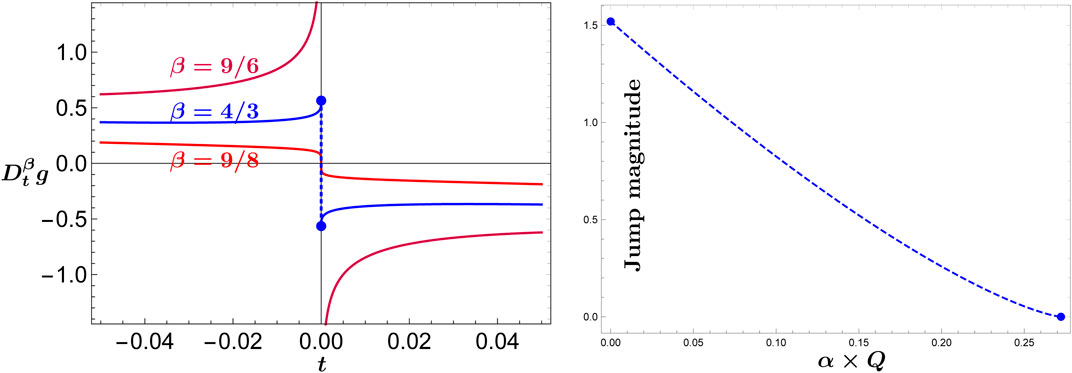
FIGURE 1. Left panel: The behavior of fractional derivatives
This result clearly shows that, for spherical symmetric AdS black hole in quintessence background, the FPT still stands at 4/3 order. Therefore, the fractional phase transition is not affected by the external quintessence field surrounding the charged AdS black hole.
2.2 Charged AdS Black Holes in Higher Dimensions
Now we consider a D dimensional charged AdS black hole to check whether higher dimension D deflects the fractional order of the phase transition from 4/3. For this case, the metric is given by
m and q are related to the ADM mass M, while Q stands for the black hole charge [25]:
with
Thermodynamics of higher dimension black holes has been investigated in Ref. 26 as well as their critical behaviors revealed as phase transition between small and large black holes. The critical points were derived at
where the specific volume is given, in the geometric units, by
The rescaled Gibbs free energy is
Note that for
Next step, we solve Eq. 24 and expand the Gibbs free energy for each dimension spacetime
Since the equation of state near the critical point behaves as
with a discontinuity taking place at

TABLE 1. Limits and fractional order phase transition at the critical point for D dimensional RN-AdS BH.
Table 1 decidedly shows that, whatever the dimension D of the RN-AdS black hole, the fractional order of phase transition near the critical point arises decidedly at
2.3 5D Gauss-Bonnet-AdS Black Hole
First we briefly introduce the action of Gauss-Bonnet black hole and its main thermodynamic features.
The action of this theory reads as
A spherically symmetric static solution of this theory has been derived, and the metric function determined through solving the real roots of a polynomial equation [27, 28].
It is founded to seek a connection between the higher derivatives in Gauss-Bonnet term and the phase transition, checking whether it affects the FPT’s order. Here, we use as prototype
where
where the specific volume is
while the rescaled Gibbs free energy (
As previous analysis, since the equation of state near the critical point [29] is reduced to
Again, we find that the phase transition near the critical point is fractional and happens at order 4/3, which suggest that neither the spacetime dimension nor the higher derivative corrections introduced by means of the Gauss-Bonnet term can alter the fractional order phase transition at the critical point. Hence we assume that FPT is located at 4/3 order, whatever the external factors (space dimension, surrounding background) as far as the AdS black hole solution possesses a spherical symmetry.
The next legitimate question is what about axisymmetric black hole solutions? Is the 4/3 order of FPT universal? we attempt to respond to this issue in the subsequent section using Kerr-AdS black hole as prototype.
3 Kerr-AdS Black Holes
The Kerr solution is the only known family of exact solutions which could present the stationary axisymmetric field outside a rotating massive object.
By using Boyer-Lindquist coordinates, the Kerr asymptotically AdS black hole solutions can read as [31–33]
where
The mass M and the angular momentum J are related to the parameters m and a as follows:
Knowing that the pressure is still given by Eq. 3 and neglecting all terms of higher order in J, the equation of state in terms of temperature, specific volume, and the angular momentum reads as [26]
where the specific volume associated with the Kerr black hole is given by
The critical point occurs at
From the approximation used previously, we derive the expression of rescaled Gibbs free energy in terms of the dimensionless parameters given in Eq. 10,
and the reduced equation of state
Then, using Eqs 40 and 41, one can readily derive the phase transition order near the critical point. Indeed, t-expansion of the rescaled Gibbs free energy becomes
where the coefficients
with
The fractional order phase transition of Kerr-AdS black hole clearly arises at
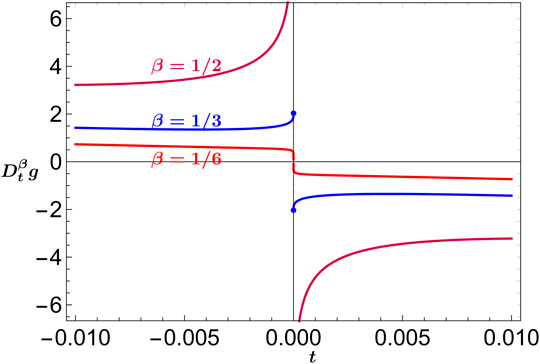
FIGURE 2. The behaviors of fractional derivatives
Therefore, near the critical point, we see that fractional order of the phase transition is no longer
4 Conclusion
Summarizing, in this paper we have studied the continuous thermodynamic phase transitions of AdS black holes according to the generalized Ehrenfest classification. By using the Caputo fractional derivatives of thermodynamic potentials for a charged black hole surrounded by quintessence and 5D Gauss-Bonnet and RN-AdSD black holes, we find that the fractional derivatives of the Gibbs free energy are always discontinuous at the critical point for
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This manuscript has been released as a preprint at arXiv database [34].
References
1. Ma MS. Fractional-order phase transition of charged AdS black holes. Phys Lett B (2019) 795:490–495. doi:10.1016/j.physletb.2019.06.054
2. Aharony O, Gubser SS, Maldacena JM, Ooguri H, Oz Y. Large N field theories, string theory and gravity. Phys Rep (2000) 323:183–386. doi:10.1016/S0370-1573(99)00083-6
3. Belhaj A, Chabab M, Moumni HE, Medari L, Sedra MB. The thermodynamical behaviors of kerr-newman AdS black holes. Chin Phys Lett (2013) 30:090402. doi:10.1088/0256-307X/30/9/090402
4. Belhaj A, Chabab M, El Moumni H, Sedra MB. On thermodynamics of AdS black holes in arbitrary dimensions. Chin Phys Lett (2012) 29:100401. doi:10.1088/0256-307X/29/10/100401
5. Chabab M, El Moumni H, Iraoui S, Masmar K, Zhizeh S. More insight into microscopic properties of RN-AdS black hole surrounded by quintessence via an alternative extended phase space. Int J Geomet Methods Mod Phys (2018) 15(10):1850171. doi:10.1142/S0219887818501712
6. Kubiznak D, Mann RB. P-V criticality of charged AdS black holes. JHEP (2012) 7:033. doi:10.1007/JHEP07(2012)033
7. Kastor D, Ray S, Traschen J. Enthalpy and the mechanics of AdS black holes. Class Quant Grav (2009) 26:195011. doi:10.1088/0264-9381/26/19/195011
8. Dolan BP. Pressure and volume in the first law of black hole thermodynamics. Class Quant Grav (2011) 28:235017. doi:10.1088/0264-9381/28/23/235017
9. Kiselev VV. Quintessence and black holes. Class Quant Grav (2003) 20:1187. doi:10.1088/0264-9381/20/6/310
10. Thomas BB, Saleh M, Kofane TC. Thermodynamics and phase transition of the Reissner-Nordström black hole surrounded by quintessence. Gen Relat Gravit (2012) 44:2181–2189. doi:10.1007/s10714-012-1382-z
11. Li GQ. Effects of dark energy on P-V criticality of charged AdS black holes. Phys Lett B (2014) 735:256–260. doi:10.1016/j.physletb.2014.06.047
12. Wu CH, Zou DC, Wang Y. P-V criticality of born-infeld AdS black holes surrounded by quintessence. Commun Theor Phys (2018) 70(4):459. doi:10.1088/0253-6102/70/4/459
13. Chabab M, Iraoui S. Thermodynamic criticality of d-dimensional charged AdS black holes surrounded by quintessence with a cloud of strings background. Gen Relat Gravit (2020) 52(8):75. doi:10.1007/s10714-020-02729-4
15. Hilfer R. Thermodynamic scaling derived via analytic continuation from the classification of Ehrenfest. Phys Scripta (1991) 44(4):321. doi:10.1088/0031-8949/44/4/002
16. Hilfer R. Multiscaling and the classification of continuous phase transitions. Phys Rev Lett (1992) 68(2):190–192. doi:10.1103/PhysRevLett.68.190
17. Hilfer R. Scaling theory and the classification of phase transitions. Mod Phys Lett B (1992) 6(13):773. doi:10.1142/S0217984992000855
18. Nagle JF. Lipid bilayer phase transition: density measurements and theory. Proc Natl Acad Sci USA (1973) 70(12):3443–3444. doi:10.1073/pnas.70.12.3443
19. Agnihotri RC, Mehrotra C, Gupta VD, Srivastava V. Fractional order phase transition in lipid bilayer: dipalmitoyllecithin. Pramana – J Phys (1982) 19(1):43–49. doi:10.1007/BF02846230
20. Riess AG, Filippenko A, Challis P, Clocchiatti A. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron J (1998) 116:1009. doi:10.1086/300499
21. Perlmutter S, Aldering G, Goldhaber G, Knop RA, Nugent P, Castro PG, et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys J (1999) 517:565–586. doi:10.1086/307221
22. Caldwell RR, Dave R, Steinhardt PJ. Cosmological imprint of an energy component with general equation of state. Phys Rev Lett (1998) 80:1582–1585. doi:10.1103/PhysRevLett.80.1582
24. Caputo M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys J (1967) 13(5):529–539. doi:10.1111/j.1365-246X.1967.tb02303.x
25. Chamblin A, Emparan R, Johnson CV, Myers RC. Charged AdS black holes and catastrophic holography. Phys Rev D (1999) 60:064018. doi:10.1103/PhysRevD.60.064018
26. Gunasekaran S, Mann RB, Kubiznak D. Extended phase space thermodynamics for charged and rotating black holes and Born-Infeld vacuum polarization. JHEP (2012) 11:110. doi:10.1007/JHEP11(2012)110
27. Wheeler JT. Symmetric solutions to the gauss-bonnet extended einstein equations. Nucl Phys B (1986) 268:737–746. doi:10.1016/0550-3213(86)90268-3
28. Wiltshire DL. Spherically symmetric solutions of einstein-maxwell theory with a gauss-bonnet term. Phys Lett B (1986) 169:36–40. doi:10.1016/0370-2693(86)90681-7
29. Cai RG, Cao LM, Li L, Yang RQ. P-V criticality in the extended phase space of Gauss-Bonnet black holes in AdS space. JHEP (2013) 9:5. doi:10.1007/JHEP09(2013)005
30. Belhaj A, Chabab M, El moumni H, Masmar K, Sedra MB. Maxwell’s equal-area law for Gauss-Bonnet-Anti-de Sitter black holes. Eur Phys J C (2015) 75(2):71. doi:10.1140/epjc/s10052-015-3299-7
31. Kerr RP. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys Rev Lett (1963) 11:237–238. doi:10.1103/PhysRevLett.11.237
32. Boyer RH, Lindquist RW. Maximal analytic extension of the Kerr metric. J Math Phys (1967) 8:265. doi:10.1063/1.1705193
33. Carter B. Hamilton-Jacobi and Schrodinger separable solutions of Einstein’s equations. Commun Math Phys (1968) 10(4):280–310. doi:10.1007/BF03399503
Keywords: AdS black holes, Gauss-Bonnet, Kerr black holes, phase transitions, fractional order
Citation: Chabab M and Iraoui S (2021) Fingerprinting the Fractional Order Phase Transitions in AdS Black Holes. Front. Phys. 8:620430. doi: 10.3389/fphy.2020.620430
Received: 22 October 2020; Accepted: 23 December 2020;
Published: 14 April 2021.
Edited by:
Frank Franz Deppisch, University College London, United KingdomReviewed by:
Meng-Sen Ma, Shanxi Datong University, ChinaDe-Cheng Zou, Yangzhou University, China
Joel Saavedra, Pontificia Universidad Católica de Valparaíso, Chile
Copyright © 2021 Chabab and Iraoui. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mohamed Chabab, bWNoYWJhYkB1Y2EuYWMubWE=; Samir Iraoui, c2FtaXIuaXJhb3VpQGNlZC51Y2EubWE=
 Mohamed Chabab
Mohamed Chabab Samir Iraoui
Samir Iraoui