Data Analysis and Background Subtraction in Neutron Spin Echo Spectroscopy

With the constantly improving performance of neutron spin echo (NSE) spectrometers it becomes possible to perform measurements on increasingly complex samples and to study more and more delicate effects. To properly study such effects, proper background correction becomes increasingly important. In this paper, we will review different methods to subtract the buffer from NSE measurements and study the effect of small errors in the subtraction of the background. In the large dynamic range of modern neutron spin-echo spectrometers multiple effects become visible in a single measurement. Specifically, for vesicles both membrane undulations and translational diffusion have an effect on the intermediate scattering function in the NSE time window and here, we will investigate how taking this into account differently affects the results obtained from data analysis.

1 Introduction

After the invention of neutron spin echo (NSE) spectroscopy by Mezei [1] in 1972 it took more than another decade before the technique was used to study membrane dynamics, at first using droplet microemulsions [2]. Later, bicontinuous microemulsions [3] and lipid bilayers [4] were studied. The development of the Zilman-Granek model [5], adapting a model for semi-flexible polymers by Farge and Maggs [6] for the two dimensional case of bilayers and starting from a Helfrich bending Hamiltonian [7] meant a major breakthrough for the field as it managed to explain the anomalous scaling of the relaxation rate $\text{Γ}\propto {\kappa }^{-1/2}$ and the stretched exponential shape of the intermediate scattering function with a stretch exponent of 2/3 that was found soon after the publication of the paper in many membrane systems by NSE and dynamic light scattering (DLS) [8–10]. The expression for the normalized intermediate scattering function reads

$S_{ZG}\left(q,t\right)=\text{exp}\left(-{\left({\text{Γ}}_{ZG}{q}^{3}t\right)}^{2/3}\right)(1)$

with the modulus of the scattering vector q, Fourier time t and

${\text{Γ}}_{ZG}=0.025\gamma \sqrt{\frac{k_{B}T}{\kappa }}\frac{k_{B}T}{\eta },(2)$

where k_B is the Boltzmann constant, T is the temperature, η is the viscosity, κ is the bending rigidity and $\gamma \approx 1$ for $\kappa /k_{B}T>>1$.

Since then, membrane dynamics have become one of the major subjects studied by NSE. As an admittedly somewhat random example, in the last proposal round 2019, a little less than 40% of all proposals submitted for the NSE spectrometer IN15 [11] at the Institut Laue-Langevin were related to the study of membrane dynamics. Another (less random) example is the number of citations of papers mentioning NSE and membrane dynamics from the Web of Science core collection (November 2020) which has increased by almost a factor 30 between 2000 and 2020, accounting for more than 15% of all the citations of papers mentioning NSE compared to less than 2% in 2000.

It was realized early on that bending rigidities obtained from fitting the Zilman-Granek model to NSE data are usually too high by about a factor 10 [12, 13] while values obtained from DLS give reasonable values [8]. The simplest remedy for this problem is to use a higher effective viscosity (typically ${\eta }_{eff}=3\eta$) and attribute the discrepancies to internal dissipation in the membrane. Seifert and Langer [14] found that at the length and time scale of NSE it is not a simple bending mode but a combined bending-stretching mode that is observed with an effective bendig rigidity

$\tilde{\kappa }=\kappa +2d^{2}k,(3)$

with the monlayer elastic area compressibility modulus k and the height of the monolayer neutral surface from the bilayer midsurface d. Fortunately, the compressibility modulus of the bilayer K_a is proportional to the bending rigidity [15].

$K_a=\frac{24\kappa }{d_{bilayer}^2},(4)$

which is related to k for a symmetric bilayer by K_a = 2k [16] even though others claim to have found K_a = k [17]. The factor 24 in Eq. 4 stems from treating the chain entropy of the lipids as short polymers in non-coupling monolayers ignoring van der Waals interactions or effects from the headgroup. This yields excellent results in treating data from micropipette suction [15] but different theoretical treatments can lead to factors between 4 and 48 [18] instead of 24 in Eq. 4 depending on the level of coupling between the monolayers and the distribution of lateral pressure across the membrane. The remaining parameter in Eq. 4d_bilayer is the mechanical thickness of the bilayer. For saturated and monounsaturated it can be replaced by the thickness of the hydrophobic part of the bilayer, but deviations are observed for more complicated bilayers such as systems with polyunsaturated lipids [15] or bilayers with cholesterol [19]. Inserting Eq. 4 in Eq. 3 with K_a = 2k gives

$\tilde{\kappa }=\kappa +24{\left(d/d_{bilayer}\right)}^2,(5)$

where the exact value of d is not known but is commonly assumed to be between 0.5 and 1 times the monolayer thickness [20, 21]. Watson and Brown [20] have shown that Eq. 5 can simply be used in the framework of the Zilman Granek model replacing κ by $\tilde{\kappa }$ which simply leads to a different prefactor in Eq. 2. The current consensus is to use a value of 0.0069 instead of 0.025 [22] which is close to the commonly used three times higher effective viscosity and corresponds to setting d at $\sqrt{\left(0.025/0.0069-1\right)/24}\cdot 2=0.66$ times the hydrophobic monolayer thickness. Different prefactors were used in different papers and Table 1 in the review by Gupta et al. [23] gives a comprehensive overview. However, it should be kept in mind that these prefactors are merely the result of matching values obtained from NSE measurements by fitting Eq. 1 with values from other methods.

Another complication comes from the fact that in the derivation of the approximate form of the Zilman-Granek model in Eq. 1 an averaging over the wavelengths of the undulations has to be performed. Monkenbusch et al. [13] have shown for length and time scales relevant for microemulsions that the explicit length scale influences the result when explicitly evaluating the nested integrals that are otherwise approximated to give Eq. 1.

Given these uncertainties in the theoretical treatment, the prefactor in Eq. 2 should be considered as a simple fudge factor and for a relative comparison between data from structurally similar vesicles Eq. 1 is perfectly sufficient as long as care is taken not to over interpret absolute values of κ.

This paper can not and will not try to resolve all the aforementioned theoretical uncertainties but focus on the effect of the exact fitting procedure of the data. While many publications simply fit data with Eq. 1, diffusion of vesicles certainly has an influence on the intermediate scattering function and in Section 2 we will investigate how values of κ are influenced by different methods of taking into account translational diffusion. In addition it will be investigated how the use of the explicit form of the Zilman-Granek model as in Monkenbusch et al. [13] influences the obtained results on length scales relevant to lipid vesicles.

In Section 3 the effect of the background subtraction will be examined in detail. While the details of the procedure for the subtraction of the background are comparably unimportant as long as the data is simply analyzed by fitting a single stretched exponential it becomes increasingly important as more subtle effects are investigated as for example thickness fluctuations [22, 24, 25] or short range motions of the lipids in the membrane [26, 27].

All of this is done in the hope that it will allow to extract more robust information from NSE experiments, which may in turn help to further develop the underlying theory.

2 Data Analysis

A closer look at Eq. 1 reveals that the q³ dependence of the undulation mode is merely the result of keeping the q dependence of the relaxation rate in the parentheses with the 2/3 exponent and Eq. 1 could equally well be rewritten as $S_{ZG}=\text{exp}\left(-{\text{Γ}}_{ZG}^{2/3}{q}^2{t}^{2/3}\right)$ which shows a q² dependence just like simple diffusion. Therefore, observing a q³ dependence when fitting Eq. 1 does not unambiguously verify the validity of the Zilman-Granek model and the telltale sign is in fact the stretched exponential shape of the curve. Looking at the first derivative of Eq. 1

$S_{ZG}^{\prime }\left(q,t\right)=-\frac{2/3\exp {\left(-{\left({\text{Γ}}_{ZG}{q}^{3}t\right)}^{2/3}\right)}^{2/3}{\left({\text{Γ}}_{ZG}{q}^3\right)}^{2/3}}{t^{1/3}}(6)$

and comparing it to the derivative of the simple exponential describing diffusion ($S_{diff}\left(q,t\right)\prime =-D{q}^2\text{exp}\left(-D{q}^{2}t\right)$, with diffusion coefficient D) it is clear that at short times the decay is much steeper for a stretched exponential contribution following the Zilman-Granek model than for simple diffusion because of the $t^{1/3}$ term in the denominator of Eq. 6 which also ensures that at long times the simple exponential will eventually decay faster. Figure 1) shows the ratio between the slopes of the Zilman-Granek stretched exponential and the simple exponential of translational diffusion using typical values both for D and Γ_ZG. A diffusion coefficient of 0.2 Ų/ns corresponds to a hydrodynamic radius $R_H=k_{B}T/\left(6\pi \eta D\right)=100$ nm at room temperature in D²O and Γ_ZG = 5 ų/ns, using the usual prefactor 0.0069 corresponds to a bending rigidity of 26 k_BT which is a reasonable value for a phospholipid bilayer. It can be seen that the ratio quickly drops to values on the order of two or less already below 100 ns. In practice, on IN15 a q value of 0.05 could be measured with a neutron wavelength of 13.5 Å, which would allow to reach almost 500 ns, 0.1 1/Å could be measured at a wavelength of 10 Å which would allow to reach fourier times up to almost 200 ns and q = 0.2 1/Å has to be measured using 6 Å neutrons, which would allow to measure Fourier times up to almost 50 ns. In any case, while the initial decay is dominated by the Zilman-Granek contribution, near the end of the Fourier time range the ratio of decays has dropped to values close to one and it is clear that the contribution from translational diffusion can not be neglected in the analysis of the data. From Figure 1 it might seem as if the Zilman-Granek contribution would be the least visible at high q. However, at higher q, the intermediate scattering function has already mostly decayed during the initial fast decay as can be seen in Figure 2. With the values used here, S_ZG has already decayed to about 0.2 while S_diff ∼ 0.8, still. In practice such a high q value can result in somewhat lengthy acquisition times, since the formfactor of the vesicle has mostly decayed.

FIGURE 1

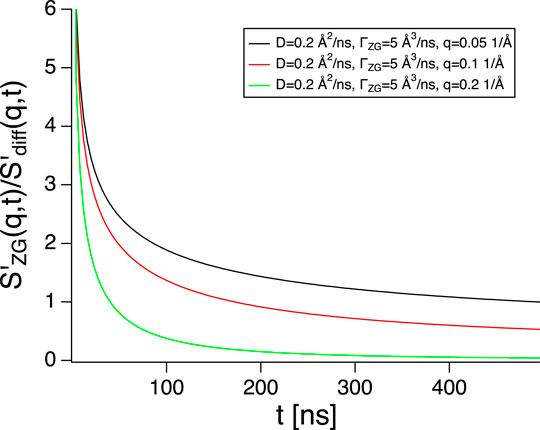
FIGURE 1. Ratio between the slope of the Zilman-Granek stretched exponential (see Eq. 6) and the derivative of simple exponential for diffusion with parameters typical for fluid phase lipid vesicles. Only at short times the contribution from diffusion is negligible.

FIGURE 2

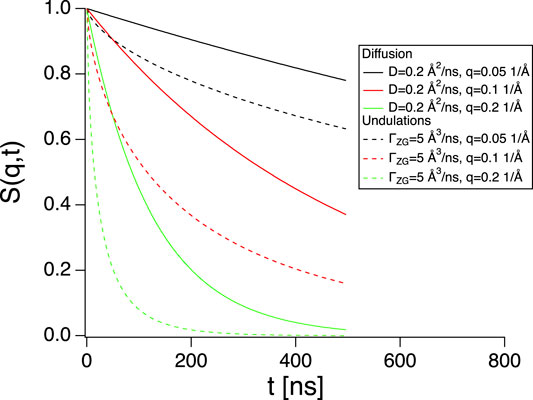
FIGURE 2. Intermediate scattering functions for diffusion (S_diff(q, t), full lines) and membrane undulations (S_ZG(q, t), dashed lines) using parameters indicated in the graph. Diffusion gives a non-negligible contribution.

Let us now turn our attention to a practical example. Fluid phase phosphatidylcholine (PC) vesicles with a radius of about 100 nm at a lipid concentration of 2 mg/ml have been measured at IN15. Fitting a simple exponential to determine an apparent diffusion coefficient ($S\left(q,t\right)=A\text{exp}\left(-D_{\text{app}}{q}^{2}t\right)$) (equivalent of fitting a simple Lorentzian to determine a linewidth in $S\left(q,\omega \right)$) gives fairly constant values of D_app (see Figure 3) and does not give a q³ dependence. In fact values slightly decrease with increasing q as the dynamic window of the measurement increasingly covers the long t part of the curve with its slow decay. Upon closer inspection, a small dip can be seen at 0.09 1/Å which might stem from correlations between membranes resulting in de Gennes narrowing [28] ($D\left(q\right)=D_0/S\left(q\right)$, with the static structure factor S(q))), which would imply that a few vesicles are not entirely unilamellar. At the lowest q, a slight increase in D_app can be seen. This behavior can be observed quite frequently in NSE data, when only a relatively weak decay of S(q, t) takes place in the NSE time window and the curves are not perfectly normalized to 1. Here, the curve for 0.029 1/Å does not decay below 0.8 and only has a value of 0.98 at the shortest times (see Figure 4). This effect is mostly taken into account by applying a prefactor to the exponential as additional fit parameter as has been the case for the determination of D_app but becomes more severe without as can be seen in Figures 5 and 6. Looking at the curves in Figure 4 it is clear that S(q, t) is not a simple exponential and the values for D_app in Figure 3 are too large for the simple diffusion of a vesicle with a 100 nm radius, so it can be concluded that we are in fact observing membrane dynamics. Fitting Eq. 1 to the data yields values of Γ_ZG on the order of 5 ų/ns (see Figure 5), realistic values of the bending rigidity, which is however no surprise at all, since the prefactors were chosen such that they give reasonable values.

FIGURE 3

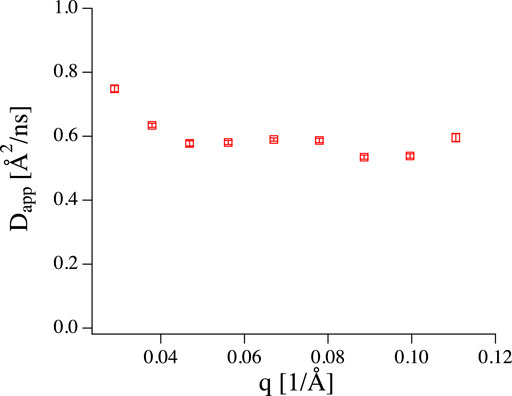
FIGURE 3. Apparent diffusion coefficient obtained from fitting NSE data of 100 nm vesicles (2 mg/ml) with a simple exponential. The value is too large for simple diffusion, but no q³ dependence is present.

FIGURE 4

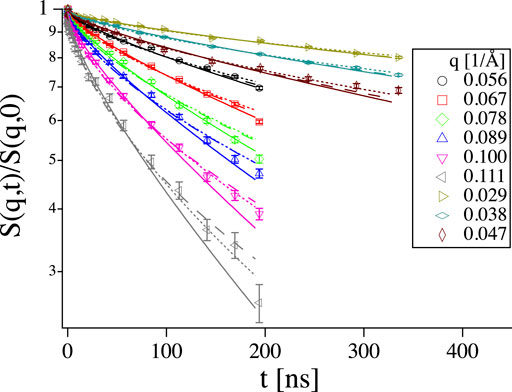
FIGURE 4. Intermediate scattering function of the same vesicles as in Figure 3 with different fits: Dashed lines: Eq. 8, full lines: Eq. 7, dotted lines: Eq. 1. All fit functions yield reasonable fits.

FIGURE 5

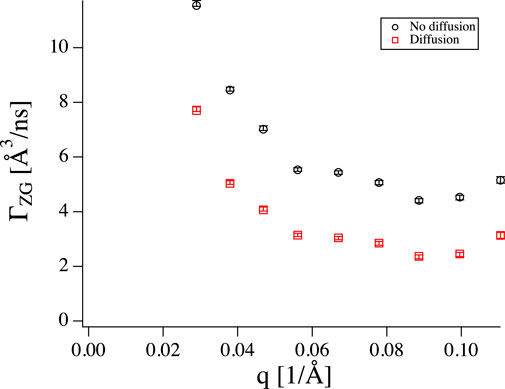
FIGURE 5. Γ_ZG obtained from fitting Eq. 1 (black circles) and Eq. 7 (red squares) to the vesicle data. Including diffusion leads to systematically lower values.

FIGURE 6

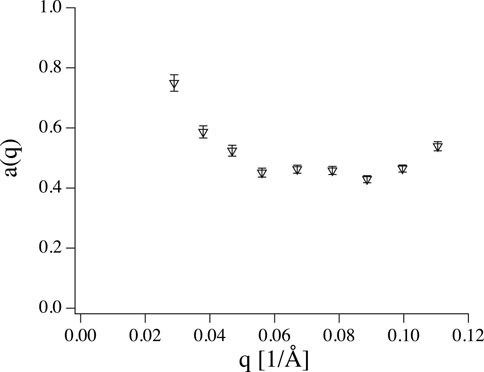
FIGURE 6. Amplitude a(q) obtained from fitting data shown in Figure 4 to Eq. 8 with Γ_ZG as shared parameter (dashed lines). Leaving a(q) free it takes values significantly smaller than 1.

The simplest way to include diffusion in the fit is by multiplication of the diffusion term with the Zilman-Granek expression:

$S\left(q,t\right)=\text{exp}\left(-D{q}^{2}t\right)\text{exp}\left(-{\left({\text{Γ}}_{ZG}{q}^{3}t\right)}^{2/3}\right).(7)$

Fitting two fairly similar relaxation rates which only differ in the exact shape of the curve is fairly difficult. Therefore, D should be known from an independent measurement such as DLS. Using D = 0.208 Ų/ns a value of Γ_ZG = 3 ų/ns is obtained which would correspond to a fairly high $\kappa =73$$k_{B}T$, which again is by no means surprising since the prefactor was chosen such that it would yield reasonable values of κ in fits without diffusion and adding a second dynamic contribution obviously leads to a decrease of the relaxation rate of the other.

The undulation motion of the membrane has a limited amplitude and consequently its visibility depends on q. Therefore, it is in principle necessary to include an amplitude a(q):

$S\left(q,t\right)=\text{exp}\left(-D{q}^{2}t\right)\left(\left(1-a\left(q\right)\right)+a\left(q\right)\text{exp}\left(-{\left({\text{Γ}}_{ZG}{q}^{3}t\right)}^{2/3}\right)\right),(8)$

where Eq. 7 is the special case where a = 1. Unfortunately, Eq. 8 inflates the number of fit parameters but conceptionally κ should be q independent and using a single κ for all q values reduces the number of fit parameter to a reasonable value. Performing the fit on the data in Figure 4 results in the amplitudes shown in Figure 6 and Γ_ZG = 12 ų/ns, which is much higher than the value obtained by simply fitting Eq. 1 due to the reduced contribution of the Zilman-Granek term.

The Milner-Safran model [29] describes membrane fluctuations for small microemulsion droplets [30] and provides an explicit expression for the amplitude. Mell et al. [31] have tried to apply Zilman-Granek model but using the amplitudes from the Milner-Safran model. They found rather mediocre agreement between theory and data. The problem might result from the fact that in the Millner-Safran theory a sphere is expanded in spherical harmonics to describe the fluctuations. This requires some excess area, relative to a perfect sphere, which minimizes the surface to volume ratio and the volume is conserved since the material can not be exchanged on the nanosecond time scale of the undulations. The longest undulation wavelength corresponds to half the circumference of the sphere and with equipartition the amplitude of that mode (n = 2) is given by Eq. 6 of Schneider et al. [32].

$\langle U^2\rangle =\frac{k_{B}T}{16\kappa }{R}^2(9)$

which gives $\sqrt{\langle U^2\rangle }=5.6$ nm for $\kappa =20$k_BT and R = 100 nm which in turn would result in unreasonably large excess areas and therefore, it is safe to assume that long wavelength undulations are not present in a real phospholipid vesicle system as predicted by the Milner-Safran theory.

This raises another interesting question. What is the range of undulation wavelengths that is actually relevant for NSE measurements of lipid vesicles? Half the vesicles circumference is an upper limit which is most likely not reached due to the lack of excess area in the vesicles. To satisfy equipartition, long wavelength undulations need rather large amplitudes, which results in a strong deformation of the vesicles from their ideal spherical shape and increases the surface to volume ratio. Since the volume of the vesicles is conserved over the nanosecond timescale of the undulations some excess surface are is needed to perform undulation motions [29] and the amount of excess area that would be needed for the long wavelength undulations with their large amplitudes may not be available in practice. Monkenbusch et al. [13] mapped the parameter space but in a range more relevant to microemulsions by evaluating the complete expression of the Zilman-Granek expression:

$s\left(q,t\right)\sim {{{\displaystyle \int }}^{\text{}}}_0^1\text{d}\mu {{{\displaystyle \int }}^{\text{}}}_0^{R_{max}}\text{d}r{J}_0\left(qr\sqrt{1-{\mu }^2}\right)\times \text{exp}\left(\frac{-k_{B}T}{2\pi \kappa }{q}^2{\mu }^2{{{\displaystyle \int }}^{\text{}}}_{k_{min}}^{k_{max}}\text{d}k\frac{1-J_0\left(kr\right)\text{exp}\left(-\kappa /\left(4\eta \right)k^{3}t\right)}{k^3}\right)(10)$

where J₀ is the 0 order Bessel function, R_max is the maximum length scale, related to the minimum undulation wavevector $k_{min}=2\pi /R_{max}$ and the maximum wavevector is given by a cut-off length on the order of the molecular length which has relatively little influence on the result. Figure 7 compares the result for Eq. 1 and 10 for q = 0.05 1/Å, $\kappa =20$$k_{B}T$ with different R_max. It can be seen that R_max does have an influence on the intermediate scattering function. The result from Eq. 1 falls right between R_max = 100 and R_max = 150 which is not too far from the maximum length $\pi R$ in typical vesicles, which are usually between 50 and 100 nm in radius. In the future, it might be interesting to investigate vesicles of different sizes. However this might be challenging since smaller vesicles are difficult to produce and larger vesicles tend to be unstable. While Eq. 10 is still computationally expensive due to the nested integrals, with modern computers it is possible to use Eq. 10 as a fit function. For example, the curves in Figure 7 were calculated with 128 points on a 2016 MacBook Pro in about 30, 9 and 2 s for R_max 150, 100 and 50 nm using not particularly optimized C code. A more a fundamental problem is that either κ or R_max should be known to fit the other.

FIGURE 7

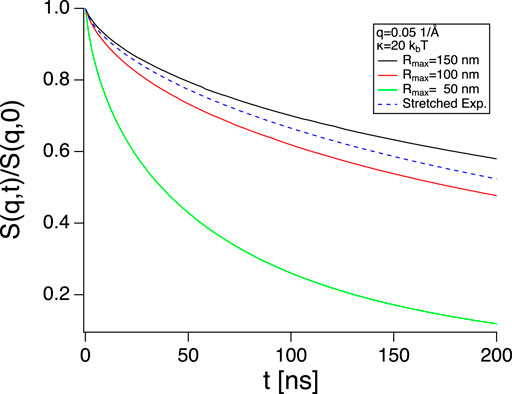
FIGURE 7. S(q, t) calculated using Eq. 10 with different R_max (full lines) and Eq. 1 (dashed blue line, using κ not $\tilde{\kappa }$) using parameters indicated in the graph. The maximum length scale clearly has an effect on S(q, t).

3 Background Subtraction

As new experiments are looking for increasingly subtle effects in membranes using NSE, such as thickness fluctuations of the membrane [22, 25] or short scale motions of lipids [26] a careful background subtraction becomes increasingly important.

Background correction in NSE [33] is greatly complicated by the fact that the incoherent scattering process changes the polarisation of the beam to -1/3 of its initial value [34]. As a result the shape of the background can be a rather complicated combination of coherent and incoherent dynamics with an amplitude of opposite sign (see Figure 8).

FIGURE 8

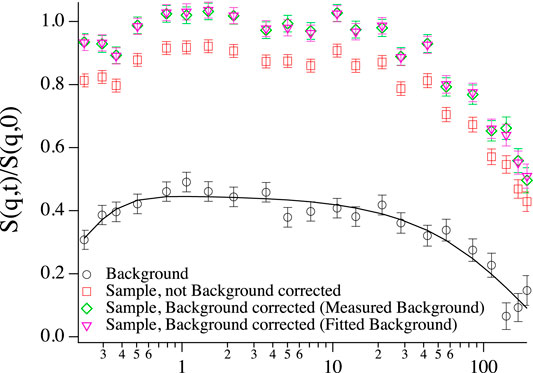
FIGURE 8. Intermediate scattering function of vesicles at low concentration (∼1 mg/ml) at q = 0.1 1/Å, background corrected with directly subtracted background (green diamonds), background corrected with fitted background (purple triangles), without background correction (red squares) and the corresponding background that was subtracted from the sample to give the background subtracted data sets (black circles, black line: double exponential fit) with fast incoherent dynamics at short times, which are still visible in the background corrected sample and background correction could not fully account for it.

In addition scattering from the instrument itself contributes a mostly elastic signal. This complicated shape of the background sets a high-q limit for the measurement of coherent dynamics in aqueous solution by NSE. The form factor typically decays as $q^{-4}$ at high q while the incoherent scattering coming mostly from the background has a constant intensity with q and the subtraction of a background with a complicated shape from a weak signal quickly starts requiring a level of precision which would make acquisition times prohibitively long. As a rule of thumb, the coherent signal should ideally be noticeably higher than the incoherent signal. As long as it is on the same order of magnitude, measurements start becoming lengthy but are still feasible. With the intensity of deuterated buffer, and typical concentrations of lipid vesicles, this means that anything above 0.2 1/Å becomes extremely lengthy to measure.

After correcting for resolution effects [35] the non-normalized intermediate scattering function of a sample with coherent intensity $I_{coh}$ and incoherent intensity I_inc will give

$s\left(q,t\right)=I_{coh}{f}_{coh}\left(t\right)-1/3I_{inc}{f}_{inc}\left(t\right),(11)$

where f = 1 at t = 0. This signal is normalized by the difference of the polarized intensity in up and down direction with $I_{up}=I_{coh}+1/3I_{inc}$ and $I_{down}=2/3I_{inc}$ so that the normalized intermediate scattering function reads

$S\left(q,t\right)=\frac{I_{coh}{f}_{coh}\left(t\right)-1/3I_{inc}{f}_{inc}\left(t\right)}{I_{coh}-1/3I_{inc}}.(12)$

A few remarks on Eq. 12 are in order. If the decay rate of $f_{inc}$ is higher than that of $f_{coh}$ and $I_{inc}$ is sufficiently large relative to $I_{coh}$, S(q, t) can have values larger than 1. If both the nominator and denominator in Eq. 12 are negative, their negative signs will cancel out and incoherent scattering will appear as a relaxation with a positive amplitude. There can be fast dynamics, mostly in the background, which prevent the curve from tending to one within the dynamic window of the measurement.

While it is possible to directly subtract the transmission weighted background measurement directly from the individual detector images that are afterward used to calculate the echo, this requires the phase of the echo to be extremely stable [36]. Therefore, the standard procedure on IN15 is to calculate s(q, t) for sample and background individually and subtract the background echo from the sample echo to obtain the background corrected non-normalized intermediate scattering function

$s_{cor}\left(q,t\right)=s_{sample}\left(q,t\right)-T_{sb}{s}_{bkg}\left(q,t\right),(13)$

where $T_{sb}$ is the transmission of the sample relative to the background. For normalization the transmission weighted up and down intensities of the background measurement are subtracted from the up and down intensities of the sample

$S_{cor}\left(q,t\right)=\frac{s_{cor}\left(q,t\right)}{I_{coh,sample}-1/3I_{inc,sample}-T_{sb}{I}_{coh,bkg}+1/3T_{sb}{I}_{inc,bkg}}.(14)$

Assuming that $s_{sample}\left(q,t\right)$ contains coherent and incoherent contributions from the background (solvent and instrument) and from the part we are interested (e.g., vesicles), then

$s_{sample}\left(q,t\right)=I_{coh,ves}{f}_{coh,ves}\left(t\right)-1/3I_{inc,ves}{f}_{inc,ves}\left(t\right)+T_{sb}\left(I_{coh,bkg}{f}_{coh,bkg}\left(t\right)-1/3I_{inc,bkg}{f}_{inc,bkg}\left(t\right)\right),(15)$

and the subtraction according to Eq. 13 eliminates all background contributions but leaves both $f_{coh,ves}\left(t\right)$ and $f_{inc,ves}\left(t\right)$ untouched. However, assuming that both show the same time dependence, which should be valid at large q, the incoherent contribution from the relevant part of the sample manifests simply as a reduction of the amplitude of the signal, which normalization according to Eq. 14 should take care of as long as the condition $I_{coh,ves}-1/3I_{inc,ves}\ne 0$ is fulfilled. Otherwise no signal can be detected. This procedure is generally quite robust but has its limitations as soon as the background contains several contributions with different phase, in which case the background should be subtracted detector image by detector image. This background subtraction procedure also delicately depends on both correct values of the transmission and the ratio of coherent to incoherent scattering. With aqueous samples, this can easily lead to some small inaccuracies since it is almost inevitable that the D₂O of the solvent exchanges with H₂O in the surrounding air. The degree of exchange can easily be slightly different between sample and background, for example because the background sample was prepared in a larger container than the other samples and standing open for longer during the preparation of the other samples using solvent from that container. If the sample compound itself contains a large number of exchangeable hydrogen atoms, it can even be advantageous to deliberately add H₂O to the background sample to match the coherent to incoherent ratio in the solvent of the sample [37]. Even if the samples and their background have been prepared with greatest care, there can still be small effects from multiple scattering which lead to a slightly increased apparent incoherent background. Following Eq. 33 from Shibayama et al. [38] with 2 mm sample thickness and assuming a relatively high concentration of 1 v% hydrogenated material (for which for simplicity we take the cross section of H₂O) results in a correction on the order of 0.005, which may still be important but typically, imperfections in the normalization stemming from sample preparation are on the order of a few percent.

Instead of subtracting a completely measured curve s_bkg(q, t) in Eq. 13, in some situations it can be advantageous to subtract a curve that is the result of a fit to s_bkg(q, t). If the shape is known and simple enough, it can save quite some time to only measure a few Fourier time points of s_bkg(q, t) and fit the rest of the expression. To give an example, fully deuterated polymer melts show an essentially flat background with fast dynamics that are not in the time window of NSE. Even if the full curve has been measured, it can be preferable to use a fitted background to avoid extra noise from a noisy background measurement. On the other hand, one runs the risk of introducing artifacts by using an oversimplified fit function for the background. Sometimes, even a double exponential fit can fail to capture all subtleties of the background. To the author’s experience, it is generally preferable to measure the full background curve, whenever possible. After all, a fitted background can still be used after measuring the full curve, while the opposite case is more difficult. In Figure 8 both versions of background subtraction are shown. Since the double exponential fit (black line) nicely describes the measured background, there is not much of a difference between the two versions of background correction, except for the third to last point, which is artificially high in the green curve where the background was directly subtracted, since the same point seems somewhat low in the measured background and the background fit straightens out this artifact.

The intricate details of background subtraction do not matter too much as long as the signal from the sample is large compared to the background. Unfortunately, some of the most interesting phenomena are best seen where the intensity is weak. Both shape fluctuations of microemulsion droplets [30, 39] and thickness fluctuations of membranes [22, 24, 25, 40] are best seen in their respective form factor minima. The result of an imperfect background subtraction usually is a curve that does not have an amplitude of exactly one together with a slight increase or flattening of S(q, t) at short times, which is the result of a not perfectly subtracted incoherent contribution. Fitting such a curve with an amplitude fixed at 1, can lead to too high relaxation rates (see Figures 5 and 6), while leaving the amplitude as a free fit parameter leads to larger error bars and can potentially result in too low fitted relaxation rates.

Another kind of phenomenon where careful background subtraction is crucial are the short length scale motions observed by Gupta et al. [26], where a different exponent x in the evolution of the mean square displacement $\langle R^2\rangle =-6\text{ln}\left(S\left(q,t\right)\right)/q^2\sim t^x$ at short times is attributed to an anomalous local motion of the head groups. Instead of x = 1 for diffusion or x = 2/3 for undulations a smaller value of 0.26 is found. This is an extremely subtle effect that prevails up to about $\langle R^2\rangle =10$ Ų which implies a decay of S(q, t) at 0.15 1/Å from one to about 0.96. To complicate things more, imperfect background subtraction would have the exact same effect on the $\langle R^2\rangle$ with an intercept that is not exactly one and some residual incoherent contribution from the background, which slows down the decay of S(q, t) at short times. The curve in Figure 9 (left) is not brought up to exactly one at short times but only to about 0.95, converting to $\langle R^2\rangle$ shows a small scaling exponent x at short times even after background subtraction. However, the contribution has almost disappeared when brute force renormalising S(q, t) with a factor 1/0.96. This shows that it is extremely difficult to differentiate such effects from an imperfect background subtraction.

FIGURE 9

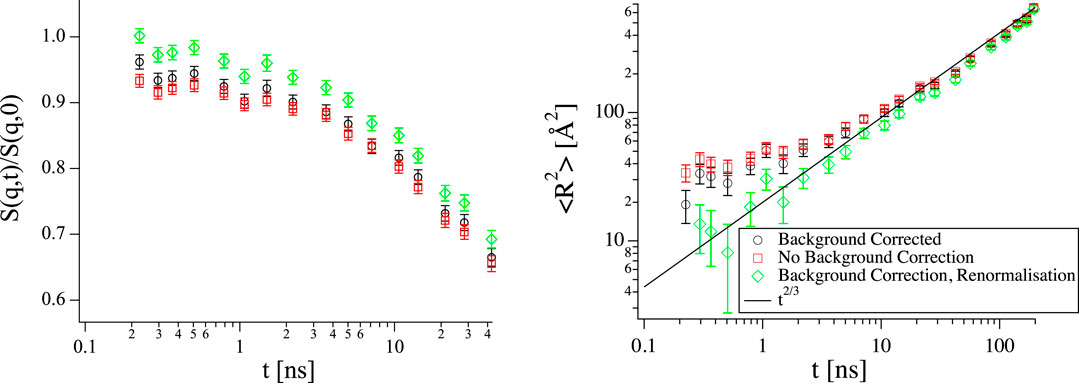
FIGURE 9. Left: Short time range of S(q, t) from the same vesicle sample as in Figure 4 at q = 0.11 1/Å with logarithmic x-axis, the same color code as in the right hand panel applies. Right: Mean square displacement calculated from the curves on the left. The black line shows scaling with t^2/3 as expected for the Zilman-Granek model. The Background corrected sample does not exactly go up to one at short times (left). As a result a scaling with low scaling exponent x appears at short times in $\langle R^2\rangle$(right). This behavior disappears when brute force renormalizing the curve with a factor 1/0.96 which ensures that the curve starts at 1 (left) and $\langle R^2\rangle$ scales as t^2/3 even at the shortest time (right).

4 Conclusion

In this paper the effect of background subtraction and data treatment on the information that can be gained from neutron spin echo (NSE) experiments on bilayers was discussed. The diffusion of typical lipid vesicles with radii between 50 and 100 nm as they are used in NSE experiments to investigate membrane dynamics does have an effect on the time and length scale covered by modern NSE spectrometers.

As long as vesicles of the same size and therefore same diffusion coefficient are compared, it is not strictly necessary to include translational diffusion in the analysis but it should be kept in mind that the absolute values of the bending rigidity that are obtained from the data without taking into account diffusion have only a limited significance. Unfortunately, the renormalization factors that are currently in use are based on data that was analyzed without diffusion to give values of the bending rigidity that agree with values obtained from other methods. If diffusion is taken into account when fitting data, there is still uncertainty concerning the value of the amplitude a(a) in Eq. 8. Depending on whether it is fixed at one or left as a free parameter in the fit, the apparent value of the bending rigidity can change in either direction compared to the case without contribution from diffusion.

Nevertheless, as soon as bending rigidities from vesicles with different radii are compared it is advised to include a contribution from diffusion. Given the similar time scales, the diffusion coefficient should be obtained from an independent measurement such as DLS, which has its intricacies as well, since in the relatively concentrated samples used in NSE, the diffusion coefficient obtained at low q by DLS is most likely affected by de Gennes narrowing [28] ($D\left(q\right)=D_0/S\left(q\right)$, with the static structure factor S(q)) while it is (almost) not in the NSE q range. Therefore, the diffusion coefficient should ideally be determined in a dilute sample. If this is not possible, the effect of de Gennes narrowing can either be calculated from a measured structure factor (e.g., by SANS), simply be estimated from a suitable model or D can be calculated via the Stokes-Einstein equation from a size measured by SANS or another suitable technique. While this helps in making values obtained from vesicles with different sizes comparable, it still does not prevent the obtained values from being unreliable as far as their absolute values are concerned and given both the experimental uncertainties concerning the exact fitting procedure and the theoretical uncertainties concerning exact prefactors in the equations used for fitting, we will probably have to accept that we can only have a reliable relative comparison. What would put NSE in a position to provide reliable absolute values would be an expression for a(q), which would allow to refine parameters from theory such as the height of the neutral surface in Eq. 3.

While usually background subtraction is not discussed in too much detail in NSE, it becomes increasingly important as more subtle effects are being studied and incorrect background subtraction and it was shown how imperfect background subtraction can lead to artifacts.

All of this shows that there are some challenges ahead on the way to gaining even more detailed information on membrane dynamics from NSE measurements.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: dx.doi.org/10.5291/ILL-DATA.TEST-2861 dx.doi.org/10.5291/ILL-DATA.TEST-2712.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Raw data of the NSE curves shown here are available under dx.doi.org/10.5291/ILL-DATA.TEST-2861 and dx.doi.org/10.5291/ILL-DATA.TEST-2712. The author would like to thank Andrew Dennison, Andrew Parnell and Michael Gradzielski for letting him use their data in this paper as much as Olaf Holderer for sharing his Python code for Eq. 10. Financial support from the BMBF Project No. 05K13KT1 is gratefully acknowledged.

References

1. Mezei F. Neutron spin echo: a new concept in polarized thermal neutron techniques. Z Phys A Hadrons Nuclei (1972) 255:146–60. doi:10.1007/BF01394523

CrossRef Full Text | Google Scholar

2. Huang JS, Milner ST, Farago B, Richter D. Study of dynamics of microemulsion droplets by neutron spin-echo spectroscopy. Phys Rev Lett (1987) 59:2600–3. doi:10.1103/PhysRevLett.59.2600

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Farago B, Monkenbusch M, Goecking K, Richter D, Huang J. Dynamics of microemulsions as seen by neutron spin echo. Physica B (1995) 213–214:712–7. doi:10.1016/0921-4526(95)00257-A

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Pfeiffer W, König S, Legrand JF, Bayerl T, Richter D, Sackmann E. Neutron spin echo study of membrane undulations in lipid multibilayers. Europhys Lett (1993) 23:457. doi:10.1209/0295-5075/23/6/013

CrossRef Full Text | Google Scholar

5. Zilman AG, Granek R. Undulations and dynamic structure factor of membranes. Phys Rev Lett (1996) 77:4788–91. doi:10.1103/PhysRevLett.77.4788

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Farge E, Maggs AC. Dynamic scattering from semiflexible polymers. Macromolecules (1993) 26:5041–4. doi:10.1021/ma00071a009

CrossRef Full Text | Google Scholar

7. Helfrich W. Elastic properties of lipid bilayers - theory and possible experiments. Z Naturforsch C Biosci: J Biosci (1973) 28:693–703. doi:10.1515/znc-1973-11-1209

CrossRef Full Text | Google Scholar

8. Freyssingeas E, Roux D, Nallet F. Quasi-elastic light scattering study of highly swollen lamellar and sponge phases. J Phys II (1997) 7:913–29. doi:10.1051/jp2:1997162

CrossRef Full Text | Google Scholar

9. Nagao M, Seto H, Kawabata Y, Takeda T. Temperature and pressure effects on structural formations in a ternary microemulsion. J Appl Crystallogr (2000) 33:653–6. doi:10.1107/S0021889899013679

CrossRef Full Text | Google Scholar

10. Mihailescu M, Monkenbusch M, Endo H, Allgaier J, Gompper G, Stellbrink J, et al. Dynamics of bicontinuous microemulsion phases with and without amphiphilic block-copolymers. J Chem Phys (2001) 115:9563–77. doi:10.1063/1.1413509

CrossRef Full Text | Google Scholar

11. Farago B, Falus P, Hoffmann I, Gradzielski M, Thomas F, Gomez C. The IN15 upgrade. Neutron News (2015) 26:15–7. doi:10.1080/10448632.2015.1057052

CrossRef Full Text | Google Scholar

12. Komura S, Takeda T, Kawabata Y, Ghosh SK, Seto H, Nagao M. Dynamical fluctuation of the mesoscopic structure in ternary -water-n-octane amphiphilic systems. Phys Rev E (2001) 63:041402. doi:10.1103/PhysRevE.63.041402

CrossRef Full Text | Google Scholar

13. Monkenbusch M, Holderer O, Frielinghaus H, Byelov D, Allgaier J, Richter D. Bending moduli of microemulsions; comparison of results from small angle neutron scattering and neutron spin-echo spectroscopy. J Phys Condens Matter (2005) 17:S2903–9. doi:10.1088/0953-8984/17/31/017

CrossRef Full Text | Google Scholar

14. Seifert U, Langer SA. Viscous modes of fluid bilayer membranes. Europhys Lett (1993) 23:71–6. doi:10.1209/0295-5075/23/1/012

CrossRef Full Text | Google Scholar

15. Rawicz W, Olbrich K, McIntosh T, Needham D, Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys J (2000) 79:328–39. doi:10.1016/j.bpj.2009.11.026

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Nagle JF. Area compressibility moduli of the monolayer leaflets of asymmetric bilayers from simulations. Biophys J (2019) 117:1051–6. doi:10.1016/j.bpj.2019.08.016

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Doktorova M, Levine MV, Khelashvili G, Weinstein H. A new computational method for membrane compressibility: bilayer mechanical thickness revisited. Biophys J (2019) 116:487–502. doi:10.1016/j.bpj.2018.12.016

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Bloom M, Evans E, Mouritsen OG. Physical properties of the fluid lipid-bilayer component of cell membranes: a perspective. Q Rev Biophys (1991) 24:293–397. doi:10.1017/S0033583500003735

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Pan JJ, Tristram-Nagle S, Nagle JF. Effect of cholesterol on structural and mechanical properties of membranes depends on lipid chain saturation. Phys Rev E (2009) 80:021931. doi:10.1103/PhysRevE.80.021931

CrossRef Full Text | Google Scholar

20. Watson MC, Brown FLH. Interpreting membrane scattering experiments at the mesoscale: the contribution of dissipation within the bilayer. Biophys J (2010) 98:L9–11. doi:10.1016/j.bpj.2009.11.026

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Lee J, Choi S, Doe C, Faraone A, Pincus PA, Kline SR. Thermal fluctuation and elasticity of lipid vesicles interacting with pore-forming peptides. Phys Rev Lett (2010) 105:038101. doi:10.1103/PhysRevLett.105.038101 |

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Nagao M, Kelley EG, Ashkar R, Bradbury R, Butler PD. Probing elastic and viscous properties of phospholipid bilayers using neutron spin echo spectroscopy. J Phys Chem Lett (2017) 8:4679–84. doi:10.1021/acs.jpclett.7b01830

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Gupta S, de Mel JU, Schneider GJ. Dynamics of liposomes in the fluid phase. Curr Opin Colloid Interface Sci (2019) 42:121–36. doi:10.1016/j.cocis.2019.05.003

CrossRef Full Text | Google Scholar

24. Nagao M, Chawang S, Hawa T. Interlayer distance dependence of thickness fluctuations in a swollen lamellar phase. Soft Matter (2011) 7:6598–605. doi:10.1039/C1SM05477E

CrossRef Full Text | Google Scholar

25. Woodka AC, Butler PD, Porcar L, Farago B, Nagao M. Lipid bilayers and membrane dynamics: insight into thickness fluctuations. Phys Rev Lett (2012) 109:058102. doi:10.1103/PhysRevLett.109.058102

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Gupta S, de Mel JU, Perera RM, Zolnierczuk P, Bleuel M, Faraone A, et al. Dynamics of phospholipid membranes beyond thermal undulations. J Phys Chem Lett (2018) 9:2956–60. doi:10.1021/acs.jpclett.8b01008

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Gupta S, Schneider GJ. Modeling the dynamics of phospholipids in the fluid phase of liposomes. Soft Matter (2020) 16:3245–56. doi:10.1039/C9SM02111F

PubMed Abstract | CrossRef Full Text | Google Scholar

28. de Gennes PG. Liquid dynamics and inelastic scattering of neutrons. Physica (1959) 25:825–39. doi:10.1016/0031-8914(59)90006-0

CrossRef Full Text | Google Scholar

29. Milner ST, Safran SA. Dynamical fluctuations of droplet microemulsions and vesicles. Phys Rev A (1987) 36:4371–9. doi:10.1103/PhysRevA.36.4371

CrossRef Full Text | Google Scholar

30. Farago B, Gradzielski M. The effect of the charge density of microemulsion droplets on the bending elasticity of their amphiphilic film. J Chem Phys (2001) 114:10105–22. doi:10.1063/1.1362690

CrossRef Full Text | Google Scholar

31. Mell M, Moleiro L, Hertle Y, Fouquet P, Schweins R, López-Montero I, et al. Bending stiffness of biological membranes: what can be measured by neutron spin echo? Eur Phys J E (2013) 36:1–13. doi:10.1140/epje/i2013-13075-2

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Schneider M, Jenkins J, Webb W. Thermal fluctuations of large quasi-spherical bimolecular phospholipid vesicles. J Phys France (1984) 45:1457–72. doi:10.1051/jphys:019840045090145700

CrossRef Full Text | Google Scholar

33. Farago B. The basics of neutron spin-echo (2003). Available at: https://www.osti.gov/etdeweb/servlets/purl/20009251.

CrossRef Full Text | Google Scholar

34. Mezei F. The principles of neutron spin echo. In: F Mezei, editor Neutron spin echo spectroscopy: basics, trends and applications. Berlin, Heidelberg: Springer Berlin Heidelberg (1980). p. 1–26.

CrossRef Full Text | Google Scholar

35. Mezei F. Fundamentals of neutron spin echo spectroscopy. In: Neutron spin echo spectroscopy: basics, trends and applications. Berlin, Heidelberg: Springer Berlin Heidelberg (2003). p. 5–14.

CrossRef Full Text | Google Scholar

36. Farago B. in preparation (2020).

CrossRef Full Text | Google Scholar

37. Farago B. Private communication (2020).

CrossRef Full Text | Google Scholar

38. Shibayama M, Nagao M, Okabe S, Karino T. Evaluation of incoherent neutron scattering from softmatter. J Phys Soc Jpn (2005) 74:2728–36. doi:10.1143/JPSJ.74.2728

CrossRef Full Text | Google Scholar

39. Nagao M, Seto H. Concentration dependence of shape and structure fluctuations of droplet microemulsions investigated by neutron spin echo spectroscopy. Phys Rev E (2008) 78:011507. doi:10.1103/PhysRevE.78.011507

CrossRef Full Text | Google Scholar

40. Nagao M. Observation of local thickness fluctuations in surfactant membranes using neutron spin echo. Phys Rev E (2009) 80:031606. doi:10.1103/PhysRevE.80.031606

CrossRef Full Text | Google Scholar