First-Principles Investigation on Electrochemical Performance of Na-Doped LiNi1/3Co1/3Mn1/3O2

The cathode material LiNi_1/3Co_1/3Mn_1/3O₂ for lithium-ion battery has a better electrochemical property than LiCoO₂. In order to improve its electrochemical performance, Na-doped LiNi_1/3Co_1/3Mn_1/3O₂ is one of the effective modifications. In this article, based on the density functional theory of the first-principles, the conductivity and the potential energy of the Na-doped LiNi_1/3Co_1/3Mn_1/3O₂ are calculated with Materials Studio and Nanodcal, respectively. The calculation results of the band gap, partial density of states, formation energy of intercalation of Li⁺, electron density difference, and potential energy of electrons show that the new cathode material Li_1−xNa_x Ni_1/3Co_1/3Mn_1/3O₂ has a better conductivity when the Na-doping amount is x = 0.05 mol. The 3D and 2D potential maps of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ can be obtained from Nanodcal. The maps demonstrate that Na-doping can reduce the potential well and increase the removal rate of lithium-ion. The theoretical calculation results match well with experimental results. Our method and analysis can provide some theoretical proposals for the electrochemical performance study of doping. This method can also be applied to the performance study of new optoelectronic devices.

Introduction

Since Sony introduced commercial lithium-ion batteries (LIBs) that used LiCoO₂ as cathode, LIBs have been used in electric vehicles (EVs), hybrid electric vehicles (HEVs), and mobile electronic devices for their good cycle performance, long life, less self-discharge, high specific capacity, and working voltage [1]. In the current era of LIBs, there is an ever-growing demand for even higher energy densities to power mobile devices with increased power consumption.

Cathode materials are one of the key materials to determine the electrochemical performance of LIBs. Recently, the ternary cathode material LiNi_xCo_yMn_zO₂ (NCM, 0 < x, y, z < 1) has been paid much attention for its lower price and better electrochemical performance. LiNi_1/3Co_1/3Mn_1/3O₂, LiNi_0.5Co_0.2Mn_0.3O₂, and LiNi_0.4Co_0.2Mn_0.4O₂ [2, 3] are often studied by scholars and experts. Their precursors are made by hydroxide coprecipitation reaction combined with solid-phase sintering step [4]. LiNi_1/3Co_1/3Mn_1/3O₂ is considered a promising cathode material for commercial LIBs due to its low price, high conductivity, excellent cycle performance, high reversibility, and stable structure [5]. However, the commercial LiNi_1/3Co_1/3Mn_1/3O₂ has already reached its theoretical limit, with poor cycling performance at high rate and thermal stability at high cutoff voltage, which limit its further application in higher-power systems such as EVs and HEVs [6].

Surface modification [6, 7] and doping [8, 9] are analyzed experimentally to improve the electrochemical performance of LiNi_1/3Co_1/3Mn_1/3O₂ for high-power electric devices. The discharging capacity and rate capacity can dramatically be improved by coating with Li₂MoO₄ [7]. The lithium difluorophosphate (LiPO₂F₂) electrolyte additive drops are applied to significantly improve the electrochemical performance of LiNi_1/3Co_1/3Mn_1/3O₂ cell at room and low temperature [10]. Some cations [11], anions [12], and polyanions [13] are doped to substitute part of Ni, Co, Mn, or oxygen sites to improve the electrochemical performance of LiNi_1/3Co_1/3Mn_1/3O₂. The K-doped LiNi_0.5Co_0.2Mn_0.3O₂ has a higher column efficiency, larger reversible discharging capacity, and rate capacity. Because bigger metal ions K⁺ can extend the space of Li-O, decrease the cation mixing (Li⁺/Ni²⁺), and enhance the structure stability [14]. The Na-doped LiNi_1/3Co_1/3Mn_1/3O₂ had been extensively investigated by Li et al. [15]; their experimental investigations showed that Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ has a more excellent electrochemical performance.

Samples and raw materials needed in the NCM ternary cathode material experiments are of high cost, and some experiments may be conducted several times; thus, the entire experiment will need a long time. However, based on first-principles [16–18], the physical and electrochemical properties can be calculated and analyzed by Materials Studio, Nanodcal, and MATLAB; the results can give some theoretical advice or investigation directions about the relevant experiments, and the theoretical calculation can effectively shorten the whole investigation period and reduce the cost [16]. In this article, the Na-doped layer-structure Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ is studied theoretically with density functional theory of first-principles; the results show that the electrochemical performance of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ is affected by the proportion of Na-substitution and the best proportion of Na-substitution in LiNi_1/3Co_1/3Mn_1/3O₂ is in agreement with that of experiments [15].

Principle

The Theory Foundation of the First-Principles

Quantum mechanics is about the properties of molecules and atoms, which is closer to the nature of all things in the universe, so it is called the first principle. In fact, according to the nuclear charge number of atoms and some simulated environmental parameters (such as electron quantity and static mass), the first principle means to solve the Schrödinger equation as shown in Equation (1).

$\widehat{\mathit{H}}\mathit{\psi }\left(\mathit{r}\right)=\mathit{E\psi }\mathrm{(}\mathit{r}\mathrm{),}(1)$

where $\widehat{\mathit{H}}$ is the Hamiltonian and $\mathit{E}$ is the system's energy. The solution of the Equation (1) is the eigenvalue (energy value) and eigenfunction (wave function), which are used to analyze the related properties of particles. However, for the multiparticle system, it is impossible to solve the Schrödinger equation exactly because of a complex electronic interaction in the system, so it is necessary to simplify and approximate it reasonably. The mass of the nucleus is much larger than that of the electron, and the velocity of the nucleus is much smaller than that of the electron. For the electron, the nucleus can be assumed to be stationary, and then the Schrödinger equation can be approximated adiabatically, as shown in Equation (2).

$\widehat{\mathit{H}}\mathrm{(}\mathit{R}\mathrm{)}\mathit{\psi }\left(\mathit{r}\right)=\mathit{E}\mathrm{(}\mathit{R}\mathrm{)}\mathit{\psi }\mathrm{(}\mathit{r}\mathrm{),}(2)$

where $\widehat{\mathit{H}}\mathrm{(}\mathit{R}\mathrm{)}$ is the adiabatical Hamiltonian and $\mathit{E}\mathrm{(}\mathit{R}\mathrm{)}$ is the system's adiabatical energy.

Density Functional Theory

The density functional theory originates from the Thomas–Fermi model proposed by Thomas [19] and Fermi [20]. This model ignores the exchange-correlation between electrons. On this assumption, the Schrödinger equation can be converted into a simpler wave equation, and then the function of the total energy about the electronic system is determined only by the electron density function $\mathit{r}\left(\mathit{r}\right)$, which is called density functional theory (DFT). This model is too rough to be used directly. Based on the Thomas–Fermi model, under the Born–Oppenheimer approximation, nonrelativistic adiabatic approximation, and single-electron approximation, Hohenberg and Kohn proposed the more exact density functional method (HK theorems) [21, 22]. The physical properties of matter can be analyzed by self-consistent calculation. According to HK theorems, properties of particles’ ground state can be expressed by particle number density ρ(r) instead of the wave function, the system degrees turning 3N into 3, so a lot of computing resources can be saved.

However, HK theorems still have the following three problems: firstly, how to determine the particle number density function ρ(r); secondly, how to determine the kinetic energy functional T [ρ(r)]; lastly, how to determine the exchange-correlation energy functional E_xc [ρ(r)].

Kohn–Sham Equation and Exchange-Correlation Functional

The first and the second problems can be solved by the Kohn–Sham equation [23], as shown in Equation (3).

$\left\{-{\nabla }^2+V_{\mathrm{KS}}\left[\rho \left(\mathit{r}\right)\right]\right\}{\phi }_i\left(\mathit{r}\right)=E_i{\phi }_i\left(\mathit{r}\right),(3)$

where $V_{\mathrm{KS}}\left[\rho \left(\mathit{r}\right)\right]=V_{\mathrm{ne}}\left[\rho \left(\mathit{r}\right)\right]+V_{\mathrm{coul}}\left[\rho \left(\mathit{r}\right)\right]+V_{\mathrm{xc}}\left[\rho \left(\mathit{r}\right)\right]$, $V_{\mathrm{ne}}\left[\rho \left(\mathit{r}\right)\right]$ is the attraction potential between nuclei, $V_{\mathrm{coul}}\left[\rho \left(\mathit{r}\right)\right]$ is the Coulomb potential between electrons, and $V_{\mathrm{xc}}\left[\rho \left(\mathit{r}\right)\right]$ is the exchange-correlation potential. In Equation (3), the Hamiltonian with the interacting particles is replaced with that of the noninteracting particles, and the interacting particles are described by the exchange-correlation functional E_xc [ρ(r)]; then, the single-electron equation can be obtained.

The last problem is generally solved by the local density approximation (LDA) and the general gradient approximation (GGA). LDA can give more accurate results for the system with small change of electron density relative in the space. Considering the ununiformity of the electron density, GGA can give more exact results than LDA [24].

With the development of computer technology, computing power has been improved dramatically, and programs based on DFT have gradually become a universal means to study the properties of materials. Multielectron system is the research object of DFT, and HK theorems are the theoretical basis of this method.

Method and Model

Based on PW91 (Perdew-Wang) [25] method with the PBE (Perdew-Burke-Ernzenhof) [26] exchange-correlation functional, DFT calculations have been carried out using GGA in the CAmbridge Serial Total Energy Package (CASTEP) program of Materials Studio 8.0. The CASTEP is the quantum mechanical procedure of the plane wave pseudopotential method. An ultrasoft pseudopotential is used to describe the Coulomb attraction potential between the inner layer electrons around the nucleus and that of the outer layer [27], A plane wave cutoff of 340 eV and a k-point mesh of 4 × 4 × 1 in the Monkhorst–Pack [28] sampling scheme are used. The parameter about the self-consistent calculation is 1 × 10⁻⁶ eV/atom. To obtain the local stable structure of material, the structural geometry is optimized until the average force on every atom falls less than 0.3 eV/nm, the maximum displacement tolerance is less than 1 × 10⁻⁴ nm, and the maximum stress tolerance less than 0.05 GPa.

For this theoretical calculation, the electronic conductivity of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ is calculated by the CASTEP program with the virtual mixed atom method. The chemical formula assumes Li and Na as 1 mol, the doping amount of Na is x mol, and then the doping amount of Li is 1-x mol. The Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ cell model is shown in Figure 1. Li and Na occupy 3a, Ni_1/3Co_1/3Mn_1/3 occupies 3b, O atoms occupy 6c, and the space group is $R\overline{3}m$. Based on the model of Figure 1, 4 × 3 × 2 supercell model is built. Virtual atomic mixing can speed up the calculation and meet the precision requirements. The results of calculation of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ (x = 0.01, 0.02, 0.03 ... 0.10) are analyzed in this article.

FIGURE 1

FIGURE 1. The cell of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O_2.

Results and Discussion

Band Gap and Partial Density of States

The band gap and the partial density of states (PDOS) of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ were calculated when Na-doping amount x = 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, and 0.10 mol. The electronic conductivity of the material depends on the number of electrons contained in the conduction band. The wider the band gap is, the less easily the valence band electrons can leap to the conduction band and the worse the conductivity of the material is. After Na-doping, the whole band structure of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ is not affected, but the energy gap has changed significantly. The relevant data of the band gap is shown in Table 1, and the diagram of the relationship between x and the band gap is shown in Figure 2. Compared with the pristine, the change of the band gap is most obvious when x = 0.01 mol. The results show that its band gap is decreasing when x increases, and Na-doping can effectively improve the conductivity of LiNi_1/3Co_1/3Mn_1/3O₂.

TABLE 1

TABLE 1. Band gap value of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ with different Na-doping amount x.

FIGURE 2

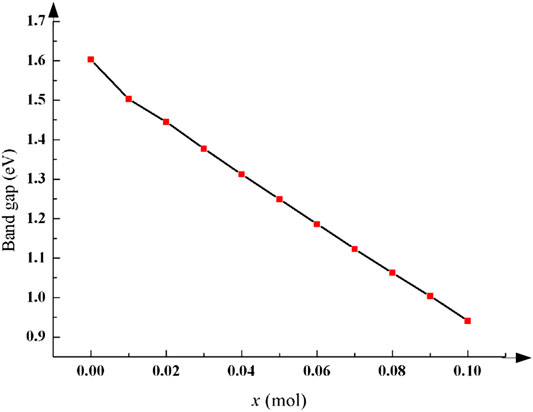
FIGURE 2. The band gap of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ declines after Na-doping and the conductivity is improved significantly.

The peak of the PDOS reflects the number of electrons in this energy. The bonding and the density of states near the Fermi level can be obtained by PDOS, and the influence of Na-doping on the conductivity of LiNi_1/3Co_1/3Mn_1/3O₂ can be analyzed. Their PDOS are shown in Figure 3 when x = 0, 0.01 and 0.05 mol. The colored lines represent the density of states of different orbitals.

FIGURE 3

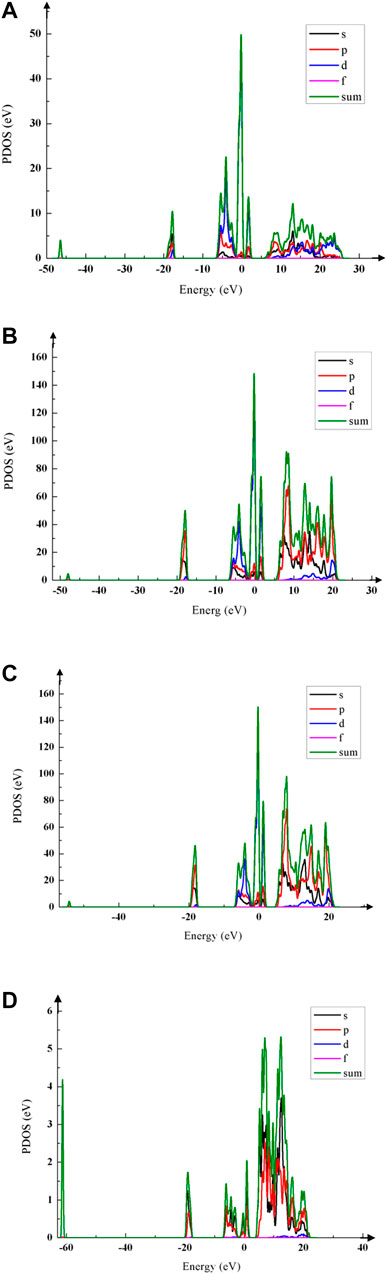
FIGURE 3. PDOS schemas of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ with different Na-doping amount x. (A) When x = 0 mol, LiNi_1/3Co_1/3Mn_1/3O₂ is not doped. (B) When x = 0.01 mol, PDOS peak of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ is higher than that of the pristine. (C) When x = 0.05 mol, the PDOS peak rises to about 157 eV, its conductivity is best. (D) When x = 0.10 mol, the PDOS peak declines dramatically to 5.5 eV, which is much lower than that of the pristine.

Figures 3A–D show that Na-doping has a great influence on the number of electrons near the Fermi level. When x = 0.01 mol (shown in Figure 3B), the PDOS peak is about 148 eV that is higher than that of the pristine (shown in Figure 3A). When x = 0.03–0.06 mol, the PDOS peak near Fermi level increases to 157 eV and its conductivity becomes better; when x = 0.06–0.09 mol, the PDOS peak begins to decline, its conductivity becomes worse; when x = 0.10 mol, the PDOS peak is lower than that of the pristine. Thus, the right amount of Na-doping should be x < 0.06 mol.

Formation Energy of Intercalation of Li⁺ and Cell Volume

The greater the formation energy of metal oxide is, the more stable the matter is, the more difficult it is for atoms to separate from molecules. The formation energy of the intercalation of Li⁺ (${\mathit{E}}_{\mathrm{f}}$) is shown in Equation (4).

${\mathit{E}}_{\mathrm{f}}={\mathit{E}}_{\mathrm{t}}-{\mathit{E}}_{\mathrm{dl}}-{\mathit{E}}_{\mathrm{dil}},(4)$

where ${\mathit{E}}_{\mathrm{t}}$ is the total energy of the supercell, ${\mathit{E}}_{\mathrm{dl}}$ is the deintercalation energy of Li⁺, and ${\mathit{E}}_{\mathrm{dil}}$ is the energy of the supercell after the deintercalation of Li⁺. The 4 × 3 × 2 supercell models are built before Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ is intercalated/deintercalated of Li⁺ and when it is intercalated/deintercalated of Li⁺ and deintercalated of Li⁺. The calculation of the cell's volume shows that the volume of Na-doped LiNi_1/3Co_1/3Mn_1/3O₂ is not extremely getting bigger though Na⁺ is bigger than Li⁺ and the structure keeps stable very well. The results of the energies in Equation (4) show that E_f has changed with the Na-doping amount (shown in Figure 4). It can be seen that Na-doping can effectively enhance the cycling performance of LiNi_1/3Co_1/3Mn_1/3O₂. E_f decreases when x < 0.05 mol, and it rises gradually when x > 0.06 mol, so the right amount x is 0.05–0.06 mol.

FIGURE 4

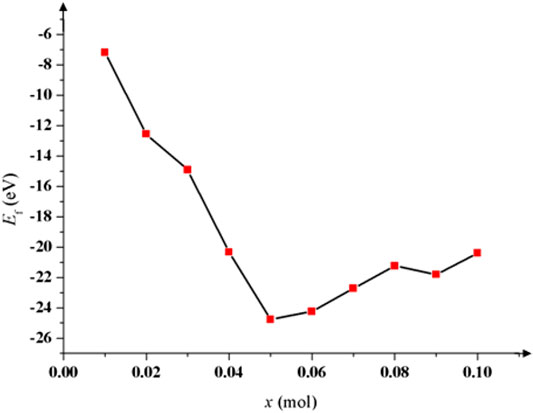
FIGURE 4. Formation energy of intercalation of Li⁺ with different doping amount x of Na. When x = 0.05 mol, E_f is lowest and the cycling performance is best.

Electron Density Difference

The change of electrons’ distribution near the local atoms with Na-doping amount x is analyzed by the electron density difference of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂. The results are shown in Figure 5. Compared with the pristine (Figure 5A), there is no change in the color of the electron cloud around atoms when x = 0.01 mol (Figure 5B), but the electron cloud has more coverage, which exhibits that its conductivity is becoming better; when x = 0.05 mol, their color starts to get darker, meaning that the free electrons increase, but the electron cloud's coverage shrinks a little (Figure 5C). The electron cloud's color gets darker than before when x > 0.05 mol, and the electron cloud's coverage expands again (Figure 5D). So, Na-doping can improve the conductivity of LiNi_1/3Co_1/3Mn_1/3O₂, and the best amount of Na-doping is x = 0.05–0.10 mol.

FIGURE 5

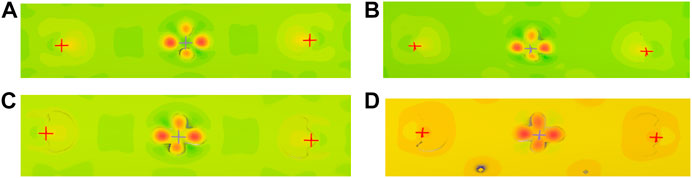
FIGURE 5. Electron density difference of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂. (A) When x = 0, the color and coverage of the electron cloud around atoms are shown. (B) When x = 0.01 mol, there is no difference for the color between x = 0.01 mol and x = 0 mol, and the coverage of the electron cloud expands. (C) When x = 0.05 mol, its color gets darker. (D) When x = 0.10, the orange color indicates that its conductivity is improved extremely.

Potential Energy of Electrons

For a system, its internal energy cannot change when there is no external force. In a potential well, the particles have the greatest kinetic energy and smallest potential, and particles can move freely in this potential well. If there is no external energy, it is difficult for them to cross over the potential well to other positions in the molecule. Therefore, the potential energy of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ can be analyzed to judge how difficult it is for electrons to escape from the potential well after doping. The 3D potential energy map of Li_0.95Na_0.05Ni_1/3Co_1/3Mn_1/3O₂ is shown in Figure 6. The blue represents the smaller negative potential energy and the red represents the larger positive potential energy. To analyze the influence of Na-doping on the potential energy well, the 2D potential energy diagram of Li_0.95Na_0.05Ni_1/3Co_1/3Mn_1/3O₂ is also obtained (shown in Figure 7). If electrons in a potential well (marked blue “*”) get enough energy to escape from the potential well, they can move to other places in the molecule. At the same time, the barriers will prevent electrons from moving along the x-axis, so electrons must move along the minimum potential energy path marked blue “*” (shown in Figure 7). Finally, the electrons are deintercalated from the cathode to the anode.

FIGURE 6

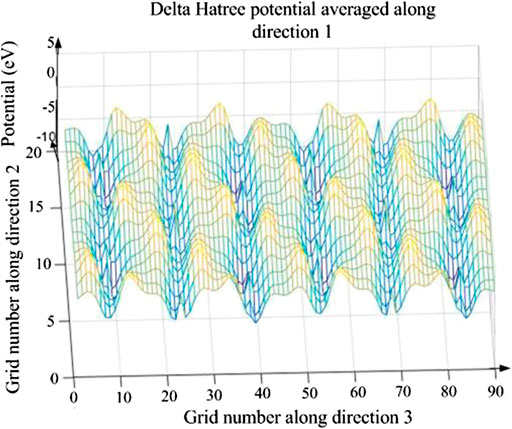
FIGURE 6. The 3D potential energy map of Li_0.95Na_0.05Ni_1/3Co_1/3Mn_1/3O₂. The potential barrier and potential well take turns, which is consistent with the layered structure of Li_0.95Na_0.05Ni_1/3Co_1/3Mn_1/3O₂.

FIGURE 7

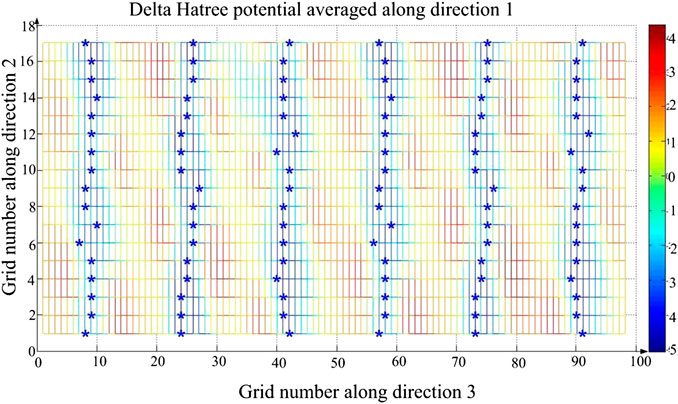
FIGURE 7. The 2D potential energy map of Li_0.95Na_0.05Ni_1/3Co_1/3Mn_1/3O₂. The blue mark "*" represents the minimum potential energy, so the electrons will move along the path marked blue "*".

In Figure 7, the blue mark “*” corresponds to the position and the potential energy. All the potential energy decreases from 17 to 1, and the change in each set is not exactly the same. As the amount of Na-doping increases, the average of the minimum potential energy decreases, which indicates that Na-doping will make the Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ potential well lower and it is easier for the electrons to escape from the potential well, and so it is for the charging reaction. Thus, its rate performance of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ can be effectively improved.

Conclusion

The physical and electrochemical properties of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ are calculated and analyzed by DFT. The band structure of LiNi_1/3Co_1/3Mn_1/3O₂ can keep stable after Na-doping, and the electronic potential energy becomes lower when the amount x of Na-doping rises; based on the analysis of the band gap and partial density of state, Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ has the best conductivity and rate performance when x = 0.03–0.06 mol; when x = 0.05 mol, the formation energy of intercalation of Li⁺ is lowest, the electrons are easiest to remove; according to the analysis of the electron density difference of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂, it has the best conductivity when x = 0.05–0.10 mol. In conclusion, the Na-doped LiNi_1/3Co_1/3Mn_1/3O₂ has better electrochemical performance when x = 0.05 mol, which is coherent with experimental results. The sample of Li_1−xNa_xNi_1/3Co_1/3Mn_1/3O₂ can be synthesized by coprecipitation reaction combined with solid-phase sintering steps. Though the electrochemical performance of Li_0.95Na_0.05Ni_1/3Co_1/3Mn_1/3O₂ is proved theoretically and experimentally to be better than that of LiNi_1/3Co_1/3Mn_1/3O₂, energy densities and specific capacity should be improved further with other modification methods. Our method and analysis based on the first-principles can provide some theoretical proposals for the electrochemical performance study of doping, and this method can be applied to the performance study of new optoelectronic devices.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

YG designed models, analyzed some data, and wrote the manuscript. KS, PL, and WY carried out calculations. LL and FC gave some proposals. XH analyzed some results.

Funding

This research was funded by the Science and Technology Project Foundation of Zhongshan City of Guangdong Province of China (no. 2018B1127), the Guangdong Basic and Applied Basic Research Foundation (no. 2020A1515010420), the Key Research Platforms and Research Projects in Universities and Colleges of Guangdong Provincial Department of Education (no. 2018KQNCX334), the Zhongshan Innovative Research Team Program (no. 180809162197886), Guangdong Provincial Key Laboratory of Optical Information Materials and Technology (no. 2017B030301007), the National Natural Science Foundation of China (no. 11775047), the union project of National Natural Science Foundation of China and Guangdong Province (no. U1601214), Science and Technology Program of Guangzhou (no. 2019050001), and the Scientific and Technological Plan of Guangdong Province (no. 2018B050502010).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Li M, Hou XH, Sha YJ, Wang J, Hu SJ, Liu X, et al. Facile spray-drying/pyrolysis synthesis of core-shell structure graphite/silicon-porous carbon composite as a superior anode for Li-ion batteries. J Power Sources (2014) 248:721–8. doi:10.1016/j.jpowsour.2013.10.012

CrossRef Full Text | Google Scholar

2. Jung SK, Gwon H, Hong J, Park K. Understanding the degradation mechanisms of Li Ni_0.5Co_0.2Mn_0.3O₂ cathode material in lithium ion batteries. Adv Energy Mater (2014) 4(1):94–8. doi:10.1002/aenm.201300787

CrossRef Full Text | Google Scholar

3. Zou BK, Ding CX, Chen CH. Research progress in ternary cathode materials Li ( Ni, Co, Mn) O₂ for lithium ion batteries. Sci Sin Chim (2014) 44(7):1104–15. doi:10.1360/N032014-00019

CrossRef Full Text | Google Scholar

4. Xu QJ, Zhou LZ, Liu MS, Pan HT, Deng XQ. Research progress in cathode material of Li-Ni-Co-Mn-O for lithium ion battery. J Shanghai Univ Electr Power (2012) 28(2):143–8. doi:10.3969/j.issn.1006-4729.2012.02.010

CrossRef Full Text | Google Scholar

5. Zhang HL, Zhao HB, Xu JJ, Zhang JJ. Optimizing Li₂O-2B₂O₃ coating layer on LiNi_0.8Co_0.1Mn_0.1O₂ (NCM811) cathode material for high-performance lithium-ion batteries. Int J Green Energy (2020) 17(7):447–55. doi:10.1080/15435075.2020.1763362

CrossRef Full Text | Google Scholar

6. Li JH, Liu ZQ, Wang YF, Wang RG. Investigation of facial B₂O₃ surface modification effect on the cycling stability and high-rate capacity of LiNi_1/3Co_1/3Mn_1/3O₂ cathode. J Alloys Compd (2020) 834:155150. doi:10.1016/j.jallcom.2020.155150

CrossRef Full Text | Google Scholar

7. Ren XY, Du JL, Pu ZH, Wang RB, Gan L, Wu Z. Facile synthesis of Li₂MoO₄ coated LiNi_1/3Co_1/3Mn_1/3O₂ composite as a novel cathode for high-temperature lithium batteries. Ionics (2020) 26:1617–27. doi:10.1007/s11581-020-03474-z

CrossRef Full Text | Google Scholar

8. Li L, Liu Q, Huang JJ, Luo SY, Feng CQ. Synthesis and electrochemical properties of Zn-doping LiNi_1/3Co_1/3Mn_1/3O₂ cathode material for lithium-ion battery application. J Mater Sci Mater Electron (2020) 31:12409–16. doi:10.1007/s10854-020-03787-9

CrossRef Full Text | Google Scholar

9. Shao ZC, Guo J, Zhao Z, Xia JL, Zhang Y. Preparation and properties of Al₂O₃-doping LiNi_1/3Co_1/3Mn_1/3O₂ cathode materials. Adv Manuf Process (2016) 31(8):1004–8. doi:10.1080/10426914.2015.1117618

CrossRef Full Text | Google Scholar

10. Chen JW, Xing LD, Yang XR, Liu X, Li TJ, Li WS. Outstanding electrochemical performance of high-voltage LiNi_1/3Co_1/3Mn_1/3O₂ cathode achieved by application of LiPO₂F₂ electrolyte additive. Electrochim Acta (2018) 290:568–76. doi:10.1016/j.electacta.2018.09.077

CrossRef Full Text | Google Scholar

11. Teng R, Yu HT, Guo CF, Wang XD, Yi TF. Effect of cation doping on the electrochemical properties of li₂MoO₃ as a promising cathode material for lithium-ion battery. Ionics (2020) 26(17):4413–22. doi:10.1007/s11581-020-03607-4

CrossRef Full Text | Google Scholar

12. Xing L, Peng H, Wang MS, Zhao X, Xu J, Wang ZQ, et al. Enhanced electrochemical performance of Zr^- modified layered LiNi_1/3Co_1/3Mn_1/3O₂ cathode material for lithium-ion batteries. Chemelectrochem (2016) 3(1):130–7. doi:10.1002/celc.201500360

CrossRef Full Text | Google Scholar

13. He R, Zhang LH, Yan MF, Gao YH, Liu ZF. Effects of Cr₂O₃-modified LiNi_1/3Co_1/3Mn_1/3O₂ cathode material on the electrochemical performance of lithium-ion batteries. J Mater Sci (2016) 52:4599–607. doi:10.1007/s10853-016-0704-z

CrossRef Full Text | Google Scholar

14. Yang ZG, Guo XD, Xiang W, Hua WB, Zhang J, He FR, et al. K-doped layered LiNi_0.5Co_0.2Mn_0.3O₂ cathode material: towards the superior rate capability and cycling performance. J Alloys Compd (2017) 699:358–65. doi:10.1016/j.jallcom.2016.11.245

CrossRef Full Text | Google Scholar

15. Li YH, Liu JY, Lei YK, Lai CY, Xu QJ. Enhanced electrochemical performance of Na-doped cathode material LiNi_1/3Co_1/3Mn_1/3O₂ for lithium-ion batteries. J Mater Sci (2017) 52:13596–605. doi:10.1007/s10853-017-1449-z

CrossRef Full Text | Google Scholar

16. Kabiraj A, Mahapatra S. High-throughput first-principles-calculations based estimation of lithium ion storage in monolayer rhenium disulfide. Commun Chem (2018) 1:81. doi:10.1038/s42004-018-0082-3

CrossRef Full Text | Google Scholar

17. Ng MF, Sullivan MB. First-Principles Characterization of Lithium Cobalt Pyrophosphate as a cathode material for solid-State li-ion batteries. J Phys Chem C (2019) 123(49):29623–9. doi:10.1021/acs.jpcc.9b09946

CrossRef Full Text | Google Scholar

18. Wang WW, Zhong Y, Zheng DH, Liu HD, Kong YF, Zhang LX, et al. P-type conductivity mechanism and defect structure of nitrogen-doped LiNbO₃ from first-principles calculations. Phys Chem Chem Phys (2020) 22(1):20–7. doi:10.1039/c9cp05019a

CrossRef Full Text | Google Scholar

19. Thomas LH. The calculation of atomic fields. Math Proc Camb Phil Soc (1927) 23:542. doi:10.1017/S0305004100011683

CrossRef Full Text | Google Scholar

20. Fermi EZ. Eine statistische methode zur bestimmung einiger eigenschaften des atoms und ihre anwendung auf die theorie des periodischen systems der elemente. Ztschrift für Physik A Hadrons and Nucl (1928) 48(1):73–9. doi:10.1007/BF01351576

CrossRef Full Text | Google Scholar

21. Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev (1964) 136(3B):B864–B871. doi:10.100/CUL-ID:1483532

CrossRef Full Text | Google Scholar

22. Jones RO, Gunnarsson O. The density functional formalism, its applications and prospects. Rev Mod Phys (1989) 61(3):689–746. doi:10.1103/RevModPhys.61.689

CrossRef Full Text | Google Scholar

23. Kohn W, Sham L. Self-consistent equations including exchange and correlation effects. Phys Rev A (1965) 140:1133–8. doi:10.1103/physrev.140.a1133

CrossRef Full Text | Google Scholar

24. Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, Singh DJ, et al. Erratum: atoms, molecules, solids, and surface: applications of the generalized gradient approximation for exchange and correlation. Phys Rev B (1992) 46(11):6671–87. doi:10.1103/PhysRevB.46.6671

CrossRef Full Text | Google Scholar

25. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B (1999) 59:1758–75. doi:10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

26. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Vanderbilt D. Soft self-consistent pseudopotentials in generalized eigenvalue formalism. Phys Rev B (1990) 41(11):7892–5. doi:10.1103/PhysRevB.41.7892

CrossRef Full Text | Google Scholar

28. Monkhorst HJ, Pack JD. Special points for brillouin-zone integrations. Phys Rev B (1976) 13:5188–92. doi:10.1103/PhysRevB.16.1748

CrossRef Full Text | Google Scholar