Control of THz Surface Plasmons by Geometric Phases

Surface plasmons (SPs) are expected to have a wide range of applications in many fields, so they have recently attracted much attention. However, most of the previous studies achieved the manipulation of SPs through designing the structure of the individual meta-atom. When developing the next generation of integrated photonic devices and components, it is essential to seek out new methods of software control, which enable more diverse modulation and higher efficiency. Here, the tunable emission of SPs with metasurfaces is systematically studied. SPs are a source of on-chip plasmonic vortices (PVs). To verify the controllability of the directional excitation of SPs, we designed beam deflectors with different angles of surface waves (SWs). Furthermore, PVs with different topological charges were generated by arranging spatially varied microslits. The proposed control strategy provides a common platform for various promising applications, such as on-chip generation of the propagation control of SPs and PVs.

Introduction

Surface plasmons (SPs) are bound electromagnetic waves that propagate along the metal-dielectric interface and decay exponentially in the direction perpendicular to the interface [1], They promise unique applications ranging from sub-wavelength lasing, biological sensing, near-field imaging, holography, and sensing, to plasmonic circuitry [2–12]. It is worth noting that an on-chip plasmonic device, which is much smaller than similar products in free space, has attracted widespread attention [13, 14]. Although it is challenging to control the wavefront of SPs, this is necessary in order to enable various functional SP devices [15]. Investigations into SPs initially focused on far-infrared and visible frequencies, and were then extended to terahertz and microwave regimes. In the early years, prisms, periodic ripples, and topological defects were the most common methods of emitting SWs. However, prism coupling requires a large volume, which is impractical for integration into a compact micro-SW device. There is a growing demand for simplifying the design and manufacture of integrated plasma devices, and thus for plasma technology research, and so exploring new methods for manipulating SPs during launch has become an intriguing research topic.

A metasurface [16, 17] is a two-dimensional (2D) metamaterial [18–20], which has excellent maneuver ability when forming the wavefront of the outgoing electromagnetic wave. The key feature of the metasurface platform is the ability to construct a local abrupt phase [21–24], amplitude [25, 26], and polarization [27–31]. Metasurfaces are also applicable to the field of SPs, and SP couplers [32–35], SP wavefront control, and SP holography [36–38] have been implemented. In addition, the terahertz (THz) range of the electromagnetic spectrum contains absorption lines of various rotating and vibrating molecules, so it has attracted attention as a fingerprint region for many spectroscopy and sensing applications. Metasurfaces designed with appropriate sub-wavelength sub-atoms and arranged in a prescribed spatial distribution have become an ideal tool for the fine control of SPs. In particular, the sub-wavelength metal slot resonator is one of the most commonly used unit elements when designing metasurfaces for SP manipulation. Metasurfaces composed of metal slits have excellent flexibility, and the wavefront of the coupled SP can be controlled arbitrarily, using iterative algorithms [39], holographic principles [40], Pancharatnam-Berry phase (PB phase) concepts [33], or coupled mode theory [41]. They can pave the way for future research if the SPs can be controlled in the THz regime.

In the 1990s, it was found that phase vortex beams by Allen at al. [42], which have a phase term that can be described by $exp\left(-il\theta \right)$, have an orbital angular momentum of light (OAM) of $l\hslash$ per photon, where l is the topological charge, θ is the azimuthal angle, and $\hslash$ is Planck's constant h divided by $2\pi$. OAM is the angular momentum component of the beam, which depends on the spatial distribution of the light field. Unlike the spin angular momentum (SAM) associated with the spin of a photon, OAM is infinite, so more degrees of freedom can be used. Similar to optical vortices, SPs with orbital angular momentum are defined as SVs. The SPs propagate along the interface.

In this article, we used the commercial electromagnetic software CST to demonstrate the manipulation of SPs, emitted by metasurfaces composed of metallic microslits. Phase control is achieved by interference between a pair of slits on the metal surface. The spatial spacing and direction of the paired microslits can be adjusted to give almost any phase distribution, thereby allowing abnormal SP emission. The proposed metasurface can match the momentum difference between free-space light and SPs, can be used as an effective SP element coupler, and can also support the propagation of coupled SPs, showing higher efficiency in a large excitation range. This is because evanescent waves such as ordinary SPP will quickly dampen or decay, but metamaterials are a good medium that can greatly improve its efficiency. More importantly, the phase of the coupled SP can be continuously controlled by carefully changing the rotation angle of the microslits, which can provide great flexibility in the manipulation of SP emissions. Furthermore, for verifying the demonstration, we proposed a PV generator which consists of spatially varying microslits arranged in a ring carved in aluminum film. In this way, the PV generator can generate any combination of spin-dependent OAMs for the SP on the metal/dielectric interface. The proposed methodology illustrates the powerful function of combining the Pancharatnam-Berry phase with the complex SP startup, and it may provide a novel method for designing various SP devices.

Experiment, Results, and Discussion

As shown in Figure 1A, the sub-wavelength metallic microslit structure was highly effective due to its ability to confine electric fields. This function is very different from the well-known bar structure, which can be explained by Babinet's principle. The unit cell had a length of L = 200 μm, a width of W = 50 μm, and a unit cell length of p = 300 μm. The metallic microslit was made on a 200 nm thick aluminum film on a modified polyimide (MPI) substrate. Figure 1B shows the SP radiation pattern (E_z component) of the microslit design, which acts as an in-plane magnetic dipole with a resonance wavelength of ${\lambda }_{sp}$. In order to prove the correctness of the design strategy, the CST Microwave Studio basic finite integration technique was used to simulate the field distribution of SPs. The SP propagating along the metal surface is usually referred to as surface plasmon polarons under visible light and infrared. However, at the THz frequency, an SP is called a Zenneck terahertz surface wave (ZTSW). Its field strength is not tightly bound to the metal surface, and the resonance wavelength of ${\lambda }_{ZTSW}$ is almost equal to the vacuum wavelength of ${\lambda }_0$ [43, 44]. This can be attributed to the fact that at terahertz frequencies metals behave as perfect electrical conductors and do not allow waves to penetrate. In the simulations, the slit pairs were carved on a 200 nm thick aluminum layer ($\sigma =3.72e7 S/m$) which was deposited on a 50 µm thick MPI substrate with a relative permittivity of ${\epsilon }^{\prime }=3.1$ and a loss tangent of $\delta =0.006$ at 1.0 THz.

FIGURE 1

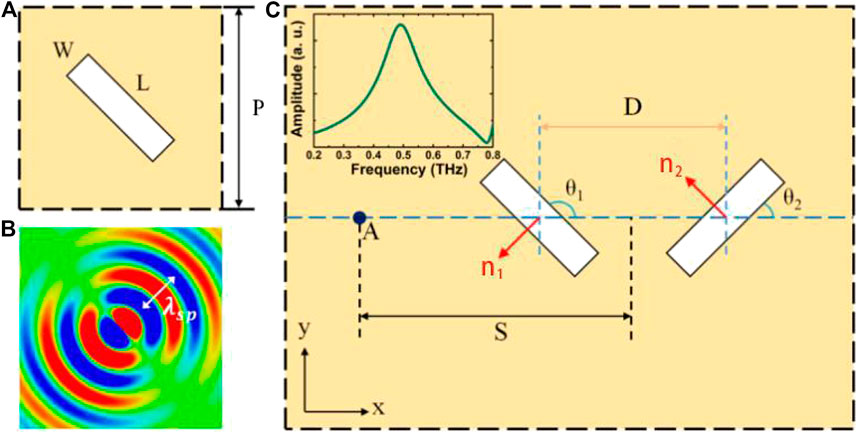
FIGURE 1. (A) The unit cell schematic of the proposed metasurface. The geometric parameters of the microslit were L = 200 μm, W = 50 μm, and p = 300 μm. (B) The simulated SP radiation pattern was excited by a narrow sub-wavelength microslit on the aluminum film under the incidence of a normal plane wave. (C) A schematic diagram of a pair of microslit resonators. They were used to derive the SP emission field at point A at a distance S from the center of the pair of microslits. D is the distance between the centers of the microslits.

The coupling of the microslit pair, as shown in Figure 1C, is excited by the plane wave and the electric field ${\overrightarrow{E}}_{in}=\left(E_x, E_y\right)$ at normal incidence, so the field at point A $\left(S\ge D/2\right)$ is the superposition of the SP field in the two microslits [45]:

${\overrightarrow{E}}_A=I sign\left(S\right)\left[\left({\overrightarrow{E}}_1·{\widehat{e}}_x\right)e^{i{k}_{sp}\left|s+\frac{D}{2}\right|}+\left({\overrightarrow{E}}_2·{\widehat{e}}_x\right)e^{i{k}_{sp}\left|s-\frac{D}{2}\right|}\right]\widehat{a}(1)$

where I represents the field amplitude of SP; ${\overrightarrow{E}}_1=\left({\overrightarrow{E}}_{in}, {\widehat{n}}_1\right){\widehat{n}}_1$ and ${\overrightarrow{E}}_2=\left({\overrightarrow{E}}_{in}, {\widehat{n}}_2\right){\widehat{n}}_2$ are incident polarization components along ${\widehat{n}}_1$ and ${\widehat{n}}_2$, where ${\widehat{n}}_1=\left(cos{\theta }_1, sin{\theta }_1\right)$ and ${\widehat{n}}_2=\left(cos{\theta }_2, sin{\theta }_2\right)$ are unit vectors perpendicular to the two microslits respectively; ${\theta }_1$ and ${\theta }_2$ represent the angles of ${\overrightarrow{E}}_1$ and ${\overrightarrow{E}}_2$ with respect to the x-axis, respectively, while ${\theta }_2-{\theta }_1=90°$;  ${\widehat{e}}_x$ is the unit vector in the positive x direction; $k_{sp}=2\pi /{\lambda }_{sp}$ is the SP wave number; $\widehat{a}$ is the unit vector given by $-\left[-i{k}_z,0,k_{sp}sign\left(S\right)\right]/\sqrt{{\left|k_z\right|}^2+{\left|k_{sp}\right|}^2}$, where $k_z=\sqrt{k_0^2-k_{sp}^2}$ is the vacuum wave number and $k_0$ is the vacuum wave number. If the incident wave is circularly polarized by $\left(E_x,E_y\right)=\sqrt{2}/2\left(1,\sigma i\right)$, where $\sigma \in \left\{+,-\right\}$ represents left-hand circular polarization (LCP) and right-hand circular polarization (RCP), respectively, and if it represents $k_{sp}D=\pi$, then Eq. (1) can be simplified to

${\overrightarrow{E}}_A=i\sqrt{2}/2I sign\left(S\right)e^{i{k}_{sp}S}{e}^{i2\sigma {\theta }_1}\widehat{a}(2)$

It can be easily obtained from Eq. (2) that the amplitude of the SP field at A is fixed, while the phase is freely controllable with a sign determined by the circular-polarization handedness and shift by the orientation angle. This shows that circular polarization can be used to switch the sign of the phase, thereby controlling the shape of the SP wavefront while maintaining the SP amplitude constant. In addition, a nearly arbitrary phase profile could be achieved even using a single straight column of microslit resonators because the phase shift enables the cover of whole $2\pi$ range. Simultaneously, as shown in the inset of Figure 1C, the simulated amplitude of $E_z$ reaches the maximum value under the designed geometry.

From the generalized Snell law, the SP coupling can be realized through constructing the phase of the microslits to satisfy $\frac{d\phi }{dx}=k_{sp}$. In this way, each row of microslits satisfying the coupling phase condition $\frac{d\phi }{dx}=k_{sp}$ can be regarded as the source of the secondary output SP. However, although the output SPs are in phase with each other and together produce a normal wavefront, they can be transmitted in only the x direction. In this case, the introduction of the phase gradient along the y direction $\frac{d\phi }{dy}$ is a non-negligible factor in achieving the arbitrary modulation of launching SPs. The Pancharatnam-Berry phase enables the accurate control of the phase of the electromagnetic wave due to the double relationship between the angle of geometric rotation and the angle of the output SPs. As shown in Figure 2A, the phase of the proposed microslit structure can cover the entire $2\pi$ range by rotating the angle between the microslits. At the same time, the amplitude of the wave is close to 50%. Based on this, the spatial distribution of the phase discontinuity at the interface between the two media can be freely constructed, where the abnormal refraction angle can be expressed as ${\theta }_t=\arcsin \left(\frac{1}{k_0}\frac{d\phi }{dy}\right)$.

FIGURE 2

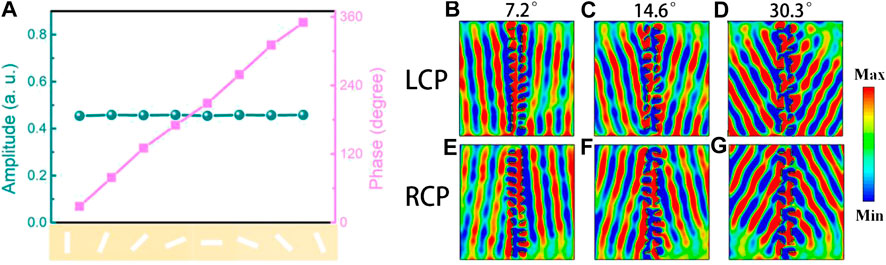
FIGURE 2. Simulated $E_z$ -field distributions of the ZTSW from a linear-phase-profile structure under normal incidences of LCP with a (B) 7.2°, (C) 14.6°, and (D) 30.3° deflected angle. The corresponding $E_z$ -field distributions of the ZTSW under normal incidences of RCP with a (E) 7.2°, (F) 14.6°, and (G) 30.3° deflected angle while the geometry and rotation of the microslits were fixed. (G) Simulated amplitude and phase shift of microslits shown at 0.49 THz.

To demonstrate the proposed scheme, we numerically demonstrated three types of metasurface with different phase gradients in the y direction. Figures 2B,E show different SP launches when the incident THz waves are LCP and RCP, respectively. The angle shift between two adjacent microslits is 22.5° in the y direction, which means that the metasurface can complete the shape of the wavefront within 8 unit cells. The anomalous angle of SP launch can be calculated easily as ${\theta }_t=7.2°$. Increasing the phase shift between adjacent microslits will increase the anomalous angle of SP launch and so achieve 2π modulation at a shorter distance. The angle shift between the two adjacent microslits was increased to 45° and 90°, and the anomalous angles of SP launch became ${\theta }_t=14.6°$ and ${\theta }_t=30.3°$, respectively. The simulated corresponding real part of the $E_z$ -field distributions is shown in Figures 2C,D,F,G. It can be seen that the sign of the anomalous refracted angle was reversed due to the different chirality of incidence. In simple terms, manipulation of the SP launch was realized by precisely designing the phase shift between the adjacent microslits in the y direction.

The reason SP launching can be accurately and continuously manipulated is the proper relationship between adjacent microslit structures. And the distance D between the adjacent microslits played a vital role in achieving the launch of high efficiency SPs. The calculated field distributions at distance D of 200–400 μm, with a step of 50 μm, while keeping ${\theta }_2-{\theta }_1=90°$ under LCP incidence at 0.496 THz, is shown in Figure 3. The mismatch spacing significantly affected the coupling between the microslits, which prevented the wavefront of SPs from being modulated effectively. It can be seen that the field distribution changed dramatically with varying D, which shows that the SP launch was sensitive to the spacing of the microslits. The rugged wavefronts at $D\ne 302 um$ indicate that an additional SP launching order occurs. There is no doubt that similar results will also be found under RCP incidence. It is worth noting that, as D gets larger, the overall area of simulation needs to grow, in order to ensure that the number of structures is consistent.

FIGURE 3

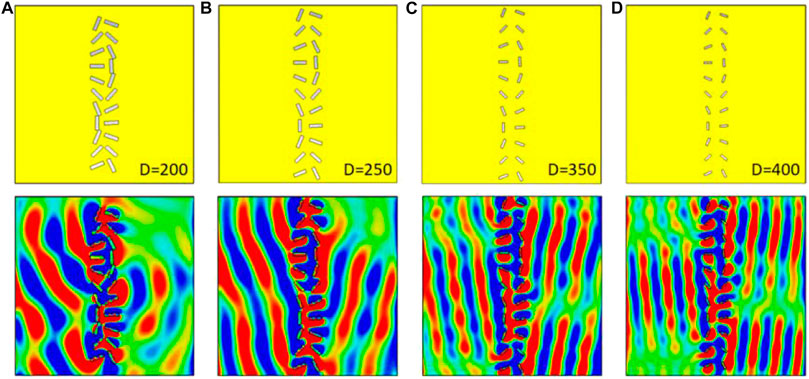
FIGURE 3. Calculated $E_z$ -field distributions of ZTSW under normal incidence of LCP at 0.496 THz with a distance D of (A) 200 μm, (B) 250 μm, (C) 350 μm, and (D) 400 μm. The top panel is a schematic of the structures.

To verify the controllability of launching SPs, a configuration was set up for generating a phase distribution by changing the orientation angle of each microslit (Figure 4). First, the microslits were distributed uniformly around a circle. Their orientation angles ${\theta }_1$ were changed by $n\pi \left(n=0, \pm 1, \pm 2\dots \right)$ clockwise around the circumference. The orientation of ${\theta }_2$ can be easily obtained due to the fixed difference between the ${\theta }_1$ and ${\theta }_2$. More importantly, the SP launched by each microslit had a different initial rotation, which was dependent on its orientation angle ${\theta }_i$. We observed the distributions of the $E_z$ -fields. The overall phase shift of SPs propagating toward the center across a whole turn equals to $2\left(n-1\right)\sigma \pi$, which can be acknowledged by observing the relationship between the number of the topological charges carried by structures and the arrangement of the microslits. It can be understood as the contribution of two parts: one is the phase shift caused by the change in the orientation angle, which can be represented by $2n\sigma \pi$. The other is the phase shift associated with the reverse mode, given by $-2\sigma \pi$. Obviously, the latter is caused by a fixed change in the azimuth of the antenna position, which is completely independent of l. In this way, the topological charges of the PVs can be expressed as $l=\sigma \left(n-1\right)$, which can be flexibly modulated by varying n.

FIGURE 4

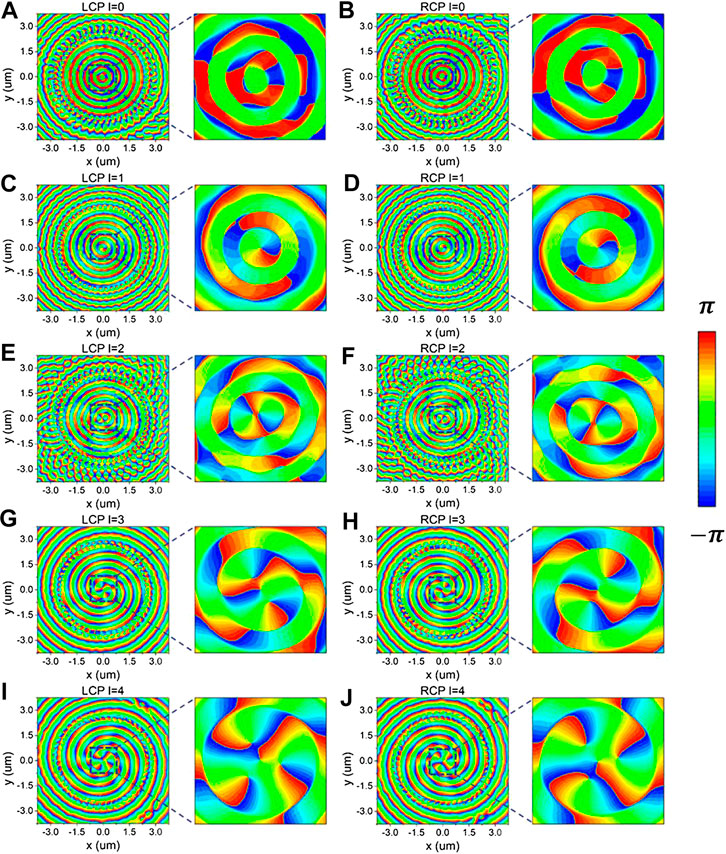
FIGURE 4. When the incident is LCP, the $E_z$ -field phase distribution on the PV generator is calculated and the topological charges are 0 (A), 1 (C), 2 (E), 3 (G), and 4 (I), respectively. And the $E_z$ -field phase distribution of the PV generator are shown in (B), (D), (F), (H), and (J) when the incident is RCP.

Figures 4A,B show the phase distribution of the $E_z$ -field for LCP and RCP, respectively. The phase distribution in the center of the structure clearly shows that the topological charge is 0 because there is no spiral phase. The structure also shows no difference between the responses to LCP and RCP incidence. However, Figures 4C,D show a clear difference in response to LCP and RCP. Figures 4C,D illustrate the corresponding simulated SP field distributions, where the phase evolution along the intensity distribution of the “doughnut” is equal to 2π, corresponding to a topological charge of 1 plasmon vortex. The direction of the phase change is closely related to the polarization of the incident wave. It is important to note that the direction of the SV phase change was reversed when the sign of the incidence changed. Figures 4E–J show the distributions of the $E_z$ -field with different topological charges carried by PVs. It can be seen that the direction of the phase change was unchanged with the increase of the topological charges under the same polarized incidence. Although the vertices of phase were not connected when the topological charge n was greater than 2, it can be seen clearly that the phase had occurred during the change of $2n\pi$. Therefore, the proposed structures were able to effect multi-channel information communication by varying the parameter n.

Conclusion

In conclusion, anomalous launching and PV generators of SPs are theoretically demonstrated in a THz near-field metasurface platform by geometric phase. It should be noted that the diameter of the sub-wavelength metal microslit was less than $\lambda /2\sim \lambda /3$. Through the simple arrangement of the microslits, arbitrary phase distribution could be realized under any excitation mode. In addition, compared with conventional SP launching manipulation with phase discontinuities, the structure we proposed enabled continuous phase change. A PV with a topological charge of 1 \ 2 \ 3 \ 4 was discussed, and the design scheme could be applied to PV with any charge only by introducing the geometric phase. These findings illustrate the importance of phase control in the SP launch process, which suggests promising THz imaging and sensing applications. Combining the SPs activated by the metasurface can open a gateway to electrically reconfigurable applications, including capturing particles and communicating on-chip information.

Experimental Section

Simulations were carried out by using the commercially available software package CST Microwave Studio. An open boundary condition was applied to the x and z directions to prevent reflections from the boundaries. For the deflector structure, a periodic boundary condition was used on the y direction with a 3,500 um × 3,500 um simulation area, but as the distance D changed, the simulation range changed accordingly; while for the OAM generator structure, an open boundary condition was applied to the y direction with a 6,500 um × 6,500 um simulation area. A normally incident circularly-polarized plane wave at 0.49 THz excited ZTSW on the substrate side and field distribution was observed from the air side.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

SW proposed the idea; PW, SH, CZ, and MH conducted pattern designs and numerical simulations; PW, SH, and YX fabricated the sample; PW performed the measurements; and SH and PW prepared the manuscript. XL and MX and MH supervised the overall projects. SW, PW, and SH analysed the data and discussed the results.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Barnes WL, Dereux A, Ebbesen TW. Surface plasmon subwavelength optics. Nature. (2003) 424:824–30. doi:10.1038/nature01937

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Nie S, Emory SR. Probing single molecules and single nanoparticles by surface-enhanced Raman scattering. Science. (1997) 275:1102–6. doi:10.1126/science.275.5303.1102

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Oulton RF, Sorger VJ, Zentgraf T, Ma RM, Gladden C, Dai L, et al. Plasmon lasers at deep subwavelength scale. Nature. (2009) 461:629–32. doi:10.1038/nature08364

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Berini P, Leon ID. Nat, Surface plasmon-polariton amplifiers and lasers. Nat Photon. (2011) 6:16–24. doi:10.1038/nphoton.2011.285

CrossRef Full Text | Google Scholar

5. Ebbesen TW, Genet C, Bozhevolnyi SI. Surface-plasmon circuitry. Phys Today. (2008) 61:44. doi:10.1063/1.2930735

CrossRef Full Text | Google Scholar

6. Sorger VJ, Oulton RF, Ma R, Zhang X. Toward integrated plasmonic circuits. MRS Bull. (2012) 37:728. doi:10.1557/mrs.2012.170

CrossRef Full Text | Google Scholar

7. Liu J, Gao Y, Ran L, Guo K, Lu Z, Liu S. Focusing surface plasmon and constructing central symmetry of focal field with linearly polarized light. Appl Phys Lett. (2015) 106:013116. doi:10.1063/1.4905307

CrossRef Full Text | Google Scholar

8. Xu Y, Zhang X, Tian Z, Gu J, Ouyang C, Li Y, et al. Mapping the near-field propagation of surface plasmons on terahertz metasurfaces. Appl Phys Lett. (2015) 107:021105. doi:10.1063/1.4926967

CrossRef Full Text | Google Scholar

9. Xu Q, Zhang X, Xu Y, Ouyang C, Tian Z, GuJ , et al. Polarization-controlled surface plasmon holography. Laser Photon Rev. (2016) 11:1600212. doi:10.1002/lpor.201600212

CrossRef Full Text | Google Scholar

10. Xu Q, Zhang X, Xu Y, Li Q, Li Y, Ouyang C, et al. Plasmonic metalens based on coupled resonators for focusing of surface plasmons. Sci Rep. (2016) 6:37861. doi:10.1038/srep37861

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yashunsky V, Lirtsman V, Zilbershtein A, Bein A, Schwartz B, Aroeti B, et al. Surface plasmon-based infrared spectroscopy for cell biosensing. J Biomed Opt. (2012) 17:081409. doi:10.1117/1.JBO.17.8.081409

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Tan Q, Guo Q, Liu H, Huang X, Zhang S. Controlling the plasmonic orbital angular momentum by combining the geometric and dynamic phases. Nanoscale. (2017) 9:4944–4949. doi:10.1039/c7nr00124j

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Gao Y, Gan Q, Xin Z, Cheng X, Bartoli FJ. Plasmonic mach-zehnder interferometer for ultrasensitive on-chip biosensing. ACS Nano. (2011) 5:9836–44. doi:10.1021/nn2034204

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Liu Y, Palomba S, Park Y, Zentgraf T, Yin X, Zhang X. Compact magnetic antennas for directional excitation of surface plasmons. Nano Lett. (2012) 12:4853–8. doi:10.1021/nl302339z

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Epstein I, Tsur Y, Arie A. Surface-plasmon wavefront and spectral shaping by near-field holography. Laser Photon Rev. (2016) 10:360. doi:10.1002/lpor.201500242

CrossRef Full Text | Google Scholar

16. Yu N, Capasso F. Flat optics with designer metasurfaces. Nat Mater. (2014) 13:139. doi:10.1038/nmat3839

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Chen HT, Taylor AJ, Yu N. A review of metasurfaces: physics and applications. Rep Prog Phys. (2016) 79:076401. doi:10.1088/0034-4885/79/7/076401

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Smith DR, Pendry JB, Wiltshire MC. Metamaterials and negative refractive index. Science. (2004) 305:788–92. doi:10.1126/science.1096796

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Shalaev VM. Optical negative-index metamaterials. Nat Photon. (2007) 1:41. doi:10.1364/META.2006.TuC3

CrossRef Full Text | Google Scholar

20. Soukoulis CM, Wegener M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat Photon. (2011) 5:523. doi:10.1038/nphoton.2011.154

CrossRef Full Text | Google Scholar

21. Yu N, Genevet P, Kats MA, Aieta F, Tetienne JP, Capasso F, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science. (2011) 334:333–7. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Ni X, Emani NK, Kildishev AV, Boltasseva A, Shalaev VM. Broadband light bending with plasmonic nanoantennas. Science. (2012) 335:427. doi:10.1126/science.1214686

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zhang X, Tian Z, Yue W, Gu J, Zhang S, Han J, et al. Broadband terahertz wave deflection based on C-shape complex metamaterials with phase discontinuities. Adv Mater Weinheim. (2013) 25:4567–72. doi:10.1002/adma.201204850

CrossRef Full Text | Google Scholar

24. Zhang X, Zhu Y, Mao C, Xu W, Ding H, Xie J, et al. Manipulating terahertz plasmonic vortex based on geometric and dynamic phase. Advanced Optical Materials. (2018) 1801328. doi:10.1002/adom.201801328

CrossRef Full Text | Google Scholar

25. Liu L, Zhang X, Kenney M, Su X, Xu N, Ouyang C, et al. Broadband metasurfaces with simultaneous control of phase and amplitude. Adv Mater Weinheim. (2014) 26:5031–6. doi:10.1002/adma.201401484

CrossRef Full Text | Google Scholar

26. Kim M, Wong AMH, Eleftheriades GV. Optical Huygens’ metasurfaces with independent control of the magnitude and phase of the local reflection coefficients. Phys. Rev. X. (2014) 4:041042. 10.1103/PhysRevX.4.041042

CrossRef Full Text | Google Scholar

27. Yu N, Aieta F, Genevet P, Kats MA, Gaburro Z, Capasso F. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. (2012) 12:6328–33. doi:10.1021/nl303445u

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Cong L, Xu N, Han J, Zhang W, Singh R. A tunable dispersion-free terahertz metadevice with Pancharatnam-Berry-phase-enabled modulation and polarization control. Adv Mater Weinheim. (2015) 27:6630–6. doi:10.1002/adma.201502716

CrossRef Full Text | Google Scholar

29. Cong L, Xu , Zhang W, Singh R. Polarization control in terahertz metasurfaces with the lowest order rotational symmetry. Adv. Opt. Mater. (2015) 3:1176. doi:10.1002/adom.201500100

CrossRef Full Text | Google Scholar

30. Cong L, Srivastava YK, Singh R. Inter and intra-metamolecular interaction enabled broadband high-efficiency polarization control in metasurfaces. Appl Phys Lett. (2016) 108:011110. doi:10.1063/1.4939564

CrossRef Full Text | Google Scholar

31. Wu PC, Tsai WY, Chen WT, Huang YW, Chen TY, Chen JW, et al. Versatile polarization generation with an aluminum plasmonic metasurface. Nano Lett. (2017) 17:445–452. doi:10.1021/acs.nanolett.6b04446

PubMed Abstract | CrossRef Full Text | Google Scholar

32 Sun S, He Q, Xiao S, Xu Q, Li X, Zhou L. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat Mater. (2012) 11:426–31. doi:10.1038/nmat3292

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Lin J, Mueller JP, Wang Q, Yuan G, Antoniou N, Yuan XC, et al. Polarization-controlled tunable directional coupling of surface plasmon polaritons. Science. (2013) 340:331–4. doi:10.1126/science.1233746

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Huang L, Chen X, Bai B, Tan Q, Jin G, Zentgraf T, et al. Helicity dependent directional surface plasmon polariton excitation using a metasurface with interfacial phase discontinuity. Light Sci. Appl. (2013) 2:e70. doi:10.1038/lsa.2013.26

CrossRef Full Text | Google Scholar

35. Pors A, Nielsen MG, Bernardin T, Weeber J-C, Bozhevolnyi SI. Efficient unidirectional polarization-controlled excitation of surface plasmon polaritons. Light Sci Appl. (2014) 3:e197. doi:10.1038/lsa.2014.78

CrossRef Full Text | Google Scholar

36. Spektor G, David A, Gjonaj B, Bartal G, Orenstein M. Metafocusing by a metaspiral plasmonic lens. Nano Lett. (2015) 15:5739–43. doi:10.1021/acs.nanolett.5b01571

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Genevet P, Wintz D, Ambrosio A, She A, Blanchard R, Capasso F. Controlled steering of Cherenkov surface plasmon wakes with a one-dimensional metamaterial. Nat Nanotechnol. (2015) 10:804–9. doi:10.1038/nnano.2015.137

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Xiao S, Zhong F, Liu H, Zhu S, Li J. Flexible coherent control of plasmonic spin-Hall effect. Nat Commun. (2015) 6:8360. doi:10.1038/ncomms9360

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Tanemura T, Balram KC, Ly-Gagnon DS, Wahl P, White JS, Brongersma ML, Miller DA, et al. Multiple-wavelength focusing of surface plasmons with a nonperiodic nanoslit coupler. Nano Lett. (2011) 11:2693–8. doi:10.1021/nl200938h

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Wintz D, Genevet P, Ambrosio A, Woolf A, Capasso F. Holographic metalens for switchable focusing of surface plasmons. Nano Lett. (2015) 15:3585–9. doi:10.1021/acs.nanolett.5b01076

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Zhang X, Xu Q, Li Q, Xu Y, Gu J, Tian Z, et al. Asymmetric excitation of surface plasmons by dark mode coupling. Sci. Adv. (2016) 2:e1501142. doi:10.1126/sciadv.1501142

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Allen L, Beijersbergen MW, Spreeuw RJ, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A. (1992) 45:8185–8189. doi:10.1103/physreva.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Jeon T, Grischkowsky D. THz Zenneck surface wave (THz surface plasmon) propagation on a metal sheet. Appl. Phys. Lett. (2006) 88:061113. doi:10.1063/1.2171488

CrossRef Full Text | Google Scholar

44. Gong M, Jeon TI, Grischkowsky D. THz surface wave collapse on coated metal surfaces. Opt. Express. (2009) 17:17088–101. doi:10.1364/OE.17.017088

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Zhang X, Xu Y, Yue W, Tian Z, Gu J, Li Y, et al. Anomalous surface wave launching by handedness phase control. Adv. Mater Weinheim. (2015) 27:7123–9. doi:10.1002/adma.201502008

CrossRef Full Text | Google Scholar