Vibration Characteristics of Quartz Crystal and Analysis of System Error in Fiber Optic Voltage Sensor

The additional deformation of the quartz crystal under the vibration stress disturbance greatly affects the measurement accuracy of the fiber optic voltage sensor. In this paper, the influence of different vibration directions on quartz crystal deformation is analyzed by the finite element method based on the analysis and derivation of the system error mathematical model of the quasi-reciprocal reflected fiber optic voltage sensor. Furthermore, the effect of additional quartz crystal deformation on the output precision of the system is calculated. The results show that the vibration stress along the axial direction mainly causes the quartz crystal to deform in height, and the vibration stress along the radial direction mainly causes the quartz crystal to deform the circumference. Among them, the deformation of the crystal radial circumference is the main reason to influence the system output accuracy. In addition, the size and deformation parameters of the quartz crystal are related to the output error of the sensor system. This paper provides the parameter optimization and design guidance for improving the anti-mechanical vibration performance of the sensor head of the fiber optic voltage sensor and provides a theoretical basis for the suppression method of the system error.

Introduction

The voltage sensors play an extremely important role in fields of power measurement and relay protection. With the continuous improvement of voltage levels, traditional electromagnetic transformers have gradually revealed their drawbacks in terms of measurement range, insulation protection, and application range [1, 2]. The optical voltage sensor (OVS), with its outstanding advantages such as high safety performance, excellent insulation performance, no magnetic saturation, large dynamic range, and so on, is gradually replacing traditional voltage transformer [3, 4]. At present, OVS research mostly included the electro-optic crystal OVS based on the Pockels effect and the all-fiber OVS based on the converse piezoelectric effect [5–7]. Compared with the electro-optic crystal OVS based on the Pockels effect, the all-fiber OVS based on the converse piezoelectric effect has a simple optical system structure. It does not require optical lens system (lens, polarizer, analyzer, wave plate) and optical collimation. Optical fiber is used for signal transmission and detection. In addition to the quartz crystal, the system no longer needs other discrete optical components, which has advantages in improving the stability and reliability of the long-term operation of the system [8].

Asea Brown Boveri (ABB) company proposed a reflective fiber optic voltage sensor (RFOVS) by using the non-reciprocity principle of Faraday rotator [9]. In this structure, a compensation fiber of equal length is spliced at ${90}^{\circ }$ to the axis after the sensing fiber. Theoretically, the structure is reciprocal and can completely offset the influence of external disturbance factors on the optical path. However, it is difficult to achieve the same length for the two-part optical fiber in the actual process, so the non-reciprocity error is introduced. The reciprocity error become more significant and complicated under the influence of external environmental disturbance. This error was analyzed in depth and proposed a relevant suppression method in the previous study [10]. It is well known that the quartz crystal is the core device of direct sensitive voltage in RFOVS. The length of sensing fiber wound on quartz crystal can be changed due to the deformation of the quartz crystal, which ultimately affects the output of the RFOVS system. In practical applications, quartz crystal deformation is easily affected by the environment, such as ambient temperature and external vibration. However, the research on OVS mainly focuses on thermal induced error [11–17] at present. There are little reports on the vibration performance of RFOVS system. In addition, due to the limitation of the fabrication process, the double crystal compensation scheme cannot guarantee the identical crystal parameters. The additional devices also reduce the reliability of the system. Therefore, in the practical application, it is an important to solve the environmental adaptability problem of RFOVS to deeply study the vibration characteristics of quartz crystal and explore the relationship between vibration stress and output accuracy of RFOVS system.

In this paper, the non-reciprocal error mathematical model of RFOVS system was established. Then, the influence of deformation of quartz crystal under the vibration stress on the output performance of RFOVS system was analyzed. Furthermore, the influence of different quartz crystal physical parameters on the system output error was investigated and the quantitative relationship between the system output error and the physical parameters of the quartz crystal under vibration stress disturbance was obtained. This study provides a theoretical basis for the suppression method of vibration error of RFOVS system and has a certain guiding significance for the optimization of RFOVS sensor head. It also provides a reference for the complex environment application of OVS.

Sensor Configuration and Operation

The configuration of RFOVS based on the converse piezoelectric effect is shown in Figure 1 [9]. The light wave from an amplified spontaneous emission (ASE, center wavelength $\lambda \approx 1\text{,}550\text{nm}$) passes through the coupler and enters the polarizer to become polarized light. The polarized light at ${45}^{\circ }$ splice point is divided into two orthogonal polarization modes. After the optical signal is modulated by the phase modulator, the two orthogonal polarization modes are transmitted along the fast and slow axis of the polarization-maintaining fiber, respectively. Then, after passing through a Faraday rotator, the polarization plane of the two orthogonal linear polarization modes is rotated ${45}^{\circ }$ and enters into two polarization-maintaining optical fibers with equal length and axial splice of ${90}^{\circ }$ successively. Optical signals in the polarization-maintaining fiber winding on the quartz crystal perceive the deformation of quartz crystal due to the converse piezoelectric effect. After ${90}^{\circ }$ splice point, the two orthogonal polarization modes propagated along the fast and slow axis of the fiber are interchanged once. Then it goes into the compensating fiber of the same length for further transmission. After the light signal is reflected by the reflector and returns along the original path. It passes through the ${90}^{\circ }$ splice point again, and the two modes of orthogonal polarization propagated in the fast and slow axis are exchanged again. Thus, the phase difference of birefringence cancels with each other, and only the phase difference introduced by the converse piezoelectric effect of quartz crystal is retained. Then the optical signal carrying voltage information passes through the Faraday rotator, and the polarization plane of the light rotates again by ${45}^{\circ }$, realizing the interchange of two orthogonal polarization modes. After the optical signal goes through the polarization-maintaining delay fiber and phase modulator in turn, and the light wave interfere at polarizer. The phase signal is converted into the optical intensity signal, then the optical intensity signal coupled into the photodetector.

FIGURE 1

FIGURE 1. Reflective fiber optic voltage sensor configuration.

Quartz crystal is the core component of the sensor unit. It generates elastic deformation due to the converse piezoelectric effect under the electric field, which results in the length change and refractive index change of the sensing fiber wound on it. Therefore, the two orthogonal linear polarization modes transmitted along the fast and slow axis of the sensing fiber produce a phase difference related to the voltage. The voltage to be measured can be obtained by detecting the phase difference.

The phase difference caused by the change in length ($\Delta {\phi }_l$) and the change in refractive index ($\Delta {\phi }_n$) can be expressed by the following formula:

$\Delta \phi =\Delta {\phi }_l+\Delta {\phi }_n=\frac{2\pi }{\lambda }\left[\left(n_{x1}-n_{y1}\right)\Delta L+L_1\left(\Delta n_{x1}-\Delta n_{y1}\right)\right](1)$

where, $n_{x1}$, $n_{y1}$ are the refractive index along the x and y axes, respectively, $\Delta L$ is the length variation of sensing optical fiber, $L_1$ is the length of sensing optical fiber, $\Delta n_{x1}$, $\Delta n_{y1}$ is the variation of refractive index along the x and y axes, respectively.

Firstly, the variation of fiber length is the main reason for the phase difference of light wave. The optical fiber is evenly and tightly wound on the quartz crystal. The change in the length of the optical fiber directly reflects the deformation of the quartz crystal [8]. The relationship between deformation of quartz crystal and the voltage to be measured is given by Eq. 2:

$\Delta L=N\cdot \Delta l=N\cdot \frac{-d_{11}\pi RU}{d}(2)$

where, $\Delta l$ is the length variation of one turn sensing fiber, $N$ is the number of turns wound on the quartz crystal, $d_{11}$ is the piezoelectric coefficient of quartz crystal, $R$ is the radius of quartz crystal, $d$ is the height of quartz crystal, $U$ is the voltage to be measured.

Secondly, the phase difference caused by the elastic optical effect of the optical fiber [18] is expressed by the following formula:

$\Delta {\phi }_n={\displaystyle \int \begin{array}{c}2\pi R\\ 0\end{array}}-5.5\times {10}^5{r}^{2}N\left({\kappa }_1^2-{\kappa }^2\right)dR=-5.5\times {10}^5{r}^2\frac{d_{11}\pi NU}{d\cdot R}(3)$

where $\kappa$, ${\kappa }_1$ are the curvature of sensing fiber before and after quartz crystal deformation, $r$ is the radius of the sensing fiber.

Combined with formulas 1–3, the phase difference caused by the converse piezoelectric effect of quartz crystal can be deduced:

$\Delta \phi =\Delta {\phi }_l+\Delta {\phi }_n=-d_{11}\pi R\frac{U}{d}\left[\frac{2\pi }{\lambda }\left(n_{x1}-n_{y1}\right)+\left(5.5\times {10}^5\times r^2\cdot \frac{1}{R^2}\right)\right]\cdot N(4)$

It can be seen from the formula 4 that there is a linear relationship between the voltage to be measured and the phase difference. The phase difference depends on the voltage to be measured, the refractive index of optical fiber, the radius and height of quartz crystal and the number of winding turns. However, in practical applications, quartz crystal is deformed not only by the converse piezoelectric effect, but also by the vibration stress. The deformation of quartz crystal due to vibration stress is perceived by the optic fiber wound on quartz crystal, which affects the measurement accuracy of RFOVS. Therefore, it is necessary to analyze the influence of the additional deformation of the quartz crystal caused by the vibration stress on the output accuracy of the system.

Theoretical Modeling and Simulation

Mathematical Modeling of the System

To model the RFOVS, we apply Jones matrix [19, 20] analysis to the system of Figure 1. In this paper, we make the following assumptions. (1) The amplitude extinction coefficient of the polarizer is $\epsilon =0$. (2) All fusion points are ideal. (3) The Faraday rotator is ideal. (4) The sensing fiber and the compensating fiber are equal in length ($L_1=L_2$).

Sensing Fiber

${\overleftrightarrow{M}}_1=\left(\begin{array}{cc}{e}^{i\left[\frac{2\pi }{\lambda }\left(n_{x1}{L}_1+n_{x1}(\Delta L_1+\Delta l_1)+(L_1+\Delta l_1)\Delta n_{x1}\right)\right]}& 0\\ 0& e^{i\left[\frac{2\pi }{\lambda }\left(n_{y1}{L}_1+n_{y1}(\Delta L_1+\Delta l_1)+(L_1+\Delta l_1)\Delta n_{y1}\right)\right]}\end{array}\right)(5)$

where $\Delta l_1$ indicates that the length variation of optical fiber due to the deformation of quartz crystal caused by vibration stress.

Compensating Fiber

$\overleftrightarrow{M_2}=\left(\begin{array}{cc}{e}^{i\left[\frac{2\pi }{\lambda }\left(n_{x1}{L}_2\right)\right]}& 0\\ 0& e^{i\left[\frac{2\pi }{\lambda }\left(n_{y1}{L}_2\right)\right]}\end{array}\right)(6)$

where, $L_2$ is the length of compensating optical fiber, $n_{x1}$, $n_{y1}$ are the refractive index along the x and y axes, respectively.

If the impact of vibration stress on the quartz crystal is not considered, then $\Delta l_1=0$. The ideal output light intensity of the system can be expressed by the following formula:

$\Delta I_{out}=E_x^2\sin \left(2\Delta \phi +{\phi }_f\right)(7)$

where, $\Delta \varphi$ is the phase difference caused by converse piezoelectric effect, ${\phi }_f$ is the feedback phase shift.

$\Delta \phi =\frac{2\pi }{\lambda }\left[\left(n_{x1}-n_{y1}\right)\Delta L_1+\left(\Delta n_{x1}-\Delta n_{y1}\right)L_1\right](8)$

If the influence of vibration stress on the quartz crystal is considered, then $\Delta l_1\ne 0$. The output light intensity of the system can be expressed by the following formula:

$\Delta I_{out}^{\text{'}}=E_x^2\sin \left(2\Delta \phi +2\Delta {\phi }_E+{\phi }_f\right)(9)$

$\Delta {\phi }_E=\frac{2\pi }{\lambda }\left[\left(n_{x1}-n_{y1}\right)+\left(\Delta n_{x1}-\Delta n_{y1}\right)\right]\cdot \Delta l_1(10)$

It can be seen from formula 10 that the main source of the error is the variation of fiber length. Since the deformation of each point of the quartz crystal is different, it is necessary to calculate the length change of one turn of the fiber through the method of integration. Therefore, the error phase caused by vibration stress is given by the following formula:

$\Delta {\phi }_E=\frac{2\pi }{\lambda }\left[{\displaystyle \underset{0}{\overset{2\pi R}{\int }}\left(n_{x1}-n_{y1}\right)\Delta \dot{P}(\mathrm{R},\mathrm{t})dR}+{\displaystyle \underset{0}{\overset{2\pi R}{\int }}\left(\Delta n_{x1}-\Delta n_{y1}\right)\Delta \dot{P}(\mathrm{R},\mathrm{t})dR}\right](11)$

where, $\Delta \dot{P}(\mathrm{R},\mathrm{t})$ represents the vibration stress of the quartz crystal.

By combining Eqs 7 and 9, the system output error expression can be obtained:

$\epsilon =\frac{\Delta I_{out}^{\text{'}}-\Delta I_{out}}{\Delta I_{out}}\times 100\%(12)$

It can be seen from formula 9 that the fiber length change caused by vibration stress of quartz crystal and the fiber length change caused by converse piezoelectric effect of quartz crystal are mixed together, and the system cannot distinguish this error phase. In practical application, the output accuracy and stability of RFOVS system is affected by external vibration disturbance. Therefore, it is significant to analyze the error phase shifts caused by the vibration stress on the output accuracy of the system.

Vibration characteristics of the quartz crystal

The geometrical model of quartz crystal was established by finite element method. The geometry and mesh division of the quartz crystal are shown in Figure 2. Quartz crystal simulation parameters are given in Table 1 [21]. As shown in Figure 3, it is the calculation result of the first 4 characteristic frequency of quartz crystal. The first 4 characteristic frequencies are 3302.2, 3302.5, 11166.8, 15648.8 Hz, respectively. Characteristic frequency means that when an object vibrates freely, its displacement changes with time according to the sine or cosine law. The vibration frequency has nothing to do with the initial conditions, but only related to the inherent characteristics of the system (such as quality, shape, material, etc.) The study of the characteristic frequency helps ensure product stability. It can be seen from the results that the first-order characteristic frequency of quartz crystal is very high, which is advantageous to avoid the influence of low-order resonance.

FIGURE 2

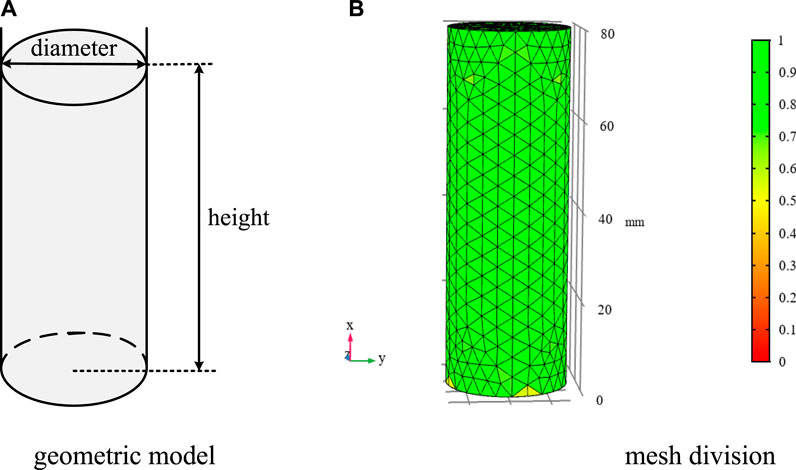
FIGURE 2. The geometry and mesh division of the quartz crystal. (A) Geometric model. (B) Mesh division.

TABLE 1

TABLE 1. Relevant parameter settings used in simulations.

FIGURE 3

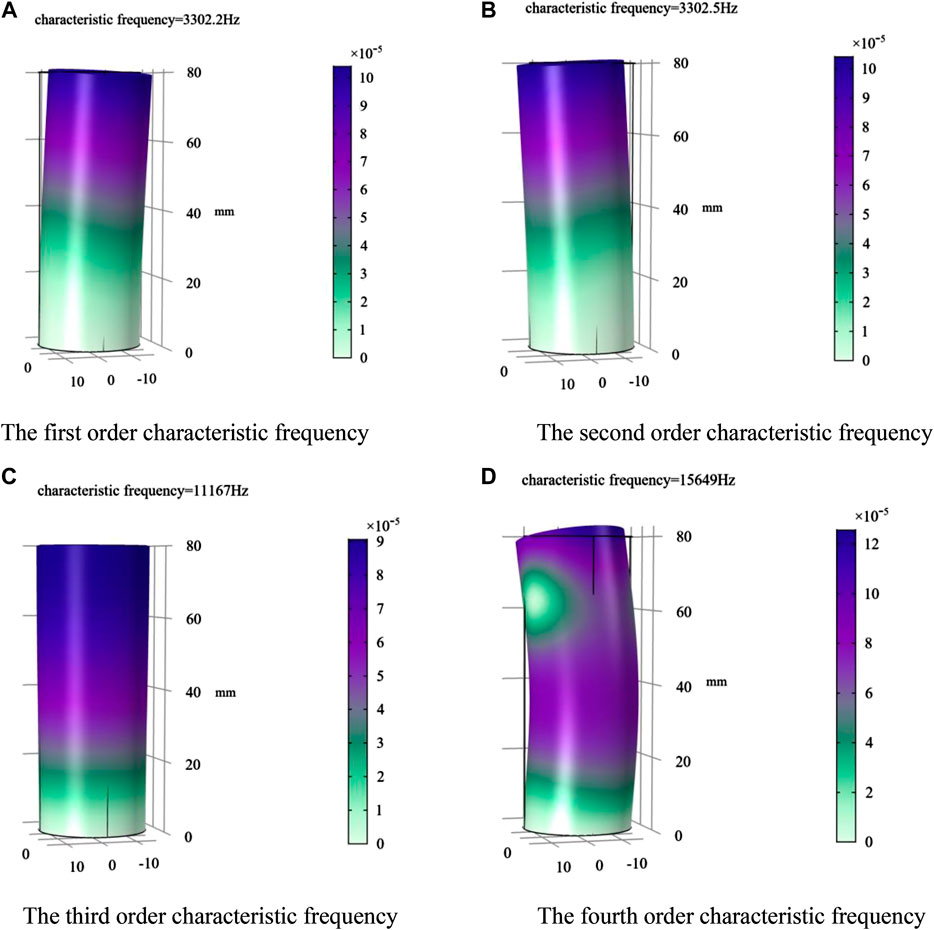
FIGURE 3. The characteristic frequency of quartz crystal. (A) The first order characteristic frequency. (B) The second order characteristic frequency. (C) The third order characteristic frequency. (D) The fourth order characteristic frequency.

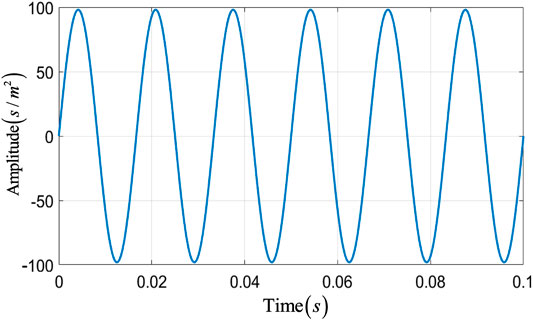
When the external vibration frequency is near the characteristic frequency, the quartz crystal is most likely to resonate, and the deformation is the largest, which has the most serious impact on the accuracy of the RFOVS system. Therefore, the analysis and control of the first 4 order frequencies are particularly important. As mentioned in previous paper [22, 23], in the practical application process of the RFOVS, the external vibration frequency is difficult to reach 3,000 Hz. Therefore, the quartz crystal is not easily affected by resonance. Based on the practical application of the RFOVS, this paper firstly applies sinusoidal excitation to quartz crystal in different directions to analyze its deformation law. Then the influence of vibration factors on the output accuracy of the system was analyzed. The vibration load curve is shown in Figure 4.

FIGURE 4

FIGURE 4. Vibration load curve (10 g 60 Hz).

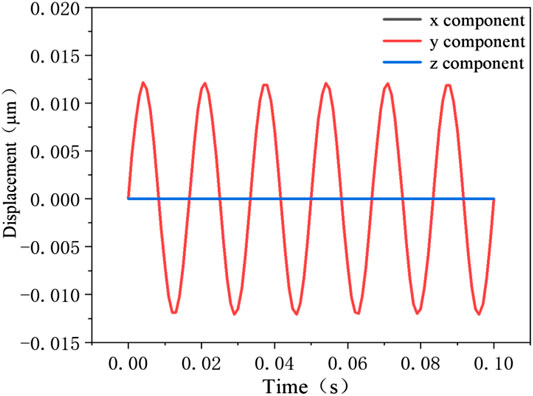
First, sinusoidal loading was applied to the x direction of the quartz crystal. The quartz crystal is fixed at one (bottom). The deformation result is shown in Figure 5. It can be seen from the simulation result that the deformation component in the x direction ($\times {10}^{-9}$ mm) is significantly larger than the y direction ($\times {10}^{-12}$ mm) and z direction ($\times {10}^{-11}$ mm). This indicates that the axial height variation of quartz crystal is mainly caused by applying vibration load in x direction. In addition, the sinusoidal load was applied in the y direction to calculate the deformation of x, y and z components of the circumference of the quartz crystal. As shown in Figure 6, the result shows that the variation of y direction circumference is mainly caused by the loading of the quartz crystal in y direction. Similarly, when a load is applied in the z direction, the quartz crystal mainly produces the variation of circumference in the z direction. For the quartz crystal, the vibration load along y axis and z axis produced the same system error. Therefore, this paper only analyzed the influence of vibration along x axis and along y axis on the system output.

FIGURE 5

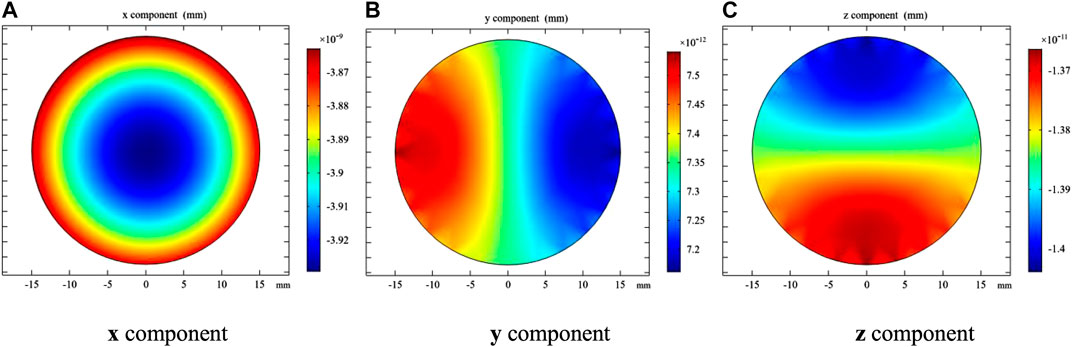
FIGURE 5. The height deformation of a quartz crystal. (A) x component. (B) y component. (C) z component.

FIGURE 6

FIGURE 6. The circumference deformation of quartz crystal.

Results and Discussion

The Relationship Between Vibration Amplitude and System Output Error

In the previous part, the influence of vibration load in different directions on quartz crystal deformation has been clarified. Firstly, the analysis of system vibration error under different amplitudes in the x direction was carried out. Quartz crystal height changes mainly due to x axis vibration. Therefore, the system output error can be calculated by combining Eqs 4 and 12. In this simulation calculation, quartz crystal height is 80 mm, radius is 15 mm, acceleration range is 2–10 g, frequency is 60 Hz and the voltage to be measured is 110 kV. As shown in Figure 7A, the vibration amplitude is almost linearly related to the system output error. However, because the quartz crystal height variation is very small, the quartz crystal height variation caused by vibration stress along the x axis has little influence on the system output accuracy. The system output can meet the accuracy level of 0.2 S. On the other hand, sinusoidal vibration load was applied along the y axis, and the system output error is shown in Figure 7B. It can be seen from the result that the vibration amplitude has a great influence on the output error of the system. In addition, compared with the height variation of quartz crystal, the vibration along the y axis mainly caused the circumference change of quartz crystal, which results in the length change of the fibre wound on quartz crystal. Therefore, the vibration has a serious impact on the output accuracy of the system. The system failed to meet the accuracy requirements of 0.2 S.

FIGURE 7

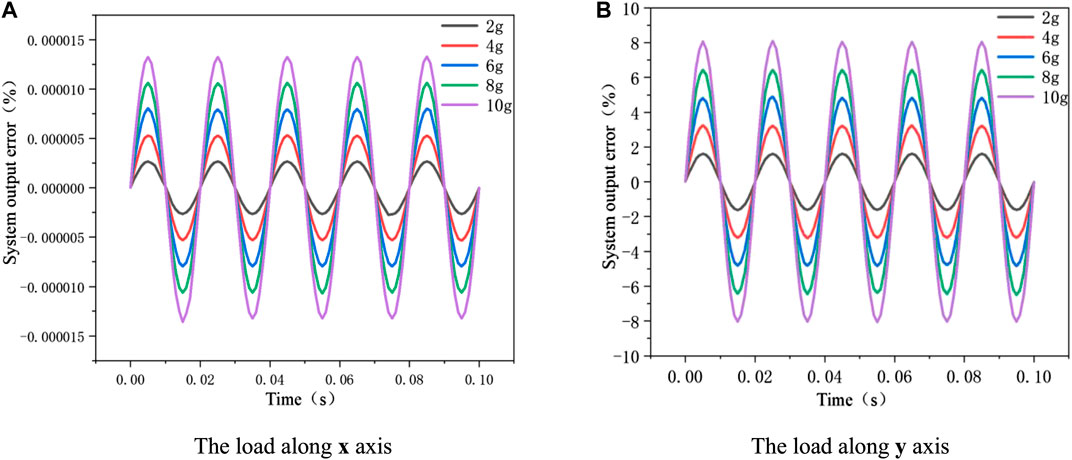
FIGURE 7. The relationship between vibration amplitude and system output error. The relationship between quartz crystal size and system output error. (A) The load along x axis. (B) The load along y axis.

In the last part, the effects of different vibration amplitudes along the x axis and the y axis on the system output were analyzed, respectively. The results show that the system output error has a linear relationship with the vibration amplitude. In addition, compared with the quartz crystal height variation, the circumference variation is the main factor caused the system output error. Therefore, in this part, the law between different quartz crystal size (radius and height) and system output error under certain amplitude was investigated. In this simulation calculation, quartz crystal height range of 70–100 mm, step length of 10 mm, radius range of 10–25 mm, step length of 5 mm, acceleration of 10 g, frequency of 60 Hz, and voltage to be measured of 110 kV are selected. The system output error of quartz crystal vibrating along x axis and y axis with different height and radius are studied, respectively.

The calculation results are shown in Figure 8. As can be seen from Figure 8A, the system output error caused by the height change of quartz crystal is still very small, and the difference of output error under different heights is also very small. However, it can be seen from Figure 8B that the radial circumference change of quartz crystal still has a great influence on the system output error. Moreover, different quartz crystal height also has a certain influence on the system output error. The higher the height, the more serious the system output error. This is mainly because increasing the height of quartz crystal reduced its stability under vibration force, resulting in larger output error of the system.

FIGURE 8

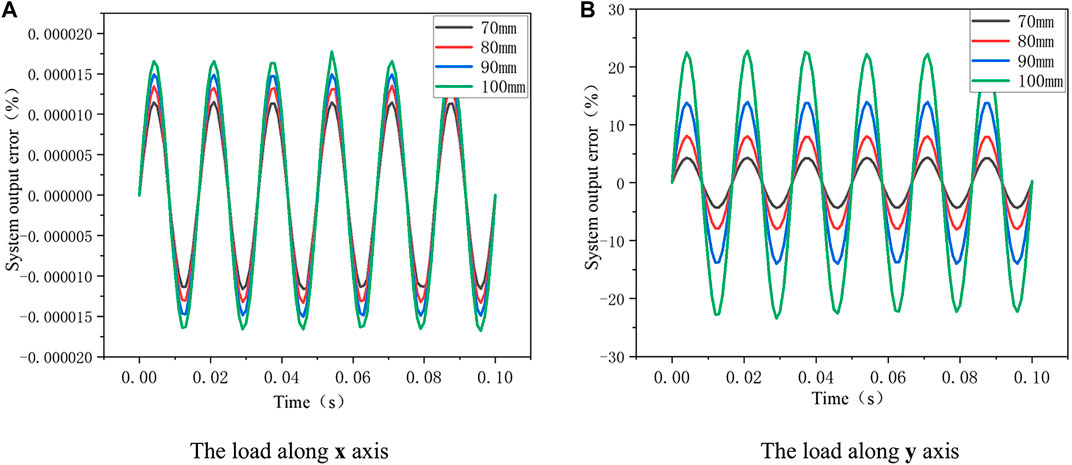
FIGURE 8. The relationship between different quartz crystal height and system Output error. (A) The load along x axis. (B) The load along y axis.

In the previous part, the results show that the quartz crystal height change has little influence on the system output error. So only the crystal height change is calculated. As can be seen from Figure 9A, the height variation is very small. The maximum height variation only around 0.0125 μm, and different quartz crystal radius have little effect on the height variation. It is known from the previous analysis that the main reason caused the system output error is the circumference change of quartz crystal. It can be seen from Figure 9B that the different quartz crystal radius has a significant impact on the system output error. The larger the crystal radius is, the smaller the output error of the system will be. This is mainly because increasing the radius can improve the stability of quartz crystal under vibration force and reduce the deformation of crystal circumference. This result is consistent with the previous analysis about quartz crystal height. It also provides guidance and basis for the optimization of sensor head.

FIGURE 9

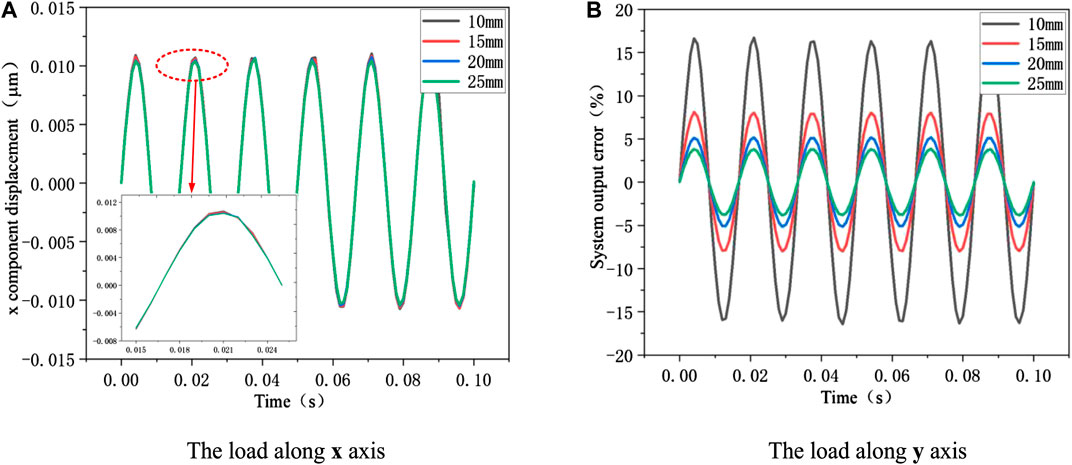
FIGURE 9. The relationship between different quartz crystal radius and system Output error. (A) The load along x axis. (B) The load along y axis.

Conclusion

In summary, the aim of the present research was to explore the relationship of output error versus vibration stress. The most obvious findings to emerge from this study are that the model of output error was established, and the relationship between system output error and vibration stress was investigated, respectively. This study indicates that the system output error is mainly caused by the deformation of radial circumference of quartz crystal. Furthermore, the relationship between the system output error and vibration stress was linear. Meanwhile, different quartz crystal size also has a certain effect on the system output error. Reasonable selection of quartz crystal radius and height can suppress the output error of the RFOVS system. The finding of this investigation complements those of earlier studies and provides a theoretical basis for error suppression. More broadly, further research will need to be done to explore error compensation algorithm to achieve the purpose of improving the accuracy of the system.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

HY: Conceptualization, Methodology, Resources, Writing-Review & Editing, Supervision, Project administration and Funding acquisition. YG: Conceptualization, Software, Formal analysis, Data Curation, Writing-Original Draft and Visualization. CD, SX, LX and WH: Software and Validation. SJ: Writing-Review & Editing, Supervision and Investigation. All authors participated in data evaluation, discussion, and interpretation.

Funding

This work was supported by the Youth Science Found Project of National Natural Science Foundation of China (NSFC) (61703090) and the Qian Xuesen Youth Innovation Fund.

Conflict of Interest

WH was employed by the company No. 16 Institution of Aerospace & Technology Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1 Klaus B, Andreas F, Georg MM, Lin Y, Miklos L. Fiber optic current and voltage sensors for electric power transmission systems. Fiber Optic Sensors Appl XV (2018) 10654:1065402. doi:10.1117/12.2303945

CrossRef Full Text | Google Scholar

2 Sadik K, George GK. Experimental comparison of conventional and optical VTs, and circuit model for optical VT. IEEE Trans Power Deliv (2011) 26:1571–8. doi:10.1109/TPWRD.2010.2100831

CrossRef Full Text | Google Scholar

3 Marceli NG, Marcelo MW. A temperature-independent optical voltage transformer based on FBG-PZT for 13.8 kV distribution lines. Measurement (2019) 147:106891. doi:10.1016/j.measurement.2019.106891

CrossRef Full Text | Google Scholar

4 Li CS. Optical voltage sensors: principle, problem and research proposal. Opt Commun, Opt Fiber Sens, Opt Mem Big Data Storage (2016) 10158:101581N. doi:10.1117/12.2248375

CrossRef Full Text | Google Scholar

5 Klaus B, Jadran K, Pascal P. Fiber optic voltage sensor for 420 kV electric. Opt Eng (2000) 39:3060–7. doi:10.1117/1.1315023

CrossRef Full Text | Google Scholar

6. Feng P, Xia X, Yan X, Ren SY. An optical AC voltage sensor based on the transverse Pockels effect. Sensors (2011) 11:6593–602. doi:10.3390/s110706593

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Akiko K, Kunihiko H. Directly high-voltage measuring system based on Pockels effect. IEEE Trans Power Deliv (2013) 28:1306–13. doi:10.1109/TPWRD.2013.2250315

CrossRef Full Text | Google Scholar

8 Bohnert KM, Nehring J. Fiber-optic sensing of electric field components. Appl Optic (1988) 27:4814–8. doi:10.1364/AO.27.004814

PubMed Abstract | CrossRef Full Text | Google Scholar

9 Bohnert K, Wildermuth S, Frank A, Brändle H. Fiber-optic voltage sensor using fiber gyro technology. Proc Eng (2010) 5:1091–4. doi:10.1016/j.proeng.2010.09.300

CrossRef Full Text | Google Scholar

10 Yang HR, Guo YC, Jiao SX, Hong W, Xu SB, Zhang YJ. Analysis and suppression of nonreciprocal phase shift error of the optical voltage sensor based on the converse piezoelectric effect. Opt Fiber Technol (2020) 55:102142. doi:10.1016/j.yofte.2020.102142

CrossRef Full Text | Google Scholar

11 Alex D, Rodrigo MB, Anderson WS, Elnatan CF, José ASD. A temperature-independent interrogation technique for FBG sensors using monolithic multilayer piezoelectric actuators. IEEE Trans Instrument Measur (2016) 65:2476–84. doi:10.1109/TIM.2016.2594021

CrossRef Full Text | Google Scholar

12 Xiao X, Xu Y, Dong Z. Thermodynamic modeling and analysis of an optical electric-field sensor. Sensors (2015) 15:7125–35. doi:10.3390/s150407125

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Olivier S, Sergio VM, Joris P, Klaus B. Signal processing for electro-optic voltage sensor. Sensors, IEEE (2013). doi:10.1109/ICSENS.2013.6688615

CrossRef Full Text | Google Scholar

14 Deng W, Li H, Zhang C, Wang P. Optimization of detection accuracy of closed-loop optical voltage sensors based on Pockels effect. Sensors (2017) 17:1723. doi:10.3390/s17081723

CrossRef Full Text | Google Scholar

15 Li H, Cui LY, Lin ZL, Li LJ, Wang R, Zhang CX. Signal detection for optical AC and DC voltage sensors based on Pockels effect. IEEE Sensor J (2013) 13:2245–52. doi:10.1109/JSEN.2013.2249581

CrossRef Full Text | Google Scholar

16 Li L, Zhang W, Li H, Pan R (2013). Linear birefringence-free optical voltage sensor based on dual-crystal structure. Appl Optic. 52:8706–13. doi:10.1364/AO.52.008706

CrossRef Full Text | Google Scholar

17 Müller GM, Quan W, Lenner M, Yang L, Frank A, Bohnert K (2016). Fiber-optic current sensor with self-compensation of source wavelength changes. Opt Lett 41:2867–70. doi:10.1364/OL.41.002867

PubMed Abstract | CrossRef Full Text | Google Scholar

18 Ulrich R, Rashleigh SC, Eickhoff W (1980). Bending-induced birefringence in single-mode fibers. Opt Lett 5:273–5. doi:10.1364/OL.5.000273

PubMed Abstract | CrossRef Full Text | Google Scholar

19 Short SX, De Arruda JU, Tselikov AA, Blake JN. Elimination of birefringence induced scale factor errors in the in-line sagnac interferometer current sensor. J Lightwave Technol (1998) 16:1844–50. doi:10.1109/50.721071

CrossRef Full Text | Google Scholar

20 Short SX, De Arruda JU, Tselikov AA, Blake JN. Imperfect quarter-waveplate compensation in sagnac interferometer-type current sensors. J Lightwave Technol (1998) 16:1212–9. doi:10.1109/50.701399

CrossRef Full Text | Google Scholar

21 Kagawa Y, Yamabuchi T. Finite element simulation of a composite piezoelectric ultrasonic transduce. IEEE Trans Son Ultrason (1979) 26:81–8. doi:10.1109/T-SU.1979.31071

CrossRef Full Text | Google Scholar

22 Bohnert K, Gabus P, Nehring J, Brändle H. Temperature and vibration insensitive fiber-optic current sensor. J Lightwave Technol (2002) 20:267–76. doi:10.1109/50.983241

CrossRef Full Text | Google Scholar

23 Ju SH, Lin H-T, Huang J-Y. Dominant frequencies of train-induced vibrations. J Sound Vib (2009) 319:247–59. doi:10.1016/j.jsv.2008.05.029

CrossRef Full Text | Google Scholar