Abstract
The solar wind is a highly turbulent medium exhibiting scalings of the fluctuations ranging over several decades of scales from the correlation length down to proton and electron gyroradii, thus suggesting a self-similar nature for these fluctuations. During its journey, the solar wind encounters the region of space surrounding Earth dominated by the geomagnetic field which is called magnetosphere. The latter is exposed to the continuous buffeting of the solar wind which determines its characteristic comet-like shape. The solar wind and the magnetosphere interact continously, thus constituting a coupled system, since perturbations in the interplanetary medium cause geomagnetic disturbances. However, strong variations in the geomagnetic field occur even in absence of large solar perturbations. In this case, a major role is attributed to solar wind turbulence as a driver of geomagnetic activity especially at high latitudes. In this review, we report about the state-of-art related to this topic. Since the solar wind and the magnetosphere are both high Reynolds number plasmas, both follow a scale-invariant dynamics and are in a state far from equilibrium. Moreover, the geomagnetic response, although closely related to the changes of the interplanetary magnetic field condition, is also strongly affected by the intrinsic dynamics of the magnetosphere generated by geomagnetic field variations caused by the internal conditions.
1. Introduction
Ref. [1] discovered an important connection between the solar wind and the magnetosphere: the level of magnetospheric storminess depends strongly on the direction of the z component of the interplanetary magnetic field (IMF) given in geocentric solar magnetospheric (GSM) coordinates. In particular, the geomagnetic activity is driven mainly by interplanetary structures with intense, long-duration and southward turning of magnetic fields (), reconnecting with the Earth’s magnetic field, following the scenario proposed by Ref. [2]. This process initiates the substorm sequence, with a net transfer of solar wind energy to Earth [3–6]. Overall, the magnetospheric activity results into several phenomena including geomagnetic substorms and storms, turbulence, ionospheric currents and auroras, and magnetic reconnection [7], thus determining a system far from equilibrium [8]. The response of the magnetosphere to the forcing exerted by the solar wind is not simply proportional to the input. When a critical threshold is reached, the magnetospheric system tends to reconfigure through a sequence of energy-loading and stress-developing processes [9, 10], determining episodic and abrupt, rather than slow and gradual, changes in the magnetosphere. This behavior motivates the description of the Earth’s magnetosphere as a complex system in which several nonlinearly sub-systems co-exist and are multiply interconnected on a wide range of spatial and temporal scales [11–15]; (and references therein).
Although there is a remarkable literature focusing on the geoeffectiveness of large interplanetary perturbations as Interplanetary counterpart of Coronal Mass Ejections (ICMEs), predominant during maximum of the solar cycle, and Corotating Intercation Regions (CIRs), more frequent during minimum e.g., [16–21], a significant geomagnetic activity is sometimes present even in the absence of such large perturbations. Within this framework and to understand the perspective of this review, a distinguishing feature of the solar wind system driver, namely turbulence, cannot be ignored. In fact, early solar wind observations by Mariner 2 in 1962 provided the first power spectral density (PSD) of magnetic field fluctuations that closely resembled a typical turbulent spectrum [22], interpreted as the proof that non-linear interactions among turbulent eddies were actively transferring energy from large to small scales. References [23, 24] highlighted that the energy cascade process is caused by the non-linear interaction of Alfvén waves. [25, 26], indeed, identified for the first time a strong correlation between velocity and magnetic field fluctuations that correspond to large amplitude Alfvén waves always propagating away from the Sun [27]. On the other hand, observations by Ref. [25] resulted to be critical for the paradigm adopted by Ref. [22] to explain the presence of a turbulence spectrum. As a matter of fact, if all the Alfvén waves were propagating outward, and there were no inward modes to interact with and produce a turbulent cascade, where did the turbulent spectrum observed by Coleman come from? This debate led Ref. [28] to the formulation of a new model in which both inward and outward Alfvén modes, present in the solar wind in different amounts, interact nonlinearly, producing a turbulent energy cascade. In fast solar wind streams mainly, fluctuations show a high Alfvénic character and are non-compressive, or in other words, the fluctuations in the proton density and in the magnitude of the magnetic field are remarkably depleted, being thus purely directional fluctuations, as expected for Alfvén waves. Solar wind turbulence is invoked to explain different processes occurring not only in the heliosphere (e.g., solar wind heating and acceleration, energetic particle acceleration, and cosmic-ray propagation) but also in the solar wind-magnetosphere coupling with particular reference to the auroral activity caused by reconnection between the southward components of the Alfvénic fluctuations magnetic fields and magnetospheric fields. Without establishing a connection between solar wind turbulence and geomagnetic response, these geomagnetic disturbances have earlier been called high-intensity (AE peak values exceeding 1,000 nT and never droping below 200 nT) long-duration (greater than 2 days) continuous AE-activity or HILDCAA [29] which are separated from magnetic storm main phases. Moreover, the auroral intensifications during HILDCAAs are not substorm expansion events, nor convection bay events [30]. Figure 1, panel A), shows an example of solar wind parameters, interplanetary magnetic field and geomagnetic indices of a typical HILDCAA event triggered by Alfvénic fluctuations, following a geomagnetic storm. This figure has been adapted from and has been described in details in Ref. [31].
FIGURE 1
(A) From top to bottom: time series of solar wind bulk speed (), temperature (), number density (); magnetic field components (, , ) and magnitude (B); geomagnetic indices: SYM-H, AU/AL and AE. Adapted from Figure 1 of Ref. 31. (B) Probability distribution function of AE index, P (AE), (black dots). The solid line refers to a nonlinear best fit obtained as the superposition of two Log-normal distribution functions. The two dotted lines show the two components relative to quiet and active periods, respectively. The vertical dashed line is the threshold discriminating active and quiet periods, evaluated from the data. Adapted from Figure 1 of Ref. 74. (C) Probability distribution function of Dst index, P (Dst) (black dots). The solid line refers to a nonlinear best fit obtained as the superposition of two Log-normal distribution functions. The individual lognormal distributions are shown as the dashed and dashed-dot lines. Adapted from Figure 2 of Ref. 115. (D) Probability distribution function of AE burst lifetime (black dots) fitted by a power law (solid line) for small timescale and by a lognormal distribution (dashed line) for larger timescales. Adapted from Figure 7 of Ref. 70. (E) Comparison of the best fit functions of the burst lifetime distribution functions for SYM-H (red), ϵ (green), and (blue). Adapted from Figure 2 of Ref. 80.
Within this framework, this review focuses on the effects of solar wind turbulence on the geomagnetic response, providing a brief overview of the state-of-art with particular reference to the scale-invariant dynamics of the solar wind and the magnetosphere (section 2) and proposed connection between solar wind turbulence and geomagnetic response (section 3). Section 4 sums up the results and contains a brief discussion.
2. Scale-Invariant Dynamics of the Solar Wind and the Magnetosphere
The solar wind dynamics is associated with many characteristic spatial and temporal scales, thus retaining a multi-scale nature [32]. The PSD of magnetic-field fluctuations cover an extended scale range, from several days to the proton and electron gyroperiods and can generally be characterized by four distinguishable dynamical ranges of scales, usually represented in the frequency domain (e.g., [33–37]; and references therein): i) a scaling of in the energy-containing range [38–41]; ii) a scaling of [42] or [23, 24] in the inertial range or at magnetohydrodynamics (MHD) scales; iii) a scaling of at sub-ion scales with a broader range of slopes, with α approximately [–4, –2] strongly related to the power of the fluctuations in the inertial range [43, 44]; iv) even steeper scaling at electron scales [33–35]. The reader is redirected to other seminal papers and reviews (e.g., [32, 36]; and references therein) for a thorough description of solar wind turbulence, being outside the scope of the present review to go into further detail.
It must be noted, however, that beside the strong connection existing between the solar wind and the magnetosphere via reconnection processes, the solar wind and the magnetosphere are both high Reynolds number plasmas [45]. As a result, we would expect that not only the solar wind but also the magnetosphere shows a scale-invariant dynamics and power-law PSD (e.g., [46–51]). On the other hand, geomagnetic indices are widely used to study the magnetospheric output and are indicative of the most important magnetospheric current systems. Although, historically, the first geomagnetic indices were related to a global description of the geomagnetic activity (Kp index introduced by Ref. [52]; and derived indices), more specific indices are now used. They take into account the separate contribution of the auroral activity, dominated by the auroral electroject dynamics (the auroral electrojet indices, AE, AU, AL, AO defined and developed by Ref. [53], and the low-latitude activity, dominated by the ring current dynamics. The latter includes the disturbance storm, Dst, index derived by Refs. [54, 55] and the a longitudinally asymmetric (ASY) and a symmetric (SYM) disturbance index introduced and derived for both the horizontal (dipole pole) direction H (SYM-H, ASY-H) and the orthogonal (East-West) direction D (SYM-D, ASY-D). In particular, the SYM-H index, derived by Ref. [56] is essentially the same as Sugiura’s hourly Dst index, although 1 min values are derived from different sets of stations and a slightly different coordinate system. Both AE and Dst (and SYM-H) show a bimodal behavior being characterized by two components relative to quiet and disturbed periods as shown in Figure 1 panel B) and C).
Observational evidence of the non-linear behavior of the magnetosphere in terms of the geomagnetic indices was given by Ref. [57] and later by, e.g., [58] who showed that the AE and Dst PSD, respectively, are characterized by a power law. In addition, the AE index has a multifractal (intermittent) structure both in quiet and disturbed periods and its fluctuations are not distributed according to a Gaussian distribution rather by a leptokurtic distribution [59–63], with AE more intermittent at maximum of solar activity than at solar minimum [64, 65].
Reference [66] found that AE burst lifetime (defined as the duration for which the measurement exceeds a given threshold value, see also Ref. [67]) probability distribution functions (PDFs) are characterized by power laws (see also Ref. [68, 69], as shown in Figure 1, panel d), adapted from Ref. [70]. References [71, 72] interpreted these results suggesting that the magnetosphere can be described in terms of a stochastic non-linear system that evolves toward metastable configurations identifying a state of self-organized criticality (SOC) [73] independent from initial conditions. The traditional SOC systems are characterized by energy dissipation in the form of avalanches. According to the theory, the events generated in this way are not correlated and would follow a Poissonian distribution. However, observations show waiting time distributions of the geomagnetic indices following power laws as for correlated events (e.g., [70, 74]), thus suggesting to attribute to an external forcing, the solar wind, the long time correlation found in the geomagnetic response, supporting the idea of forced and/or self-organized criticality (FSOC) systems [72, 75]. Evidence suggesting a significant SOC component in the dynamics of substorms in the magnetosphere was presented by Ref. [76] showing observations of bursty bulk flows, fast flows, localized dipolarization plasma turbulence, and multiple localized reconnection sites that would provide the basic avalanche phenomenon in the establishment of SOC in the plasma sheet. According to Ref. [77]; the magnetosphere can be assimilated to a metastable system, consisting of a collection of temporarily stable states. Some of them are related to the others by relatively quick transition processes, which can be identified as the loading-unloading component during substorms. For a comprehensive review on SOC, the interested reader is redirected to the papers by Refs. [78, 79].
SOC models are invoked also to explain power laws lifetime distributions of the SYM-H index [80] as shown in Figure 1E), adapted from Ref. [80]. In particular, the scaling properties of SYM-H for both quiet and active periods are described by power law scaling behaviors, each with a single nonlinear scaling exponent, characteristic of fractional Brownian motion (fBm) [81, 82]. However, the significant differences between quiet and active intervals suggests, according to their interpretation, that the basic dynamics of SYM-H could be captured by a modification to fBm [83], indicating that the SYM-H time series, rather than being monofractal, is probably weakly multifractal.
3. Connecting Solar Wind Turbulence and Geomagnetic Response
Significant effort has been made in establishing the relationship between fluctuations in the energy delivered by the solar wind to the magnetosphere and variations in the magnetospheric response. Common quantities, referred as coupling parameters, used to study the coupling between the solar wind and the magnetosphere are [84] measuring the interplanetary magnetic field advected in the magnetosphere by the reconnection process and the ϵ parameter [85] which estimates the fraction of the solar-wind Poynting flux through the dayside magnetosphere.
Several studies have been performed to compare the behavior of the coupling parameters and the interplanetary magnetic field with the geomagnetic indices. Reference [86] showed that the burst lifetime PDFs of the coupling parameters are finite-range power laws with an exponential cut-off. Although the burst lifetime PDFs of AU, AL and AE have the same power law component, a second component can be recognized in the auroral indices distributions and are highlighted in Figure 1, panel B) and d), showing AE PDFs and AE burst lifetime PDFs, respectively, adapted from Refs. [70, 74]; respectively. The power law component is directly linked to the solar wind input at short (about 20 min) lag [87] and it is commonly referred as “directly driven component”, in which energy is directly dissipated in the auroral ionosphere and ring current with a delay of about 20 min being due to the inductance of the magnetosphere-ionosphere system. This component is associated with the DP2 current systems consisting of the eastward electrojet centered in the evening sector and the westward electrojet centered in the late morning sector [88–90]. The second component is related to the global magnetospheric output that is an intrinsic property of the magnetosphere. This is linked to the DP1 current system dominated by the westward electrojet in the midnight sector and it is referred as “loading unloading component”, indicating that the energy from the solar wind is first stored in the magnetotail and then is suddenly released to be deposited in the auroral ionosphere and ring current as a consequence of external changes in the interplanetary medium or internal triggering processes [87, 91–93] such as, e.g., magnetic reconnection in the tail [94].
Reference [70] confirmed previous results and showed in addition that while the power law associated to the directly driven component depends on the phase of the solar cycle, the second component related to the loading-unloading mechanisms does not change accordingly, supporting the idea that it is related to the intrinsic response of the magnetosphere. Studying the statistical properties of fluctuations in AU, AL and AE indices and in the ϵ parameter, Ref. [95] found that the fluctuations are self-similar up to 4 h for AU and AL and up to 2 h for AE. Fluctuations on shorter time scales are found to have similar long-tailed (leptokurtic) PDFs, consistent with an underlying nonlinear process. [96]; using the Local Intermittency Measure (LIM) technique to extract the intermittent component of the AE index, found that this corresponds to the impulsive unloading process. Further investigations by Ref. [97] focused on the scaling properties of the solar wind driver and geomagnetic indices during solar minimum and maximum. They found that fluctuations in the AL index exhibit scaling properties insensitive to the phase of the solar cycle while the scaling exponent of AU changes with the solar cycle and the trend follows that of the ϵ parameter. This is consistent with the AU index more closely monitoring activity on the dayside and AL reflecting activity in the magnetotail [97].
Similar to Ref [80], ref [86] performed a comparative studies between the behavior of the input parameters and the geomagnetic response at low latitudes by means of the SYM-H index and found power law distributions for all parameters. Although during solar minimum the scaling exponents obtained for SYM-H, and ϵ were essentially the same, this was not the case for solar maximum. The authors interpreted the similar values between coupling parameters and SYM-H during solar minimum as merely fortuitous and that the scaling properties of the low-latitude magnetosphere are not purely a direct response to the scale-free properties of the solar wind but are due to inherent properties of the magnetosphere. The same authors questioned the role of the solar wind as a direct driver for the SYM-H (or Dst) scaling in agreement with Ref. [98]. This results agrees with SYM-H being the product of a SOC system [99] and would be consistent with the observation that the ring current is frequently the product of multiple spatial and temporal fine structures (e.g., [100]). In this case, Dst (and SYM-H) is produced by superposition of multiple processes, rather than by a single monolithic ring current, which operate in a SOC state. The effect of interplanetary magnetic field fluctuations on the geomagnetic response at low latitudes, using the SYM-H index, was studied using higher order statistical moments [101]. While the asymmetry of the probability density functions (described in terms of the skewness) does not seem to be important as a geoeffective parameter, there is a relationship between the kurtosis of the two parameters, thus appearing to be a representative geoeffective parameter, which can influence the reconnection process at the Earth’s magnetopause and the efficiency of the solar wind–magnetosphere coupling.
Correlations between the basic characteristics of turbulence in the upstream solar wind and various geomagnetic indices have also shown that geomagnetic activity increases with an increase in the amplitude of the turbulence in the solar wind. Reference [45] highlighted that the amplitude of the turbulence in the solar wind upstream of the Earth is strongly correlated with the geomagnetic activity during both northward and southward IMF. During southward , when magnetic reconnection operates at the magnetopause, the antiparallel orientations of interplanetary and magnetospheric magnetic fields are essential. On the contrary, during northward a viscous coupling of the solar wind flow to the magnetosphere is enhanced and therefore the level of turbulence in the solar wind is the key parameter. In this case, an increased upstream turbulence leads to a larger eddy viscosity (which reflects in a larger Reynolds stress), determining more momentum transport from the solar wind flow into the magnetosphere. This causes a greater convection in the magnetosphere, which drives stronger current systems between the magnetosphere and the ionosphere, and which leads to raised geomagnetic indices. This is in agreement with a later study by Ref. [102] on the role of the solar wind fluctuations in geomagnetic activity during southward and northward IMF. They demonstrated that, in both cases, high power fluctuations in systematically result in a greater level of geomagnetic activity on timescales consistent with viscous processes. Within the same framework, Ref. [103] showed that the substorm activity is associated not only to flux loading rather also to high solar wind velocity, causing viscous terms to have an important role in substorm loading or onsets than previously supposed. On the other hand, the triggering of geomagnetic activity can be caused by the passage of a velocity-shear layer determining sudden changes in the cross-polar-cap potential and ionospheric Joule dissipation are seen as the shear layers pass and eventually generating ULF oscillations responsible for the energization of the outer electron radiation belt [104]. It must be noted that a southward direction of the IMF as the primary driver of the geomagnetic activity is not the only crucial parameter. Indeed, an important role is played also by the energy carried by solar wind fluctuations. Reference [105] studied the correlation between the solar wind total (kinetic + magnetic) energy and the Dst index and found that high-energy solar wind plasma can severely perturb the near-Earth space environment even without reconnecting with the geomagnetic field at the dayside magnetopause.
The first statistical evidence of the role played by Alfvénic turbulence in the solar wind-magnetosphere coupling was shown by Ref. [106] who performed a comparitive study over different phases of the solar cycle. In particular, these authors identified the turbulent Alfvénic content of the solar wind fluctuations using the normalized cross-helicity, , indicating the predominance of an Alfvénic mode (either inward or outward) with respect to the other, and the normalized residual energy, , indicating a predominance of magnetic energy on kinetic energy or viceversa. For Alfvénic fluctuations, and . For further details refer to Ref. [106]. It was found that the level of AE depends not only on the presence of Alfvénic fluctuations but also on the amplitude of such fluctuations as shown in Figure 2, panel A) and B), adapted from Ref. [106]. These results were further supported by another study by the same authors [107] who presented the first statistical evidence of the presence of a slow Alfvénic solar wind during maximum of solar activity and found to be very similar to the fast wind on many respects and not only for the Alfvénic content of the fluctuations [44, 108–112]. [107] demonstrated that the nature of these kind of fluctuations plays a major role in the geomagnetic activity rather than the type of wind selected on the basis of the flow speed. On the other hand, the same statistical relationship was not established between solar wind turbulence and low-latitude geomagnetic response (see Figure 2 panel C), adapted from Ref. [98]. In addition, Ref. [65] performed a statistical study on the intermittency of and AE. They focused on their respective extreme (say intermittent) events and studied the distribution of the elapsed time, or waiting time, between consecutive events, finding distributions characterized by well-defined power laws which would suggest the existence of long term correlations typical of turbulent processes. These events were found to be weakly dependent on the phase of the solar cycle. However, these results have been overall questioned by observations of the turbulent fluctuations downstream of the Earth’s bow shock that show that the shock destroys the information from the solar wind. If this is the case, the turbulent spectrum that eventually forms far from the shock is due to the local property of the magnetosheath (e.g., [47]) and therefore, according to this study, the property of power laws in the interplanetary magnetic field does not map into the property of power laws in the inner magnetosphere.
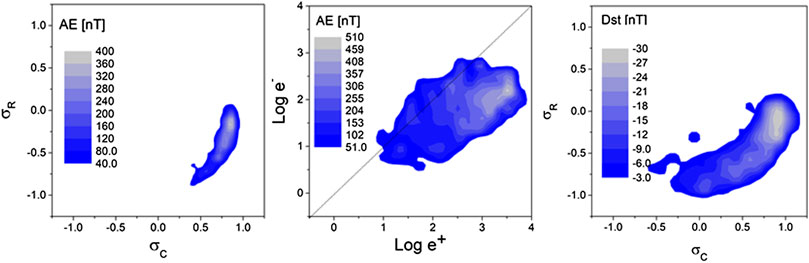
FIGURE 2
(A) Average AE values (indicated by the color scale) computed over square bins of ; (B) Average AE values (indicated by the color scale) computed over square bins of . The solid black line indicates the locus of all points which meets the condition: = . Both adapted from Ref. 106. (C) Average Dst values computed for every square bin , adapted from Ref. 98.
4. Discussion
The solar wind and the magnetosphere are high Reynolds number plasma environments [45], both showing scale-invariant dynamics and power-law PSDs. Several studies have been carried out to investigate the turbulent nature of the solar wind (e.g., [32, 36]; and references therein) and the magnetosphere (e.g., [46–51]) separately, invoking turbulence and a SOC approach to describe the dynamics of the two plasma environments, respectively. At this stage, an obvious question arises: whether SOC is different from turbulence. Since they basically exhibit several similarities (e.g., power-law functions in the power spectrum, scale-free size distributions, and many degrees of freedom), the answer to this question is rather difficult. We refer the reader to Ref. [79] that have been exhaustively discussed this topic, invoking a SOC-turbulence duality as a generic feature of astrophysical plasmas, although the explicit complementarity between the two has not been demonstrated. According to the same authors, SOC can be identified as a state of near-critical turbulence, which is in the transition between the laminar state and the fully developed turbulence state. On the other hand, several models have been used within the SOC approach to reproduce the observed fluctuation spectra in terms of sandpile cellular automata models. These models are clearly useful to improve forecasting (or, at least, nowcasting) within the framework of Space Weather studies. Although they are overall capable of reproducing the observations, they also show some limitations in explaining for example the turbulent behavior of the Earth's plasma sheet [13].
On the other hand, since the solar wind and the magnetosphere constitute a coupled system, at a later stage, a scientific effort has been carried out to establish a link between solar wind turbulence and geomagnetic response (e.g., [45, 65, 70, 80, 86, 97, 98, 101, 106, 107]). The previous papers have identified a direct link between the so-called “directly driven component”, characteristic of the magnetosphere dynamics at auroral latitudes, and solar wind turbulence. This link is eventually established via reconnection processes between the southward components of the Alfvénic fluctuations magnetic fields and magnetospheric fields. On the other hand, the connection between the turbulent solar wind and the geomagnetic response at low latitudes has been questioned [80, 98], although the magnetic storms recovery phase has been found to be related to large-amplitude Alfvén waves [113, 114]. Conversely, the previous results have been distrusted by observations performed across the Earth’s bow shock that would destroy the information from the solar wind. Therefore, according to this study, the property of power laws in the interplanetary magnetic field cannot be directly related to the property of power laws in the inner magnetosphere [47]. This conjecture would allow other interpretations aiming at identifying the trigger of the geomagnetic activity as, for instance, i) the role played by viscous coupling especially during northward IMF [45, 102, 103]; ii) the presence of velocity-shear layers that eventually lead to the generation of ULF oscillations responsible for the energization of the outer electron radiation belt [104], iii) the role of the energy associated to solar wind fluctuations in determining Dst perturbations even without reconnecting with the geomagnetic field at the dayside magnetopause [105].
To summarize, the solar wind and the magnetosphere are nonlinear environments, forming a coupled system, mainly via reconnection processes. The magnetosphere reacts nonlinearly to the system’s driver. Being a metastable system characterized by quick transition processes, it loads the energy accumulated in an impulsive way when a critical threshold is reached to reconfigure toward an equilibrium configuration. Given the complexity of the system, the authors are in favor of using a statistical approach rather than a one-to-one study. In this case, there is some evidence of the statistical relationship between solar wind turbulence and the geomagnetic response, although this is cannot be considered, for sure, the only physical mechanism involved in the magnetosphere’s dynamics.
Funding
DT was partially supported by the Italian Space Agency (ASI) under contract I/013/12/0.
Statements
Author contributions
All authors listed have made a substantial, direct and intellectual contribution to the work and approved it for publication. In particular, the paper was conceived and written by RD with the support and critical feedback of DT and RB.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1.
FairfieldDHCahillLJJr.Transition region magnetic field and polar magnetic disturbances. J Geophys Res (1966). 71:155–69. 10.1029/JZ071i001p00155.
2.
DungeyJW. Interplanetary magnetic field and the auroral zones. Phys Rev Lett (1961). 6:47–8. 10.1103/PhysRevLett.6.47.
3.
RussellCTMcPherronRL. Semiannual variation of geomagnetic activity. J Geophys Res (1973). 78:82–108. 10.1029/JA078i001p00092.
4.
BakerDNAkasofuS-IBaumjohannWBieberJFairfieldJWHonesEWJr.et alSubstorms in the magnetosphere. NASA Publication (1984). NASA RP-1120.
5.
BakerDNPulkkinenTIAngelopoulosVBaumjohannWMcPherronRL. The neutral line model of substorms: past results and present view. J Geophys Res (1966). 101:12975–3010. 10.1029/95JA03753.
6.
GonzalezWDJoselynJAKamideYKroehlHWRostokerGTsurutaniBTet alWhat is a geomagnetic storm?. J Geophys Res (1994). 99:5771–92. 10.1029/93JA02867.
7.
TsurutaniBTHajraREcherEGjerloevJW. Extremely intense (SML = -2500 nt) substorms: isolated events that are externally triggered?Ann Geophys (2015). 33:519–24. 10.5194/angeo-33-519-2015.
8.
ConsoliniGMichelisPDTozziR. On the Earth’s magnetospheric dynamics: nonequilibrium evolution and the fluctuation theorem. J Geophys Res (2008). 113:A08222. 10.1029/2008JA013074.
9.
KlimasJUritskyVMVassiliadisDBakerDN. A mechanism for the loading-unloading substorm cycle missing in MHD global magnetospheric simulation models. Geophys Res Lett (2005). 32:L14108. 10.1029/2005GL022916.
10.
BakerDNKlimasJVassiliadisD. Nonlinear dynamics in the Earth’s magnetosphere. In: TsonisAAElsnerJB, editors. Nonlinear dynamics in geosciences. Berlin, Germany: Springer (2007). p. 53–67.
11.
ChangT. Low-dimensional behavior and symmetry-breaking of stochastic systems near criticality can these effects be observed in space and in the laboratory?. IEEE Trans Plasma Sci (1992). 20:691–4. 10.1109/27.199515.
12.
KlimasAJVassiliadisDBakerDNRobertsDA. The organized nonlinear dynamics of the magnetosphere. J Geophys Res (1996). 101:13089–114. 10.1029/96JA00563.
13.
WatkinsNWFreemanMPChapmanSCDendyRO. Testing the soc hypothesis for the magnetosphere. J Atmos Sol Terr Phys (2001). 63:1435–45. 10.1016/S1364-6826(00)00245-5.
14.
ConsoliniG. Self-organized criticality: a new paradigm for the magnetotail dynamics. Fractals (2002). 10:275–83. 10.1142/S0218348X02001397.
15.
ValdiviaJRoganJMunozVGomberoffLKlimasAVassiliadisDet alThe magnetosphere as a complex system. Adv Space Res (2005). 35:961–71. 10.1016/j.asr.2005.03.144.
16.
GoslingJTBameSJMcComasDJ. Coronal mass ejections and large geomagnetic storms. Geophys Res Lett (1990). 17:901–4. 10.1029/GL017i007p00901.
17.
TsurutaniBTGonzalezWDGonzalezALCTangFArballoJKOkadaM. Interplanetary origin of geomagnetic activity in the declining phase of solar cycle. J Geophys Res (1995). 100:21717–33. 10.1029/95JA01476.
18.
GonzalezWDTsurutaniBTClua de GonzalezAL. Interplanetary origin of geomagnetic storms. Space Sci Rev (1999). 88:529–62. 10.1023/A:1005160129098.
19.
YermolaevYIYermolaevMYZastenkerGNZelenyiLMPetrukovichAASauvaudJ-A. Statistical studies of geomagnetic storm dependencies on solar and interplanetary events: a review. Planet Space Sci (2005). 53:189–96. 10.1016/j.pss.2004.09.044.
20.
LaughlinLKTurnerNE. Geoeffectiveness of CIR and CME events: factors contributing to their differences. J Southeastern Assoc Res Astron (2008). 2:19–22.
21.
YermolaevYINikolaevaNSLodkinaIGYermolaevMY. Geoeffectiveness and efficiency of CIR, sheath, and ICME in generation of magnetic storms. J Geophys Res (2012). 117:A00L07. 10.1029/2011JA017139.
22.
ColemanPJJ. Turbulence, viscosity and dissipation in the solar wind plasma. Astrophys J (1968). 153:371–88. 10.1086/149674.
23.
IroshnikovPS. Turbulence of a conducting fluid in a strong magnetic field. Sov Astron (1964). 40:742.
24.
KraichnanRH. Inertial-range spectrum of hydromagnetic turbulence. Phys Fluid (1965). 8:1385. 10.1063/1.1761412.
25.
BelcherJWDavisL. Large-amplitude Alfvén waves in the interplanetary medium, 2. J Geophys Res (1971). 76:3534–63. 10.1029/JA076i016p03534.
26.
BelcherJWSolodynaCV. Alfvén waves and directional discontinuities in the interplanetary medium. J Geophys Res (1975). 80:181–6. 10.1029/JA080i001p00181.
27.
BelcherJWDavisLJSmithEJ. Large-amplitude Alfvén waves in the interplanetary medium: Mariner 5. J Geophys Res (1969). 74:2302–8. 10.1029/JA074i009p02302.
28.
TuC-YPuZ-YWeiF-S. The power spectrum of interplanetary Alfvénic fluctuations: derivation of governing equation and its solution. J Geophys Res (1984). 89:9695–702. 10.1029/JA089iA11p09695.
29.
TsurutaniBTGonzalezWD. The cause of high-intensity long-duration continuous AE activity (HILDCAAs): interplanetary Alfvén wave trains. Planet Space Sci (1987). 35:405–12. 10.1016/0032-0633(87)90097-3.
30.
TsurutaniBTGonzalezWDGuarnieriFLKamideYZhouXArballoJK. Are high-intensity long-duration continuous AE activity (HILDCAA) events substorm expansion events?J Atmos Sol Terr Phys (2004). 66:167–76. 10.1016/j.jastp.2003.08.015.
31.
PrestesAKlausnerVGonzálezAOSerraSL. Statistical analysis of solar wind parameters and geomagnetic indices during HILDCAA/HILDCAA* occurrences between 1998 and 2007. Phys Rev Lett (2017). 60:1850–65. 10.1016/j.asr.2017.06.023.
32.
VerscharenDKleinKGMarucaBA. The multi-scale nature of the solar wind. Living Rev Sol Phys (2019). 16:5. 10.1007/s41116-019-0021-0.
33.
AlexandrovaOSaurJLacombeCMangeneyAMitchellJSchwartzSJet alUniversality of solar-wind turbulent spectrum from MHD to electron scales. Phys Rev Lett (2009). 103:165003. 10.1103/PhysRevLett.103.165003.
34.
SahraouiFGoldsteinMLRobertPKhotyaintsevYV. Evidence of a cascade and dissipation of solar-wind turbulence at the electron gyroscale. Phys Rev Lett (2009). 102:231102. 10.1103/PhysRevLett.102.231102.
35.
AlexandrovaOChenCHKSorriso-ValvoLHorburyTSBaleSD. Solar wind turbulence and the role of ion instabilities. Space Sci Rev (2013). 178:101–39. 10.1007/s11214-013-0004-8.
36.
BrunoRCarboneV. The solar wind as a turbulence laboratory. Living Rev Sol Phys (2013). 10:208. 10.12942/lrsp-2013-2.
37.
GoldsteinMLWicksRTPerriSSahraouiF. Kinetic scale turbulence and dissipation in the solar wind: key observational results and future outlook. Philos Trans Roy Soc (2015). A373:20140147. 10.1098/rsta.2014.0147.
38.
MatthaeusWHGoldsteinML. Low-frequency 1/f noise in the interplanetary magnetic field. Phys Rev Lett (1986). 57:495–8. 10.1103/PhysRevLett.57.495.
39.
DmitrukPMatthaeusHW. Low-frequency 1/f fluctuations in hydrodynamic and magnetohydrodynamic turbulence. Phys Rev E (2007). 76:036305. 10.1103/PhysRevE.76.036305.
40.
MatteiniLStansbyDHorburyTSChenCHK. On the 1/f spectrum in the solar wind and its connection with magnetic compressibility. Astrophys J Lett (2018). 869:L32. 10.3847/2041-8213/aaf573.
41.
BrunoRTelloniDSorriso-ValvoLMarinoRMarcoRDD’AmicisR. On the low-frequency break observed in the slow solar wind magnetic spectra. Astron Astrophys (2019). 627:A96. 10.1051/0004-6361/201935841.
42.
KolmogorovAN. The local structure turbulence in incompressible viscous fluids for very large Reynolds numbers. Dokl Akad Nauk SSSR (1941). 30:301–5.
43.
BrunoRTrenchiLTelloniD. Spectral slope variation at proton scales from fast to slow solar wind. Astrophys J Lett (2014). 793:L15. 10.1088/2041-8205/793/1/L15.
44.
D’AmicisRMatteiniLBrunoR. On the slow solar wind with high Alfvénicity: from composition and microphysics to spectral properties. Mon Not Roy Astron Soc (2019). 483:4665–77. 10.1093/mnras/sty3329.
45.
BorovskyJEFunstenHO. Role of solar wind turbulence in the coupling of the solar wind to the Earth’s magnetosphere. J Geophys Res (2003). 108:1246. 10.1029/2002JA009601.
46.
AlexandrovaOLacombeCMangeneyA. Spectra and anisotropy of magnetic fluctuations in the Earth’s magnetosheath: cluster observations. Ann Geophys (2008). 26:3585–96. 10.5194/angeo-26-3585-2008.
47.
HuangSYHadidLZSahraouiFYuanZGDengXH. On the existence of the Kolmogorov inertial range in the terrestrial magnetosheath turbulence. Astrophys J Lett (2017). 836:L10. 10.3847/2041-8213/836/1/L10
48.
ChhiberRChasapisABandyopadhyayRParasharTNMatthaeusWHMarucaBAet alHigher-order turbulence statistics in the Earth’s magnetosheath and the solar wind using Magnetospheric multiscale observations. J Geophys Res (2018). 123:9941–54. 10.1029/2018JA025768
49.
LiHJiangWWangCVerscharenDZengCRussellCTet alEvolution of the Earth’s magnetosheath turbulence: a statistical study based on mms observations. Astrophys J Lett (2020). 898:L43. 10.3847/2041-8213/aba531
50.
KozakLVPetrenkoBALuiATYKronbergEAGrigorenkoEEProkhorenkovAS. Turbulent processes in the Earth’s magnetotail: spectral and statistical research. Ann Geophys (2018). 36:1303–18. 10.5194/angeo-36-1303-2018
51.
Di MareFSorriso-ValvoLRetinoAMalaraFHasegawaH. Evolution of turbulence in the Kelvin-Helmholtz instability in the terrestrial magnetopause. Atmosphere (2019). 10:561. 10.3390/atmos10090561
52.
BartelsJ. Potsdamer erdmagnetische. Ztschrift Geophys (1938). 14:68–78.
53.
DavisTNSugiuraM. Auroral electrojet activity index AE and its universal time variations. J Geophys Res (1966). 71:785–801. 10.1029/JZ07i003p00785
54.
SugiuraM. Hourly values of equatorial Dst for the IGY. Ann IGY (1964). 35:9.
55.
SugiuraMKameiT. Equatorial Dst index 1957-1986. In: BerthelierAMenvielleM, editors. IAGA bulletin 40. Saint Maur, France: Int. Serv. of Geomagn. Indices Publ. Off. (1991). p. 246.
56.
IyemoriT. Storm-time magnetospheric currents inferred from mid-latitude geomagnetic field variations. J Geomagn Geoelectr (1990). 42:1249–65. 10.5636/jgg.42.1249
57.
TsurutaniBTSugiuraMIyemoriTGoldsteinBEGonzalezWDAkasofuS-Iet alThe nonlinear response of AE to the IMF Bs driver - a spectral break at 5 hours. Geophys Res Lett (1990). 17:269–82. 10.1029/GL017i003p00279
58.
WeiHLBillingsSABalikhinM. Analysis of the geomagnetic activity of the Dst index and self-affine fractals using wavelet transforms. Nonlinear Process Geophys (2004). 11:303–12. 10.5194/npg-11-303-2004
59.
ConsoliniGMarcucciMFCandidiM. Multifractal structure of auroral electrojet index data. Phys Rev Lett (1996). 76:4082–5. 10.1103/PhysRevLett.76.4082
60.
ConsoliniGMichelisPD. Non-Gaussian distribution function of AE index fluctuations: evidence of time intermittency. Geophys Res Lett (1998). 9:419–23. 10.1029/1998GL900073
61.
VorosZ. On multifractality of high-latitude geomagnetic fluctuations. Ann Geophys (2000). 18:1273–82. 10.1007/s00585-000-1273-6
62.
DorotovicIVorosK. On the Earth’s plasma sheet response to the magnetic turbulence in the solar wind. In: DanesyADGDPoedtsSAndriesJ, editors.Proceedings of the 11th European solar physics meeting the dynamic Sun: challenges for theory and observations; 2005 Sep 11–16; Leuven, Belgium. Noordwijk, Netherlands: ESA Publications (2005). p. 13.
63.
RypdalMRypdalK. Stochastic modeling of the AE index and its relation to fluctuations in Bz of the IMF on time scales shorter than substorm duration. J Geophys Res (2010). 115:A11216. 10.1029/2010JA015463
64.
VorosZJankovicovaDKovacsP. Scaling and singularity characteristics of solar wind and magnetospheric fluctuations. Nonlinear Process Geophys (2002). 9:149–62. 10.5194/npg-9-149-2002
65.
D’AmicisRBrunoRBavassanoB. Alfvénic turbulence in high speed solar wind streams as a driver for auroral activity. J Atmos Sol Terr Phys (2009). 71:1014–22. 10.1016/j.jastp.2008.05.002
66.
ConsoliniG. Sandpile cellular automata and magnetospheric dynamics. In: AielloSIucciNSironiGTravesAVillanteU, editors. Proceedings of the 8th GIFCO conference: cosmic physics in the year 2000. Bologna, Italy: SIF (1997). p. 123–6.
67.
TakaloJ. Correlation dimension of AE data. [PhD thesis]. Jyväskylä, Finland: University of Jyviskylii (1993).
68.
LuiATYChapmanSCLiouKNewellPTMengnadCIBrittnacherMet alIs the dynamic magnetosphere an avalanching system?. Geophys Res Lett (2000). 27:911–4. 10.1029/1999GL010752
69.
UritskyVMKlimasAJVassiliadisDChuaDParksG. Scale-free statistics of spatiotemporal auroral emissions as depicted by POLAR UVI images: dynamic magnetosphere is an avalanching system. J Geophys Res (2002). 107:1426. 10.1029/2001JA000281
70.
D’AmicisRBrunoRVillanteU. A comparative study of probability distribution functions and burst lifetime distributions of Bs and AE at solar maximum and minimum. In: LuiATYKamideYConsoliniG, editors. Multiscale coupling of Sun-Earth processes. Burlington, MA: Elsevier (2005). p. 399–409.
71.
ChangTS. Self-organized criticality, multi-fractal spectra, sporadic localized reconnections and intermittent turbulence in the magnetotail. Phys Plasmas (1999). 6:4137–45. 10.1063/1.873678
72.
ConsoliniGChangTS. Magnetic field topology and criticality in geotail dynamics: relevance to substorm phenomena. Space Sci Rev (2001). 95:309–21. 10.1023/A:1005252807049
73.
BakPTangCWiesenfeldK. Self-organized criticality: an explanation of the 1/f noise. Phys Rev Lett (1987). 59:381. 10.1103/PhysRevLett.59.381.
74.
ConsoliniGMichelisPD. Fractal time statistics of AE-index burst waiting times: evidence of metastability. Nonlinear Process Geophys (2002). 9:419–23. 10.5194/npg-9-419-2002
75.
SánchezRNewmanDECarrerasBA. Waiting-time statistics of self-organized-criticality systems. Phys Rev Lett (2002). 88:068302. 10.1103/PhysRevLett.88.068302
76.
KlimasAJValdiviaJAVassiliadisDBakerDNHesseMTakaloJ. Self-organized criticality in the substorm phenomenon and its relation to localized reconnection in the magnetospheric plasma sheet. J Geophys Res (2000). 105:18765–80. 10.1029/1999JA000319
77.
SitnovMISharmaASPapadopoulosKVassiliadisDValdiviaJAKlimasAJet alPhase transition-like behavior of the magnetosphere during substorms. J Geophys Res (2000). 105:12955–74. 10.1029/1999JA000279
78.
SharmaASAschwandenMJCrosbyNBKlimasAJMilovanovAVMoralesLet al25 Years of self-organized criticality: space and laboratory plasmas. Space Sci Rev (2016). 198:167–216. 10.1007/s11214-015-0225-0
79.
AschwandenMJCrosbyNBDimitropoulouMGeorgoulisMKHergartenSMcAteerJet al25 Years of self-organized criticality: solar and astrophysics. Space Sci Rev (2016). 198:47–166. 10.1007/s11214-014-0054-6
80.
WanlissJWeygandJM. Power law burst lifetime distribution of the SYM-H index. Geophys Res Lett (2007). 34:L04107. 10.1029/2006GL028235
81.
WanlissJ. Nonlinear variability of SYM-H over two solar cycles. Earth Planets Space (2004). 56:e13–6. 10.1186/BF03352507
82.
WanlissJ. Fractal properties of SYM-H during quiet and active times. J Geophys Res (2005). 110:A03202. 10.1029/2004JA010544
83.
PeltierR-FLévy-VéhelJ. Multifractional brownian motion : definition and preliminary results (1995). INRIA. RR-2645.
84.
BurtonRKMcPherronRLRussellCT. An empirical relationship between interplanetary conditions and Dst. J Geophys Res (1975). 80:4204. 10.1029/JA080i031p04204
85.
PerreaultPAkasofuSI. A study of geomagnetic storms. Geophys J (1978). 54:547–73. 10.1111/j.1365-246X.1978.tb05494.x
86.
FreemanMWatkinsNWRileyDJ. Evidence for a solar wind origin of the power law burst lifetime distribution of the AE indices. Geophys Res Lett (2000). 27:1087–90. 10.1029/1999GL010742
87.
BargatzeLFBakerDNMcPherronRLHonesEW. Magnetospheric impulse response for many levels of magnetospheric activity. J Geophys Res (1985). 90:6387–94. 10.1029/JA090iA07p06387
88.
ObayashiTNishidaA. Large-scale electric field in the magnetosphere. Space Sci Rev (1968). 8:3–31. 10.1007/BF00362569
89.
NishidaA. DP 2 and polar substorm. Space Sci Rev (1971). 19:205–21. 10.1016/0032-0633(71)90200-5
90.
KamideYBaumjohannW. Magnetosphere-ionosphere coupling. New York: Springer-Verlag (1993).
91.
TsurutaniBTSlavinJAKamideYZwicklRDKingJHRussellCT. Coupling between the solar wind and the magnetosphere: CDAW 6. J Geophys Res (1985). 90:1191–9. 10.1029/JA090iA02p01191
92.
RostokerGAkasofuS-IBaumjohannWKamideYMcPherronRL. The roles of direct input of energy from the solar wind and unloading of stored magnetotail energy in driving magnetospheric substorms. Space Sci Rev (1987). 46:93–111. 10.1007/BF00173876
93.
LiouKNewellPTMengC-IBrittnacherMParksG. Characteristics of the solar wind controlled auroral emissions. J Geophys Res (1998). 103:17543–57. 10.1029/98JA01388
94.
AngelopoulosVMcFaddenJPLarsonDCarlsonCWMendeSBFreyHet alTail reconnection triggering substorm onset. Science (2008). 321:931–5. 10.1126/science.1160495
95.
HnatBChapmanSCRowlandsGWatkinsNWFreemanMP. Scaling of solar wind ϵ and the AU, AL and AE indices as seen by WIND. Geophys Res Lett (2002). 29:2078. 10.1029/2002GL016054.
96.
ConsoliniGMichelisPD. Local intermittency measure analysis of AE index: the directly driven and unloading component. Geophys Res Lett (2005). 32:L05101. 10.1029/2004GL022063
97.
HnatBChapmanSCRowlandsG. Scaling and a Fokker-Planck model for fluctuations in geomagnetic indices and comparison with solar wind as seen by Wind and ACE. J Geophys Res (2005). 110:A08206. 10.1029/2004JA010824
98.
D’AmicisRBrunoRBavassanoB. Geomagnetic activity driven by solar wind turbulence. Adv Space Res (2010). 46:514–20. 10.1016/j.asr.2009.08.031
99.
PaczuskiMSBoettcherSBaiesiM. Interoccurrence times in the Bak-Tang-Wiesenfeld sandpile model: a comparison with the observed statistics of solar flares. Phys Rev Lett (2005). 95:181102. 10.1103/PhysRevLett.95.181102
100.
LuiATYMcEntireRWKrimigisSM. Evolution of the ring current during two geomagnetic storms. J Geophys Res (1987). 92:7459–70. 10.1029/JA092iA07p07459
101.
JankovicovaDVorosZSimkaninJ. The influence of solar wind turbulence on geomagnetic activity. Nonlinear Process Geophys (2008). 15:53–9. 10.5194/npg-15-53-2008
102.
OsmaneADimmockAPNaderpourRPulkkinenTINykyriK. The impact of solar wind ulf bz fluctuations on geomagnetic activity for viscous timescales during strongly northward and southward imf. J Geophys Res (2015). 120:9307–22. 10.1002/2015JA021505
103.
NewellPTGjerloevJWMitchellEJ. Space climate implications from substorm frequency. J Geophys Res (2013). 118:6254–65. 10.1002/jgra.50597
104.
BorovskyJE. The effect of sudden wind shear on the Earth’s magnetosphere: statistics of wind shear events and CCMC simulations of magnetotail disconnections. J Geophys Res (2012). 117:A06224. 10.1029/2012JA017623
105.
TelloniDCarboneFAntonucciEBrunoRGrimaniCVillanteUet alStudy of the influence of the solar wind energy on the geomagnetic activity for Space Weather science. Astrophys J (2020). 896:149. 10.3847/1538-4357/ab91b9
106.
D’AmicisRBrunoRBavassanoB. Is geomagnetic activity driven by solar wind turbulence?Geophys Res Lett (2007). 34:L05108. 10.1029/2006GL028896
107.
D’AmicisRBrunoRBavassanoB. Response of the geomagnetic activity to solar wind turbulence during solar cycle 23. J Atmos Sol Terr Phys (2011). 73:653. 10.1016/j.jastp.2011.01.012
108.
D’AmicisRBrunoR. On the origin of highly Alfvénic slow solar wind. Astrophys J (2015). 805:84. 10.1088/0004-637X/805/1/84
109.
StansbyDMatteiniLHorburyTSPerroneDD’AmicisRBercicL. The origin of slow Alfvénic solar wind at solar minimum. Mon Not Roy Astron Soc (2020). 492:39–44. 10.1093/mnras/stz3422
110.
PerroneDD’AmicisRMarcoRDMatteiniLStansbyDBrunoRet alHighly Alfvénic slow solar wind at 0.3 au during a solar minimum: helios insights for Parker Solar Probe and Solar Orbiter. Astron Astrophys (2020). 633:A166. 10.1051/0004-6361/201937064
111.
D’AmicisRMatteiniLBrunoRVelliM. Large amplitude fluctuations in the Alfvénic solar wind. Sol Phys (2020). 295:46. 10.1007/s11207-020-01606-2
112.
TelloniDBrunoRD’AmicisRCarboneFMarcoRDPerroneD. Wave-polarization analysis of the Alfvénic slow solar wind at kinetic scales. Astrophys J (2020). 897:167. 10.3847/1538-4357/ab980a
113.
GuarnieriFLTsurutaniBTGonzalezWDEcherEGonzalezALCGrandeMet alICME and CIR storms with particular emphasis on HILDCAA events. In: GopalswamyNBhattacharyyaA, editors. Solar influence on the heliosphere and Earth’s environment: recent progress and prospects; 2006 Feb 19–20; Goa, India. Mumbai, India: Indian Institute of Geomagnetism (2006). p. 266.
114.
TsurutaniBTGonzalezWDGonzalezALCGuarnieriFLGopalswamyNGrandeMet alCorotating solar wind streams and recurrent geomagnetic activity: a review. J Geophys Res (2006). 111:A07S01. 10.1029/2005JA011273
115.
WanlissJAAnhVVYuZ-GWatsonS. Multifractal modeling of magnetic storms via symbolic dynamics analysis. J Geophys Res (2005). 110:A08214. 10.1029/2004JA010996
Summary
Keywords
solar wind, interplanetary magnetic field, turbulence, geomagnetic response, geomagnetic activity indices, magnetic storm and substorm
Citation
D’Amicis R, Telloni D and Bruno R (2020) The Effect of Solar-Wind Turbulence on Magnetospheric Activity. Front. Phys. 8:604857. doi: 10.3389/fphy.2020.604857
Received
10 September 2020
Accepted
27 October 2020
Published
25 November 2020
Volume
8 - 2020
Edited by
Joseph Eric Borovsky, Space Science Institute, United States
Reviewed by
Zoltan Voros, Austrian Academy of Sciences, Austria
Adnane Osmane, University of Helsinki, Finland
Updates
Copyright
© 2020 D'Amicis, Telloni and Bruno.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: R. D’Amicis, raffaella.damicis@inaf.it
This article was submitted to Space Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.