Ion Acoustic Peregrine Soliton Under Enhanced Dissipation

The effect of enhanced Landau damping on the evolution of ion acoustic Peregrine soliton in multicomponent plasma with negative ions has been investigated. The experiment is performed in a multidipole double plasma device. To enhance the ion Landau damping, the temperature of the ions is increased by applying a continuous sinusoidal signal of frequency close to the ion plasma frequency ∼1 MHz to the separation grid. The spatial damping rate of the ion acoustic wave is measured by interferometry. The damping rate of ion acoustic wave increases with the increase in voltage of the applied signal. At a higher damping rate, the Peregrine soliton ceases to show its characteristics leaving behind a continuous envelope.

Introduction

The Peregrine soliton is an isolated large-amplitude wave commonly known as rogue waves. These are extreme and rare wave events that usually appear on the ocean surfaces. It has two unique properties that distinguish the Peregrine soliton from ordinary solitons. Firstly, this large-amplitude wave is localized in both time and space axis; secondly, it has amplitude amplification of more than ∼3 times that of the background wave height. One generic mechanism considered responsible for the evolution of rogue waves is modulational instability. In this process, phase and amplitude modulation grow due to a delicate balance between nonlinearity and group velocity dispersion. Different solutions of nonlinear Schrodinger equation (NLSE) deal with such type of instability. In 1983, Peregrine derived a rational solution of NLSE in the context of water waves as a limit of a wide class of solutions to the NLSE [1]. This solution was later known as Peregrine soliton, which has been considered as a prototype of a rogue wave. Almost 3 decades later, the Peregrine soliton has been experimentally observed in various nonlinear mediums such as fiber optics, water, and plasma [2–4]. The NLSE, in its many forms, provides the solutions of extreme wave events (rogue waves, breathers, and envelope solitons) [5–7, 9]. Using the NLSE framework, the vigours properties of rogue waves have been theoretically studied in different plasma systems, such as electron-positron plasma [8], magnetized plasma [9], plasma with nonextensive electron velocity distribution [10], nonthermal plasma [11], and dusty plasma [12–16]. Recently, Tsai et al. [17] confirmed the presence of dust acoustic rogue waves in a self-excited laboratory dusty plasma medium. The existence of rogue waves has also been studied in a degenerate Thomas-Fermi plasma system [18]. The NLSE was derived for this purpose by considering cold inertial ions and Thomas-Fermi distributed electrons and positrons. Similar studies in electron-positron-ion plasma using a semirelativistic fluid model predicted the evolution of both bright and dark type envelope solitons [19, 20].

In multicomponent plasma with a critical concentration of negative ions, an initial amplitude-modulated ion wave packet undergoes self-modulation due to modulational instability and gives rise to the formation of bright and dark (hole) ion acoustic Peregrine soliton [4, 21]. The criteria for the generation of bright and hole Peregrine soliton out of an initial amplitude-modulated perturbation depend on the relative phase between the carrier and the envelope. The evolution of envelope-like solitons in such plasma is too described by the NLSE [22, 23]. The NLSE also supports the existence of higher-order and multiple Peregrine solitons [7, 24–26]. In our previous works, we have experimentally observed both second-order Peregrine soliton and multi-Peregrine soliton in multicomponent plasma containing negative ions [27, 28]. It was found that the characteristics of initial perturbations such as the amplitude (steepness) and modulation length (and depth) play a crucial role in the generation of both kinds of solitons.

Landau damping is a collisionless process because of which a longitudinal space charge wave (e.g., ion acoustic wave) in plasma decays exponentially with time. It occurs due to energy exchange between the waves and particles in plasma when their velocities are comparable. Eventually, Landau damping prevents the growth of instability and creates a region of stability in the parameter space. In laboratory discharge plasma with Maxwellian electrons, ion waves suffer Landau damping which become dominant when ion temperature is comparable to electron temperature ($T_i\sim T_e$). Various research works have been performed to study the solitary waves in plasmas containing additional components like multispecies ions, negative ions, and dust particles [29–34]. Landau damping modifies the nature of solitary waves in such plasmas, and it has been extensively studied both experimentally and theoretically [35–39]. The first experiment to detect the Landau damping of ion acoustic wave was performed in a highly ionized cesium and potassium plasma [40]. In a Q machine plasma experiment, Landau damping was found to prevent the formation of solitary waves by dominating over the steepening effect of nonlinearity [41]. However, the strength of Landau damping reduces in the presence of negatively charged dust particles in a Q machine plasma [42, 43]. In the double plasma (DP) device, experiments on shock and solitary waves under enhanced Landau damping have been performed [44, 45]. The study showed that the presence of lighter ions enhances the damping, which prevents the formation of solitons in a DP device [46].

The purpose of this paper is to report the experimental investigation of the Landau damping effect on Peregrine soliton in multicomponent plasma with a critical concentration of negative ions. The experimental setup and procedure to enhance the strength of Landau damping are discussed in Experimental Setup. The experimental measurement of Landau damping rate using interferometry and the observation of Peregrine soliton under enhanced damping are conferred in Results and Discussion. Finally, we present the concluding remarks in Conclusion.

Experimental Setup

Production of Multicomponent Plasma

The experiment is carried out in a DP device of a length of 120 cm and a diameter of 30 cm with a surface plasma confinement facility [21, 27]. The device consists of two magnetic cages separated by a floating mesh grid in between. Argon plasma is produced in both chambers at an operating pressure of $3.8\times {10}^{-4}$ Torr by the independent dc discharge process. The discharge voltages and currents are maintained at 60 V and 10–50 mA, respectively. The plasma parameters are measured with the help of an axially movable planar Langmuir probe. The measured electron temperature and density are in the range of 1–2 eV and 10⁸–10⁹ cm⁻³, respectively. Next, to produce the multicomponent plasma, SF₆ gas is inserted into the chamber through a fine control needle valve at a partial pressure of $(1 – 4)\times {10}^{-5}$ Torr and as a result, the ${\text{F}}^{-}$ ions are produced mainly through a dissociative attachment process. For the present experiment, the multicomponent plasma is thus created, which contains electrons and ${\text{Ar}}^{+}$ and ${\text{F}}^{-}$ ions. The density of ${\text{F}}^{-}$ ions is finely controlled to maintain the critical density ratio of negative to positive ion, i.e., $n_{-}/n_{+}=0.1$, where $n_{-}$ is the negative ion (${\text{F}}^{-}$) density and $n_{+}$ is the positive ion $\left({\text{Ar}}^{+}\right)$ density. The I–V characteristics curves are obtained for Ar and Ar + SF₆ plasma separately, and the electron and ion saturation currents are measured from it. From these saturation currents, the critical density ratio is calculated by the formula $r=1-I_{es}/I_{es0}$, where $I_{es}$ and $I_{es0}$ are the Langmuir probe saturation current with and without SF₆, respectively. After attaining the desired conditions, a slowly amplitude-modulated sinusoidal wave packet is applied to the source anode as the initial perturbation to excite the Peregrine soliton. The mean free path of the ion-neutral collision is estimated to be in the order of meters; hence, the generated plasma can be considered as collisionless [47, 48].

Method to Enhance the Strength of Landau Damping

In a DP device, the electron to ion temperature ratio is usually high ($\ge 10$), and hence the propagating wave suffers negligible Landau damping. For this reason, the DP device is used for wave experiments in plasma from the early days [49, 50]. Two methods are widely used to enhance Landau damping in a DP device. The first one is to mix lighter mass ions to increase the number of resonant particles. In a pioneering experiment, the addition of a trace of light helium ions to a xenon plasma has led to Landau damping of ion acoustic wave [41]. In the presence of lighter helium ions, the wave phase velocity and temperature ratio changes only up to 10%, which induces the Landau damping, providing all other plasma parameters unaltered. This technique was applied to examine the enhanced Landau damping effect on shock propagation in a DP device [44]. The damping rate was found to be proportional to the wave number in the linear regime. The second method is to apply a radio frequency (rf) signal (frequency ∼ ${\omega }_{pi}$) to the separation grid of a DP device to heat the ions [45]. The ions near the grid oscillate at this frequency and gain energy. Hence, by adjusting the amplitude of the rf signal, plasma ion temperature enhancement can be obtained. The experimental investigation of collisionless damping effect on the propagation of ion acoustic solitary waves has already been performed by using this method [45], where an rf signal of frequency 1.78 MHz with a peak to peak voltage (V_HF) ranging from 0 to 400 mV was applied to the separation grid. This value of V_HF is too small to affect the plasma parameters other than the ion temperature. In the present experiment, an rf signal of frequency f_HF = 900 kHz is applied to the separation grid to heat the ions from a function generator. The desired Landau damping rate is obtained by varying the peak to peak voltage ($V_{HF}$) in the range 0–100 mV. In Figure 1, the schematic of the experimental arrangement to control the Landau damping strength is presented.

FIGURE 1

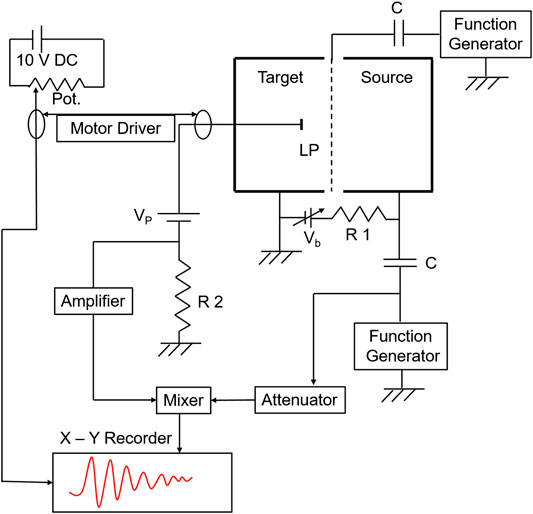
FIGURE 1. Block diagram of the experimental arrangement to enhance the Landau damping as well as measure the dispersion relation of ion acoustic waves.

Results and Discussion

Measurement of Landau Damping Rate of Ion Acoustic Wave

Experimentally, we first examine the linear dispersion relation of ion acoustic wave in the present argon plasma condition using interferometry. For this, continuous sinusoidal waves of frequency 100–800 kHz (100 kHz in step) with amplitude ≤200 mV are applied to the source anode from a function generator through a 1 μF capacitor. A reference signal from the function generator is applied to the balanced mixer’s right input through an attenuator. The plane Langmuir probe collects the signal continuously against the axial position with a motorized probe driving system. The probe is biased above the plasma potential in order to detect perturbations in electron saturation current. The signal is detected by the probe that is coupled to the left input of the mixer. The output of the mixer is fed to the Y axis of the X–Y recorder. The probe distance from the grid is calibrated using a separate voltage source with a potentiometer attached to the motor driving system and is connected to the X axis of the X–Y recorder. Figure 2 shows a typical linear dispersion relation for ion acoustic waves in a normal argon plasma. The solid line represents the theoretical dispersion relation, which is obtained by putting the experimental plasma parameters in Eq. 1. The theoretical relation (Eq. 1) is derived by considering the Maxwellian distribution having T_e >> T_i [51].

$\frac{{\omega }^2}{k_r^2}=\frac{K_B{T}_e}{m_i}\left(\frac{1+\frac{3T_i}{T_e}}{1+k_r^2{\lambda }_D^2}\right).(1)$

FIGURE 2

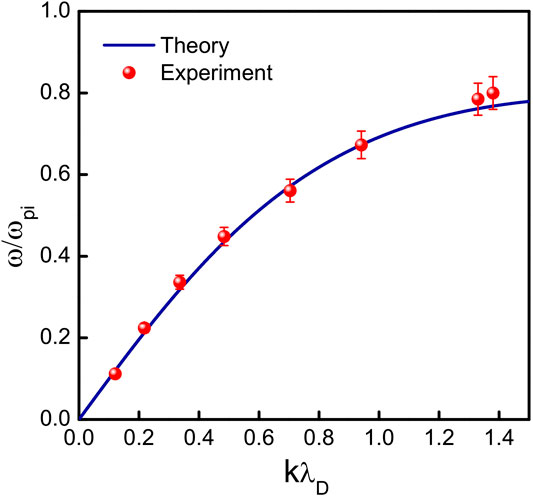
FIGURE 2. Dispersion relation of ion acoustic wave. The solid line is the theoretical curve calculated from Eq. 1.

Here $\omega$ is the frequency component, $k_r$ is the real wavenumber, $T_i$ and $T_e$ are the ion and electron temperatures, respectively, and $m_i$ is the ion mass. The Debye length, ${\lambda }_D=0.02 \text{cm}$, and ion plasma frequency, ω_pi = 892 kHz, are measured from the plasma parameters. In Figure 2, it is observed that the measured $\omega -k$ relation fits well with the theoretical one. The phase velocity of the ion acoustic wave measured from the lower $k{\lambda }_D$ region is $\sim 1.04\times {10}^5{\text{cms}}^{-1}$.

Usually, the Landau damping rate is calculated from the real ($k_r$) and imaginary ($k_i$) parts of the wavenumber. As the wave varies in space as $exp\left(ikx\right)$, the imaginary part of the wavenumber will produce spatial exponential damping. Here, the spatial damping rate ($k_i/k_r$) of the wave is calculated from the phase plots for a fixed value of V_HF. The phase plots for V_HF = 0 and 100 mV at applied frequency 500 kHz are shown in Figure 3. The fast reduction of amplitude at V_HF = 100 mV signifies the increment in Landau damping rate. Generally, in basic plasma wave experiments, the effect of Landau damping is often observed as damping of an exciting wave during propagation. We observe the impact of damping through resonant particles traveling at wave phase velocity. The graphs of the measured damping rate ($k_i/k_r$) with normalized frequency are shown in Figure 4. The theoretical plot is obtained from the following relation [51]:

$\frac{1}{2 \pi } \frac{k_i}{k_r}=\frac{{\left(\frac{T_e}{T_i}\right)}^{3/2}exp\left\{\left(\frac{T_e}{3T_i}\right)\left(1-\frac{{\omega }^2}{{\omega }_{pi}^2}\right)\left(1+\frac{3T_i}{T_e}\right)\right\}.}{2{\pi }^{3/2}{\left(1-\frac{{\omega }^2}{{\omega }_{pi}^2}\right)}^{1/2}} (2)$

FIGURE 3

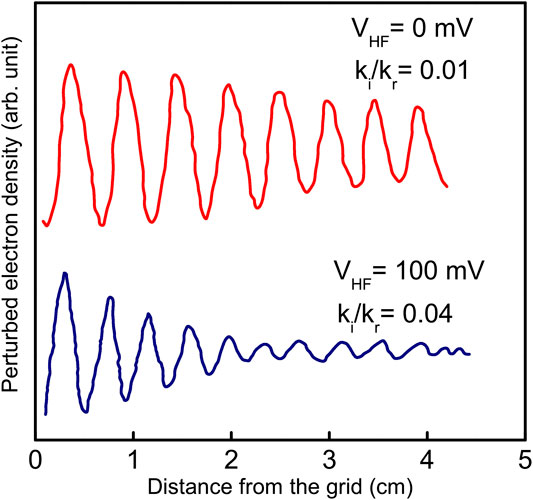
FIGURE 3. Typical interferometer pattern for a 500 kHz signal at V_HF = 0 and 100 mV. The measured damping rates are also shown.

FIGURE 4

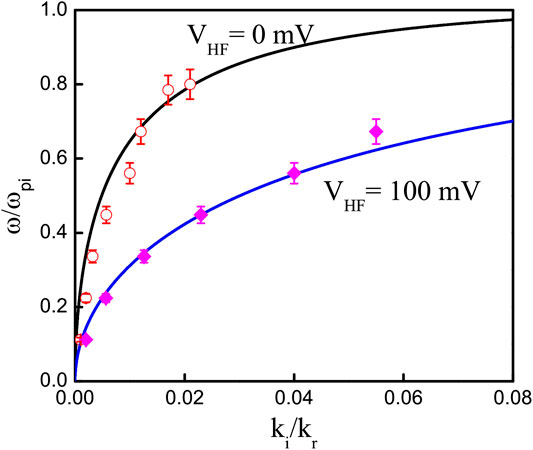
FIGURE 4. Normalized wavenumber $\omega /{\omega }_{pi}$ as a function of the spatial damping rate $k_i/k_r$. The solid curves are theoretically obtained from Eq. 2. The open and closed symbols are experimentally measured values at V_HF = 0 and V_HF = 100 mv, respectively.

The damping rate of the ion acoustic wave increases as the amplitude of the rf signal is increased. In Figure 4, the solid lines are calculated for V_HF = 0 and V_HF = 100 mV from Eq. 2, whereas the open and closed symbols are calculated values of $k_i/k_r$ for V_HF = 0 and V_HF = 100 mV, respectively. The experimental points are found to coincide with the theory nicely.

Peregrine Soliton Under Enhanced Landau Damping

Initially, to excite the Peregrine soliton, an amplitude-modulated continuous sinusoidal wave of carrier frequency 380 kHz and modulation frequency 30 Hz is synthesized using a pair of function generators. The carrier frequency is typically selected at nearly half of the ion plasma frequency (f_pi ∼ 892 kHz). The excitation amplitude of the carrier wave is varied from 2 to 9 V. Example of the evolution of Peregrine soliton at different initial amplitude is shown in Figure 5 at a fixed distance from the grid x = 9 cm. The initially applied signal is shown at the top. For carrier amplitude V_c = 5 V, the perturbation resembles the applied perturbation, which indicates linear wave propagation. The carrier amplitude is small, and the effective nonlinearity is just below the threshold, due to which the perturbation is linear. Gradually, with the increase in excitation amplitude, the wave packet suffers steepening due to nonlinearity. When the self-modulation of the wave packet reaches 100% at V_c = 8 V, the nonlinearity is entirely balanced by the group velocity dispersion, leading to the formation of Peregrine soliton. The amplitude amplification factor of the Peregrine soliton is found to be ∼3 (ratio of the peak amplitude of the wave packet to the background carrier wave amplitude). The group velocity of the perturbation is $\mathrm{\sim }2\times {10}^5{\text{ cms}}^{-1}$.

FIGURE 5

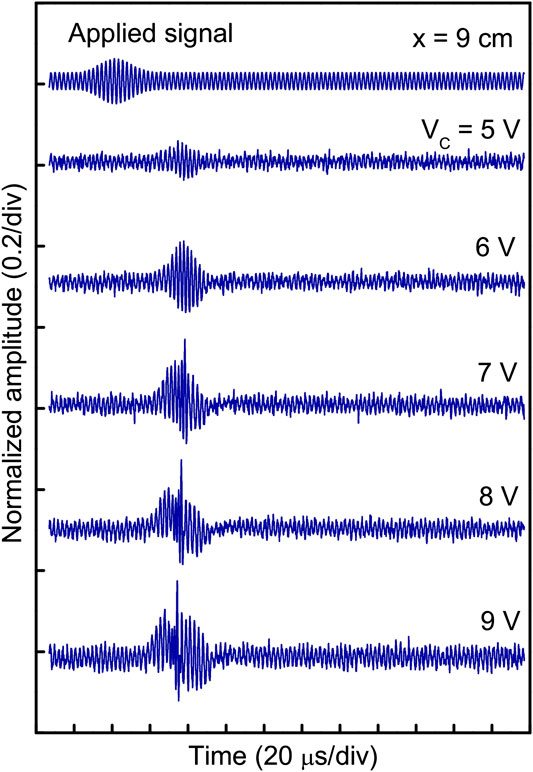
FIGURE 5. Typical examples experimentally observed Peregrine soliton at x = 9 cm from the grid. The top trace is the applied signal with carrier and modulation frequencies 380 and 30 kHz, respectively.

Next, a high-frequency rf signal is applied to the grid to enforce Landau damping on the evolution of Peregrine soliton while keeping the probe distance fixed at 9 cm (with V_c = 8 V). The frequency of the applied continuous signal is kept fixed at 900 kHz, which is in the range of ion plasma frequency. Modification of the Peregrine soliton due to the dissipative effect is shown in Figures 6A,B. At V_HF = 0 mV, i.e., without the rf voltage, the Peregrine soliton is undisturbed. As V_HF increases, the Peregrine soliton amplitude decreases, which signifies the enhancement of the strength of Landau damping. At V_HF = 60 mV, the peak of the Peregrine soliton completely disappears. As indicated by the damping rate calculation, an increase in V_HF provides strong Landau damping. As shown in Figures 6A,B, the amplitude of the Peregrine soliton decreases with an increase in V_HF. Although the amplitude of the background carrier wave is increased at high V_HF, which indicates the increase in ion temperature.

FIGURE 6

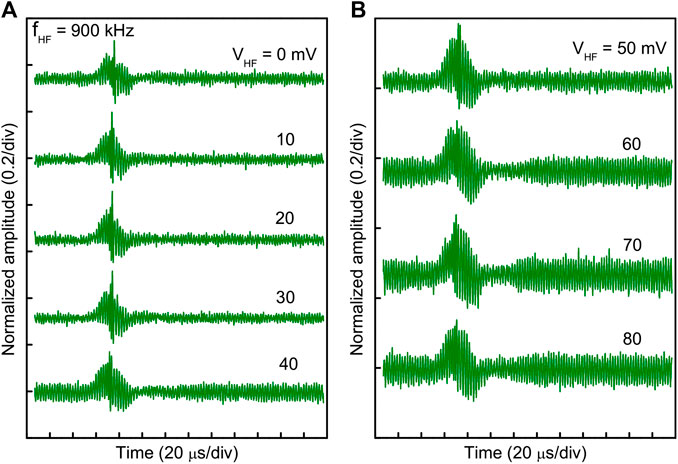
FIGURE 6. Observed oscilloscope trace at a fixed probe position 9 cm from the separation grid showing the transition of ion acoustic Peregrine soliton to an envelope with an increase in V_HF. (A) For V_HF = 0–40 mV. (B) For V_HF = 50–80 mV.

A close observation of the evolution indicates that the solitary peak amplitude gradually decreases with the reduction of compression in the middle of the wave packet (due to which wave energy focuses on forming a soliton). An increase in ion temperature raises the number of resonant ions near the phase velocity of the wave, due to which Landau damping is enhanced, and the wave becomes less dispersive. As nonlinearity remains the same, now both dissipation (due to enhanced Landau damping) and dispersion compete to balance the nonlinearity.

Continuous Wavelet Transformation Analysis

The continuous wavelet transformation (CWT) analysis is performed for time-series data (presented in Figures 6A,B) and shown in Figures 7, 8. The time-series data are presented along with the CWT scalogram (3-dimensional surface plot of the absolute coefficient matrix) to clarify the temporal locations of the envelope. In Figure 7A, the CWT analysis of the Peregrine soliton for a temporal data length of 250 μs is shown (which corresponds to the top trace of Figure 6A). The CWT scalogram shows the broadening of the frequency spectrum at 75 µs, i.e., at the isolated peak location. For better resolution, CWT analysis is performed for a temporal length of 50–100 μs and shown in Figure 7B. A deep hole (dark blue) in front of the soliton peak is observed here. This hole represents the complete self-modulation of the initially applied wave packet due to modulational instability.

FIGURE 7

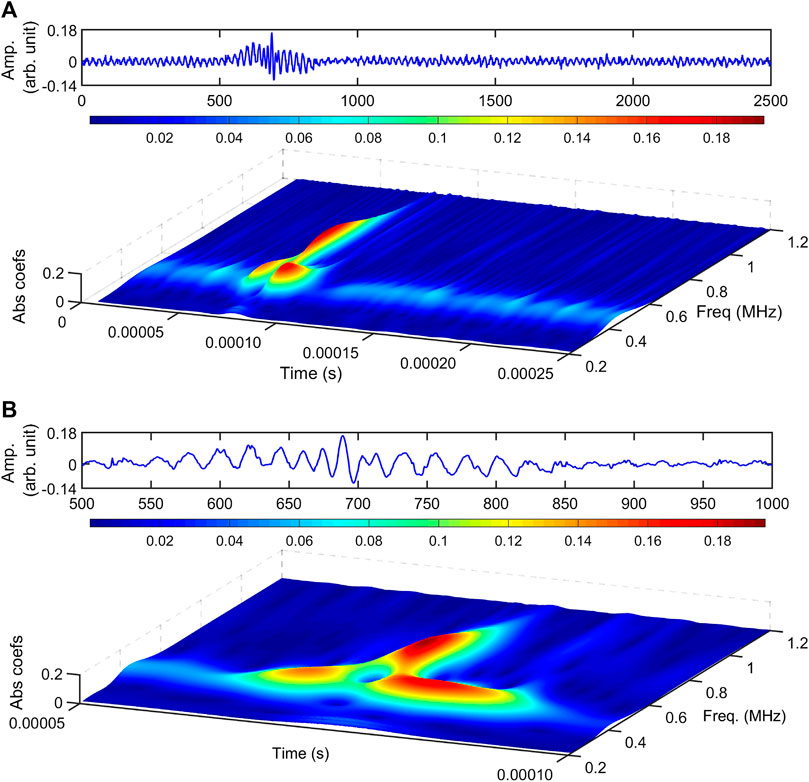
FIGURE 7. Typical CWT scalogram of fundamental Peregrine soliton without application of V_HF. The probe position is at 9 cm. (A) Time series (top) and CWT scalogram (bottom) for Peregrine soliton for data length 0–250 µs. (B) Enlarged view of (A) for data length 50–100 µs.

FIGURE 8

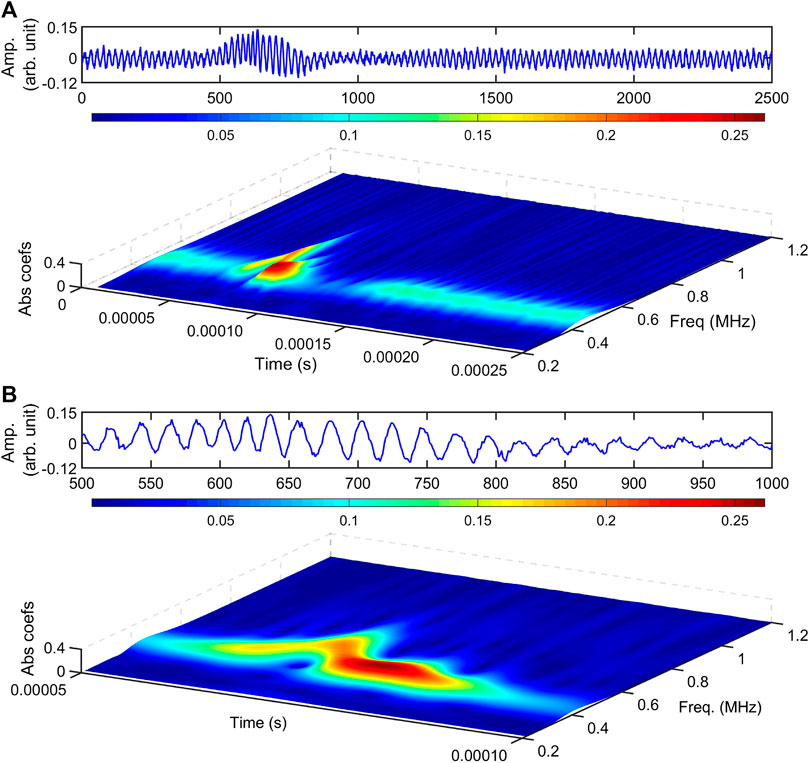
FIGURE 8. Typical CWT scalogram of fundamental Peregrine soliton with the application of V_HF = 80 mV. The probe position is at 9 cm. (A) Time series (top) and CWT scalogram for data length 0–250 µs (bottom). (B) Enlarged view of (A) for data length 50–100 µs.

The CWT scalogram, along with the time-series data of envelope with enhanced Landau damping (with V_HF = 80 mV), is shown in Figures 8A,B. Here, the reduction in the broadening of the frequency spectrum is clearly observed. Also, in Figure 8B, it is noticed that the deep hole in front of the largest wave crest almost disappears. Figure 7B shows the focusing of energy on the narrow wave group in the middle of the wave packet, whereas in Figure 8B, a continuous wave envelope is noticed. This signifies that wave energy focusing due to modulational instability vanishes because of the strong Landau damping (at V_HF = 80 mV).

Conclusion

The evolution of ion acoustic Peregrine soliton under dissipation is observed in multicomponent plasma with negative ions. The strength of the Landau damping is increased by heating of ions via rf signal (close to the ion plasma frequency) application to the separation grid. The spatial damping rate of the ion acoustic wave is measured from the interferometer phase plot. The experimentally measured damping rate shows good agreement with the theory. The results show the modification of the evolution characteristics of Peregrine soliton. With high rf amplitude (V_HF ≥ 60 mV), the soliton peak disappears, leaving behind an envelope only. At high V_HF, the damping rate increases due to the rise in the thermal velocity of ions and thereby increasing resonant ions numbers close to the phase velocity of the wave. Once the dissipative effect becomes more substantial, the delicate balance between nonlinearity and group velocity dispersion gets affected, and the soliton disappears. However, a theoretical model considering the enhanced Landau damping effect is yet to be established and will be considered as a future study.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

PP has done the experiment and data analysis as well as writing the manuscript.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author would like to thank H. Bailung for his guidance throughout the experiment.

References

1. Peregrine D. Water waves, nonlinear Schrödinger equations and their solutions. J Aust Math Soc Ser B Appl Math (1983) 25:16–43. doi:10.1017/S0334270000003891

CrossRef Full Text | Google Scholar

2. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The Peregrine soliton in nonlinear fibre optics. Nat Phys (2010) 6:790. doi:10.1038/nphys1740

CrossRef Full Text | Google Scholar

3. Chabchoub A, Hoffmann NP, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett (2011) 106:204502. doi:10.1103/PhysRevLett.106.204502 |

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Bailung H, Sharma SK, Nakamura Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011) 107:255005. doi:10.1103/PhysRevLett.107.255005 |

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Moslem WM, Shukla PK, Eliasson B. Surface plasma rogue waves. EPL (Europhysics Lett) (2011) 96:25002. doi:10.1209/0295-5075/96/25002

CrossRef Full Text | Google Scholar

6. El-Tantawy SA, Wazwaz AM, Ali Shan S. On the nonlinear dynamics of breathers waves in electronegative plasmas with Maxwellian negative ions. Phys Plasmas (2017) 24:022105. doi:10.1063/1.4975090

CrossRef Full Text | Google Scholar

7. Akbari-Moghanjoughi M. Electrostatic rogue-waves in relativistically degenerate plasmas. Phys Plasmas (2014) 21:102111. doi:10.1063/1.4897928

CrossRef Full Text | Google Scholar

8. Moslem WM. Langmuir rogue waves in electron-positron plasmas. Phys Plasmas (2011) 18:10–4. doi:10.1063/1.3559486

CrossRef Full Text | Google Scholar

9. Veldes GP, Borhanian J, McKerr M, Saxena V, Frantzeskakis DJ, Kourakis I. Electromagnetic rogue waves in beam–plasma interactions. J Optic (2013) 15:064003. doi:10.1088/2040-8978/15/6/064003

CrossRef Full Text | Google Scholar

10. Moslem WM, Sabry R, El-Labany SK, Shukla PK. Dust-acoustic rogue waves in a nonextensive plasma. Phys Rev E - Stat Nonlinear Soft Matter Phys (2011) 84:066402. doi:10.1103/PhysRevE.84.066402

CrossRef Full Text | Google Scholar

11. Wang Y, Li J, Dai C, Chen X, Zhang J. Solitary waves and rogue waves in a plasma with nonthermal electrons featuring Tsallis distribution. Phys Lett (2013) 377:2097–104. doi:10.1016/j.physleta.2013.06.008

CrossRef Full Text | Google Scholar

12. Abdelsalam UM, Moslem WM, Khater AH, Shukla PK. Solitary and freak waves in a dusty plasma with negative ions. Phys Plasmas (2011) 18:092305. doi:10.1063/1.3633910

CrossRef Full Text | Google Scholar

13. Chahal BS, Singh M, Shalini, Saini NS. Dust ion acoustic freak waves in a plasa with two temperature electrons featuring Tsallis distributio. Physica A (2018) 491:935–45. doi:10.1016/j.physa.2017.10.004

CrossRef Full Text | Google Scholar

14. Shalini, Saini NS. Dust ion acoustic rogue waves in superthermal warm ion plasma. J Plasma Phys (2015) 81:905810316. doi:10.1017/S0022377815000082

CrossRef Full Text | Google Scholar

15. Singh K, Kaur N, Saini NS. Head-on collision between two dust acoustic solitary waves and study of rogue waves in multicomponent dusty plasma. Phys Plasmas (2017) 24:063703. doi:10.1063/1.4984996

CrossRef Full Text | Google Scholar

16., Saini NS, Kaur B, Singh M, Bains AS. Dust kinetic Alfvén solitary and rogue waves in a dusty plasma with two temperature n solitary and rogue waves in a dusty plasma with two Dust kinetic Alfv e temperature nonextensive ions. Phys Plasmas (2017) 24:073701. doi:10.1063/1.4989712

CrossRef Full Text | Google Scholar

17. Tsai Y, Tsai J, Lin I. Generation of acoustic rogue waves in dusty plasmas through three-dimensional particle focusing by distorted waveforms. Nat Phys Lett (2016) 12:537–77. doi:10.1038/NPHYS3669

CrossRef Full Text | Google Scholar

18. Ata-ur-Rahman . Electrostatic rogue waves in a degenerate Thomas-Fermi plasma. Braz J Phys (2019) 49:517–25. doi:10.1007/s13538-019-00676-3

CrossRef Full Text | Google Scholar

19. Rahman A, Kerr MM, El-taibany WF, Kourakis I, Qamar A. Amplitude modulation of quantum-ion-acoustic wavepackets in electron-positron-ion plasmas : modulational instability, envelope modes, extreme waves. Phys Plasmas (2015) 22:022305. doi:10.1063/1.4907247

CrossRef Full Text | Google Scholar

20. Kourakis I, Mc Kerr M, Ur-Rahman A. Semiclassical relativistic fluid theory for electrostatic envelope modes in dense electron-positron-ion plasmas: modulational instability and rogue waves. J Plasma Phys (2013) 79:1089–94. doi:10.1017/S0022377813001323

CrossRef Full Text | Google Scholar

21. Sharma SK, Bailung H. Observation of hole Peregrine soliton in a multicomponent plasma with critical density of negative ions. J Geophys Res Sp Phys (2013) 118:919–24. doi:10.1002/jgra.50111

CrossRef Full Text | Google Scholar

22. Bailung H, Nakamura Y. Observation of modulational instability in a multi-component plasma with negative ions. J Plasma Phys (1993) 50:231–42. doi:10.1017/S0022377800027033

CrossRef Full Text | Google Scholar

23. Saito M, Watanabe S, Tanaca H. Modulational instability of ion wave in plasma with negative ion. J Phys Soc Japan (1984) 53:2304–10.

CrossRef Full Text | Google Scholar

24. El-Tantawy SA, El-bedwehy NA, El-Labany SK. Ion-acoustic super rogue waves in ultracold neutral plasmas with nonthermal electrons Ion-acoustic super rogue waves in ultracold neutral plasmas with nonthermal electrons. Phys Plasmas (2013) 20:072102. doi:10.1063/1.4812630

CrossRef Full Text | Google Scholar

25. El-Tantawy SA, Ali S, Maroof R, Wazwaz AM, El-Labany SK. On the super freak waves in multicomponent plasmas having two-negative ions: Xe+ − F− − SF6−and Ar+ − F− −SF6−plasmas. Indian J Phys (2017) 91:939–46. doi:10.1007/s12648-017-0982-6

CrossRef Full Text | Google Scholar

26. El-Tantawy SA, El-Bedwehy NA, El-Labany SK. Ion-acoustic super rogue waves in ultracold neutral plasmas with nonthermal electrons. Phys Plasmas (2013) 20:072102. doi:10.1063/1.4812630

CrossRef Full Text | Google Scholar

27. Pathak P, Sharma SK, Nakamura Y, Bailung H. Observation of second order ion acoustic Peregrine breather in multicomponent plasma with negative ions. Phys Plasmas (2016) 23:022107. doi:10.1063/1.4941968

CrossRef Full Text | Google Scholar

28. Pathak P, Sharma SK, Nakamura Y, Bailung H. Observation of ion acoustic multi-Peregrine solitons in multicomponent plasma with negative ions. Phys Lett (2017) 381:4011–8. doi:10.1016/j.physleta.2017.10.046

CrossRef Full Text | Google Scholar

29. McKenzie JF, Verheest F, Doyle TB, Hellberg MA. Compressive and rarefactive ion-acoustic solitons in bi-ion plasmas. Phys Plasmas (2017) 11:1762. doi:10.1063/1.1688332

CrossRef Full Text | Google Scholar

30. Gill TS, Kaur H, Saini NS. Ion-acoustic solitons in a plasma consisting of positive and negative ions with nonisothermal electrons. Phys Plasmas (2003) 10:3927. doi:10.1063/1.1611486

CrossRef Full Text | Google Scholar

31. Xue J. Head-on collision of dust-acoustic solitary waves. Phys Rev E - Stat Nonlinear Soft Matter Phys (2004) 69:016403. doi:10.1103/PhysRevE.69.016403

CrossRef Full Text | Google Scholar

32. Sharma SK, Boruah A, Bailung H. Head-on collision of dust-acoustic solitons in a strongly coupled dusty plasma. Phys Rev E - Stat Nonlinear Soft Matter Phys (2014) 89:013110. doi:10.1103/PhysRevE.89.013110

CrossRef Full Text | Google Scholar

33. Boruah A, Sharma SK, Nakamura Y, Bailung H. Observation of dust acoustic multi-solitons in a strongly coupled dusty plasma. Phys Plasmas (2016) 23:93704. doi:10.1063/1.4962566

CrossRef Full Text | Google Scholar

34. Boruah A, Sharma SK, Bailung H, Nakamura Y. Oblique collision of dust acoustic solitons in a strongly coupled dusty plasma. Phys Plasmas (2015) 22:781035. doi:10.1063/1.4931735

CrossRef Full Text | Google Scholar

35. Karpman VI, Shklyar DR. Nonlinear Landau damping in an inhomogeneous plasma. Sov Phys - JETP (1975) 40:53–6.

Google Scholar

36. Ott E, Sudan RN. Nonlinear theory of ion acoustic waves with Landau damping. Phys Fluids (1969) 12:2388. doi:10.1063/1.1692358

CrossRef Full Text | Google Scholar

37. VanDam JW, Taniuti T. Nonlinear ion acoustic waves with Landau Damping.pdf. J Phys Soc Japan (1973) 35:1973.

Google Scholar

38. Mendonca JT, Bingham R. Plasmon beam instability and plasmon Landau damping of ion acoustic waves. Phys Plasmas (2002) 9:2604. doi:10.1063/1.1479142

CrossRef Full Text | Google Scholar

39. Amendt P. Pseudomoment fluid modeling : electron Landau damping of ion-acoustic waves. Phys Plasmas (2001) 8:1437. doi:10.1063/1.1355681

CrossRef Full Text | Google Scholar

40. Wong AY, Motley RW, D’Angelo N. Landau damping of ion acoustic waves in highly ionized plasmas. Phys Rev (1964) 133:A436. doi:10.1103/PhysRev.133.A436

CrossRef Full Text | Google Scholar

41. Alexeff I, Jones WD, Montgomeryt D. Controlled Landau damping of ion acoustic waves. Phys Rev Lett (1967) 19:422–5.

CrossRef Full Text | Google Scholar

42. Luo QZ, D’Angelo N, Merlino RL. Experimental study of shock formation in a dusty plasma. Phys Plasmas (1999) 6:3455. doi:10.1063/1.873605

CrossRef Full Text | Google Scholar

43. Luo QZ, D’Angelo N, Merlino RL. Shock formation in a negative ion plasma. Phys Plasmas (1998) 5:2868–70. doi:10.1063/1.873007

CrossRef Full Text | Google Scholar

44. Nakamura Y, Bailung H, Saitou Y. Observation of ion-acoustic shock waves undergoing Landau damping. Phys Plasmas (2004) 11:3925. doi:10.1063/1.1771654

CrossRef Full Text | Google Scholar

45. Saitou Y, Nakamura Y. Ion-acoustic soliton-like waves undergoing Landau damping. Phys Lett (2005) 343:397–02. doi:10.1016/j.physleta.2005.06.035

CrossRef Full Text | Google Scholar

46. Kozima H, Yamagiwa K, Tanaka T, Matsubara H, Yoshino H. Experimental study of an ion acoustic soliton with dissipation. J Phys Soc Japan (1989) 58:504–510.

CrossRef Full Text | Google Scholar

47. Brown SC. Basic data of plasma physics. New York, NY: Wiley (1969).

Google Scholar

48. Mizuno Y. Plasma Physics. Tokyo, Japan: Kyoritu (1984). (in Japanese).

Google Scholar

49. Taylor RJ, Ikezi H, Mackenzie KR. A large double plasma device for plasma beam and wave studies A large double plasma device for plasma beam and wave studies. Rev Sci Instrum (1972) 43:1675. doi:10.1063/1.1685522

CrossRef Full Text | Google Scholar

50. Nakamura Y, Ooyama M, Ogino T. Observation of spherical ion acoustic solitons. Phys Rev Lett (1980) 45:1565–69.

CrossRef Full Text | Google Scholar

51. Wong AY ed. Introduction to experimental plasma physics. Los Angeles, CA: University of California at Los Angeles (1977).

Google Scholar