- 1Shanghai Key Laboratory of Modern Optics and Systems, University of Shanghai for Science and Technology, Shanghai, China
- 2Shanghai Institute of Intelligent Science and Technology, Tongji University, Shanghai, China
The dynamical switching of a toroidal dipole resonance channel is demonstrated by tuning the Fermi level of a Dirac semimetal film sandwiched between the back substrates. As the Fermi level is increased from 30 to 150 meV, the resonance frequency is switched from 0.283 to 0.201 THz because of the transition from toroidal mode to hybrid mode. The hybrid mode is formed by the interaction between the toroidal mode and the plasmonic mode (induced by a Dirac semimetal film with metallic properties). The influence of the sandwiched dielectric layer (between the toroidal metasurface pattern and the Dirac semimetal film) on the switching effect was also investigated. This active dual-channel terahertz switching may have potential applications in advanced terahertz communication.
Introduction
Artificial subwavelength resonator arrays have been regarded as so-called “metamaterials” to manipulate novel electromagnetic responses, and have been widely applied to electromagnetically induced transparency [1–7], the Fano effect [8–12], perfect absorption [13–15], polarization conversion [16–18], and so on. The toroidal dipole effect, a novel type of electromagnetic excitation, can be visualized as a vortex of a closed-loop magnetic field excited by the currents flowing on the surface of ring-shaped structures [19]. In 2010, a toroidal dipole effect combined with three-dimensional (3D) metamaterials was verified at microwave frequencies [20]. However, there is, inevitably, complexity involved in the fabrication of a 3D metamaterial. A toroidal dipole effect in two-dimensional (2D) metamaterials has gained widespread attention because the toroidal dipole manifests as poloidal currents on the surface of split rings, which is distinctly different from the traditional electric and magnetic dipoles [21, 22]. Compared with 3D metamaterials, there are some benefits to developing 2D metamaterials because of their simpler fabrication and scalability [22]. Toroidal dipoles in 2D metamaterials offer weak electromagnetic scattering compared with electric and magnetic dipoles, and could reduce the radiative loss from an electric dipole [22]. In addition, such a configuration is easy to fabricate by conventional photolithography and a lift-off process. Moreover, an active tunable toroidal dipole possesses unique advantages, such as channel switching in the field of terahertz communication and an adjustable transmission spectrum [23–25]. For instance, the combination of a toroidal metasurface and a graphene layer can actively adjust and modulate the resonance intensity of a toroidal dipole from the “ON” state to the “OFF” state [23, 24]. In 2019, Song et al. [25] presented a tunable terahertz toroidal metamaterial based on the modulation of the conductivity of vanadium dioxide.
A Dirac semimetal film (DSF), as a new quantum material [26], has attracted more attention because of its topological band structure, which is similar to that of graphene [27]. The energy and momentum of this DSF meet the linear dispersion relationship in the 3D direction of K space, so it is also called 3D graphene. Compared with graphene, DSF has unique properties: i) it is less susceptible to interference from a dielectric environment; ii) there are no excess electrons on its surface; iii) it shows a stable performance; and iv) it is easier to prepare. In addition, the dielectric equation for the DSF can be dynamically adjusted by changing its Fermi energy level/bias voltage/conductivity, resulting in its transition from a dielectric to a semimetal/metal state. The tunable metamaterials based on the DSF have been reported to adjust the terahertz electric and magnetic dipole response [28–30]. To the best of our knowledge, only a few studies have reported a tunable toroidal resonance by utilizing a DSF.
In this study, a tunable terahertz toroidal dipole metamaterial composed of split-ring resonators (SRRs) with a symmetric structure is proposed. Also, the frequency-dependent resonance of a toroidal dipole has been studied with different thicknesses of the dielectric layer between the DSF layer and the SRR layer. By varying the Fermi level of the DSF, the transmission spectra of the toroidal dipole are simulated when the thicknesses of the dielectric layer are set to 5 and 24 μm. Channel switching of the toroidal dipole resonance by changing the Fermi level is presented with various effects under different thicknesses of the dielectric layer. The results demonstrate that the thickness of the dielectric layer has a crucial effect on the tunable properties of the toroidal dipole metamaterial with the DSF. The physical mechanism of channel switching is further explored by analyzing the distribution of the surface current and magnetic field. Consequently, this study shows that channel switching of the toroidal dipole resonance has the potential to be applied to terahertz information exchange and terahertz communication.
Design and Results
The proposed SRRs are designed with the symmetric metallic pattern shown in Figure 1A. The specific parameters of the metallic pattern are also illustrated in Figure 1A. The centerline of the metallic pattern is defined as the vertical symmetry axis, as shown by the red dotted line in Figure 1A. Figure 1B shows the 3D view of the structure. The thicknesses of the metallic layer (regarded as a perfect electric conductor in the simulation), dielectric layer, DSF layer, and the substrate are set at 0.2 μm, 5 μm, 30 nm, and 50 μm, respectively. The dielectric layer and substrate are made of polyimide with a permittivity of 3.5.
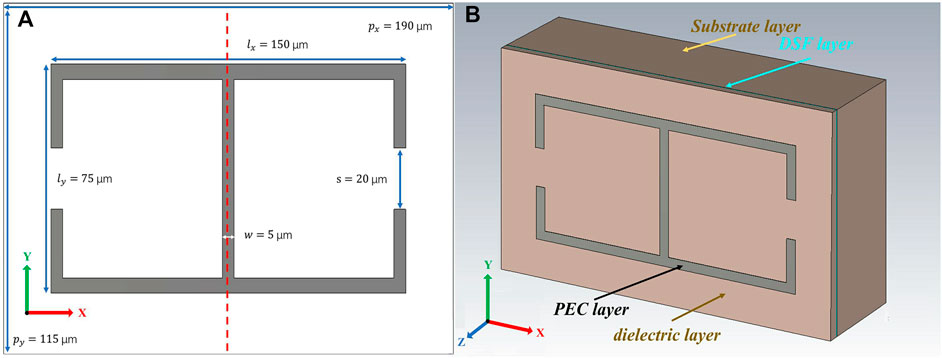
FIGURE 1. (A) Front view of the toroidal dipole structure. (B) The proposed tunable toroidal dipole made of a metallic pattern (perfect electric conductor (PEC)) layer, a dielectric layer, a Dirac semimetal film (DSF), and a substrate layer.
To explore the electromagnetic properties of the model, a full-wave electromagnetic simulation based on the standard finite-element method was carried out. In the simulation, the incident wave is modeled as a Floquet port above the unit cell with the metallic pattern boundary condition attached to the x- and y-directions. The poloidal conductive current of the resonators can be excited by the interaction of the incident plane wave and the electric field. The electric field direction is parallel to the centerline. The simulated transmission spectrum of the toroidal dipole is presented in Figure 2A, with a toroidal dipole resonance observed near 0.283 THz. At the resonance frequency, the surface current and magnetic current distribution are simulated to study the resonance characteristics of the toroidal dipole, as illustrated in Figures 2B,C. When the incident electric field is parallel to the centerline, the excited surface current flows on each loop of the SRRs, and the currents of the two loops are basically opposite, as shown in Figure 2C. The inverse oscillation of the excited currents generates a set of magnetic dipoles with inverse polarization, creating a circular head-to-tail arrangement of magnetic dipoles. Figure 2B reveals the formation of the closed magnetic vortex. In light of the concept of a toroidal dipole, the localized plasmons in a gapped structure play an important role in determining the direction of the surface current. In addition, the intensity of the magnetic field, as shown in Figure 1D in the form of color mapping, gradually decreases along the direction from the centerline of the metallic pattern to the gapped structure. Consequently, it is further explained that the excitation of the toroidal dipole directly leads to the spatial localization of the magnetic field and the formation of a closed magnetic vortex.
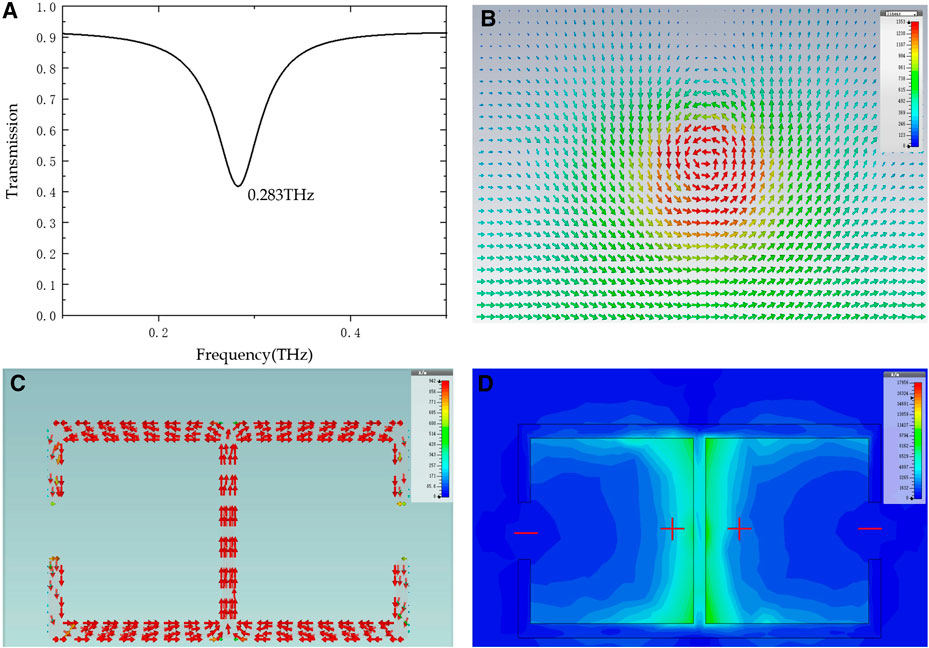
FIGURE 2. (A) Simulated transmission spectrum of the proposed structure with a Fermi level of 30 meV. (B) Magnetic current distribution. (C) Surface current. (D) The magnetic field distribution of the structure. (B–D) are at a resonance frequency of 0.283 THz.
The complex conductivity of the DSF surface obeys the Kubo formula. By using the random-phase approximation at the long-wavelength limit, the dynamic conductivity of the DSF is represented as [26]:
Here,
where
According to Eqs 1–3, we calculate the complex permittivity values at different frequencies, as shown in Figure 3. The real and imaginary parts of the permittivity of the DSF are highly sensitive to the EF. The conductivity and metallicity of the DSF are positively correlated with the EF. Then, these discrete values of the complex permittivity are imported into the characteristic parameters of the Dirac semimetal to complete the modeling.
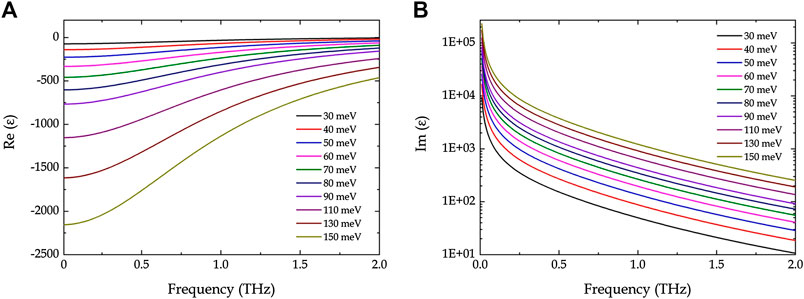
FIGURE 3. (A) Real and (B) imaginary parts of the Dirac semimetal film (DSF) dielectric functions under different Fermi levels. The parameters of the DSF are set as g = 4,
The transmission spectra of the proposed toroidal dipole are simulated and depicted in Figure 4 for different thicknesses of the dielectric layer. The EF and thickness of the DSF are 30 meV and 30 nm, respectively. With d2 increased from 1 to 15 μm, the resonant dip in the transmission spectra increases rapidly, showing a sharper formant. As d2 is varied from 15 to 27 μm, the resonant dip increases slowly. Actually, the dielectric layer of the polyimide acts as a cavity, and for different thicknesses there are different distribution fields. The interaction between the metallic pattern and the DSF becomes strong with d2 ranging from 1 to 15 μm. A small change in d2 has a significant impact on the transmission spectrum. As d2 is large enough, the interaction between the metallic pattern and the DSF becomes weak, which creates a slight change in the transmission spectrum with d2 ranging from 15 to 27 μm. These results confirm that the thickness of the dielectric layer significantly impacts the performance of the toroidal dipole. In the following, we will discuss the influence of the Fermi level on the toroidal resonance with different thicknesses of the dielectric layer (d2 = 5 and 24 μm). The thickness of the DSF is fixed at 30 nm.
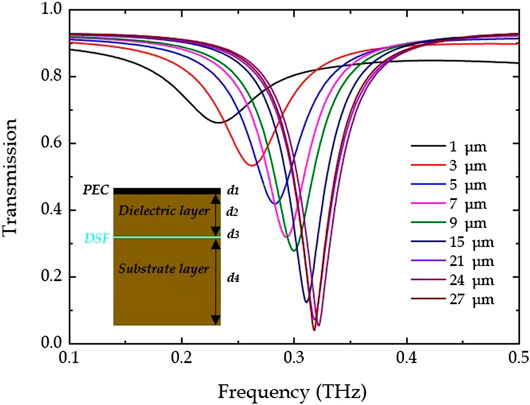
FIGURE 4. Simulated transmission spectra as a function of the thickness of the dielectric layer (d2) with EF = 30 meV and the thickness of the perfect electric conductor (PEC), Dirac semimetal film (DSF), and substrate layer set as d1 = 0.2 μm, d3 = 30 nm, and d4 = 50 μm, respectively. (inset) The cross-sections of the model are shown.
The complicated surface conductivity of the DSF can be actively dominated by adjusting the EF, which can possibly be achieved by alkaline surface doping [26]. The resonance frequency of the toroidal dipole depends on the electron density of the DSF, determined by the EF. To illustrate the frequency adjustability of the toroidal dipole resonance, the toroidal dipole resonance under different Fermi levels in the case of d3 = 30 nm is investigated. The transmission spectra of the toroidal metasurface under various Fermi levels are shown in Figure 5A (d2 = 5 μm) and Figure 5C (d2 = 24 μm). As seen in Figures 5A,B, the transmission amplitude of the resonance dip increases gradually and the resonance frequency is almost stable at 0.28 THz when the EF is increased from 30 to 70 meV and the tuning range of the toroidal resonance intensity is decreased from 0.813 to 0.418. As the EF is increased from 70 to 110 meV, the resonance frequency is redshifted to 0.20 THz with its intensity almost unchanged. With the increase of the EF from 110 to 150 meV, the resonance frequency at 0.20 THz is relatively uniform and the amplitude decreases from 0.802 to 0.435. Accordingly, the tunable transmission spectrum shows a channel-switching effect of toroidal dipole resonance by adjusting the EF to tune the conductivity of the DSF. In addition, the simulation results indicate that the electromagnetic properties of the DSF have a significant influence on the transmission spectrum.
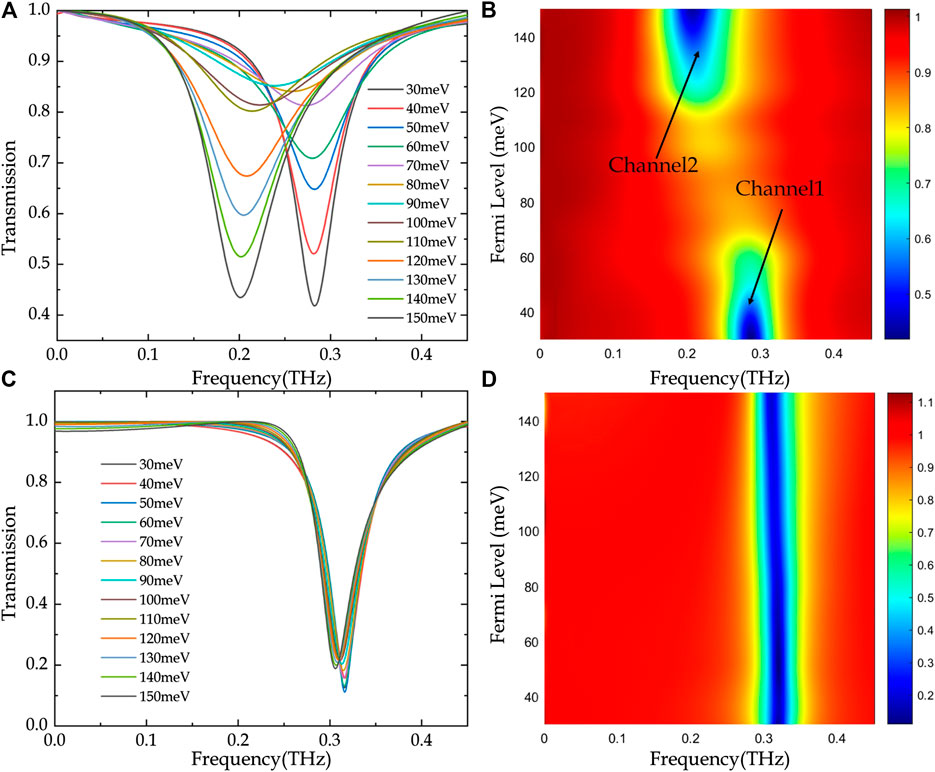
FIGURE 5. (A, C) Simulated transmission spectra as a function of the Fermi levels of the Dirac semimetal film (DSF) and (B, D) Fermi levels as a function of the frequency and transmission. The thicknesses of the DFS and substrate (polyimide) are set at 30 nm and 50 μm, respectively. The thicknesses of the dielectric layer are set at (A, B) 5 μm and (C, D) 24 μm.
The transmission spectra of the toroidal dipole are also simulated for d2 = 24 μm. As the EF is varied from 30 to 150 meV, the amplitude of the resonance dip ranges from 0.11 to 0.22, and the resonance frequency shifts from 0.316 to 0.306 THz. Figures 5C,D illustrates that the channel switching of the toroidal dipole resonance cannot be achieved by changing the EF below d2 = 24 μm.
Figure 6 shows the distribution of the surface current and the magnetic field under different Fermi levels with d2 = 5 μm (Figures 6A,B) and 24 μm (Figures 6C,D). When EF = 30 meV and d2 = 5 μm, the DSF presents dielectric-like properties, as shown in Figure 6A, which shows little difference from the toroidal metasurface without the DSF. Meanwhile, Figure 6B shows that the DSF ultimately presents metallic-like properties with EF = 150 meV, which forms a hybrid mode generated by the interaction between the toroidal effect and the plasmonic effect (induced by the DSF with metallic properties) [31]. In the hybrid mode, the magnetic current of the toroidal dipole cannot pass through the DSF layer completely; the DSF layer acts as a block owing to its metallic properties. The plasmonic effect interferes with the existing toroidal effect, leading to a shift in the resonance frequencies. Compared with Figure 6C at EF = 30 meV and d2 = 24 μm, Figure 6D shows that the distribution areas of the magnetic field have been slightly weakened with the EF raised to 150 meV, while the DSF layer still has an effective blocking effect owing to the metallic-like properties of the DSF. Since d2 is large enough, the DSF has a small impact of interference on the toroidal effect, and the resonance frequency has a slight red shift.
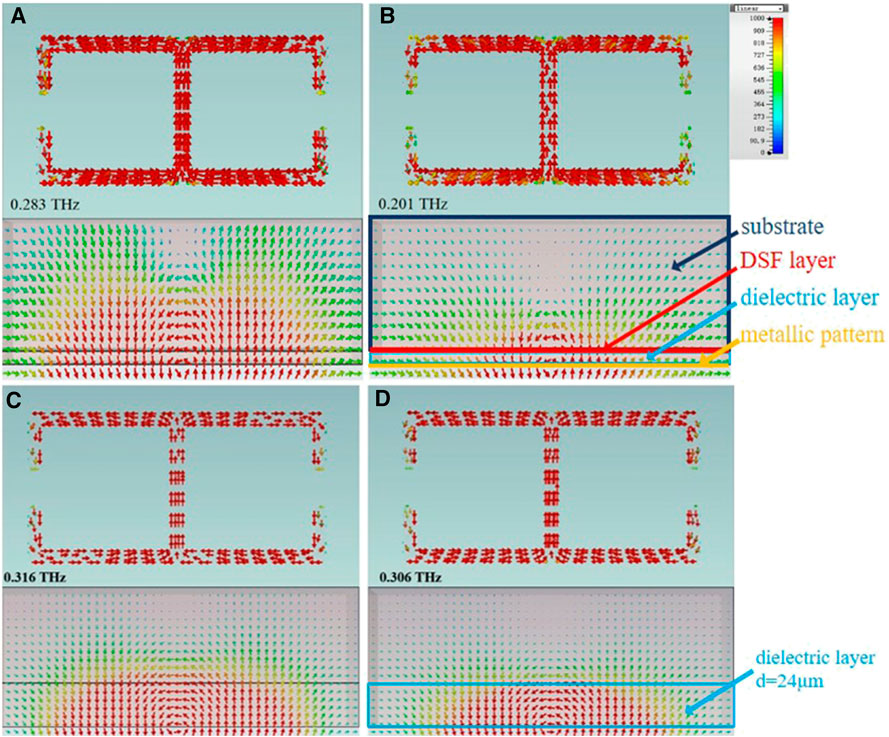
FIGURE 6. Current distribution and magnetic field distribution with d2 = (A, B) 5 μm and (C, D) 24 μm, corresponding to EF = (A, C) 30 meV and (B, D) 150 meV. DSF, Dirac semimetal film; PEC, perfect electric conductor.
Conclusion
In conclusion, toroidal dipole resonance tuned by a DSF has been shown to achieve active channel switching at terahertz frequencies. The thickness of the dielectric layer is equal to 5 μm, so that the Dirac semimetal can effectively tune the toroidal dipole created by the symmetric SRR structure. Active dual-channel switching of the toroidal dipole resonance is the result of the transition from the toroidal effect to the hybrid mode, which results from the interaction between the toroidal and plasmonic modes. When the Fermi level of the DSF is varied from 30 to 150 meV, the resonance frequency has a significant red shift from 0.28 to 0.20 THz. The amplitude of the resonance dip first increases from 0.418 to 0.813 and then decreases to 0.435. Our results may provide potential applications in terahertz communication components such as modulators and switching.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
The Authors’ contributions are presented below: Study concept and design, LC, DL, YS; Acquisition of data, YS, DL, JX; Analysis and interpretation of data, YS, LC; Critical revision of the manuscript for important intellectual content, LC, YW; Statistical analysis, YS, JX, YW; Obtained funding, LC; Drafting of the manuscript, YS, DL.
Funding
This project was supported by the National Key R&D Program of China (2018YFF13000), the National Natural Science Foundation of China (No. 61988102), the Shuguang Program Supported by the Shanghai Education Development Foundation and the Shanghai Municipal Education Commission, China (No. 18SG44), the 111 Project (D18014), and the International Joint Lab Program supported by the Science and Technology Commission Shanghai Municipality (17590750300).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Sayon Guilavogui for his language editing contribution.
References
1. Tassin P., Zhang L., Koschny T., Economou EN, Souloulis CM. Planar designs for electromagnetically induced transparency in metamaterials. Opt Express (2010) 17(7):5595–605. doi:10.1364/oe.17.005595
2. Xu H, Lu Y, Lee YP, Ham BS. Studies of electromagnetically induced transparency in metamaterials. Opt Express (2010) 18(17):17736–17747. doi:10.1364/OE.18.017736
3. Sun Y, Tong YW, Xue CH, Ding YQ, Li YH, Jiang H, et al. Electromagnetic diode based on nonlinear electromagnetically induced transparency in metamaterials. Appl Phys Lett (2013) 103(9):0919041–0919045. doi:10.1063/1.4819854
4. Chen L, Gao CM, Xu JM, Zang XF, Cai B, Zhu YM. Observation of electromagnetically induced transparency-like transmission in terahertz asymmetric waveguide-cavities systems. Opt Lett. (2013) 38:1379. doi:10.1364/OL.38.001379
5. Li Y, Zhang J, Qu S, Wang J, Chen H, Xu Z, et al. Wideband selective polarization conversion mediated by three-dimensional metamaterials. J Appl Phys (2014) 115(23):063908. doi:10.1063/1.4883762
6. Lu T, Qiu P, Lian J, Zhang D, Zhuang S. Ultrathin and broadband highly efficient terahertz reflective polarization converter based on four L-shaped metamaterials. Opt Mater (2019) 95, 109230. doi:10.1016/j.optmat.2019.109230
7. Zhao G, Li Y. Terahertz broadband polarization converter based on metamaterials. In: International conference on optical instruments and technology 2017: micro/nano Photonics. materials and devices; 2018 January 12; Bejing, China (2018).
8. Luk'Yanchuk B, Zheludev NI, Maier SA, Halas NJ, Nordlander P, Giessen H, et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat Mater (2010) 9(9):707–715. doi:10.1038/nmat2810
9. Lassiter JB, Sobhani H, Fan JA, Kundu J, Capasso F, Nordlander P, et al. Fano resonances in plasmonic nanoclusters: geometrical and chemical tunability. Nano Lett (2010) 10(8):3184–3189. doi:10.1021/nl102108u
10. Amin M, Farhat M, Bağcı H. A dynamically reconfigurable Fano metamaterial through graphene tuning for switching and sensing applications. Sci Rep (2013) 3(7):2105. doi:10.1038/srep02105
11. Chen L, Wei YM, Zang XF, Zhu YM, Zhuang SL. Excitation of dark multipolar plasmonic resonances at terahertz frequencies. Sci Rep (2016) 6:22027. doi:10.1038/srep22027
12. Chen L, Xu N, Singh L, Cui T, Singh R, Zhu Y, et al. Defect-induced Fano resonances in corrugated plasmonic metamaterials. Adv Opt Mater (2017) 5(8):1600960. doi:10.1002/adom.201600960
13. Zhang S, Genov DA, Wang Y, Liu M, Zhang X. Plasmon-induced transparency in metamaterials. Phys Rev Lett (2008) 101(4):218–221. doi:10.1103/PhysRevLett.101.047401
14. Zhu Y, Hu X, Fu Y, Yang H, Gong Q. Ultralow-power and ultrafast all-optical tunable plasmon-induced transparency in metamaterials. Sci Rep (2013) 3:2338. doi:10.1038/srep02338
15. Chai Z, Hu X, Zhu Y, Zhang F, Yang H, Gong Q. Low-power and ultrafast all-optical tunable plasmon-induced transparency in plasmonic nanostructures. Appl Phys Lett (2013) 102(20):2011191–2011195. doi:10.1063/1.4807765
16. Hao JM, Wang J, Liu XL, Padilla WJ, Zhou L, Qiu M. High performance optical absorber based on a plasmonic metamaterial. Appl Phys Lett (2010) 96(25):251104. doi:10.1063/1.3442904
17. Song Z, Wang Z, Wei M. Broadband tunable absorber for terahertz waves based on isotropic silicon metasurfaces. Mater Lett (2019) 234:138–141. doi:10.1016/j.matlet.2018.09.084
18. Song Z, Wang K, Li J, Liu QH. Broadband tunable terahertz absorber based on vanadium dioxide metamaterials. Opt Express (2018) 26(6):7148–7154. doi:10.1364/OE.26.007148
19. Zel'Dovich IB. Electromagnetic interaction with parity violation. J Exp Theor Phys (1958) 6(6):1184.
20. Papasimakis N, Fedotov VA, Kaelberer T, Tsai DP, Zheludev NI, et al. Toroidal dipolar response in a metamaterial. Science (2010) 330(6010):1510–1512. doi:10.1126/science.1197172
21. Gupta M, Singh R. Toroidal metasurfaces in a 2D flatland. Rev Phy (2020) 5(100040):2405–4283. doi:10.1016/j.revip.2020.100040
22. Gupta M, Savinov V, Xu N, Cong L, Dayal G, Wang S, et al. Sharp toroidal resonances in planar terahertz metasurfaces. Adv Mater Weinheim (2016) 28(37):8206–8211. doi:10.1002/adma.201601611
23. Liu GD, Zhai X, Xia SX, Lin Q, Zhao CJ, Wang LL. Toroidal resonance based optical modulator employing hybrid graphene-dielectric metasurface. Opt Express (2017) 25(21):26045–26054. doi:10.1364/OE.25.026045
24. Chen X, Fan W. Study of the interaction between graphene and planar terahertz metamaterial with toroidal dipolar resonance. Opt Lett (2017) 42(10):2034. doi:10.1364/OL.42.002034
25. Song Z, Deng Y, Zhou Y, Liu Z. Terahertz toroidal metamaterial with tunable properties. Opt Express (2019) 27(4):5792. doi:10.1364/OE.27.005792
26. Kotov OV, Lozovik YE. Dielectric response and novel electromagnetic modes in three-dimensional Dirac semimetal films. Phys Rev B (2016) 93(23):235417. doi:10.1103/physrevb.93.235417
27. Young SM, Zaheer S, Teo JCY, Kane CL, Mele EJ, Rappe AM. Dirac semimetal in three dimensions. Phys Rev Lett (2012) 108 (14), 1404051–1404055. doi:10.1103/PhysRevLett.108.140405
28. Chen H, Zhang H, Zhao Y, Liu S, Cao M, Zhang Y. Broadband tunable terahertz plasmon-induced transparency in Dirac semimetals. Optic Laser Technol. (2018) 104:210–215. doi:10.1016/j.optlastec.2018.02.034
29. Chen H, Zhang H, Liu M, Zhao Y, Guo X, Zhang Y. Realization of tunable plasmon-induced transparency by bright-bright mode coupling in Dirac semimetals. Opt Mater Express (2017) 7(9):3397–3407. doi:10.1364/ome.7.003397
30. Chen H, Zhang H, Guo X, Liu S, Zhang Y. Tunable plasmon-induced transparency in H-shaped Dirac semimetal metamaterial. Appl Opt (2018) 57(4):752–756. doi:10.1364/AO.57.000752
Keywords: dirac semimetal, toroidal dipole, frequency switching, terahertz communication, metasurface
Citation: Sun Y, Liao D, Xu J, Wu Y and Chen L (2020) Active Switching of Toroidal Resonances by Using a Dirac Semimetal for Terahertz Communication. Front. Phys. 8:602772. doi: 10.3389/fphy.2020.602772
Received: 04 September 2020; Accepted: 06 November 2020;
Published: 10 December 2020.
Edited by:
Jinhui Shi, Harbin Engineering University, ChinaReviewed by:
Kuang Zhang, Harbin Institute of Technology, ChinaChunmei Ouyang, Tianjin University, China
Copyright © 2020 Sun, Liao, Xu, Wu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lin Chen, bGluY2hlbkB1c3N0LmVkdS5jbg==
†These authors have contributed equally to this work
 Yuanbao Sun1†
Yuanbao Sun1† Lin Chen
Lin Chen