Peregrine Solitons of the Higher-Order, Inhomogeneous, Coupled, Discrete, and Nonlocal Nonlinear Schrödinger Equations

This study reviews the Peregrine solitons appearing under the framework of a class of nonlinear Schrödinger equations describing the diverse nonlinear systems. The historical perspectives include the various analytical techniques developed for constructing the Peregrine soliton solutions, followed by the derivation of the general breather solution of the fundamental nonlinear Schrödinger equation through Darboux transformation. Subsequently, we collect all forms of nonlinear Schrödinger equations, involving systematically the effects of higher-order nonlinearity, inhomogeneity, external potentials, coupling, discontinuity, nonlocality, higher dimensionality, and nonlinear saturation in which Peregrine soliton solutions have been reported.

1 Introduction

In 1834, the British engineer J. S. Russell observed a hump of water propagating in a narrow canal created by a boat that maintained its speed and shape for several miles. Unlike a repeated pattern of sinusoidal waves or a spreading out of water wave pulses, the most remarkable feature of the observed single hump is that it was not a series of peaks and troughs wave; instead, it has a “solitary wave” structure with only one peak oscillating with a constant velocity and unchanging profile with time which led him to advert it a “wave of translation”. He followed his observations by intensive experiments in a water wave tank leading to demonstrating that, in contrast with the linear case where increasing the amplitude has nothing to do with the wave speed, the speed of the solitary wave is related to its height through $v=\sqrt{g\left(d+h\right)}$ and its envelope profile can take the form of $h{\text{sech}}^2\left[k\left(x-vt\right)\right]$, where h, d, k, g, x, and t denote the wave height, the tank depth, the wavenumber, the gravitational acceleration, the propagation direction, and the time, respectively [1].

The conclusions made by Russell were argued by many mathematical theories such as the wave theory of G. B. Airy which indicates that the crest of a wave of a finite amplitude propagates faster than its remaining structure and eventually breaks [2] and G. G. Stokes theory which states that only the periodic waves can be in a finite and permanent profile [3]. In contrast to these mathematical arguments, in 1895 the Dutch mathematician D. Korteweg and his student G. de Vries came up with a model that describes the propagation of long surface waves in a narrow water channel [4]. A considerable conclusion of Korteweg and de Vries’s model was its admissibility of a special solution that travels with constant speed and amplitude, which was in an exact match with Russel’s description. Currently, this model is known as the Korteweg–de Vries (KdV) equation. Disappointedly, the significance of this solution and Russell’s observations were overlooked and not understood until 1965 when N. J. Zabusky and M. D. Kruskal pioneered numerical solutions to the KdV equation [5] and observed solitary wave pulses interact between themselves elastically as if they are real particles and return to their initial properties after the collision, except for some phase shifts. This results in a localized solution that remains stable and constant during the propagation which is now referred to as a bright soliton or briefly as a soliton. Nowadays, it is well known that solitons are constructed due to a dynamic balance between the group velocity dispersion and the nonlinearity of the system.

Nonlinear systems have attracted increasing interest after C. S. Gardner and his colleagues J. M. Greene, M. D. Kruskal, and R. M. Miura in 1967 introduced a method [6] now known as the inverse scattering transform (IST) that yields a solution to initial value problems (IVPs) for nonlinear partial differential equations (NPDEs). The IST method may be seen as an extension to the Fourier transform for NPDEs. The integrability of the nonlinear Schrödinger equation (NLSE) was discovered in 1972 when V. Zakharov and A. B. Shabat generalized the IST method and derived, for the first time, its soliton solution upon associating the NLSE to a linear system of differential equations [7]. The integrable NLSE equation is, in principle, admitting infinitely many independent solutions. Later on, the IST method was adopted to find a wide class of solutions to the NLSE and its various versions. Recently, all known solutions of the fundamental NLSE and its different versions were collected by [8].

The first breather type solution on a finite background of the NLSE was achieved in 1977 by E. A. Kuznetsov [9] and independently by Y. C. Ma [10] in 1979; now it is accordingly named Kuznetsov-Ma breather. Such a solution is periodic in time and localized in space. The Kuznetsov-Ma breather was derived by solving the initial value problem of the NLSE where the initial profile is a continuous wave (CW) on a background superposing with a soliton solution. The soliton profile in this context can be considered as a perturbation source on the CW. The modulational instability analysis is used to study the dynamics of the Kuznetsov-Ma breather when the amplitude of the soliton is much smaller than the background of the CW. The Kuznetsov-Ma breather solution can be also seen as a soliton on a finite background. In 1983, D. H. Peregrine [11] derived an exact solution to the focusing NLSE equation that is localized in both time and space domains, on a nonzero background. As a result of its dual localization which is the feature of a solitary wave, currently, this solution is known as Peregrine soliton. Physically, the Peregrine soliton models the closet prototype of rogue waves and thus usually takes the full name Peregrine rogue waves [12–14]. Rogue waves have been first studied in the context of oceanography [12, 15, 16]. Peregrine soliton is the lowest order rational solution of the NLSE that takes the form of one dominant peak, appears from “nowhere”, causes danger, and “disappears without a trace” [17, 18]. Its dominant peak is accompanied by two side holes that exist as a result of energy conservation. Due to its danger, oceanographers often call it using some other names such as the “freak waves”, the “killer waves”, the “monster waves”, the “abnormal waves”, and the “extreme waves” and rarely use the words “rogon waves”, “giant waves”, or “steep waves”. The highest amplitude of the Peregrine soliton equals two to three times the amplitude of the surrounding background waves.

Shortly, after the revelation of the Peregrine soliton, N. Akhmediev et al., in 1985, found another breather type solution on a finite background to the NLSE which is, contrary to the Kuznetsov-Ma breather, breathing periodically in space and localized in time domain [19]. This solution is now referred to as Akhmediev breather. In relation to the modulational instability analysis, when the frequency of the applied perturbation tends to zero (the soliton’s frequency approaches zero), the Kuznetsov-Ma breather tends to a Peregrine soliton. More precisely, taking the temporal period of the Kuznetsov-Ma breather solution to infinity results in a Peregrine soliton. Interestingly, the Akhmediev breather solution also turns out into a Peregrine soliton when the spacial period tends to infinity.

Together with the Kuznetsov-Ma and the Akhmediev breathers, the Peregrine soliton belongs to the family of the solitons on a nonzero background. This family can be represented in one general breather solution form in which the Peregrine soliton can be recovered. The Peregrine soliton, particularly, is considered as the first-order rational solution of a series of infinite recurrence orders of rational solutions. The second-order Peregrine soliton appears with a higher amplitude than the first-order Peregrine soliton [17, 20]. Higher-order of rational solutions and Peregrine soliton hierarchy are also revealed in Refs. 20 and 21.

Although the formation of Peregrine soliton requires ideal mathematical conditions which could be practically impossible, earlier intensive experiments are performed to randomly observe optical rogue waves [23, 24], acoustic rogue waves [25], and rogue waves in parametrically excited capillary waves [26]. In 2010, B. Kibler et al. succeeded for the first time in demonstrating experimentally the dynamics of the Peregrine soliton in nonlinear fiber optics under nonideal excitation condition modeled by the NLSE [27]. Soon after, Peregrine solitons have been observed in deep water wave tanks [28].

Rogue waves can be naturally created via various generating mechanisms. From the perspective of the MI analysis, there is always a chance for these modulations on the CW background to create multiple breathers that are scattering in random directions. Collisions between these grown breathers probably proceed a formation of wave amplification. Higher peaks than the ones associated with the breathers can be generated from the growth of Akhmediev breathers [18, 29–31]. A similar result can be obtained when the collided breathers are Kuznetsov-Ma breathers [20]. Another possible mechanism for the rogue waves’ creation is when the collision occurs between multiple solitons carrying different heights and propagating with different phases [32–36]. At the collision point, the amplitude of the peak becomes higher than the solitons individually, thanks to the nonlinear interaction between them. For other scenarios, see also [20, 30, 37–42].

Considerable efforts have been directed toward testing the stability of the Peregrine soliton behavior, analytically and numerically, against external perturbations [43–46, 46, 47, 47–54]. The stability issue is of important interest to experimentalists, as they seek to reproduce or generate solutions under a laboratory setting. Determining the stability of the solution allows the estimation of the range of practical applications that the solution can occupy. Generally, the studies reveal that, due to the high double localization and sharp structure associated with the Peregrine soliton solution, it, consequently, exhibits high sensitivity to small perturbations or changes in the initial conditions and thus reveals unstable characteristics. Other interesting works on the stability of the Peregrine soliton can be found for instance in [55–65].

Peregrine soliton is of crucial importance due to its doubly dimensional localization in space and time and because it defines a limit case of a wide range of solutions to the NLSE. Thus, it has received huge attention from mathematicians, physicists, and engineers. Its investigations have been rolled up through many contexts such as observation of Peregrine solitons in a multicomponent plasma with negative ions [66, 67], phase properties of Peregrine soliton in the hydrodynamic and optical domains [68], implementation of breather-like solitons extracted from the Peregrine rogue wave in the nonlinear fibers [69], demonstrating experimentally and numerically the generation and breakup of the Peregrine soliton in telecommunications fiber [70], optical rogue waves in an injected semiconductor laser [71], and Peregrine solution in the presence of wind forcing in deep water wave tank laboratories [72].

Besides the experimental observations, numerous numerical simulations and theoretical studies have been performed to demonstrate and predict the occurrence of such a unique type of soliton on a finite background in diverse physical media, for example, in Bose-Einstein condensates [73], freak waves as limiting Stokes waves in the ocean [74], in a mode-locked fiber laser [75], in singly resonant optical parametric oscillators [76], Peregrine solitons and algebraic soliton pairs in Kerr nonlinear media [77], the interaction of two in-phase and out-of-phase Peregrine solitons in a Kerr nonlinear media [41], and recently in lattice systems [78]. For other studies, see also [18, 21, 29, 79–85].

In this work, we aim at reviewing the theoretical studies that have been performed for Peregrine solitons of NLSEs with different setups and conditions. The work is arranged as follows. In Section 2, we derive the general breather class of the NLSE via the Darboux transformation and Lax pair method. We show that the Peregrine soliton solution is a limiting case of the general breather solution. An alternative route is then presented where we implement a specific seed solution to derive directly the Peregrine soliton solution. Section 3 is devoted to reviewing the Peregrine solitons of higher-order and inhomogeneous NLSEs. In Section 4, the Peregrine solitons of NLSEs with external constant and variable potentials are reviewed. Section 5 discusses the Peregrine solitons in coupled NLSEs, known as the Manakov system or the vector NLSE (N-coupled NLSEs), the coupled Gross-Pitaevskii equations, the coupled Hirota equations, the coupled cubic-quintic NLSEs, the PT-symmetric coupled NLSEs, and the higher-order coupled NLSEs. In Section 6, we review the works done on Peregrine solitons of the discrete NLSEs, the Ablowitz-Ladik equations, the generalized Salerno equation, and the Hirota equations. In Section 7, the Peregrine solitons in nonlocal NLSEs are presented. The nonlocal NLSE is a non-Hermitian and PT-symmetric equation with the nonlinearity term potential $V\left(x,t\right)u\left(x,t\right)=u\left(x,t\right)u^{\ast }\left(-x,t\right)u\left(x,t\right)$, where $u\left(x,t\right)$ is the mean field wavefunction, satisfying the PT-symmetric condition, $V\left(x,t\right)=V^{\ast }\left(-x,t\right)$. The nonlocality can also be seen in the presence of the reverse time dependency where $V\left(x,t\right)=V^{\ast }\left(x,-t\right)$ or with the combination of spatial and temporal nonlocalities $V\left(x,t\right)=V^{\ast }\left(-x,-t\right)$. In Section 8, we discuss the Peregrine solitons of higher dimensional and mixed NLSEs. In Section 9, the Peregrine solitons in saturable NLSEs will be discussed. We end up in Section 10 by the main conclusions and outlook for future work. The solutions for all the NLSEs considered are provided in the Supplementary Material.

2 Analytical Derivation of the Fundamental Peregrine Soliton

Various analytical methods are used to solve different versions of the NLSE such as the inverse scattering transform [86–93], the Adomian Decomposition method [94], the Homotopy Analysis method [95, 96], the similarity transformation method [97–102], and the Darboux transformation and Lax pair method [103–106], just to name a few. This section is devoted to deriving the general breather solution of the fundamental NLSE using the Darboux transformation and Lax pair method [107]. We show that, under certain limits, the general breather solution reduces to the Akhmediev breather, the Kuznetsov-Ma breather, the Peregrine soliton, the single bright soliton, or the continuous wave solution. The Darboux transformation method is an applicable method for solving only linear systems and cannot be directly applied for nonlinear systems. A crucial additional step is required to make it applicable for nonlinear systems as well. It is to search for an appropriate pair of matrices that associates the nonlinear equation to a linear system. This pair was introduced firstly in 1968 by P. D. Lax [108] and now named Lax pair. The Lax pair should be associated with the nonlinear system through what is called a compatibility condition. The next step is to solve the obtained linear system using a seed solution, which is a known exact solution to the nonlinear system. This technique gives remarkable merit which is the applicability to perform new exact solutions. Each seed solution performs another exact solution that belongs to the family of the seed solution. The latter obtained solution could be used as a new seed solution for the next performance round. All achieved solutions will belong to the same family of the initial seed solution. It is well known that using the trivial solution, $u\left(x,t\right)=0$, as a seed in the Darboux transformation method for the NLSE will produce the single bright soliton solution. The single bright soliton solution can act as a seed solution in the next round to generate the two-soliton solution. Keeping on the same track, multisoliton solutions can be generated in this way. In order to generate the general breather solution of the NLSE, a nontrivial seed solution is needed, namely, the continuous wave solution $u\left(x,t\right)=A{e}^{i{A}^{2}t}$, where A is an arbitrary real amplitude of the wave. Here we include the final results. For the details of the mathematical derivation see Supplementary Appendix.

The fundamental NLSE can be written in dimensionless form as

$i{u}_t+\frac{1}{2}{u}_{xx}+|u{|}^{2}u=0,(1)$

where $u=u\left(x,t\right)$ is the complex wave function and the subscripts denote partial derivatives with respect to t and x. The general breather solution of Eq. 1 can be compactly written as*

$\begin{array}{c}u\left[1\right]=A{e}^{i{A}^{2}t}\\ \times \left\{1-\frac{\sqrt{8}{\lambda }_{1r}}{A}\frac{\left(A^2+{\text{Γ}}^2\right)\text{cos}\left(q_1\right)+i\left(A^2-{\text{Γ}}^2\right)\text{sin}\left(q_1\right)+2A\left[{\text{Γ}}_r\text{cosh}\left(q_2\right)-i{\text{Γ}}_i\text{sinh}\left(q_2\right)\right]}{2A{\text{Γ}}_r\text{cos}\left(q_1\right)+\left({\text{Γ}}^2+A^2\right)\text{cosh}\left(q_2\right)}\right\},\end{array}(2)$

where

$q_1={\delta }_1+\sqrt{2}[\sqrt{2}x{\text{Δ}}_i-2t\left({\text{Δ}}_i{\lambda }_{1i}+{\text{Δ}}_r{\lambda }_{1r}\right)],q_2={\delta }_2+\sqrt{2}[\sqrt{2}x{\text{Δ}}_r-2t\left({\text{Δ}}_r{\lambda }_{1i}-{\text{Δ}}_i{\lambda }_{1r}\right)]$

${\text{Δ}}_r=\text{Re}\left[\sqrt{2{\left({\lambda }_{1r}-i{\lambda }_{1i}\right)}^2-A^2}\right],{\text{Δ}}_i=\text{Im}\left[\sqrt{2{\left({\lambda }_{1r}-i{\lambda }_{1i}\right)}^2-A^2}\right]$

${\text{Γ}}_r={\text{Δ}}_r+\sqrt{2}{\lambda }_{1r},{\text{Γ}}_i={\text{Δ}}_i-\sqrt{2}{\lambda }_{1i},\text{and}\text{Γ}=\sqrt{{\text{Γ}}_r^2+{\text{Γ}}_i^2}$

This is the general breather solution of the NLSE with five arbitrary real parameters, ${\lambda }_{1r}$, ${\lambda }_{1i}$, ${\delta }_1$, ${\delta }_2$, and A, which can be, with certain sets of parameter’s values, reduced to different types of solutions within the same family. For the sake of obtaining the Akhmediev breather, the Kuznetsov-Ma breather, the Peregrine soliton, the single bright soliton, and the continuous wave solution as limiting cases of solution Eq. 2, the first four free parameters are held on ${\lambda }_{1r}=0.05$, ${\lambda }_{1i}=0$, ${\delta }_i=0$, and ${\delta }_r=0$, while we choose A to be the variable parameter.

(1) Continuous wave: In the limit $A\to \sqrt{2}{\lambda }_{1r}$, the general breather solution returns back to the seed solution with an amplitude $A=-\sqrt{2}{\lambda }_{1r}$ (Figure 1A)

$u\left[1\right]=-\sqrt{2}{\lambda }_{1r}{e}^{2i{\lambda }_{1r}^{2}t}.(3)$

(2) Soliton: In the trivial limit, when $A\to 0$, the general breather solution reduces to a soliton solution which is localized in x and does not change as it propagates, fixed shape along t direction (Figure 1B)

$u\left[1\right]=-2\sqrt{2}{\lambda }_{1r}{e}^{4i{\lambda }_{1r}^{2}t}\text{sech}\left(2\sqrt{2}{\lambda }_{1r}x\right).(4)$

(3) Kuznetsov-Ma breather: When $\left|A\right|<\sqrt{2}{\lambda }_{1r}$ the general breather solution becomes periodic only in t and localized in x, which is referred to as a KM breather (Figure 1E).

(4) Akhmediev breather: When $\left|A\right|>\sqrt{2}{\lambda }_{1r}$ the general breather solution becomes periodic in x and localized in t, which is currently known as an Akhmediev breather (Figure 1D).

(5) Peregrine soliton: In the nontrivial limit, when $A\to -\sqrt{2}{\lambda }_{1r}$, the period goes to infinity and the breather solution reduces to the Peregrine soliton which is localized in both x and t and given by the rational expression (Figure 1C)

$u\left[1\right]=\sqrt{2}{\lambda }_{1r}{e}^{2i{\lambda }_{1r}^{2}t}\left(\frac{-3-16i{\lambda }_{1r}^{2}t+8{\lambda }_{1r}^2{x}^2+16i{\lambda }_{1r}^4{t}^2}{1+8{\lambda }_{1r}^2{x}^2+16{\lambda }_{1r}^4{t}^2}\right).(5)$

*There are different forms of the general breather solution in the literature. Three more expressions are listed in [8].

FIGURE 1

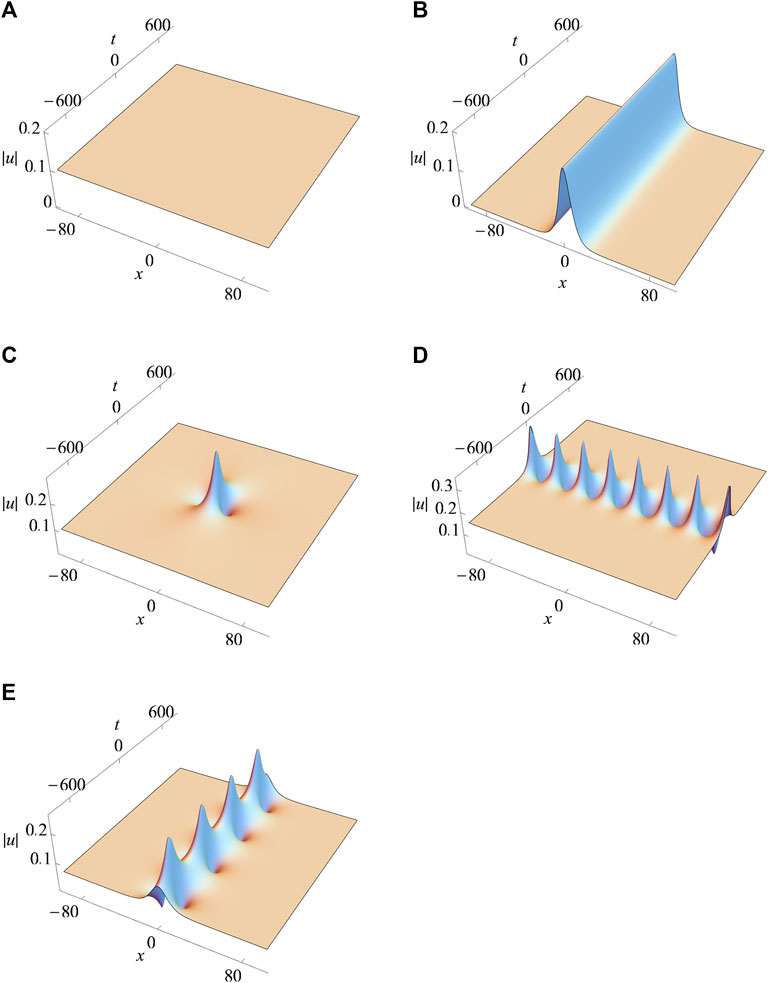
FIGURE 1. The five members of the solution class (2) all at ${\lambda }_{1r}=0.07$. (A) CW at $A=\sqrt{2}{\lambda }_{1r}$, (B) soliton at $A=0$, (C) Peregrine soliton at $A=-\sqrt{2}{\lambda }_{1r}$, (D) Akhmediev breather at $A=1.5\sqrt{2}{\lambda }_{1r}$, (E) Kuznetsov-Ma breather at $A=\sqrt{2}{\lambda }_{1r}/1.5$.

3 Peregrine Solitons of Higher-Order and Inhomogeneous NLSES

This section is dedicated to review existing Peregrine soliton solutions of the inhomogeneous NLSE with higher-order effects and potentials reported in the literature. In general, the higher-order NLSE (HNLSE) encompasses the effects of the higher-order dispersion, the higher-order nonlinearity, the stimulated Raman self-frequency shift, and the self-steepening effects in addition to group velocity dispersion (GVD) and cubic nonlinearity of fundamental NLSE. Such HNLSEs play a significant role in describing the dynamics of the ultrashort pulse propagation, supercontinuum generation [109], Heisenberg spin chain [110], ocean waves [16], and so forth. However, our context will be adhering to the Peregrine soliton solutions realized for such HNLSEs with different higher-order dispersive and nonlinear effects under certain circumstances. Diverse HNLSEs have been reported in the literature, namely, the Hirota equation [111], the Lakshmanan-Porsezian-Daniel equation [110], the quintic NLSE [22], the sextic NLSE [112, 113], heptic NLSE [112], and octic NLSE [112]. This section attempts to review the occurrence of the Peregrine solution reported in the aforementioned HNLSEs. Additionally, the inhomogeneous NLSE which is commonly termed as variable coefficient NLSE is also explored for the occurrence of Peregrine solutions [114, 115]. Understanding such inhomogeneous NLSEs plays a significant role in describing the nonuniform, defective, and irregular space-time dependence of the physical systems as well as discovering the apt control parameters required for diverse complex systems [85, 116–118]. The higher-order and inhomogeneous NLSEs, in which Peregrine solutions are reported, are listed below.

3.1 The Interaction of the Optical Rogue Waves Described by a Generalized HNLSE With (Space-, Time-) Modulated Coefficients [118]

$\begin{array}{c}i{\psi }_z=\beta \left(z,t\right){\psi }_{tt}+[V\left(z,t\right)+i\gamma \left(z,t\right)]\psi +g\left(z,t\right)|\psi {|}^2\psi +i[{\alpha }_1\left(z\right){\psi }_{ttt}+{\alpha }_2\left(z\right)\frac{\partial \left(|\psi {|}^2\psi \right)}{\partial t}+{\alpha }_3\left(z\right)\psi \frac{\partial |\psi {|}^2}{\partial t}]\\ +[\mu \left(z\right)+i\sigma \left(z,t\right)]{\psi }_t.\end{array}(6)$

In the above equation, $\beta \left(z,t\right)$, $V\left(z,t\right)$, $\gamma \left(z,t\right)$, and $g\left(z,t\right)$ represent the (space-, time-) modulated coefficients of GVD, external potential, gain/loss, and SPM, respectively. ${\alpha }_1\left(z\right)$, ${\alpha }_2\left(z\right)$, and ${\alpha }_3\left(z\right)$ account for third-order dispersion, self-steepening, and stimulated Raman scattering coefficients, respectively. $\mu \left(z\right)$ and $\sigma \left(z,t\right)$ denote the coefficients of differential gain or loss parameter and (space-, time-) modulated walk-off, respectively. (Solutions: See S1 $\&$ S2.)

3.2 The Fourth-Order Integrable Generalized NLSE With Higher-Order Nonlinear Effects Describing the Propagation of Femtosecond Pulse Through a Nonlinear Silica Fiber [119]

$i{\psi }_t+{\psi }_{xx}+2|\psi {|}^2\psi +{\gamma }_1\left({\psi }_{xxxx}+6{\psi }_x^2{\psi }^{\text{*}}+4|{\psi }_x{|}^2\psi +8|\psi {|}^2{\psi }_{xx}+2{\psi }^2{\psi }_{xx}^{\text{*}}+6|\psi {|}^4\psi \right)=0.(7)$

Here ${\gamma }_1$ indicates the strength of higher-order linear and nonlinear effects. (Solution: See S3.)

3.3 The Fifth-Order NLSE Describing One-Dimensional Anisotropic Heisenberg Ferromagnetic Spin Chain [120]

$\begin{array}{l}i{\psi }_t+\frac{1}{2}\left({\psi }_{xx}+2|\psi {|}^2\psi \right)-i\alpha \left({\psi }_{xxx}+6|\psi {|}^2{\psi }_x\right)+\gamma [{\psi }_{xxx}+6|\psi {|}^4\psi +2{\psi }^2{\psi }_{xx}^{\text{*}}+4\psi |{\psi }_x{|}^2+6{\psi }^{\text{*}}{\left({\psi }_x\right)}^2\\ +8\left|\psi {|}^2{\psi }_{xx}\right]-i\delta [{\psi }_{xxxxx}+30|\psi {|}^4{\psi }_x+20{\psi }^{\text{*}}{\psi }_x{\psi }_{xx}+10|\psi {|}^2{\psi }_{xxx}+10{\left(\psi |{\psi }_x{|}^2\right)}_x]=0,\end{array}(8)$

where the parameters α, γ, and δ are the coefficients of third-order dispersion, fourth-order dispersion, and fifth-order dispersion, respectively. (Solution: See S4.)

3.4 The Dynamics of Ultrashort Optical Pulses Propagating Through an Optical Fiber Described by a Higher-Order NLSE [121]

$i{\psi }_x+{\alpha }_2{K}_2\left(\psi \right)-i{\alpha }_3{K}_3\left(\psi \right)+{\alpha }_4{K}_4\left(\psi \right)-i{\alpha }_5{K}_5\left(\psi \right)=0,(9)$

where $K_2$, $K_3$, $K_4$, and $K_5$ are cubic, Hirota, Lakshmanan-Porsezian-Daniel, and quintic operators, respectively.

$\{\begin{array}{l}{K}_2={\psi }_{tt}+2\psi |\psi {|}^2,\hfill \\ K_3={\psi }_{ttt}+6{\psi }_t|\psi {|}^2,\hfill \\ K_4={\psi }_{tttt}+8|\psi {|}^2{\psi }_{tt}+6|\psi {|}^4\psi +4|{\psi }_t{|}^2\psi +6\overline{\psi }{\psi }_t^2+2{\psi }^2{\overline{\psi }}_{tt},\hfill \\ K_5={\psi }_{ttttt}+10|\psi {|}^2{\psi }_{ttt}+10{\left(\psi |{\psi }_t{|}^2\right)}_t+20\overline{\psi }{\psi }_t{\psi }_{tt}+30|\psi {|}^4{\psi }_t.\hfill \end{array}$

${\alpha }_i(i=\mathrm{1,2,3,4,5})$ are real constants. (Solution: See S5.)

3.5 The Sixth-Order NLSE With a Single Higher-Order Dispersion Term Describing the Dynamics of Modulation Instability, Rogue Waves, and Spectral Analysis [122]

$i{\psi }_z+{\delta }_2{\text{Γ}}_2\left(\psi \right)+{\delta }_6{\text{Γ}}_6\left(\psi \right)=0,(10)$

where ${\delta }_2$ and ${\delta }_6$ are the second- and sixth-order dispersion coefficients, respectively. ${\text{Γ}}_2$ and ${\text{Γ}}_6$ are cubic and sextic operator, respectively. In this analysis, the second-order dispersion coefficient value is fixed as ${\delta }_2=1/2$.

$\{\begin{array}{c}{\text{Γ}}_2={\psi }_{tt}+2\psi |\psi {|}^2,\\ {\text{Γ}}_6={\psi }_{tttttt}+{\psi }^2\left[60{\left|{\psi }_t\right|}^2{\psi }^{\text{*}}+50{\psi }_{tt}{\left({\psi }^{\text{*}}\right)}^2+2{\psi }_{tttt}^{\text{*}}\right]+\psi [12{\psi }^{\text{*}}{\psi }_{tttt}+18{\psi }_t^{\text{*}}{\psi }_{ttt}+8{\psi }_t{\psi }_{ttt}^{\text{*}}\\ +70{\left({\psi }^{\text{*}}\right)}^2{\psi }_t^2+22|{\psi }_{tt}{|}^2]+10{\psi }_t\left[3{\psi }^{\text{*}}{\psi }_{ttt}+5{\psi }_t^{\text{*}}{\psi }_{tt}+2{\psi }_t{\psi }_{tt}^{\text{*}}\right]+10{\psi }^3\left[2{\psi }^{\text{*}}{\psi }_{tt}^{\text{*}}+{\left({\psi }_t^{\text{*}}\right)}^2\right]\\ +20{\psi }^{\text{*}}{\psi }_{tt}^2+20\psi {\left|\psi \right|}^6.\end{array}$

(Solution: See S6.)

3.6 An Infinite Hierarchy of the Integrable NLSE [112]

$\begin{array}{l}F\left[\psi \left(x,t\right)\right]=i{\psi }_x+{\alpha }_2{K}_2\left[\psi \left(x,t\right)\right]-i{\alpha }_3{K}_3\left[\psi \left(x,t\right)\right]+{\alpha }_4{K}_4\left[\psi \left(x,t\right)\right]-i{\alpha }_5{K}_5\left[\psi \left(x,t\right)\right]\\ +{\alpha }_6{K}_6\left[\psi \left(x,t\right)\right]-i{\alpha }_7{K}_7\left[\psi \left(x,t\right)\right]+{\alpha }_8{K}_8\left[\psi \left(x,t\right)\right]-i{\alpha }_9{K}_9\left[\psi \left(x,t\right)\right]+\dots =0,\end{array}(11)$

where $K_2$, $K_3$, $K_4$, $K_5$, $K_6$, $K_7$, $K_8$, and $K_9$ are cubic, Hirota, Lakshmanan-Porsezian-Daniel, quintic, sextic, heptic, octic, and ninth-order operators, respectively. ${\alpha }_j(j=\mathrm{1,2,3,4,5,6,7,8,9},\dots )$ are real constants. The higher-order operators up to $K_8$ are provided below

$\{\begin{array}{l}{K}_2={\psi }_{tt}+2\psi |\psi {|}^2,\\ K_3={\psi }_{ttt}+6{\psi }_t|\psi {|}^2,\\ K_4={\psi }_{tttt}+8|\psi {|}^2{\psi }_{tt}+6|\psi {|}^4\psi +4|{\psi }_t{|}^2\psi +6{\psi }_t^2{\psi }^{\text{*}}+2{\psi }^2{\psi }_{tt}^{\text{*}},\\ K_5={\psi }_{ttttt}+10|\psi {|}^2{\psi }_{ttt}+10{\left(\psi |{\psi }_t{|}^2\right)}_t+20{\psi }^{\text{*}}{\psi }_t{\psi }_{tt}+30|\psi {|}^4{\psi }_t,\\ K_6={\psi }_{tttttt}+\left[60{\psi }^{\text{*}}\right|{\psi }_t{|}^2+50{\left({\psi }^{\text{*}}\right)}^2{\psi }_{tt}+2{\psi }_{tttt}^{\text{*}}]{\psi }^2+\psi [12{\psi }^{\text{*}}{\psi }_{tttt}+8{\psi }_t{\psi }_{ttt}^{\text{*}}+22|{\psi }_{tt}{|}^2]\\ +\psi [18{\psi }_{ttt}{\psi }_t^{\text{*}}+70{\left({\psi }^{\text{*}}\right)}^2{\psi }_t^2]+20{\left({\psi }_t\right)}^2{\psi }_{tt}^{\text{*}}+10{\psi }_t[5{\psi }_{tt}{\psi }_t^{\text{*}}+3{\psi }^{\text{*}}{\psi }_{ttt}]+20{\psi }^{\text{*}}{\psi }_{tt}^2\\ +10{\psi }^3[{\left({\psi }_t^{\text{*}}\right)}^2+2{\psi }^{\text{*}}{\psi }_{tt}^{\text{*}}]+20\psi |\psi {|}^6,\\ K_7={\psi }_{ttttttt}+70{\psi }_{tt}^2{\psi }_t^{\text{*}}+112{\psi }_t|{\psi }_{tt}{|}^2+98|{\psi }_t{|}^2{\psi }_{ttt}+70{\psi }^2\left[{\psi }_t\right[(\psi )2+2{\psi }^{\text{*}}{\psi }_{tt}^{\text{*}}]+{\psi }^{\text{*}}(2{\psi }_{tt}{\psi }_t^{\text{*}}\\ +{\psi }_{ttt}{\psi }^{\ast })]+28{\psi }_t^2{\psi }_{ttt}^{\ast }+14\psi [{\psi }^{\ast }(20|{\psi }_t{|}^2{\psi }_t+{\psi }_{ttttt})+3{\psi }_{ttt}{\psi }_{tt}^{\ast }+2{\psi }_{tt}{\psi }_{ttt}^{\ast }+2{\psi }_{tttt}{\psi }_t^{\ast }\\ +{\psi }_t{\psi }_{tttt}^{\text{*}}+20{\psi }_t{\psi }_{tt}{\left({\psi }^{\text{*}}\right)}^2]+140|\psi {|}^6{\psi }_t+70{\psi }_t^3{\left({\psi }^{\text{*}}\right)}^2+14\left(5{\psi }_{tt}{\psi }_{ttt}+3{\psi }_t{\psi }_{tttt}\right){\psi }^{\text{*}},\\ K_8={\psi }_{tttttttt}+14{\psi }^3\left[40\right|{\psi }_t{|}^2{\left({\psi }^{\text{*}}\right)}^2+20{\psi }_{tt}{\left({\psi }^{\text{*}}\right)}^3+2{\psi }_{tttt}^{\text{*}}{\psi }^{\text{*}}+3{\left({\psi }_{tt}^{\text{*}}\right)}^2+4{\psi }_t^{\text{*}}{\psi }_{ttt}^{\text{*}}]\\ +{\psi }^2[28{\psi }^{\text{*}}\left(14{\psi }_{tt}{\psi }_{tt}^{\text{*}}+11{\psi }_{ttt}{\psi }_t^{\text{*}}+6{\psi }_t{\psi }_{ttt}^{\text{*}}\right)+238{\psi }_{tt}{\left({\psi }_t^{\text{*}}\right)}^2+336|{\psi }_t{|}^2{\psi }_{tt}^{\text{*}}+560{\psi }_t^2{\left({\psi }^{\text{*}}\right)}^3\\ +98{\psi }_{tttt}{\left({\psi }^{\text{*}}\right)}^2+2{\psi }_{tttttt}^{\text{*}}]+2\psi \{21{\psi }_t^2[9{\left({\psi }_t^{\text{*}}\right)}^2+14{\psi }^{\text{*}}{\psi }_{tt}^{\text{*}}]+{\psi }_t[728{\psi }_{tt}{\psi }_t^{\text{*}}{\psi }^{\text{*}}+238{\psi }_{ttt}{\left({\psi }^{\text{*}}\right)}^2\\ +6{\psi }_{ttttt}^{\text{*}}]+34|{\psi }_{ttt}{|}^2+36{\psi }_{tttt}{\psi }_{tt}^{\text{*}}+22{\psi }_{tt}{\psi }_{tttt}^{\text{*}}+20{\psi }_{ttttt}{\psi }_t^{\text{*}}+161{\psi }_{tt}^2{\left({\psi }^{\text{*}}\right)}^2+8{\psi }_{tttttt}{\psi }^{\text{*}}\}\\ +182{\psi }_{tt}|{\psi }_{tt}{|}^2+308{\psi }_{tt}{\psi }_{ttt}{\psi }_t^{\text{*}}+252{\psi }_t{\psi }_{ttt}{\psi }_{tt}^{\text{*}}+196{\psi }_t{\psi }_{tt}{\psi }_{ttt}^{\text{*}}+168{\psi }_t{\psi }_{tttt}{\psi }_t^{\text{*}}+42{\psi }_t^2{\psi }_{tttt}^{\text{*}}\\ +14{\psi }^{\text{*}}\left(30{\psi }_t^3{\psi }_t^{\text{*}}+4{\psi }_{ttttt}{\psi }_t+5{\psi }_{ttt}^2+8{\psi }_{tt}{\psi }_{tttt}\right)+490{\psi }_t^2{\psi }_{tt}{\left({\psi }^{\text{*}}\right)}^2\\ +140{\psi }^4{\psi }^{\text{*}}[{\left({\psi }_t^{\text{*}}\right)}^2+{\psi }^{\text{*}}{\psi }_{tt}^{\text{*}}]+70\psi |\psi {|}^8.\end{array}$

(Solution: See S7.)

3.7 A Generalized Variable Coefficient Inhomogeneous NLSE With Varying Dispersion, Nonlinearity, Gain, and External Potentials [123]

$i{\psi }_t+\frac{1}{2}\beta \left(t\right){\psi }_{xx}+G\left(t\right)|\psi {|}^2\psi -\left(2\alpha \left(t\right)x+\frac{1}{2}\text{Ω}\left(t\right)x^2\right)\psi =i\frac{\gamma \left(t\right)}{2}\psi .(12)$

Here, $\beta \left(t\right)$ and $G\left(t\right)$ are the dispersion and nonlinearity management parameters. $\alpha \left(t\right)$, $\text{Ω}\left(t\right)$, and $\gamma \left(t\right)$ represent linear and harmonic oscillator potential and gain ($\gamma \left(t\right)<0$) or loss ($\gamma \left(t\right)>0$) coefficients, respectively. (Solutions: See S8 $\&$ S9.)

3.8  A Special Case of Eq. 12: The Variable Coefficient Inhomogeneous NLSE for Optical Signals [124]

$i{\psi }_x+\frac{1}{2}\beta \left(x\right){\psi }_{tt}+\chi \left(x\right)|\psi {|}^2\psi +\alpha \left(x\right)t^2\psi =i\gamma \left(x\right)\psi .(13)$

Here, $\beta \left(x\right)$, $\chi \left(x\right)$, $\alpha \left(x\right)$, and $\gamma \left(x\right)$ denote GVD, nonlinearity, normalized loss rate, and loss/gain coefficients, respectively. (Solutions: See S10 $\&$ S11.)

3.9 An Electron-Plasma Wave Packet With a Large Wavelength and Small Amplitude Propagating Through the Plasma Described by an Inhomogeneous NLSE With a Parabolic Density and Constant Damping Interaction [125]

$i{\psi }_z+{\psi }_{tt}+2|\psi {|}^2\psi -\left(\alpha t-{\beta }^2{t}^2\right)\psi +i\beta \psi =0,(14)$

where α and β are linear and damping coefficient, respectively. $\alpha t$ and ${\beta }^2{t}^2$ account for the profiles of linear and parabolic density. (Solution: See S12.)

3.10 The Propagation of the Femtosecond Pulse Through an Inhomogeneous Fiber With Selective Linear and Nonlinear Coefficients Described by an Inhomogeneous Hirota Equation [126]

${\psi }_z={\alpha }_1\left(z\right)\left(i{\psi }_{tt}+\frac{1}{3\delta }{\psi }_{ttt}\right)+{\alpha }_4\left(z\right)\left(i\delta \psi |\psi {|}^2+|\psi {|}^2{\psi }_t\right)+{\alpha }_6\left(z\right)\psi ,(15)$

where ${\alpha }_6=\frac{{\alpha }_{1,z}{\alpha }_4-{\alpha }_1{\alpha }_{4,z}}{2{\alpha }_1{\alpha }_4}$. Here ${\alpha }_1\left(z\right)$, ${\alpha }_2\left(z\right)$, and ${\alpha }_6$ represent the contribution of the dispersion, nonlinearity, and gain/loss coefficient, respectively; δ is a constant. (Solution: See S13.)

3.11 The NLSE Describing the Water Waves in the Infinite Water Depth [127]

$i\left({\psi }_t+c_g{\psi }_x\right)-\frac{{\omega }_0}{8k_0^2}{\psi }_{xx}-\frac{1}{2}{\omega }_0{k}_0^2|\psi {|}^2\psi =0,(16)$

where $c_g=\partial \omega /\partial k$ is the group velocity. The angular frequency ${\omega }_0=\sqrt{g{k}_0}$, where $k_0$ and g are the wave number and the acceleration due to gravity, respectively. (Solution: See S14.)

4 Peregrine Solitons With External Potentials

This section deals with reviewing the Peregrine soliton solutions reported in the NLSE with diverse external potentials. In nonlinear dynamics, a waveform which can exhibit a localized translation resulting from the counteracting dispersive and nonlinear effects is coined as “soliton”. Such classical soliton is also referred to as autonomous soliton, owing to the role of time as an independent variable and its absence in the nonlinear evolution equation. Those autonomous solitons can preserve their shape and velocity before and after collisions with an introduction of a phase shift [5]. However, in real circumstances, physical systems may be subjected to external space- and time-dependent forces. In such a case, these systems are known as nonautonomous systems and their corresponding solitons are known as nonautonomous solitons [128–130]. Furthermore, it is confirmed that solitons in such systems still have the ability to preserve their profile after collisions and adapt to the external potentials as well as to dispersive and nonlinear variations, but sacrificing the stability in amplitude, speed, and spectra [116, 131, 132]. In addition, such nonautonomous NLSEs can be generalized to describe the unusual phenomenon of rogue waves in different situations [85, 105, 123, 133–137]. Those rogue waves are characterized by spatiotemporal localization and possess the amplitudes greater than twice as that of the surrounding background [11, 13, 17, 18]. Further, dynamics of such rogue waves have been demonstrated experimentally in nonlinear optics [23, 24, 27, 138], plasma physics [139], Bose-Einstein condensation (BEC) [73], and atmospheric dynamics [140]. One of the basic waveforms of the rogue wave is the Peregrine soliton [11] whose appearance in the nonautonomous NLSEs under the influence of various external potentials will be presented below.

4.1 The Gross-Pitaevskii (GP) Equation Describing Matter Rogue Wave in BEC With Time-Dependent Attractive Interatomic Interaction in Presence of an Expulsive Potential [141]

$i{\psi }_t-\frac{1}{2}{\psi }_{xx}+a\left(t\right)|\psi {|}^2\psi +\frac{1}{2}{\lambda }^2{x}^2\psi =0,(17)$

where $a\left(t\right)$ is the nonlinear coefficient, defined by $a\left(t\right)=\left|a_s\left(t\right)\right|/a_B$ with $a_s\left(t\right)$ the s-wave scattering length and $a_B$ the Bohr radius. The aspect ratio is given by $\lambda =\left|{\omega }_0\right|/{\omega }_{\perp }$, where ${\omega }_0$ and ${\omega }_{\perp }$ are oscillator frequencies in the direction of cigar and transverse axes, respectively. (Solution: See S15.)

4.2 A Generic (1 + 1)-Dimensional NLSE With Variable Coefficients in Dimensionless Form [142]

$i{\psi }_t+\frac{D}{2}{\psi }_{xx}-g|\psi {|}^2\psi -V\psi =0,(18)$

where D and g represent the coefficient of dispersion and nonlinearity and V is an external potential denoting the trap confining the atoms in BECs. (Solutions: See S16 $\&$ S17.)

4.3 NLSE Describing the Nonlinear Optical Systems With the Spatially Modulated Coefficients in Presence of a Special Quadratic External Potential in the Dimensionless Form [143]

$i{\psi }_z+d\left(x\right){\psi }_{xx}+2\gamma \left(z,x\right)|\psi {|}^2\psi +V\left(z,x\right)\psi =0.(19)$

Here, $d\left(x\right)$ and $\gamma \left(z,x\right)$ are the diffraction and the nonlinearity coefficients, respectively. $V\left(z,x\right)=d\left(x\right)\left(a{x}^2+b\right)$ denotes the external potential modulated by the diffraction coefficient, with a and b being the real constants. (Solution: See S18.)

4.4 A GNLSE With Distributed Coefficients Describing the Amplification or Absorption of Optical Pulse Propagating Through a Monomode Optical Fiber [144]

$i{\psi }_z-\frac{1}{2}\beta \left(z\right){\psi }_{tt}+\gamma \left(z\right)|\psi {|}^2\psi +id\left(z\right)\psi =0,(20)$

where $\beta \left(z\right)$, $\gamma \left(z\right)$, and $d\left(z\right)$ are GVD, nonlinearity, and amplification/absorption coefficients, respectively. (Solution: See S19.)

4.5 NLSE Describing the Rogue Wave Dynamics under a Linear Potential [105]

$i{\psi }_t+\frac{1}{2}{\psi }_{xx}+\gamma \left(t\right)\left(x-x_0\left(t\right)\right)+|\psi {|}^2\psi =0,(21)$

where $\gamma \left(t\right)$ and $x_0\left(t\right)$ are real arbitrary functions. (Solutions: See S20 $\&$ S21.)

4.6 NLSE Describing Rogue Wave Under a Quadratic Potential [105]

$i{\psi }_t+\frac{1}{2}{\psi }_{xx}+\frac{1}{2}\left({\dot{\gamma }}^2-\ddot{\gamma }\right)x^2\psi +e^{\gamma }|\psi {|}^2\psi =0,(22)$

where $\gamma \left(t\right)$ is an integrability condition of the above equation, relating the coefficients of the quadratic potential and the nonlinearity. (Solution: See S22.)

4.7 A GP Equation With an External Potential Describing the Mean Field Dynamics of a Quasi-One-Dimensional BEC [145]

$i{\psi }_t+\frac{1}{2}{\psi }_{xx}+\gamma \left(t\right)|\psi {|}^2\psi +V\left(x,t\right)\psi -\frac{i}{2}g\left(t\right)\psi =0,(23)$

where the nonlinearity parameter is defined by $\gamma \left(t\right)=\frac{a_s\left(t\right)}{a_B}$, with $a_s\left(t\right)$ the scattering length and $a_B$ the Bohr radius. $V\left(x,t\right)=\frac{1}{2}{\text{Ω}}^2\left(t\right)x^2+h\left(t\right)x$ denotes the external potential, ${\text{Ω}}^2\left(t\right)=-\frac{{\omega }_0^2\left(t\right)}{{\omega }_{\perp }^2}$ with ${\omega }_0$ and ${\omega }_{\perp }$ representing the trap frequency in the axial direction and the radial trap frequency, respectively. $h\left(t\right)$ and $g\left(t\right)$ denote the linear potential and gain/loss coefficients for atomic and thermal cloud. (Solution: See S23.)

4.8 A GNLSE Describing the Pulse Propagation Through Tapered Graded-Index Nonlinear Waveguide Amplifier [146]

$i{\psi }_z+\frac{1}{2}{\psi }_{xx}+F\left(z\right)\frac{x^2}{2}\psi -\frac{i}{2}G\left(z\right)\psi +|\psi {|}^2\psi =0,(24)$

where $F\left(z\right)$ and $G\left(z\right)$ are the dimensionless tapering function and gain profile, respectively. (Solutions: See S24 $\&$ S25.)

4.9 The Propagation of Rogue Waves Described by a Nonautonomous NLSE With an External Harmonic Potential [147]

$i{\psi }_t+\frac{\alpha \left(t\right)}{2}{\psi }_{xx}+\left(-i\gamma \left(t\right)+\frac{\omega \left(t\right)r^2}{2}+\beta \left(t\right)|\psi {|}^2\right)\psi =0,(25)$

where $\alpha \left(t\right)$, $\gamma \left(t\right)$, and $\beta \left(t\right)$ represent the coefficients of the dispersion, the distributed gain/loss, and the Kerr nonlinearity, respectively. $\omega \left(t\right)r^2/2$ represents the harmonic potential. (Solutions: See S26 $\&$ S27.)

4.10 An Inhomogeneous NLSE With an External Potential to Tune the Width and Shape of the Pulse [148]

$i{\psi }_t+{\psi }_{xx}+2|\psi {|}^2\psi +{\alpha }^2{x}^2\psi +i\alpha \psi =0,(26)$

where α is a real number. (Solution: See S28.)

4.11 The (1 + 1)-Dimensional Nonautonomous NLSE With a Linear Potential [149]

$i{\psi }_z+\frac{\beta \left(z\right)}{2}{\psi }_{tt}+\chi \left(z\right)|\psi {|}^2\psi -2\alpha \left(z\right)t\psi -i\gamma \left(z\right)\psi =0,(27)$

where $\beta \left(z\right)$ and $\chi \left(z\right)$ are the coefficients of varying dispersion and nonlinearity, respectively. The term $2\alpha \left(z\right)t\psi$ denotes an approximate form of self-induced Raman effect. $\gamma \left(z\right)$ is the gain parameter. (Solutions: See S29 $\&$ S30.)

4.12 A Nonautonomous NLSE With Variable Coefficients in Presence of Varying Linear and Harmonic Potentials Describing the Optical Pulse Propagation [150]

$i{\psi }_z\left(z,t\right)+\frac{d\left(z\right)}{2}{\psi }_{tt}\left(z,t\right)+r\left(z\right)|\psi \left(z,t\right){|}^2\psi \left(z,t\right)+{\nu }_1\left(z\right)t\psi \left(z,t\right)+{\nu }_2\left(z\right)t^2\psi \left(z,t\right)=0,(28)$

where $d\left(z\right)$ describes the varying dispersion. $r\left(z\right)$ is a transformation coefficient that relates the nonlinear coefficient with the gain/loss coefficient. ${\nu }_1\left(z\right)$ and ${\nu }_2\left(z\right)$ denote the varying linear and harmonic potential, respectively. (Solution: See S31.)

4.13 A NLSE Describing Varying Dispersion With an External Harmonic Oscillator Potential [151]

$i{\psi }_z+\frac{D\left(z\right)}{2}{\psi }_{tt}+R\left(z\right)|\psi {|}^2\psi +i\left(\alpha \left(z\right)+\delta D\left(z\right)P\left(z\right)t\right){\psi }_t-\frac{i}{2}\text{Γ}\left(z\right)\psi =0.(29)$

Here $D\left(z\right)$, $R\left(z\right)$, $\alpha \left(z\right)$, $P\left(z\right)$, and $\text{Γ}\left(z\right)$ are varying dispersion in a harmonic oscillator potential form, varying nonlinearity, velocity of propagation, nonlinear focus length, and gain/loss coefficient, respectively. (Solutions: See S32 $\&$ S33.)

4.14 NLSE With Spatially Modulated Coefficients and a Special External Potential in the Dimensionless Form [39]

$i{\psi }_z+\frac{1}{2}\beta \left(x\right){\psi }_{xx}+\chi \left(x\right)|\psi {|}^2\psi +\frac{1}{2}\beta \left(x\right)\left(-\frac{1}{4}{x}^2+m+\frac{1}{2}\right)\psi =0.(30)$

Here, $\beta \left(x\right)$ and $\chi \left(x\right)$ denote coefficients of the diffraction and the nonlinearity, respectively. The external potential is a simple quadratic potential modulated by the diffraction coefficient, where m is a nonnegative integer referred to as the quantum modal parameter. (Solution: See S34.)

4.15 A Quasi-One-Dimension Gross-Pitaevskii Equation Describing BEC With Time-Dependent Quadratic Trapping Potential [152]

$i{\psi }_t+\frac{1}{2}{\psi }_{xx}+\sigma \gamma \left(t\right)|\psi {|}^2\psi +f\left(t\right)\frac{x^2}{2}\psi +h\left(t\right)x\psi -\frac{i}{2}g\left(t\right)\psi =0.(31)$

Here $\gamma \left(t\right)=2a_s\left(t\right)/a_B$ with $a_s$ and $a_B$ being the atomic scattering length and the Bohr radius. Further, $f\left(t\right)=-{\omega }_0^2\left(t\right)/{\omega }_{\perp }^2$, $h\left(t\right)=-\alpha \left(t\right)/{\omega }_{\perp }^2{a}_{\perp }$, and $g\left(t\right)=\eta \left(t\right)/\hslash {\omega }_{\perp }$ are the atoms confined in a cylindrical trap, time-dependent parabolic trap, and linear time-dependent potential, respectively, with $a_{\perp }={\left(\hslash /m{\omega }_{\perp }\right)}^{1/2}$. Here, $\sigma =+1\left(-1\right)$ corresponds to $a_s\left(t\right)<0\left(>0\right)$ defining attractive (repulsive) time-dependent scattering length. ${\omega }_0$ and ${\omega }_{\perp }$ are the trap frequency in the axial direction and the radial trap frequency, respectively. $\alpha \left(t\right)$ and $\eta \left(t\right)$ represent the interaction of linear time-dependent potential trap and gain/loss term incorporates the interaction of condensate with normal atomic cloud through three body interactions, respectively. (Solutions: See S35 $\&$ S36.)

5 Peregrine Solitons in Coupled NLSES

This section presents the Peregrine soliton solutions reported in the context of coupled NLSEs (CNLSEs), starting from basic vector NLSEs or the Manakov model [153] to the CNLSEs with the effects of higher-order dispersion/diffraction, self-focusing/defocusing, and other higher-order nonlinear effects [109, 154]. Such CNLSEs play a vital role in describing the interaction of multiple components of a vector wave or multiple scalar waves in numerous physical systems. In literature, several reports have demonstrated the significance of the CNLSEs in nonlinear science, namely, birefringent optical fibers [155], BEC [156], oceanic studies [157], biophysics [158], and even finance [159]. Recently, vector rogue waves featured with more than one component have been given special attention in nonlinear science, for their striking dynamics when compared to those of the scalar systems. A plethora of studies has been reported to understand such phenomena, which demonstrate new excitation patterns manifesting the vector rogue waves compared to that of the scalar rogue waves with well-known eye-shaped patterns [16, 160, 161]. Bludov et al. originally reported the numerical existence of the rogue waves in a two-component BEC described by the coupled GP equation with variable scattering lengths [162], followed with substantial analytical studies describing the spatiotemporal distribution of dark rogue waves [163], higher-order solutions [164], and baseband modulation stability featuring bright-dark and dark-dark rogue waves [165]. Furthermore a multi-rogue wave reveals four-petaled flower in spatiotemporal distribution [166] and resonant interactions [167] in a three-component coupled NLSEs. In addition, these rogue waves have also been found to demonstrate unusual distribution of rogue waves in spatiotemporal distribution plane when compared to the scalar ones. Moreover, integrable mixed CNLSEs (M-CNLSEs) feature-rich solutions of the multi-rogue wave structures including rogue wave doublet, bright-dark composites, bright-dark triplet, and bright-bright and bright-dark quartets are also constructed to understand the rogue wave dynamics in multicomponent physical systems [168]. This section will be confined within our aim to present the Peregrine soliton solution under the framework of CNLSEs.

5.1 A Manakov Model [169–173]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1=0,\\ i{\psi }_{2t}+{\psi }_{2xx}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2=0,\end{array}(32)$

(solutions: See S37, S38, S39, S40, S41, S42 $\&$ S43.)

5.2 Special Cases of the Manakov System

 i. The Manakov system of the form [174]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}+2\mu \left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1=0,\\ i{\psi }_{2t}+{\psi }_{2xx}+2\mu \left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2=0,\end{array}(33)$

where μ is a real constant. (Solution: See S44.)

 ii. The two-coupled NLSE describing the wave evolution dynamics through a two-mode nonlinear fiber in dimensionless form [175]

$\begin{array}{l}i{\psi }_{1z}+{\psi }_{1tt}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1=0,\\ i{\psi }_{2z}+{\psi }_{2tt}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2=0.\end{array}(34)$

(Solution: See S45.)

 iii. The Manakov model in the normal dispersion regime [63]

$\begin{array}{l}i{\psi }_{1z}-{\psi }_{1tt}+\sigma \left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1=0,\\ i{\psi }_{2z}-{\psi }_{2tt}+\sigma \left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2=0,\end{array}(35)$

where $z,t,\sigma$ are the propagation distance, retarded time, and the strength of the cubic nonlinearity, respectively. (Solution: See S46.)

 iv. The focusing CNLSE of the form [38, 164]

$\begin{array}{l}i{\psi }_{1t}+\frac{1}{2}{\psi }_{1xx}+\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1=0,\\ i{\psi }_{2t}+\frac{1}{2}{\psi }_{2xx}+\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2=0.\end{array}(36)$

(Solutions: See S47 $\&$ S48.)

 v. The Manakov system [165]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}-2s\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1=0,\\ i{\psi }_{2t}+{\psi }_{2xx}-2s\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2=0,\end{array}(37)$

where the constant s takes the value $-1$ or $+1$ for focusing or defocusing regime, respectively. (Solution: See S49.)

 vi. The Manakov system describing the propagation of optical pulses through the birefringent optical fibers [176]

$\begin{array}{l}i{\psi }_{1x}+\frac{D}{2}{\psi }_{1tt}+\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1=0,\\ i{\psi }_{2x}+\frac{D}{2}{\psi }_{2tt}+\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2=0.\end{array}(38)$

Dispersion (D) indicates the normal dispersion for ($D=-1$) and the anomalous dispersion for ($D=1$). (Solution: See S50.)

5.3 The Three-Component CNLSE [177]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2+|{\psi }_3{|}^2\right){\psi }_1=0,\\ i{\psi }_{2t}+{\psi }_{2xx}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2+|{\psi }_3{|}^2\right){\psi }_2=0,\\ i{\psi }_{3t}+{\psi }_{3xx}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2+|{\psi }_3{|}^2\right){\psi }_3=0.\end{array}(39)$

5.4 A Special Case of Eq. (39): The Three-Component CNLSE [178]

$\begin{array}{l}i{\psi }_{1t}+\frac{1}{2}{\psi }_{1xx}+\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2+|{\psi }_3{|}^2\right){\psi }_1=0,\\ i{\psi }_{2t}+\frac{1}{2}{\psi }_{2xx}+\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2+|{\psi }_3{|}^2\right){\psi }_2=0,\\ i{\psi }_{3t}+\frac{1}{2}{\psi }_{3xx}+\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2+|{\psi }_3{|}^2\right){\psi }_3=0.\end{array}(40)$

(Solutions: See S51 $\&$ S52.)

5.5 The Three-Component Manakov System in the Defocusing Regime [179]

$\begin{array}{l}i{\psi }_{1z}+i\delta {\psi }_{1t}+{\psi }_{1tt}-\sigma \left(|{\psi }_1{|}^2+|{\psi }_2{|}^2+|{\psi }_3{|}^2\right){\psi }_1=0,\\ i{\psi }_{2z}-i\delta {\psi }_{2t}+{\psi }_{2tt}-\sigma \left(|{\psi }_1{|}^2+|{\psi }_2{|}^2+|{\psi }_3{|}^2\right){\psi }_2=0,\\ i{\psi }_{3z}+{\psi }_{3tt}-\sigma \left(|{\psi }_1{|}^2+|{\psi }_2{|}^2+|{\psi }_3{|}^2\right){\psi }_3=0,\end{array}(41)$

where δ denotes the group velocity mismatch and σ describes the coefficient of cubic nonlinearity. (Solution: See S53.)

5.6 The CNLSE Describing the Nonlinear Interaction of the Short Wave (A) and the Long Wave (U) [180]

$\begin{array}{l}i\frac{\partial A}{\partial \xi }+\frac{1}{2}\frac{{\partial }^{2}A}{\partial {\tau }^2}+UA=0,\\ \frac{\partial U}{\partial \xi }-\frac{\partial |A{|}^2}{\partial \tau }=0.\end{array}(42)$

(Solution: See S54.)

5.7 The Integrable M-CNLSE [168]

$i{\psi }_t^{\left(l\right)}+{\psi }_{xx}^{\left(l\right)}+{\psi }^{\left(l\right)}{\displaystyle \sum }_{j=1}^M{\delta }_j|{\psi }^{\left(j\right)}{|}^2=0,l=\mathrm{1,2},\dots M.(43)$

Here ${\delta }_j$ s can be positive (negative) value defining focusing (defocusing) nonlinearity. (Solution: See S55.)

5.8 A Two-Coupled NLSE in Dimensionless Form [163]

$i{\psi }_{1z}+{\sigma }_1{\psi }_{1tt}+\left[2g_1\right|{\psi }_1{|}^2+2g_2\left|{\psi }_2{|}^2\right]{\psi }_1=0,$

$i{\psi }_{2z}+{\sigma }_2{\psi }_{2tt}+\left[2g_1\right|{\psi }_1{|}^2+2g_2\left|{\psi }_2{|}^2\right]{\psi }_2=0,(44)$

where ${\sigma }_1$ and ${\sigma }_2$ define the sign of GVD, taking the value $+1$ or $-1$ for anomalous or normal GVD, respectively. $g_1$ and $g_2$ are nonlinearity parameters determining the properties of Kerr medium with electrostriction mechanism. (Solution: See S56.)

5.9 The Coupled Derivative NLSE [181]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}-\frac{2}{3}i\mathit{ϵ}{\left[\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1\right]}_x=0,\\ i{\psi }_{2t}+{\psi }_{2xx}-\frac{2}{3}i\mathit{ϵ}{\left[\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2\right]}_x=0,\end{array}(45)$

where ϵ takes the value $\pm 1$. (Solution: See S57.)

5.10 A CNLSE With Negative Coherent Coupling Describing the Propagation of Orthogonally Polarized Optical Waves in an Isotropic Medium [182]

$\begin{array}{l}i{\psi }_{1z}+{\psi }_{1tt}+2\left(|{\psi }_1{|}^2+2|{\psi }_2{|}^2\right){\psi }_1-2{\psi }_1^{\text{*}}{\psi }_2^2=0,\\ i{\psi }_{2z}+{\psi }_{2tt}+2\left(2|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2-2{\psi }_1^2{\psi }_2^{\text{*}}=0.\end{array}(46)$

(Solutions: See S58 $\&$ S59.)

5.11 An Integrable Generalization of the CNLSE [183]

$\begin{array}{l}{\psi }_{1xt}+\alpha {\beta }^2{\psi }_1-2i\alpha \beta {\psi }_{1x}-\alpha {\psi }_{1xx}+i\alpha {\beta }^2{\psi }_1{\psi }_2{\psi }_{1x}=0,\\ {\psi }_{2xt}+\alpha {\beta }^2{\psi }_2-2i\alpha \beta {\psi }_{2x}-\alpha {\psi }_{2xx}-i\alpha {\beta }^2{\psi }_1{\psi }_2{\psi }_{2x}=0,\end{array}(47)$

where α and β are constants. (Solution: See S60.)

5.12 A Coupled NLSE With Special External Potential in a Parabolic Form [184]

$\begin{array}{l}i{\psi }_{1z}+\beta \left(x\right){\psi }_{1xx}+2\chi \left(x\right)\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1+U\left(x\right){\psi }_1=0,\\ i{\psi }_{2z}+\beta \left(x\right){\psi }_{2xx}+2\chi \left(x\right)\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2+U\left(x\right){\psi }_2=0,\end{array}(48)$

where $U\left(x\right)=\beta \left(x\right)\left(a{x}^2+b\right)$ is a parabolic external potential modulated by the diffraction coefficient, with real constants a and b. $\beta \left(x\right)$ and $\chi \left(x\right)$ denote the effective diffraction coefficient and the nonlinearity coefficient, respectively. (Solution: See S61.)

5.13 The Gross-Pitaevskii Equations [185]

$\begin{array}{l}i{\psi }_{1t}=-{\psi }_{1xx}+\left(g_1|{\psi }_1{|}^2+g|{\psi }_2{|}^2\right){\psi }_1+\beta \left(t\right){\psi }_2,\\ i{\psi }_{2t}=-{\psi }_{2xx}+\left(g|{\psi }_1{|}^2+g_2|{\psi }_2{|}^2\right){\psi }_2+\beta \left(t\right){\psi }_1,\end{array}(49)$

where $g_1$ and $g_2$ are the dimensionless nonlinear coefficients for the quasi-one-dimensional condensate. The factor g can take two values $g=\pm 1$. The $\beta \left(t\right)$ in the last term can be used to switch between the two hyperfine states, originated from the external magnetic field. (Solution: See S62.)

5.14 A Coupled GNLSE [186]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}-2{\psi }_1^2{\psi }_2+4{\beta }^2{\psi }_1^3{\psi }_2^2+4i\beta {\left({\psi }_1{\psi }_2\right)}_x{\psi }_1=0,\\ i{\psi }_{2t}-{\psi }_{2xx}+2{\psi }_1{\psi }_2^2-4{\beta }^2{\psi }_1^2{\psi }_2^3+4i\beta {\left({\psi }_1{\psi }_2\right)}_x{\psi }_2=0,\end{array}(50)$

where β is a constant, describing the strength of higher-order terms. (Solution: See S63.)

5.15 A CNLSE [187]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}+2\left(|{\psi }_1{|}^2+2|{\psi }_2{|}^2\right){\psi }_1-2{\psi }_1^{\text{*}}{\psi }_2^2=0,\\ i{\psi }_{2t}+{\psi }_{2xx}+2\left(|{\psi }_2{|}^2+2|{\psi }_1{|}^2\right){\psi }_2-2{\psi }_2^{\text{*}}{\psi }_1^2=0.\end{array}(51)$

(Solution: See S64.)

5.16 The Two-Component CNLSE With Four-Wave Mixing Term [188]

$\begin{array}{l}i{\psi }_{1t}+\frac{1}{2}{\psi }_{1xx}+\sigma \left(|{\psi }_1{|}^2+2|{\psi }_2{|}^2\right){\psi }_1+\sigma {\psi }_2^2{\psi }_1^{\text{*}}=0,\\ i{\psi }_{2t}+\frac{1}{2}{\psi }_{2xx}+\sigma \left(2|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2+\sigma {\psi }_1^2{\psi }_2^{\text{*}}=0,\end{array}(52)$

where $\sigma =\pm 1$ accounts for attractive $(+)$ or repulsive $(-)$ interactions.

5.17 A Special Case of Eq. 52: An Integrable CNLSE [189]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}+2|{\psi }_1{|}^2{\psi }_1+4|{\psi }_2{|}^2{\psi }_1+2{\psi }_2^2{\psi }_1^{\text{*}}=0,\\ i{\psi }_{2t}+{\psi }_{2xx}+2|{\psi }_2{|}^2{\psi }_2+4|{\psi }_1{|}^2{\psi }_2+2{\psi }_1^2{\psi }_2^{\text{*}}=0.\end{array}(53)$

(Solutions: See S65 $\&$ S66.)

5.18 The Evolution of Two Orthogonally Polarized Components in an Isotropic Medium Described by the Normalized CNLSE [190, 191]

$\begin{array}{l}i{\psi }_{1z}+{\psi }_{1tt}+2\left(|{\psi }_1{|}^2-2|{\psi }_2{|}^2\right){\psi }_1-2{\psi }_1^{\text{*}}{\psi }_2^2=0,\\ i{\psi }_{2z}+{\psi }_{2tt}+2\left(2|{\psi }_1{|}^2-|{\psi }_2{|}^2\right){\psi }_2+2{\psi }_2^{\text{*}}{\psi }_1^2=0.\end{array}(54)$

(Solutions: See S67 $\&$ S68.)

5.19 A System of Linearly Coupled NLSEs for Field Variables [60]

$\begin{array}{l}i{\psi }_{1z}=-{\psi }_{1xx}+\left({\chi }_1|{\psi }_1{|}^2+\chi |{\psi }_2{|}^2\right){\psi }_1+i\gamma {\psi }_1-{\psi }_2,\\ i{\psi }_{2z}=-{\psi }_{2xx}+\left(\chi |{\psi }_1{|}^2+{\chi }_1|{\psi }_2{|}^2\right){\psi }_2-i\gamma {\psi }_2-{\psi }_1,\end{array}(55)$

where ${\chi }_1$ and χ denote the SPM and XPM coefficients, respectively. γ represents the PT-balanced gain. (Solution: See S69.)

5.20 A CNLSE Describing the Dynamics of Light Propagation Through PT-Symmetric Coupled Waveguides [192]

$\begin{array}{l}i{\psi }_{1z}+\frac{1}{2}{\psi }_{1xx}+\left({\chi }_1|{\psi }_1{|}^2+\chi |{\psi }_2{|}^2\right){\psi }_1=-{\psi }_2+i\gamma {\psi }_1,\\ i{\psi }_{2z}+\frac{1}{2}{\psi }_{2xx}+\left(\chi |{\psi }_1{|}^2+{\chi }_1|{\psi }_2{|}^2\right){\psi }_2=-{\psi }_1-i\gamma {\psi }_2,\end{array}$

where the parameters χ (or ${\chi }_1>0$) and χ (or ${\chi }_1<0$) correspond to the focusing and defocusing case, respectively. The γ in the last term describes PT-balanced gain in the first and loss in the second waveguide. The relation ${\psi }_2\left(x,z\right)=\pm {\psi }_1\left(x,z\right)\text{exp}\left(\pm i\theta \right)$ is used which casts above equations into the single equation of the form

$i{\psi }_z+\frac{1}{2}{\psi }_{xx}+\left({\chi }_1+\chi |\right)\psi {|}^2\psi \pm \text{cos}\left(\theta \right)\psi =0.(56)$

(Solutions: See S70 $\&$ S71.)

5.21 A CNLSE With the Four-Wave Mixing Term Which Describes the Pulse Propagation in a Birefringent Fiber [193–196]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}+2\left(a|{\psi }_1{|}^2+c|{\psi }_2{|}^2+b{\psi }_1{\psi }_2^{\text{*}}+b^{\text{*}}{\psi }_1^{\text{*}}{\psi }_2\right){\psi }_1=0,\\ i{\psi }_{2t}+{\psi }_{2xx}+2\left(a|{\psi }_1{|}^2+c|{\psi }_2{|}^2+b{\psi }_1{\psi }_2^{\text{*}}+b^{\text{*}}{\psi }_1^{\text{*}}{\psi }_2\right){\psi }_2=0.\end{array}(57)$

Here a and c are real constants, describing the self-phase modulation and cross-phase modulation effects, respectively. b is a complex constant, describing the four-wave mixing effects. (Solutions: See S72, S73, S74 $\&$ S75.)

5.22 A Focusing-Defocusing Type CNLSE [197]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}+2\gamma \left(|{\psi }_1{|}^2-|{\psi }_2{|}^2\right){\psi }_1-\gamma \left({\psi }_1^2+{\psi }_2^2\right){\psi }_1^{\text{*}}=0,\\ i{\psi }_{2t}+{\psi }_{2xx}+2\gamma \left(|{\psi }_1{|}^2-|{\psi }_2{|}^2\right){\psi }_2+\gamma \left({\psi }_1^2+{\psi }_2^2\right){\psi }_2^{\text{*}}=0,\end{array}(58)$

where γ denotes the strength of nonlinearity. (Solution: See S76.)

5.23 A CNLSE With Variable Coefficients [198]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}+v\left(x,t\right){\psi }_1+g\left(t\right)\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1+i\gamma \left(t\right){\psi }_1=0,\\ i{\psi }_{2t}+{\psi }_{2xx}+v\left(x,t\right){\psi }_2+g\left(t\right)\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2+i\gamma \left(t\right){\psi }_2=0,\end{array}(59)$

where $v\left(x,t\right)$, $g\left(t\right)$, and $\gamma \left(t\right)$ are the coefficients of the external potential, nonlinearity, and gain, respectively. (Solutions: See S77 $\&$ S78.)

5.24 The Generalized CNLSE for Two Components [199]

$\begin{array}{l}i{\psi }_{1z}+{\alpha }_1\left(z\right){\psi }_{1xx}+{\beta }_1\left(z\right)|{\psi }_1{|}^2{\psi }_1+{\delta }_1\left(z\right)|{\psi }_2{|}^2{\psi }_1+{\nu }_1\left(x,z\right){\psi }_1+i{\gamma }_1\left(z\right){\psi }_1=0,\\ i{\psi }_{2z}+{\alpha }_2\left(z\right){\psi }_{2xx}+{\beta }_2\left(z\right)|{\psi }_1{|}^2{\psi }_2+{\delta }_2\left(z\right)|{\psi }_2{|}^2{\psi }_2+{\nu }_2\left(x,z\right){\psi }_2+i{\gamma }_2\left(z\right){\psi }_2=0,\end{array}(60)$

where ${\alpha }_1\left(z\right)$ and ${\alpha }_2\left(z\right)$ are diffraction (dispersion) coefficients. ${\beta }_1\left(z\right)$ and ${\beta }_2\left(z\right)$ are nonlinear coefficients. ${\delta }_1\left(z\right)$ and ${\delta }_2\left(z\right)$ are the coefficient of gain/loss. ${\nu }_1$ and ${\nu }_2$ are the two real valued functions of spatial coordinates x and z, describing the external potentials. ${\gamma }_1$ and ${\gamma }_2$ are real valued functions of the propagation distance z. (Solutions: See S79 $\&$ S80.)

5.25 The Coupled Inhomogeneous NLSE [200]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1-\left(\alpha x-{\beta }^2{x}^2\right){\psi }_1+i\beta {\psi }_1=0,\\ i{\psi }_{2t}+{\psi }_{2xx}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2-\left(\alpha x-{\beta }^2{x}^2\right){\psi }_2+i\beta {\psi }_2=0,\end{array}(61)$

where α denotes the coefficient of the linear density profile and β is the coefficient of damping. $\alpha x$ and ${\beta }^2{x}^2$ correspond to the linear and parabolic density profiles. (Solution: See S81.)

5.26 The Higher-Order CNLSE With Variable Coefficients [201]

$\begin{array}{l}i{\psi }_{jz}-\frac{1}{2}{\beta }_2\left(z\right){\psi }_{jtt}-\gamma \left(z\right)\left({\displaystyle \sum }_{n=1}^2{a}_{nj}|{\psi }_n{|}^2\right){\psi }_j+i{\beta }_3\left(z\right){\psi }_{jttt}+i\chi \left(z\right)\left({\displaystyle \sum }_{n=1}^2{a}_{nj}|{\psi }_n{|}^2\right){\psi }_{jt}\\ +i\delta \left(z\right)\left({\displaystyle \sum }_{n=1}^2{a}_{nj}{\psi }_{nt}{\psi }_j^{\text{*}}\right){\psi }_j+i\text{Γ}\left(z\right){\psi }_j=0,j=\mathrm{1,2.}\end{array}(62)$

Here ${\beta }_2\left(z\right)$, $\gamma \left(z\right)$, ${\beta }_3\left(z\right)$, $\chi \left(z\right)$, $\delta \left(z\right)$, and $\text{Γ}\left(z\right)$ are coefficients of group velocity dispersion, nonlinearity (SPM and XPM), TOD, SS, SFS, and loss/gain, respectively. (Solution: See S82.)

5.27 The Coupled Hirota Equations [202]

$\begin{array}{l}i{\psi }_{1t}+\frac{1}{2}{\psi }_{1xx}+\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1+i\mathit{ϵ}[{\psi }_{1xxx}+\left(6|{\psi }_1{|}^2+3|{\psi }_2{|}^2\right){\psi }_{1x}+3{\psi }_1{\psi }_2^{\text{*}}{\psi }_{2x}]=0,\\ i{\psi }_{2t}+\frac{1}{2}{\psi }_{2xx}+\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2+i\mathit{ϵ}[{\psi }_{2xxx}+\left(6|{\psi }_2{|}^2+3|{\psi }_1{|}^2\right){\psi }_{2x}+3{\psi }_2{\psi }_1^{\text{*}}{\psi }_{1x}]=0,\end{array}(63)$

where ϵ is a constant that provides the strength of higher-order effects and scales the integrable perturbations of the simple Manakov system. (Solutions: See S83 $\&$ S84.)

5.28 A Coupled Cubic-Quintic NLSE Describing the Pulse Propagation in Non-Kerr Media [203]

$\begin{array}{l}i{\psi }_{1z}+{\psi }_{1tt}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1+{\left({\rho }_1|{\psi }_1{|}^2+{\rho }_2|{\psi }_2{|}^2\right)}^2{\psi }_1-2i{\left[\left({\rho }_1|{\psi }_1{|}^2+{\rho }_2|{\psi }_2{|}^2\right){\psi }_1\right]}_t\\ +2i\left({\rho }_1{\psi }_1^{\text{*}}{\psi }_{1t}+{\rho }_2{\psi }_2^{\text{*}}{\psi }_{2t}\right){\psi }_1=0,\\ i{\psi }_{2z}+{\psi }_{2tt}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2+{\left({\rho }_1|{\psi }_1{|}^2+{\rho }_2|{\psi }_2{|}^2\right)}^2{\psi }_2-2i{\left[\left({\rho }_1|{\psi }_1{|}^2+{\rho }_2|{\psi }_2{|}^2\right){\psi }_2\right]}_t\\ +2i\left({\rho }_1{\psi }_1^{\text{*}}{\psi }_{1t}+{\rho }_2{\psi }_2^{\text{*}}{\psi }_{2t}\right){\psi }_2=0,\end{array}(64)$

where ${\rho }_1$ and ${\rho }_2$ are the real parameters. (Solution: See S85.)

5.29 A Coupled Cubic-Quintic NLSE Describing the Effects of Quintic Nonlinearity on the Propagation of Ultrashort Pulse in a Non-Kerr Media [204]

$\begin{array}{l}i{\psi }_{1t}+{\psi }_{1xx}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_1+{\left({\rho }_1|{\psi }_1{|}^2+{\rho }_2|{\psi }_2{|}^2\right)}^2{\psi }_1-2i{\left[\left({\rho }_1|{\psi }_1{|}^2+{\rho }_2|{\psi }_2{|}^2\right){\psi }_1\right]}_x\\ +2i\left({\rho }_1{\psi }_1^{\text{*}}{\psi }_{1x}+{\rho }_2{\psi }_2^{\text{*}}{\psi }_{2x}\right){\psi }_1=0,\\ i{\psi }_{2t}+{\psi }_{2xx}+2\left(|{\psi }_1{|}^2+|{\psi }_2{|}^2\right){\psi }_2+{\left({\rho }_1|{\psi }_1{|}^2+{\rho }_2|{\psi }_2{|}^2\right)}^2{\psi }_2-2i{\left[\left({\rho }_1|{\psi }_1{|}^2+{\rho }_2|{\psi }_2{|}^2\right){\psi }_2\right]}_x\\ +2i\left({\rho }_1{\psi }_1^{\text{*}}{\psi }_{1x}+{\rho }_2{\psi }_2^{\text{*}}{\psi }_{2x}\right){\psi }_2=0,\end{array}(65)$

where ${\rho }_1$ and ${\rho }_2$ are real constants. (Solution: See S86.)

5.30 A Fourth-Order CNLSE Describing the Ultrashort Pulse Propagation in a Birefringent Optical Fiber [205]

$\begin{array}{l}i{\psi }_{\alpha t}+{\psi }_{\alpha xx}+2{\psi }_{\alpha }{\displaystyle \sum }_{\rho =1}^2|{\psi }_{\rho }{|}^2+\gamma [{\psi }_{\alpha xxxx}+2{\psi }_{\alpha }{\displaystyle \sum }_{\rho =1}^2|{\psi }_{\rho x}{|}^2+2{\psi }_{\alpha x}{\displaystyle \sum }_{\rho =1}^2{\psi }_{\rho }{\psi }_{\rho x}^{\text{*}}+6{\psi }_{\alpha x}{\displaystyle \sum }_{\rho =1}^2{\psi }_{\rho }^{\text{*}}{\psi }_{\rho x}\\ +4{\psi }_{\alpha xx}{\displaystyle \sum }_{\rho =1}^2|{\psi }_{\rho }{|}^2+4{\psi }_{\alpha }{\displaystyle \sum }_{\rho =1}^2{\psi }_{\rho }^{\text{*}}{\psi }_{\rho xx}+2{\psi }_{\alpha }{\displaystyle \sum }_{\rho =1}^2{\psi }_{\rho }{\psi }_{\rho xx}^{\text{*}}+6{\psi }_{\alpha }{\left({\displaystyle \sum }_{\rho =1}^2|{\psi }_{\rho }{|}^2\right)}^2]=0,\end{array}(66)$

where $\alpha =1,2$. γ is a real parameter that denotes the strength of higher-order linear and nonlinear effects. (Solution: See S87.)

5.31 A NLS-Type System With Self-Consistent Sources Associated With the Two-Component Homogeneous Plasma [206]

$\begin{array}{l}{\psi }_{1t}-\frac{i\alpha }{2}{\psi }_{1xx}+i\alpha \sigma |{\psi }_1{|}^2{\psi }_1-k_0{\psi }_2{\psi }_3^{\text{*}}=0,\\ {\psi }_{2x}-{\psi }_1{\psi }_3=0,{\psi }_{3x}-2i{k}_0{\psi }_3-\sigma {\psi }_1^{\text{*}}{\psi }_2=0,\end{array}(67)$

where α, σ, and $k_0$ denote the coefficients of dispersion, nonlinearity, and coupling, respectively. (Solution: See S88.)

6 Peregrine Solitons in Discrete NLSE

This section delivers the Peregrine soliton solutions presented in the literature in the framework of discrete NLSEs. Since its origin from the mid-1960s, the general NLSE of continuous form plays a significant role in unraveling the physical phenomena and insights which lead to numerous scientific and technological applications in various nonlinear systems. Further, owing to its outstanding versatility, different forms of continuous NLSEs, namely, scalar and vector NLSEs, have been proposed with suitable additional terms to predict various dynamical situations in numerous nonlinear systems [90, 109, 207]. From the past three decades, apart from continuous nonlinear systems, considerable efforts have also been made to investigate the nonlinear discrete systems characterized by structural discontinuities and lattices. These systems find potential applications in electronic circuits [208, 209], optical waveguides [210], nonlinear lattices [211], spatial energy concentrators [212], coupled nonlinear waveguide arrays [213], BEC trapped in periodic optical lattices [214], photorefractive crystals [215], and so forth. Those nonlinear discrete systems, discrete NLSEs, can be modeled through discretizing the continuous NLSE via appropriate transformations. In such discrete NLSEs, the energy evolution is in a semidiscrete form characterized by the spatial discretization and temporal continuity [90].

Additionally, the pioneering work by Ablowitz and Ladik led to a cutting-edge method for constructing a family of semidiscrete and doubly discrete nonlinear systems associated with their linear operator pairs, necessary for obtaining the solutions of the nonlinear systems via the inverse scattering transform (IST) [216]. Further, those formulations include an integrable semidiscretization of NLSE as well as doubly discrete integrable NLSE referred to as integrable discrete NLSE (IDNLSE) [217]. These equations form basic discrete equations which serve as a model for the plethora of applications where exact solutions can be realized through diverse methods such as Darboux and Bäcklund transformations in addition to the IST [86, 87, 89, 90, 93, 218]. Firstly, the DNLSE was reported by Christodoulides et al., in a nonlinear array of coupled waveguides displaying discrete self-focusing [219], followed by the experimental realization of discrete spatial solitons in AlGaAs nonlinear waveguide arrays [213]. Solitons resulting in these systems are due to the interplay between discreteness and self-trapping nonlinearity and coined as spatial discrete solitons or lattice solitons [220]. On the other hand, Peregrine solitons of DNLSEs display different dynamical behavior compared to that of the continuous counterpart and find interesting applications in spatial energy concentrators [212], photonic lattices [221], anharmonic lattices [222], Heisenberg spin chains [223], self-trapping on a dimer [224], and so forth. These Peregrine solitons that arise in discrete systems are studied in a broad category under the context of i) the DNLSEs [90, 219], ii) the Ablowitz-Ladik equations [90, 225], iii) the discrete Hirota equations (a combination of DNLSE and discrete complex modified KdV equations) [90, 226], and iv) the Salerno equation (an interpolation of the cubic DNLSE and the integrable Ablowitz-Ladik equation) [227]. Here, we present the class of DNLSEs where the Peregrine solitons were reported.

6.1 The Focusing and Defocusing Ablowitz-Ladik (AL) Equation [228]

$i\frac{d{\psi }_n}{dt}=\left(1\pm |{\psi }_n{|}^2\right)\left({\psi }_{n+1}+{\psi }_{n-1}\right).(68)$

In the above AL equation, the term $|{\psi }_n{|}^2$ with $+$ and $-$ sign represents focusing and defocusing regimes, respectively. (Solution: See S89.)

6.2 The DNLSE Describing an Array of Coupled Nonlinear Waveguides [229]

$i\frac{d{\psi }_n}{dt}+{\psi }_{n+1}+{\psi }_{n-1}-2{\psi }_n+\sigma |{\psi }_n{|}^2{\psi }_n=0.(69)$

Here, the constant σ takes the value $``+1"$ denoting the focusing nonlinearity and $``-1"$ denoting the defocusing nonlinearity. (Solution: See S90.)

6.3 An Optical Field Propagating Through a Tight Binding Waveguide Array Described by the DNLSE [230]

$i\frac{d{\psi }_j}{dz}=-J_j\left({\psi }_{j+1}+{\psi }_{j-1}\right)+V_j{\psi }_j+g|{\psi }_j{|}^2{\psi }_j,(70)$

where $J_j$ is the coupling coefficient between j-th waveguide and adjacent waveguides. $V_j$ is the propagation constant of the j-th waveguide. g is the constant describing nonlinear interaction. (Solution: See S91.)

6.4 The Discrete NLSE [231]

$i\frac{d{\psi }_n}{dt}={\psi }_{n+1}-2{\psi }_n+{\psi }_{n-1}+{\psi }_n{\psi }_n^{\text{*}}\left({\psi }_{n+1}+{\psi }_{n-1}\right).(71)$

(Solution: See S92.)

6.5 The Integrable AL Equation [232, 233]

$i\frac{d{\psi }_n}{dt}+\left({\psi }_{n-1}+{\psi }_{n+1}\right)\left(1+|{\psi }_n{|}^2\right)-2{\psi }_n=0.(72)$

(Solutions: See S93 $\&$ S94.)

6.6 The Modified AL Equation [234]

$i\frac{d{\psi }_n}{dt}+\left({\psi }_{n-1}+{\psi }_{n+1}\right)\left(1+|{\psi }_n{|}^2\right)-2\left(q^2+1\right){\psi }_n=0.(73)$

(Solution: See S95.)

6.7 The Generalized Ablowitz-Ladik-Hirota Lattice Equation With Variable Coefficients [235]

$i{\psi }_{n,t}+[\text{Λ}\left(t\right){\psi }_{n+1}+{\text{Λ}}^{\text{*}}\left(t\right){\psi }_{n-1}]\left(1+g\left(t\right)|{\psi }_n{|}^2\right)-2v_n\left(t\right){\psi }_n+i\gamma \left(t\right){\psi }_n=0.(74)$

Here, the tunnel coupling constant between the sites is given by $\text{Λ}\left(t\right)=\alpha \left(t\right)+i\beta \left(t\right)$, with $\alpha \left(t\right)$ and $\beta \left(t\right)$ the differentiable real valued functions. $g\left(t\right)$, $v_n\left(t\right)$, and $\gamma \left(t\right)$ represent time-modulated interstice nonlinearity, space-time-modulated inhomogeneous frequency shift, and time-modulated effective gain/loss constants, respectively. (Solution: See S96.)

6.8 The Generalized Salerno Equation [64]

$i\frac{d{\psi }_n}{dt}=-\frac{1}{2}\left({\psi }_{n+1}-2{\psi }_n+{\psi }_{n-1}\right)-\mu |{\psi }_n{|}^2{\psi }_n-\frac{1}{2}\left(1-\mu \right)|{\psi }_n{|}^2\left({\psi }_{n+1}+{\psi }_{n-1}\right).(75)$

Above equation corresponds to the DNLSE, when $\mu =1$, and reduces to the AL system, when $\mu =0$, respectively. (Solution: See S97.)

6.9 The Discrete Hirota Equation [233]

$i\frac{d{\psi }_n}{dt}+[\left(a-ib\right){\psi }_{n-1}+\left(a+ib\right){\psi }_{n+1}]\left(1+|{\psi }_n{|}^2\right)-2{\psi }_n=0.(76)$

(Solution: See S98.)

6.10 A Spatially Discrete Hirota Equation [236]

$\begin{array}{l}\frac{d{\psi }_n}{dt}=\alpha \left(1+|{\psi }_n{|}^2\right)[{\psi }_{n+2}-2{\psi }_{n+1}+2{\psi }_{n-1}-{\psi }_{n-2}+{\psi }_n^{\text{*}}\left({\psi }_{n+1}^2-{\psi }_{n-1}^2\right)-|{\psi }_{n-1}{|}^2{\psi }_{n-2}\\ +|{\psi }_{n+1}{|}^2{\psi }_{n+2}+{\psi }_n\left({\psi }_{n-1}^{\text{*}}{\psi }_{n+1}-{\psi }_{n+1}^{\text{*}}{\psi }_{n-1}\right)]-i\beta \left(1+|{\psi }_n{|}^2\right)\left({\psi }_{n+1}+{\psi }_{n-1}\right)+2i\beta {\psi }_n,\end{array}(77)$

where α and β are real constants. (Solution: See S99.)

6.11 A Single Ablowitz-Ladik Equation With Only One Component [237]

$i\frac{d{\psi }_n^{\left(1\right)}}{dt}+\frac{1}{2h^2}\left({\psi }_{n-1}^{\left(1\right)}+{\psi }_{n+1}^{\left(1\right)}-2{\psi }_n^{\left(1\right)}\right)+\frac{1}{2}\left({\psi }_{n-1}^{\left(1\right)}+{\psi }_{n+1}^{\left(1\right)}\right)|{\psi }_n^{\left(1\right)}{|}^2=0,(78)$

where $1/h^2$ is a real coefficient. (Solution: See S100.)

6.12 The Discrete AL Equation [238]

$i\frac{d{\psi }_n}{dt}=\frac{{\psi }_{n+1}+{\psi }_{n-1}-2{\psi }_n}{h^2}+\sigma |{\psi }_n{|}^2\left({\psi }_{n+1}+{\psi }_{n-1}\right).(79)$

Here $\sigma =+1$ and $-1$ for focusing and defocusing nonlinearity, respectively. h is a real parameter. (Solution: See S101.)

6.13 The Coupled AL Equations Describing the Coupled Discrete Nonlinear Wave Systems [51]

$\begin{array}{l}{\psi }_{n,t}^{\left(1\right)}=-i\left(\sigma +|{\psi }_n^{\left(1\right)}{|}^2\right)\left({\psi }_n^{\left(2\right)\text{*}}+{\psi }_{n-1}^{\left(2\right)\text{*}}\right),\\ {\psi }_{n,t}^{\left(2\right)}=i\left(\sigma +|{\psi }_n^{\left(2\right)}{|}^2\right)\left({\psi }_{n+1}^{\left(1\right)\text{*}}+{\psi }_n^{\left(1\right)\text{*}}\right).\end{array}(80)$

Here $\sigma =+1$ and $-1$ denote the focusing and defocusing nonlinearity, respectively. (Solution: See S102.)

6.14 The System of Differential-Difference Equations on the Doubly Infinite Lattice [239, 240]

$\begin{array}{l}i\frac{d{\psi }_n^{\left(1\right)}}{dt}={\psi }_{n+1}^{\left(1\right)}-2{\psi }_n^{\left(1\right)}+{\psi }_{n-1}^{\left(1\right)}-{\psi }_n^{\left(1\right)}{\psi }_n^{\left(2\right)}\left({\psi }_{n+1}^{\left(1\right)}+{\psi }_{n-1}^{\left(1\right)}\right),\\ -i\frac{d{\psi }_n^{\left(2\right)}}{dt}={\psi }_{n+1}^{\left(2\right)}-2{\psi }_n^{\left(2\right)}+{\psi }_{n-1}^{\left(2\right)}-{\psi }_n^{\left(1\right)}{\psi }_n^{\left(2\right)}\left({\psi }_{n+1}^{\left(2\right)}+{\psi }_{n-1}^{\left(2\right)}\right)\end{array}(81)$

with ${\psi }_n^{\left(2\right)}=\sigma {\psi }_n^{\left(1\right)\text{*}}$. (Solutions: See S103 $\&$ S104.)

6.15 The Coupled AL Equation With Variable Coefficients Describing the Optical Field Through the Tight Binding Waveguide Array [241]

$\begin{array}{l}i\frac{d{\psi }_n^{\left(1\right)}}{dt}+[1+g_1\left(t\right)|{\psi }_n^{\left(1\right)}{|}^2+g_2\left(t\right)\left|{\psi }_n^{\left(2\right)}{|}^2\right][{\text{Λ}}_1\left(t\right){\psi }_{n+1}^{\left(1\right)}+{\text{Λ}}_1^{\text{*}}\left(t\right){\psi }_{n-1}^{\left(1\right)}]-2v_1\left(n,t\right){\psi }_n^{\left(1\right)}+i{\gamma }_1\left(t\right){\psi }_n^{\left(1\right)}=0,\\ i\frac{d{\psi }_n^{\left(2\right)}}{dt}+[1+g_1\left(t\right)|{\psi }_n^{\left(2\right)}{|}^2+g_2\left(t\right)\left|{\psi }_n^{\left(1\right)}{|}^2\right][{\text{Λ}}_2\left(t\right){\psi }_{n+1}^{\left(2\right)}+{\text{Λ}}_2^{\text{*}}\left(t\right){\psi }_{n-1}^{\left(2\right)}]-2v_2\left(n,t\right){\psi }_n^{\left(2\right)}+i{\gamma }_1\left(t\right){\psi }_n^{\left(2\right)}=0.\end{array}(82)$

Here the tunnel coupling coefficients between sites are given by ${\text{Λ}}_1\left(t\right)=a\left(t\right)+ib\left(t\right)$, ${\text{Λ}}_2\left(t\right)=c\left(t\right)+id\left(t\right)$ with $a\left(t\right)$, $b\left(t\right)$, $c\left(t\right)$, and $d\left(t\right)$ being differentiable functions. $g_1\left(t\right)$ and $g_2\left(t\right)$ denote the time-modulated interstice nonlinearity. The space-time-modulated inhomogeneous frequency shifts are denoted by $v_1\left(t\right)$ and $v_2\left(t\right)$. ${\gamma }_1\left(t\right)$ and ${\gamma }_2\left(t\right)$ represent the time-modulated effective gain and loss term. (Solution: See S105.)

7 Peregrine Solitons in Nonlocal NLSEs

The objective of this section is to present the existing Peregrine soliton solutions reported in the literature under the context of nonlocal NLSEs. In nonlinear systems, NLSEs play a ubiquitous role in understanding the diverse nonlinear phenomena, finding potential applications from fundamental to advanced technologies [109]. Out of such diverse manifestations of NLSEs, the NLSE with parity-time symmetry has shown an extensive recent research interest. This equation displays invariance under the joint transformations of time $t\to -t$, space $x\to -x$ (both time and space reversal symmetry), and complex conjugation. Its original prediction was by Bender et al. in a class of non-Hermitian PT invariant Hamiltonians in quantum mechanics [242]. PT-symmetric systems have gained great attention in diverse fields of research. Apart from the quantum mechanics, PT-symmetric systems have been investigated in many other physical systems, namely, nonlinear optics [243], plasmonics [244], BEC [245], electronics [246], and acoustics [247]. Such PT-symmetric systems allow the realization of a new class of gain/loss balanced dissipative as well as conservative systems which features unusual dynamics and control which cannot be realized in the conventional systems [248]. In the background of NLSEs, PT-symmetric systems involve two different models, namely, i) the nonlinear optical system where the optical potential is fixed PT-symmetric [243, 249–251] and ii) the coupled and multicomponent NLSE with a balance gain/loss [60, 252, 253].

Recently, Ablowitz et al. introduced an exactly integrable nonlocal PT-symmetric NLSE where the nonlinearity is nonlocal as well as PT-symmetric [254]. Furthermore, they constructed a discrete one-soliton solution via a left-right Riemann-Hilbert formulation in an exactly solvable PT-symmetric DNLSE which then discretized the above reported NLSE [255]. Since then, a numerous nonlocal integrable NLSEs have been reported such as the reverse time NLSE [93], the reverse space-time NLSE [93, 256], the nonlocal derivate NLSE [93, 257], PT-symmetric Davey-Stewartson equation [93, 258], and the reverse space-time complex modified KdV equation [93, 259, 260], to explore the exciting behaviors of nonlocal solutions in such systems. Recently, intense research investigations have been made in rogue waves to understand and control their appearance in nonlinear optics [155], BEC [156], hydrodynamics [157], biophysics [158], and so forth. In general, these rogue waves are mathematically expressed in a rational form which exhibits both spatial and temporal localization. Moreover, they possess interesting dynamical patterns and are found to be observed in a large number of local nonlinear integrable systems [17, 21, 173, 261, 262]. In the following, we list out the Peregrine soliton solution under the context of different nonlocal PT-symmetric NLSEs with space reversal, time reversal, and space-time reversal.

7.1 The Nonlocal NLSE With Parity-Time Symmetric Self-Induced Potential [263]

$i{\psi }_z+\frac{1}{2}{\psi }_{xx}+\psi \left(x,z\right){\psi }^{\text{*}}\left(-x,z\right)\psi \left(x,z\right)=0.(83)$

(Solutions: See S106 $\&$ S107.)

7.2 The Reverse Time Nonlocal NLSE [256]

$i{\psi }_t\left(x,t\right)={\psi }_{xx}\left(x,t\right)+2{\psi }^2\left(x,t\right)\psi \left(x,-t\right).(84)$

(Solution: See S108.)

7.3 A Nonlocal NLSE With the PT-Symmetric Potential [264]

$i{\psi }_t\left(x,t\right)={\psi }_{xx}\left(x,t\right)+2{\psi }^2\left(x,t\right){\psi }^{\text{*}}\left(-x,t\right).(85)$

(Solution: See S109.)

7.4 A Nonlocal NLSE [265]

$i{\psi }_t\left(x,t\right)={\psi }_{xx}\left(x,t\right)-2{\psi }^2\left(x,t\right){\psi }^{\text{*}}\left(-x,t\right).(86)$

(Solution: See S110.)

7.5 A Nonlocal NLSE With the Self-Induced PT-Symmetric Potential [266]

$i{\psi }_t\left(x,t\right)+{\psi }_{xx}\left(x,t\right)+\frac{1}{2}{\psi }^2\left(x,t\right){\psi }^{\text{*}}\left(-x,t\right)=0.(87)$

(Solution: See S111.)

7.6 A Reverse Time Nonlocal NLSE [267]

$i{\psi }_t\left(x,t\right)={\psi }_{xx}\left(x,t\right)+2\sigma {\psi }^2\left(x,t\right)\psi \left(x,-t\right).(88)$

Here, the constant σ takes the values $+1$ and $-1$ for focusing and defocusing nonlinearity, respectively. (Solution: See S112.)

7.7 A Nonlocal NLSE [268]

$i{\psi }_t\left(x,t\right)={\psi }_{xx}\left(x,t\right)+2\sigma {\psi }^2\left(x,t\right){\psi }^{\text{*}}\left(-x,t\right).(89)$

Here, σ takes the value $+1$ or $-1$ for focusing or defocusing nonlinearity, respectively. (Solution: See S113.)

7.8 A Nonlocal Derivative NLSE [269]

$i{\psi }_t\left(x,t\right)+{\psi }_{xx}\left(x,t\right)+\sigma {\left[{\psi }^2\left(x,t\right){\psi }^{\text{*}}\left(-x,t\right)\right]}_x=0,(90)$

where σ takes the value $+1$ or $-1$ for focusing or defocusing nonlinearity, respectively. (Solution: See S114.)

7.9 A Nonlocal Third-Order NLSE [270]

$i{\psi }_t+ic{\psi }_x+{\psi }_{xx}+\sigma \psi {\left[\psi \left(-x,t\right)\right]}^{\text{*}}\psi +i\lambda {\psi }_{xxx}+3i\lambda \sigma \psi {\left[\psi \left(-x,t\right)\right]}^{\text{*}}{\psi }_x=0,(91)$

where λ, σ, and c are real constants. (Solution: See S115.)

7.10 An Integrable Three-Parameter Nonlocal Fifth-Order NLSE [271]

$i{\psi }_t+S\left(\psi ,r\right)+\alpha H\left(\psi ,r\right)+\gamma P\left(\psi ,r\right)+\delta Q\left(\psi ,r\right)=0,(92)$

where $\psi \equiv \psi \left(x,t\right),r\equiv r\left(x,t\right)$ are complex fields; α, γ, and δ are all real parameters.

Here, a) $S\left(\psi ,r\right)$ denotes the nonlocal NLS part

$S\left(\psi ,r\right)=\frac{1}{2}{\psi }_{xx}+{\psi }^{2}r,(93)$

b) $H\left(\psi ,r\right)$ represents the nonlocal Hirota part

$H\left(\psi ,r\right)={\psi }_{xxx}+6\psi {\psi }_{x}r,(94)$

c) $P\left(\psi ,r\right)$ denotes the nonlocal Lakshmanan-Porsezian-Daniel (LPD) part

$P\left(\psi ,r\right)={\psi }_{xxxx}+8\psi r{\psi }_{xx}+6{\psi }^3{r}^2+4\psi {\psi }_x{r}_x+6{\psi }_x^{2}r+2{\psi }^2{r}_{xx},(95)$

and d) $Q\left(\psi ,r\right)$ is the nonlocal quintic part

$Q\left(\psi ,r\right)={\psi }_{xxxxx}+10\psi r{\psi }_{xxx}+10{\left(\psi {\psi }_x{r}_x\right)}_x+20r{\psi }_x{\psi }_{xx}+30{\psi }^2{r}^2{\psi }_x,(96)$

where $r\left(x,t\right)=\sigma {\psi }^{\text{*}}\left(-x,t\right)$ and $\sigma =\pm 1$. (Solutions: See S116, S117, S118 $\&$ S119.)

7.11 The Nonlocal Variant of the NLSE in a Dimensionless Form [272]

$i\frac{\partial \psi }{\partial t}+\frac{1}{2}\frac{{\partial }^2\psi }{\partial x^2}+\theta \psi -\mu \psi =0,$

$\nu \frac{{\partial }^2\theta }{\partial x^2}-2q\theta =-2|\psi {|}^2,(97)$

where θ represents the optically induced deviation of the director angle, ν is the nonlocality parameter, μ is the propagation constant, and q is the parameter that represents the square of the applied static electric field that pretilts the nematic dielectric. Using Fourier transform θ can be rewritten as

$\theta =F^{-1}\left[\frac{F\left[2\right|\psi {|}^2]}{\nu k^2+2}\right].$

Here k is the wave number relevant to the Fourier variable. (Solution: See S120.)

7.12 The Generalized PT-Symmetric Nonlocal Coupled NLSE With Nonlocal SPM, XPM, and FWM of the Following Form [273]

$\begin{array}{l}i\frac{\partial {\psi }_1\left(x,t\right)}{\partial t}+\frac{{\partial }^2{\psi }_1\left(x,t\right)}{\partial x^2}+[a{\psi }_1\left(x,t\right){\psi }_1^{\text{*}}\left(-x,t\right)+b{\psi }_1\left(x,t\right){\psi }_2^{\text{*}}\left(-x,t\right)\\ +c{\psi }_2\left(x,t\right){\psi }_2^{\text{*}}\left(-x,t\right)+d{\psi }_1^{\text{*}}\left(-x,t\right){\psi }_2\left(x,t\right)]{\psi }_1\left(x,t\right)=0,\\ i\frac{\partial {\psi }_2\left(x,t\right)}{\partial t}+\frac{{\partial }^2{\psi }_2\left(x,t\right)}{\partial x^2}+[a{\psi }_1\left(x,t\right){\psi }_1^{\text{*}}\left(-x,t\right)+b{\psi }_1\left(x,t\right){\psi }_2^{\text{*}}\left(-x,t\right)\\ +c{\psi }_2\left(x,t\right){\psi }_2^{\text{*}}\left(-x,t\right)+d{\psi }_1^{\text{*}}\left(-x,t\right){\psi }_2\left(x,t\right)]{\psi }_2\left(x,t\right)=0,\end{array}(98)$

where a and c correspond to the nonlocal SPM and XPM, respectively, while $b,d$ represent the nonlocal FWM terms. (Solution: See S121.)

8 Peregrine Solitons in Higher Dimensional and Mixed NLSEs

This section aims at presenting the Peregrine soliton solutions of higher dimensional and mixed NLSEs reported in the existing literature. The one-dimensional (1D) cubic NLSE or (1 + 1)-dimensional ((1 + 1)-D) cubic NLSE appears in diverse fields of physics, namely, nonlinear optics, plasma physics, BEC, condensed matter physics, and superfluids [109]. A successful first, completely integrable property of such (1 + 1)-D NLSE has been reported by Ablowitz et al., through the inverse scattering transform technique [87]. Higher dimensional NLSEs of such a basic (1 + 1)-D NLSE can be obtained by replacing the second spatial derivative through the Laplacian. Moreover, higher dimensional NLSEs are not integrable, but localized solutions are found to exist in two transverse directions [274, 275]. However, the obtained solutions are not robust against perturbations and found to be unstable after a finite distance. Also, the (3 + 1)-D NLSEs are not integrable, but localized solutions for these equations have been reported through the numerical simulations [6] and via the similarity transformations [275–277]. In particular, this section is related to the Peregrine soliton solution. The Peregrine solitons found profound interest in diverse areas of physics, namely, optical systems [278], BEC [73], hydrodynamics [12], and superfluids [25]. Originally, such Peregrine soliton solutions have been reported in the two-dimensional graded-index waveguides using the similarity transformation [279], followed by their appearance in a two-dimensional graded-index grating waveguide [280] and two-dimensional coupled NLSEs with distributed coefficients [281]. The Peregrine soliton solutions in a (3 + 1)-D inhomogeneous NLSE with variable coefficients [282] and a (3 + 1)-D higher-order coupled NLSE [283] have also been reported. These Peregrine solitons play an inevitable role in describing the dynamics of ocean waves, nonlinear optics, and BEC. Hence, this section considers reporting the Peregrine soliton solutions of various higher dimensional NLSEs and mixed NLSEs. Here, the mixed NLSEs refer to the higher dimensional NLSEs with other physical effects, namely, inhomogeneity, external potential, variable coefficient, and nonlocality. Such higher dimensional and mixed NLSEs in which Peregrine soliton solutions are reported will be listed in this section.

8.1 The Three-Dimensional Inhomogeneous NLSE With Variable Coefficients in a Dimensionless Form [282]

$i{\psi }_t=-\frac{1}{2}{\nabla }^2\psi +v\left(r,t\right)\psi +g\left(t\right)|\psi {|}^2\psi +i\gamma \left(t\right)\psi .(99)$

8.2 A Special Case of Eq. 99 [284]

$i{\psi }_t=-\frac{\beta \left(t\right)}{2}{\nabla }^2\psi +v\left(r,t\right)\psi +g\left(t\right)|\psi {|}^2\psi +i\gamma \left(t\right)\psi =0,(100)$

where $\psi =\psi \left(\mathbf{r},t\right)$, $\mathbf{r}\in {\mathrm{ℝ}}^3$, $\mathbf{r}=\left(x,y,z\right)$, $\nabla \equiv \left({\partial }_x,{\partial }_y,{\partial }_z\right)$ with ${\partial }_x=\partial /{\partial }_x$. $v\left(\mathbf{r},t\right)$ is an external potential with a real valued function of time and spatial coordinates. $\beta \left(t\right)$, $g\left(t\right)$, and $\gamma \left(t\right)$ denote the coefficients of linearity, nonlinearity, and gain/loss, respectively. (Solutions: See S122, S123 $\&$ S124.)

8.3 A (2 + 1)-Dimensional NLSE With an External Potential [285]

$i{\psi }_t+{\psi }_{xx}+{\psi }_{yy}-g\left(x,y,t\right)|\psi {|}^2\psi -V\left(x,y,t\right)\psi =0,(101)$

where $g\left(x,y,t\right)$ is the coefficient of nonlinearity and $V\left(x,y,t\right)$ is an external potential. (Solutions: See S125 $\&$ S126.)

8.4 The 3D Variable Coefficient NLSE of the Form With Linear and Parabolic Potentials [286]

$i{\psi }_t+\frac{\beta \left(t\right)}{2}\text{Δ}\psi +\chi \left(t\right)|\psi {|}^2\psi +V\left(t,x,y,z\right)\psi =i\gamma \left(t\right)\psi ,(102)$

where $\psi =\psi \left(t,x,y,z\right)$ is the order parameter in BECs or the complex envelope of the electric field in optical communication system. Here $\text{Δ}={\partial }_x^2+{\partial }_y^2+{\partial }_z^2$ is the 3-dimensional Laplacian operator. The functions $\beta \left(t\right)$, $\chi \left(t\right)$, and $\gamma \left(t\right)$ are the coefficients of the diffraction, nonlinearity, and gain/loss. Here, the potential $V=V_1\left(t\right)\left(x+y+z\right)+V_2\left(t\right)Y^2$, where $V_1\left(t\right)$ and $V_2\left(t\right)$ are linear and parabolic potential strengths and $Y^2=x^2+y^2+z^2$. (Solution: See S127.)

8.5 A (2 + 1)-Dimensional NLSE With Variable Coefficients [287]

$i{\psi }_t+{\psi }_{xy}+\alpha \left(x,y,t\right)\psi +\beta \left(t\right)\psi {\partial }_x^{-1}{\partial }_y|\psi {|}^2+i\gamma \left(t\right)\psi =0,(103)$

where $\psi =\psi \left(x,y,t\right)$, with the propagation variables x, y and transverse variable t. $\alpha \left(x,y,t\right)$ is an external potential which is the real valued function of space and time. $\beta \left(t\right)$ and $\gamma \left(t\right)$ are the coefficients of nonlinearity and gain/loss. The inverse d-bar operator, ${\partial }_x^{-1}={\partial }_z^{-1}+{\partial }_{\overline{z}}^{-1}$, $z=x+iy$, ${\partial }_z=\frac{1}{2}\left({\partial }_x-i{\partial }_y\right)$, ${\partial }_{\overline{z}}=\frac{1}{2}\left({\partial }_x+i{\partial }_y\right)$, and $\left({\partial }_{\overline{z}}f\right)=\frac{1}{\pi }\underset{{\mathrm{ℝ}}^2}{{\displaystyle \int }}\frac{f\left(x\prime ,y\prime \right)dx\prime dy\prime }{z-z\prime }$. (Solution: See S128.)

8.6 A Two-Dimensional Nonlocal NLSE [288]

$i{\psi }_t=-{\psi }_{xx}-\sigma \psi {{{\displaystyle \int }}^{\text{}}}_{-\infty }^{+\infty }|\psi {|}^{2}dy=0,(104)$

where $\psi \equiv \psi \left(x,y,t\right)$ is a two-dimensional field envelope and $\sigma \left(>0\right)$ is the nonlinearity coefficient. (Solution: See S129.)

8.7 A (2 + 1)-Dimensional Variable Coefficient NLSE With Partial Nonlocality [289]

$i{\psi }_t+\beta \left(t\right){\psi }_{xx}+\chi \left(t\right)\psi {{{\displaystyle \int }}^{\text{}}}_{-\infty }^{+\infty }|\psi {|}^{2}dy=0,(105)$

where $\psi =\psi \left(t,x,y\right)$. $\beta \left(t\right)$ and $\chi \left(t\right)$ are the coefficients of diffraction and nonlinearity, respectively. (Solution: See S130.)

8.8 A (2 + 1)-Dimensional Variable Coefficient Partially Nonlocal NLSE [290]

$i\frac{\partial \psi }{\partial z}+\beta \left(z\right)\frac{{\partial }^2\psi }{\partial x^2}+\chi \left(z\right)\psi {{{\displaystyle \int }}^{\text{}}}_{-\infty }^{+\infty }|\psi {|}^{2}dy+\gamma \left(z\right)x^2\psi =0,(106)$

where $\psi =\psi \left(z,x,y\right)$ describing the optical field or wave function of condensate. $\beta \left(z\right)$ and $\gamma \left(z\right)$ are the coefficients of diffraction and tapering effect/harmonic trapping potential, respectively. The nonlinearity is localized in x-direction and nonlocalized in y-direction with the coefficient function $\chi \left(z\right)$. (Solution: See S131.)

8.9 A (2 + 1)-Dimensional (2D) Nonlocal NLSE Satisfying the Two-Dimensional Parity-Time-Symmetric Potential $V\left(x,y\right)=V^{\text{*}}\left(-x,-y\right)$ [291, 292]

$i{\psi }_t+{\psi }_{xy}+\psi r=0,r_y={\left[\psi \left(x,y,t\right)\psi {\left(-x,-y,t\right)}^{\text{*}}\right]}_x,(107)$

where $\psi =\psi \left(x,y,t\right)$ and $V\left(x,y,t\right)=\psi \left(x,y,t\right){\psi }^{\text{*}}\left(x,y,t\right)$. (Solutions: See S132 $\&$ S133.)

8.10 A Two-Dimensional Nonlocal NLSE [293]

$i{\psi }_t+{\psi }_{xx}+{\psi }_{yy}-2{\psi }_{xy}+2\psi V=0,V=\psi \left(x,y,t\right){\psi }^{\text{*}}\left(-x,-y,t\right),(108)$

where $\psi =\psi \left(x,y,t\right)$. (Solution: See S134.)

8.11 The Integrable “Reverse Space” 2D Nonlocal NLSE [294]

$\left(i{\partial }_t+{\partial }_{xy}^2\right)\psi \left(x,y,t\right)-\frac{\lambda }{2}\psi \left(x,y,t\right)\left({\partial }_z^{-1}+{\partial }_{\overline{z}}^{-1}\right){\partial }_y\left[\psi \left(x,y,t\right){\psi }^{\text{*}}\left(-x,-y,t\right)\right]=0,\lambda =\pm 1.(109)$

8.12 A Reverse Space-Time Nonlocal NLSE [294]

$\left(i{\partial }_t+{\partial }_{xy}^2\right)\psi \left(x,y,t\right)-\frac{\lambda }{2}\psi \left(x,y,t\right)\left({\partial }_z^{-1}+{\partial }_{\overline{z}}^{-1}\right){\partial }_y\left[\psi \left(x,y,t\right){\psi }^{\text{*}}\left(-x,y,-t\right)\right]=0,\lambda =\pm 1.(110)$

Here $z\equiv x+iy$ and ${\partial }_{z,\overline{z}}^{-1}$ are operators inverse to ${\partial }_z\equiv \left(1/2\right)\left({\partial }_x-i{\partial }_y\right)$ and ${\partial }_{\overline{z}}\equiv \left(1/2\right)\left({\partial }_x+i{\partial }_y\right)$. (Solutions: See S135 $\&$ S136.)

8.13 A Two-Dimensional Two-Coupled Variable Coefficient NLSE [281]

$\begin{array}{l}i{\psi }_{1z}+\frac{\beta \left(z\right)}{2}\left({\psi }_{1xx}+{\psi }_{1yy}\right)+R\left(z\right){\displaystyle \sum }_{k=1}^2|{\psi }_k{|}^2{\psi }_1=i\gamma \left(z\right){\psi }_1,\\ i{\psi }_{2z}+\frac{\beta \left(z\right)}{2}\left({\psi }_{2xx}+{\psi }_{2yy}\right)+R\left(z\right){\displaystyle \sum }_{k=1}^2|{\psi }_k{|}^2{\psi }_2=i\gamma \left(z\right){\psi }_2,\end{array}(111)$

where ${\psi }_j={\psi }_j\left(x,y,z\right)$, $j=\mathrm{1,2}$. The real analytic spatial functions, $\beta \left(z\right)$, $R\left(z\right)$, and $\gamma \left(z\right)$ represent the diffraction, nonlinearity, and gain/loss parameter, respectively. (Solution: See S137.)

8.14 The Variable Coefficient NLSE Describing the Inhomogeneous Nonlinear Waveguide [295]

$\begin{array}{l}i{\psi }_{1z}+\frac{\beta }{2}\left({\psi }_{1xx}+{\psi }_{1yy}\right)+\chi \left(z\right)\left(r_{11}|{\psi }_1{|}^2+r_{12}|{\psi }_2{|}^2\right){\psi }_1+\frac{1}{2}f\left(z\right)\left(x^2+y^2\right){\psi }_1=ig\left(z\right){\psi }_1,\\ i{\psi }_{2z}+\frac{\beta }{2}\left({\psi }_{2xx}+{\psi }_{2yy}\right)+\chi \left(z\right)\left(r_{21}|{\psi }_1{|}^2+r_{22}|{\psi }_2{|}^2\right){\psi }_2+\frac{1}{2}f\left(z\right)\left(x^2+y^2\right){\psi }_2=ig\left(z\right){\psi }_2,\end{array}(112)$

where ${\psi }_1\left(x,y,z\right)$ and ${\psi }_2\left(x,y,z\right)$ are the two normalized orthogonal components of electric fields. β, $\chi \left(z\right)$, g(z), and f(z) denote the dispersion, nonlinearity, gain, and geometry of tapered waveguide coefficients, respectively. $r_{11}$ and $r_{22}$ are the self-phase modulation coefficients for ${\psi }_1\left(x,y,z\right)$, ${\psi }_2\left(x,y,z\right)$ and $r_{12}$ and $r_{21}$ are the cross-phase modulation coefficients. (Solution: See S138.)

8.15 The Variable Coefficient CNLSE [296]

$\begin{array}{l}i{\psi }_{1z}+\frac{1}{2}[{\beta }_1\left(z\right){\psi }_{1xx}+{\beta }_2\left(z\right){\psi }_{1yy}+{\beta }_3\left(z\right){\psi }_{1tt}]+\chi \left(z\right)\left({\sigma }_{11}|{\psi }_1{|}^2+{\sigma }_{12}|{\psi }_2{|}^2\right){\psi }_1=i\gamma \left(z\right){\psi }_1,\\ i{\psi }_{2z}+\frac{1}{2}[{\beta }_1\left(z\right){\psi }_{2xx}+{\beta }_2\left(z\right){\psi }_{2yy}+{\beta }_3\left(z\right){\psi }_{2tt}]+\chi \left(z\right)\left({\sigma }_{21}|{\psi }_1{|}^2+{\sigma }_{22}|{\psi }_2{|}^2\right){\psi }_2=i\gamma \left(z\right){\psi }_2,\end{array}(113)$

where ${\psi }_1\left(z,x,y,t\right)$ and ${\psi }_2\left(z,x,y,t\right)$ are the two normalized complex mode fields. ${\beta }_1\left(z\right)$ and ${\beta }_2\left(z\right)$ are the coefficients of diffractions along the x and y transverse coordinates. ${\beta }_3\left(z\right)$ is the coefficient of dispersion. $\chi \left(z\right)$ is the SPM, accounting for the self-focusing ($\chi >0$) or the self-defocusing ($\chi <0$) nonlinearity. The parameters ${\sigma }_{11}$, ${\sigma }_{12}$, ${\sigma }_{21}$, and ${\sigma }_{22}$ determine the ratio of the coupling strengths of the cross-phase modulation to the SPM. For linearly polarized eigenmodes, ${\sigma }_{11}={\sigma }_{22}=1$, ${\sigma }_{12}={\sigma }_{21}=2/3$, in case of circularly polarized eigen modes, ${\sigma }_{11}={\sigma }_{22}=1$, ${\sigma }_{12}={\sigma }_{21}=2$ and for the elliptically polarized eigen modes, ${\sigma }_{11}={\sigma }_{22}=1$, $2<{\sigma }_{12}={\sigma }_{21}<2/3$. The parameter $\gamma \left(z\right)$ represents the loss when $\gamma \left(z\right)<0$ or gain when $\gamma \left(z\right)>0$. (Solution: See S139.)

9 Peregrine Solitons in Saturable NLSES

This section presents the Peregrine soliton solutions reported in the literature under the family of the saturable NLSEs. In nonlinear dynamics, the ultrashort optical pulse propagation through the dielectric waveguides like optical fibers is governed by the NLSEs. The key parameter that plays a decisive role in the nonlinear effects of such optical fibers is an intensity dependent variation of the refractive index, also known as the optical Kerr effect. The Kerr index induced refractive index results in the self-phase modulation which ultimately broadens the optical spectrum. Moreover, it is well known that the Kerr nonlinearity determines the nonlinear response of the optical medium up to a certain level of input power, but when input power level exceeds a certain value, the role of higher-order nonlinear susceptibility is inevitable. This eventually results in the saturation of the nonlinear response of the system. In general, all nonlinearities saturation is owing to the upper limit for change in the refractive index of the material medium and thereafter system does not display any change in the nonlinear index even at very high input power levels [109]. Also, it is demonstrated that the saturation in cubic nonlinearity is equivalent to the occurrence of the third-, fifth-, and seventh-order nonlinear susceptibility [297]. Such nonlinear index saturation has been originally observed in dual core nonlinear directional couplers by Stegeman et al. [298], followed by plethora of studies to understand the detrimental effects of nonlinear saturation in the coupling behaviors of directions couplers [299–302]. The propagation of solitons through the materials with nonlinear saturation has also been expressed through numerical and analytical methods. The dynamics of such system provide the evidence of the existence of bistable solitons of the same duration with different peak powers [303]. Moreover, the dynamics of ultrashort pulse propagation through the fibers with saturable nonlinearity in the normal dispersion regime has also been analyzed to determine the minimum duration of the output pulse of fiber-grating compressor [304]. In addition, the nonlinear saturation effects play a significant role in the MI gain spectrum of the ultrashort pulse propagation through the semiconductor doped fibers [305–307]. This section lists out the saturable NLSEs in which Peregrine soliton solutions were reported.

9.1 A NLSE Describes Quasi-1D Bose-Einstein Condensates [308]

$i{\psi }_t=-\frac{1}{2}{\psi }_{xx}+V\left(x\right)\psi +\frac{1-\left(3/2\right)|\psi {|}^2}{\sqrt{1-|\psi {|}^2}}\psi ,(114)$

where $V\left(x\right)=\frac{1}{2}{\text{Ω}}^2{x}^2$ is an external potential of harmonic form. $\text{Ω}$ is the normalized trap strength. (Solution: See S140.)

10 Summary and Outlook

The historical review of the discovery of the Peregrine soliton goes side by side with the mathematical steps of its derivation. We have adopted here the most common method of derivation, namely, the use of Lax pair and Darboux transformation. Employing the continuous wave as a seed solution, we have analytically derived the general breather solution of the NLSE through the Darboux transformation and Lax pair technique. We have shown that this class of solution turns out, under certain limits, into its five members, the Akhmediev breather, the Kuznetsov-Ma breather, the Peregrine soliton, the single bright soliton, and the continuous wave solution. When the temporal period of the Kuznetsov-Ma breather approaches infinity, it falls into the Peregrine soliton. A similar result is obtained when the spacial period of the Akhmediev breather tends to infinity. We have then collected all Peregrine soliton solutions of the NLSE and its various variations that are found in the literature. Particularly, we have recorded the Peregrine soliton solutions in higher-order and inhomogeneous NLSEs, in NLSE with external potentials, in coupled NLSEs, in discrete NLSEs, in nonlocal NLSEs, in higher dimensional and mixed NLSEs, and finally in saturable NLSEs. The Peregrine waves in saturable nonlinear systems are not sufficiently explored. Concerning studies in such systems will yield more information about modulation instability and new frequency generations, that will play a crucial role in nonlinear optical fields.

While studying the various nonlinear dynamics modeled by the NLSEs is a developing and attractive area of research, this work will be a useful guideline to keep track of new NLS frameworks that admit Peregrine soliton solutions, youthful stability investigations, up-to-date formation mechanisms, and fresh experimental observations. One future extension of this work is a deep exploration of the existence of Peregrine solitons in higher coupled NLSEs and higher dimensional systems. The accompanying features of these systems could support the robustness of the Peregrine soliton against different perturbations and initial conditions and thus generate more stable rogue wave structures. Additionally, it may be interesting to investigate numerically complex nonintegrable systems in order to achieve more stable rogue waves. Constructing such models experimentally allows for the monitorization of randomly many possible nonlinear dynamics. This opens the door to a better understanding of the preactions accomplished by extreme events such as rogue waves.

As the multisoliton interaction is one of the formation mechanisms of the rogue waves and it is recently reported in the bioenergy transport mechanism in the helical protein [32], this evidence may also be extended to different biomechanisms. Moreover, one of the not fully explored aspects, yet very important, is the knowledge of how a variety of initial conditions are influencing the rogue wave formation. In nonlinear optics, the knowledge of initial conditions plays an essential role in generating, on purpose, rogue waves in order to produce high energy light pulses. Last but not least, with regard to the dispersion and nonlinearity management, it may be interesting to consider interactions of multi-Peregrine solitons modeling by higher dimensional NLSEs. Recently, photonic rogue waves are analytically reported in lattice systems [78]. This will be useful in understanding wave interactions in diverse crystal structures.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge the support of UAE University through grants UAEU-UPAR(1) 2019 and UAEU-UPAR(11) 2019.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.596886/full#supplementary-material

References

1. Russell JS, Taylor J. Report on waves: made to the meetings of the british association. Cambridge, MA: Harvard University (1845). p. 88.

Google Scholar

2. Airy GB. Tides and waves. Munich, Germany: B. Fellows (1845). p. 396.

Google Scholar

3. Stokes G. On the theory of oscillatory waves. Cambridge, UK: Pitt Press (1847). p. 15.

Google Scholar

4. Korteweg DJ, de Vries G. Xli. on the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. London, Edinburgh, Dublin Philos Mag J Sci (1895). 39:422–43. doi:10.1080/14786449508620739.

CrossRef Full Text | Google Scholar

5. Zabusky NJ, Kruskal MD. Interaction of “solitons” in a collisionless plasma and the recurrence of initial states. Phys Rev Lett (1965). 15:240–3. doi:10.1103/PhysRevLett.15.240.

CrossRef Full Text | Google Scholar

6. Gardner CS, Greene JM, Kruskal MD, Miura RM. Method for solving the korteweg-devries equation. Phys Rev Lett (1967). 19:1095–7. doi:10.1103/PhysRevLett.19.1095.

PubMed abstract | CrossRef Full Text | Google Scholar

7. Zakharov VE, Shabat AB. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of wave in nonlinear media. Sov Phys JETP (1972). 34:62–7.

Google Scholar

8. Al Khawaja U, Al Sakkaf L. Handbook of exact solutions to the nonlinear Schrödinger equations. Bristol, UK: Institute of Physics Publishing (2019). 375 p.

Google Scholar

9. Kuznetsov EA. Solitons in a parametrically unstable plasma. Akad Nauk SSSR Doklady (1977). 236:575–7.

Google Scholar

10. Ma YC. The perturbed plane-wave solutions of the cubic schrödinger equation. Stud Appl Math (1979). 60:43–58. doi:10.1002/sapm197960143.

CrossRef Full Text | Google Scholar

11. Peregrine DH. Water waves, nonlinear schrödinger equations and their solutions. J Aust Math Soc (1983). 25:16–43. doi:10.1017/S0334270000003891.

CrossRef Full Text | Google Scholar

12. Kharif C, Pelinovsky E, Slunyaev A. Rogue Waves in the ocean. Berlin, Heidelberg: Springer-Verlag (2009). 216 p.

Google Scholar

13. Shrira VI, Geogjaev VV. What makes the peregrine soliton so special as a prototype of freak waves? J Eng Math (2010). 67:11–22. doi:10.1007/s10665-009-9347-2.CrossRef Full Text

Google Scholar

14. Osborne A. Nonlinear ocean wave and the inverse scattering transform. In: R Pike, and P Sabatier, editors Scattering. Cambridge, MA: Academic Press (2002). p. 637–66.

Google Scholar

15. Broad WJ. Rogue giants at sea. The New York Times (2006). 11.

Google Scholar

16. Calini A, Schober CM. Rogue waves in higher order nonlinear schrödinger models. In: Pelinovsky, E, and Kharif, C, editors. Extreme Ocean Waves. Dordrecht, Netherlands: Springer (2008). p. 31–51.

Google Scholar

17. Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Phys Lett A (2009). 373:675–8. doi:10.1016/j.physleta.2008.12.036.CrossRef Full Text

Google Scholar

18. Akhmediev N, Soto-Crespo JM, Ankiewicz A. Extreme waves that appear from nowhere: on the nature of rogue waves. Phys Lett A (2009). 373:2137–45. doi:10.1016/j.physleta.2009.04.023.CrossRef Full Text

Google Scholar

19. Akhmediev N, Eleonskii VM, Kulagin NE. Generation of periodic trains of picosecond pulses in an optical fiber: exact solutions. Sov Phys JETP (1985). 62:894–9.

Google Scholar

20. Kedziora DJ, Ankiewicz A, Akhmediev N. Second-order nonlinear schrödinger equation breather solutions in the degenerate and rogue wave limits. Phys Rev E (2012). 85:066601. doi:10.1103/PhysRevE.85.066601.

PubMed abstract | CrossRef Full Text | Google Scholar

21. Akhmediev N, Ankiewicz A, Soto-Crespo JM. Rogue waves and rational solutions of the nonlinear schrödinger equation. Phys Rev E (2009). 80:026601. doi:10.1103/PhysRevE.80.026601.

PubMed abstract | CrossRef Full Text | Google Scholar

22. Chowdury A, Kedziora DJ, Ankiewicz A, Akhmediev N. Breather solutions of the integrable quintic nonlinear schrödinger equation and their interactions. Phys Rev E (2015). 91:022919. doi:10.1103/PhysRevE.91.022919.

PubMed abstract | CrossRef Full Text | Google Scholar

23. Solli DR, Ropers C, Koonath P, Jalali B. Optical rogue waves. Nature (2007). 450:1054–7. doi:10.1038/nature06402.

CrossRef Full Text | Google Scholar

24. Hammani K, Finot C, Dudley JM, Millot G. Optical rogue-wave-like extreme value fluctuations in fiber raman amplifiers. Optic Express (2008). 16:16467–74. doi:10.1364/OE.16.016467.

PubMed abstract | CrossRef Full Text | Google Scholar

25. Ganshin AN, Efimov VB, Kolmakov GV, Mezhov-Deglin LP, McClintock PVE. Observation of an inverse energy cascade in developed acoustic turbulence in superfluid helium. Phys Rev Lett (2008). 101:065303. doi:10.1103/PhysRevLett.101.065303.

CrossRef Full Text | Google Scholar

26. Shats M, Punzmann H, Xia H. Capillary rogue waves. Phys Rev Lett (2010). 104:104503. doi:10.1103/PhysRevLett.104.104503.

CrossRef Full Text | Google Scholar

27. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The peregrine soliton in nonlinear fibre optics. Nat Phys (2010). 6:790–5. doi:10.1038/nphys1740.

CrossRef Full Text | Google Scholar

28. Chabchoub A, Hoffmann NP, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett (2011). 106:204502. doi:10.1103/PhysRevLett.106.204502.

CrossRef Full Text | Google Scholar

29. Akhmediev N, Soto-Crespo J, Ankiewicz A. How to excite a rogue wave. Phys Rev A (2009). 80:043818. doi:10.1103/PhysRevA.80.043818.

CrossRef Full Text | Google Scholar

30. Frisquet B, Kibler B, Millot G. Collision of akhmediev breathers in nonlinear fiber optics. Phys Rev X (2013). 3:041032. doi:10.1103/PhysRevX.3.041032.

CrossRef Full Text | Google Scholar

31. Chowdury A, Kedziora D, Ankiewicz A, Akhmediev N. Breather-to-soliton conversions described by the quintic equation of the nonlinear schrödinger hierarchy. Phys Rev E (2015). 91:032928. doi:10.1103/PhysRevE.91.032928.

CrossRef Full Text | Google Scholar

32. Liu J, Jin DQ, Zhang XL, Wang YY, Dai CQ. Excitation and interaction between solitons of the three-spine α-helical proteins under non-uniform conditions. Optik (2018). 158:97–104. doi:10.1016/j.ijleo.2017.11.200.

CrossRef Full Text | Google Scholar

33. Akhmediev N, Soto-Crespo J, Ankiewicz A. Could rogue waves be used as efficient weapons against enemy ships?. Eur Phys J Spec Top (2010). 185:259–66. doi:10.1140/epjst/e2010-01253-8.

CrossRef Full Text | Google Scholar

34. Taki M, Mussot A, Kudlinski A, Louvergneaux E, Kolobov M, Douay M. Third-order dispersion for generating optical rogue solitons. Phys Lett A (2010). 374:691–5. doi:10.1016/j.physleta.2009.11.058.

CrossRef Full Text | Google Scholar

35. Genty G, de Sterke CM, Bang O, Dias F, Akhmediev N, Dudley JM. Collisions and turbulence in optical rogue wave formation. Phys Lett A (2010). 374:989–96. doi:10.1016/j.physleta.2009.12.014.

CrossRef Full Text | Google Scholar

36. Demircan A, Amiranashvili S, Brée C, Mahnke C, Mitschke F, Steinmeyer G. Rogue wave formation by accelerated solitons at an optical event horizon. Appl Phys B (2014). 115:343–54. doi:10.1007/s00340-013-5609-9.

CrossRef Full Text | Google Scholar

37. Ablowitz MJ, Horikis TP. Interacting nonlinear wave envelopes and rogue wave formation in deep water. Phys Fluids (2015). 27:012107. doi:10.1063/1.4906770.

CrossRef Full Text | Google Scholar

38. Wang XB, Han B. Characteristics of rogue waves on a soliton background in the general coupled nonlinear schrödinger equation. Commun Theor Phys (2019). 71:152. doi:10.1088/0253-6102/71/2/152.

CrossRef Full Text | Google Scholar

39. Zhong WP, Belić M, Zhang Y. Second-order rogue wave breathers in the nonlinear schrödinger equation with quadratic potential modulated by a spatially-varying diffraction coefficient. Optic Exp (2015). 23:3708–16. doi:10.1364/OE.23.003708.

CrossRef Full Text | Google Scholar

40. Wang Q, Li X. Collision properties of rogue waves in optical fiber. Optic Commun (2019). 435:255–64. doi:10.1016/j.optcom.2018.11.037.

CrossRef Full Text | Google Scholar

41. Zhen-Kun W, Yun-Zhe Z, Yi H, Feng W, Yi-Qi Z, Yan-Peng Z. The interaction of peregrine solitons. Chin Phys Lett (2014). 31:090502. doi:10.1088/0256-307X/31/9/090502.

CrossRef Full Text | Google Scholar

42. Ankiewicz A, Kedziora DJ, Akhmediev N. Rogue wave triplets. Phys Lett A (2011). 375:2782–5. doi:10.1016/j.physleta.2011.05.047.

CrossRef Full Text | Google Scholar

43. Al Khawaja U, Bahlouli H, Asad-uz-zaman M, Al-Marzoug S. Modulational instability analysis of the peregrine soliton. Commun Nonlinear Sci Num Simul (2014). 19:2706–14. doi:10.1016/j.cnsns.2014.01.002.

CrossRef Full Text | Google Scholar

44. Schober C, Strawn M. Stability analysis of the peregrine solution via squared eigenfunctions. AIP Conf Proc (2017). 1895:040004. doi:10.1063/1.5007371.

CrossRef Full Text | Google Scholar

45. Calini A, Schober C. Observable and reproducible rogue waves. J Optic (2013). 15:105201. doi:10.1088/2040-8978/15/10/105201.

CrossRef Full Text | Google Scholar

46. Islas A, Schober CM. Numerical investigation of the stability of the rational solutions of the nonlinear schrödinger equation. Appl Math Comput (2017). 305:17–26. doi:10.1016/j.amc.2017.01.060.

CrossRef Full Text | Google Scholar

47. Calini A, Schober C. Numerical investigation of stability of breather-type solutions of the nonlinear schrödinger equation. Nat Hazards Earth Syst Sci (2014). 14:1431. doi:10.5194/nhess-14-1431-2014.

CrossRef Full Text | Google Scholar

48. Calini A, Schober CM, Strawn M. Linear instability of the peregrine breather: numerical and analytical investigations. Appl Numer Math (2019). 141:36–43. doi:10.1016/j.apnum.2018.11.005.

CrossRef Full Text | Google Scholar

49. Ankiewicz A, Devine N, Akhmediev N. Are rogue waves robust against perturbations?. Phys Lett A (2009). 373:3997–4000. doi:10.1016/j.physleta.2009.08.053.

CrossRef Full Text | Google Scholar

50. Onorato M, Proment D. Approximate rogue wave solutions of the forced and damped nonlinear Schrödinger equation for water waves. Phys Lett A (2012). 376:3057–9. doi:10.1016/j.physleta.2012.05.063.

CrossRef Full Text | Google Scholar

51. Wen XY, Yan Z, Malomed BA. Higher-order vector discrete rogue-wave states in the coupled Ablowitz-Ladik equations: exact solutions and stability. Chaos (2016). 26:123110. doi:10.1063/1.4972111.

CrossRef Full Text | Google Scholar

52. Muñoz C. Instability in nonlinear schrödinger breathers. Proyecciones (2017). 36:653–83. doi:10.4067/S0716-09172017000400653.

CrossRef Full Text | Google Scholar

53. Chen S, Soto-Crespo JM, Grelu P. Coexisting rogue waves within the (2 + 1)-component long-wave–short-wave resonance. Phys Rev E (2014). 90:033203. doi:10.1103/PhysRevE.90.033203.

CrossRef Full Text | Google Scholar

54. Klein C, Haragus M. Numerical study of the stability of the peregrine breather. Preprint repository name [Preprint] (2015). Available from: https://arxiv.org/abs/1507.06766.

CrossRef Full Text | Google Scholar

55. Chan HN, Chow KW, Kedziora DJ, Grimshaw RHJ, Ding E. Rogue wave modes for a derivative nonlinear schrödinger model. Phys Rev E (2014). 89:032914. doi:10.1103/PhysRevE.89.032914.

CrossRef Full Text | Google Scholar

56. Kharif C, Touboul J. Under which conditions the benjamin-feir instability may spawn an extreme wave event: a fully nonlinear approach. Eur Phys J Spec Top (2010). 185:159–68. doi:10.1140/epjst/e2010-01246-7.

CrossRef Full Text | Google Scholar

57. Van Gorder RA. Orbital instability of the peregrine soliton. J Phys Soc Jpn (2014). 83:054005. doi:10.7566/JPSJ.83.054005. doi:10.1140/epjst/e2010-01246-7.

CrossRef Full Text | Google Scholar

58. Cuevas-Maraver J, Malomed BA, Kevrekidis PG, Frantzeskakis DJ. Stabilization of the peregrine soliton and kuznetsov–ma breathers by means of nonlinearity and dispersion management. Phys Lett A (2018). 382:968–72. doi:10.1016/j.physleta.2018.02.013.

CrossRef Full Text | Google Scholar

59. El-Tantawy S, Shan SA, Akhtar N, Elgendy A. Impact of electron trapping in degenerate quantum plasma on the ion-acoustic breathers and super freak waves. Chaos, Solit Fractals (2018). 113:356–64. doi:10.1016/j.chaos.2018.04.037.

CrossRef Full Text | Google Scholar

60. Bludov YV, Driben R, Konotop VV, Malomed B. Instabilities, solitons and rogue waves in -coupled nonlinear waveguides. J Optic (2013). 15:064010. doi:10.1088/2040-8978/15/6/064010.

CrossRef Full Text | Google Scholar

61. Shin H. Deformation of a peregrine soliton by fluctuating backgrounds. Phys Rev E (2013). 88:032919. doi:10.1103/PhysRevE.88.032919.

CrossRef Full Text | Google Scholar

62. Cuevas-Maraver J, Kevrekidis PG, Frantzeskakis DJ, Karachalios NI, Haragus M, James G. Floquet analysis of kuznetsov-ma breathers: a path towards spectral stability of rogue waves. Phys Rev E (2017). 96:012202. doi:10.1103/PhysRevE.96.012202.

CrossRef Full Text | Google Scholar

63. Li JH, Chan HN, Chiang KS, Chow KW. Breathers and ‘black’ rogue waves of coupled nonlinear schrödinger equations with dispersion and nonlinearity of opposite signs. Commun Nonlinear Sci Num Simul (2015). 28:28–38. doi:10.1016/j.cnsns.2015.03.019.

CrossRef Full Text | Google Scholar

64. Hoffmann C, Charalampidis E, Frantzeskakis D, Kevrekidis P. Peregrine solitons and gradient catastrophes in discrete nonlinear schrödinger systems. Phys Lett A (2018). 382:3064–70. doi:10.1016/j.physleta.2018.08.014.

CrossRef Full Text | Google Scholar

65. Birem M, Klein C. Multidomain spectral method for schrödinger equations. Adv Comput Math (2016). 42:395–423. doi:10.1007/s10444-015-9429-9.

CrossRef Full Text | Google Scholar

66. Bailung H, Sharma SK, Nakamura Y. Observation of peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011). 107:255005. doi:10.1103/PhysRevLett.107.255005.

CrossRef Full Text | Google Scholar

67. Pathak P, Sharma SK, Nakamura Y, Bailung H. Observation of ion acoustic multi-peregrine solitons in multicomponent plasma with negative ions. Phys Lett A (2017). 381:4011–8. doi:10.1016/j.physleta.2017.10.046.

CrossRef Full Text | Google Scholar

68. Xu G, Hammani K, Chabchoub A, Dudley JM, Kibler B, Finot C. Phase evolution of peregrine-like breathers in optics and hydrodynamics. Phys Rev E (2019). 99:012207. doi:10.1103/PhysRevE.99.012207.

CrossRef Full Text | Google Scholar

69. Yang G, Wang Y, Qin Z, Malomed BA, Mihalache D, Li L. Breather like solitons extracted from the peregrine rogue wave. Phys Rev E (2014). 90:062909. doi:10.1103/PhysRevE.90.062909.

CrossRef Full Text | Google Scholar

70. Hammani K, Kibler B, Finot C, Morin P, Fatome J, Dudley JM, et al. Peregrine soliton generation and breakup in standard telecommunications fiber. Opt Lett (2011). 36:112–4. doi:10.1364/OL.36.000112.

CrossRef Full Text | Google Scholar

71. Zamora-Munt J, Garbin B, Barland S, Giudici M, Leite JRR, Masoller C, et al. Rogue waves in optically injected lasers: origin, predictability, and suppression. Phys Rev A (2013). 87:035802. doi:10.1103/PhysRevA.87.035802.

CrossRef Full Text | Google Scholar

72. Chabchoub A, Hoffmann N, Branger H, Kharif C, Akhmediev N. Experiments on wind-perturbed rogue wave hydrodynamics using the peregrine breather model. Phys Fluids (2013). 25:101704. doi:10.1063/1.4824706.

CrossRef Full Text | Google Scholar

73. Bludov YV, Konotop VV, Akhmediev N. Matter rogue waves. Phys Rev A (2009). 80:033610. doi:10.1103/PhysRevA.80.033610.

CrossRef Full Text | Google Scholar

74. Dyachenko AI, Zakharov VE. Modulation instability of stokes wave freak wave. J Exp Theor Phys Lett (2005). 81:255–9. doi:10.1134/1.1931010.

CrossRef Full Text | Google Scholar

75. Zaviyalov A, Egorov O, Iliew R, Lederer F. Rogue waves in mode-locked fiber lasers. Phys Rev A (2012). 85:013828. doi:10.1103/PhysRevA.85.013828.

CrossRef Full Text | Google Scholar

76. Oppo GL, Yao AM, Cuozzo D. Self-organization, pattern formation, cavity solitons, and rogue waves in singly resonant optical parametric oscillators. Phys Rev A (2013). 88:043813. doi:10.1103/PhysRevA.88.043813.

CrossRef Full Text | Google Scholar

77. Chen S, Song LY. Peregrine solitons and algebraic soliton pairs in kerr media considering space–time correction. Phys Lett A (2014). 378:1228–32. doi:10.1016/j.physleta.2014.02.042.

CrossRef Full Text | Google Scholar

78. Rivas D, Szameit A, Vicencio RA. Rogue waves in disordered 1d photonic lattices. Sci Rep (2020). 10:1–8. doi:10.1038/s41598-020-69826-x.

CrossRef Full Text | Google Scholar

79. Osborne AR, Onorato M, Serio M. The nonlinear dynamics of rogue waves and holes in deep-water gravity wave trains. Phys Lett A (2000). 275:386–93. doi:10.1016/S0375-9601(00)00575-2.

CrossRef Full Text | Google Scholar

80. Osborne AR. The random and deterministic dynamics of ‘rogue waves’ in unidirectional, deep-water wave trains. Mar Struct (2001). 14:275–93. doi:10.1016/S0951-8339(00)00064-2.

CrossRef Full Text | Google Scholar

81. Yan Z. Nonautonomous “rogons” in the inhomogeneous nonlinear schrödinger equation with variable coefficients. Phys Lett A (2010). 374:672–9. doi:10.1016/j.physleta.2009.11.030.

CrossRef Full Text | Google Scholar

82. Dai CQ, Wang YY, Tian Q, Zhang JF. The management and containment of self-similar rogue waves in the inhomogeneous nonlinear schrödinger equation. Ann Phys (2012). 327:512–21. doi:10.1155/2016/7879517.

CrossRef Full Text | Google Scholar

83. Xu S, He J, Wang L. Two kinds of rogue waves of the general nonlinear schrödinger equation with derivative. Europhys Lett (2012). 97:30007. doi:10.1209/0295-5075/97/30007.

CrossRef Full Text | Google Scholar

84. Yang G, Li L, Jia S. Peregrine rogue waves induced by the interaction between a continuous wave and a soliton. Phys Rev E (2012). 85:046608. doi:10.1103/PhysRevE.85.046608.

CrossRef Full Text | Google Scholar

85. Zhao LC. Dynamics of nonautonomous rogue waves in Bose–Einstein condensate. Ann Phys (2013). 329:73–9. doi:10.1016/j.aop.2012.10.010.

CrossRef Full Text | Google Scholar

86. Ablowitz MJ. Lectures on the inverse scattering transform. Stud Appl Math (1978). 58:17–94. doi:10.1002/sapm197858117.

CrossRef Full Text | Google Scholar

87. Ablowitz MJ, Segur H. Solitons and the inverse scattering transform. Philadelphia, PA: Siam (1981). 434 p.

Google Scholar

88. Drazin PG, Johnson RS. Solitons: an introduction. Cambridge, UK: Cambridge University Press (1989). 226 p.

Google Scholar

89. Ablowitz MJ, Ablowitz M, Clarkson P, Clarkson PA. Solitons, nonlinear evolution equations and inverse scattering. Bull London Math Soc (1993). 25:620–2. doi:10.1112/blms/25.6.620.

CrossRef Full Text | Google Scholar

90. Ablowitz M, Prinari B, Trubatch A. Discrete and continuous nonlinear schrödinger systems. Cambridge, UK: Cambridge University Press (2005). 276 p.

Google Scholar

91. Aktosun T. Inverse scattering transform and the theory of solitons. Preprint repository name [Preprint] (2009). Available from: https://arxiv.org/abs/0905.4746.

Google Scholar

92. Ablowitz MJ. Nonlinear dispersive waves: asymptotic analysis and solitons. Cambridge, UK: Cambridge University Press (2011). 348 p.

Google Scholar

93. Ablowitz MJ, Musslimani ZHF. Inverse scattering transform for the integrable nonlocal nonlinear schrödinger equation. Nonlinearity (2016). 29:915. doi:10.1088/0951-7715/29/3/915.

CrossRef Full Text | Google Scholar

94. Adomian G. Solving frontier problems of physics: the decomposition method; with a preface by yves cherruault. Dordrecht, Netherlands: Kluwer Academic Publishers (1994). 12 p.

Google Scholar

95. Liao SJ. An explicit, totally analytic approximate solution for blasius’ viscous flow problems. Int J Non Lin Mech (1999). 34:759–78. doi:10.1016/S0020-7462(98)00056-0.

CrossRef Full Text | Google Scholar

96. Liao S. On the homotopy analysis method for nonlinear problems. Appl Math Comput (2004). 147:499–513. doi:10.1016/S0096-3003(02)00790-7.

CrossRef Full Text | Google Scholar

97. Ye J, Zheng C. Exact projective excitations of nonautonomous nonlinear schrödinger system in (1 + 1)-dimensions. J Mod Phys (2012). 3:702. doi:10.4236/jmp.2012.38095.

CrossRef Full Text | Google Scholar

98. Zhao D, He XG, Luo HG. Transformation from the nonautonomous to standard nls equations. Eur Phys J D (2009). 53:213–6. doi:10.1140/epjd/e2009-00051-7.

CrossRef Full Text | Google Scholar

99. Pérez-García VM, Torres PJ, Konotop VV. Similarity transformations for nonlinear schrödinger equations with time-dependent coefficients. Phys Nonlinear Phenom (2006). 221:31–6. doi:10.1016/j.physd.2006.07.002.

CrossRef Full Text | Google Scholar

100. Kundu A. Integrable nonautonomous nonlinear schrödinger equations are equivalent to the standard autonomous equation. Phys Rev E (2009). 79:015601. doi:10.1103/PhysRevE.79.015601.

CrossRef Full Text | Google Scholar

101. Kruglov V, Peacock A, Harvey J. Exact self-similar solutions of the generalized nonlinear schrödinger equation with distributed coefficients. Phys Rev Lett (2003). 90:113902. doi:10.1103/PhysRevLett.90.113902.

CrossRef Full Text | Google Scholar

102. Al Khawaja U, Boudjemâa A. Binding energy of soliton molecules in time-dependent harmonic potential and nonlinear interaction. Phys Rev E (2012). 86:036606. doi:10.1103/PhysRevE.86.036606.

CrossRef Full Text | Google Scholar

103. Al Khawaja U. Soliton localization in bose–einstein condensates with time-dependent harmonic potential and scattering length. J Phys Math Theor (2009). 42:265206. doi:10.1088/1751-8113/42/26/265206.

CrossRef Full Text | Google Scholar

104. Guo B, Ling L, Liu Q. Nonlinear schrödinger equation: generalized darboux transformation and rogue wave solutions. Phys Rev E (2012). 85:026607. doi:10.1103/PhysRevE.85.026607.

CrossRef Full Text | Google Scholar

105. Al Khawaja U, Taki M. Rogue waves management by external potentials. Phys Lett A (2013). 377:2944–9. doi:10.1016/j.physleta.2013.09.012.

CrossRef Full Text | Google Scholar

106. Al Khawaja U. Exact solitonic solutions of the gross-pitaevskii equation with a linear potential. Phys Rev E (2007). 75:066607. doi:10.1103/PhysRevE.75.066607.

CrossRef Full Text | Google Scholar

107. Matveev VB, Matveev V. Darboux transformations and solitons. Berlin, Germany: Springer (1991). p. 120.

Google Scholar

108. Lax PD. Integrals of nonlinear equations of evolution and solitary waves. Commun Pure Appl Math (1968). 21:467–90. doi:10.1002/cpa.3160210503.

CrossRef Full Text | Google Scholar

109. Agrawal G. Nonlinear fiber optics. 6th ed. Cambridge, MA: Academic Press (2019). p. 728.

Google Scholar

110. Lakshmanan M, Porsezian K, Daniel M. Effect of discreteness on the continuum limit of the heisenberg spin chain. Phys Lett A (1988). 133:483–8. doi:10.1016/0375-9601(88)90520-8.

CrossRef Full Text | Google Scholar

111. Hirota R. Exact envelope-soliton solutions of a nonlinear wave equation. J Math Phys (1973). 14:805–9. doi:10.1063/1.1666399.

CrossRef Full Text | Google Scholar

112. Ankiewicz A, Kedziora DJ, Chowdury A, Bandelow U, Akhmediev N. Infinite hierarchy of nonlinear schrödinger equations and their solutions. Phys Rev E (2016). 93:012206. doi:10.1103/PhysRevE.93.012206.

CrossRef Full Text | Google Scholar

113. Sun WR. Breather-to-soliton transitions and nonlinear wave interactions for the nonlinear schrödinger equation with the sextic operators in optical fibers. Ann Phys (2017). 529:1600227. doi:10.1002/andp.201600227.

CrossRef Full Text | Google Scholar

114. Ruprecht PA, Holland MJ, Burnett K, Edwards M. Time-dependent solution of the nonlinear schrödinger equation for bose-condensed trapped neutral atoms. Phys Rev A (1995). 51:4704–11. doi:10.1103/PhysRevA.51.4704.

CrossRef Full Text | Google Scholar

115. Dai CQ, Wang YY, Tian Q, Zhang JF. The management and containment of self-similar rogue waves in the inhomogeneous nonlinear schrödinger equation. Ann Phys (2012). 327:512–21. doi:10.1016/j.aop.2011.11.016.

CrossRef Full Text | Google Scholar

116. Chen HH, Liu CS. Solitons in nonuniform media. Phys Rev Lett (1976). 37:693–7. doi:10.1103/PhysRevLett.37.693.

CrossRef Full Text | Google Scholar

117. Raghavan S, Agrawal GP. Spatiotemporal solitons in inhomogeneous nonlinear media. Optic Commun (2000). 180:377–382. doi:10.1016/S0030-4018(00)00727-6.

CrossRef Full Text | Google Scholar

118. Yan Z, Dai C. Optical rogue waves in the generalized inhomogeneous higher-order nonlinear schrödinger equation with modulating coefficients. J Optic (2013). 15:064012. doi:10.1088/2040-8978/15/6/064012.

CrossRef Full Text | Google Scholar

119. Wang LH, Porsezian K, He JS. Breather and rogue wave solutions of a generalized nonlinear schrödinger equation. Phys Rev E (2013). 87:053202. doi:10.1103/PhysRevE.87.053202.

CrossRef Full Text | Google Scholar

120. Sun WR, Tian B, Zhen HL, Sun Y. Breathers and rogue waves of the fifth-order nonlinear schrödinger equation in the heisenberg ferromagnetic spin chain. Nonlinear Dynam (2015). 81:725–32. doi:10.1007/s11071-015-2022-4.

CrossRef Full Text | Google Scholar

121. Wang XB, Zhang TT, Dong MJ. Dynamics of the breathers and rogue waves in the higher-order nonlinear schrödinger equation. Appl Math Lett (2018). 86:298–304. doi:10.1016/j.aml.2018.07.012.

CrossRef Full Text | Google Scholar

122. Yue Y, Huang L, Chen Y. Modulation instability, rogue waves and spectral analysis for the sixth-order nonlinear schrödinger equation. Commun Nonlinear Sci Numer Simulat (2020). 89:105284. doi:10.1016/j.cnsns.2020.105284.

CrossRef Full Text | Google Scholar

123. Wu X, Hua G, Ma Z. Novel rogue waves in an inhomogenous nonlinear medium with external potentials. Commun Nonlinear Sci Numer Simulat (2013). 18:3325–36. doi:10.1016/j.cnsns.2013.05.007.

CrossRef Full Text | Google Scholar

124. Manzetti S. Mathematical modeling of rogue waves: a survey of recent and emerging mathematical methods and solutions. Axioms (2018). 7:1–19. doi:10.3390/axioms7020042.

CrossRef Full Text | Google Scholar

125. Sun WR, Tian B, Jiang Y, Zhen HL. Double-wronskian solitons and rogue waves for the inhomogeneous nonlinear schrödinger equation in an inhomogeneous plasma. Ann Phys (2014). 343:215–27. doi:10.1016/j.aop.2014.01.018.

CrossRef Full Text | Google Scholar

126. He J, Tao Y, Porsezian K, Fokas A. Rogue wave management in an inhomogeneous nonlinear fibre with higher order effects. J Nonlinear Math Phys (2013). 20:407–19. doi:10.1080/14029251.2013.855045.

CrossRef Full Text | Google Scholar

127. Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi F. Rogue waves and their generating mechanisms in different physical contexts. Phys Rep (2013). 528:47–89. doi:10.1016/j.physrep.2013.03.001.

CrossRef Full Text | Google Scholar

128. Tappert FD, Zabusky NJ. Gradient-induced fission of solitons. Phys Rev Lett (1971). 27:1774–6. doi:10.1103/PhysRevLett.27.1774.

CrossRef Full Text | Google Scholar

129. Ponomarenko SA, Agrawal GP. Do solitonlike self-similar waves exist in nonlinear optical media? Phys Rev Lett (2006). 97:013901. doi:10.1103/PhysRevLett.97.013901.

CrossRef Full Text | Google Scholar

130. Serkin VN, Hasegawa A, Belyaeva TL. Nonautonomous solitons in external potentials. Phys Rev Lett (2007). 98:074102. doi:10.1103/PhysRevLett.98.074102.

CrossRef Full Text | Google Scholar

131. Serkin VN, Hasegawa A. Novel soliton solutions of the nonlinear schrödinger equation model. Phys Rev Lett (2000). 85:4502–5. doi:10.1103/PhysRevLett.85.4502.

CrossRef Full Text | Google Scholar

132. Serkin VN, Hasegawa A. Exactly integrable nonlinear schrödinger equation models with varying dispersion, nonlinearity and gain: application for soliton dispersion. IEEE J Sel Top Quant Electron (2002). 8:418–31. doi:10.1109/JSTQE.2002.1016344.

CrossRef Full Text | Google Scholar

133. Yan Z, Konotop VV. Exact solutions to three-dimensional generalized nonlinear schrödinger equations with varying potential and nonlinearities. Phys Rev E (2009). 80:036607. doi:10.1103/PhysRevE.80.036607.

CrossRef Full Text | Google Scholar

134. Kumar CN, Gupta R, Goyal A, Loomba S, Raju TS, Panigrahi PK. Controlled giant rogue waves in nonlinear fiber optics. Phys Rev A (2012). 86:025802. doi:10.1103/PhysRevA.86.025802.

CrossRef Full Text | Google Scholar

135. Zhao LC. Dynamics of nonautonomous rogue waves in bose–einstein condensate. Ann Phys (2013). 329:73–9. doi:10.1016/j.aop.2012.10.010.

CrossRef Full Text | Google Scholar

136. Chen HY, Zhu HP. Controllable behaviors of spatiotemporal breathers in a generalized variable-coefficient nonlinear schrödinger model from arterial mechanics and optical fibers. Nonlinear Dynam (2015). 81:141–9. doi:10.1007/s11071-015-1978-4.

CrossRef Full Text | Google Scholar

137. Dai CQ, Wang YY. Controllable combined peregrine soliton and kuznetsov–ma soliton in PT-symmetric nonlinear couplers with gain and loss. Nonlinear Dynam (2015). 80:715–21. doi:10.1007/s11071-015-1900-0.

CrossRef Full Text | Google Scholar

138. Erkintalo M, Genty G, Dudley JM. Rogue-wave-like characteristics in femtosecond supercontinuum generation. Opt Lett (2009). 34:2468–70. doi:10.1364/OL.34.002468.

CrossRef Full Text | Google Scholar

139. Moslem WM. Langmuir rogue waves in electron-positron plasmas. Phys Plasmas (2011). 18:032301. doi:10.1063/1.3559486.

CrossRef Full Text | Google Scholar

140. Stenflo L, Marklund M. Rogue waves in the atmosphere. J Plasma Phys (2010). 76:293–5. doi:10.1017/S0022377809990481.

CrossRef Full Text | Google Scholar

141. Wen L, Li L, Li ZD, Song SW, Zhang XF, Liu WM. Matter rogue wave in bose-einstein condensates with attractive atomic interaction. Euro Phys J D (2011). 64:473–8. doi:10.1140/epjd/e2011-20485-4.

CrossRef Full Text | Google Scholar

142. He JS, Charalampidis EG, Kevrekidis PG, Frantzeskakis DJ. Rogue waves in nonlinear schrödinger models with variable coefficients: application to bose-einstein condensates. Phys Lett A (2014). 378:577–83. doi:10.1016/j.physleta.2013.12.002.

CrossRef Full Text | Google Scholar

143. Zhong W, Chen L, Belić M, Petrović N. Controllable parabolic-cylinder optical rogue wave. Phys Rev E (2014). 90:043201. doi:10.1103/PhysRevE.90.043201.

CrossRef Full Text | Google Scholar

144. Sun Y, Tian B, Liu L, Wu X. Rogue waves for a generalized nonlinear schrödinger equation with distributed coefficients in a monomode optical fiber. Chaos, Solit Fractals (2018). 107:266–74. doi:10.1016/j.chaos.2017.12.012.

CrossRef Full Text | Google Scholar

145. Loomba S, Pal R, Kumar CN. Controlling rogue wave triplets in Bose–Einstein condensate. J Phys B Atom Mol Opt Phys (2015). 48:105003. doi:10.1088/0953-4075/48/10/105003.

CrossRef Full Text | Google Scholar

146. Goyal A, Gupta R, Loomba S, Kumar CN. Riccati parameterized self-similar waves in tapered graded-index waveguides. Phys Lett A (2012). 376:3454–7. doi:10.1016/j.physleta.2012.07.041. doi:10.1088/0953-4075/48/10/105003.

CrossRef Full Text | Google Scholar

147. Ali S, Younis M. Rogue wave solutions and modulation instability with variable coefficient and harmonic potential. Frontiers in Physics (2020). 7:255. doi:10.3389/fphy.2019.00255.

CrossRef Full Text | Google Scholar

148. Tao Y, He J, Porsezian K. Deformed soliton, breather, and rogue wave solutions of an inhomogeneous nonlinear schrödinger equation. Chin Phys B (2013). 22:074210. doi:10.1088/1674-1056/22/7/074210.

CrossRef Full Text | Google Scholar

149. Dai CQ, Zheng CL, Zhu HP. Controllable rogue waves in the nonautonomous nonlinear system with a linear potential. Eur Phys J D (2012). 66:1. doi:10.1140/epjd/e2012-20718-0.

CrossRef Full Text | Google Scholar

150. Jia H, Yang R, Tian J, Zhang W. Controllable excitation of higher-order rogue waves in nonautonomous systems with both varying linear and harmonic external potentials. Optic Commun (2018). 415:93–100. doi:10.1016/j.optcom.2018.01.026.

CrossRef Full Text | Google Scholar

151. Loomba S, Gupta R, Kaur H, Rajan MSM. Self-similar rogue waves in an inhomogeneous generalized nonlinear schrödinger equation. Phys Lett A (2014). 378:2137–41. doi:10.1016/j.physleta.2014.05.028.

CrossRef Full Text | Google Scholar

152. Panigrahi PK, Gupta R, Goyal A, Kumar CN. Riccati generalization of self-similar solutions of nonautonomous gross-pitaevskii equation. Eur Phys J Spec Top (2013). 222:655–63. doi:10.1140/epjst/e2013-01870-7.

CrossRef Full Text | Google Scholar

153. Manakov S. On the theory of two-dimensional stationary self-focusing of electromagnetic waves. J Exp Theor Phys Lett (1974). 38:248

Google Scholar

154. Kivshar YS, Malomed BA. Dynamics of solitons in nearly integrable systems. Rev Mod Phys (1989). 61:763–915. doi:10.1103/RevModPhys.61.763.

CrossRef Full Text | Google Scholar

155. Radhakrishnan R, Lakshmanan M. Bright and dark soliton solutions to coupled nonlinear schrödinger equations. J Phys Math Gen (1995). 28:2683–92. doi:10.1088/0305-4470/28/9/025.

CrossRef Full Text | Google Scholar

156. Busch T, Anglin JR. Dark-bright solitons in inhomogeneous bose-einstein condensates. Phys Rev Lett (2001). 87:010401. doi:10.1103/PhysRevLett.87.010401.

CrossRef Full Text | Google Scholar

157. Dhar AK, Das KP. Fourth-order nonlinear evolution equation for two stokes wave trains in deep water. Phys Fluid A Fluid Dynam (1991). 3:3021. doi:10.1063/1.858209.

CrossRef Full Text | Google Scholar

158. Scott AC. Launching a davydov soliton: I. soliton analysis. Phys Scripta (1984). 29:279–83. doi:10.1088/0031-8949/29/3/016.

CrossRef Full Text | Google Scholar

159. Yan Z. Vector financial rogue waves. Phys Lett A (2011). 375:4274–9. doi:10.1016/j.physleta.2011.09.026.

CrossRef Full Text | Google Scholar

160. Akhmediev N, Pelinovsky E. Editorial - introductory remarks on “discussion debate: Rogue waves - towards a unifying concept?”. Eur Phys J Spec Top (2010). 185:1–4. doi:10.1140/epjst/e2010-01233-0.

CrossRef Full Text | Google Scholar

161. Kharif C, Pelinovsky E. Physical mechanisms of the rogue wave phenomenon. Eur J Mech B Fluid (2003). 22:603–34. doi:10.1016/j.euromechflu.2003.09.002.

CrossRef Full Text | Google Scholar

162. Bludov YV, Konotop VV, Akhmediev N. Vector rogue waves in binary mixtures of bose-einstein condensates. Eur Phys J Spec Top (2010). 185:169–80. doi:10.1140/epjst/e2010-01247-6.

CrossRef Full Text | Google Scholar

163. Zhao LC, Liu J. Localized nonlinear waves in a two-mode nonlinear fiber. J Opt Soc Am B (2012). 29:3119–27. doi:10.1364/JOSAB.29.003119.

CrossRef Full Text | Google Scholar

164. Zhao LC, Guo2 B, Ling L. High-order rogue wave solutions for the coupled nonlinear schrödinger equations-ii. J Math Phys (2016). 57:043508. doi:10.1063/1.4947113.

CrossRef Full Text | Google Scholar

165. Baronio F, Conforti M, Degasperis A, Lombardo S, Onorato M, Wabnitz S. Vector rogue waves and baseband modulation instability in the defocusing regime. Phys Rev Lett (2014). 113:034101. doi:10.1103/PhysRevLett.113.034101.

CrossRef Full Text | Google Scholar

166. Zhao LC, Liu J. Rogue-wave solutions of a three-component coupled nonlinear schrödinger equation. Phys Rev E (2013). 87:013201. doi:10.1103/PhysRevE.87.013201.

CrossRef Full Text | Google Scholar

167. Baronio F, Conforti M, Degasperis A, Lombardo S. Rogue waves emerging from the resonant interaction of three waves. Phys Rev Lett (2013). 111:114101. doi:10.1103/PhysRevLett.111.114101.

CrossRef Full Text | Google Scholar

168. Rao J, Porsezian K, Kanna T, Cheng Y, He J. Vector rogue waves in integrable m-coupled nonlinear schrödinger equations. Phys Scripta (2019). 94:075205. doi:10.1088/1402-4896/ab1482.

CrossRef Full Text | Google Scholar

169. Baronio F, Degasperis A, Conforti M, Wabnitz S. Solutions of the vector nonlinear schrödinger equations: evidence for deterministic rogue waves. Phys Rev Lett (2012). 109:044102. doi:10.1103/PhysRevLett.109.044102.

CrossRef Full Text | Google Scholar

170. Mu G, Qin Z, Grimshaw R. Dynamics of rogue waves on a multisoliton background in a vector nonlinear schrödinger equation. SIAM J Appl Math (2015). 75:1–20. doi:10.1137/140963686.

CrossRef Full Text | Google Scholar

171. Guo BL, Ling LM. Rogue wave, breathers and bright-dark-rogue solutions for the coupled schrödinger equations. Chin Phys Lett (2011). 28:110202. doi:10.1088/0256-307x/28/11/110202.

CrossRef Full Text | Google Scholar

172. He J, Guo L, Zhang Y, Chabchoub A. Theoretical and experimental evidence of non-symmetric doubly localized rogue waves. Proc R Soc A (2014). 470:20140318. doi:10.1098/rspa.2014.0318.

CrossRef Full Text | Google Scholar

173. Zhai BG, Zhang WG, Wang XL, Zhang HQ. Multi-rogue waves and rational solutions of the coupled nonlinear schrödinger equations. Nonlinear Anal R World Appl (2013). 14:14–27. doi:10.1016/j.nonrwa.2012.04.010.

CrossRef Full Text | Google Scholar

174. Vishnu Priya N, Senthilvelan M, Lakshmanan M. Akhmediev breathers, ma solitons, and general breathers from rogue waves: a case study in the manakov system. Phys Rev E (2013). 88:022918. doi:10.1103/PhysRevE.88.022918.

CrossRef Full Text | Google Scholar

175. Zhao LC, Xin GG, Yang ZY. Rogue-wave pattern transition induced by relative frequency. Phys Rev E (2014). 90:022918. doi:10.1103/PhysRevE.90.022918.

CrossRef Full Text | Google Scholar

176. Chen S, Soto-Crespo JM, Grelu P. Dark three-sister rogue waves in normally dispersive optical fibers with random birefringence. Optic Express (2014). 22:27632–42. doi:10.1364/OE.22.027632.

CrossRef Full Text | Google Scholar

177. Xu T, Chen Y. Localized waves in three-component coupled nonlinear schrödinger equation. Chin Phys B (2016). 25:090201. doi:10.1088/1674-1056/25/9/090201.

CrossRef Full Text | Google Scholar

178. Wang XB, Han B. The three-component coupled nonlinear schrödinger equation: Rogue waves on a multi-soliton background and dynamics. Europhys Lett (2019). 126:15001. doi:10.1209/0295-5075/126/1500.

CrossRef Full Text | Google Scholar

179. Chan HN, Chow KW. Rogue wave modes for the coupled nonlinear schrödinger system with three components: a computational study. Appl Sci (2017). 7(1–12):559. doi:10.3390/app7060559.

CrossRef Full Text | Google Scholar

180. Chen S, Grelu P, Soto-Crespo JM. Dark- and bright-rogue-wave solutions for media with long-wave–short-wave resonance. Phys Rev E (2014). 89:011201. doi:10.1103/PhysRevE.89.011201.

CrossRef Full Text | Google Scholar

181. Xu T, He G. The coupled derivative nonlinear schrödinger equation: conservation laws, modulation instability and semirational solutions. Nonlinear Dynam (2020). 100:2823–37. doi:10.1007/s11071-020-05679-3.

CrossRef Full Text | Google Scholar

182. Sun WR, Tian B, Xie XY, Chai J, Jiang Y. High-order rogue waves of the coupled nonlinear schrödinger equations with negative coherent coupling in an isotropic medium. Commun Nonlinear Sci Numer Simulat (2016). 39:538–44. doi:10.1016/j.cnsns.2016.04.005.

CrossRef Full Text | Google Scholar

183. Feng L, Zhang T. Breather wave, rogue wave and solitary wave solutions of a coupled nonlinear schrödinger equation. Appl Math Lett (2018). 78:133–40. doi:10.1016/j.aml.2017.11.011.

CrossRef Full Text | Google Scholar

184. Zhong W, Beli M, Malomed BA. Rogue waves in a two-component manakov system with variable coefficients and an external potential. Am Phys Soc (2015). 92:053201. doi:10.1103/PhysRevE.92.053201.

CrossRef Full Text | Google Scholar

185. Bludov YV, Konotop VV, Akhmediev N. Vector rogue waves in binary mixtures of bose–einstein condensates. Eur Phys J Spec Top (2010). 185:169–80. doi:10.1140/epjst/e2010-01247-6.

CrossRef Full Text | Google Scholar

186. Mukam SPT, Souleymanou A, Kuetche VK, Bouetou TB. Generalized darboux transformation and parameter-dependent rogue wave solutions to a nonlinear schrödinger system. Nonlinear Dynam (2018). 93:373–83. doi:10.1007/s11071-018-4198-x.

CrossRef Full Text | Google Scholar

187. Li ZD, Wang Y-Y, He PB. Formation mechanism of asymmetric breather and rogue waves in pair-transition-coupled nonlinear schrödinger equations. Chin Phys B (2019). 28:010504. doi:10.1088/1674-1056/28/1/010504.

CrossRef Full Text | Google Scholar

188. Zhang G, Yan Z, Wen XY. Modulational instability, beak-shaped rogue waves, multi-dark-dark solitons and dynamics in pair-transition-coupled nonlinear schrödinger equations. Proc R Soc A (2017). 473:1–19. doi:10.1098/rspa.2017.0243.

CrossRef Full Text | Google Scholar

189. Zhao LC, Ling L, Yang ZY, Liu J. Pair-tunneling induced localized waves in a vector nonlinear schrödinger equation. Commun Nonlinear Sci Numer Simulat (2015). 23:21–7. doi:10.1016/j.cnsns.2014.10.031.

CrossRef Full Text | Google Scholar

190. Guo R, Liu YF, Hao HQ, Qi FH. Coherently coupled solitons, breathers and rogue waves for polarized optical waves in an isotropic medium. Nonlinear Dynam (2015). 80:1221–30. doi:10.1007/s11071-015-1938-z.

CrossRef Full Text | Google Scholar

191. Chen SS, Tian B, Sun Y, Zhang CR. Generalized darboux transformations, rogue waves, and modulation instability for the coherently coupled nonlinear schrödinger equations in nonlinear optics. Ann Phys (2019). 531:1900011. doi:10.1002/andp.201900011.

CrossRef Full Text | Google Scholar

192. Dai C, Huang W. Multi-rogue wave and multi-breather solutions in PT-symmetric coupled waveguides. Appl Math Lett (2014). 32:35–40. doi:10.1016/j.aml.2014.02.013.

CrossRef Full Text | Google Scholar

193. Vishnu Priya N, Senthilvelan M. Generalized darboux transformation and nth order rogue wave solution of a general coupled nonlinear schrödinger equations. Commun Nonlinear Sci Numer Simulat (2015). 20:401–20. doi:10.1016/j.cnsns.2014.06.001.

CrossRef Full Text | Google Scholar

194. Li HM, Tian B, Wang DS, Sun WR, Xie XY, Liu L. Rogue waves for a coupled nonlinear schrödinger system in a multi-mode fibre. J Mod Optic (2016). 63:1924–31. doi:10.1080/09500340.2016.1177617.

CrossRef Full Text | Google Scholar

195. Vishnu Priya N, Senthilvelan M. On the characterization of breather and rogue wave solutions and modulation instability of a coupled generalized nonlinear schrödinger equations. Wave Motion (2015). 54:125–33. doi:10.1016/j.wavemoti.2014.12.001.

CrossRef Full Text | Google Scholar

196. Vishnu Priya N, Senthilvelan M, Lakshmanan M. Dark solitons, breathers, and rogue wave solutions of the coupled generalized nonlinear schrödinger equations. Phys Rev E (2014). 89:062901. doi:10.1103/PhysRevE.89.062901.

CrossRef Full Text | Google Scholar

197. Wang YF, Guo BL, Liu N. Optical rogue waves for the coherently coupled nonlinear schrödinger equation with alternate signs of nonlinearities. Appl Math Lett (2018). 82:38–42. doi:10.1016/j.aml.2018.01.007.

CrossRef Full Text | Google Scholar

198. Yu F, Yan Z. New rogue waves and dark-bright soliton solutions for a coupled nonlinear schrödinger equation with variable coefficients. Appl Math Comput (2014). 233:351–8. doi:10.1016/j.amc.2014.02.023.

CrossRef Full Text | Google Scholar

199. Cheng X, Wang J, Li J. Controllable rogue waves in coupled nonlinear schrödinger equations with varying potentials and nonlinearities. Nonlinear Dynam (2014). 77:545–52. doi:10.1007/s11071-014-1316-2.

CrossRef Full Text | Google Scholar

200. Sun WR, Tian B, Liu RX, Liu DY. Triple wronskian vector solitons and rogue waves for the coupled nonlinear schrödinger equations in the inhomogeneous plasma. J Math Anal Appl (2015). 424:1006–20. doi:10.1016/j.jmaa.2014.11.056.

CrossRef Full Text | Google Scholar

201. Li J, Han J, Du Y, Dai C. Controllable behaviors of peregrine soliton with two peaks in a birefringent fiber with higher-order effects. Nonlinear Dynam (2015). 82:1393–8. doi:10.1007/s11071-015-2246-3.

CrossRef Full Text | Google Scholar

202. Wang X, Chen Y. Rogue-wave pair and dark-bright-rogue wave solutions of the coupled hirota equations. Chin Phys B (2014). 23:070203. doi:10.1088/1674-1056/23/7/070203.

CrossRef Full Text | Google Scholar

203. Zhang Y, Nie X-J, Zha Z. Rogue wave solutions for the coupled cubic–quintic nonlinear schrödinger equations in nonlinear optics. Phys Lett (2014). 378:191–7. doi:10.1016/j.physleta.2013.11.010.

CrossRef Full Text | Google Scholar

204. Xu T, Chen Y, Lin J. Localized waves of the coupled cubic–quintic nonlinear schrödinger equations in nonlinear optics. Chin Phys B (2017). 26:120201. doi:10.1088/1674-1056/26/12/120201.

CrossRef Full Text | Google Scholar

205. Lan Z. Rogue wave solutions for a coupled nonlinear schrödinger equation in the birefringent optical fiber. Appl Math Lett (2019). 98:128–34. doi:10.1016/j.aml.2019.05.028.

CrossRef Full Text | Google Scholar

206. Meng GQ, Qin JL, Yu GL. Breather and rogue wave solutions for a nonlinear schrödinger-type system in plasmas. Nonlinear Dynam (2015). 81:739–51. doi:10.1007/s11071-015-2024-2.

CrossRef Full Text | Google Scholar

207. Askaryan GA. Effects of the gradient of a strong electromagnetic beam on electrons and atoms. Sov Phys-JETP (1962). 15:1088–90.

Google Scholar

208. Marquié P, Bilbault JM, Remoissenet M. Observation of nonlinear localized modes in an electrical lattice. Phys Rev E (1995). 51:6127–33. doi:10.1103/PhysRevE.51.6127.

CrossRef Full Text | Google Scholar

209. Bilbault JM, Marquié P. Energy localization in a nonlinear discrete system. Phys Rev E (1996). 53:5403–8. doi:10.1103/PhysRevE.53.5403.

CrossRef Full Text | Google Scholar

210. Aceves AB, De Angelis C, Peschel T, Muschall R, Lederer F, Trillo S, et al. Discrete self-trapping, soliton interactions, and beam steering in nonlinear waveguide arrays. Phys Rev E (1996). 53:1172–89. doi:10.1103/PhysRevE.53.1172.

CrossRef Full Text | Google Scholar

211. Hennig D, Tsironis G. Wave transmission in nonlinear lattices. Phys Rep (1999). 307:333–432. doi:10.1016/S0370-1573(98)00025-8.

CrossRef Full Text | Google Scholar

212. Bludov YV, Konotop VV, Akhmediev N. Rogue waves as spatial energy concentrators in arrays of nonlinear waveguides. Opt Lett (2009). 34:3015–7. doi:10.1364/OL.34.003015.

CrossRef Full Text | Google Scholar

213. Eisenberg HS, Silberberg Y, Morandotti R, Boyd AR, Aitchison JS. Discrete spatial optical solitons in waveguide arrays. Phys Rev Lett (1998). 81:3383–6. doi:10.1103/PhysRevLett.81.3383.

CrossRef Full Text | Google Scholar

214. Anderson BP, Kasevich MA. Macroscopic quantum interference from atomic tunnel arrays. Science (1998). 282:1686–9. doi:10.1126/science.282.5394.1686.

CrossRef Full Text | Google Scholar

215. Fleischer JW, Carmon T, Segev M, Efremidis NK, Christodoulides DN. Observation of discrete solitons in optically induced real time waveguide arrays. Phys Rev Lett (2003). 90:023902. doi:10.1103/PhysRevLett.90.023902.

CrossRef Full Text | Google Scholar

216. Ablowitz MJ, Kaup DJ, Newell AC, Segur H. The inverse scattering transform-fourier analysis for nonlinear problems. Stud Appl Math (1974). 53:249–315. doi:10.1002/sapm1974534249.

CrossRef Full Text | Google Scholar

217. Ablowitz MJ, Ladik JF. Nonlinear differential-difference equations. J Math Phys (1975). 16:598–603. doi:10.1063/1.522558.

CrossRef Full Text | Google Scholar

218. Ablowitz MJ, Ladik JF. Nonlinear differential-difference equations and fourier analysis. J Math Phys (1976). 17:1011. doi:10.1063/1.523009.

CrossRef Full Text | Google Scholar

219. Christodoulides DN, Joseph RI. Discrete self-focusing in nonlinear arrays of coupled waveguides. Opt Lett (1988). 13:794–6. doi:10.1364/OL.13.000794.

CrossRef Full Text | Google Scholar

220. Chen Z, Segev M, Christodoulides DN. Optical spatial solitons: historical overview and recent advances. Rep Prog Phys (2012). 75:086401. doi:10.1088/0034-4885/75/8/086401.

CrossRef Full Text | Google Scholar

221. Rivas D, Szameit A, Vicencio RA. Rogue waves in disordered 1d photonic lattices. Sci Rep (2020). 10:13064. doi:10.1038/s41598-020-69826-x.

CrossRef Full Text | Google Scholar

222. Takeno S, Hori K. A propagating self-localized mode in a one-dimensional lattice with quartic anharmonicity. J Phys Soc Jpn (1990). 59:3037–40. doi:10.1143/JPSJ.59.3037.

CrossRef Full Text | Google Scholar

223. Ishimori Y. An integrable classical spin chain. J Phys Soc Jpn (1982). 51:3417–8. doi:10.1143/JPSJ.51.3417.

CrossRef Full Text | Google Scholar

224. Kenkre VM, Campbell DK. Self-trapping on a dimer: time-dependent solutions of a discrete nonlinear schrödinger equation. Phys Rev B (1986). 34:4959–61. doi:10.1103/PhysRevB.34.4959.

CrossRef Full Text | Google Scholar

225. Ablowitz MJ. Nonlinear evolution equations-continuous and discrete. Soc Ind Appl Math Rev (1977). 19:663–84. doi:10.1137/1019105.

CrossRef Full Text | Google Scholar

226. Hirota R. Nonlinear partial difference equations. I. a difference analogue of the Korteweg-De Vries equation. J Phys Soc Jpn (1977). 43:1424–33. doi:10.1143/JPSJ.43.1424.

CrossRef Full Text | Google Scholar

227. Salerno M. Quantum deformations of the discrete nonlinear schrödinger equation. Phys Rev A (1992). 46:6856–9. doi:10.1103/PhysRevA.46.6856.

CrossRef Full Text | Google Scholar

228. Ohta Y, Yang J. General rogue waves in the focusing and defocusing ablowitz–ladik equations. J Phys Math Theor (2014). 47:255201. doi:10.1088/1751-8113/47/25/255201.

CrossRef Full Text | Google Scholar

229. Bludov YV, Konotop VV, Akhmediev N. Rogue waves as spatial energy concentrators in arrays of nonlinear waveguides. Opt Lett (2009). 34:3015–7. doi:10.1364/OL.34.003015.

CrossRef Full Text | Google Scholar

230. Efe S, Yuce C. Discrete rogue waves in an array of waveguides. Phys Lett A (2015). 379:1251–5. doi:10.1016/j.physleta.2015.02.031.

CrossRef Full Text | Google Scholar

231. Li M, Shui JJ, Xu T. Generation mechanism of rogue waves for the discrete nonlinear schrödinger equation. Appl Math Lett (2018). 83:110–5. doi:10.1016/j.aml.2018.03.018.

CrossRef Full Text | Google Scholar

232. Ankiewicz A, Akhmediev N, Lederer F. Approach to first-order exact solutions of the ablowitz-ladik equation. Phys Rev E (2011). 83(6):056602. doi:10.1103/PhysRevE.83.056602.

CrossRef Full Text | Google Scholar

233. Ankiewicz A, Akhmediev N, Soto-Crespo JM. Discrete rogue waves of the ablowitz-ladik and hirota equations. Phys Rev E (2010). 82(7):026602. doi:10.1103/PhysRevE.82.026602.

CrossRef Full Text | Google Scholar

234. Akhmediev N, Ankiewicz A. Modulation instability, fermi-pasta-ulam recurrence, rogue waves, nonlinear phase shift, and exact solutions of the ablowitz-ladik equation. Phys Rev E (2011). 83:046603. doi:10.1103/PhysRevE.83.046603.

CrossRef Full Text | Google Scholar

235. Yan Z, Jiang D. Nonautonomous discrete rogue wave solutions and interactions in an inhomogeneous lattice with varying coefficients. J Math Anal Appl (2012). 395:542–9. doi:10.1016/j.jmaa.2012.05.058.

CrossRef Full Text | Google Scholar

236. Yang J, Zhu ZN. Higher-order rogue wave solutions to a spatial discrete hirota equation. Chin Phys Lett (2018). 35:090201. doi:10.1088/0256-307x/35/9/090201.

CrossRef Full Text | Google Scholar

237. Ankiewicz A, Devine N, Ünal M, Chowdury A, Akhmediev N. Rogue waves and other solutions of single and coupled ablowitz–ladik and nonlinear schrödinger equations. J Optic (2013). 15:064008. doi:10.1088/2040-8978/15/6/064008.

CrossRef Full Text | Google Scholar

238. Wen XY, Yan Z. Modulational instability and dynamics of multi-rogue wave solutions for the discrete ablowitz-ladik equation. J Math Phys (2018). 59:073511. doi:10.1063/1.5048512.

CrossRef Full Text | Google Scholar

239. Prinari B. Discrete solitons of the focusing ablowitz-ladik equation with nonzero boundary conditions via inverse scattering. J Math Phys (2016). 57:083510. doi:10.1063/1.4961160.

CrossRef Full Text | Google Scholar

240. Ortiz AK, Prinari B. Inverse scattering transform for the defocusing ablowitz–ladik system with arbitrarily large nonzero background. Stud Appl Math (2019). 143:373–403. doi:10.1111/sapm.12282.

CrossRef Full Text | Google Scholar

241. Li L, Yu F. Optical discrete rogue wave solutions and numerical simulation for a coupled ablowitz–ladik equation with variable coefficients. Nonlinear Dynam (2018). 91:1993–2005. doi:10.1007/s11071-017-3998-8.

CrossRef Full Text | Google Scholar

242. Bender CM, Boettcher S. Real spectra in non-hermitian hamiltonians having PT-symmetry. Phys Rev Lett (1998). 80:5243–6. doi:10.1103/PhysRevLett.80.5243.

CrossRef Full Text | Google Scholar

243. Musslimani ZH, Makris KG, El-Ganainy R, Christodoulides DN. Optical solitons in PT periodic potentials. Phys Rev Lett (2008). 100:030402. doi:10.1103/PhysRevLett.100.030402.

CrossRef Full Text | Google Scholar

244. Benisty H, Degiron A, Lupu A, Lustrac AD, Chénais S, Forget S, et al. Implementation of pt symmetric devices using plasmonics: principle and applications. Optic Express (2011). 19:18004. doi:10.1364/OE.19.018004.

CrossRef Full Text | Google Scholar

245. Cartarius H, Wunner G. Model of a PT-symmetric bose-einstein condensate in a δ-function double-well potential. Phys Rev A (2012). 86:013612. doi:10.1103/PhysRevA.86.013612.

CrossRef Full Text | Google Scholar

246. Schindler J, Li A, Zheng MC, Ellis FM, Kottos T. Experimental study of active lrc circuits with PT symmetries. Phys Rev A (2011). 84:040101. doi:10.1103/PhysRevA.84.040101.

CrossRef Full Text | Google Scholar

247. Zhu X, Ramezani H, Shi C, Zhu J, Zhang X. PT-symmetric acoustics. Phys Rev X (2014). 4:031042. doi:10.1103/PhysRevX.4.031042.

CrossRef Full Text | Google Scholar

248. Sinha D, Ghosh PK. Integrable nonlocal vector nonlinear schrödinger equation with self-induced parity-time-symmetric potential. Phys Lett A (2017). 381:124–8. doi:10.1016/j.physleta.2016.11.002.

CrossRef Full Text | Google Scholar

249. Hu S, Ma X, Lu D, Yang Z, Zheng Y, Hu W. Solitons supported by complex -symmetric Gaussian potentials. Phys Rev A (2011). 84:043818. doi:10.1103/PhysRevA.84.043818.

CrossRef Full Text | Google Scholar

250. Shi Z, Jiang X, Zhu X, Li H. Bright spatial solitons in defocusing kerr media with -symmetric potentials. Phys Rev A (2011). 84:053855. doi:10.1103/PhysRevA.84.053855.

CrossRef Full Text | Google Scholar

251. Rüter CE, Makris KG, El-Ganainy R, Christodoulides DN, Segev M, Kip D. Observation of parity–time symmetry in optics. Nat Phys (2010). 6:192–5. doi:10.1038/nphys1515. doi:10.1103/PhysRevA.84.053855.

CrossRef Full Text | Google Scholar

252. Barashenkov IV, Suchkov SV, Sukhorukov AA, Dmitriev SV, Kivshar YS. Breathers in -symmetric optical couplers. Phys Rev A (2012). 86:053809. doi:10.1103/PhysRevA.86.053809.

CrossRef Full Text | Google Scholar

253. Konotop VV, Yang J, Zezyulin DA. Nonlinear waves in -symmetric systems. Rev Mod Phys (2016). 88:035002. doi:10.1103/RevModPhys.88.035002.

CrossRef Full Text | Google Scholar

254. Ablowitz MJ, Musslimani ZH. Integrable nonlocal nonlinear schrödinger equation. Phys Rev Lett (2013). 110:064105. doi:10.1103/PhysRevLett.110.064105.

CrossRef Full Text | Google Scholar

255. Ablowitz MJ, Musslimani ZH. Integrable discrete symmetric model. Phys Rev E (2014). 90:032912. doi:10.1103/PhysRevE.90.032912.

CrossRef Full Text | Google Scholar

256. Yang B, Chen Y. Several reverse-time integrable nonlocal nonlinear equations: Rogue-wave solutions. Chaos (2018). 28:053104. doi:10.1063/1.5019754.

CrossRef Full Text | Google Scholar

257. Zhou ZX. Darboux transformations and global solutions for a nonlocal derivative nonlinear schrödinger equation. Commun Nonlinear Sci Numer Simulat (2018). 62:480–8. doi:10.1016/j.cnsns.2018.01.008.

CrossRef Full Text | Google Scholar

258. Fokas AS. Integrable multidimensional versions of the nonlocal nonlinear schrödinger equation. Nonlinearity (2016). 29:319–24. doi:10.1088/0951-7715/29/2/319.

CrossRef Full Text | Google Scholar

259. Ma LY, Shen SF, Zhu ZN. Soliton solution and gauge equivalence for an integrable nonlocal complex modified korteweg-de vries equation. J Math Phys (2017). 58:103501. doi:10.1063/1.5005611.

CrossRef Full Text | Google Scholar

260. Luo XD. Inverse scattering transform for the complex reverse space-time nonlocal modified korteweg-de vries equation with nonzero boundary conditions and constant phase shift. Chaos (2019). 29:073118. doi:10.1063/1.5090426.

CrossRef Full Text | Google Scholar

261. Ankiewicz A, Clarkson PA, Akhmediev N. Rogue waves, rational solutions, the patterns of their zeros and integral relations. J Phys Math Theor (2010). 43:122002. doi:10.1088/1751-8113/43/12/122002.

CrossRef Full Text | Google Scholar

262. Dubard P, Gaillard P, Klein C, Matveev V. On multi-rogue wave solutions of the nls equation and positon solutions of the kdv equation. Eur Phys J Spec Top (2010). 185:247–58. doi:10.1140/epjst/e2010-01252-9.

CrossRef Full Text | Google Scholar

263. Gupta SK, Sarma AK. Peregrine rogue wave dynamics in the continuous nonlinear schrödinger system with parity-time symmetric kerr nonlinearity. Commun Nonlinear Sci Numer Simulat (2016). 36:141–7. doi:10.1016/j.cnsns.2015.11.017.

CrossRef Full Text | Google Scholar

264. Yang B, Yang J. On general rogue waves in the parity-time-symmetric nonlinear schrödinger equation. J Math Anal Appl (2020). 487:124023. doi:10.1016/j.jmaa.2020.124023.

CrossRef Full Text | Google Scholar

265. Sakthivinayagam P, Chen J. PT-symmetric cubic-quintic nonlinear schrödinger equation with dual power nonlinearities and its solitonic solutions. Optik (2020). 217:164665. doi:10.1016/j.ijleo.2020.164665.

CrossRef Full Text | Google Scholar

266. Liu W. High-order rogue waves of the benjamin ono equation and the nonlocal nonlinear schrödinger equation. Mod Phys Lett B (2017). 31:1750269. doi:10.1142/S0217984917502694.

CrossRef Full Text | Google Scholar

267. Yang B, Chen Y. General rogue waves and their dynamics in several reverse time integrable nonlocal nonlinear equations. Preprint repository name [Preprint] (2017). Available from: https://arxiv.org/abs/1712.05974.

Google Scholar

268. Yang B, Yang J. Rogue waves in the nonlocal PT-symmetric nonlinear schrödinger equation. Lett Math Phys (2019). 109:945–73. doi:10.1007/s11005-018-1133-5.

CrossRef Full Text | Google Scholar

269. Yang B, Yang J. Transformations between nonlocal and local integrable equations. Stud Appl Math (2018). 140:178–201. doi:10.1111/sapm.12195.

CrossRef Full Text | Google Scholar

270. Xu Z, Chow K. Breathers and rogue waves for a third order nonlocal partial differential equation by a bilinear transformation. Appl Math Lett (2016). 56:72–7. doi:10.1016/j.aml.2015.12.016.

CrossRef Full Text | Google Scholar

271. Yang Y, Wang X, Cheng X. Higher-order rational solutions for a new integrable nonlocal fifth-order nonlinear schrödinger equation. Wave Motion (2018). 77:1–11. doi:10.1016/j.wavemoti.2017.10.012.

CrossRef Full Text | Google Scholar

272. Ward CB, Kevrekidis PG, Horikis TP, Frantzeskakis DJ. Rogue waves and periodic solutions of a nonlocal nonlinear schrödinger model. Phys Rev Res (2020). 2:013351. doi:10.1103/PhysRevResearch.2.013351.

CrossRef Full Text | Google Scholar

273. Vinayagam P, Radha R, Al Khawaja U, Ling L. New classes of solutions in the coupled PT-symmetric nonlocal nonlinear schrödinger equations with four wave mixing. Commun Nonlinear Sci Numer Simulat (2018). 59:387–95. doi:10.1016/j.cnsns.2017.11.016.

CrossRef Full Text | Google Scholar

274. Chiao RY, Garmire E, Townes CH. Self-trapping of optical beams. Phys Rev Lett (1964). 13:479–82. doi:10.1103/PhysRevLett.13.479.

CrossRef Full Text | Google Scholar

275. Bergé L. Wave collapse in physics: principles and applications to light and plasma waves. Phys Rep (1998). 303:259–370. doi:10.1016/S0370-1573(97)00092-6.

CrossRef Full Text | Google Scholar

276. Vlasov V, Petrishev I, Talanov V. Averaged description of wave beams in linear and nonlinear media. Radiofiz (1971). 14:1353–63. doi:10.1007/BF01029467.

CrossRef Full Text | Google Scholar

277. Gagnon L. Exact solutions for optical wave propagation including transverse effects. J Opt Soc Am B (1990). 7:1098–102. doi:10.1364/JOSAB.7.001098.

CrossRef Full Text | Google Scholar

278. Montina A, Bortolozzo U, Residori S, Arecchi FT. Non-Gaussian statistics and extreme waves in a nonlinear optical cavity. Phys Rev Lett (2009). 103:173901. doi:10.1103/PhysRevLett.103.173901.

CrossRef Full Text | Google Scholar

279. Zhu HP. Nonlinear tunneling for controllable rogue waves in two dimensional graded-index waveguides. Nonlinear Dynam (2013). 72:873–82. doi:10.1007/s11071-013-0759-1.

CrossRef Full Text | Google Scholar

280. Dai CQ, Zhu HP. Superposed kuznetsov-ma solitons in a two-dimensional graded-index grating waveguide. J Opt Soc Am B (2013). 30:3291–7. doi:10.1364/JOSAB.30.003291.

CrossRef Full Text | Google Scholar

281. Manikandan K, Senthilvelan M, Kraenkel RA. On the characterization of vector rogue waves in two-dimensional two coupled nonlinear schrödinger equations with distributed coefficients. Eur Phys J B (2016). 89:218. doi:10.1140/epjb/e2016-70420-0.

CrossRef Full Text | Google Scholar

282. Yan Z, Konotop VV, Akhmediev N. Three-dimensional rogue waves in nonstationary parabolic potentials. Phys Rev E (2010). 82:036610. doi:10.1103/PhysRevE.82.036610.

CrossRef Full Text | Google Scholar

283. Yu F. Multi-rogue waves for the (3+1)-dimensional coupled higherorder nonlinear schrödinger equations in optical fiber. Sci Sin Math (2014). 44:151–63. doi:10.1360/012014-10.

CrossRef Full Text | Google Scholar

284. Yu F. Nonautonomous rogue wave solutions and numerical simulations for a three-dimensional nonlinear schrödinger equation. Nonlinear Dynam (2016). 85:1929. doi:10.1007/s11071-016-2806-1.

CrossRef Full Text | Google Scholar

285. Wang G. Symmetry analysis and rogue wave solutions for the (2+1)-dimensional nonlinear schrödinger equation with variable coefficients. Appl Math Lett (2016). 56:56–64. doi:10.1016/j.aml.2015.12.011.

CrossRef Full Text | Google Scholar

286. Zhu H, Chen Y. Spatiotemporal superposed rogue-wave-like breathers in a (3+1)-dimensional variable-coefficient nonlinear schrödinger equation. Nonlinear Anal Model Contr (2016). 21:77–91. doi:10.15388/NA.2016.1.5.

CrossRef Full Text | Google Scholar

287. Wang X, Han B. On the breathers and rogue waves to a (2+1)-dimensional nonlinear schrödinger equation with variable coefficients. Waves Random Complex Media (2019) 1–11. doi:10.1080/17455030.2019.1646944.

CrossRef Full Text | Google Scholar

288. Yan Z. Rogon-like solutions excited in the two-dimensional nonlocal nonlinear schrödinger equation. J Math Anal Appl (2011). 380:689–96. doi:10.1016/j.jmaa.2011.01.071.

CrossRef Full Text | Google Scholar

289. Dai CQ, Liu J, Fan Y, Yu DG. Two-dimensional localized peregrine solution and breather excited in a variable-coefficient nonlinear schrödinger equation with partial nonlocality. Nonlinear Dynam (2017). 88:1373–83. doi:10.1007/s11071-016-3316-x.

CrossRef Full Text | Google Scholar

290. Chen YX, Xu FQ, Hu YL. Excitation control for three-dimensional peregrine solution and combined breather of a partially nonlocal variable-coefficient nonlinear schrödinger equation. Nonlinear Dynam (2019). 95:1957–64. doi:10.1007/s11071-018-4670-7.

CrossRef Full Text | Google Scholar

291. Liu Y, Li B. Rogue waves in the (2+1)-dimensional nonlinear schrödinger equation with a parity-time-symmetric potential. Chin Phys Lett (2017). 34:010202. doi:10.1088/0256-307X/34/1/010202.

CrossRef Full Text | Google Scholar

292. Peng WQ, Tian SF, Zhang TT, Fang Y. Rational and semi-rational solutions of a nonlocal (2 + 1)-dimensional nonlinear schrödinger equation. Math Methods Appl Sci (2019). 42:6865–77. doi:10.1002/mma.5792.

CrossRef Full Text | Google Scholar

293. Liu W, Zhang J, Li X. Rogue waves in the two dimensional nonlocal nonlinear schrödinger equation and nonlocal klein-gordon equation. PloS One (2018). 13:e0192281. doi:10.1371/journal.pone.0192281.

CrossRef Full Text | Google Scholar

294. Cao Y, Malomed BA, He J. Two (2+1)-dimensional integrable nonlocal nonlinear schrödinger equations: breather, rational and semi-rational solutions. Chaos Solit Fractals (2018). 114:99–107. doi:10.1016/j.chaos.2018.06.029.

CrossRef Full Text | Google Scholar

295. De KK, Goyal A, Raju TS, Kumar CN, Panigrahi PK. Riccati parameterized self-similar waves in two-dimensional graded-index waveguide. Optic Commun (2015). 341:15–21. doi:10.1016/j.optcom.2014.11.101.

CrossRef Full Text | Google Scholar

296. Wang YY, Dai CQ, Zhou GQ, Fan Y, Chen L. Rogue wave and combined breather with repeatedly excited behaviors in the dispersion/diffraction decreasing medium. Nonlinear Dynam (2017). 87:67–73. doi:10.1007/s11071-016-3025-5.

CrossRef Full Text | Google Scholar

297. Chen YF, Beckwitt K, Wise FW, Aitken BG, Sanghera JS, Aggarwal ID. Measurement of fifth- and seventh-order nonlinearities of glasses. J Opt Soc Am B (2006). 23:347–52. doi:10.1364/JOSAB.23.000347.

CrossRef Full Text | Google Scholar

298. Stegeman GI, Seaton CT. Effects of saturation and loss on nonlinear directional couplers. Appl Phys Lett (1987). 50:1035. doi:10.1063/1.97962.

CrossRef Full Text | Google Scholar

299. Caglioti E, Trillo S, Wabnitz S, Daino B, Stegeman GI. Power-dependent switching in a coherent nonlinear directional coupler in the presence of saturation. Appl Phys Lett (1987). 51:293. doi:10.1063/1.98476.

CrossRef Full Text | Google Scholar

300. Chen Y. Twin core nonlinear couplers with saturable nonlinearity. Electron Lett (1990). 26:1374. doi:10.1049/el:19900883.

CrossRef Full Text | Google Scholar

301. Chen Y. Mismatched nonlinear couplers with saturable nonlinearity. J Opt Soc Am B (1991). 8:986–92. doi:10.1364/JOSAB.8.000986.

CrossRef Full Text | Google Scholar

302. Khadzhi PI, Orlov OK. Light propagation in a directional coupler with saturable nonlinearity. Tech Phys (2000). 45:1164–9. doi:10.1134/1.1318103.

CrossRef Full Text | Google Scholar

303. Gatz S, Herrmann J. Soliton propagation in materials with saturable nonlinearity. J Opt Soc Am B (1991). 8:2296–302. doi:10.1364/JOSAB.8.002296.

CrossRef Full Text | Google Scholar

304. Herrmann J. Propagation of ultrashort light pulses in fibers with saturable nonlinearity in the normal-dispersion region. J Opt Soc Am B (1991). 8:1507–11. doi:10.1364/JOSAB.8.001507.

CrossRef Full Text | Google Scholar

305. Coutaz JL, Kull M. Saturation of the nonlinear index of refraction in semiconductor-doped glass. J Opt Soc Am B (1991). 8:95–8. doi:10.1364/JOSAB.8.000095.

CrossRef Full Text | Google Scholar

306. Hickmann JM, Cavalcanti SB, Borges NM, Gouveia EA, Gouveia-Neto AS. Modulational instability in semiconductor-doped glass fibers with saturable nonlinearity. Opt Lett (1993). 18:182–4. doi:10.1364/OL.18.000182.

CrossRef Full Text | Google Scholar

307. da Silva GL, Gleria I, Lyra ML, Sombra ASB. Modulational instability in lossless fibers with saturable delayed nonlinear response. J Opt Soc Am B (2009). 26:183–8. doi:10.1364/JOSAB.26.000183.

CrossRef Full Text | Google Scholar

308. Charalampidis EG, Cuevas-Maraver J, Frantzeskakis DJ, Kevrekidis PG. Rogue waves in ultracold bosonic seas. Rom Rep Phys (2018). 70:1–25.

Google Scholar

309. Akhmediev N, Korneev V, Mitskevich N. N-modulation signals in a single-mode optical waveguide under nonlinear conditions. Sov Phys JETP (1988). 67:89–95. doi:10.1016/j.revip.2019.100037.

CrossRef Full Text | Google Scholar