Electronic Nematic States Tuned by Isoelectronic Substitution in Bulk FeSe1−xSx

Isoelectronic substitution is an ideal tuning parameter to alter electronic states and correlations in iron-based superconductors. As this substitution takes place outside the conducting Fe planes, the electronic behaviour is less affected by the impurity scattering experimentally and relevant key electronic parameters can be accessed. In this short review, I present the experimental progress made in understanding the electronic behaviour of the nematic electronic superconductors, FeSe_1−xS_x. A direct signature of the nematic electronic state is in-plane anisotropic distortion of the Fermi surface triggered by orbital ordering effects and electronic interactions that result in multi-band shifts detected by ARPES. Upon sulphur substitution, the electronic correlations and the Fermi velocities decrease in the tetragonal phase. Quantum oscillations are observed for the whole series in ultra-high magnetic fields and show a complex spectra due to the presence of many small orbits. Effective masses associated to the largest orbit display non-divergent behaviour at the nematic end point (x ∼ 0.175(5)), as opposed to critical spin-fluctuations in other iron pnictides. Magnetotransport behaviour has a strong deviation from the Fermi liquid behaviour and linear T resistivity is detected at low temperatures inside the nematic phase, where scattering from low energy spin-fluctuations are likely to be present. The superconductivity is not enhanced in FeSe_1−xS_x and there are no divergent electronic correlations at the nematic end point. These manifestations indicate a strong coupling with the lattice in FeSe_1−xS_x and a pairing mechanism likely promoted by spin fluctuations.

1 Introduction

Nematic electronic states have been suggested to play an important role in understanding the electronic behavior of high temperature superconductors like cuprates and iron-based superconductors, quantum Hall systems, and Sr₃Ru₂O₇ [1]. Often the nematic electronic state breaks the rotational symmetry of a tetragonal plane lattice from four-fold symmetric (C₄) down to two-fold symmetric (C₂) [1]. This symmetry breaking is expected to have a number of consequences on the electronic properties leading to a series of effects involving anisotropic single-particle properties, showing a distorted Fermi surface (that can be triggered like a Pomeranchuk instability in the presence of interactions [2]), anisotropic spin-fluctuation spectra, and anisotropic transport properties that can lead to non-Fermi-liquid behavior [3]. Theoretically, in the proximity to a nematic quantum critical point, the nematic fluctuations with wave-vector q = 0 can enhance the critical temperature by pairing through the exchange of nematic fluctuations in all symmetry channels [4, 5]. In real systems, the nematic electronic phase is intimately coupled with the lattice. This coupling has significant consequences on the observed response, such as the presence of the tetragonal-to-orthorhombic structural transition at the same temperature where the nematic electronic order develops. This finite coupling of the electronic system with the lattice is expected to alter the response of the nematic critical fluctuations on superconductivity and the non-Fermi liquid power-law dependencies in transport [6–9].

Iron-based superconductors offer a unique playground to understand unconventional superconductivity and explore the normal competing electronic phases, such as nematic electronic phases and spin-density wave phases. Often the nematic and spin-density phases neighbor each other in the phase diagrams of iron-based superconductors, making it difficult to assess whether the spin or nematic fluctuations are the most relevant for stabilizing superconductivity [10]. A unique system, the chalcogenides FeSe_1−xS_x, provides an essential route to investigate the interplay between nematicity and superconductivity, in the absence of long-range magnetism. Furthermore, the isoelectronic substitution can access the experimental manifestations around a putative nematic critical point, undisturbed by the presence of a magnetic critical point, as found in other systems, like BaFe₂(As_1−xP_x)₂ [11]. The parent compound of this family, FeSe, displays a nematic electronic phase and a tetragonal-to-orthorhombic transition below 90 K [12] and no long range magnetic order was detected despite a rich spectrum of low and high-energy spin fluctuations [13–15].

The bulk superconductivity of FeSe has a relatively low critical temperature close to 9 K but it can be enhanced toward 40 K by applied external pressure [16, 17]. The nematic phase of FeSe is also suppressed at low pressures [16–19] before a new magnetic state is stabilized at high pressures [19, 20], that competes with the high-T_c phase [17]. Besides applied pressure, the bulk superconductivity of FeSe can be enhanced toward 40 K via the intercalation between the van der Waals layers of a molecular spacer [21], and by gating of thin flakes [22]. In a monolayer on FeSe, on a suitable substrate, the transition temperatures reach record values toward 65 K; a strong interfacial electron-phonon coupling and a charge transfer through the interface is proposed as a source for this two-dimensional high-T_c superconductivity [23, 24]. This effect is surprisingly absent in a monolayer of FeS [25] and in the absence of substrate in thin flakes of FeSe [26].

Isoelectronic substitution is a clean and efficient way to tune phase diagrams of iron-based superconductors, by gently suppressing the relevant electronic interactions and competing electronic phases with superconductivity, and to access quantum critical points [34]. For the FeSe family this is achieved by replacing elements with a similar number of electrons outside the Fe planes, using sulphur or tellurium ions on selenium ions sites. The availability of single crystals of these materials have allowed intense interest and study of their physical properties, summarized in recent reviews in Refs. 15, 35–37. Furthermore, by combining physical and chemical pressures, the relative position of the nematic electronic phase in relation to the spin-density wave phase can be varied and thus the influence of two competing electronic phases on superconductivity can be disentangled [38, 39]. The scope of this review is to summarize the recent experimental efforts in understanding the electronic behavior of FeSe_1−xS_x that can provide a unique insight into the role played by the nematicity, Fermi surfaces, proximity to a putative nematic critical point and electronic correlations in relation to superconductivity in the absence of any long-range magnetic order.

2 Phase Diagram of FeSe_1−xS_x

Figure 1A shows the phase diagram of FeSe_1−xS_x as a function of isoelectronic substitution with sulphur obtained from transport measurements. The isoelectronic substitution achieved by replacing selenium ions for sulfur ions outside the Fe plane causes an positive internal chemical pressure as these ions have different ionic radii (S²⁻ is 1.70 Å compared with 1.87 Å for Se²⁻) [40, 41]. The nematic electronic phase of FeSe, due to its finite coupling with the underlying lattice, triggers a structural transition from a tetragonal to an orthorhombic phase at T_s [12]. This transition gives rise to a well-defined anomaly in the transport measurements (Figure 1C) that helps to build the nematic phase diagram and to identify the expected position of each measured single crystal inside the nematic phase, as shown in Figure 1A.

FIGURE 1

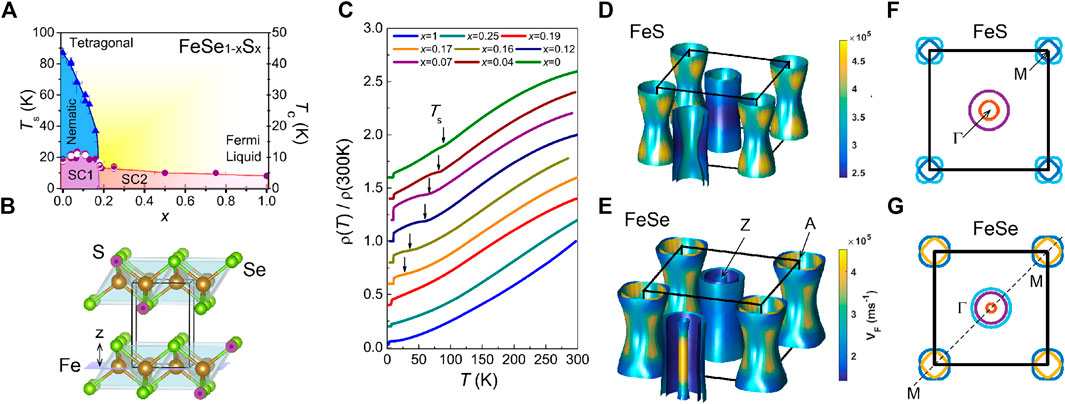
FIGURE 1. Phase diagram of FeSe_1−xS_x. (A) Phase diagram of FeSe_1−xS_x based on Ref. 27. (C) The resistivity vs. temperature of FeSe_1−xS_x normalized at room temperature, after Refs. 27–29. The data are shifted vertically and the arrows indicate the position of the nematic transition that coincides with the tetragonal to orthorhombic transition at T_s. This transition is better visualized using the first derivative of the resistivity, as discussed in Refs. 27, 28, 30. (B) The tetragonal unit cell of FeSe_1−xS_x (solid lines). FeSe_1−xS_x crystalizes in the P4/nmm space group (No.129) with atoms Fe: 2a (3/4,1/4,0) and Se: 2c (1/4,1/4, z_Se). The position of the chalcogen above the Fe plane is indicated by the parameter z that affects significantly the band structure. Calculated Fermi surface using density functional theory (DFT using GGA approximation and spin-orbit coupling) of FeS in (D) and FeSe in (E) using experimental lattice parameters at room temperature for FeSe [31] and FeS [32, 33]). The Fermi surfaces are colored using the Fermi velocities indicated by the corresponding color bar. The middle hole band with lower velocity in FeSe has a dominant d_xy character whereas the other hole and electron bands have mixed d_xz/yz character. The high-symmetry cut of the Fermi surface in the $\text{Γ}$-M plane (k_z = 0) for FeS in (E) and FeSe in (F). The dashed line indicates the direction of the high symmetry cuts in ARPES measurements.

The isoelectronic substitution with sulfur in FeSe leads to the efficient suppression of the nematic electronic state, similarly to the effect of applied pressure [42] (Figure 1A). In contrast to applied pressure, the nematic phase can be completely suppressed with sulfur substitution and no spin-density wave phase was detected for any available single crystals. The lowest detected value of T_s is about 25 K, followed by an abrupt drop at the nematic end point (NEP) which occurs close to x ∼ 0.175(5), [27, 29, 40, 43, 44]. Thus, FeSe_1−xS_x family is unique and permits the exploration of the nematic electronic phase transition in the vicinity of a putative nematic critical point.

Inside the nematic phase, the superconducting transition temperature displays a small dome reaching T_c ∼ 11 K close to x ∼ 0.11, varying from 8.7 (3) K for FeSe inside the nematic phase toward 6.5–5 K just outside it [29, 30, 44, 45]. For higher x values inside the tetragonal phase, the superconductivity hardly changes reaching only 4.5 (5) K toward FeS [32, 33]. The suppression of the nematic phase transition in FeSe_1−xS_x coincides with a decrease in the superconducting transition temperature T_c close to NEP. STM studies have detected a rather abrupt change in the superconducting order parameter at the nematic phase boundaries, implying that different types of pairing may be operational inside (SC1) and outside the nematic phase (SC2), as shown in Figure 1A [30, 46]. Recently, it has been suggested theoretically that a topological transition associated with the creation of a Bogoliubov Fermi surface could occur as a function of x in FeSe_1−xS_x [47, 48].

In order to understand in depth the electronic properties of FeSe_1−xS_x a good knowledge of the exact composition and the sulfur variation in each batch is required. This can be challenging for techniques, like neutron-diffraction and muon spin rotation, that require a large mass of sample made of hundreds of small single crystals [49]. At room temperature FeSe_1−xS_x crystalizes in the P4/nmm space group (No. 129), as shown in Figure 1B. The lattice parameters of FeSe are a = 3.7651 Å, c = 5.5178 Å, z_Se = 0.2672 [31] whereas FeS has a much smaller c axis (a = 3.6802 Å, c = 5.0307 Å, z_S = 0.2523) [32, 33]. The lattice parameters measured by X-ray diffraction for each crystal of FeSe_1−xS_x can be used to determine the composition of each sample. Assuming the formation of a solid solution as a function of composition, the values of the lattice parameters at room temperature, p, (that can be a,b and c or z_Se/S) for a certain composition x can be estimated using an empirical Vegard’s law p_x = xp_S + (1 − x) p_Se

2.1 Single Crystal Growth

Single crystals of FeSe_1−xS_x are normally grown by the KCl/AlCl₃ chemical vapor transport method from the FeSe end toward x ∼ 0.4 [12, 29, 40, 43, 44, 50, 51]. The growth of higher concentrations and FeS was achieved using a hydrothermal reaction of iron powder with sulfide solution, which in general is a more invasive method and can lead to single crystals with higher concentration of impurities [29, 32, 33, 52]. Epitaxial thin films of FeSe_1−xS_x with x < 0.43 were grown via pulsed laser deposition [53]. A potential anomaly was observed in the resistivity curves for films with large x, suggested to be linked to a magnetic transition [53], but these findings have not been yet confirmed in single crystals [44, 53]. The exact x composition for samples in each batch is normally checked using compositional analysis using energy-dispersive X-ray spectroscopy (EDX) or electron-probe micro-analysis (EPMA) [12, 27, 44, 50, 53]. The nominal composition, x_nom, used during the growth process is often smaller than the real composition x (by about 80%) and the higher the composition the larger degree of variation occurs within the same batch [44, 53]. For example, the phase diagrams of FeSe_1−xS_x reported in Refs. 54, 55 uses the nominal values x_nom. Thus, the linear resistivity in 35T occurs inside the nematic phase, as the measured zero resistivity shows an anomaly at T_s ∼ 51 K for a nominal composition x_nom ∼ 0.16 that would correspond around x ∼ 0.13 [28]. The residual resistivity ratio, defined as the ratio between room temperature resistivity and the resistivity at the onset of superconductivity, varies between 15 and 44 [27, 28] and it is often used as a proxy to assess the quality of each single crystal. In high magnetic field, quantum oscillations were observed for all composition of FeSe_1−xS_x reflecting their high quality with large mean free path (up to ∼350 Å) [27, 39]. For higher x composition, the mean free path decreases slightly and new hexagonal phases could be stabilized [27]. The superconductivity of Fe_1+δSe can also be destroyed by very small changes in its stoichiometry [31].

3 Electronic Structure of FeSe_1−xS_x

The main features of the electronic structure of FeSe_1−xS_x can be understood by considering the two-dimensional square lattice of Fe ions, separated by Se/S atoms residing above and below the Fe layer, as shown in Figure 1B. Due to the strong bonding between the Fe-Fe and Fe-(Se/S) sites, an Fe atom can be placed inside the center of an almost perfect tetrahedron of Fe(Se/S)₄ that determines the electronic properties of these materials. Band structure calculations show that the Fermi surface of FeSe_1−xS_x consists of well-separated hole pockets at the center of the Brillouin zone and electron pockets at the zone corners that form quasi-two dimensional Fermi surfaces, as shown in Figures 1D,E. The position of the chalcogen ion in relation to the Fe plane, z, affects significantly the predicted number and the orbital character of the hole bands, FeSe having an additional middle hole band with d_xy character which is pushed below the Fermi level in FeS (Figures 1D,E). There are two predicted cylindrical electron bands which hardly change in shape across this series, similar to the isoelectronic series BaFe₂(As_1−xP_x)₂ [56]. The positive chemical pressure in FeSe_1−xS_x results in a lattice contraction and the reduction of the c axis [41] and it would bring the Fe(Se/S) layers closer together, increasing the bandwidth and potentially leading to the suppression of the electronic correlations [29, 57]. As discussed below, DFT calculations provide essential guide to understand the origin of the observed Fermi surfaces of FeSe_1−xS_x, but the size are smaller, the number of hole bands is reduced compared with calculations and the k_z dependence is changed.

4 ARPES Studies of FeSe_1−xS_x

ARPES is highly suited for the exploration of FeSe_1−xS_x as these systems can be easily cleaved in-situ due to weak van der Waals bonds between the FeSe layers which also enable the development of devices of two-dimensional superconductors by mechanical exfoliation [22, 26]. Furthermore, ARPES studies can evaluate the role of orbital character on the nematic electronic states, as the matrix element effects affect the intensity of different bands with different orbital character. In certain conditions, ARPES spectra of iron-based superconductors does not show certain branches due to the underlying symmetry, in particular for the electron bands [59–61], as the intensity depends strongly on the polarisation of the incident beam as well as the incident photon energy. A representation of the orbital character of different pockets at high symmetry points is shown in Figure 2H.

FIGURE 2

FIGURE 2. Low-temperature ARPES data for FeSe_1−xS_x. Band dispersion around high symmetry points, (A)$\text{Γ}$, (B)Z, and (C) M collected using horizontally and vertically linearly polarized synchrotron light (LH and LV) at low temperatures at 13 K for different x compositions (after Refs. 29, 35, 40). Momentum dependent cuts (MDCs) are shown above each dispersion which allows to extract the k_F values at the Fermi level (the instrumental resolution is ∼3 meV). The top of the parabolic band dispersion for the outer hole band at the $\text{Γ}$ point for x = 0.18 is getting closer to the Fermi level (∼5 meV) compared with FeSe (∼17 meV). (D) DFT calculations high symmetry cuts for FeS for the same symmetry points like the ARPES data with energies in meV. These dispersions can be compared with experiments to extract the renormalization factor for each band. The colors indicate the different orbital character. The Fermi surface map for the hole bands at the Z point in (E) and for the electron bands at the A point in (F), after Refs. 29, 35, 40, and 58. Inside the nematic phase, the existence of twining below T_s can cause superposition of the signal from two domains, rotated by 90°. The orbital character of the map varies around the Fermi surface as depicted for the tetragonal case in (H). The dashed line indicates the cuts in (A–C) and the orientation of the maps in (E) and (F). (G) The energy dependent cuts (EDCs) centered at the high symmetry M point for different composition. The energy separation between the two most intense peaks is defined by ${\text{Δ}}_M$, a proxy for the orbital ordering effect. The positions of the high symmetry M1 and M3 points for x = 0.18 are indicated by arrows. (H) Schematic of the tetragonal Fermi surfaces in the Z-A plane containing different orbital characters. The dashed line is a cut along the diagonal of the unit cell used in the ARPES measurements in panels a–c.

Extensive experimental ARPES studies on FeSe found that system has many relevant electronic ingredients for a multiband system [35, 59, 62–66]. The experimental Fermi surface of FeSe is unusually small having 2 electron pockets and a single hole pocket (instead of 3), a factor 5 smaller than that predictions of the band-structure calculations (Figure 1E). Such a small Fermi surface could be sensitive to topological changes in magnetic fields or under applied strain. To bring the DFT calculated Fermi surfaces in agreement with experiments, band shifts need to be applied in opposite direction for hole and electrons of more than 200 meV for FeSe [62] and less than 100 meV for FeS [67]. Band shifts also occur at high temperatures inside the tetragonal phase of FeSe and these effects are caused by higher energy interactions [68] as well as the changes in the chemical potential [69], as found in many iron-based superconductors [70]. Furthermore, like many other iron chalcogenides, FeSe exhibits strong orbitally-dependent electronic correlations due to the larger band renormalization factor ∼7–9 of the d_xy band compared with ∼3–4 for the d_xz/yz band [62, 71]. These values are obtained by comparing the experimental band dispersion to those from DFT calculations in the tetragonal phase, as shown in Figure 1 [62, 71]. At high binding energies, ARPES spectra detected Hubbard-like bands suggesting the existence of incoherent many-body excitations originating from Fe 3d states, in addition to the renormalized quasiparticle bands near the Fermi level [63, 72]. Many high energy features of the observed ARPES data can be accounted for by considering the strong local Coulomb interactions on the spectral function via dynamical mean-field theory, including the formation of a Hubbard-like band [63, 72]. Another inherent challenge for ARPES studies inside the nematic phase is the likely presence of sample twinning (rotated by 90°), by cooling thorough the structural transition, and a lot of recent effort has been dedicated to address this issue by applying strain to FeSe [65, 66, 73].

4.1 Hole Pockets of FeSe_1−xS_x

The evolution of the hole pockets of FeSe_1−xS_x with x substitution for the two high symmetry points Z (at the top of the Brillouin zone) and $\text{Γ}$ (at the center of the Brillouin zone) at low temperatures is shown in Figures 2A,B, respectively. The observed energy dispersions of FeSe_1−xS_x are all renormalized and shifted, as compared to the DFT dispersions, leading to much smaller hole and electron pockets, as compared with calculations [62]. The renormalization values corresponding to the two main hole dispersions (with d_xz/d_xz orbital character) are around 3–4 and hardly change for any compositions inside the nematic phase toward x ∼ 0.180.18, but they are reduced to a factor of ∼1–2.3 for FeS, suggesting that the suppression of electronic correlations occurs from FeSe toward FeS [29, 57]. Additionally, the highly renormalized d_xy band, found at ∼50 meV below the Fermi level, remains relatively unaffected across the nematic phase transition to x ∼ 0.18 and it cannot be resolved for FeS due to the disorder effects [29]. The d_xy hole band is notoriously difficult to observe in experiments due to matrix element effects and being strongly incoherent in iron-chalcogenides [74] but its dispersion can be revealed due to band mixing caused by the spin-orbit coupling effects [29, 75]. As a function of x substitution, the Fermi velocities increase by ∼10% inside the nematic phase but more significantly outside toward FeS, reflecting the suppression of electronic correlations, as shown in Figure 4E.

FIGURE 3

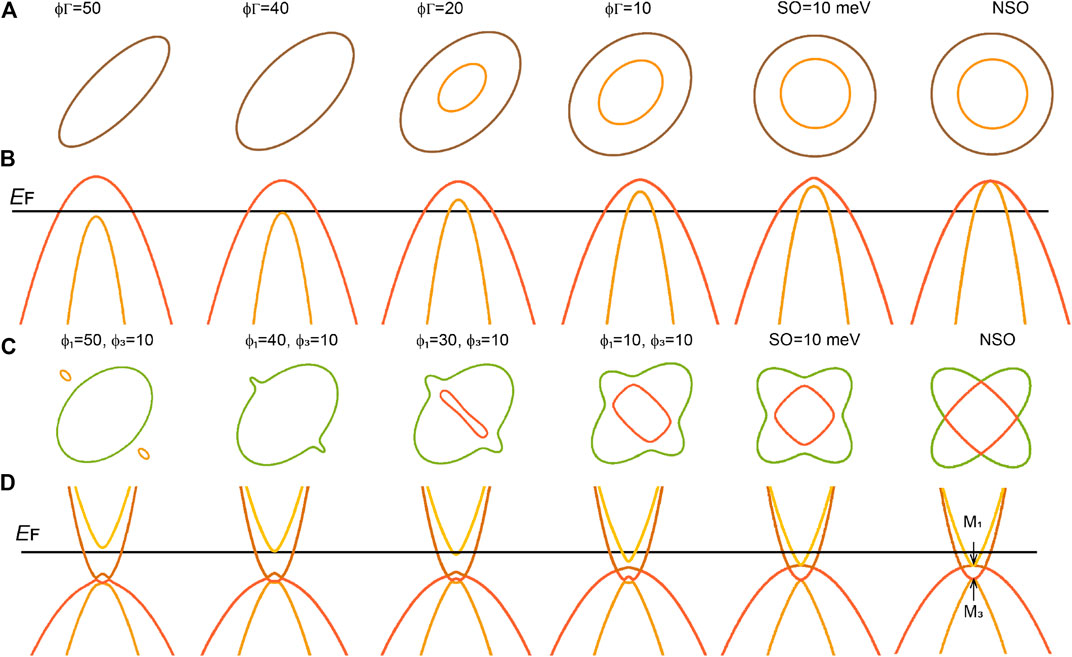
FIGURE 3. Simulations of the effect of nematicity on the ARPES data. Simulations of the Fermi surface maps and band dispersions in a nematic and tetragonal phase, as described in detail in Refs. 76, 77. This model parameters are adjusted to match the experimental data for the tetragonal x = 0.18 in Figures 2B,C and the spin-orbit coupling is considered as being 10 meV. The starting values used in simulations are ${\mathit{ϵ}}_1$ = −16, ${\mathit{ϵ}}_3$ = −35, m₁ = 0.05, m₃ = 4 × 10⁻⁴, $a_1$ = 964, $a_3$ = −2,862, v = −327, p₁ = −2,589, p₃ = −589. The simulations on the right side assume the absence of spin-orbit coupling. The orbital order induced affects the electron and holes band dispersion in different way. (A) At the $\text{Γ}$ point the band splitting is determined both by the spin-orbit coupling and nematicity, giving a band splitting of $\sqrt{{\text{Δ}}_{SO}^2+{\varphi }_{\text{Γ}}^2}$, and the hole pockets become elongated in (B). One of the inner hole pocket is pushed below the Fermi level. (C) At the M point the effect of nematicity is influenced by the anisotropy of the on-site energies of the d_xz (${\varphi }_1$) and d_yz orbitals, anisotropic d_xy hopping (${\varphi }_3$) as well as the spin-orbit coupling [76] and the electron pockets changes shape significantly in (D). The in-plane maps illustrate the representation expected for a single domain sample. In real experiments, the superposition of two different domains rotated by 90° could occur.

FIGURE 4

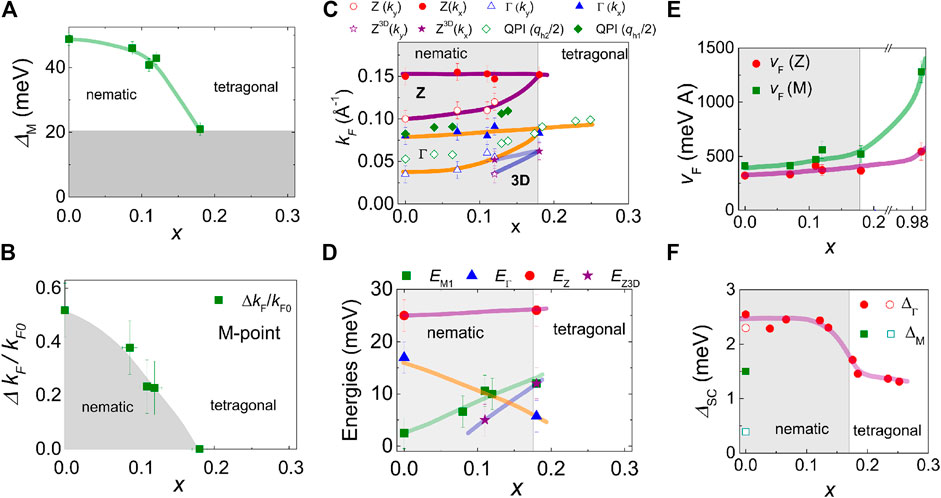
FIGURE 4. Low temperature parameters extracted from APRES data of FeSe_1−xS_x. (A) The variation of the low temperature splitting parameter, ${\text{Δ}}_M$, extracted from EDCs at the M point, with x substitution, shown in Figure 1G. A splitting of 20 meV is already present for the tetragonal x = 0.18 suggesting the effect of nematicity is less than ${\text{Δ}}_M$ for x = 0 [29, 40]. (B) The relative distortion of the electron Fermi surface at the M point, $\text{Δ}{k}_F/k_{F0}$, at T ∼ 13 K in relation with the tetragonal phase k_F0, as a function of x substitution (after Ref. 40). (C) The variation of the Fermi k_F vector with x for the hole pockets extracted from the MDC cuts and assuming that the data arises from two superimposed ellipses. The value of the q/2 scattering vectors from QPI are compared with those from ARPES data, after Ref. 46. (D) The variation of the energy of the top or bottom of the bands at different high-symmetry points. (E) The Fermi velocities extracted form the slope of the energy dispersion as a function of momentum for the hole and the electron bands, after Refs. 29, 40. (F) The x variation of the superconducting gap, $\left|{\text{Δ}}_{SC}\right|$, extracted for the hole band for FeSe_1−xS_x and the electron band for FeSe, after Refs. 46, 78. Another potential small gap of 0.39 meV (open square) was invoked from specific heat data for FeSe [79].

The ARPES studies at the two high symmetry points using different incident energies allows for the evaluation of the k_z hole dispersion of the cylindrical Fermi surfaces of FeSe_1−xS_x and the sensitivity of the second inner hole band to any band shifts inside the nematic phase. The inner hole band, which forms a small 3D inner hole pocket around the Z point, is observed in the tetragonal phase of FeSe but it is pushed below the Fermi level inside the nematic phase [62]. With sulfur substitution, the inner hole band is shifted gradually up and it crosses the Fermi level only at the Z point from x ∼ 0.11 [40] and grows in size at x ∼ 0.18. The inner hole band does not cross the Fermi level at the $\text{Γ}$ point for any compositions up to x ∼ 0.18; however, it has been suggested that this pocket could grow in size and become a two-dimensional cylinder for FeS (Figures 1D,E) [29, 57, 67]. Interestingly, the Fermi surface of the tetragonal phase for x ∼ 0.18 is very similar to the Fermi surface of FeSe at high temperature. Thus, there is a direct correspondence between the temperature and sulfur substitution in FeSe of the nematic electronic structure of FeSe_1−xS_x [29, 40].

4.2 Simulations of the Effect of Nematicity on the Low-Energy Electronic Structure

To understand the effect of nematicity and the orbital effects at each high symmetry point, simulations based on a model developed in Refs. 76, 77 for a single domain sample are shown in Figure 3. The parameters for the simulations are adjusted to match the ARPES experimental data for x = 0.18 in Figures 2B,C [29] and the other variable are listed in Figure 3. In the tetragonal phase of FeSe_1−xS_x, the hole Fermi surface are expected to be circular and C₄ symmetric, originating from the d_xz/yz bands, as shown in Figure 2E. In the absence of nematicity the two hole dispersions at the center of the Brillouin zone are expected to be split only by the spin-orbit coupling [76], as shown in Figure 3A. Experimentally, the band separation gives a spin-orbit of ∆_so ∼ 13(3) meV for FeSe in the tetragonal phase at high temperatures and for the tetragonal x ∼ 0.18 at low temperatures [62, 63, 80]. As the nematic order is turned on, ${\varphi }_{\text{Γ}}$ [76], the hole pocket is expected to become distorted and the splitting between the two hole band dispersions increases, as shown in Figure 3. In addition, the increase in the orbital ordering effects moves the inner 3D hole pocket at the Z point completely below the Fermi level, as shown in Figure 2 [40, 81]. Experimentally, at low temperature FeSe has only one quasi-two dimensional hole Fermi surface (compared with 3 predicted by the DFT calculations) with an elliptical in-plane area at the high symmetry points, as shown in Figure 2E. The signature of this nematic electronic phase can be induced by orbital-ordering effects and electronic interactions that can drive a Pomeranchuck instability of the Fermi surface [2]. Other scenarios have been addressed theoretically in detail in other works [82–86]. Since samples of FeSe_1−xS_x inside the nematic phase can form twin domains rotated by 90° below T_s often ARPES experiments visualizes two superposed ellipses, as shown in Figure 2E, but only a single ellipse may be observed in detwinned measurements on FeSe [63, 64, 81]. As the orbital ordering is reduced with S substitution, the splitting between the inner d_yz bands and outer d_yz hole band dispersion is smaller and at low temperatures from x ∼ 0.11, the inner hole band crosses the Fermi level at the Z point, leading to the formation of the small 3D hole pocket. Inside the nematic phase, the in-plane Fermi surfaces are highly anisotropic, indicated by the splitting of the two different k_F values (obtained from the MDC cuts of two different domains), as shown in Figure 3. With increasing x, in-plane Fermi surface becomes a circle for both hole pockets for the tetragonal x ∼ 0.18 but the cylindrical hole Fermi surface has a strong k_z dependence [29].

4.3 Electron Pockets of FeSe_1−xS_x

Whereas the behavior of the hole bands is well understood and consistent between different experimental reports, the behavior of the electron bands remains a highly debated subject. The P4/nmm unit cell of tetragonal FeSe includes two Fe sites which are related by a glide symmetry [76] and ARPES measurements should detect electron bands emerging from two-crossed ellipses [58, 87], similar to other systems, such as LiFeAs or NaFeAs [80]. The electron pockets suffer a significant change inside the nematic phase and the relevance of different orbital contribution is still being debated. At the corner of the Brillouin zone (M and A point) in the tetragonal phase, there are two degenerate doublet states, M1 and M3, at the zone corner protected by the space-group symmetry, even when spin-orbit coupling is taken into account [76], as shown in Figures 3C,D. Therefore, any splitting and shifts of the bands at M (or A) would reduce the crystal symmetry in the presence of the spin-orbit coupling. The nematic order can be triggered by the development of the anisotropy in the on-site energies of the d_xz and d_yz orbitals (${\varphi }_1$ term) and anisotropic d_xy hopping (${\varphi }_3$ term) [76]. The two-crossed ellipse, corresponding to the electron pockets (Figure 2H), are expected to have a finite splitting between the inner and outer orbits, due to the spin-orbit coupling in the tetragonal phase, as shown in Figure 3C. Inside the nematic phase, by increasing both the ${\varphi }_1$ and ${\varphi }_3$, the degeneracy at the M1 and M3 points are lifted and the bands split apart; this promotes the in-plane distortion of the Fermi surface along its longest axis (Figures 3C,D). Further increasing ${\varphi }_1$, which is related to orbital order induced by the increase orbital polarization of the d_xz vs. d_yz bands, the inner electron band is pushed up and eventually it can disappear; thus only a single electron pocket is present, as shown in Figure 3D. Furthermore, orbitally-induced shifts could shrink the electron pocket along one direction, transforming it into two small Fermi pockets, whereas along the other direction, the electron pocket is enlarged into a peanut shape [63, 88]. Indeed, at low temperatures, the band giving rise to the inner electron pocket at the M point is very close to the Fermi level about 3 meV for FeSe (within experimental resolution of 3 meV). This proximity creates the conditions for a topological transition of the electron pocket into a peanut or Dirac-like crossing, under other perturbations, such as applied strain [65, 73], as found for thin films of FeSe under internal strain from the substrate [88].

Experimentally, in the tetragonal phase the inner electron band dispersions at M (or A) are expected to have d_xz/d_yz orbital character when probed along the diagonal of the Brillouin zone, as shown in Figure 2H. The outer electron band with d_xy orbital character is harder to observe due to matrix element effects and the incident energy used (Figures 2C,J). This behavior is detected for the tetragonal FeSe_1−xS_x with x = 0.18 shown in Figure 2C; [29] and FeSe above T_s [40, 58, 62]. In the nematic phase, the changes for the electron bands are drastic, with M1 point shifting up whereas the M3 shifts down, and additional splitting could take place around these two degenerate points, as shown in Figure 2C. The energy separation between the two intense features at the M point below T_s (EDC cuts), is defined by ∆_M which is ∼50 meV for bulk FeSe [62, 64, 89]. This splitting is much larger than what would be expected from DFT calculations simply taking into account its small orthorhombic distortion (∼5 meV) [62]. The elongated directions of the elliptical Fermi surfaces at the M point are rotated by 90° with respect to that at the $\text{Γ}$ point due to the momentum-dependent sign-changing orbital polarization, where the d_xz band shifts upward at the $\text{Γ}$ point but downward at the M point [81, 90]. Interestingly, 20 meV already separates the two doublets in the tetragonal phase at the M point, in the absence of nematicity, for the tetragonal system with x = 0.18 (see Figure 2G), and FeSe at high temperatures [63]. This implies that the energy scale of the nematic order could be smaller that 50 meV, as shown in Figure 4A [35].

A direct signature of the nematicity is the in-plane distortion of the Fermi surface. Inside the nematic phase for the electron pockets this can be related to the development of the orbital polarisation ∆n = n_xz−n_yz. The orbitally dependent band shifts cause the inner sections of the electron pockets with d_yz orbital character to contract whereas the d_xz sections to expand, but forming a cross-shape due to effect of sample twinning, as shown in Figure 1F. The degree of anisotropy of the Fermi surface can be related to (k_F−k_F0)/k_F0 [40]. where the k_F-vector is that corresponding to the inner d_yz portion of the electron pocket, and k_F0 is the Fermi k-vector in the tetragonal phase for each compound. Figure 4B shows the evolution of the Fermi surface elongation with x substitution and indicates that the nematic phase is responsible for this in-plane distortions, which is completely suppressed in the tetragonal phase.

4.4 Comparison Between ARPES and QPI

The presence of both highly elongated and isotropic Fermi surfaces of FeSe_1−xS_x is likely to significantly influence other measurements. Scanning tunneling microscopy (STM) studies shows highly anisotropic quasiparticle interference (QPI) patterns inside the nematic state, becoming isotropic in the tetragonal phase [46, 78]. The resulting QPI spectra exhibit electron-like and hole-like dispersions along different directions (q_a and q_b, respectively) corresponding to the intraband back-scatterings in the electron bands at the Brillouin zone corner and in the hole band at the zone center, respectively. Thus, the QPI spectra reflect the evolution of the scattering processes across the series FeSe_1−xS_x.

To clarify the qualitative relation between the QPI branches and the band structure, the scattering q vectors from the intraband backscattering can be compared with the Fermi wavevector extracted directly from ARPES dispersions at the Fermi level, as shown in Figure 4C. The Fermi momenta of FeSe of a distorted deformed Fermi cylinder can be estimated from the scattering vectors at zero energy (q/2∼k_F) to be ∼0.05 and 0.08 Å⁻¹ for the hole band and ∼0.04 Å⁻¹ for the electron band [37, 46]. On the other hand, the Fermi wavevector from ARPES for FeSe for the elliptical hole pocket at the $\text{Γ}$ point varies between ∼0.035 and 0.08 Å⁻¹ [40, 62], but is larger at the Z point (∼0.1 and 0.15 Å⁻¹), as shown in Figure 4C. These values are close to those from laser ARPES data (which are usually measured around 7 eV which corresponds to a k_z position closer to the $\text{Γ}$ point), varying between $0.036\pi /a\sim 0.038$ and $0.11\pi /a\sim 0.092$ Å⁻¹. Thus, the resulting elongated hole ellipse of FeSe, with a high aspect ratio (∼3), is one of the most anisotropic Fermi surfaces among all the iron-based superconductors [91].

A direct comparison between ARPES and QPI data on FeSe_1−xS_x suggest that the scattering vectors in QPI are likely to correspond to the in-plane Fermi vectors at the center of the Brillouin zone (k_z = 0). This is in agreement with the assignment of the scattering vectors in Ref. 78. They are less sensitive to k_z dependent scattering processes outside of this plane, despite recent theoretical suggestions for FeSe [92], as the k_F vectors at Z are much larger than the scattering vectors (q/2) extracted from QPI, as shown in Figure 4C. In the case of the electrons pockets, the QPI scattering vector is close to those of the small inner electron wave vector (∼0.02(1) Å⁻¹) rather than to the long elongated axis of the ellipse (0.14 (1) Å⁻¹), found in ARPES [35, 58]. Furthermore, the estimated Fermi energies from the QPI dispersions, for the hole bands are of 10–20 meV [46], in good agreement with the top of the hole band at the $\text{Γ}$ point of ∼17 meV from ARPES [35, 62]. Laser ARPES data (measured away from a high-symmetry point) give slightly lower values of ∼6.7 meV or 10 meV for the hole band [91, 93]. For the electron bands the Fermi energies of 5–10 meV from QPI are close to the 3–5 meV corresponding to the inner electron band dispersion [35, 63]. With increasing x, the bottom of the inner electron bands at the M point is pushed lower below the Fermi level from about 3 meV toward 15 meV for x = 0.18 [29, 95]. The outer hole band crossing at the Z point lies around 25 (3) meV from x = 0 to x = 0.18, but decrease more significantly for the hole point at the $\text{Γ}$ point (Figure 4D). These shifts bring the cylindrical hole band into the regime to undergo a possible Lifshitz transition at the nematic end point, as suggested by quantum oscillations [27].

The evolution of the QPI scattering vectors along one direction performed in a single domain of FeSe_1−xS_x have been associated to two scattering vectors along short elliptical axis in different scattering planes: q_h2 at k_z = 0 ($\text{Γ}$ point) and q_h1 at k_z = $\pi /c$ (Z-point) [46]. The QPI dispersion associated with the q_h1 scattering vector at the Z-point was suggested to disappear close to x ∼ 0.1, whereas q_h2 increases toward x ∼ 0.25, as shown in Figure 4C. However, there is no evidence for the disappearance of hole bands up to x = 0.18 in ARPES data at the Z point, as shown in Figures 2A–C and Figure 4C. An alternative explanation could invoke a scenario in which the two scattering vectors (q_h1 and q_h2), would merge into a single value for a isotropic Fermi surface close to x ∼ 0.17. Thus, for an isotropic system a single hole dispersion could be visible in the QPI and in that case the scattering vectors along orthogonal direction would be similar to those from ARPES at the $\text{Γ}$ point. As QPI is less sensitive to k_z dependent scattering processes, the small 3D hole band at the Z point in Figure 4C is not detected [46]. Further experimental QPI experiments with cuts along different directions as well as theoretical work will be needed to reconcile quantitative features obtained from ARPES and QPI for FeSe_1−xS_x.

5 Quantum Oscillations in High Magnetic Fields

A powerful technique to access directly the Fermi surface of FeSe_1−xS_x is via quantum oscillations in very high magnetic fields and at low temperatures below 1.5 K [27, 42, 62, 95]. Quantum oscillations originate from the oscillations in the density of states in the presence of the Landau quantization of a metallic system in an applied magnetic field. The quantum oscillations are periodic in 1/B and the frequency of these oscillations relates directly to extremal areas of the Fermi surface via Osanger relation ($F_i=\hslash /2\pi e\cdot A_{k_z,i}$ with frequencies in Tesla ∼10⁻¹⁶ (Å⁻²) of the cross-section area of each orbit). For a slightly-warped cylindrical Fermi surface two frequencies would be observed at the center (k_z = 0) and the top of the Brillouin zone $\left(k_z=\pi /c\right)$, and in the case of twinned crystals the cross section areas of different domains would coincide. Quantum oscillations are normally observed only in clean single crystals as the cyclotron energy which separates Landau levels needs to be larger than the broadening of the levels $\hslash /\tau$ due to scattering. Quantum oscillations have been observed for all x compositions of FeSe_1−xS_x [27, 42, 67, 96]. The isoelectronic substitution result in relatively similar mean free paths (using the Dingle analysis for the maximum hole band orbit [98]), having values of $\ell$ ∼ 277 (35) Å for FeSe and $\ell$ ∼ 283 (20) Å for x ∼ 0.19 [27]. Besides impurity scattering effects, the amplitude of the quantum oscillations is significantly suppressed for heavier quasiparticle masses as a result of the smearing of the Landau levels by the Fermi-Dirac distribution and often heavier masses cannot be observed.

5.1 Comparison Between ARPES and Quantum Oscillations

As compared with ARPES, quantum oscillations are insensitive to surface states and the signal is dominated by the bulk response thus giving an unambiguous probe of the bulk Fermi surface. Furthermore, they have a much better k-space resolution of 10³ of the area of the Brillouin zone that allows very accurate determination of the cross-section orbits on the Fermi surface, for a particular magnetic field orientation. However, the location of the orbits in the k-space is not easily known for multiband systems (Figures 1D–G) making the assignment of the potential frequencies for a multi-band system difficult. In these circumstances, the angular dependence of the observed orbits is used as a guide to assign the different orbits to Fermi surfaces as the minimum and maximum orbits will have different angular dependencies and it is expected that the cyclotron effective mass for the same band is likely to have similar values [42, 62]. Even in twinned samples, the quantum oscillations are likely to be unaffected as the cross-section areas originating from different domains would be the same, however, any differences only be noticeable at very high rotation angles where the quantum oscillation amplitude disappears. The experimental Fermi surface of FeSe_1−xS_x could potentially have four different sheets, that could generate up to seven or eight extremal orbits at the high symmetry points due the strong k_z dependence, as shown in Figure 5D. In a system with many similar small orbits (with k_F values below 0.08 Å) the expected frequencies would be found below 200 T. A clear separation between individual small frequencies is hampered by the limited magnetic field window (20–45 T) caused by the presence of superconductivity and large upper critical field (<20 T) (Figure 5A. This low frequency region is also affected by extrinsic effects in a fast Fourier transform (Figure 5C, such as the 1/f noise and the peak created by a background polynomial, making any reliable assignment of the small frequencies difficult.

FIGURE 5

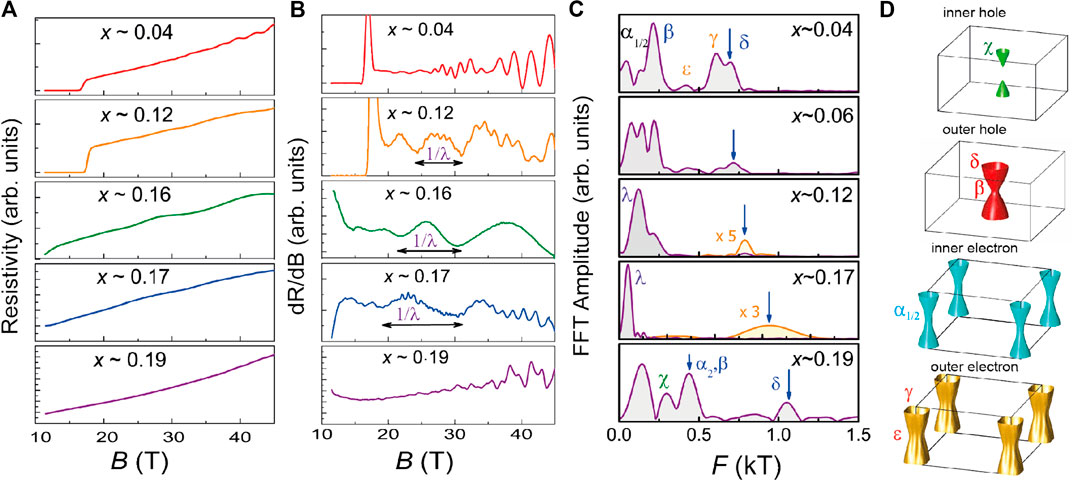
FIGURE 5. Quantum oscillations in FeSe_1−xS_x. (A) The in-plane longitudinal resistivity ρ_xx(B) as a function of magnetic field B for different compositions, x, measured at T ∼ 0.35 K (B) The oscillatory part of the resistivity visualized better by the first derivative of resistivity dρ_xx/dB, as a function of magnetic field from (A–F) at the lowest measured temperature. The horizontal line indicates the period of the low-frequency oscillations $\left(\sim 1/\lambda \right)$. (C) The frequency spectra of the oscillatory signal ($\text{Δ}{\rho }_{osc}$/ρ) obtained by subtracting a polynomial background and using a fast Fourier transform (FFT). A multiplied FFT spectrum is used to emphasize the weak high frequency δ frequency for certain x compositions indicated by vertical arrows. The proposed Fermi surface and the different extremal areas for FeSe_1−xS_x obtained by shrinking the calculated tetragonal Fermi surface of FeSe from Figure 1E. Frequencies below 200T cannot be reliably assigned due to a possible overlap of at least 3 different small frequencies (α₁, α₂, and χ). These graphs are adapted from Ref. 27.

An interesting insight into the origin of the quantum oscillation amplitudes was provided by magnetotransport and Hall effect in ultra-high magnetic fields up to 90 T in FeSe [98]. By comparing the changes in the relative amplitudes of the quantum oscillations of the ${\rho }_{xx}$ and ${\rho }_{xy}$ components, and considering the positive sign of the high-field Hall signal at very low temperatures [98], the mobile carriers were assigned to the hole band (β and δ orbits) [42, 62, 96]. The frequencies of quantum oscillations assigned to the quasi-two dimensional hole cylinder of FeSe are 220 T for β orbit at the $\text{Γ}$ point and 660 T for the δ orbit at the Z point, when magnetic field $B\left|\right|c$. The cyclotron effective masses associated with these two orbits are around 4.5(5) m_e, in good agreement between different studies [35, 42, 62]. The estimated frequencies of the hole pockets using the k_F values from ARPES data (Figure 4C) are consistently smaller than those assigned in quantum oscillations (by ∼150 T or 24% smaller for the δ orbit at the Z point and $\sim 100$ T or 50% smaller for the β orbit at the $\text{Γ}$ point for FeSe). One obvious difference between the two techniques is related to sensitivity to surface states in ARPES, compared with bulk, that is normally probed by quantum oscillations. ARPES resolution, k_z dependence and the energy and momentum integrations is expected to affect the precise k_F values. Variation of the values for the top of the hole band at the $\text{Γ}$ point of 6.7–15 meV is found between different reports for FeSe [62, 93], and this will affect the precise determination of the k_F values. On the other hand, the high frequency values from quantum oscillations have a much better agreement between different reports [42, 62, 96]. Quantum oscillations are measured below 1 K in high magnetic field above 20 T whereas ARPES is measured in zero field above 10 K (∼1 meV). As inner pockets of FeSe_1−xS_x are small, magnetic field could induce additional spin-polarization of the Fermi surfaces in very high magnetic fields (3–4 meV). Another discrepancy between quantum oscillations and ARPES is related to the orbitally averaged effective masses that are larger for the outer electron bands (∼7 m_e) compared with the hole bands (4.5 m_e) in quantum oscillations [42, 62]. In contrast, the Fermi velocities extracted from ARPES are larger at the A point (0.66 eV Å) compared with hole bands at the Z point (0.4–0.5 eV Å) [65]. However, the velocities in ARPES are extracted for only one of the highly symmetry direction and the values are not orbitally averaged (Figure 2).

Quantum oscillations in iron-based superconductors detect clearly electron Fermi surfaces with lighter effective masses in LaFePO [99], LiFe(As/P) [100] and BaFe₂As₂ [56]. These orbits originate from inner and outer quasi-two dimensional cylinders due to the finite spin-orbit coupling, as depicted for FeSe_1−xS_x in Figure 3C. In FeSe, the orbital differentiation is much more pronounced than in iron pnictides, as the d_xy band is involved in the formation of outer flower-shaped electron orbit (Figure 2H). This would lead to a much heavier orbitally averaged cyclotron mass of ∼7 m_e, associated with the outer electron orbit around the A point (γ orbit of ∼560 T) for FeSe, as shown in Figure 6A [42, 62]. Based on k_F values at the A point determined from ARPES with Fermi vector values of 0.03 (1) and 0.19 (1) Å⁻¹ [65], the area of a flower-shaped orbit would be ∼350 T (or ∼35% of γ orbit) whereas for a single ellipse pocket reaches only ∼190 T, which is or ∼66% smaller than the γ orbit from quantum oscillations. In ultra high magnetic fields, potential breakdown orbits could be generated by tunneling across the gaps created by the spin-orbit coupling, but the necessary magnetic fields are likely to be very large and the orbits would be smaller than that of the flower-shaped orbit [101]. The nematicity has a drastic effect on the electron bands and it can lead to highly elongated pockets with a very small inner electron band, as shown in Figure 3C. At 13 K, the inner band at the M point gets very close to the Fermi level within 3 meV for FeSe (within the experimental resolution). Thus, any small changes in the band positions relative to the chemical potential (1–2 meV) that could occur at low temperatures below 1.5 K and in high magnetic fields could potentially push the inner electron bands above the Fermi level at the M point and lead to single elliptical orbit or an elliptical pocket and two tiny electron pockets, as shown in Figure 3C.

FIGURE 6

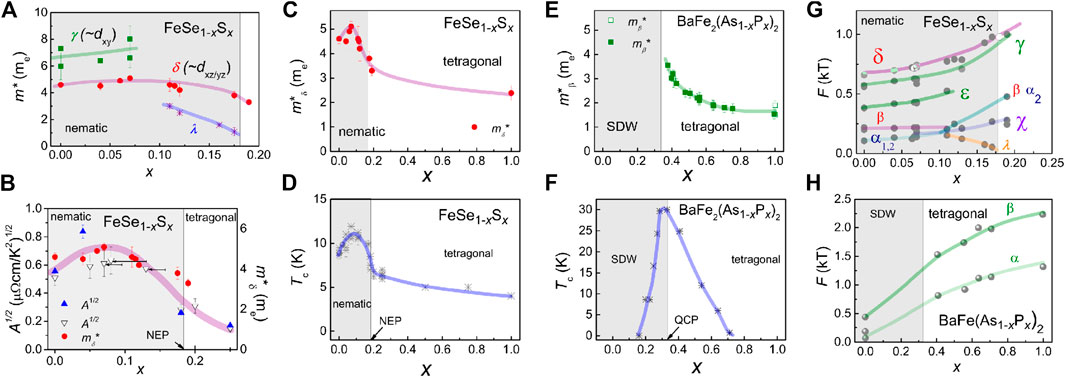
FIGURE 6. Electronic correlations of FeSe_1−xS_x compared with BaFe₂(As_xP_1−x)₂. (A) The quasiparticle effective masses of the high frequencies, γ and δ and the dominant low frequency, λ. Solid lines are guides to the eyes. Grey areas indicate either the nematic phase for FeSe_1−xS_x or the spin-density wave (SDW) for BaFe₂(As_xP_1−x)₂. (B) Comparison between the Fermi liquid coefficient A and the effective masses for different compositions of FeSe_1−xS_x. The band masses of the δ orbit (from Ref. 27) are compared to A^1/2, extracted from the low temperatures Fermi-liquid behavior, and shown as solid triangles (after Ref. 28). Data shown as open triangles were reported in Ref. 54 using nominal x_nom values and they are shifted in x to smaller values (as indicated by horizontal arrows) to match the real concentration based on the values of T_s, as reported previously [27, 43]. The nematic end point (NEP) occurs close to x ∼ 0.175(5)[27, 43] and the solid thick lines are guides to the eye. The comparison between the effective mass of maximum orbit of the outer hole (at the Z point), δ, in FeSe_1−xS_x in (C) and the maximum orbit β of the outer electron band (at the A point) in tetragonal phase of BaFe₂(As_xP_1−x)₂[56, 106] in (E) together with the evolution of the superconducting critical temperature, T_c in (D) and (F), respectively. The quantum oscillations data for FeS are from Ref. 96. A qualitative correlation is found between the T_c and the electronic correlations for the two systems, but superconductivity in the vicinity of the SDW is a fact 3 stronger than in FeSe_1−xS_x. Superconductivity is enhanced at the magnetic critical point in BaFe$2$(As_xP_1−x)₂ but this does not occur at the nematic end point in FeSe_1−xS_x, suggesting that the nematic fluctuations are not the main driver for superconductivity. Instead, a local peak in $T_c$ inside the nematic phase may signify an enhanced low-energy spin fluctuation in this regime [44]. The evolution of the multiple observed quantum oscillations frequencies of FeSe_1−xS_x in (G) compared with those of BaFe₂(As_xP_1−x)₂ in (H). The lines are guides to the eye to indicate the potential origin of the observed frequencies. Frequencies of FeS are also larger [95]. Pronounced Fermi surface shrinking is observed in both systems as the electronic correlations are enhanced.

Recent studies promotes the idea that FeSe would only have a single electron pocket in the corner of the Brillouin zone. For a peanut-like pocket at the A point [65] its area is almost a factor 3 smaller than the γ pocket in quantum oscillations, the change compensation of the system would be lost and the magnetotransport data of FeSe cannot be explained [98]. The proximity of the inner electron band to the Fermi level is highly sensitive to small energetic alterations within experimental resolution (∼3 meV), any differences in Fe stoichiometry, surface effects or the possible changes that can occur under applied uniaxial stress, as found for thin films of FeSe under strain from a substrate [91]). Thus, different scenarios related to the fate and the number of the electron pockets (Figure 3C) need to be considered, besides other theoretical reasons [65, 66, 102–104].

Figure 5C show the complex fast Fourier spectra of FeSe_1−xS_x due to the presence of multiple small Fermi surfaces areas. The signature associated with the inner electron band in quantum oscillations would be a peak in the Fast Fourier transform below 100 T. Previously, it was assumed that FeSe has a single cylindrical electron pocket, with areas varying between 50 T pocket for its minimum and 550 T (γ) for its maximum [42]. This variation would suggest a much more warped Fermi surface cylinder for the electron band (factor 10 between the two high symmetry areas), as compared with the hole band, for FeSe, in disagreement with the k_z dependence determined from ARPES studies [35, 62, 65]. The quantum oscillations spectra could assign the lowest frequency below 100 T to the inner quasi-two dimensional electron pocket, whereas γ and ϵ around 440 T could correspond to the outer electron band (Figure 5D) [35, 62]. A small inner electron pocket is not easy to observe using spectroscopic techniques, nor does it have a large contribution to the density of states, but it plays an important role in magnetotransport due to its high mobility [40]. With sulfur substitution for small x < 0.09, quantum oscillations show similar features to those of FeSe, as shown in Figure 5C. As the nematic effects are progressively removed, the inner electron orbits would increase in size, reaching a value of 200 T in FeS [67].

5.2 Evolution of Fermi Surface Areas of FeSe_1−xS_x

The overall evolution of the Fermi surface of FeSe_1−xS_x implies that the majority of the cross-sectional areas expand as a function of chemical pressure, in particular the maximum orbits located at the top of the Brillouin zone, as shown in Figure 6G [27]. For the outer hole band (δ orbit), the increase in areas reflects the transition from an in-plane anisotropic to isotropic Fermi surface, as the ellipse transforms into a circle, and as the in-plane areas increase due to changes in the lattice parameters [29, 35, 40]. These trends are in contrast to the small Fermi surfaces observed under applied pressure in FeSe, suggested to result from Fermi surface reconstruction inside the spin-density phase [18]. However, the Fermi surfaces of FeSe_1−xS_x are severely reduced in size compared with those predicted by DFT calculations (varying from a factor of 5 for FeSe toward a factor 3 for x ∼ 0.17). This shrinking is an important consequence of strong orbitally-dependent inter- and intra-band electronic interactions, significantly large in iron chalcogenides [62, 105], but also found in many iron-based superconductors [56, 99]. These effects are suppressed once the bandwidth increases with sulfur substitution toward FeS [29] or with phosphorus substitution in BaFe₂(As_xP_1−x)₂, as shown in Figures 6G,H [56]. The largest orbit detected in FeS is almost a factor 2 larger than for x ∼ 0.19 [67] but it is still a factor 2 smaller than that predicted by band structure, and band-shifts of 0.1 eV are required to bring experiment in agreement with DFT calculations [67]. The Fermi energies estimated from quantum oscillations of FeS have significantly increased to 27–102 meV [67], compared with 3–18 meV estimated for FeSe [42].

Transport measurements in a multi-band system like FeSe_1−xS_x are normally dominated by the pockets with the highest mobility carriers in a parallel resistor model. The magnetoresistance at low temperatures shows a prominent low frequency oscillation from x = 0.12 toward NEP (Figures 5A,B) [27]. Outside the nematic phase, the background magnetoresistance is almost quadratic in magnetic field and the dominant low-frequency oscillation has disappeared (Figure 5). This dominant low frequency is not detected at higher sulfur substitution or higher pressures beyond the nematic end point inside the tetragonal phase [27, 39]. In quantum oscillations, the disappearance of a frequency could be linked to a possible Liftshitz transition, which is a topological change of the Fermi surface in which the neck of a quasi-two dimensional is disconnected while the top of the cylinder expands such that the volume remains the same [107]. ARPES data indicate that a small inner 3D hole pocket centered at Z is expected to emerge from x ∼ 0.11, as shown in Figure 1. This small 3D pocket is supposed to grow in size with x, rather than to disappear. However, in high magnetic fields, this 3D hole pocket could become heavily spin-polarized and, therefore, one of its polarized sheet could disappear at the nematic phase boundaries. Another scenario can rely on the strong increase in the interlayer warping as a function of chemical or applied pressure, as the conducting layers come closer together when c axis decreases. DFT calculations of FeSe and FeS show indeed that the hole bands are highly sensitive to the position of the chalcogen atom above the Fe plane [29, 58, 62]. ARPES studies for the tetragonal x ∼ 0.18 suggest that the hole band at the $\text{Γ}$ point is smaller compared with FeSe and the top of the band is about 5 meV above the Fermi level, as shown in Figure 4D [29, 35]. Thus, the orbit associated with the hole band at the $\text{Γ}$ point could be a prime candidate for the observed disappearance of a significant frequency in quantum oscillations. Other scenarios could invoke magnetic field-induced Lifshitz transitions affecting the bands with very small Fermi energies, such as the inner hole and electron bands, that are comparable to the Zeeman energy (3–4 meV) [108]. Multi-band interference effects as well as oscillations of the chemical potential could be considered as other potential theoretical avenues to understand these effects in magnetic fields [109].

5.2 Electronic Correlations at a Putative Nematic Critical Point

The cyclotron-averaged effective masses of the quasiparticles for each extremal orbit can be extracted from the temperature dependence of the amplitude of the quantum oscillations [27, 110]. The quasiparticle masses associated with the largest hole orbit δ around the Z point increase slowly from 4.3(3) m_e toward a local maximum around x < 0.11 before the values continue to decrease outside the nematic phase to around 3.2 (5) m_e for x ∼ 0.19. In the end compound FeS, quantum oscillations have revealed very light effective masses ranging from 0.6–2.1 m_e [67, 95]. The overall trends shows that cyclotron masses are larger inside the nematic phase of FeSe_1−xS_x but they are getting lighter with the increasing bandwidth [57]. The reduction of the electronic correlations toward FeS is supported by the enhanced velocities from ARPES, shown in Figure 4E [29]. The effective mass of the prominent small frequency oscillation (λ) is small below 2 m_e. Due to its heavy mass and its possible proximity to the δ orbit, the γ orbit (with some orbitally averaged d_xy character) cannot be detected over the entire range but it is expected to follow similar trends to the hole bands effective mass (δ) and to the electronic contribution to the specific heat (Figure 6A) [27, 30].

The nematic state of FeSe_1−xS_x is a correlated electronic state based on the quasiparticle effective masses. Interestingly, the electronic correlations assigned to the orbits with predominant d_xz/d_yz character (outer hole band, δ) follow similar trends as T_c, as shown in Figures 6C,D, suggesting that this quasi-two dimensional hole band is likely to play a dominant role in the pairing mechanism. The trends in the effective masses are in good agreement with those from specific heat studies on FeSe_1−xS_x that show a slight increase in the Sommerfeld coefficient (7–9 mJ/mol K) inside the nematic phase before being smoothly suppressed, without any enhancement at the nematic end point [30, 111, 112]. Additionally, the Fermi liquid behavior A^1/2 coefficient extracted from the low temperature resistivity measurement has the same trends like the cyclotron mass [28], as shown in Figure 6, and it decreases slowly in the tetragonal phase [52]. Note that these values of the A^1/2 coefficient agree with those reported in Ref. 54, once adjusted for the correct value of x based on the T_s of each sample, shown by the open triangle in Figure 6B.

To asses the nematic critical behavior in FeSe_1−xS_x, it is worth emphasizing that the electronic correlations and the orbitally averaged cyclotron masses do not show any divergence close to NEP (x ∼ 0.175(5)), as shown in Figure 6C [27]. Instead, the effective mass of FeSe_1−xS_x reaches the largest value deep inside the nematic phase, where the superconductivity is the strongest and the low-energy spin-fluctuations are expected to be the largest [44]. The lack of divergent effective masses at NEP points toward a finite coupling of the electronic system with the underlying lattice that can suppressed the critical nematic fluctuations, except along certain directions in FeSe_1−xS_x [6]. Nematic susceptibility as a function of chemical pressure suggest the possibility of having a nematic critical point in FeSe_1−xS_x [43]. However, at low temperatures there are no divergent electronic correlation in any of the measured quantities in the vicinity of the nematic end point, suggesting an important role for the coupling of the electronic system with the lattice in this system [27, 28].

Signatures of quantum criticality caused by diverging spin fluctuations were detected in quantum oscillations in BaFe₂(As_1−xP_x)₂, by approaching the spin-density wave phase from the tetragonal phase. The cyclotron effective mass of the outer electron bands increases from 1.8 to 3.5 m_e over a large compositional range (x = 0.4–1) in the tetragonal phase, as shown in Figure 6E [56, 106]. This enhancement of the effective mass in BaFe₂(As_1−xP_x)₂ correlates directly with the strong increase in the superconducting transition temperature. The quantum oscillations frequencies originate from the lighter electron bands in BaFe₂(As_1−xP_x)₂ and their frequencies get smaller as the system evolves from the metallic tetragonal phase toward the spin-density wave phase. These trends are similar to those expected for FeSe_1−xS_x. It is worth emphasizing that for both systems only the effective mass is reported, not the mass enhancement in relation to the band mass, due to the complexity involved in establishing the details of the correct band structure for the mixed isoelectronic systems. Figure 6 compares the effective masses for the two isoelectronic systems and it suggests that the relevant interactions that enhance the effective masses in FeSe_1−xS_x are the same that enhance superconductivity. These pairing interactions are strongest deep inside the nematic phase not at the nematic end point. Their origin could be the spin fluctuations in both systems and they are also likely to be responsible for the linear resistivity observed inside the nematic phase for FeSe_1−xS_x [28] and for BaFe₂(As_1−xP_x)₂ for x ∼ 0.33 [114]. The superconductivity is strongly enhanced in the proximity of a magnetic critical point in BaFe₂(As_1−xP_x)₂, as opposed to the small abrupt drop in T_c at the nematic end point FeSe_1−xS_x (see Figure 6D). This suggests that a strong nematoelastic effect suppresses the critical nematic fluctuations and the superconducting mechanism has a non-nematic origin in FeSe_1−xS_x [7].

5.3 The Nematic Susceptibility of FeSe_1−xS_x

A direct measurement to test for the existence of an intrinsic nematic electronic state is the determination of the nematic susceptibility, that is the related to the in-plane resistivity anisotropy under a small amount of external strain [114]. These type of studies have established that the tetragonal-to-orthorhombic structural transition in iron pnictides is driven by the electronic instability of the system [114]. The Curie-Weiss behavior of nematic susceptibility near a nematic transition is expected to display a generic mean-field behavior. The nematic fluctuations of the nematic order parameter, which couple linearly to the orthorhombic distortion via the nematoelastic coupling, are expected to be suppressed but this may not be the case if the nematic fluctuations are driven by the spin fluctuations [116]. The nematic susceptibility of Ba(Fe_1−xCo_x)₂As₂ follows a Curie-Weiss dependence and the mean field nematic critical temperature closely tracks the actual structural transition temperature, being suppressed to zero at the optimal doping [114]. The divergence of the nematic susceptibility above T_s indicates the tendency toward an electronic nematic phase transition and the Weiss temperature indicates the strength of nematic fluctuations [114]. At a critical nematic point, the nematic susceptibility should diverge at zero temperature (in proportion to 1/T) and power law behaviors in temperature and composition are expected [116].

Nematic susceptibility measurements for FeSe and FeSe_1−xS_x [43, 62], [117] indicate a large divergence above the T_s, similar to what was previously observed in Ba(Fe_1−xCo_x)₂As₂, but in the absence of magnetic order [114]. Nematic susceptibility of FeSe has an opposite sign to other pnictides [118], but similar to other chalcogenides, like FeTe [75], as the resistance along the a (AFM) direction is larger than that along b axis (FM direction). A sign-change in the in-plane anisotropy could be induced by the different scattering rates by spin fluctuations corresponding to different Fermi velocities at the hot-spots for electron- and hole-doped pnictides [119]. In FeSe, despite the lack of long-range magnetic order, the anisotropy of the in-plane resistance below T_s follows qualitatively a model assuming that the electrons are mainly scattered by magnetic fluctuations [117, 120]. Elastoresistance measurements in FeSe_1−xS_x superconductors found that the nematic transition temperature decreases with x [43], whereas the nematic fluctuations are strongly enhanced, similar to Ba(Fe_1−xCo_x)₂As₂. The observation of strong nematic fluctuations is consistent with the presence of a nematic quantum critical point, but this observation is insufficient to determine whether these fluctuations are driven by quantum criticality. Static Raman susceptibility studies show similar trends to the nematic susceptibility, and additionally it was suggested the possible stabilization of stripe quadrupole order in FeSe_1−xS_x [121]. Future studies to establish a suitable power law of the nematic susceptibility are needed [116] in order to identify whether this point represent a critical point in FeSe_1−xS_x. However, the lack of divergent electronic correlations in quantum oscillations or enhanced superconductivity at the nematic end point suggest a strong suppression of critical fluctuations in FeSe_1−xS_x.

5.4 Magnetotransport Behaviour of FeSe_1−xS_x

In multi-band systems with different carrier mobilities, the magnetoresistivity components ${\rho }_{xx}$ and ${\rho }_{xy}$ have a complicated behavior in magnetic field. In the presence of a single dominant scattering time, the magnetoresistance is expected to follow Kohler’s rule and a B² dependence [122]. In the tetragonal phase of FeSe_1−xS_x, a quadratic dependence of the magnetoresistance is found up to 69 T both at high temperature above T_s or at low temperature outside the nematic phase boundaries for x ≥ 0.19 [28]. On the other hand, inside the nematic phase of FeSe_1−xS_x, Kohler’s rule is violated and the magnetoresistance of FeSe_1−xS_x, follows an unusual B^∼1.55 power law in high magnetic fields [28]. Furthermore, scaling to a modified Kohler’s rule as a function of the Hall angle was found in the vicinity of the nematic end point [123]. Another way to understand this complex behavior is to separate different components of magnetoresistance, as suggested in Ref. 55. The coefficient of one of the extracted component has the same temperature dependence as the resistivity slope in 34 T in FeSe (Figure 7), once adjusted for the correct compositions as Refs. 54, 55 uses the nominal sulfur concentration. Furthermore, other types of magnetoresistivity scaling found for BaFe₂(As_1−xP_x)₂ [125], are not found for FeSe_1−xS_x [28, 55], and these effects are likely to occur for samples with higher impurity scattering [55].

FIGURE 7

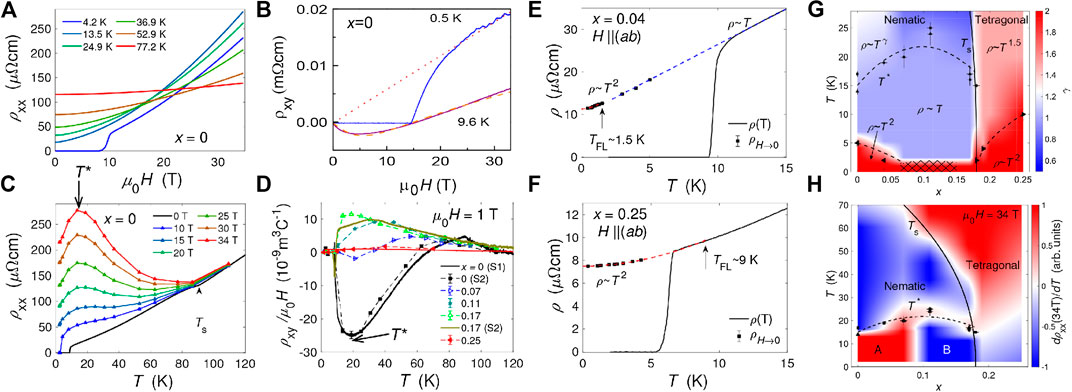
FIGURE 7. Magnetotransport behaviour of FeSe_1−xS_x. (A) Longitudinal magnetoresistance, ${\rho }_{xx}$ and (B) Hall component, ${\rho }_{xy}$ of FeSe at different fixed temperatures, after Refs. 28, 40. The dotted and dashed lines are fits to two-band and three-band models, detailed in [40]. (C) The temperature dependence of magnetoresistance in fixed magnetic field indicating significant effects inside the nematic phase. Below T* there is an unusual drop in magnetoresistance of FeSe suggesting potential changes in scattering and/or the electronic structure. (D) Hall effect coefficient in low magnetic fields ($B={\mu }_{0}H\le 1$T), indicating a sign change and the dominance of different highly mobile carriers across the nematic phase. The low-temperature linear resistivity for x = 0.04 (E) and x = 0.25 (F). The solid lines are the zero-field resistivity data. Solid circles represent the zero-field extrapolated values from high field longitudinal resistance measurements when $B\left|\right|\left(ab\right)$ plane [28]. The dashed lines represent fits to a Fermi-liquid behaviour found below T_FL, as indicated by arrows. (G) The low-temperature resistivity exponent below T*, extrapolated from high magnetic fields, indicating the unusual transport behaviour of the nematic phase. (D) The colour plot of the slope of resistivity in 34T between the nematic A and B phases. Solid squares represent T_s and solid triangles T_c. T* indicated by stars represents the peak in magnetoresistance and the maximum in of the Hall coefficient R_H. Solid lines indicate the nematic and superconducting phase boundaries and the dashed lines are guides to the eye. All the samples show clear quantum oscillations in the transverse magnetoresistance below 1.5 K [27], consistent with the presence of the Fermi-liquid behavior at low temperatures for all samples. These data are adapted after Ref. 28.

5.5 Highly Mobile Small Carriers in FeSe_1−xS_x Beyond the Two-Band Model

A compensated two-carrier model can describe the behavior of the magnetoresistance and the Hall effect of FeSe_1−xS_x in the tetragonal phase [28, 98]. For a compensated metal, the sign of the Hall coefficient depends on the difference between the hole and electron carrier mobilities [98]. At high temperatures in the tetragonal phase, the Hall effect is linear and the Hall coefficient, $R_{\text{H}}={\rho }_{xy}/B$, is close to zero as the hole and electron pockets have rather similar mobilities [98]. Inside the nematic phase, the Hall coefficient for FeSe, extrapolated in the low-field limit (below 1 T), is negative at low temperatures with a minimum around 20 K [29, 98]. These anomalies indicate that the magnetotransport behavior of FeSe cannot be described using a two-band compensated model, and an additional higher mobility charge carrier is required (with carrier concentration of 0.7 × 10²⁰ cm⁻³, a factor 5 smaller than the size of the largest band) [98, 125, 126]. This component would correspond to a Fermi surface of small volume that could be linked to the inner electron band with frequencies below 100 T and a light effective mass (∼2 m_e) [27, 42, 62]. With increasing x, the Hall coefficient at low temperatures is positive for x ∼ 0.11, suggesting the dominance of highly mobile hole carriers, as shown in Figure 7D [28]. This sign change occurs for the same composition at which the highly mobile 3D hole pocket center is detected in ARPES studies at the Z-point around x ∼ 0.11, shown in Figure 2 [40]. High mobility carriers have been suggested to dominate the magnetotransport behavior across the whole nematic phase of FeSe_1−xS_x [126, 127], Furthermore, FeSe under pressure shows similar trends to the chemical pressure effect and the normal-state Hall resistivity changes sign from negative to positive, showing dominant highly mobile hole carriers at high pressures [79].

The orbital order significantly affects band shifts for the electron bands and it can generate very small pockets, as shown in Figure 3. The presence of the small number of highly mobile carrier was suggested to be linked to the Dirac-like dispersions in the nematic phase on some sections of the electron pockets [125, 128]. Large orbital-dependent shifts of ∆_M ∼ 70 meV in FeSe thin films on SrTiO₃ have been found to generate Dirac-like dispersion around the M point [88], but these shifts are much larger than those of ∆_M ∼ 50 meV in bulk FeSe. Magnetotransport cannot distinguish whether there are two tiny electron-like pockets or one small electron pocket (Figure 3C for large ${\varphi }_3$ values), besides the almost compensated hole and electron bands in FeSe. It is clear that a two-band picture containing an single electron and hole pocket and assuming isotropic scattering fails to describe magnetotransport behavior of FeSe [98].

Significant changes in scattering could occur for a elongated nematic Fermi surface of FeSe_1−xS_x [35, 62]. Two scattering wave-vectors are detected by STM [46] suggesting different scattering processes along certain directions of an elongated ellipse [9]. A flower-shaped electron orbit would have a strongly varying angular velocity [129] and the scattering rate could vary strongly due to the changes of the orbital character on various sections induced by spin fluctuations [117, 130]. Hall effect in iron-based superconductors is also affected by the spin fluctuations that induce mixing of the electron and hole currents [131]. All these effects could lead to highly anisotropic scattering rates in FeSe_1−xS_x that are suppressed with x substitution. Indeed, in the tetragonal phase a single scattering process dominates the magnetotransport, as Kohler’s rule is obeyed [28]. Further theoretical work is needed to understand transport and magnetotransport data of FeSe_1−xS_x. Future models should account for anisotropic scattering and scattering of quasiparticles from the domain walls, when the nematic domain size (determined by the quenched disorder) is smaller than the normal state mean-free path [1].

FeSe_1−xS_x displays deviation from the Fermi liquid theory, expected for conventional metals, that affect the temperature and field dependencies of electron transport. The magnetoresistance of FeSe_1−xS_x increases significantly once a system enters the nematic state and shows an unusual temperature dependence that varies strongly with x, as shown in Figures 7A,B for FeSe. The temperature dependence of the resistivity slope in 34 T in FeSe changes sign at a characteristic temperature, T^* below 14 K, and the Hall coefficient R_H display a negative maximum, as shown in Figures 7B,D. Interestingly, T^* seems to be the characteristic scale for low-energy spin fluctuations in FeSe_1−xS_x [44, 132, 133]. Magnetostriction measurements in magnetic field for FeSe showed that the lattice distortion continues to increase down to T_c, different from BaFe₂As₂, where there is a intimate connection between the magnetic order and structural distortion [121]. With sulfur substitution, T^* shifts to a slightly higher temperature of ∼20 K, and eventually disappears in the tetragonal phase, as the low-energy spin fluctuations are completely suppressed [44, 134]. Changes in magnetotransport and in the resistivity slope occur from x ∼ 0.11 (Figure 7H) in the presence of the additional highly mobile 3D band, labeled as the nematic B phase [28]. It is clear that magnetic field could affect scattering inside the nematic phase that could be still dominated by spin fluctuations and it can spin polarize the multi-band small Fermi-surface of FeSe_1−xS_x. Further theoretical work will be required to explain the observed effects in magnetic fields and experimental studies in single domains crystals are needed to address the extrinsic scattering at the nematic domain boundaries.

5.6 Anomalous Transport Behavior

Linear resistivity at low temperatures is usually found near an antiferromagnetic critical point, such as in BaFe₂(As_1−xP_x) [11] and reflect scattering induced by critical spin-fluctuations [135]. FeSe_1−xS_x has a low temperature region with a linear resistivity across the whole nematic phase below T^* (using extrapolated in-plane high magnetic field data), as shown in Figures 7E,G. Low energy spin-fluctuations are present inside the nematic state in FeSe_1−xS_x [44, 132, 134], and μSR studies place FeSe near an itinerant antiferromagnetic quantum critical point at very low temperatures [136]. This region with linear T resistivity below T^* occurs over a limited temperature regime and the Fermi-liquid behavior recovers below T_FL and all compositions show quantum oscillations (Figures 7E–G) [27]. Deviations from Fermi-liquid behavior were also reported for FeSe [11] and linear T resistivity was detected in 35 T for x_nom ∼ 0.16 with T_s ∼ 50 K, which corresponds to x ∼ 0.13 inside the nematic phase [37, 54]. Thus, all existing experimental transport data for FeSe_1−xS_x in high magnetic fields up to 45 T suggest that the low-temperature linear resistivity occurs inside the nematic phase, rather than at the nematic end point, and, as in the case of the electronic correlations and T_c, it is likely a manifestation of the spin fluctuation scattering mechanism inside the nematic phase FeSe_1−xS_x.

In the tetragonal phase of FeSe_1−xS_x the resistivity exponent seem to vary with temperature [28, 52] and a resistivity with T^3/2 dependence is found over a large temperature range up to 120 K, in agreement with studies under pressure [39]. Theoretical models suggest that the exact temperature exponent of resistivity, in vicinity of nematic critical points is highly dependent on the presence of cold spots on different Fermi surfaces, due to the symmetry of the nematic order parameter [9, 137, 138] or due to the scattering from acoustic phonons [8] near the nematic end point. Near a Pomeranchuk instability the transport decay rate is linear in temperature everywhere on the Fermi surface except at cold spots on the Brillouin zone diagonal, leading to a resistivity proportional to T^3/2 for a clean 2D system or to a linear T dependence in the presence of impurities [137]. Furthermore, the scale at which the crossover to Fermi liquid behavior occurs at low temperatures depends on the strength of the coupling to the lattice [6], responsible for the lack of divergent critical fluctuation at the nematic end point in FeSe_1−xS_x [27, 28, 39].

6 Superconductivity of FeSe_1−xS_x

The normal nematic electronic phase and the anomalous scattering of FeSe_1−xS_x affects significantly its superconducting state. The gap structure of FeSe is two-fold symmetric, reaching small values on the major axis of the elliptical hole pocket and it is changing its sign between the hole and the small electron pocket [78, 139]. While nematicity is an intrinsic property of the bulk FeSe_1−xS_x, nematic fluctuations may not be the primary force driving the superconducting pairing [140], despite the fact that the relative orthorhombic distortion is reduced as the superconductivity increases in FeSe_1−xS_x [111]. Neutron scattering have detected substantial stripe spin fluctuations that are enhanced abruptly inside the nematic phase and a sharp spin resonance develops in the superconducting state with an energy of ∼4 meV, consistent with an electron-boson coupling mode [141]. By de-twinning crystals of FeSe via a BaFe₂As₂ substrate, the neutron diffraction spectra reveal that the spin fluctuations are highly anisotropic [13]. Theoretically, low-energy spin excitation were suggested to be stabilized by the frustrated magnetism among the local Fe moments [86, 142] or antiferroquadrupolar state in FeSe [143]. These low-energy spin-fluctuations are likely to provide the pairing channel in FeSe [144, 145] and this can manifest via nesting of d_yz sections of the hole and electron bands; the d_xy portions do not participate in pairing due to the orbital selective strong correlation effects [78, 146]. In this scenario, a maximum gap on the Fermi surface sections with d_yz character, and a small gap on sections with d_xz or d_xy character would occur, similar to experiments [78, 147]. Most of the thermodynamic and thermal conductivity studies of bulk FeSe in the superconducting phase have been modeled by accounting for two different nodeless superconducting gaps [148, 149]. The presence of nodes in the superconducting gap of FeSe has also been suggested by other studies [113, 150, 151]. The multi-gap superconductivity is preserved as a function of chemical pressure in FeSe_1−xS_x [112, 139], and tunneling experiments found that the vortex core anisotropy is strongly suppressed once Fermi surface becomes isotropic [151]. High-resolution thermal expansion showed a lack of coupling between the orthorhombic distortion and superconductivity in FeSe [12], whereas with increasing substitution toward x ∼ 0.15 the effect seems to be the opposite [111]. The jump in specific heat (∆C_el/γ_nT_c) for different x varies slightly around 2, which is above the weak coupling limit of the BCS theory believed to be caused by the multi-band effects [112].

For isotropic isoelectronic iron-based superconductors, the height of pnictogen acts as a switch between high-T_c nodeless and low-T_c nodal pairings [152]. FeS, like other end member compounds, displays weak correlations and nodal superconductivity, similar to other systems like LaFePO and LiFeP [153–156], as the chalcogen position is closer to the iron planes compared to their isoelectronic sister-compounds, like LiFeAs. On the other hand for FeSe, there has been suggestions both of nodal and nodeless superconductivity [113, 157, 158, 159, 160]. Abrupt changes in the superconductivity occur at the nematic end point, potentially stabilized by different pairing channels inside and outside the nematic phase [30, 46]. There is no superconductivity enhancement at the nematic end point in FeSe_1−xS_x, suggesting the presence of a non-nematic pairing mechanism and/or the lack of divergent critical fluctuations, similar to the behavior of the quasiparticle effective masses [27, 39]. The coupling to the relevant lattice strain restrict the critical behavior only along certain high symmetry directions and this can affect the nematic critical fluctuations and do not enhance superconductivity [6, 7].

6.1 BCS-BEC Crossover of the Multiband FeSe_1−xS_x

FeSe_1−xS_x are multi-band systems with relatively small Fermi energies at low temperatures. There has been a lot of interest to asses whether these systems are candidates in the crossover regime between the BCS to the BEC state, expected for ∆_SC/E_F ≤ 1 [161, 162]. These effects have been suggested to occur in Fe_1+ySe_xTe_1−x, as the hole band as the $\text{Γ}$ point is tuned at the Fermi level by Fe deficiency and ∆_SC/E_F varies 0.16 to 0.50 [163]. This ratio is also relevant for assessing the possibility of stabilization of a FFLO state in FeSe [164] and a good knowledge of the value of the superconducting gap and the Fermi energy of the multi-band and highly warped Fermi surfaces is needed. The amplitudes of the highly anisotropic superconducting gaps of FeSe around the hole pocket vary between ∆_SC ∼ 2.5 (or 2.3) ($\text{Γ}$ point) from STM to 1.5 meV–3 meV from laser ARPES [94]. For the electron pocket (at the M point) the values of the gap vary between 3.5 and 1.5 meV [46, 78] and another potential small gap of 0.39 meV was invoked from specific heat data [79] (Figure 4F). The top of the hole band (associated to the Fermi energy E_F) is k_z dependent having a value of 16 meV at $\text{Γ}$ point and 25 meV at the Z point (Figure 4D) [35, 62], whereas laser ARPES reports values of 6.7–10 meV [91, 93]. Based on these values, ∆_SC/E_F ∼ 0.1–0.15 for the hole band at the $\text{Γ}$ point in FeSe. This ratio will decrease using the parameters at Z point and the correct values of E_F need to take into account the strong k_z dependence of the cylindrical Fermi surface and the mass anisotropy for each pocket. As a function of x, the gap associated with the hole band remains relatively constant inside the nematic phase, but it is getting smaller toward 1.5 meV in the tetragonal phase (see Figure 4F) [46]. The top of hole band and the $\text{Γ}$ is somewhat reduced toward 5 meV for x ∼ 0.18 but increases slightly for the Z point at 26 meV; the bottom of the inner electron band is around ∼15 meV (see Figure 4F). The variation of these parameters will affect the estimates of ${\text{Δ}}_{SC}/E_{\text{F}}$ and one needs to consider the multiple bands and gaps of FeSe_1−xS_x together with the k_z dependence of the Fermi surface and the superconducting gap [93, 164]. Furthermore, the Fermi velocities increase with x pushing the system away from the BCS-BEC crossover regime, as not all the bands satisfy the crossover condition.

Another way to assess the proximity to the crossover is to check whether the size of the Cooper pair, given by the coherence length ${\xi }_{ab}$, is smaller than the mean inter-particle spacing 1/k_F and $\xi k_F\ll 1$[15, 161]. Using the in-plane coherence length for FeSe of ξ = 4.6–5.7 nm [42, 45] and the values of k_F ∼ 0.038–0.15 for the hole bands (Figure 4), it suggests that $\xi$k_F ∼ 1.75–8.55 is large and the Cooper pairs are quite extended suggesting that the superconductivity of FeSe need to be understood considering its multi-band effects. Further aspects of the pairing mechanism of FeSe and other iron-chalcogenides are discussed in detail in recent reviews [15, 37].

7 Conclusion

FeSe_1−xS_x has opened an new area of exploration of the electronic nematic state and its role in the stabilization of the unconventional superconductivity. These systems are multi-band systems which are highly sensitive to orbitally-dependent electronic interactions that affect the evolution of the electronic structure with sulfur substitution. Fermi surface of FeSe_1−xS_x are mainly quasi-two dimensional warped cylinders but an additional 3D hole pocket is present with increasing sulfur concentration from x ∼ 0.11. The Fermi energies have a broad range, that generally increases with x substitution, but they are smaller for the inner electron and hole pockets, making them prone to electronic instabilities. The development of nematic electronic phase with strong anisotropic electronic structure influences the scattering and leads to unusual magnetoresistance inside the nematic phase. Linear resistivity and anomalous magnetotransport is detected inside the nematic phase and is likely to reflect the role played by the spin fluctuations in this regime. FeSe_1−xS_x show no signatures of enhanced T_c and divergent electronic correlations at the nematic end point, which are likely to be quenched by the finite coupling with the lattice. This coupling could also be the origin of the non-Fermi liquid behavior outside the nematic phase. The superconductivity of FeSe_1−xS_x has a small enhancement inside the nematic phase and a somehow abrupt change at the nematic end point. This behavior is different from the isoelectronic family BaFe₂(As_1−xP_x)₂ where quantum critical fluctuations enhance both superconductivity and effective masses of the quasiparticles on approaching the spin-density phase and linear resistivity is found at the magnetic critical point. The study of FeSe_1−xS_x compared with other isoelectronic iron-based superconductors emphasis the important role played by the magnetic rather than nematic fluctuations for enhancing superconductivity in iron-based superconductors.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

I acknowledge the financial support provided by EPSRC (EP/I004475/1, EP/I017836/1, EP/M020517/1), Oxford Centre for Applied Superconductivity and Diamond Light Source for experimental access to the I05 Beamline. I am grateful for the experimental access and technical support received from the high magnetic field facilities at the NHMFL, Tallahassee, USA, HMFL, Nijmegen and LNCMI, Toulouse, France. Our research performed in high magnetic fields was supported by HFML-RU/FOM and LNCMI-CNRS, members of the European Magnetic Field Laboratory (EMFL) and by EPSRC (UK) via its membership to the EMFL (Grant No. EP/N01085X/1) The work performed at the National High Magnetic Field Laboratory, was supported by National Science Foundation Cooperative Agreement No. DMR-1157490 and the State of Florida. I am grateful to the KITP programme for providing the scientific interaction which was supported by the National Science Foundation under Grant No. NSF PHY-1748958. I am also grateful for an EPSRC Career Acceleration Fellowship (EP/I004475/1). I also acknowledge the University of Oxford Open Access block grant for funding open access fee.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I am very grateful to numerous collaborators for their important scientific contribution dedicated to the understanding of the electronic structure of FeSe_1−xS_x. I would like to thank warmly to Amir Haghighirad, Shiv Singh, Thomas Wolf and Shigeru Kasahara for the growth of high quality crystals; Timur Kim, Matthew Watson, Pascal Reiss and Kylie MacFarquharson for their contributions to ARPES studies; Pascal Reiss, Matthew Bristow, Zachary Zajicek, Samuel Blake, Mara Bruma, David Graf, Alix McCollam,William Knafo for their contributions to high magnetic field studies; Joe Prentice, Roemer Hinlopen, Oliver Humphries, Oliver Squire, Gladys Lee, James Bate, Andrew Smith, Tom Nicholas, Abhinav Naga, Jan Memedovic, Joshua Bell, Michele Ghini, Nathaniel Davies for their individual contributions to experimental and computational aspects that have enhancee our research. I am grateful to Rafael Fernandes for sharing his computer code and Andreas Kreisel, Peter Hirschfeld, M. Watson, Roser Valenti, Karim Zantout and Zachary Zajicek for useful comments on this manuscript.

References

1. Fradkin E, Kivelson SA, Lawler MJ, Eisenstein JP, Mackenzie AP. Nematic Fermi fluids in condensed matter physics. Ann Rev Condens Matter Phys (2010) 1:153–78.

CrossRef Full Text | Google Scholar

2. Pomeranchuk II. On the stability of a Fermi liquid. J Exp Theor Phys Lett (1959) 8:361.

Google Scholar

3. Vojta M. Lattice symmetry breaking in cuprate superconductors: stripes, nematic, and superconductivity. Adv Phys (2009) 58:699–820. doi:10.1080/00018730903122242

CrossRef Full Text | Google Scholar

4. Lederer S, Schattner Y, Berg E, Kivelson SA. Superconductivity and non-Fermi liquid behavior near a nematic quantum critical point. Proc Natl Acad Sci USA (2017) 114:4905. doi:10.1073/pnas.1620651114

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Lederer S, Schattner Y, Berg E, Kivelson SA. Enhancement of superconductivity near a nematic quantum critical point. Phys Rev Lett (2015) 114:097001. doi:10.1103/PhysRevLett.114.097001

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Paul I, Garst M. Lattice effects on nematic quantum criticality in metals. Phys Rev Lett (2017) 118:227601. doi:10.1103/PhysRevLett.118.227601

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Labat D, Paul I. Pairing instability near a lattice-influenced nematic quantum critical point. Phys Rev B (2017) 96:195146.

CrossRef Full Text | Google Scholar

8. de Carvalho VS, Fernandes RM. Resistivity near a nematic quantum critical point: impact of acoustic phonons. Phys Rev B (2019) 100. doi:10.1103/PhysRevB.100.115103

CrossRef Full Text | Google Scholar

9. Wang X, Berg E. Scattering mechanisms and electrical transport near an Ising nematic quantum critical point. Phys Rev B (2019) 99:235136. doi:10.1103/physrevb.99.235136

CrossRef Full Text | Google Scholar

10. Fernandes RM, Chubukov AV, Schmalian J. What drives nematic order in iron-based superconductors?. Nat Phys (2014) 10:97–104. doi:10.1038/nphys2877

CrossRef Full Text | Google Scholar

11. Kasahara S, Shibauchi T, Hashimoto K, Ikada K, Tonegawa S, Okazaki R, et al. Evolution from non-Fermi- to Fermi-liquid transport via isovalent doping in superconductors. Phys Rev B (2010) 81:184519.

CrossRef Full Text | Google Scholar

12. Böhmer AE, Hardy F, Eilers F, Ernst D, Adelmann P, Schweiss P, Wolf T, Meingast C. Lack of coupling between superconductivity and orthorhombic distortion in stoichiometric single-crystalline FeSe. Phys Rev B (2013) 87:180505. doi:10.1016/j.physc.2012.07.005

CrossRef Full Text | Google Scholar

13. Chen T, Chen Y, Kreisel A, Lu X, Schneidewind A, Qiu Y, et al. Anisotropic spin fluctuations in detwinned FeSe. Nat Mater (2019) 18:709–16. doi:10.1038/s41563-019-0369-5

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang Q, Shen Y, Pan B, Zhang X, Ikeuchi K, Iida K, et al. Magnetic ground state of FeSe. Nat Commun (2016) 7:12182. doi:10.1038/ncomms12182

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Kreisel A, Hirschfeld PJ, Andersen BM, On the remarkable superconductivity of FeSe and its close cousins. Symmetry (2020) 12 (9): 1402. doi:10.3390/sym12091402

CrossRef Full Text | Google Scholar

16. Medvedev S, McQueen TM, Troyan IA, Palasyuk T, Eremets MI, Cava RJ, et al. Electronic and magnetic phase diagram of β-Fe_1.01Se with superconductivity at 36.7 K under pressure. Nat Mater (2009) 8:630–33. doi:10.1038/nmat2491

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Sun JP, Matsuura K, Ye GZ, Mizukami Y, Shimozawa M, Matsubayashi K, et al. Dome-shaped magnetic order competing with high-temperature superconductivity at high pressures in FeSe. Nat Commun (2016) 7:12146. doi:10.1038/ncomms12146

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Terashima T, Kikugawa N, Kasahara S, Watashige T, Shibauchi T, Matsuda Y, et al. Pressure-induced antiferromagnetic transition and phase diagram in FeSe. J Phys Soc Japan (2015) 84:063701. doi:10.7566/JPSJ.84.063701

CrossRef Full Text | Google Scholar

19. Kothapalli K, Böhmer AE, Jayasekara WT, Ueland BG, Das P, Sapkota A, et al. Strong cooperative coupling of pressure-induced magnetic order and nematicity in FeSe. Nat Commun (2016) 7:12728. doi:10.1038/ncomms12728

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Bendele M, Ichsanow A, Pashkevich Y, Keller L, Strässle T, Gusev A, et al. Coexistence of superconductivity and magnetism in FeSe under pressure. Phys Rev B (2012) 85:064517. doi:10.1103/PhysRevB.85.064517

CrossRef Full Text | Google Scholar

21. Burrard-Lucas M, Free DG, Sedlmaier SJ, Wright JD, Cassidy SJ, Hara Y, et al. Enhancement of the superconducting transition temperature of FeSe by intercalation of a molecular spacer layer. Nat Mater (2013) 12:15–9. doi:10.1038/nmat3464

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lei B, Cui JH, Xiang ZJ, Shang C, Wang NZ, Ye GJ, et al. Evolution of high-temperature superconductivity from a low-T_c phase tuned by carrier concentration in FeSe thin flakes. Phys Rev Lett (2016) 116:077002. doi:10.1103/PhysRevLett.116.077002

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Huang D, Hoffman JE. Monolayer FeSe on SrTiO₃. Ann Rev Condens Matter Phys (2017) 8:311–36. doi:10.1146/annurev-conmatphys-031016-025242

CrossRef Full Text | Google Scholar

24. Rebec SN, Jia T, Zhang C, Hashimoto M, Lu DH, Moore RG, Shen ZX. Coexistence of replica bands and superconductivity in FeSe monolayer films. Phys Rev Lett (2017) 118:067002. doi:10.1103/PhysRevLett.118.067002

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Shigekawa K, Nakayama K, Kuno M, Phan GN, Owada K, Sugawara K, Takahashi T, Sato T. Dichotomy of superconductivity between monolayer FeS and FeSe. Proc Natl Acad Sci USA (2019) 116:24470–4474. doi:10.1073/pnas.1912836116

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Farrar LS, Bristow M, Haghighirad AA, McCollam A, Bending SJ, I Coldea A. Suppression of superconductivity and enhanced critical field anisotropy in thin flakes of FeSe. Npj Quantum Mat (2020) 5:29. doi:10.1038/s41535-020-0227-3

CrossRef Full Text | Google Scholar

27. Coldea AI, Blake SF, Kasahara S, Haghighirad AA, Watson MD, Knafo W, et al. Evolution of the low-temperature Fermi surface of superconducting FeSe_1−xS_x across a nematic phase transition. Npj Quantum Mat (2019) 4:2. doi:10.1038/s41535-018-0141-0

CrossRef Full Text | Google Scholar

28. Bristow M, Reiss P, Haghighirad AA, Zajicek Z, Singh SJ, Wolf T, et al. Anomalous high-magnetic field electronic state of the nematic superconductors FeSe_1−xS_x. Phys Rev Res (2020) 2:013309. doi:10.1103/PhysRevResearch.2.013309

CrossRef Full Text | Google Scholar

29. Reiss P, Watson MD, Kim TK, Haghighirad AA, Woodruff DN, Bruma M, et al. Suppression of electronic correlations by chemical pressure from FeSe to FeS. Phys Rev B (2017) 96:121103. doi:10.1103/PhysRevB.96.121103

CrossRef Full Text | Google Scholar

30. Sato Y, Kasahara S, Taniguchi T, Xing X, Kasahara Y, Tokiwa Y, et al. Abrupt change of the superconducting gap structure at the nematic critical point in FeSe_1−xS_x. Proc Natl Acad Sci USA (2018) 115:1227–231. doi:10.1073/pnas.1717331115

PubMed Abstract | CrossRef Full Text | Google Scholar

31. McQueen TM, Huang Q, Ksenofontov V, Felser C, Xu Q, Zandbergen H, et al. Extreme sensitivity of superconductivity to stoichiometry in FeSe (Fe1+dSe). Phys Rev B (2009) 79:014522. doi:10.1103/PhysRevB.79.014522

CrossRef Full Text | Google Scholar

32. Lai X, Zhang H, Wang Y, Wang X, Zhang X, Lin J, Huang F. Observation of superconductivity in tetragonal FeS. J Am Chem Soc (2015) 137:10148–0151. doi:10.1021/jacs.5b06687

CrossRef Full Text | Google Scholar

33. Guo Z, Sun F, Chen Y, Mao Y, Wan L, Yan X, et al. Synthesis, structure and superconductivity of FeSe_1−xS_x (0 ≤ x ≤ 1) solid solution crystals. Cryst Eng Comm (2019) 21:2994–999. doi:10.1039/c9ce00038k

CrossRef Full Text | Google Scholar

34. Abrahams E, Si Q. Quantum criticality in the iron pnictides and chalcogenides. J Phys Cond Mat (2011) 23:223201. doi:10.1088/0953-8984/23/22/223201

CrossRef Full Text | Google Scholar

35. Coldea AI, Watson MD. The key ingredients of the electronic structure of FeSe. Annu Rev Cond Matt Phys (2018) 9:125–46. doi:10.1146/annurev-conmatphys-033117-054137

CrossRef Full Text | Google Scholar

36. Böhmer AE, Kreisel A. Nematicity, magnetism and superconductivity in FeSe. J Phys Condens Matter (2017) 30:023001. doi:10.1088/1361-648x/aa9caa

CrossRef Full Text | Google Scholar

37. Shibauchi T, Hanaguri T, Matsuda Y. Exotic superconducting states in FeSe-based materials (2020) J. Phys. Soc. Jpn. 89:102002. doi:10.7566/JPSJ.89.102002

Google Scholar

38. Matsuura K, Mizukami Y, Arai Y, Sugimura Y, Maejima N, Machida A, et al. Maximizing T_c by tuning nematicity and magnetism in FeSe_1−xS_x superconductors. Nat Commun (2017) 8:1143. doi:10.1038/s41467-017-01277-x

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Reiss P, Graf D, Haghighirad AA, Knafo W, Drigo L, Bristow M, et al. Quenched nematic criticality separating two superconducting domes in an iron-based superconductor under pressure. Nat Phys (2020) 16:89–94. doi:10.1038/s41567-019-0694-2

CrossRef Full Text | Google Scholar

40. Watson MD, Kim TK, Haghighirad AA, Blake SF, Davies NR, Hoesch M, et al. Suppression of orbital ordering by chemical pressure in FeSe_1−xS_x. Phys Rev B (2015) 92:121108. doi:10.1103/physrevb.92.121108

CrossRef Full Text | Google Scholar

41. Mizuguchi Y, Tomioka F, Tsuda S, Yamaguchi T, Takano Y. Substitution effects on FeSe superconductor. J Phys Soc Jpn (2009) 78:074712. doi:10.1143/jpsj.78.074712

CrossRef Full Text | Google Scholar

42. Terashima T, Kikugawa N, Kiswandhi A, Choi E-S, Brooks JS, Shigeru K, et al. Anomalous Fermi surface in FeSe seen by Shubnikov-de Haas oscillation measurements. Phys Rev B (2014) 90:144517. doi:10.1103/PhysRevB.90.144517

CrossRef Full Text | Google Scholar

43. Hosoi S, Matsuura K, Ishida K, Wang H, Mizukami Y, Watashige T, et al. Nematic quantum critical point without magnetism in FeSe_1−xS_x superconductors. Proc Natl Acad Sci USA (2016) 113:8139. doi:10.1073/pnas.1605806113

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Wiecki P, Rana K, Böhmer AE, Lee Y, Bud’ko SL, Canfield PC, et al. Persistent correlation between superconductivity and antiferromagnetic fluctuations near a nematic quantum critical point in FeSe_1−xS_x. Phys Rev B (2018) 98:020507. doi:10.1103/PhysRevB.98.020507

CrossRef Full Text | Google Scholar

45. Bristow M, Haghighirad AA, Watson MD, Reiss P, Zajicek Z, Prentice J, et al. Multi-band effects and dominant inter-band pairing responsible for the upper critical fields of bulk FeSe (2021). in preparation

Google Scholar

46. Hanaguri T, Iwaya V, Kohsaka Y, Machida T, Watashige T, Kasahara S, et al. Two distinct superconducting pairing states divided by the nematic end point in FeSe_1−xS_x. Sci Adv (2018) 4:eaar6419. doi:10.1126/sciadv.aar6419

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Setty C, Bhattacharyya S, Cao Y, Kreisel A, Hirschfeld PJ. Topological ultranodal pair states in iron-based superconductors. Nat Commun (2020) 11:523. doi:10.1038/s41467-020-14357-2

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Setty C, Cao Y, Kreisel A, Bhattacharyya S, Hirschfeld PJ. Bogoliubov Fermi surfaces in spin-systems: model Hamiltonians and experimental consequences. Phys Rev B (2020) 102:064504.

CrossRef Full Text | Google Scholar

49. Holenstein S, Stahl J, Shermadini Z, Simutis G, Grinenko V, Chareev DA, et al. Extended magnetic dome induced by low pressures in superconducting FeSe_1−xS_x. Phys Rev Lett (2019) 123:147001. doi:10.1103/PhysRevLett.123.147001

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Chareev D, Osadchii E, Kuzmicheva T, Lin J-Y, Kuzmichev S, Volkova O, et al. Single crystal growth and characterization of tetragonal FeSe superconductors. Cryst Eng Comm (2013) 15:1989–993. doi:10.1039/C2CE26857D

CrossRef Full Text | Google Scholar

51. Böhmer AE, Taufour V, Straszheim WE, Wolf T, Canfield PC. Variation of transition temperatures and residual resistivity ratio in vapor-grown FeSe. Phys Rev B (2016) 94:024526. doi:10.1103/PhysRevB.94.024526

CrossRef Full Text | Google Scholar

52. Yi X, Xing X, Qin L, Feng J, Meng L, Zhang Y, et al. Hydrothermal synthesis and complete phase diagram of FeSe_1−xS_x$\left(0\le x\le 1\right)$single crystals. arXiv:2010.05191 (2020).

Google Scholar

53. Nabeshima F, Ishikawa T, Oyanagi K-i, Kawai M, Maeda A. Growth of superconducting epitaxial films of sulfur substituted FeSe via pulsed laser deposition. J Phys Soc Jpn (2018) 87:073704. doi:10.7566/JPSJ.87.073704

CrossRef Full Text | Google Scholar

54. Licciardello S, Buhot J, Lu J, Ayres J, Kasahara S, et al. Electrical resistivity across a nematic quantum critical point. Nature (2019) 567:213–17. doi:10.1038/s41586-019-0923-y

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Licciardello S, Maksimovic N, Ayres J, Buhot J, Čulo M, Bryant B, et al. Coexistence of orbital and quantum critical magnetoresistance in. Phys Rev Res (2019) 1:023011. doi:10.1103/PhysRevResearch.1.023011

CrossRef Full Text | Google Scholar

56. Shishido H, Bangura AF, Coldea AI, Tonegawa S, Hashimoto K, Kasahara S, et al. Evolution of the Fermi surface of BaFe₂(As_1–xP_x)₂ on entering the superconducting dome. Phys Rev Lett (2010) 104:057008. doi:10.1103/PhysRevLett.104.057008

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Miao J, Niu XH, Xu DF, Yao Q, Chen QY, Ying TP, et al. Electronic structure of FeS. Phys Rev B (2017) 95: 205127.

Google Scholar

58. Watson MD, Kim TK, Rhodes LC, Eschrig M, Hoesch M, Haghighirad AA, et al. Evidence for unidirectional nematic bond ordering in FeSe. Phys Rev B (2016) 94:201107. doi:10.1103/PhysRevB.94.201107

CrossRef Full Text | Google Scholar

59. Sobota JA, Yu H, Shen Z-X. Electronic structure of quantum materials studied by angle-resolved photoemission spectroscopy. arXiv:2008.02378 (2020).

Google Scholar

60. Brouet V, Fuglsang Jensen M, Lin PH, Taleb-Ibrahimi A, Le Fèvre P, Bertran F, et al. Impact of the two Fe unit cell on the electronic structure measured by ARPES in iron pnictides. Phys Rev B (2012) 86:075123.

CrossRef Full Text | Google Scholar

61. Moreschini L, Lin P-H, Lin C-H, Ku W, Innocenti D, Chang YJ, et al. Consequences of broken translational symmetry in FeSe_1−xS_x. Phys Rev Lett (2014) 112:087602. doi:10.1103/PhysRevLett.112.087602

CrossRef Full Text | Google Scholar

62. Watson MD, Kim TK, Haghighirad AA, Davies NR, McCollam A, Narayanan A, et al. Emergence of the nematic electronic state in FeSe. Phys Rev B (2015) 91:155106. doi:10.1103/PhysRevB.91.155106

CrossRef Full Text | Google Scholar

63. Watson M. D., Backes S., Haghighirad A. A., Hoesch M., Kim T. K., Coldea A. I., et al. (2017). Formation of Hubbard‐like bands as a fingerprint of strong electron‐electron interactions in FeSe. Phys. Rev. B 95, 081106. doi:10.1103/PhysRevB.95.081106

CrossRef Full Text | Google Scholar

64. Shimojima T, Suzuki Y, Sonobe T, Nakamura A, Sakano M, Omachi J, et al. Lifting of orbital degeneracy at the structural transition in detwinned FeSe. Phys Rev B (2014) 90:121111. doi:10.1103/PhysRevB.90.121111

CrossRef Full Text | Google Scholar

65. Watson M. D., Haghighirad A. A., Rhodes L. C., Hoesch M., Kim T. K. (2017). Electronic anisotropies revealed by detwinned angle‐resolved photo‐emission spectroscopy measurements of FeSe. New J. Phys. 19, 103021. doi:10.1088/1367-2630/aa8a04

CrossRef Full Text | Google Scholar

66. Yi M, Pfau H, Zhang Y, He Y, Wu H, Chen T, et al. Nematic energy scale and the missing electron pocket in FeSe. Phys Rev X (2019) 9:041049. doi:10.1103/PhysRevX.9.041049

CrossRef Full Text | Google Scholar

67. Terashima T, Kikugawa N, Graf D, Hirose HT, Uji S, Matsushita Y, et al. Accurate determination of the Fermi surface of tetragonal FeS via quantum oscillation measurements and quasiparticle self-consistent GW calculations. Phys Rev B (2019) 99:134501. doi:10.1103/PhysRevB.99.134501

CrossRef Full Text | Google Scholar

68. Kushnirenko YS, Kordyuk AA, Fedorov AV, Haubold E, Wolf T, Büchner B, et al. Anomalous temperature evolution of the electronic structure of FeSe. Phys Rev B (2017) 96:100504. doi:10.1103/PhysRevB.96.100504

CrossRef Full Text | Google Scholar

69. Rhodes LC, Watson MD, Haghighirad AA, Eschrig M, Kim TK. Strongly enhanced temperature dependence of the chemical potential in FeSe. Phys Rev B (2017) 95:195111. doi:10.1103/PhysRevB.95.195111

CrossRef Full Text | Google Scholar

70. Brouet V, Lin PH, Texier Y, Bobroff J, Taleb-Ibrahimi A, Le Fèvre P, et al. Large temperature dependence of the number of carriers in co-doped BaFe₂As₂. Phys Rev Lett (2013) 110:167002. doi:10.1103/PhysRevLett.110.167002

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Maletz J, Zabolotnyy VB, Evtushinsky DV, Thirupathaiah S, Wolter AUB, Harnagea L, et al. Unusual band renormalization in the simplest iron-based superconductor FeSe. Phys Rev B (2014) 89:220506. doi:10.1103/PhysRevB.89.220506

CrossRef Full Text | Google Scholar

72. Evtushinsky DV, Aichhorn M, Sassa Y, Liu ZH, Maletz J, Wolf T, et al. Direct observation of dispersive lower Hubbard band in iron-based superconductor FeSe. (2016) arXiv:1612.02313.

Google Scholar

73. Cai C, Han TT, Wang ZG, Chen L, Wang YD, Xin ZM, et al. Anomalous spectral weight transfer in the nematic state of iron-selenide superconductor. Chin Phys B (2020) 29:077401. doi:10.1088/1674-1056/ab90ec

CrossRef Full Text | Google Scholar

74. Liu ZK, Yi M, Zhang Y, Hu J, Yu R, Zhu J-X, et al. Experimental observation of incoherent-coherent crossover and orbital-dependent band renormalization in iron chalcogenide superconductors. Phys Rev B (2015) 92:235138. doi:10.1103/PhysRevB.92.235138

CrossRef Full Text | Google Scholar

75. Zhang Y, He C, Ye ZR, Jiang J, Chen F, Xu M, et al. Symmetry breaking via orbital-dependent reconstruction of electronic structure in detwinned NaFeAs. Phys Rev B (2012) 85:085121. doi:10.1103/PhysRevB.85.085121

CrossRef Full Text | Google Scholar

76. Fernandes RM, Oskar V. Distinguishing spin-orbit coupling and nematic order in the electronic spectrum of iron-based superconductors. Phys Rev B (2014) 90:214514. doi:10.1103/PhysRevB.90.214514

CrossRef Full Text | Google Scholar

77. Christensen MH, Fernandes RM, Chubukov AV. Orbital transmutation and the electronic spectrum of FeSe in the nematic phase. Phys Rev Res (2020) 2:013015. doi:10.1103/PhysRevResearch.2.013015

CrossRef Full Text | Google Scholar

78. Sprau PO, Kostin A, Kreisel A, Böhmer AE, Taufour V, Canfield PC, et al. Discovery of orbital-selective Cooper pairing in FeSe. Science (2016) 357:75. doi:10.1126/science.aal1575

CrossRef Full Text | Google Scholar

79. Sun Y, Kittaka S, Nakamura S, Sakakibara T, Irie K, Nomoto T, et al. Gap structure of FeSe determined by angle-resolved specific heat measurements in applied rotating magnetic field. Phys Rev B (2017) 96:220505. doi:10.1103/PhysRevB.96.220505

CrossRef Full Text | Google Scholar

80. Borisenko SV, Evtushinsky DV, Liu Z-H, Morozov I, Kappenberger R, Wurmehl S, et al. Direct observation of spin-orbit coupling in iron-based superconductors. Nat Phys (2016) 12:311–17. doi:10.1038/nphys3594

CrossRef Full Text | Google Scholar

81. Suzuki Y, Shimojima T, Sonobe T, Nakamura A, Sakano M, Tsuji H, et al. Momentum-dependent sign-inversion of orbital polarization in superconducting FeSe. Phys Rev B (2015) 92:205117. doi:10.1103/PhysRevB.92.205117

CrossRef Full Text | Google Scholar

82. Chubukov AV, Khodas M, Fernandes RM. Magnetism, superconductivity, and spontaneous orbital order in iron-based superconductors: which comes first and why?. Phys Rev X (2016) 6:041045. doi:10.1103/PhysRevX.6.041045

CrossRef Full Text | Google Scholar

83. Xing R-Q, Classen L, Khodas M, Chubukov AV. Competing instabilities, orbital ordering, and splitting of band degeneracies from a parquet renormalization group analysis of a four-pocket model for iron-based superconductors: application to FeSe. Phys Rev B (2017) 95:085108. doi:10.1103/PhysRevB.95.085108

CrossRef Full Text | Google Scholar

84. Jiang K, Hu J, Ding H, Wang Z. Interatomic Coulomb interaction and electron nematic bond order in FeSe. Phys Rev B (2016) 93:115138. doi:10.1103/PhysRevB.93.115138

CrossRef Full Text | Google Scholar

85. Scherer DD, Jacko A, Christoph F, Ersoy S, Stefan B, Roser V, et al. Interplay of nematic and magnetic orders in FeSe under pressure. Phys Rev B (2017) 95:094504. doi:10.1103/PhysRevB.95.094504

CrossRef Full Text | Google Scholar

86. Glasbrenner JK, Mazin II, Jeschke HO, Hirschfeld PJ, Fernandes RM, Valentí R. Effect of magnetic frustration on nematicity and superconductivity in iron chalcogenides. Nat Phys (2015) 11:953–58. doi:10.1038/nphys3434

CrossRef Full Text | Google Scholar

87. Fedorov A, Yaresko A, Kim TK, Kushnirenko Y, Haubold E, Wolf T, et al. Effect of nematic ordering on electronic structure of FeSe. Sci Rep (2016) 6:36834. doi:10.1038/srep36834

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Zhang Y, Yi M, Liu Z-K, Li W, Lee JJ, Moore RG, et al. Distinctive orbital anisotropy observed in the nematic state of a FeSe thin film. Phys Rev B (2016) 94:115153. doi:10.1103/PhysRevB.94.115153

CrossRef Full Text | Google Scholar

89. Zhang P, Qian T, Richard P, Wang XP, Miao H, Lv BQ, et al. Observation of two distinct/band splittings in FeSe. Phys Rev B (2015) 91:214503. doi:10.1103/PhysRevB.91.214503

CrossRef Full Text | Google Scholar

90. Zhang Y, Lee JJ, Moore RG, Li W, Yi M, Hashimoto M, et al. Superconducting gap anisotropy in monolayer FeSe thin film. Phys Rev Lett (2016) 117:117001. doi:10.1103/PhysRevLett.117.117001

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Liu D, Li C, Huang J, Lei B, Wang L, Wu X, et al. Orbital origin of extremely anisotropic superconducting gap in nematic phase of FeSe superconductor. Phys Rev X (2018) 8:031033. doi:10.1103/PhysRevX.8.031033

CrossRef Full Text | Google Scholar

92. Rhodes LC, Watson MD, Kim TK, Eschrig M. k_z selective scattering within quasiparticle interference measurements of FeSe. Phys Rev Lett (2019) 123:216404. doi:10.1103/PhysRevLett.123.216404

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Hashimoto T, Ota Y, H, Suzuki Y, Shimojima T, Watanabe S, et al. Superconducting gap anisotropy sensitive to nematic domains in FeSe. Nat Commun (2018) 9:282. doi:10.1038/s41467-017-02739-y

PubMed Abstract | CrossRef Full Text | Google Scholar

94. MacFarquharson K, Reiss P, Haghighirad AA, Kim T, Coldea AI. Revealing the coexistence of the bulk and surface electronic states by in-situ K dosing in the tetragonal superconductor FeSeS (2021). in preparation.

Google Scholar

95. Terashima T, Kikugawa N, Graf D, Hirose HT, Uji S, Matsushita Y, et al. Accurate determination of the Fermi surface of tetragonal FeS via quantum oscillation measurements and quasiparticle self-consistent GW calculations. Phys. Rev. B (2019) 99:134501. doi:10.1103/PhysRevB.99.134501

CrossRef Full Text | Google Scholar

96. Audouard A, Duc F., Drigo L, Toulemonde P, Karlsson S, Strobel P, et al. Quantum oscillations and upper critical magnetic field of the iron-based superconductor FeSe. Europhys Lett (2015) 109:27003. doi:10.1209/0295-5075/109/27003

CrossRef Full Text | Google Scholar

97. Shoenberg D. Magnetic oscillations in metals. Cambridge: Cambridge University Press (1984).

98. Watson MD, Yamashita T, Kasahara S, Knafo W, Nardone M, Béard J, et al. Dichotomy between the hole and electron behavior in multiband superconductor FeSe probed by ultrahigh magnetic fields. Phys Rev Lett (2015) 115:027006. doi:10.1103/PhysRevLett.115.027006

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Coldea AI, Fletcher JD, Carrington A, Analytis JG, Bangura AF, Chu JH, et al. Fermi surface of superconducting LaFePO determined from quantum oscillations. Phys Rev Lett (2008) 101:216402. doi:10.1103/PhysRevLett.101.216402

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Putzke C, Coldea AI, Guillamón I, Vignolles D, McCollam A, LeBoeuf D, et al. de Haas-van Alphen study of the fermi surfaces of superconducting LiFeP and LiFeAs. Phys Rev Lett (2012) 108, 047002. doi:10.1103/PhysRevLett.108.047002

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Putzke C, Coldea AI, Guillamon I, Vignolles D, McCollam A, LeBoeuf D, et al. Reply to comment by Borisenko et al. on article ‘A de Haas-van Alphen study of the Fermi surfaces of superconducting LiFeP and LiFeAs’. arXiv:1108.3956 (2011).

Google Scholar

102. Rhodes LC, Watson MD, Haghighirad AA, Evtushinsky DV, Kim TK. Revealing the single electron pocket of FeSe in a single orthorhombic domain. Phys Rev B (2020) 101:235128. doi:10.1103/PhysRevB.101.235128

CrossRef Full Text | Google Scholar

103. Huh SS, Seo JJ, Kim BS, Cho SH, Jung JK, Kim S, et al. Absence of Y-pocket in 1-Fe Brillouin zone and reversed orbital occupation imbalance in FeSe. Commun Phys (2020) 3:52. doi:10.1038/s42005-020-0319-1

CrossRef Full Text | Google Scholar

104. Rhodes LC, Böker J, Müller MA, Eschrig M, Eremin IM. Non-local nematicity and the missing electron pocket in FeSe (2020) arXiv:2009.00507.

Google Scholar

105. Fanfarillo L, Mansart J, Toulemonde P, Cercellier H, Le Fèvre P, Bertran F, et al. Orbital-dependent Fermi surface shrinking as a fingerprint of nematicity in FeSe. Phys Rev B (2016) 94:155138. doi:10.1103/PhysRevB.94.155138

CrossRef Full Text | Google Scholar

106. Walmsley P, Putzke C, Malone L, Guillamón I, Vignolles D, Proust C, et al. Quasiparticle mass enhancement close to the quantum critical point in BaFe₂(As_1–xP_x)₂. Phys Rev Lett (2013) 110:257002. doi:10.1103/PhysRevLett.110.257002

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Lifshitz I, Kosevich A. On the theory of the Shubnikov-de Haas effect. Sov Phys JETP (1956) 2:636.

Google Scholar

108. Ptok A. Lifshitz transitions induced by magnetic field. Acta Phys Pol A (2019) 135:55. doi:10.12693/APhysPolA.135.55

CrossRef Full Text | Google Scholar

109. Mark V. High magnetic fields: a tool for studying electronic properties of layered organic metals. Chem Rev (2004) 104:5737–82. doi:10.1021/cr0306891

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Shoenberg D. Magnetic oscillations in metals. Cambridge, England: Cambridge University Press (1984).

111. Wang L, Hardy F, Wolf T, Peter A, Fromknecht R, Schweiss P, et al. Superconductivity-enhanced nematicity and “s+d” gap symmetry in FeSe_1–xS_x. Phys Stat Solidi (B) (2016) 254:1600153. doi:10.1002/pssb.201600153

CrossRef Full Text | Google Scholar

112. Abdel-Hafiez M, Zhang Y-Y, Cao Z-Y, Duan C-G, Karapetrov G, Pudalov VM, et al. Superconducting properties of sulfur-doped iron selenide. Phys Rev B (2015) 91:165109. doi:10.1103/PhysRevB.91.165109

CrossRef Full Text | Google Scholar

113. Kasahara S, Watashige T, Hanaguri T, Kohsaka Y, Yamashita T, Shimoyama Y, et al. Field-induced superconducting phase of FeSe in the BCS-BEC cross-over. Proc Natl Acad Sci USA (2014) 111:16309. doi:10.1073/pnas.1413477111

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Chu JH, Kuo HH, Analytis JG, Fisher IR. Divergent nematic susceptibility in an iron arsenide superconductor. Science (2012) 337:710–12. doi:10.1126/science.1221713

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Karahasanovic U, Schmalian J. Elastic coupling and spin-driven nematicity in iron-based superconductors. Phys Rev B (2016) 93:064520. doi:10.1103/PhysRevB.93.064520

CrossRef Full Text | Google Scholar

116. Palmstrom JC, Walmsley P, Straquadine JAW, Sorensen ME, Hannahs ST, Burns DH, et al. Comparison of temperature and doping dependence of nematic susceptibility near a putative nematic quantum critical point (2019). arXiv:1912.07574.

Google Scholar

117. Tanatar MA, Böhmer AE, Timmons EI, Schütt M, Drachuck G, Taufour V, et al. Origin of the resistivity anisotropy in the nematic phase of FeSe. Phys Rev Lett (2016) 117:127001. doi:10.1103/PhysRevLett.117.127001

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Kuo HH, Chu JH, Palmstrom JC, Kivelson SA, Fisher IR. Ubiquitous signatures of nematic quantum criticality in optimally doped Fe-based superconductors. Science (2016) 352:958–62. doi:10.1126/science.aab0103

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Blomberg EC, Tanatar MA, Fernandes RM, Mazin II, Shen B, Wen HH, et al. Sign-reversal of the in-plane resistivity anisotropy in hole-doped iron pnictides. Nat Commun (2013) 4:1914. doi:10.1038/ncomms2933

PubMed Abstract | CrossRef Full Text | Google Scholar

120. He M, Wang L, Hardy F, Xu L, Wolf T, Peter A, et al. Evidence for short-range magnetic order in the nematic phase of FeSe from anisotropic in-plane magnetostriction and susceptibility measurements. Phys Rev B (2018) 97:104107. doi:10.1103/PhysRevB.97.104107

CrossRef Full Text | Google Scholar

121. Zhang WL, Wu SF, Kasahara S, Shibauchi T, Matsuda Y, Blumberg G. Stripe quadrupole order in the nematic phase of FeSe_1−xS_x (2017). arXiv:1710.09892.

Google Scholar

122. Pippard AB. Magnetoresistance in metals, Cambridge studies in low temperature Physics. Cambridge, UK: Cambridge University Press (1989).

123. Huang WK, Hosoi S, ulo M, Kasahara S, Sato Y, Matsuura K, et al. Non-Fermi liquid transport in the vicinity of nematic quantum critical point of ${\text{FeSe}}_{1-x}{\text{S}}_x$superconductor. Phys Rev Res (2020) 2:033367. doi:10.1103/PhysRevResearch.2.033367

CrossRef Full Text | Google Scholar

124. Hayes IM, McDonald RD, Breznay NP, Helm T, Philip JW. Moll, mark wartenbe, arkady shekhter, and James G. Analytis, Scaling between magnetic field and temperature in the high-temperature superconductor BaFe₂(As_1–xP_x)₂. Nat Phys (2016) 12:916–19. doi:10.1038/nphys3773

CrossRef Full Text | Google Scholar

125. Huynh KK, Tanabe Y, Urata T, Oguro H, Heguri S, Watanabe K, et al. Electric transport of a single-crystal iron chalcogenide FeSe superconductor: evidence of symmetry-breakdown nematicity and additional ultrafast Dirac cone-like carriers. Phys Rev B (2014) 90:144516. doi:10.1103/PhysRevB.90.144516

CrossRef Full Text | Google Scholar

126. Sun Y, Pyon S, Tamegai T. Electron carriers with possible Dirac-cone-like dispersion in (x=0 and 0.14) single crystals triggered by structural transition. Phys Rev B (2016) 93:104502. doi:10.1103/PhysRevB.93.104502

CrossRef Full Text | Google Scholar

127. Ovchenkov YA, Chareev DA, Kulbachinskii VA, Kytin VG, Presnov DE, Volkova OS, et al. Highly mobile carriers in iron-based superconductors. Supercond Sci Technol (2017) 30:035017. doi:10.1088/1361-6668/aa570a

CrossRef Full Text | Google Scholar

128. Tan SY, Fang Y, Xie DH, Feng W, Wen CHP, Song Q, et al. Observation of Dirac cone band dispersions in FeSe thin films by photoemission spectroscopy. Phys Rev B (2016) 93:104513. doi:10.1103/PhysRevB.93.104513

CrossRef Full Text | Google Scholar

129. Ong NP. Geometric interpretation of the weak-field Hall conductivity in two-dimensional metals with arbitrary Fermi surface. Phys Rev B Condens Matter (1991) 43:193–201. doi:10.1103/physrevb.43.193

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Luo CW, Cheng PC, Wang S-H, Chiang J-C, Lin J, Wu KH, et al. Unveiling the hidden nematicity and spin subsystem in FeSe. Npj Quantum Mat (2017) 2:32. doi:10.1038/s41535-017-0036-5

CrossRef Full Text | Google Scholar

131. Fanfarillo L, Cappelluti E, Castellani C, Benfatto L. Unconventional Hall effect in pnictides from interband interactions. Phys Rev Lett (2012) 109:096402. doi:10.1103/PhysRevLett.109.096402

PubMed Abstract | CrossRef Full Text | Google Scholar

132. Shi A, Arai T, Kitagawa S, Yamanaka T, Ishida K, Anna E, et al. Pseudogap behavior of the nuclear SpinLattice relaxation rate in FeSe probed by ⁷⁷Se-NMR. J Phys Soc Jpn (2018) 87:013704. doi:10.7566/JPSJ.87.013704

CrossRef Full Text | Google Scholar

133. Baek SH, Ok JM, Kim JS, Aswartham S, Morozov I, Chareev D, et al. Separate tuning of nematicity and spin fluctuations to unravel the origin of superconductivity in FeSe. Npj Quantum Mater (2020) 5:8. doi:10.1038/s41535-020-0211-y

CrossRef Full Text | Google Scholar

134. Grinenko V, Dengre S, Sarkar R, Chareev DA, Vasiliev AN, Efremov DV, et al. Anomalous Knight shift and low-energy spin dynamics in the nematic state of FeSe_1–xS_x (2019). arXiv:1903.00530.

Google Scholar

135. Rosch A. Interplay of disorder and spin fluctuations in the resistivity near a quantum critical point. Phys Rev Lett (1999) 82:4280–283. doi:10.1103/PhysRevLett.82.4280

CrossRef Full Text | Google Scholar

136. Grinenko V, Sarkar R, Materne P, Kamusella S, Yamamshita A, Takano Y, et al. Low-temperature breakdown of antiferromagnetic quantum critical behavior in FeSe. Phys Rev B (2018) 97:201102. doi:10.1103/PhysRevB.97.201102

CrossRef Full Text | Google Scholar

137. Dell’Anna L, Metzner W. Electrical resistivity near Pomeranchuk instability in two dimensions. Phys Rev Lett (2007) 98:136402. doi:10.1103/PhysRevLett.98.136402

PubMed Abstract | CrossRef Full Text | Google Scholar

138. Maslov DL, Yudson VI, Chubukov AV. Resistivity of a non-galilean-invariant Fermi liquid near Pomeranchuk quantum criticality. Phys Rev Lett (2011) 106:106403. doi:10.1103/PhysRevLett.106.106403

PubMed Abstract | CrossRef Full Text | Google Scholar

139. Xu HC, Niu XH, Xu DF, Jiang J, Yao Q, Chen QY, et al. Highly anisotropic and twofold symmetric superconducting gap in nematically ordered FeSe_0.93–0.07. Phys Rev Lett (2016) 117:157003. doi:10.1103/PhysRevLett.117.157003

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Acharya S, Pashov D, van Schilfgaarde M. Role of nematicity in controlling spin fluctuations and superconducting T_c in bulk FeSe. arXiv:2005.07729 (2020).

Google Scholar

141. Wang Q, Shen Y, Pan B, Hao Y, Ma M, Zhou F, et al. Strong interplay between stripe spin fluctuations, nematicity and superconductivity in FeSe. Nat Mater (2016) 15:159–163. doi:10.1038/nmat4535

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Wang F, Kivelson SA, Lee D-H. Nematicity and quantum paramagnetism in FeSe. Nat Phys (2015) 11:959–63. doi:10.1038/nphys3456

CrossRef Full Text | Google Scholar

143. Yu R, Si Q. Antiferroquadrupolar and ising-nematic orders of a frustrated bilinear-biquadratic heisenberg model and implications for the magnetism of FeSe. Phys Rev Lett (2015) 115:116401. doi:10.1103/PhysRevLett.115.116401

PubMed Abstract | CrossRef Full Text | Google Scholar

144. Imai T, Ahilan K, Ning FL, McQueen TM, Cava RJ. Why does undoped FeSe become a high-Tc superconductor under pressure?. Phys Rev Lett (2009) 102:177005. doi:10.1103/PhysRevLett.102.177005

PubMed Abstract | CrossRef Full Text | Google Scholar

145. Benfatto L, Valenzuela B, Fanfarillo L. Nematic pairing from orbital-selective spin fluctuations in FeSe. Npj Quantum Mater (2018) 3:56. doi:10.1038/s41535-018-0129-9

CrossRef Full Text | Google Scholar

146. Kreisel A, Andersen BM, Sprau PO, Kostin A, Davis JCS, Hirschfeld PJ. Orbital selective pairing and gap structures of iron-based superconductors. Phys Rev B (2017) 95:174504. doi:10.1103/PhysRevB.95.174504

CrossRef Full Text | Google Scholar

147. Rhodes LC, Watson MD, Haghighirad AA, Evtushinsky DV, Eschrig M, Kim TK. Scaling of the superconducting gap with orbital character in FeSe. Phys Rev B (2018) 98:180503. doi:10.1103/PhysRevB.98.180503

CrossRef Full Text | Google Scholar

148. Lin J-Y, Hsieh YS, Chareev DA, Vasiliev AN, Parsons Y, Yang HD. Coexistence of isotropic and extended s-wave order parameters in FeSe as revealed by low-temperature specific heat. Phys Rev B (2011) 84:220507. doi:10.1103/PhysRevB.84.220507

CrossRef Full Text | Google Scholar

149. Bourgeois-Hope P, Chi S, Bonn DA, Liang R, Hardy WN, Wolf T, et al. Thermal conductivity of the iron-based superconductor FeSe: nodeless gap with a strong two-band character. Phys Rev Lett (2016) 117:097003. doi:10.1103/PhysRevLett.117.097003

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Song CL, Wang YL, Cheng P, Jiang YP, Li W, Zhang T, et al. Direct observation of nodes and twofold symmetry in FeSe superconductor. Science (2011) 332:1410. doi:10.1126/science.1202226

PubMed Abstract | CrossRef Full Text | Google Scholar

151. Moore SA, Curtis JL, Di Giorgio C, Lechner E, Abdel-Hafiez M, Volkova OS, et al. Evolution of the superconducting properties in FeSe_1−xS_x. Phys Rev B (2015) 92:235113. doi:10.1103/PhysRevB.92.235113

CrossRef Full Text | Google Scholar

152. Kuroki K, Usui H, Onari S, Arita R, Aoki H. Pnictogen height as a possible switch between high- nodeless and low- nodal pairings in the iron-based superconductors. Phys Rev B (2009) 79:224511. doi:10.1103/PhysRevB.79.224511

CrossRef Full Text | Google Scholar

153. Fletcher JD, Serafin A, Malone L, Analytis JG, Chu JH, Erickson AS, et al. Evidence for a nodal-line superconducting state in LaFePO. Phys Rev Lett (2009) 102:147001. doi:10.1103/PhysRevLett.102.147001

PubMed Abstract | CrossRef Full Text | Google Scholar

154. Hashimoto K, Kasahara S, Katsumata R, Mizukami Y, Yamashita M, Ikeda H, et al. Nodal versus nodeless behaviors of the order parameters of LiFeP and LiFeAs superconductors from magnetic penetration-depth measurements. Phys Rev Lett (2012) 108:047003. doi:10.1103/PhysRevLett.108.047003

PubMed Abstract | CrossRef Full Text | Google Scholar

155. Xing J, Lin H, Li Y, Li S, Zhu X, Yang H, et al. Nodal superconducting gap in tetragonal FeS. Phys Rev B (2016) 93:104520. doi:10.1103/PhysRevB.93.104520

CrossRef Full Text | Google Scholar

156. Yang Y, Wang W-S, Lu H-Y, Xiang Y-Y, Wang Q-H. Electronic structure and -wave superconductivity in FeS. Phys Rev B (2016) 93:104514.

CrossRef Full Text | Google Scholar

157. Hardy F, He M, Wang L, Wolf T, Schweiss P, Merz M, et al. Calorimetric evidence of nodal gaps in the nematic superconductor FeSe. Phys Rev B (2019) 99:035157. 10.1103/PhysRevB.99.035157

CrossRef Full Text | Google Scholar

158. Bourgeois-Hope P, Chi DA, Bonn R, Liang W, Hardy N, Wolf T, et al. Thermal conductivity of the iron-based superconductor FeSe: nodeless gap with a strong two-band character. Phys. Rev. Lett. (2016), 117: 097003.

159. Jiao L, Huang CL, Rößler S, Koz C, Rößler UK, Schwarz U, et al. Superconducting gap structure of FeSe. Sci Rep (2017) 7:44024. doi:10.1038/srep44024

PubMed Abstract | CrossRef Full Text | Google Scholar

160. Randeria M, Taylor E. Crossover from Bardeen-Cooper-Schrieffer to Bose-Einstein condensation and the unitary fermi gas. Annu Rev Condens Matter Phys (2014) 5:209–32. doi:10.1146/annurev-conmatphys-031113-133829

CrossRef Full Text | Google Scholar

161. Chen Q, Stajic J, Tan S, Levin K. BCS-BEC crossover: from high temperature superconductors to ultracold superfluids. Phys Rep (2005) 412:1–88. doi:10.1016/j.physrep.2005.02.005

CrossRef Full Text | Google Scholar

162. Rinott S, Chashka KB, Amit R, Rienks EDL, Amina T-I, Patrick LF, et al. Tuning across the BCS-BEC crossover in the multiband superconductor Fe_1+ySe_xTe_1−x: an angle-resolved photoemission study. Sci Adv (2017) 3:e1602372. doi:10.1126/sciadv.1602372

PubMed Abstract | CrossRef Full Text | Google Scholar

163. Kasahara S, Sato Y, Licciardello S, Čulo M, Arsenijević S, Ottenbros T, et al. Evidence for an FFLO state with segmented vortices in the BCS-BEC-Crossover superconductor FeSe. Phys Rev Lett (2020) 124:107001. doi:10.1103/PhysRevLett.124.107001

PubMed Abstract | CrossRef Full Text | Google Scholar

164. Kushnirenko YS, Fedorov AV, Haubold E, Thirupathaiah S, Wolf T, Aswartham S, et al. Three-dimensional superconducting gap in FeSe from angle-resolved photoemission spectroscopy. Phys Rev B (2018) 97:180501. doi:10.1103/PhysRevB.97.180501

CrossRef Full Text | Google Scholar