Higher-Order Statistics in Compressive Solar Wind Plasma Turbulence: High-Resolution Density Observations From the Magnetospheric MultiScale Mission

Turbulent density fluctuations are investigated in the solar wind at sub-ion scales using calibrated spacecraft potential. The measurement technique using the spacecraft potential allows for a much higher time resolution and sensitivity when compared to direct measurements using plasma instruments. Using this novel method, density fluctuations can be measured with unprecedentedly high time resolutions for in situ measurements of solar wind plasma at 1 a.u. By investigating 1 h of high-time resolution data, the scale dependant kurtosis is calculated by varying the time lag τ to calculate increments between observations. The scale-dependent kurtosis is found to increase towards ion scales but then plateaus and remains fairly constant through the sub-ion range in a similar fashion to magnetic field measurements. The sub-ion range is also found to exhibit self-similar monofractal behavior contrasting sharply with the multi-fractal behavior at large scales. The scale-dependent kurtosis is also calculated using increments between two different spacecraft. When the time lags are converted using the ion bulk velocity to a comparable spatial lag, a discrepancy is observed between the two measurement techniques. Several different possibilities are discussed including a breakdown of Taylor’s hypothesis, high-frequency plasma waves, or intrinsic differences between sampling directions.

1.Introduction

The solar wind is an excellent example of turbulent plasma where disordered fluctuations are observed in velocity, temperature, and density as well as in electromagnetic fields [1–5]. At large scales, a fluid description of the plasma is valid and fluctuations transverse to the mean magnetic field direction dominate. This region is often termed the inertial range, where magnetic fields and density are often observed with a power spectral density that has a −5/3 spectral index [6–8]. However, the presence of several different species (protons, electrons, and heavy ions), each with their characteristic scales, causes several different distinct ranges to be present in the plasma [9–11]. When fluctuations approach proton scales, kinetic effects become important, the magnetic spectra steepen [7], and fluctuations become more compressive [12]. In this range, usually called sub-ion range, the Kolmogorov-like phenomenology can be adapted using Hall-MHD and kinetic models. These predict different spectral scaling exponents, typically near the observed values $\sim -8/3$ (see e.g., Ref. [13]). There are also observations and numerical simulations that suggest the third order law based on Hall MHD is valid, supporting the hypothesis that there is another fluid like cascade in this region [14, 15]. However, the additional presence of kinetic effects, such as Landau damping [16] suggest that another fluid like cascade is not completely sufficient to describe the phenomenology. At smaller scales electron kinetic effects become important and the morphology of the magnetic spectrum is unclear [17–20]. At the sub-ion scales, density measurements are challenging due to the need for high time resolution. Investigating density fluctuations can be especially taxing due to the lower (compared to instruments that measure fields) sampling rates. One novel way to measure the electron density at the same time resolution as electric field measurements is to calibrate the spacecraft potential [3, 21–29]. In the solar wind typically the two dominant currents to and from the spacecraft are the photoelectron current $I_{ph}$ and the electron thermal current $I_e$. If all other current sources are small it can be assumed that both of these currents are equal and have opposite signs. This is typically the case in the solar wind at 1 a.u. Using lower time resolution electron density and temperature data from plasma instruments, the electron thermal current can be calculated as a function of the spacecraft potential. The variation of the current with the potential can be modelled by a superposition of exponential functions. By using the obtained model and the direct measurement of electron temperature the electron density can be derived from the spacecraft potential.

Turbulent flows tend to develop vortices or eddies, which are intermittently distributed in the flow [30, 31] and are often termed coherent structures. Due to the presence of a strong ambient magnetic field in a plasma, coherent structures become elongated along the magnetic field direction [20, 32, 33]. Furthermore, the plasma allows other types of structures to form such as current sheets, flux ropes, or magnetic vortices [34–38]. These structures are associated with large gradients¹ in the measured variables (such as electron density), which are often investigated by calculating differences of time-lagged or spatially lagged variables and evaluating their scale-dependent statistics. A time-lagged increment is defined as:

$\delta n_e\left(t,\tau \right)=n_e\left(t+\tau \right)-n_e\left(t\right),(1)$

where $n_e$ is the plasma electron density, t is the sample time and τ a time scale where $\tau \ge \delta t$ where $\delta t$ is the time resolution.

Similarly, a spatial lag between two measurement points at position vectors $\overrightarrow{{\lambda }_1}$ and $\overrightarrow{{\lambda }_2}$ are defined as

$\delta n_e\left(\overrightarrow{{\lambda }_{\mathrm{1,2},t}}\right)=n_e\left(\overrightarrow{{\lambda }_{1,t}}\right)-n_e\left(\overrightarrow{{\lambda }_{2,t}}\right).(2)$

To quantify how intermittent a given time interval is, higher-order statistics of increments such as the kurtosis are calculated. Kurtosis is defined as;

$\kappa =\frac{\langle \delta n_e^4\rangle }{{\langle \delta n_e^2\rangle }^2},(3)$

and measures the deviation of a probability distribution function from being Gaussian, specifically how heavy the tails of the distribution are. For a Gaussian process, the kurtosis is equal to three. An intermittent signal would be expected to have a scale dependence in the kurtosis [e.g., 39–42] and a departure from self-similar or monofractal scaling² [43–46].

Previous studies in the solar wind have shown that the kurtosis of magnetic and velocity fluctuations do exhibit a scale dependence in the inertial range [47, 48], suggesting that the inertial range is strongly intermittent. Furthermore, magnetic field measurements also indicate that this range is characterized by multifractal behavior, a standard framework to model intermittency [12, 44]. Different components of the magnetic field have also been shown to have different intermittency properties. The component of the magnetic field along the mean-field direction (also termed the compressive component) has also been shown to be more intermittent at large scales [49] when compared to the transverse components. This was interpreted as a combination of the transverse fluctuations phases being randomized by large scale Alfvénic fluctuations, in effect reducing the kurtosis³. Meanwhile, in the large scale compressive component, Alfvénic fluctuations have very little effect as they are incompressible. Additionally, compressible coherent structures are more prevalent causing the kurtosis to be larger. At smaller scales below proton characteristic scales, there are conflicting observations. In the study of Alexandrova et al. [13] the kurtosis was found to increase rapidly in the sub-ion range. This is similar to the result of Chhiber et al. [42] in the magnetosheath i.e., a rapid increase in the kurtosis of the fluctuations in the sub-ion range. Meanwhile, observations of Kiyani et al. [44] show that the sub-ion range in the solar wind is monofractal, juxtaposing strongly with the multifractal inertial range. Other studies in the solar wind have observed the fluctuations in density Chen et al. [45] and magnetic field Chhiber et al. [42] which do not have a strong increase of the scale-dependent kurtosis in the sub-ion range. A recent analysis based on empirical mode decomposition concluded that the sub-ion scale turbulence of density fluctuations is not intermittent [50]. However, in the study of Sorriso-Valvo et al. [46] different methods applied to density measurements of the same intervals yielded different results. The various different results point to the fact that higher order statistics obtained in plasma turbulence are not universal, but may depend on the specific interval.

The majority of the studies mentioned have used single spacecraft measurements and have used a time lag (Eq. 1) to obtain the fluctuation. This is limited to investigating a single direction (i.e., along the bulk velocity vector), and also requires an assumption that the plasma does not evolve over the timescale it requires to be measured, so that the spacecraft see a one-dimensional spatial cut through the plasma. This assumption is termed Taylor’s frozen in flow hypothesis [51]. To avoid assuming this, multi-point missions such as Cluster and the Magnetospheric MultiScale mission were developed which allow increments to be calculated using two different spacecraft, overcoming the inherent Spatio-temporal ambiguity associated with single spacecraft observations.

Calculating spatially separated increments defined in Eq. 2 has the advantage that multiple directions can be sampled, but are limited to a single scale for a tetrahedral constellation of four points i.e., six baselines in different direction of size of order $\left|\overrightarrow{{\lambda }_{\mathrm{1,2}}}\right|$. At the distance of the order of tens of kilometers, magnetic field increments calculated from two points can vary wildly from being close to Gaussian [42], to being strongly leptokurtic [41]. However, due to magnetic field instrument’s sensitivity in the sub-ion range, a comparison between time-lagged and spatially lagged measurements is difficult.

The goal of this paper is to use density fluctuations in the solar wind estimated from the spacecraft potential on the Magnetospheric MultiScale mission to obtain an extremely high time resolution measurement of the electron density [52]. Although there are limitations to this technique, it also has several advantages, most notably the higher time resolution, fewer data gaps, and the absence of large errors due to low particle counts. Using this novel method, density fluctuations can be measured with unprecedented time resolutions. Such time resolutions are not possible using plasma measurements, and exceed what has been done in the current literature with spacecraft potential. This method applied to the MMS spacecraft allows density fluctuations to be measured deep into the sub ion range up to 40 Hz. This range of scales has only previously been accessible to magnetic field measurements in the solar wind [e.g., 12]. Previous studies of density with spacecraft potential [e.g., 53, 54] have been limited to $\sim 7.5$ Hz due to sensitivity or a Nyquist frequency of 16 Hz using a direct measurement [e.g., 40, 46, 55]. The novel spacecraft potential measurement will be compared to the direct measurement from the plasma instrument and to the magnetic field data which are both available but similar to the previous studies [41, 42] are limited to a smaller range of time scales due to the limited sensitivity in the magnetic field measurement in the sub-ion scales. In the following section, we will present the data. This will be followed by the results of the kurtosis of the density fluctuations, a discussion and a conclusion.

2.Data/Methodology

Data is used from the Magnetospheric MultiScale mission [56] (MMS) when an hour-long interval of burst mode data in the slow solar wind was available. The MMS mission consists of four identical spacecraft in a tetrahedral configuration optimized for studying magnetic reconnection in the Earth’s Magnetosphere. However, there are also intervals of solar wind plasma which have been sampled by MMS. The close spacings of MMS of the order of a few km to tens of km make it an excellent mission to study sub-ion scale turbulence. A 1-h long burst mode interval is analyzed here which was previously studied in [42, 57]. The spacecraft are located at $\left[x_{GSE},y_{GSE},z_{GSE}]=[16.5,17.5,6.3\right]R_E$ and were not magnetically connected to the foreshock. The subscript GSE denotes the Geocentric Solar Ecliptic coordinate system, where the x component points from Earth towards the Sun, z points to the North solar ecliptic. This is very far from the nominal bow shock nose which is approximately at $x_{GSE}=10R_E$ [58]. Furthermore there are no signatures of backstreaming ions or electric field fluctuations in this interval [52] and the magnetic field is predominantly in $y_{GSE}$ direction meaning that there is no connection with the foreshock. The magnetic field is measured by the fluxgate magnetometers [59] which have a sampling rate of 128 Hz in burst mode and sensitivity which allows the study of the magnetic fluctuations at inertial (fluid scales) and ion kinetic scales before noise becomes significant near 5 Hz for this interval. We do not use the Search coil magnetometer as it is already at the noise level. The plasma measurements are provided by the Fast Plasma Investigation’s (FPI) Dual Ion Spectrometers and Dual Electron Spectrometers and have sampling rates of 6.6 and 33 Hz respectively [60].

The Spacecraft potential can be used to estimate the electron density (see e.g., [3, 21–29, 52]). A detailed description of the calibration process and of the spin removal is presented in [52]. It is important to note that the spacecraft have a characteristic charging timescale, and respond to the ambient electron density after that timescale. Assuming constant photoelectron emission this time scale is very large of the order of kiloHertz [32]. This is far outside of our range of interest. Even if we relax the assumption that the photoelectron emission is constant such as when large amplitude electric fields are present the charging timescale is still much larger than the largest scale we survey [61]. Therefore in the solar wind we do not expect any finite charging effects in the solar wind at these scales. The spin is removed by constructing an empirical model of the spacecraft charging by binning the potential based on the spacecraft phase angle. A model is fitted to the median in each bin and then subtracted. For this interval, spin effects were present also in the FPI electron data. These have been removed using the same approach. The spacecraft potential is calculated from measurements performed with the Spin Plane Double Probe instruments [62] and has a sampling rate of 8.192 kHz. The spacecraft potential is measured from the four spin plane probes. The four measured probe to spacecraft potentials are averaged to give the spacecraft potential. If one probe is unavailable i.e. for MMS4 due to one probe becoming unbiased due to a dust strike then the average of two opposing probes is used rather than all four probes [61, 63, 64]. This results in a difference in the quality of the measurement when comparing spacecraft 1 through 3 with 4. The electron density data from FPI the has an upper limit of 3 Hz for electrons due to Poission noise from finite counting statistics. For the spacecraft potential we used the upper limit of 40 Hz to avoid noise from the preamplifier. The limit of 40 Hz was chosen so that the signal from the spacecraft potential is three times larger than a quiet interval when the spacecraft potential is regulated by the Active Spacecraft POtential Control (ASPOC) instrument [65] is operating [52].

An overview of the event is given in Figure 1. Both measurement techniques show good agreement for the electron density. An important caveat of the spacecraft potential is that it can be severely affected by dust strikes or similar inverted signatures discussed by [e.g., 66–68]. These events are characterized by an abrupt jump or drop in the density estimation which can affect the calculation of higher-order statistics [69, 70]. In our sample, there is a sharp decrease in the potential at one point which is likely due to a dust strike, or an inverted signature as discussed by [67]. Such strikes, present in the spacecraft potential data set, are removed here by linear interpolation as they are not density perturbations intrinsic to the solar wind. Rather the perturbation in density is the result of the dust vaporizing on contact with the spacecraft and cause a density perturbation due to the dust/spacecraft interaction. This can be seen in the bottom panel of Figure 1. The interval has a low ion bulk speed of 377 km s⁻¹, a mean electron density from FPI of 8.8 cm⁻³ and ion and electron plasma beta (dimensionless ratio of plasma pressure to magnetic pressure) of ${\beta }_i=0.4$ and ${\beta }_e=0.7$. There are no signatures of large scale events such as Interplanetary coronal mass ejections in the day before or the day after the event from OMNI. This means that the interval is characteristic of typical slow solar wind. It is important to note that the measurement of the ion temperature is unreliable from MMS [e.g., 57, 71] and here we use OMNI data [72] for the calculation of the ion plasma beta.

FIGURE 1

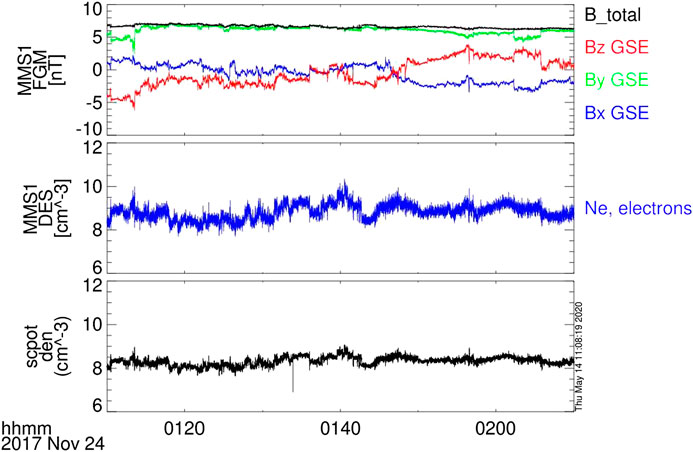
FIGURE 1. Measured data from MMS1 during the interval studied. Top panel shows the three magnetic field components and the magnitude. Middle panel shows the electron density measured from the FPI-DES instrument. Bottom panel shows the electron density measured from the spacecraft potential calibration method.

This interval is a typical example of the slow solar wind. The spacecraft separations are in the range $r\in \left[\mathrm{15,20}\right]$km. Based on Taylor’s frozen in flow hypothesis [51] this corresponds to a timescale of ${\tau }_{sc}\in \left[0.04,0.06\right]$ s. When considering inter-spacecraft fluctuations, the time resolution needs to be sufficient to distinguish the changes, otherwise some fluctuation may be advected over the spacecraft before it has been sampled [e.g., 57]. Out of the three measurements which we use in this study (magnetic field, electron density from FPI, and electron density from the spacecraft potential), the lowest time resolution is the FPI electrons at 0.03 s. This is sufficiently small so that no blurring of the information occurs when calculating increments between two spacecraft which are radially aligned (i.e., along the solar wind bulk flow direction). That is to say advection time of a fluctuation in the radial direction of 15 km/377 km/s = 0.04 s which is larger than the time resolution of the FPI electrons.

3.Results

The power spectral densities of the spacecraft potential-derived electron density, the trace magnetic field and the magnetic field magnitude are shown in Figure 2. The frequencies corresponding to the different spatial scales the ion and electron inertial lengths ($d_i,d_e$) the ion and electron gyroradii (${\rho }_i,{\rho }_e$), as well as the combined scales [73], are indicated. A typical inertial range scaling is observed at low frequencies for both the electron density and the magnetic fluctuations, with a power-law scaling exponent close to $-5/3$. Spectral breaks are found by fitting a power law from either side of the break and is indicated by the vertical dashed black lines. There is a flattening in the magnetic field spectra near 5 Hz which is due to instrumental noise. The decrease at higher frequencies ($f>10$Hz) is due to an anti-aliasing filter and is not of physical origin. The electron density from the spacecraft potential shows a power law until 100 Hz where the spectrum flattens. In the region above 100 Hz the spectrum is flat indicating white noise, the kurtosis is 3 (see Figure 3) at a value of three and the structure functions are also flat regardless of the order (see Figure 6). This is likely due to noise and is consistent with the Poisson noise in the electronics [62]. Although, pre-amplifier noise may be significant at smaller frequencies and has a non-zero spectral index. In order to avoid noise effects, here we limit our analysis to the range up to 40 Hz. At ion scales there is a flattening in the central region of the electron density spectra [45, 74] which we term a transition region.

FIGURE 2

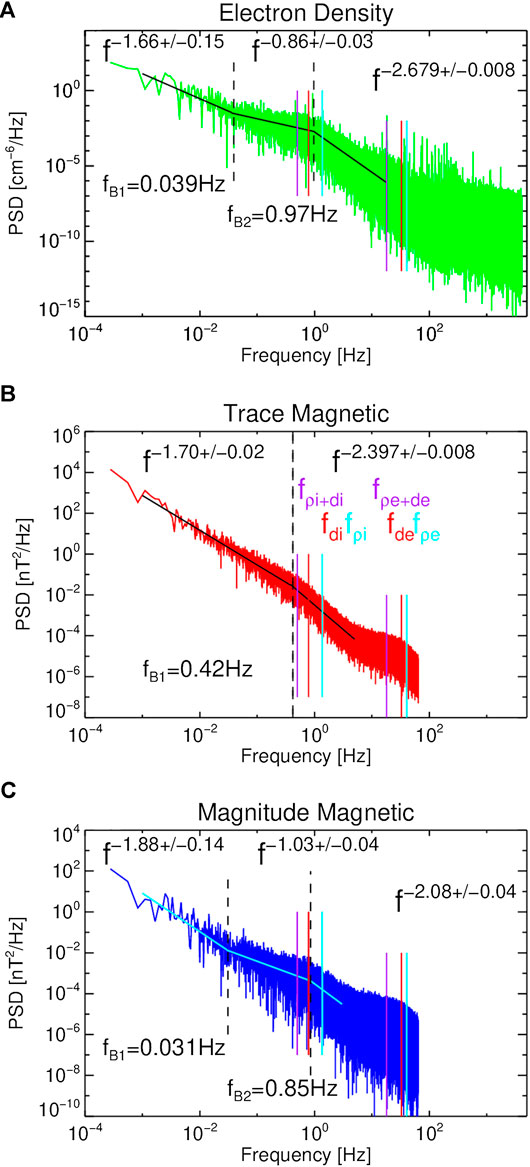
FIGURE 2. Power spectral densities from MMS1. (A) shows the electron density from the spacecraft potential, (B) shows the trace magnetic field from the fluxgate magnetometer (C) shows the magnetic field magnitude from FGM. The colored lines denote several of the characteristic scales, while the black dashed lines denote the spectral breaks. The power-law fits and the break frequencies are indicated on the plots.

FIGURE 3

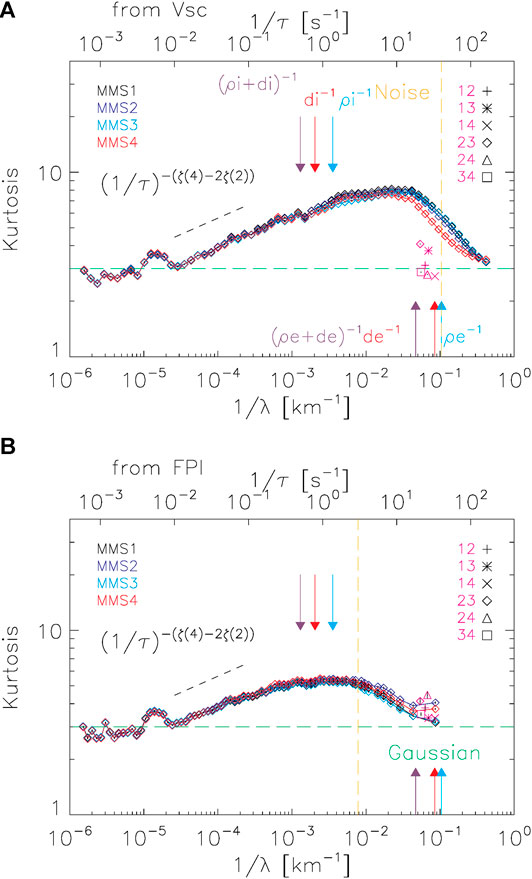
FIGURE 3. Scale-dependent kurtosis for electron density fluctuations obtained from the spacecraft potential (A) and FPI (B). The orange vertical line denotes the region where instrumental noise becomes significant for the two different measurements. The green horizontal line denotes a kurtosis of 3, characteristic of a Gaussian process. The arrows denote the same characteristic scales as previously in Figure 2. The lines denote the time-lagged values from different spacecraft, and the pink data points denote the kurtosis calculated from two spacecraft measurements. Black-dashed lines indicate power-laws expected from the scaling of the structure functions, and are displayed for reference. Error bars are indicated based on 100 bootstrap resamplings but they are smaller than the plotting symbols.

Figure 3 shows the scale-dependent kurtosis of the density fluctuations calculated from both the direct measurement from FPI and from the spacecraft potential. Both time lags (lines) and spatial lags (points) are used for this calculation. An unfortunate consequence of sampling heavily tailed distributions such as turbulent fluctuations is that some large fluctuations might significantly alter higher-order statistics. To ensure better statistical consistency we follow the scheme presented in Kiyani et al. [70]. This involves removing the largest fluctuation in the probability distribution function, recalculating the kurtosis, and repeating until the kurtosis converges. This has the advantage that outliers from either side of the heavy tails will be removed, and do not need any a priori information e.g., the standard deviation [75, 76]. Practically, this does not remove many data points. In our scheme of convergence we set a maximum limit of at most $0.1\text{\%}$ removed data points. The error bars, prevalently smaller than the symbols, denote the estimated error from one hundred bootstrap resamplings of the fluctuations.

At the largest scales, the kurtosis $\kappa \simeq 3$ indicates approximately Gaussian distributions. There is a bump in the kurtosis at a scale of ${\lambda }^{-1}\sim {10}^{-5}$ km⁻¹ which is likely related to the finite signal length. In the inertial range, the kurtosis increases roughly as a power law, as expected from the scaling properties of turbulence. The expected scaling laws are indicated for reference, the exponents $\simeq 0.1$ being estimated using the structure functions scaling exponents (see below) and Eq. 4. As the time lags become smaller near ion scales there is a plateau and then the value of the kurtosis starts to decrease near the combined electron scale before the noise floor. The noise floor is indicated by the orange dashed line at 3 Hz for the FPI data and 40 Hz for the potential data. Both density measurements show similar scale-dependent kurtoses at large scales. However, due to FPI data reaching the noise floor sooner, at a higher frequency they begin to disagree. The time-lagged measurements from the four spacecraft agree well with one another. The data points from MMS4 differ slightly in the spacecraft potential possibly due to the probe failure mentioned previously. This may be a result of two probes being used from MMS4 rather than four probes on the other spacecraft. The PDFs show some skewness. At small scales, this is necessary in order to have non-vanishing odd-order moments. At large scales, we still observe skewed PDFs, which are probably a finite sample effect, for example due to the presence of statistically underrepresented large-scale structures which may affect the statistics. We do not discuss those scales in this paper. The pink data points show the kurtoses calculated from the spatial lags. The values of the kurtosis from the spatial lags are small, close to being Gaussian for both measurements. A salient feature here is that for the FPI data the time and spatial lags agree, however, the time lag is unreliable due to noise. This is a similar result to the magnetic field in [42]. However, the spacecraft potential is less affected by noise and there is a disagreement between the time and spatial lags.

Figure 4 shows the scale-dependent kurtosis for the magnetic field measurements $\mathbf{B}\left(t\right)$. To put the fluctuations in a physically relevant co-ordinate system, we convert the fluctuations from the Geocentric Solar Ecliptic system to a mean-field scale-dependent coordinate system [32]. This is defined for each pair of measurements that make an increment as ${\mathbf{B}}_{loc}(t,\tau )=\left[\mathbf{B}\left(t\right)+\mathbf{B}\left(t+\tau \right)\right]/2$ for a time lag, or ${\mathbf{B}}_{loc,\mathrm{1,2}}\left(t\right)=\left[{\mathbf{B}}_1\left(t\right)+{\mathbf{B}}_2\left(t\right)\right]/2$ for spatially lagged measurements. The perpendicular components are defined as the cross product of the local magnetic field and the radial direction from the Sun, and the cross product of the local magnetic field with the first perpendicular direction. The three components of the magnetic field are displayed in Figure 4 with the lines denoting the time-lagged quantities and the points denoting spatially lagged quantities. We recover the same result as [42], i.e., there is an approximately power-law increase in the inertial range towards ion scales, and then a reduction before the signals become noise dominated. However, as we use a different coordinate system we also have information about the compressive and the transverse components. At these scales, the transverse components seem to dominate the kurtosis.

FIGURE 4

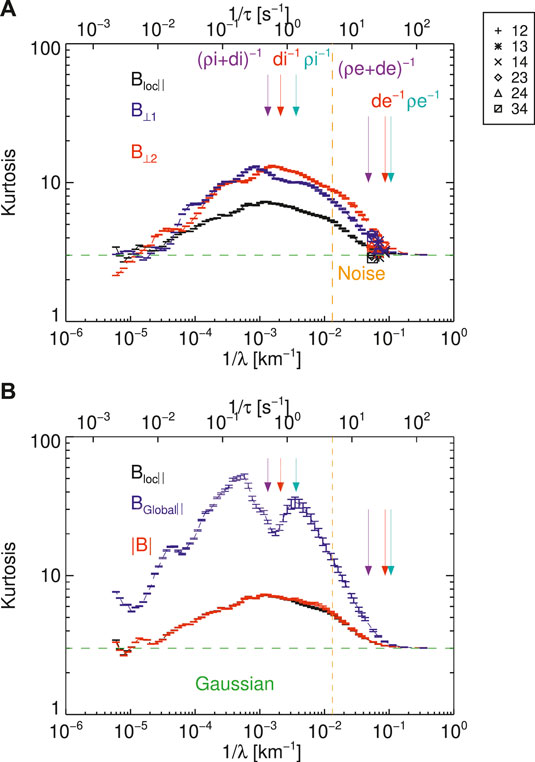
FIGURE 4. (A) The scale-dependent kurtosis for the magnetic field components in a local mean-field co-ordinate system. The connected lines denote the time-lagged increments and the points denote the spatially lagged values. (B) Three different measures of the compressible magnetic field component. Blue denotes the global mean field over the entire interval, red denotes the magnitude of the magnetic field and black denotes the same local mean-field as in (A). The green horizontal line denotes a kurtosis of 3 which corresponds to a Gaussian distribution. The orange vertical line denotes 5 Hz where instrumental noise becomes significant in the fluxgate magnetometer data. The colored arrows denote the characteristic ion scales the cyclotron scale, the inertial length and the Larmor radius.

We also compare our results to other measures of the compressive magnetic field in Figure 4B. Here the kurtosis of the global magnetic field (which is defined as the mean direction of the field over the entire interval) and of the magnitude of the magnetic field are plotted along with that of the local magnetic field. The local magnetic field and the magnitude agree very well with one another, which is expected for the solar wind as the fluctuations in the magnitude are small $\delta B/B_0\ll 1$. However, the global magnetic field is much more intermittent. This suggests that when using a global magnetic field some of the intermittent transverse fluctuations might be contributing to the compressible part if there is an abrupt change in the magnetic field direction away from the global mean field direction. On the other hand, the local magnetic field may follow the fluctuations too closely and therefore gradients may not be fully captured, which would result in a lower kurtosis for the local magnetic field definition. This is essentially because the direction of a local magnetic field is not a fixed direction but is also varies in time (or space), reducing the strength of the gradients. For a more detailed discussion on the use of local vs. global mean magnetic field, the reader is directed to the discussion of [77]. Here, we remark that both local and global magnetic fields have limitations, where a local definition may underestimate the intermittency while a global magnetic field may overestimate it.

Figure 5 shows the probability distribution functions (PDF) for the electron density fluctuations from FPI and the spacecraft potential. These PDFs show the spatial lags (b, d) and the time lags (a, c) where τ corresponds to the spatial lag sizes assuming Taylot's hypothesis. The fluctuations here have been normalized to the standard deviation for each scale. Both spatial lags show approximately Gaussian distributions with low kurtosis values. The pairs which include MMS4 for the spacecraft potential are noticeably different which is again likely to the probe failure on MMS4. The time lags based on the FPI data also show a similar distribution. However, the time lags from the spacecraft potential are leptokurtic and show prominent heavy tails.

FIGURE 5

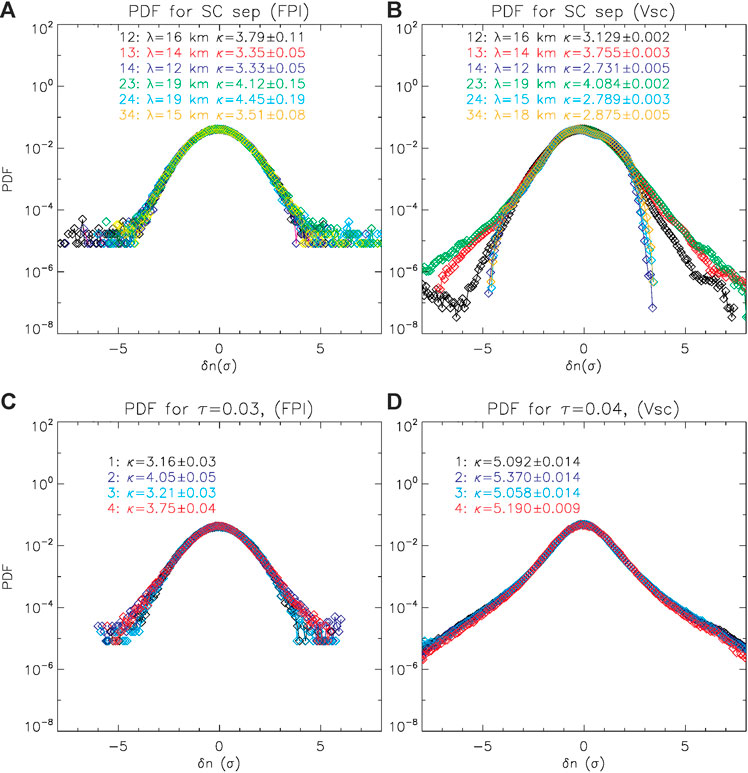
FIGURE 5. Probability distribution functions for standardized density fluctuations based on spatially lagged measurements from FPI-DES (A) from spacecraft potential (B) and for time lags at a comparable scale to the spatial lags for FPI (C) and for the spacecraft potential (D).

Figure 6 shows the m-th order structure functions from m = 1 to m = 6. These are defined as:

$S_m\left(\tau \right)={\langle {\left|\delta n_e\left(t,\tau \right)\right|}^m\rangle }_t(4)$

FIGURE 6

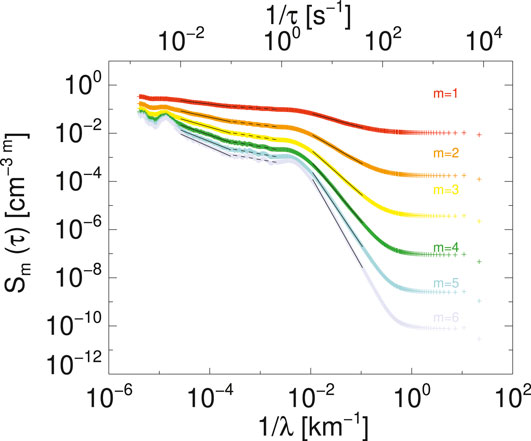
FIGURE 6. The m-th order structure functions for m = 1 to m = 6. The straight lines denote fits over three different time lag ranges the inertial scales $\frac{1}{\tau }=\left[0.01,0.1\right]s^{-1}$ the transition scales $\frac{1}{\tau }=\left[0.1,0.8\right]s^{-1}$ and the sub-ion range $\frac{1}{\tau }=\left[\mathrm{4,40}\right]s^{-1}$.

For an intermittent signal at higher orders of m ($m>3$), $S_m$ becomes more difficult to estimate due to the assumptions of ergodicity in the statistical approach and the reality of the finite length of time series [e.g., 69, 70, 78]. Higher orders accentuate the effects of the largest fluctuations and outliers in the data, which can cause the estimation of $S_m$ to degrade if the largest amplitude fluctuations are not sufficiently sampled in the signal. Therefore the quality of the structure-function obtained is dependent on the statistics of the extreme fluctuations in the signal. In particular, the estimation is difficult when using time lags when the increments at a given time lag have large amplitudes and the time-lagged series is strongly intermittent, which is usually the case in turbulent flows. This can somewhat be mitigated by having a longer time interval so that rare events are sufficiently sampled. However, our data lengths in MMS and Cluster are typically very short [e.g., 41, 79] because of orbital constraints. For MMS at best there are some intervals with a few hours of continuous burst mode in the solar wind.

The maximum order that can be estimated accurately is dependent on the intermittency in the signal, and the length of the time interval used. A rough estimate for the largest order that can be estimated is $\text{log}\left(N\right)-1$ where N is the number of data points. For the number of data points, here $N\simeq 20\times {10}^6$ this corresponds to the largest possible order of 6 [40]. However using the approach of [69], and analyzing a timescale of 0.5s where the scale-dependent kurtosis is near its peak a maximum order of 4 is obtained. Structure functions from orders 1 through 6 are shown in Figure 6 although orders larger than 4 should be interpreted with caution as discussed.

The structure functions show two distinct ranges with power-law behaviour $S_m\left(\tau \right)\propto {\tau }^{\zeta \left(m\right)}$. A possible suggestion of a power-law behaviour is also present in the transition range, at intermediate scales. However, it is difficult to resolve the inertial range and the transition range as they don’t cover a very large range of scales.

The variation with the order m of the scaling exponents ${\zeta }_m$ obtained by fitting the structure functions to the inertial range and the sub-ion range is investigated.

For a monofractal scale-invariant process the scaling index expected to vary linearly as $\zeta \left(m\right)\propto m$, while for a multifractal process the scaling exponent will have a nonlinear relationship to the order. Physically this means that more than one moment of order m is needed to fully capture the details of the PDF, and the signal is more intermittent. The relationship between the scaling exponent and the order (with step $\delta m=0.1$) is shown in Figure 7 for two of the ranges which correspond to the fits shown in black in Figure 6. As the transition range is shorter than a decade in scale and the scaling exponents are strongly concave we are not able to fit a p-model to them and we do not display them. The scaling relations of the inertial are concave, while the sub-ion range shows a linear relation. A linear fitting is performed for orders below $m=3$ which is shown in black and the order four is marked by the orange line. This is one order below the maximum physical m estimated from the technique of [69]. Before m = 4 is reached, the inertial departs from the linear scaling. This suggests that there is multifractality in the inertial range. This is in stark contrast to the sub-ion range which exhibits linear scaling even at orders $m>4$. Similar relations between the scaling exponent and the order are obtained for the magnetic field in Figure 8. However, as there is a smaller range available due to the noise floor occurring at a lower frequency than the electron density meaning that the sub-ion range is fitted over a smaller range of scales and is not as reliable as the electron density. For the two transverse components, there are only two ranges fitted, the ion inertial and the sub-ion range as there is no apparent transition range in the trace spectra in Figure 2A. Some studies have observed transitions in the trace magnetic spectra between the ion inertial and ion gyroradius scales, which may be related to ion damping, the interplay of Hall and convective terms or plasma instabilities [e.g., see 11, 80 and references therein]. However the spectral signature of this region is different to the flattening observed in the density spectra. Typically the transition observed in the magnetic spectra is very steep $\sim -3.4$ although the same process may affect the density and magnetic spectra differently. However in this interval we have no evidence of a transition in the trace spectra for this interval. For the compressive component, there are three ranges. However, similarly to the density spectra the transition range is too short to be fitted satisfactorily. The inertial ranges show weak concave relations while the sub-ion range shows mono-fractal behavior. This behavior has been observed in magnetic field observations of [12, 44], and in ion density fluctuations [45].

FIGURE 7

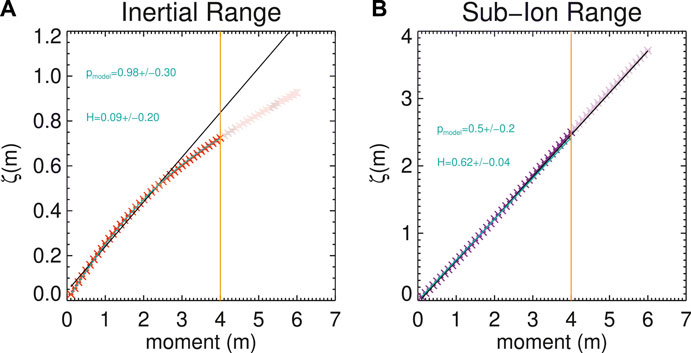
FIGURE 7. Scaling exponents ζ as a function of the moment m for the inertial (A) transition (B) and sub-ion ranges. The exponents here correspond to the black lines in Figure 6. The cyan lines denote p-model fits, and the black line denotes a linear fit to orders below 3.

FIGURE 8

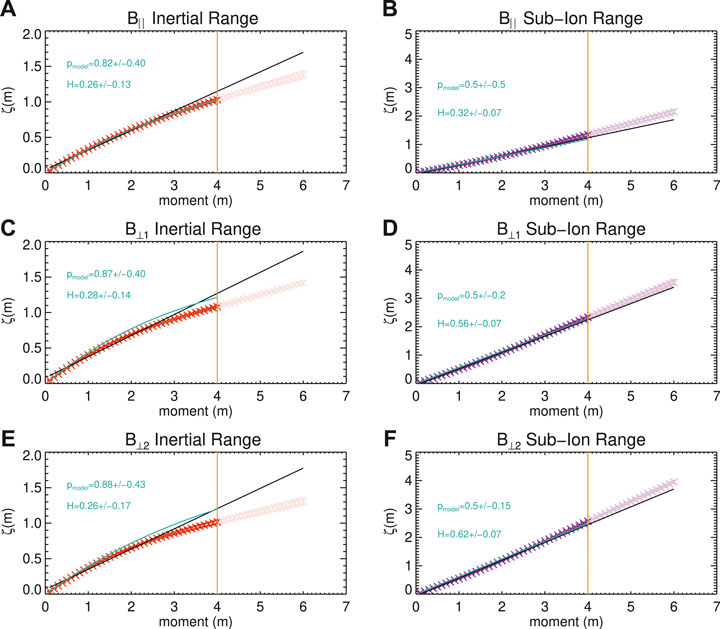
FIGURE 8. Scaling exponents ζ as a function of the moment m for the magnetic field. (A, B) denote the compressive component for the two ranges mentioned previously. (C, E) denote the scaling index for the inertial range for the two transverse components (D, F) denote the scaling exponent for the sub-ion range transverse components.

In order to obtain a more quantitative estimate of the level of intermittency, each scaling exponent curve can be fitted to a standard p-model of intermittent turbulence [81]. In such phenomenological framework, intermittency is modeled as the result of a multifractal multiplicative cascade for the fraction of volume in which the energy is transferred across scales. It predicts a simple relation for the scaling exponents: ${\zeta }_m=1-{\text{log}}_2\left[p_{model}^{mH}+{\left(1-p_{model}\right)}^{mH}\right]$, where H is the Hurst exponent, related to the spectral index through $\alpha =2H+1$ or to the structure function scaling exponents through ${\zeta }_m=mH$, and indicating the roughness of the signal. In the present work, H has been left as a free fitting parameter of the model. The second fitting parameter $p_{model}\in \left[0.5,1\right]$, related to the fraction of volume where the energy transfer is concentrated during the intermittent cascade, so that larger $p_{model}$ corresponds to larger intermittency.

The scaling exponents presented in the various panels of Figures 7, 8 have been fitted to a p-model, and the quality of the fit is excellent in all cases. Note that the p-model fit was performed only using exponents up to the fourth order, to ensure statistical convergence. However, we point out that the fitting parameters remain basically unchanged when all six orders are included. We therefore include the higher orders (with lighter colour plotting symbols) in the figures, with the caveat that they might be poorly statistically described. The solid cyan lines in the Figures 7, 8 represent those fits, and the resulting intermittency parameters $p_{model}$ are given in each panel. The fitted values of H are always compatible with the scaling exponents of the second order structure functions, within error bars. This confirms the possibility to describe the turbulence using the P-model, and corroborates the meaningfulness of the intermittency parameter $p_{model}$ For the electron density, a strong intermittency value $p_{model}=0.98\pm 0.30$ was found in the inertial range, in agreement with the large scaling exponent of the kurtosis. We do not show the scaling exponents or fit a p-model for the transition range, the bad quality of the fit did not allow modeling the data with the p-model. This is consistent with the extreme curvature of the scaling exponent (not shown), which for large orders m becomes a decreasing function of the order. This feature is typically forbidden for an “ideal” turbulent field, which requires monotonic increase of ${\zeta }_m$ (constant exponents are expected in the presence of topological discontinuities, for example in the absence of dissipation as described by the Burgers equation for neutral flows) [31]. The indication of this observation is that the stochastic fluctuations of the transition region are not simply the result of a turbulent cascade, but other physical processes must occur in generating the exceptionally strong gradients in that range of scale. This is not surprising, since in this range kinetic effects start to be relevant in the dynamics, so that wave-particle interactions may play an additional role in generating density fluctuations. Specifically this may be consistent with damping of compressive slow mode waves which are cascaded as a passive scalar, and are heavily damped as they reach the ion scales, in addition to an active cascade of kinetic Alfvén waves [e.g 74, 82].

In the sub-ion range, the p-model fitting parameter $p_{model}=0.5\pm 0.2$ indicates clearly the absence of intermittency, again in agreement with visual description of the PDFs and of the kurtosis, and with recent results on density intermittency [50]. Finally, the magnetic field components present high level of intermittency in the inertial range ($p_{model}\simeq 0.8$), and strictly mono-fractal scaling in the sub-ion range ($p_{model}\simeq 0.5$).

4.Discussion

The evolution of the scale-dependent kurtosis is shown to increase throughout the inertial range until it reaches the proton characteristic scales whereafter it decreases in the magnetic field or plateaus as in the density. This behavior is different from that in the magnetosheath, where the scale-dependent kurtosis continues to increase down to the smallest scales [42]. This may be due to the magnetosheath turbulence being strongly driven by the shock while the solar wind turbulence is decaying and the kurtosis decreases with radial distance [e.g., 83, 84]. This is to say that turbulence in the solar wind at large heliocentric distances is far from the drivers, e.g., velocity shears between streams, shocks, etc. Another possibility is that high-frequency wave activity in the solar wind may act in the sub-ion range to reduce the kurtosis [48]. These waves would need to have the property of having strong wavevector anisotropy $k_{\perp }\gg k_{\parallel }$, and approximate equal power in the compressive and stransverse components. In this region of large $k_{\perp }$these waves could be either Ion Bernstein [e.g., 85] or Kinetic Alfvén waves [e.g., 54]. The damping rates of such waves are highly sensitive to the propagation direction and the plasma beta. In the magnetosheath, due to processing at the shock the ion temperature (and consequently the ion beta) are much higher [e.g., 86]. At higher plasma β, linear plasma waves are typically more heavily damped [87]. This suggests that such waves could exist in the solar wind and act to reduce the kurtosis while in the magnetosheath they cannot exist leading to the magnetosheath being more similar to a neutral fluid.

One of the more puzzling results here is that there is a difference between the time and the spatial lags of the electron density from spacecraft potential. For the magnetic field data and the density from FPI, there is an agreement between the time and the spatial lags. However, this is somewhat misleading as the time lags are heavily affected by instrumental noise. As instrumental noise is uncorrelated between spacecraft the spatial lags are more robust to the effects of noise. In the spacecraft potential data, the time lag corresponding to the spatial separation occurs before instrumental noise becomes significant and show a leptokurtic distribution. The spatial lags show approximately Gaussian distributions. This could be due to several reasons. Firstly, there may be a physical difference between the different directions i.e., that there are more structures in the direction of the bulk flow (time lags) as opposed to other directions (spatial lags). This may be a naturally occurring difference or there could be a sampling effect related to the bulk flow direction [88]. Another possibility is that Taylor’s hypothesis breaks down in this region. In the numerical study of [89] they concluded that the Taylor’s hypothesis is likely to be violated at small scales for intervals where the Alfvén speed is comparable to the bulk speed [e.g., in the magnetosheath 90]. The geometry of the magnetic field with respect to the bulk velocity direction also plays a role with more radial configurations of the magnetic field being more likely to violate the hypothesis. In this interval $V_{sw}/V_A=7.6$, the magnetic field makes a large angle ($86\pm {11}^{\circ }$) with the bulk velocity and the hypothesis should be well satisfied for large scales. However, at small scales such as we study here, the hypothesis may still break down despite the interval having a large bulk speed and a favorable magnetic field configuration. A breakdown in Taylor’s hypothesis could be due to wave activity or that structures evolve at faster timescales at these scales. The waves that can exist in the sub-ion range such as kinetic Alfvén waves [91], or fast mode branch waves such as Ion Bernstein waves, or parallel whistler waves [92, 93] are very dispersive. Furthermore wave activity could act to reduce the kurtosis here similarly to how MHD-scale Alfvén waves act at larger scales [49]. Another possibility is that electron scale coherent structures evolve very quickly. For example, vortices could merge such as is discussed in neutral fluid turbulence in a process called vortex collapse [e.g., 94] or could develop or be destroyed on time scales faster than the advection time. This hypothesis could be tested directly with several spacecraft that are aligned with the bulk flow direction at a range of distnaces. Other possibilities are that the timing accuracy is not sufficient to compare inter-spacecraft increments, although this seems unlikely. Another issue could be that the resampling required to put the time series from different spacecraft on the same timeline causes some issues at the edges of the time series [42]. To ensure that outliers due to this effect are not present data points at the edges (the first and last 4 s) of the resampled time series are removed at each edge. Finally, we remark that coherent structures are characterized by phase coherence across many scales, therefore when looking at time lags larger scale coherent structures may affect the smaller scales, whereas using spatial lags the larger scale fluctuations could be more effectively filtered. It is however important to note that the structure of coherent structures may be complex with larger coherent structures, possibly having smaller “daughter” structures associated with them [95].

The scale-dependent kurtosis of the magnetic field gives complementary information to the density. In Figure 4 we see that the compressive component is smaller than the transverse components. This is different from observations of larger scales where the opposite is true [49], this may reflect a difference in the nature of coherent structures. At large scales coherent structures are likely strongly compressive, magnetic holes or boundaries between streams, while in the ion ranges the structures may be predominantly incompressible or very weakly compressible such as Alfvénic vortices and current sheets [34, 37]. There is a large difference between the scale-dependent kurtosis using a global mean as opposed to a local mean or the magnitude of the magnetic field. Using a global field may result in a larger kurtosis as it is potentially polluted by some of the transverse coherent structures. However, when using a local field gradients may not be able to be identified. In this case the local magnetic field agrees well with the values of the kurtosis of magnetic field magnitude and the density. The good agreement between the local magnetic field and the magnitude is likley because the fluctuations are small. However as the fluctuations are larger in the magnetosheath the magnitude may not be reliable, and one should use a local definition. However, it should be stressed that both approaches to calculating a local field have advantages and limitations, and the choice has implications for the interpretation of the results as shown here.

When comparing the spatial lags of the magnetic field and the density we see agreement between all of the different methods, that they all have small kurtoses. This complements previous measurements of the power of compressive and transverse fluctuations i.e. that they have similar powers in the sub-ion range [12, 20]. One potential explanation for this is that the fluctuations are kinetic Alfvén wave-like. As the KAW develops a larger wavenumber in the perpendicular direction it becomes strongly compressive. In the sub-ion range, this could account for equal power in the compressive and two transverse components [e.g., 12, 96].

Structure-function anaysis presented in Figures 7,8 also suggests that the sub-ion range for magnetic and density fluctuations are monofractal. For the density measurements, the scaling exponents are somewhat smaller than what is expected based on the Fourier spectrum in Figure 2. This may be due to the flattening in the spectrum at ion scales, meaning that there is a shorter range of scales available for fitting compared to the magnetic field data. The flattening of the spectra at ion scales could be due to the competition of large scale slow waves and small scale kinetic Alfvén waves, Hall effects, or an increase in the compressible coherent structures at this range. In this range, the scaling indices are anomalous⁴ suggesting a larger degree of multifractality in the density fluctuations. However, the scale-dependent kurtosis reaches a plateau and is not very different in Figure 3 when the scales close to the transition range are compared to the sub-ion range. Here we reach a similar conclusion to [46], that different measures of intermittency capture different properties of intermittency. The scaling indices in the sub-ion range of magnetic and density fluctuations suggest monofractal scaling, in agreement with the spatially lagged kurtoses which show predominantly Gaussian statistics. However, the time-lagged measurements show leptokurtic distributions.

5.Conclusion

To summarize; we have investigated compressive and incompressive intermittency in the solar wind. Using the exceptionally high resolution data provided from MMS allows a view deep into the sub-ion scale with unprecedented time resolution for an in situ measurement of electron density fluctuations. Further more the multiple measurement points allow an investigation of different directions in the plasma. Previous studies of the electron density have been limited to single point measurements and are only able to sample along the bulk flow direction. The results are found to be similar to those found with the magnetic field in [12, 44] and in ion density fluctuations at larger scales than are studied here [45]. In these studies, the scale-dependent kurtosis was not found to evolve significantly and the evolution of scaling index with the order suggested monofractal scaling or only very weak multifractality when juxtaposed with the inertial and transition ranges.

A discrepancy was observed between temporal and spatial lags and we have put forward several possible explanations for this. This could be due to a breakdown in Taylor’s hypothesis. This could be investigated using two spacecraft data where the baseline is aligned with the bulk flow. This would give a direct measurement of whether Taylor’s hypothesis is valid. However, for this interval none of the spacecraft pairs are aligned closely enough to the bulk velocity direction to make such a comparison. Other possibilities include directional differences. To investigate this possibility detailed comparisons with numerical simulations may be needed, and more sampling points than the four points that MMS or Cluster offer. One strong possibility is high-frequency waves which may affect these scales of randomizing the phases of the signal, reducing the kurtosis. Waves such as those described tend to have strong wavevector anisotropies ($k_{\perp }\gg k_{\parallel }$) [e.g., 97, 98] and could cause different kurtoses in different directions. Furthermore, such waves would also be strongly dispersive and could also lead to a violation of Taylor’s hypothesis. Alternatively it may be coherent structures in this interval are all much larger than the spacecraft baseline sizes. In this case there would not be much difference between the different spacecraft, whereas the gradients in the time lags would be larger. One final possibility is that there could be a sampling effect inherent with the bulk velocity direction [e.g., 88]. This could cause a bias in the bulk flow direction so that more structures are seen in this direction than compared to others.

The differences in the different measurement techniques support the statement in [46] that to investigate intermittency a variety of different techniques should be employed. We also remark that four-point measurements have revolutionized in situ plasma turbulence study. However, four points are inherently limited to providing either homogeneous coverage of the plasma at a single scale or multi-scale coverage at the cost of losing directional information. The natural next step in investigating space plasma turbulence is to go beyond four points to obtain multi-direction multi-scale measurements [99–101].

Data Availability Statement

The Magnetospheric MultiScale mission data are available from https://lasp.colorado.edu/mms/sdc/public/. The processed spacecraft potential can be accessed at https://www.iwf.oeaw.ac.at/en/research/researchnbspgroups/space-plasma-physics/sc-plasma-interaction/mmsaspoc-data-analysis/.

Author Contributions

OR, JT and LS, performed the analysis of the data. The initial manuscript was drafted by OR. OR and RN developed of the density dataset. JT, LS, ZV, and RN contributed to the interpretation of the data and several improvements in the manuscript.

Funding

The calibration of the spacecraft potential data at IWF is supported by Austrian FFG projects ASAP15/873685. JT was funded by a Fulbright Austria-Marshall Plan grant. RN was supported by Austrian FWF projects I2016-N20. ZV was supported by the Austrian FWF projects P28764-N27.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge the MMS instrument teams for FPI, FGM, and SDP for providing excellent data which made this study possible.

References

1. Bale, SD, Kellogg, PJ, Mozer, FS, Horbury, TS, and Reme, H. Measurement of the electric fluctuation spectrum of magnetohydrodynamic turbulence. Phys Rev Lett (2005). 94:215002. doi:10.1103/PhysRevLett.94.215002

CrossRef Full Text | Google Scholar

2. Podesta, JJ, Roberts, DA, and Goldstein, ML. Power spectrum of small-scale turbulent velocity fluctuations in the solar wind. J Geophys Res (2006). 111:A10109. doi:10.1029/2006JA011834

CrossRef Full Text | Google Scholar

3. Roberts, OW, Narita, Y, Li, X, Escoubet, CP, and Laakso, H. Multipoint analysis of compressive fluctuations in the fast and slow solar wind. J Geophys Res Space Phys (2017). 122:6940–63. doi:10.1002/2016JA023552

CrossRef Full Text | Google Scholar

4. Šafránková, J, Nemecek, Z, Nemec, F, Prech, L, Chen, CHK, and Zastenker, GN. Power spectral density of fluctuations of bulk and thermal speeds in the solar wind. Astrophys J (2016). 825:121. doi:10.3847/0004-637X/825/2/121

CrossRef Full Text | Google Scholar

5. Roberts, OW, Narita, Y, Nakamura, R, Vörös, Z, and Gershman, D. Anisotropy of the spectral index in ion scale compressible turbulence: MMS observations in the magnetosheath. Front Phys (2019). 7: 1–16. doi:10.3389/fphy.2019.00184

CrossRef Full Text | Google Scholar

6. Tu, CY, and Marsch, E. MHD structures, waves and turbulence in the solar wind: observations and theories. Space Sci Rev (1995). 73:1–210. doi:10.1007/BF00748891

CrossRef Full Text | Google Scholar

7. Smith, CW, Vasquez, BJ, and Hamilton, K. Interplanetary magnetic fluctuation anisotropy in the inertial range. J Geophys Res (2006). 111:A09111. doi:10.1029/2006JA011651

CrossRef Full Text | Google Scholar

8. Bruno, R, and Carbone, V. The solar wind as a turbulence laboratory. Living Rev Sol Phys (2013). 10, 2. http://www.livingreviews.org/lrsp-2013-2. doi:10.12942/lrsp-2013-2

CrossRef Full Text | Google Scholar

9. Kiyani, KH, Osman, KT, and Chapman, SC. Dissipation and heating in solar wind turbulence: from the macro to the micro and back again. Phil Trans Math Phys Eng Sci (2015). 373:20140155. doi:10.1098/rsta.2014.0155

CrossRef Full Text | Google Scholar

10. Verscharen, D, Klein, KG, and Maruca, BA. The multi-scale nature of the solar wind. Living Rev Sol Phys (2019). 16:5. doi:10.1007/s41116-019-0021-0

CrossRef Full Text | Google Scholar

11. Sahraoui, F, Hadid, L, and Huang, S. Magnetohydrodynamic and kinetic scale turbulence in the near-Earth space plasmas: a (short) biased review. Rev Mod Plasma Phys (2020). 4:4. doi:10.1007/s41614-020-0040-2

CrossRef Full Text | Google Scholar

12. Kiyani, K, Chapman, S, Sahraoui, F, Hnat, B, Fauvarque, O, and Khotyaintsev, YV. Enhanced magnetic compressibility and isotropic scale invariance at sub-ion larmor scales in solar wind turbulence. Astrophys J (2013). 763:10. doi:10.1088/0004-637X/763/1/10

CrossRef Full Text | Google Scholar

13. Alexandrova, O, Lacombe, C, and Mangeney, A. Spectra and anisotropy of magnetic fluctuations in the Earth’s magnetosheath: cluster observations. Ann Geophys (2008). 26:3585–96. doi:10.5194/angeo-26-3585-2008

CrossRef Full Text | Google Scholar

14. Ferrand, R, Galtier, S, Sahraoui, F, Meyrand, R, Andrés, N, and Banerjee, S. On exact laws in incompressible hall magnetohydrodynamic turbulence. Astrophys J (2019). 881:50. doi:10.3847/1538-4357/ab2be9

CrossRef Full Text | Google Scholar

15. Bandyopadhyay, R, Sorriso-Valvo, L, Chasapis, A, Hellinger, P, Matthaeus, WH, Verdini, A, et al. In situ observation of hall magnetohydrodynamic cascade in space plasma. Phys Rev Lett (2020). 124:225101. doi:10.1103/PhysRevLett.124.225101

CrossRef Full Text | Google Scholar

16. Chen, CH, Klein, KG, and Howes, GG. Evidence for electron Landau damping in space plasma turbulence. Nat Commun (2019). 10:740. doi:10.1038/s41467-019-08435-3

CrossRef Full Text | Google Scholar

17. Alexandrova, O, Saur, J, Lacombe, C, Mangeney, A, Mitchell, J, Schwartz, S, et al. Universality of solar-wind turbulent spectrum from MHD to electron scales. Phys Rev Lett (2009). 103:165003. doi:10.1103/PhysRevLett.103.165003

CrossRef Full Text | Google Scholar

18. Alexandrova, O, Lacombe, C, Mangeney, A, Grappin, R, and Maksimovic, M. Solar wind turbulent spectrum at plasma kinetic scales. Astrophys J (2012). 760:121. doi:10.1088/0004-637X/760/2/121

CrossRef Full Text | Google Scholar

19. Sahraoui, F, Huang, SY, Belmont, G, Goldstein, ML, Rétino, A, Robert, P, et al. Scaling OF the electron dissipation range OF solar wind turbulence. Astrophys J (2013). 777:15. doi:10.1088/0004-637X/777/1/15

CrossRef Full Text | Google Scholar

20. Roberts, OW, Narita, Y, and Escoubet, CP. Direct measurement of anisotropic and asymmetric wave vector spectrum in ion-scale solar wind turbulence. Astrophys J (2017). 851:L11. doi:10.3847/2041-8213/aa9bf3

CrossRef Full Text | Google Scholar

21. Pedersen, A. Solar wind and magnetosphere plasma diagnostics by spacecraft electrostatic potential measurements. Ann Geophys (1995). 13:118–29. doi:10.1007/s00585-995-0118-8

CrossRef Full Text | Google Scholar

22. Escoubet, CP, Pedersen, A, Schmidt, R, and Lindqvist, PA. Density in the magnetosphere inferred from ISEE 1 spacecraft potential. J Geophys Res Space Phys (1997). 102:17595–609. doi:10.1029/97JA00290

CrossRef Full Text | Google Scholar

23. Pedersen, A, Décréau, P, Escoubet, CP, Gustafsson, G, Laakso, H, Lindqvist, PA, et al. Four-point high time resolution information on electron densities by the electric field experiments (EFW) on cluster. Ann Geophys (2001). 19:1483–9. doi:10.5194/angeo-19-1483-2001

CrossRef Full Text | Google Scholar

24. Pedersen, A, Lybekk, B, André, M, Eriksson, A, Masson, A, Mozer, FS, et al. Electron density estimations derived from spacecraft potential measurements on cluster in tenuous plasma regions. J Geophys Res Space Phys (2008). 113:A07S33. doi:10.1029/2007JA012636

CrossRef Full Text | Google Scholar

25. Lybekk, B, Pedersen, A, Haaland, S, Svenes, K, Fazakerley, AN, Masson, A, et al. Solar cycle variations of the cluster spacecraft potential and its use for electron density estimations. J Geophys Res Space Phys (2012). 117:A01217. doi:10.1029/2011JA016969

CrossRef Full Text | Google Scholar

26. Yao, S, He, JS, Marsch, E, Tu, CY, Pedersen, A, Rème, H, et al. Multi-scale anti-correlation between electron density and magnetic field strength in the solar wind. Astrophys J (2011). 728:146. doi:10.1088/0004-637X/728/2/146.

CrossRef Full Text | Google Scholar

27. Andriopoulou, M, Nakamura, R, Torkar, K, Baumjohann, W, and Hoelzl, B. Deriving plasma densities in tenuous plasma regions, with the spacecraft potential under active control. J Geophys Res Space Phys (2015). 120:9594–616. doi:10.1002/2015JA021472

CrossRef Full Text | Google Scholar

28. Andriopoulou, M, Nakamura, R, Wellenzohn, S, Torkar, K, Baumjohann, W, Torbert, RB, et al. Plasma density estimates from spacecraft potential using MMS observations in the dayside magnetosphere. J Geophys Res Space Phys (2018). 123:2620–9. doi:10.1002/2017JA025086

CrossRef Full Text | Google Scholar

29. Torkar, K, Nakamura, R, Wellenzohn, S, Jeszenszky, H, Torbert, RB, Lindqvist, PA, et al. Improved determination of plasma density based on spacecraft potential of the magnetospheric multiscale mission under active potential control. IEEE Trans Plasma Sci (2019). 47:3636–47. doi:10.1109/TPS.2019.2911425

CrossRef Full Text | Google Scholar

30. Kolmogorov, AN. A refinement of previous hypotheses concerning the local structure of turbulence. J Fluid Mech (1962). 13:83–5. doi:10.1017/s0022112062000518

CrossRef Full Text | Google Scholar

31. Frisch, U. Turbulence: The Legacy of A. N. Kolmogorov. Cambridge, England: Cambridge University Press (1995).

Google Scholar

32. Chen, C, Mallet, A, Schekochihin, A, Horbury, T, Wicks, RT, and Bale, S. Three-dimensional structure of solar wind turbulence. Astrophys J (2012). 758:2. doi:10.1088/0004-637X/758/2/120

CrossRef Full Text | Google Scholar

33. Roberts, OW, Toledo-Redondo, S, Perrone, D, Zhao, J, Narita, Y, Gershman, D, et al. Ion-scale kinetic Alfvén turbulence: MMS measurements of the Alfvén ratio in the magnetosheath. Geophys Res Lett (2018). 45:7974–84. doi:10.1029/2018GL078498

CrossRef Full Text | Google Scholar

34. Perrone, D, Alexandrova, O, Mangeney, A, Maksimovic, M, Lacombe, C, Rakoto, V, et al. Compressive coherent structures at ION scales IN the slow solar wind. Astrophys J (2016). 826:196. doi:10.3847/0004-637X/826/2/196

CrossRef Full Text | Google Scholar

35. Roberts, OW, Li, X, Alexandrova, O, and Li, B. Observation of an MHD Alfvén vortex in the slow solar wind. J Geophys Res Space Phys (2016). 121:3870–81. doi:10.1002/2015JA022248

CrossRef Full Text | Google Scholar

36. Vörös, Z, Yordanova, E, Echim, MM, Consolini, G, and Narita, Y. Turbulence-generated proton-scale structures in the terrestrial magnetosheath. Astrophys J Lett (2016). 819:L15 1–6. doi:10.3847/2041-8205/819/1/L15

CrossRef Full Text | Google Scholar

37. Perrone, D, Alexandrova, O, Roberts, OW, Lion, S, Lacombe, C, Walsh, A, et al. Coherent structures at ion scales in fast solar wind: cluster observations. Astrophys J (2017). 849:49. doi:10.3847/1538-4357/aa9022.

CrossRef Full Text | Google Scholar

38. Wang, X, Tu, CY, He, JS, and Wang, LH. Ion-scale spectral break in the normal plasma beta range in the solar wind turbulence. J Geophys Res Space Phys (2018). 123:68–75. doi:10.1002/2017JA024813.

CrossRef Full Text | Google Scholar

39. Wu, P, Perri, S, Osman, K, Wan, M, Matthaeus, W, Shay, M, et al. Intermittent heating IN solar wind and kinetic simulations. Astrophys J Lett (2013). 763:L30. doi:10.1088/2041-8205/763/2/L30.

CrossRef Full Text | Google Scholar

40. Chen, CHK, Leung, L, Boldyrev, S, Maruca, BA, and Bale, S. Ion-scale spectral break of solar wind turbulence at high and low beta. Geophys Res Lett (2014). 41:8081–88. doi:10.1002/2014GL062009.

CrossRef Full Text | Google Scholar

41. Chasapis, A, Matthaeus, WH, Parashar, TN, Fuselier, SA, Maruca, BA, Phan, TD, et al. High-resolution statistics of solar wind turbulence at kinetic scales using the magnetospheric multiscale mission. Astrophys J (2017). 844:L9. doi:10.3847/2041-8213/aa7ddd.

CrossRef Full Text | Google Scholar

42. Chhiber, R, Chasapis, A, Bandyopadhyay, R, Parashar, TN, Matthaeus, WH, Maruca, BA, et al. Higher-order turbulence statistics in the Earth’s magnetosheath and the solar wind using magnetospheric multiscale observations. J Geophys Res Space Phys (2018). 123:9941–54. doi:10.1029/2018JA025768.

CrossRef Full Text | Google Scholar

43. Macek, WM. Multifractality and intermittency in the solar wind. Nonlinear Process Geophys (2007). 14:695–700. doi:10.5194/npg-14-695-2007

CrossRef Full Text | Google Scholar

44. Kiyani, KH, Chapman, SC, Khotyaintsev, YV, Dunlop, MW, and Sahraoui, F. Global scale-invariant dissipation in collisionless plasma turbulence. Phys Rev Lett (2009). 103:075006. doi:10.1103/PhysRevLett.103.075006

CrossRef Full Text | Google Scholar

45. Chen, CHK, Sorriso-Valvo, L, Šafránková, J, and Němeček, Z. Intermittency OF solar wind density fluctuations from ION to electron scales. Astrophys J (2014). 789:L8. doi:10.1088/2041-8205/789/1/L8

CrossRef Full Text | Google Scholar

46. Sorriso-Valvo, L, Carbone, F, Leonardis, E, Chen, CH, Šafránková, J, and Němeček, Z. Multifractal analysis of high resolution solar wind proton density measurements. Adv Space Res (2017). 59:1642–51. doi:10.1016/j.asr.2016.12.024

CrossRef Full Text | Google Scholar

47. Sorriso-Valvo, L, Carbone, V, Veltri, P, Consolini, G, and Bruno, R. Intermittency in the solar wind turbulence through probability distribution functions of fluctuations. Geophys Res Lett (1999). 26:1801–4. doi:10.1029/1999GL900270

CrossRef Full Text | Google Scholar

48. Wan, M, Osman, KT, Matthaeus, WH, and Oughton, S. Investigation of intermittency in magnetohydrodynamics and solar wind turbulence: scale-dependent kurtosis. Astrophys J (2012). 744:171. doi:10.1088/0004-637X/744/2/171

CrossRef Full Text | Google Scholar

49. Bruno, R, Carbone, V, Sorriso-Valvo, L, and Bavassano, B. Radial evolution of solar wind intermittency in the inner heliosphere. J Geophys Res Space Phys (2003). 108:1130. doi:10.1029/2002JA009615

CrossRef Full Text | Google Scholar

50. Carbone, F, Sorriso-Valvo, L, Alberti, T, Lepreti, F, Chen, CHK, Němeček, Z, et al. Arbitrary-order hilbert spectral analysis and intermittency in solar wind density fluctuations. Astrophys J (2018). 859:27. doi:10.3847/1538-4357/aabcc2

CrossRef Full Text | Google Scholar

51. Taylor, GI. The spectrum of turbulence. Proc Math Phys Eng Sci (1938). 164:476–90. doi:10.1098/rspa.1938.0032

CrossRef Full Text | Google Scholar

52. Roberts, OW, Nakamura, R, Torkar, K, Narita, Y, Holmes, JC, Voros, Z, et al. Sub-ion scale Compressive turbulence in the solar wind: MMS spacecraft potential observations. The Astrophys J Suppl S (2020). 250:35. doi:10.3847/1538-4365/abb45d

Google Scholar

53. Chen, C, Howes, GG, Bonnell, JW, Mozer, FS, Klein, KG, and Bale, S. Kinetic scale density fluctuations in the solar wind. In: Solar wind 13: proceeding of the thirteenth international solar wind conference solar wind, 1539; Pasadena, CA; (2013). p. 143–6. doi:10.1063/1.4811008

CrossRef Full Text | Google Scholar

54. Chen, C, Boldyrev, S, Xia, Q, and Perez, JC. Nature of subproton scale turbulence in the solar wind. Phys Rev Lett (2013). 110:225002. doi:10.1103/PhysRevLett.110.225002

CrossRef Full Text | Google Scholar

55. Safrankova, J, Nemecek, Z, Prech, L, and Zastenker, G. Ion kinetic scale in the solar wind observed. Phys Rev Lett (2013). 110:025004. doi:10.1103/PhysRevLett.110.025004

CrossRef Full Text | Google Scholar

56. Burch, JL, Moore, TE, Torbert, RB, and Giles, BL. Magnetospheric multiscale overview and science objectives. Space Sci Rev (2016). 199:5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

57. Bandyopadhyay, R, Chasapis, A, Chhiber, R, Parashar, TN, Maruca, BA, Matthaeus, WH, et al. Solar wind turbulence studies using MMS fast plasma investigation data. Astrophys J (2018). 866:81. doi:10.3847/1538-4357/aade93

CrossRef Full Text | Google Scholar

58. Jeřáb, M, Něměek, Z, Šafránková, J, Jelínek, K, and Měrka, J. Improved bow shock model with dependence on the IMF strength. Planet Space Sci (2005). 53:85–93. doi:10.1016/j.pss.2004.09.032

CrossRef Full Text | Google Scholar

59. Russell, CT, Anderson, BJ, Baumjohann, W, Bromund, KR, Dearborn, D, Fischer, D, et al. The magnetospheric multiscale magnetometers. Space Sci Rev (2016). 199:189–256. doi:10.1007/s11214-014-0057-3

CrossRef Full Text | Google Scholar

60. Pollock, C, Moore, T, Jacques, A, Burch, J, Gliese, U, Saito, Y, et al. Fast plasma investigation for magnetospheric multiscale. Space Sci Rev (2016). 199:331–406. doi:10.1007/s11214-016-0245-4

CrossRef Full Text | Google Scholar

61. Roberts, OW, Nakamura, R, Torkar, K, Graham, DB, Gershman, DJ, Holmes, J, et al. Estimation of the electron density from spacecraft potential during high frequency electric field fluctuations. J Geophys Res Space Phys (2020). 125:e2020JA027854. doi:10.1029/2020JA027854

CrossRef Full Text | Google Scholar

62. Lindqvist, PA, Olsson, G, Torbert, RB, King, B, Granoff, M, Rau, D, et al. The spin-plane Double probe electric field instrument for MMS. Space Sci Rev (2016). 199:137–65. doi:10.1007/s11214-014-0116-9

CrossRef Full Text | Google Scholar

63. Khotyaintsev, YV, Lindqvist, PA, and Nilsson, T. Spin-plane Double Probe instrument/ Axial Double Probe instrument (SDP/ADP) data products guide (2017). Technical Report.

Google Scholar

64. Graham, DB, Vaivads, A, Khotyaintsev, YV, Eriksson, AI, André, M, Malaspina, DM, et al. Enhanced escape of spacecraft photoelectrons caused by Langmuir and upper hybrid waves. J Geophys Res Space Phys (2018). 123:7534–53. doi:10.1029/2018JA025874

CrossRef Full Text | Google Scholar

65. Torkar, K, Nakamura, R, Tajmar, M, Scharlemann, C, Jeszenszky, H, Laky, G, et al. Active spacecraft potential control investigation. Space Sci Rev (2016). 199:515–44. doi:10.1007/s11214-014-0049-3

CrossRef Full Text | Google Scholar

66. Ye, S, Vaverka, J, Nouzak, L, Sternovsky, Z, Zaslavsky, A, Pavlu, J, et al. Understanding cassini RPWS antenna signals triggered by dust impacts. Geophys Res Lett (2019). 46:10941–50. doi:10.1029/2019GL084150

CrossRef Full Text | Google Scholar

67. Vaverka, J, Pavlů, J, Nouzák, L, Šafránková, J, Němeček, Z, Mann, I, et al. One-year analysis of dust impact-like events onto the MMS spacecraft. J Geophys Res Space Phy 124 (2019). 8179–90. doi:10.1029/2019JA027035

CrossRef Full Text | Google Scholar

68. Escoubet, CP, Hwang, KJ, Toledo-Redondo, S, Turc, L, Haaland, SE, Aunai, N, et al. Cluster and MMS simultaneous observations of magnetosheath high speed jets and their impact on the magnetopause. Front Astron Space Sci (2020). 6:78. doi:10.3389/fspas.2019.00078

CrossRef Full Text | Google Scholar

69. Dudok de Wit, T. Can high-order moments be meaningfully estimated from experimental turbulence measurements? Phys Rev (2004). 70:055302. doi:10.1103/PhysRevE.70.055302

CrossRef Full Text | Google Scholar

70. Kiyani, K, Chapman, SC, and Hnat, B. Extracting the scaling exponents of a self-affine, non-Gaussian process from a finite-length time series. Phys Rev (2006). 74:051122. doi:10.1103/PhysRevE.74.051122

CrossRef Full Text | Google Scholar

71. Bandyopadhyay, R, Matthaeus, WH, Chasapis, A, Russell, CT, Strangeway, RJ, Torbert, RB, et al. Direct measurement of the solar-wind taylor microscale using MMS turbulence campaign data. APJ (2020). 899:63. doi:10.3847/1538-4357/ab9ebe

Google Scholar

72. King, JH, and Papitashvili, N. Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J Geophys Res (2005). 110:A02104. doi:10.1029/2004JA010649

CrossRef Full Text | Google Scholar

73. Bruno, R, and Trenchi, L. Radial dependence OF the frequency break between fluid and kinetic scales IN the solar wind fluctuations. Astrophys J Lett (2014). 787 24. doi:10.1088/2041-8205/787/2/L24

CrossRef Full Text | Google Scholar

74. Chandran, BDG, Quataert, E, Howes, GG, Xia, Q, and Pongkitiwanichakul, P. Constraining low-frequency alfvenic turbulence in the solar wind using density-fluctuation measurements. Astrophys J (2009). 707:1668–75. doi:10.1088/0004-637X/707/2/1668

CrossRef Full Text | Google Scholar

75. Veltri, P. MHD turbulence in the solar wind: self-similarity, intermittency and coherent structures. Plasma Phys Control Fusion (1999). 41:A787–95. doi:10.1088/0741-3335/41/3A/071

CrossRef Full Text | Google Scholar

76. Chapman, SC, Hnat, B, Rowlands, G, and Watkins, NW. Scalling collapse and structure functions: identifying self-affinity in finite length time series. Nonlinear Process Geophys (2005). 12:767–74. doi:10.5194/npg-12-767-2005

CrossRef Full Text | Google Scholar

77. Oughton, S, and Matthaeus, WH. Critical balance and the physics of magnetohydrodynamic turbulence. Astrophys J (2020). 897:37. doi:10.3847/1538-4357/ab8f2a

CrossRef Full Text | Google Scholar

78. Tennekes, H, and Wyngaard, JC. The intermittent small-scale structure of turbulence: data-processing hazards. J Fluid Mech (1972). 55:93–103. doi:10.1017/S0022112072001661

CrossRef Full Text | Google Scholar

79. Roberts, OW, Li, X, and Jeska, L. A statistical study OF the solar wind turbulence at ION kinetic scales using the K -filtering technique and cluster data. Astrophys J (2015). 802:1–13. doi:10.1088/0004-637X/802/1/2

CrossRef Full Text | Google Scholar

80. Alexandrova, O, Chen, CHK, Sorriso-Valvo, L, Horbury, TS, and Bale, SD. Solar wind turbulence and the role of ion instabilities. Space Sci Rev (2013). 178:101–39. doi:10.1007/s11214-013-0004-8

CrossRef Full Text | Google Scholar

81. Meneveau, C, and Sreenivasan, KR. Simple multifractal cascade model for fully developed turbulence. Phys Rev Lett (1987). 59:1424–1427. doi:10.1103/PhysRevLett.59.1424

CrossRef Full Text | Google Scholar

82. Schekochihin, AA, Cowley, SC, Dorland, W, Hammett, GW, Howes, GG, Quataert, E, et al. Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys J Suppl (2009). 182:310–77. doi:10.1088/0067-0049/182/1/310

CrossRef Full Text | Google Scholar

83. Wawrzaszek, A, Echim, M, Macek, WM, and Bruno, R. Evolution of intermittency in the slow and fast solar wind beyond the ecliptic plane. Astrophys J Lett (2015). 814: L19. doi:10.1088/2041-8205/814/2/L19

CrossRef Full Text | Google Scholar

84. Parashar, TN, Cuesta, M, and Matthaeus, WH. Reynolds number and intermittency in the expanding solar wind: predictions based on voyager observations. Astrophys J 884 (2019). L57. doi:10.3847/2041-8213/ab4a82

CrossRef Full Text | Google Scholar

85. Narita, Y, Plaschke, F, Nakamura, R, Baumjohann, W, Magnes, W, Fischer, D, et al. Wave telescope technique for MMS magnetometer. Geophys Res Lett (2016). 43:4774–80. doi:10.1002/2016GL069035.Received

CrossRef Full Text | Google Scholar

86. Krasnoselskikh, V, Balikhin, M, Walker, SN, Schwartz, S, Sundkvist, D, Lobzin, V, et al. The dynamic quasiperpendicular shock: Cluster discoveries. Space Science Reviews (2013). 178:535–598. doi:10.1007/s11214-013-9972-y

CrossRef Full Text | Google Scholar

87. Gary, S. Theory of space plasma microinstabilities. Cambridge, England: Cambridge University Press (1993).

Google Scholar

88. Turner, AJ, Gogoberidze, G, Chapman, S, Hnat, B, and Müller, WC. Nonaxisymmetric anisotropy of solar wind turbulence. Phys Rev Lett (2011). 107:095002. doi:10.1103/PhysRevLett.107.095002

CrossRef Full Text | Google Scholar

89. Perri, S, Valentini, F, Sorriso-Valvo, L, Reda, A, and Malara, F. On the estimation of the current density in space plasmas: multi- versus single-point techniques. Planet Space Sci (2017). 140:6–10. doi:10.1016/j.pss.2017.03.008

CrossRef Full Text | Google Scholar

90. Stawarz, JE, Eriksson, S, Wilder, FD, Ergun, RE, Schwartz, SJ, Pouquet, A, et al. Observations of turbulence in a kelvin-helmholtz event on 8 september 2015 by the magnetospheric multiscale mission. J Geophys Res Space Phy (2016). 121:11021–11034. doi:10.1002/2016JA023458

CrossRef Full Text | Google Scholar

91. Chen, C, Bale, S, Salem, C, and Maruca, B. Residual energy spectrum of solar wind turbulence. Astrophys J (2013). 770:125. doi:10.1088/0004-637X/770/2/125

CrossRef Full Text | Google Scholar

92. Lacombe, C, Alexandrova, O, Matteini, L, Santolík, O, Cornilleau-Wehrlin, N, Mangeney, A, et al. Whistler mode waves and the electron heat flux in the solar wind: cluster observations. Astrophys J (2014). 796:5. doi:10.1088/0004-637X/796/1/5

CrossRef Full Text | Google Scholar

93. Roberts, OW, Alexandrova, O, Kajdič, P, Turc, L, Perrone, D, Escoubet, CP, et al. Variability of the magnetic field power spectrum in the solar wind at electron scales. Astrophys J (2017). 850:120. doi:10.3847/1538-4357/aa93e5

CrossRef Full Text | Google Scholar

94. Novikov, EA, and Sedov, YB. Vortex collapse. Sov Phys JETP (1979). 50:297–301

Google Scholar

95. Greco, A, Perri, S, Servidio, S, Yordanova, E, and Veltri, P. The complex structure of magnetic field discontinuities in the turbulent solar wind. Astrophys J (2016). 823:L39. doi:10.3847/2041-8205/823/2/L39

CrossRef Full Text | Google Scholar

96. Narita, Y. Non-elliptic wavevector anisotropy for magnetohydrodynamic turbulence. Ann Geophys (2015). 33:1413–9. doi:10.5194/angeo-33-1413-2015

CrossRef Full Text | Google Scholar

97. Roberts, OW, Li, X, and Li, B. Kinetic plasma turbulence in the fast solar wind measured by cluster. Astrophys J (2013). 769:58. doi:10.1088/0004-637X/769/1/58

CrossRef Full Text | Google Scholar

98. Roberts, OW, and Li, X. Evidence of the ion cyclotron resonance at proton kinetic scales in the solar wind. Astrophys J (2015). 802:1–11. doi:10.1088/0004-637X/802/1/1

CrossRef Full Text | Google Scholar

99. Klein, KG, Alexandrova, O, Bookbinder, J, Caprioli, D, Case, AW, Chandran, BDG, et al. [Plasma 2020 decadal] Multipoint measurements of the solar wind: a proposed advance for studying magnetized turbulence. Arxiv [Preprint]. 1903.05740. (2019).

Google Scholar

100. TenBarge, JM, Alexandrova, O, Boldyrev, S, Califano, F, Cerri, SS, Chen, CHK, et al. [Plasma 2020 decadal] Disentangling the spatiotemporal structure of turbulence using multi-spacecraft data. Arxiv [Preprint]. 1903.05710. (2019).

Google Scholar

101. Matthaeus, WH, Bandyopadhyay, R, Brown, MR, Borovsky, J, Carbone, V, Caprioli, D, et al. [Plasma 2020 decadal] The essential role of multi-point measurements in turbulence investigations: the solar wind beyond single scale and beyond the Taylor Hypothesis. Arxiv [Preprint]. 1903.06890 (2019).

Google Scholar