- Department of Health Technology, Technical University of Denmark, Kongens Lyngby, Denmark
Mesoscopic environments and particles diffusing in them are often studied by tracking such particles individually while their Brownian motion explores their environment. Environments may be, e.g., a domain in a cell membrane, an interior compartment of a cell, or an engineered nanopit. Particle trajectories are typically determined from time-lapse recorded movies. These are recorded with sufficient exposure time per frame to be able to detect and localize particles in each frame. Since particles move during this exposure time, particles image with motion blur. This motion blur can compromise estimates of diffusion coefficients and the size of the confining domain if not accounted for correctly. We do that here. We give explicit and exact expressions for the variance of measured positions and the mean-squared displacement of a Brownian particle confined in, respectively, a 1D box, a 2D box, a 2D circular disc, and a 3D sphere. Our expressions are valid for all exposure times, irrespective of the size of the confining space and the value of the diffusion coefficient. They apply also in the common case where the exposure time is smaller than the time-lapse due, e.g., to “dead time” caused by the readout process in the camera. These expressions permit determination of diffusion coefficients and domain sizes for given movies for the simple geometries we consider. More important, the trends observed in our exact results when parameter values are varied are valid also for more complex geometries for which no exact analytical solutions exist. Wherever the underlying physics is the same, the exact quantitative description of its consequences provided here is portable as a qualitative and semi-quantitative understanding of its consequences in general. The results may also be useful for other types of reflected Brownian motion than those occurring in single-particle tracking, e.g., in nuclear magnetic resonance imaging techniques. For use in that particular context, we briefly discuss the effects of confinement on anisotropic Brownian motion imaged with motion blur.
1 Introduction
In many branches of science, individual particles or molecules are labeled fluorescently in order to track and characterize their motion. To this end, they must be sufficiently isolated from each other in time and/or space, e.g., by sparse labeling [1] or super-resolution microscopies [2]. Only then may their centers be found with a precision that increases with the number of photons recorded [3]. When it does, nanometer precision is obtained routinely. In this manner, single-particle tracking is used extensively to uncover, e.g., the organization and dynamics of biology at its shortest length scale [4] and its interactions with nanoparticles [5]. One key advantage of single-particle tracking is that, with sufficiently long trajectories, it yields single-particle results. With sample-averaging unnecessary, it can detect heterogeneity in a population. Moreover, if such heterogeneity is absent, it can detect anomalous behavior in individual particles. Thus spotted before averaging, such outliers can be excluded from samples before sample-averages are calculated. This can improve accuracy and precision of estimates substantially.
Since the molecules and particles are studied under ambient conditions, they undergo Brownian motion. Various methods of various qualities are used to estimate diffusion coefficients from recorded particle trajectories describing free Brownian motion [6, 7]. Here, we address how to do similar estimates for Brownian motion in confined spaces: for example, a domain in a cell membrane, a compartment inside a cell, or an engineered nanopit [4, 8–10]. Such motion in confined domains and the properties of the domains themselves are important. Indeed, nano-domains in cell membranes, such as lipid nano-domains and nano-domains created by cellular filaments, are involved in multiple biological mechanisms, such as signal processing, membrane trafficking, and various diseases [11–13]. Moreover, single-particle tracking of nano-particles is often used to characterize lab-on-a-chip devices and thus the importance of single-particle tracking for characterization of particles and their confining environments.
The implementation of single-particle tracking may, however, itself confound results obtained with it. In order to track a fluorescently labeled particle or molecule, one records a time-lapse movie of micrographs of the particle. Typically, the dim signal from its fluorescent label is recorded with a highly sensitive camera. Each frame of the time-lapse movie must have recorded enough photons from the label to permit detection and localization of the particle in that frame [14]. So, a sufficiently long exposure time is used. The particle, however, moves during exposure. Since typical exposure times last tens of milliseconds, they are much longer than the characteristic time-scale of the particle's inertial motion. The particle thus undergoes Brownian motion while being imaged. This creates motion blur, and the observed position essentially is the time-average over positions visited by the particle during exposure. This has consequences for the statistics of motion, such as variances of measured positions of the particle and its mean-squared displacement (MSD).
While the effects of motion blur on the statistics of free Brownian motion have been studied in detail [6, 14–16], less effort has been devoted to its effects in the case of confined Brownian motion. Clearly, if the exposure time is very long, the particle visits all of a confining domain many times during a single exposure time. Thus, if the domain is smaller than the diffraction limit, super-localization techniques will locate the particle at the centroid of the confining domain if at all. Such consequences of motion blur have been observed [17], and approximate formulas that correct for these effects have been developed for specific geometries [18]. Their quality, unfortunately, depends on the values of experimental parameters. Therefore, we here derive exact expressions for the variances of positions and the MSD for Brownian particles in confinement recorded with motion blur. Specifically, we treat the cases of 1D Brownian motion confined to a box, 2D Brownian motion confined, respectively, to a box and to a circular disc, and 3D Brownian motion confined to a sphere. Our formulas are valid for all frame rates, irrespective of the value of the diffusion coefficient and the size of the confining domain. We also model the common case of “dead time” making the exposure time shorter than the inverse frame rate. While our exact results are derived for uniform and isotropic Brownian motion, we also discuss the implications of confinement and motion blur on anisotropic Brownian motion confined to a 2D disc. We do this using simulated trajectories. We compare the statistics obtained from those trajectories to the theory for the isotropic case.
We note that confined (sometimes called reflected) Brownian motion also plays an important role in other research fields, e.g., in probability theory and nuclear magnetic resonance (NMR) imaging. Time-averaging also may influence results there, e.g., in pulsed field-gradient spin-echo NMR, where the diffusion of the spins during the finite duration of the pulse causes that the pores in materials appear smaller than they are (for a review, see [19, Sec. II.B]).
2 Results
2.1 True Positions Versus Measured Positions
In order to track a fluorescently labeled particle in a fluorescence microscopy experiment, one records a movie of it. Typically, one uses a constant time-lapse,
Finite exposure time can be accounted for by introducing the shutter function
Since the particle moves during the recording of its position, its measured position is affected by motion blur. That position,
provided that it started at position
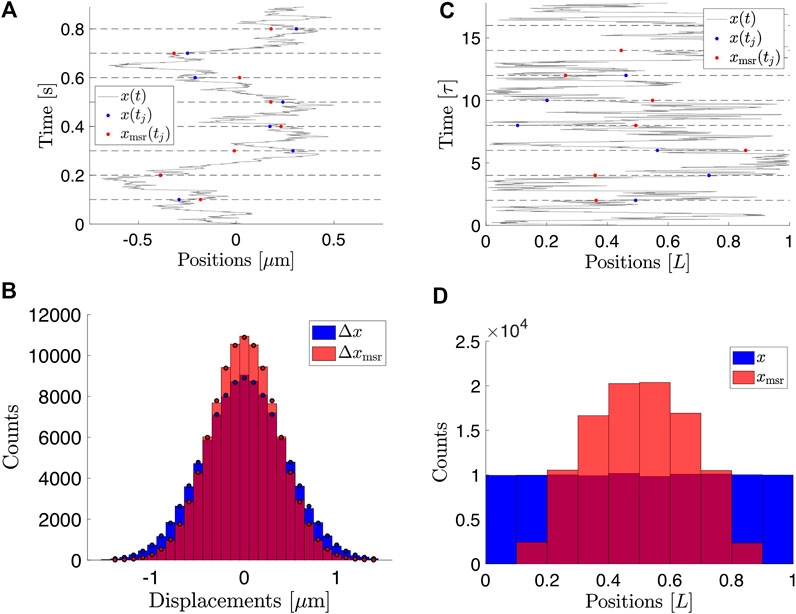
FIGURE 1. Consequences of finite exposure time for the measured positions of a Brownian particle. (A) Simulated positions of a free Brownian particle with
Below, we explore the consequences of this time-averaging on the variance and the mean-squared displacement (MSD) for Brownian motion in confining spaces. For free Brownian motion, these effects are discussed at length in, e.g., [6, 14, 15].
In real measurements, the measured position of a particle also contains a localization error due to photon shot noise. In practice, localization errors may be important in the analysis of experimental data, but we present our formulas without localization errors to keep them simple. In Section 4.5, we briefly describe how to account also for localization errors.
2.2 Free Brownian Motion
We consider a particle embedded in a fluid at rest at finite temperature, subject only to the fluctuating thermal forces from the fluid surrounding it. We assume that the time-lapse
with the initial condition
With the boundary conditions
That is, the conditional probability density is normal with mean
2.2.1 Statistics of Displacements for Instantaneously Sampled Positions
As a consequence, consecutive sampled positions of a Brownian particle are related by displacements
An example of time-lapse sampled positions of a Brownian particle is shown in Figure 1A.
Equation 2 also gives the mean-squared displacement,
with its signature proportionality to the time lag
2.2.2 Motion Blur Reduces Variances of Displacements and Correlates Them
Since motion blur effectively acts as a low-pass filter, the statistical properties of displacements
So, the motion blur reduces the variance of the displacements and introduces a nearest-neighbor correlation between them. Both effects are proportional to
The MSD of the measured positions for
Consequently, a fit of a straight line to the MSD estimated from positions subject to motion blur will return the true value of D on average. However, unless data are very rich, superior alternatives for the determination of D exist also for this case [6, 7].
2.3 Brownian Motion in 1D Confinement
To account for the statistical effects of confinement, we first consider the simplest possible case, a particle diffusing in 1D in a box of length L. Let x denote the coordinate of the particle with axis chosen such that the box has
For initial condition
Here, we have introduced the characteristic time-scale
Brownian motion confined to a 2D square or rectangular box is described by the independent motion of each of two Cartesian coordinates in their respective 1D boxes.
2.3.1 Variance of Positions Recorded With Motion Blur for a Brownian Particle in a 1D Box
In the limiting case of instantaneous recording of exact positions, there is uniform probability density
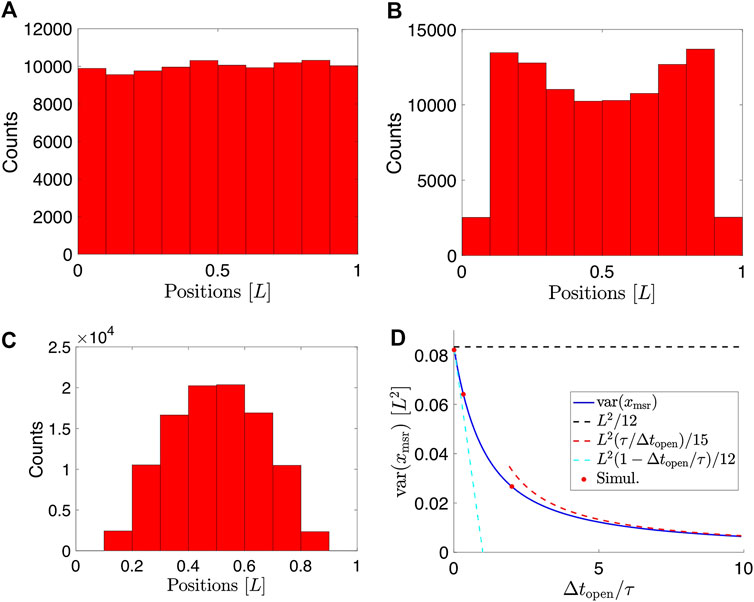
FIGURE 2. Histograms of measured positions for
In practice,
The variance of the measured positions is
where the average
where
The time-ordered auto-correlation function can be expressed via the conditional probability density in Eq. 13,
The calculation is straightforward, but lengthy (Supplementary Material). Using Eqs. 15, 16, 17, we get that the variance for a particle in 1D confinement is
This expression is exact and agrees with simulated data for Brownian motion in 1D confinement, as shown in Figure 2D. The result for the variance was also derived in [24] in the context of the apparent pore sizes in materials when studied with pulsed gradient-field spin-echo NMR.
We note that the sum in Eq. 18 converges rapidly. Terms with
When the exposure time
In the opposite limit,
Note that for
Since both parameters of interest, D and L, appear in the expressions for the variance, it is not possible to determine both of them independently based on the variance alone. Access to the full distribution of the measured positions would, in principle, allow this (Figure 2A–C). The MSD, however, also grants access to this information, as we shall see below.
2.3.2 MSD of Positions Recorded With Motion Blur, for a Brownian Trajectory in a Box
Obviously, the MSD must be bounded for confined Brownian motion. Here, we consider this MSD for positions recorded with motion blur:
since
The details of the calculation may be found in the Supplementary Material. This expression is exact and agrees with simulated data for a Brownian particle confined to a 1D box (Figure 3). For
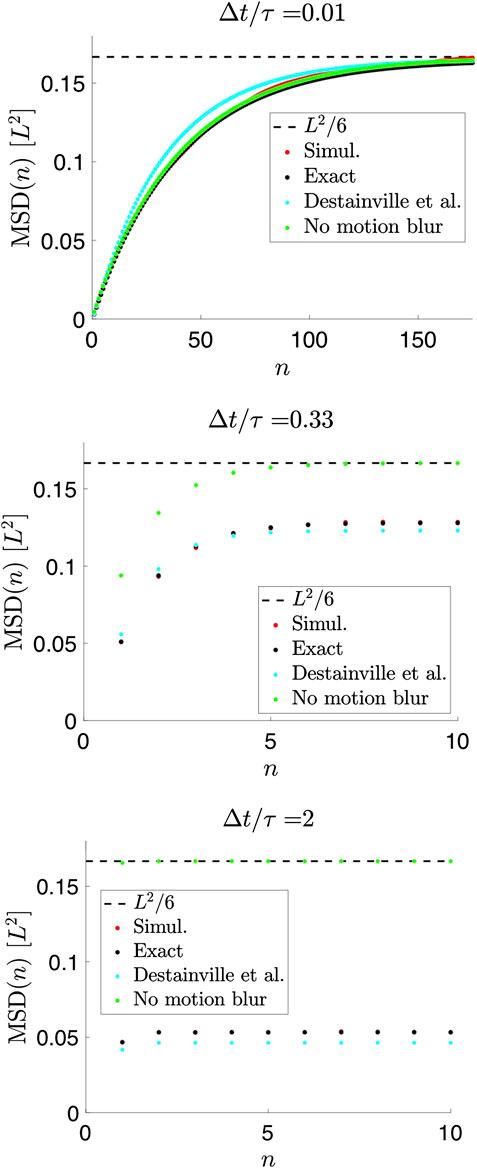
FIGURE 3. Mean-squared displacements (MSDs) of measured positions for a Brownian particle in a 1D box for
For
Thus, motion blur, described to lowest order in
Figure 3 also illustrates that both D and L, in principle, can be determined from data, provided that
In the absence of motion blur and localization errors—i.e., if positions are recorded instantaneously with infinite precision—the MSD can be calculated exactly for all values of n directly from Eq. 13 (Figure 3) [22],
Results for the MSD similar to our Eq. 22 were previously found by Destainville and Salomé [18] in order to improve analysis of data from [17]. Considering a fully open shutter (
This is similar, but not identical to Eq. 22, see Figure 3, likely because their parameters were chosen to produce the correct scaling properties from a single term, i.e., similar to our term with
2.4 2D Brownian Motion Confined to a Disc
Another relevant case to consider is that of a Brownian particle confined to a 2D circular disc with radius
For the case of Brownian motion confined to a 2D disc, the solution to the diffusion Fokker–Planck equation for the conditional probability density for the particle’s position
where
2.4.1 Variance of Positions Recorded With Motion Blur, for a Brownian Trajectory on a 2D Disc
For the 2D case, we define the measured position similarly to Eq. 1. The variance of the measured positions is calculated in a manner similar to the 1D case, and the result is
For details of the calculation, see Supplementary Material. This exact expression agrees with simulated data (Figure 4A–C) of particles undergoing Brownian motion confined to a 2D disc and subject to motion blur (Figure 4D).
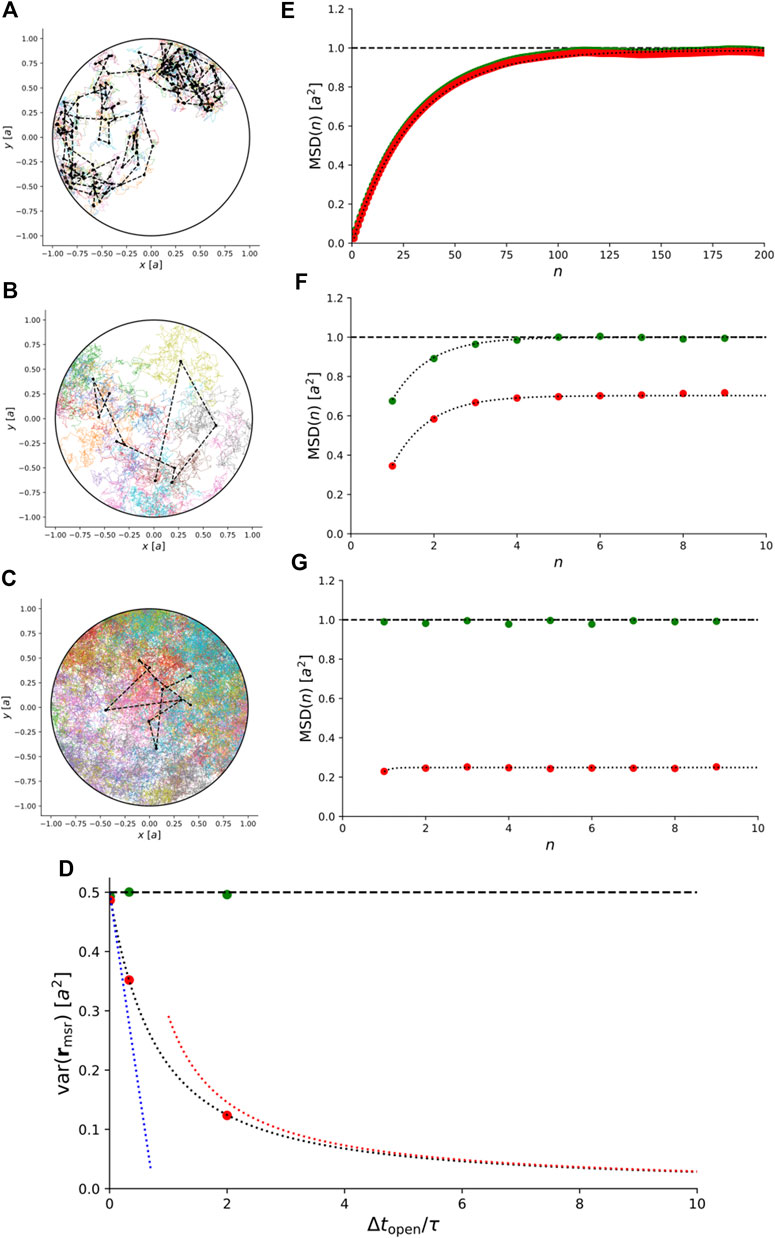
FIGURE 4. Simulations of 2D Brownian motion confined to a circular domain with radius a. (A)–(C) Simulated trajectories for
In the limit where the exposure time,
which is equal to the variance of a particle’s positions under instantaneous (and noise-free) recording (see Supplementary Material).
On the other hand, for
To arrive at this expression, we evaluated the relevant sum following [25], see Supplementary Material.
These limiting behaviors are also indicated in Figure 4D. Qualitatively, the implications of the variance of particle positions confined to a 2D circular domain and with positions recorded using finite exposure time are similar to the case of a particle confined to a box.
2.4.2 MSD of Positions Recorded With Motion Blur, for a Brownian Trajectory on a 2D Disc
A calculation similar to that for the 1D case yields the MSD of a 2D Brownian trajectory on a disc (Supplementary Material),
This expression is exact for all values of
In the case of instantaneous and noise-free recording of positions, it has been shown that the MSD can be calculated from Eq. 27 [22, 25]. The result is
That is, Eq. 32 is the 2D version of Eq. 24, valid for instantaneous (and noise-free) sampling. We note that this expression is recovered from our result, Equation (31), in the limit of
2.5 3D Brownian Motion Confined to a 3D Sphere
We now consider a Brownian particle confined to a 3D sphere with radius
The solution to the diffusion Fokker–Planck equation for the conditional probability density for the particle’s position
Here,
2.5.1 Variance of Positions Recorded With Motion Blur, for a Brownian Trajectory in a 3D Sphere
For the 3D case, we define once again the measured position similarly to Eq. 1. The calculation of the variance of the measured positions is similar to the 1D case leading to the result (for details, see Supplementary Material),
Figure 5A–C show trajectories of particles undergoing confined Brownian motion in a 3D sphere. The exact result for the variances of the measured positions agrees with the simulated data (Figure 5D). When the exposure time is small compared to the characteristic timescale, i.e.,
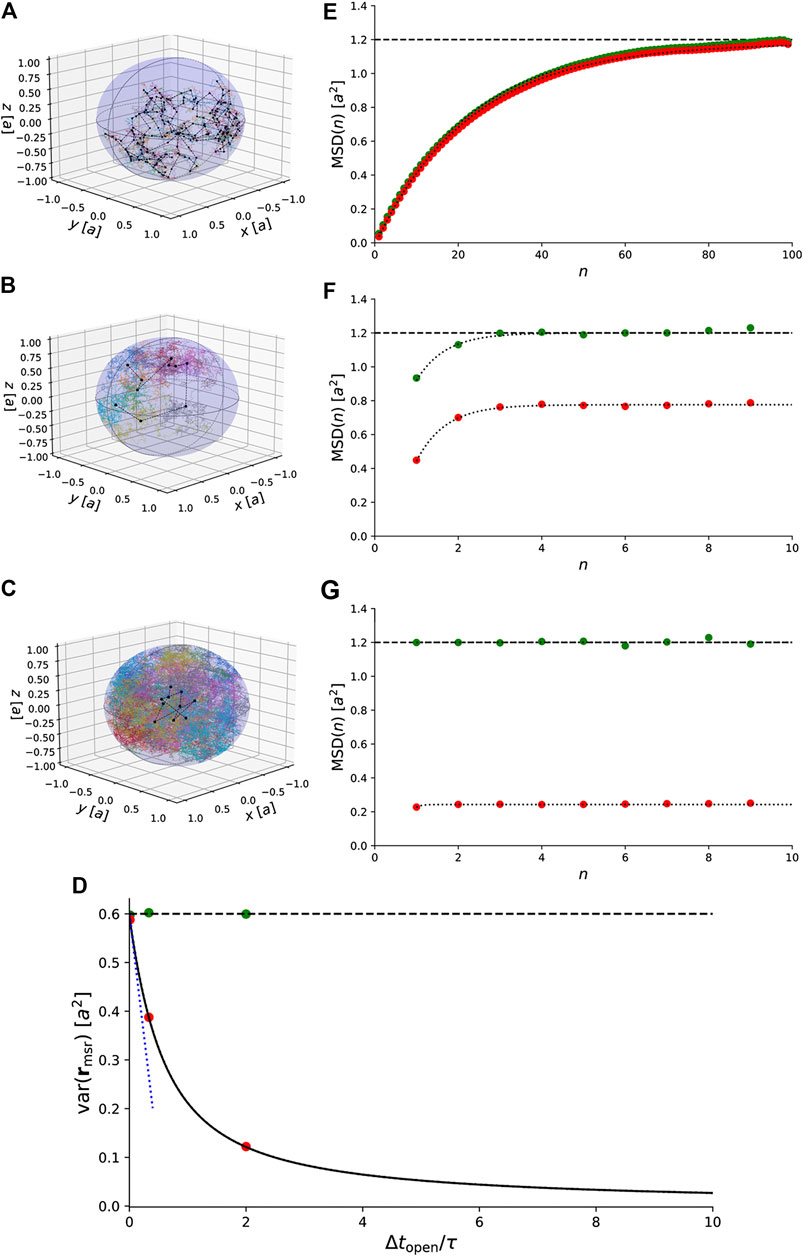
FIGURE 5. Simulations of 3D Brownian motion confined to a spherical domain with radius a. (A)–(C) Simulated trajectories for
Details of the calculation are presented in Supplementary Material.
2.5.2. MSD of Positions Recorded With Motion Blur, for a Brownian Trajectory in a 3D Sphere
A calculation similar to the one done for the 1D case gives the MSD for a 3D Brownian trajectory confined within a 3D sphere. The result is
This expression is exact for all values of
In the absence of motion-blur—i.e., in the case of instantaneous recording of exact positions—the MSD can be calculated directly from the propagator in Eq. 34 with the result [22]
This result is also indicated in Figure 5E–G.
2.6 2D Anisotropic Brownian Motion Confined to a 2D Disc
So far, we only considered isotropic Brownian motion, i.e., with identical diffusion coefficients in all directions. Now, we discuss the implications of confinement on anisotropic Brownian motion that is imaged with motion blur. For simplicity, we restrict the discussion to anisotropic 2D Brownian motion confined to a disc. In this case, the probability density is described by a Fokker–Planck equation, which in Cartesian coordinates reads (compare with Eq. 2)
Here, we have chosen Cartesian coordinates with axes along the two primary axes of the diffusion tensor without loss of generality. The isotropic case is recovered for
and the boundary condition becomes
By introducing elliptic coordinates and rewriting Eq. 40 in these coordinates, a solution for the propagator can be found by separation of temporal and spatial variables, exactly as for the other cases considered above. The solution for the spatial part is given in terms of Mathieu functions [26], but the structure of these functions complicates a compact analytic solution.
Instead, we simulated trajectories of anisotropic Brownian motion confined to a 2D disc and recorded them with
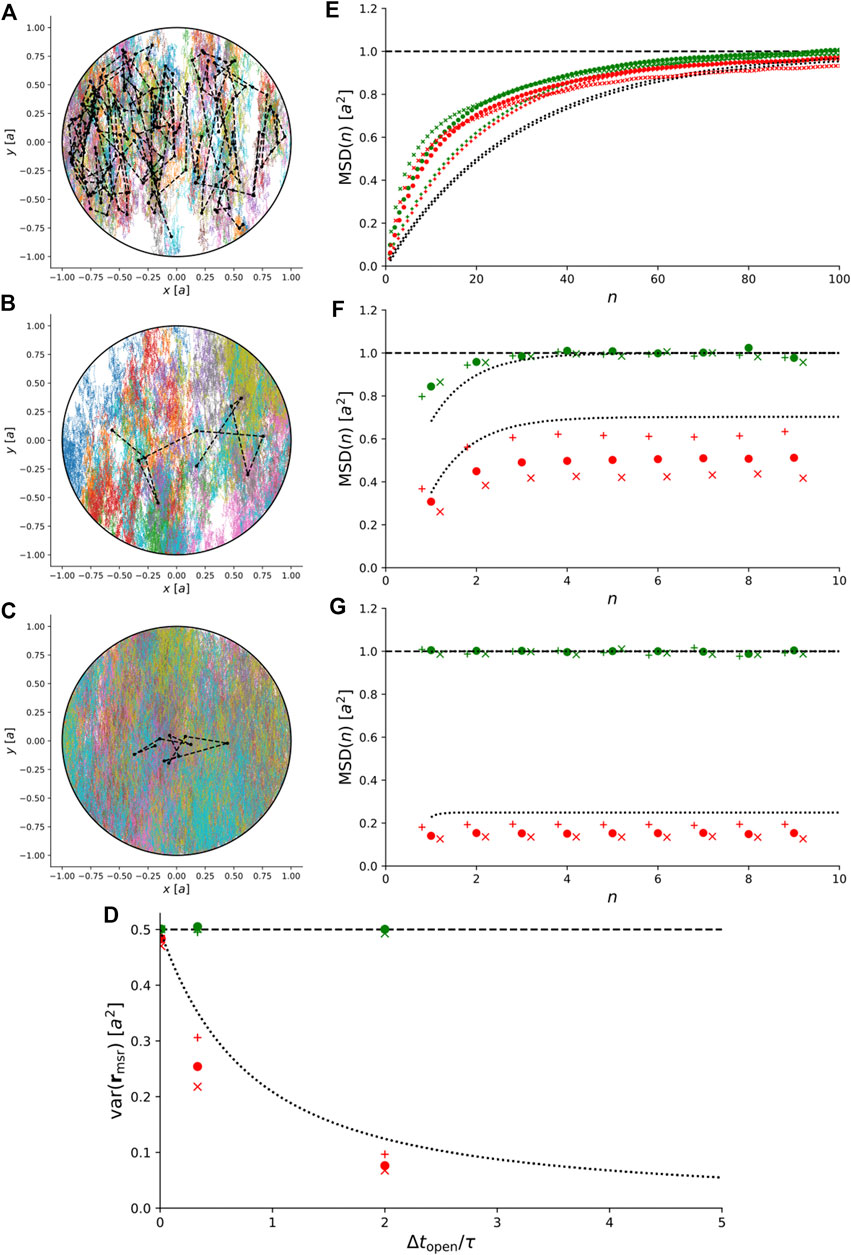
FIGURE 6. Simulations of 2D anisotropic Brownian motion confined to a circular domain with radius a. (A)–(C) Simulated trajectories for
For comparison, Figure 6D–G also show the exact theoretical results for variance and MSD for isotropic Brownian motion, i.e., for
This illustrates that for anisotropic Brownian motion, the coupling between confinement and motion blur is non-trivial and care must be taken to rule out anisotropic diffusion before our exact results for isotropic Brownian motion are used to interpret experimental results.
3 Discussion
In this work, we presented exact formulas for the variance and MSD of positions of a particle undergoing Brownian motion in confining spaces. These formulas remain valid when random Gaussian localization errors make true and recorded positions differ, provided that these localization errors are independently and identically distributed, which often is the case or may be assumed. To account for the localization error, our formulas should be offset merely by
We assumed normal Brownian motion throughout this article, and our formulas are guaranteed to apply only for such motion. On the other hand, we used only second moments of distributions, so results may in principle generalize to other cases with finite second moment if they exist. In some cases, particles may exhibit more complicated, types of motion, such as sub-diffusion due to interactions with other molecules in a membrane or “hop-diffusion”: particles may be almost confined to nano-domains but “hop” between neighboring domains [17, 27].
Other complication we ignored. Particles experience increased viscous drag near surfaces, as described by Faxén [28], and may experience attractive depletion forces near surfaces if many smaller particles—e.g., macromolecules—are present. Results of simulations and experiments, in which these and other effects are, respectively, simulated or suspected, can now be compared to the exact statistics given above for cases of steric confinement alone.
Additionally, while the approach described here delivers results for individual molecules, precision on estimates for parameters requires long trajectories [4]. In applications, the number of data points in a trajectory depends, e.g., on the fluorescent label and may be much lower than that used in our simulations. In such cases, one may compromise as regards true single-molecule results and average over a sample of several or many molecules to improve statistics of results obtained with our formulas [4].
Our formulas should facilitate that as much information as possible can be extracted about the mobility of the particles and the confining domains. To do this, one should account for the fact that the estimated MSD-values are correlated, since they are obtained from the same trajectory. This makes optimal fitting to MSDs complicated [16]. Additionally, in the present case of confined Brownian motion, such correlations most likely also depend on the position of the particle relative to the boundaries. Our formulas could, in principle, also facilitate a more accurate use of the MSD as a basis for classifying the type of motion [27].
The covariance-based estimator (CVE) introduced and demonstrated in [6, 7, 29] is an attractive alternative; however, away from surfaces, it estimates the bulk value of D, does that even from short segments of the trajectory, and does this optimally, provided its SNR =
In conclusion, there is still work to do in the field of analysis of single-molecule and single-particle trajectories. Trajectories of self-propelled particles, e.g., are better understood as persistent random motion. Tools for analysis of such trajectories with accounting for motion blur and/or effects of confinement would amount to quite an oeuvre even for the simplest model, the Ornstein-Uhlenbeck process, we predict, based on [30], though methods developed in [31, 32] may help. Here, we have exhausted a small fraction of this field with exact formulas for the variances and MSDs for simple Brownian motion, valid when particle positions are recorded using finite exposure time, which is the typical case by far. These formulas should help researchers to get the most out of their data for motion of Brownian particles and the domains that confine them, e.g., for particles diffusing in cell membranes [4, 10, 17].
4 Materials and Methods
4.1 Simulations
Equation (3) describes the propagator
where
4.2 Simulation of Free Brownian Motion With Motion Blur
We simulate the effect of motion blur by dividing the time-lapse
4.3 Simulation of Brownian Motion in Confinement
For free diffusion, it was possible to simulate a trajectory by sampling random numbers from the probability density function in Eq. 3, as the function is a Gaussian. In principle, one could simulate diffusion of a particle diffusing between walls at
This protocol assumes that
For more complex geometries, e.g., the 2D disc, closed boundaries can be implemented as described in [33]. For the case of anisotropic Brownian motion confined to a 2D disc, the implementation of the reflecting boundary is complicated. So, we implemented it by exploiting that anisotropic Brownian motion confined to a circular domain is equivalent to isotropic Brownian motion confined to an elliptical domain, see Section 2.6. With this transformation, the reflecting boundary conditions may be implemented, essentially, as described in [33]. After generating such transformed trajectories, we scaled positions back to original space.
4.4 Calculation of the Mean-Squared Displacement From Data
We estimated the mean-squared displacement from the simulated positions with [7]
where
4.5 Influence of Localization Errors
If the expected number of photons collected from the label on a particle is constant in time, the standard deviation,
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
KM and JP conceived the idea, did the research, and wrote the first draft of the manuscript. HF wrote the second version of the manuscript.
Funding
This work was supported by the Novo Nordisk Foundation Challenge Programme (NNF16OC0022166 to KM and HF).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.583202/full#supplementary-material.
Footnotes
1Note that by time-lapse, we mean the inverse frame rate: the lapse between, e.g., the start of consecutive frames. The “time-lapse” between the end of recording of one frame and the beginning of the next frame we call dead time.
2In [18], the definition of τ is
3If we had started out with the slightly more general case of confinement to an ellipse with axes parallel to the axes of the diffusion tensor, we would also land on this result after rescaling.
References
1. Schmidt T, Schütz GJ, Baumgartner W, Gruber HJ, Schindler H. Imaging of single molecule diffusion. Proc Natl Acad Sci Unit States Am (1996) 93:2926–9. doi:10.1073/pnas.93.7.2926
2. Manley S, Gillette JM, Patterson GH, Shroff H, Hess HF, Betzig E, et al. High-density mapping of single-molecule trajectories with photoactivated localization microscopy. Nat Methods (2008) 5:155–7. doi:10.1038/nmeth.1176
3. Mortensen KI, Churchman LS, Spudich JA, Flyvbjerg H. Optimized localization analysis for single-molecule tracking and super-resolution microscopy. Nat Methods (2010) 7:377–81. doi:10.1038/nmeth.1447
4. Arnspang EC, Sengupta P, Mortensen KI, Jensen HH, Hahn U, Jensen EBV, et al. Regulation of plasma membrane nanodomains of the water channel aquaporin-3 revealed by fixed and live photoactivated localization microscopy. Nano Lett (2019) 19:699–707. doi:10.1021/acs.nanolett.8b03721
5. Ruthardt N, Lamb DC, Bräuchle C. Single-particle tracking as a quantitative microscopy-based approach to unravel cell entry mechanisms of viruses and pharmaceutical nanoparticles. Mol Ther (2011) 19:1199–211. doi:10.1038/mt.2011.102
6. Vestergaard CL, Blainey PC, Flyvbjerg H. Optimal estimation of diffusion coefficients from single-particle trajectories. Phys Rev E (2014) 89:022726. doi:10.1103/PhysRevE.89.022726
7. Vestergaard CL, Pedersen JN, Mortensen KI, Flyvbjerg H. Estimation of motility parameters from trajectory data. Eur Phys J Spec Top (2015) 224:1151–68. doi:10.1140/epjst/e2015-02452-5
8. Clausen MP, Arnspang EC, Ballou B, Bear JE, Lagerholm BC. Simultaneous multi-species tracking in live cells with quantum dot conjugates. PloS One (2014) 9. doi:10.1371/journal.pone.0097671
9. Schütz GJ, Kada G, Pastushenko VP, Schindler H. Properties of lipid microdomains in a muscle cell membrane visualized by single molecule microscopy. EMBO J (2000) 19:892–901. doi:10.1093/emboj/19.5.892
10. Kure JL, Andersen CB, Mortensen KI, Wiseman PW, Arnspang EC. Revealing plasma membrane nano-domains with diffusion analysis methods. Membranes (2020) 10:314. doi:10.3390/membranes10110314
11. Adebiyi A, Soni H, John TA, Yang F. Lipid rafts are required for signal transduction by angiotensin ii receptor type 1 in neonatal glomerular mesangial cells. Exp Cell Res (2014) 324:92–104. doi:10.1016/j.yexcr.2014.03.011
12. Helms JB, Zurzolo C. Lipids as targeting signals: lipid rafts and intracellular trafficking. Traffic (2004) 5:247–54. doi:10.1111/j.1600-0854.2004.0181.x
13. Raghu H, Sodadasu PK, Malla RR, Gondi CS, Estes N, Rao JS. Localization of uPAR and MMP-9 in lipid rafts is critical for migration, invasion and angiogenesis in human breast cancer cells. BMC Canc (2010) 10:647. doi:10.1186/1471-2407-10-647
14. Vestergaard CL. Optimizing experimental parameters for tracking of diffusing particles. Phys Rev E (2016) 94:022401. doi:10.1103/PhysRevE.94.022401
15. Berglund AJ. Statistics of camera-based single-particle tracking. Phys Rev E (2010) 82:011917. doi:10.1103/PhysRevE.82.011917
16. Michalet X, Berglund AJ. Optimal diffusion coefficient estimation in single-particle tracking. Phys Rev E (2012) 85:061916. doi:10.1103/PhysRevE.85.061916
17. Ritchie K, Shan XY, Kondo J, Iwasawa K, Fujiwara T, Kusumi A. Detection of non-brownian diffusion in the cell membrane in single molecule tracking. Biophys J (2005) 88:2266–77. doi:10.1529/biophysj.104.054106
18. Destainville N, Salomé L. Quantification and correction of systematic errors due to detector time-averaging in single-molecule tracking experiments. Biophys J (2006) 90:L17–L19. doi:10.1529/biophysj.105.075176
19. Grebenkov DS. Nmr survey of reflected Brownian motion. Rev Mod Phys (2007) 79:1077–137. doi:10.1103/RevModPhys.79.1077
20. Risken H. The Fokker–Planck equation: methods of solution and applications. Berlin: Springer (1984).
21. Bullerjahn JT, von Bülow S, Hummer G. Optimal estimates of self-diffusion coefficients from molecular dynamics simulations. J Chem Phys (2020) 153:021101. doi:10.1063/5.0008312
22. Bickel T. A note on confined diffusion. Phys Stat Mech Appl (2007) 377:24–32. doi:10.1016/j.physa.2006.11.008
23. Wong WP, Halvorsen K. The effect of integration time on fluctuation measurements: calibrating an optical trap in the presence of motion blur. Optic Express (2006) 14:12517–31. doi:10.1364/OE.14.012517
24. Mitra PP, Halperin BI. Effects of finite gradient-pulse widths in pulsed-field-gradient diffusion measurements. J Magn Reson, Ser A (1995) 113:94–101. doi:10.1006/jmra.1995.1060
25. Riseborough PS, Hänggi P. Diffusion on surfaces of finite size: Mössbauer effect as a probe. Surf Sci (1982) 122:459–73. doi:10.1016/0039-6028(82)90096-6
27. Clausen MP, Lagerholm BC. Visualization of plasma membrane compartmentalization by high-speed quantum dot tracking. Nano Lett (2013) 13:2332–7. doi:10.1021/nl303151f
28. Happel J, Brenner H. Low Reynolds number hydrodynamics. Upper Saddle River, NJ:Prentice-Hall (1965).
29. Vestergaard CL, Blainey PC, Flyvbjerg H. Single-particle trajectories reveal two-state diffusion-kinetics of hOGG1 proteins on DNA. Nucl Acids Res (2018) 46:2446–58. doi:10.1093/nar/gky004
30. Pedersen JN, Li L, Gradinaru C, Austin RH, Cox EC, Flyvbjerg H. How to connect time-lapse recorded trajectories of motile micro-organisms with dynamical models in continuous time. Phys Rev E (2016) 94:062401. doi:10.1103/PhysRevE.94.062401
31. Brueckner DB, Fink A, Schreiber C, Roettgermann PJF, Raedler JO, Broedersz CP. Stochastic nonlinear dynamics of confined cell migration in two-state systems. Nat Phys (2019) 15:595–601. doi:10.1038/s41567-019-0445-4
32. Brueckner DB, Ronceray P, Broedersz CP. Inferring the dynamics of underdamped stochastic systems. Phys Rev Lett (2020) 125:058103. doi:10.1103/PhysRevLett.125.058103
Keywords: time-averaging, mean-squared displacement, motion blur analysis, confined diffusion, single-molecule, particle tracking, reflected Brownian motion
Citation: Mortensen KI, Flyvbjerg H and Pedersen JN (2021) Confined Brownian Motion Tracked With Motion Blur: Estimating Diffusion Coefficient and Size of Confining Space. Front. Phys. 8:583202. doi: 10.3389/fphy.2020.583202
Received: 14 July 2020; Accepted: 23 November 2020;
Published: 13 January 2021.
Edited by:
Giovanni Volpe, University of Gothenburg, SwedenReviewed by:
Nicolas Francisco Lori, University of Minho, PortugalMarco G. Mazza, Loughborough University, United Kingdom
Copyright © 2021 Mortensen, Flyvbjerg and Pedersen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kim I. Mortensen, a2ltb0BkdHUuZGs=; Jonas N. Pedersen, am5wZUBkdHUuZGs=
 Kim I. Mortensen
Kim I. Mortensen Henrik Flyvbjerg
Henrik Flyvbjerg Jonas N. Pedersen
Jonas N. Pedersen