Challenges in Monte Carlo Simulations as Clinical and Research Tool in Particle Therapy: A Review

The use and interest in Monte Carlo (MC) techniques in the field of medical physics have been rapidly increasing in the past years. This is the case especially in particle therapy, where accurate simulations of different physics processes in complex patient geometries are crucial for a successful patient treatment and for many related research and development activities. Thanks to the detailed implementation of physics processes in any type of material, to the capability of tracking particles in 3D, and to the possibility of including the most important radiobiological effects, MC simulations have become an essential calculation tool not only for dose calculations but also for many other purposes, like the design and commissioning of novel clinical facilities, shielding and radiation protection, the commissioning of treatment planning systems, and prediction and interpretation of data for range monitoring strategies. MC simulations are starting to be more frequently used in clinical practice, especially in the form of specialized codes oriented to dose calculations that can be performed in short time. The use of general purpose MC codes is instead more devoted to research. Despite the increased use of MC simulations for patient treatments, the existing literature suggests that there are still a number of challenges to be faced in order to increase the accuracy of MC calculations for patient treatments. The goal of this review is to discuss some of these remaining challenges. Undoubtedly, it is a work for which a multidisciplinary approach is required. Here, we try to identify some of the aspects where the community involved in applied nuclear physics, radiation biophysics, and computing development can contribute to find solutions. We have selected four specific challenges: i) the development of models in MC to describe nuclear physics interactions, ii) modeling of radiobiological processes in MC simulations, iii) developments of MC-based treatment planning tools, and iv) developments of fast MC codes. For each of them, we describe the underlying problems, present selected examples of proposed solutions, and try to give recommendations for future research.

1 Introduction

The use of Monte Carlo (MC) techniques and their interest in the field of medical physics have been rapidly increasing in the past years. This is the case especially in particle therapy, where high accuracy in dose calculations, patient geometry, beam model, and all aspects in the physics of interactions are crucial elements for a successful planning of patient treatment and its verification. Thanks to the possibility to track particles in 3D in a fully detailed geometry and to take into account all relevant physics processes on their way, MC simulations have become an essential calculation tool.

Applications in particle therapy where MC simulations have proven to be a very useful tool are several. For instance, they are crucial in the design and commissioning of novel clinical facilities, allowing for shielding calculations and full treatment head simulations. MC simulations are also a valuable tool for the commissioning of treatment planning systems (TPS), where they can provide accurate look-up tables describing 3D dose distributions of particle beams, that include electromagnetic and nuclear interactions of the primary particles and all secondaries produced. Furthermore, MC simulations allow to accurately include various radiobiological effects in dose calculations, thanks to the possibility of coupling to dedicated models. These properties make MC simulations suitable for dose calculations of complex patient cases. Especially if highly heterogeneous tissues are involved, MC methods are generally considered to be more accurate than analytical calculation methods [1–3]. Finally, thanks to the capability of performing detailed simulations of nuclear interactions, MC are also fundamental for the development of in-beam treatment monitoring strategies through positron-emission tomography, the detection of prompt photons, or other fragments from nuclear de-excitation.

A vast amount of works concerning MC simulations in particle therapy have been published in the past decades. Several reviews are also available, including, for instance, general works about MC techniques in particle therapy [4–7], MC simulations for range monitoring [8], the role of MC simulations in radiobiological modeling of treatment outcomes [9], and MC simulations in GPU dose calculations [10]. The high demand for accurate calculation tools and the general consensus that MC simulations can provide the requested accuracy for complex dose calculations have led to a more widespread use of these tools in daily clinical practice, especially in proton therapy, where commercial treatment planning systems have started to offer MC calculation tools. In most cases, these are specifically developed and optimized codes. However, the use of general purpose and fully detailed MC codes is still limited. Among the reasons are the complexity of the usage of the codes, the excessive computation times, the need to improve nuclear interaction models, the lack of data for tuning these models, and the complexity to combine radiobiology and physics into a single calculation tool.

In this review, we discuss some of the ongoing developments and challenges that remain to be faced in order to improve the accuracy of MC simulations and to facilitate their use in clinics and in research. Undoubtedly, a multidisciplinary approach is required to overcome many of the remaining challenges. It is beyond the scope of this review to include all the available literature and topics that regard MC simulations in particle therapy. Here, we try to identify some of the aspects where the community involved in applied nuclear physics, radiation biophysics, and computing development can contribute to find solutions. We have selected four specific challenges for this review:

(1) The development of models in MC to describe nuclear physics interactions, including data to benchmark MC codes.

(2) The development of MC simulations including calculations of RBE, LET, and microdosimetry.

(3) The development of MC-based treatment planning

(4) The development of fast MC codes.

Below, we take an in-depth look at these issues, and describe the problematics, the ongoing developments, and the future directions, trying to emphasize the role of applied nuclear physics in overcoming these challenges. A complete review of all ongoing works about the above topics is beyond the scope of this work. Therefore, the selection of works that were chosen to be highlighted in this article should be considered as non-exhaustive.

2 Development of Nuclear Interaction Models in MC Codes

Charged hadrons of energies relevant in particle therapy (up to a few hundred MeV/nucleon) interact in tissue by electromagnetic and nuclear interactions [11]. Concerning the former, inelastic collisions with atomic electrons, resulting in ionization and atomic excitation, cause the particle to continuously lose energy along its path. Energy losses can be well described by the Bethe-Bloch formalism, predicting an increasing energy loss with decreasing particle energy. This is the main process governing the shape of the Bragg peak for charged particle beams in material. Also, discrete inelastic energy losses can occur in the form of delta-rays. Moreover, charged particles undergo numerous elastic Coulomb scatterings from the nuclei themselves (multiple Coulomb scattering, MCS), causing lateral broadening of the incoming particle beam. Modeling electromagnetic interactions is highly complicated in MC codes, but usually considered sufficiently accurate. On the contrary, hadronic physics models are still not considered completely satisfactory [12].

In this section, we try to point out the most important difficulties and challenges in nuclear physics model building, quoting the features of some of the most widely used MC codes used for particle therapy. Then, we shall summarize the possible impact of nuclear interaction modeling in dose calculation and in the evaluation of additional quantities useful for particle therapy. In particular, we shall focus the discussion on secondary particle production for range monitoring purposes. Finally, we shall present a summary of existing experimental data which are useful for tuning and benchmarking calculation models.

2.1 Main Problematics in the Development of Nuclear Interaction Models

There are many aspects of hadronic interactions that are relevant for correctly describing interactions of protons or heavier ions in the energy range relevant to particle therapy. Among them, we point out nuclear reaction cross section, elastic cross section, secondary particles, and fragment production, considering at the same time multiplicity, angle, and energy distributions. Secondary nucleons, particles, and fragments produced in nuclear reactions can considerably affect the spatial pattern of energy deposition and must be carefully taken into account. In particular, for the case of ion projectiles, nuclear fragmentation reactions are responsible for the deterioration of the physical selectivity in the longitudinal and transverse dimension, especially around the Bragg peak region. The amount of fragments produced generally increases with the mass and charge of the primary particle.

The commonly used general purpose modern MC codes make use of phenomenological models. Although a common approach is to fit existing data to predict certain quantities, in our opinion, they should be built upon reliable physical bases to have full predictive capability. In practice, this means that these models have to be built according to a “microscopic” approach, that is, starting from the fundamental properties of the nucleus and of its constituents. All relevant conservation laws have to be fulfilled, and correlations within each single interaction must be preserved. The treatment of nuclear environment and all phases following the primary fast interaction (pre-equilibrium, evaporation, fission, and de-excitation) is to be taken into account.

Models of this kind have necessarily a number of parameters that must be tuned by means of experimental data at single interaction level. In order to achieve a reliable level of predictive power, the number of these parameters should be kept minimal and their dependence on projectiles, targets, and energies should be predetermined without adapting them to the specific situation. On the one hand, this approach allows in principle to achieve a high degree of reliability. On the other hand, this might result in complex algorithms which can be demanding in terms of computing power with respect to simpler solutions, such as the parametric interpolation (or extrapolation) of existing data. It must also be pointed out that is not always possible, within a given model, to achieve the same level of accuracy at all energies or in the whole accessible phase space. Furthermore, in the therapeutic energy range, it is not always possible to rely upon a single model. Great care has to be taken in order to ensure the proper continuity in the transition from one model to another. Different MC codes have found different solutions to the above problems. In the following, we shall summarize the nuclear models adopted for a few of the most relevant MC codes presently used in particle therapy.

2.2 Approaches and Proposed Solutions to Model Nuclear Interactions

2.2.1 GEANT4

GEANT4 is used by a large number of experiments and projects in a variety of application domains, including medical physics and radiation protection. In the case of GEANT4 [13–15], the user has the possibility of selecting different models by specifying the so-called physics list. Reference physics lists are available in Ref. 16. In the context of particle therapy, an often recommended choice is the one called QGSP_BIC_EMY, which includes, beyond a Quark Gluon String model for the multi-GeV energy range, a Binary Cascade model. The GEANT4 Binary Cascade is a hybrid between a classical intranuclear cascade and a quantum molecular dynamic model [17–19] for the simulation of inelastic scattering of hadrons and light ions of intermediate energies. It is considered valid down to 200 MeV. New developments are under investigation to improve models for energies below this value, an example of which was published recently [20]. However, this study also highlighted the need for many more improvements in nuclear interaction modeling and calculation speed.

There are user-friendly interfaces to GEANT4 which are used by different groups working in particle therapy. For instance, the TOPAS (TOol for PArticle Simulation) toolkit [21, 22] wraps and extends the GEANT4 Simulation Toolkit to facilitate the use of MC simulations in radiotherapy environments. It allows the user to configure pre-built components (nozzles, patient geometry, dosimetry, and imaging components) to simulate a wide variety of treatments with no required knowledge of any programming language. Another example is GATE (GEANT4 Application for Tomographic Emission) [23]. It has been developed by the OpenGate collaboration and encapsulates the GEANT4 libraries, providing a toolkit mostly oriented to nuclear medicine by easily including detailed geometry of many imaging devices. It has been tested in the context of particle therapy, especially for range monitoring applications [24–26].

In order to respond to the need of benchmarking the code against reference data, the GEANT4 community has recently developed a testing system, denominated G4-Med [27], which is specifically oriented to medical physics. Among the different options, it offers the possibility of benchmarking both electromagnetic and hadronic physics processes and models available in the pre-built, physics lists. A whole chapter is dedicated to the topic of hadronic models in the specific context of particle therapy. Total cross section of hadron–nucleus and nucleus-–nucleus collisions have been compared to the data publicly available in the EXFOR database. Different subjects have been considered: yields, charge changing, and double differential cross sections. Tests concerning comparisons with Bragg peaks have been also reported. A detailed discussion on the quality of these benchmarks can be found in the report.

In addition to this recent work, in the context of proton therapy, we point out the work of Hall et al. [28], where GEANT4 results were compared to accurate measurement of longitudinal absolute dose profiles for 177 MeV protons at different radial distances from the beam axis, up to a radius of 10 cm. The test is sensitive to the dose envelope originating from nuclear interactions. Excellent agreement is reported over five orders of magnitude in the dose scale.

2.2.2 FLUKA

In the case of FLUKA [29, 30], the number of available physics models is limited. The code automatically selects the appropriate model for each interaction according to the energy of projectile. The nuclear environment, down to a few MeV, is provided by the interaction model called PEANUT (Pre-Equilibrium Approach to NUclear Thermalization) [31–33]. Interactions proceed along the steps of a generalized intranuclear cascade, followed by pre-equilibrium particle emission and by an equilibrium phase. For residual having A $<$ 16, a Fermi breakup model is implemented [34]. In the emission of nucleons, a coalescence model is considered. The excitation energy still remaining after nuclear evaporation is dissipated by emission of γ rays. Competition of gamma ray emission with particle evaporation is considered. In the case of nucleus–nucleus collisions, for incident energies below $\sim$130 MeV/u, FLUKA makes use of the BME (Boltzmann master equation) model [35], which simulates the thermalization of a composite nucleus created in the complete or incomplete fusion of two ions. For increasing energy, FLUKA relies on the RQMD (Relativistic Quantum Molecular Dynamic) model [17, 36], which can also be run in intranuclear cascade mode.

2.2.3 PHITS

A QMD approach has been chosen also in the PHITS (Particle and Heavy Ion Transport code System) code [37, 38] for the treatment of hadron–nucleus and nucleus–nucleus collisions. Here, the JQMD (JAERI Quantum Molecular Dynamics) code is used [18]. JQMD is combined with the JAM (Jet AA Microscopic Transport Model) code [39], which implements a hadronic cascade approach, capable of dealing with hadron–hadron collisions up to center-of-mass energy $\sqrt{s}\sim$100 GeV. At the end of the dynamical stage of the interaction, excited residual nuclei are treated by the GEM (Generalized Evaporation Model) model [40] to generate light particle evaporation and fission processes. Benchmarks of PHITS are reported in Ref. 41.

2.2.4 MCNP

MCNP (Monte Carlo NParticle), now in the version MCNP6 [42], developed at Los Alamos National Laboratories, is one of the most important general purpose three-dimensional MC codes. It is well known in nuclear physics and used for studies including criticality, shielding, and detector response, but also dosimetry and many other applications, such as medical ones. As far as hadron–nucleus and nucleus–nucleus interactions are concerned, also MCNP makes use of different models depending on energy. For incident energy below 1 GeV, of relevance for particle therapy, interactions are mostly treated by means of the INC (intranuclear cascade) approach. The MCNP6 default option for reactions induced by d, t, ³He, ⁴4He is the ISABEL INC generator, described in Ref. 43, and can be used also for nucleons and heavy ions with E $<$ 1 GeV. It can optionally include pre-equilibrium reactions described by the MPM (multistage pre-equilibrium model) [44]. Evaporation reactions are treated with EVAP [45], while for fission, RAL [46] or HETFIS [47, 48] can be chosen. A newer and improved model is CEM03.03 [49–51] which has its own treatment of pre-equilibrium, evaporation, and fission reactions. It considers also coalescence of nucleons into complex particles up to ⁴He and Fermi breakup of excited or unstable nuclei with mass numbers up to A = 12. Another recent alternative for the INC approach is INCL [52] for nucleons, d, t, ³He, and ⁴He at energies up to several GeV. It does not consider pre-equilibrium and makes use of the abration–ablation model implemented in the ABLA code [53, 54], developed at GSI, to describe evaporation and fission.

2.2.5 SHIELD-HIT

SHIELD-HIT, in its last version SHIELD-HIT12A [55, 56], is a MC particle transport program optimized for proton and ion particle therapy. Nuclear reactions are treated within the MSDM (multistage dynamical model) generator [57]. It is composed of a fast cascade stage of nuclear reaction, which, according to projectile energy, is treated by the DCM (Dubna Cascade Model) [58] or by the QGSM (Quark-Gluon String Model) [59, 60]. At the end of the cascade stage, nucleons which are close to each other in phase space can coalesce to form a complex particle. Pre-compound emission of nuclei is handled by a cascade-exciton model [61]. Subsequent equilibrium de-excitation is handled by Fermi breakup, according to the implementation described in Ref. 62. Then, evaporation/fission competition and multi-fragmentation of highly excited nuclei follow.

2.3 Impact of Nuclear Reaction Models on Dose Calculations

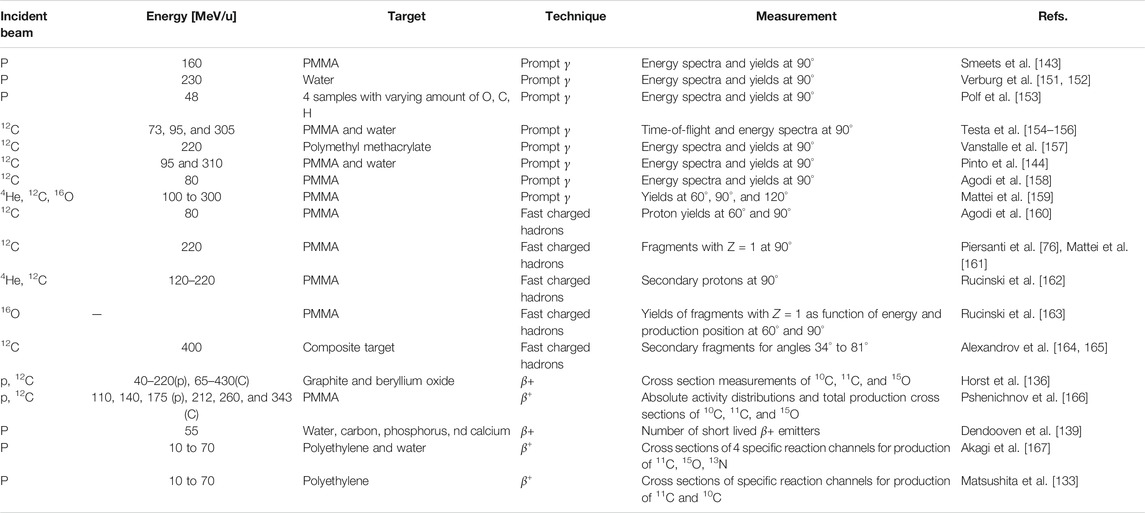
Nuclear interactions cause the attenuation of primary ions and build up of secondary ions, aspects that are crucial for accurate dose delivery and dosimetry [12]. Inelastic interactions are responsible for beam attenuation of the primary beam with penetration depth, and elastic interactions contribute to beam broadening. In the case of carbon ions, it was estimated with MC simulations that up to about 40% of the dose in the region between the entrance channel and the Bragg peak is delivered by fragments [63]. Thus, wrongly modeled cross sections would clearly lead to discrepancies in longitudinal and lateral dose distributions between measurements and MC simulations. A vast amount of works exist, mostly in the context of proton and carbon therapy, showing excellent agreements between MC codes and dosimetric measurements, both in terms of lateral and longitudinal dose (Bragg peak measurements). An example of a measured Bragg peak together with a GEANT4 MC simulation is shown in Figure 1. Results with analogous quality of agreement have been obtained also for other codes, including FLUKA comparisons with HIT [1], CNAO [64], and GSI [65].

FIGURE 1

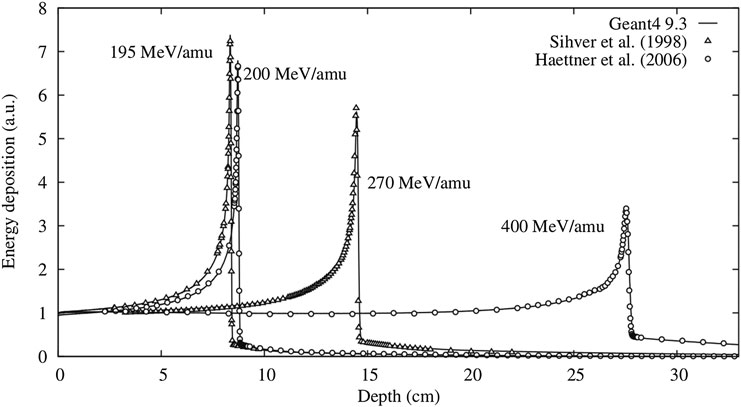
FIGURE 1. From Lechner et al. [66]: an example of an excellent agreement between data and GEANT4 MC simulations in predicting the depth–dose profile of carbon ion beams.

From these nice agreements in dose distributions, one may conclude that we have reached a satisfactory level of accuracy of the description of nuclear reactions in MC codes for physical dose calculations. However, this is only partially true, and several important improvements in the context of dose calculations remain to be done:

• For particles other than protons and carbon ions, the agreement in physical dose between MC codes and measurements is still not fully satisfactory. For instance, some significant discrepancies were found between simulations and data of spread-out Bragg peaks of Helium atoms in water [67, 68]. These differences were attributed to an underestimation of dose contributions from secondary particles produced at large angles.

• Nuclear interactions strongly affect biological dose [12]. Secondary fragments produced during nuclear interactions lead to an altered spatial dose distribution, because different fragments have different ranges and angular distributions. Some of these fragments may hardly contribute to the physical dose, but they can lead to a modification of the LET spectra, which results in a difference of RBE for the same delivered dose. Thus, even when longitudinal and lateral physical dose measurements show excellent agreements with a MC code, this does not automatically imply that the biological dose in the patient is correctly calculated. In Section 4, we discuss the importance of biological aspects in more detail.

• Other aspects different from nuclear interactions can affect the prediction of dose distribution. For instance, in proton therapy, δ-ray electron build-up effects are important in the dose build-up region [69], and should be correctly accounted for in physical and biological dose calculations.

Summarizing, physical dose is indeed an important measure to validate the description of nuclear reaction models in MC codes, and newly developed models should always be validated with dose measurements. However, evaluating physical dose alone is not enough, as will become clear in the next paragraph.

2.4 Impact on the Calculation of Secondary Particle Production

Although dose calculation is the primary role of MC application in particle therapy, there are other aspects in which this kind of tool turns out to be essential. These are related to the capability of providing a reliable prediction of secondary particles produced in nuclear interactions. We have mentioned above that nuclear reactions influence the spectrum of fragments and how this can be crucial for the correct evaluation of both physical and biological doses. Moreover, although of scarce numerical relevance for dosimetry, production of secondary particles is relevant for various other issues, including the implementation of range monitoring techniques, neutron production, shielding, treatment facility design, or full treatment head simulations. In the following, we discuss the issues that we consider most complex: range monitoring and neutron production.

2.4.1 Calculation of Secondary Products for Range Monitoring Purposes

The nuclear processes that can yield secondary radiation suited for range monitoring application are three: the production of ${\beta }^{+}$ emitting nuclei, the de-excitation of nuclei by means of prompt photon emission, and the fragmentation of ion projectiles into fast hadrons capable of escaping out of the patient. In all cases, a MC prediction of the measured distributions is essential for their effective use for range monitoring purposes. Here, we summarize the main issues which are of interest for these processes as far as MC codes are concerned.

• Production of ${\beta }^{+}$ emitting nuclides. Nuclear ${\beta }^{+}$ decays produce positrons that annihilate with electrons, resulting in an almost back-to-back 511 keV photon pair that can be detected. The most likely ${\beta }^{+}$ emitting isotopes that can be formed are ¹⁰C, ¹¹C, ¹⁵O, and ¹³N. Much research has been dedicated to range monitoring with PET, summarized, for instance, in various reviews [8, 70–72]. The capability of MC codes to provide a reliable prediction of the production of these isotopes is strongly correlated to the quality that the physics models achieve in managing the fragmentation process in general, and all the other stages occurring in the nuclei following the fast interaction. An alternative approach to full modeling, whenever validated experimental measurement of production cross sections exist (as, for instance, those available in EXFOR database), is to fit them and interface them to the simulated track length distribution. In range monitoring, both approaches are being used. The general situation is that the most important general purpose codes are able to predict the production of the most abundant nuclides (like ¹¹C or ¹⁵O) with a sufficient quality. The main challenge remains in the capability of predicting nuclides with short lifetimes, where also the available experimental measurements are scarce. Data that can be used to improve the accuracy of MC models for the production of short-lived isotopes for range monitoring are discussed in Section 2.5. All stages concerning transport of positrons and their decay can be considered more standard and manageable without particular difficulty.

• Prompt gamma from nuclear de-excitation. Prompt gamma imaging methods are based on the detection of prompt photons that are emitted in the de-excitation phase of a nuclear interaction. The distribution of prompt gammas is correlated with the beam range. A recent review is written by Krimmer et. al. [73]. In the past years, MC developers started to pay particular attention to correctly predicting prompt gamma distributions. Also, in this case, the complexity of non-elastic nuclear reactions makes it difficult to accurately reproduce the level and shape of prompt γ emission. Of course the quality in the prediction of residual nuclei and of their excitation, as for the case of ${\beta }^{+}$ emitters, is important. Whenever possible, photon energies and branching ratios should be sampled according to existing databases of known nuclear levels and transitions. For example, they can be derived from data provided by the most recent release of the RIPL [74] data provided by IAEA. However, not only the level energies, but also spin and parity have an influence on photon emission. Furthermore, the shape of emission lines is subject to Doppler broadened due to nuclear recoil, and this also deserves attention in the development of the interaction model.

• Production of fast charged hadrons. The principle of range monitoring in ion therapy by means of hadrons escaping the patient (mainly protons) was proposed about a decade ago [75] and since then investigated by different research groups, see Section 2.5. Fast hadron production is clearly part of nuclear fragmentation, and therefore we are again dealing with the physics models which are relevant to dose calculations. However, as discussed in Ref. 76, the most accurate result in the measurement of a proton emission distribution correlated with a longitudinal dose profile, is achieved by detecting particles emitted at large angles with respect to the beam direction. This involves a limited region of the available phase space and it is not trivial for available calculation models to reproduce with the same quality both fragmentation at small angles (the most important as far as dose is concerned) and the emission at large angles. As discussed later, there is a lack of experimental data useful for model tuning and benchmarking, and available data are limited in angle and primary energy [77, 78]. Double differential cross sections are eagerly needed. More available data will be discussed in Section 2.5.

2.4.2 Calculation of Neutron Production and Interaction

MC codes allow to evaluate neutron production during a particle therapy treatment. The simulation of neutrons with energy exceeding $\sim$10 MeV is provided by the same models discussed so far for charged particles. The situation is different for lower energies, since neutron cross sections have a complex structure. They cannot be calculated and usually one has to rely upon evaluated nuclear data files. Different libraries are accessible (ENDF/B, JEFF, JENDL, CENDL, ROSFOND, and BROND) [79, 80] and are periodically updated. By means of dedicated software codes, it is possible to obtain cross sections to be used within MC codes.

Simulations have been used to evaluate the risk of secondary cancer due to neutron exposure, especially in the comparison between passive and active scanning (see for instance [81–85]). At present, there is some consensus that risks deriving from neutrons are negligible with respect to those associated to the primary beam, at least as far proton therapy is concerned. The contribution of neutrons to dose is therefore normally neglected in treatment planning. However, there remain other cases in which the calculation of neutron interactions is important:

• for prompt γ detection for range monitoring purposes, the evaluation of background deriving from neutron interactions is relevant.

• The long-term effects of neutron production should be done with MC models that include radiobiological models [83, 84].

• In Boron neutron capture therapy (BNCT) [86, 87], which is based on the direct use of neutrons. It is one of the cases in which treatment planning and dosimetry are strongly based on MC. One of the main reference codes for BNCT is MCNP [42, 88], which was used for treatment planning [89]. More recently also PHITS [37, 38] has entered in use for this purpose [90]. A comparison of results obtained with GEANT4 for different physics list, and with FLUKA, is reported in Ref. 91. MC simulations are also widely used in BNCT to design new beams for the specific application [92, 93].

For reliable neutron production models, benchmarking nuclear interaction models with neutron data are important. Fortunately, a large amount of neutron production data at an enormous energy range is already available from reactor experiments and radiation protection in space, as we will see in Section 2.5. Finally, even though neutrons might not seem very interesting in the context of charged particle therapy, we point out that neutron data are very powerful to constrain nuclear interaction models.

2.5 Data for Benchmarking and Tuning Nuclear Physics Codes

To determine the effects of secondary particles and to exploit them in range monitoring, MC models can be used to predict the yields and characteristics of the secondary particles. The accuracy of the predictions ultimately relies on the ability to correctly model the relevant production cross sections. In our opinion, experimentally measured cross sections are the most valuable data that are needed to tune the models in the relevant range of ion species, energies, and target mass. In particular, single and double differential cross sections are the most interesting measurements.

A collection of measured cross sections in the energy range from 100 MeV/u up to 10 GeV/u can be found in reviews by Norbury [94], Sihver [95], and Bauhoff [96], focusing mostly on radiation protection in space. Moreover, the handbook by Heilbronn and Nakamura [97] contains lots of data for neutron production, mostly from design studies of heavy ion accelerator facilities and radiation protection in space. In the context of radiotherapy, much effort has been done in the last decades to improve the accuracy of MC codes in the energy range up to 400 MeV/u for tissue-like targets. However, although a large amount of valuable data are available for the purpose of benchmarking and tuning calculation models, at present, there still remain significant gaps. In the following, we summarize some of the most relevant measurements that have to be considered. We divide them into three categories: i) measurements of cross sections on thin targets, ii) measurements performed on thick targets, and iii) measurements specifically oriented for range monitoring purposes.

2.5.1 Measurements of Cross Sections on Thin Targets

These measurement concern total cross sections, partial cross sections, and single and double differential cross sections of specific processes. While total cross sections are valuable to predict primary beam attenuation, partial cross sections, and single and double differential cross sections are important to predict yields, angles, and energies of secondary particles. The usage of thin targets is most appropriate for tuning MC models, because the energy of the beam does not decrease, and the model parameters can be isolated from transport issues. A non-exhaustive selection of cross section measurements that have frequently been used for tuning nuclear models in MC simulations in the particle therapy energy range is reported in Table 1.

TABLE 1

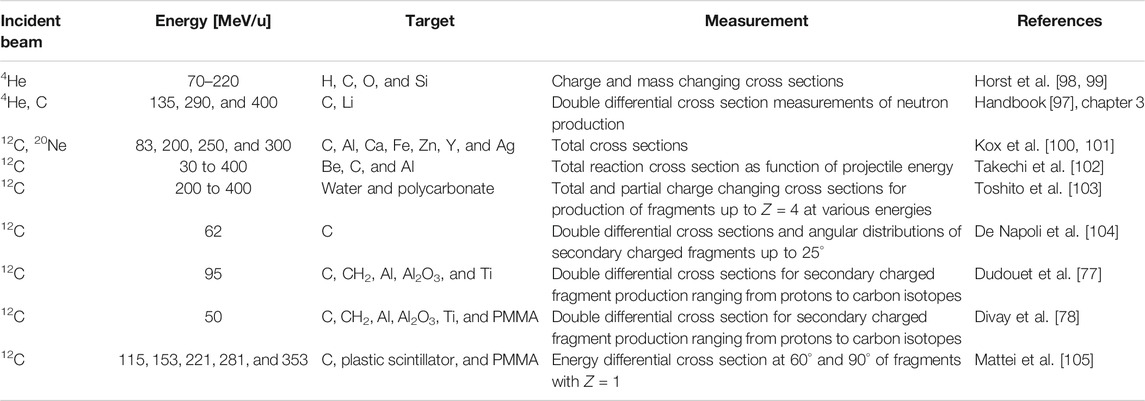
TABLE 1. Cross section measurements on thin targets for tissue-like targets in the energy range up to 400 MeV/u.

The majority of the cross section measurements in Table 1 are for carbon projectiles; however, the growing amount of interest in particle therapy with other projectiles has led to recent new initiatives. For instance, valuable new cross section measurements for ⁴He [98, 99] are displayed in Figure 2. This figure illustrates a general problem with many cross sections: there are differences between data sets, and for analytical or MC model parameterizations, it is ambiguous with which measurements the tuning should be done. New data are thus useful to resolve ambiguities between data sets.

FIGURE 2

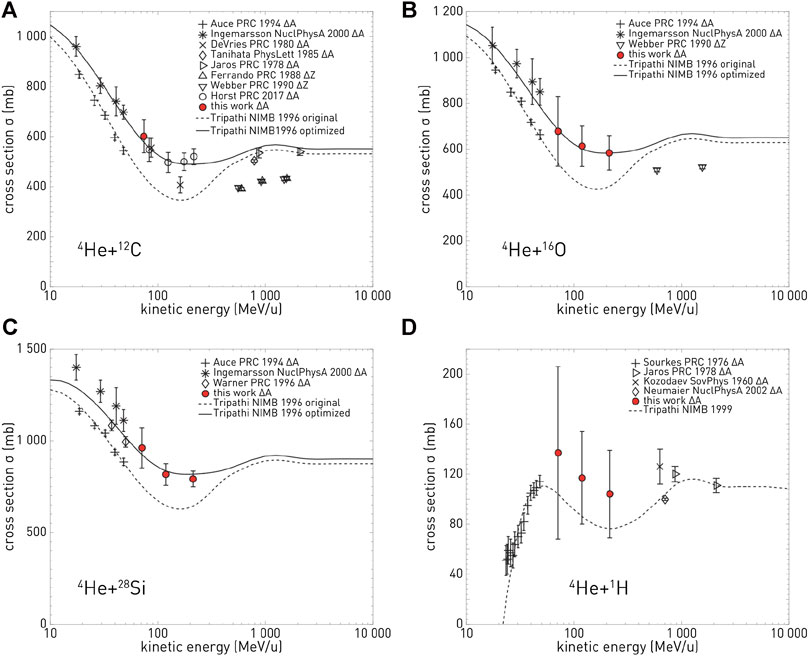
FIGURE 2. Cross section measurements from Horst et al. [99]: in red, the new measured mass-changing cross sections for ⁴He ions on C (top left), O (top right), Si (bottom left), and H (bottom right) targets, compared with different data from the literature and with two parameterizations of the measurements.

As reported in 2010 by Böhlen [63], a tuning of the hadronic models in FLUKA and GEANT4 was based on some of the measurements in Table 1, revealing several shortcomings in both codes, in particular at lower energies. Further developments in the improvement of the nuclear models in GEANT4 were reported afterward [104, 106, 107], and new efforts are currently in progress [20]. PHITS, FLUKA, and MCNP6 were recently benchmarked with experimental data for neutron production cross sections [108].

Concerning protons, the work by Braunn et. al. [109], aimed at benchmarking the TALYS nuclear reaction code, contains a large number of references of total proton–nucleus cross section measurements as a function of energy in the range up to 250 MeV with tissue-like targets.

Despite the progress made over the years, Table 1 shows that double differential cross section measurements for charged fragment production are still scarce, while such measurements are the most essential for tuning nuclear reaction models. Measurements that are specifically aimed at improving the knowledge for particle therapy are planned in 2021 by the FOOT collaboration [110]. The ultimate goal of this experiment is to provide measurements of energy differential cross sections for the production of charged fragments with an accuracy of 5–10%. This would provide reference data sets for model benchmarking with a high level of accuracy. However, for processes or phase space regions where there is a complete lack of data, even less accurate measurement would be valuable.

2.5.2 Measurements on Thick Targets

These measurements include cross sections, primary beam attenuation studies, Faraday cup measurements, fragmentation yields, and emission angles. Rather than being directly useful for model tuning, these measurements allow us to assess the overall accuracy of MC codes, that is, transport, nuclear, and electromagnetic interactions together. A vast amount of measurements on thick targets have been done in the last decades; however, only a handful are useful for MC benchmarking. First, they should include a clear description of the experimental setup. Second, the physical quantities should be reported in absolute units. In Table 2, a selection of valuable measurements is presented. Of these measurements, the cross section measurements by Schall [111], Heattner [112, 113], and Golvschenko [114, 115] are most suitable for benchmarking MC codes at particle therapy energies, and these data were used for benchmarking FLUKA [63], GEANT4 [63], PHITS [116], and SHIELD-HIT [55, 56]. Examples of studies aimed at studying emission angles and fragment yields were performed for PHITS [117], FLUKA [118], and GEANT4 [119], allowing for additional improvements in these codes. A recent experimental work of Aricò et al. [120] points out that there are differences in secondary fragment production between water and PMMA targets. Furthermore, simulations were performed using FLUKA, and some differences were found between experimental measurements and calculations. All these differences should be taken into account when dosimetric measurements are performed using PMMA instead of water phantoms.

TABLE 2

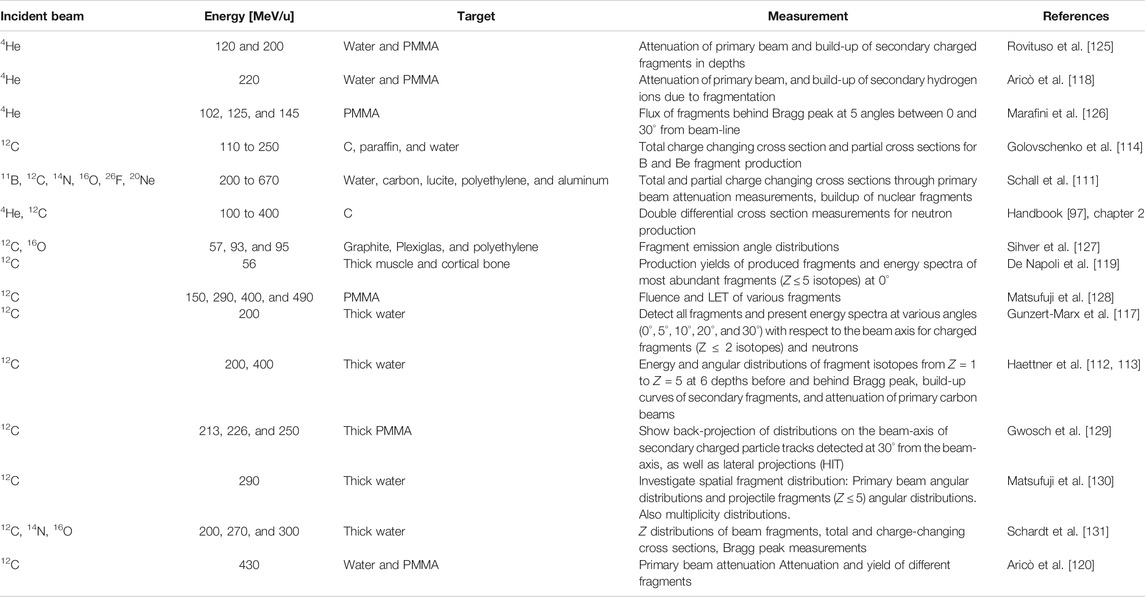
TABLE 2. A non-exhaustive selection of measurements on thick targets relevant to particle therapy: projectile, energy, target material, measurement, literature with MC-data comparisons, and reference with first author.

A different approach is represented by charge measurements performed by means of a multilayer Faraday Cup. For example, in the work of Rinaldi et al. [121], a FLUKA simulation of protons at 160 MeV was compared to existing experimental data. This is an integral test which allows to estimate the accuracy of MC models in reproducing the overall range of nuclear secondaries produced in target fragmentation. However, as remarked by the authors, it cannot provide any specific check of a particular reaction channel. Besides FLUKA, also other MC codes have been previously compared to the same kind of measurements. For instance, SHIELD-HIT is considered in Henkner et al. [122], MCNPX in Mascia et al. [123], and GEANT4 in Zacharatou et al. [124] and in Hall et al. [28].

2.5.3 Measurements That Were Performed in the Context of Range Monitoring

These measurements are those that specifically concern the production of secondaries which can be exploited for range monitoring, a topic where the reliability of nuclear models in MC is of particular relevance. These secondaries include ${\beta }^{+}$ emitting nuclei, prompt gammas, and energetic secondary charged fragments. We summarize a selection of these measurements in Table 3. Again the list is non-exhaustive, and we selected only those measurements that were reported in absolute physics quantities on homogeneous targets, since we consider these as the most suitable for the benchmarking of MC models.

TABLE 3

TABLE 3. Summary of measurements in the context of range monitoring studies.

As far as ${\beta }^{+}$ emitting nuclei are concerned, a large amount of measurements is available for offline, in-room, and online monitoring. Most of them are measurements of the detection of the activity spatial distribution. However, the data which are particularly useful for MC model tuning are cross section measurements. Actually there are not yet enough cross section data available. Existing data have large uncertainties, and to achieve a range accuracy below 1 mm, more accurate cross section measurements are needed [132]. The case for which more data are available is that of ¹¹C production in p-¹²C collisions. Figure 3, taken from the work of Matsushita et al. [133], illustrates a situation which points out that considerable systematic differences exist between different data sets. Clearly, the uncertainty of the predictions of MC models can be, at best, of the same order as the experimental uncertainty. FLUKA was compared with these cross section data, starting from the work of Sommerer [134], and the quality of results, as summarized in Figure 7 of the article of Battistoni et al. [135], can be considered satisfactory. The comparison with data for ¹¹C and ¹⁵O production is shown. These are the two most relevant radionuclides in case of PET monitoring in proton therapy, but other isotopes can be important, especially in in-beam PET. Less data are available in case of ¹⁰C production. Recently, new cross section data for ¹⁰C, ¹¹C, and O¹⁵, very useful for future benchmark studies, were published by different groups [133, 136], where the work of Horst et al [136] concerns also data relative to C–C and C–O collisions. Since recently, the use of PET monitoring technique is under consideration also in the case of ion therapy [137]. The prediction capability for short-lived ${\beta }^{+}$ emitters remains subject to uncertainties. A recent comparison [138] between GEANT4 for short-lived ${\beta }^{+}$ emitting nuclei with data [139] clearly demonstrated the need for improvement.

FIGURE 3

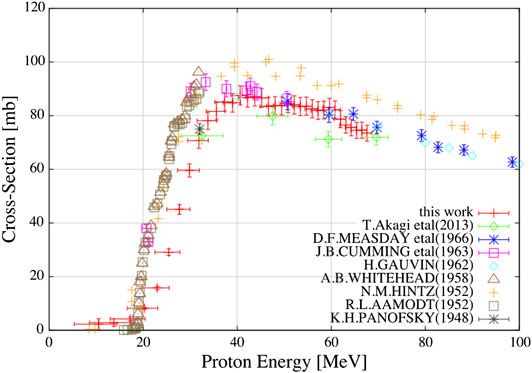
FIGURE 3. Cross section measurements for ¹¹C from different groups in the past 70 years, with new recent measurements included. Reproduced with permission from Matsushita et al. [133] Discrepancies between various measurements are visible.

Regarding prompt gammas, soon after the first proposal to use prompt gamma detection for particle therapy [140], it was realized that existing MC models were not reliable, see, for instance [141]. This has led to many new developments, among which the Envision project [142], in the context of European FP7 program, dedicated to imaging in ion therapy, which also stimulated new efforts for the improvement of existing codes and the development of new ones. For instance, valuable measurements in the framework of Envision were reported by Smeets et al. [143] and Pinto et al. [144], as well as several studies aimed at improving the accuracy of MC codes like MCNPX [143], GEANT4 [145], and TOPAS [146]. The study by Dedes et al. [145] revealed that prompt gamma yields were strongly overestimated by GEANT4 [145]. Improvements in GEANT4 were reported in 2016 [147], and good results for the FLUKA code concerning the prediction of both yields and energies of prompt gammas are obtained [135].

Finally, charged fast hadrons were considered more recently for range monitoring purposes [148–150] in the context of ion therapy. Table 3 summarizes various measurements that are useful for MC benchmarking. From the point of view of fundamental cross sections of interest in this case, also data reported in Table 1 are very useful. However, the approach aiming at achieving more spatial precision [149] requires the use of fragments emitted at large angles (mostly protons). Simulating such processes is challenging, because only a few of the total number of charged hadron secondaries produced are emitted at large angles. In fact, the standard available biasing techniques (importance biasing and biasing of inelastic cross section) do not apply in this context, especially when a comparison with experimental data on the basis of event-by-event reconstruction is required. It would be possible to develop dedicated variance reduction techniques for this purpose. In addition there is lack of data at large production angles to benchmark production models. A recent attempt to perform this kind of measurements for ¹²C interactions on different elements is reported in Ref. 105.

2.6 Future Directions in Model Development

In the last decade, many important developments of interest for particle therapy concerned the use of MC. So far, the attention has been mainly focused on the treatments with proton and ¹²C beams. Therefore, also the efforts in the development of nuclear models were necessarily concentrated on the interactions of these projectiles. More recently, the attention is focusing on ⁴He interactions, since this appears to be most probable application of new ion beams for therapy [168]. The case of ¹⁶O projectiles is also a next study case. Consequently, future work to improve MC models should be oriented in the same direction.

It turns out that adopted hadronic models are in general adequate for physical dose calculations. However, it is clear that none of the models considered in the above-discussed MC codes, or others, is capable, alone, to provide reliable predictions in all clinical and research applications. Due to their intrinsic phenomenological nature, experimental data are needed to drive model development and to allow their benchmark. In this respect, our claim is that the most valuable data for this purpose are single and double differential cross sections, measured on thin target experiments. Unfortunately, in the whole range of interest for particle therapy, there is still a significant lack of measurements, mainly concerning nucleus–nucleus interactions. In the next years, new data are expected from the FOOT experiment [110]. Of course, also indirect approaches and measurements on thick targets, often involving multiple interactions and different energies, are very important for model validation.

Finally, we would like to point out that a judgment of the level of accuracy of certain model may strongly depend on the scope of use. The capability of correctly reproducing in detail the cross sections may not be necessary in all cases. For instance, a model can be accurate in reproducing the physical dose but not enough for range verification techniques. In any case, MC models require a continuous work of upgrade and development. This concerns both the improvement of physics modeling and the optimization of their algorithmic implementation. Actually, the complexity of the description of interactions can result in elevated consumption of computing time. As we shall discuss also in the next sections, this aspect remains one of the major limitations in the use of general purpose MC codes in clinical practice.

3 Monte Carlo and Radiobiological Modeling

3.1 Rationale

The capability of performing a reliable calculation of physical dose is a necessary condition for an MC to be used in particle therapy. However, this is not sufficient, and the evaluation of effective biological dose is eventually required. This is a fundamental aspect which is particularly important in ion therapy. In fact, one of the most important reasons for the use of carbon or heavier ions in particle therapy is their increased relative biological effectiveness (RBE) in the Bragg peak region. A primary ion beam will give rise to a mixed radiation field with particles and nuclear fragments of different charge, energy, and LET. Each of them will have a different biological impact, even for the same imparted physical dose in the same kind of tissue. This is related to the different ionization density which the different particles will produce on length scales comparable to the size of DNA structure and cell nuclei. Many complex biological aspects are involved that may give rise to significant uncertainties in effective biological dose calculations. Thus, the study of radiobiological effects cannot be limited just to the physics of the interactions of radiation with matter, but should include the modeling of biological factors. Below, we discuss strategies that have recently been developed to take into account some biological effects in MC dose calculations in clinical and research context.

3.2 The Track Structure Approach

This review mainly concerns MC codes adopting the condensed history approach, while radiobiological calculations are most properly performed by means of track structure codes. These are codes designed to track the passage of electrons and ions simulating each individual basic interaction and recording positions and energy depositions of all produced particles. Besides the description of physical processes, radiochemistry models must be implemented in these codes to take into account the many body processes relevant for radiobiological purposes. Track structure codes are in general able to perform calculations on microscopic (nanometric) volume scales in liquid water, making their application in simulations of actual treatments highly unpractical from the point of view of computing power. However, they remain fundamental, together with mathematical models of the cell structure, for the investigation of all basic mechanisms related to biological effects of radiation. Among the examples of codes belonging to this class, we can quote PARTRAC [169], able to perform calculations on microscopic scales in liquid water, and TRAX [170, 171], which can deal with different materials. Results obtainable by these codes can in principle be coupled with the radiation field simulation achievable with general purpose MC codes.

A recent approach aiming to merge the track structure approach into the framework of a general purpose MC code is the GEANT4-DNA project [172]. It was started in the context of the studies for radiation protection in space missions. The code currently includes the interactions of light particles (electrons) and ions including hydrogen and helium isotopes down to the eV scale in liquid water. An example of the tracking capabilities of the code is shown in Figure 4, where the 2D pattern generated in liquid water by a single 1 keV electron is shown.

FIGURE 4

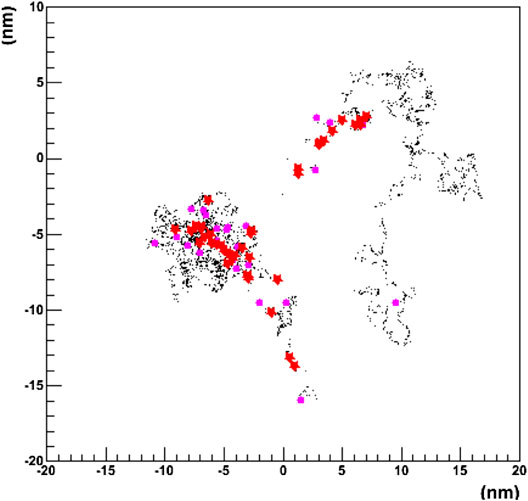
FIGURE 4. Projected 2D pattern generated by a single 1 keV electron in liquid water using the GEANT4-DNA physics processes. The primary particle originates at the (0,0) position. Different colors represent different physics processes [172].

Thanks to the geometrical modeling capabilities of GEANT4, it allows to implement the geometry of biological targets at sub-micrometric scales. In particular, it can use either a voxelized or an atomistic approach. The latter allows to model targets at nanometric scales, such as the DNA molecule, using the combination of standard mathematical volumes, as shown in Figure 5. A chemistry model can be coupled to simulate indirect effects of radiation due to the generation of molecular radical species.

FIGURE 5

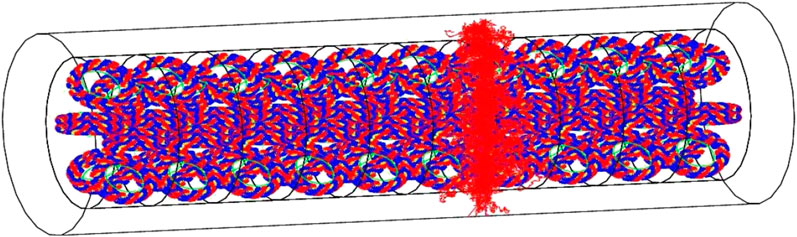
FIGURE 5. Visualization of a whole chromatin fiber irradiated by a single 500 keV He⁺ particle, emitted perpendicularly to the main revolution axis of the fiber. Individual bases are modeled as sectors of cylindrical shells, with an inner radius of 0.5 nm and an outer radius of 1.185 nm. They have a thickness of 0.33 nm. The positions of 100 pairs of bases are parameterized into a DNA helix loop. [172].

Another attempt is being made in the context of the TOPAS [21, 22] project, where an extension was developed called TOPAS-nBio [22, 173], which is aimed at the modeling of detailed biological effects at the nanometer scale, facilitating and extending the use of GEANT4-DNA models for subcellular geometries, physics, and chemistry processes.

3.3 Coupling of General Purpose MC Codes With Radiobiological Models

A common approach to evaluate the RBE-weighted dose ($D_{RBE}$) in a MC simulation is to obtain the RBE by exploiting the survival probability S of cells as function of physical dose D as predicted by the linear quadratic dependence, inspired by the dual radiation model of [174] formulated as

$S=e^{-\alpha D-\beta D^2}.[1]$

Here, α and β are parameters, which depend on several variables including those of biological nature, such as the tissue type, and of physical nature, like particle type, energy, dose, and LET. The RBE factor, for a given survival level S, is then given by

$RBE=2{\beta }_i[-{\alpha }_X+\sqrt{{\alpha }_X^2-4{\beta }_{X}lnS}]/2{\beta }_X[-{\alpha }_i+\sqrt{{\alpha }_i^2-4{\beta }_{i}lnS}],[2]$

where ${\alpha }_X$ and ${\beta }_X$ are the coefficients for photons, while ${\alpha }_i$ and ${\beta }_i$ are the coefficients for the ions of interest (at a given LET).

When general purpose condensed history MC codes are considered, the most common approach is to rely on a precomputed database of the coefficients α and β. They can be estimated by numerical radiobiological models, such as the local effect model (LEM) [175–178] or the microdosimetric kinetic model (MKM) [179–185]. Alternatively, they can be obtained from experimental data or from track structure simulations. One of the first examples of this approach within a MC can be found in the work of Kase et al. [186], using GEANT4 in the context of ion therapy activity at NIRS. In the case of FLUKA [135], a general interface is available to the user in order to provide a database in terms of α and β for different tissue types and for the different components of the radiation field as a function of energy per nucleon. As implemented also in other codes, in order to compute the biological effect, FLUKA performs the calculation of dose-weighted averages ${\overline{\alpha }}_j$ and ${\overline{\beta }}_j$:

${\overline{\alpha }}_j=\frac{{{\displaystyle \sum }}_i\text{Δ}{d}_{i,j}\cdot {\alpha }_{i,j}}{{{\displaystyle \sum }}_i\text{Δ}{d}_{i,j}}\text{and}\sqrt{{\overline{\beta }}_j}=\frac{{{\displaystyle \sum }}_i\text{Δ}{d}_{i,j}\cdot \sqrt{{\beta }_{i,j}}}{{{\displaystyle \sum }}_i\text{Δ}{d}_{i,j}},[3]$

where $\text{Δ}{d}_{i,j}$ is the dose from the ith charged particle (composing the mixed radiation field) with associated ${\alpha }_{i,j}$ and ${\beta }_{i,j}$ in voxel j and i runs over all particles depositing dose in voxel j. Eventually, RBE and RBE-weighted dose values can be determined for each voxel of the irradiated target knowing the absorbed dose and the dose-weighted averages ${\overline{\alpha }}_j$ and ${\overline{\beta }}_j$

As an example, we report in Figure 6$\overline{\alpha }$ and $\overline{\beta }$ (left panel) and the absorbed dose and $D_{RBE}$ (right panel) for a carbon ion biologically optimized spread-out Bragg peak, as available at CNAO. The SOBP was calculated for a homogeneous dose distribution of 3 Gy-RBE in a cubic shaped target of side 6 cm centered at 9 cm depth in water. The FLUKA weighting was achieved for a cell line having ${\left(\alpha /\beta \right)}_X$ = 2 Gy, as obtained from photon irradiation measurements.

FIGURE 6

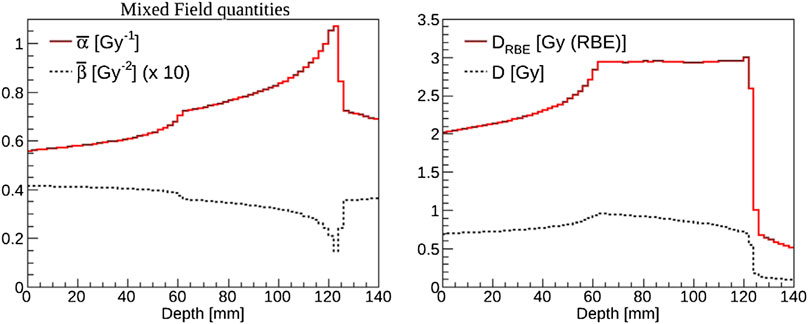
FIGURE 6. Example of biological weighting of dose performed with FLUKA [135] in the case of a carbon ion spread-out Bragg peak for a cube-shaped target of side 6 cm centered at 9 cm in water. Left panel: $\overline{\alpha }$ (solid line) and $\overline{\beta }$ (dashed line) calculated as a function of depth in water. The β results have been rescaled by a factor of ten for display purposes. Right panel: absorbed dose (dashed line) and $D_{RBE}$ (solid line) values calculated as a function of depth in water.

Another example where this approach was applied is a newly developed radiobiological model denominated BIANCA [187, 188], implemented in the form of MC simulation as well, which takes into account the development of complex DNA lesions, chromosomic aberrations, and their capability of inducing clonogenic cell death. In Ref. 188, the coupling of BIANCA with the FLUKA MC is reported. This work shows a comparison of survival data of CHO cells after an irradiation mimicking a clinically relevant scenario using carbon ions and protons. An interesting result of this work is reported in Figure 7.

FIGURE 7

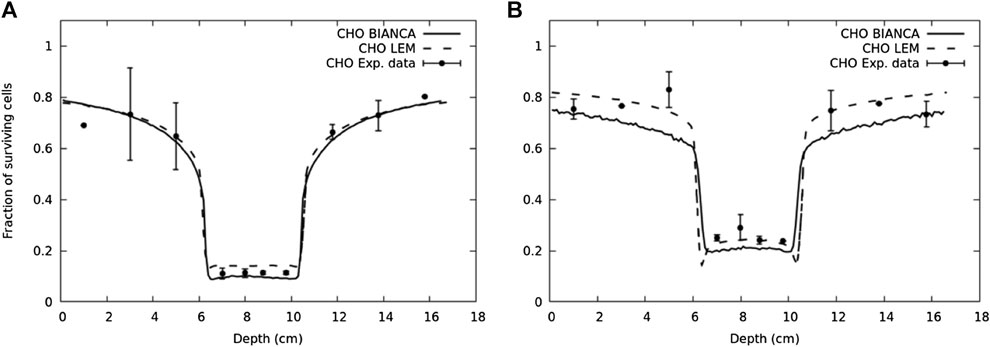
FIGURE 7. Surviving fraction for CHO cells in a typical two-port irradiation with carbon ions (panel (A)) and protons (panel (B)) [188]. The solid lines represent the predictions performed by BIANCA interfaced to FLUKA, the points are experimental data taken from Ref. 189, and the dashed lines represent the prediction performed by LEM model [189].

Different RBE models can produce different results, and this can result in different dose prescriptions. This aspect has been studied in detail for carbon ion therapy at CNAO with the help of MC calculation. The starting point is that it was considered to take as reference the clinical protocols assessed in the past in the NIRS Japanese center. At NIRS the MKM radiobiological model was used, while, for several years, the treatment planning system of CNAO, as in the rest of Europe, was based on the LEM-I model. Since 2012, Fossati et al. [190] showed that for the same D_RBE, significant variations of the physical dose D in the target volume, up to 15–20%, were found when comparing the two approaches. In order to minimize target physical dose variations, and possible consequent risks of undercoverage of target, prescription dose conversion factors, as suggested in Ref. 190 in a study with water phantoms, were validated for a series of patient cases by Molinelli et al. [191] by means of simulations performed with the FLUKA MC, where the alpha, beta radiobiological parameters from LEM-I were used according to the procedure described in this section. Further studies using MC simulations are reported in the work Magro et al. [192]. A Matlab-based tool was developed to generate a biological database, that is, a set of input tables of some model-specific parameters for a variety of particles, based on the MKM mode. This database was benchmarked with published ICRU energy loss tables. Then, using this database together with the information about the mixed-radiation field (particle type, energy, etc), FLUKA can calculate the RBE-weighted dose of the mixed-radiation field in each voxel. To clinically benchmark the coupling of FLUKA with the NIRS approach, a few real patient treatments were simulated, corresponding to different prescripted dose levels. The simulation results (physical dose, effective dose, and RBE) were compared to the results obtained by means of the TPS adopted at NIRS. Some discrepancies were found, but the general level of agreement was considered satisfactory. A similar investigation has been more recently performed for ⁴He ions, as reported in the work of Mein et al. [193] using both MC and an analytical calculation platform.

3.4 Semi-Analytical Approaches

The dose average linear energy transfer ($LE{T}_D$) is frequently used as physical quantity to describe the biological effectiveness of the mixed radiation field. $LE{T}_D$ is the dose-weighted mean value of the particle LET distribution at depth z in the radiation field consisting of dose contribution $D_i$ from all particle species i and is defined as

$LE{T}_D\left(z\right)=\frac{{\text{Σ}}_i{{\displaystyle \int }}^{\text{}}LE{T}_i\left(E\right)D_i\left(E,z\right)dE}{{\text{Σ}}_i{{\displaystyle \int }}^{\text{}}{D}_i\left(E,z\right)dE}=\frac{{\text{Σ}}_i{{\displaystyle \int }}^{\text{}}LE{T}_i^2\left(E\right){\varphi }_i\left(E,z\right)dE}{{\text{Σ}}_i{{\displaystyle \int }}^{\text{}}LE{T}_i\left(E\right){\varphi }_i\left(E,z\right)dE}.[4]$

The quantities $LE{T}_i\left(E\right)$ and ${\varphi }_i\left(E,z\right)$ can be evaluated by means of MC codes so that $LE{T}_D$ can be calculated by means of Eq. 4. This can be exploited to evaluate RBE in the case of proton therapy, where it is possible to make use of phenomenological models which predict proton RBE as a function of LET, dose, and the (α, β) tissue-specific parameters for photons. The most common models of this type, derived from the analysis of proton RBE experimental data, are those of Wedenberg [194], Wilkens [195], McNamara [196], and Carabe [197].

Dependence of RBE on LET can be fitted in different ways. For example, in the Wedenberg model [194], RBE is given by

$RBE\left(LET,D,{\left(\alpha /\beta \right)}_X\right)=-\frac{1}{2D}{\left(\frac{\alpha }{\beta }\right)}_X+\frac{1}{D}\sqrt{\frac{1}{4}{\left(\frac{\alpha }{\beta }\right)}_X^2+\left(qLET+{\left(\frac{\alpha }{\beta }\right)}_X\right)D+D^2}[5]$

where q is a parameter obtained by experimental data, different for each cell line.

Instead, the RBE expressions of McNamara [196] is given by

$RBE\left(LET,D,{\left(\alpha /\beta \right)}_X\right)=\frac{1}{2D}\left(\sqrt{{\left(\frac{\alpha }{\beta }\right)}_X^2+4D{\left(\frac{\alpha }{\beta }\right)}_X\left(p_0+\frac{p_1}{{\left(\alpha /\beta \right)}_X}LET\right)+4D^2{\left(p_2+p_3\sqrt{{\left(\frac{\alpha }{\beta }\right)}_X}LET\right)}^2}-{\left(\frac{\alpha }{\beta }\right)}_X\right)[6]$

where $p_0=0.999064$, $p_1=0.35605$ Gy keV⁻¹ μm, $p_2=1.1012$, and $p_3=0.0038703$ Gy^−0.5 keV μm.

These kind of approaches can be useful in proton therapy to take into account variations in RBE, as alternative to the common assumption in clinical treatments of a constant RBE value of 1.1. In principle, it is possible to introduce these parameterizations also in ion therapy; however, it is usually preferred to make use of more sophisticated phenomenological or mechanistic models.

3.5 Future Directions and Developments

Considering the present state of the art, the possibility of making use of track structure simulation within a MC calculation of particle therapy treatments seems to be confined, for the moment, to research activities. In fact, the exceptionally high computing time which is required by such an approach can discourage to adopt this solution for a systematic study of clinical cases, and treatment planning in particular, even when accelerating techniques or large clusters are employed. It can be considered sometimes for retrospective analyses of clinical data. In general, the use of an interface to pre-calculated tables from external radiobiological models will remain the most practical solution for MC simulations.

Future developments, useful for biologically oriented treatment planning, need to consider not only RBE but also other important radiobiological quantities. One of the most important parameters is the oxygen enhancement ratio (OER) and its dependence on physical variables. This parameter is particularly interesting in view of the use of high-LET radiation for the treatment of hypoxic tumors, as discussed, for instance, in the works of Scifoni and Sokol et al. [198–200].

The development of new generation treatment planning is also considering the radiobiological effect of target fragmentation in proton therapy. As proposed in Ref. 201, this phenomenon may contribute to an increase of RBE especially in the entrance channel, and neglecting this contribution can bring to an underestimation of damage to the healthy tissues. The investigation of this particular aspect, usually not considered so far, requires both experimental activity and MC simulations. This is also a theme where the importance of modeling nuclear interactions, as discussed in Section 2, is emerging [202, 203].

Other topics in which MC simulation can be important in the context of radiobiology is the comprehension of possible mechanisms leading to the enhancement of radiobiological effectiveness. An attempt in this direction is the recent suggestion concerning the additions of specific radioisotopes (like ¹¹B or ¹⁹F) to exploit nuclear reactions triggered by protons on these nuclei. These reactions can generate short-range high-LET alpha particles inside the tumors, thereby allowing a highly localized DNA-damaging action [204]. Another interesting challenge is coming from the possible extension of the FLASH Radiotherapy approach [205, 206] to particle therapy, that is, the delivery of very high dose rates ($\ge$ 100 Gy/s). It has been suggested that such high dose rates can enhance differential effects between normal tissue behavior with respect to the tumor. From the point of view of MC codes, no changes are expected for the physics of interactions of radiation in matter, while specific radiobiological models are still under investigation and development.

4 Development of MC-Based Treatment Planning

4.1 Introduction

Over the past years, the superior accuracy of MC calculations with respect to analytical calculations has been confirmed in many studies. This is thanks to the more accurate implementation of physical (and possibly radiobiological) processes, the fact that the material composition is included in calculations, and the precise tracking algorithms. At present, MC dose calculations are therefore successfully used for various purposes in treatment planning and related research. Although the applications of MC in treatment planning are mostly in forward dose calculations (to compute the dose distribution in a tissue given a treatment plan), new developments are ongoing to include them in inverse dose calculations (to find a treatment plan whose execution will achieve a desired dose distribution).

In the next paragraphs, we shall first summarize some considerations on the role of MC in the present use of MC in treatment planning systems. Then, we shall present an example of developments in MC-based treatment planning systems, and we finish with some consideration about the underlying problematics and developments.

4.2 Present Usage of MC in Treatment Planning

MC simulations play an important role in the development and commissioning of treatment planning systems. Different treatment planning systems exist for particle therapy. A discussion of these tools goes beyond the purpose of the present review, but a few general issues can be mentioned. For dose delivery with spot spanning, commercial treatment planning systems are usually based on fast analytic dose engines using pencil beam algorithms. Such algorithms are often developed with the help of MC dose calculations, since it is not possible to rely completely upon analytic expressions or available tabulations. Many treatment planning systems require that the user provides specific measurements and MC simulations of pencil beams in water as a part of the TPS commissioning process for a given facility.

Moreover, MC simulations are currently often used for verifying the treatment plans of commercial treatment planning systems for complex patient dose calculations. Such verifications are often desired in situations which are characterized by large density heterogeneities (see, e.g., [1–3]), at least for a limited number of patient cases. The TPS prescription is used as input to the MC, which performs a forward dose calculation, that can be compared with the analytical result.

The clinical interest in high-accuracy MC tools is demonstrated by the fact that vendors of commercial treatment planning systems have since recently started to provide the user with MC-based dose calculation kernels for proton therapy, albeit only for forward calculations:

• The RayStation ^® [207] TPS provides the user the possibility to perform forward MC dose calculations for protons, based on a condensed history MC for primary and secondary protons, while heavier secondaries are considered only using a continuous slowing down approximation [208]. This MC dose engine has been validated also in clinical context [209]. Here, the authors demonstrated the superior accuracy of the MC dose engine with respect to the analytical algorithm in specific situations: in the presence of range shifters, large air gaps, or when beam directions are tangential to the patient surface. This may also depend on patient anatomy [2, 3]. RayStation also includes a tool allowing for an easy comparison between the MC and the analytical result, so discrepancies can be easily identified.

• The Eclipse treatment planning system provides users a MC dose algorithm for proton therapy, AcurosPT [210]. Here, computational run time is minimized by simplifying and eliminating less significant physics processes. The algorithm was benchmarked with TOPAS.

4.3 Recent New Developments in MC-Based TPS

There are several promising new developments in the usage of MC calculations in treatment planning. For instance, in the context of ion therapy, new developments are ongoing in the TRiP98 (treatment planning for particles) [211, 212] tool. This TPS was created as analytical dose calculation and optimization tool and used clinically for carbon ion radiotherapy at GSI until 2008, taking advantage from the development of the LEM radiobiological model carried on at GSI [175–178, 213, 214]. In the clinical applications of TRiP98, the LEM-I version was adopted. It also served as prototype for the clinical TPS Syngo^® RT Planning Software [215]. The original TRiP98 used a 1-dimensional deterministic transport algorithm, and the broadening of the ion beam as a function of depth was accounted for by means of a double Gaussian function. In order to overcome this kind of limitations, a fast MC algorithm was developed within TRiP98, as reported in the article of Iancu et al. [216]. This dose kernel could potentially also be used for plan optimization.

Also, in the development of ion treatment planning at HIMAC, MC has played a role. As reported in a dedicated textbook [217], GEANT4 was used to build the prediction of ion species and their kinetic energies of the therapeutic carbon-ion beam and to predict the dose mean-specific energy (z*) which is necessary for their microdosimetric radiobiological model.

A recent example of MC dose calculation tool for both proton and heavy ion therapy is the work of Russo et al. [218, 219]. It describes a TPS computing kernel for different ion types, called PlanKIT (Planning Kernel for Ion Therapy), developed within a collaboration between IBA and INFN, currently only used for research. This TPS is based on the use of a “Beamlet Superposition (BS) model.” The concept, similar to what is adopted in other projects, is that an ion beam can be thought of as composed of subunits, here called Beamlet, that are obtained splitting the beam phase space in smaller phase spaces. The total irradiation result is obtained by summing the interactions of the different beamlets, computed with FLUKA MC simulations. In this way, it is possible to produce universal Look-Up tables of physical and radiobiological quantities, like dose, track-averaged, and dose-averaged LET and, by coupling to the MKM radiobiological model, α and β coefficients to derive RBE according to the linear quadratic model. The main advantages deriving from this approach were two: i) the possibility to simulate the irradiation with different ions species and ii) the evaluation of several physical and radiobiological quantities at the same time. At present, only forward calculations can be performed with PlanKIT.

All above mentioned examples, with exception of the TriP98 research, are examples where MC is used as forward dose calculation tool. Considering the recognized quality of results in dose calculation which can be obtained by means of simulation, it is natural to consider also the possibility of coupling MC to an optimization code for inverse dose calculations, so that MC accuracy would be assured for all stages in treatment planning, from development to clinical use. This would have a few important advantages:

• It would allow to include the most accurate description of physics, geometry, beam models, and materials during all stages of treatment planning, including plan optimization, that is, the calculation process to obtain all beam weights by optimizing the dose in terms of target coverage and OAR dose.

• It would allow to consider the actual composition of tissues. In fact, TPS calculations are usually performed just considering a water equivalent path length environment. For electromagnetic processes, this is generally not a problem, but for processes involving nuclear interactions, it may lead to errors, especially in calculations for high density regions in the patient (bone and implants), or in modeling treatment heads and beam shape devices.

• It would be possible to simultaneously predict dose and secondary particle production, useful for treatment verification techniques.

One of the first attempts to proceed in this direction has been reported in the work of Mairani et al. [220], which describes the development of a MC treatment planning (MCTP tool) for proton therapy based on the FLUKA code. The workflow of this solution is illustrated in Figure 8.

FIGURE 8

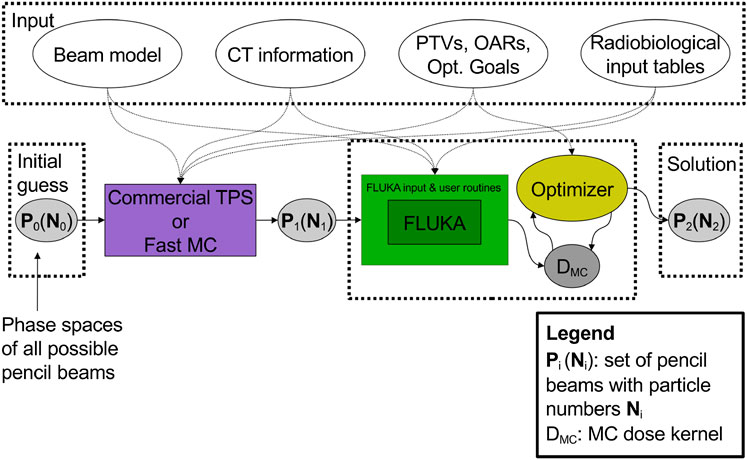
FIGURE 8. Workflow of the multi-step procedure for dose calculation and optimization of the work of Mairani et al. [220].

The procedure requires as input a set of pre-optimized pencil beams P¹(N¹). Here, N¹ is the initial pre-optimized guess for the fluences that is obtained with a commercial TPS or fast MC, starting from all the possible beams P₀ available in a given therapy facility in terms of energy values and positions. Then, the MC-optimized solution, P₂(N₂), is obtained iteratively by an optimizer algorithm which runs over a MC calculated dose kernel, that is, 2-dimensional matrix of $d_{i,j}$ values (dose in voxel j of patient geometry deposited by pencil beam i). Hereby, an RBE-weighed dose kernel is achieved by either using a fixed RBE value of 1.1 or using pre-computed tables of radiobiological coefficients, as described in Section 3. An optimizer code, taking as input the MC dose kernel, produces the treatment plan by minimizing a cost function which takes into account the prescribed dose to the planned target volume (PTV) and a set of dose limits for organs at risk (OAR).

This approach has been initially validated at CNAO by comparing the results to those achieved by the standard TPS adopted in the facility. Figure 9 reports the results of one of those comparisons.

FIGURE 9

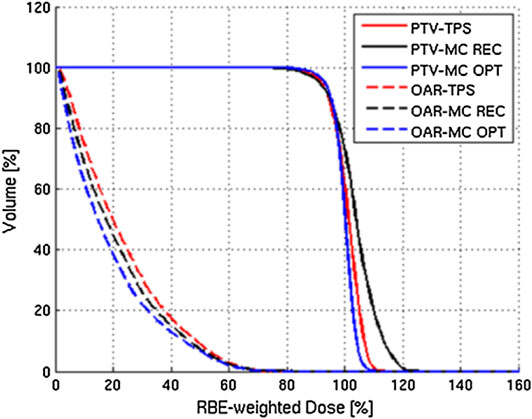
FIGURE 9. Example of results of the MC TPS tool of Mairani et al. [220]: DVHs for PTV and OAR calculated for a three-field patient case (chordoma in the head–neck district). The standard TPS results (labeled TPS) are compared with the MC-recalculated (labeled MC REC) and MCTP (labeled MC OPT) ones.

The project was soon extended to ion therapy, as described in the work by Böhlen et al. [221]. Since then, it has been used mainly for research purposes. For instance, we can quote two examples: i) the investigation of the robustness of ion beam therapy treatment plans with respect to uncertainties in biological treatment [222] and ii) the study and validation of treatments with different ion species, including ⁴He and ¹⁶O (also protons and C), by comparing results with dosimetric measurements, as performed at the Heidelberg Ion Therapy Center [223].

4.4 Developments and Perspectives

As mentioned in the conclusions of Section 3, work is ongoing in view of a new generation of TPS considering new features, as other radiobiological parameters and target fragmentation, and the possible use of new ions other than ¹²C. In all these cases, the use of MC will undoubtedly remain important both for development and check. A new case study where simulation can play a fundamental role (provided that the coupling with radiobiological modeling is properly implemented) is the optimization calculations for multiple ion treatments, as described by Sokol et al. [200]. Here, the combination of ⁴He and ¹⁶O beams has been considered as advantageous to achieve the “kill painting” approach [198, 224]. The first studies have been performed by means of the multi-ion biological optimization (MIBO) version of TRiP98 where specific algorithms to consider OER were added.

The MC approach discussed in Section 4.3 to treatment planning is surely of great interest and is potentially an innovative breakthrough. A few issues are still hampering the application in clinical practice. The most obvious difficulty is the large computing power that is required by full MC calculations, several hours for a multi-field proton therapy treatment plan [220]. From a clinical point of view, treatment planning with full MC can become attractive only if the required time is comparable to that employed using the standard approach, even if the quality of physics can be superior. Of course it is possible to reduce computation time by running parallel independent histories on a cluster of CPUs. However, the use of a very large cluster is not straightforward for all therapy centers. Instead, a more promising road is the development of fast MC techniques. This will be reviewed in Section 5. As we shall see, new attempts to develop MC treatment planning environments are under way [225, 226].

Finally, higher computation speed is not the unique requirement. In order to facilitate the use of MC in treatment planning in a clinical environment, it is important to develop the necessary software interfaces for the integration with TPS and image processing.

5 Development of Fast MC Codes

As mentioned previously, a major issue hindering widespread clinical implementation of MC simulations is computational efficiency. The complexity in the implementation of physics models and transport algorithms is very demanding in terms of computing power. Considering that a normal MC simulation of a treatment often requires transporting a large number of particles, usually large computer clusters have to be used. For this reason, in the last years, the interest for the development of fast simulation techniques has grown considerably. These attempts make either use of new technologies in computing hardware, or they adopt dedicated algorithmic solutions. Since it is often sufficient to have a code fully dedicated to dose calculation, a significant contribution to the speedup is also obtained by simplifying the structure of the code with respect to a general purpose MC, focusing only on the relevant processes. In this Section, we highlight a few examples of fast MC code development.

5.1 Current Methods to Speed up Monte Carlo Simulations

5.1.1 Usage of Graphics Processing Units (GPU)

The progress in the use of graphics processing units (GPU) allowed a new effective direction in the search for higher computation speed. This approach, pushed by computed graphics, has allowed for the development of techniques for general purpose computing exploiting the high degree of parallel operation which characterize these hardware units. This has brought to the approach denominated “General Purpose computing with Graphics Processing Units” (GPGPU). MC is one of those computing cases which can profit from the high degree of parallelism allowed by this technology, since events may be processed in many different cores at the same time. A comprehensive review about advantages and challenges about GPU proton dose calculations (analytical and MC) was written by Jia et al. [10].

The GPGPU architectures have evolved in time, and since about 2007 commercial solutions are available with full possibility of programming. Probably, the most diffused and interesting hardware units are those produced by NVIDIA^® through the CUDA^® (Compute Unified Device Architecture) platform [227]. CUDA^® is a development environment which allows the writing of applications by means of the extension of diffused programming languages, like C/C++, overcoming the difficulties of assembly languages. CUDA^® compilers for other languages are also commercially available. Programs exploiting the GPGPU architecture can be also written using the OpenCL (Open Computing Language) software libraries. MC algorithms must in general be rewritten in order to efficiently exploit GPU features, taking also into account possible limitations and bottlenecks, as those coming from the interactions between CPU and GPU memories. Limits such as the size of global and shared memory, maximum number of threads per block, and number of stream multiprocessors are GPU dependent. In the case of MC simulations, there exist some limitations to the effective number of parallel threads in a GPU. The large number of cores (typically thousands) cannot, in practice, be totally exploited at all times. The random structure in MC algorithms generates the so-called thread divergence, which limits the actual number of cores which effectively run in parallel. However, the achievable gain factor remains in any case significant.

A recent example of a MC simulation framework exploiting the GPU approach for pencil beam dose calculations is the FRED (Fast paRticle thErapy Dose evaluator) [225] code, developed in the context of treatment planning for proton therapy. Using effective models for particle-medium electromagnetic and nuclear interactions, it allows for tracking and scoring of energy deposition of primary and secondary particles, also in a voxel geometry imported from CT scans. Single pencil-beam dose simulations have been validated. A merit of this framework is that, since the beginning of its development, it already contained all the optimization tools for full treatment plan MC-based calculations. Moreover, not only the use of the water path length approximation is possible, but also simulating realistic materials. The tracing kernel can achieve an event processing rate of 10 million primary/s on a single GPU card. This performance allows to recalculate a treatment plan at 1% of the total particles in a few minutes.

As an example of the quality achievable with this tool, in Figure 10, we show the dose comparison between measurements, FRED, and the commercial TPS used at CNAO, for a spread-out Bragg Peak (SOBP) corresponding to a uniform dose irradiation in a 6-cm sided cube volume at 15 cm of depth in water. Panels (a) and (c) show the longitudinal dose profiles, while panels (b) and (d) show the transversal profiles.

FIGURE 10

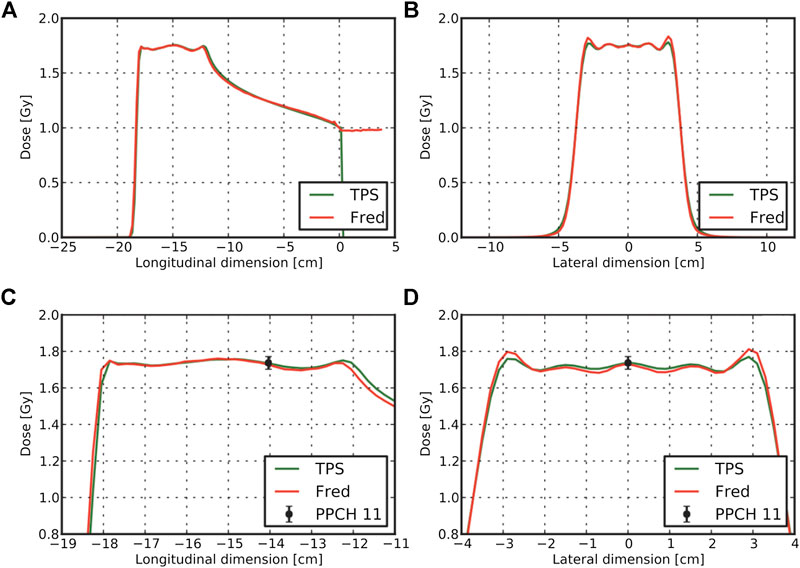
FIGURE 10. Results for the comparison of FRED results with TPS adopted at CNAO for a SOBP cube at 15 cm depth in water resulting from a treatment plan with protons. TPS and FRED dose lineouts through the cube center are shown in panels (A) and (B). Enlarged version of the profiles together with the measured dose level for a pinpoint ionization chamber is visible in panels (C) and (D) [225].

Preclinical application of FRED is presently being studied in Kracow, also in conjunction with the development of plastic-scintillator-based PET detectors for particle therapy delivery monitoring [228]. Further development of FRED for carbon ion treatments is in progress.

Moving to an example in a more clinical context, complete 4-D patient dose calculations in proton therapy including respiratory motion can be ran on GPUs, as reported in Ref. [229]. The GPU calculations include the distribution of the treatment plan according to breathing phase, calculations, and dose accumulation from the various breathing phases. Proton transport simulations were done according to the track-repeating algorithm (described below). Simplified approaches for electromagnetic and nuclear physics processes were used. Validation of the GPU dose calculations was done against GEANT4/TOPAS in terms of secondary particle yields, energy and angular distributions, and for treatment plans [230]. The calculations are fast enough to have allowed for the development of a GPU-based TPS [231].

A GPU-based proton MC tool (GPUMCD) has been developed by Maneval et al. [232]. They introduced a rigorous formalism for energy loss calculation at the typical proton energies used in therapy. The purpose was to accelerate the MC dose calculations by allowing larger steps while preserving accuracy. A lookup table linking the fractional energy loss per step length, ϵ, to the equivalent restricted stopping power L_eq was created. The mean energy loss for any step length was simply defined as the product of the step length with L_eq. The proton CSDA (continuous slowing-down approximation) was modeled with the L_eq formalism and added to GPUMCD. GEANT4 had been used as reference for the validation. This formalism was found to lead to an intrinsic efficiency gain factor ranging between 30–630, increasing with the prescribed accuracy of simulations. It can be considered a promising variance reduction technique for computing proton dose distributions. Combined with GPU acceleration, the total acceleration provided by the L_eq formalism with respect to CPU-based GEANT4 simulations was found to be the order of 10⁵.

Still in proton therapy, a calculation package for proton dose calculations, gPMC (GPU Proton Monte Carlo), was developed [233]. This framework aims at improving speed without applying simplified approaches. Protons are transported according to a class II condensed history scheme and continuous slowing down. Production of delta-electrons is considered, but their kinetic energy is deposited locally. Regarding nuclear interactions, the empirical strategy developed in Ref. 234 is adopted (described in more detail below). Only proton–proton elastic reactions, proton–oxygen elastic reactions, and inelastic interactions were included. The framework was validated using TOPAS/GEANT4 and performing the gamma passing rate analysis. It can be noted that the authors of this work explicitly mention some technical problems, typically encountered in the interaction between GPUs and CPU, and their solution. Since then, developers of GPU-based MC codes have progressively learned how to manage and overcome these difficulties.

For carbon therapy, recently a framework called goCMC (GPU OpenCL Carbon Monte Carlo) was developed, simulating particle transport in voxelized geometry [235]. The package operates using the OpenCL framework. Electromagnetic processes are modeled by the standard class II condensed history scheme with a continuous slowing down approach. Regarding nuclear interactions, only 4 (inelastic) reactions are included, and secondary particle production is simulated using pre-computed tables, containing particle yields, energy, and scattering angle probabilities. The disadvantage of this method is that energy and momentum conservation is not assured event-by-event, as in full MC simulations. The method was validated for mono-energetic mono-directional beams against GEANT4 and data, using the gamma analysis and dosimetric quantities. A new development, oriented to provide a real MC-based treatment planning is presented in Ref. [226]. An example of results is given in Figure 11, for three patient cases (prostate, pancreas, and brain) treated with ¹²C ions. The total time needed, including MC simulation, optimization, and final dose calculation, ranged from about 800 to 6,400 s, depending also on the adopted hardware.

FIGURE 11

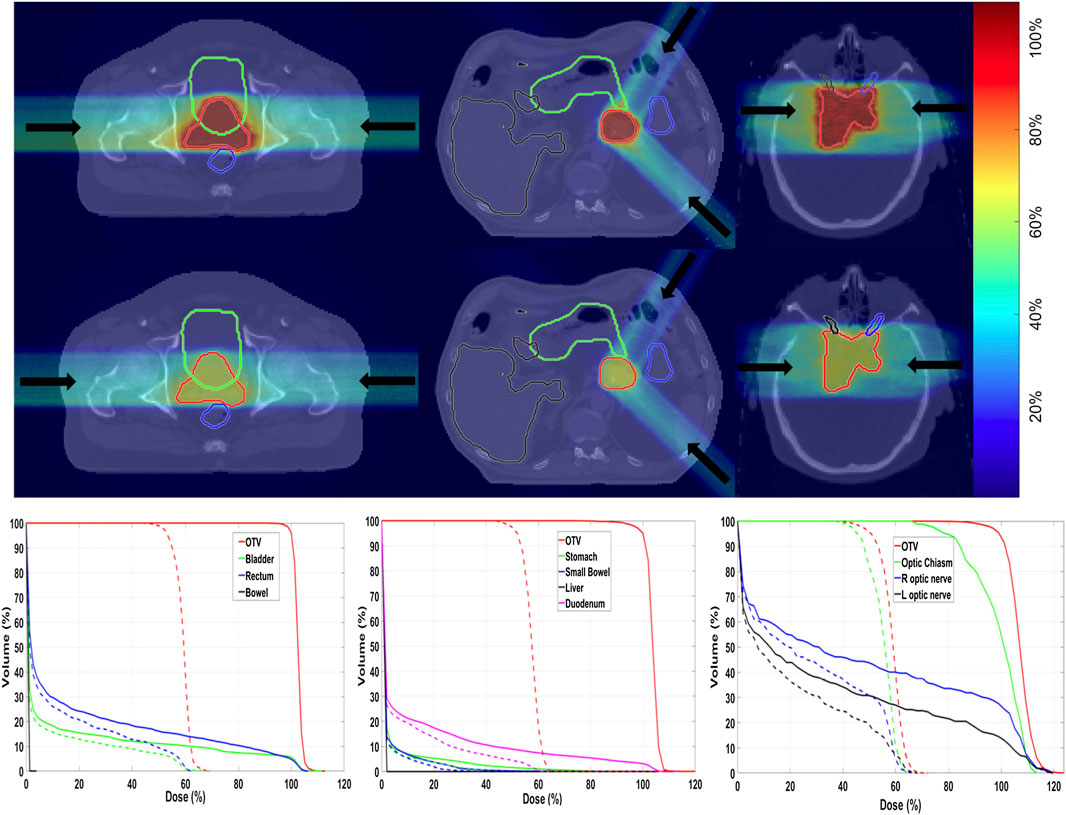
FIGURE 11. Example of TPS calculation with the GPU framework described in Ref. 226. First and second rows are biological dose and physical dose, overlaid on CT images, in three patient cases. From left to right: prostate, pancreatic, and brain cancers. The color bar indicates the dose levels relative to the prescription dose. Arrows indicate beam directions. The bottom row is the corresponding dose–volume histograms (DVHs). Solid lines and dashed lines denote biological dose and physical dose, respectively. The OTV represents the optimization target volume, a similar concept to CTV.

Recently, a GPU simulation framework called FRoG (Fast Recalculation on GPU) was developed allowing to simulate protons, carbon, helium, and oxygen ions [236]. Although Frog is reported to have MC accuracy, the framework used an analytical dose calculator.

5.1.2 Usage of Phase-Space Files

Rather than fully modeling the beam line and treatment head, a fixed machine output for a given installation can be used for treatment simulations. In that case, “phase-space files” can be produced for a given treatment head, containing the physical properties (energy, direction) of the primary particles that exit a given treatment head. This technique is common in conventional radiotherapy. In particle therapy with passive scattering techniques, usage of phase space files is typically not possible because the treatment head varies. However, even for active scanning techniques applying this method is not straightforward, because of facility dependence of the characteristics of outgoing particles, for instance, due to differences in the beam line devices or differences in operational beam parameters like beam size. In that case, using “optimized” phase space files could be an option [237–239], in which the parameters are somehow tuned until the simulations match the measurements (typically longitudinal and lateral dose profiles) at a certain treatment site. This method was recently applied at the Shanghai Proton and Heavy Ion Center [239].

5.1.3 Track-Repeating Algorithms

The track-repeating approach, originally proposed by Li et al. [240] for protons, is based on the idea to use pre-generated events during simulation to accelerate dose simulations. First, a full MC simulation is performed to generate events of protons interacting in water, with various initial beam energies. These events, including particle trajectories with path length, scattering angles, energy losses, and deposits in water for each step, are stored in a large database. All the physics interactions (in water), including secondary particles, are thus calculated by a general purpose MC code. Then, during particle transport in a given medium, the particle track length in a given material is adjusted to that of water, using the local density. For materials such as bone, corrections can be included by considering the different stopping power. Angles are adjusted according to the direction of the incident particle. At each step, appropriate tracks are selected from this pre-generated database, which are tracked further. This so-called track-repeating approach is different from the normal MC simulation, where physics interactions are sampled on the fly at each step. The track-repeating approach was clinically validated [241] against data and GEANT4, using the gamma index analysis and dosimetric quantities (DVHs) and is in use at the Shanghai particle therapy facility [238]. Figure 12 shows a comparison between the fast dose calculator (CDC) described by Yepes et al. [241].

FIGURE 12

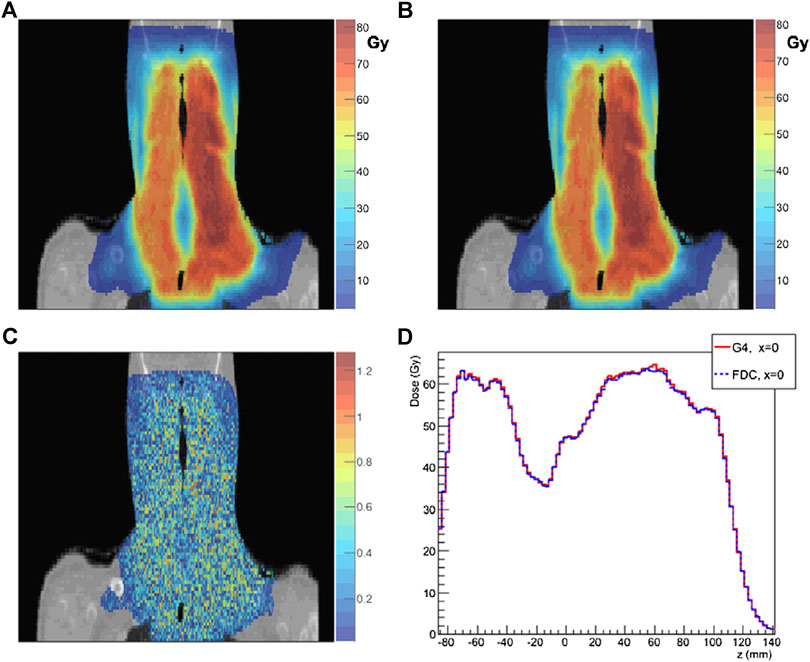
FIGURE 12. Comparison of results from the FDC developed by Yepes et al. [241] and GEANT4. Dose distribution for a particular coronal section of a head-and-neck patient: as (A) GEANT4 and (B) FDC. (C) 2 mm/2% gamma-index for the voxels on that particular section of FDC relative to GEANT4. (D) For the same section, the dose along the z-axis (inferior-superior) for x = 0 calculated with GEANT4 and FDC for that section.

A GPU implementation was also performed by the authors [242]. The usage of pre-generated tracks from a database was also adopted by [243], reusing ideas from available codes from conventional radiotherapy. The advantage of their approach is that they use pre-generated events in many different materials, rather than only in water. They used MCNPX for the generation of the pre-calculated tracks, as well as for the validation of the code. The latter was based on depth–dose curves along the central axis and lateral dose distributions.

A possible shortcoming of the track repeating approach, in the context of particle therapy, concerns nuclear interactions. While there are assessed methods to perform scaling of stopping power for different materials and densities with respect to water, there may be a substantial dependence of nuclear cross sections on the actual elemental composition. It is therefore questionable whether using events based on the physics interactions in water is sufficiently accurate. Regarding the calculation of dose, which is dominated by electromagnetic interactions, the accuracy is probably sufficient. In those cases where an accurate description of nuclear interaction is desired, as those we have discussed in Sections 2.3 and 2.4, this could not be the case. This problem could probably be overcome by pre-generating full events also in other materials.

5.1.4 Voxel Monte Carlo Algorithms

Based on ideas from traditional radiotherapy algorithms, a Voxel MC code for proton (VMCpro) therapy was developed [234]. Here, protons are step-by-step traced through a voxelized volume (typically a CT scan). One step is equal to the distance between the voxel boundaries, unless a discrete interaction took place within the voxel. The geometrical step length is calculated from the geometrical step length in water according to the ratio of densities and the ratio of the stopping power in a given voxel density to that in water, using an empirical fit formula. A multiple scattering angle is sampled at the new position, and the proton is rotated accordingly. Nuclear interactions are modeled as corrections to electromagnetic processes, treating all soft tissues as water. In the quoted article, the authors claim that they succeeded to achieve, at that time, a computing speed higher by a factor of 13 with respect to FLUKA and of 35 with respect to GEANT4.

5.1.5 Macro Monte Carlo Simulations

In the work of Fix e al. [244], a method inherited from electron dose calculations is adapted to proton therapy: Macro Monte Carlo simulations (MMC). In this method, full MC simulations (in this case with GEANT4) of protons in different spheres of different materials with many energies are performed, and exiting particles with all their characteristics are stored (macro-steps). The dose distribution in a voxelized grid can be obtained by a sequence of macro steps. The method was validated by comparing depth–dose curves and lateral dose curves with GEANT4.

5.1.6 Other Approaches

An example of a dedicated in-house proton MC code developed at PSI for assessing possible deficiencies of analytical dose calculations in inhomogeneous patient tissue is described in Ref. [245]. Here, a slab-by-slab approach is adopted for proton transport, calculating energy loss and taking into account multiple Coulomb scattering in the voxel. However, nuclear interactions are simulated analytically, with no tracking of secondary particles. The code was tested on a variety of patient plans.

Yet another approach of speeding up MC simulations for protons is with simplified Monte Carlo (SMC) simulations [246]. The approach is based on an effective model to take into account all physics processes relevant to dose calculations, using measured depth–dose curves in water. At each voxel, two effects are modeled. First, the residual range of protons is decreased according to the local material properties and corresponding energy loss. Second, MCS is modeled according to a Gaussian distribution. Thus, rather than sampling detailed interaction processes step by step, they capture all net effects (including nuclear interactions) in terms of dose deposition in each voxel. The code was also implemented on a GPU platform.

5.2 GPU-Based MC for Radiobiological Calculations

The use of GPU allowed to develop efficient MC applications specifically oriented to radiobiological purposes. As discussed in Section 3, the quantitative evaluation of radiation damage in biological cells, such as DNA strand breaks and base damage, in general take a considerably long execution time. This is particularly relevant for track structure computations. We report here three interesting examples.

In the work of Kalantzis et al. [247], the authors present an implementation of a MC code for microdosimetric calculations of low energy electrons and protons tracks on a GPU under the above quoted CUDA^® platform developed by NVIDIA^®. Performance and accuracy have been tested on a commercially available general purpose GPU. They also developed a hybrid implementation employing OpenMP (an application program interface (API) used to explicitly direct multi-threaded, shared memory parallelism among CPU cores) and CUDA^® in order to demonstrate the potential of utilizing simultaneously a multi-core CPU and a GPU for further acceleration of the MC simulations.

Another interesting example is reported by Okada et al. [248], where a new MC simulator named MPEXS-DNA is described, allowing high computing performance by using a GPU. The code has been developed for track structure and radiolysis simulations at the subcellular scale. Physics and chemical processes are based on GEANT4-DNA processes available in GEANT4 version 10.02 p03. The validation was performed by comparison with existing experimental data and simulation results obtained by other simulation codes, including PARTRAC [169]. By using NVIDIA^® GPU devices adopting the Volta architecture, MPEXS-DNA has achieved speedup factors up to 2,900 against GEANT4-DNA simulations performed with a single CPU core.

Finally, Tsai et al. [249] present a GPU-based fast microscopic MC simulation package, gMicroMC. They also built a human lymphocyte nucleus DNA model and implemented a DNA damage calculation method to compute single- and double-strand breaks of different complexities. The comparison of the simulation results with those generated by GEANT4-DNA gives good agreement. They achieved speedup factors of $\sim$540 times for the entire simulation process, as compared to the computations by GEANT4-DNA executed on a CPU using a single thread.

5.3 Role of Full MC Frameworks

From the amount of literature written about fast simulation frameworks, it is evident that there is a large interest in speeding up calculation codes, as this brings us a step closer to application in a clinical environment. At the same time, we have seen that all fast codes have validated their calculations also by means of comparison with general purpose MC codes. Thus, we can conclude that codes like MCNPX, GEANT, or FLUKA remain important role also for the development of new calculation methods to be adopted in particle therapy. Summarizing, we can conclude that in the context of fast MC developing, there are two main tasks for full general purpose codes:

• To generate realistic pre-generated data bases for track-repeating approaches.

• To serve as validation for accelerated simulation codes.

In the case of phase space file and track-repeating algorithms, attention has to be paid to possible artifacts. The size of pre-calculated samples need to be carefully considered. In fact, when using standard sampling techniques, the very long period in the cycling of random number generation algorithms allows a totally safe margin against the possible repetition of the same events. Instead, when sampling from a file of pre-generated events, which is necessarily limited in size, more attention has to be paid if the same configuration has to be used more than once. In this case, there is the risk of generating fake structures and correlations in the distribution of scored variables.

In addition it has to be remarked that for specific applications going beyond dose calculations, like, for instance, the case of range monitoring, general purpose MC codes still remain the most appropriate tool.

6 Discussion

In this review, we have discussed some of the ongoing research and challenges that remain to be faced in order to improve MC simulations for particle therapy so as to facilitate their use in clinics and in research. One of the challenges is the improvement of nuclear interaction models. In particular, there is still the need of more new experimental data sets of double differential cross section measurements for radiotherapeutic beams and tissue like targets, since this is essential for benchmarking and tuning nuclear interaction models. Although the calculation of physical dose has already reached in most cases a satisfactory level of accuracy, improved models can lead to more accurate biological dose calculations and improved range monitoring methods, not only for carbon and protons but also for new ions like helium and oxygen. New experimental activities designed for this purpose are at present in progress [110].

Another important challenge for MC development concerns the reliability of modeling radiobiological factors in simulations. The coupling with radiobiological models, or databases, may allow to evaluate the onset of initial DNA damages, but the task of treating all later processes governed by radiochemical processes is out of scope, at least in general purpose MC codes. The uncertainties in this context are particularly difficult to mitigate. The experimental radiobiological measurements, which provide results that are the most useful references for RBE evaluation, still exhibit important uncertainties, as demonstrated in the data base of the particle irradiation data ensemble (PIDE) project [250].

Regarding MC-based treatment planning, many interesting developments are ongoing, and MC-based biological dose calculations are entering more and more in the clinical workflow for all patients. Fast MC codes based on GPU-based calculations or special algorithms are very valuable to come a step closer toward MC-based biological treatment planning. However, such fast MC calculations should always be carefully validated with full MC codes, which then maintain their important role.

There are certainly other topics which are still relevant to the development of MC simulations in particle therapy that we have not considered in this review. For instance, we have not discussed the possible benefits related to improving the description of patient composition in MC simulations, through new imaging techniques. Currently, MC simulations of all processes in patients are based on CT scans. When hadronic interactions are relevant, the actual nuclear composition of tissues has a relevance. Parameterization as a function of CT Hounsfield numbers, like the one by Schneider et al. [251], provides mean values. Improvements could derive by the adoption of imaging techniques with a higher resolving power in distinguishing material differences, like Dual Energy computed tomography (DECT) or multi-energy computed tomography (MECT). Research and development on new approaches like proton-CT can be also an alternative solution. Also, much research is ongoing to how to simulate time-dependent geometries (4D-MC simulations) to include motion effects in dose calculations, which was not treated in this review. There are also some arguments which are related to quality control, dosimetry, and microdosimetry which surely benefit from the use of MC. New developments in this direction are ongoing [252]. Last, but not least, we have not entered in the discussion about the importance of easy user interfaces for MC codes. Several interesting developments in this context are ongoing [21, 22, 253]. Examples on this subject, in view of clinical application of MC in proton therapy, have been recently published [254–256]. The spread of MC tools in clinical practice can be also facilitated providing nonexpert users with clear tutorials and easy installation procedures.

Despite the important progresses achieved so far in the application of MC simulations in particle therapy, we are still far away from efficient MC simulation codes that can model the physical interactions and biological response of tissue at multi-scale level, that is, from the level of DNA segments (nm) to large populations of cells (cm). Such MC codes should include simulation of physical, physicochemical, and chemical processes in human tissue, within short time scales and without the need of enormous computing resources. It is also clear that MC tools, for their nature, need to be continuously improved and maintained, also from the point of view of computing technology. Frequent code upgrades, close collaboration, and resources are also necessary to further improve the usage of MC calculations. Not only developers but also users of MC simulations in particle therapy can contribute by validating their simulation framework with measurements, whereby it is essential that the beam model and dose delivery system are accurately simulated. Finally, the diversity of the literature studied in this review highlights the need for a balanced multidisciplinary multi-scale approach to realize such codes, combining physics, biology, chemistry, medicine, and computing. Bridging the gaps between the various research fields is therefore of prime importance for the development of efficient MC tools in particle therapy.

7 Conclusion

Having access to accurate MC simulation codes is considered crucial in particle therapy, not only because such codes provide more accurate calculations of dose in patients but also in several research fields including range verification techniques, neutron dose calculations, modeling of biological effects, and research to new treatment techniques. In this review, we have discussed a few of the challenges that are to be faced before MC simulations can be widely and efficiently used by the particle therapy community. Improving nuclear interaction physics models, radiobiological modeling, MC-based treatment planning, and development in fast MC codes are the topics selected for this review, but many other topics remain to be addressed.

We have tried to emphasize how the successful development of these codes is a task that need a multidisciplinary approach, as in fact is true for the whole subject of particle therapy. Applied nuclear physicists can have an important role in bringing the particle physics community a step closer toward an efficient use of MC simulations. In particular, the expertise and data from nuclear physics experiments are very important to improve the radiobiological modeling of tissue response to particle treatments in MC simulations.

Author Contributions

SM promoted this work; GB and AK performed editing and reviewing. AK coordinated the work.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work has been carried out in the context of MC-INFN experiment of INFN. The authors wish to thank A. Schiavi for the useful suggestions and help in reviewing the manuscript.

References

1. Parodi K, Mairani A, Brons S, Hasch B, Sommerer F, Naumann J, et al. Monte Carlo simulations to support start-up and treatment planning of scanned proton and carbon ion therapy at a synchrotron-based facility. Phys Med Biol. (2012). 57:3759–84. doi:10.1088/0031-9155/57/12/3759

CrossRef Full Text | Google Scholar

2. Grassberger C, Daartz J, Dowdell S, Ruggieri T, Sharp G, Paganetti H. Quantification of proton dose calculation accuracy in the lung. Int J Radiat Oncol Biol Phys. (2014). 89:424–30. doi:10.1016/j.ijrobp.2014.02.023

CrossRef Full Text | Google Scholar

3. Schuemann J, Giantsoudi D, Grassberger C, Moteabbed M, Min CH, Paganetti H. Assessing the clinical impact of approximations in analytical dose calculations for proton therapy. Int J Radiat Oncol Biol Phys. (2015). 92:1157–64. doi:10.1016/j.ijrobp.2015.04.006.

CrossRef Full Text | Google Scholar

4. Seco J, Verhaegen F. Monte Carlo techniques in radiation therapy. Boca Raton, FL: CRC Press (2013). 334 p.

Google Scholar

5. Paganetti H. Proton therapy physics. Boca Raton, FL: CRC Press (2012). 691 p.

Google Scholar

6. Paganetti H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Phys Med Biol. (2012). 57:R99–117. 10.1088/0031-9155/57/11/R99

CrossRef Full Text | Google Scholar

7. Dedes G, Parodi K. Monte Carlo simulations of particle interactions with tissue in carbon ion therapy. Int J Part Ther. (2015). 2:447–58. 10.14338/IJPT-15-00021

CrossRef Full Text | Google Scholar

8. Kraan AC. Range verification methods in particle therapy: underlying physics and Monte Carlo modeling. Front Oncol. (2015). 5:150. doi:10.3389/fonc.2015.00150.

PubMed Abstract | CrossRef Full Text | Google Scholar

9. El Naqa I, Pater P, Seuntjens J. Monte Carlo role in radiobiological modelling of radiotherapy outcomes. Phys Med Biol. (2012). 57:R75–97. doi:10.1088/0031-9155/57/11/R75.

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Jia1 X, Pawlicki T, Murphy K, Mundt A. Proton therapy dose calculations on GPU: advances and challenges. Transl Canc Res. (2012). 1:207–16. doi:10.3978/j.issn.2218-676X.2012.10.03

CrossRef Full Text | Google Scholar

11. Zyla P, Barnett R, Beringer J, Dahl O, Dwyer DA, Groom DE, et al. The review of particle physics. Prog Theor Exp Phys. (2020). 2020:083C01. doi:10.1093/ptep/ptaa104

CrossRef Full Text | Google Scholar

12. Durante M, Paganetti H. Nuclear physics in particle therapy: a review. Rep Prog Phys. (2016). 79:096702. doi:10.1088/0034-4885/79/9/096702.

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. GEANT4 - a simulation toolkit. Nucl Instrum Methods. (2003). 506:250–303. doi:10.1016/S0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

14. Allison J, Amako K, Apostolakis J, Araujo H, Arce P, Asai M, et al. GEANT4 developments and applications. IEEE Trans Nucl Sci. (2006). 53:270–8. doi:10.1109/TNS.2006.869826

CrossRef Full Text | Google Scholar

15. Allison J, Amako K, Apostolakis J, Arce P, Asai M, Aso T, et al. Recent development in GEANT4. Nucl Instrum Methods A. (2016). 835:186–225. doi:10.1016/j.nima.2016.06.125

CrossRef Full Text | Google Scholar

16.GEANT4. GEANT4 physics list. (2019). Available from: https://geant4.web.cern.ch/node/628.

17. Bleicher M, Zabrodin E, Spieles C, Bass S, Ernst C, Soff S, et al. Relativistic hadron-hadron collisions in the ultra-relativistic quantum molecular dynamics model. J Phys G. (1999). 25:1859. doi:10.1088/0954-3899/25/9/308

CrossRef Full Text | Google Scholar

18. Niita K, Chiba S, Maruyama S, Maruyama T, Takada H, Fukahori T, et al. Analysis of the (N,xN) reactions by quantum molecular dynamics plus statistical decay model. Phys Rev C. (1995). 52:2620–35. doi:10.1103/physrevc.52.2620

CrossRef Full Text | Google Scholar

19. Sorge H. Flavor production in Pb(160 AGeV) on Pb collisions: effect of color ropes and hadronic rescattering. Phys Rev C. (1995). 52:3291.

Google Scholar

20. Mancini-Terracciano C, Asai M, Caccia B, Cirrone G, Dotti A, Faccini R, et al. Preliminary results coupling stochastic mean field and Boltzmann-Langevin One Body models with GEANT. Phys Med. (2019). 67:116–22. doi:10.1016/j.ejmp.2019.10.026

CrossRef Full Text | Google Scholar

21. Perl J, Shin J, Schumann J, Faddegon B, Paganetti H. TOPAS: an innovative proton Monte Carlo platform for research and clinical applications. Med Phys. (2012). 39:6818–37. doi:10.1118/1.4758060.

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Faddegon B, Ramos-Méndeza J, Schuemann J, McNamara A, Shin J, Perl J, et al. The TOPAS tool for particle simulation, a Monte Carlo simulation tool for physics, biology and clinical research. Phys Med. (2020). 72:114–21. doi:10.1016/j.ejmp.2020.03.019

CrossRef Full Text | Google Scholar

23. Jan S, Santin G, Strul D, Staelens S, Assié K, Autret D, et al. Gate: a simulation toolkit for pet and spect. Phys Med Biol. (2004). 49:4543–61. doi:10.1088/0031-9155/49/19/007.

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Grevillot L, Bertrand D, Dessy F, Freud N, Sarrut D. A Monte Carlo pencil beam scanning model for proton treatment plan simulation using GATE/GEANT4. Phys Med Biol. (2011). 56:5203–19. doi:10.1088/0031-9155/56/16/008.

PubMed Abstract| CrossRef Full Text | Google Scholar

25. Jan S, Frisson T, Sarrut D. Gate simulation of 12c hadrontherapy treatment combined with a pet imaging system for dose monitoring: a feasibility study. IEEE Trans Nucl Sci. (2013). 60:423–9. doi:10.1109/TNS.2012.2233496

CrossRef Full Text | Google Scholar

26. Resch A, Elia A, Fuchs H, Carlino A, Palmans H, Stock M, et al. Evaluation of electromagnetic and nuclear scattering models in GATE/GEANT4 for proton therapy. Med Phys. (2019). 46:2444–56. doi:10.1002/mp.13472.

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Arce P, Bolst D, Cutajar D, Guatelli S, Le A, Rosenfeld A, et al. Report on G4-Med, a GEANT4 benchmarking system for medical physics applications developed by the GEANT4 medical simulation benchmarking group. Med Phys. (2020). doi:10.1002/mp.14226.

CrossRef Full Text | Google Scholar

28. Hall D, Makarova A, Paganetti H, Gottschalk B. Validation of nuclear models in GEANT4 using the dose distribution of a 177 MeV proton pencil beam. Phys Med Biol. (2016). 61:N1–10. doi:10.1088/0031-9155/61/1/N1

CrossRef Full Text | Google Scholar

29. Böhlen T, Cerutti F, Chin M, Fassò A, Ferrari PAO, Mairani A, et al. The FLUKA code: developments and challenges for high energy and medical applications. Nucl Data Sheets. (2014). 120:211–4. doi:10.1016/j.nds.2014.07.049

CrossRef Full Text | Google Scholar

30. Ferrari A, Sala P, Fassò A, Ranft J. FLUKA: a multi-particle transport code. CERN (2005). INFN/TC 05/11, SLAC-R-773.

CrossRef Full Text

31. Fassò A, Ferrari A, Ranft J, Sala P. FLUKA: status and prospective for hadronic applications. In: A Kling, F Barāo, M Nakagawa, L Távora, and P Vaz, editors. Proc. MonteCarlo 2000 conference; Berlin, Germany: Springer-Verlag (2001). p. 159–64.

Google Scholar

32. Fassò A, Ferrari A, Ranft J, Sala P. FLUKA: performances and applications in the intermediate energy range. In: P Dragovitsch, S Linn, and M Burbank, editors. Proc. 1 AEN/NEA specialists’ meeting on shielding aspects of accelerators, targets and irradiation facilities (SATIF 1). Paris, France: OECD (1995). p. 287–304.

Google Scholar

33. Ferrari A, Sala P. The physics of high energy reactions. In: A Gandini, and G Reffo, editors. Proc. workshop on nuclear reaction data and nuclear reactors physics, design and safety. Singapore: World Scientific (1998). 424 p.

Google Scholar

34. Ferrari A, Ranft J, Roesler S, Sala P. Cascade particles, nuclear evaporation, and residual nuclei in high energy hadron-nucleus interactions. Eur Phys J C (EPJ C), - Part Fields. (1996). 70:413–26. doi:10.1007/s002880050119

CrossRef Full Text | Google Scholar

35. Cavinato M, Fabrici E, Gadioli E, Erba E, Risi E. Boltzmann master equation theory of angular distributions in heavy-ion reactions. Nucl Phys A. (1998). 643:15–29. doi:10.1016/S0375-9474(98)00545-4

CrossRef Full Text | Google Scholar

36. Sorge H, Stocker H, Greiner W. Relativistic quantum molecular dynamics approach to nuclear collisions at ultrarelativistic energies. Nucl Phys A. (1989). 498:567–76. doi:10.1016/0375-9474(89)90641-6

CrossRef Full Text | Google Scholar

37. Sato T, Iwamoto Y, Hashimoto S, Ogawa T, Furuta T, Abe S, et al. Features of particle and heavy ion transport code system (PHITS) version 3.02. J Nucl Sci Technol. (2018). 55:684–90. doi:10.1080/00223131.2017.1419890

CrossRef Full Text | Google Scholar

38. Sato T, Niita K, Matsuda N, Hashimoto S, Iwamoto Y, Noda S, et al. Particle and heavy ion transport code system PHITS, version 2.52. Nucl Sci Technol. (2013). 50:913–23. doi:10.1080/00223131.2013.814553

CrossRef Full Text | Google Scholar

39. Nara Y, Otuka H, Ohnishi A, Niita K, Chiba S. Relativistic nuclear collisions at 10 AGev energies from p+Be to Au+Au with the hadronic cascade model. Phys Rev C. (2000). 61:024901. doi:10.1103/PhysRevC.61.024901

CrossRef Full Text | Google Scholar

40. Furihata S. Statistical analysis of light fragment production from medium energy proton-induced reactions. Nucl Instrum Methods B. (2000). 171:251–8. doi:10.1016/S0168-583X(00)00332-3

CrossRef Full Text | Google Scholar

41. Iwamoto Y, Sato T, Hashimoto S, Ogawa T, Furuta T, Abe S, et al. Benchmark study of the recent version of the PHITS code. J Nucl Sci Technol. (2017). 54:617–35. doi:10.1080/00223131.2017.1297742

CrossRef Full Text | Google Scholar

42. Goorley T, James M, Booth T, Brown F, Bull J, Cox LJ, et al. Initial MCNP6 release overview MCNP6 version 0.1. Nucl Technol. (2012). 180:298–315. doi:10.13182/NT11-135.

CrossRef Full Text | Google Scholar

43. Yariv Y, Frankel Z. Intranuclear cascade calculation of high- energy heavy-ion interactions. Phys Rev C. (1979). 20:2227–43. doi:10.1103/PhysRevC.20.2227

CrossRef Full Text | Google Scholar

44. Prael R, Bozoian M. Adaption of the multistage preequilibrium model for the Monte Carlo method (1988). LANL. LA-UR-88-3238.

45. Dresner L. Evap - a fortran program for calculating the evaporation of various particles from excited compound nuclei (1962). ORNL. TM196. doi:10.2172/4638868.

CrossRef Full Text | Google Scholar

46. Atchison F. Spallation and fission in heavy metal nuclei under medium energy proton bombardment. In: G Bauer, editor. Meeting on targets for neutron beam spallation sources; 1979 Jun 11–12; Jülich, Germany. Jülich, Germany: Forschungszentrum Jülich (1980). p. 17–46.

Google Scholar

47. Barish J, Gabriel T, Alsmiller FS, Alsmiller RG. HETFIS high-energy nucleon meson transport code with fission (1981). Oak Ridge National Laboratory. ORNL/TM-7882.

Google Scholar

48. Alsmiller FS, Alsmiller RG, Gabriel T, Lillie R, Barish J. A phenomenological model for particle production from the collisions of nucleons and pions with fissile elements at medium energies. Nucl Sci Eng. (1981). 79:147–61. doi:10.13182/NSE81-A27403

CrossRef Full Text | Google Scholar

49. Mashnik S, Sierk A. CEM03.03 user manual (2012). Los Alamos National Laboratory. LA-UR-12-01364.

Google Scholar

50. Gudima KK, Mashnik SG, Toneev VD. Cascade-exciton model of nuclear reactions. JINR Commun. (1980). 80:774–7.

Google Scholar

51. Gudima KK, Mashnik SG, Toneev VD. Cascade-exciton model of nuclear reactions. Nucl Phys A. (1983). 401:329–61. doi:10.1016/0375-9474(83)90532-8

CrossRef Full Text | Google Scholar

52. Boudard A, Cugnon J, Leray S, Volant C. Intranuclear cascade model for a comprehensive description of spallation reaction data. Phys Rev C. (2002). 66:044615. doi:10.1103/PhysRevC.66.044615

CrossRef Full Text | Google Scholar

53. Gaimard J, Schmidt K. A reexamination of the abrasion-ablation model for the description of the nuclear fragmentation reactions. Nucl Phys A. (1991). 531:709–45. doi:10.1016/0375-9474(91)90748-U

CrossRef Full Text | Google Scholar

54. Junghans A, de Jong M, Clerc H, Ignatyuk A, Kudyaev G, Schmidt K. Projectile-fragment yields as a probe for the collective enhancements in the nuclear level density. Nucl Phys A. (1998). 629:635–55. doi:10.1016/S0375-9474(98)00658-7

CrossRef Full Text | Google Scholar

55. Hansen DC, Lühr A, Sobolevsky N, Bassler N. Optimizing SHIELD-HIT for carbon ion treatment. Phys Med Biol. (2012). 57:2393–409. doi:10.1088/0031-9155/57/8/2393.

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Bassler N, Hansen D, Lühr A, Thomsen B, Petersen J, Sobolevsky N. SHIELD-HIT12A - a Monte Carlo particle transport program for ion therapy research. J Phys: Conf. Ser. (2014). 489:012004. doi:10.1088/1742-6596/489/1/012004

CrossRef Full Text | Google Scholar

57. Botvina AS, Dementyev AV, Smirnova ON, Sobolevsky NM, Toneev VD. International codes and model intercomparison for intermediate energy activation yields (1997). NEA/OECD. NSC/DOC (97)-1.

Google Scholar

58. Toneev VD, Gudima KK. Particle emission in light and heavy ion reactions. Nucl Phys A. (1983). 400:173–89. doi:10.1016/0375-9474(83)90433-5

CrossRef Full Text | Google Scholar

59. Amelin NS, Gudima KK, Toneev VD. Further development of the quark-gluon strings model for describing high-energy collisions with nuclear target. Sov J Nucl Phys. (1990). 52:172–8.

Google Scholar

60. Amelin NS, Gudima KK, Toneev VD. Further development of the quark-gluon strings model for describing high-energy collisions with nuclear target. Yad Fiz. (1990). 52:272.

Google Scholar

61. Gudima KK, Mashnik SG, Toneev VD. Cascade-exciton model of nuclear reactions (1976). Nuclear Physics and Radiation Physics. ZFK--324.

Google Scholar

62. Botvina AS, Iljinov AS, Mishustin IN, Bondorf JP, Donangelo R, Sneppen K. Statistical simulation of the break-up of highly excited nuclei. Nucl Phys. (1987). 475:663–86. doi:10.1016/0375-9474(87)90232-6

CrossRef Full Text | Google Scholar

63. Böhlen TT, Cerutti F, Dosanjh M, Ferrari A, Gudowska I, Mairani A, et al. Benchmarking nuclear models of FLUKA and GEANT4 for hadron therapy. Phys Med Biol. (2010). 55:5833–47. doi:10.1088/0031-9155/55/19/014

CrossRef Full Text | Google Scholar

64. Mirandola A, Molinelli S, Vilches Freixas G, Mairani A, Gallio E, Panizza D, et al. Dosimetric commissioning and quality assurance of scanned ion beams at the Italian national center for oncological hadrontherapy. Med Phys. (2015). 42:5287. doi:10.1118/1.4928397.

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Sommerer F, Parodi K, Ferrari A, Poljanc K, Enghardt W, Aiginger H. Investigating the accuracy of the FLUKA code for transport of therapeutic ion beams in matter. Phys Med Biol. (2006). 51:4385–98. doi:10.1088/0031-9155/51/17/017

CrossRef Full Text | Google Scholar

66. Lechner A, Ivanchenko VN, Knobloch J. Validation of recent GEANT4 physics models for application in carbon ion therapy. Nucl Instrum Methods B. (2010). 268:2343–54. doi:10.1016/j.nimb.2010.04.008

CrossRef Full Text | Google Scholar

67. Tessonnier T, Mairani A, Brons S, Sala P, Cerutti F, Ferrari A, et al. Helium at the Heidelberg ion beam facility center: comparisons between FLUKA MC code predictions and dosimetric measurements. Phys Med Biol. (2017). 62:6784–803. doi:10.1088/1361-6560/aa7b12

CrossRef Full Text | Google Scholar

68. Tessonnier T, Mairani A, Brons S. Experimental dosimetric comparison of ¹H, ⁴He, ¹²C and ¹⁶O scanned ion beams. Phys Med Biol. (2017). 62:3958–82. doi:10.1088/1361-6560/aa6516

CrossRef Full Text | Google Scholar

69. Pfuhl U, Horst F, Weber U. Dose build-up effects induced by delta electrons and target fragments in proton Bragg curves - measurements and simulations. Phys Med Biol. (2018). 63:175002. doi:10.1088/1361-6560/aad8fc

CrossRef Full Text | Google Scholar

70. Knopf A, Lomax A. In vivo proton range verification: a review. Phys Med Biol. (2013). 58:R131–160. doi:10.1088/0031-9155/58/15/R131

CrossRef Full Text | Google Scholar

71. Parodi K, Polf JC. In vivo range verification in particle therapy. Med Phys. (2018). 45:e1036. doi:10.1002/mp.12960.

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Zhu X, El Fahkri G. Proton therapy verification with PET imaging. Theranostics. (2013). 3:731–40. doi:10.7150/thno.5162

CrossRef Full Text | Google Scholar

73. Krimmer J, Dauvergne D, Létang J, Testa E. Prompt-gamma monitoring in hadrontherapy: a review. Nucl Instrum Methods Phys Res Sect A Accel Spectrom Detect Assoc Equip. (2017). 10:1016. doi:10.1016/j.nima.2017.07.063

CrossRef Full Text | Google Scholar

74. Capote R, Herman M, Oblozinsky P, Young P, Goriely S, Belgya T, et al. RIPL – reference input parameter library for calculation of nuclear reactions and nuclear data evaluations. Nucl Data Sheets. (2009). 110:3107–214. doi:10.1016/j.nds.2009.10.004

CrossRef Full Text | Google Scholar

75. Amaldi U, Hajdas W, Iliescu S, Malakhov N, Samaratti J, Sauli F, et al. Advanced quality assurance for CNAO. Nucl Instrum Methods A. (2010). 617:248–9. doi:10.1016/j.nima.2009.06.087

CrossRef Full Text | Google Scholar

76. Piersanti L, Bellini F, Bini F, Collamati F, De Lucia E, Durante M, et al. Measurement of charged particle yields from PMMA irradiated by a 220 MeV/u C beam. Phys Med Biol. (2012). 59:1857–72. doi:10.1088/0031-9155/59/7/1857

CrossRef Full Text | Google Scholar

77. Dudouet J, Juliani D, Labalme M, Cussol D, Angélique J, Braunn B, et al. Double-differential fragmentation cross-section measurements of 95 MeV/nucleon C beams on thin targets for hadron therapy. Phys Rev C. (2013). 88:024606. doi:10.1103/PhysRevC.88.024606

CrossRef Full Text | Google Scholar

78. Divay C, Colin J, Cussol D, Finck C, Karakaya Y, Labalme M, et al. Differential cross section measurements for hadron therapy: 50 MeV/nucleon C reactions on H, C, O, Al, and Ti targets. Phys Rev C. (2017). 95:044602. doi:10.1103/PhysRevC.95.044602

CrossRef Full Text | Google Scholar

79. Chadwick M, Herman M, Oblozinsky P, Dunn ME, Danon Y, Kahler A, et al. ENDF/B-VII.1 nuclear data for science and technology: cross sections, covariances, fission product yields and decay data. Nucl Data Sheets. (2011). 112:2887–996. doi:10.1016/j.nds.2011.11.002

CrossRef Full Text | Google Scholar

80.JENDL. JENDL (2011). Available from: http://wwwndc.jaea.go.jp/jendl/jendl.html.

Google Scholar

81. Schneider U, Lomax A, Timmermann B. Second cancers in children treated with modern radiotherapy techniques. Radiother Oncol. (2008). 89:135–40. doi:10.1016/j.radonc.2008.07.017.

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Newhauser WD, Fontenot JD, Mahajan A, Kornguth D, Stovall M, Zheng Y, et al. The risk of developing a second cancer after receiving craniospinal proton irradiation. Phys Med Biol. (2009). 54:2277–91. doi:10.1088/0031-9155/54/8/002.

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Newhauser WD, Durante M. Assessing the risk of second malignancies after modern radiotherapy. Nat Rev Canc. (2011). 11:438–48. doi:10.1038/nrc3069.

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Schneider U, Hälg R. The impact of neutrons in clinical proton therapy. Front Oncol. (2015). 5:235. doi:10.3389/fonc.2015.00235.

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Hälg R, Schneider U. Neutron dose and its measurement in proton therapy-current state of knowledge. Br J Radiol. (2020). 93:20190412. doi:10.1259/bjr.20190412.

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Barth RF, Soloway AH, Fairchild RG. Boron neutron capture therapy of cancer. Canc Res. (1990). 50:1061.

PubMed Abstract | Google Scholar

87. Barth R. A critical assessment of boron neutron capture therapy: an overview. J Neuro Oncol. (2003). 62:1–5. doi:10.1007/BF02699929

CrossRef Full Text | Google Scholar

88.Team XMC. MCNP - a general Monte Carlo n-particle transport code, version 5,- volume I: overview and theory (2003). Los Alamos National Laboratory. Tech. Rep. LA-UR-03-1987.

Google Scholar

89. Goorley J, Kiger W, Zamenhof RGR. Reference dosimetry calculations for neutron capture therapy with comparison of analytical and voxel models. Med Phys. (2002). 29:145–56. doi:10.1118/1.1428758

CrossRef Full Text | Google Scholar

90. Kumada H, Yamamoto K, Matsumura A, Yamamoto T, Nakagawa Y. Development of JCDS, a computational dosimetry system at JAEA for boron neutron capture therapy. J Phys Conf. 74 (2007). 012010. doi:10.1088/1742-6596/74/1/021010

CrossRef Full Text | Google Scholar

91. Chen Z, Yang P, Lei Q, Wen Y, He D, Wu Z, et al. Comparison of BNCT dosimetry calculations using different GEANT4 physics lists. Radiat Protect Dosim. (2019). 187:88–97. doi:10.1093/rpd/ncz144.

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Herrera MS, González SJ, Minsky DM, Kreiner AJ. Evaluation of performance of an accelerator-based BNCT facility for the treatment of different tumor targets. Phys Med. (2013). 29:436. doi:10.1016/j.ejmp.2013.01.006.

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Bortolussi S, Altieri S. Thermal neutron irradiation field design for boron neutron capture therapy of human explanted liver. Med Phys. (2007). 34:4700. doi:10.1118/1.2795831.

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Norbury J, Miller J, Adamczyk A, Heilbronn L, Townsend L, Blattnig S, et al. Nuclear data for space radiation. Radiat Meas. (2012). 12:315–63. doi:10.1016/j.radmeas.2012.03.004

CrossRef Full Text | Google Scholar

95. Sihver L, Lantz M, Takechi M, Kohama A, Ferrari A, Cerutti F, et al. A comparison of total reaction cross section models used in particle and heavy ion transport codes. Adv Space Res. (2012). 49:812–9. doi:10.1016/j.asr.2011.11.029

CrossRef Full Text | Google Scholar

96. Bauhoff W. Tables of reaction and total cross sections for proton-nucleus scattering below 1 GeV. Atomic Data Nucl Data Tables. (1986). 35:429–47. doi:10.1016/0092-640X(86)90016-1

CrossRef Full Text | Google Scholar

97. Nakamura T, Heilbronn L. Handbook on secondary particle production and transport. Singapore: World Scientific (2006). p. 236.

Google Scholar

98. Horst F, Schuy C, Weber U. Measurements of He charge and mass changing cross sections for He+C collisions in the energy range 80-220 MeV/u for applications in ion beam therapy. Phys Rev C. (2017). 96:024624. doi:10.1103/PhysRevC.96.024624

CrossRef Full Text | Google Scholar

99. Horst F, Arico G, Brinkman K, Brons S, Ferrari A, Haberer T, et al. Measurements of He charge and mass changing cross sections on H,C, O, and Si targets in the energy range 70-220 MeV/u for radiation transport calculations in ion-beam therapy. Phys Rev C. (2019). 99:014603. doi:10.1103/PhysRevC.99.014603

CrossRef Full Text | Google Scholar

100. Kox S, Gamp A, Cherkaoui R, Cole AJ, Longequeue N, Menet J, et al. Direct measurements of heavy ion total reaction cross section at 30 and 83 MeV/nucleon. Nucl Phys A. (1984). 420:162–72. doi:10.1016/0375-9474(84)90663-8

CrossRef Full Text | Google Scholar

101. Kox S, Gamp A, Perrin C, Arvieux J, Bertholet R, Bruandet JF, et al. Trends of total reaction cross sections for heavy ion collisions in the intermediate energy range. Phys Rev C. (1987). 35:1678–91. doi:10.1103/physrevc.35.1678

CrossRef Full Text | Google Scholar

102. Takechi M, Fukuda M, Mihara M, Tanaka K, Chinda T, Matsumasa T, et al. Reaction cross sections at intermediate energies and Fermi-motion effects. Phys Rev C. (2009). 79:061601. doi:10.1103/PhysRevC.79.061601

CrossRef Full Text | Google Scholar

103. Toshito T, Kodama K, Sihver L, Yusa K, Ozaki M, Amako K, et al. Measurements of total and partial change-changing cross sections for 200 and 400 MeV/nucleon C on water and polycarbonate. Phys Rev C. (2007). 75:054606. doi:10.1103/PhysRevC.75.054606

CrossRef Full Text | Google Scholar

104. De Napoli M, Agodi C, Battistoni G, Blancato A, Cirrone G, Cuttone G, et al. Carbon fragmentation measurements and validation of the GEANT4 nuclear reaction models for hadron therapy. Phys Med Biol. (2012). 57:7651. doi:10.1088/0031-9155/57/22/7651

CrossRef Full Text | Google Scholar

105. Mattei I, Alexandrov A, Alunni Solestizi L, Ambrosi G, Argirò S, Bartosik N, et al. Measurement of C fragmentation cross sections on C, O, and H in the energy range of interest for particle therapy applications. IEEE Trans Radiat Plasma Med Sci. (2020). 4:269. doi:10.1109/TRPMS.2020.2972197

CrossRef Full Text | Google Scholar

106. Braunn B, Boudard A, Colin J, Cugnon J, Cussol D, David J, et al. Comparisons of hadrontherapy-relevant data to nuclear interaction codes in the GEANT4 toolkit. J Phys Conf. (2013). 420:1. doi:10.1088/1742-6596/420/1/012163

CrossRef Full Text | Google Scholar

107. Dudouet J, Cussol D, Durand D, Labalme M. Benchmarking GEANT4 nuclear models for hadron therapy with 95 MeV/nucleon carbon ions. Phys Rev C. (2014). 89:054616. doi:10.1103/PhysRevC.89.054616

CrossRef Full Text | Google Scholar

108. Tsai P, Lai B, Heilbronn L, Sheu R. Benchmark of neutron production cross sections with Monte Carlo codes. Nucl Instrum Methods Phys Res B. (2018). 416:16–29. doi:10.1016/j.nimb.2017.11.029

CrossRef Full Text | Google Scholar

109. Braunn B, Boudard A, David J. Assessment of nuclear-reaction codes for proton induced reactions on light nuclei below 250 MeV. Eur Phys J Plus. (2015). 130:153. 10.1140/epjp/i2015-15153-x

CrossRef Full Text | Google Scholar

110. Spighi R, Alexandrov A, Alpat B, Ambrosi G, Argirò S, Battistoni G, et al. Foot: fragmentation of target experiment. Nuovo Cim C. (2019). 42:134.

Google Scholar

111. Schall I, Schardt D, Geissel H, Irnich H, Kankeleit E, Kraft G, et al. Charge-changing nuclear reactions of relativistic light-ion beams (5Z10) passing through thick absorbers. Nucl Instrum Methods B. (1996). 117:221–34. doi:10.1016/0168-583X(96)00325-4

CrossRef Full Text | Google Scholar

112. Haettner E, Iwase H, Schardt D. Experimental fragmentation studies with C therapy beams. Radiat Protect Dosim. (2006). 122:485. doi:10.1093/rpd/ncl402

CrossRef Full Text | Google Scholar

113. Haettner E, Iwase H, Krämer M, Kraft G, Schardt D. Experimental study of nuclear fragmentation of 200 and 400 Mev/u C ions in water for applications in particle therapy. Phys Med Biol. (2013). 58:8265–79. doi:10.1088/0031-9155/58/23/8265.

CrossRef Full Text | Google Scholar

114. Golovchenko A, Skvarc J, Yasuda N, Giacomelli M, Tretyakova SP, Ilić R, et al. Total charge-changing and partial cross-section measurements in the reactions of 110-250 MeV/nucleon C in carbon, paraffin and water. Phys Rev C. (2002). 66:014609. doi:10.1103/PhysRevC.66.014609

CrossRef Full Text | Google Scholar

115. Golovchenko A, Skvarc J, Yasuda N, Giacomelli M, Tretyakova SP, Ilić R, et al. Erratum: total charge-changing and partial cross-section measurements in the reactions of 110-250 MeV/nucleon C in carbon, paraffin and water. Phys Rev C. (2002). 66:039901. doi:10.1103/PhysRevC.66.039901

CrossRef Full Text | Google Scholar

116. Puchalska M, Tessonnier T, Parodi K, Sihver L. Benchmarking of PHITS for carbon ion therapy. Int J Part Ther. (2018). 4:48. doi:10.14338/IJPT-17-00029.1

CrossRef Full Text | Google Scholar

117. Gunzert-Marx K, Iwase H, Schardt D, Simon R. Secondary beam fragments produced by 200 MeV u C ions in water and their dose contributions in carbon ion radiotherapy. New J Phys. (2008). 10:075003. doi:10.1088/1367-2630/10/7/075003

CrossRef Full Text | Google Scholar

118. Aricò G, Gehrke T, Jakubek J, Gallas R, Berke S, Jäkel O, et al. Investigation of mixed ion fields in the forward direction for 220.5 MeV/u helium ion beams: comparison between water and PMMA targets. Phys Med Biol. (2017). 62:8003–24. doi:10.1088/1361-6560/aa875e.

CrossRef Full Text | Google Scholar

119. De Napoli M, Romano F, D’Urso D, Licciardello T, Agodi C, Candiano G, et al. Nuclear reaction measurements on tissue-equivalent materials and GEANT4 Monte Carlo simulations for hadrontherapy. Phys Med Biol. (2014). 59:7643. doi:10.1088/0031-9155/59/24/7643

CrossRef Full Text | Google Scholar

120. Aricò G, Gehrke T, Gallas R, Mairani A, Jäkel O, Martišíková M. Investigation of single carbon ion fragmentation in water and PMMA for hadron therapy. Phys Med Biol. (2019). 64:055018. doi:10.1088/1361-6560/aafa46

CrossRef Full Text | Google Scholar

121. Rinaldi I, Ferrari A, Mairani A, Paganetti H, Parodi K, Sala P. An integral test of FLUKA nuclear models with 160 MeV proton beams in multi-layer Faraday cups. Phys Med Biol. (2011). 56:4001–11. doi:10.1088/0031-9155/56/13/016

CrossRef Full Text | Google Scholar

122. Henkner K, Sobolevsky N, Jäkel O, Paganetti H. Test of the nuclear interaction model in SHIELD-HIT and comparison to energy distributions from GEANT4. Phys Med Biol. (2009). 54:N509–N517. doi:10.1088/0031-9155/54/22/N01.

CrossRef Full Text | Google Scholar

123. Mascia A, De Marco J, Chow P, Solberg T. Benchmarking of the MCNPX nuclear interaction models for use in the proton therapy energy range. Proc. 14th ICCR; Seoul, South Korea. Piscataway, NJ:IEEE Nuclear and Plasma Sciences Society (2004)). 478–81.

124. Zacharatou Jarlskog C, Paganetti H. Physics setting for using GEANT4 toolkit in proton therapy. IEEE Trans Nucl Sci. (2008). 55:1018–25. doi:10.1109/TNS.2008.922816

CrossRef Full Text | Google Scholar

125. Rovituso M, Schuy C, Weber U, Brons S, Cortés-Giraldo M, La Tessa C, et al. Fragmentation of 120 and 200 MeV/u He ions in water and PMMA targets. Phys Med Biol. (2017). 62:1310–26. doi:10.1088/1361-6560/aa5302

CrossRef Full Text | Google Scholar

126. Marafini M, Paramatti R, Pinci D, Battistoni G, Collamati F, De Lucia E, et al. Secondary radiation measurements for particle therapy applications: nuclear fragmentation produced by He ion beams in a PMMA target. Phys Med Biol. (2017). 62:1291–309. doi:10.1088/1361-6560/aa5307

CrossRef Full Text | Google Scholar

127. Sihver L, Giacomelli M, Ota S, Skvarc J, Yasuda N, Ilic R, et al. Projectile fragment emission angles in fragmentation reactions of light ions in the energy region 200 MeV/nucleon: experimental study. Radiat Meas. (2013). 48:73–81. doi:10.1016/j.radmeas.2012.08.006

CrossRef Full Text | Google Scholar

128. Matsufuji N, Fukumura A, Komori M, Kanai T, Kohno T. Influence of fragment reaction of relativistic heavy charged particles on heavy-ion radiotherapy. Phys Med Biol. (2003). 48:1605–23. doi:10.1088/0031-9155/48/11/309.

CrossRef Full Text | Google Scholar

129. Gowsch K, Hartmann B, Jakubek J, Granja C, Soukup P, Jäkel O, et al. Non-invasive monotoring of therapeutic carbon ion beams in a homogeneous phantom by tracking of secondary ions. Phys Med Biol. (2013). 58:3755–73. doi:10.1088/0031-9155/58/11/3755

CrossRef Full Text | Google Scholar

130. Matsufuji N, Komori M, Sasaki H, Akiu K, Ogawa M, Fukumura A, et al. Spatial fragment distribution from a therapeutic pencil-like carbon beam in water. Phys Med Biol. (2005). 50:3393–403. doi:10.1088/0031-9155/50/14/014.

CrossRef Full Text | Google Scholar

131. Schardt D, Schall I, Geissel H, Irnich H, Kraft G, Magel A, et al. Nuclear fragmentation of high-energy heavy-ion beams in water. Adv Space Res. (1996). 17:87–94. doi:10.1016/0273-1177(95)00516-h.

CrossRef Full Text | Google Scholar

132. España S, Zhu X, Daartz J, El Fakhri G, Bortfeld T, Paganetti H. The reliability of proton-nuclear interaction cross-section data to predict proton-induced pet images in proton therapy. Phys Med Biol. (2011). 56:2687–98. doi:10.1088/0031-9155/56/9/003

CrossRef Full Text | Google Scholar

133. Matsushita K, Nishio T, Takana S, Tsuneda M, Sugiura A, Leki K. Measurement of proton induced target fragmentation cross sections in carbon. Nucl Phys A. (2016). 946:104–16. doi:10.1016/j.nuclphysa.2015.11.007

CrossRef Full Text | Google Scholar

134. Sommerer F, Cerutti F, Parodi K, Ferrari A, Enghardt W, Aiginger H. In-beam PET monitoring of mono-energetic O and C beams: experiments and FLUKA simulations for homogeneous targets. Phys Med Biol. (2009). 54:3979–96. doi:10.1088/0031-9155/54/13/003

CrossRef Full Text | Google Scholar

135. Battistoni G, Bauer J, Böhlen T, Cerutti F, Chin M, et al. The FLUKA code: an accurate simulation tool for particle therapy. Fron Oncol. (2016). 6:116. doi:10.3389/fonc.2016.00116

CrossRef Full Text | Google Scholar

136. Horst F, Adi W, Aricò G, Brinkmann K, Durante M, Reidel M, et al. Measurement of PET isotope production cross sections for protons and carbon ions on carbon and oxygen targets for applications in particle therapy range verification. Phys Med Biol. (2019). 64:205012. doi:10.1088/1361-6560/ab4511

CrossRef Full Text | Google Scholar

137. Ferrero V, Bisogni M, Camarlinghi N, Fiorina E, Giraudo G, Morrocchi M, et al. Double-field hadrontherapy treatment monitoring with the inside in-beam PET scanner: proof of concept. IEEE Trans Radiat Plasma Medical Sci. (2018). 2:588–93. 10.1109/TRPMS.2018.2870478

CrossRef Full Text | Google Scholar

138. Bongrand A, Busato E, Force P, Martin F, Montarou G. Use of short-lived positron emitters for in-beam and real-time β. Phys Med. (2020). 69:248–55. doi:10.1016/j.ejmp.2019.12.015.

CrossRef Full Text | Google Scholar

139. Dendooven P, Buitenhuis H, Diblen F, Heeres PN, Biegun AK, Fiedler F, et al. Short-lived positron emitters in beam-on PET imaging during proton therapy. Phys Med Biol. (2015). 60:8923–47. doi:10.1088/0031-9155/60/23/8923.

CrossRef Full Text | Google Scholar

140. Min C, Kim C. Prompt gamma measurements for locating the dose falloff region in the proton therapy. Appl Phys Lett. (2006). 89:183517. 10.1063/1.2378561

CrossRef Full Text | Google Scholar

141. Le Foulher F, Bajard M, Chevallier M, Dauvergne D, Freud N, Henriquet P, et al. Monte Carlo simulations of prompt-gamma emission during carbon ion irradiation. IEEE Trans Nucl Sci. (2010). 57:2768–72. doi:10.1109/ANIMMA.2009.5503665

CrossRef Full Text | Google Scholar

142.European NoVel Imaging Systems for ION therapy. Envision project. (2012). Available from: https://envision.web.cern.ch/.

Google Scholar

143. Smeets J, Roellinghoff F, Prieels D, Stichelbaut F, Benilov A, Busca P, et al. Prompt gamma imaging with a slit camera for real time range control in proton therapy. Phys Med Biol. (2012). 57:3371–405. doi:10.1088/0031-9155/57/11/3371.

CrossRef Full Text | Google Scholar

144. Pinto M, Bajard M, Brons S, Chevallier M, Dauvergne D, Dedes G, et al. Absolute prompt-gamma yield measurements for ion beam therapy monitoring. Phys Med Biol. (2015). 60:565–94. doi:10.1088/0031-9155/60/2/565

CrossRef Full Text | Google Scholar

145. Dedes G, Pinto M, Dauvergne D, Freud N, Krimmer J, Létang JM, et al. Assessment and improvements of GEANT4 hadronic models in the context of prompt-gamma hadrontherapy monitoring. Phys Med Biol. (2014). 59:1747–72. doi:10.1088/0031-9155/59/7/1747.

CrossRef Full Text | Google Scholar

146. Testa M, Min CH, Verburg JM, Schümann J, Lu H, Paganetti H. Range verification of passively scattered proton beams based on prompt gamma time patterns. Phys Med Biol. (2014). 59:4181–95. doi:10.1088/0031-9155/59/15/4181.

CrossRef Full Text | Google Scholar

147. Pinto M, Dauvergne D, Freud N, Krimmer J, Létang JM, Testa E. Assessment of GEANT4 prompt-gamma emission yields in the context of proton therapy monitoring. Front Oncol. (2016). 28:10. 10.3389/fonc.2016.00010

CrossRef Full Text | Google Scholar

148. Muraro S, Battistoni G, Collamati F, De Lucia E, Faccini R, Ferroni F, et al. Monitoring of hadrontherapy treatments by means of charged particle detection. Front Oncol. (2016). 6:177. doi:10.3389/fonc.2016.00177.

CrossRef Full Text | Google Scholar

149. Traini G, Mattei I, Battistoni G, Bisogni MG, De Simoni M, Dong Y, et al. Review and performance of the dose profiler, a particle therapy treatments online monitor. Phys Med. (2019). 65:84–93. doi:10.1016/j.ejmp.2019.07.010.

CrossRef Full Text | Google Scholar

150. Félix-Bautista R, Gehrke T, Ghesquière-Diérickx L, Reimold M, Amato C, Turecek D, et al. Experimental verification of a non-invasive method to monitor the lateral pencil beam position in an anthropomorphic phantom for carbon-ion radiotherapy. Phys Med Biol. (2019). 64:175019. doi:10.1088/1361-6560/ab2ca3

CrossRef Full Text | Google Scholar

151. Verburg MJ, Riley K, Bortfeld T, Seco J. Energy and time resolved detection of prompt gamma rays for proton range verification. Phys Med Biol. (2013). 58:L37–49. doi:10.1088/0031-9155/58/20/L37

CrossRef Full Text | Google Scholar

152. Verburg J, Seco J. Proton range verification through prompt gamma-ray spectroscopy. Phys Med Biol. (2014). 59:7089–106. doi:10.1088/0031-9155/59/23/7089.

CrossRef Full Text | Google Scholar

153. Polf J, Panthi R, Mackin D, McCleskey M, Saastamoinen A, Roeder B, et al. Measurement of characteristic prompt gamma rays emitted from oxygen and carbon in tissue- equivalent samples during proton beam irradiation. Phys Med Biol. (2013). 58:5821–31. doi:10.1088/0031-9155/58/17/5821.

CrossRef Full Text | Google Scholar

154. Testa E, Bajard M, Chevallier M, Dauvergne D, Le Foulher F, Poizat J, et al. Monitoring the Bragg peak location of 73 MeV/u carbon ion beams by means of prompt gamma-ray measurements. Appl Phys Lett. (2008). 93:093506. doi:10.1063/1.2975841

CrossRef Full Text | Google Scholar

155. Testa E, Bajard M, Chevallier M, Dauvergne D, Le Foulher F, Freud N, et al. Dose profile monitoring with carbon ions by means of prompt-gamma measurements. Nucl Instrum Methods B. (2009). 267:993–6. doi:10.1016/j.nimb.2009.02.031

CrossRef Full Text | Google Scholar

156. Testa M, Bajard M, Chevallier M, Dauvergne D, Freud N, Henriquet P, et al. Real-time monitoring of the Bragg peak position in ion therapy by means of single photon detection. Radiat Environ Biophys. (2010). 49:337–43. doi:10.1007/s00411-010-0276-2.

CrossRef Full Text | Google Scholar

157. Vanstalle M, Mattei I, Sarti A, Bellini F, Bini F, Collamati F, et al. Benchmarking GEANT4 hadronic models for prompt-γ monitoring in carbon ion therapy. Med Phys. (2017). 44:4276–86. doi:10.1002/mp.12348

CrossRef Full Text | Google Scholar

158. Agodi C, Bellini F, Cirrone G, Collamati F, Cuttone G, De Lucia E, et al. Precise measurement of prompt photon emission for carbon ion therapy. J Instrum. (2012). 7:P03001. doi:10.1088/1748-0221/7/03/P03001

CrossRef Full Text | Google Scholar

159. Mattei I, Bini F, Collamati F, De Lucia E, Frallicciardi P, Iarocci E, et al. Secondary radiation measurements for particle therapy applications: prompt photons produced by He, C and O ion beams in a PMMA target. Phys Med Biol. (2017). 62:1438–55. doi:10.1088/1361-6560/62/4/1438

CrossRef Full Text | Google Scholar

160. Agodi C, Battistoni G, Bellini F, Cirrone GAP, Collamati F, Cuttone G, et al. Charged particle’s flux measurement from PMMA irradiated by 80 MeV/u carbon ion beam. Phys Med Biol. (2012). 57:5667–78. doi:10.1088/0031-9155/57/18/5667

CrossRef Full Text | Google Scholar

161. Mattei I, Battistoni G, Collini F, De Lucia E, Durante M, Fiore S, et al. Addendum: measurement of charged particle yields from PMMA irradiated by a 220 MeV/u C beam. Phys Med Biol. (2017). 62:8483. doi:10.1088/1361-6560/aa8b35

CrossRef Full Text | Google Scholar

162. Rucinski A, Battistoni G, Collamati F, De Lucia E, Faccini R, Frallicciardi PM, et al. Secondary radiation measurements for particle therapy applications: charged particles produced by ⁴He and ¹²C ion beams in a PMMA target at large angle. Phys Med Biol. (2018). 63:055018. doi:10.1088/1361-6560/aaa36a

CrossRef Full Text | Google Scholar

163. Rucinski A, Traini G, Baratto Roldan A, Battistoni G, De Simoni M, Dong Y, et al. Secondary radiation measurements for particle therapy applications: charged secondaries produced by ¹⁶O ion beams in a PMMA target at large angles. Phys Med. (2019). 64:45–53. doi:10.1016/j.ejmp.2019.06.001

CrossRef Full Text | Google Scholar

164. Aleksandrov A, Consiglio L, De Lellis G, Di Crescenzo A, Lauria A, Montesi M, et al. Measurement of large angle fragments induced by 400 MeV/u carbon ion beams. Meas Sci Technol. (2015). 26:094001. 10.1088/0957-0233/26/9/094001

CrossRef Full Text | Google Scholar

165. Alexandrov A, De Lellis G, Di Crescenzo A, Lauria A, Montesi M, Pastore A, et al. Measurements of ¹²C ions beam fragmentation at large angle with an emulsion cloud chamber. J Instrum. (2017). 12:P08013. 10.1088/1748-0221/12/08/P08013

CrossRef Full Text | Google Scholar

166. Pshenichnov I, Mishustin I, Greiner W. Distributions of positron-emitting nuclei in proton and carbon-ion therapy studied with GEANT4. Phys Med Biol. (2006). 51:6099–112. doi:10.1088/0031-9155/51/23/011.

CrossRef Full Text | Google Scholar

167. Akagi T, Yagi M, Yamashita T, Murakami M, Yamakawa Y, Kitamura K, et al. Experimental study for the production cross section of positron emitters induced from C and O nuclei by low-energy proton beams. Radiat Meas. (2013). 59:262–9. doi:10.1016/j.radmeas.2013.07.005

CrossRef Full Text | Google Scholar

168. Tommasino F, Scifoni E, Durante M. New ions for therapy. Int J Par Therapy. (2016). 2:428–38. doi:10.14338/IJPT-15-00027.1.

CrossRef Full Text | Google Scholar

169. Dingfelder M, Hantke D, Inokuti M, Paretzke H. Electron inelastic-scattering cross sections in liquid water. Radiat Phys Chem. (1998). 53:1–18. doi:10.1016/S0969-806X(97)00317-4

CrossRef Full Text | Google Scholar

170. Krämer M, Kraft G. Calculations of heavy-ion track structure. Radiat Environ Biophys. (1994). 33:91–109. doi:10.1016/0168-583X(95)00538-2

CrossRef Full Text | Google Scholar

171. Wälzlein C, Krämer M, Scifoni E, Durante M. Advancing the modeling in particle therapy: from track structure to treatment planning. Appl Radiat Isot. (2014). 83:171–6. doi:10.1016/j.apradiso.2013.01.019

CrossRef Full Text | Google Scholar

172. Incerti S, Baldacchino G, Bernal M, Capra R, Champion C, Francis Z, et al. The GEANT4-DNA project. Int J Model Simul Sci Comput. (2010). 1:157–78. doi:10.1142/S1793962310000122

CrossRef Full Text | Google Scholar

173. Schuemann J, McNamara A, Ramos-Méndez J, Perl J, Held K, Paganetti H, et al. TOPAS-nBio: an extension to the TOPAS simulation toolkit for cellular and sub-cellular radiobiology. Radiat Res. (2019). 191:125–38. doi:10.1667/RR15226.1.

CrossRef Full Text | Google Scholar

174. Kellerer A, Rossi H. A generalized formulation of dual radiation action. Radiat Res. (1978). 75:471–88. doi:10.2307/3574835

CrossRef Full Text | Google Scholar

175. Scholz M, Kraft G. Track structure and the calculation of biological effects of heavy charged particles. Adv Space Res. (1996). 18:5–14. doi:10.1016/0273-1177(95)00784-C

CrossRef Full Text | Google Scholar

176. Scholz M, Kellerer A, Kraft-Weyrather W, Kraft G. Computation of cell survival in heavy ion beams for therapy - the model and its approximation. Radiat Environ Biophys. (1997). 36:59–66. doi:10.1007/s004110050055.

CrossRef Full Text | Google Scholar

177. Krämer M, Scholz M. Treatment planning for heavy-ion radiotherapy: calculation and optimization of biologically effective dose. Phys Med Biol. (2000). 45:3319–30.

178. Krämer M, Scholz M. Rapid calculation of biological effects in ion radiotherapy. Phys Med Biol. (2006). 51:1959–70. doi:10.1088/0031-9155/51/8/001.

CrossRef Full Text | Google Scholar

179. Hawkins R. A statistical theory of cell killing by radiation of varying linear energy transfer. Radiat Res. (1994). 140:366–74.

180. Hawkins R. A microdosimetric-kinetic model of cell death from exposure to ionizing radiation of any let, with experimental and clinical application. Int J Radiat Biol. (1996). 69:739–55. doi:10.1080/095530096145481

CrossRef Full Text | Google Scholar

181. Hawkins R. A microdosimetric-kinetic model for the effect of non-Poisson distribution of lethal lesions on the variation of RBE with LET. Radiat Res. (2003). 160:61–9. doi:10.1667/rr3010

CrossRef Full Text | Google Scholar

182. Kase Y, Kanai T, Matsumoto Y, Furusawa Y, Okamoto H, Asaba T, et al. Microdosimetric measurements and estimation of human cell survival for heavy-ion beams. Radiat Res. (2006). 166:629–38. doi:10.1667/RR0536.1.

CrossRef Full Text | Google Scholar

183. Kase Y, Kanai T, Matsufuji N, Furusawa Y, Elsässer T, Scholz M. Biophysical calculation of cell survival probabilities using amorphous track structure models for heavy-ion irradiation. Phys Med Biol. (2008). 53:37–59. doi:10.1088/0031-9155/53/1/003.

CrossRef Full Text | Google Scholar

184. Inaniwa T, Furukawa T, Kase Y, Matsufuji N, Toshito T, Matsumoto Y, et al. Treatment planning for a scanned carbon beam with a modified microdosimetric kinetic model. Phys Med Biol. (2010). 55:6721–37.doi:10.1088/0031-9155/55/22/008.

CrossRef Full Text | Google Scholar

185. Inaniwa T, Kanematsu N, Matsufuji N, Kanai T, Shirai T, Noda K, et al. Reformulation of a clinical-dose system for carbon-ion radiotherapy treatment planning at the national institute of radiological sciences Japan. Phys Med Biol. (2015). 60:3271–86.doi:10.1088/0031-9155/60/8/3271.

CrossRef Full Text | Google Scholar

186. Kase Y, Kanematsu N, Kanai T, Matsufuji N. Biological dose calculation with Monte Carlo physics simulation for heavy-ion radiotherapy. Phys Med Biol. (2006). 51:N467–75. doi:10.1088/0031-9155/51/24/N03.

CrossRef Full Text | Google Scholar

187. Carante M, Aimè C, Tello Cajiao J, Ballarini F. BIANCA, a biophysical model of cell survival and chromosome damage by protons, C-ions and He-ions at energies and doses used in hadrontherapy. Phys Med Biol. (2018). 63:075007. doi:10.1088/1361-6560/aab45f

CrossRef Full Text | Google Scholar

188. Carante M, Aricò G, Ferrari A, Kozlowska W, Mairani A, Ballarini F. First benchmarking of the BIANCA model for cell survival prediction in a clinical hadron therapy scenario. Phys Med Biol. (2019). 64:215008. doi:10.1088/1361-6560/ab490f

CrossRef Full Text | Google Scholar

189. Elsässer T, Weyrather W, Friedrich T, Durante M, Iancu G, Krämer M, et al. Quantification of the relative biological effectiveness for ion beam radiotherapy: direct experimental comparison of proton and carbon ion beams and a novel approach for treatment planning. Int J Radiat Oncol Biol Phys. (2010). 78:1177–83. doi:10.1016/j.ijrobp.2010.05.014

CrossRef Full Text | Google Scholar

190. Fossati P, Molinelli S, Matsufuji N, Ciocca M, Mirandola A, Mairani A, et al. Dose prescription in carbon ion radiotherapy: a planning study to compare NIRS and LEM approaches with a clinically-oriented strategy. Phys Med Biol. (2012). 57:7543–54. doi:10.1088/0031-9155/57/22/7543.

CrossRef Full Text | Google Scholar

191. Molinelli S, Magro G, Mairani A, Matsufuji N, Kanematsu N, Inaniwa T, et al. Dose prescription in carbon ion radiotherapy: how to compare two different RBE-weighted dose calculation systems. Radiother Oncol. (2016). 120:307–12. doi:10.1016/j.radonc.2016.05.031.

CrossRef Full Text | Google Scholar

192. Magro G, Dahle T, Molinelli S, Ciocca M, Fossati P, Ferrari A, et al. The FLUKA Monte Carlo code coupled with the NIRS approach to clinical dose calculation in carbon ion therapy. Phys Med Biol. (2017). 62:3814–27. doi:10.1088/1361-6560/aa642b

CrossRef Full Text | Google Scholar

193. Mein S, Dokic I, Klein C, Tessonnier T, Böhlen T, Magro G, et al. Biophysical modeling and experimental validation of relative biological effectiveness (RBE) for ⁴He ion beam therapy. Radiat Oncol. (2019). 14:123. doi:10.1186/s13014-019-1295-z.

CrossRef Full Text | Google Scholar

194. Wedemberg M, Lind B, Hardemark B. A model for the relative biological effectiveness of protons: the tissue specific parameter of photons is a predictor for the sensitivity to let changes. Acta Oncol. (2013). 52:580–8. doi:10.3109/0284186X.2012.705892

CrossRef Full Text | Google Scholar

195. Wilkens J, Oelfke U. Analytical linear energy transfer calculations for proton therapy. Med Phys. (2003). 30:806–15. doi:10.1118/1.1567852.

CrossRef Full Text | Google Scholar

196. McNamara A, Schuemann J, Paganetti H. A phenomenological relative biological effectiveness (RBE) model for proton therapy based on all published in vitro cell survival data. Phys Med Biol. (2015). 60:8399–416. doi:10.1088/0031-9155/60/21/8399.

CrossRef Full Text | Google Scholar

197. Carabe A, Moteabbed M, Depauw N, Schuemann J, Paganetti H. Range uncertainty in proton therapy due to variable biological effectiveness. Phys Med Biol. (2012). 57:1159–72. doi:10.1088/0031-9155/57/5/1159.

CrossRef Full Text | Google Scholar

198. Scifoni E, Tinganelli W, Kraft-Weyrather W, Durante M, Maier A, Krämer M. Including oxygen enhancement ratio in ion beam treatment planning: model implementation and experimental verification. Phys Med Biol. (2013). 58:3871–95. doi:10.1088/0031-9155/58/11/3871

CrossRef Full Text | Google Scholar

199. Sokol O, Scifoni E, Tinganelli W, Kraft-Weyrather W, Wiedemann J, Maier A, et al. Oxygen beams for therapy: advanced biological treatment planning and experimental verification. Phys Med Biol. (2017). 62:7798–813. doi:10.1088/1361-6560/aa88a0.

CrossRef Full Text | Google Scholar

200. Sokol O, Krämer M, Hild S, Durante M, Scifoni E. Kill painting of hypoxic tumors with multiple ion beams. Phys Med Biol. (2019). 64:045008. doi:10.1088/1361-6560/aafe40.

CrossRef Full Text | Google Scholar

201. Tommasino F, Durante M. Proton radiobiology. Cancers. (2015). 7:353–81. doi:10.3390/cancers7010353

CrossRef Full Text | Google Scholar

202.TIFPA. Modeling and verification for ion beam treatment planning (2020). Available from: http://www.tifpa.infn.it/projects/move-it/.

203. Petringa G, Romano F, Manti L, Pandola L, Attili A, Cammarata F, et al. Radiobiological quantities in proton-therapy: estimation and validation using GEANT4-based Monte Carlo simulations. Phys Med. (2019). 58:72–80. doi:10.1016/j.ejmp.2019.01.018.

CrossRef Full Text | Google Scholar

204. Cirrone G, Manti L, Margarone D, Petringa G, Giuffrida L, Minopoli A, et al. First experimental proof of proton boron capture therapy (PBCT) to enhance protontherapy effectiveness. Sci Rep. (2018). 8:1141. doi:10.1038/s41598-018-19258-5.

CrossRef Full Text | Google Scholar

205. Vozenin MC, Hendry J, Limoli C. Biological benefit of ultra-high dose rate flash radiotherapy: sleeping beauty awoken. Clin Oncol. (2019). 31:407–415. doi:10.1016/j.clon.2019.04.001

CrossRef Full Text | Google Scholar

206. Colangelo NW, Azzam E. The importance and clinical implications of FLASH ultra-high dose-rate studies for proton and heavy ion radiotherapy. Radiat Res. (2020). 193:1–4. doi:10.1667/RR15537.1

CrossRef Full Text | Google Scholar

207. Laboratories R. Raystation carbon ion planning (2020). Available from: http://www.raysearchlabs.com.

Google Scholar

208. Saini J, Maes D, Egan A, Bowen S, St James S, Janson M, et al. Dosimetric evaluation of a commercial proton spot scanning Monte-Carlo dose algorithm: comparisons against measurements and simulations. Phys Med Biol. (2017). 62:7659–81. doi:10.1088/1361-6560/aa82a5.

CrossRef Full Text | Google Scholar

209. Widesott L, Lorentini S, Fracchiolla F, Farace P, Schwarz M. Improvements in pencil beam scanning proton therapy dose calculation accuracy in brain tumor cases with a commercial Monte Carlo algorithm. Phys Med Biol. (2018). 63:145016. doi:10.1088/1361-6560/aac279.

CrossRef Full Text | Google Scholar

210. Lin L, Huang S, Kang M, Hiltunen P, Vanderstraeten R, Lindberg J, et al. A benchmarking method to evaluate the accuracy of a commercial proton Monte Carlo pencil beam scanning treatment planning system. J Appl Clin Med Phys. (2017). 18:44–9. doi:10.1002/acm2.12043.

CrossRef Full Text | Google Scholar

211. Krämer M, Jäkel O, Haberer T, Kraft G, Schardt D, Weber U. Treatment planning for heavy-ion radiotherapy: physical beam model and dose optimization. Phys Med Biol. (2000). 45:3299–317. doi:10.1088/0031-9155/45/11/313.

CrossRef Full Text | Google Scholar

212. Krämer M, Durante M. Ion beam transport calculations and treatment plans in particle therapy. Eur Phys J D. (2010). 60:195–202. doi:10.1140/epjd/e2010-00077-8

CrossRef Full Text | Google Scholar

213. Jäkel O, Krämer M, Karger C, Debus J. Treatment planning for heavy ion radiotherapy: clinical implementation and application. Phys Med Biol. (2001). 46:1101–16. doi:10.1088/0031-9155/46/4/314

CrossRef Full Text | Google Scholar

214. Krämer M. Treatment planning for heavy-ion radiotherapy: biological optimization of multiple beam ports. J Radiat Res. (2001). 42:39–46. 10.1269/jrr.42.39.

CrossRef Full Text | Google Scholar

215. Syngo TPS. Tech. Rep. Manheim, Germany: Siemens AG (2009).

Google Scholar

216. Iancu G, Kraemer M, Zink K, Durante M. Implementation of an efficient Monte Carlo algorithm in TriP: physical dose calculation. Int J Part Therapy. (2015). 2:415–25. 10.14338/IJPT-14-00030.1

CrossRef Full Text | Google Scholar

217. Kanematsu N, Inaniwa T. Treatment planning of carbon-ion radiotherapy. H Tsujii, T Kamada, T Shirai, K Noda, H Tsuji, and K Karsawa, editors. Tokyo, Japan: Springer (2014).

Google Scholar

218. Russo G, Attili A, Battistoni G, Bertrand D, Bourhaleb F, Cappucci F, et al. A novel algorithm for the calculation of physical and biological irradiation quantities in scanned ion beam therapy: the beamlet superposition approach. Phys Med Biol. (2016). 61:183–214. doi:10.1088/0031-9155/61/1/183.

CrossRef Full Text | Google Scholar

219. Manganaro L, Russo G, Cirio R, Dalmasso F, Giordanengo S, Monaco V, et al. A Monte Carlo approach to the microdosimetric kinetic model to account for dose rate time structure effects in ion beam therapy with application in treatment planning simulations. Med Phys. (2017). 44:1577–89. doi:10.1002/mp.12133.

CrossRef Full Text | Google Scholar

220. Mairani A, Böhlen TT, Schiavi A, Tessonnier T, Molinelli S, Brons S, et al. A Monte Carlo-based treatment planning tool for proton therapy. Phys Med Biol. (2013). 58:2471–90. doi:10.1088/0031-9155/58/8/2471.

CrossRef Full Text | Google Scholar

221. Böhlen T, Bauer S, Dosanjh M, Ferrari A, Haberer T, Parodi K, et al. A Monte Carlo-based treatment-planning tool for ion beam therapy. J Radiat Res. (2013). 54:i77–i81. 10.1093/jrr/rrt050

CrossRef Full Text | Google Scholar

222. Böhlen T, Brons S, Dosanjh M, Ferrari A, Fossati P, Haberer T, et al. Investigating the robustness of ion beam therapy treatment plans to uncertainties in biological treatment parameters. Phys Med Biol. (2012). 57:7983–8004. doi:10.1088/0031-9155/57/23/7983.

CrossRef Full Text | Google Scholar

223. Tessonnier T, Böhlen T, Ceruti F, Ferrari A, Sala P, Brons S, et al. Dosimetric verification in water of a Monte Carlo treatment planning tool for proton, helium, carbon and oxygen ion beams at the Heidelberg ion beam therapy center. Phys Med Biol. (2017). 62:6579–94. doi:10.1088/1361-6560/aa7be4.

CrossRef Full Text | Google Scholar

224. Tinganelli W, Durante M, Hirayama R, Krämer M, Maier A, Kraft-Weyrather W, et al. Kill-painting of hypoxic tumours in charged particle therapy. Sci Rep. (2015). 5:17016. doi:10.1038/srep17016.

CrossRef Full Text | Google Scholar

225. Schiavi A, Senzacqua M, Pioli S, Mairani A, Magro G, Molinelli S, et al. Fred: a GPU-accelerated fast-Monte Carlo code for rapid treatment plan recalculation in ion beam therapy. Phys Med Biol. (2017). 62:7482–504. doi:10.1088/1361-6560/aa8134.

CrossRef Full Text | Google Scholar

226. Qin N, Shen C, Tsai M, Pinto M, Tian Z, Dedes G, et al. Full Monte Carlo-based biological treatment plan optimization system for intensity modulated carbon ion therapy on GPU. Int J Radiat Biol Phys. (2018). 100:235–43. 10.1016/j.ijrobp.2017.09.002

CrossRef Full Text | Google Scholar

227.NVIDA Corporation. NVIDA corporation (2020). Available from: http://www.nvidia.com.

Google Scholar

228. Rucinski A, Barana J, Battistoni G, Chrostowska A, Durante M, Gajewski J, et al. Investigations on physical and biological range uncertainties in Kraców proton beam therapy center. Acta Phys Pol B. (2020). 51:9–16. doi:10.5506/APhysPolB.51.9

CrossRef Full Text | Google Scholar

229. Pepin M, Tryggestad E, Seum Wan Chan Tseung H, Johnson JE, Herman MG, Beltran C. A Monte‐Carlo‐based and GPU‐accelerated 4D‐dose calculator for a pencil beam scanning proton therapy system. Med Phys. (2018). 45:5293–304. doi:10.1002/mp.13182

CrossRef Full Text | Google Scholar

230. Seum Wan Chan Tseung H, Ma J, Beltran C. A fast GPU-based Monte Carlo simulation of proton transport with detailed modeling of nonelastic interactions. Med Phys. (2015). 42:2967–78. doi:10.1118/1.4921046

CrossRef Full Text | Google Scholar

231. Ma J, Beltran C, Seum Wan Chan Tseung H, Herman M. A GPU-accelerated and Monte Carlo-based intensity modulated proton therapy optimization system. Med Phys. (2014). 41:121707. doi:10.1118/1.4901522

CrossRef Full Text | Google Scholar

232. Maneval D, Bouchard H, Ozell B, Després P. Efficiency improvement in proton dose calculations with an equivalent restricted stopping power formalism. Phys Med Biol. (2017). 63:015019. doi:10.1088/1361-6560/aa9166

CrossRef Full Text | Google Scholar

233. Jia X, Schümann J, Paganetti H, Jiang SB. GPU-based fast Monte Carlo dose calculation for proton therapy. Phys Med Biol. (2012). 57:7783–97. doi:10.1088/0031-9155/57/23/7783.

CrossRef Full Text | Google Scholar

234. Fippel M, Soukup M. A Monte Carlo dose calculation algorithm for proton therapy. Med Phys. (2004). 31:2263–73. doi:10.1118/1.1769631

CrossRef Full Text | Google Scholar

235. Qin N, Pinto M, Tian Z, Dedes G, Pompos A, Jiang S, et al. Initial development of goCMC: a GPU-oriented fast cross-platform Monte Carlo engine for carbon ion therapy. Phys Med Biol. (2017). 62:3682–99. doi:10.1088/1361-6560/aa5d43.

CrossRef Full Text | Google Scholar

236. Mein S, Choi K, Kopp B, Tessonnier T, Bauer J, Ferrari A, et al. Fast robust dose calculation on GPU for high-precision ¹H, ⁴He, ¹²C and ¹⁶O ion therapy: the FRoG platform. Sci Rep. (2018). 8:14829. doi:10.1038/s41598-018-33194-4

CrossRef Full Text | Google Scholar

237. Martins J, Saxena R, Neppl S, Alhazmi A, Reiner M, Veloza S, et al. Optimization of phase space files from clinical linear accelerators. Phys Med. (2019). 64:54–68. doi:10.1016/j.ejmp.2019.06.007.

CrossRef Full Text | Google Scholar

238. Wang Q, Schlegel N, Moyers M, Lin J, Hong L, Chen H, et al. Validation of the fast dose calculator for Shanghai proton and heavy ion center. Biomed Phys Eng Express. (2018). 4:06500. 10.1088/2057-1976/aae039

CrossRef Full Text | Google Scholar

239. Wang Q, Zhu C, Bai X, Deng Y, Schlegel N, Adair A, et al. Automatic phase space generation for Monte Carlo calculations of intensity modulated particle therapy. Biomed Phys Eng Express. (2020). 6:025001. doi:10.1088/2057-1976/ab7152.

CrossRef Full Text | Google Scholar

240. Li JS, Shahine B, Fourkal E, Ma CM. A particle track-repeating algorithm for proton beam dose calculation. Phys Med Biol. (2005). 50:1001–10. doi:10.1088/0031-9155/50/5/022

CrossRef Full Text | Google Scholar

241. Yepes PP, Eley JG, Liu A, Mirkovic D, Randeniya S, Titt U, et al. Validation of a track repeating algorithm for intensity modulated proton therapy: clinical cases study. Phys Med Biol. (2016). 61:2633–45. doi:10.1088/0031-9155/61/7/2633.

CrossRef Full Text | Google Scholar

242. Yepes PP, Mirkovic D, Taddei PJ. A GPU implementation of a track-repeating algorithm for proton radiotherapy dose calculations. Phys Med Biol. (2010). 55:7107–20. doi:10.1088/0031-9155/55/23/S11.

CrossRef Full Text | Google Scholar

243. Jabbari J, Seuntjens J. A fast Monte Carlo code for proton transport in radiation therapy based on MCNPX. Med Phys. (2014). 39:156–63. doi:10.4103/0971-6203.139004

CrossRef Full Text | Google Scholar

244. Fix M, Frei D, Volken W, Born E. Macro Monte Carlo for dose calculation of proton beams. Phys Med Biol. (2013). 58:2027–44. doi:10.1088/0031-9155/58/7/2027.

CrossRef Full Text | Google Scholar

245. Tourovsky A, Lomax AJ, Schneider U, Pedroni E. Monte Carlo dose calculations for spot scanned proton therapy. Phys Med Biol. (2005). 50:971–81. doi:10.1088/0031-9155/50/5/019.

CrossRef Full Text | Google Scholar

246. Kohno R, Takada Y, Sakae T, Terunuma T, Matsumoto K, Nohtomi A, et al. Experimental evaluation of validity of simplified Monte Carlo method in proton dose calculations. Phys Med Biol. (2003). 48:1277–88. doi:10.1088/0031-9155/48/10/303.

CrossRef Full Text | Google Scholar

247. Kalantzis G, Tachibana H. Accelerated event-by-event Monte Carlo microdosimetric calculations of electrons and protons tracks on a multi-core CPU and a CUDA-enabled GPU. Comput Methods Progr Biomed. (2014). 113:116–25. doi:10.1016/j.cmpb.2013.09.009

CrossRef Full Text | Google Scholar

248. Okada S, Murakami K, Incerti S, Amako K, Sasaki T. MPEXS-DNA, a new gpu-based Monte Carlo simulator for track structures and radiation chemistry at subcellular scale. Med Phys. (2019). 1483–500. doi:10.1002/mp.13370.

CrossRef Full Text | Google Scholar

249. Tsai M, Tian Z, Qin N, Yan C, Lai Y, Hung SH, et al. A new open-source GPU-based microscopic Monte Carlo simulation tool for the calculations of DNA damages caused by ionizing radiation – part I: core algorithm and validation. Med Phys. (2020). 47:1958–70. doi:10.1002/mp.14037

CrossRef Full Text | Google Scholar

250.PIDE. Particle irradiation data ensable project (2019). Available from: https://www.gsi.de/work/forschung/biophysik/forschungsfelder/radiobiological_modelling/pide_project.htm.

251. Schneider W, Bortfled T, Schlegel W. Correlation between CT numbers and tissue parameters needed for Monte Carlo simulations of clinical dose distributions. Phys Med Biol. (2000). 45:459–78. 10.1088/0031-9155/45/2/314

CrossRef Full Text | Google Scholar

252. Bolst D, Guatelli S, Tran L, Chartier L, Davis J, Biasi G, et al. Validation of GEANT4 for silicon microdosimetry in heavy ion therapy. Phys Med Biol. (2020). 65:045014. doi:10.1088/1361-6560/ab586a.

CrossRef Full Text | Google Scholar

253. Jan S, Benoit D, Becheva E, Carlier T, Cassol F, Descourt P, et al. GATE V6: a major enhancement of the GATE simulation platform enabling modelling of CT and radiotherapy. Phys Med Biol. (2011). 56:881–901. doi:10.1088/0031-9155/56/4/001

CrossRef Full Text | Google Scholar

254. Shin J, Kooy H, Paganetti H, Clasie B. DICOM-RT ion interface to utilize MC simulations in routine clinical workflow for proton pencil beam radiotherapy. Phys Med. (2020). 74:1. doi:10.1016/j.ejmp.2020.04.018.

CrossRef Full Text | Google Scholar

255. Deng W, Younkin J, Souris K, Huang S, Augustine K, Fatyga M, et al. Technical note: integrating an open source Monte Carlo code “MCsquare” for clinical use in intensity-modulated proton therapy. Med Phys. (2020). 47:2558–574. doi:10.1002/mp.14125

CrossRef Full Text | Google Scholar

256. Guterres Marmitt G, Pin A, Ng Wei Siang K, Janssens G, Souris K, Cohilis M, et al. Platform for automatic patient quality assurance via Monte Carlo simulations in proton therapy. Phys Med. (2020). 70:49–57. doi:10.1016/j.ejmp.2019.12.018.

CrossRef Full Text | Google Scholar