Tipping Points in Opinion Dynamics: A Universal Formula in Five Dimensions

A universal formula is shown to predict the dynamics of public opinion including eventual sudden and unexpected outbreaks of minority opinions within a generic parameter space of five dimensions. The formula is obtained by combining and extending several components of the Galam model of opinion dynamics, otherwise treated separately, into one single update equation, which then deploys in a social space of five dimensions. Four dimensions account for a rich diversity of individual traits within a heterogeneous population, including differentiated stubbornness, contrarianism, and embedded prejudices. The fifth dimension is the size of the update groups being discussed. Having one single formula allows one to explore the complete geometry of the underlying landscape of opinion dynamics. Attractors and tipping points, which shape the topology of the different possible dynamics flows, are unveiled. Driven by repeated discussion among small groups of people during a social or political public campaign, the phenomenon of minority spreading and parallel majority collapse are thus revealed ahead of their occurrence. Accordingly, within the opinion landscape, unexpected and sudden events such as Brexit and Trump victories become visible within a forecast time horizon, making them predictable. Despite the accidental nature of the landscape, evaluating the parameter values for a specific case allows one to single out which basin of attraction is going to drive the associate dynamics, and thus, a prediction of the outcome becomes feasible. The model may apply to a large spectrum of social situations including voting outcomes, market shares, and societal trends, allowing us to envision novel winning strategies in competing environments.

1. Introduction

Majoritarian social decisions have been traditionally justified by Condorcet’s jury theorem which states that, in majoritarian group decisions, the errors in individual judgment are canceled out to arbitrary accuracy as the number of voters increases. This implies the stable dominance of rational majority in democratic decision-making. In reality, however, democratic majoritarianism can produce seemingly unexpected sudden shifts, as exemplified by political events such as the 2016 Brexit victory and Trump election. There is also a glaring contradiction in democracy in which there exist powerful interest groups that exert disproportionate power despite their minority status.

Such unexpected and paradoxical outcomes of opinion dynamics are challenging puzzles, which are yet to be elucidated. In particular, with public opinion being nowadays a major key to trigger eventual changes in modern societies as well as collapses of political regimes, the understanding of the mechanisms behind the making of public opinion becomes a major issue of vital interest.

It happened that from the beginning of sociophysics [1], the study of opinion dynamics has been a main topic of research, which has shed new and disruptive light about these paradoxical features resulting from majority group decision [2–6]. A great deal of models have been, and are yet to be, proposed to describe opinion dynamics in social systems [7–12]. Most of them consider homogeneous populations with a local update rule and discrete variables. A series of these models were shown to be included within a single unifying frame [13]. Continuous variables have also been used [14, 15]. Yet, despite ongoing active research [16–21] up-to-date, the opinion dynamics issue is still lacking a comprehensive and robust framework, especially a reliable predictive tool.

Among those models stands the seminal Galam model [22–26], which combines local majority rule updates with local symmetry breaking driven by unconscious prejudices and cognitive biases in case of an even-size group at a tie. The model has revealed some heuristic capacity with the successful predictions of a few political events such as 2016 Brexit victory [24, 27], Trump election [28], and 2005 French rejection of the European constitution project [29]. It has been subsequently extended to incorporate heterogeneous populations with three different psychological traits, which are heterogeneous prejudices, inflexibility or stubbornness [30–37], and contrarianism [38–41]. However, only specific combinations of these traits have been investigated [42–44]. An additional limitation has been the restriction of update groups to sizes 2, 3, and 4.

In this work, by investigating further the Galam model in a generic parameter space of five dimensions, we obtain a single universal update equation to follow the temporal evolution of opinion distribution among a heterogeneous population with any combination of rational, stubborn, and contrarian agents for any average of hidden prejudices and for an arbitrary size of groups being discussed.

The update equation allows one to explore the complete geometry of the underlying landscape. In particular, attractors and tipping points which shape the faith of possible dynamics flows are unveiled. The underlying dynamics path of public opinion driven by repeated discussion among small groups of people during a social or political public campaign becomes predictable. Future occurrence of sudden minority spreading and parallel majority collapse ahead of their actual occurrence is revealed as shown with 2016 Brexit and Trump victories. They became visible within a forecast time horizon and in turn predictable.

In addition, having the full five-dimensional landscape makes predictions more feasible and robust because, then, the precise evaluation of the parameter values is not required. Instead, what matters is identifying the relevant basin of attraction where the dynamics will take place. However, along the basin boundaries, more-precise estimates of the parameters are necessary.

Having a universal formula which accounts for generic psychological features makes the model applicable to a large spectrum of social situations including voting outcomes, market shares, and societal trends. The results also allow us to envision novel winning strategies in competing environments to win a public debate or a market share.

The rest of the article is organized as follows. In Section 2, we outline the derivation of the universal formula aggregating the various components of the Galam model. A few illustrations of sudden and unexpected minority outbreaks yielded by the equation are exhibited in Section 3. Section 4 contains some explicit expressions for the evolution equation for (some) few specific values of the group size r. We analyze the mathematical structure of the universal update equation through the identification of its fixed points in Section 5. Section 6 explores some aspects of the five-dimensional parameter space of the model pointing out the existence of critical points. The results are illustrated with several numerical examples. Concluding remarks are presented in the last section.

2. The Universal Formula in Five-Dimensional Parameter Space

We consider a population with N agents, each capable of taking two states 1 and 0, respectively, representing two exclusive opinions A and B. At a given time t, the corresponding proportions of agents holding A and B are denoted as $p_t$ and $\left(1-p_t\right)$. To make legitimate use of proportions and probabilities, we focus on cases with $N>100$ [26]. Choosing an initial time $t=0$, we investigate the time evolution of $p_0$ driven by informal local discussion among agents at successive discrete time steps with $p_0\to p_1\to p_2\to \dots$

To account for this complicated and unknown process, we use the Galam dynamical model, which monitors the opinion dynamics by a sequential iterated scheme. To implement one scheme, agents are first randomly distributed within small groups of size r. Then, within each group, a majority rule is applied to update local agent opinions. Each agent has one vote to determine the actual local majority. However, to account for the heterogeneity of psychological traits among agents, not all of them obey the majority rule by shifting the opinion if holding the local minority choice. Three types of agents, floaters, inflexibles, and contrarians, are considered. After local updates are performed, all groups are dismantled and agents are reshuffled, thus erasing the local correlations which were created by applying the local majority rules.

• The floaters vote to determine the local majority and, afterward, the ones holding the minority opinion shift to adopt the majority opinion. However, in case of a tie in a local even-size group, floaters adopt the choice in tune with the leading prejudice among the group members [3]. This prejudice-driven tie breaking is activated unconsciously by the agents. Accordingly, at a tie, opinion A is chosen with probability k and opinion B is chosen with probability $\left(1-k\right)$. The value of k satisfies $0\le k\le 1$ and is a function of the distribution of prejudices within the social group.

• The inflexibles also vote to determine the local majority, but contrary to the floaters, in case they hold the minority choice, they stick to it. They are stubborn and keep on with their own pre-decided choice whatever the local majority is. Accordingly, an A-inflexible stays in state 1 and a B-inflexible stays in 0. The same holds true at a tie. Their respective proportions denoted as a and b are external fixed parameters with the constraint $0\le a+b\le 1$.

• The contrarians are floaters, who, once groups are dismantled, decide individually to shift the opinion to oppose the group majority they contributed to. The attitude is independent of the majority choice, either A or B. The proportion of contrarians among floaters is denoted as c satisfying $0\le c\le 1$. The value of c is also a fixed external parameter with the case $c>1/2$ corresponding to a situation where a majority of floaters systematically flip to the other opinion creating an ongoing alternative shifting between A and B. The proportion of floaters A and B is given by $\left(1-a-b\right)$, and the proportion of contrarians among all agents is given by $\tilde{c}=\left(1-a-b\right)c$.

At time t, once a scheme is completed with $p_t\to p_{t+1}$, another one is performed to obtain $p_{+1}\to p_{t+2}$ and so forth till the debate ends with an eventual vote at a given time, which determines the total number of updates to be implemented. The frequency of updates is a function of the intensity of the ongoing debate. For any real situation, the debate initial proportion $p_0$ is evaluated using polls.

Let us now evaluate the function $P_{a,b,c,k}^{\left(r\right)}$ yielding $p_{t+1}$ from $p_t$, given the values, as follows:

$p_{t+1}=P_{a,b,c,k}^{\left(r\right)}\left(p_t\right).(1)$

However, since the contrarian phenomenon is mathematically identical to a random flipping of floaters with probability c among reshuffled agents, we can decouple the c effect from the local update writing as

$p_{t+1}=\left(1-c\right)\left[P_{a,b,k}^{\left(r\right)}\left(p_t\right)-a\right]+c\left[1-P_{a,b,k}^{\left(r\right)}\left(p_t\right)-b\right],(2)$

which simplifies as

$p_{t+1}=\left(1-2c\right)P_{a,b,k}^{\left(r\right)}\left(p_t\right)+c\left(1+a-b\right).(3)$

To evaluate $P_{a,b,k}^{\left(r\right)}$, we note that in a given configuration of a group of size r with $\left(r-\mu \right)$ agents holding opinion A and μ agents holding opinion B, the contributions to $P_{a,b,k}^{\left(r\right)}$ result from two different families. One family includes contributions with a majority of A and equality of A and B (for even size at a tie with probability k), while the other family corresponds to contributions with a minority of A and equality of A and B (for even size at a tie with probability $\left(1-k\right)$). These families are denoted, respectively, as $P_{a,b,c}^{\left(r,\mu \right)}$ and $Q_{a,b,c}^{\left(r,\mu \right)}$ under the constraint $\mu \le \left[r/2\right]$, where $\left[x\right]$ is the integer part of x. Eq. 1 can be rewritten as

$P_{a,b,k}^{\left(r,\mu \right)}\left(p_t\right)={\displaystyle \sum }_{\mu =0}^{\left[\frac{r}{2}\right]}\left\{K_k^{\left(r,\mu \right)}{P}_{a,b}^{\left(r,\mu \right)}\left(p_t\right)+K_{1-k}^{\left(r,\mu \right)}{Q}_{a,b}^{\left(r,\mu \right)}\left(p_t\right)\right\},(4)$

with

$\begin{array}{c}{K}_k^{\left(r,\mu \right)}=1+\left(k-1\right){\delta }_{r,2\mu }=1\left(r\ne 2\mu \right)\\ =k\left(r=2\mu \right),\end{array}(5)$

which allows factorization of the k dependence.

The quantity $P_{a,b}^{\left(r,\mu \right)}\left(p\right)$, which accounts for the contribution to A after one update from configurations with $\left(r-\mu \right)$ agents with opinion A and μ agents with opinion B, can be decomposed as the sum of contributions with α A-inflexibles and β B-inflexibles, where integer α runs from 0 to $\left(r-\mu \right)$ and β runs from 0 to μ giving (see Figure 1 left)

$P_{a,b}^{\left(r,\mu \right)}\left(p\right)=\stackrel{r-\mu }{{\displaystyle \sum }_{\alpha =0}}\stackrel{\mu }{{\displaystyle \sum }_{\beta =0}}{P}_{a,b,\alpha ,\beta }^{\left(r,\mu \right)}\left(p\right).(6)$

Since $\mu \le \left[r/2\right]$ (A majority or tie), contributions to $p_{t+1}$ from Eq. 6 come from all agents except B-inflexibles minus contrarians after the update, yielding

$\begin{array}{c}{P}_{a,b,\alpha ,\beta }^{\left(r,\mu \right)}\left(p\right)=\left(\begin{array}{c}r\\ \mu \end{array}\right)\left(\begin{array}{c}\mu \\ \beta \end{array}\right)\left(\begin{array}{c}r-\mu \\ \alpha \end{array}\right){\left(1-p-b\right)}^{\mu -\beta }\\ \times {\left(p-a\right)}^{r-\mu -\alpha }{b}^{\beta }{a}^{\alpha }\left(\frac{r-\beta }{r}\right).\end{array}(7)$

Similarly, the quantity $Q_{a,b}^{\left(r,\mu \right)}\left(p\right)$, which accounts for the contribution to A from configurations with μ agents with opinion A and $\left(r-\mu \right)$ agents with opinion B, can be decomposed as the sum of contributions with $\alpha =0,\dots ,\mu$A-inflexibles and $\beta =0,\dots ,\left(r-\mu \right)$B-inflexibles giving (see Figure 1 right)

$Q_{a,b}^{\left(r,\mu \right)}\left(p\right)=\stackrel{\mu }{{\displaystyle \sum }_{\alpha =0}}\stackrel{r-\mu }{{\displaystyle \sum }_{\beta =0}}{Q}_{a,b,\alpha ,\beta }^{\left(r,\mu \right)}\left(p\right).(8)$

Since $\mu \le \left[r/2\right]$ (A minority or tie), contributions to $p_{t+1}$ from Eq. 8 come only from A-inflexibles after the update, yielding

$\begin{array}{c}{Q}_{a,b,\alpha ,\beta }^{\left(r,\mu \right)}\left(p\right)=\left(\begin{array}{c}r\\ \mu \end{array}\right)\left(\begin{array}{c}\mu \\ \alpha \end{array}\right)\left(\begin{array}{c}r-\mu \\ \beta \end{array}\right){\left(1-p-b\right)}^{r-\mu -\beta }\\ \times {\left(p-a\right)}^{\mu -\alpha }{b}^{\beta }{a}^{\alpha }\left(\frac{\alpha }{r}\right).\end{array}(9)$

With the use of the formulas ${\left(x+y\right)}^n={{{\displaystyle \sum }}^{\text{}}}_{j=0}^n\left(\begin{array}{c}n\\ j\end{array}\right)x^{n-j}{y}^j$ and $ny{\left(x+y\right)}^{n-1}={{{\displaystyle \sum }}^{\text{}}}_{j=0}^n\left(\begin{array}{c}n\\ j\end{array}\right)j{x}^{n-j}{y}^j$, the summation over α and β leads us to

$P_{a,b}^{\left(r,\mu \right)}\left(p\right)=\left(\begin{array}{c}r\\ \mu \end{array}\right)p^{r-\mu }{\left(1-p\right)}^{\mu }\left[1-\frac{\mu }{r\left(1-p\right)}b\right](10)$

and

$Q_{a,b}^{\left(r,\mu \right)}\left(p\right)=\left(\begin{array}{c}r\\ \mu \end{array}\right)p^{\mu }{\left(1-p\right)}^{r-\mu }\left[\frac{\mu }{rp}a\right].(11)$

With the use of identities

$\begin{array}{c}{\displaystyle \sum }_{\mu =0}^{\left[\frac{r}{2}\right]}{K}_{1-k}^{\left(r,\mu \right)}\left(\begin{array}{c}r\\ \mu \end{array}\right)p^{\mu }{\left(1-p\right)}^{r-\mu }\\ +{\displaystyle \sum }_{\mu =0}^{\left[\frac{r}{2}\right]}{K}_k^{\left(r,\mu \right)}\left(\begin{array}{c}r\\ \mu \end{array}\right)p^{r-\mu }{\left(1-p\right)}^{\mu }\\ ={\left(p+1-p\right)}^r=1\end{array}(12)$

and

$\begin{array}{c}{\displaystyle \sum }_{\mu =0}^{\left[\frac{r}{2}\right]}{K}_k^{\left(r,\mu \right)}\left(\begin{array}{c}r\\ \mu \end{array}\right)\frac{\mu }{rp}{p}^{\mu }{\left(1-p\right)}^{r-\mu }\\ +{\displaystyle \sum }_{\mu =0}^{\left[\frac{r}{2}\right]}{K}_{1-k}^{\left(r,\mu \right)}\left(\begin{array}{c}r\\ \mu \end{array}\right)\frac{r-\mu }{rp}{p}^{r-\mu }{\left(1-p\right)}^{\mu }\\ ={\frac{1}{rp}{\partial }_{\eta }{\left(\eta p+1-p\right)}^r|}_{\eta =1}={\left(p+1-p\right)}^{r-1}=1,\end{array}(13)$

we arrive at the compact expression of the evolution function $P_{a,b,k}^{\left(r\right)}$ for general group size r in the form

$P_{a,b,k}^{\left(r\right)}\left(p\right)={\text{Π}}_0^{\left(r\right)}\left(p,k\right)+a{\text{Π}}_1^{\left(r\right)}\left(p,k\right)-b{\text{Π}}_2^{\left(r\right)}\left(p,k\right),(14)$

where

${\text{Π}}_0^{\left(r\right)}\left(p,k\right)={\displaystyle \sum }_{\mu =0}^{\left[\frac{r}{2}\right]}\left(\begin{array}{c}r\\ \mu \end{array}\right)K_k^{\left(r,\mu \right)}{p}^{r-\mu }{\left(1-p\right)}^{\mu },(15)$

${\text{Π}}_1^{\left(r\right)}\left(p,k\right)={\displaystyle \sum }_{\mu =0}^{\left[\frac{r}{2}\right]}\left(\begin{array}{c}r\\ \mu \end{array}\right)K_{1-k}^{\left(r,\mu \right)}\frac{\mu }{rp}{p}^{\mu }{\left(1-p\right)}^{r-\mu },(16)$

${\text{Π}}_2^{\left(r\right)}\left(p,k\right)={\displaystyle \sum }_{\mu =0}^{\left[\frac{r}{2}\right]}\left(\begin{array}{c}r\\ \mu \end{array}\right)K_k^{\left(r,\mu \right)}\frac{\mu }{r\left(1-p\right)}{p}^{r-\mu }{\left(1-p\right)}^{\mu }.(17)$

Note that the relation ${\text{Π}}_2^{\left(r,\mu \right)}\left(p,k\right)={\text{Π}}_1^{\left(r,\mu \right)}\left(1-p,1-k\right)$. Also, note that the relation

$P_{a,b}^{\left(r,\mu \right)}\left(p\right)+Q_{b,a}^{\left(r,\mu \right)}\left(1-p\right)=\left(\begin{array}{c}r\\ \mu \end{array}\right)p^{r-\mu }{\left(1-p\right)}^{\mu }.(18)$

This guarantees the covariance of $P_{a,b,k}^{\left(r\right)}\left(p\right)$ with respect to the renaming of opinions A and B as follows:

$P_{a,b,k}^{\left(r\right)}\left(p\right)+P_{b,a,1-k}^{\left(r\right)}\left(1-p\right)=1.(19)$

At this stage, to obtain the complete update equation, we use Eq. 3 as

$\begin{array}{c}{P}_{a,b,c,k}^{\left(r\right)}\left(p\right)\\ =\left(1-2c\right)\left[{\text{Π}}_0^{\left(r\right)}\left(p,k\right)+a{\text{Π}}_1^{\left(r\right)}\left(p,k\right)-b{\text{Π}}_2^{\left(r\right)}\left(p,k\right)\right]\\ +c\left(1+a-b\right),\end{array}(20)$

which allows calculation of the opinion dynamics for any set of parameters $\left(a,b,c,k\right)$ given any group size r for any initial support $p_0$for opinion A. We thus have calculated a universal formula to predict opinion dynamics in a parameter space of five dimensions.

FIGURE 1

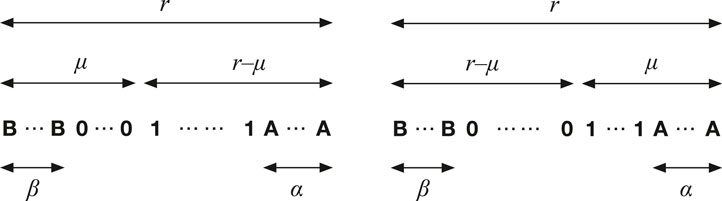
FIGURE 1. Diagrams representing a group of r agents made up of α A-inflexibles (shown as $\mathbf{A}$), β B-inflexibles (shown as $\mathbf{B}$), and $r^{\alpha }-\beta$ floaters and contrarians. Agents are split into two opinions with μ having one opinion and $\left(r-\mu \right)$ being the other with $\mu <\left[r/2\right]$. The left diagram is the case in which opinion A holds the majority, and the right diagram is the case in which B holds the majority.

We now go one step further to make our equation further realistic by considering a distribution of size with $r=\mathrm{1,2},\dots ,L$, where L is the largest update size. Usually, in most social situations, L is around $\mathrm{4,5}$, or 6. The size weight $w_r$ of groups of size r has to be evaluated from observation under the constraint ${{{\displaystyle \sum }}^{\text{}}}_{r=1}^{r=L}{w}_r=1$. Including the size $r=1$ allows consideration of agents who do not take part in local discussion during each update. Then, using Eq. 2, the associated global proportion of A supporters becomes

$\begin{array}{c}{G}_{a,b,c,k}^{\left\{L\right\}}\left(p\right)\\ =\stackrel{r=L}{{\displaystyle \sum }_{r=1}}{w}_r{P}_{a,b,c,k}^{\left\{r\right\}}\left(p\right)\\ =\left(1-2c\right)\stackrel{r=L}{{\displaystyle \sum }_{r=1}}{w}_r\left[{\text{Π}}_0^{\left(r\right)}\left(p,k\right)+a{\text{Π}}_1^{\left(r\right)}\left(p,k\right)-b{\text{Π}}_2^{\left(r\right)}\left(p,k\right)\right]+c\left(1+a-b\right).\end{array}(21)$

In principle, Eq. 21 allows one to contribute to the issue of connecting the topology of a given network and the dynamics occurring through the network [45]. Indeed, the set of values of weights $w_r$ and L could then be extracted from the network.

3. A Few Illustrations of Sudden and Unexpected Minority Outbreaks

To make our universal update equation more concrete, we list explicit expressions for the series of values $r=\mathrm{3,4,5,6,7,8,9}$ in Appendix A. In addition, to distinguish the dynamical effects that come from the current update equation from the ones already present in the former model, we recall that the impact of unconscious prejudices has been studied for group size $r=4$ and the effect of having inflexible or stubborn agents has been studied for groups of size 3. Each yields separately the phenomenon of minority spreading as exhibited for instance with $k=1$ and $a=0.20\text{ and }b=0$ in Figure 2. The corresponding update formulas are recovered from Eq. 2 with $P_{\mathrm{0,0,0,1}}^{\left(4\right)}\left(p\right)={\text{Π}}_0^{\left(4\right)}\left(p,k\right)=p^2\left(3p^2-8p+6\right)$ and $P_{0.20,\mathrm{0,0},k}^{\left(3\right)}\left(p\right)={\text{Π}}_0^{\left(3\right)}\left(p,k\right)+0.20{\text{Π}}_1^{\left(3\right)}\left(p,k\right)=-2p^3+3.20p^2+0.20\left(1-2p\right)$. Note that $P_{0.20,\mathrm{0,0},k}^{\left(3\right)}\left(p\right)$ is independent of k as expected for an odd-size group. Minority spreading occurs in both cases, but rather slowly for the second one.

FIGURE 2

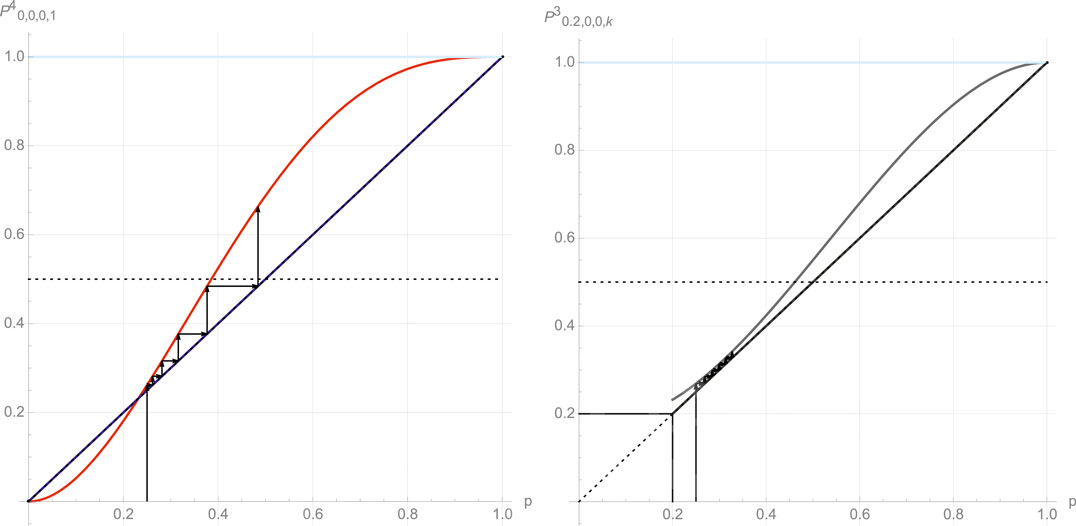
FIGURE 2. Left: evolution of the proportion of A support $P_{\mathrm{0,0,0,1}}^{\left\{4\right\}}\left(p\right)$ as a function of p. The arrows show the minority spreading starting from an initial support $p=0.25$. Right: evolution of the proportion of A support $P_{0.2,\mathrm{0,0},k}^{\left\{3\right\}}\left(p\right)$ as a function of p. The arrows show the minority spreading starting from an initial support $p=0.25$.

While each effect was accounting for, alone, now the universal formula allows us to investigate the combination of both effects, either going along the same support for A ($P_{0.20,\mathrm{0,0,1}}^{\left(4\right)}\left(p\right)$) or competing for and against A ($P_{\mathrm{0,0.20},\mathrm{0,1}}^{\left(4\right)}\left(p\right)$) as shown in Figure 3 for the case $r=4$. Combination enhances drastically the minority spreading, but competition shows that $20\text{\%}$ of B-inflexibles do overcome the full benefit of the prejudice effect.

FIGURE 3

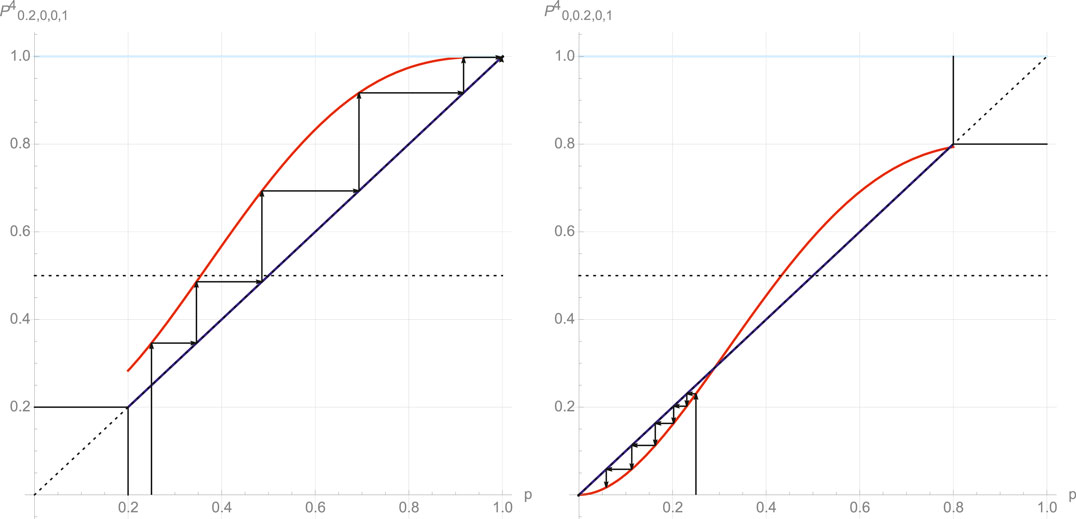
FIGURE 3. Left: evolution of the proportion of A support $P_{0.20,\mathrm{0,0,1}}^{\left\{4\right\}}\left(p\right)$ as a function of p. The arrows show the speeding up of the A minority spreading starting from an initial support $p=0.25$. Right: evolution of the proportion of A support $P_{\mathrm{0,0.2},0,k}^{\left\{4\right\}}\left(p\right)$ as a function of p. The arrows show the A minority now shrinking from an initial support $p=0.25$.

We proceed to illustrating the capacity of the current update equation to yield sudden and unexpected minority outbreaks exhibiting a couple of striking cases with groups of sizes $r=3$ and $r=4$.

In Figure 4, each graph shows two curves for the evolution of p, the proportion of the support for A, as a function of the number of updates with the same value of r. The two sets of parameter values are shown in each figure. Only very little differences differentiate the two sets of parameters, while the two associated curves exhibit drastic difference in their respective outcomes. The graph in the left is an example of the case $r=3$ with the common starting value $p=0.2$. Two lines are those of $a=0.170$ and $a=0.172$ and common values $b=c=0$, showing the drastic difference caused by a minuscule change in the parameter a. Likewise, the graph in the right is an example of the case $r=4$ with the common starting value $p=0.2$. Two lines are those of $c=0.04$ and $c=0.05$, and common values $a=b=0.10$ and $k=0.6$, showing the effect caused by a $1\text{\%}$ change in the parameter c.

FIGURE 4

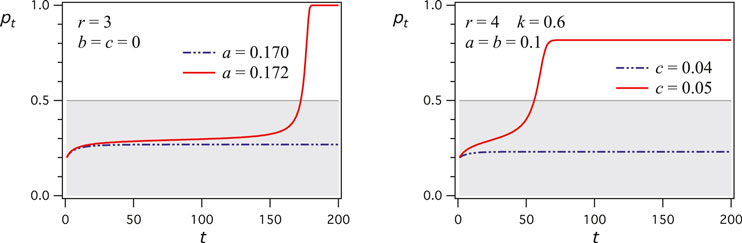
FIGURE 4. Evolution of p, the proportion of the support for A, as a function of the number of updates t. Left: A $r=3$ case with starting value $p=0.2$. Two lines are those of $a=0.170$ and $a=0.172$, and common values $b=c=0$. Right: A $r=4$ case with starting value $p=0.2$. Two lines are those of $c=0.04$ and $c=0.05$, and common values $a=b=0.10$ and $k=0.6$.

4. Fixed Points of the Dynamics

The dynamics implemented by repeated applications of Eq. 2 exhibits a rather large spectrum of different scenarios within the five-dimensional space spanned by $0\le a\le p\le 1$, $0\le b\le 1-p\le 1$, $0\le c\le 1$, $a+b+c\le 1$, $0\le k\le 1$, and $1\le r\le \infty$. The phase diagram landscape is shaped by the various attractors and tipping surfaces, which are the solutions of the fixed-point equation

$p^{\mathrm{\star }}=P_{a,b,c,k}^{\left(r\right)}\left(p^{\mathrm{\star }}\right).(22)$

It is of interest to mention that Eq. 22 is a polynomial of degree r in p and thus exhibits r solutions of which no more than three are real and contained within the $0-1$ range. This assessment results from playing with the equation and hand-waving arguments but a mathematical proof is still on hold.

In case of three fixed points $p_0^{\mathrm{\star }}$, $p_s^{\mathrm{\star }}$, and $p_1^{\mathrm{\star }}$ in ascending order, the smallest $p_0^{\mathrm{\star }}\le 1/2$ is stable and represents B-majoritarian final state, while the largest $p_1^{\mathrm{\star }}\ge 1/2$ is also stable, representing A-majoritarian final state. The medium-valued $p_s^{\mathrm{\star }}$ is unstable, acts as a separator for the basins of attraction to $p_0^{\mathrm{\star }}$ and $p_1^{\mathrm{\star }}$, and is a tipping point of the dynamics.

Since making a visual representation is impossible in five dimensions, being interested in the evolution of an initial value $p_0$ given fixed values of $\left(a,b,c,k,r\right)$, the operative use of the phase diagram is to select two-dimensional slices showing the evolution of $p_0$ as a function of repeated updates with $p_0\to p_1\to \dots \to p_n$, where n is the number of iterations. With respect to prediction about a real event, what matters is to determine if $p_n>1/2$ (opinion A victory), $p_n<1/2$ (opinion A failure), or $p_n\approx 1/2$ (hung outcome).

An alternative practical use of the phase diagram is to extract the two-dimensional slices, which shows the function $p_{t+1}=P_{a,b,c,k}^{\left(r\right)}\left(p_t\right)$ for a fixed set of values $\left(a,b,c,k,r\right)$. These curves display the eventual attractors and tipping points underlying the dynamics from which predictions can be made. These points are located at the crossing of $p_{t+1}=P_{a,b,c,k}^{\left(r\right)}\left(p_t\right)$ and the diagonal $p_{t+1}=p_t$.

Indeed, all “slices” share the common property of having at least one single attractor for the dynamics. In addition, a series of slices exhibit one additional attractor and a tipping point located between the two attractors. For those cases, varying some of the parameters $\left(a,b,c,k\right)$ may lead either to have one attractor and the tipping point to coalesce at critical values, yielding then a single-attractor dynamics. The other scheme is having the two attractors to merge at the tipping point to produce another single-attractor dynamics. To have a single-attractor dynamics implies one identified opinion is certain to win whatever its initial support is. This means that the debate or the campaign duration lasts for enough time to cross $1/2$, i.e., $50\text{\%}$, of the ballots for an election. Figure 5 and Figure 6 show a series of cases illustrating the above two scenarios.

FIGURE 5

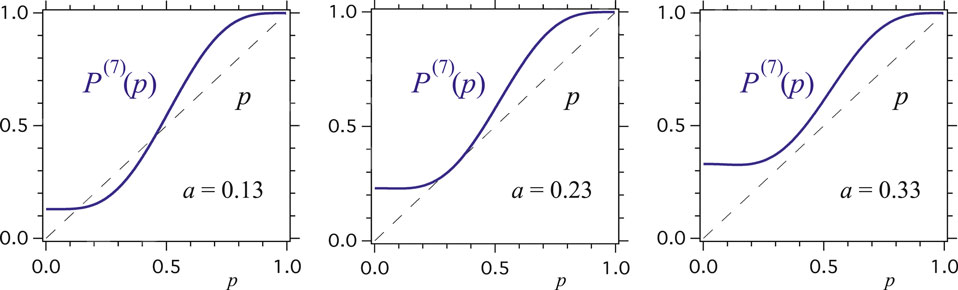
FIGURE 5. Examples of the evolution function $P_{a,b,c,k}^r\left(p\right)$ around critical value $a=a_c$ for $b=c=0$. The group size is chosen to be $r=7$.

FIGURE 6

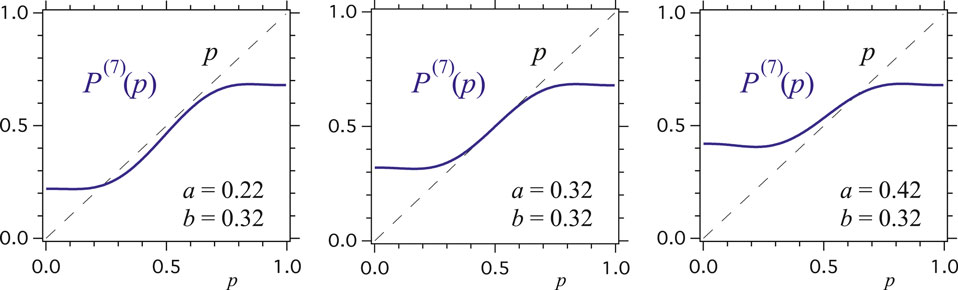
FIGURE 6. Examples of the evolution function $P_{a,b,c,k}^r\left(p\right)$ around triple critical value $a=b=a_t$ for $c=0$. The group size is chosen to be $r=7$.

5. Exploring the Phase Diagram

From Eq. 22, when $b=c=0$, increasing the parameter a makes $p_0^{\mathrm{\star }}$ and $p_s^{\mathrm{\star }}$ merge into a single value at $a=a_c$ and then disappear to make $p_1^{\mathrm{\star }}$ the sole final state of the system (see Figure 7). The critical value a for $b=0$, which we call $a_c\left(c\right)$, is obtained from

$p^{\mathrm{\star }}-P_{a_c\left(c\right),0,c,k}^{\left(r\right)}\left(p^{\mathrm{\star }}\right)=0,(23)$

$1-{\partial }_p{P}_{a_c\left(c\right),0,c,k}^{\left(r\right)}\left(p^{\mathrm{\star }}\right)=0.(24)$

In particular, for $c=0$, the critical value $a_c\left(0\right)$, which we simply call $a_c$, and its associated $p_c^{\mathrm{\star }}$ are obtained from

$\begin{array}{l}{\text{Π}}_0^{\left(r\right)}\left(p_c^{\mathrm{\star }},k\right){\text{Π}}_1^{\left(r\right)\prime }\left(p_c^{\mathrm{\star }},k\right)-{\text{Π}}_0^{\left(r\right)\prime }\left(p_c^{\mathrm{\star }},k\right){\text{Π}}_1^{\left(r\right)}\left(p_c^{\mathrm{\star }},k\right)\\ +{\text{Π}}_0^{\left(r\right)}\left(p_c^{\mathrm{\star }},k\right)-p_c^{\mathrm{\star }}{\text{Π}}_0^{\left(r\right)\prime }\left(p_c^{\mathrm{\star }},k\right)=0,\end{array}(25)$

$a_c=\frac{p_c^{\mathrm{\star }}-{\text{Π}}_0^{\left(r\right)}\left(p_c^{\mathrm{\star }},k\right)}{{\text{Π}}_1^{\left(r\right)}\left(p_c^{\mathrm{\star }},k\right)}.(26)$

With small but non-zero b, the system goes through transition between two stable fixed-point phase and single fixed-point phase, when a is varied, at a critical value higher than $a_c$.

FIGURE 7

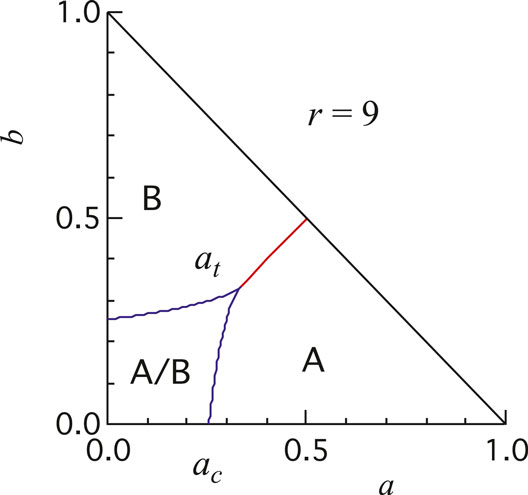
FIGURE 7. An example of the phase diagram of the parameter space $\left\{a,b\right\}$. The group size here is chosen to be $r=9$. The regions marked as A, B, and $A/B$ represent parameter values with which the system converges unconditionally to A majority, unconditionally to B majority, and to either A or B majority depending on the initial configuration, respectively.

Above a certain value of b, the system goes from B-majoritarian single fixed-point phase to A-majoritarian single fixed-point phase without passing through three fixed-point phase (see Figure 7). The transition is characterized by triple critical point $a=b=a_t\left(c\right)$:

$p_t^{\mathrm{\star }}-P_{a_t\left(c\right),a_t\left(c\right),c,k}^{\left(r\right)}\left(p_t^{\mathrm{\star }}\right)=0,(27)$

$1-{\partial }_p{P}_{a_t\left(c\right),a_t\left(c\right),c,k}^{\left(r\right)}\left(p_t^{\mathrm{\star }}\right)=0.(28)$

Limiting ourselves to $c=0$ for now, the triple point $a_t$$=a_t\left(0\right)$ and its associated $p_t^{\mathrm{\star }}$ are obtained as $p_t^{\mathrm{\star }}=1/2$ and

$a_t=\frac{1-{\text{Π}}_0^{\left(r\right)\prime }\left(\frac{1}{2},k\right)}{2{\text{Π}}_1^{\left(r\right)\prime }\left(\frac{1}{2},k\right)}.(29)$

It is instructive to draw the phase diagram on an $\left\{a,b\right\}$ plane. There is a region of small values of a and b in which final majority can go either way depending on its initial support. For large values of a and/or b, final majority is predetermined due to the strong influence of inflexibles. When a or b exceeds $a_t$, two inflexible-dominated regions are placed next to each other without an intermediate floater-determinable region. An example of $r=9$is shown in Figure 7.

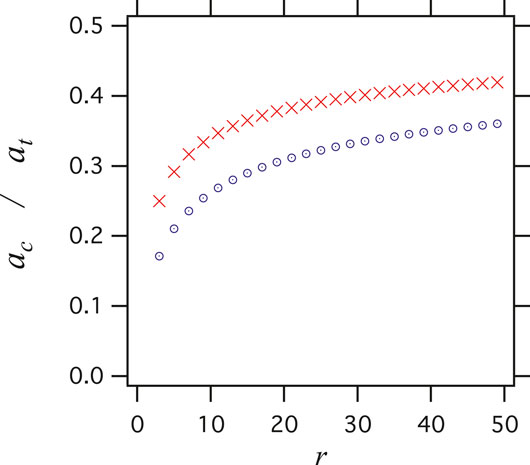
The r-dependence of $a_c$ and $a_t$ can be seen in Figure 8. We list just some of them as follows: For $r=3$, we have $a_c=0.1714$ and $a_t=0.25$, and for $r=5$, $a_c=0.2104$ and $a_t=0.2917$. For $r=7$, we have $a_c=0.2358$ and $a_t=0.3167$, and for $r=9$, $a_c=0.2452$ and $a_t=0.3339$.

FIGURE 8

FIGURE 8. Critical parameters $a_c$ and $a_t$ as functions of group size r.

Overall, approaching $r=\infty$limit, $a_r=a_t=0.5$ is very slow, and for reasonably small group size $r\approx 10$, $a_c\approx 1/4$ and $a_t\approx 1/3$ hold, which are closer to the case $r=3$ than $r=\infty$. Even at $r\approx 50$, we have surprisingly small $a_c\approx 1/3$ and $a_t\approx 2/5$.

It is again instructive to look at the phase diagram on the $\left\{a,b\right\}$ plane with different values of c (Figure 9). It should be very clear now that for all groups of size r, the effect of contrarians on the final majority formation is to decrease the role of floaters and increase the power of inflexibles. This fact, which has originally been found in $r=3$, for example, turns out to be a generic feature of the Galam model.

FIGURE 9

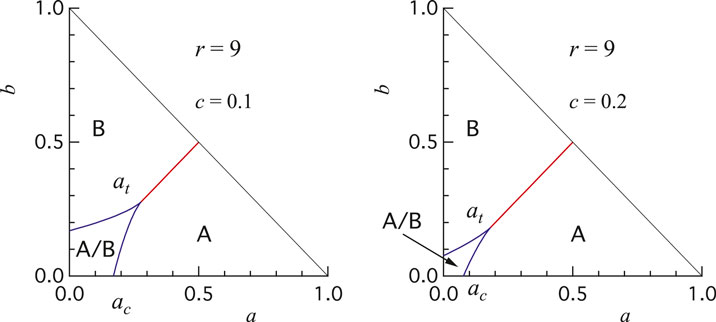
FIGURE 9. Phase diagram on $\left\{a,b\right\}$ plane for $r=9$. Left for $c=0.1$ and right for $c=0.2$. The regions marked as A, B, and $A/B$ represent parameter values with which the system converges unconditionally to A majority, unconditionally to B majority, and to either A or B majority depending on the initial configuration, respectively.

6. Summary

In this study, we have obtained a universal formula for the temporal evolution of agents following the Galam opinion dynamics in a parameter space of five dimensions, which are the respective proportions of inflexibles of each side (stubbornness), the proportion of contrarians, the mean value of shared prejudices, and the update group size.

The associated opinion landscape is found to be shaped by several attractors and tipping points, which yield a rich variety of non linearities and singularities in the opinion flows. Sudden upheavals such as minority spreading and majority collapse are thus given a rationale unveiling the hidden mechanisms behind the occurrence of unexpected and sudden shifts in the distribution of opinions such as with the Brexit victory and Trump election. The time dependence of the corresponding phenomena is also exhibited.

For large group sizes, although the effects of inflexible agents waved out with simple majority rule holding, the results vary very slowly, showing that earlier insights obtained from group sizes three and four remain intact. In contrast, for even sizes, although the prejudice effect weakens with increasing size, it stays effective. Moreover, having the update equation for any group size r makes it possible to consider combinations of group sizes, which in turn opens the path to account for underlying networks.

The study of one specific case has showed the existence of critical points $a_c$ and $a_t$, which corner and branch out the lines separating the inflexibles-dominant and floaters-determinable phases. The admixture and increase of contrarians effectively assist the dominance of inflexibles and reduce the parameter region in which initial composition of floaters can determine the outcome of majority opinion formation. The increase in group size r induces modest but clear increase in both $a_c$ and $a_t$. Accordingly, when the local discussion involves more agents, a larger committed minority is necessary to impose its will on the majority, or, identically, a larger enlightened minority is necessary for its persuasion of the majority.

Obtaining the complete phase diagram of the dynamics of opinions yields a robust forecasting frame for which predictions become more reliable since what matters is the identification of the basin of attraction in which the dynamics is taking place, thus providing some flexibility in the accuracy of parameter evaluation. However, along the basin boundaries, higher precision is required for estimation of the value of the parameters. Given a specific issue, locating the corresponding relevant attractor allows anticipation of a possible unexpected shift of opinion trend ahead of its occurrence.

It is of importance to emphasize one instrumental feature of the model that it does not rely on data beside the use of few polls. Indeed, the model is not data-driven, allowing one to build the general landscape of the dynamics, whose topology is shaped by the various tipping points and attractors, which have been identified from the universal formula.

However, at this stage, making the framework operational for robust predictions is still to be implemented since specific tools must be designed to evaluate the value of parameters, i.e., the proportions of inflexibles of each side and contrarians, as well as the effective average of active prejudices connected to a given issue. This challenge cannot be addressed by physics solely. An interdisciplinary frame with social scientists is at stake to create effective new tolls to evaluate quantitatively those parameters.

Yet, it has been shown that rough qualitative estimates are sufficient to identify which basin is going to drive the dynamics for some cases as illustrated for the Brexit and French referendum about the project of the European constitution for which most activated prejudices were acting in favor of the choice no.

Accordingly, at this stage, predictions are qualitative about winning or losing a vote and not about a precise value of the voting outcome. The forecast is about toward an increase in support to obtain above fifty percent or a decrease to end up below fifty percent. Therefore, interdisciplinary efforts have to be made to reach solid quantitative predictions. Nevertheless, having the universal formula allows one to elaborate winning strategies in competing environments, widening previous discussed paths [46–50].

To conclude, we have obtained a potentially ready-to-use universal formula which, although operative tools for precise tuning of parameters are still lacking, provides already a new ground to make a large spectrum of predictions of winning strategies about outcomes of opinion dynamics, including voting, market shares, and societal trends.

Explicit Evolution Equations for $r=\mathrm{3,4,5,6,7,8,9}$

To make our universal update equation more concrete, we list explicit expressions for the series of values $r=\mathrm{3,4,5,6,7,8,9}$ as follows:

$r=3$

$\begin{array}{c}{\text{Π}}_0^{\left(3\right)}\left(p,k\right)=p^2\left(3-2p\right),\\ {\text{Π}}_1^{\left(3\right)}\left(p,k\right)={\left(1-p\right)}^2,\\ {\text{Π}}_2^{\left(3\right)}\left(p,k\right)=p^2.\end{array}(30)$

$r=4$

$\begin{array}{c}{\text{Π}}_0^{\left(4\right)}\left(p,k\right)=p^3\left(4-3p\right)+6k{p}^2{\left(1-p\right)}^2,\\ {\text{Π}}_1^{\left(4\right)}\left(p,k\right)={\left(1-p\right)}^2\left(1+2p\right)-3kp{\left(1-p\right)}^2,\\ {\text{Π}}_2^{\left(4\right)}\left(p,k\right)=p^3+3k{p}^2\left(1-p\right).\end{array}(31)$

$r=5$

$\begin{array}{c}{\text{Π}}_0^{\left(5\right)}\left(p,k\right)=p^3\left(10-15p+6p^2\right),\\ {\text{Π}}_1^{\left(5\right)}\left(p,k\right)={\left(1-p\right)}^3\left(1+3p\right),\\ {\text{Π}}_2^{\left(5\right)}\left(p,k\right)=p^3\left(4-3p\right).\end{array}(32)$

$r=6$

$\begin{array}{c}{\text{Π}}_0^{\left(6\right)}\left(p,k\right)=p^4\left(14-24p+10p^2\right)+20k{p}^3{\left(1-p\right)}^3,\\ {\text{Π}}_1^{\left(6\right)}\left(p,k\right)={\left(1-p\right)}^3\left(1+3p+6p^2\right)-10k{p}^2{\left(1-p\right)}^3,\\ {\text{Π}}_2^{\left(6\right)}\left(p,k\right)=p^4\left(5-4p\right)+10k{p}^3{\left(1-p\right)}^2.\end{array}(33)$

$r=7$

$\begin{array}{c}{\text{Π}}_0^{\left(7\right)}\left(p,k\right)=p^4\left(35-84p+70p^2-20p^3\right),\\ {\text{Π}}_1^{\left(7\right)}\left(p,k\right)={\left(1-p\right)}^4\left(1+4p+10p^2\right),\\ {\text{Π}}_2^{\left(7\right)}\left(p,k\right)=p^4\left(15-24p+18p^2\right).\end{array}(34)$

$r=8$

$\begin{array}{c}{\text{Π}}_0^{\left(8\right)}\left(p,k\right)=p^5\left(56-140p+120p^2-35p^3\right)+70k{p}^4{\left(1-p\right)}^4,\\ {\text{Π}}_1^{\left(8\right)}\left(p,k\right)={\left(1-p\right)}^4\left(1+4p+10p^2+20p^3\right)-35k{p}^3{\left(1-p\right)}^4,\\ {\text{Π}}_2^{\left(8\right)}\left(p,k\right)=p^5\left(21-35p+15p^2\right)+35k{p}^4{\left(1-p\right)}^3.\end{array}(35)$

$r=9$

$\begin{array}{c}{\text{Π}}_0^{\left(9\right)}\left(p,k\right)=p^5\left(126-420p+540p^2-315p^3+70p^4\right),\\ {\text{Π}}_1^{\left(9\right)}\left(p,k\right)={\left(1-p\right)}^5\left(1+5p+15p^2+35p^3\right),\\ {\text{Π}}_2^{\left(9\right)}\left(p,k\right)=p^5\left(56-140p+120p^2-35p^3\right).\end{array}(36)$

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, and further inquiries can be directed to the corresponding author.

Author Contributions

All authors have contributed equally to the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors express their gratitude to Ms. Miwa Ohtsuki and Professor Shinichiro Inaba for their encouragements during the completion of this work. This manuscript has been released as a pre-print at arXiv [51].

References

1. Galam, S, Gefen, Y, and Shapir, Y. Sociophysics: a new approach of sociological collective behaviour. I. mean‐behaviour description of a strike. J Math Sociol (1982). 9:1–13. doi: 10.1080/0022250x.1982.9989929. CrossRef Full Text

Google Scholar

2. Brazil, R. The physics of public opinion, Physics World (2012).

Google Scholar

3. Galam, S. Sociophysics: A physicist’s Modeling of Psycho-political Phenomena. New York, NY: Springer (2012).

Google Scholar

4. Castellano, C, Fortunato, S, and Loreto, V. Statistical physics of social dynamics. Rev Mod Phys (2009). 81:591–646. doi: 10.1103/revmodphys.81.591. CrossRef Full Text

Google Scholar

5. Schweitzer, F. Sociophysics. Phys Today (2018). 71:40–6. doi: 10.1063/pt.3.3845. CrossRef Full Text

Google Scholar

6. Noorazar, H. Recent advances in opinion propagation dynamics: a 2020 survey. Eur Phys J Plus (2020). 135:521. doi: 10.1140/epjp/s13360-020-00541-2.

CrossRef Full Text | Google Scholar

7. Sznajd-Weron, K, and Sznajd, J. Opinion evolution in closed community Int J Mod Phys C (2000). 11:1157–65. doi: 10.1142/s0129183100000936. CrossRef Full Text

Google Scholar

8. Ochrombel, R. Simulation of Sznajd sociophysics model with convincing single opinions Int J Mod Phys C (2001). 12:1091. doi: 10.1142/s0129183101002346. CrossRef Full Text

Google Scholar

9. Corcos, A, Eckmann, J-P, Malaspinas, A, Malevergne, Y, and Sornette, D. Imitation and contrarian behaviour: hyperbolic bubbles, crashes and chaos. Quant Finance (2002). 2:264–81. doi: 10.1088/1469-7688/2/4/303. CrossRef Full Text

Google Scholar

10. Behera, L, and Schweitzer, F. On spatial consensus formation: Is the Sznajd model different from a voter model? Int J Mod Phys C (2003). 14:1331–54. doi: 10.1142/s0129183103005467. CrossRef Full Text

Google Scholar

11. Tessone, CJ, Toral, R, Amengual, P, Wio, HS, and San Miguel, M. Neighborhood models of minority opinion spreading. Eur Phys J B (2004). 39:535–44. doi: 10.1140/epjb/e2004-00227-5. CrossRef Full Text

Google Scholar

12. Sanchez, JR. A modified one-dimensional Sznajd model. arXiv: cond-mat/0408518 (2004).

Google Scholar

13. Galam, S. Local dynamics vs. social mechanisms: A unifying frame. Europhys Lett (2005). 70:705–11. doi: 10.1209/epl/i2004-10526-5.

CrossRef Full Text | Google Scholar

14. Deffuant, G, Neau, D, Amblard, F, and Weisbuch, G. Mixing beliefs among interacting agents. Adv Complex Syst (2000). 03:87–98. doi: 10.1142/s0219525900000078. CrossRef Full Text

Google Scholar

15. Hegselmann, R, and Krause, U. Opinion dynamics and bounded confidence models, analysis, and simulation. J Artif Soc Soc Simulat (2002). 5:(3).

Google Scholar

16. Rodriguez, N, Bollen, J, and Ahn, Y-Y. Collective Dynamics of Belief Evolution under Cognitive Coherence and Social Conformity. PloS One (2016). 11:e0165910. doi: 10.1371/journal.pone.0165910. CrossRef Full Text

Google Scholar

17. Battiston, F, Cairoli, A, Nicosia, V, Baule, A, and Latora, V. Interplay between consensus and coherence in a model of interacting opinions. Phys Nonlinear Phenom (2016). 323-324:12–9. doi: 10.1016/j.physd.2015.10.013. CrossRef Full Text

Google Scholar

18. Marsan, GA, Bellomo, N, and Gibelli, L. Stochastic evolutionary differential games toward a systems theory of behavioral social dynamics. Math Model Methods Appl Sci (2016). 26:1051–93. doi: 10.1142/s0218202516500251. CrossRef Full Text

Google Scholar

19. Cheon, T, and Morimoto, J. Balancer effects in opinion dynamics. Phys Lett (2016). 380:429–34. doi: 10.1016/j.physleta.2015.11.012. CrossRef Full Text

Google Scholar

20. Cheon, T, and Galam, S. Dynamical Galam model. Phys Lett (2018). 382:1509–15. doi: 10.1016/j.physleta.2018.04.019. CrossRef Full Text

Google Scholar

21. Lynn, CW, Papadopoulos, L, Lee, DD, and Bassett, DS. Surges of collective human activity emerge from simple pairwise correlations. Phys Rev (2019). 9. doi: 10.1103%2FPhysRevX.9.011022.

CrossRef Full Text | Google Scholar

22. Galam, S. Majority rule, hierarchical structures, and democratic totalitarianism: A statistical approach. J Math Psychol (1986). 30:426–34. doi: 10.1016/0022-2496(86)90019-2. CrossRef Full Text

Google Scholar

23. Galam, S, Chopard, B, Masselot, A, and Droz, M. Competing species dynamics: Qualitative advantage versus geography. Eur Phys J B (1998). 4:529–31. doi: 10.1007/s100510050410. CrossRef Full Text

Google Scholar

24. Galam, S. The dynamics of minority opinions in democratic debate. Phys Stat Mech Appl (2004). 336:56–62. doi: 10.1016/j.physa.2004.01.010. CrossRef Full Text

Google Scholar

25. Galam, S. Heterogeneous beliefs, segregation, and extremism in the making of public opinions. Phys Rev E (2005). 71:046123. doi: 10.1103/physreve.71.046123. CrossRef Full Text

Google Scholar

26. Fasano, G, Sorato, A, and Ellero, A. A modified Galam’s model for word-of-mouth information exchange, Physica A (2009). 388:3901–10. doi: 10.1016%2Fj.physa.2009.06.002

CrossRef Full Text | Google Scholar

27. Galam, S. Are referendum a machinery to turn our prejudices into rational choices? An unfortunate answer from sociophysics, in The Routlrdge Handbook to Referendums and Direct Democracy, Eds. Morel, L, and Qvortrup, M, Routledge 19, 334–47 (2018).

Google Scholar

28. Galam, S. The Trump phenomenon, an explanation from sociophysics. Int J Mod Phys B (2017). 31:1742015. doi: 10.1142/s0217979217420152. CrossRef Full Text

Google Scholar

29. Lehir, P. Les mathématiques s’invitent dans le débat européen, (interview of S. Galam). Monde (2005). 26/02:23.

Google Scholar

30. Galam, S, and Moscovici, S. Towards a theory of collective phenomena: consensus and attitude changes in groups. Eur J Soc Psychol (1991). 21:49–74. doi: 10.1002/ejsp.2420210105. CrossRef Full Text

Google Scholar

31. Galam, S, and Jacobs, F. The role of inflexible minorities in the breaking of democratic opinion dynamics. Phys Stat Mech Appl (2007). 381:366–76. doi: 10.1016/j.physa.2007.03.034. CrossRef Full Text

Google Scholar

32. Martins, A, and Galam, S. Building up of individual inflexibility in opinion dynamics, Phys Rev E (2013). 87, 042807. doi: 10.1103/physreve.87.042807. CrossRef Full Text

Google Scholar

33. Crokidakis, N, and de Oliveira, PMC. Inflexibility and ind+ependence: phase transitions in the majority-rule model. Phys Rev E (2015). 92:062122. doi: 10.1103/physreve.92.062122. CrossRef Full Text

Google Scholar

34. Mobilia, M. Nonlinear q-voter model with inflexible zealots. Phys Rev E (2015). 92:012803. doi: 10.1103/physreve.92.012803. CrossRef Full Text

Google Scholar

35. Pickering, W, Szymanski, BK, and Lim, C. Analysis of the high dimensional naming game with committed minorities. Phys Rev E (2016). 93:052311. doi: 10.1103/physreve.93.052311. CrossRef Full Text

Google Scholar

36. Burghardt, K, Rand, W, and Girvan, M. Competing opinions and stubbornness: connecting models to data. Phys Rev E (2016). 93:032305. doi: 10.1103/physreve.93.032305. CrossRef Full Text

Google Scholar

37. Juul, JS, and Porter, MA. Hipsters on networks: How a minority group of Individuals can lead to an anti-establishment majority. arXiv:1707.07187v2 (2018).

Google Scholar

38. Galam, S. Contrarian deterministic effects on opinion dynamics: "the hung elections scenario". Phys Stat Mech Appl (2004). 333:453–60. doi: 10.1016/j.physa.2003.10.041. CrossRef Full Text

Google Scholar

39. Tanabe, S, and Masuda, N. Complex dynamics of a nonlinear voter model with contrarian agents. Chaos (2013). 23:043136. doi: 10.1063/1.4851175. CrossRef Full Text | Pubmed

Google Scholar

40. Lee, E, Holme, P, and Lee, SH. Modeling the dynamics of dissent. Phys Stat Mech Appl (2017). 486:262–72. doi: 10.1016/j.physa.2017.05.047. CrossRef Full Text

Google Scholar

41. Gambaro, JP, and Crokidakis, N. The influence of contrarians in the dynamics of opinion formation. Phys Stat Mech Appl (2017). 486:465–72. doi: 10.1016/j.physa.2017.05.040. CrossRef Full Text

Google Scholar

42. Jacobs, F, and Galam, S. Two-opinions-dynamics generated by inflexibles and non-contrarian and contrarian floaters. arXiv:0803.3150v1 (2008).

Google Scholar

43. Crokidakis, N, Blanco, VH, and Anteneodo, C. Impact of contrarians and intransigents in a kinetic model of opinion dynamics. Phys Rev E (2014). 89:013310. doi: 10.1103/physreve.89.013310. CrossRef Full Text

Google Scholar

44. Kalil, N, Miguel, MS, and Toral, R. Zealots in the mean-field noisy voter model. Phys. Rev. E (2018). 97:012310.

Google Scholar

45. Battiston, F, Cencetti, G, Iacopini, I, Latora, V, Lucas, M, Patania, A, et al. Networks beyond pairwise interactions: Structure and dynamics. Phys Rep (2020). 874:1–92. doi: 10.1016/j.physrep.2020.05.004. CrossRef Full Text

Google Scholar

46. Wang, Z, Xia, C, Chen, Z, and Chen, G. Epidemic Propagation With Positive and Negative Preventive Information in Multiplex Networks. IEEE Trans Cybern (2020). [Epub ahead of print]. doi: 10.1109/TCYB.2019.2960605

Google Scholar

47. Wang, Z, Guo, Q, Sun, S, and Xia, C. The impact of awareness diffusion on SIR-like epidemics in multiplex networks. Appl Math Comput (2019). 349:134–47. doi: 10.1016/j.amc.2018.12.045. CrossRef Full Text

Google Scholar

48. Li, J, Wang, J, Sun, S, and Xia, C. Cascading crashes induced by the individual heterogeneity in complex networks. Appl Math Comput (2018). 323:182–92. doi: 10.1016/j.amc.2017.11.059. CrossRef Full Text

Google Scholar

49. Javarone, MA. Network Strategies in the Election Campaigns. J Stat Mech - Theory Exp (2014). 8:P08013. doi: 10.1088%2F1742-5468%2F2014%2F8%2FP08013

CrossRef Full Text | Google Scholar

50. Javarone, MA, and Squartini, T. Conformism-driven phases of opinion formation on heterogeneous networks: The q-voter model case. J Stat Mech - Theory Exp (2015). P10002. doi: 10.1088%2F1742-5468%2F2015%2F10%2FP10002

Google Scholar

51. Galam, S, and Cheon, T. Tipping Point Dynamics: A Universal Formula, arXiv:1901.09622v1 (2019).

Google Scholar