Seismic Response Time-Frequency Analysis of Bedding Rock Slope

Introduction

The Sichuan-Tibet railway starts from Chengdu, passes through Ya'an, Kangding, Changdu, and Linzhi to Lhasa, with a total length of 1,800 km. Influenced by the collision and compression of the Indian plate on the Eurasian plate, the terrain along the Sichuan-Tibet railway is characterized by high mountains, deep valleys, and crisscross gullies. There are many active fault zones in the transition zone between the plateau and the basin, which are the root cause of earthquakes. Frequent seismic activity and a fragile geological environment are factors that easily induce large-scale landslides. The Wenchuan Ms 8.0 earthquake, Lushan Ms 7.0 earthquake, and Ludian Ms 6.5 earthquake have all caused a large number of slope collapses [1–4]. The bedding rock slope is a very common type of slope distributed in the Sichuan-Tibet railway construction area [5, 6]. Due to the influence of internal structural characteristics, the stability of this type of slope is poor, and it is very prone to collapse in the event of an earthquake [7, 8]. This seriously affects the safety of the Sichuan-Tibet railway during the construction and operation period.

Seismic stability of bedding rock slopes has always been a hot issue in geological disaster research. In general, the most commonly used method in stability analysis is the quasi-static method. In this method, the influence of peak ground motion parameters on slope stability is considered, and the instantaneous action of earthquake is equivalent to load acting on the center of gravity of sliding mass [9–12]. Earthquake modeling in the laboratory scale is one of the most powerful methods to reveal the dynamic response and failure process of slopes in the event of strong earthquakes [13–15]. Li L Q [16] studied the seismic response of bedding and toppling rock slope through large-scale shaking table tests. According to the acceleration and earth pressure of different parts of the slope, it was found that the acceleration amplifying factor was larger than the earth pressure amplifying factor at the slope surface. The earth pressure amplifying factor at the top surface for a toppling rock slope was close to that of a bedding rock slope. Fan G [17] also used a shaking table test to study the bedding slope with a weak interlayer. The results show that the dynamic failure mode of the slope mainly included the horizontal and vertical staggered cracks, the extrusion of the weak interlayer, and the fracture of the slope top. Salmi and Hosseinzadeh [18] used the Universal Distinct Element Code software package to evaluate the stability of rock slope and identify the critical failure mode. The study found that bedding sliding was the main failure mode of the slope, and the nature of discontinuities plays a key role in the slope instability. Liu et al. [19] used the programming language FISH in FLAC (3D) to realize the process of slope vibration degradation, and used the numerical calculation method to analyze the stability of the slope in the event of an earthquake and the long-term stability of the slope under frequent microseisms. The above study only considers the acceleration and earth pressure parameters of the seismic wave, and ignores the influence of the frequency and duration of the seismic wave on the slope stability.

In the whole process of earthquake motion, the seismic wave is very complex, and the slope will show obvious non-linear characteristics [20, 21]. Hilbert-Huang transform (HHT) is a self-adaptive time-frequency analysis method suitable for non-linear and unstable signal processing proposed by Huang et al. [22]. This method has high time-frequency resolution for seismic signals, and can more accurately describe the energy distribution of seismic signals in time-frequency. Moreover, the Hilbert marginal spectrum obtained by integrating the Hilbert spectrum represents the distribution of the signal energy amplitude in the frequency domain. Therefore, HHT has been widely used in the seismic response analysis of non-linear non-stationary dynamic systems in the field of civil engineering [23–25].

In this paper, the potential rock bedding slope disaster points in the Sichuan-Tibet railway construction area are selected, and the similar system of the model is designed. The shaking table test of the rock bedding slope with a weak structural plane is carried out to study the seismic dynamic response characteristics and failure process of this kind of slope. On this basis, the HHT method is used to analyze the characteristics of seismic waves in time and frequency domains. The results can provide reference for the formulation of slope disaster prevention and mitigation measures.

Overview of Shaking Table Test

A shaking table physical simulation test is one of the most powerful means of revealing the strong vibration response and failure process of slopes [26, 27]. An earthquake simulation shaking table test was carried out in the laboratory of the School of Architecture and Civil Engineering, Xinyang Normal University. The shaking table is a large-scale one-way seismic simulation shaking table with a table size of 3 × 3 m. The table structure is a steel welded single-layer grid. The maximum load capacity of the table is 10 t and the maximum speed is 0.7 m/s. The frequency of this shaking table is 0.1–50 Hz, the displacement range is ±125 mm, and the maximum acceleration is 15 m/s², which can meet the requirements of this shaking table test. This test uses a 64-channel BBM data acquisition system, the maximum reference error ≤ 0.5%. The signal adaptor is connected to the charge converter to convert the voltage signal, the maximum reference error is ≤ 1 %. Data acquisition, monitoring signal, and online analysis are carried out synchronously, as shown in Figure 1.

FIGURE 1

Figure 1. Data acquisition system for shaking table test.

Design and Manufacture of Slope Model

The model box used in this model test is a rigid model box welded by angle steel, channel steel, and steel plate. The model box is 2.0 m long, 2.0 m wide and 1.5 m high, as shown in Figure 2. A polyethylene foam with a thickness of 10 cm is placed between the steel plate and the model as a shock-absorbing layer to reduce the influence of the model box boundary effect [26]. The slope prototype is the bedding rock slope at the exit of a tunnel on the Sichuan-Tibet railway. In this test, the density (ρ), elastic modulus (E), and geometric size (L) are used as control parameters, and a similar system of the model is designed through the “π theorem” [28, 29]. The scale ratio of the model is 1:10, and the time similarity ratio is 1:3.16. Simplifying the slope to facilitate model establishment. After simplification, the slope angle of the rock layer is 35° and the slope foot angle is 60°. The thickness of the rock layer is 6 cm and the thickness of the weak interlayer is 1 cm, as shown in Figure 3. In addition, the raw materials of the simulation materials used in the experiment are gypsum, clay, river sand, and water [30]. Through repeated material ratio tests, it is determined that the ratio of the simulated rock material is gypsum:clay:river sand:water = 1:5.38:1.52:0.27, and the ratio of the weak structure plane simulated material is clay:river sand:water = 1:6.89:0.25. Through density tests, direct shear tests, and triaxial compression tests, the density of the rock material is 1.908 g/cm³, the cohesion is 15.5 kPa, the internal friction angle is 37.9°, the density of the structural surface material is 1.72 g/cm³. The cohesion force is 2.7 kPa and the internal friction angle is 41.7°.

FIGURE 2

Figure 2. Test model box.

FIGURE 3

Figure 3. Test model.

Measuring Point Layout

In this test, one-way acceleration sensors, three-way acceleration sensors, and cable displacement sensors are arranged at different positions in the slope model to obtain the seismic response of the bedding rock slope. The acceleration sensor adopts the three-way acceleration sensor (Type: 1C101) and one-way acceleration sensor (Type: 1C301) produced by the Donghua Testing Company. One-way acceleration sensors are mainly used to test the distribution of the acceleration field in the bedrock, and three-way acceleration sensors are used to monitor the acceleration field in the slope. The cable displacement sensors are also produced by the Donghua Testing Company and its type is 5G203. It is used to monitor the displacement change of the slope during the earthquake. In addition, in order to more accurately describe the response of the entire model during the earthquake, this test used an independently developed high-frequency digital camera system to record it. The layout of the measuring points is shown in Figure 4.

FIGURE 4

Figure 4. Arrangement of measuring points of the shaking table.

Loading Mode

According to the results of field investigation and seismic risk assessment, the Wenchuan Wolong wave and El Centro wave are selected for loading in this test. The acceleration peak value of the input seismic wave is normalized, and the duration is adjusted according to a similar relationship. Figure 5 shows the two kinds of adjusted seismic wave acceleration time-history curves. The acceleration peaks of the two seismic waves are 0.1, 0.2, 0.4, 0.7, and 0.9 g, respectively, and load in order from small to large. Before each peak earthquake wave is loaded, the model is scanned for white noise with an amplitude of 0.05 g. The loading conditions are shown in Table 1.

FIGURE 5

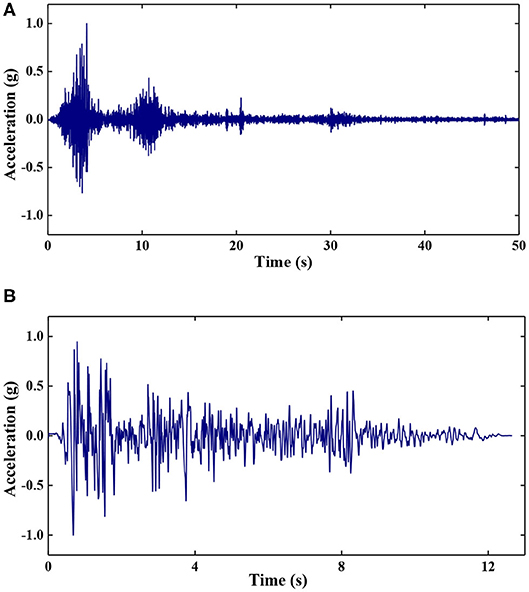
Figure 5. Horizontal seismic wave acceleration curve after adjustment of test input. (A) Acceleration time-history curve of the Wenchuan Wolong wave and (B) Acceleration time-history curve of the El Centro wave.

TABLE 1

Table 1. Loading condition of shaking table test.

Seismic Response of the Bedding Rock Slope

Acceleration Amplification Effect of the Slope

Under the action of an earthquake, the acceleration response of different parts of the slope often present different changing laws [31, 32]. In this test, the Y-direction acceleration of measuring points A1, A2, A3, A4, and A5 is taken as the basis of the acceleration response of the slope surface, and the Y-direction acceleration of measuring points A1, A6, A7, A8, and A9 is taken as the basis of the acceleration response of the slope body. The acceleration peak amplification factor (PGA) is defined as the ratio of the y-direction acceleration peak value of each measuring point above to the y-direction acceleration peak value of the A10 measuring point, which is arranged on the vibration table top. Taking the El Centro earthquake wave as an example, the variation law of the slope and PGA with different heights under different seismic amplitudes is described.

Figures 6A,B show the variation of PGA with elevation at each measurement point in the slope and at the slope surface at different seismic amplitudes. The GPA on the slope surface gradually increased along the height direction, while the GPA of the slope body showed a trend of decreasing first and then increasing. The bedding rock slope has an obvious “elevation effect” under earthquake action. With the increase of seismic amplitude, the dynamic shear strength and modulus of slope materials decrease gradually, while the damping ratio increases, which enhances the isolation and damping capabilities of the slope. In the process of seismic wave propagation from bottom to top, the loss of energy increases, the PGA amplification coefficient of each measuring point decreases gradually, and the elevation effect decreases. When the amplitude of the seismic wave reaches 0.9 g, the GPA amplification coefficient of the slope and each measuring point of the slope decreases significantly, especially at the height of 100 cm.

FIGURE 6

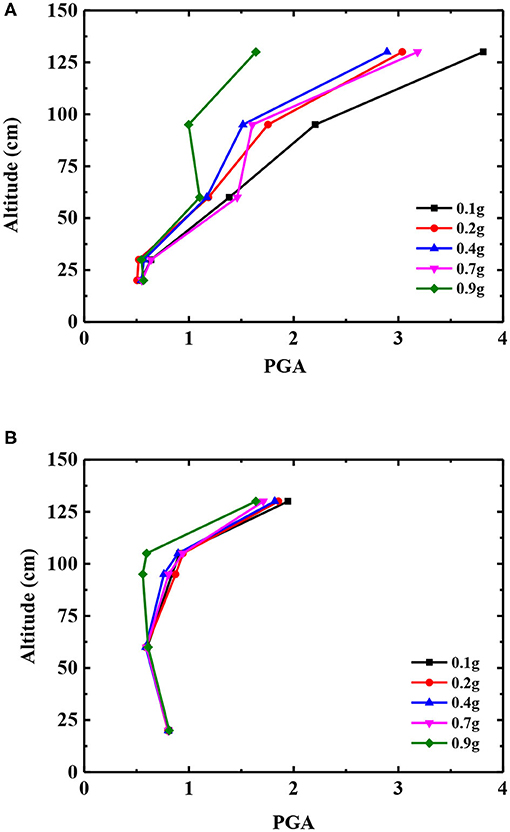
Figure 6. PGA of slope surface and body under different seismic amplitudes. (A) Slope surface and (B) Slope body.

The reason for the above phenomenon is that the internal structure of the slope is damaged. Under the action of a 0.9 g earthquake, the middle and upper part of the slope gradually slide down along the interlayer structure, and the rear edge of the slope begins to separate from the model box. Due to the block of the middle and lower “locking section” of the slope body, there are tensile cracks perpendicular to the rock layer at the height of 100 cm on the slope surface, as shown in Figure 7. The top of the slope is gradually separated from the slope body, and the inconsistency of the movement of the slope on both sides of the structural plane increases, so the GPA magnification coefficient decreases. In addition, the internal friction and friction energy consumption of the block increase, which further reduces the amplification coefficient of GPA.

FIGURE 7

Figure 7. Failure phenomenon of the bedding rock slope. (A) Left view and (B) Front view.

Acceleration Response Spectrum of Slope

The shape of the acceleration response spectrum of the bedding rock slope under earthquake action has important reference value for understanding the dynamic response characteristics of the slope. In this section, the Y-acceleration time history of each measuring point of the slope and the slope under the action of an El Centro seismic wave with a peak acceleration of 0.2 g is selected for analysis. It is worth noting that this acceleration response spectrum calculation uses the damping ratio commonly used in engineering 5% [33].

It can be seen from Figure 8 that the peak of the acceleration response spectrum gradually increases along the elevation under the action of the 0.2 g El Centro seismic wave. The shape of the acceleration response spectrum of the slope has a double peak in the lower part of the slope (height below 60 cm), and single peak in the upper part (height above 60 cm). The excellent period is concentrated around T = 0.6 s, and the amplitude of the response spectrum corresponding to the short period (T = 0.0–1.2 s) has a certain amplification along the elevation. The shape of the acceleration response spectrum of the slope along elevation is basically the same, the predominant period is approximately T = 0.4 s, and the amplitude of the response spectrum corresponding to the short period part (T = 0.0–1.2 s) also has a certain amplification effect along elevation. Compared with the amplitude of the acceleration response spectrum of the slope surface and slope body, the peak value of the acceleration response spectrum of the slope surface above 25 cm is obviously larger than that of the slope body. The difference value gradually increases with the elevation, showing the “trend effect.”

FIGURE 8

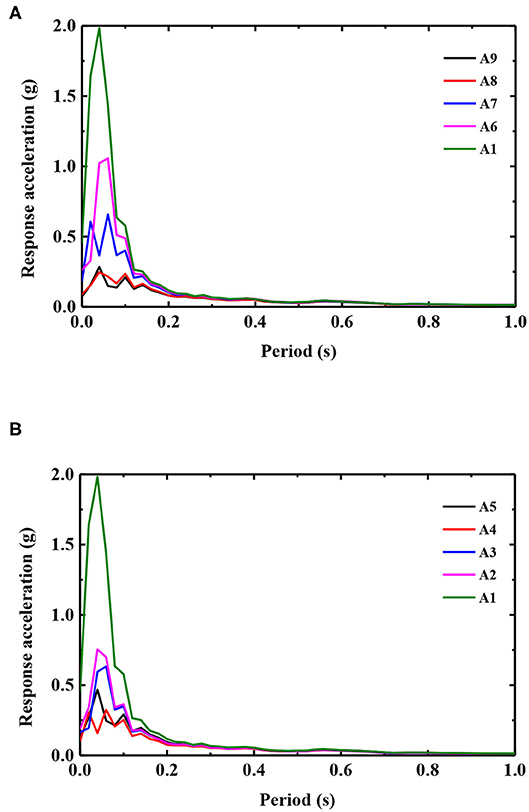
Figure 8. Acceleration response spectrum of the slope surface and body under 0.2 g seismic amplitude. (A) Slope surface and (B) Slope body.

Displacement Response of the Slope

Figure 9 shows the displacement of the slope surface under different earthquake amplitudes. Under the peak earthquake of 0.1, 0.2, 0.4, and 0.7 g, the displacement response of the slope surface is smaller, and the displacement of each measuring point is <5 mm. When the amplitude of the seismic wave reaches 0.9 g, the displacement of the slope increases significantly, and the slope begins to be damaged. In addition, due to the existence of an interlayer structure surface, the movement of different parts of the slope is not consistent, and the displacement of the slope increases with the increase of elevation. With the increase of seismic amplitude, the non-uniform movement between the rock layers further increases. As a result, the shear slip of the top of the slope relative to the main body, the separation of the back edge of the slope and the model box, and the tension crack gradually extend to the structural plane in the slope locking section, which causes the whole slope to fail.

FIGURE 9

Figure 9. Displacement of the slope surface with different seismic amplitudes.

Seismic Response Time-Frequency Analysis

Hilbert-Huang Transform

A Hilbert-Huang transform includes two parts: EMD empirical mode decomposition and Hilbert spectrum analysis. EMD empirical mode decomposition assumes that any signal is a composite signal composed of different intrinsic modal functions (IMFs), and each IMF component must meet two conditions: (1) the number of extreme points and zero crossing points were the same or have at most one difference, (2) the mean of the upper and lower envelope of the signal was zero. In this way, any signal can be decomposed into multiple IMFs. Then, the Hilbert spectrum and marginal spectrum are obtained by Hilbert transformation for each eigenmode function [34, 35].

For the seismic signal F(t), which was decomposed into multiple IMFs, its Hilbert transformation is as follows:

$\begin{array}{ll}G(t)=\frac{1}{\pi }K{\displaystyle {\int }_{-\infty }^{\infty }}\frac{F(\delta )}{t-\delta }d\delta & (1)\end{array}$

where K is a Cauchy principal value. Established analytic signal P(t):

$\begin{array}{ll}P(t)=F(t)+jG(t)=a(t)e^{j\Phi (t)}& (2)\end{array}$

where a(t) is the amplitude function; and Φ(t) is the phase function.

$\begin{array}{ll}a(t)=\sqrt{F^2(t)+G^2(t)}& (3)\end{array}$

$\begin{array}{ll}\Phi (t)=arctan\frac{G(t)}{F(t)}& (4)\end{array}$

The instantaneous frequency of the signal could be obtained by differentiating the phase. Therefore, the Hilbert transform of the decomposed IMF component can obtain the distribution law of the signal on the time-frequency-energy scale, which is the form of the Hilbert spectrum:

$\begin{array}{ll}H(\omega ,t)=Re{\displaystyle \sum _{i=1}^{n+1}}{a}_i(t)·e^{j\int {\omega }_i(t)dt}& (5)\end{array}$

By integrating the time in the expression formula of the Hilbert spectrum, the distribution law of the signal on the frequency-amplitude scale can be obtained, which is the form of the corresponding marginal spectrum:

$\begin{array}{ll}h(\omega ,t)={\displaystyle {\int }_{-\infty }^{\infty }}H(\omega ,t)dt& (6)\end{array}$

Hilbert Spectrum Analysis

According to the above method, the acceleration time history of each measuring point on the slope under the action of 0.1, 0.2, 0.4, 0.7, and 0.8 g Wenchuan Wolong seismic waves is transformed by HHT. The Hilbert spectrum of each measuring point under the action of different amplitude seismic waves is obtained. The characteristics of the seismic signal energy in the time-frequency domain are represented by a two-dimensional plane contour map, and the Hilbert spectrum under the action of a 0.2 g Wenchuan Wolong seismic wave is shown in Figures 10, 11.

FIGURE 10

Figure 10. Hilbert spectrum of the slope surface. (A) A1, (B) A6, (C) A7, (D) A8, and (E) A9.

FIGURE 11

Figure 11. Hilbert spectrum of the slope body. (A) A1, (B) A2, (C) A3, (D) A4, and (E) A5.

According to the comprehensive analysis of Figures 10, 11, it can be found that the Hilbert Huang transform can accurately describe the time-frequency characteristics of the seismic signal. From Figures 10, 11, it can be seen that the energy of the Wenchuan Wolong earthquake wave gradually increases from bottom to top. In the time domain, the energy is mainly concentrated in 2–6 and 12–15 s, corresponding to the time node when the compression wave of the Wolong earthquake reaches the double peak value. The predominant frequency is concentrated between 5 and 40 hz. With the increase of elevation, the former increases and the latter decreases. The above phenomenon may be related to the first natural frequency of the slope test model, which causes the amplification of the surrounding frequency components. This is consistent with the conclusion that the slope soil has a filtering effect on the high frequency component of the seismic wave and an amplifying effect on the low frequency component [36, 37]. For the bedding rock slope soil, the natural frequency is relatively small, which can enlarge the frequency band around the natural frequency of the seismic wave, and filter the frequency band in other ranges.

Hilbert Marginal Spectrum Analysis

The Hilbert energy spectrum of each measuring point on the slope under the action of 0.1, 0.2, 0.3, 0.4, and 0.6 g Wenchuan Wolong seismic waves is integrated in time, and the Hilbert marginal spectrum of each measuring point under the action of different amplitude seismic waves is obtained. The marginal spectrum of the slope under the action of 0.2 and 0.9 g Wenchuan Wolong seismic waves is shown in Figures 12, 13.

FIGURE 12

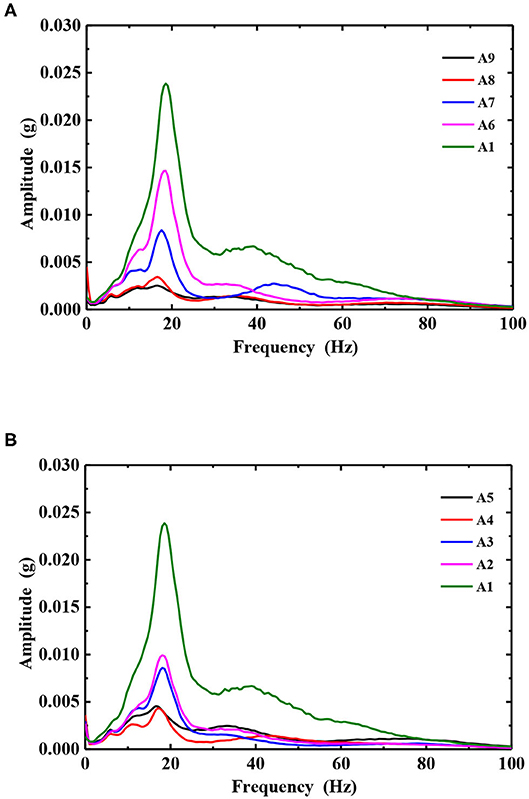
Figure 12. The Hilbert marginal spectrum of the slope surface and body under 0.2 g of seismic amplitude. (A) Slope surface and (B) Slope body.

FIGURE 13

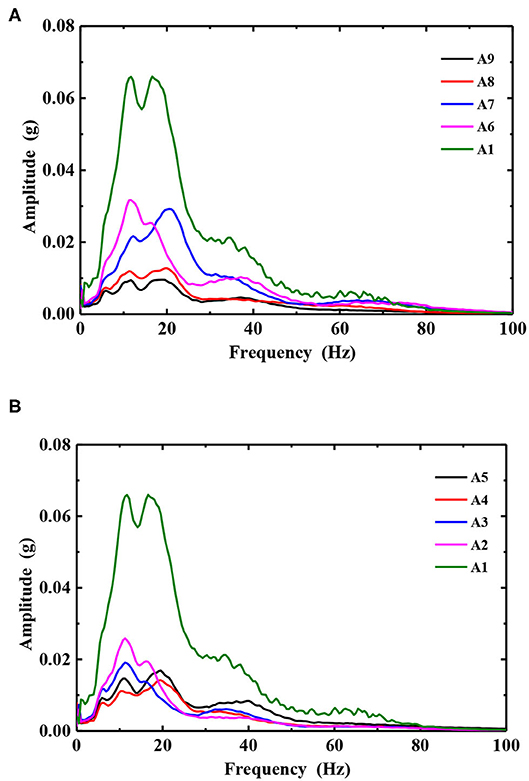
Figure 13. The Hilbert marginal spectrum of slope surface and body under 0.9 g of seismic amplitude. (A) Slope surface and (B) Slope body.

It can be seen from Figures 12, 13 that under the action of a 0.2 g seismic wave, the shape of the marginal spectrum of each measuring point on the slope and in the slope is basically the same, all of which are single peaks. The distribution of the marginal spectrum frequency is relatively pure, and the predominant frequency is about 18 Hz. The peak value of the marginal spectrum increases with the increase of elevation. Under the action of a 0.6 g seismic wave, the shape of the marginal spectrum changes from a single peak to a double peak. The predominant frequency of A1, A2, and A3 measuring points has changed, which is concentrated around 12 Hz. That is to say, with the increase of the peak value of the input ground motion, the high frequency component of the site is weakened and the low frequency component is increased. The A6 and A7 measuring points of the slope surface have a similar marginal spectral peak, while the A3, A4, and A5 measuring points of the slope body have a similar marginal spectral peak. The difference of the peak value of the marginal spectrum indicates that earthquake damage has occurred in the slope [23, 25]. In order to further reveal the damage development process of the slope, the peak value of the marginal spectrum of each measuring point under the action of different amplitude seismic waves is extracted for analysis, as shown in Figures 14, 15.

FIGURE 14

Figure 14. PGA of the slope surface under different amplitudes.

FIGURE 15

Figure 15. PGA of the slope body under different amplitudes.

Figures 14, 15 show the energy change characteristics in the frequency domain during the bottom-up propagation of the seismic wave in the slope. Under the action of 0.1, 0.2, 0.4, and 0.7 g seismic waves, the peak value of the marginal spectrum increases linearly with the height, and there is no obvious inflection point for the peak value of the marginal spectrum. It shows that the continuity of each part of the slope is good, and that the energy of the seismic wave can be transferred upward smoothly. When the seismic amplitude reaches 0.9 g, the change rule of the peak value of the marginal spectrum under the height of 100 cm on the slope does not change. The turning point can be seen at the height of 100 cm on the slope surface, and the same phenomenon also occurs in the slope body. The peak value of the marginal spectrum above 100 cm on the slope is basically consistent with that under a 0.7 g seismic wave. It shows that there is damage and a tension crack at the height of 100 cm, which affects the upward propagation of the seismic wave. The degree of earthquake damage near the slope is stronger than that inside the slope. However, the slope has good continuity at other positions without damage. This is basically consistent with the failure phenomenon observed in the test.

Conclusion

In this paper, based on the large-scale shaking table experiment of similar materials and the HHT method, the seismic dynamic response and instability mechanism of the bedding rock slope under different seismic amplitude values are systematically studied, and the following conclusions are drawn:

Firstly, the bedding rock slope has an obvious elevation effect under earthquake action. With the increase of the seismic amplitude value, the energy loss of the seismic wave in the process of bottom-up propagation increases, the PGA amplification coefficient of the slope body and each measuring point of the slope decreases gradually, and the elevation effect weakens. When the amplitude of the seismic wave reaches 0.9 g, the GPA amplification coefficient of the slope and each measuring point of the slope decreases significantly, especially at the height of 100 cm.

Secondly, under the action of an earthquake, the peak value of the acceleration response spectrum of the slope gradually increases along the elevation. The shape of the acceleration response spectrum of the slope has a double peak value in the lower part (height below 60 cm) and a single peak value in the upper part (height above 60 cm). The predominant period is about t = 0.6 s. The acceleration response spectrum of the slope body is basically the same along the elevation, and the predominant period is about t = 0.4 s. Compared with the amplitude of the acceleration response spectrum of the slope surface and the slope body, the peak value of the acceleration response spectrum of the slope surface above 25 cm is significantly higher than that of the slope body, showing a trend effect.

Thirdly, due to the existence of an interlayer structural plane, the movement of different parts of the slope is not consistent, and the displacement of the slope increases with the increase of elevation. The failure mechanism of the bedding rock slope is mainly divided into two stages. The first stage: under the action of gravity and seismic force, the top rock of the slope starts to slide along the structural plane, the trailing edge of the slope is separated from the model box, and a tensile crack that gradually expands into the structural plane is generated in the locking section of the slope. The second stage: as the ground motion continues, the inconsistent motion between the rock layers increases further, the tensile cracks penetrate the structural plane, the top slope body slides out along the shear slip surface, and the entire slope becomes unstable and is destroyed.

Fourthly, the characteristics of the seismic signal in time–frequency domain can be better described by the Hilbert Huang transform. In the time domain, the energy is mainly concentrated in 2–6 and 12–15 s, corresponding to the time node when the compression wave of the Wolong earthquake reaches the double peak value. The predominant frequency is concentrated between 5 and 40 hz. With the increase of elevation, the former increases and the latter decreases.

Fifthly, the change of the peak value of the marginal spectrum clearly shows the development process of the earthquake damage inside the slope. The change rule of the peak value of the marginal spectrum under the height of 100 cm of the slope has not changed. At the height of 100 cm, the inflection point can be seen obviously, and the same phenomenon also occurs in the slope. It shows that the damage occurs at the height of 100 cm, and the degree of earthquake damage near the slope is stronger than that inside the slope. The recognition results of the marginal spectrum are in good agreement with the experimental results.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author Contributions

LZ was the site representative of the field tests. CY was the project administrator and the person responsible for model tests, they proposed the research ideas. SM finished the first version of the manuscript. XG and MY finished the data process work. YL helped LZ finish the field tests. All authors contributed to the article and approved the submitted version.

Funding

This study was supported in part by the National Key Research and Development Plan (No. 2018YFE0207100); the Natural Science Foundation of China (Contract No. 41731288); the Sichuan Provincial Science and Technology Support Project (Nos. 18MZGC0186, 18MZGC0247, 2018JY0549); the China National Railway Group Co. Ltd Scientific Research Project (Nos. SY2016G003, N2019G002; P2019T001); the China Academy of Railway Sciences Corporation Limited Research and Development Fund (No. 2019YJ026); the 2017–2019 Young Elite Scientist Sponsorship Program by CAST. 2019 Young Top Talents Sponsorship Program of China Ten Thousand People Plan (No. 2019YJ300); the 2018 Sichuan Province Ten Thousand People Plan; the Nanchang Railway Bureau Scientific Research Project (No. 20171106), and the China Railway Eryuan Engineering Group Co. Ltd Scientific Research Project [No. KYY2019145(19-20)].

Conflict of Interest

The authors declare that this study received funding from China National Railway Group Co. Ltd, China Academy of Railway Sciences Corporation Limited, and China Railway Eryuan Engineering Group Co. Ltd. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.

References

1. Huang R, Fan X. The landslide story. Nat Geosci. (2013) 6:325–6. doi: 10.1038/ngeo1806

CrossRef Full Text | Google Scholar

2. Tang C, Ma G, Chang M, Li WL, Zhang DD, Jia T. Landslides triggered by the 20 April 2013 Lushan earthquake, Sichuan province, China. Eng Geol. (2015) 187:45–55. doi: 10.1016/j.enggeo.2014.12.004

CrossRef Full Text | Google Scholar

3. Wang WP, Yin YP, Yang LW, Zhang N, Wei YJ. Investigation and dynamic analysis of the catastrophic rockslide avalanche at Xinmo, Maoxian, after the Wenchuan Ms 8.0 earthquake. Bull Eng Geol Environ. (2020) 79:495–512. doi: 10.1007/s10064-019-01557-4

CrossRef Full Text | Google Scholar

4. Yingying T, Chong X, Jian C. Spatial distribution and susceptibility analyses of pre-earthquake and coseismic landslides related to the Ms 6.5 earthquake of 2014 in Ludian, Yunan, China. Geocarto Int. (2016) 32:978–89. doi: 10.1080/10106049.2016.1232316

CrossRef Full Text | Google Scholar

5. Zhang S, Guang-Ze Z, Liang-Wen J, Guang WU. Analysis of the characteristics of major geological disasters and geological alignment of Sichuan-Tibet railway. Railway Stand Des. (2016) 1:14–9. doi: 10.13238/j.issn.1004-2954.2016.01.003

CrossRef Full Text

6. Huang R, Li W. Research on development and distribution rules of Geohazards induced by Wenchuan earthquake on 12th May. Chin J Rock Mech Eng. (2008) 27:2585–92. doi: 10.3321/j.issn:1000-6915.2008.12.028

CrossRef Full Text

7. Chigira M, Wu X, Inokuchi T, Wang G. Landslides induced by the 2008 Wenchuan earthquake, Sichuan, china. Geomorphology. (2010) 118:225–38. doi: 10.1016/j.geomorph.2010.01.003

CrossRef Full Text | Google Scholar

8. Zhen-Lin C, Xiao HU, Qiang XU. Experimental study of motion characteristics of rock slopes with weak intercalation under seismic excitation. J Mt Sci. (2016) 13:178–88. doi: 10.1007/s11629-014-3212-0

CrossRef Full Text | Google Scholar

9. Yin Y, Sun P, Zhang M, Li B. Mechanism on apparent dip sliding of oblique inclined bedding rockslide at Jiweishan, Chongqing, China. Landslides. (2011) 8:49–65. doi: 10.1007/s10346-010-0237-5

CrossRef Full Text | Google Scholar

10. Yu-Chuan Y, Hui-Ge X, Xing-Guo Y, Ming-Liang C, Jia-Wen Z. Experimental study on the dynamic response and stability of bedding rock slopes with weak interlayers under heavy rainfall. Environ Earth Sci. (2018) 77:433. doi: 10.1007/s12665-018-7624-y

CrossRef Full Text | Google Scholar

11. Danqing S, Ailan C, Zhu C, Xiurun G. Seismic stability of a rock slope with discontinuities under rapid water drawdown and earthquakes in large-scale shaking table tests. Eng Geol. (2018) 245:153–68. doi: 10.1016/j.enggeo.2018.08.011

CrossRef Full Text | Google Scholar

12. Gischig VS, Eberhardt E, Moore JR, Hungr O. On the seismic response of deep-seated rock slope instabilities–insights from numerical modeling. Eng Geol. (2015) 193:1–18. doi: 10.1016/j.enggeo.2015.04.003

CrossRef Full Text | Google Scholar

13. Brito VP, Costa RF, Gomes MAF, Parteli EJR. Sliding susceptibility of a rough cylinder on a rough inclined perturbed surface. Physica A. (2003) 335:47–58. doi: 10.1016/j.physa.2003.11.012

CrossRef Full Text | Google Scholar

14. Parteli EJR, Gomes MAF, Brito VP. Nontrivial temporal scaling in a Galilean stick-slip dynamics. Phys Rev E Stat Nonlin Soft Matter Phys. (2005) 71(3 Pt 2A):036137. doi: 10.1103/PhysRevE.71.036137

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Parteli EJR, Gomes MAF, Montarroyos E, Brito VP. Omori law for sliding of blocks on inclined rough surfaces. Physica A. (2001) 292:536–44. doi: 10.1016/S0378-4371(00)00629-4

CrossRef Full Text | Google Scholar

16. Long-qi L, Neng-pan J, Zhang S, Deng XX. Shaking table test to assess seismic response differences between steep bedding and toppling rock slopes. Bull Eng Geol Environ. (2017) 78:1–13. doi: 10.1007/s10064-017-1186-1

CrossRef Full Text | Google Scholar

17. Fan G, Zhang J, Wu J, Yan K. Dynamic response and dynamic failure mode of a weak intercalated rock slope using a shaking table. Rock Mech Rock Eng. (2016) 49:1–14. doi: 10.1007/s00603-016-0971-7

CrossRef Full Text | Google Scholar

18. Salmi EF, Hosseinzadeh S. Slope stability assessment using both empirical and numerical methods: a case study. Bull Eng Geol Environ. (2015) 74:13–25. doi: 10.1007/s10064-013-0565-5

CrossRef Full Text | Google Scholar

19. Liu X, Liu Y, He C, Li X. Dynamic stability analysis of the bedding rock slope considering the vibration deterioration effect of the structural plane. Bull Eng Geol Environ. (2018) 77:87–103. doi: 10.1007/s10064-016-0945-8

CrossRef Full Text | Google Scholar

20. Yang C, Zhang J, Zhang M. A prediction model for horizontal run-out distance of landslides triggered by Wenchuan earthquake. Earthquake Eng Eng Vibr. (2013) 12:201–8. doi: 10.1007/s11803-013-0163-3

CrossRef Full Text | Google Scholar

21. Dong LJ, Wesseloo J, Potvin Y. Discriminant models of blasts and seismic events in mine seismology. Int J Rock Mech Min Sci. (2016) 86:282–91. doi: 10.1016/j.ijrmms.2016.04.021

CrossRef Full Text | Google Scholar

22. Huang NE, Shen Z, Long SR, Wu MC, Shih HH, Zheng Q. et al. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis. Proceedings A. (1998) 454:903–95. doi: 10.1098/rspa.1998.0193

CrossRef Full Text | Google Scholar

23. Fan G, Zhang JJ, Fu X, Zhou LR. Dynamic failure mode and energy-based identification method for a counter-bedding rock slope with weak intercalated layers. J Mt Sci. (2016) 13:2111–23. doi: 10.1007/s11629-015-3662-z

CrossRef Full Text | Google Scholar

24. Fan G, Zhang LM, Zhang JJ, Yang CW. Time-frequency analysis of instantaneous seismic safety of bedding rock slopes. Soil Dyn Earthquake Eng. (2017) 94:92–101. doi: 10.1016/j.soildyn.2017.01.008

CrossRef Full Text | Google Scholar

25. Yan K, Liu F, Zhu C, Wang Z, Zhang J. Dynamic responses of slopes with intercalated soft layers under seismic excitations. Chin J Rock Mech Eng. (2017) 36:2686–98. doi: 10.13722/j.cnki.jrme.2017.0440

CrossRef Full Text

26. Huang R, Li G, Ju N. Shaking table test on strong earthquake response of stratified rock slopes. Chin J Rock Mech Eng. (2013) 32:865–75. doi: 10.3969/j.issn.1000-6915.2013.05.003

CrossRef Full Text | Google Scholar

27. Xu Q, Liu H, Zou W, Fan X, Chen J. Large-scale shaking table test study of acceleration dynamic responses characteristics of slopes. Chin J Rock Mech Eng. (2010) 29:2420–8. doi: 10.1016/S1876-3804(11)60004-9

CrossRef Full Text | Google Scholar

28. Yuan W. Simulation Theory and Static Model Test. Chengdu: Southwest Jiaotong University Press (1998).

29. Zhang M. Study of similitude laws for shaking table tests. Earthquake Eng Eng Vibr. (1997) 17:52–8. doi: CNKI:SUN:DGGC.0.1997-02-006

30. Changwei Y, Xinmin L, Jianjing Z, Zhiwei C, Cong S, Hongbo G. Analysis on mechanism of landslides under ground shaking: a typical landslide in the Wenchuan earthquake. Environ Earth Sci. (2014) 72:3457–66. doi: 10.1007/s12665-014-3251-4

CrossRef Full Text | Google Scholar

31. Chen XL, Gao RX, Gong W. Random seismic response and dynamic fuzzy reliability analysis of bedding rock slopes based on pseudoexcitation method. Int J Geomech. (2018) 18:04017165. doi: 10.1061/(ASCE)GM.1943-5622.0001084

CrossRef Full Text | Google Scholar

32. Dong L, Wesseloo J, Potvin Y, Li X. Discrimination of mine seismic events and blasts using the fisher classifier, naive Bayesian classifier and logistic regression. Rock Mech Rock Eng. (2016) 49:183–211. doi: 10.1007/s00603-015-0733-y

CrossRef Full Text | Google Scholar

33. Yang-Chang W. Research on the Ground Motion Characteristics of Rock Slope and the Landslide Genesis Mechanism, Stability Identification and Damage Scope Evaluation System of Base-Covered Slope. Chengdu: Southwest Jiaotong University (2013).

34. Huang NE. Introduction to the Hilbert-Huang transform and its related mathematical problems. Interdiscip Math. (2005) 1–26. doi: 10.1142/9789812703347_0001

CrossRef Full Text | Google Scholar

35. Huang NE, Wu Z. A review on Hilbert-Huang transform: method and its applications to geophysical studies. Rev Geophys. (2008) 46:1–23. doi: 10.1029/2007RG000228

CrossRef Full Text | Google Scholar

36. Changwei Y, Ning F, Jianjing Z, Junwei B, Jun Z. Research on time-frequency analysis method of seismic stability of covering-layer type slope subjected to complex wave. Environ Earth Sci. (2015) 74:5295–306. doi: 10.1007/s12665-015-4540-2

CrossRef Full Text | Google Scholar

37. Dong L, Zou W, Li X, Shu W, Wang Z. Collaborative localization method using analytical and iterative solutions for microseismic/acoustic emission sources in the rockmass structure for underground mining. Eng Fract Mech. (2018) 210:95–112. doi: 10.1016/j.engfracmech.2018.01.032

CrossRef Full Text | Google Scholar