Analysis of Stock Price Motion Asymmetry via Visibility-Graph Algorithm

1. Introduction

The use of network science to perform time series analysis has emerged in recent decades. Of the numerous approaches to rendering a time series into a complex network, three major categories of approaches have most attracted researchers’ attention [1–11]. The first approach uses recurrence networks and was introduced by Donner and Zou et al. in 2009 [5–8]. This approach analyzes phase space recurrence of a time series from a geometric point of view by interpreting the recurrence matrix of a time series as the adjacency matrix of a complex network. Transition networks represent the second major approach to transform a time series into a complex network. These networks are constructed by partitioning the phase space of a dynamic system and were introduced by Nicolis et al. in 2005 [9]. Hence, a node in a transition network represents a certain discrete state or pattern that describes the dynamic system. Direct links are established if one of the nodes is followed by another with nonzero probability along the time series [10]. The third category is the algorithmic group of visibility graphs (VG) [11]. In 2008, Lacasa et al. proposed an effective method called the visibility-graph algorithm (VGA) for converting a time series into a graph network by analyzing the mutual visibility relationships between points and cutting points in a computational geometry landscape [12, 13]. This concept has attracted great interest and numerous extensions of the standard VGA have been proposed. Luque et al. [14] came up with a simplified VGA called a horizontal visibility graph (HVG) to transform a time series into a complex network. Specifically, two observations are connected in an HVG if and only if there are no obstacles in between [15]. Based on the concepts of the VG and HVG, parametric VGs introduce a viewing angle $\alpha$ and allow one to study the dependence of network structural measures on $\alpha$ [16]. Limited penetrable VG (LPVG) is a less restricted HVG in which two observations are connected if either one has a larger value than the obstacles in between [17, 18].

Analyses of financial time series via a VG approach have been studied intensively [19–29]. For example, Long Yu discovered small-world characteristics in visibility-graph networks converted from the time series of the price of gold and its returns [24]. Moreover, Yao et al. found that exchange-rate networks converted from the currency-rate time series of the US dollar, euro, yen, and sterling against the Chinese yuan share consistent topological characteristics with hierarchical structures and mixed small-world and scale-free properties. They also discovered that network communities are actually composed of large numbers of trending points and small numbers of discrete peaks and trough points [25]. Furthermore, a novel method that combined VGA with link prediction was proposed by Zhang et al. to forecast the time series. Using fuzzy logic, better predictability can be achieved by fusing the direct and indirect effects of historical data [26].

Asymmetry in financial time series has generally been explored via statistical analysis [30–42]. Typically, it is found that the distribution of time horizons over which a detrended stock index moves from an arbitrary initial return to a predetermined positive level deviates to a symmetrically predetermined negative level [37–40]. This property is known as the gain-loss asymmetry and has been regarded as a characteristic of financial time series [30, 34, 36, 37]. Another well-known asymmetry, which describes the negative correlation between volatility and the direction of price motion, is the leverage effect [41]. Recently, Jiang et al. investigated asymmetry in large-scale price fluctuations. Analyses reveal that dynamic relaxation before and after large fluctuations is characterized by a power law with exponents $p_{+}$ and $p_{-}$. On minute time scales, large-fluctuation dynamics are time-reversely symmetric with $p_{+}=p_{-}$. On daily time scales, however, large price fluctuations that approach financial crashes are asymmetric with $p_{-}\ne p_{+}$ [42]. We shall point out that the results of these studies are rather generic in the sense that only the price increases and decreases are considered. In fact, price motions can be classified in more detail into accelerated or decelerated rise (AR; DR) and fall (AF; DF), depending upon the convexity or concavity of the price motion trajectories. Symmetry analysis should also be performed by taking these four types of price motion trajectories into account. However, since different price motion modes can form different convoluted temporal structures, it would be quite difficult to decompose these price movements via statistical approaches.

In this paper, we propose to study the financial time series asymmetry via visibility-graph networks based on the intuition that network approaches may be more effective in identifying different price motion trajectories. Hence the terminology of symmetry in this study specifically refers to the topological symmetry of the price motion trajectories. In particular, in a stock price series, we are concerned with whether concave and convex price motions can form a time-reversed symmetry. The research question reads as follows: whether those accelerated/decelerated price rises are statistically symmetric with those decelerated/accelerated falls. It is worth mentioning that conventional VGA analysis cannot be applied directly to investigation of the topologically asymmetric properties of financial series because the method is incapable of distinguishing different stock price rise and fall trajectories by mapping the time series as a whole onto an undirected network. To solve this problem, an idea from Yan et al. (2012) [43] is borrowed to address discrimination between price movements via visibility and invisibility-graph (IVG) networks. Using these graph networks, asymmetry in stock index motion can be measured using concave or convex indicator distributions or expected returns that are conditional on node degrees, instead of the conventional waiting-time statistics.

Recently, fruitful results have been achieved in the investigation of time series time reversibility using the HVG method [44–51]. In a study on how crises affect the motions of US stock prices, different market price behaviors are identified by examining the series irreversibility evolved over the time [50, 51]. Based on the notion that the reversed and original processes are statistically distinguishable if a stationary process is time-reversible, we may postulate that a topological symmetric time series must be a time-reversible one, and vice versa. A quantitative analysis of this postulation is also conducted.

The whole paper consists of four sections. Following the introduction of the study in Section 1, the methodology is detailed in Section 2. Asymmetry in price motion trajectories and speeds is analyzed using graph networks in Section 3 and 4, respectively. Finally, conclusions are described in Section 5.

2. Methodology

2.1. Basic Algorithms

Graph networks for AR and DF motions of a stock index can be constructed by mapping a time series of length $L$, $X\left(t_i\right)\left(i<L\right)$ onto a graph network using VGA. To start, two arbitrary data points $\left(t_a,x_a\right)$ and $\left(t_b,x_b\right)$, where $a<b,$ are specified. Two vertical lines are drawn exactly at $t_a$ and $t_b$, with heights equal to the values of $x_a$ and $x_b$, $\text{respectively}.$Next, the endpoints of the two vertical lines are connected via a straight line whenever vertical lines from any other data points within the range ($t_a,$$t_b)$ do not cut off the connection. That is, if any intermediate data point $\left(t_c,x_c\right)$ fulfills the condition

$\begin{array}{c}{x}_c<x_b+\left(x_a-x_b\right)\frac{t_b-t_c}{t_b-t_a}, a<c<b,\end{array}(1)$

the two data points $\left(t_a,x_a\right)$ and $\left(t_b,x_b\right)$ are visible to each other.

The invisibility-graph algorithm (IVGA) [43] can be used to build up the networks that describe DR and AF motions of a stock index. In contrast to the VGA, here, the data points $\left(t_a,x_a\right)$ and $\left(t_b,x_b\right)$ are connected only if the point $\left(t_c,x_c\right)$ intersects the connecting line. Hence, the relationship between these three data points is transformed into the following:

$\begin{array}{c}{x}_c>x_b+\left(x_a-x_b\right)\frac{t_b-t_c}{t_b-t_a}, a<c<b.\end{array}(2)$

Based on Yan’s study [43], three conditions are further applied to distinguish AR and DF in VG as well as DR and AF in IVG. These conditions are stated as follows:

1. Any data point in the time series can be linked only to data points located on its left-hand side.

2. The link between $\left(t_a,x_a\right)$ and $\left(t_b,x_b\right)$ ($t_a<t_b$) is connected only if $x_b>x_a$ when constructing the graph network for price increases, and vice versa when constructing the graph network for price decreases.

3. A moving time scope $S$ is used to construct a graph network throughout the entire time series; therefore, there is no link between $\left(t_a,x_a\right)$ and $\left(t_b,x_b\right)$ if $\left|a-b\right|>S$.

With these three additional conditions, VGA and IVGA can capture rise and fall trends by eliminating links converted from the short-term disturbing price motions. We demonstrate the capture of time series topological symmetry in Figures 1 and 2. The networks in Figures 1 and 2 are built from an artificial time series that combines the original Hang Seng Index sample data with its mirror-symmetric counterpart. Figure 1 shows that VGA can distinguish the concave trajectory of the price rise from other price motions. For those data points located on the concave upward trend (from node 11 to node 14 in the original HSI section and from node 24 to node 26 in the reversed HSI section), the degree numbers of AR nodes are higher. For other data points, in contrast, the degree numbers are lower. VGA can also distinguish concave decreasing price motions as well (from node 3 to node 5 in the original HSI section and from node 15 to node 19 in the reversed HSI section). In Figure 2, however, the convex trajectories of price motions are captured effectively by IVGA based on the degree distributions for price rise (from node 10 to node 12 in the original HSI section and from node 26 to node 28 in the reversed HSI section) and price fall (from node 1 to node 3 in the original HSI section and node 17 to node 19 in the reversed HSI section). Obviously, the artificial time series has perfectly symmetric price motion trajectories since the concave (convex) rise in the original HSI section has a corresponding convex (concave) fall in the reversed HSI section. The identical rising and falling degree distributions of VGs and IVGs in Figures 1 and 2 reveal that this artificial time series does have a perfect topological symmetry. Given the definition of time reversibility, a topologically symmetrical time series must be a time-reversible one. The reason lies in that if a time series is topologically symmetrical, the reversed and original processes should be statistically indistinguishable with regard to the degree distributions of nodes.

FIGURE 1

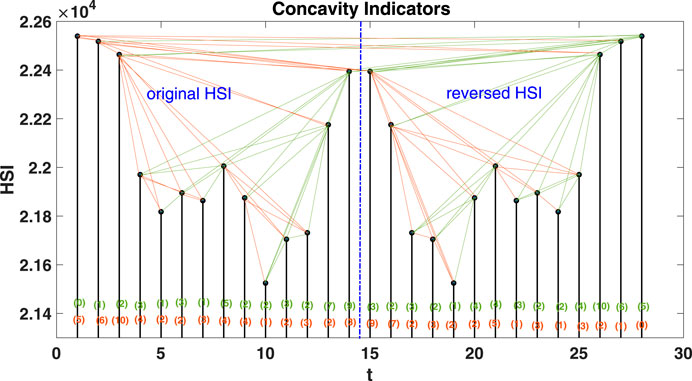
FIGURE 1. Application of VGA to the daily Hang Seng Index from August 13, 2013, to September 2, 2013, and its time-reversely mirrored data set. Note that the perfect reflection symmetry between AR [nodes 10–14] and DF [nodes 1–5] is demonstrated via identically distributed degrees in the two networks.

FIGURE 2

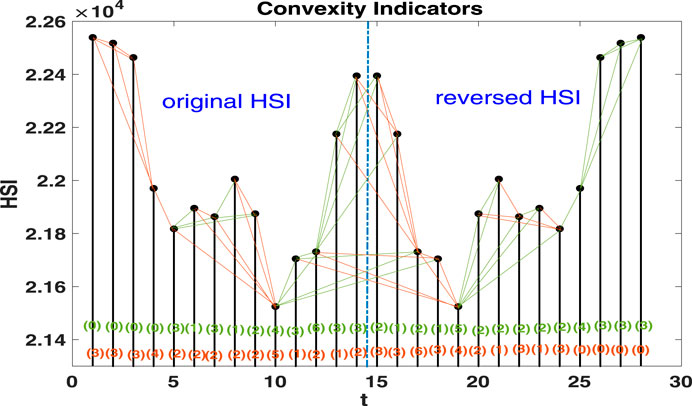
FIGURE 2. Application of the modified IVGA to the daily Hang Seng Index from August 13, 2013, to September 2, 2013, and its time-reversely mirrored data. Note that perfect reflectional symmetry between DR [nodes 5–8 in (A)] and AF [nodes 6–10 in (B)] is demonstrated via identically distributed degrees in the two networks.

2.2. Concave and Convex Motion Indicators

To formalize the algorithms shown above, we specify a node $b$ in a time series of length $L$ and set a time scope $S\left(S<L/2\right)$. Based on Eq. 1, node $a,$ which has a link to node $b$ in the visibility-graph network, should belong to the following set:

$\begin{array}{c}A=\left[\left(t_a,x_a\right)|x_a>x_b+\left(x_c-x_b\right)\frac{t_b-t_a}{t_b-t_c},a<c<b<L\right].\end{array}(3)$

Employing the three additional conditions described in Section 2.1, the subsets of nodes that connect to node $b$ in the price rise and price fall trajectories are defined as follows:

$\begin{array}{c}{A}_R=\left\{\left(t_a,x_a\right)|\left(t_a,x_a\right)\in A,x_b>x_a \text{and} \left|a-b\right|\le S \right\},\\ A_F=\left\{\left(t_a,x_a\right)|\left(t_a,x_a\right)\in A,x_b<x_a \text{and} \left|a-b\right|\le S \right\}. \end{array}(4)$

Hence, the degree of node $b$ in the visibility-graph rise and fall networks reads as

$\begin{array}{c}{\mathit{D}}_{VG}^X\left(\mathit{b}\right)=n\left({\mathit{A}}_X\right),\text{with} X=R, F.\end{array}(5)$

By definition, $D_{VG}^X\in \left[1,2S\right], X=R, F$. The concave motion indicator for a node $i$ is proposed to be the following:

$\begin{array}{c}{\mathit{I}}_{CC}^X\left(\mathit{i}\right)=\frac{{\mathit{D}}_{VG}^X\left(\mathit{i}\right)}{\mathit{S}},\text{with}X=R, F.\end{array}(6)$

Note that, for an ideal concave trajectory consisting of $L$ data points, the concave indicators along the time axis can be sketched as in Figure 3. For a realistic time series, the distribution of this indicator measures how perfectly a concave curve could fit the ideal AR or DF price motion trajectory.

FIGURE 3

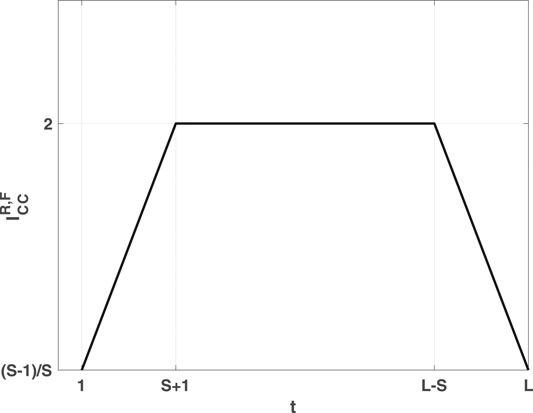
FIGURE 3. The distribution of concave indicators $I_{CC}^{R,F}$ in an ideal concave trajectory of length $L$ with time scope $S$.

Hence, the mean value of $I_{CC}^{R,F}$ can be a measure of the smoothness of AR or DF price motions. The higher the $\overline{I_{CC}^{R,F}}$, the less the zigzag price variation, and vice versa.

In the same manner, the mathematical set that describes the invisibility-graph network can be written as

$\begin{array}{c}{A}^{\prime }=\left\{\left(t_a,x_a\right)|x_a<x_b+\left(x_c-x_b\right)\frac{t_b-t_a}{t_b-t_c},a<c<b<L\right\}.\end{array}(7)$

Subsets of the rise and fall trend read, respectively, as follows:

$\begin{array}{c}{A}_R^{\prime }=\left\{\left(t_a,x_a\right)|\left(t_a,x_a\right)\in A^{\prime },x_b>x_a\text{and}\left|a-b\right|\le S \right\},\\ A_F^{\prime }=\left\{\left(t_a,x_a\right)|\left(t_a,x_a\right)\in A^{\prime },x_b<x_a\text{and}\left|a-b\right|\le S \right\}.\end{array}(8)$

The degree of node $b$ in the invisibility rise and fall networks is

$\begin{array}{c}{D}_{IVG}^X\left(b\right)=n\left({A^{\prime }}_X\right),\text{with}X=R, F.\end{array}(9)$

Convex motion indicators can thus be defined via

$\begin{array}{c}{I}_{CV}^X\left(i\right)=\frac{D_{IVG}^X\left(i\right)}{S}, \text{with}X=R, F,\end{array}(10)$

the distribution of which measures how perfectly a convex curve can fit an ideal DR or AF motion price trajectories. Likewise, $\overline{I_{CV}^X}$ measures the smoothness of the price motion trajectory.

A quantitative measure of the topological asymmetry in price motion trajectory can be done via the distinguishability between distributions of the concave and convex rise/fall indicators defined above. Specifically, denoting the distribution of rise indicators as $P\left(I_{CC,CV}^R\right)$ and the distribution of fall indicators as $P\left(I_{CC,CV}^F\right)$, a topologically symmetric time series should have $P\left(I_{CC,CV}^R\right)=P\left(I_{CC,CV}^F\right)$.

On the other hand, the degree of topological asymmetry is measured by calculating the Kullback-Leibler divergence (KLD) of $P\left(I_{CC,CV}^R\right)$ and $P\left(I_{CC,CV}^F\right)$. Stemming from information theory, KLD is employed as a measure of the distance between two probability distributions [52, 53]. KLD of concave/convex rise and fall indicators distributions can be calculated as follows:

$\begin{array}{c}D\left(P\Vert Q\right)\underset{¯}{\underset{¯}{def}}{\displaystyle \sum P\left(I_Y^R\right)\log \frac{P\left(I_Y^R\right)}{Q\left(I_Y^F\right)},\text{with} Y=CC, CV}, \end{array}(11)$

which equals 0 if and only if $P\left(I_Y^R\right)=Q\left(I_Y^F\right)$ and exceeds 0 otherwise.

3. Asymmetry in Trajectories of Price Motion

Analyses that include the application of VGA and IVGA to the stock indices of various countries and regions are presented in this section. Eight data sets from international stock market indices that span from June 28, 1999, to June 28, 2019, were selected. These include the Hong Kong Hang Seng, Dow Jones Industrial Average, Japanese Nikkei 225, London FTSE 100, German DAX, French CAC 40, Shanghai SSE Composite, and Indian BSE. Here, we set the time scope as S = 262 since the number can be interpreted as the trading days in a year.

Networks converted from the Hang Seng Index are used to demonstrate how the concave and convex motion indicators [Eqs 6 and 10] change along with the time evolution of price.

In the upper panel of Figure 4, the long-lasting bubble right before the subprime mortgage crisis in 2008 is characterized by clusters of large concave rise indicators. The large concave fall indicators in the lower panel of Figure 4, however, characterize the decelerated fall of the index over 3 years after it reaches 18,000 points on March 27, 2000. The large convex rise indicators in the upper panel of Figure 5 show that the Hang Seng Index exhibits a decelerated rise from 2009 to 2011 after the subprime mortgage crisis. The notorious 2008–2009 crisis is represented by the extraordinarily large values of convex fall indicators in the lower panel of Figure 5. Both figures show that the concave rise indicator changes asynchronously with its fall counterpart, just as the convex fall indicator changes asynchronously with its rise counterpart.

FIGURE 4

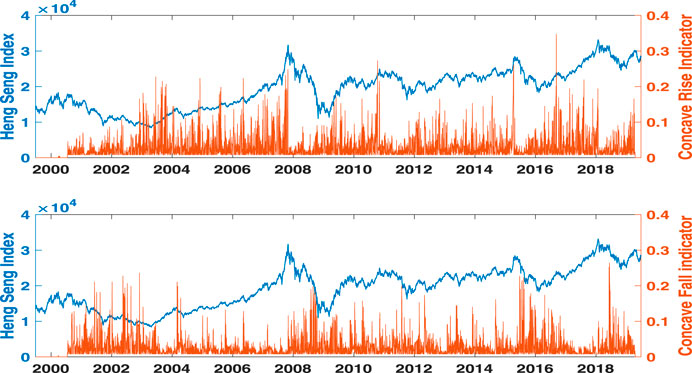
FIGURE 4. Price motion indicators measure AR and DF in the Hang Seng Index from June 28, 1999, to June 28, 2019. Concave rise and fall indicators are shown in the upper and lower panels, respectively. The Hang Seng Index is plotted using blue lines, while the indicators use red bars. The time scope is set to S = 262, which is equal to the number of trading days per year.

FIGURE 5

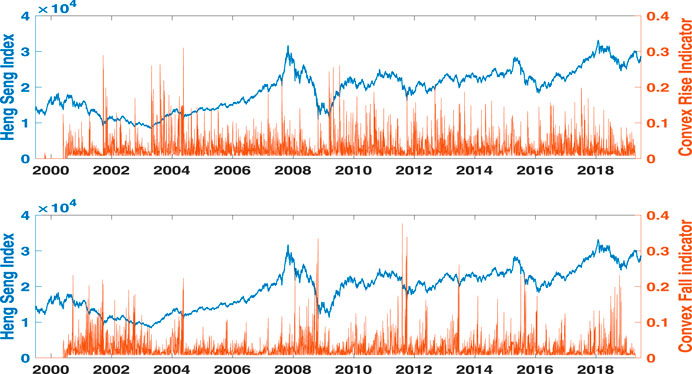
FIGURE 5. Price motion indicators measure DR and AF in the Hang Seng Index from June 28, 1999, to June 28, 2019. Convex rise and fall indicators are shown in the upper and lower panels, respectively. The Hang Seng Index is plotted using blue lines and indicators are represented using red bars. Here, the time scope is set to S = 262, which is equal to the number of trading days per year.

To illustrate asymmetry in the price motion trajectories for these eight financial time series, distributions of $I_{CC}^{R,F}$ and $I_{CV}^{R,F}$ are obtained from the statistics of VG and IVG networks, respectively. Distributions of rise and fall $I_{CC}$ for the eight stock indices are shown in Figures 6A–H. As in the small $I_{CC}$ regime, the rise distributions are similar to the fall distributions in all cases. However, as $I_{CC}$ becomes larger than ${10}^{-2}$, the rise distributions start to deviate from the fall distributions. This suggests that the AR and DF motions of stock indices are essentially asymmetric. Similarly, distributions of rise and fall $I_{CV}$ are displayed in Figures 7A–H. Again, deviation in rise and fall distributions can be found in the range $I_{CV}>{10}^{-2}$, indicating that DR and AF motions of stock indices are essentially asymmetric, too.

FIGURE 6

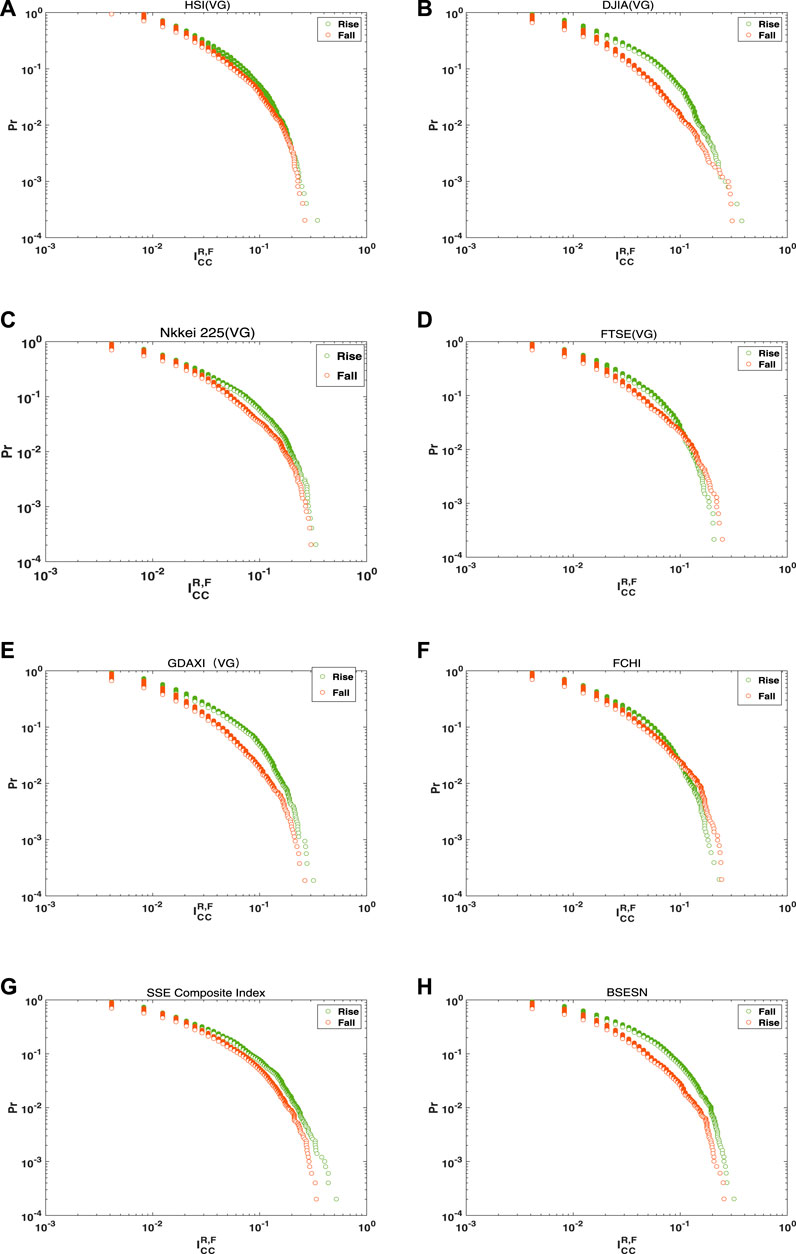
FIGURE 6. Rise and fall $I_{CC}^{R, F}$ distributions for eight stock indices: (A) Hong Kong Hang Seng; (B) Dow Jones Industrial Average; and (C) Japanese Nikkei 225, London FTSE 100, German DAX, French CAC40, Shanghai SSE Composite, and Indian BSE.

FIGURE 7

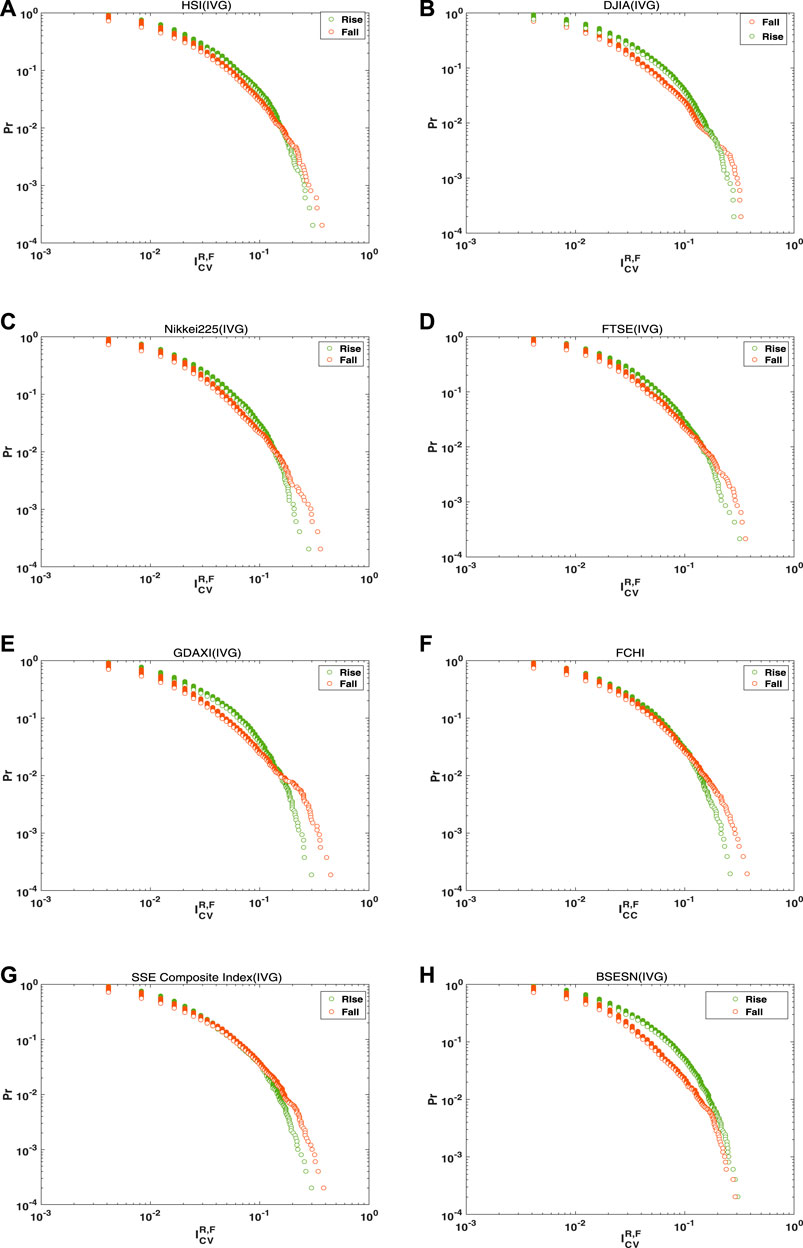
FIGURE 7. Distributions of rise and fall $I_{CV}^{R, F}$ values for the eight stock indices: (A) Hong Kong Hang Seng; (B) Dow Jones Industrial Average; and (C) Japanese Nikkei 225, London FTSE 100, German DAX, French CAC40, Shanghai SSE Composite, and Indian BSE.

Average values of rise and fall indicators are also calculated for the eight stock indices. The rise and fall $\overline{I_{CC}}$ and $\overline{I_{CV}}$ values are listed in Tables 1 and 2, respectively. The SSEC AR and DF motions are smoothest since its $\overline{I_{CC}^R}$ and $\overline{I_{CC}^F}$ rank first in magnitude among the others in the table. With regard to the DR motions of stock indices, the Indian market behaves in the smoothest manner because the $\overline{I_{CV}^R}$ of the BSESN is larger than those of any other indices. On the other hand, the zigzag AF appears less frequently in the Chinese stock market than in other markets, as suggested by the fact that the SSEC has the largest $\overline{I_{CV}^F}$ in Table 2. These observations are consistent with empirical evidence that emerging financial markets are less efficient than developed markets. The presence of fewer price oscillation in emerging markets implies that investors are more likely to form a herd.

TABLE 1

TABLE 1. Rise and fall $\overline{I_{CC}}$ values of eight stock indices.

TABLE 2

TABLE 2. Rise and fall $\overline{I_{CV}}$ values of eight stock indices.

As the time scale can be an important factor that influences the topological asymmetry in stock price motion, we measure the KLD between the rise and fall distributions of $I_{CC}$ and $I_{CV}$ with different time scopes as $S=100,130,160,\dots ,610$. Values of KLD between the rise and fall $I_{CC}$ distributions are shown in Figure 8 as functions of the time scope for the eight stock indices, as well as for a purely random time series. Compared with the KLD of the random series depicted in blue line dots, the DJIA and BSESN have an impressively higher value than any other stock indices. This indicates higher degrees of asymmetry between AR and DF price motions for these two indices. On the other hand, the dependence of KLD on the time scope is rather weak outside of the DJIA, SSEC, and BSESN.

FIGURE 8

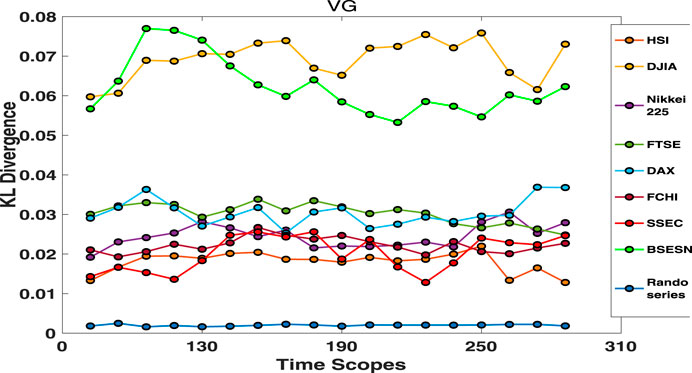
FIGURE 8. KL divergence between $I_{CC}$ rise and fall distributions as functions of time scopes for eight stock indices and a random series.

The KL-divergence values between rise and fall $I_{CV}$ distributions are shown as functions of time scopes in Figure 9 for the eight stock indices, as well as for the purely random series. Except in the case of BSESN data, the overall degree of asymmetry between DR and AF price motions is weaker than that in Figure 8. However, the dependence of the KL divergence on the time scope strengthens in all cases except for the FCHI, FTSE, and Nikkei 225.

FIGURE 9

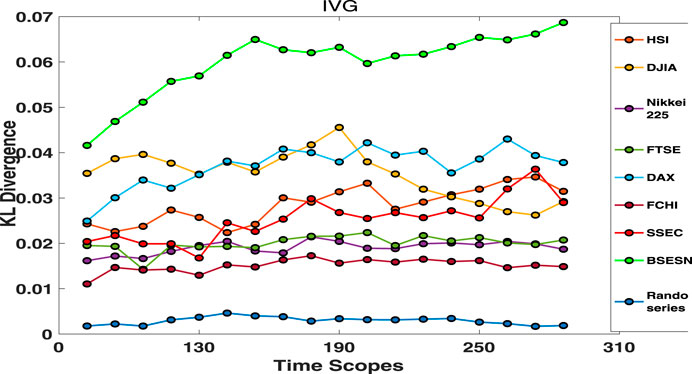
FIGURE 9. KL divergences between $I_{CV}$ rise and fall distributions as functions of the time scope for eight stock indices and a pure random series.

FIGURE 10

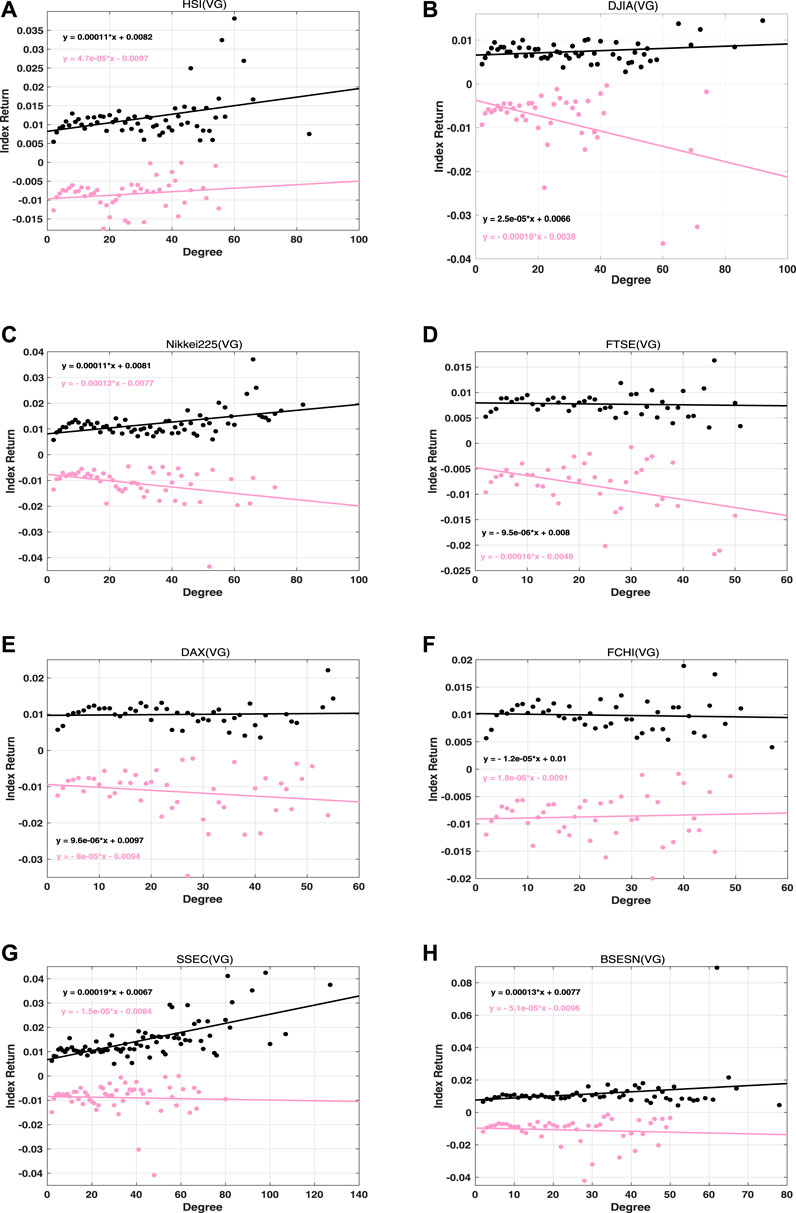
FIGURE 10. Conditional expected index returns for the degree of rise and fall price motions within VG networks for the eight stock indices. Red indicates a rise and black indicates a fall.

In Figures 8 and 9, we note that the KLDs for random series are close to 0 and vary little as the parameter $S$ changes. This is in agreement with the postulation that time-reversible time series are topologically symmetrical. On the other hand, the bigger KLDs for stock indices shown in the same figures are consistent with the finding in the previous study on time irreversibility in stock indices via the HVG method [45], which states that a chaotic time series results in a bigger KLD between in- and out-distributions than a Gaussian time series does.

In addition, KLDs of the BSESN are found to be dramatically higher than those of other stock markets in Figures 8 and 9. In particular, the observation that the BSESN KLD follows an increasing trend in Figure 9 indicates that the Indian stock market index exhibits a long-term, low-speed rise. This is in line with observations that the Indian stock market was in a bull market for over 20 years until the coronavirus outbreak. The KLD results in Figure 8 also show that the DJIA has relatively large topological asymmetry between AR and DF price motions during the period from 1999 to 2019, which indicates that the price is pushed upwards mostly by AF motions in the USA bull markets. As Yan et al. [43] published, the AR price motion implies a superexponential growth typically caused by investors’ herding behavior. Over the past decade, there have been several reports on herd buying behavior of AAPL and MSFT [54, 55]. A report published on December 4, 2019 [56], said “The Dow Jones Industrial Average owes Apple and Microsoft corporation a big thanks.” These reports may explain why AR motions dominate the movement of DJIA index.

4. Asymmetry in Speeds of Price Motion

Yan et al. argued that a higher degree number $k_a$ indicates a higher possibility that the time series is growing at a superexponential rate at time tick $a$; hence, the degree number of VG/IVG could be a good indicator for the proximity to the point of a bubble-and-crash regime shift [43]. However, we should point out that such an argument may not be accurate because the high VG degree number can also be a result of a relatively low-speed and smooth growth as long as the time scope is large enough. As the price approaches the critical point in stock markets, the magnitude of fluctuations becomes dramatically large. Therefore, the correlation between degree number $k_a$ and price return $r_a$ should be a more appropriate indicator showing the possibility for the stock index to grow/drop at the exponential rate (for AR and DF motions) or at the logarithmic rate (for DR and AF motions). Comparisons of these indicators may reveal the asymmetry in the speeds of price growth and drop.

In order to measure the asymmetry in the speeds of price motion, the expected price return $r$ over a unit time span is calculated conditionally on the node degree $k$ in VG and IVG networks. The conditional expected index return is defined as follows:

$\begin{array}{c}\langle r|k\rangle =\frac{{\sum }_a{r}_a\delta \left(k_a-k\right)}{{\sum }_a\delta \left(k_a-k\right)}, \end{array}(12)$

where $r_a=\log P_a-\log P_{a-1}$. $P_a$ is the stock index, $k_a$ is the node degree at time tick $a$, and $\delta \left(x\right)$ is the Kronecker delta function. The conditional expected price rise and fall returns on the node degree in VG and IVG networks are defined as follows in order to illustrate the asymmetry in the speeds of price growth and price drop for the eight aforementioned financial time series:

$\begin{array}{c}\langle r_{rise}|k\rangle =\frac{{\displaystyle {\sum }_{a}H\left(r_a\right)r_a\delta \left(k_a-k\right)}}{{\displaystyle {\sum }_a\delta \left(k_a-k\right)}}, \end{array}(13)$

$\begin{array}{c}\begin{array}{c}\langle r_{fall}|k\rangle =\frac{{\displaystyle {\sum }_a\left[1-H\left(r_a\right)\right]r_a\delta \left(k_a-k\right)}}{{\sum }_a\delta \left(k_a-k\right)}, \end{array}\end{array}(14)$

where $H\left(x\right)$ is a Heaviside step function [12].

The expected rise and fall returns that are conditioned on the VG node degree for eight stock indices are plotted in Figure 10, while those conditioned on the IVG node degree are in Figure 11. Expected return data points are fitted linearly and shown as black lines for rise motions and pink lines for fall motions, respectively, in Figures 10 and 11. The slopes of the fitting lines show the correlated relationships between expected returns and degree regardless of whether the trajectories are concave or convex. The larger the absolute slope, the more significantly a stock index exhibits a superexponential or a logarithmic motion.

FIGURE 11

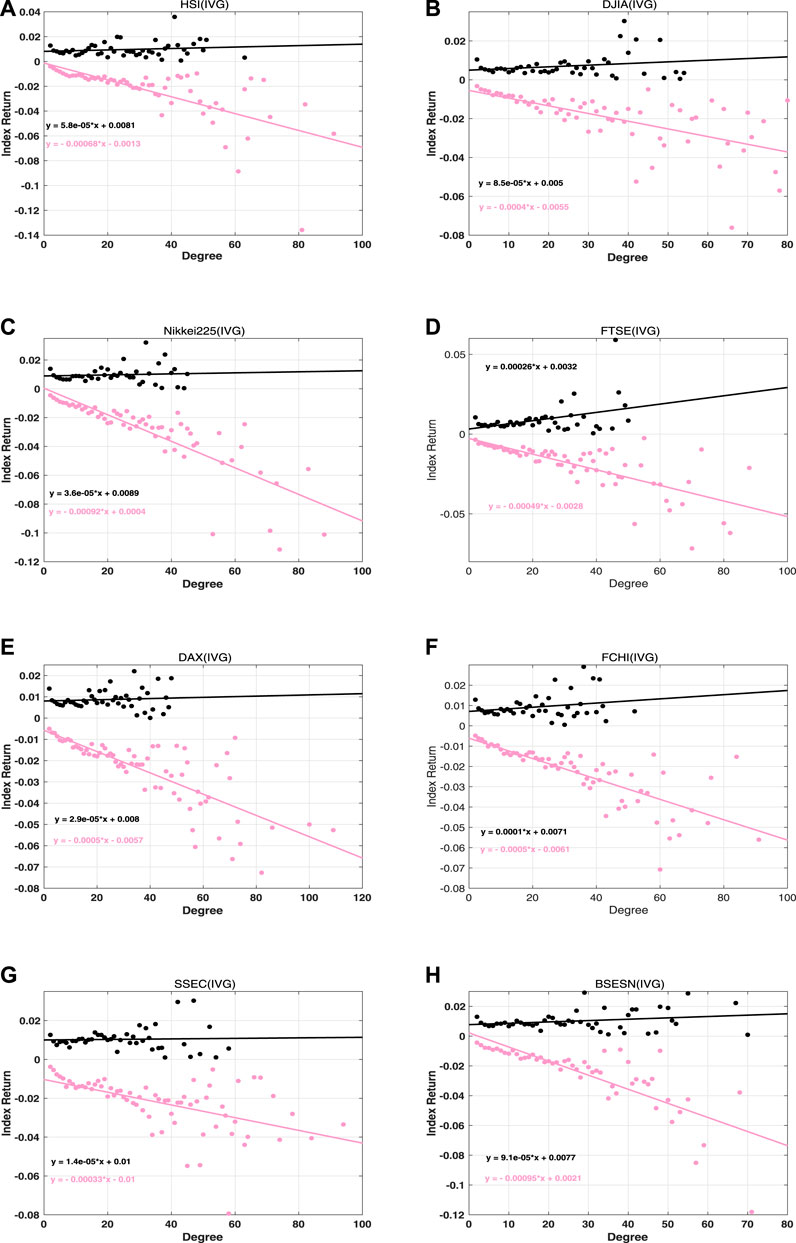
FIGURE 11. Conditional expected index returns based on the degree of rise and fall price motions in IVG networks for the eight stock indices. Red indicates a rise and black indicates a fall.

For concave price trajectories in Figure 10, stock indices can be classified into four categories. For category I, which includes the DAX and FCHI, the rise in absolute slope is almost the same as the fall in absolute slope, and both the rise and fall slopes are quite small. This implies that AR and DF are not the main forms in which these two stock markets exhibit bubbles and crashes. For category II, which includes the DJIA and FTSE, the absolute rise slope is far smaller than the fall slope. This suggests that it is possible for the price to decrease at a logarithmic fall rate after stock crashes in these two markets. For case III, which includes the HSI, SSEC, and BSESN, the absolute rise slope is larger than the fall slope. Obviously, these markets are likely to increase via a superexponential growth rate within bubble regimes. For case IV, which includes the Nikkei 225, the absolute rise slope and absolute fall slope are almost the same. However, their values are bigger than those noted in case I. This means that the Nikkei 225 rise and fall trajectories contain many concave motions in the bubble-and-crash regime. For the convex trajectories in Figure 11, the absolute fall slopes exceed the rise slopes for all of the stock indices. This implies that all of the markets crash at logarithmic rates. We also note that the FTSE and FCHI have rather large absolute rise slopes, which means that the price approaches the critical point in the DR way within the bubble regimes.

Overall, the findings in this section agree with the previous studies of gain-loss asymmetry [37–40]. In particular, stock market prices fall faster than they rise in developed countries. The analysis in this study provides a clearer picture regarding the conclusion made in Ref. [40] that the rise speed overtakes the fall speed in developing country stock markets, such as those of India and China. Indeed, the speed of AR price motion is larger than that of DF motion, while the speed of AF price motion exceeds that of DR motion, just as in mature markets.

5. Conclusion

In this paper, we developed a new concept of financial time series asymmetry based on the topological distinguishability of price motion trajectories. A new application of VGA and IVGA was developed to capture different types of price motion trajectories. Measures based on VGA and IVGA were employed to analyze asymmetry in price motion trajectories as well as in price motion speeds. To analyze topological asymmetry in price motion trajectories, we compared the distributions of concave and convex indicators for both rise and fall price motions. Deviations in rise and fall indicator distributions among VG and IVG networks showed that AR-DF and DR-AF stock index motions are asymmetric with each other. To investigate the influences of time scopes, the relation between KLD and time scope was also illustrated. Unlike with the random series, the KLD of stock index rise and fall indicator distributions is significant and the dependence of KLD on time scopes is strong. This is especially true for Indian and American stock indices.

Furthermore, we calculated the conditional expected index return on node degree to show asymmetry in price motion speeds. The rise and fall conditional expected index returns on VG or IVG network node degrees were distributed in an asymmetric manner, which indicates that asymmetry is embedded in AR-DF and DR-AF price motion speeds when the stock index approaches a bubble-and-crash regime shift. Our result was in line with gain-loss asymmetry overall. However, it offered details regarding why AF motions in emerging markets (e.g., China and India) contribute to faster rises and slower falls.

As a byproduct of this study, we also get some knowledge of the relationship between the topological symmetry and the time reversibility of a time series. By the definition of time reversibility, we proved, with an artificially combined piece of HSI time series, that the topologically symmetrical time series must be time-reversible. On the other hand, by checking the topological symmetry of a random series, the numerical evidence, which supports the postulation that a time-irreversible series must be topologically asymmetric, has also been found.

Future research will include exploration of topological asymmetry in other empirical data that exhibits chaotic behaviors, such as sunspots, heartbeats, and earthquake waves. The relation between topological symmetry and time reversibility is also to be investigated theoretically. Finally, the most important task is to explore how topological symmetry among financial time series affects the time reversibility. In this sense, we must study the network properties of VG and IVG networks and identify network characteristics right before large-scale price changes.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

RL and YC contributed to the conception of the study; RL performed the data analyses and wrote the article; CY helped perform the analysis with constructive discussions.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.539521/full#supplementary-material.

References

1. Zhang J, Small M. Complex network from pseudoperiodic time series: topology versus dynamics. Phys Rev Lett (2006). 96:238701. doi:10.1103/physrevlett.96.238701.

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zhang J, Luo X, Small M. Detecting chaos in pseudoperiodic time series without embedding. Phys Rev (2006). 73:016216. doi:10.1103/physreve.73.016216.

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zhang J, Sun J, Luo X, Zhang K, Nakamura T, Small M. Characterizing pseudoperiodic time series through the complex network approach. Phys Nonlinear Phenom (2008). 237:2856–65. doi:10.1016/j.physd.2008.05.008.

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Xu X, Zhang J, Small M. Superfamily phenomena and motifs of networks induced from time series. Proc Natl Acad Sci Unit States Am (2008). 105:19601–5. doi:10.1073/pnas.0806082105.

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Marwan N, Donges JF, Zou Y, Donner RV, Kurths J. Complex network approach for recurrence analysis of time series. Phys Lett A (2009). 373:4246–54. doi:10.1016/j.physleta.2009.09.042.

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Donner RV, Zou Y, Donges JF, Marwan N, Kurths J. Recurrence networks—a novel paradigm for nonlinear time series analysis. New J Phys (2010). 12(3):033025. doi:10.1088/1367-2630/12/3/033025.

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Donner RV, Zou Y, Donges JF, Marwan N, Kurths J. Ambiguities in recurrence-based complex network representations of time series. Phys Rev E (2010). 81:015101. doi:10.1103/physreve.81.015101.

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Donner RV, Small M, Donges JF, Marwan N, Zou Y, Xiang R, et al. Recurrence-based time series analysis by means of complex network methods. Int J Bifurcation Chaos (2011). 21:1019–46. doi:10.1142/s0218127411029021.

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Nicolis G, Cantu AG, Nicolis C. Dynamical aspects of interaction networks. Int J Bifurcation Chaos (2005). 15:3467–80. doi:10.1142/s0218127405014167.

PubMed Abstract | CrossRef Full Text | Google Scholar

10. McCullough M, Small M, Stemler T, Ho-Ching Iu H. Time lagged ordinal partition networks for capturing dynamics of continuous dynamical systems. Chaos (2015). 25:053101. doi:10.1063/1.4919075.

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Nuñez AM, Lacasa L, Gomez JP, Luque B. Visibility algorithms: a short review. In: Y Zhang, editor. New frontiers in graph theory. Rijeka, Croatia: IntechOpen (2012). p. 119–52.

PubMed AbstractGoogle Scholar

12. Lacasa L, Luque B, Ballesteros F, Luque J, Nuño JC. From time series to complex networks: the visibility graph. Proc Natl Acad Sci Unit States Am (2008). 105:4972–5. doi:10.1073/pnas.0709247105.

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Lacasa L, Luque B, Luque J, Nuño JC. The visibility graph: a new method for estimating the Hurst exponent of fractional Brownian motion. Europhys Lett (2009). 86:30001. doi:10.1209/0295-5075/86/30001.

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Luque B, Lacasa L, Ballesteros F, Luque J. Horizontal visibility graphs: exact results for random time series. Phys Rev E (2009). 80:046103. doi:10.1103/physreve.80.046103.

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Lacasa L, Toral R. Description of stochastic and chaotic series using visibility graphs. Phys Rev E (2010). 82:036120. doi:10.1103/physreve.82.036120.

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bezsudnov IV, Snarskii AA. From the time series to the complex networks: the parametric natural visibility graph. Phys Stat Mech Appl (2014). 414:53–60. doi:10.1016/j.physa.2014.07.002.

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhou T-T, Jin N-D, Gao Z-K, Luo Y-B. Limited penetrable visibility graph for establishing complex network from time series. Acta Phys Sin (2012). 61(3):030506. doi:10.7498/aps.61.030506.

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Gao Z-K, Hu L-D, Zhou T-T, Jin N-D. Limited penetrable visibility graph from two-phase flow for investigating flow pattern dynamics. Acta Phys Sin (2013). 62(11):110507. doi:10.7498/aps.62.110507.

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Stephen M, Gu C, Yang H. Visibility graph based time series analysis. PloS One (2015). 10:e0143015. doi:10.1371/journal.pone.0143015.

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Vamvakaris MD, Pantelous AA, Zuev KM. Time series analysis of S&P 500 index: a horizontal visibility graph approach. Phys Stat Mech Appl (2018). 497:41–51. doi:10.1016/j.physa.2018.01.010.

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Fan X, Li X, Yin J, Tian L, Liang J. Similarity and heterogeneity of price dynamics across China's regional carbon markets: a visibility graph network approach. Appl Energy (2019). 235:739–46. doi:10.1016/j.apenergy.2018.11.007.

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Qian M-C, Jiang Z-Q, Zhou W-X. Universal and nonuniversal allometric scaling behaviors in the visibility graphs of world stock market indices. J Phys Math Theor (2010). 43:335002. doi:10.1088/1751-8113/43/33/335002.

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wang N, Dong L, Wang Q. Visibility graph analysis on quarterly macroeconomic series of China based on complex network theory. Phys Stat Mech Appl (2012). 391:6543–55. doi:10.1016/j.physa.2012.07.054.

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Long Y. Visibility graph network analysis of gold price time series. Phys Stat Mech Appl (2013). 392:3374–84. doi:10.1016/j.physa.2013.03.063.

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Yao C-zhong, Lin J-N. A visibility graph approach to CNY exchange rate networks and characteristic analysis. Discrete Dyn Nat Soc (2017). 2017:5632374. doi:10.1155/2017/5632374.

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Zhang R, Ashuri B, Deng Y. A novel method for forecasting time series based on fuzzy logic and visibility graph. Adv Data Anal Classif (2017). 11:759–83. doi:10.1007/s11634-017-0300-3.

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Liu C, Zhou W-X, Yuan W-K. Statistical properties of visibility graph of energy dissipation rates in three-dimensional fully developed turbulence. Phys Stat Mech Appl (2010). 389:2675–81. doi:10.1016/j.physa.2010.02.043.

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ni X-H, Jiang Z-Q, Zhou W-X. Degree distribution of the visibility graphs mapped from fractional Brownian motions and multifractal random walks. Phys Lett Sec A (2008). 373:3822. doi:10.1016/j.physleta.2009.08.041.

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Liu C, Zhou W-X, Yuan W-K. Statistical properties of visibility graph of energy dissipation rates in three-dimensional fully developed turbulence. Physica A (2010). 389:2675–81. doi:10.1016/j.physa.2010.02.043.

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Siven JV, Todd Lins J. Gain/loss asymmetry in time series of individual stock prices and its relationship to the leverage effect. Preprint repository name [Preprint] (2009). Available from: https://arxiv.org/abs/0911.4679

PubMed AbstractGoogle Scholar

31. Tsay RS Analysis of financial time series. Hoboken, NJ: John Wiley & Sons (2005). p. 720.

PubMed AbstractGoogle Scholar

32. Yan J. Asymmetry, fat-tail, and autoregressive conditional density in financial return data with systems of frequency curves. Iowa City, Iowa: University of Iowa: Department of Statistics and Actuarial Science (2005). p. 26.

PubMed AbstractGoogle Scholar

33. Verhoeven P, McAleer M. Fat tails and asymmetry in financial volatility models. Math Comput Simulat (2004). 64:351–61. doi:10.1016/s0378-4754(03)00101-0.

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Jensen MH, Johansen A, Simonsen I. Inverse statistics in economics: the gain–loss asymmetry. Phys Stat Mech Appl (2003). 324(1-2):338–43. doi:10.1016/s0378-4371(02)01884-8.

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Donangelo R, Jensen MH, Simonsen I, Sneppen K. Synchronization model for stock market asymmetry. J Stat Mech (2006). 11:L11001. doi:10.1088/1742-5468/2006/11/L11001.

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Grudziecki M, Gnatowska E, Karpio K, Orłowski A, Załuska-Kotur M. New results on gain-loss asymmetry for stock markets time series. Acta Phys Pol (2008). 114:569. doi:10.12693/aphyspola.114.569.

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Siven J, Lins J, Hansen J. A multiscale view on inverse statistics and gain/loss asymmetry in financial time series. J Stat Mech Theory Exp (2008). 2009:P02004. doi:10.1088/1742-5468/2009/02/P02004.

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Zhou W-X, Yuan W-K. Inverse statistics in stock markets: universality and idiosyncracy. Phys Stat Mech Appl (2005). 353:433–44. doi:10.1016/j.physa.2005.02.011.

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Chen H, Noronha G, Singal V. The price response to S&P 500 index additions and deletions: evidence of asymmetry and a new explanation. J Finance (2004). 59:1901–30. doi:10.1111/j.1540-6261.2004.00683.x.

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Karpio K, Kotur M, Orłowski A. Gain–loss asymmetry for emerging stock markets. Phys Stat Mech Appl (2007). 375:599–604. doi:10.1016/j.physa.2006.10.003.

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Bouchaud J-P, Matacz A, Potters M. Leverage effect in financial markets: the retarded volatility model. Phys Rev Lett (2001). 87:228701. doi:10.1103/PhysRevLett.87.228701.

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Jiang X, Chen T, Zheng B. Time-reversal asymmetry in financial systems. Phys Stat Mech Appl (2013). 392:5369–75. doi:10.1016/j.physa.2013.07.006.

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Yan W, Serooskerken E. Forecasting financial extremes: a network degree measure of super-exponential growth. PloS One (2015). 10:e0128908. doi:10.1371/journal.pone.0128908.

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Lacasa L, Nuñez A, Roldán É, Parrondo JMR, Luque B. Time series irreversibility: a visibility graph approach. Eur Phys J B (2012). 85:217. doi:10.1140/epjb/e2012-20809-8.

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Lacasa L, Ryan F. Time reversibility from visibility graphs of nonstationary processes. Phys Rev E (2015). 92:022817. doi:10.1103/PhysRevE.92.022817.

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Flanagan R, Lacasa L. Irreversibility of financial time series: a graph-theoretical approach. Phys Lett A (2016). 380:1689–97. doi:10.1016/j.physleta.2016.03.011.

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Xiong H, Shang P, Xia J, Wang J. Time irreversibility and intrinsics revealing of series with complex network approach. Phys Stat Mech Appl (2018). 499:241–9. doi:10.1016/j.physa.2018.02.041.

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Wu Z, Shang P, Xiong H. An improvement of the measurement of time series irreversibility with visibility graph approach. Phys Stat Mech Appl (2018). 502:370–8. doi:10.1016/j.physa.2018.02.131.

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Xie F, Fu Z, Piao L, Mao Z. Time irreversibility of mean temperature anomaly variations over China. Theor Appl Climatol (2016). 123:161–70. doi:10.1007/s00704-014-1347-0.

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Vamvakaris MD, Pantelous AA, Zuev KM. Time series analysis of S&P 500 index: a horizontal visibility graph approach. Phys Stat Mech Appl (2018). 497:41–51. doi:10.1016/j.physa.2018.01.010.

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Vamvakaris MD, Pantelous AA, Zuev. K. Investors’ behavior on S&P 500 index during periods of market crashes: a visibility graph approach. In: F Economou, K Gavriilidis, GN Gregoriou, V Kallinterakis, editors. Handbook of investors’ behavior during financial crises. San Diego, CA: Academic Press (2017). p. 401–17.

PubMed Abstract | Google Scholar

52. Kullback S, Leibler RA. On information and sufficiency. Ann Math Stat (1951). 22(1):79–86. doi:10.1214/aoms/1177729694.

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Erven T, Harremoës P. R\'enyi divergence and kullback-leibler divergence (2012). Available from: https://arxiv.org/abs/1206.2459

PubMed Abstract |Google Scholar

54. Klebnikov S. Apple, Microsoft, Amazon, Google and Facebook make up a record chunk of the S&P 500. Here’s why that might be dangerous (2020). Available from: https://www.forbes.com/sites/sergeiklebnikov/2020/07/24/apple-microsoft-amazon-google-and-facebook-make-up-a-record-chunk-of-the-sp-500-heres-why-that-might-be-dangerous/#432d745a4f6b

PubMed Abstract | Google Scholar

55.Global Market Strategist for US Institutional Equities. How Apple and Microsoft could blow up the stock market (2019). Available from: https://edition.cnn.com/2019/11/01/investing/tech-stocks-faang/index.html

PubMed Abstract | Google Scholar

56. Derrick J. Why the Dow Jones industrial average owes Apple and Microsoft a big thanks (2019). Available from: https://finance.yahoo.com/news/why-dow-jones-industrial-average-183102086.html?soc_src=social-sh&soc_trk=ma.

PubMed Abstract | Google Scholar