Toward a Corrected Knife-Edge-Based Reconstruction of Tightly Focused Higher Order Beams

The knife-edge method is an established technique for profiling of even tightly focused light beams. However, the straightforward implementation of this method fails if the materials and geometry of the knife-edges are not chosen carefully or, in particular, if knife-edges are used that are made of pure materials. Artifacts are introduced in these cases in the shape and position of the reconstructed beam profile due to the interaction of the light beam under study with the knife. Hence, corrections to the standard knife-edge evaluation method are required. Here we investigate the knife-edge method for highly focused radially and azimuthally polarized beams and their linearly polarized constituents. We introduce relative shifts for those constituents and report on the consistency with the case of a linearly polarized fundamental Gaussian beam. An adapted knife-edge reconstruction technique is presented and proof-of-concept tests are shown, demonstrating the reconstruction of beam profiles.

1 Introduction

A paraxially propagating linearly polarized fundamental Gaussian beam undergoes, upon high numerical aperture focusing, an elongation of its focal spot along the polarization axis of the input beam [1–3]. In contrast, radially and azimuthally polarized beams are still symmetric with respect to their electric and magnetic field distributions when tightly focused. Nonetheless, both cases have in common that for non-paraxial propagation, the field distributions exhibit significant contributions of longitudinal field components, which, for the case of radial polarization, are peaking on the optical axis [2, 4, 5]. A paraxial radially polarized mode can be decomposed into two orthogonally polarized Hermite-Gaussian (HG) modes: an x-polarized HG₁₀ and a y-polarized HG₀₁ mode. In contrast, an azimuthally polarized mode is a superposition of a y-polarized HG₁₀ and an x-polarized HG₀₁ mode. Similar to linearly polarized Gaussian beams, tight focusing of these linearly polarized constituents also results in a symmetry breaking of the focal spot. Due to the rich structure of the focal spot achieved by various field engineering techniques, a precise measurement of such complicated vectorial fields is rather challenging. Nevertheless it is crucial to experimentally analyze and profile tightly focused vectorial beams in a real-world setup before utilizing them for experiments in nano-optics or plasmonics (see, for instance, Refs. 6–10 and others).

In the literature, many methods for beam characterization have been described, such as the so-called knife-edge [11–14], point scan method [15], particle scan [16], or slit method [17], to just name a few. In the knife-edge method, a beam-block realized by a sharp edge made from an opaque material (such as a knife or razor-blade) is line-scanned through the beam perpendicular to its optical axis while the transmitted power is monitored by a detector for multiple scanning directions. From the resulting photocurrent curves (power vs. position of the edge relative to the beam) the so-called beam-projections onto the scanning-line and finally the beam shape can be tomographically reconstructed [2, 5].

In a more recent study, knife-edges made from pure materials (metals, semiconductors, etc.) were systematically studied and polarization dependent effects in the knife-edge profiling method were observed [18]. Those effects result in a shift and a deformation of the measured projections and depend on the polarization and wavelength of the input beam, and the materials of the knife-edge samples. Caused by the aforementioned distortions introduced by knife-edges made from pure materials, a proper reconstruction of the beam under study seems to be impossible using a standard evaluation method. But recently we have demonstrated that the interaction between the knife-edge and a highly focused linearly polarized fundamental Gaussian beam can be understood in terms of the moments of the beam (beam profile times a polynomial) and, therefore, an adapted beam reconstruction and fitting technique can be successfully applied in this case [19].

The aim of the study presented in this article is an extension of the previously discussed method by applying the knowledge already obtained for linearly polarized fundamental Gaussian beams [18, 19] and to develop an adapted knife-edge reconstruction technique for highly focused linearly polarized first order Hermite-Gaussian beams [20], which are the constituents of radially and azimuthally polarized beams.

2 Theoretical Considerations

2.1 Basics of the Knife-Edge Method

The principle of the knife-edge method is depicted in Figure 1. For experimental reasons we consider here beam profiling by two adjacent edges of a single rectangularly shaped metallic knife-pad. The photocurrent generated inside the photodiode is proportional to the power P detected by the photodiode and is recorded for each beam position $x_0$ with respect to the knife-edge

$P=P_0{\displaystyle {\int }_{-\infty }^{\infty }dy}{\displaystyle {\int }_{-\infty }^{0}I\left(x+x_0,y,z=0\right)dx},(1)$

where $P_0$ is a proportionality coefficient and I is the electric field intensity. In the conventional knife-edge method, the derivative $\partial P/\partial x_0$ of the photocurrent curve with respect to the beam position $x_0$ reconstructs a projection of the intensity onto the xz-plane at $z=0$ (projection onto the x-axis) [11]. In a next step, the two-dimensional electric field intensity distribution can be reconstructed from projections measured along different directions using the Radon back-transform, if polarization-dependent effects can be neglected [2, 5].

FIGURE 1

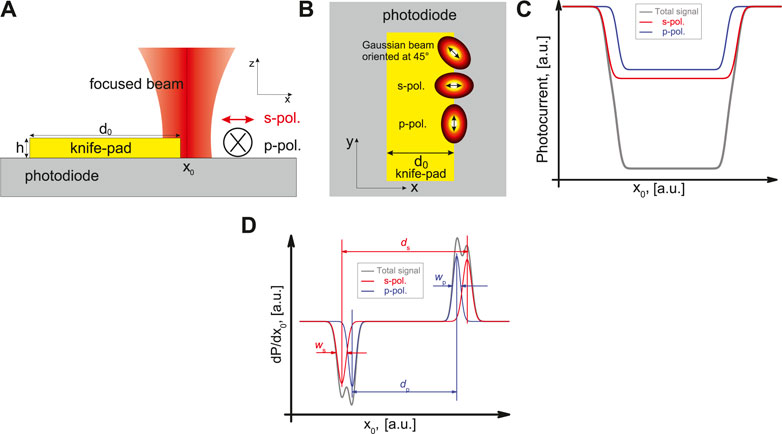
FIGURE 1. Schematic depiction of the knife-edge method xz-plane (A) and xy-plane (B). The state of polarization always refers to the orientation of the electric field of the incoming beam relative to the knife-edge in the xy-plane. Typical beam profiling data (photocurrent curves) (C) and their derivatives (beam-projections) (D) for a linearly polarized Gaussian beam (oriented at 45° (total signal) - gray, s-polarization - red, p-polarization - blue).

In this context it has to be mentioned that the term intensity usually refers to the total electric energy density and at the same time to the z-component of the Poynting-vector $\mathbf{S}$, because they are proportional to each other in the limit of paraxial light beams. In the case of tightly focused light beams (non-paraxial propagation), electric fields can exhibit strong longitudinal electric field components, resulting in different distributions of ${\left|\mathbf{E}\left(x,y\right)\right|}^2$ and $S_z\left(x,y\right)$. It was shown that the integral Eq. 1 adopted from the conventional knife-edge method allows for the reconstruction of the beam profile in terms of its total electric energy density distribution ${\left|\mathbf{E}\left(x,y\right)\right|}^2$ also in case of tightly focused vectorial beams if special edge-materials, thicknesses and certain wavelengths are chosen [2]. Nevertheless, with pure knife-edge materials of different thicknesses and for different wavelengths of the input beam, the retrieved projections do not correspond to the expected projections of the electric energy density distributions as they appear strongly distorted [18].

To better understand those shifts and distortions in the measured projections, we start with a fundamental Gaussian beam, which has its electric field oriented at 45° to the knife-edge. With a polarizer in front of the focusing objective oriented either perpendicular or parallel to the knife-edge, the incident beam can be decomposed in its linearly polarized constituents with the electric field of the incoming beam being either perpendicular (s) or parallel (p) to the knife-edge, see Figures 1A,B. A photocurrent curve can be recorded for each orientation of the polarizer. The sum of those two photocurrent curves should result in the signal recorded without the polarizer (total signal), see Figure 1C. Taking the derivative $\partial P/\partial x_0$ of the photocurrent curves with respect to the beam position $x_0$ should reconstruct the expected Gaussian beam profile. However, this is not the case as shown in Figure 1D. The projections of the Gaussian beam with its electric field oriented at 45° to the knife-edge is strongly distorted. In an exaggerated picture, they exhibit two distinct lobes. However, when a polarizer is used the situation looks different: each linear constituent preserves in principle its Gaussian shape and only smaller distortions can be found. Nonetheless, it becomes evident that s- and p-projections are shifted ($d_s\ne d_p\ne d_0$ with $d_0$ the width of the metal pad (see Figure 1A)) and asymmetrically deformed, causing also deviations in the retrieved beam diameters $w_s$ and $w_p$ (see Figure 1D). The above-mentioned effects are caused by the fact that the knife-edge is not only blocking the beam while line-scanning but it is also excited by the beam plasmonically (if the pad is made from metal). Furthermore, the power flow through the knife-edge is polarization-dependent and proportional to the value of the projection of the electric energy density onto the edge [18, 21]. Obviously, if one does not account for these effects, the standard scheme is not valid without corrections unless the knife-edge parameters are carefully chosen [1]. It is worth noting here that during the reconstruction of light beams with diameters larger than several wavelengths such effects are negligible as the distortions are much smaller than the projection of the beam.

Of particular interest for this article is now the question how higher order (first order) beams behave in the context of the previous discussion, see Figure 2. Similar to the rotated linearly polarized Gaussian beam a radially polarized beam is a superposition of two orthogonally polarized modes (x-pol. HG₁₀, y-pol. HG₀₁). In an equivalent fashion, an azimuthally polarized beam is a superposition of two linearly polarized constituents (y-pol. HG₁₀, x-pol. HG₀₁). In the case of tightly focused cylindrical vector beams, the retrieved total beam projections will be strongly modified if their linearly polarized constituents are shifted and distorted, see Figures 2A,B. Therefore it is important to investigate whether the distortions observed in these linearly polarized first order constituents can also be described using analogical parameters $d_s$ and $d_p$, as in the case of a fundamental linearly polarized Gaussian beam [18]. Furthermore, it is crucial to study whether the apparent shifts $d_s$, $d_p$ of the projections correlate with the previously investigated case. Additionally, we also discuss the applicability of an adapted reconstruction method, discussed and introduced for tightly focused fundamental Gaussian beams recently [19] for the case of knife-edges made from pure materials, in contrast to studies presented earlier [1], where very special parameters had to be chosen for the knife-edges.

FIGURE 2

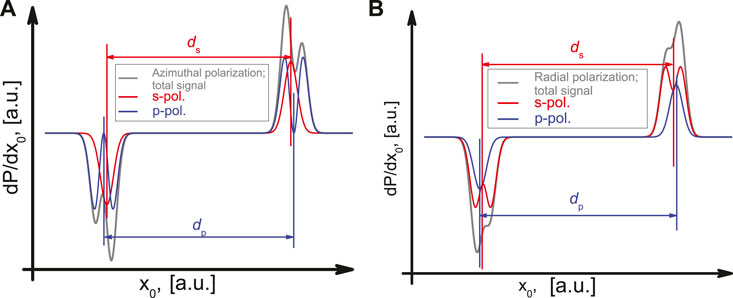
FIGURE 2. Typical derivatives of beam profiling data (photocurrent curves) for azimuthally (A) and radially (B) polarized beams (gray) and their linear constituents (s-polarization - red, p-polarization - blue).

2.2 Approximation of Vector Beams via Paraxial Modes

We start with a discussion of the basis functions that would be most suitable for further development of an adapted knife-edge technique. An accurate description of highly focused beams is possible either by vectorial diffraction theory, leading to a numerical calculation of diffraction integrals, see for instance [3, 4], or by the so-called complex source approach, which enables an analytical description of tightly focused fields [22, 23]. The disadvantage of both approaches is their complexity, which makes them unsuitable for the development of an adapted knife-edge technique. Our aim here is to use an orthogonal set of analytical functions, which would be sufficient for an approximate description of highly focused fields. Electric (and magnetic) field components that are solutions to Maxwell’s equations can be expressed in terms of two independent functions $f_1\left(\mathbf{r}\right)$ (x-polarized) and $f_2\left(\mathbf{r}\right)$ (y-polarized) of the paraxial wave equation [24]:

$\begin{array}{c}{E}_x=f_1\left(\mathbf{r}\right)+\frac{1}{4k^2}\left[\frac{{\partial }^2{f}_1\left(\mathbf{r}\right)}{\partial x^2}+\frac{{\partial }^2{f}_1\left(\mathbf{r}\right)}{\partial y^2}\right]+\frac{1}{2k^2}\frac{{\partial }^2{f}_2\left(\mathbf{r}\right)}{\partial x\partial y},\\ E_y=f_2\left(\mathbf{r}\right)-\frac{1}{4k^2}\left[\frac{{\partial }^2{f}_2\left(\mathbf{r}\right)}{\partial x^2}+\frac{{\partial }^2{f}_2\left(\mathbf{r}\right)}{\partial y^2}\right]+\frac{1}{2k^2}\frac{{\partial }^2{f}_1\left(\mathbf{r}\right)}{\partial x\partial y},\\ E_z=\frac{\text{i}}{k}\left[\frac{\partial f_1\left(\mathbf{r}\right)}{\partial x}+\frac{\partial f_2\left(\mathbf{r}\right)}{\partial y}\right],\end{array}(2)$

We can further simplify these expressions by keeping only the leading terms in $f_1\left(\mathbf{r}\right)$ and $f_2\left(\mathbf{r}\right)$, i.e., we drop the second derivatives from the expressions Eq. 2, in case a lower order derivative appears. This can be done because the second derivatives are of order $1/k^2{l}_0^2$, where $l_0$ is some characteristic length. Next, we identify functions $f_1\left(\mathbf{r}\right)$ and $f_2\left(\mathbf{r}\right)$ as the x- and y-polarized constituents of the incident beam. Furthermore we introduce the so-called elegant HG modes [26] as follows,

$f_{\mathrm{1,2}}^{\left(m,n\right)}\left(\mathbf{r}\right)={\sigma }^{\left(m+n\right)/2+1}{H}_m\left(x\sigma \right)H_n\left(y\sigma \right)\text{exp}\left[\text{i}kz-{\sigma }^2\left(x^2+y^2\right)-\text{i}\left(1+\frac{m+n}{2}\right)\text{arctan}\xi \right],(3)$

with

$\sigma =\frac{1}{{\omega }_0\sqrt{1+\text{i}\xi }},\xi =z/z_0,z_0=k{\omega }_0^2/2,(4)$

and ${\omega }_0$ the beam width. We note here that although individual Hermite-Gaussian modes are not exact solutions to Maxwell’s equations, corrections can be found and expressed as an infinite sum according to the method of Lax et al. [25]. Those can be related to complex sourced vortices [23]. The main advantage of using the elegant version of Hermite-Gaussian modes over standard modes is the following useful relation [26],

$f_{\mathrm{1,2}}^{\left(m,n\right)}\left(\mathbf{r}\right)=\frac{{\partial }^{m+n}{f}_{\mathrm{1,2}}^{\left(\mathrm{0,0}\right)}\left(\mathbf{r}\right)}{\partial x^m\partial y^n},(5)$

which greatly simplifies further considerations and enables us to rewrite Eq. 2 as

$\begin{array}{c}{E}_x\left(\mathbf{r}\right)={\displaystyle \sum _{m=m_1}^{m_2}{\displaystyle \sum _{n=n_1}^{n_2}{a}_{m,n}{f}_1^{\left(m,n\right)}\left(\mathbf{r}\right)}}+\frac{1}{2k^2}{\displaystyle \sum _{m=m_3}^{m_4}{\displaystyle \sum _{n=n_3}^{n_4}{b}_{m,n}{f}_2^{\left(m+1,n+1\right)}\left(\mathbf{r}\right)}},\\ E_y\left(\mathbf{r}\right)=\frac{1}{2k^2}{\displaystyle \sum _{m=m_1}^{m_2}{\displaystyle \sum _{n=n_1}^{n_2}{a}_{m,n}{f}_1^{\left(m+1,n+1\right)}\left(\mathbf{r}\right)}}+{\displaystyle \sum _{m=m_3}^{m_4}{\displaystyle \sum _{n=n_3}^{n_4}{b}_{m,n}{f}_2^{\left(m,n\right)}\left(\mathbf{r}\right)}},\\ E_z\left(\mathbf{r}\right)=\frac{\text{i}}{k}{\displaystyle \sum _{m=m_1}^{m_2}{\displaystyle \sum _{n=n_1}^{n_2}{a}_{m,n}{f}_1^{\left(m+1,n\right)}\left(\mathbf{r}\right)}}+\frac{\text{i}}{k}{\displaystyle \sum _{m=m_3}^{m_4}{\displaystyle \sum _{n=n_3}^{n_4}{b}_{m,n}{f}_2^{\left(m,n+1\right)}\left(\mathbf{r}\right)}},\end{array}(6)$

where the expansion coefficients $a_{m,n}$ and $b_{m,n}$ uniquely describe a tightly focused field and its linearly polarized constituents. In a similar fashion we can express the projections of the electric field energy densities of s- or p-polarized projections of arbitrary beams in the focal plane. We multiply Eq. 6 with its complex conjugate and integrate over the y-axis, so that indices n disappear from the sum Eq. 6. In this manner we arrive at the following expressions for p- and s-polarized projections,

$\begin{array}{l}{U}_{E,x}\left(x\right)={\displaystyle \sum _{m_1,m_2}{B}_{m_1,m_2}{g}_1^{\left(m_1\right)}\left(x\right)g_1^{\left(m_2\right)}\left(x\right)},\\ U_{E,y}\left(x\right)={\displaystyle \sum _{m_1,m_2}{B}_{m_1,m_2}{g}_2^{\left(m_1\right)}\left(x\right)g_2^{\left(m_2\right)}\left(x\right)},\\ U_{E,z}\left(x\right)={\displaystyle \sum _{m_1,m_2}{\alpha }_{m_1,m_2}{B}_{m_1,m_2}{g}_1^{\left(m_1+1\right)}\left(x\right)g_1^{\left(m_2+1\right)}\left(x\right)},\end{array}(7)$

where $B_{m_1,m_2}$ are unknowns describing the intensity profiles, functions $g_{\mathrm{1,2}}^{\left(m\right)}$ are projections of HG-modes $f_{\mathrm{1,2}}^{\left(m,n\right)}$ onto the xz-plane and ${\alpha }_{m_1,m_2}$ are coefficients, which correct the amplitudes of the z-components in Eq. 6. They have to be obtained separately.

We now discuss an azimuthally and radially polarized beam and their linear constituents in more detail. A paraxial radially polarized beam is a superposition of two orthogonal HG modes, an x-polarized $f_1^{\left(\mathrm{1,0}\right)}$ and a y-polarized $f_2^{\left(\mathrm{0,1}\right)}$ mode, whereas a paraxial azimuthally polarized beam is obtained by a superposition of a y-polarized $f_2^{\left(\mathrm{1,0}\right)}$ and an x-polarized $f_1^{\left(\mathrm{0,1}\right)}$ mode. Under tight focusing conditions, each HG-mode changes and new components of the electric field appear, which can be described using Eq. 2. However, we restrict ourselves here to the approximations of Eq. 6, which we use to determine the shape of projections in the form of Eq. 7. We compare now projections, which we derive using Eq. 7, with projections calculated by Richards-Wolf integrals [3] for the cases discussed in the experimental part. As a proof-of-concept, we demonstrate the fitting procedure for one particular wavelength and for several projections of Hermite-Gaussian input beams in Figure 3, where we use as a criterion for convergence that the paraxial beam overlaps with the central part of the obtained exact projections. This way, the central part of the p-polarized projection of an HG₁₀ beam (y-polarized HG₁₀ mode) was fitted by a paraxial beam function from Eq. 7. The result of the fitting procedure is shown in Figure 3A. We can see that the paraxial model describes the y-component sufficiently well. The central part of the s-polarized projection of a HG₁₀ beam (x-polarized HG₁₀) was also fitted using the aforementioned paraxial beam functions, see Figures 3B,C. Here we can see that the x-component can be approximated well, whereas the z-component shows minor discrepancies with respect to the paraxial function. Lastly, we have fitted the s- and p-polarized projection of an HG₀₁ beam (x-, y-polarized HG₀₁) using paraxial beam functions from Eq. 7. The results presented in Figures 3D,E prove again the appropriateness of the chosen approximation.

FIGURE 3

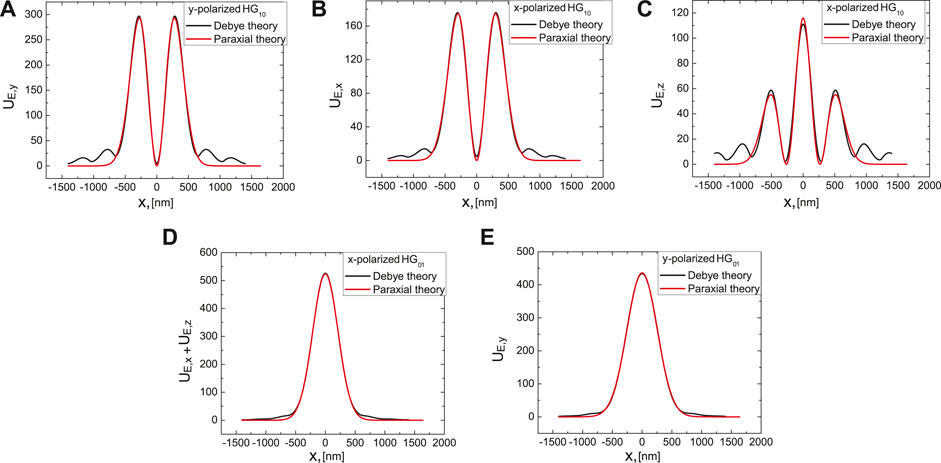
FIGURE 3. Comparison of calculated components of the projections of electric field energy densities between an approximation (paraxial theory, red) and exactly calculated projections using Richards-Wolf integrals (vectorial diffraction theory (Debye), black). The wavelength is $\lambda =700\text{nm}$, the numerical aperture $\left(NA\right)$ is 0.9, the focal length is $f=2.0\text{mm}$ and the beam width of HG modes at the entrance pupil is $w_0=1.74\text{mm}$. Indices for Hermite-Gaussian modes are shown in the graphs.

2.3 Corrections to the Knife-Edge Based Reconstruction Scheme for Modes of First Order

In our previous work [19], we presented a numerical technique to correct for artifacts in profiling of linearly polarized fundamental Gaussian beams, which are introduced by the interaction of the knife-edge with the focused light field [21]. This approach finally enables the usage of any kind of opaque material as a knife-edge material. Here, we now discuss a generalization of this numerical technique, which will also allow for the correction of artifacts observed in beam profiling of s- and p-polarized projections of the electric field intensity, which can be represented using Eq. 7. For that purpose, we start the discussion with a short excursus, describing the light-matter interaction between the focused light beam and the knife-edge as it is recorded by a detector, see Eq. 1.

First, the integration in Eq. 1 over the y-axis reduces the dimensionality of the electric field energy density. Therefore, beam profiling of this kind does not result directly in the reconstruction of the electric field intensity distribution I but its projection $U_E$ onto the xz-plane. Thus, eigenmodes of the knife-edge problem consist of two independent classes: transverse electric (in our notation p-polarized) and transverse magnetic (s-polarized) modes. The projection of the electric field energy density, i.e., $U_E$ in the case of p-polarization has a non-vanishing component $U_{E,y}$ parallel to the knife-edge and a z-component $U_{E,z}$, indistinguishable in shape from $U_{E,y}$ because of the symmetry of Eq. 7. The s-modes have two non-vanishing and distinguishable components of the projection $U_E$, where the main component $U_{E,x}$ is perpendicular (s-polarization) to the knife-edge [18, 27, 28]. In order to analyze the interaction of the focal electric field distribution $E_b$ of a highly focused beam with the knife-edge, we need to start by decomposing it into its s- and p-polarized constituents. In this manner the resulting beam will be described by a sum (Eq. 6). We start by taking the derivative of Eq. 1 and rewriting the result as [19, 21].

$\frac{\partial P}{P_0\partial x_0}=U_E\left(x_0\right)+{\displaystyle \sum _{n=1}^{\infty }{C}_n\frac{{\partial }^n{U}_E\left(x_0\right)}{\partial x_0^n}},(8)$

with $C_n={\left({\text{i}}^{n}n!\right)}^{-1}{\partial }^n\widehat{T}/\partial k_x^n$. Here $U_E\left(x\right)$ is the projection of the electric field energy density onto the xz-plane at the position of the knife-edge, and $\widehat{T}\left(k_x\right)$ is a spectral representation of the polarization-dependent knife-edge interaction operator.

The physical meaning behind Eq. 8 is the following. The first term in the sum $\left(n=1\right)$ is a result of the local response of the knife-edge to the s- or p-polarized electric field components, and it is mainly associated with the translation operator $U_E\left(x+dx\right)\approx U_E\left(x\right)+dx\partial U_E\left(x\right)/\partial x$. Indeed, if we take either the projection of the s-polarized constituents of a radially polarized beam (see Eq. 7) or p-polarized constituents of an azimuthally polarized beam and plot the resulting beam profiles for various values of $C_1$, we result in a profile, which is displaced into the knife-edge or away from it, see Figures 4A,B. As the expansion coefficient $C_1$ increases, artifacts such as negative values and distortions of $U_E$ can be observed in the resulting profile. We note that the coefficients $C_n$ are knife-edge specific, and they have to be obtained either experimentally [19] or numerically from the analytical model [18, 21].

FIGURE 4

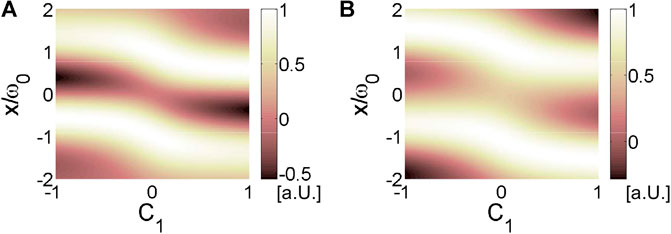
FIGURE 4. Dependence of calculated beam projections of (A)$x-$ and (B)$y-$ polarized HG₁₀ modes on the coefficients $C_1$ according to Eq. 9 for a response to the local electric field.

We substitute now the expressions from Eq. 7 into Eq. 8 and obtain for s- and p-projections

$\frac{\partial P}{P_0\partial x_0}={\displaystyle \sum _{m_1,m_2}{B}_{m_1,m_2}}\left[G_{m_1,m_2}^{\left(s,p\right)}+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{l=0}^n\frac{C_{n}n!}{l!\left(n-l\right)!}{G}_{m_1+1,m_2+n-l}^{\left(s,p\right)}}}\right],(9)$

where

$G_{m_1,m_2}^{\left(p\right)}=g_2^{\left(m_1\right)}\left(x\right)g_2^{\left(m_2\right)}\left(x\right),G_{m_1,m_2}^{\left(s\right)}=g_1^{\left(m_1\right)}\left(x\right)g_1^{\left(m_2\right)}\left(x\right)+{\alpha }_{m_1,m_2}{g}_1^{\left(m_1+1\right)}\left(x\right)g_1^{\left(m_2+1\right)}\left(x\right).(10)$

We recently demonstrated that for functions with Gaussian envelopes, derivatives up to fourth order are sufficient [19]. Thus, the inner sum in Eq. 9 contains up to 14 different combinations of HG polynomials for a single unknown $B_{m_1,m_2}$. It is noteworthy that by choosing lower limits of the indices $m_1$ and $m_2$, the fitting algorithm becomes more robust, however resulting also in a reduced accuracy. Nonetheless, if $C_n$ coefficients were determined either numerically or experimentally, the algorithm can still be used for beam reconstruction.

3 Experimental Results and Adapted Fit Algorithm

In the following section we briefly discuss the experimental setup, the principle of the measurement and the studied knife-edge sample. A detailed discussion of the experimental concept was introduced earlier in Refs. 18 and 21. The experiments were performed at wavelengths between 535 and 700 nm using a tunable laser system from TOPTICA. The emitted laser beam is coupled into a single-mode photonic crystal fiber (PCF) to obtain a Gaussian beam profile. After collimation this linearly polarized Gaussian beam is converted into a radially or azimuthally polarized mode by using a liquid crystal polarization converter (LCPC) (see Figure 5A) [29]. Afterward the beam is filtered by a Fourier spatial filter (FSF), consisting of two lenses and a pinhole to achieve a high mode quality. The resulting beam is guided into a high NA microscope objective by a set of mirrors, and focused onto the knife-edge sample. For measurements with the fundamental x- and y-polarized linear constituents of the radially or azimuthally polarized modes, a linear polarizer is used in front of the objective. The knife-edges are line-scanned through the focal spot by a piezostage, and the power of the light beam that is not blocked by the knife-edge is detected by a photodiode placed directly underneath. This way projections of the beam profile are measured as already discussed in Section 2.1. For the measurements, knife-edges made of gold with a thickness $h=70\text{nm}$ and a width $d_0=3\text{μm}$ (±50 nm) are fabricated on commercial silicon (Si) photodiodes as substrate (see Figure 5B). Similar samples have been utilized and discussed already in Ref. 21.

FIGURE 5

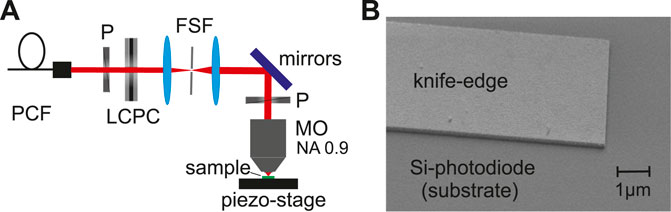
FIGURE 5. Schematic illustration of the experimental setup (A) (P, Polarizer; LCPC, liquid crystal polarization converter; FSF, Fourier spatial filter; MO, microscope objective), SEM image of the used knife-edge sample (B) (gold with a thickness h = 70 nm and a width $d_0$$\approx$ 3 μm fabricated on a silicon photodiode).

We start the discussion of our experimental results by demonstrating the appearnace of the aforementioned artifacts while beam profiling a radially and an azimuthally polarized beam and their linearly polarized constituents at two different wavelengths, see Figures 6A,B. In all cases one can notice the impact of the wavelength on the shape and relative position of the measured beam projections. While for a wavelength of $\lambda =535\text{nm}$ the shape of the p-polarized linear constituent of an azimuthally polarized beam seems to be sufficiently preserved, see Figure 6A, further analysis reveals a shift of the profile into the knife-edge and a significantly modified beam width. The projection of the s-polarized constituent in this case has a Gaussian shape, its width however is also modified and its center is shifted away from the knife-edge. This behavior is comparable to the artifacts observed in beam profiling of linearly polarized fundamental Gaussian beams [18], as shown recently. While the projection of the p-polarized constituent of a radially polarized beam is shifted into the knife-edge, the projection of the s-polarized constituent of a radially polarized beam is strongly altered in all cases Figures 6A,B. We find that the contribution of the z-component of the electric field in the measured beam profile in the latter case is much weaker than expected as the reconstructed HG₁₀ mode shows a minimum reaching almost zero. Therefore the observed profile is more typical for the linearly polarized constituent of a azimuthally than for a radially polarized beam. The projection of the p-polarized constituent of an azimuthally polarized beam not only experiences relative shifts (see Figure 6B), but one notices negative values of the projection curve at the center of the beam. This finding is especially surprising, considering the fact that a p-polarized HG₁₀ mode has no z-component in the center of the beam. It should be noted here that in contrast to actual electric field intensity energy density distribution of a beam of light, the projected intensities can reach values below zero.

FIGURE 6

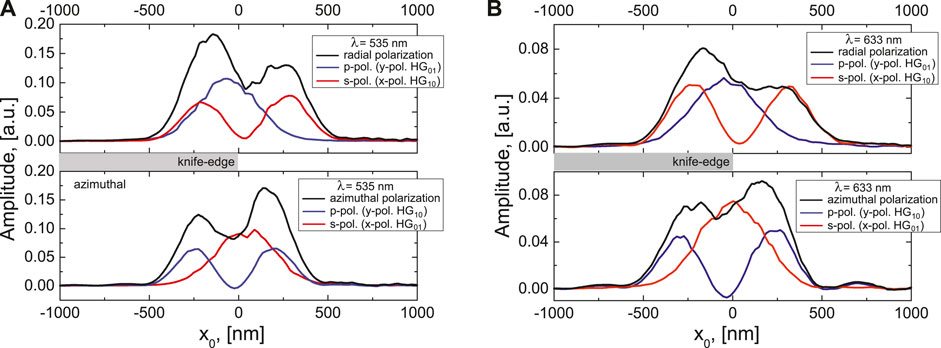
FIGURE 6. Experimentally measured projections of radially and azimuthally polarized beams (black) and their linear s-, p- polarized constituents (red, blue) for (A)$\lambda =535\text{nm}$, (B)$\lambda =633\text{nm}$. The accuracy of determining the actual position of the projections relative to the knife-edge is limited by the error in measuring the width $d_0$ of the knife-edge in an SEM.

As a next step, we have retrieved specific points from the projections of all linearly polarized constituents, indicated in Figures 1 and 2 by the red and blue vertical lines respectively, to determine the shift of the projections $d_s$ and $d_p$ from the knife-edges in a systematic way. We found, in agreement with theoretical predictions, that the projections of s- and p-polarized constituents of both radially and azimuthally polarized beams experience similar shifts of their relative positions with respect to the knife-edge indicating that s-polarized projections move away from the knife-edge whereas p-polarized projections move into the knife-edge. Similar phenomena were recently reported for linearly polarized Gaussian beams, see Ref. 21. Finally, we compare the measured relative shifts $d_s-d_p$ between s- and p-polarized projections of a linearly polarized Gaussian beam and radially and azimuthally polarized beams, see Figure 7A. As expected, their relative shifts are also comparable to each other for different wavelengths, hinting at an experimental verification of the coefficients $C_n$ in Eq. 8. As indicated before, coefficients $C_n$ depend on the specific knife-edge sample and being independent of the beam shape, which is actually profiled as long as the polarization state is linear.

FIGURE 7

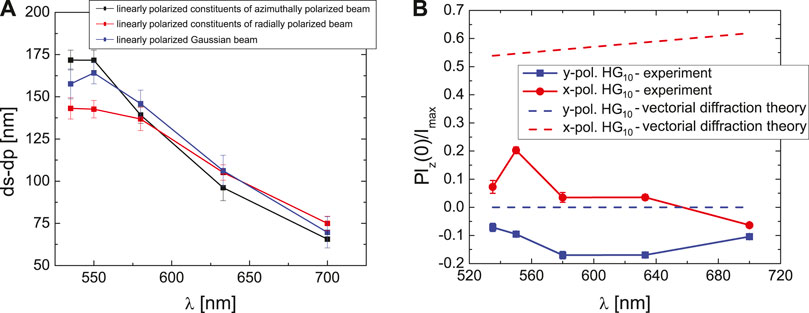
FIGURE 7. Experimentally measured relative shift $d_s-d_p$ for linearly, s- and p-polarized Gaussian beams (black) and for the linearly s- and p-polarized constituents of radially (red) and azimuthally (blue) polarized beams for different wavelengths λ(A). Comparison between the projected intensity (PI) for the z-component of the electric field in the center of the measured beam (experiment) and numerically obtained values from vectorial diffraction theory [3] (B).

In a next step, we compare the measured intensities for the z-component of the electric field of the projected linear constituents at the specific points (see Figure 2) with those obtained numerically from Debye integrals [3], see Figure 7B. In all cases we have normalized the on-axis intensity at the point $z=0$ to the maximum value of the s- and p- polarized HG₁₀ modes. We notice that the conventionally reconstructed linear constituent of the radially polarized beam has on-axis intensity, which is many times smaller than numerically expected. For one particular wavelength, the on-axis intensity reaches $20\text{\%}$ of the maximum value, which is almost three times smaller than one might expect from the numerical simulations. At a wavelength of $\lambda =700\text{nm}$ we observe negative values of the projected on-axis intensities. The same is observed for all wavelengths for the reconstructed projections of a HG₁₀ mode in the case of azimuthal polarization. In all cases our experimental observations are in line with our expectations from previous sections.

Based on the ansatz proposed in Eq. 9, we have implemented a least-square fitting algorithm as a proof-of-concept, where we have restricted ourselves to up to the fourth derivative of the electric field energy density projection $U_E\left(x_0\right)$ and use calculated beam widths from Debye theory as a fixed parameter. For the sake of simplicity, we have used approximations from Eq. 7 for the components of the s- and p-polarized beams in the plane of the projection. In addition the real position of the knife-edge was predetermined before fitting to reduce the number of free parameters in the fitting routine and to fix the coordinate frame. For this purpose, we experimentally measure the distances $d_0$ between both edges using a scanning electron microscope (SEM), find the center $x_c$ between the peak values of both projections in one scan and finally set the actual positions of both knife-edges to be at $x_c\pm d_0/2$. An example of such a fitting procedure is presented in Figure 8 for s- and p-polarized constituents of radially and azimuthally polarized beams at wavelengths of 535 and 700 nm. It turns out that for all investigated wavelengths between 535 and 700 nm, by simultaneously ensuring $d_s=d_p=d_0$, the fitting algorithm has successfully converged toward realistic beam projections, resulting in a good overlap between the theoretical expectations from vectorial diffraction theory and reconstructed beam profiles.

FIGURE 8

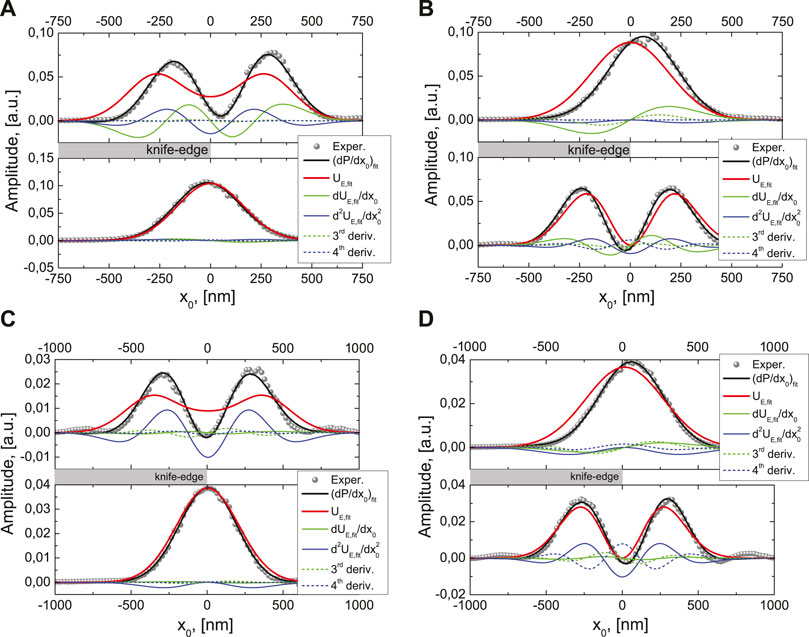
FIGURE 8. Depiction of the adapted knife-edge method for linear constituents of tightly focused radially (A,C) and azimuthally (B,D) polarized beams. The derivatives of the experimentally measured photocurrents (gray circles) and the fitted curve (black) with the beam profile (red) are shown together with its first four derivatives at $\lambda =535\text{nm}$(A,B) and $\lambda =700\text{nm}$(C,D). The states of polarization are s (first row) and p (second row).

Lastly, we have used those successfully converged iterations to numerically determine the coefficients $C_n$ in Eq. 9 for each wavelength, which we have used in our experiments. This numerical determination of the knife-edge parameters greatly reduces the number of unknowns in the reconstruction algorithm and gives us the opportunity to numerically reconstruct radially and azimuthally polarized beams directly without the need of using a polarizer in front of the focusing objective for separating linearly polarized constituents. An example of such numerically reconstructed electric field density projections is presented in Figure 9 at wavelengths of 535 and 633 nm. As one can see, the distortions observed while straightforwardly implementing the knife-edge method have disappeared after implementation of the adapted fit algorithm.

FIGURE 9

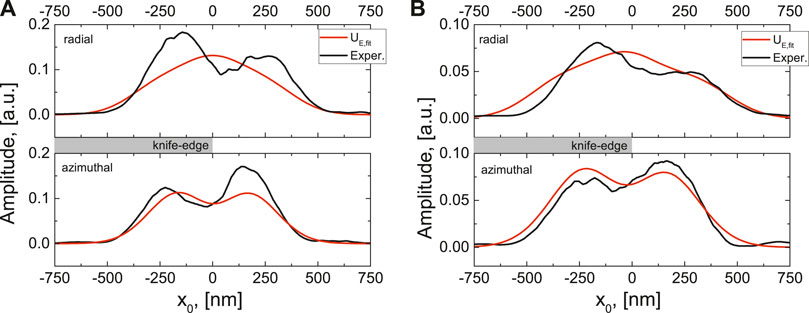
FIGURE 9. Depiction of the adapted knife-edge method for tightly focused radially and azimuthally polarized beams. Experimentally measured projections of radially and azimuthally polarized beams (black) and their reconstructed beam profiles (red) for (A)$\lambda =535\text{nm}$, (B)$\lambda =633\text{nm}$.

In the end we would like to stress that the implementation of the fitted knife-edge algorithm performs an additional smoothing of some fine scale numerical artifacts. This can happen because the beams in our basis are perfect and symmetric in shape. One can argue, that by approximating the beam as a combination of Hermite-Gaussian modes, the algorithm restores only “perfect” shapes of a beam. Furthermore, if this method is applied to an irregularly shaped beam, it could completely remove the irregularities and artificially reconstruct it into a “perfect” shape beam. This is a natural outcome given the fact that the beams are very tightly focused here, and numerically observed irregularities have very high transverse wave-vectors, which would require an introduction of evanescent Hermite-Gaussian fields in order to describe them. However, we would like to point out that Eq. 8 can be rewritten without implementation of Hermite-Gaussian polynomials and the whole adapted knife-edging algorithm can be implemented as a system of linear equations for a few adjacent x-coordinates. This implementation would produce less smooth curves than those we observe in Figures 8 and 9.

4 Conclusion

In conclusion, we have analyzed the performance of the knife-edge method for pure materials applied to linearly polarized Hermite-Gaussian modes of first order, which are the constituents of radially and azimuthally polarized beams. For the correction of the observed modifications in these knife-edge measurements we presented a straight-forward and easy to implement method that is based on the adapted knife-edge reconstruction scheme. This way we are able to retrieve the beam projections of linearly polarized Hermite-Gaussian modes, for which shifts and deformations of the reconstructed projections as observed in conventional knife-edge measurements can be corrected.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

SO and PB conceived the idea. SO developed the theoretical frame work and analyzed the theoretical data. CH and PM performed the experiments and analyzed the experimental data. PB and GL supervised the project. All authors contributed equally to the manuscript.

Funding

SO acknowledges funding by the European Social Fund according to the activity “Improvement of researchers” qualification by implementing world-class R&D projects’ of Measure No. 09.3.3-LMT-K-712.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Stefan Malzer, Isabel Gäßner, Olga Rusina, and Irina Harder for their valuable support in preparing the samples. This manuscript has been released as a pre-print on the pre-print server arXiv (S. Orlov et al., arXiv:1610.08643 [physics.optics]).

References

1. Quabis S, Dorn R, Eberler M, Glöckl O, Leuchs G. Focusing light to a tighter spot. Optic Commun (2000) 179:1–7. doi:10.1016/s0030-4018(99)00729-4

CrossRef Full Text | Google Scholar

2. Dorn R, Quabis S, Leuchs G. The focus of light-linear polarization breaks the rotational symmetry of the focal spot. J Mod Optic (2003) 50:1917–26. doi:10.1080/09500340308235246

CrossRef Full Text | Google Scholar

3. Richards B, Wolf E. Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system. Proc R Soc A (1959) 253:358–79. doi:10.1098/rspa.1959.0200

CrossRef Full Text | Google Scholar

4. Youngworth KS, Brown TG. Focusing of high numerical aperture cylindrical-vector beams. Opt Express (2000) 7:77–87. doi:10.1364/oe.7.000077

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dorn R, Quabis S, Leuchs G. Sharper focus for a radially polarized light beam. Phys Rev Lett (2003) 91:233901. doi:10.1103/physrevlett.91.233901

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kindler J, Banzer P, Quabis S, Peschel U, Leuchs G. Waveguide properties of single subwavelength holes demonstrated with radially and azimuthally polarized light. Appl Phys B (2007) 89:517–20. doi:10.1007/s00340-007-2874-5

CrossRef Full Text | Google Scholar

7. Züchner T, Failla AV, Hartschuh A, Meixner AJ. A novel approach to detect and characterize the scattering patterns of single Au nanoparticles using confocal microscopy. J Microsc (2008) 229:337–43. doi:10.1111/j.1365-2818.2008.01910.x

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Banzer P, Kindler J, Quabis S, Peschel U, Leuchs G. Extraordinary transmission through a single coaxial aperture in a thin metal film. Opt Express (2010) 18:10896–904. doi:10.1364/oe.18.010896

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Banzer P, Peschel U, Quabis S, Leuchs G. On the experimental investigation of the electric and magnetic response of a single nano-structure. Opt Express (2010) 18:10905–23. doi:10.1364/oe.18.010905

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Bauer T, Orlov S, Leuchs G, Banzer P. Towards an optical far-field measurement of higher-order multipole contributions to the scattering response of nanoparticles. Appl Phys Lett (2015) 106:091108. doi:10.1063/1.4914117

CrossRef Full Text | Google Scholar

11. Firester AH, Heller ME, Sheng P. Knife-edge scanning measurements of subwavelength focused light beams. Appl Opt (1977) 16:1971–4. doi:10.1364/ao.16.001971

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Khosrofian JM, Garetz BA. Measurement of a Gaussian laser beam diameter through the direct inversion of knife-edge data. Appl Opt (1983) 22:3406–10. doi:10.1364/ao.22.003406

PubMed Abstract | CrossRef Full Text | Google Scholar

13. de Araújo MA, Silva R, de Lima E, Pereira DP, de Oliveira PC. Measurement of Gaussian laser beam radius using the knife-edge technique: improvement on data analysis. Appl Opt (2009) 48:393–6. doi:10.1364/ao.48.000393

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Brost G, Horn PD, Abtahi A. Convenient spatial profiling of pulsed laser beams. Appl Opt (1985) 24:38–40. doi:10.1364/ao.24.000038

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Schneider MB, Webb WW. Measurement of submicron laser beam radii. Appl Opt (1981) 20:1382–8. doi:10.1364/ao.20.001382

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bauer T, Orlov S, Peschel U, Banzer P, Leuchs G. Nanointerferometric amplitude and phase reconstruction of tightly focused vector beams. Nat Photon (2013) 8:23–7. doi:10.1038/nphoton.2013.289

CrossRef Full Text | Google Scholar

17. McCally RL. Measurement of Gaussian beam parameters. Appl Opt (1984) 23:2227. doi:10.1364/ao.23.002227

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Marchenko P, Orlov S, Huber C, Banzer P, Quabis S, Peschel U, et al. Interaction of highly focused vector beams with a metal knife-edge. Opt Express (2011) 19:7244–61. doi:10.1364/oe.19.007244

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Huber C, Orlov S, Banzer P, Leuchs G. Corrections to the knife-edge based reconstruction scheme of tightly focused light beams. Opt Express (2013) 21:25069–76. doi:10.1364/oe.21.025069

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Orlov S, Huber C, Marchenko P, Banzer P, Leuchs G. Corrected knife-edge-based reconstruction of tightly focused higher order beams (2016). arXiv:1610.08643.

Google Scholar

21. Huber C, Orlov S, Banzer P, Leuchs G. Influence of the substrate material on the knife-edge based profiling of tightly focused light beams. Opt Express (2016) 24:8214–27. doi:10.1364/oe.24.008214

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Orlov S, Peschel U. Complex source beam: a tool to describe highly focused vector beams analytically. Phys Rev A (2010) 82:063820. doi:10.1103/physreva.82.063820

CrossRef Full Text | Google Scholar

23. Orlov S, Banzer P. Vectorial complex-source vortex beams. Phys Rev A (2014) 90:023832. doi:10.1103/physreva.90.023832

CrossRef Full Text | Google Scholar

24. Erikson WL, Singh S. Polarization properties of Maxwell-Gaussian laser beams. Phys Rev E (1994) 49:5778–86. doi:10.1103/physreve.49.5778

CrossRef Full Text | Google Scholar

25. Lax M, Louisell WH, McKnight WB. From Maxwell to paraxial wave optics. Phys Rev A (1975) 11:1365. doi:10.1103/physreva.11.1365

CrossRef Full Text | Google Scholar

26. Siegman AE. Lasers. Mill Valley, CA: University Science Books (1986). 1322 p.

Google Scholar

27. Sturman B, Podivilov E, Gorkunov M. Eigenmodes for metal-dielectric light-transmitting nanostructures. Phys Rev B (2007) 76:125104. doi:10.1103/physrevb.76.125104

CrossRef Full Text | Google Scholar

28. Kocabaş ŞE, Veronis G, Miller DAB, Fan S. Modal analysis and coupling in metal-insulator-metal wavequides. Phys Rev B (2009) 79:035120. doi:10.1103/PhysRevB.79.035120

CrossRef Full Text | Google Scholar

29. Stalder M, Schadt M. Linearly polarized light with axial symmetry generated by liquid-crystal polarization converters. Opt Lett (1996) 21:1948–50. doi:10.1364/ol.21.001948

PubMed Abstract | CrossRef Full Text | Google Scholar