- 1Dipartimento di Fisica e Astronomia, Universitá di Bologna, , Bologna, Italy
- 2Hamburger Sternwarte, Hamburg, Germany
- 3Istituto di Radio Astronomia, INAF, Bologna, Italy
- 4Institute of Neurosurgery, Department of Neurosciences, Biomedicine, and Movement Sciences, University of Verona, Verona, Italy
- 5Azienda Ospedaliera‐Universitaria di Modena, Modena, Italy
We investigate the similarities between two of the most challenging and complex systems in Nature: the network of neuronal cells in the human brain, and the cosmic network of galaxies. We explore the structural, morphological, network properties and the memory capacity of these two fascinating systems, with a quantitative approach. In order to have an homogeneous analysis of both systems, our procedure does not consider the true neural connectivity but an approximation of it, based on simple proximity. The tantalizing degree of similarity that our analysis exposes seems to suggest that the self-organization of both complex systems is likely being shaped by similar principles of network dynamics, despite the radically different scales and processes at play.
Introduction
Central to our vision of Nature are two fascinating systems: the network of neurons in the human brain and the cosmic web of galaxies.
The human brain is a complex temporally and spatially multiscale structure in which cellular, molecular and neuronal phenomena coexist. It can be modeled as a hierarchical network (i.e., “the human connectome” [1]), in which neurons cluster into circuits, columns, and different interconnected functional areas. The structure of the neuronal network allows the linking between different areas, all devoted to process specific spatiotemporal activities over their neurons, forming the physical and biological basis of cognition [e.g., Ref. 2]. Some of major challenges of contemporary neuroscience are to disentangle the structure of the connectome (e.g., the complete map of the neural connections in a brain), to understand how this structure can produce complex cognitive functions, and to define the role of glial cells and of the microenvironment in the interneuronal physiology.
The Universe, according to the large collection of telescope data gathered over many decades, seems to be reasonably well described by a “consensus” physical model called the
Although the relevant physical interactions in the above two systems are completely different, their observation through microscopic and telescopic techniques have captured a tantalizing similar morphology, to the point that it has often been noted that the cosmic web and the web of neurons look alike [e.g., Refs. 6 and 7].
In this work, we apply methods from cosmology, neuroscience, and network analysis to explore this thought-provoking question quantitatively for the first time, to our knowledge.
Materials and Methods
Immunohistochemistry and Microscopy
We analyzed several independent samples of cerebral and of cerebellar human cortex were formalin-fixed and paraffin-embedded [8], sampling slices of depth
Cosmological Simulations
We used synthetic samples of the cosmic web from a high-resolution (
Results
Absolute Numbers, Internal Proportions, and Composition
We first quote data available from the literature, which allow us a first sketchy comparison of the absolute sizes of both systems. The radius of the observable Universe is
According to recent estimates, the adult human brain contains
It can be noticed that the two systems are organized in well defined networks, with
In the case of the Universe we refer to the present-day composition, based on Planck Collaboration et al. [15], as the relative energy distribution is a function of time in the
In summary: 1) the brain is composed by water (
Strikingly, in both cases
Morphological Comparison
Small samples of the human cerebral and cerebellar cortex were harvested during corticectomy to approach subcortical tumors (Section 2.1). The neuronal cells have been then stained with clone 2F11 monoclonal antibody against neurofilaments, which are neuron-specific intermediate filaments in the cytoplasm of neurons that provide structural support to the neuronal cytoskeleton, along with microtubules and microfilaments. It has been shown that the number, spacing, and areal density of neurofilaments in neurons are measures with a strong dependency on axon caliber [e.g., Refs. 19–21]. Although also microtubules density depends on axon caliber, it has been shown that microtubules often form small clusters in the vicinity of membranous organelles [22]. For this reason we consider neurofilaments might be more homogeneously arranged in the neuron, and likely to be a better target to visualize the spatial distribution of neurons in the slices. For the cosmic web, we analyzed each one of the 12 thin slices from the simulated volume (Section 2.2), to assess the effect of cosmic variance. Such 2-dimensional approach mimics what is done with brain samples, and due to the large degree of isotropy of the cosmic web on such large scales this approach can also be used to readily translate our statistics into the 3-dimensional case.
Figure 1 gives an overview of the details of structures observed at various scales (from

FIGURE 1. Maps of normalized density contrast,
We will use in this work statistical tools to 1) compare the distribution of structure across the entire continuum range of spatial scales of our samples, also compared to other natural complex systems (Section 3.3); 2) measure the properties of connectivity between nodes in the network, estimating the tendency to form highly clustered configurations (see Section 3.4).
Spectral Analysis
We used here a statistics commonly used in cosmology: the density power spectrum,
In the case of the cosmological simulation,
The resulting power spectra are shown in Figure 2. It shall be stressed that power spectra are free to be slid horizontally in the plot, in the sense that the reference scale L related to
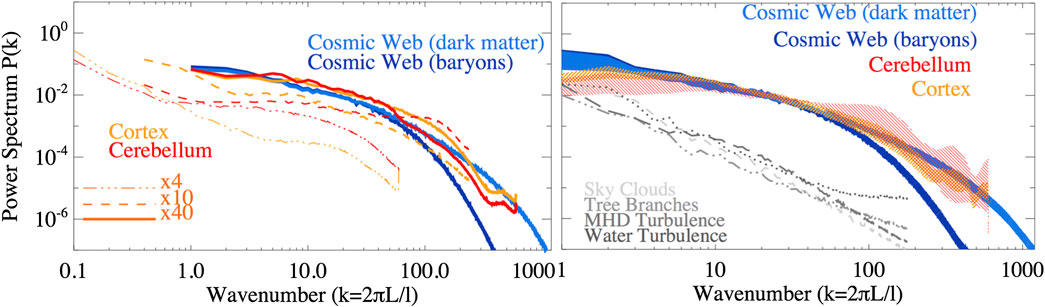
FIGURE 2. Left: power spectra of density fluctuations in all samples (in the case of brain samples, spectra from slices of different size and magnification factors are shown). Right: power spectra of density fluctuations (in the case of brain tissues, only the
On the other hand, the fluctuations measured on
Lastly, we produced control power spectra for other randomly drawn samples of natural networks (sky clouds, tree branches, water turbulence, and magneto-hydrodynamic turbulence - all available at https://cosmosimfrazza.myfreesites.net/cosmic-web-and-brain-network-datasets), with the goal of double checking that our method is not biased to produce similarity between truly different physical systems. As shown by the gray lines in the right panel of Figure 2, such systems display a more regular power-law spectral behavior, clearly at variance with what found in the main networks analyzed in this work - even if in the latter case we did not perform a full analysis across the entire dynamical range of such systems, looking for the emergence of possible spectral features as in the case of the brain and the cosmic samples.
However, power spectra are blind to phase correlations in the continuous field, hence two morphologically different distributions can still produce similar spectra [28]. In the following section we will thus also rely on non-spectral methods to compare the different samples.
Network Analysis
Network science have proliferated into various physical disciplines, including neuroscience [e.g., Ref. 29–32] as well as cosmology [e.g., Refs. 33 and 34]. Complex network analysis can partially soften the problem of not having perfectly consistent density estimators across our samples, in the sense that defining the nodes of the various networks is less sensitive to the exact mapping details of the images. We focus here on two simple network parameters commonly used in graph theory and network analysis [e.g., Refs. 35 and 36]. The first is the degree centrality,
where
in which
While sophisticated methods to identify nodes and filaments in the simulated cosmic network [e.g., Ref. 4] or in the neuronal network [e.g., Ref. 37] have been proposed, here we explore a simpler approach with the advantage of being readily applicable to both networks. The method is inspired by standard “halo finding” procedures in cosmology to identify the self-gravitating halos in the cosmic web [38]. In detail: 1) we marke the highest intensity peaks in all maps (i.e., pixels in the top
We then built the adjacent matrix of nodes,
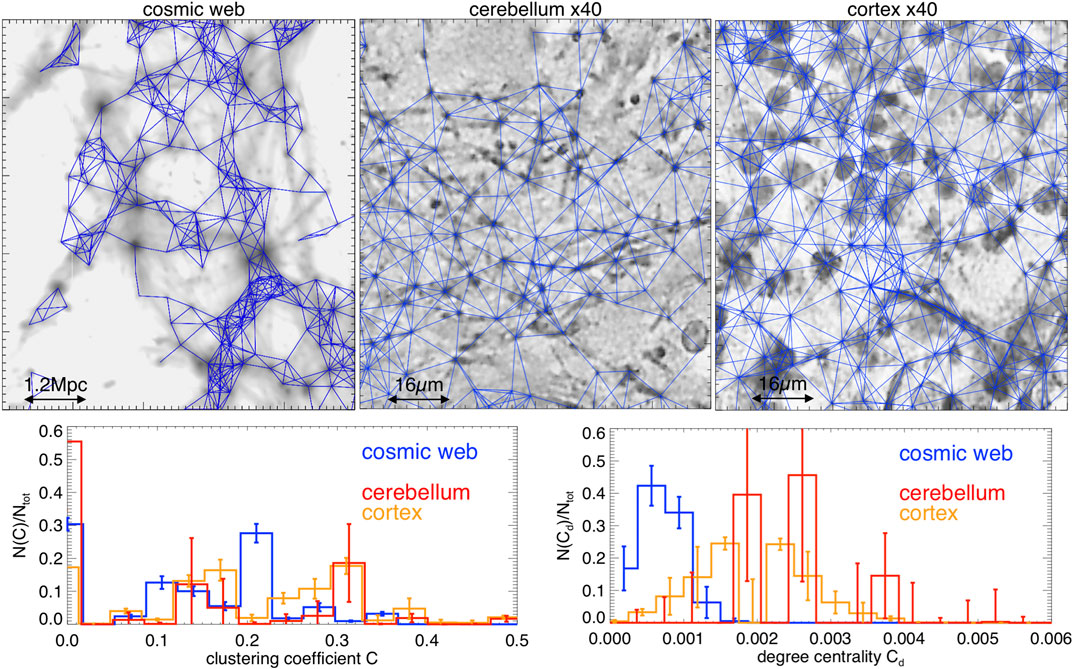
FIGURE 3. Top panels: zoomed details of the reconstructed connections between nodes for three example of networks in our sample (blue lines, superimposed to the density contrast maps). Bottom panels: distributions of clustering coefficient and of degree centrality for all slices (the error bars give the scatter within each investigated sample of slices). The reconstructed connections do not take into account the long-range neural connections, and the clusters shown are purely spatial.
This method selects from
Both statistics clearly show that the brain and cosmic web networks are very different from Erdös–Rényi random networks of the same size, which would instead predict for the two parameters
We point out that in this study we analyzed only a fraction of the cortex, and not the whole Central Nervous System, whose architecture is obviously different. Actually, while proximity can accurately describe the cosmic web, neural webs are based on connections and therefore our analysis is not sensitive to long-range connectivity. But indeed long-range connectivity is known to be a crucial feature of neural webs. We defer the application of more complex network statistics [e.g., Ref. 40]) to future work.
Discussion
We have presented a detailed comparison between the neuronal network and the cosmic web, two of the most fascinating and complex networks in Nature, with the goal of assessing the level of similarity between these two physical systems in an objective way.
We have also applied homogeneous statistical approaches to real lab samples of both the brain and the cerebellar cortex (Section 2.1), and to slices of the simulated distribution of dark matter and ordinary in the cosmic web (Section 2.2), and quantified their morphological and network properties using spectral analysis (Section 3.3) as well as network parameters from graph theory (Section 3.4). Within the range of simplifying assumptions we used to define both networks (e.g., based on the proximity of nodes identified from the continuous matter distribution rendered by different imaging techniques) our findings hint at the fact that similar network configurations can emerge from the interaction of entirely different physical processes, resulting in similar levels of complexity and self-organization, despite the dramatic disparity in spatial scales (i.e.,
We are aware that this approach has several limitations. First, our comparison focused on density of matter. The selection of neurofilaments to outline the neuronal network was based on the fact that they are quite evenly expressed in the cytoplasmic compartment of the neurons. Our results should be further validated with different markers, as microfilaments or microtubules. Second, we assumed that the highest stain density is located at the level of neuronal Soma, which is an approximation, leading to a non-standard definition of nodes. Further studies are required to validate our results with functional neural network data and without losing anatomical-visual definition. Third, our study has been based on histological slices, which can obviously show only a tiny portion of the brain network itself. Moreover, while the cosmic web uses proximity to define its network, neural webs are based on connections that can be significantly long-range spatially, and which could not be properly assessed through our analysis due to technical limitation of the method. For the above limitations, we could not present a systematic and complete connectivity analysis of networks, as we focused on simple proximity and not on long-range connectivity. A key Frontier of this line of comparative research is the possibility of measuring the memory capacity of both networks, a task presently made challenging by the radically different approaches presently available to measure to monitor the flow of information within them. An interesting factoid well illustrates that possible similarities also exist in this respect. The total memory capacity of the human brain has been recently estimated using section electron microscopy to reconstruct the 3D distribution of dendritic spines and of their synapses, and finding 26 distinct synaptic strengths, which accounts to an average of
Together with the rest of the analysis presented in this work, such similarities are meant to motivate the development of more powerful and discriminating algorithms to pinpoint analogies and differences of these fascinating systems, almost at the conceivable extremes of spatial scales in the Universe.
Data Availability Statement
All brain samples analysed in this work, as well as relevant samples of the simulated cosmic web and the reconstructed network connectivity are publicly accessible at this URL: https://cosmosimfrazza.myfreesites.net/cosmic-web-and-brain-network-datasets.
Ethics Statement
This study was carried out in accordance with the recommendations of the University Hospital of Modena. All subjects gave written informed consent in accordance with the Declaration of Helsinki.
Author Contributions
Both authors contributed to the writing of the manuscript and to the interpretation of results. FV is responsible for the production of the cosmological simulations and for numerical methods adopted in the paper. AF is responsible for the extraction of the brain samples used in this work.
Funding
FV acknowledges financial support from the ERC Starting Grant “MAGCOW”, no. 714196.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We gratefully acknowledge Elena Zunarelli (Department of Anatomic Pathology, University Hospital Policlinico di Modena, Modena, Italy) for producing the slices used in Figure 1. The cosmological simulation of this work have been produced using the ENZO code (http://enzo-project.org), which is the product of a collaborative effort of scientists at many universities and national laboratories. The simulations/analysis of this work have been produced on Piz Daint supercomputer at CSCS-ETHZ (Lugano, Switzerland) and on Marconi at CINECA (Bologna, Italy) under projects s805 and INA17_C4A28 with (FV as Principal Investigator). FV acknowledges the usage of online storage tools kindly provided by the INAF Astronomical Archive (IA2) initiave (http://www.ia2.inaf.it). We gratefully acknowledge careful reading of this manuscript by D. Wittor.
References
1. Sporns O. The human connectome: a complex network. Ann N Y Acad Sci. (2011). 1224:109–25. doi:10.1111/j.1749-6632.2010.05888.x
2. Battaglia D, Witt A, Wolf F, Geisel T. Dynamic effective connectivity of inter-areal brain circuits. PLoS Comput Biol. (2012). 8:1–20. doi:10.1371/journal.pcbi.1002438
3. Schneider P. Extragalactic astronomy and cosmology: an introduction. Berlin, Heidelberg: Springer (2015). doi:10.1007/978-3-642-54083-7
4. Libeskind NI, van de Weygaert R, Cautun M, Falck B, Tempel E, Abel T, et al. Tracing the cosmic web. Mon Not R Astron Soc Lett. (2018). 473:1195–217. doi:10.1093/mnras/stx1976
5. Doré O, Hirata C, Wang Y, Weinberg D, Eifler T, Foley RJ, et al. WFIRST: the essential cosmology space observatory for the coming decade. arXiv:1904.01174. arXiv e-prints (2019)., https://arxiv.org/abs/1904.01174
6. Lima M, Brain + Universe (2009). Visual complexity. http://www.visualcomplexity.com/vc/blog/?p=234
7. Neyrinck M, Elul T, Silver M, Mallouh E, Aragón-Calvo M, Banducci S, et al. Exploring Connections Between Cosmos & Mind Through Six Interactive Art Installations in “As Above As Below”. arXiv:2008.05942. arXiv e-prints (2020).
8. Hsu SM. [39] immunohistochemistry. M Wilchek, and EA Bayer, editors Avidin-biotin technology. Methods in enzymology. Vol. 184. Cambridge, MA: Academic Press (1990). p. 357–63. doi:https://doi.org/10.1016/0076-6879(90)84293-P
9. Bryan GL, Norman ML, O’Shea BW, Abel T, Wise JH, Turk MJ, et al. ENZO: an adaptive mesh refinement code for astrophysics. Astrophys J. (2014). 211:19. doi:10.1088/0067-0049/211/2/19
10. Vazza F, Brueggen M, Gheller C, Hackstein S, Wittor D, Hinz PM. Simulations of extragalactic magnetic fields and of their observables. Class Quant Grav. (2017). 34:234001. doi:10.1088/1361-6382/aa8e60
11. Condon JJ, Matthews AM.
12. Conselice CJ, Wilkinson A, Duncan K, Mortlock A. The evolution of galaxy number density at z < 8 and its implications. Astrophys J. (2016). 830:83. doi:10.3847/0004-637X/830/2/83
13. Azevedo FA, Carvalho LR, Grinberg LT, Farfel JM, Ferretti RE, Leite RE, et al. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J Comp Neurol. (2009). 513:532–41. doi:10.1002/cne.21974
14. Herculano-Houzel S. The remarkable, yet not extraordinary, human brain as a scaled-up primate brain and its associated cost. Proc Natl Acad Sci USA. (2012). 109:10661–8. doi:10.1073/pnas.1201895109
15.Planck Collaboration, Ade PAR, Aghanim N, Arnaud M, Ashdown M, Aumont J, et al. Planck 2015 results. XIII. Cosmological parameters. Astron Astrophys. (2016). 594:63. doi:10.1051/0004-6361/201525830
16. O’brien JS, Sampson EL. Lipid composition of the normal human brain: gray matter, white matter, and myelin. J Lipid Res. (1965). 6(4):537–44.
17.Biochemistry and the central nervous system. A.M.A. Archives Neurol Psychiatry. (1957). 77:56. doi:10.1001/archneurpsyc.1957.02330310066012
18. Pfeifer S, McCarthy IG, Stafford SG, Brown ST, Font AS, Kwan J, et al. The Bahamas project: effects of dynamical dark energy on large-scale structure. arXiv e-prints (2020) arXiv:2004.07670.
19. Maxwell W, Graham D. Loss of axonal microtubules and neurofilaments after stretch-injury to guinea pig optic nerve fibers. J Neurotrauma. (1997). 14:603–14. doi:10.1089/neu.1997.14.603
20. Jafari SS, Nielson M, Graham DI, Maxwell WL. Axonal cytoskeletal changes after nondisruptive axonal injury. ii. intermediate sized axons. J Neurotrauma. (1998). 15:955–66. doi:10.1089/neu.1998.15.955. PMID: 9840768
21. Fournier AJ, Hogan JD, Rajbhandari L, Shrestha S, Venkatesan A, Ramesh KT. Changes in neurofilament and microtubule distribution following focal axon compression. PLoS One. (2015). 10:1–21. doi:10.1371/journal.pone.0131617
22. Price R, Lasek R, Katz M. Microtubules have special physical associations with smooth endoplasmic reticula and mitochondria in axons. Brain Res. (1991). 540:209–16. doi:https://doi.org/10.1016/0006-8993(91)90509-T
23. Vazza F, Brunetti G, Gheller C, Brunino R, Brüggen M. Massive and refined. II. The statistical properties of turbulent motions in massive galaxy clusters with high spatial resolution. Astron Astrophys. (2011). 529:A17. doi:10.1051/0004-6361/201016015
24. Manto M, Gruol D, Schmahmann J, Koibuchi N, Rossi F. Handbook of the cerebellum and cerebellar disorders. Berlin, Heidelberg: Springer (2013). p. 1–24. doi:10.1007/978-94-007-1333-8
25. Sylos Labini F, Vasilyev NL, Baryshev YV. Power law correlations in galaxy distribution and finite volume effects from the sloan digital sky survey data release four. Astron Astrophys. (2007). 465:23–33. doi:10.1051/0004-6361:20065321
26. Sylos Labini F, Vasilyev NL, Baryshev YV. Large-scale fluctuations in the distribution of galaxies from the two-degree galaxy redshift survey. Astron Astrophys. (2009). 496:7–23. doi:10.1051/0004-6361:200810575
27. Sylos Labini F Inhomogeneities in the universe. Class Quant Grav. (2011). 28:164003. doi:10.1088/0264-9381/28/16/164003
28. Coles P. Phase correlations and topological measures of large-scale structure. Data Anal. (2009). 665:493–522. doi:10.1007/978-3-540-44767-2_15
29. Bassett DS, Bullmore E. Small-world brain networks. Neuroscientist. (2006). 12:512–23. doi:10.1177/1073858406293182. PMID: 17079517
30. Meng L, Xiang J. Brain network analysis and classification based on convolutional neural network. Front Comput Neurosci. (2018). 12:95. doi:10.3389/fncom.2018.00095
31. Joyce KE, Laurienti PJ, Burdette JH, Hayasaka S. A new measure of centrality for brain networks. PLoS One. (2010). 5:1–13. doi:10.1371/journal.pone.0012200
32. Sporns O, Honey CJ, Ktter R. Identification and classification of hubs in brain networks. PLoS One. (2007). 2:e1049. doi:10.1371/journal.pone.0001049
33. de Regt R, Apunevych S, von Ferber C, Holovatch Y, Novosyadlyj B. Network analysis of the COSMOS galaxy field. Mon Not R Astron Soc Lett. (2018). 477:4738–448. doi:10.1093/mnras/sty801
34. Tsizh M, Novosyadlyj B, Holovatch Y, Libeskind NI. Large-scale structures in the
35. Hansen DL, Shneiderman B, Smith MA, Himelboim I. Social network analysis: measuring, mapping, and modeling collections of connections. In: DL Hansen, B Shneiderman, MA Smith, and I Himelboim, editors Analyzing social media networks with NodeXL. 2nd ed. Chap. 3, Morgan Kaufmann (2020). p. 31–51. doi:https://doi.org/10.1016/B978-0-12-817756-3.00003-0
36. Golbeck J. Network structure and measures. In: J Golbeck, editor Analyzing the social web. Chap. 2. Boston: Morgan Kaufmann (2013). p. 25–44. doi:https://doi.org/10.1016/B978-0-12-405531-5.00003-1
37. Stanley M, Moussa M, Paolini B, Lyday R, Burdette J, Laurienti P. Defining nodes in complex brain networks. Front Comput Neurosci. (2013). 7:169. doi:10.3389/fncom.2013.00169
38. Knebe A, Knollmann SR, Muldrew SI, Pearce FR, Aragon-Calvo MA, Ascasibar Y, et al. Haloes gone MAD14: the halo-finder comparison project. Mon Not Roy Astron Soc. (2011). 415:2293–318. doi:10.1111/j.1365-2966.2011.18858.x
39. Albert R, Barabási AL. Statistical mechanics of complex networks. Rev Mod Phys. (2002). 74:47–97. doi:10.1103/RevModPhys.74.47
40. van den Heuvel MP, Sporns O. Rich-club organization of the human connectome. J Neurosci. (2011). 31:15775–86. doi:10.1523/JNEUROSCI.3539-11.2011
41. Bartol TM, Bromer C, Kinney J, Chirillo MA, Bourne JN, Harris KM, et al. Nanoconnectomic upper bound on the variability of synaptic plasticity. Elife. (2015). 4:e10778. doi:10.7554/eLife.10778
42. Vazza F On the complexity and the information content of cosmic structures. Mon Not R Astron Soc: Lett. (2017). 465:4942–55. doi:10.1093/mnras/stw3089
Keywords: cosmology: theory, neuroscience, network analysis, complex systems, large‐scale structure formation
Citation: Vazza F and Feletti A (2020) The Quantitative Comparison Between the Neuronal Network and the Cosmic Web. Front. Phys. 8:525731. doi: 10.3389/fphy.2020.525731
Received: 16 January 2020; Accepted: 28 September 2020;
Published: 16 November 2020.
Edited by:
Francesco Caravelli, Los Alamos National Laboratory (DOE), United StatesReviewed by:
Mark Neyrinck, University of the Basque Country, SpainMarius Cautun, Leiden University, Netherlands
Michael Silver, University of California, Berkeley, United States
Copyright © 2020 Vazza and Feletti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: F. Vazza, ZnJhbmNvLnZhenphMkB1bmliby5pdA==
 F. Vazza
F. Vazza A. Feletti4,5
A. Feletti4,5