Quasiclassical Theory of C4-Symmetric Magnetic Order in Disordered Multiband Metals

Recent experimental studies performed in the normal state of iron-based superconductors have discovered the existence of the C₄-symmetric (tetragonal) itinerant magnetic state. This state can be described as a spin density wave with two distinct magnetic vectors ${\overrightarrow{Q}}_1$ and ${\overrightarrow{Q}}_2$. Given an itinerant nature of magnetism in iron-pnictides, we develop a quasiclassical theory of tetragonal magnetic order in disordered three-band metal with anisotropic band structure. Within our model we find that the C₄-symmetric magnetism competes with the C₂-symmetric state with a single $\overrightarrow{Q}$ magnetic structure vector. Our main results is that disorder promotes tetragonal magnetic state which is in agreement with earlier theoretical studies.

1. Introduction

Quasiclassical approach to interacting many-body systems has proved to be a powerful tool in describing their transport and thermodynamic properties. Within this method, the quantum mechanical averages of an operator corresponding to a physical quantity are replaced with the averages of its classical counterpart over all classical trajectories. Alternatively, one can formulate the quasiclassical theory by using the quasiclassical functions which are obtained from the quantum mechanical single-particle propagators by integrating them over all single particle energies. Qualitatively, for a superconductor with pairing gap Δ and quasiparticles with Fermi momentum p_F and Fermi velocity v_F, this procedure corresponds to averaging over the short length scales of the problem $~p_F^{-1}$ and retaining the physics at long scales ~ v_F/Δ. Quasiclassical theory was particularly useful in the comparatively recent analysis of the problem of far-from-equilibrium order parameter dynamics in charge-neutral superfluids [1–5].

Most recently, several non-trivial phenomena have been observed in a family of iron-based superconductors and their alloys [6]. One example of such phenomena is an observation of the peak in the penetration depth in BaFe₂(As_1−xP_x)₂ as a function of phosphorus concentration [7–10], in Ba_1−xK_xFe₂As₂ as a function of potassium concentration [11] and, most recently in Ba(Fe_1−xCo_x)₂As₂ as a function of cobalt concentration [12]. Another example is the experimental observation of the spin-density-wave order which is characterized by two magnetic ordering vectors, ${\overrightarrow{Q}}_1$ and ${\overrightarrow{Q}}_2$, in various iron-based superconducting alloys [13–20].

Due to the fact that in iron-based superconductors the superconductivity is often observed near magnetic instability, quasiclassical approaches initially developed for the purely superconducting states have been re-formulated to specifically include the effects of competition between superconducting and magnetic phases as well as the effects of disorder [21–24]. The experimental observations of the peak in the London penetration depth remains only partially understood [25, 26] which provides an additional motivation to look for possible explanations of this effect.

In turn, the experimental discovery of the double-$\overrightarrow{Q}$ magnetic state in iron-based superconductors has lead to an appearance of many theoretical works discussing the emergence of this state and its various properties as well as its relation with other magnetic states [27–35]. Most recently, the effects of disorder on the stability of the single- and double-$\overrightarrow{Q}$ states have been discussed [36]. In particular, it was found that disorder leads to suppression of the single-$\overrightarrow{Q}$ state in favor the double-$\overrightarrow{Q}$ one.

Inspired by the earlier work on this problem, in this paper we use a slightly simplified version of the model introduced in reference [36] to formulate a quasiclassical theory of the double-$\overrightarrow{Q}$ state in iron-based superconductors. Specifically, we consider the disordered model which incorporates both interband and intraband disorder. In agreement with the earlier results [36], we find that when the interband disorder can be ignored, the intraband disorder promotes the emergence of the double-$\overrightarrow{Q}$ state.

This paper is organized as follows. In the next section II introduce the model Hamiltonian. Section III is devoted to the formulation of the quasiclassical approach with the derivation of the quasiclassical equations. In section IV contains the results of the Landau expansion for the free energy using the quasiclassical equations. Section V contains the discussion of the results and comments related to the further development of the presented formalism in the context of the physics of iron-based superconductors. Sections with acknowledgments and Appendix with some technical details conclude the paper.

2. Model

In what follows we first introduce the model Hamiltonian, which consists of three terms:

$\begin{array}{ll}\widehat{H}={\widehat{H}}_0+{\widehat{H}}_{\text{sdw}}+{\widehat{H}}_{\text{dis}}.& (1)\end{array}$

The first term on the right hand side of this expression is a single-particle Hamiltonian which describes the band-structure consisting of three bands: hole-like band at the Γ point and two electron-like bands centered at ${\overrightarrow{Q}}_X=(\pi ,0)$, ${\overrightarrow{Q}}_Y=(0,\pi )$ of the two-dimensional Brillouin zone. We use the compact notations to write down $\widehat{H}$₀ using the six-component spinor ${\widehat{\Psi }}_{\text{k}}^{†}=\left({\widehat{c}}_{\text{k}\uparrow }^{†}, {\widehat{c}}_{\text{k}\downarrow }^{†}, {\widehat{d}}_{\text{k}\uparrow }^{†}, {\widehat{d}}_{\text{k}\downarrow }^{†}, {\widehat{f}}_{\text{k}\uparrow }^{†}, {\widehat{f}}_{\text{k}\downarrow }^{†}\right)$:

$\begin{array}{ll}{\widehat{H}}_0={\displaystyle \sum _{\text{k}}}{\widehat{\Psi }}_{\text{k}}^{†}\left(\begin{array}{ccc}{\epsilon }_{\Gamma }(\text{k}){\widehat{\sigma }}_0& 0& 0\\ 0& {\epsilon }_X(\text{k}){\widehat{\sigma }}_0& 0\\ 0& 0& {\epsilon }_Y(\text{k}){\widehat{\sigma }}_0\end{array}\right){\widehat{\Psi }}_{\text{k}},& (2)\end{array}$

where ${\widehat{\sigma }}_0$ is a unit 2 × 2 matrix and single particle energy spectra are given by ε_Γ(k) = ξ_k, ${\xi }_{\text{k}}={ϵ}_0-k^2/2$, ε_X(k) = −ξ_k + δ₀ + δ₂ cos 2ϕ_k, ε_Y(k) = −ξ_k + δ₀ − δ₂ cos 2ϕ_k, ϵ₀ is the energy which amounts to the off-set between the bands and k = (k cos ϕ_k, k sin ϕ_k). Here δ₀ is a parameter which is defined relative to the chemical potential μ and describes the deviation from nesting: the bands are perfectly nested when δ₀ = 0. Lastly, δ₂ is an anisotropy parameter which accounts for the ellipticity of the corresponding Fermi pockets [36].

The second term, $\widehat{H}$_sdw, appearing in (1) accounts for the spin-density-wave order within the mean-field approximation:

$\begin{array}{ll}{\widehat{H}}_{\text{sdw}}=-{\displaystyle \sum _{\text{k}}}{\widehat{\Psi }}_{\text{k}}^{†}\left(\begin{array}{ccc}0& {\overrightarrow{m}}_X·\overrightarrow{\sigma }& {\overrightarrow{m}}_Y·\overrightarrow{\sigma }\\ {\overrightarrow{m}}_X·\overrightarrow{\sigma }& 0& 0\\ {\overrightarrow{m}}_Y·\overrightarrow{\sigma }& 0& 0\end{array}\right){\widehat{\Psi }}_{\text{k}}.& (3)\end{array}$

Here ${\overrightarrow{m}}_X$, ${\overrightarrow{m}}_Y$ are the magnetizations corresponding to two structure vectors ${\overrightarrow{Q}}_X$ and ${\overrightarrow{Q}}_Y$. In what follows, we will assume that magnetic state has Ising-like anisotropy, so we replace ${\overrightarrow{m}}_{X,Y}·\overrightarrow{\sigma }\to m_{X,Y}{\widehat{\sigma }}_3$. Within the mean-field approach we have adopted here, the order parameters m_X,Y must be computed self-consistently.

Finally, the last term on the r.h.s. side of Equation (1) introduces the disorder potential in a system. In principle, the disorder should scatter quasiparticles within each band (intraband scattering) as well as between the bands (interband scattering). The disorder unavoidably leads to the suppression of itinerant magnetism. In this paper we will limit ourselves to the case of an intraband disorder only, for an interband disorder scattering only plays a crucial role in the problem of co-existence of magnetism and superconductivity [21–23], while for the problem at hand it will only lead the faster suppression of the magnetic order. Thus, we write for the last term in (1)

$\begin{array}{ll}{\widehat{H}}_{\text{dis}}=u{\displaystyle \int }{d}^2\text{r}{\Psi }^{†}(\text{r})\Psi (\text{r}){\displaystyle \sum _i}\delta (\text{r}-{\text{R}}_i)& (4)\end{array}$

and the summation is performed over the impurity sites.

3. Quasiclassical Equations

In order to formulate the quasiclassical theory, we first introduce a single-particle correlation function

$\begin{array}{ll}{G}_{\alpha \beta }(x,x^{\prime })=-{\langle {\widehat{T}}_{\tau }\left({\widehat{\Psi }}_{\alpha }(x){\widehat{\Psi }}_{\beta }^{†}(x^{\prime })\right)\rangle }_{\text{g.s.}}& (5)\end{array}$

in the Matsubara representation, ${\widehat{\Psi }}_{\alpha }(x)={\widehat{\Psi }}_{\alpha }(\text{r},\tau )$, and the averaging is performed over the ground state of the Hamiltonian (Equation 1). Next step consists in employing the equations of motion for the propagator (5):

$\begin{array}{l}-\frac{\partial }{\partial \tau }\widehat{G}-{\widehat{H}}_{\text{r}}\widehat{G}-\widehat{\Sigma }○\widehat{G}=\delta (x-x^{\prime })𝟙,\\ \frac{\partial }{\partial {\tau }^{\prime }}\widehat{G}-\widehat{G}{\widehat{H}}_{{\text{r}}^{\prime }}-\widehat{G}○\widehat{\Sigma }=\delta (x-x^{\prime })𝟙.& (6)\end{array}$

Here $\widehat{H}$_r acts on r, the self-energy part $\widehat{\Sigma }$ is generated by the disorder potential and its action on the propagator is

$\begin{array}{ll}\widehat{\Sigma }○\widehat{G}={\displaystyle \underset{0}{\overset{1/T}{{\displaystyle \int }}}}d{\tau }^{″}{\displaystyle \int }{d}^2{\text{r}}^{″}{\Sigma }_{\alpha \gamma }(x,x^{″})G_{\gamma \beta }(x^{″},x^{\prime }).& (7)\end{array}$

The summation over the repeated indices is assumed. Next, we perform the Wigner transformation

$\begin{array}{ll}\widehat{G}(x,x^{\prime })={\displaystyle \int }\frac{d^2\text{k}}{{(2\pi )}^2}{e}^{i\text{k}·(\text{r}-{\text{r}}^{\prime })}\widehat{G}\left(\tau -{\tau }^{\prime };\frac{\text{r}+{\text{r}}^{\prime }}{2},\text{k}\right).& (8)\end{array}$

In the presence of the quenched disorder, propagators will be dependent on R = (r + r′)/2. In what follows we assume that the disorder in uncorrelated and will average the propagator over the disorder distribution which corresponds to self-consistent Born approximation. Lastly, we introduce the following matrices:

$\begin{array}{l}{\widehat{{M}}}_1=\left(\begin{array}{ccc}0& 0& 0\\ 0& {\widehat{\sigma }}_0& 0\\ 0& 0& {\widehat{\sigma }}_0\end{array}\right),{\widehat{{M}}}_2=\left(\begin{array}{ccc}0& 0& 0\\ 0& {\widehat{\sigma }}_0& 0\\ 0& 0& -{\widehat{\sigma }}_0\end{array}\right),\\ {\widehat{{M}}}_3=\left(\begin{array}{ccc}{\widehat{\sigma }}_0& 0& 0\\ 0& -{\widehat{\sigma }}_0& 0\\ 0& 0& -{\widehat{\sigma }}_0\end{array}\right),{\widehat{{P}}}_X=\left(\begin{array}{ccc}0& {\widehat{\sigma }}_3& 0\\ -{\widehat{\sigma }}_3& 0& 0\\ 0& 0& 0\end{array}\right),\\ {\widehat{{P}}}_Y=\left(\begin{array}{ccc}0& 0& {\widehat{\sigma }}_3\\ 0& 0& 0\\ -{\widehat{\sigma }}_3& 0& 0\end{array}\right),{\widehat{{Q}}}_X=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& {\widehat{\sigma }}_0\\ 0& {\widehat{\sigma }}_0& 0\end{array}\right).& (9)\end{array}$

Quasiclassical equations can now be derived after we multiply the first equation (6) from the left and the second equation from the right by ${\widehat{{M}}}_3$. Subtracting the resulting first equation from the second one we find

$\begin{array}{l}\left[{\omega }_n{\widehat{{M}}}_3,\widehat{{G}}(i{\omega }_n,{\varphi }_{\text{k}})\right]+i{\delta }_0\left[{\widehat{{M}}}_1,\widehat{{G}}(i{\omega }_n,{\varphi }_{\text{k}})\right]\\ +i{\delta }_2\text{ cos}(2{\varphi }_{\text{k}})\left[{\widehat{{M}}}_2,\widehat{{G}}(i{\omega }_n,{\varphi }_{\text{k}})\right]\\ +i\left[\left({\widehat{H}}_{\text{sdw}}+{\widehat{\Sigma }}_{\text{dis}}(i{\omega }_n)\right){\widehat{{M}}}_3,\widehat{{G}}(i{\omega }_n,{\varphi }_{\text{k}})\right]=0,& (10)\end{array}$

where we introduced the quasiclassical function, $\left[\widehat{f},\widehat{g}\right]$ implies the usual commutation relation and

$\begin{array}{ll}\widehat{{G}}(i{\omega }_n,{\varphi }_{\text{k}})=\frac{i}{\pi }{\displaystyle \int }{\widehat{{M}}}_3\widehat{G}(i{\omega }_n,\text{k})d{\xi }_{\text{k}},& (11)\end{array}$

where $\widehat{G}$(iω_n, k) is the Matsubara transform of the matrix function $\widehat{G}$(τ, k). The self-energy part is determined by the quasiclassical function and disorder scattering rate $\Gamma =\pi {\nu }_F|u{|}^2$ (ν_F is the density of states at the Fermi level per valley per spin):

$\begin{array}{ll}{\widehat{\Sigma }}_{\text{dis}}(i\omega )=-i\Gamma {\displaystyle \underset{0}{\overset{2\pi }{{\displaystyle \int }}}}\frac{d\varphi }{2\pi }{\widehat{{M}}}_3\widehat{{G}}(i\omega ,i{\varphi }_{\text{k}}).& (12)\end{array}$

In the absence of disorder, quasiclassical equation (10) is linear in $\widehat{{G}}$ and therefore is not sufficient to find $\widehat{{G}}$ unambiguously. In order to define the problem completely, one has to complement (11) with a certain constraint. To derive this constraint, we introduce a new (matrix) function [37]

$\begin{array}{l}\widehat{{B}}(\tau ,{\tau }^{\prime };{\varphi }_{\text{k}})={\displaystyle \underset{0}{\overset{1/T}{{\displaystyle \int }}}}\widehat{{G}}(\tau ,{\tau }^{″};{\varphi }_{\text{k}})\widehat{{G}}({\tau }^{″},{\tau }^{\prime };{\varphi }_{\text{k}})d{\tau }^{″}.\end{array}$

Equation for this matrix function can be easily derived from (10). It then follows that quasiclassical functions must satisfy the following normalization condition:

$\begin{array}{ll}{\widehat{{G}}}^2(i{\omega }_n,{\varphi }_{\text{k}})=𝟙.& (13)\end{array}$

As we will demonstrate below, inclusion of disorder potential does not violate this condition. In order to solve the quasiclassical equations (10) self-consistently, we need to specify the matrix structure of the function $\widehat{{G}}$.

3.1. Clean System

We start by setting the disorder scattering rate to zero, Γ = 0, for it would allow us to keep the resulting expressions more compact. Most of the results derived in this section are easily generalized for the case when Γ ≠ 0 (see below).

In the absence of the magnetic order, the expression for the function $\widehat{{G}}$ follows from (11) by comparing the solution of the quasiclassical equations with the expression found from the expression for the single-particle propagator, so that a term proportional to ${\widehat{{M}}}_3$ must appear in the expression for $\widehat{{G}}$. This conjecture also implies that there should also appear two other terms proportional to ${\widehat{{M}}}_1$ and ${\widehat{{M}}}_2$ so we write the following ansatz

$\begin{array}{ll}{\widehat{{G}}}_0=\frac{1}{2}(g_1+g_2){\widehat{{M}}}_1+\frac{1}{2}(g_2-g_1){\widehat{{M}}}_2+g_3{\widehat{{M}}}_3.& (14)\end{array}$

The commutators which include $\widehat{H}$_sdw must lead to the appearance of the three more terms in $\widehat{{G}}$: each one of the two of them being proportional to the corresponding magnetizations, while the third one being proportional to the product of m_X and m_Y. The calculation yields the following expression

$\begin{array}{ll}\widehat{{G}}-{\widehat{{G}}}_0=p_x{\widehat{{P}}}_X+p_y{\widehat{{P}}}_Y+q_x{\widehat{{Q}}}_X.& (15)\end{array}$

After plugging this ansatz into the quasiclassical equations and collecting the terms proportional to the same matrices (these matrices are different from those introduced above and will not be listed here), we derive the following set of quasiclassical equations:

$\begin{array}{l}\left[2i{\Omega }_n+{\delta }_2\text{ cos}(2\varphi )\right]p_x+m_X(g_2-2g_3)=-m_Y{q}_x,\\ \left[2i{\Omega }_n-{\delta }_2\text{ cos}(2\varphi )\right]p_y+m_Y(g_1-2g_3)=-m_X{q}_x,\\ 2{\delta }_2\text{ cos}(2\varphi )q_x=m_Y{p}_x-m_X{p}_y& (16)\end{array}$

and Ω_n = ω_n − iδ₀/2. Furthermore, given the expression (15) the constraint condition (13) reduces to the set of the following simple relations:

$\begin{array}{l}{q}_x=-g_1\frac{p_y}{p_x}=-g_2\frac{p_x}{p_y},{(g_3-g_1-g_2)}^2=1,\\ p_x^2=g_1(2g_3-g_1-g_2),p_y^2=g_2(2g_3-g_1-g_2).& (17)\end{array}$

Note, that by combining the first two relations with the last two ones one also finds $q_x^2=g_1{g}_2$. With the help of relations (17) it is also straightforward to show that the third equation in (16) is redundant, so overall we have got the system of six non-linear equations with six unknowns. These equations must also be supplemented by the self-consistency conditions for the magnetizations, which in terms of the quasiclassical functions have the following form:

$\begin{array}{ll}{m}_{X,Y}=-2\pi {\nu }_F{g}_{\text{sdw}}T\text{Im}{\displaystyle \sum _{{\omega }_n>0}}\langle p_{x,y}(i{\omega }_n,{\varphi }_{\text{k}})\rangle ,& (18)\end{array}$

where 〈f〉 denotes averaging over ϕ_k and g_sdw is the coupling constant.

The first two quasiclassical equations (16) can be re-written in a compact form using relations (17). Indeed, by introducing the auxiliary variables

$\begin{array}{ll}{u}_1=\frac{m_X\sqrt{g_1}}{\sqrt{2+g_1+g_2}},u_2=\frac{m_Y\sqrt{g_2}}{\sqrt{2+g_1+g_2}},& (19)\end{array}$

the quasiclassical equations acquire the following form

$\begin{array}{l}{u}_1\left[2i{\Omega }_n+{\delta }_2\text{ cos}(2\varphi )-u_1-u_2\right]=m_X^2,\\ u_2\left[2i{\Omega }_n-{\delta }_2\text{ cos}(2\varphi )-u_1-u_2\right]=m_Y^2.& (20)\end{array}$

Perhaps, for the clarity of our subsequent discussion it would be useful to mention that in the case when magnetizations are vanishingly small, m_X,Y ≪ πT, functions $g_{1,2}\propto m_{X,Y}^2$, q_x ∝ m_Xm_Y, while p_x,y ∝ m_X,Y.

We have to analyze the solution of the equations (20) in two special cases only: (i) single-$\overrightarrow{Q}$ state for which we set m_Y = 0 and m_X = m₁ and (ii) double-$\overrightarrow{Q}$ state in which $m_X=m_Y=m_2/\sqrt{2}$.

3.1.1. Single-$\overrightarrow{Q}$ State

Since in this case p_y = q_x = g₂ = 0, we have

$\begin{array}{ll}{p}_x(i{\omega }_n,\varphi )=\left(\frac{m_1^2+u_1^2}{m_1^2-u_1^2}\right)\frac{2m_1}{2i{\Omega }_n+{\delta }_2\text{ cos}(2\varphi )}.& (21)\end{array}$

In turn, function u₁(iω_n, ϕ) is determined by one of the two roots of the quadratic equation [first equation in (20) with u₂ = 0] which recovers the correct expression for the non-interacting propagator:

$\begin{array}{ll}{u}_1=Z_n(\varphi )-\gamma \sqrt{Z_n^2(\varphi )-m_1^2},& (22)\end{array}$

where Z_n(ϕ) = iΩ_n + (δ₂/2) cos(2ϕ) and γ is the pre-factor which guarantees that in the limit when m₁ → 0, u₁ also vanishes.

3.1.2. Double-$\overrightarrow{Q}$ State

The solution of the equations (20) in this cases reduces to the solution of a single cubic equation

$\begin{array}{ll}(x+2i{\Omega }_n)\left[x^2-{\delta }_2^2{\text{ cos}}^2(2\varphi )+m_2^2\right]=2i{\Omega }_n{m}_2^2.& (23)\end{array}$

Functions u₁ and u₂ can then be computed from

$\begin{array}{ll}{u}_{1,2}=\frac{1}{2}\left(1+\frac{2i{\Omega }_n}{x_a}\right)\left[x_a\pm {\delta }_2\text{ cos}(2\varphi )\right],& (24)\end{array}$

where x_a is one of the roots of Equation (23).

It is a priori not clear which one of the three roots must be chosen. An additional difficulty in choosing the correct root consists in the fact that after finding an analytic expressions for the roots (23) it turns out that depending on the limiting case (m_X,Y → 0 or δ₂ → 0, for example) different roots recover the correct expressions for the quasiclassical functions. The procedure we have adopted consisted in analyzing all three complex roots of (23) and picking up the one for which all the equations (16,17) are satisfied and in addition Im[p_x,y] < 0. The latter condition guarantees the positive contribution to magnetization (Equation 18), and minimum in free energy.

3.1.3. Results

We have used these expressions to evaluate the dependence of the order parameters m₁ and m₂ on the anisotropy parameter δ₂ for a fixed value of δ₀ and fixed temperature. Naturally, we find that both m₁ and m₂ are the same for the same values of the model parameters. The results of the calculations for the temperature dependence of the magnetizations m₁ and m₂ are presented on Figure 1A. Perhaps it is not too surprising that we found the values of m₁ and m₂ equal to each other within the error bars of the numerical calculations. Therefore, self-consistency equations cannot be used to determine which of the two states would be more favorable and we will have to compute the free energy for each state.

FIGURE 1

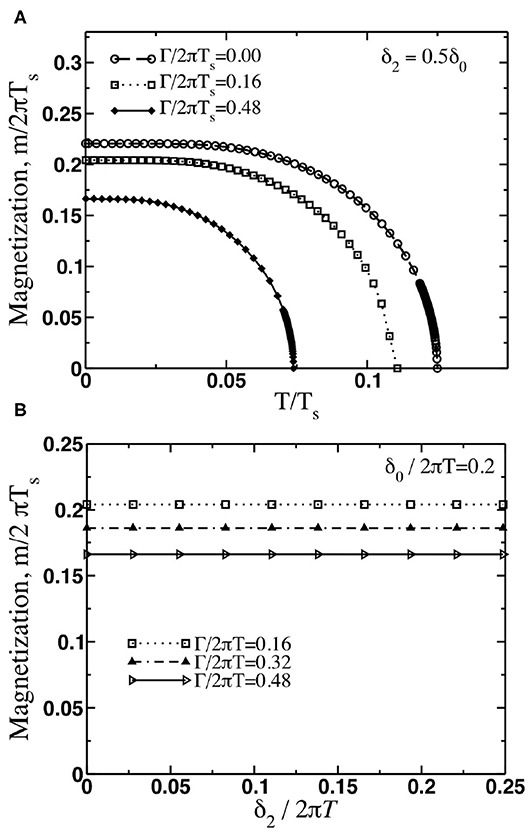
Figure 1. Dependence of magnetizations m₁ and m₂ on temperature and anisotropy parameter δ₂ obtained by the numerical analysis of the self-consistency equations (18). Within the numerical accuracy, we found that m₁ = m₂. (A) Magnetization as a function of temperature are plotted for various values of scattering rate Γ and δ₂ = 0.5δ₀ with δ₀ = 2πT_s where T_s is a Curie temperature in isotropic system without impurities. (B) Magnetization as a function of the Fermi surface anisotropy parameter δ₂ and T = 0.1T_s.

3.2. Disordered System

Quasiclassical equations for the disordered system naturally have similar form as equations (16) for the fact that the matrix structure of the quasiclassical function does not change as soon as Γ becomes non-zero. The calculation of the commutation relations (10) yields

$\begin{array}{l}\left[2i{\tilde{\Omega }}_n+{\Delta }_n(\varphi )\right]p_x+(m_X-i\Gamma \langle p_x\rangle )(g_2-2g_3)\\ =i\Gamma \langle q_x\rangle p_y-(m_Y-i\Gamma \langle p_y\rangle )q_x,\\ \left[2i{\tilde{\Omega }}_n-{\Delta }_n(\varphi )\right]p_y+(m_Y-i\Gamma \langle p_y\rangle )(g_1-2g_3)\\ =i\Gamma \langle q_x\rangle p_x-(m_X-i\Gamma \langle p_x\rangle )q_x.& (25)\end{array}$

In these equations ${\tilde{\Omega }}_n={\Omega }_n+(\Gamma /4)(4\langle g_3\rangle -\langle g_1\rangle -\langle g_2\rangle )$ and Δ_n(ϕ) = δ₂ cos(2ϕ) + i(Γ/2)(〈g₁〉 − 〈g₂〉). Just like in the case Γ = 0 the third equation is redundant and therefore is not listed here.

Equations (25) show that disorder renormalization plays out differently for single-$\overrightarrow{Q}$ and double-$\overrightarrow{Q}$ states. Given these disorder renormalizations, in order to solve the self-consistency equation (18), the angular averages (〈g₃〉 and 〈p_x〉 in a single-$\overrightarrow{Q}$ state, for example) had to be computed by iterations. We found that the values of the corresponding magnetizations still remain essentially identical for non-zero Γ (Figure 1B). We also found, that qualitative behavior of both m₁(δ₂) and m₂(δ₂) does not change with an inclusion of disorder.

Lastly, we would like to mention that the inclusion of the interband disorder with scattering rate Γ_π would not change the dependence of the magnetization on the anisotropy parameters, but only leads to a faster suppression of the magnetization with an increase in Γ_π.

4. Free Energy

To derive an expression for the free energy in terms of the quasiclassical functions, we can employ an expression for the effective action corresponding to the model Hamiltonian (1). Omitting the disorder potential for now, we have [36] ${F}(m_X,m_Y)=(m_X^2+m_Y^2)/g_{\text{sdw}}-S(\lambda =1)$ with

$\begin{array}{ll}S(\lambda )=T{\displaystyle \sum _{i{\omega }_n}}{\displaystyle {{\displaystyle \int }}_{\text{k}}}\text{Tr log}\left(\widehat{𝟙}+\lambda {\widehat{G}}_0(i{\omega }_n,\text{k})\widehat{W}\right).& (26)\end{array}$

Here $\widehat{G}$₀(iω_n, k) is the single-particle propagator for the non-interacting system, $\widehat{W}=-m_X{\widehat{{S}}}_X-m_Y{\widehat{{S}}}_Y$ and

$\begin{array}{ll}{\widehat{{S}}}_X=\left(\begin{array}{ccc}0& {\widehat{\sigma }}_3& 0\\ {\widehat{\sigma }}_3& 0& 0\\ 0& 0& 0\end{array}\right),{\widehat{{S}}}_Y=\left(\begin{array}{ccc}0& 0& {\widehat{\sigma }}_3\\ 0& 0& 0\\ {\widehat{\sigma }}_3& 0& 0\end{array}\right).& (27)\end{array}$

The expression for the free energy in terms of the quasiclassical functions can be derived by following the steps in the calculation of reference [38]. First, we note

$\begin{array}{ll}\frac{\partial S}{\partial \lambda }=-i\pi {\nu }_F{\displaystyle \underset{0}{\overset{\pi }{{\displaystyle \int }}}}\frac{d{\varphi }_{\text{k}}}{\pi }\text{Tr}\left[{\widehat{{M}}}_3{\widehat{{G}}}_{\lambda }(i{\omega }_n,{\varphi }_{\text{k}})\widehat{W}\right],& (28)\end{array}$

where ${\widehat{{G}}}_{\lambda }(i{\omega }_n,{\varphi }_{\text{k}})$ is found from solving the quasiclassical equations (10) in which order parameters have been rescaled by parameter λ, m_X,Y → λm_X,Y. The resulting expression for the free energy reads

$\begin{array}{l}{F}(m_X,m_Y)=\frac{m_X^2+m_Y^2}{g_{\text{sdw}}}\\ -2i\pi {\nu }_{F}T{\displaystyle \sum _{i{\omega }_n}}{\displaystyle \underset{0}{\overset{1}{{\displaystyle \int }}}}d\lambda \left(m_X\langle p_{\lambda x}\rangle +m_Y\langle p_{\lambda y}\rangle \right).& (29)\end{array}$

This expression can also be employed for the case of non-zero disorder by using the solution of equations (25) with the rescaled magnetizations.

It is a hopeless task to evaluate the free energy (29) analytically, but it is amenable to the numerical analysis. However, our numerical computation of the free energy for the single-Q and double-Q states ran into an unexpected problem: the difference between the free energies of the corresponding states fall within the numerical error of the calculation. Thus, in order to determine which one of the two magnetic states will be energetically favorable, below we derive the Landau expansion.

4.1. Free Energy Expansion in Powers of the Magnetization

Having found an expression for the free energy, we consider the temperatures slightly below the critical temperature, so that both magnetizations are sufficiently small compared to πT. Then, we can formally obtain the solution of the quasiclassical equations (25) by expanding functions p_x and p_y in powers of m_X and m_Y.

4.1.1. Clean Case

In the case of the clean system the expression up to the fourth order in powers of magnetization reads

$\begin{array}{l}{F}\left(m_X,m_Y\right)=a_2\left(m_X^2+m_Y^2\right)+b_4{\left(m_X^2+m_Y^2\right)}^2\\ -g_4{\left(m_X^2-m_Y^2\right)}^2+O(m^6),& (30)\end{array}$

where the corresponding coefficients are given by b₄ = (a₄ + a_XY)/2, g₄ = (a_XY − a₄)/2 with

$\begin{array}{l}{a}_2=\frac{1}{g_{\text{sdw}}}-8{\nu }_{F}T{\displaystyle \sum _{{\omega }_n>0}}{\displaystyle \underset{0}{\overset{\pi }{{\displaystyle \int }}}}\frac{{\omega }_{n}d{\varphi }_{\text{k}}}{4{\omega }_n^2+{({\delta }_0\pm {\delta }_2\text{ cos}(2{\varphi }_{\text{k}}))}^2},\\ a_4=4{\nu }_F\text{Im}\left\{T{\displaystyle \sum _{{\omega }_n>0}}{\displaystyle \underset{0}{\overset{\pi }{{\displaystyle \int }}}}\frac{d{\varphi }_{\text{k}}}{{\left[2i{\Omega }_n\pm {\delta }_2\text{ cos}(2{\varphi }_{\text{k}})\right]}^3}\right\},\\ a_{XY}=-8{\nu }_F\text{Re}\left\{T{\displaystyle \sum _{{\omega }_n>0}}{\displaystyle \underset{0}{\overset{\pi }{{\displaystyle \int }}}}\frac{{\Omega }_{n}d{\varphi }_{\text{k}}}{{\left[4{\Omega }_n^2+{\delta }_2^2{\text{cos}}^2(2{\varphi }_{\text{k}})\right]}^2}\right\}.\end{array}$

The sign of the coefficient g₄ is crucial for it determines which one of the two states becomes energetically more favorable. Indeed, let us assume that we choose the model parameters such that both m₁ and m₂ are much smaller than πT. For a fixed value of m₁ = m₂ it follows that when g₄ > 0 the single-$\overrightarrow{Q}$ will have the lower energy compared to the double-$\overrightarrow{Q}$ one. However, one needs to keep in mind that this line of arguments holds only when the coefficients in the free energy expansion are all of the order O(1) and coefficient b₄ remains positive for a given set of values of parameters δ₀/2πT and δ₂/2πT.

4.1.2. Disordered Case

The question arises as to how non-zero disorder will affect the stability of the single-$\overrightarrow{Q}$ state [36]. The calculation of the quasiclassical functions is similar to the one in the clean case, with the only exception that the averages over the angle ϕ need to be computed self-consistently. For example, the first order corrections to functions p_x and p_y are

$\begin{array}{l}{p}_x^{(1)}=\frac{2\left(m_X-i\Gamma \langle p_x^{(1)}\rangle \right)}{2i(|{\omega }_n|+\Gamma )\text{ sign}({\omega }_n)+{\delta }_0+{\delta }_2\text{ cos}(2\varphi )},\\ p_y^{(1)}=\frac{2\left(m_Y-i\Gamma \langle p_y^{(1)}\rangle \right)}{2i(|{\omega }_n|+\Gamma )\text{ sign}({\omega }_n)+{\delta }_0-{\delta }_2\text{ cos}(2\varphi )}.& (31)\end{array}$

After integrating both parts of these expressions over ϕ, we can easily solve for $\langle p_x^{(1)}\rangle$ and $\langle p_y^{(1)}\rangle$.

The calculation of the expressions for the coefficients of the Landau expansion in this case gives

$\begin{array}{l}{A}_4=4{\nu }_F\text{Im}\{T{\displaystyle \sum _{{\omega }_n>0}{\left(\frac{\eta (i{\omega }_n)-i\Gamma }{\eta (i{\omega }_n)+i\Gamma }\right)}^3}\\ \times {\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d{\varphi }_{\text{k}}}{{\left[2i({\Omega }_n+\Gamma )\pm {\delta }_2\text{ cos}(2{\varphi }_{\text{k}})\right]}^3}}\},\\ A_{\text{XY}}=-8{\nu }_F\text{Re}\{T{\displaystyle \sum _{{\omega }_n>0}{\left(\frac{\eta (i{\omega }_n)-i\Gamma }{\eta (i{\omega }_n)+i\Gamma }\right)}^3}\\ \times {\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{({\Omega }_n+\Gamma )d{\varphi }_{\text{k}}}{{\left[4{({\Omega }_n+\Gamma )}^2+{\delta }_2^2{\text{ cos}}^2(2{\varphi }_{\text{k}})\right]}^2}}\}\\ -2\pi {\nu }_F\Gamma \text{Re}\left\{T{\displaystyle \sum _{{\omega }_n>0}{\left(\frac{\eta (i{\omega }_n)-i\Gamma }{\eta (i{\omega }_n)+i\Gamma }\right)}^3}{z}^2(i{\omega }_n)\right\}.& (32)\end{array}$

Functions η(iω_n) and z(iω_n) appear as a result of disorder renormalization and are listed in Appendix. The coefficient g₄ in free energy is now given by g₄ = (A_XY − A₄)/2. Compared with the clean case, we see that expression for the coefficient A_XY contains an extra term proportional to Γ. The dependence of g₄ on disorder can be easily analyzed numerically. The results of the numerical computations are shown in Figure 4.

4.2. Phase Diagram

To determine the phase diagram in the space of anisotropy parameters δ₀ and δ₂, we need to find a point where the free energies of both states become degenerate, g₄(δ_0c, δ_2c) = 0. In Figure 2 we show the phase diagram for the clean system. It agrees qualitatively with the one obtained previously [36] for small values of δ₂/2πT ≪ 1, single-$\overrightarrow{Q}$ state becomes energetically favorable when the value of electron-hole asymmetry δ₀ is above a critical value δ_0c/2πT ~ 0.3.

FIGURE 2

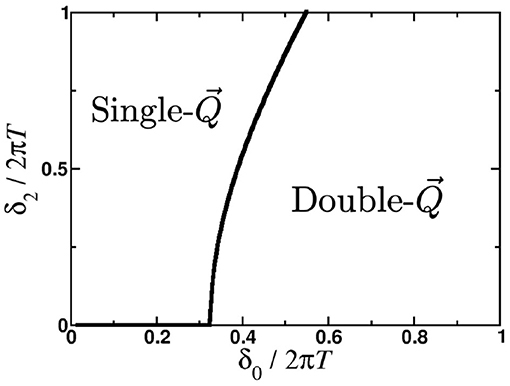
Figure 2. Results of the numerical analysis of the coefficient g₄ in the free energy expansion for the clean system, Γ = 0. The solid line marks the first order transition line along which the coefficient g₄ is zero and the energies of the single-$\overrightarrow{Q}$ and double-$\overrightarrow{Q}$ states are degenerate.

FIGURE 3

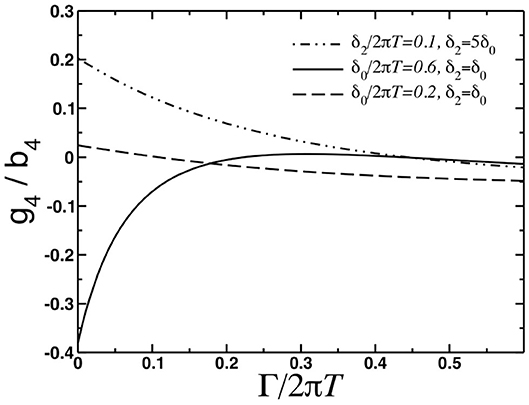
Figure 3. Plot of the nematic coupling constant g₄ which appears in free energy as a function of the disorder scattering rate for various values of the parameters δ₀ and δ₂.

With an addition of disorder, phase diagram is modified and the results are presented on Figure 3 For small disorder the critical line separating two phases slightly moves to higher values of δ₂. Perhaps unexpectedly, a small region of single-$\overrightarrow{Q}$ state appears at large (compared to δ₂) values of δ₀. Upon further increase in the values of the disorder scattering rate, the phase boundary separating two states moves to higher values of δ₂ and also extends to higher values of δ₀. Overall, we may conclude that disorder promotes double-$\overrightarrow{Q}$ state over the single-$\overrightarrow{Q}$ state.

FIGURE 4

Figure 4. Results of the numerical analysis of the coefficient g₄ in the free energy expansion for the disordered system. With the increase in the value of the disorder scattering rate, the single-$\overrightarrow{Q}$ state is a ground state for higher and higher values of the anisotropy parameter δ₂ which accounts for the ellipticity of the electron-like pockets.

5. Discussion

As we have already pointed out in the Introduction, our main goal was to demonstrate how the quasi-classical method can be applied to analyse the competition between magnetic states in multiband metals in the presence of disorder. Having accomplished that goal, we can now generalize it to investigate the problem of an interplay between superconductivity and magnetism. It is already well-established that by including the interband disorder scattering Anderson-Abrikosov-Gor'kov theorem makes it possible for superconductivity and magnetism to co-exist in a certain region of the phase diagram, which size is determined by the ratio of the intra- and inter-band scattering rates [22, 23]. The question is then would be to check if superconducting order may provide an additional contribution in determining which of the two competing magnetic states would be energetically favorable. These results may be employed to provide a qualitative understanding as to why nematicity has been observed in stoichiometric iron selenide in contrast to electron-doped iron selenide.

Lastly, we would like to mention that the inclusion of the interband disorder scattering would not affect our results in any substantial way. Indeed, compared to the case of intraband disorder, the inclusion of the interband scattering leads primarily to the faster suppression of the critical temperature, without affecting the ground state energies of the single- and double-$\overrightarrow{Q}$ states significantly.

To summarize, in this paper we have formulated the quasi-classical approach to analyze the relative stability of the single- and double-$\overrightarrow{Q}$ spin-density-wave states with respect to band and effective mass anisotropy as well as disorder scattering. Generally, we find that with an increase in intraband disorder scattering rate, the system favors the single-$\overrightarrow{Q}$ for moderately high values of the Fermi surface anisotropy parameter, δ₂.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

MD has performed numerical and analytical calculations. MK has performed the analytical calculations. All authors participated in the discussions of the ideas and the ways to solve the problem, and participated in writing the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was financially supported by the National Science Foundation grant NSF-DMR-BSF-2002795, and in part, by the U.S. Department of Energy, Basic Energy Sciences, grant DE-SC0016481 (MD). MK was supported by the Israel Science Foundation 1287/15.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Alex Levchenko for bringing this problem to our attention and many fruitful conversations. Useful discussions with R. M. Fernandes and E. König were gratefully acknowledged.

References

1. Barankov RA, Levitov LS, Spivak BZ. Collective Rabi oscillations and solitons in a time-dependent BCS pairing problem. Phys Rev Lett. (2004) 93:160401. doi: 10.1103/PhysRevLett.93.160401

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Yuzbashyan EA, Altshuler BL, Kuznetsov VB, Enolskii VZ. Solution for the dynamics of the BCS and central spin problems. J Phys A Math Gen. (2005) 38:7831. doi: 10.1088/0305-4470/38/36/003

CrossRef Full Text | Google Scholar

3. Yuzbashyan EA, Altshuler BL, Kuznetsov VB, Enolskii VZ. Nonequilibrium Cooper pairing in the nonadiabatic regime. Phys Rev B. (2005) 72:220503. doi: 10.1103/PhysRevB.72.220503

CrossRef Full Text | Google Scholar

4. Yuzbashyan EA, Tsyplyatyev O, Altshuler BL. Relaxation and persistent oscillations of the order parameter in fermionic condensates. Phys Rev Lett. (2006) 96:097005. doi: 10.1103/PhysRevLett.96.097005

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Yuzbashyan EA, Dzero M, Gurarie V, Foster MS. Quantum quench phase diagrams of an s-wave BCS-BEC condensate. Phys Rev A. (2015) 91:033628. doi: 10.1103/PhysRevA.91.033628

CrossRef Full Text | Google Scholar

6. Shibauchi T, Carrington A, Matsuda Y. A quantum critical point lying beneath the superconducting dome in iron pnictides. Annu Rev Condensed Matter Phys. (2014) 5:113–35. doi: 10.1146/annurev-conmatphys-031113-133921

CrossRef Full Text | Google Scholar

7. Hashimoto K, Yamashita M, Kasahara S, Senshu Y, Nakata N, Tonegawa S, et al. Line nodes in the energy gap of superconducting BaFe₂(As_1−xP_x)₂ single crystals as seen via penetration depth and thermal conductivity. Phys Rev B. (2010) 81:220501. doi: 10.1103/PhysRevB.81.220501

CrossRef Full Text | Google Scholar

8. Gordon RT, Kim H, Salovich N, Giannetta RW, Fernandes RM, Kogan VG, et al. Doping evolution of the absolute value of the London penetration depth and superfluid density in single crystals of Ba(Fe_1−xCo_x)₂As₂. Phys Rev B. (2010) 82:054507. doi: 10.1103/PhysRevB.82.054507

CrossRef Full Text | Google Scholar

9. Hashimoto K, Cho K, Shibauchi T, Kasahara S, Mizukami Y, Katsumata R, et al. A sharp peak of the zero-temperature penetration depth at optimal composition in BaFe₂(As_1−xP_x)₂. Science. (2012) 336:1554–7. doi: 10.1126/science.1219821

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lamhot Y, Yagil A, Shapira N, Kasahara S, Watashige T, Shibauchi T, et al. Local characterization of superconductivity in BaFe₂(As_1−xP_x)₂. Phys Rev B. (2015) 91:060504. doi: 10.1103/PhysRevB.91.060504

CrossRef Full Text | Google Scholar

11. Kim H, Tanatar MA, Straszheim WE, Cho K, Murphy J, Spyrison N, et al. Competition between superconductivity and magnetic/nematic order as a source of anisotropic superconducting gap in underdoped Ba_1−xK_xFe₂As₂. Phys Rev B. (2014) 90:014517. doi: 10.1103/PhysRevB.90.014517

CrossRef Full Text | Google Scholar

12. Joshi KR, Nusran NM, Tanatar MA, Cho K, Bud'ko SL, Canfield PC, et al. Quantum phase transition inside the superconducting dome of Ba(Fe_1−xCo_x)₂As₂ probed by optical magneto-sensing using NV-centers in diamond. arXiv. (2019) 190300053.

Google Scholar

13. Kim MG, Kreyssig A, Thaler A, Pratt DK, Tian W, Zarestky JL, et al. Antiferromagnetic ordering in the absence of structural distortion in Ba(Fe_1−xMn_x)₂As₂. Phys Rev B. (2010) 82:220503. doi: 10.1103/PhysRevB.82.220503

CrossRef Full Text | Google Scholar

14. Avci S, Chmaissem O, Allred JM, Rosenkranz S, Eremin I, Chubukov AV, et al. Magnetically driven suppression of nematic order in an iron-based superconductor. Nat Commun. (2014) 5:3845. doi: 10.1038/ncomms4845

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wang L, Hardy F, Böhmer AE, Wolf T, Schweiss P, Meingast C. Complex phase diagram of Ba_1−xNa_xFe₂As₂: A multitude of phases striving for the electronic entropy. Phys Rev B. (2016) 93:014514. doi: 10.1103/PhysRevB.93.014514

CrossRef Full Text | Google Scholar

16. Hassinger E, Gredat G, Valade F, de Cotret SR, Juneau-Fecteau A, Reid JP, et al. Pressure-induced Fermi-surface reconstruction in the iron-arsenide superconductor Ba_1−xK_xFe₂As₂: evidence of a phase transition inside the antiferromagnetic phase. Phys Rev B. (2012) 86:140502. doi: 10.1103/PhysRevB.86.140502

CrossRef Full Text | Google Scholar

17. Böhmer AE, Hardy F, Wang L, Wolf T, Schweiss P, Meingast C. Superconductivity-induced re-entrance of the orthorhombic distortion in Ba_1−xK_xFe₂As₂. Nat Commun. (2015) 6:7911. doi: 10.1038/ncomms8911

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Allred JM, Avci S, Chung DY, Claus H, Khalyavin DD, Manuel P, et al. Tetragonal magnetic phase in Ba_1−xK_xFe₂As₂ from x-ray and neutron diffraction. Phys Rev B. (2015) 92:094515. doi: 10.1103/PhysRevB.92.094515

CrossRef Full Text | Google Scholar

19. Hassinger E, Gredat G, Valade F, de Cotret SR, Cyr-Choinière O, Juneau-Fecteau A, et al. Expansion of the tetragonal magnetic phase with pressure in the iron arsenide superconductor Ba_1−xK_xFe₂As₂. Phys Rev B. (2016) 93:144401. doi: 10.1103/PhysRevB.93.144401

CrossRef Full Text | Google Scholar

20. Allred JM, Taddei KM, Bugaris DE, Krogstad MJ, Lapidus SH, Chung DY, et al. Double-Q spin-density wave in iron arsenide superconductors. Nat Phys. (2016) 12:493–8. doi: 10.1038/nphys3629

CrossRef Full Text | Google Scholar

21. Fernandes RM, Vavilov MG, Chubukov AV. Enhancement of T_c by disorder in underdoped iron pnictide superconductors. Phys Rev B. (2012) 85:140512. doi: 10.1103/PhysRevB.85.140512

CrossRef Full Text | Google Scholar

22. Vavilov MG, Chubukov AV. Phase diagram of iron pnictides if doping acts as a source of disorder. Phys Rev B. (2011) 84:214521. doi: 10.1103/PhysRevB.84.214521

CrossRef Full Text | Google Scholar

23. Dzero M, Khodas M, Klironomos AD, Vavilov MG, Levchenko A. Magnetic penetration depth in disordered iron-based superconductors. Phys Rev B. (2015) 92:144501. doi: 10.1103/PhysRevB.92.144501

CrossRef Full Text | Google Scholar

24. Kirmani AA, Dzero M, Levchenko A. Quasiclassical circuit theory of contiguous disordered multiband superconductors. Phys Rev Res. (2019) 1:033208. doi: 10.1103/PhysRevResearch.1.033208

CrossRef Full Text | Google Scholar

25. Levchenko A, Vavilov MG, Khodas M, Chubukov AV. Enhancement of the London penetration depth in pnictides at the onset of spin-density-wave order under superconducting dome. Phys Rev Lett. (2013) 110:177003. doi: 10.1103/PhysRevLett.110.177003

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Chowdhury D, Swingle B, Berg E, Sachdev S. Singularity of the London penetration depth at quantum critical points in superconductors. Phys Rev Lett. (2013) 111:157004. doi: 10.1103/PhysRevLett.111.157004

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lorenzana J, Seibold G, Ortix C, Grilli M. Competing orders in FeAs layers. Phys Rev Lett. (2008) 101:186402. doi: 10.1103/PhysRevLett.101.186402

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Eremin I, Chubukov AV. Magnetic degeneracy and hidden metallicity of the spin-density-wave state in ferropnictides. Phys Rev B. (2010) 81:024511. doi: 10.1103/PhysRevB.81.024511

CrossRef Full Text | Google Scholar

29. Kang J, Tešanović Z. Theory of the valley-density wave and hidden order in iron pnictides. Phys Rev B. (2011) 83:020505. doi: 10.1103/PhysRevB.83.020505

CrossRef Full Text | Google Scholar

30. Giovannetti G, Ortix C, Marsman M, Capone M, van den Brink J, Lorenzana J. Proximity of iron pnictide superconductors to a quantum tricritical point. Nat Commun. (2011) 2:398. doi: 10.1038/ncomms1407

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Brydon PMR, Schmiedt J, Timm C. Microscopically derived Ginzburg-Landau theory for magnetic order in the iron pnictides. Phys Rev B. (2011) 84:214510. doi: 10.1103/PhysRevB.84.214510

CrossRef Full Text | Google Scholar

32. Fernandes RM, Chubukov AV, Knolle J, Eremin I, Schmalian J. Preemptive nematic order, pseudogap, and orbital order in the iron pnictides. Phys Rev B. (2012) 85:024534. doi: 10.1103/PhysRevB.85.024534

CrossRef Full Text | Google Scholar

33. Cvetkovic V, Vafek O. Space group symmetry, spin-orbit coupling, and the low-energy effective Hamiltonian for iron-based superconductors. Phys Rev B. (2013) 88:134510. doi: 10.1103/PhysRevB.88.134510

CrossRef Full Text | Google Scholar

34. Kang J, Wang X, Chubukov AV, Fernandes RM. Interplay between tetragonal magnetic order, stripe magnetism, and superconductivity in iron-based materials. Phys Rev B. (2015) 91:121104. doi: 10.1103/PhysRevB.91.121104

CrossRef Full Text | Google Scholar

35. Gastiasoro MN, Andersen BM. Competing magnetic double-Q phases and superconductivity-induced reentrance of C₂ magnetic stripe order in iron pnictides. Phys Rev B. (2015) 92:140506. doi: 10.1103/PhysRevB.92.140506

CrossRef Full Text | Google Scholar

36. Hoyer M, Fernandes RM, Levchenko A, Schmalian J. Disorder-promoted C₄-symmetric magnetic order in iron-based superconductors. Phys Rev B. (2016) 93:144414. doi: 10.1103/PhysRevB.93.144414

CrossRef Full Text | Google Scholar

37. Aleiner IL, Efetov KB. Supersymmetric low-energy theory and renormalization group for a clean Fermi gas with a repulsion in arbitrary dimensions. Phys Rev B. (2006) 74:075102. doi: 10.1103/PhysRevB.74.075102

CrossRef Full Text | Google Scholar

38. Thuneberg EV, Kurkijärvi J, Rainer D. Elementary-flux-pinning potential in type-II superconductors. Phys Rev B. (1984) 29:3913–23. doi: 10.1103/PhysRevB.29.3913

CrossRef Full Text | Google Scholar

A. Coefficients in the Free Energy Expansion

In this section we provide the details of the calculation for the Landau free energy expansion. Both p_λx and p_λy can be determined approximately for small values of m_X and m_Y from the quasiclassical equations. We start with the derivation for the clean case, Γ = 0.

A.1. First Order Corrections

Up to the linear order in m_j from Equation (16) I find $g_3^{(0)}=\text{sign}({\omega }_n)$ and

$\begin{array}{ll}{p}_{\lambda x}^{(1)}=\frac{2\lambda m_X\text{sign}({\omega }_n)}{2i{\omega }_n+{\delta }_0+{\delta }_2\text{ cos}(2\varphi )},p_{\lambda y}^{(1)}=\frac{2\lambda m_Y\text{sign}({\omega }_n)}{2i{\omega }_n+{\delta }_0-{\delta }_2\text{ cos}(2\varphi )}.& (\mathrm{A1})\end{array}$

A.2. Third Order Corrections

The second order correction to p_λj is zero. To determine the third order correction, we first need to compute the second order corrections to g_j's. To do that, we first use equations (20) (and presume for simplicity that ω_n > 0):

$\begin{array}{ll}{u}_{\lambda 1}^{(2)}=\frac{{\lambda }^2{m}_X^2}{2i{\omega }_n+{\delta }_0+{\delta }_2\text{ cos}(2\varphi )},u_{\lambda 2}^{(2)}=\frac{{\lambda }^2{m}_Y^2}{2i{\omega }_n+{\delta }_0-{\delta }_2\text{ cos}(2\varphi )},& (\mathrm{A2})\end{array}$

so that

$\begin{array}{l}{g}_{\lambda 1}^{(2)}=\frac{2{(\lambda m_X)}^2}{{\left[2i{\omega }_n+{\delta }_0+{\delta }_2\text{ cos}(2\varphi )\right]}^2},\\ g_{\lambda 2}^{(2)}=\frac{2{(\lambda m_Y)}^2}{{\left[2i{\omega }_n+{\delta }_0-{\delta }_2\text{ cos}(2\varphi )\right]}^2},\\ g_{\lambda 3}^{(2)}=g_{\lambda 1}^{(2)}+g_{\lambda 2}^{(2)}.& (\mathrm{A3})\end{array}$

In addition, for the function q_x we find

$\begin{array}{ll}{q}_{\lambda x}^{(2)}=-\frac{2{\lambda }^2{m}_X{m}_Y}{{(2i{\omega }_n+{\delta }_0)}^2-{\delta }_2^2{\text{ cos}}^2(2\varphi )}.& (\mathrm{A4})\end{array}$

The choice of sign follows from considering the trivial case of δ₂ = 0.

Given all these expressions, we go back to equations (16) to obtain the following expression:

$\begin{array}{l}{p}_{\lambda x}^{(3)}=\frac{4{(\lambda m_X)}^3}{{\left[2i{\Omega }_n+{\delta }_2\text{ cos}(2\varphi )\right]}^3}\\ +\frac{8i{\lambda }^3{\Omega }_n{m}_X{m}_Y^2}{{\left[2i{\Omega }_n+{\delta }_2\text{ cos}(2\varphi )\right]}^2{\left[2i{\Omega }_n-{\delta }_2\text{ cos}(2\varphi )\right]}^2}.& (\mathrm{A5})\end{array}$

Similarly, for $p_{\lambda y}^{(3)}$ we found

$\begin{array}{l}{p}_{\lambda y}^{(3)}=\frac{4{(\lambda m_Y)}^3}{{\left[2i{\Omega }_n-{\delta }_2\text{ cos}(2\varphi )\right]}^3}\\ +\frac{8i{\lambda }^3{\Omega }_n{m}_Y{m}_X^2}{{\left[2i{\Omega }_n+{\delta }_2\text{ cos}(2\varphi )\right]}^2{\left[2i{\Omega }_n-{\delta }_2\text{ cos}(2\varphi )\right]}^2}.& (\mathrm{A6})\end{array}$

After plugging these expressions into Equation (29) and grouping the similar terms, we arrive to Equation (30).

A.3. Functions η(iω_n) and z(iω_n)

The formulas for the coefficients in Landau free energy expansion (32) include the following functions:

$\begin{array}{l}{\eta }^{-1}(i{\omega }_n)=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\pi }{{\displaystyle \int }}}}\frac{d\varphi }{2i({\omega }_n-i{\delta }_0/2+\Gamma )\pm {\delta }_2\text{ cos}(2\varphi )},\\ z(i{\omega }_n,{\delta }_0)=-\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\pi }{{\displaystyle \int }}}}\frac{d\varphi }{4{({\omega }_n-i{\delta }_0/2+\Gamma )}^2+{\delta }_2^2{\text{ cos}}^2(2\varphi )}.& (\mathrm{A7})\end{array}$