- Department of Physics and Columbia Astrophysics Laboratory, Columbia University, New York, NY, United States
The science returns of gravitational wave astronomy will be maximized if electromagnetic counterparts to gravitational-wave sources can be identified. Kilonovae are promising counterparts to compact binary mergers, both because their long timescales and approximately isotropic emission make them relatively easy to observe, and because they offer astronomers a unique opportunity to probe astrophysical heavy-element nucleosynthesis and merger-driven mass ejection. In the following, I review progress in theoretical modeling that underpinned advances in our understanding of kilonovae leading up the first detection of a neutron star merger, GW170817. I then review the important lessons from this event and discuss the challenges and opportunities that await us in the future.
1. Introduction
Multi-messenger astronomy refers to the revolutionary possibility of combining electromagnetic (EM) and gravitational-wave (GW) observations to gain new insight into astrophysical phenomena. In the current era of ground-based gravitational-wave detectors, the mergers of compact objects—black holes (BHs) and neutron stars (NSs)—are the systems most accessible to multi-messenger astronomy, and their routine observation promises to teach us more about stellar binary evolution, dynamics in the strong gravity regime, the production and evolution of astrophysical jets, the NS equation of state (EOS), and the origin of the heavy elements. Among mergers' EM counterparts, “kilonovae,” radioactively-powered, quasi-isotropic transients that shine at optical and infrared wavelengths and evolve on timescales of days to weeks, are unique in their ability to shed light on merger-driven mass ejection and nucleosynthesis.
2. Background on R-Process Transients
The idea that compact object mergers produce radioactively-powered EM emission in addition to gravitational wave signals is rooted in the realization [1–3] that mergers could synthesize unstable nuclei whose decays would power an electromagnetic transient [4].
More specifically, the partial disruption of a NS in a NS2 or NSBH merger produces a neutron-rich outflow capable of assembling a broad range of heavy, unstable nuclei via rapid neutron capture, or the r-process. As first outlined by [5] and [6], the r-process occurs in explosive environments featuring a high flux of free neutrons, which allows successive captures of free neutrons onto light seed nuclei on timescales shorter than typical β-decay lifetimes. This drives the composition of the gas toward heavy, neutron-rich regions of the chart of the nuclides, in many cases close to the neutron drip line. When neutron capture ceases, the newly-born nuclei decay toward stability, producing an abundance pattern with characteristic peaks around mass numbers A = 82, 130, 196. The stable and long-lived daughters account for about half of the elements in the Periodic Table more massive than Iron.
The complexity of r-process nucleosynthesis allows for variation in the final abundance pattern. While a lack of relevant experimental data (e.g., nuclear masses and neutron-capture cross sections) for many nuclei involved in the r-process present a challenge for theoretical r-process simulations [7, 8], even if nuclear physics uncertainties were eliminated, abundance yields would still be sensitive to conditions when nucleosynthesis begins. Traditionally [9, e.g.], gasses with the potential to undergo an r-process have been parametrized in terms of three variables: expansion timescale (τexp), entropy per baryon (sB), and initial electron fraction (Ye), which is defined as the number of protons per baryon and quantifies the relative number of free neutrons available to build up heavy nuclei.
The final abundance pattern depends on the interplay of all these factors [e.g., [10]]. However, for conditions expected for compact object mergers (i.e., neutron-rich, low-entropy gasses), abundances appear from simulations to be particularly sensitive to Ye, with Ye ≈ 0.25 emerging as a threshold above which the r-process fails to burn nuclei beyond the second r-peak [11, 12]. Such a truncated r-process is termed a “light” r-process, as opposed to the “heavy” r-process, which takes place under very neutron-rich conditions and synthesizes stable and semi-stable nuclei up to A ~ 260. In a merger, the NS material that forms the expanding gas is very neutron rich [13], and will remain so unless weak-current interactions are strong enough to push the composition toward a more moderate Ye[14]. The potential for r-process variability is illustrated in Figure 1.
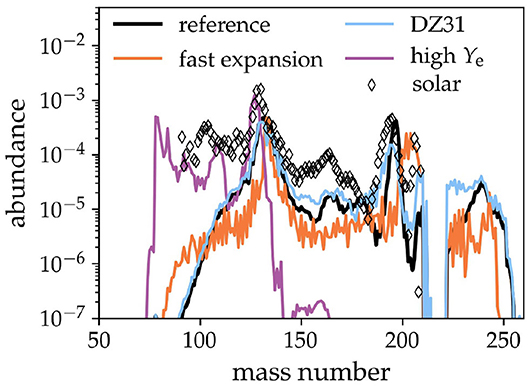
Figure 1. The impact of nuclear physics and astrophysical uncertainties on predicted r-process abundances. The reference case (black curve) was calculated using the FRDM mass model [15] for a low-entropy, neutron-rich gas. Every other curve differs from the reference case in only one way. The orange curve shows the impact of decreasing the expansion time, while the purple curve demonstrates the much stronger effect of raising Ye. The influence of the choice of nuclear mass model is illustrated by the light blue curve. Scaled solar r-process abundances from [16] are plotted as black diamonds. This figure was adapted from Figure 1 of [17] with permission from J. Barnes.
The role of r-process nucleosynthesis and decay in generating EM signals associated with compact object mergers was first discussed by [4], who derived the earliest theoretical model of r-process-powered transient emission. Since this groundbreaking work, the community has undertaken increasingly detailed studies of all the major parameters governing the nature of r-process transients, from the energy supplied by the r-process, to the ejected mass, to the optical properties of r-process atoms and ions.
3. Key Parameters
While detailed computational models are required to fully explain the evolution of radioactive astrophysical transients, the basic character of these systems are functions of a few physical parameters whose relationships to the emission can be understood from basic physical principles.
In simple (semi-)analytic models [à la, [18]], a transient's luminosity peaks when the expansion time t equals the timescale for photons to diffuse through the ejecta, , where Mej and vej are the mass and characteristic velocity of the ejecta, respectively, and κ is its effective opacity. The luminosity at peak is roughly equivalent to the instantaneous rate at which radioactive decay is heating the ejecta. This correspondence reappears on the tail of the light curve, when the ejecta is mostly transparent and the luminosity directly reflects radioactive heating. Consideration of the above reveals that the energy released (per unit mass) in the radioactive decays of r-process nuclei is a crucial determinant of kilonova emission, as are the mass, velocity, and opacity of merger-driven outflows. The effects of these parameters on kilonovae's bolometric light curves are presented in Figure 2.
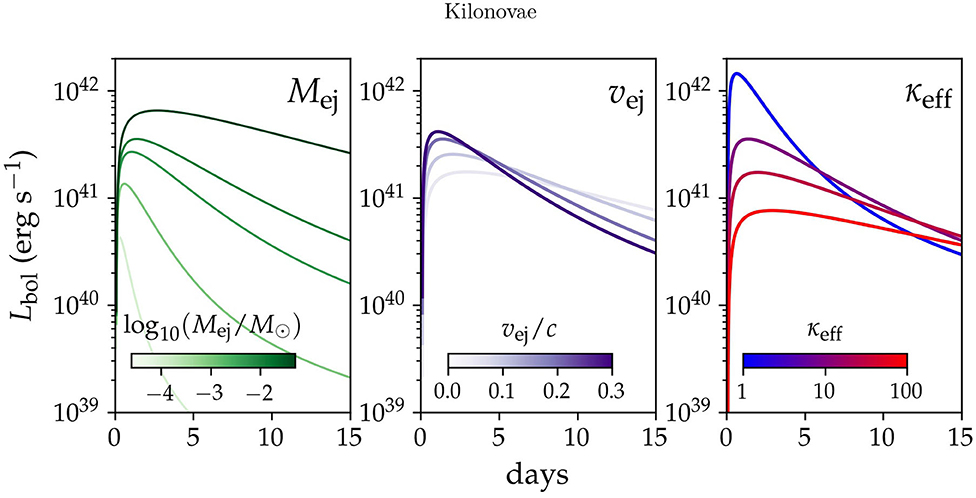
Figure 2. Toy-model bolometric kilonova light curves, similar to those of [19], illustrating the effects of ejecta mass (left), velocity (middle), opacity (right) on emission. R-process heating has been approximated as a simple power law with ζ = 1.3. In the middle and right panels, Mej is set to 0.01M⊙. The value of κeff is 10 cm2 g−1 in the left and middle panels, and vej is 0.2c in the left and right panels. Thermalization has been estimated from the numerical results of [17].
3.1. R-Process Heating and Radioactivity
The dominant decay channel for unstable r-process nuclei is β-decay [(Z, N) → (Z+1, N−1); 20], which emits high-energy β-particles, neutrinos, and γ-rays. In most realizations of the r-process, select nuclei will also undergo α-decay ((Z, N) → (Z−2, N−2)) and fission, releasing energy in the form of more massive α-particles and fission fragments. [17, 21–23]. These suprathermal particles and photons transfer heat the ejecta as they interact with it, and the thermal photons produced by the heated gas diffuse outward to form the light curve. The emerging luminosity, as well as the relationship between luminosity and ejected mass, depend both on the rate at which the r-process produces energy and the efficiency with which that energy is converted to thermal photons.
When [4] constructed the first kilonova models, they treated the overall normalization of energy from r-process decay as a free parameter proportional to the rest mass energy of the ejected material. In other words, the sum of all the energy released from radioactivity was taken to equal with f allowed to vary. Despite this simplification, their model of the r-process uncovered what turned out to be a robust feature of r-process radioactivity. By assuming the lifetimes τ of decaying nuclei were evenly distributed logarithmically and ignoring the correlation between τ and decay energy, Li et al. [4] calculated that r-process decay should release energy like Ėrad∝1/t. More rigorous calculations using full r-process nuclear reaction networks [20, 24, 25] as well as more robust analytic treatments [26] modified this picture, finding that, when heating is dominated by the β-decays of a broad ensemble of nuclei, the energy production is well-approximated by a steeper power-law, with ζ = 1.2−1.4.
However, while power-law heating is a useful model, uncertainties in r-process calculations resulting from unmeasured quantities, as well as the sensitivity of the r-process to its astrophysical environment, leave room for variability in nucleosynthesis and decay, and therefore Ėrad. In particular, the behavior of Ėrad is likely to deviate from a power-law if α-decay or fission becomes dominant over β-decay, or if only a small number of nuclei are contributing to the heating [22, 23, 27].
More detailed nuclear calculations also revealed the absolute scale of the energy released by r-process decay, allowing [20] to predict that the peak luminosity of transients from NS2 mergers would be about a thousand time brighter than a classical nova, motivating the term “kilonova.”
Metzger et al. [20] was also the first to estimate the fraction of the energy from r-process decay able to effectively heat the gas (the “thermalization fraction”). More detailed numerical work on thermalization was carried out by [17], who found that thermalization increased for denser ejecta configurations, lower-energy decay spectra, and radioactivity profiles that favored α-decay or fission relative to β-decay. These themes were revisted in [28]. Later analytic work [27, 29], showed that thermalization also depends on how the decay spectrum and Ėrad evolve with time. The potential variation in r-process heating [see e.g., [23]], and the sensitivity of the thermalization efficiency to that variation, suggest that further detailed numerical studies may be useful for understanding the true allowed range of kilonova heating and luminosity.
3.2. Mass Ejection
There are three main channels through which merging compact objects ejecta mass [see reviews by [30, 31]]. All produce an outflow neutron rich enough to support at least a light r-process.
High-velocity tidally shredded outflows are produced during the final stages of inspiral when a NS is disrupted by the differential gravitational field of its binary companion. While the quantity of ejected mass depends on the NS EOS (less compact EOSs are more easily shredded) as well as the mass ratio of the binary and the spins of the component stars [32–35], it is generally expected to be small [~10−4M⊙; [36, 37]] for a NS2 merger, though it can be substantially larger (~0.1M⊙) for a NSBH merger provided the NS disrupts outside the innermost stable circular orbit [38, 39]. Tidal shredding produces a cold, low-entropy outflow with an abundance of free neutrons. It is therefore expected to undergo a robust r-process with nucleosynthesis beyond the third peak [e.g., [13]].
In contrast, dynamically squeezed matter is subject to enough weak interactions to inhibit the synthesis of the heaviest elements. Dynamical squeezing occurs when merging NSs finally collide [36, 37, 40]. The violence of the collision expels material from the contact interface via shocks, which accelerate the resulting outflow to high velocities and heat it to high temperatures, allowing the production of thermal electron/positron pairs and neutrinos. Absorption of these particles then raises the Ye of the gas [41, 42].
The mass of this component increases with NS compactness [36], since NSs with smaller radii make contact at a smaller separation, and therefore a higher velocity, leading to more energetic collisions capable of unbinding more matter (this trend holds only up to a point; mass ejection is minimal if the colliding NSs are compact enough to collapse promptly to a BH [43], though mass asymmetry can offset this effect [37]).
Some simulations [36, 44] suggest that, in certain cases, this outflow will feature a high-velocity, low-mass (~10−5M⊙) tail of material whose rapid expansion hinders neutron capture, resulting in a composition dominated by lighter nuceli and leftover free neutrons [21]. Under such conditions, the free-neutron decay could power a short-lived transient peaking on timescales close to the free-neutron half life [45].
The most robust mass ejection channel may be winds from accretion disks surrounding the mergers' central remnants (CRs). In NSBH mergers, the disk is formed from disrupted NS matter that remains gravitationally bound. For NS2 mergers, the primary source of disk material is a NS CR, which pushes material off its surface as it transitions from differential to solid-body rotation [46] (The prompt collapse of a CR therefore inhibits disk formation for NS2 mergers.) Disk material is unbound through some combination of viscous heating [47], magnetic turbulence [48], α-recombination [49], and ν-absorption [50, 51].
The effect of weak interactions on the disk composition is uncertain, and likely depends strongly on the CR. While a central NS would be strong source of neutrinos [e.g., [52]], a central BH would not be; in the latter case, weak interactions in the disk would be limited to those driven by thermal neutrinos and positrons produced by the disk itself [53]. Many studies [48, 54, 55] have found that, for a BH CR, the accretion disk regulates its composition to a low Ye, though the exact distribution of Ye appears to be sensitive to the neutrino transport method adopted [e.g., [56]].
As with other mass ejection methods, the mass of the disk (and therefore the disk wind) depends on the binary parameters and NS EOS [e.g., [40]]. Less compact NS EOSs produce more massive disks, and therefore more massive disk outflows. The EOS also affects the composition (at least for NS2 mergers) by controlling the fate of the CR, and the exposure of the disk to neutrino irradiation [57–59].
3.3. Opacity
The distinct compositions burned in the various outflows generated in NS2 and NSBH mergers have major effects on kilonova emission because the composition of the gas determines the opacity of the ejecta, which in turn influences the light curve and the spectral energy distribution (SED).
As the gas expands, it cools to temperatures (~few × 103 K) that support low levels of ionization. Under these conditions, the dominant source of opacity is bound-bound (“line”) opacity [60]. In the bound-bound regime, the absorption of photons by atoms results not in ionization, but in the excitation of its bound electrons to a higher-energy configuration. While the probability that any particular absorption will occur is a function of the many-body quantum mechanics governing the absorbing atom, the effective continuum opacity depends on the number of opportunities for a photon of a given energy to suffer an absorption—i.e., on the density of moderate to strong lines in wavelength space.
Determining bound-bound opacity is particularly challenging for r-process compositions, since there is limited experimental data on energy levels and absorption probabilities for many of the species burned by the r-process. Nevertheless, general trends can be deduced from simple heuristics. First, the more unique species are present in a composition, the greater the number of lines, and the higher the opacity. Second, and more significantly, the presence of atomic species with a high degree of complexity (i.e., with a greater number of distinct electronic configurations) will increase opacity.
Atomic complexity is a function of the size of an atom's valence electron shell. A valence shell that accommodates a larger number of electrons allows for more distinct electronic configurations; each configuration has a slightly different energy, so the net effect is a greater number of energy levels, more transitions between energy levels, and a higher opacity [see e.g., [61]]. This picture has been borne out both by available experimental data [62] and by atomic structure calculations, with groups using different atomic structure modeling codes all finding a striking increase in opacity as valence shell size increases [61, 63, 64].
The relationship between atomic complexity and opacity has profound implications for kilonovae. Lanthanides and actinides are the most complex elements in the Periodic Table. These species have a high number of closely spaced energy levels, resulting in an abundance of low-energy bound-bound transitions and a high opacity that extends out into the near infrared (NIR). While lanthanides and actinides are easily synthesized by the heavy r-process, they are produced in negligible quantities in a light r-process event [11, 12]. The opacity of the kilonova ejecta—and the color of its emission—therefore depend sensitively on the nucleosynthesis that took place in its ejecta.
As first explained in [65], the high opacity of a lanthanide-rich (heavy r-process) ejecta delays and dims the light curve peak, while the extreme density of lines at optical wavelengths pushes the emission redward, causing the spectrum to peak in the NIR [see also [62]]. Of course, not all outflows from compact object mergers will undergo a heavy r-process. Light r-process compositions, will have a lower opacity. The emission associated with these outflows will have a faster rise; a sharper, brighter light-curve peak; and an SED concentrated at blue/optical wavelengths, similar to the original predictions of [20].
Kilonova emission may be due to a combination of signals from multiple outflows characterized by different histories of nucleosynthesis: a “red” component associated with a lanthanide-rich outflow, and a “blue” component from a composition that failed to burn lanthanides [58, 65]. The outcome of the r-process is closely tied to the manner of mass ejection and, in the case of disk winds, the nature or lifetime of the CR. The presence or relative prominence of red or blue kilonova components can therefore reveal the mass ejection mechanisms at play, and even shine an (indirect) light on the NS EOS.
4. Lessons From GW170817
The theory outlined above was established before a compact object merger was definitively detected, but was corroborated by the first such detection. On August 17, 2017, the LIGO*-Virgo network picked up a signal consistent with the inspiral of a merging neutron star binary [66]. A spatially-coincident short-gamma ray burst was observed contemporaneously [67–69], increasing confidence in the signal and triggering a worldwide search by observational astronomers for a radioactive counterpart, which was soon identified in a galaxy a mere 40 Mpc distant [70–77]. These observations yielded a wealth of data which, in combination with theory, crystallized into a fairly coherent picture of the post-merger system.
The bolometric light-curve evolution was consistent with an approximately power-law injection of energy, as expected from the decay of a large ensemble of r-process nuclei [78]. The transient's broadband evolution showed signs of two distinct components, with the blue and optical bands rising to an early peak and declining swiftly thereafter, while emission in the redder bands evolved on a much longer (~2 week) timescale [e.g., [70, 72, 72, 78, 79]]. The disparate behavior at red and blue wavelengths was interpreted by most groups [72, 80–82] to require two separate outflows [but see [83]]: a lanthanide-poor one driving the early blue component, and a lanthanide-rich one powering the extended red and NIR emission.
Since long-lived red emission is difficult to explain without invoking the uniquely high opacity of the lanthanides and actinides produced in abundance by the heavy r-process [84, 85], the broadband light curves confirmed that GW170817 had indeed triggered r-process nucleosynthesis, and that its optical counterpart was in fact a kilonova.
The identification of kilonova spectral features with particular r-process ions would further corroborate this conclusion, and early work on GW170817 demonstrated the promise of such an approach. For example, [86] linked one feature of the kilonova spectrum to singly-ionized Strontium, thus claiming the first detection of an individual r-process element in an electromagnetic transient. Future studies of kilonova spectra will increase confidence in such identifications and improve our ability to constrain compositions from spectral analysis.
In the meantime, kilonova spectra encode information critical for a rigorous reconstruction of the outflow(s) that produced their electromagnetic emission. The spectrum of the GW170817 kilonova was originally dominated by a smooth blue blackbody [73, 87–89], which was replaced after a few days by pseudo-blackbody peaking in the NIR and exhibiting broad absorption features [74, 90]. While the dramatic shift from blue to redder wavelengths is consistent with the kilonova's broadband evolution, the spectrum provided additional information on the velocities of the outflows associated with each component of the emission. The lack of features in the blue spectrum suggested velocities high enough to smooth out any absorption lines, vej ~ 0.3c [e.g., [73, 80]]. In contrast, the broad absorption troughs in the red spectrum indicate a slower outflow with vej ~ 0.1c.
The combination of spectral and photometric data suggested that the merger launched a high-velocity, lanthanide-poor outflow in addition to a lower-velocity outflow rich in lanthanides. Some authors [e.g., [80, 85, 87]] have attributed the “blue” component to shock-heated, dynamically “squeezed” ejecta. However, the mass required to explain the luminosity (Mblue ≈ 0.01M⊙) is higher than predicted by numerical relativity simulations [36, 37, 41, 91], motivating others to consider alternate scenarios [92, 93].
The kilonova's red component has been somewhat more securely associated with a wind unbound from the accretion disk surrounding the CR. The mass (Mred ≈ 0.04M⊙ and velocity inferred for this component are consistent with expectations from simulations [48, 55], and the conditions in the disk are thought to be favorable for heavy r-process nucleosynthesis as long as the CR collapses instantly to a BH or survives for only a limited time as a hyper- or supramassive NS [although see [56] for an illustration of the how the treatment of neutrino transport in disks can alter the predicted nucleosynthetis].
5. Open Questions and a Look to the Future
GW170817 allowed the astronomy community to make inroads on some of most pressing questions multimessenger astronomy promises to help untangle. First, it demonstrated a long-theorized [94–99] association between short gamma-ray bursts and compact object mergers. Second, it allowed the derivation of the first multi-messenger constraints on the NS EOS [e.g. [100, 101]]. It also allowed an entirely original and independent calculation of the Hubble Constant H0 [102, 103]. Finally, it conclusively identified mergers as an astrophysical site of r-process nucleosynthesis [70, 72, 80, 90, among many others]. However, the mysteries surrounding mergers and post-merger phenomena are far from resolved.
One major remaining question is related to the source of the blue kilonova component. While the emission seems to be powered by radioactivity, the NS EOS required to produce such a massive outflow via dynamical squeezing is seemingly too compact to simultaneously explain the similarly high mass of the red disk wind component. (Recall that disk wind represents a fraction of the total disk mass, and that less compact EOS's favor heavier accretion disks.) Further observations of kilonovae, especially at early times, will be instrumental in revealing the nature of the blue component and providing additional tools for evaluating the NS EOS [104].
A second question is the role of mergers in astrophysical r-process production. GW170817 proved that NS2 mergers are a site of the r-process nucleosynthesis, and simple estimates suggest that the entire r-process content of the Universe may originate in compact object mergers [80, 105]. However, these arguments hinge on the (still very uncertain) merger rates and average r-process mass per event, not to mention the largely unconstrained contribution from NSBH mergers.
In addition to these uncertainties, there are concerns about whether mergers can explain r-process enrichment everywhere it is observed [106]. For example, r-process-enriched extremely metal poor stars seem to require an early-Universe source of the r-process, while mergers typically occur at a delay of hundreds of millions or even billions of years relative to star formation [e.g., 107]. Likewise, it is difficult to explain enrichment in ultra-faint dwarf galaxies [108] with mergers, given that the velocities pre-merger binaries acquire when their component stars go supernova generally exceed the low escape velocities of these low-mass galaxies [109]. A variety of alternative r-process sites have been proposed [110–113]; however, a complete census of merging systems will clarify rates and ejected mass, and illuminate the role of mergers in burning the heaviest elements.
Additional observations will also unveil the full diversity of merging systems and kilonovae (this is an especially enticing prospect given how distinct the second NS2 merger, GW190425, was from the first [114]). Neutron star-black hole (NSBH) mergers, which have not yet been observed, should provide an additional source of heterogeneity, as they are expected to produce ejecta that is more massive [32], more neutron-rich [115], and less isotropic [39] than a typical NS2 merger. There is also likely to be substantial diversity among kilonovae from NSBH mergers, since mass ejection is sensitive to parameters such as mass ratio and component star spin [e.g., [116]]. Observations of NSBH mergers and their kilonovae are therefore crucial for documenting the full range of compact objects mergers' radioactively powered EM emission.
We can hope, in the next several years, to better constrain merger rates, and to understand how merging systems are distributed by total binary mass, mass ratio, and binary type (NS2 v. NSBH). We can map out the relationship between binary and kilonova parameters, a map that will become increasingly accurate as parallel advances and theory and nuclear physics experiment (e.g., the Facility for Rare Isotopes Beams; [117]) allow us to more confidently infer ejected mass from observations. We can determine how common various components are (and we can hope to observe as-yet unseen components, like tidal tails or neutron precursors) and assess whether the net enrichment from these components is consistent observed stellar r-process abundances (and variations in those abundances). Ideally, we will develop the tools to measure or constrain abundance yields from the spectra of individual merger events. Our deeper understanding of kilonovae will allow us to confidently progress on the questions—r-process origins, NS EOS, H0—that multi-messenger astronomy is uniquely well-poised to address.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
JB was supported by the National Aeronautics and Space Administration (NASA) through the Einstein Fellowship Program, grant number PF7-180162.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Lattimer JM, Schramm DN. Black-hole-neutron-star collisions. Astrophys J. (1974) 192:L145–7. doi: 10.1086/181612
2. Lattimer JM, Schramm DN. The tidal disruption of neutron stars by black holes in close binaries. Astrophys J. (1976) 210:549–67. doi: 10.1086/154860
3. Symbalisty E, Schramm DN. Neutron star collisions and the r-process. Astrophys Lett. (1982) 22:143.
4. Li LX, Paczyński B. Transient events from neutron star mergers. Astrophys J Lett. (1998) 507:L59–62. doi: 10.1086/311680
5. Burbidge EM, Burbidge GR, Fowler WA, Hoyle F. Synthesis of the elements in stars. Rev Modern Phys. (1957) 29:547–650. doi: 10.1103/RevModPhys.29.547
6. Cameron AGW. On the origin of the heavy elements. Astrophys J. (1957) 62:9–10. doi: 10.1086/107435
7. Mendoza-Temis J, Vargas CE, Bagatella-Flores N. r-process nucleosynthesis calculations in neutron-star mergers (NSM): main nuclear physics requirements. In: Morriset C, Delgado-Inglada G, García-Rojas J, editors. Cosmic Feast of the Elements. Puebla: Universidad Nacional Autónoma de México (2017). p. 22.
8. Cowan JJ, Sneden C, Lawler JE, Aprahamian A, Wiescher M, Langanke K, et al. Making the heaviest elements in the universe: a review of the rapid neutron capture process. arXiv preprint arXiv:1901.01410.
9. Qian YZ, Woosley SE. Nucleosynthesis in neutrino-driven winds. I. The physical conditions. Astrophys J. (1996) 471:331. doi: 10.1086/177973
10. Qian YZ. The origin of the heavy elements: recent progress in the understanding of the r-process [review article]. Prog Particle Nuclear Phys. (2003) 50:153–99. doi: 10.1016/S0146-6410(02)00178-3
11. Wanajo S, Sekiguchi Y, Nishimura N, Kiuchi K, Kyutoku K, Shibata M. Production of all the r-process nuclides in the dynamical ejecta of neutron star mergers. Astrophys J. (2014). 789:L39. doi: 10.1088/2041-8205/789/2/L39
12. Lippuner J, Roberts LF. r-process lanthanide production and heating rates in kilonovae. Astrophys J. (2015) 815:82. doi: 10.1088/0004-637X/815/2/82
13. Meyer BS. Decompression of initially cold neutron star matter: a mechanism for the r-process? Astrophys J. (1989) 343:254. doi: 10.1086/167702
14. Meyer BS, McLaughlin GC, Fuller GM. Neutrino capture and r-process nucleosynthesis. Phys Rev C. (1998) 58:3696–710. doi: 10.1103/PhysRevC.58.3696
15. Möller P, Nix JR, Myers WD, Swiatecki WJ. Nuclear ground-state masses and deformations. Atom Data Nucl Data Tabl. (1995) 59:185–381. doi: 10.1006/adnd.1995.1002
16. Arnould M, Goriely S, Takahashi K. The r-process of stellar nucleosynthesis: astrophysics and nuclear physics achievements and mysteries. Phys Rep. (2007) 450:97–213. doi: 10.1016/j.physrep.2007.06.002
17. Barnes J, Kasen D, Wu MR, Martinez-Pinedo G. Radioactivity and thermalization in the ejecta of compact object mergers and their impact on kilonova light curves. Astrophys J. (2016) 829:110. doi: 10.3847/0004-637X/829/2/110
18. Arnett WD. Type I supernovae. I - Analytic solutions for the early part of the light curve. Astrophys J. (1982) 253:785–97. doi: 10.1086/159681
20. Metzger BD, Martinez-Pinedo G, Darbha S, Quataert E, Arcones A, Kasen D, et al. Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. Mnthly Notices R Astron Soc. (2010) 406:2650–62. doi: 10.1111/j.1365-2966.2010.16864.x
21. Mendoza-Temis JdJ, Wu MR, Langanke K, Martinez-Pinedo G, Bauswein A, Janka HT. Nuclear robustness of the r process in neutron-star mergers. Phys Rev C. (2015) 92:055805. doi: 10.1103/PhysRevC.92.055805
22. Zhu Y, Wollaeger RT, Vassh N, Surman R, Sprouse TM, Mumpower MR, et al. Californium-254 and kilonova light curves. Astrophys J Lett. (2018) 863:L23. doi: 10.3847/2041-8213/aad5de
23. Wu MR, Barnes J, Martinez-Pinedo G, Metzger BD. Fingerprints of heavy-element nucleosynthesis in the late-time lightcurves of kilonovae. Phys Rev Lett. (2019) 122:062701. doi: 10.1103/PhysRevLett.122.062701
24. Roberts LF, Kasen D, Lee WH, Ramirez-Ruiz E. Electromagnetic transients powered by nuclear decay in the tidal tails of coalescing compact binaries. Astrophys J Lett. (2011) 736:L21. doi: 10.1088/2041-8205/736/1/L21
25. Korobkin O, Rosswog S, Arcones A, Winteler C. On the astrophysical robustness of the neutron star merger r-process. Mnthly Notices R Astron Soc. (2012) 426:1940–9. doi: 10.1111/j.1365-2966.2012.21859.x
26. Hotokezaka K, Sari R, Piran T. Analytic heating rate of neutron star merger ejecta derived from Fermi's theory of beta decay. Mnthly Notices R Astron Soc. (2017) 468:91–6. doi: 10.1093/mnras/stx411
27. Kasen D, Barnes J. Radioactive heating and late time kilonova light curves. Astrophys J. (2019) 876:128. doi: 10.3847/1538-4357/ab06c2
28. Hotokezaka K, Nakar E. Radioactive heating rate of r-process elements and macronova light curve. arXiv preprint arXiv:1909.02581. doi: 10.3847/1538-4357/ab6a98
29. Waxman E, Ofek EO, Kushnir D. Late-time kilonova light curves and implications to GW170817. Astrophys J. (2019) 878:93. doi: 10.3847/1538-4357/ab1f71
30. Fernández R, Metzger BD. Electromagnetic signatures of neutron star mergers in the advanced LIGO era. Annu Rev Nuclear Particle Sci. (2016) 66:23–45. doi: 10.1146/annurev-nucl-102115-044819
31. Shibata M, Hotokezaka K. Merger and mass ejection of neutron star binaries. Annu Rev Nuclear Particle Sci. (2019) 69:41–64. doi: 10.1146/annurev-nucl-101918-023625
32. Kyutoku K, Ioka K, Shibata M. Anisotropic mass ejection from black hole-neutron star binaries: Diversity of electromagnetic counterparts. Phys Rev D. (2013) 88:041503. doi: 10.1103/PhysRevD.88.041503
33. Kawaguchi K, Kyutoku K, Nakano H, Okawa H, Shibata M, Taniguchi K. Black hole-neutron star binary merger: Dependence on black hole spin orientation and equation of state. Phys Rev D. (2015) 92:024014. doi: 10.1103/PhysRevD.92.024014
34. Lehner L, Liebling SL, Palenzuela C, Caballero OL, O'Connor E, Anderson M, et al. Unequal mass binary neutron star mergers and multimessenger signals. Classic Quant Gravity. (2016) 33:184002. doi: 10.1088/0264-9381/33/18/184002
35. Dietrich T, Bernuzzi S, Ujevic M, Tichy W. Gravitational waves and mass ejecta from binary neutron star mergers: effect of the stars' rotation. Phys Rev D. (2017) 95:044045. doi: 10.1103/PhysRevD.95.044045
36. Bauswein A, Goriely S, Janka HT. Systematics of dynamical mass ejection, nucleosynthesis, and radioactively powered electromagnetic signals from neutron-star mergers. Astrophys J. (2013) 773:78. doi: 10.1088/0004-637X/773/1/78
37. Hotokezaka K, Kiuchi K, Kyutoku K, Okawa H, Sekiguchi Yi, Shibata M, et al. Mass ejection from the merger of binary neutron stars. Phys Rev D. (2013) 87:024001. doi: 10.1103/PhysRevD.87.024001
38. East WE, Pretorius F, Stephens BC. Eccentric black hole-neutron star mergers: effects of black hole spin and equation of state. Phys Rev D. (2012) 85:124009. doi: 10.1103/PhysRevD.85.124009
39. Kyutoku K, Ioka K, Okawa H, Shibata M, Taniguchi K. Dynamical mass ejection from black hole-neutron star binaries. Phys Rev D. (2015) 92:044028. doi: 10.1103/PhysRevD.92.044028
40. Oechslin R, Janka HT, Marek A. Relativistic neutron star merger simulations with non-zero temperature equations of state. I. Variation of binary parameters and equation of state. Astron Astrophys. (2007) 467:395–409. doi: 10.1051/0004-6361:20066682
41. Sekiguchi Y, Kiuchi K, Kyutoku K, Shibata M. Dynamical mass ejection from binary neutron star mergers: Radiation-hydrodynamics study in general relativity. Phys Rev D. (2015). 91:064059. doi: 10.1103/PhysRevD.91.064059
42. Radice D, Galeazzi F, Lippuner J, Roberts LF, Ott CD, Rezzolla L. Dynamical mass ejection from binary neutron star mergers. Mnthly Notices R Astron Soc. (2016) 460:3255–71. doi: 10.1093/mnras/stw1227
43. Bauswein A, Baumgarte TW, Janka HT. Prompt merger collapse and the maximum mass of neutron stars. Phys Rev Lett. (2013) 111:131101. doi: 10.1103/PhysRevLett.111.131101
44. Kyutoku K, Ioka K, Shibata M. Ultrarelativistic electromagnetic counterpart to binary neutron star mergers. Mnthly Notices R Astron Soc. (2014) 437:L6–10. doi: 10.1093/mnrasl/slt128
45. Metzger BD, Bauswein A, Goriely S, Kasen D. Neutron-powered precursors of kilonovae. Mnthly Notices R Astron Soc. (2015) 446:1115–20. doi: 10.1093/mnras/stu2225
46. Oechslin R, Janka HT. Torus formation in neutron star mergers and well-localized short gamma-ray bursts. Mnthly Notices R Astron Soc. (2006) 368:1489–99. doi: 10.1111/j.1365-2966.2006.10238.x
47. Metzger BD, Piro AL, Quataert E. Time-dependent models of accretion discs formed from compact object mergers. Mnthly Notices R Astron Soc. (2008) 390:781–97. doi: 10.1111/j.1365-2966.2008.13789.x
48. Siegel DM, Metzger BD. Three-dimensional GRMHD simulations of neutrino-cooled accretion disks from neutron star mergers. Astrophys J. (2018) 858:52. doi: 10.3847/1538-4357/aabaec
49. Fernández R, Metzger BD. Delayed outflows from black hole accretion tori following neutron star binary coalescence. Mnthly Notices R Astron Soc. (2013) 435:502–17. doi: 10.1093/mnras/stt1312
50. Surman R, McLaughlin GC, Hix WR. Nucleosynthesis in the outflow from gamma-ray burst accretion disks. Astrophys J. (2006) 643:1057–64. doi: 10.1086/501116
51. Metzger BD, Thompson TA, Quataert E. On the conditions for neutron-rich gamma-ray burst outflows. Astrophys J. (2008) 676:1130–50. doi: 10.1086/526418
52. Dessart L, Ott CD, Burrows A, Rosswog S, Livne E. Neutrino signatures and the neutrino-driven wind in binary neutron star mergers. Astrophys J. (2009) 690:1681–705. doi: 10.1088/0004-637X/690/2/1681
53. Popham R, Woosley SE, Fryer C. Hyperaccreting black holes and gamma-ray bursts. Astrophys J. (1999) 518:356–74. doi: 10.1086/307259
54. Just O, Bauswein A, Ardevol Pulpillo R, Goriely S, Janka HT. Comprehensive nucleosynthesis analysis for ejecta of compact binary mergers. Mnthly Notices R Astron Soc. (2015) 448:541–67. doi: 10.1093/mnras/stv009
55. Fernández R, Tchekhovskoy A, Quataert E, Foucart F, Kasen D. Long-term GRMHD simulations of neutron star merger accretion discs: implications for electromagnetic counterparts. Mnthly Notices R Astron Soc. (2019) 482:3373–93. doi: 10.1093/mnras/sty2932
56. Miller JM, Ryan BR, Dolence JC, Burrows A, Fontes CJ, Fryer CL, et al. Full transport model of GW170817-like disk produces a blue kilonova. Phys Rev D. (2019) 100:023008. doi: 10.1103/PhysRevD.100.023008
57. Metzger BD, Fernández R. Red or blue? A potential kilonova imprint of the delay until black hole formation following a neutron star merger. Mnthly Notices R Astron Soc. (2014) 441:3444–53. doi: 10.1093/mnras/stu802
58. Kasen D, Fernández R, Metzger BD. Kilonova light curves from the disc wind outflows of compact object mergers. Mnthly Notices R Astron Soc. (2015) 450:1777–86. doi: 10.1093/mnras/stv721
59. Lippuner J, Fernández R, Roberts LF, Foucart F, Kasen D, Metzger BD, et al. Signatures of hypermassive neutron star lifetimes on r-process nucleosynthesis in the disc ejecta from neutron star mergers. Mnthly Notices R Astron Soc. (2017) 472:904–18. doi: 10.1093/mnras/stx1987
60. Pinto PA, Eastman RG. The physics of type IA supernova light curves. II. Opacity and Diffusion. Astrophys J. (2000) 530:757–76. doi: 10.1086/308380
61. Kasen D, Badnell NR, Barnes J. Opacities and spectra of the r-process ejecta from neutron star mergers. Astrophys J. (2013) 774:25. doi: 10.1088/0004-637X/774/1/25
62. Tanaka M, Hotokezaka K. Radiative transfer simulations of neutron star merger ejecta. Astrophys J. (2013) 775:113. doi: 10.1088/0004-637X/775/2/113
63. Tanaka M, Kato D, Gaigalas G, Kawaguchi K. Systematic opacity calculations for kilonovae. arXiv preprint arXiv:1906.08914. doi: 10.1093/mnras/staa1576
64. Fontes CJ, Fryer CL, Hungerford AL, Wollaeger RT, Korobkin O. A line-binned treatment of opacities for the spectra and light curves from neutron star mergers. Mnthly Notices R Astron Soc. (2020) 493:4143–171. doi: 10.1093/mnras/staa485
65. Barnes J, Kasen D. Effect of a high opacity on the light curves of radioactively powered transients from compact object mergers. Astrophys J. (2013) 775:18. doi: 10.1088/0004-637X/775/1/18
66. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett. (2017) 119:161101. doi: 10.1103/PhysRevLett.119.161101
67. Goldstein A, Veres P, Burns E, Briggs MS, Hamburg R, Kocevski D, et al. An ordinary short gamma-ray burst with extraordinary implications: fermi-GBM detection of GRB 170817A. Astrophys J Lett. (2017) 848:L14. doi: 10.3847/2041-8213/aa8f41
68. Savchenko V, Ferrigno C, Kuulkers E, Bazzano A, Bozzo E, Brandt S, et al. INTEGRAL Detection of the First Prompt Gamma-Ray Signal Coincident with the Gravitational-wave Event GW170817. Astrophys J Lett. (2017) 848:L15. doi: 10.3847/2041-8213/aa8f94
69. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys J Lett. (2017) 848:L13. doi: 10.3847/2041-8213/aa920c
70. Arcavi I, Hosseinzadeh G, Howell DA, McCully C, Poznanski D, Kasen D, et al. Optical emission from a kilonova following a gravitational-wave-detected neutron-star merger. Nature. (2017) 551:64–6. doi: 10.1038/nature24291
71. Coulter DA, Foley RJ, Kilpatrick CD, Drout MR, Piro AL, Shappee BJ, et al. Swope Supernova Survey (2017a). (SSS17a), the optical counterpart to a gravitational wave source. Science. (2017). 358:1556–8. doi: 10.1126/science.aap9811
72. Drout MR, Piro AL, Shappee BJ, Kilpatrick CD, Simon JD, Contreras C, et al. Light curves of the neutron star merger GW170817/SSS17a: implications for r-process nucleosynthesis. Science. (2017) 358:1570–74. doi: 10.1126/science.aaq0049
73. Shappee BJ, Simon JD, Drout MR, Piro AL, Morrell N, Prieto JL, et al. Early spectra of the gravitational wave source GW170817: evolution of a neutron star merger. Science. (2017) 358:1574–8. doi: 10.1126/science.aaq0186
74. Smartt SJ, Chen TW, Jerkstrand A, Coughlin M, Kankare E, Sim SA, et al. A kilonova as the electromagnetic counterpart to a gravitational-wave source. Nature. (2017) 551:75–9. doi: 10.1038/nature24303
75. Soares-Santos M, Holz DE, Annis J, Chornock R, Herner K, Berger E, et al. The electromagnetic counterpart of the binary neutron star merger LIGO/virgo GW170817. I. Discovery of the optical counterpart using the dark energy camera. Astrophys J Lett. (2017) 848:L16. doi: 10.3847/2041-8213/aa9059
76. Valenti S, Sand DJ, Yang S, Cappellaro E, Tartaglia L, Corsi A, et al. The discovery of the electromagnetic counterpart of GW170817: kilonova AT 2017gfo/DLT17ck. Astrophys J Lett. (2017) 848:L24. doi: 10.3847/2041-8213/aa8edf
77. Abbott BP, Abbott R, Abbott TD, Acernese F. Multi-messenger observations of a binary neutron star merger. Astrophys J Lett. (2017) 848:L12. doi: 10.3847/2041-8213/aa91c9
78. Cowperthwaite PS, Berger E, Villar VA, Metzger BD, Nicholl M, Chornock R, et al. The electromagnetic counterpart of the binary neutron star merger LIGO/virgo GW170817. II. UV, optical, and near-infrared light curves and comparison to kilonova models. Astrophys J Lett. (2017) 848:L17. doi: 10.3847/2041-8213/aa8fc7
79. Troja E, Piro L, van Eerten H, Wollaeger RT, Im M, Fox OD, et al. The X-ray counterpart to the gravitational-wave event GW170817. Nature. (2017) 551:71–4. doi: 10.1038/nature24290
80. Kasen D, Metzger B, Barnes J, Quataert E, Ramirez-Ruiz E. Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature. (2017) 551:80–4. doi: 10.1038/nature24453
81. Kasliwal MM, Nakar E, Singer LP, Kaplan DL, Cook DO, Van Sistine A, et al. Illuminating gravitational waves: A concordant picture of photons from a neutron star merger. Science. (2017) 358:1559–65. doi: 10.1126/science.aap9455
82. Tanaka M, Utsumi Y, Mazzali PA, Tominaga N, Yoshida M, Sekiguchi Y, et al. Kilonova from post-merger ejecta as an optical and near-Infrared counterpart of GW170817. Publ Astron Soc Japan. (2017) 69:102. doi: 10.1093/pasj/psx121
83. Waxman E, Ofek EO, Kushnir D, Gal-Yam A. Constraints on the ejecta of the GW170817 neutron star merger from its electromagnetic emission. Mnthly Notices R Astron Soc. (2018) 481:3423–41. doi: 10.1093/mnras/sty2441
84. Villar VA, Guillochon J, Berger E, Metzger BD, Cowperthwaite PS, Nicholl M, et al. The combined ultraviolet, optical, and near-infrared light curves of the kilonova associated with the binary neutron star merger GW170817: unified data set, analytic models, and physical implications. Astrophys J Lett. (2017) 851:L21. doi: 10.3847/2041-8213/aa9c84
85. Perego A, Radice D, Bernuzzi S. AT 2017gfo: an anisotropic and three-component kilonova counterpart of GW170817. Astrophys J Lett. (2017) 850:L37. doi: 10.3847/2041-8213/aa9ab9
86. Watson D, Hansen CJ, Selsing J, Koch A, Malesani DB, Andersen AC, et al. Identification of strontium in the merger of two neutron stars. Nature. (2019) 574:497–500. doi: 10.1038/s41586-019-1676-3
87. Nicholl M, Berger E, Kasen D, Metzger BD, Elias J, Briceño C, et al. The electromagnetic counterpart of the binary neutron star merger LIGO/virgo GW170817. III. Optical and UV spectra of a blue kilonova from fast polar ejecta. Astrophys J Lett. (2017) 848:L18. doi: 10.3847/2041-8213/aa9029
88. McCully C, Hiramatsu D, Howell DA, Hosseinzadeh G, Arcavi I, Kasen D, et al. The rapid reddening and featureless optical spectra of the optical counterpart of GW170817, AT 2017gfo, during the first four days. Astrophys J Lett. (2017) 848:L32. doi: 10.3847/2041-8213/aa9111
89. Evans PA, Cenko SB, Kennea JA, Emery SWK, Kuin NPM, Korobkin O, et al. Swift and NuSTAR observations of GW170817: detection of a blue kilonova. Science. (2017) 358:1565–70. doi: 10.1126/science.358.6370.1551-i
90. Chornock R, Berger E, Kasen D, Cowperthwaite PS, Nicholl M, Villar VA, et al. The electromagnetic counterpart of the binary neutron star merger LIGO/virgo GW170817. IV. Detection of near-infrared signatures of r-process nucleosynthesis with gemini-south. Astrophys J Lett. (2017) 848:L19. doi: 10.3847/2041-8213/aa905c
91. Radice D, Perego A, Hotokezaka K, Fromm SA, Bernuzzi S, Roberts LF. Binary neutron star mergers: mass ejection, electromagnetic counterparts, and nucleosynthesis. Astrophys J. (2018) 869:130. doi: 10.3847/1538-4357/aaf054
92. Metzger BD, Thompson TA, Quataert E. A magnetar origin for the kilonova ejecta in GW170817. Astrophys J. (2018) 856:101. doi: 10.3847/1538-4357/aab095
93. Piro AL, Kollmeier JA. Evidence for cocoon emission from the early light curve of SSS17a. Astrophys J. (2018) 855:103. doi: 10.3847/1538-4357/aaaab3
94. Paczynski B. Gamma-ray bursters at cosmological distances. Astrophys J Lett. (1986) 308:L43–6. doi: 10.1086/184740
95. Narayan R, Paczynski B, Piran T. Gamma-ray bursts as the death throes of massive binary stars. Astrophys J Lett. (1992) 395:L83–6. doi: 10.1086/186493
96. Eichler D, Livio M, Piran T, Schramm DN. Nucleosynthesis, neutrino bursts and gamma-rays from coalescing neutron stars. Nature. (1989) 340:126–8. doi: 10.1038/340126a0
97. Piran T. The physics of gamma-ray bursts. Rev Modern Phys. (2004) 76:1143–210. doi: 10.1103/RevModPhys.76.1143
98. Lee WH, Ramirez-Ruiz E. The progenitors of short gamma-ray bursts. N J Phys. (2007) 9:17. doi: 10.1088/1367-2630/9/1/017
99. Kumar P, Zhang B. The physics of gamma-ray bursts & relativistic jets. Phys Rep. (2015) 561:1–109. doi: 10.1016/j.physrep.2014.09.008
100. Margalit B, Metzger BD. Constraining the maximum mass of neutron stars from multi-messenger observations of GW170817. Astrophys J Lett. (2017) 850:L19. doi: 10.3847/2041-8213/aa991c
101. Radice D, Perego A, Zappa F, Bernuzzi S. GW170817: joint constraint on the neutron star equation of state from multimessenger observations. Astrophys J Lett. (2018) 852:L29. doi: 10.3847/2041-8213/aaa402
102. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature. (2017) 551:85–8. doi: 10.1038/nature24471
103. The LIGO Scientific Collaboration, the Virgo Collaboration, Abbott BP, Abbott R, Abbott TD, Abraham S, et al. A gravitational-wave measurement of the Hubble constant following the second observing run of Advanced LIGO and Virgo. arXiv preprint arXiv:1908.06060. Available online at: https://ui.adsabs.harvard.edu/abs/2017Natur.551...85A/exportcitation
104. Arcavi I. The first hours of the GW170817 kilonova and the importance of early optical and ultraviolet observations for constraining emission models. Astrophys J Lett. (2018) 855:L23. doi: 10.3847/2041-8213/aab267
105. Côté B, Fryer CL, Belczynski K, Korobkin O, Chruślińska M, Vassh N, et al. The origin of r-process elements in the milky way. Astrophys J. (2018) 855:99. doi: 10.3847/1538-4357/aaad67
106. Côté B, Eichler M, Arcones A, Hansen CJ, Simonetti P, Frebel A, et al. Neutron star mergers might not be the only source of r-process elements in the milky way. Astrophys J. (2019) 875:106. doi: 10.3847/1538-4357/ab10db
107. Safarzadeh M, Sarmento R, Scannapieco E. On neutron star mergers as the source of r-process-enhanced metal-poor stars in the milky way. Astrophys J. (2019) 876:28. doi: 10.3847/1538-4357/ab1341
108. Ji AP, Frebel A, Chiti A, Simon JD. R-process enrichment from a single event in an ancient dwarf galaxy. Nature. (2016) 531:610–3. doi: 10.1038/nature17425
109. Bonetti M, Perego A, Dotti M, Cescutti G. Neutron star binary orbits in their host potential: effect on early r-process enrichment. Mnthly Notices R Astron Soc. (2019) 490:296–311. doi: 10.1093/mnras/stz2554
110. Mösta P, Roberts LF, Halevi G, Ott CD, Lippuner J, Haas R, et al. r-process nucleosynthesis from three-dimensional magnetorotational core-collapse supernovae. Astrophys J. (2018) 864:171. doi: 10.3847/1538-4357/aad6ec
111. Halevi G, Mösta P. r-process nucleosynthesis from three-dimensional jet-driven core-collapse supernovae with magnetic misalignments. Mnthly Notices R Astron Soc. (2018) 477:2366–2375. doi: 10.1093/mnras/sty797
112. Siegel DM, Barnes J, Metzger BD. Collapsars as a major source of r-process elements. Nature. (2019) 569:241–4. doi: 10.1038/s41586-019-1136-0
113. Fischer T, Wu MR, Wehmeyer B, Bastian NUF, Martinez-Pinedo G, Thielemann FK. Core-collapse supernova explosions driven by the hadron-quark phase transition as rare r process site. arXiv preprint arXiv:2003.00972. doi: 10.3847/1538-4357/ab86b0
114. The LIGO Scientific Collaboration, the Virgo Collaboration, Abbott BP, Abbott R, Abbott TD, Abraham S, et al. GW190425: observation of a compact binary coalescence with total mass ~ 3.4M − ⊙. arXiv preprint arXiv:2001.01761. Available online at: https://ui.adsabs.harvard.edu/abs/2017Natur.551...85A/exportcitation
115. Roberts LF, Lippuner J, Duez MD, Faber JA, Foucart F, Lombardi JC, et al. The influence of neutrinos on r-process nucleosynthesis in the ejecta of black hole–neutron star mergers. Mnthly Notices R Astron Soc. (2017) 464:3907–19. doi: 10.1093/mnras/stw2622
116. Foucart F, Hinderer T, Nissanke S. Remnant baryon mass in neutron star-black hole mergers: Predictions for binary neutron star mimickers and rapidly spinning black holes. Phys Rev D. (2018) 98:081501. doi: 10.1103/PhysRevD.98.081501
Keywords: gravitational wave astronomy, kilonovae, kilonovae: TNS 2017 gfo, DLT17ck, SSS17a, r-process nucleosynthesis, neutron star binaries
Citation: Barnes J (2020) The Physics of Kilonovae. Front. Phys. 8:355. doi: 10.3389/fphy.2020.00355
Received: 20 March 2020; Accepted: 27 July 2020;
Published: 28 October 2020.
Edited by:
Rosalba Perna, Stony Brook University, United StatesReviewed by:
Anthony Piro, Carnegie Observatories (CIS), United StatesSayantan Choudhury, Max Planck Institute for Gravitational Physics (AEI), Germany
Copyright © 2020 Barnes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jennifer Barnes, amxiMjMzMUBjb2x1bWJpYS5lZHU=
 Jennifer Barnes
Jennifer Barnes