Electronic and Magnetic Anisotropies in FeSe Family of Iron-Based Superconductors

Chen, Tong; Yi, Ming; Dai, Pengcheng

doi:10.3389/fphy.2020.00314

MINI REVIEW article

Front. Phys., 21 August 2020

Sec. Condensed Matter Physics

Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.00314

Electronic and Magnetic Anisotropies in FeSe Family of Iron-Based Superconductors

TC
Tong Chen ^*
MY
Ming Yi ^*
PD
Pengcheng Dai ^*

Department of Physics and Astronomy, Rice University, Houston, TX, United States

Abstract

Most parent compounds of iron-based superconductors (FeSCs) exhibit a tetragonal-to-orthorhombic lattice distortion below T_s associated with an electronic nematic phase that breaks the four-fold (C₄) rotational symmetry of the underlying lattice, and then forms collinear antiferromagnetic (AF) order below T_N (T_N ≤ T_s). Optimal superconductivity emerges upon suppression of the nematic and AF phases. FeSe, which also exhibits a nematic phase transition below T_s but becomes superconducting in the nematic phase without AF order, provides a unique platform to study the interplay amongst the nematic phase and superconductivity. In this review, we focus on the experiments done on uniaxial pressure detwinned single crystals of FeSe compared to other FeSCs and highlight the importance of understanding the electronic and magnetic anisotropy in elucidating the nature of unconventional superconductivity.

1. Introduction

In unconventional superconductors such as heavy fermions, copper- and iron-based materials, the observation that superconductivity often emerges from their antiferromagnetic (AF) ordered parent compounds suggests that magnetism plays an important role in the mechanism of high-transition temperature (high-T_c) superconductivity []. In addition to forming a collinear AF structure below T_N, most parent compounds of iron-based superconductors (FeSCs) exhibit a tetragonal-to-orthorhombic structural transition below T_s and form an electronic nematic phase that breaks the four-fold (C₄) rotational symmetry in the iron plane (T_N ≤ T_s) [, ]. Since the tetragonal-to-orthorhombic structural transition for FeSCs occurs below room temperature (T_s < 295 K), the system forms 90° rotated twinned domains below T_s, making it impossible for a bulk probe to determine the intrinsic electronic and magnetic properties of the individual domains and the associated nematic phase. To alleviate this technical difficulty, mechanical detwin devices were developed first for the BaFe₂As₂ compounds [, ], and later adapted for other material families. These types of devices utilize a mechanical device to apply uniaxial pressure along one of the orthorhombic lattice directions, one can detwin single crystals of FeSCs and thus measure the intrinsic electronic and magnetic anisotropies present in the orthorhombic phase []. Therefore, uniaxial pressure detwinned FeSCs can provide a platform to study the interplay of the nematic phase, magnetic order, and superconductivity. Compared with other families of FeSCs, FeSe is highly unusual because FeSe exhibits an orthorhombic structural distortion at T_s ≈ 90 K and superconductivity at T_c ≈ 9 K [] without magnetic order. As a consequence, one can directly probe the interplay between the nematic phase and superconductivity without the complication of the static AF ordered phase. Moreover, unexpected phenomenon, say, extremely-high superconducting temperature in thin films of FeSe [, ], have been observed. And it is also proposed that exotic state like Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) state is realized in this compound [, ].

After the discovery of the unconventional superconductivity in F-doped LaFeAsO [], many FeSCs were found and classified into RFeAsO (R = La, Ce, Pr,…, the 1111 family), AFe₂As₂ (A = Ba, Sr, Ca, K, the 122 family), AFeAs (A = Li, Na, the 111 family, Figure 1A), Fe_1+yTe_1−xSe_x (the 11 family), and A_xFe_2−yAs₂ (A = K, Rb,…, the alkali iron selenide family) [–]. The 122 family, especially the electron- and hole-doped BaFe₂As₂, are the most intensively studied materials [–] because superconductivity can be induced by doping a large variety of chemicals including K/Na on Ba sites (hole-doping) [, ], Co/Ni on Fe sites (electron-doping) [, ] and P on As sites (isovalent doping) [], and large-sized single crystals can be grown by self-flux methods in most cases []. In the phase diagram of Co-doped BaFe₂As₂, the static AF order is gradually suppressed and separated from the structural transition by Co-doping in the underdoped region [, ]. The optimal superconductivity appears when the nematic phase and AF order are suppressed, suggesting that the nematic and static AF orders are competing with superconductivity [] (Figure 1B). However, FeSe does not follow this typical phase diagram (Figure 1C). Instead, in the S-doped FeSe, the structural (nematic) transition does not have an accompanying magnetic transition [, –]. Moreover, superconductivity is not suppressed with increasing S-substitution, different from the superconductivity dome in the phase diagram of Ba(Fe_1−xCo_x)₂As₂. Given the contrasting behavior between Ba(Fe_1−xCo_x)₂As₂ and FeSe_1−xS_x, it will be interesting to study the relationship between nematic phase and superconductivity in these two families of materials.

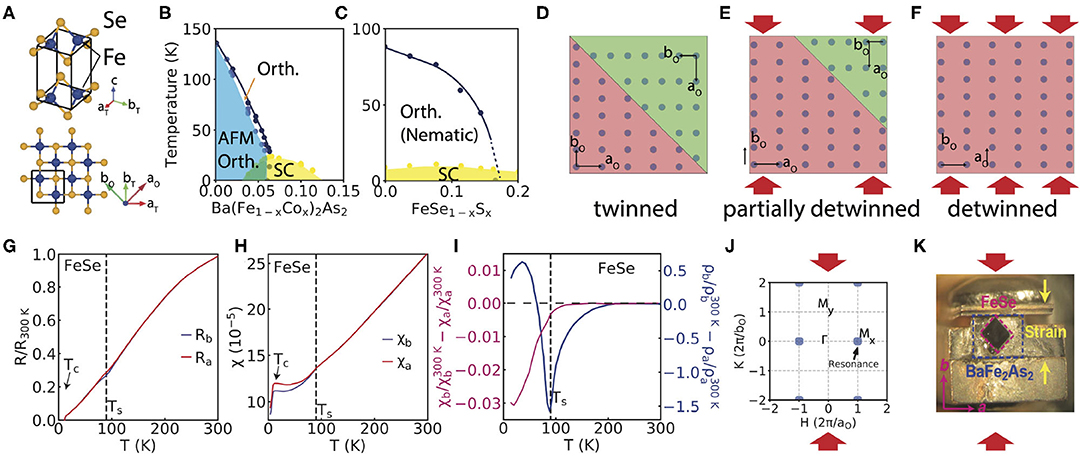
Figure 1

]. (C) Phase diagram of FeSe_1−xS_x []. (D–F) Schematic illustration of a twinned (D), partially detwinned (E), and fully detwinned (F) single crystal that contains two domains under a zero (D), intermediate (E), and large (F) mechanical force. (G) Temperature dependence of in-plane resistivity R_a (ρ_a resistivity along a direction) and R_b (ρ_a resistivity along b direction) of FeSe. (H) Temperature dependence of in-plane susceptibility χ_a and χ_b (susceptibility along a and b directions) of FeSe in a 12 T field. (I) Anisotropy of resistivity and susceptibility of FeSe []. (J) Schematic of the Brillouin Zone (BZ). The strain direction is along b-axis, defining the Γ - M_Y momentum direction in the ARPES measurements. Blue dots mark the AF wave-vector in the BZ. (K) Photo of a detwinning device []. The mechanical uniaxial strain device consists of a clamp that presses a single crystal substance of BaFe₂As₂, which can transfer the strain to the single crystal of FeSe glued on top. The strain direction is along b-axis, defining the Γ - M_Y momentum direction. Panels (G–I) are reproduced from [] with permission.

2. Nematicity and Detwinning Devices

The electronic nematic phase refers to the in-plane rotational symmetry-breaking phase below the structural transition temperature T_s in FeSCs []. Transport measurements on uniaxial strain detwinned Ba(Fe_1−xCo_x)₂As₂ provided evidence of anisotropic transport properties that were attributed to the presence of a nematic phase because the small lattice distortion below T_s is not expected to induce such a large resistivity anisotropy []. Later, the electronic and magnetic anisotropies were observed by angle-resolved photoemission spectroscopy (ARPES) [] and inelastic neutron scattering (INS) measurements on mechanically detwinned samples [], highlighting nematicity as an essential degree of freedom that interplays with magnetism and superconductivity.

Since the iron-based materials naturally form two 90° rotated twin domains below the orthorhombic transition at T_s, experiments on twinned samples usually measure the average of anisotropic properties [, ]. Thus, to study the intrinsic electronic and magnetic anisotropies, it is essential to detwin the sample (Figures 1D–F,J,K), which can be achieved by applying a uniaxial pressure through a mechanical clamp device that directly presses on the parallel edges of the crystal [, , –]. However, for materials that are structurally soft, such direct clamping is difficult to achieve. Instead, other types of detwinning strategy were developed that involve gluing the sample onto a substrate that can transfer a uniaxial strain to the sample. Piezoelectric materials [, ], glass-fiber-reinforced plastic [], and even mechanical force detwinned BaFe₂As₂ (Figure 1K) [, ] are proved to be effective substrates to detwin the FeSCs. In this review, we discuss effective strain strategy on FeSe using BaFe₂As₂ as a substrate, which is clamped in a detwin device. Since BaFe₂As₂ itself undergoes tetragonal to orthorhombic transition at 138 K, the detwinned BaFe₂As₂ single crystal would provide a natural anisotropic strain on the FeSe glued on top.

3. Electronic and Magnetic Anisotropies

3.1. Resistivity and Susceptibility

Resistivity measurements on uniaxial strain detwinned Ba(Fe_1−xCo_x)₂As₂ reveal clear evidence of in-plane anisotropy developing at a temperature above T_N and T_s [, , ]. In the undoped parent compound BaFe₂As₂, the resistivity anisotropy increases when approaching T_N = T_s ≈ 138 K from higher temperature, peaks at T_N = T_s, and then gradually decreases upon cooling. As a function of increasing electron (Co)-doping in Ba(Fe_1−xCo_x)₂As₂, the resistivity anisotropy increases and then vanishes near optimal doping, consistent with the spin nematic scenario in which the tetragonal-to-orthorhombic transition is driven by magnetic fluctuations at a temperature T_s > T_N. Since structural distortion in Ba(Fe_1−xCo_x)₂As₂ is also associated with the lifting of degeneracy in the orbital degrees of freedom below T_s [], the observed resistivity anisotropy could be a consequence of orbital order instead of magnetic fluctuations. In the magnetic susceptibility measurements on detwinned BaFe₂As₂, χ_b becomes larger than χ_a below T_N = T_s, and the anisotropy monotonically increases upon cooling [].

Since single crystals of FeSe are thin and fragile, more complicated detwinning strategies were developed to detwin FeSe, such as using a “horseshoe” device [] or glue the single crystals on different substrates [, , ]. In resistivity and susceptibility measurements on detwinned FeSe, the behavior of the anisotropy is very similar to that of BaFe₂As₂. The in-plane resistivity anisotropy in FeSe develops at a temperature above T_s, peaks at T_s, and then vanishes upon cooling (Figures 1G,I), while the absolute value of susceptibility anisotropy monotonically increases with decreasing temperature (Figures 1H,I) [].

We note that the sign of ρ_b − ρ_a and χ_b − χ_a, where ρ_a/b and χ_a/b are resistivity and magnetic susceptibility along the lattice orthorhombic a/b directions, respectively, in detwinned FeSe is opposite to that of BaFe₂As₂. The small magnitudes and the reversed sign of resistivity and susceptibility anisotropy in detwinned FeSe may be attributable to the small lattice orthorhombicity, which results in smaller orbital overlap along the a-axis, while the static collinear AF order in the BaFe₂As₂ systems, coupled with related spin fluctuations, give rise to the overwhelming ρ_b and χ_b.

3.2. Angle-Resolved Photo-Emission Spectroscopy

The electronic structure of FeSe has been intensively studied by ARPES measurements [, –]. FeSe shares common features with other FeSCs, with three hole bands near the BZ center and two electron bands at the BZ corners. However, one distinction between FeSe and iron pnictides such as doped BaFe₂As₂ is that FeSe is the only compound that does not have the long range magnetic order that appears below the nematic ordering temperature to induce additional folding in the electronic structure and Fermi surfaces (Figures 1B,C). Hence FeSe provides an ideal system to study the effect of the nematic phase on the electronic structure.

Although FeSe has been studied by ARPES in great detail, the description of the electronic structure in the nematic state is still actively debated with important consequences regarding two central problems. First, while some reports conclude that the orbital anisotropy between d_xz and d_yz in FeSe has an energy scale comparable to those in the iron pnictides [, –, , ], others report that it is much smaller in FeSe [, ]. The implication of the former is that the nematic order in FeSe is electronic in origin similar to the iron pnictides while for the latter, it is implied that the nematic order could be much more on par with the lattice distortion. The second debated question is the complete disappearance of an electron pocket in the nematic phase as observed by spectroscopy probes [], which leads to strongly anisotropic superconducting gap [, , ]. Various scenarios have been proposed for the route in which the electron pocket disappears [–].

These issues are recently examined by studies on FeSe that are detwinned by gluing single crystals of FeSe on mechanically strained BaFe₂As₂ [] (Figures 2a–m). The complete detwinning of FeSe via this method is demonstrated by comparing the signal from orthogonal directions of the crystal (Figures 2a–e). As seen at the same momentum point indicated by the arrows, the peaks from Γ − M_X and Γ − M_Y appear at distinct energies and the mixing of the two match that of the same measurement on a twinned crystal. Moreover, no portion of the signal from Γ − M_X is leaked in the signal taken along Γ − M_Y. Hence the detwinning was complete. From photoemission matrix element effects [], it was identified that the bands observed along Γ − M_X and Γ − M_Y originate from the d_xz and d_yz orbitals. The difference between the orbitals, as well as the anisotropy of d_xy orbital, cause the 50 meV energy difference at the BZ corners. [] This result confirms that the nematic order in FeSe is electronic in origin and similar to that in the iron pnictides. Second, in addition to d_xz and d_yz, the d_xy orbital also shows a nematic band shift and participates in the nematic order, which could be explained by an anisotropic hopping term. Finally, the vanishing electron pocket that contains d_xy and d_xz characters in the tetragonal state disappears by shrinking in size due to a new hybridization between the d_xy and d_xz bands as they shift at the onset of the nematic phase. Eventually deep in the nematic phase but above the superconducting phase, this electron pocket is lifted completely above the Fermi level, making way for a strongly anisotropic superconducting state.

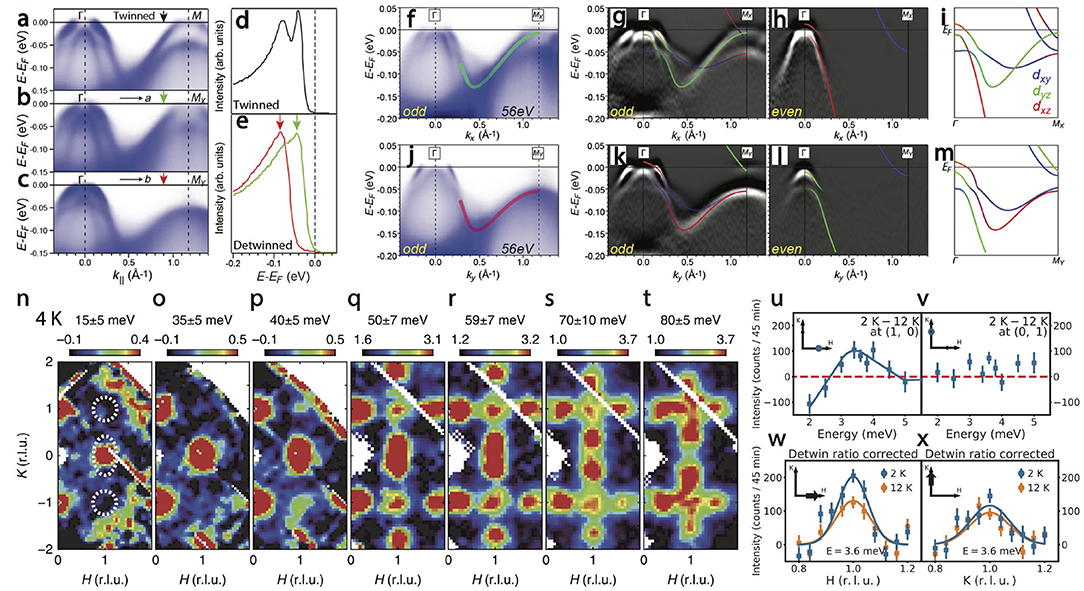
Figure 2

, , ]. (a) ARPES spectra taken along the Γ - M direction on a twinned FeSe. (b,c) ARPES spectra taken on detwinned FeSe along the Γ - M_X and Γ - M_Y directions, respectively. (d,e) Energy distribution curves taken at the momentum pointed to by arrows in (a–c). The measurements are taken with 70 eV photons under odd polarization with respect to the cut direction. (f) Spectra measured along the Γ-M_X direction with odd polarization. (g,h) Second energy derivatives of measured spectra along the Γ-M_X direction under odd and even polarization with respect to the cut direction, respectively. A schematic of bands of orbital symmetries with the allowed intensity under each polarization is overlaid. (i) The complete band schematic from both polarizations is summarized Γ - M_X. (j–m) A similar measurement as (f–i) but for the Γ-M_Y direction. (n–t) Constant energy cuts in the [H, K] plane from the neutron scattering spectra of twinned FeSe []. Measurements in n-p and q-t were carried out at 4 K with E_i = 79 and 294 meV, respectively. Symmetry equivalent data were pooled to enhance statistical accuracy. (u,v) Difference of the scattering below and above T_c as a function of energy at Q_AF = (1, 0) and (0, 1) measured in detwinned FeSe. The solid and dashed lines are guides to the eye. The peak 3.6 meV marks the neutron spin resonance. (w,x) Wave-vector scans with E = 3.6 meV at Q_AF = (1, 0) and (0, 1). The trajectory of the scans (black errors) crossing spin excitations are illustrated in the insets. n-t are adapted from reference [] with permission.

In addition, in relation to the reversed anisotropy observed in susceptibility and resistivity mentioned above, it is interesting to note that FeSe has a much more prominent reversed orbital anisotropy at the Brillouin zone (BZ) center compared to BaFe₂As₂, that is, the d_xz orbital is lifted up compared to d_yz, opposite to that of the large orbital anisotropy at the BZ corner [, ]. It is also interesting to note that a recent X-ray linear dichroism (XLD) measurement reveals a reversed orbital occupation imbalance between d_xz and d_yz for FeSe compared to BaFe₂As₂[].

3.3. Neutron Scattering

Since superconductivity in unconventional superconductors usually emerges from AF ordered parent compounds, and a neutron spin resonance, a collective spin excitation with intensity tracking the superconducting order parameter, is widely observed by INS, magnetism is believed to be a common thread to understand the microscopic origin of unconventional superconductivity [, ].

Spin excitations in parent compounds of FeSCs have been studied by neutron time-of-flight (TOF) chopper spectrometers soon after the availability of single-crystalline samples. Recently, the spin waves in fully detwinned BaFe₂As₂ are mapped out in the entire BZ using a TOF spectrometer []. It is shown that at low energies, spin waves are most intense at the AF wave-vectors Q_AF = (±1, 0). With increasing energy, spin waves become more transversely elongated and magnetic scattering starts to appear near (0, ±1) to reduce the two-fold (C₂) anisotropy. Upon further increasing energy, the transverse excitations from (±1, 0) and (0, ±1) merge together above 150 meV at (±1, ±1).

The neutron spin resonance, a signature of unconventional superconductivity, was studied in superconducting BaFe_1.915Ni_0.085As₂ []. INS experiments on twinned BaFe_1.915Ni_0.085As₂ have found order-parameter like spin resonance at wave vectors Q_AF = (1, 0, 1) and (0, 1, 1) with E ≈ 6 meV below T_c = 16.5 K []. In the normal state in detwinned BaFe_1.915Ni_0.085As₂, well-defined peaks centered at both (1, 0, 1) and (0, 1, 1) are observed. On cooling below T_c, only the scattering at (1, 0, 1) increases in intensity and forms a resonance, while it does not change across T_c at (0, 1, 1), which shows that the spin resonance has the C₂-symmetric, consistent with a highly anisotropic pairing state []. For a sample with slightly lower electron-doping, we find that spin excitations in the normal state are absent at (0, 1, 1), indicating that resonance only appears at Q_AF = (1, 0, 1) []. These results suggest that the superconductivity-induced resonance is orbital selective and arises from the electron-hole Fermi surface nesting of quasiparticles with the d_yz orbital characters [].

Spin fluctuation spectra in twinned FeSe are similar to that of BaFe₂As₂, as shown in Figures 2n–t, except that Néel spin fluctuations at Q = (1, 1) coexist with the stripe spin fluctuations at Q_AF = (1, 0) []. The crossover of their intensities at T_s indicates competition between each other, which is proposed to be the root cause for the absence of long-range magnetic order. In detwinned FeSe, spin excitations are most intense at Q_AF = (1, 0) at low energies in the normal state, and the C₂ anisotropy is reduced at lower energies, 3 − 5 meV, indicating a gapped C₄ mode. At present, there are no measurement on detwinned FeSe for excitation energies above 20 meV, and it is therefore still an open question of how the anisotropy changes up to the band top in the system for a detwinned sample [].

INS on twinned FeSe has found that superconductivity induces a spin resonance of E = 3.6 meV at (1, 0) and (0, 1) below T_c [, , ]. Figures 2u,v show temperature difference of spin excitations in detwinned FeSe below and above T_c = 9 K as a function of energy at (1, 0) and (0, 1), respectively []. While Figure 2u shows clear evidence of the resonance at 3.6 meV at (1, 0) (negative intensities indicate the opening of a spin gap), the identical temperature difference plot (Figure 2v) yields no observable temperature dependence across T_c, indicating no spin resonance or spin gap at (0, 1). Figures 2w,x show wave-vector scans after correcting for finite detwin ratio. As we can see, superconductivity induces a C₂-symmetric resonance on a background of C₄-symmetric normal state scattering. These results are consistent with anistropic superconducting gaps observed from STM measurements [], and calculation based on anisotropic superconducting gaps from STM data can reproduce the observed antitropic neutron spin resonance [].

4. Conclusion

In this short review article, we focus on recent progress on detwinned FeSe, and compare it with detwinned electron-doped BaFe₂As₂. Although optimal superconductivity appears at the expense of nematic and AF order in electron-doped BaFe₂As₂ and coexists with nematic order in FeSe, the basic behaviors of spin excitations in both classes of materials are similar. These results indicate that superconductivity in different families of FeSCs has the same microscopic origin, suggesting orbital selective superconductivity in the nematic region of the FeSCs.

Statements

Author contributions

The manuscript was written by TC, MY, and PD. All authors made the comments.

Funding

The neutron scattering work at Rice on electron-doped BaFe₂As₂ and FeSe was supported by the U.S. NSF Grant No. DMR-1700081 and the U.S. Department of Energy, BES DE-SC0012311 (PD), respectively. The single-crystal synthesis work was supported by Robert A. Welch Foundation Grant No. C-1839 (PD). The ARPES work on FeSe was supported by Robert A. Welch Foundation Grant No. C-2024 (MY) as well as the Alfred P. Sloan Foundation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1.
ScalapinoDJ. A common thread: the pairing interaction for unconventional superconductors. Rev Modern Phys. (2012) 84:1383. 10.1103/RevModPhys.84.1383
2.
DaiP. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev Modern Phys. (2015) 87:855. 10.1103/RevModPhys.87.855
3.
FernandesRMChubukovAVSchmalianJ. What drives nematic order in iron-based superconductors?Nat Phys. (2014) 10:97–104. 10.1038/nphys2877
4.
ChuJHAnalytisJGDe GreveKMcMahonPLIslamZYamamotoYet al. In-plane resistivity anisotropy in an underdoped iron arsenide superconductor. Science. (2010) 329:824–6. 10.1126/science.1190482
5.
TanatarMABlombergECKreyssigAKimMGNiNThalerAet al. Uniaxial-strain mechanical detwinning of CaFe₂As₂ and BaFe₂As₂ crystals: optical and transport study. Phys Rev B. (2010) 81:184508. 10.1103/PhysRevB.81.184508
6.
BöhmerAEKreiselA. Nematicity, magnetism and superconductivity in FeSe. J Phys Condens Matter. (2017) 30:023001. 10.1088/1361-648X/aa9caa
7.
GeJFLiuZLLiuCGaoCLQianDXueQKet al. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO₃. Nat Mater. (2015) 14:285–9. 10.1038/nmat4153
8.
ZhangZWangYHSongQLiuCPengRMolerKet al. Onset of the Meissner effect at 65 K in FeSe thin film grown on Nb-doped SrTiO₃ substrate. Sci Bull. (2015) 60:1301–4. 10.1007/s11434-015-0842-8
9.
PtokAKapciaKJPiekarzPOleśAM. The ab initio study of unconventional superconductivity in CeCoIn₅ and FeSe. N J Phys. (2017) 19:063039. 10.1088/1367-2630/aa6d9d
10.
KasaharaSSatoYLicciardelloSČuloMArsenijevićSOttenbrosTet al. Evidence for an Fulde-Ferrell-Larkin-Ovchinnikov State with segmented vortices in the BCS-BEC-crossover superconductor FeSe. Phys Rev Lett. (2020) 124:107001. 10.1103/PhysRevLett.124.107001
11.
KamiharaYWatanabeTHiranoMHosonoH. Iron-based layered superconductor La[O_1−x F_x]FeAs (x = 0.05 - 0.12) with T_c = 26 K. J Am Chem Soc. (2008) 130:3296–7. 10.1021/ja800073m
12.
NandiSKimMKreyssigAFernandesRPrattDThalerAet al. Anomalous suppression of the orthorhombic lattice distortion in superconducting Ba(Fe_1−xCo_x)₂As₂ single crystals. Phys Rev Lett. (2010) 104:057006. 10.1103/PhysRevLett.104.057006
13.
HosoiSMatsuuraKIshidaKWangHMizukamiYWatashigeTet al. Nematic quantum critical point without magnetism in FeSe_1−xS_x superconductors. Proc Natl Acad Sci USA. (2016) 113:8139–43. 10.1073/pnas.1605806113
14.
HeMWangLHardyFXuLWolfTAdelmannPet al. Evidence for short-range magnetic order in the nematic phase of FeSe from anisotropic in-plane magnetostriction and susceptibility measurements. Phys Rev B. (2018) 97:104107. 10.1103/PhysRevB.97.104107
15.
YiMPfauHZhangYHeYWuHChenTet al. Nematic energy scale and the missing electron pocket in FeSe. Phys Rev X. (2019) 9:041049. 10.1103/PhysRevX.9.041049
16.
PaglioneJGreeneRL. High-temperature superconductivity in iron-based materials. Nat Phys. (2010) 6:645–58. 10.1038/nphys1759
17.
JohnstonDC. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv Phys. (2010) 59:803–1061. 10.1080/00018732.2010.513480
18.
StewartG. Superconductivity in iron compounds. Rev Modern Phys. (2011) 83:1589. 10.1103/RevModPhys.83.1589
19.
TaftiFJuneau-FecteauADelageMEDe CotretSRReidJPWangAet al. Sudden reversal in the pressure dependence of T_c in the iron-based superconductor KFe₂As₂. Nat Phys. (2013) 9:349–52. 10.1038/nphys2617
20.
TaftiFOuelletAJuneau-FecteauAFaucherSLapointe-MajorMDoiron-LeyraudNet al. Universal V-shaped temperature-pressure phase diagram in the iron-based superconductors KFe₂As₂, RbFe₂As₂, and CsFe₂As₂. Phys Rev B. (2015) 91:054511. 10.1103/PhysRevB.91.054511
21.
WangYLuPWuJLiuJWangXZhaoJet al. Phonon density of states of single-crystal SrFe₂As₂ across the collapsed phase transition at high pressure. Phys Rev B. (2016) 94:014516. 10.1103/PhysRevB.94.014516
22.
PtokASternikMKapciaKJPiekarzP. Structural, electronic, and dynamical properties of the tetragonal and collapsed tetragonal phases of KFe₂As₂. Phys Rev B. (2019) 99:134103. 10.1103/PhysRevB.99.134103
23.
RotterMTegelMJohrendtD. Superconductivity at 38 K in the iron arsenide (Ba_1−xK_x)Fe₂As₂. Phys Rev Lett. (2008) 101:107006. 10.1103/PhysRevLett.101.107006
24.
PramanikAAbdel-HafiezMAswarthamSWolterAWurmehlSKataevVet al. Multigap superconductivity in single crystals of Ba_0.65Na_0.35Fe₂As₂: a calorimetric investigation. Phys Rev B. (2011) 84:064525. 10.1103/PhysRevB.84.064525
25.
SefatASJinRMcGuireMASalesBCSinghDJMandrusD. Superconductivity at 22 K in Co-doped BaFe₂As₂ crystals. Phys Rev Lett. (2008) 101:117004. 10.1103/PhysRevLett.101.117004
26.
LiLLuoYWangQChenHRenZTaoQet al. Superconductivity induced by Ni doping in BaFe₂As₂ single crystals. N J Phys. (2009) 11:025008. 10.1088/1367-2630/11/2/025008
27.
JiangSXingHXuanGWangCRenZFengCet al. Superconductivity up to 30 K in the vicinity of the quantum critical point in BaFe₂(As_1−xP_x)₂. J Phys Condens Matter. (2009) 21:382203. 10.1088/0953-8984/21/38/382203
28.
CanfieldPCBud'KoSL. FeAs-based superconductivity: a case study of the effects of transition metal doping on BaFe₂As₂. Annu Rev Condens Matter Phys. (2010) 1:27–50. 10.1146/annurev-conmatphys-070909-104041
29.
ChuJHAnalytisJGKucharczykCFisherIR. Determination of the phase diagram of the electron-doped superconductor Ba(Fe_1−xCo_x)₂As₂. Phys Rev B. (2009) 79:014506. 10.1103/PhysRevB.79.014506
30.
UemuraYJ. Commonalities in phase and mode. Nat Mater. (2009) 8:253–55. 10.1038/nmat2415
31.
WatsonMKimTHaghighiradABlakeSDaviesNHoeschMet al. Suppression of orbital ordering by chemical pressure in FeSe_1−xS_x. Phys Rev B. (2015) 92:121108. 10.1103/PhysRevB.92.121108
32.
ReissPWatsonMKimTHaghighiradAWoodruffDBrumaMet al. Suppression of electronic correlations by chemical pressure from FeSe to FeS. Phys Rev B. (2017) 96:121103. 10.1103/PhysRevB.96.121103
33.
SatoYKasaharaSTaniguchiTXingXKasaharaYTokiwaYet al. Abrupt change of the superconducting gap structure at the nematic critical point in FeSe_1−xS_x. Proc Natl Acad Sci USA. (2018) 115:1227–31. 10.1073/pnas.1717331115
34.
YiMLuDChuJHAnalytisJGSoriniAPKemperAFet al. Symmetry-breaking orbital anisotropy observed for detwinned Ba(Fe_1−xCo_x)₂As₂ above the spin density wave transition. Proc Natl Acad Sci USA. (2011) 108:6878–83. 10.1073/pnas.1015572108
35.
LuXParkJZhangRLuoHNevidomskyyAHSiQet al. Nematic spin correlations in the tetragonal state of uniaxial-strained BaFe_2−xNi_xAs₂. Science. (2014) 345:657–60. 10.1126/science.1251853
36.
FernandesRMSchmalianJ. Manifestations of nematic degrees of freedom in the magnetic, elastic, and superconducting properties of the iron pnictides. Superconduct Sci Technol. (2012) 25:084005. 10.1088/0953-2048/25/8/084005
37.
SongYCarrSVLuXZhangCSimsZCLuttrellNet al. Uniaxial pressure effect on structural and magnetic phase transitions in NaFeAs and its comparison with as-grown and annealed BaFe₂As₂. Phys Rev B. (2013) 87:184511. 10.1103/PhysRevB.87.184511
38.
ManHLuXChenJSZhangRZhangWLuoHet al. Electronic nematic correlations in the stress-free tetragonal state of BaFe_2−xNi_xAs₂. Phys Rev B. (2015) 92:134521. 10.1103/PhysRevB.92.134521
39.
LuXTsengKFKellerTZhangWHuDSongYet al. Impact of uniaxial pressure on structural and magnetic phase transitions in electron-doped iron pnictides. Phys Rev B. (2016) 93:134519. 10.1103/PhysRevB.93.134519
40.
TamDWSongYManHCheungSCYinZLuXet al. Uniaxial pressure effect on the magnetic ordered moment and transition temperatures in BaFe_2−xT_xAs₂ (T= Co, Ni). Phys Rev B. (2017) 95:060505. 10.1103/PhysRevB.95.060505
41.
LuXSchererDDTamDWZhangWZhangRLuoHet al. Spin waves in detwinned BaFe₂As₂. Phys Rev Lett. (2018) 121:067002. 10.1103/PhysRevLett.121.067002
42.
ManHZhangRParkJLuXKuldaJIvanovAet al. Direct observation of spin excitation anisotropy in the paramagnetic orthorhombic state of BaFe_2−xNi_xAs₂. Phys Rev B. (2018) 97:060507. 10.1103/PhysRevB.97.060507
43.
ChuJHKuoHHAnalytisJGFisherIR. Divergent nematic susceptibility in an iron arsenide superconductor. Science. (2012) 337:710–2. 10.1126/science.1221713
44.
HicksCWBrodskyDOYellandEAGibbsASBruinJABarberMEet al. Strong increase of T_c of Sr₂RuO₄ under both tensile and compressive strain. Science. (2014) 344:283–5. 10.1126/science.1248292
45.
HeMWangLAhnFHardyFWolfTAdelmannPet al. Dichotomy between in-plane magnetic susceptibility and resistivity anisotropies in extremely strained BaFe₂As₂. Nat Commun. (2017) 8:1–6. 10.1038/s41467-017-00712-3
46.
ChenTChenYKreiselALuXSchneidewindAQiuYet al. Anisotropic spin fluctuations in detwinned FeSe. Nat Mater. (2019) 18:709. 10.1038/s41563-019-0369-5
47.
TanatarMABöhmerAETimmonsEISchüttMDrachuckGTaufourVet al. Origin of the resistivity anisotropy in the nematic phase of FeSe. Phys Rev Lett. (2016) 117:127001. 10.1103/PhysRevLett.117.127001
48.
ShimojimaTSuzukiYSonobeTNakamuraASakanoMOmachiJet al. Lifting of xz/yz orbital degeneracy at the structural transition in detwinned FeSe. Phys Rev B. (2014) 90:121111. 10.1103/PhysRevB.90.121111
49.
SuzukiYShimojimaTSonobeTNakamuraASakanoMTsujiHet al. Momentum-dependent sign inversion of orbital order in superconducting FeSe. Phys Rev B. (2015) 92:205117. 10.1103/PhysRevB.92.205117
50.
WatsonMKimTHaghighiradADaviesNMcCollamANarayananAet al. Emergence of the nematic electronic state in FeSe. Phys Rev B. (2015) 91:155106. 10.1103/PhysRevB.91.155106
51.
LiuXZhaoLHeSHeJLiuDMouDet al. Electronic structure and superconductivity of FeSe-related superconductors. J Phys Condens Matter. (2015) 27:183201. 10.1088/0953-8984/27/18/183201
52.
ZhangPQianTRichardPWangXPMiaoHLvBQet al. Observation of two distinct d_xz/d_yz band splittings in FeSe. Phys Rev B. (2015) 91:214503. 10.1103/PhysRevB.91.214503
53.
XuHCNiuXHXuDFJiangJYaoQChenQYet al. Highly anisotropic and twofold symmetric superconducting gap in nematically ordered FeSe_0.93S_0.07. Phys Rev Lett. (2016) 117:157003. 10.1103/PhysRevLett.117.157003
54.
FanfarilloLMansartJToulemondePCercellierHLeFévre PBertranFmcet al. Orbital-dependent Fermi surface shrinking as a fingerprint of nematicity in FeSe. Phys Rev B. (2016) 94:155138. 10.1103/PhysRevB.94.155138
55.
FedorovAYareskoAKimTKKushnirenkoYHauboldEWolfTet al. Effect of nematic ordering on electronic structure of FeSe. Sci Rep. (2016) 6:36834. 10.1038/srep36834
56.
WatsonMHaghighiradARhodesLHoeschMKimTK. Electronic anisotropies revealed by detwinning angle-resolved photoemission spectroscopy measurements of FeSe. N J Phys. (2017) 19:103021. 10.1088/1367-2630/aa8a04
57.
ColdeaAIWatsonMD. The key ingredients of the electronic structure of FeSe. Annu Rev Condens Matter Phys. (2018) 9:125–46. 10.1146/annurev-conmatphys-033117-054137
58.
LiuDLiCHuangJLeiBWangLWuXet al. Orbital origin of extremely anisotropic superconducting gap in nematic phase of FeSe superconductor. Phys Rev X. (2018) 8:031033. 10.1103/PhysRevX.8.031033
59.
DayRPLevyGMichiardiMZwartsenbergBZonnoMJiFet al. Influence of spin-orbit coupling in iron-based superconductors. Phys Rev Lett. (2018) 121:076401. 10.1103/PhysRevLett.121.076401
60.
HuhSSSeoJJKimBSChoSHJungJKKimSet al. Absence of Y-pocket in 1-Fe Brillouin zone and reversed orbital occupation imbalance in FeSe. Commun Phys. (2020) 3:52. 10.1038/s42005-020-0319-1
61.
WatsonMYamashitaTKasaharaSKnafoWNardoneMBéardJet al. Dichotomy between the hole and electron behavior in multiband superconductor FeSe probed by ultrahigh magnetic fields. Phys Rev Lett. (2015) 115:027006. 10.1103/PhysRevLett.115.027006
62.
SprauPOKostinAKreiselABöhmerAETaufourVCanfieldPCet al. Discovery of orbital-selective Cooper pairing in FeSe. Science. (2017) 357:75–80. 10.1126/science.aal1575
63.
HuHYuRNicaEMZhuJXSiQ. Orbital-selective superconductivity in the nematic phase of FeSe. Phys Rev B. (2018) 98:220503. 10.1103/PhysRevB.98.220503
64.
KangJFernandesRMChubukovA. Superconductivity in FeSe: the role of nematic order. Phys Rev Lett. (2018) 120:267001. 10.1103/PhysRevLett.120.267001
65.
YuRZhuJXSiQ. Orbital selectivity enhanced by nematic order in FeSe. Phys Rev Lett. (2018) 121:227003. 10.1103/PhysRevLett.121.227003
66.
WangQShenYPanBZhangXIkeuchiKIidaKet al. Magnetic ground state of FeSe. Nat Commun. (2016) 7:1–7. 10.1038/ncomms12182
67.
FernandesRMVafekO. Distinguishing spin-orbit coupling and nematic order in the electronic spectrum of iron-based superconductors. Phys Rev B. (2014) 90:214514. 10.1103/PhysRevB.90.214514
68.
PfauHChenSDYiMHashimotoMRotunduCRPalmstromJCet al. Momentum dependence of the nematic order parameter in iron-based superconductors. Phys Rev Lett. (2019) 123:066402. 10.1103/PhysRevLett.123.066402
69.
WangMLuoHWangMChiSRodriguez-RiveraJASinghDet al. Magnetic field effect on static antiferromagnetic order and spin excitations in the underdoped iron arsenide superconductor BaFe_1.92Ni_0.08As₂. Phys Rev B. (2011) 83:094516. 10.1103/PhysRevB.83.094516
70.
TianLLiuPXuZLiYLuZWalkerHet al. Spin fluctuation anisotropy as a probe of orbital-selective hole-electron quasiparticle excitations in detwinned Ba (Fe_1−xCo_x)₂As₂. Phys Rev B. (2019) 100:134509. 10.1103/PhysRevB.100.134509
71.
WangQShenYPanBHaoYMaMZhouFet al. Strong interplay between stripe spin fluctuations, nematicity and superconductivity in FeSe. Nat Mater. (2016) 15:159–63. 10.1038/nmat4492
72.
MaMBourgesPSidisYXuYLiSHuBet al. Prominent role of spin-orbit coupling in FeSe revealed by inelastic neutron scattering. Phys Rev X. (2017) 7:021025. 10.1103/PhysRevX.7.021025

Summary

Keywords

detwin, superconductivity, magnetism, nematicity, orbital selectivity

Citation

Chen T, Yi M and Dai P (2020) Electronic and Magnetic Anisotropies in FeSe Family of Iron-Based Superconductors. Front. Phys. 8:314. doi: 10.3389/fphy.2020.00314

Received

28 April 2020

Accepted

09 July 2020

Published

21 August 2020

Volume

8 - 2020

Edited by

Jose P. Rodriguez, California State University, Los Angeles, United States

Reviewed by

Amalia Coldea, University of Oxford, United Kingdom; Konrad Jerzy Kapcia, Institute of Nuclear Physics (PAN), Poland

Updates

This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Tong Chen tc39@rice.eduMing Yi mingyi@rice.eduPengcheng Dai pdai@rice.edu

This article was submitted to Condensed Matter Physics, a section of the journal Frontiers in Physics

Disclaimer

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Condensed Matter Physics

MINI REVIEW article

Electronic and Magnetic Anisotropies in FeSe Family of Iron-Based Superconductors

Abstract

1. Introduction

2. Nematicity and Detwinning Devices